Abstract
When drinking water flows into the water distribution network from a reservoir, it is exposed to the risk of accidental or deliberate contamination. Serious drinking water pollution events can endanger public health, bring about economic losses, and be detrimental to social stability. Therefore, it is obviously crucial to research the water contamination source identification problem, for which scholars have made considerable efforts and achieved many advances. This paper provides a comprehensive review of this problem. Firstly, some basic theoretical knowledge of the problem is introduced, including the water distribution network, sensor system, and simulation model. Then, this paper puts forward a new classification method to classify water contamination source identification methods into three categories according to the algorithms or methods used: solutions with traditional methods, heuristic methods, and machine learning methods. This paper focuses on the new approaches proposed in the past 5 years and summarizes their main work and technical challenges. Lastly, this paper suggests the future development directions of this problem.
1. Introduction
Water is essential to human survival, and the drinking water system is a considerable resource to human health and wellbeing relating to the material life, culture, society, politics, and economy. Therefore, the safety of the water distribution system (WDS) plays an important strategic role in maintaining public health and industrial growth [1]. While drinking water quality is tested at water plants, the WDS is vulnerable to accidental or deliberate attacks due to openness, accessibility, and the aging infrastructure, leading to drinking water contamination during transportation to users. Berglund et al. believed that the WDS would be threatened by pollution invasion, physical damage, connection facility failure, and control attack, among which the number of papers on pollution invasion far exceeded other types of threats [2]. The ways for pollution to invade pipe networks include polluting water sources or pipe network nodes, incorrect pipe connections or pipeline leaks, and the lack of water quality management [3]. In January 2014, chemical pollution occurred in the Elk River, West Virginia, USA, resulting in a lack of direct drinking water supply for more than 300,000 people within 5 days [4]. In May 2016, a faulty pipe connection in Beijing’s water supply system accidentally led to graywater intrusion into drinking water pipes. On 31 May of that year, Hong Kong’s drinking water was found to contain excessive levels of lead, well above the World Health Organization’s highest level. Contamination events of the WDS have always occurred and may still occur in the future. Due to the rapid and unpredictable propagation of pollutants in the water distribution network (WDN), it is important to quickly identify the contamination source to stop the spread of pollution.
To reduce the risk to the community, it is possible to strengthen the physical equipment security of the WDS and place water quality monitoring sensors in the WDN. If water quality monitoring can be carried out at all points in the network, the WDS management would be much easier. However, due to high sensor procurement costs and budget constraints, water quality sensors are deployed on several nodes in the WDN, and the observation data obtained from a sparse set of sensors are limited. Considering the WDN with the sensor network, the water pollution response system can be divided into three parts: (1) pollution detection, where the water quality sensors are used to continuously detect water quality; when the pollutant concentration detected by the sensors exceeds the threshold, the warning system will be triggered; (2) contamination identification, where, once contamination is detected in the WDN, the extent of contamination needs to be assessed and the evolution of contaminants within the network needs to be inferred; (3) pollution control, where, in order to minimize the risk after detection, water companies need to make effective response decisions [5].
The contamination source identification (CSI) is a complicated task to deduce pollution source information from the water quality sensor observation data. It is often defined as an inverse problem looking for a group of information about the contamination source, including the location, injection time, mass, and diffusion range. Solving the CSI problem is challenging. First of all, the data obtained from the sensors are limited, resulting in potential uncertainty of the contamination source location [6]. Secondly, the scale and complexity of the WDN affect the performance of the solutions. When the number of sensors in the WDN is fixed, a larger WDN scale leads to a significant increase in the non-uniqueness of the solution [7]. In addition, the changes in the flow velocity and water demand increase the uncertainty, and the accuracy of sensor degree directly affects the performance of the solutions.
Adedoja et al. reviewed the CSI problem, summarized the relevant literature before 2018, and divided the CSI algorithms into the simulation/optimization method, probabilistic method, and other methods [8]. Gong et al. believed that the CSI problem was characterized by multimodality, expensive computing, and uncertainty; hence, the literature was divided into three types on the basis of these three characteristics [9]. However, this paper mainly focused on the simulation/optimization method. According to the existing research, the CSI solutions have been developed in three stages. Particle backtracking was a commonly used method early, which traces the state of each node at the previous timepoint by particles [7,10,11]. Then, with the development of the machine learning methods, scholars began to use the Bayesian formula to calculate the probability that the node is the contamination source [12,13,14,15,16,17,18,19,20,21]. At the same time, the simulation/optimization framework based on optimization algorithms was proposed [22]. This method iteratively searches the real contamination source by narrowing the difference between the sensor data corresponding to the preset contamination source and the real sensor observation data [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. In recent years, many new types of research have emerged on solving the CSI problem, especially the methods combined with deep learning, which provides new ideas for the CSI problem. This paper reviews the relevant literature on the CSI problem and focuses on the studies in the past 5 years. This paper classifies the CSI solutions according to the algorithms or methods used into three categories: solutions with traditional methods, heuristic methods, and machine learning methods. Moreover, this paper summarizes the basic theories related to the CSI problem, so as to provide references for researchers engaged in this field.
2. Theory of Contamination Source Identification
2.1. WDN Model
2.1.1. Composition of WDN
The WDN is a complex system consisting of a set of spatially interrelated parts, which can supply drinking water to consumers from different sources [38]. The WDN is mainly divided into two parts. One is the node collection, including nodes, source(s), and tank(s). The other is the pipelines connecting the nodes and other components attached to the pipelines such as the pumps and valves. Reservoirs are usually the sources of water, often denoting underground water sources, lakes, and rivers. Pools can serve as the containers and sources of water. The flow rate, velocity, and head loss of water in the WDN are all different, affected by the diameter, length, roughness coefficient, and other pipeline parameters. In the CSI problem, the advective transport and reaction are commonly assumed to occur in the WDN, and there is a complete instantaneous mixing process at any connecting node that receives the inflow of two or more pipeline flows [38]. This simplified model makes it convenient to study, although it does not exactly correspond to reality.
Figure 1 shows a simplified WDN model, consisting of one reservoir, one pool, eight nodes, and 12 pipelines. The black arrow represents the water flow direction. The asterisk represents the contamination is injected from point A. The triangle represents that a water quality sensor is placed at point E. Under the influence of water flow, pollutants will spread to other locations in the WDN and be detected by the water quality sensor. It can be seen from Figure 1 that the polluted water mainly flows in three directions: from point A to point B to the pool, from point A to point D to point G, and from point A to point D to point E. When the water quality sensor at point E detects that the pollutant concentration exceeds the threshold value, the sensor will set off an alarm, indicating that a pollution event has been detected.
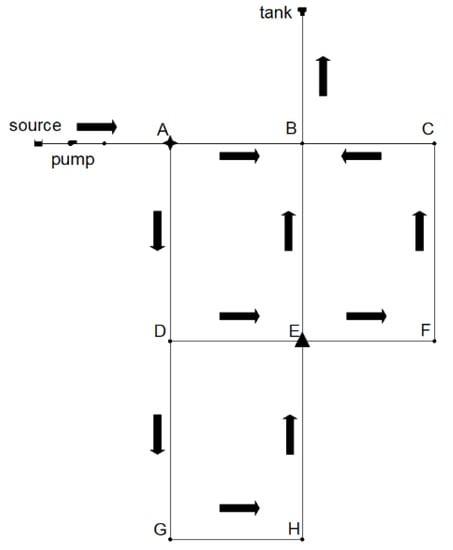
Figure 1.
Configuration of the physical system of a WDN.
2.1.2. Hydraulic Model and Quality Model
Drinking water enters the WDN from a reservoir and is used at each node. The water velocity and flow direction over time are called the hydraulic characteristics of WDN, which can be calculated using the hydraulic energy of the inlet and outlet nodes [39]. The water velocity and flow direction are determined by the pump power, water demand, tank volume, and other factors. The water demand of different nodes is not constant and usually changes daily or seasonally. Therefore, the hydraulic characteristics of WDN need to be adjusted at any time to ensure the response to the water demand. With the change in water velocity, the WDN presents a complex behavior, and the flow direction even changes in some cases [38]. The study of hydraulic characteristics is vital to the CSI problem, and almost all simulation models are based on the hydraulic model. Creaco et al. analyzed two nodal demand reconstruction methods, top-down deterministic and bottom-up stochastic approaches, as well as their influences on the hydraulic model of WDN [40]. They also described the models for water demand pulse generation and the differences in the modeling structures [41]. Some CSI methods also consider the uncertainty brought by water demand, which makes the research more consistent with the reality [27,41,42,43,44,45].
Water quality is affected by agricultural and industrial discharges, and it needs to be controlled in real time within qualitative and quantitative parameters. As chlorine is commonly used as a water disinfectant in the WDS, it can be used as an indicator of water quality deterioration [46]. In fact, the chlorine flows from the reservoir to network and reacts in the pipeline, causing the chlorine concentration to gradually decrease. Therefore, it is necessary to analyze the chlorine decay model according to the characteristics of decay reaction kinetics and correctly estimate the residual chlorine content in the WDN. This is called a water quality simulation. In most studies, the water quality simulation process follows the chlorine decay model proposed in [47].
2.1.3. Sensor Network
The sensor network can obtain observation data by detecting contamination in the WDN, which helps to quickly identify the contamination source features. The sensor placement problem (SPP) is an independent problem from the CSI problem, but sensor placement has a significant impact on the performance of the CSI methods [6].
The detection and the tracing of water pollution using sensor data are directly related to the type of sensor. Different types of sensors can detect different types of pollutants. There are two types of sensors. One type is for specific pollutants, such as sensors designed for metal ion concentration detection. These sensors have excellent performance in the detection of specific pollutants, but lack the detection ability of other pollutants. The other type is for general pollutants, commonly used in the current WDNs. These sensors have a general detection ability for most pollutants. Their detection indicators usually include residual chlorine, temperature, pH, oxidation/reduction potential, electrical conductivity, dissolved oxygen, total organic carbon, nitrogen, turbidity, and particle count. In addition, sensors can also be divided into fixed sensors and mobile sensors. A fixed sensor is placed in some fixed nodes, while a mobile sensor moves to other nodes with the flow of water after being placed in the WDN. At present, most studies on the CSI problem are based on the fixed sensor network, but researchers have also explored the application of mobile sensors in the CSI problem [48].
The location of traditional water quality monitoring points in the WDS is determined by experience, and the main points are set in dense urban areas. In the past 20 years, the SPP has been defined as a single-objective or multi-objective optimization problem. The optimization targets include the number of affected people, the number of detectable pollution events, the length of contaminated pipelines, the quality of pollutants consumed by users, and the detection time [49]. Hu et al. reviewed the SPP for water contamination detection, focusing on optimization strategies and frameworks [50].
In addition to the type and location of sensors, the reality of “false positives and false negatives” can also affect the identification of contamination. If the sensors fail to detect contamination occurring in the WDN that the sensors should have detected, the sensor reading is considered a false negative. If the sensors incorrectly detect contamination and no event has occurred in the WDN that would explain the test, the sensor reading is considered a false positive. Assuming that the response of sensors is continuous, these situations impact the CSI results and reduce the accuracy of the CSI algorithm [38].
2.2. Simulation Model
2.2.1. Simulation Software
Simulation software has been widely used in the WDS management because of its ability to simulate pollution scenarios. In the study of pollution tracing, the real pollution data are sparse. On the one hand, for natural disasters and accidental intrusion affecting water quality, water companies need to manage the pollution data safely. On the other hand, the frequency of some deliberate attacks is very low, and the pollution data are rarely observed or recorded. In reality, it is impossible to conduct real physical experiments in the WDN. Due to the lack of data, many research communities have developed modeling tools and frameworks that can provide simulations of potential contamination dispersal and control measures.
Berglund et al. reviewed the simulation modeling of WDS [2]. Most frameworks use hydraulic modeling, which can calculate the water flow direction, flow rate, and water quality transport processes. Some studies use graph theory to represent the pipe network, emphasizing the connection between nodes. Some tools and frameworks have been developed into software that combines the simulation of the underlying pipe network with statistical models and optimization methods to facilitate the study and management of the WDS. Table 1 lists the simulation software commonly used in the CSI problem and the functions they have.

Table 1.
Modeling tools for CSI.
Among the simulation software listed above, EPANET is the most widely used, developed by the United States Environmental Protection Agency. The underlying code is open-access and implemented by the C program. It can carry out hydraulic and water quality analysis for different types of the WDS by adopting a simplified approach to water quality based on advective transport and some simplified reaction kinetics [51]. EPANET can set the configuration of water source and pump, simulate the reaction of water flow with contact walls such as pipes and water head, and simulate the tracking of water source. EPANET can also use N-order reaction kinetics to simulate water quality reactions, simulate the reaction process of reactive substances, and simulate the change process of tracers of nonreactive substances over time.
EPANET can set the source water quality for each node, which can simulate the pollution intrusion scenario. Pollutants may enter from any node of the pipe network at any time. By injecting a certain concentration of pollutants into a node or several nodes of the pipe network, EPANET is invoked for hydraulic and quality simulation, and continuous data detected by sensors can be obtained. This allows a complete simulation of pollution intrusion. The source water quality parameters to be set include water demand mode, source water quality, sensor location, hydraulic simulation time, and pollution injection mode.
Models for hydraulic and water quality simulation have been constantly studied. The standard version of the EPANET model solves the advective transport equation by solving a mass balance of the fundamental plug flow substance that considers the advective transport and kinetic reaction processes. However, this method is limited exclusively to monitoring the advective transport and fate of a single chemical species, such as fluoride, which can be used in a tracer study or free chlorine to study the decay of disinfectants. To consider multiple and interacting chemical species, an extension of the EPANET model called multispecies extension (EPANET-MSX) was developed [52], capable of modeling the behavior of any chemical species within water networks. In addition, to consider dispersive processes, intrinsic to transport mechanisms and relevant in the case of laminar flow regimes, Piazza et al. proposed the EPANET dynamic dispersion model, in which diffusive–dispersive processes in two dimensions (axial and transverse) for laminar flow regimes were considered [53].
2.2.2. WDN Data
The CSI problem has corresponding benchmarks, which consist of pipe network data with supporting hydraulic and water quality models. The Center for Water Systems provides examples of WDN used by various researchers in the literature as benchmarks. The network data include basic network information, simulation input files, and other information that might be used in network analysis. Table 2 shows the benchmark network commonly used in the CSI research and the number of nodes, pipes, sources, tanks, and pumps, all of which can be used as input files of EPANET.

Table 2.
Benchmark WDN for CSI.
The CSI methods are not only tested on the benchmarks, but also tested on the real pipe networks in some studies. For example, Tao et al. [17] and Xin et al. [54] adopted the WDN in Zhenjiang City, Jiangsu Province, China. The model consisted of 3379 nodes, two sources, and 3701 pipes. The research of Bazargan-Lari et al. was applied to the WDN in District 19, south of Tehran [55].
3. CSI Methods/Algorithms
With the development of emerging algorithms and technologies, some early CSI methods have gradually lost advantages with fewer updates. Furthermore, the new methods derived from new technologies cannot be simply classified by the previous labels, especially the research of integrated technologies. This paper classifies the CSI solutions according to the algorithms or methods used into three categories: solutions with traditional methods, with heuristic methods, and with machine learning methods. The traditional methods include the mathematical method (MM) and topological properties of pipe the network. Heuristic methods include the evolutionary algorithm (EA) and rough set theory (RS). The machine learning methods include Bayesian, deep learning (DL), and other machine learning (ML) algorithms. Since Adedoja et al. provided a comprehensive summary of the studies before 2018, this paper does not reclassify this work, instead paying more attention to the research from 2018 until now. In order to facilitate comparison, labels classified according to solutions are still listed [8], in addition to the challenges brought by uncertainty that many studies focused on. The overall content is shown in Table 3.

Table 3.
Literature review of CSI methods.
3.1. Traditional Methods
Due to the existence of a series of physical models of the WDN, such as hydraulic characteristics, topological properties of the network, and the particularity of pollutant transport, some traditional methods can be used to solve the CSI problem. These methods are not limited to mathematical methods, including particle backtracking method (PBA) [7,10,11], origin tracking method [75], mixed quadratic programming [76], and topology properties of the pipe network or pollutant transmission properties.
Capano et al. proposed the dynamics of network pollution method, connecting the pollution matrix and the network topology to identify the nodes or paths that are most sensitive to pollution. They might be the key nodes or paths that help the diffusion of pollutants, which can ultimately be traced back to the pollution source node [46]. The importance linked to the topology determines the application conditions of the method, as it makes it possible to define a priori and absolutely the necessary measurement points.
Marlim et al. introduced the contamination-probable setting identifier, which mainly solved the uncertainty caused by changes in water demand and sensor misreading. The identifier applied the spatial filter based on backtracking to acquire all possible settings, thereby focusing on reducing the number of suspect injection location. This method could identify the contamination setting with a reduced number of sensors. However, it did not optimally locate the sensors, revealing that sensor information significantly affects model performance [65].
Inspired by the Kalman filter to solve the groundwater pollution source identification, Butera et al. applied it to solve the CSI problem. The experiment was carried out in Anytown network, which verified that Kalman filter could be applied in the field of the water supply system [67]. However, the sensors were located in all nodes of the network. This is unrealistic and not conducive to transplanting the method to a larger network.
Lucin et al. proposed a search space reduction method. For each potential pollution source node, an extreme pollutant scenario was simulated with an unrealistic large contamination amount constantly being injected at the analyzed node. If the sensor did not record the pollution, the node was considered not a pollution source [70]. The method uses a forward simulation model, which can be conducted easily in large-scale networks, as well as on multiple processors, due to the single instruction multiple data nature of the method’s computational process. The accompanying optimization algorithm of this method is the standard genetic algorithm (GA); thus, the computational efficiency can be improved by using a more efficient optimization algorithm.
3.2. Heuristic Methods
Heuristic methods are widely used in optimization problems because of their universality. Therefore, when the CSI problem is defined as an optimization problem, it can be solved by heuristic methods. Given a set of observed concentration data of sensor networks, an inverse problem can be constructed by combining the WDN simulation model with the optimization framework to identify the pollution source location and release history characteristics. By minimizing the error between the simulated pollution concentration obtained by the sensor in the WDN and the real observed concentration, this inverse problem iteratively searches for the most likely pollution source nodes. In this time, the CSI problem is regarded as an optimization problem [22].
Yan et al. proposed corresponding solutions to different challenges of the CSI problem based on EAs. In view of the expensive computing, they proposed to use the Gaussian model as surrogate to replace part of the EPANET simulation to reduce the calculation cost [57]. They combined it with the collaborative strategy to obtain non-unique solutions [58]. They also optimized the surrogate to further improve the accuracy and efficiency. Experiments were all carried out on the large-scale BWSN2 network [74]. In order to solve the uncertainty of CSI problem, the Gaussian model and autoregressive model were used to simulate the water demand [43], while the Poisson distribution was used in [45]. In addition, the episodic CSI problem was studied [61]. In order to improve the objective function and locate it in real time, the search for the contamination source begins immediately after the first detection of pollution data, instead of starting to trace it after collecting sufficient sensor data. In other studies, the CSI problem was regarded as a multimodal optimization problem. A niche GA was proposed to solve this multimodal problem with an improved objective function and threshold [62]. A dynamic multimodal GA based on domain knowledge was also proposed, and its effectiveness was verified on multiple WDNs [72].
Bazargan-Lari et al. proposed a method integrating the rough set theory and Monte Carlo simulation model. The method provided forecasts of water contamination zoning map for determining the spread of contamination. The Monte Carlo simulation was used to incorporate the uncertainties of pollution injection. This method was applied to the southern Section 19 of the Tehran water supply network [55]. This work was the first to explore the capabilities of rough set theory in monitoring the WDN, but lacked a study of the checkpoint pattern.
Li et al. proposed an adaptive multi-population evolutionary optimization algorithm, which adopted a collaborative strategy to identify location and pollution injection characteristics, and used a feedback learning mechanism to adjust population size adaptively, mainly to solve the problem of the non-uniqueness of solutions and real-time location [69]. The proposed method could find more candidate solutions than the adaptive dynamic optimization technology framework, which is a classic method to solve the real-time CSI problem [26].
3.3. Machine Learning Methods
3.3.1. Bayesian
In the case of discrete probabilities, the Bayesian formula is used to calculate the conditional probabilities associated with the occurrence of an event. On the basis of flow path analysis, De Sanctis et al. used the Bayesian formula to update the posterior probability of each node as the source of pollution over time [13]. On this basis, a large number of studies based on the Bayesian probability method were conducted.
Sankary et al. expanded on a previous study [77], but used a Bayesian framework to estimate the likelihood of injection upstream from the observed sensor data instead of equal injection likelihood at all upstream junctions. The Bayesian method with mobile sensor data provided better performance [48]. Compared to the fixed sensor system, this approach could improve performance on the small network and improve the localization accuracy on the larger network. The placement of fixed water quality sensors is to minimize the expected population affected [78], which can be optimized through a better SPP algorithm.
Cai et al. devised a new Bayesian framework for the CSI problem with random water demand. It integrated forward and backward tracking of contaminant movement with the probability updating of suspicious contaminant events. The mathematical formulas for proposed weighted Bayesian updating scheme were derived [44]. This study used binary sensor data to update probability in real time. However, the injection duration was not considered, which might be advantageous to probability updating.
3.3.2. Deep Learning
In recent years, the development of deep learning has promoted the progress of research in various fields, including research on the CSI problem. Whether introducing new methods or improving the efficiency of existing methods, deep learning has shown certain advantages and will be a major trend of the development of the CSI algorithms in the future.
Sun et al. proposed a method wherein the convolutional neural network (CNN) was used to solve the CSI problem on the basis of consumer complaint information. According to the automatic feature extraction of CNN, the proposed method explored the inherent characteristics of complaint patterns corresponding to contaminant intrusion nodes [59]. However, the recognition accuracy of CNN is sensitive to the noise level of the complaint delay time.
Qian et al. paid attention to the depth learning ability of the deep neural network (DNN), and used it to optimize the search space of EAs. DNN captured the relationship between time-series sensor data and the source node. The experiment compared the proposed algorithm with pure EA. The results showed that the performance of EA could be significantly improved after introducting the DNN [71].
Zhou et al. used the graph neural network (GNN) to transfer the CSI knowledge learned from different WDNs to a new WDN, which infilled insufficient training samples of the CSI problem when using deep learning. The experiment was carried out on the Wolf-Cordera network and compared with other DNNs. The results showed the superiority of the GNN in solving the CSI problem [73]. GNN is in the development stage at present. Its advantage in processing topology graphs perfectly fits the research of WDN. In this work, the contamination data of the non-sensor nodes were all filled with zeros to simplify the model training, which confused cases where the sensor did not detect contamination.
3.3.3. Other Methods
Rutkowski et al. used the learning vector quantization (LVQ) neural network as a classical pattern classification tool to identify the potential contamination source. As a result of identification, a certain subzone was marked as the location of pollution entering [56]. The method is strongly dependent on the appropriate mathematical model of the WDS, which limits its usability.
Tinelli et al. developed and demonstrated the feasibility of monitoring the WDS based on artificial intelligence by referring to the application of the support vector machine and artificial neural network (ANN) in pattern recognition and anomaly detection. The study labeled risk areas to help operators control water quality, and it was applied in the WDS of the Science City Campus of the University of Lille in France [60].
Grbcic et al. proposed using machine learning classifiers to identify pollution source, combining two machine learning algorithms [63]. They used ANN to classify the contamination source, and used random forest to perform regression prediction on contamination characteristics [64]. Then, they combined machine learning algorithms and optimization algorithms in [68] to solve the CSI problem. First, potential pollution nodes were classified using random forest, and then the optimization algorithm was used to determine the pollution injection characteristics.
4. Conclusions
This paper provided a comprehensive review of the relevant studies on the water contamination source identification problem, mainly introducing the basic theory of the CSI problem and the new research in recent years. At present, each CSI algorithm has its applicability and limitations, and further research is still needed to expand on the CSI problem.
At present, almost all studies have been carried out for a single pollution source. However, considering reality, it is completely possible for pollutants to invade the pipe network from multiple places. Algorithms for a single contamination source may not be applicable to multiple contamination source identification (MCSI). However, information about the number of contamination sources, contamination concentration, and contamination intrusion pattern are unknown in reality; thus, the universality of the algorithm will be greatly reduced. The MCSI problem has always been considered as a problem worth studying, but related research is scarce. Some researchers believe that their methods can be extended to solve the MCSI, but experiments are needed to verify these claims. The authors of [79] used a machine learning approach to identify the number of injection locations. Although a CSI method was not provided, this approach might help in the study of the MCSI. It is important to carry out research on the problem of multiple pollution sources and fully consider the uncertainties in the pipeline network to make the research more realistic.
At present, only a few studies have considered the efficiency of the algorithm. Considering the dependence of the CSI problem on simulation and the low efficiency of simulation software when simulating large-scale pipe networks, the CSI algorithm should shorten the solving time as much as possible. When considering the MCSI, the time complexity will increase exponentially as the dimensions of the decision variable increase. Only by finding out the information of pollution sources as soon as possible can we effectively curb the spread of pollution and reduce losses. The feasible methods are to reduce the dependence on simulation software or adopt parallel computing.
The research on machine learning in CSI is no longer limited to using probability estimation; it also involves using pattern recognition, anomaly detection, and other methods. Deep learning also opens up a new way to solve the CSI problem. Research in this direction is still in its infancy. Combining machine learning with the physical properties of pipe networks or with optimization methods can be a future research direction.
It is necessary to detect abnormal sensor data. Most existing studies have specified a point at which hydraulic simulation begins. This is usually before sensor contamination detection. In reality, sensor data are obtained all the time; thus, it is necessary to detect anomalies from time-series data and determine the occurrence of contamination. Data mining can be used to detect abnormal data, and different kinds of sensors can be used to improve the sensitivity to abnormal phenomena.
Author Contributions
Conceptualization, J.G. and X.Y.; methodology, J.G.; writing—original draft preparation, J.G.; writing—review and editing, J.G. and X.Y.; supervision, X.G. and C.H.; project administration, X.Y.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the NSF of China (Grant Nos. U1911205, 62073300, and 62076225). This paper was supported by the State Environmental Protection Key Laboratory of Source Apportionment and Control of Aquatic Pollution, Hubei Key Laboratory of Yangtze Catchment Environmental Aquatic Science, China University of Geosciences, Wuhan, 430078, China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kanakoudis, V.; Tsitsifli, S. Potable water security assessment—A review on monitoring, modelling and optimization techniques, applied to water distribution networks. Desalin. Water Treat. 2017, 99, 18–26. [Google Scholar] [CrossRef]
- Berglund, E.Z.; Pesantez, J.E.; Rasekh, A.; Shafiee, M.E.; Sela, L.; Haxton, T. Review of Modeling Methodologies for Managing Water Distribution Security. J. Water Resour. Plan. Manag. 2020, 146, 03120001. [Google Scholar] [CrossRef] [PubMed]
- Xin, K.L.; Tao, T.; Li, S.P.; Yan, H.X. Contamination accidents in China’s drinking water distribution networks: Status and countermeasures. Water Policy 2017, 19, 13–27. [Google Scholar] [CrossRef]
- Thomasson, E.D.; Scharman, E.; Fechter-Leggett, E.; Bixler, D.; Ibrahim, S.; Duncan, M.A.; Hsu, J.; Scott, M.; Wilson, S.; Haddy, L.; et al. Acute Health Effects After the Elk River Chemical Spill, West Virginia, January 2014. Public Health Rep. 2017, 132, 196–202. [Google Scholar] [CrossRef]
- Rodriguez, J.S.; Bynum, M.; Laird, C.; Hart, D.B.; Klise, K.A.; Burkhardt, J.; Haxton, T. Optimal Sampling Locations to Reduce Uncertainty in Contamination Extent in Water Distribution Systems. J. Infrastruct. Syst. 2021, 27, 04021026. [Google Scholar] [CrossRef]
- Seth, A.; Klise, K.A.; Siirola, J.D.; Haxton, T.; Laird, C.D. Testing Contamination Source Identification Methods for Water Distribution Networks. J. Water Resour. Plan. Manag. 2016, 142, 1–11. [Google Scholar] [CrossRef]
- De Sanctis, A.E.; Shang, F.; Uber, J.G. Real-Time Identification of Possible Contamination Sources Using Network Backtracking Methods. J. Water Resour. Plan. Manag. 2010, 136, 444–453. [Google Scholar] [CrossRef]
- Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network. Water 2018, 10, 579. [Google Scholar] [CrossRef]
- Gong, J.-Y.; Yan, X.-S.; Hu, C.-Y.; Gong, W.-Y. Survey on methods for drinking water contamination source identification based on intelligent optimization algorithm. Kongzhi Lilun Yu Yingyong/Control Theory Appl. 2021, 38, 1313–1323. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.G.; Polycarpou, M. Particle Backtracking Algorithm for Water Distribution System Analysis. J. Environ. Eng. 2002, 128, 441–450. [Google Scholar] [CrossRef]
- Laird, C.D.; Biegler, L.T.; Waanders, B.G.V.B.; Bartlett, R.A. Contamination Source Determination for Water Networks. J. Water Resour. Plan. Manag. 2005, 131, 125–134. [Google Scholar] [CrossRef]
- Dawsey, W.J.; Minsker, B.S.; VanBlaricum, V.L. Bayesian Belief Networks to Integrate Monitoring Evidence of Water Distribution System Contamination. J. Water Resour. Plan. Manag. 2006, 132, 234–241. [Google Scholar] [CrossRef]
- De Sanctis, A.; Boccelli, D.; Shang, F.; Uber, J. Probabilistic approach to characterize contamination sources with imperfect sensors. In Proceedings of the World Environmental and Water Resources Congress 2008: Ahupua’A, Honolulu, HI, USA, 12–16 May 2008; pp. 1–10. [Google Scholar]
- Neupauer, R.M.; Records, M.K.; Ashwood, W.H. Backward Probabilistic Modeling to Identify Contaminant Sources in Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 587–591. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. Bayesian networks for estimating contaminant source and propagation in a water distribution system using cluster structure. In Proceedings of the Water Distribution Systems Analysis 2010, Tucson, AZ, USA, 12–15 September 2010; pp. 426–435. [Google Scholar]
- Dawsey, W.J. Bayesian Belief Networks to Integrate Monitoring Evidence of Water Distribution System Contamination; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2012. [Google Scholar]
- Tao, T.; Huang, H.-D.; Xin, K.-L.; Liu, S.-M. Identification of contamination source in water distribution network based on consumer complaints. J. Central South Univ. 2012, 19, 1600–1609. [Google Scholar] [CrossRef]
- Wang, H.; Harrison, K.W. Improving Efficiency of the Bayesian Approach to Water Distribution Contaminant Source Characterization with Support Vector Regression. J. Water Resour. Plan. Manag. 2014, 140, 3–11. [Google Scholar] [CrossRef]
- Yang, X.; Boccelli, D.L. Bayesian Approach for Real-Time Probabilistic Contamination Source Identification. J. Water Resour. Plan. Manag. 2014, 140, 04014019. [Google Scholar] [CrossRef]
- Wagner, D.E.; Neupauer, R.M.; Cichowitz, C. Adjoint-Based Probabilistic Source Characterization in Water-Distribution Systems with Transient Flows and Imperfect Sensors. J. Water Resour. Plan. Manag. 2015, 141, 04015003. [Google Scholar] [CrossRef]
- Barandouzi, M.; Kerachian, R. Probabilistic contaminant source identification in water distribution infrastructure systems. Civil Eng. Infrastruct. J. 2016, 49, 311–326. [Google Scholar]
- Guan, J.B.; Aral, M.M.; Maslia, M.L.; Grayman, W.M. Identification of contaminant sources in water distribution systems using simulation-optimization method: Case study. J. Water Resour. Plan. Manag. 2006, 132, 252–262. [Google Scholar] [CrossRef]
- Hill, J.; van Bloemen Waanders, B.; Laird, C. Source inversion with uncertain sensor measurements. In Proceedings of the Water Distribution Systems Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–13. [Google Scholar]
- Preis, A.; Ostfeld, A. A contamination source identification model for water distribution system security. Eng. Optim. 2007, 39, 941–947. [Google Scholar] [CrossRef]
- Di Cristo, C.; Leopardi, A. Pollution source identification of accidental contamination in water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 197–202. [Google Scholar] [CrossRef]
- Liu, L.; Zechman, E.M.; Brill, J.; Downey, D.; Mahinthakumar, G.; Ranjithan, S.; Uber, J. Adaptive contamination source identification in water distribution systems using an evolutionary algorithm-based dynamic optimization procedure. In Proceedings of the Water Distribution Systems Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–9. [Google Scholar]
- Vankayala, P.; Sankarasubramanian, A.; Ranjithan, S.R.; Mahinthakumar, G. Contaminant Source Identification in Water Distribution Networks Under Conditions of Demand Uncertainty. Environ. Forensics 2009, 10, 253–263. [Google Scholar] [CrossRef]
- Zechman, E.M.; Ranjithan, S.R. Evolutionary Computation-Based Methods for Characterizing Contaminant Sources in a Water Distribution System. J. Water Resour. Plan. Manag. 2009, 135, 334–343. [Google Scholar] [CrossRef]
- Tryby, M.E.; Propato, M.; Ranjithan, S.R. Monitoring Design for Source Identification in Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 637–646. [Google Scholar] [CrossRef]
- Liu, L.; Ranjithan, S.R.; Mahinthakumar, G. Contamination Source Identification in Water Distribution Systems Using an Adaptive Dynamic Optimization Procedure. J. Water Resour. Plan. Manag. 2011, 137, 183–192. [Google Scholar] [CrossRef]
- Neupauer, R.M. Adjoint Sensitivity Analysis of Contaminant Concentrations in Water Distribution Systems. J. Eng. Mech. 2011, 137, 31–39. [Google Scholar] [CrossRef]
- Preis, A.; Ostfeld, A. Hydraulic uncertainty inclusion in water distribution systems contamination source identification. Urban Water J. 2011, 8, 267–277. [Google Scholar] [CrossRef]
- Gugat, M.; Gugat, M. Contamination Source Determination in Water Distribution Networks. SIAM J. Appl. Math. 2012, 72, 1772–1791. [Google Scholar] [CrossRef]
- Liu, L.; Zechman, E.M.; Mahinthakumar, G.; Ranjithan, S.R. Identifying contaminant sources for water distribution systems using a hybrid method. Civ. Eng. Environ. Syst. 2012, 29, 123–136. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, J.; Yan, X.; Zeng, D.; Guo, S. A MapReduce based Parallel Niche Genetic Algorithm for contaminant source identification in water distribution network. Ad Hoc Networks 2015, 35, 116–126. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, J.; Hu, C. Research on multimodal optimization algorithm for the contamination source identification of city water distribution networks. In International Conference on Bio-Inspired Computing: Theories and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 80–85. [Google Scholar]
- Yan, X.; Zhao, J.; Hu, C.; Wu, Q. Contaminant source identification in water distribution network based on hybrid encoding. J. Comput. Methods Sci. Eng. 2016, 16, 379–390. [Google Scholar] [CrossRef]
- Costa, D.M.; Melo, L.F.; Martins, F.G. Localization of Contamination Sources in Drinking Water Distribution Systems: A Method Based on Successive Positive Readings of Sensors. Water Resour. Manag. 2013, 27, 4623–4635. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, S. Contamination source identification based on sequential Bayesian approach for water distribution network with stochastic demands. IISE Trans. 2017, 49, 899–910. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G.; Savic, D. On the choice of the demand and hydraulic modeling approach to WDN real-time simulation. Water Resour. Res. 2017, 53, 6159–6177. [Google Scholar] [CrossRef]
- Shen, H.; McBean, E. False Negative/Positive Issues in Contaminant Source Identification for Water-Distribution Systems. J. Water Resour. Plan. Manag. 2012, 138, 230–236. [Google Scholar] [CrossRef]
- Xuesong, Y.; Jie, S.; Chengyu, H. Research on contaminant sources identification of uncertainty water demand using genetic algorithm. Clust. Comput. 2017, 20, 1007–1016. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, Z.; Li, T. Pollution source localization in an urban water supply network based on dynamic water demand. Environ. Sci. Pollut. Res. 2017, 26, 17901–17910. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Ye, Z.-S. Contamination Source Identification: A Bayesian Framework Integrating Physical and Statistical Models. IEEE Trans. Ind. Informatics 2021, 17, 8189–8197. [Google Scholar] [CrossRef]
- Yan, X.; Gong, J.; Wu, Q. Pollution source intelligent location algorithm in water quality sensor networks. Neural Comput. Appl. 2020, 33, 209–222. [Google Scholar] [CrossRef]
- Capano, G.; Bonora, M.A.; Carini, M.; Maiolo, M. Identification of Contamination Potential Source (ICPS): A Topological Approach for the Optimal Recognition of Sensitive Nodes in a Water Distribution Network. In International Conference on Numerical Computations: Theory and Algorithms; Springer: Cham, Switzerland, 2020; pp. 525–536. [Google Scholar]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling Chlorine Residuals in Drinking-Water Distribution Systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Sankary, N.; Ostfeld, A. Bayesian Localization of Water Distribution System Contamination Intrusion Events Using Inline Mobile Sensor Data. J. Water Resour. Plan. Manag. 2019, 145, 04019029. [Google Scholar] [CrossRef]
- Santonastaso, G.F.; Di Nardo, A.; Creaco, E.; Musmarra, D.; Greco, R. Comparison of topological, empirical and optimization-based approaches for locating quality detection points in water distribution networks. Environ. Sci. Pollut. Res. 2020, 28, 33844–33853. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Li, M.; Zeng, D.; Guo, S. A survey on sensor placement for contamination detection in water distribution systems. Wirel. Networks 2016, 24, 647–661. [Google Scholar] [CrossRef]
- Piazza, S.; Blokker, E.J.M.; Freni, G.; Puleo, V.; Sambito, M. Impact of diffusion and dispersion of contaminants in water distribution networks modelling and monitoring. Water Supply 2019, 20, 46–58. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.; Rossman, L. EPANET Multi-species extension software and user’s manual. US EPA 2008. Available online: https://cfpub.epa.gov/si/si_public_file_download.cfm?p_download_id=500759&Lab=NHSRC (accessed on 5 November 2022).
- Piazza, S.; Sambito, M.; Freni, G. A Novel EPANET Integration for the Diffusive–Dispersive Transport of Contaminants. Water 2022, 14, 2707. [Google Scholar] [CrossRef]
- Xin, K.; Tao, T.; Wang, Y.; Liu, S. Hazard and vulnerability evaluation of water distribution system in cases of contamination intrusion accidents. Front. Environ. Sci. Eng. 2012, 6, 839–848. [Google Scholar] [CrossRef]
- Bazargan-Lari, M.R.; Taghipour, S.; Habibi, M. Real-time contamination zoning in water distribution networks for contamination emergencies: A case study. Environ. Monit. Assess. 2021, 193, 336. [Google Scholar] [CrossRef]
- Rutkowski, T.; Prokopiuk, F. Identification of the Contamination Source Location in the Drinking Water Distribution System Based on the Neural Network Classifier. IFAC-PapersOnLine 2018, 51, 15–22. [Google Scholar] [CrossRef]
- Yan, X.; Yang, K.; Hu, C.; Gong, W. Pollution source positioning in a water supply network based on expensive optimization. Desalin. Water Treat. 2018, 110, 308–318. [Google Scholar] [CrossRef]
- Gong, J.; Yan, X.; Hu, C.; Wu, Q. Collaborative based pollution sources identification algorithm in water supply sensor networks. Desalin. Water Treat. 2019, 168, 123–135. [Google Scholar] [CrossRef]
- Sun, L.; Yan, H.; Xin, K.; Tao, T. Contamination source identification in water distribution networks using convolutional neural network. Environ. Sci. Pollut. Res. 2019, 26, 36786–36797. [Google Scholar] [CrossRef]
- Tinelli, S.; Juran, I. Artificial intelligence-based monitoring system of water quality parameters for early detection of non-specific bio-contamination in water distribution systems. Water Supply 2019, 19, 1785–1792. [Google Scholar] [CrossRef]
- Yan, X.; Li, T.; Hu, C.; Wu, Q. Real-time localization of pollution source for urban water supply network in emergencies. Clust. Comput. 2018, 22, S5941–S5954. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, J.; Hu, C.; Zeng, D. Multimodal optimization problem in contamination source determination of water supply networks. Swarm Evol. Comput. 2019, 47, 66–71. [Google Scholar] [CrossRef]
- Grbčić, L.; Lučin, I.; Kranjčević, L.; Družeta, S. Water supply network pollution source identification by random forest algorithm. J. Hydroinformatics 2020, 22, 1521–1535. [Google Scholar] [CrossRef]
- Grbčić, L.; Lučin, I.; Kranjčević, L.; Družeta, S. A Machine Learning-based Algorithm for Water Network Contamination Source Localization. Sensors 2020, 20, 2613. [Google Scholar] [CrossRef]
- Marlim, M.S.; Kang, D. Identifying Contaminant Intrusion in Water Distribution Networks under Water Flow and Sensor Report Time Uncertainties. Water 2020, 12, 3179. [Google Scholar] [CrossRef]
- Yan, X.S.; Hu, C.Y.; Sheng, V.S. Data-driven pollution source location algorithm in water quality monitoring sensor networks. Int. J. Bio-Inspired Comput. 2020, 15, 171–180. [Google Scholar] [CrossRef]
- Butera, I.; Gómez-Hernández, J.J.; Nicotra, S. Contaminant-Source Detection in a Water Distribution System Using the Ensemble Kalman Filter. J. Water Resour. Plan. Manag. 2021, 147, 04021029. [Google Scholar] [CrossRef]
- Grbčić, L.; Kranjčević, L.; Družeta, S. Machine Learning and Simulation-Optimization Coupling for Water Distribution Network Contamination Source Detection. Sensors 2021, 21, 1157. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yang, R.; Zhou, L.; Zeng, S.; Mavrovouniotis, M.; Yang, M.; Yang, S.; Wu, M. Adaptive Multipopulation Evolutionary Algorithm for Contamination Source Identification in Water Distribution Systems. J. Water Resour. Plan. Manag. 2021, 147, 04021014. [Google Scholar] [CrossRef]
- Lučin, I.; Grbčić, L.; Družeta, S.; Čarija, Z. Source Contamination Detection Using Novel Search Space Reduction Coupled with Optimization Technique. J. Water Resour. Plan. Manag. 2021, 147, 04020100. [Google Scholar] [CrossRef]
- Qian, K.; Jiang, J.; Ding, Y.; Yang, S.-H. DLGEA: A deep learning guided evolutionary algorithm for water contamination source identification. Neural Comput. Appl. 2021, 33, 11889–11903. [Google Scholar] [CrossRef]
- Yan, X.; Zhou, Z.; Hu, C.; Gong, W. Real-time location algorithms of drinking water pollution sources based on domain knowledge. Environ. Sci. Pollut. Res. 2021, 28, 46266–46280. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Jiang, J.; Qian, K.; Ding, Y.; Yang, S.-H.; He, L. Graph convolutional networks based contamination source identification across water distribution networks. Process Saf. Environ. Prot. 2021, 155, 317–324. [Google Scholar] [CrossRef]
- Gong, J.; Yan, X.; Hu, C. An ensemble-surrogate assisted cooperative particle swarm optimisation algorithm for water contamination source identification. Int. J. Bio-Inspired Comput. 2022, 19, 169–177. [Google Scholar] [CrossRef]
- Laird, C.; Biegler, L.; van Bloemen Waanders, B.; Bartlett, R. Time dependent contamination source determination for municipal water networks using large scale optimization. J. Water Resour. Plan. Manag. 2003, 129, 1–28. [Google Scholar]
- Laird, C.D.; Biegler, L.T.; Waanders, B.G.V.B. Mixed-Integer Approach for Obtaining Unique Solutions in Source Inversion of Water Networks. J. Water Resour. Plan. Manag. 2006, 132, 242–251. [Google Scholar] [CrossRef]
- Sankary, N.; Ostfeld, A. Inline Mobile Water Quality Sensors Deployed for Contamination Intrusion Localization. In Proceedings of the 2017 Computing and Control for the Water Industry, Sheffield, UK, 5–7 September 2017. [Google Scholar]
- Krause, A.; Leskovec, J.; Guestrin, C.; VanBriesen, J.; Faloutsos, C. Efficient Sensor Placement Optimization for Securing Large Water Distribution Networks. J. Water Resour. Plan. Manag. 2008, 134, 516–526. [Google Scholar] [CrossRef]
- Lučin, I.; Grbčić, L.; Čarija, Z.; Kranjčević, L. Machine-Learning Classification of a Number of Contaminant Sources in an Urban Water Network. Sensors 2021, 21, 245. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).