Modelling and Estimation in Lithium-Ion Batteries: A Literature Review
Abstract
1. Introduction
- Insight is provided on the fundamentals of Li-ion batteries regarding the main and side reactions, with the aim of explaining the basics in a comprehensive way;
- The modelling of LIBs is summarised and explained in a straightforward way from a state-estimation perspective;
- A complete single-particle model (SPM) is provided, as well as a review of the simplification methods for electrochemical models. Finally, the proposed SPM is simplified to extract a reduced order state-space model;
- A picture of the landscape of observers is provided, with explanations of the strengths and weaknesses of each mentioned observer, again with the intention of comprehensively elucidating the fundamentals;
- A classification of estimation methods is provided for SoC and SoH.
2. Fundamentals of Li-Ion Cells
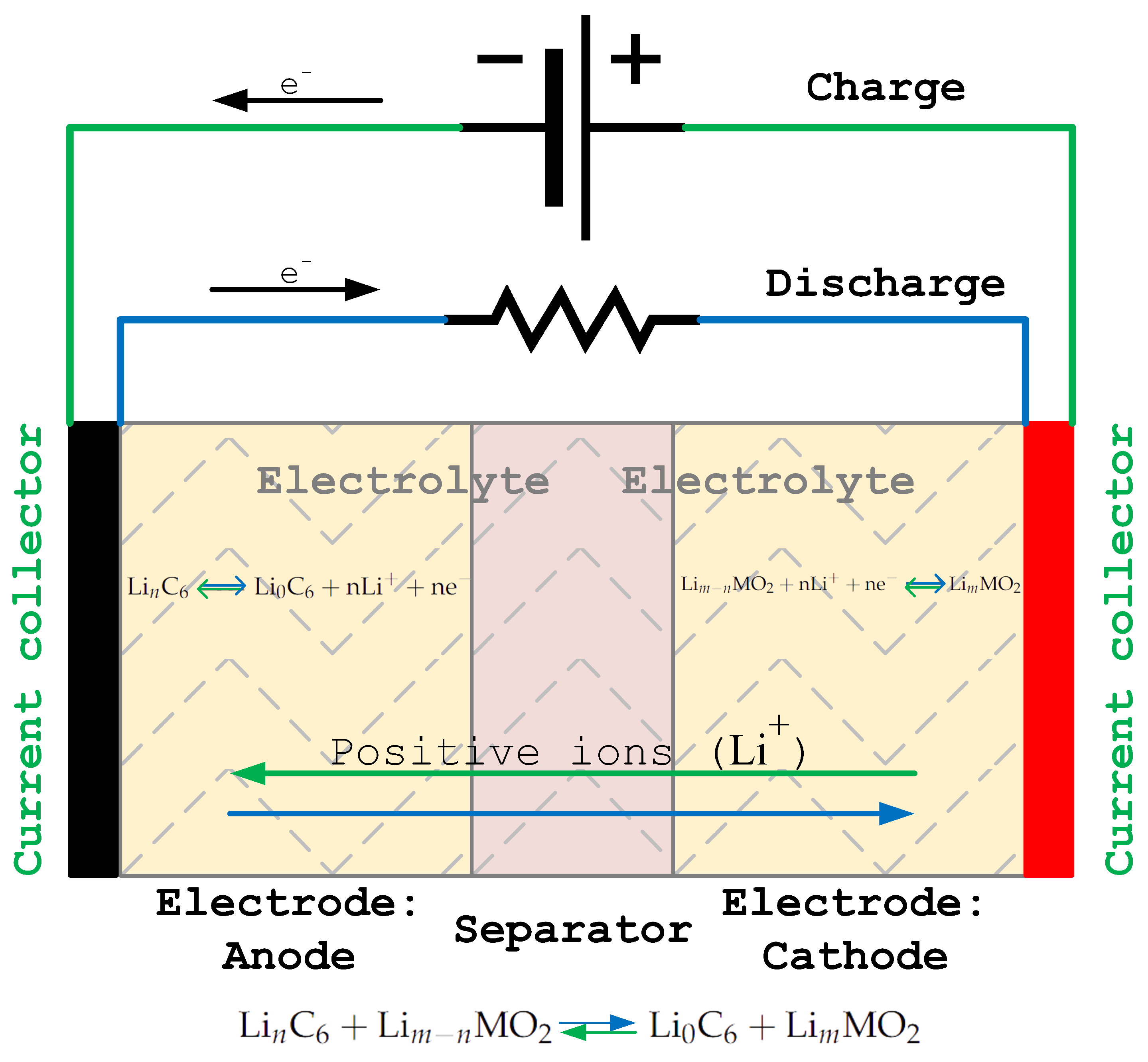
2.1. Working Principles
2.2. Side Reactions
2.2.1. Overvoltage
- Lithium plating: The graphite electrodes become saturated with lithium, leading to an effect known as lithium deposition or lithium plating. This results in the formation of dendrites within the anode, which obstruct the flow of ions. Over time, dendrites can extend into the separator, causing short circuits [25,26].
2.2.2. Undervoltage
- SEI: An undervoltage situation leads to the precipitation of insoluble products onto the electrode surface in the anode, forming a passive film known as the SEI. While the SEI is necessary to prevent unwanted reactions between the electrolyte and the electrode, it is convenient to avoid the excessive growth of the SEI, as it can also contribute to capacity fading [28,29].
2.2.3. High Currents
- Particle fracture: The particles may change volume and thus stress the electrode materials. The effect of particle fracture can indirectly cause the growth of the SEI or loss of active material [30].
2.2.4. High Temperatures
2.3. Indicators
- Capacity () [Ah]: The maximum amount of charge that can be stored inside the battery and delivered during a full discharge cycle. The capacity (usually expressed in Ah) varies according to the quantity of material in the electrodes;
- Nominal capacity () [Ah]: The original capacity of the battery when it is new and no degradation has occurred;
- State of Charge (SoC): The primary indicator in LIBs, providing information about the remaining energy inside the battery. SoC can be defined as in Equation (4), where Q is the actual capacity and is the maximum capacity of the cell, both measured in ;
- SoH: The ratio between the current maximum available capacity and the rated available capacity, which indicates the battery’s aging condition. It can be expressed mathematically as follows:
- C rate: The charging or discharging current relative to capacity. A 1C rate corresponds to full charging or discharging the battery in one hour, while 0.5C corresponds to two hours of charging. The C-rate for a 2 Ah cell being charged or discharged at 2 A is 1C, and if the current were 6 A, it would be 3C. In general, a value above 3–4 C is considered a high C-rate, although this varies notably depending on the chemistry.
2.4. Li-Ion Materials
3. Modelling
- Mechanistic models are based on the physical and chemical phenomena occurring within the battery, providing a detailed, accurate and interpretable representation of its internal behaviour.
- ECMs simulate the causality between the battery current and the voltage by constructing an electric circuit using resistors and capacitors, although they do not inherently represent the physical effects.
- Data-driven models are developed solely based on measured data and with minimum to zero use of the battery first principles, which makes them less effective in describing internal physicochemical phenomena. However, they have the potential to capture complex behaviour that is not yet fully understood from a physical perspective.
3.1. Mechanistic Models
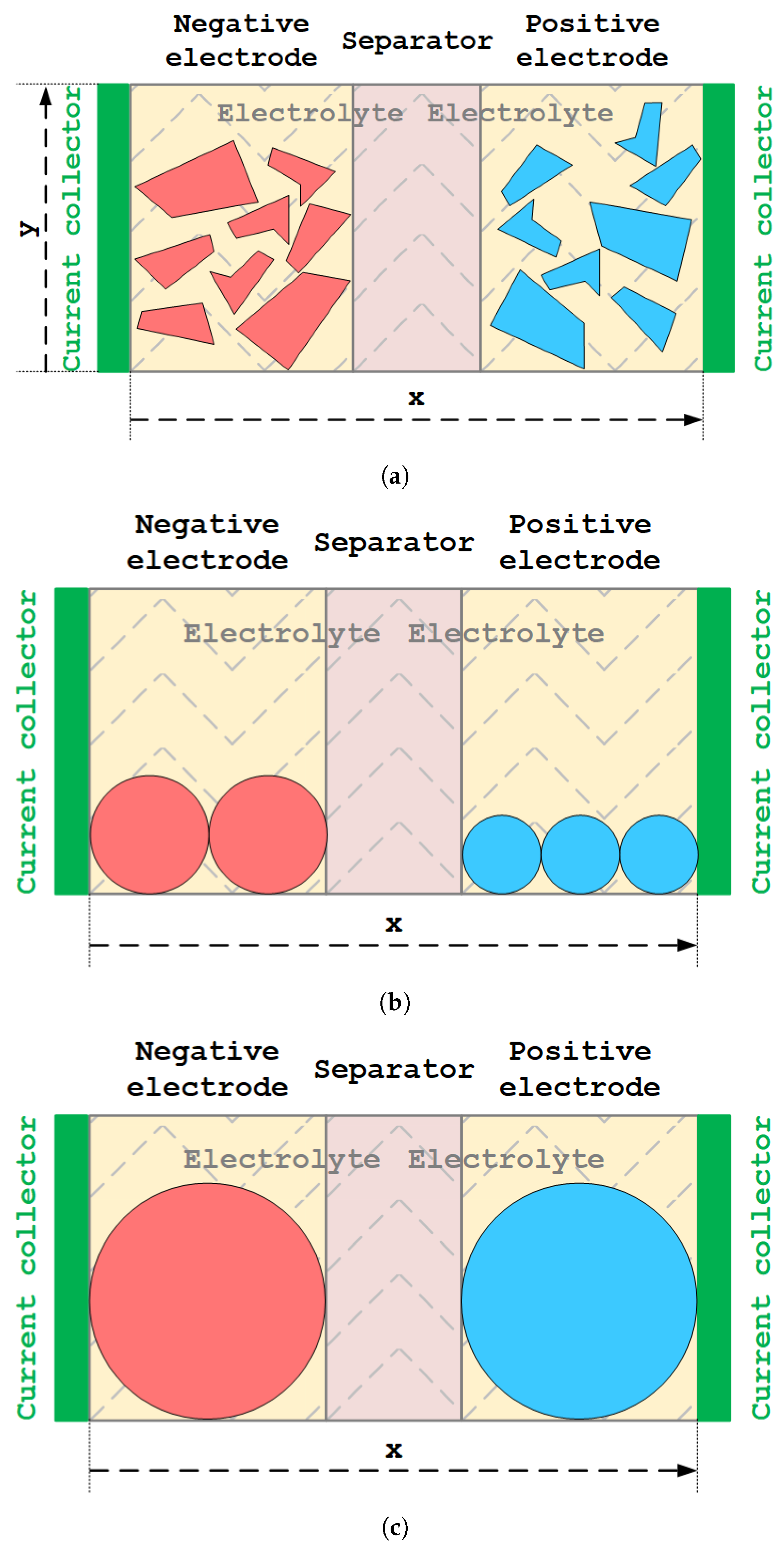
3.1.1. Microscale Model
3.1.2. Homogenised Model
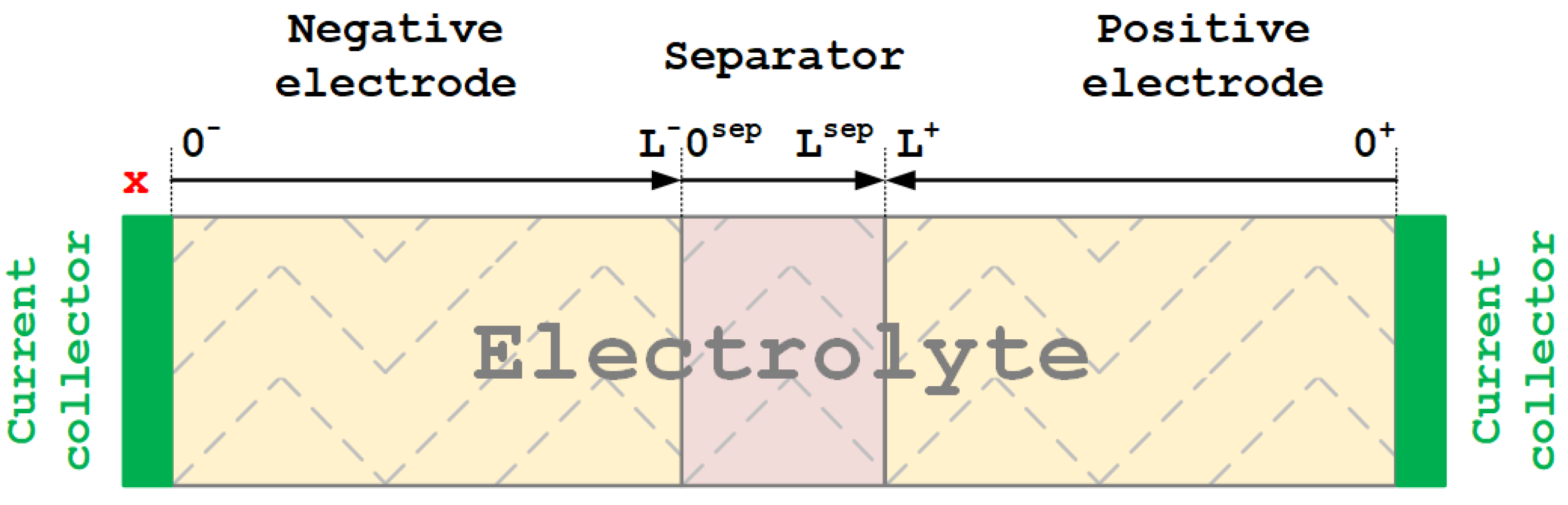
3.1.3. Doyle–Fuller–Newman Model
- Solid Phase
- Electrolyte
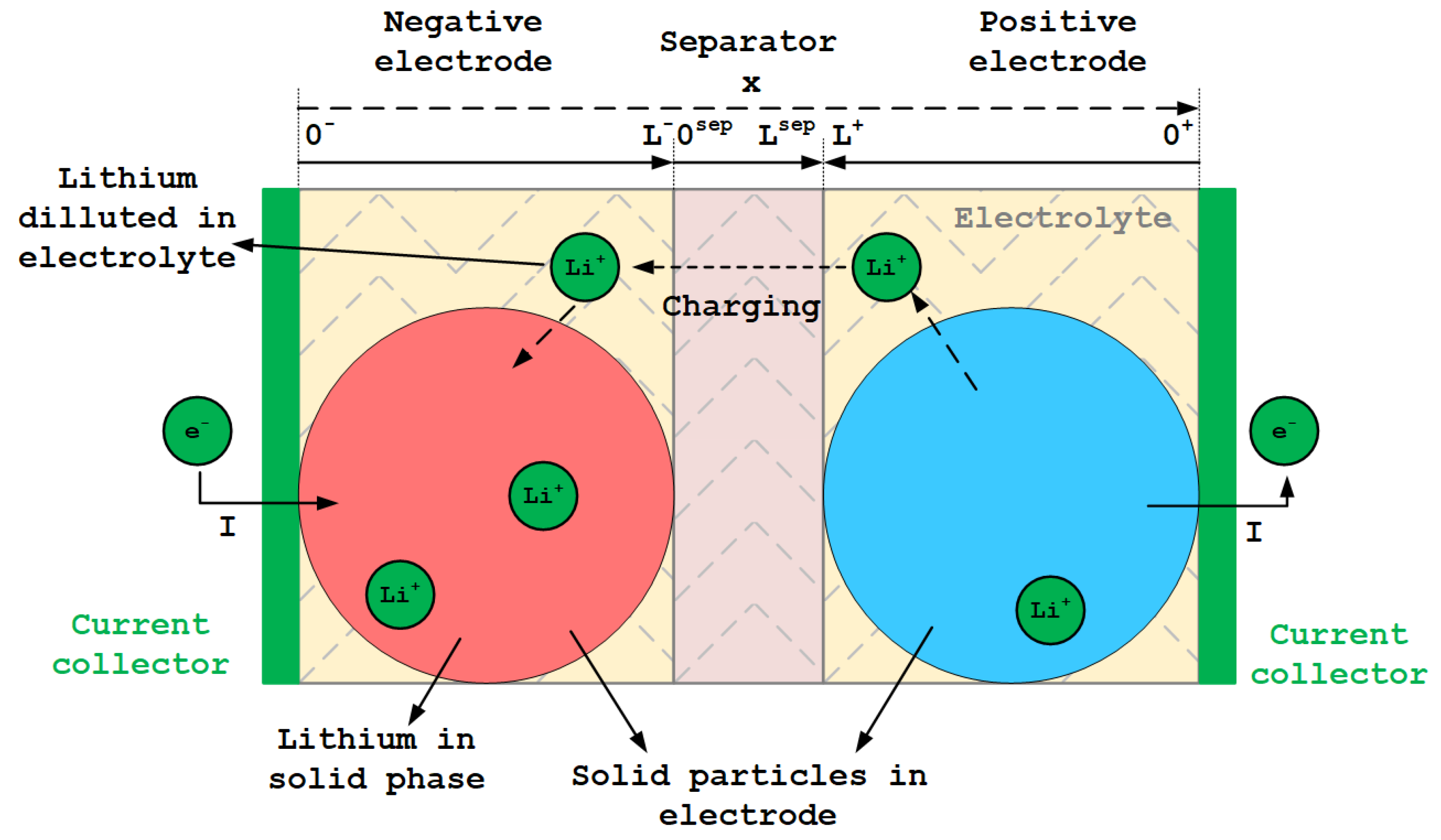
3.1.4. SPM
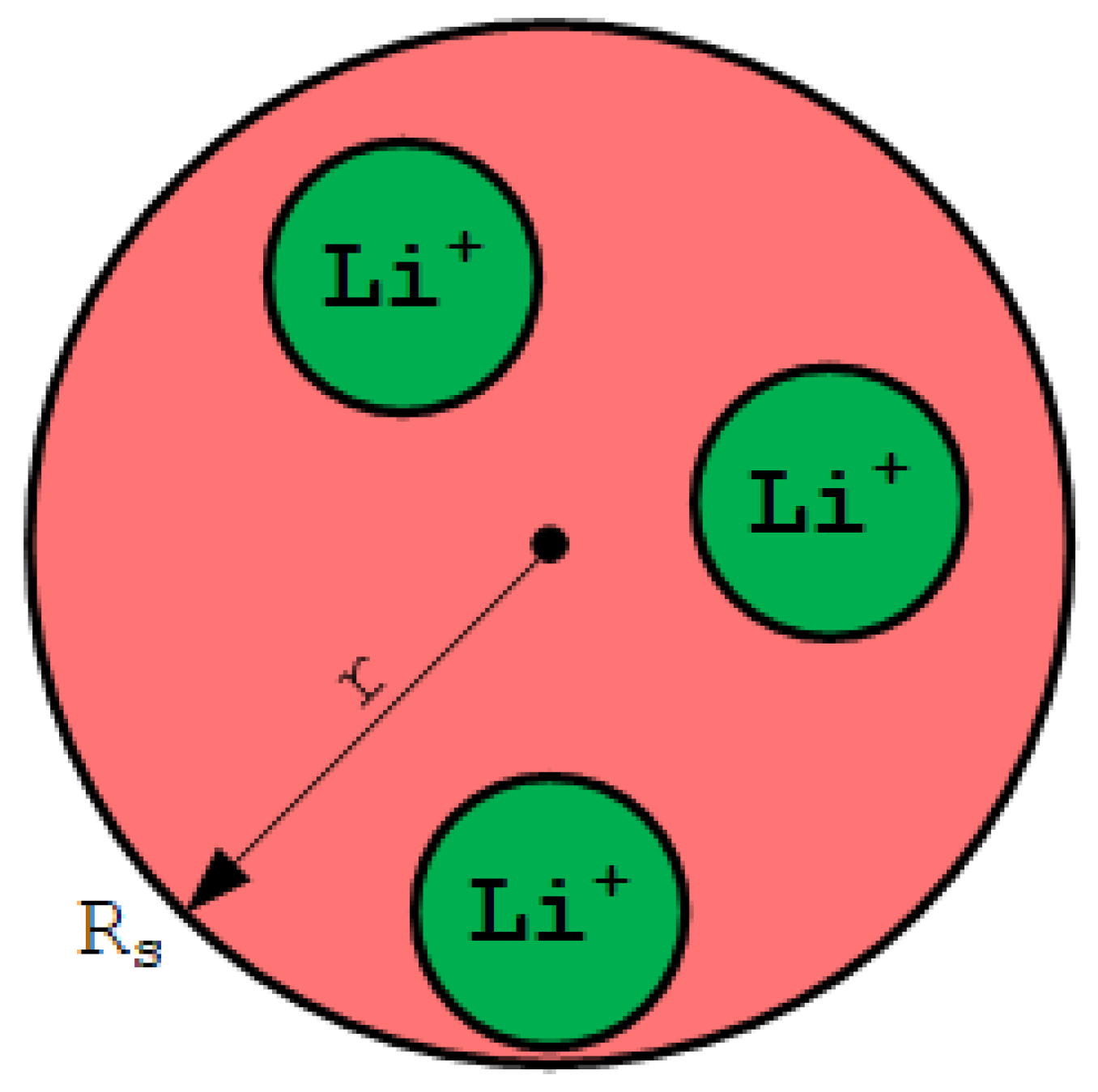
- The concentration of solid particles is homogeneous in a radial sense so that the concentration only varies on the radial coordinate (r);
- The current density in each electrode is uniformly distributed;
- The number of moles in the electrolyte and that in the solid phase are both conserved. This can establish a proportional relation between current and flux;
- The transport coefficients () of the anode and cathode are equal.
- Solid Phase
- Electrolyte
- Cell Potential
- Thermal Modelling
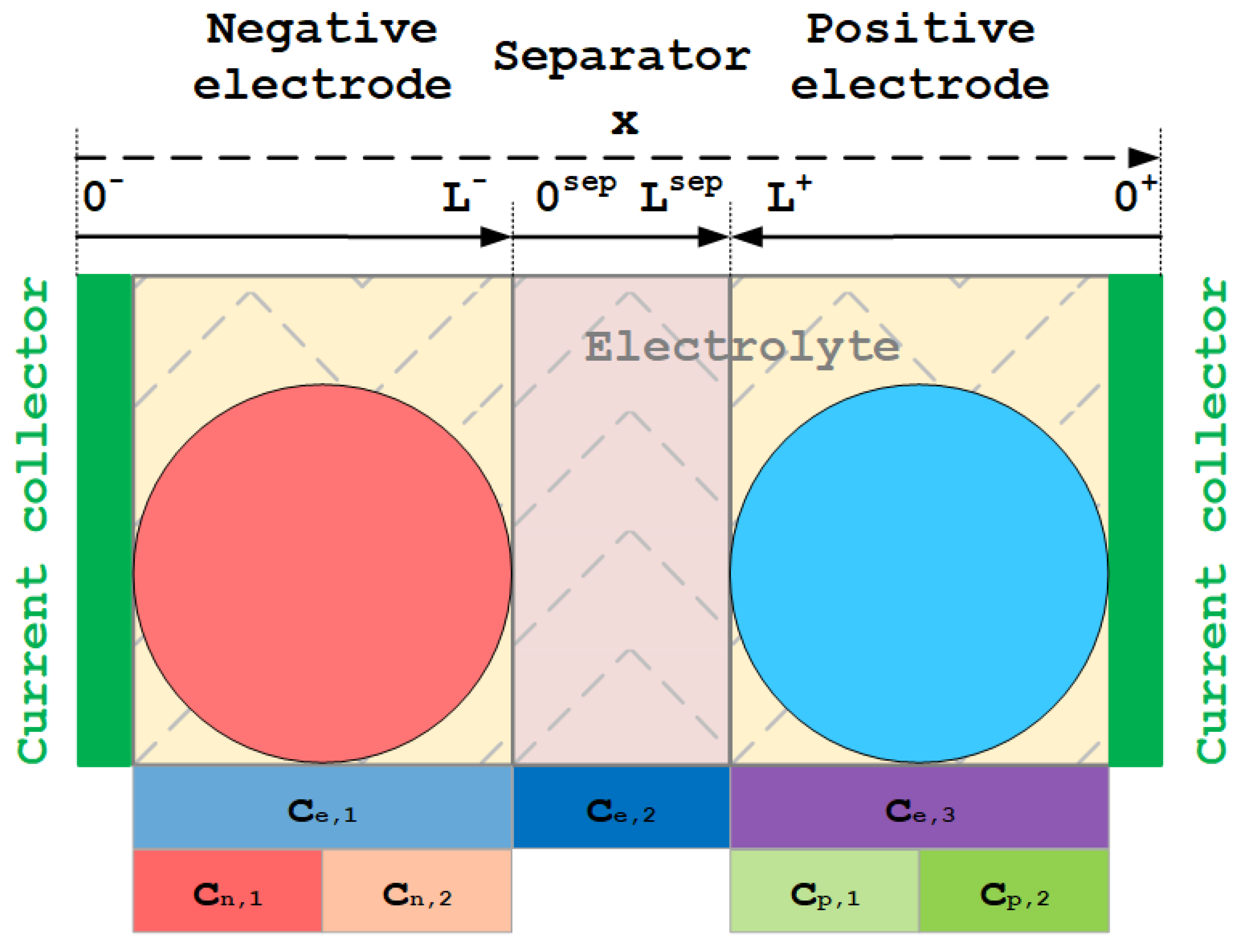
3.1.5. Finite-Order Models
- Spatial discretization: Well-known techniques such as Finite-difference Method (FDM) or Finite-volume Method (FVM) are used;
- Function approximation: Spatiotemporal variables are approximated by a finite weighted sum of assumed trial functions that are fitted using optimisation techniques;
- Frequency domain approximation: The frequency response is obtained means of Padé approximation or the residue grouping method, among other techniques;
- Physics simplification: Typically achieved using diverse SPM approaches with several variations.
- Spatial Discretization
- Function Approximation
- Frequency Domain Approximation
- Physics Simplification
- Concentration in the Solid
- Concentrations in the Electrolyte
3.2. ECMs
3.2.1. Phenomenological ECMs
3.2.2. Electrochemical ECM
3.3. Data-Driven Models
4. Estimation in Li-Ion Batteries
4.1. Estimable Information
4.1.1. SoC
- Coulomb counting method: Coulomb counting is the most straightforward approach to compute SoC in a cell. It involves integrating the current over time, thereby calculating the extracted capacity of the cell. However, this technique has two main drawbacks: the initial SoC is usually unknown, and the capacity may change depending on the C rate or the temperature, as well as the cell’s aging. Additionally, Coulomb counting is susceptible to various sources of error, as listed in [15], including current measurement error, current integration error, timing error, and measurement and process noise.
- OCV method: The OCV is closely related to SoC, meaning if one is known, the other can be determined. However, OCV can only be measured in the absence of current and after the battery has been at rest, as current causes voltage to deviate from the OCV curve, and due to hysteresis, it takes a long time to recover. Although this method is precise and straightforward, it is unsuitable for online applications. Nevertheless, it holds value in providing an OCV–SoC curve, as required in many models. The authors of [85] provided a detailed guide for OCV characterisation.
- Internal resistance method: By applying a fast current pulse and measuring the resulting voltage variation, the internal resistance can be determined and linked to SoC [86]. This method performs quite well at lower levels of SoC, where voltage tends to decrease rapidly. However, in other ranges, especially with a typical voltage plateau, SoC estimation becomes much less precise.
- Model and Look-Up table: Using a simple model properly experimentally calibrated under static conditions, OCV can be extracted. Then, for online applications, SoC can be computed using a look-up table that relates OCV to SoC.
4.1.2. SoH
- Internal resistance measurement: As a battery loses capacity and degrades, the internal resistance increases [87]. Periodically measuring it with current pulses, always at the same level of SoC, can provide information about the SoH. Internal resistance characterisation is an easier experimental method than capacity measurement and can be performed in a shorter time.
- Impedance measurement: Measurement of the impedance can also be related to SoH [88], as the battery impedance is affected by degradation. EIS is needed to characterise this phenomenon, providing valuable information, as electrochemically based models (Section 3.2.2) also use EIS to extract model parameters.
4.1.3. Parameters
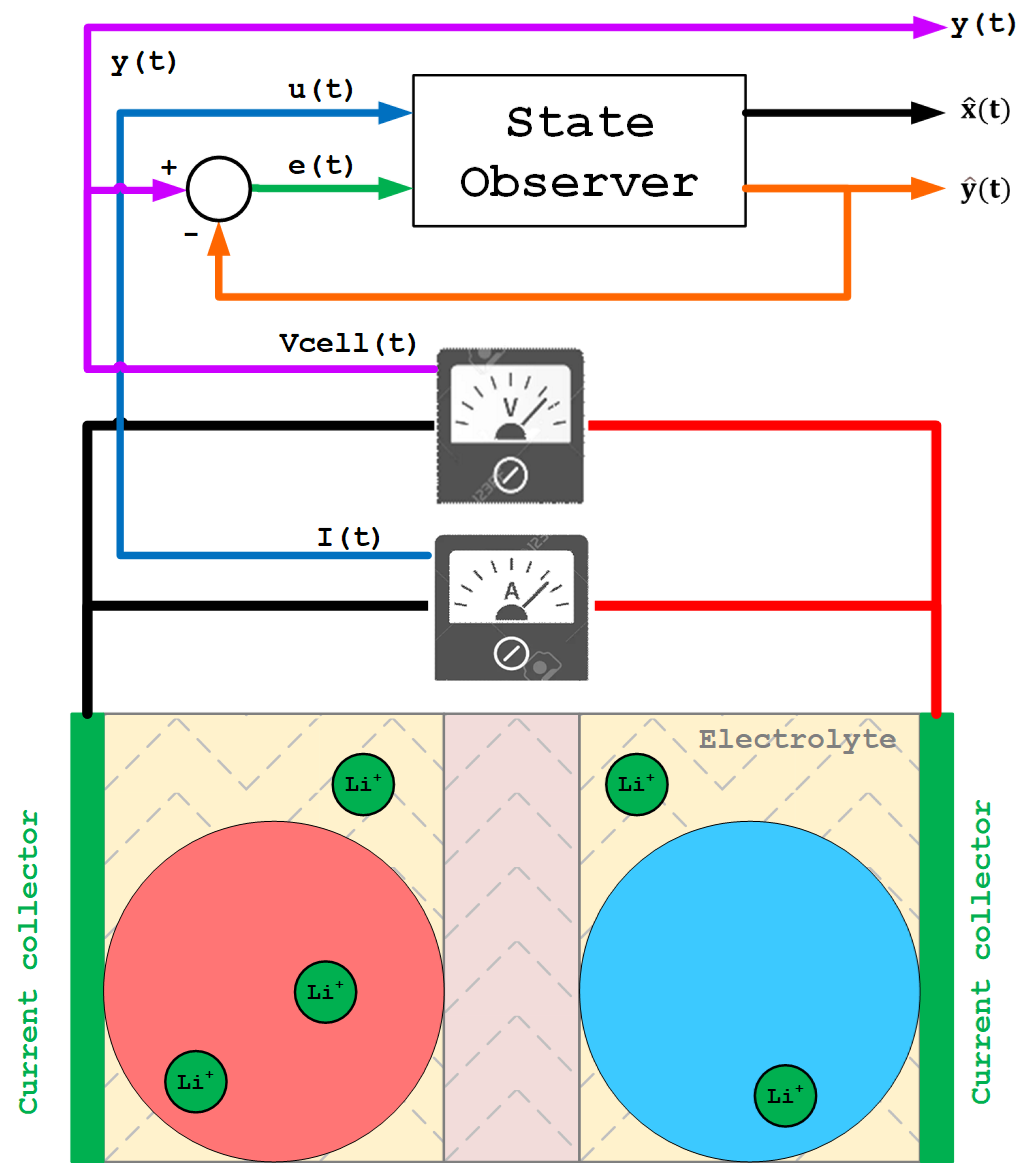
4.2. The Observation Problem
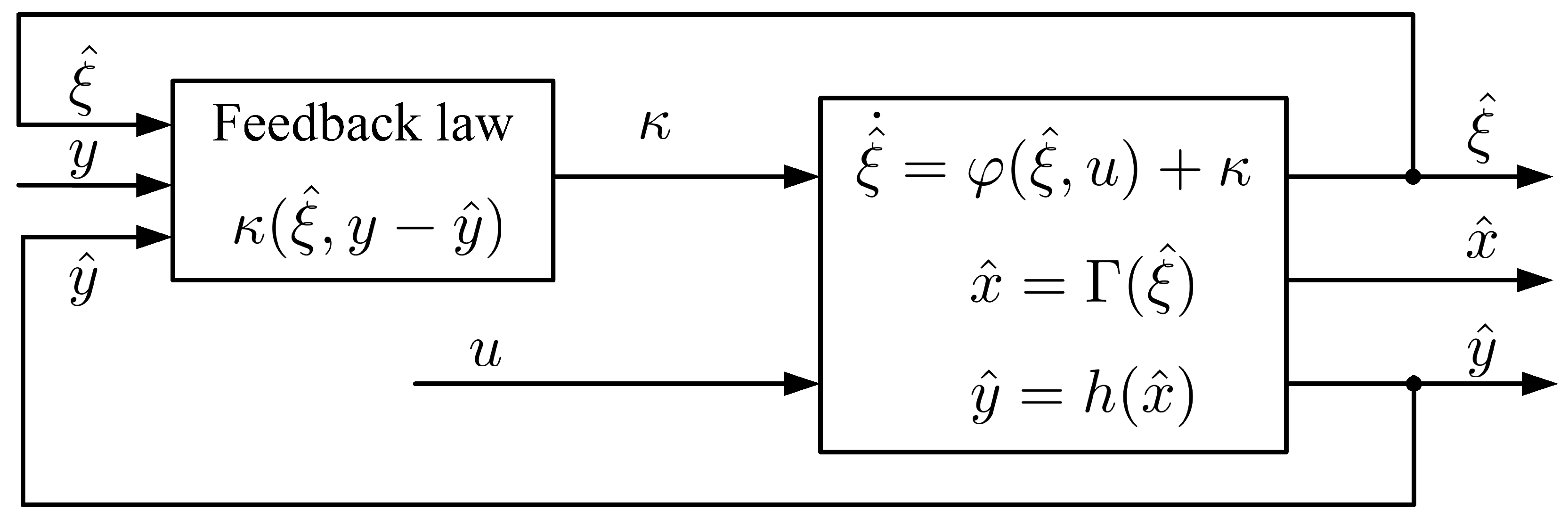
4.3. Observer Definition
- as .
- The observer dynamics (36) are depicted in a different set of coordinates () than the original system coordinates (). Consequently, the observer includes a map () that relates the observer coordinates to the coordinates of the original system.
- The dimensions of the observer may be larger than the original system dimensions.
- Not only can the dynamics of the system be nonlinear, but the observer feedback term () may also be a nonlinear function.
4.4. State-Space Model of Li-Ion Batteries
4.5. Observers in Li-Ion Batteries
4.5.1. Linear State Observers
- Extended Kalman filter [16,17,119,120,121,122,123,124,125]: This represents a classical approach to state observation for dynamic systems that effectively converts (locally) a nonlinear system into a linear one. This transformation is achieved by computing the first-order Taylor series expansion, specifically the Jacobian matrix, around the estimated operating point at each time step. Consequently, the nonlinear system is approximated as a continuum of linearised points. Additionally, assumptions are made regarding the measurement noise and process perturbations, assuming them to be zero-mean, Gaussian and independent of each other. However, it may prove inaccurate when applied to highly nonlinear systems. Moreover, there is no guarantee of convergence if the initial values of the observer estimation deviate significantly from the actual values.
- Observer [126]: This method endeavours to identify corresponding states that satisfy a mathematical optimisation problem formulated using the norm of the observer. Its primary goal is to achieve an optimal solution for a range of diverse plants representing varying levels of uncertainty or noise. Consequently, it offers certain advantages over an extended Kalman filter, including heightened robustness against model uncertainties and the ability to handle unknown noise statistics. However, the implementation of this approach demands a significant level of mathematical comprehension and relies heavily on the specific plants employed during its design. Furthermore, if the actual operating conditions differ from those used in the observer’s design, convergence is not guaranteed.
4.5.2. Nonlinear State Observers
- Unscented Kalman filter [127,128,129,130,131,132]: An unscented Kalman filter (UKF) is a nonlinear variant of a Kalman filter and typically demonstrates superior performance compared to the extended Kalman filters when confronted with highly nonlinear systems. The key to its effectiveness lies in its utilisation of unscented transformation instead of computing the Jacobian matrix for every operation point. Moreover, a UKF does not impose a requirement for a Gaussian noise distribution. The algorithm operates by generating a set of “sigma points” surrounding the mean of the entire sample set. These sigma points are then employed to determine the covariance of the state distribution. Despite the advantages offered by this approach, it lacks robustness in the face of model uncertainties or disturbances that are not modelled in a stochastic manner.It has to be remarked that there exist more variations of extended Kalman filters. Some notable examples are adaptive extended Kalman filters [120,125], adaptive unscented Kalman filters [133,134,135], sigma point Kalman filters [136,137], central difference Kalman filters [138,139,140] and cubature Kalman filters [141,142,143]. We refer the reader to [11,144] for a more in-depth presentation of all these variations.
- Sliding-mode observer [145,146,147,148,149,150,151,152]: Sliding-mode observers (SMOs) offer an effective approach to directly address nonlinear systems, leveraging the principles of sliding-mode control [153] to devise feedback laws for observer design. By incorporating a discontinuous correction term (represented by a switching term with a switching frequency extending to infinity), SMOs guide the system states towards a surface where the measured and estimated outputs become indistinguishable. As a result, if the system satisfies a particular observability property, the estimated states ultimately converge to the actual states. SMOs possess the advantageous capability to minimise modelling errors and mitigate the effects of uncertainties, all while enabling the coordinates of observer error dynamics to reach zero within a finite time frame. However, a significant drawback of this method lies in the discontinuous nature of the correction term, which often leads to high-frequency commutations, thereby increasing its computational cost. Nevertheless, the implementation of such observers can be enhanced through the use of adaptive gain techniques or zero-crossing techniques. These approaches offer avenues for improving the overall performance and computational efficiency of SMOs.
- High-gain observer [154,155]: High-gain observers (HGOs) share a similar theoretical foundation with SMOs, as both employ a correction term based on high-gain principles. However, in the case of HGOs, this correction term is continuous, thereby avoiding the persistent commutations often encountered in SMOs. HGOs excel in estimating states within nonlinear systems, but they are susceptible to the “peaking phenomenon”, whereby the states of the observer can drastically increase during the transient.This phenomenon entails that during a transient phase before convergence, the estimates may assume values that significantly deviate from the true states. Despite this drawback, HGOs still offer effective performance in state estimation for nonlinear systems, making them a valuable tool in the realm of observer design. Nonetheless, recently, some authors proposed a modification on HGOs that eliminates the peaking phenomena while reducing the noise sensitivity of the overall algorithm [156,157].
- Adaptive observer [19,158,159,160,161,162,163,164,165,166]: Observers are estimation algorithms rooted in the system’s mathematical model; they compare the information from measured trajectories with the model to generate estimations. Consequently, any disparities between the actual system and the mathematical model directly impact the accuracy of the estimations. Adaptive observers address this concern by simultaneously estimating unknown model parameters and internal states. Compared to other robust observers like HGOs and SMOs, adaptive observers generally exhibit reduced sensitivity to noise.Nevertheless, ensuring the robustness of adaptive observers necessitates the introduction of specific input signals to the system, effectively “exciting” it to accurately identify the unknown parameters.
- Circle-criterion observer [167]: Li-ion battery models usually present a semilinear structure in which the state dynamics can be separated into a linear term and a nonlinear term (see Section 4.4). Some authors have exploited the fact that the nonlinear terms usually satisfy a monotonic condition, which transforms the observer design process into a linear matrix inequality problem. It has to be mentioned that battery models can present nonmonotonic, nonlinear terms. In such cases, one a hybrid circle-criterion observer can be implemented, as proposed in [168].
4.6. Future Perspectives and Challenges
- Need for codesign of the battery model and observer: The performance of the observer highly depends on the quality of the model, few models are specifically designed for nonlinear observers. LIB models can be very complex and precise, but mostly have to be simplified (or at least endure an order-reduction process) to be used for observation applications. We believe that codesign would result in a simpler and more efficient development process.
- Further research on the application of nonlinear observers: Most models used for estimation tend to be linear or are linearised at some point, but the battery behaviour is nonlinear. The use of nonlinear observers such as the mentioned HGO or SMO and exploration of new observer architectures, such as the parameter estimation-based [169] observer and the Kazantzis–Kravaris/Luenberger observer [170], could potentially increase performance.
- Robustness against uncertainty: Most Kalman filter-based observers model noise and uncertainty stochastically. Nonetheless, this type of modelling may not always be possible in battery systems. In this sense, the authors of [173,174] developed techniques that allow for a reduction in the effects of uncertainty and noise in the estimation quality when they are not statistically modelled.
- Applications: The literature encompasses a substantial body of work on observer design, along with papers addressing optimal control in LIBs, which necessitates state estimation. Nevertheless, there is a scarcity of papers that integrate both aspects. It is imperative to formulate observer designs with a view towards their application in optimal control.
- Theory/practice gap: Since the implementation of many observers is a tortuous path, academia is far ahead of what is being implemented in industrial applications, obviously missing recent advances and advantages. If the ultimate goal of an observer is being implemented, tools to make this process feasible and economical (from an industrial point of view) are needed. This theory/practice gap in the battery literature and in the general control community was pointed out in [175].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| B-V | Butler-Volmer |
| BMS | Battery Monitoring System |
| DFN | Doyle-Fuller-Newman |
| ECM | Equivalent Circuit Model |
| EIS | Electrochemical Impedance Spectra |
| ESS | Energy Storage System |
| EV | Electric Vehicel |
| FDM | Finite-difference Method |
| FVM | Finite-volume Method |
| GPR | Gaussian process regression |
| HGO | High Gain Observer |
| Li-ion | Lithium-Ion |
| LIBs | Lithium-Ion Batteries |
| LR | Linear Regression |
| OCV | Open Circuit Voltage |
| P2D | Pseudo-2-dimensional |
| PDEs | Partial Differential Equations |
| SEI | Solid Electrolyte Interfase |
| SMO | Sliding Mode Observer |
| SoC | State of Charge |
| SoH | State of Health |
| SPM | Single Particle Model |
| SPMe | Single Particle Model with electrolyte dynamics |
| SVM | Support Vector Machine |
| UKF | Unscented Kalman Filter |
References
- Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Asri, L.I.M.; Ariffin, W.N.S.F.W.; Zain, A.S.M.; Nordin, J.; Saad, N.S. Comparative Study of Energy Storage Systems (ESSs). J. Phys. Conf. Ser. 2021, 1962, 012035. [Google Scholar] [CrossRef]
- Deng, W.; Xu, Y.; Zhang, X.; Li, C.; Liu, Y.; Xiang, K.; Chen, H. (NH4)2Co2V10O28·16H2O/(NH4)2V10O25·8H2O heterostructure as cathode for high-performance aqueous Zn-ion batteries. J. Alloys Compd. 2022, 903, 163824. [Google Scholar] [CrossRef]
- Zhou, W.; Zeng, G.; Jin, H.; Jiang, S.; Huang, M.; Zhang, C.; Chen, H. Bio-Template Synthesis of V2O3@Carbonized Dictyophora Composites for Advanced Aqueous Zinc-Ion Batteries. Molecules 2023, 28, 2147. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.N.; Li, Y.H.; Xu, D.F.; Zhou, W.; Xiang, K.X.; Chen, H. Three-dimensional hierarchically porous nitrogen-doped carbon from water hyacinth as selenium host for high-performance lithium–selenium batteries. Rare Met. 2022, 41, 3432–3445. [Google Scholar] [CrossRef]
- Wen, X.; Luo, J.; Xiang, K.; Zhou, W.; Zhang, C.; Chen, H. High-performance monoclinic WO3 nanospheres with the novel NH4+ diffusion behaviors for aqueous ammonium-ion batteries. Chem. Eng. J. 2023, 458, 141381. [Google Scholar] [CrossRef]
- Xiao, J.; Li, H.; Zhang, H.; He, S.; Zhang, Q.; Liu, K.; Jiang, S.; Duan, G.; Zhang, K. Nanocellulose and its derived composite electrodes toward supercapacitors: Fabrication, properties, and challenges. J. Bioresour. Bioprod. 2022, 7, 245–269. [Google Scholar] [CrossRef]
- Clemente, A.; Costa-Castelló, R. Redox Flow Batteries: A Literature Review Oriented to Automatic Control. Energies 2020, 13, 4514. [Google Scholar] [CrossRef]
- Puleston, T.; Clemente, A.; Costa-Castelló, R.; Serra, M. Modelling and Estimation of Vanadium Redox Flow Batteries: A Review. Batteries 2022, 8, 121. [Google Scholar] [CrossRef]
- Miao, Y.; Hynan, P.; von Jouanne, A.; Yokochi, A. Current Li-Ion Battery Technologies in Electric Vehicles and Opportunities for Advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef]
- Hannan, M.; Lipu, M.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Lee, S.B.; Thiagarajan, R.S.; Subramanian, V.R.; Onori, S. Advanced Battery Management Systems: Modeling and Numerical Simulation for Control. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 4403–4414. [Google Scholar]
- Krewer, U.; Röder, F.; Harinath, E.; Braatz, R.D.; Bedürftig, B.; Findeisen, R. Review—Dynamic Models of Li-Ion Batteries for Diagnosis and Operation: A Review and Perspective. J. Electrochem. Soc. 2018, 165, 3656–3673. [Google Scholar] [CrossRef]
- Brosa Planella, F.; Ai, W.; Boyce, A.M.; Ghosh, A.; Korotkin, I.; Sahu, S.; Sulzer, V.; Timms, R.; Tranter, T.G.; Zyskin, M.; et al. A continuum of physics-based lithium-ion battery models reviewed. Prog. Energy 2022, 4, 042003. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A Critical Look at Coulomb Counting Approach for State of Charge Estimation in Batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Rzepka, B.; Bischof, S.; Blank, T. Implementing an Extended Kalman Filter for SoC Estimation of a Li-Ion Battery with Hysteresis: A Step-by-Step Guide. Energies 2021, 14, 3733. [Google Scholar] [CrossRef]
- van Dao, Q.; Dinh, M.C.; Kim, C.S.; Park, M.; Doh, C.H.; Bae, J.H.; Lee, M.K.; Liu, J.; Bai, Z. Design of an Effective State of Charge Estimation Method for a Lithium-Ion Battery Pack Using Extended Kalman Filter and Artificial Neural Network. Energies 2021, 14, 2634. [Google Scholar]
- Li, Y.; Anderson, R.D.; Song, J.; Phillips, A.M.; Wang, X. A nonlinear adaptive observer approach for state of charge estimation of lithium-ion batteries. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 370–375. [Google Scholar]
- Bergveld, H.J.; Kruijt, W.S.; Notten, P.H.L. Basic information on batteries. In Battery Management Systems: Design by Modelling; Springer: Dordrecht, The Netherlands, 2002; pp. 31–53. [Google Scholar]
- Tang, M.H.-M. Side Reactions in Lithium-Ion Batteries. Ph.D. Dissertation, University of California, Berkeley, Berkeley, CA, USA, 2012. [Google Scholar]
- Reniers, J.M.; Mulder, G.; Howey, D.A. Review and Performance Comparison of Mechanical-Chemical Degradation Models for Lithium-Ion Batteries. J. Electrochem. Soc. 2019, 166, 3189–3200. [Google Scholar] [CrossRef]
- Zou, B.; Zhang, L.; Xue, X.; Tan, R.; Jiang, P.; Ma, B.; Song, Z.; Hua, W. A Review on the Fault and Defect Diagnosis of Lithium-Ion Battery for Electric Vehicles. Energies 2023, 16, 5507. [Google Scholar] [CrossRef]
- Lin, X.; Park, J.; Liu, L.; Lee, Y.; Sastry, A.M.; Lu, W. A Comprehensive Capacity Fade Model and Analysis for Li-Ion Batteries. J. Electrochem. Soc. 2013, 160, 1701–1710. [Google Scholar] [CrossRef]
- Waldmann, T.; Hogg, B.I.; Wohlfahrt-Mehrens, M. Li plating as unwanted side reaction in commercial Li-ion cells—A review. J. Power Sources 2018, 384, 107–124. [Google Scholar] [CrossRef]
- Schindler, S.; Bauer, M.; Petzl, M.; Danzer, M.A. Voltage relaxation and impedance spectroscopy as in-operando methods for the detection of lithium plating on graphitic anodes in commercial lithium-ion cells. J. Power Sources 2016, 304, 170–180. [Google Scholar] [CrossRef]
- Choi, N.-S.; Yeon, J.-T.; Lee, Y.-W.; Han, J.-G.; Lee, K.-T.; Kim, S.-S. Degradation of spinel lithium manganese oxides by low oxidation durability of LiPF6-based electrolyte at 60 °C. Solid State Ion. 2012, 219, 41–48. [Google Scholar] [CrossRef]
- Safari, M.; Morcrette, M.; Teyssot, A.; Delacourt, C. Multimodal Physics-Based Aging Model for Life Prediction of Li-Ion Batteries. J. Electrochem. Soc. 2009, 156, A145. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI Formation in Rechargeable Batteries: Capacity Fade, Accelerated Aging and Lifetime Prediction. J. Electrochem. Soc. 2013, 160, 243–250. [Google Scholar] [CrossRef]
- Yang, X.G.; Ge, S.; Liu, T.; Leng, Y.; Wang, C.Y. A look into the voltage plateau signal for detection and quantification of lithium plating in lithium-ion cells. J. Power Sources 2018, 395, 251–261. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Liao, C.; Wu, L.; Li, J.; Guo, Y. Effects of temperature on dynamic characteristics of li-ion batteries in electric vehicle applications. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar]
- Leuchter, J.; Bauer, P. Capacity of power-batteries versus temperature. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–8. [Google Scholar]
- Less, G.B.; Seo, J.H.; Han, S.; Sastry, A.M.; Zausch, J.; Latz, A.; Schmidt, S.; Wieser, C.; Kehrwald, D.; Fell, S. Micro-Scale Modeling of Li-Ion Batteries: Parameterization and Validation. J. Electrochem. Soc. 2012, 159, 697–704. [Google Scholar] [CrossRef]
- Summerfield, J.H.; Curtis, C.N. Modeling the Lithium Ion/Electrode Battery Interface Using Fick’s Second Law of Diffusion, the Laplace Transform, Charge Transfer Functions, and a [4, 4] Padé Approximant. Int. J. Electrochem. 2015, 2015, 496905. [Google Scholar] [CrossRef][Green Version]
- Kim, S.; Wee, J.; Peters, K.; Huang, H.Y.S. Multiphysics Coupling in Lithium-Ion Batteries with Reconstructed Porous Microstructures. J. Phys. Chem. C 2018, 122, 5280–5290. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Chaturvedi, N.A.; Klein, R.; Christensen, J.; Ahmed, J.; Kojic, A. Algorithms for Advanced Battery-Management Systems. IEEE Control Syst. 2010, 30, 49–68. [Google Scholar]
- Liu, K.; Gao, Y.; Zhu, C.; Li, K.; Fei, M.; Peng, C.; Zhang, X.; Han, Q.L. Electrochemical modeling and parameterization towards control-oriented management of lithium-ion batteries. Control Eng. Pract. 2022, 124, 105176. [Google Scholar] [CrossRef]
- Li, W.; Cao, D.; Jöst, D.; Ringbeck, F.; Kuipers, M.; Frie, F.; Sauer, D.U. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries. Appl. Energy 2020, 269, 115104. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Z.; Xie, C.; Vilathgamuwa, D.M. Physics-Based Model Predictive Control for Power Capability Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 2023, 19, 10763–10774. [Google Scholar] [CrossRef]
- Allam, A.; Onori, S. Online Capacity Estimation for Lithium-Ion Battery Cells via an Electrochemical Model-Based Adaptive Interconnected Observer. IEEE Trans. Control Syst. Technol. 2021, 29, 1636–1651. [Google Scholar] [CrossRef]
- Li, Y.; Karunathilake, D.; Vilathgamuwa, D.M.; Mishra, Y.; Farrell, T.W.; Choi, S.S.; Zou, C. Model Order Reduction Techniques for Physics-Based Lithium-Ion Battery Management: A Survey. IEEE Ind. Electron. Mag. 2022, 16, 36–51. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model With Electrolyte Dynamics. IEEE Trans. Control Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Bartlett, A.; Marcicki, J.; Onori, S.; Rizzoni, G.; Yang, X.G.; Miller, T. Electrochemical Model-Based State of Charge and Capacity Estimation for a Composite Electrode Lithium-Ion Battery. IEEE Trans. Control Syst. Technol. 2016, 24, 384–399. [Google Scholar] [CrossRef]
- Moura, S.J.; Chaturvedi, N.A.; Krstić, M. Adaptive Partial Differential Equation Observer for Battery State-of-Charge/State-of-Health Estimation Via an Electrochemical Model. J. Dyn. Syst. Meas. Control 2014, 136, 011015. [Google Scholar] [CrossRef]
- LithiumWerks Batteries. LithiumWerks ANR26650M1-B, 3.3 Volt, 2.5 Ah Lithium Iron Phosphate (LiFePO4) Battery; LithiumWerks Batteries: Farmington Hills, MI, USA, 2023. [Google Scholar]
- Wett, C.; Ganuza, C.; Ayerbe, E.; Turan, B.; Schwunk, S. Method of Lines for flexible coupling of the Single Particle Model for Lithium-Ion Batteries demonstrated by thermal modelling. J. Energy Storage 2023, 68, 107459. [Google Scholar] [CrossRef]
- Guo, M.; Sikha, G.; White, R.E. Single-Particle Model for a Lithium-Ion Cell: Thermal Behavior. J. Electrochem. Soc. 2011, 158, A122. [Google Scholar] [CrossRef]
- Basu, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Sohn, D.K.; Yeo, T. Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system. Appl. Energy 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Wang, D.; Gao, Y.; Zhang, X.; Dong, T.; Zhu, C. A novel pseudo two-dimensional model for NCM Liion battery based on electrochemical-thermal coupling analysis. In Proceedings of the 2020 3rd International Conference on Electron Device and Mechanical Engineering (ICEDME), Suzhou, China, 1–3 May 2020; pp. 110–116. [Google Scholar]
- Richardson, G.; Korotkin, I. Heat generation and a conservation law for chemical energy in Li-ion batteries. Electrochim. Acta 2021, 392, 138909. [Google Scholar] [CrossRef]
- Versypt, A.N.F.; Braatz, R.D. Analysis of Finite Difference Discretization Schemes for Diffusion in Spheres with Variable Diffusivity. Comput. Chem. Eng. 2014, 71, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Rapp, B.E. Chapter 31—Finite Volume Method. In Microfluidics: Modelling, Mechanics and Mathematics; Rapp, B.E., Ed.; Micro and Nano Technologies; Elsevier: Oxford, UK, 2017; pp. 633–654. [Google Scholar]
- Cai, L.; White, R.E. Reduction of Model Order Based on Proper Orthogonal Decomposition for Lithium-Ion Battery Simulations. J. Electrochem. Soc. 2009, 156, A154. [Google Scholar] [CrossRef]
- Dao, T.S.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- Guo, M.; White, R.E. An approximate solution for solid-phase diffusion in a spherical particle in physics-based Li-ion cell models. J. Power Sources 2012, 198, 322–328. [Google Scholar] [CrossRef]
- Smith, K.A.; Rahn, C.D.; Wang, C.Y. Model Order Reduction of 1D Diffusion Systems Via Residue Grouping. J. Dyn. Syst. Meas. Control 2008, 130, 011012. [Google Scholar] [CrossRef]
- Tran, N.T.; Vilathgamuwa, M.; Farrell, T.; Choi, S.S.; Li, Y.; Teague, J. A Padé Approximate Model of Lithium Ion Batteries. J. Electrochem. Soc. 2018, 165, 1409–1421. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical Model Based Observer Design for a Lithium-Ion Battery. IEEE Trans. Control Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Tran, M.K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- López-Villanueva, J.A.; Rodríguez-Iturriaga, P.; Parrilla, L.; Rodríguez-Bolívar, S. A compact model of the ZARC for circuit simulators in the frequency and time domains. AEU—Int. J. Electron. Commun. 2022, 153, 154293. [Google Scholar] [CrossRef]
- Bensaad, Y.; Friedrichs, F.; Baumhöfer, T.; Eswein, M.; Bähr, J.; Fill, A.; Birke, K.P. Embedded real-time fractional-order equivalent circuit model for internal resistance estimation of lithium-ion cells. J. Energy Storage 2023, 67, 107516. [Google Scholar] [CrossRef]
- Gao, Y.; Ji, W.; Zhao, X. SOC Estimation of E-Cell Combining BP Neural Network and EKF Algorithm. Processes 2022, 10, 1721. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, J.; Zhou, Y.; Pei, H. State of Charge Estimation of Lithium Battery Based on Integrated Kalman Filter Framework and Machine Learning Algorithm. Energies 2023, 16, 2155. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Zhang, Q.; Liao, W.; Rao, Z. State of charge estimation of Li-ion batteries based on deep learning methods and particle-swarm-optimized Kalman filter. J. Energy Storage 2023, 64, 107191. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine Learning Applied to Electrified Vehicle Battery State of Charge and State of Health Estimation: State-of-the-Art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Sesidhar, D.V.S.R.; Badachi, C.; Green, R.C., II. A review on data-driven SOC estimation with Li-Ion batteries: Implementation methods & future aspirations. J. Energy Storage 2023, 72, 108420. [Google Scholar]
- Selvaraj, V.; Vairavasundaram, I. A comprehensive review of state of charge estimation in lithium-ion batteries used in electric vehicles. J. Energy Storage 2023, 72, 108777. [Google Scholar] [CrossRef]
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.M.; Ker, P.J.; Muttaqi, K.M. State-of-Charge Estimation of Li-Ion Battery in Electric Vehicles: A Deep Neural Network Approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, Y.; Han, X. Research on estimation model of the battery state of charge in a hybrid electric vehicle based on the classification and regression tree. Math. Comput. Model. Dyn. Syst. 2019, 25, 376–396. [Google Scholar] [CrossRef]
- Qu, J.; Liu, F.; Ma, Y.; Fan, J. A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]
- Zhou, D.; Li, Z.; Zhu, J.; Zhang, H.; Hou, L. State of Health Monitoring and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Temporal Convolutional Network. IEEE Access 2020, 8, 53307–53320. [Google Scholar] [CrossRef]
- Ungurean, L.; Micea, M.V.; Cârstoiu, G. Online state of health prediction method for lithium–ion batteries, based on gated recurrent unit neural networks. Int. J. Energy Res. 2020, 44, 6767–6777. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer Learning With Long Short-Term Memory Network for State-of-Health Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2020, 67, 8723–8731. [Google Scholar] [CrossRef]
- You, G.W.; Park, S.; Oh, D. Diagnosis of Electric Vehicle Batteries Using Recurrent Neural Networks. IEEE Trans. Ind. Electron. 2017, 64, 4885–4893. [Google Scholar] [CrossRef]
- Choi, Y.; Ryu, S.; Park, K.; Kim, H. Machine Learning-Based Lithium-Ion Battery Capacity Estimation Exploiting Multi-Channel Charging Profiles. IEEE Access 2019, 7, 75143–75152. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Li, Y.; Tao, J. CNN and transfer learning based online SOH estimation for lithium-ion battery. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 5489–5494. [Google Scholar]
- Kaur, K.; Garg, A.; Cui, X.; Singh, S.; Panigrahi, B.K. Deep learning networks for capacity estimation for monitoring SOH of Li–ion batteries for electric vehicles. Int. J. Energy Res. 2021, 45, 3113–3128. [Google Scholar] [CrossRef]
- Strange, C.; dos Reis, G. Prediction of future capacity and internal resistance of Li-ion cells from one cycle of input data. Energy AI 2021, 5, 100097. [Google Scholar] [CrossRef]
- Hsu, C.W.; Xiong, R.; Chen, N.Y.; Li, J.; Tsou, N.T. Deep neural network battery life and voltage prediction by using data of one cycle only. Appl. Energy 2022, 306, 118134. [Google Scholar] [CrossRef]
- Li, W.; Zhang, H.; van Vlijmen, B.; Dechent, P.; Sauer, D.U. Forecasting battery capacity and power degradation with multi-task learning. Energy Storage Mater. 2022, 53, 453–466. [Google Scholar] [CrossRef]
- Pattipati, B.; Balasingam, B.; Avvari, G.V.; Pattipati, K.R.; Bar-Shalom, Y. Open circuit voltage characterization of lithium-ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Matsushima, T. Deterioration estimation of lithium-ion cells in direct current power supply systems and characteristics of 400-Ah lithium-ion cells. J. Power Sources 2009, 189, 847–854. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; van Mierlo, J.; van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Wu, J.; Deng, Z.; Lin, M.; Mao, S.; Stroe, D.I. A comprehensive overview and comparison of parameter benchmark methods for lithium-ion battery application. J. Energy Storage 2023, 71, 108197. [Google Scholar] [CrossRef]
- Xu, R.; Wang, D.; Yan, G.; Duan, J.; Guo, H.; Wang, J.; Wang, Z.; Li, X.; Li, G. Direct current internal resistance decomposition model for accurate parameters acquisition and application in commercial high voltage LiCoO2 battery. J. Energy Storage 2023, 70, 108100. [Google Scholar] [CrossRef]
- Hu, Z.; Ren, G.; Zhang, J.; Si, Y.; Duan, Y. A parameter identification and state of charge estimation method of lithium-ion battery considering temperature bias. J. Energy Storage 2023, 68, 107650. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, X. An improved parameter identification method considering multi-timescale characteristics of lithium-ion batteries. J. Energy Storage 2023, 59, 106462. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An enhanced particle filter technology for battery system state estimation and RUL prediction. Measurement 2022, 191, 110817. [Google Scholar] [CrossRef]
- Gao, M.; Liu, Y.; He, Z. Battery state of charge online estimation based on particle filter. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; Volume 4, pp. 2233–2236. [Google Scholar]
- Bi, J.; Zhang, T.; Yu, H.; Kang, Y. State-of-health estimation of lithium-ion battery packs in electric vehicles based on genetic resampling particle filter. Appl. Energy 2016, 182, 558–568. [Google Scholar] [CrossRef]
- Samadi, M.; Alavi, S.M.; Saif, M. An electrochemical model-based particle filter approach for Lithium-ion battery estimation. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3074–3079. [Google Scholar]
- Ye, M.; Guo, H.; Cao, B. A model-based adaptive state of charge estimator for a lithium-ion battery using an improved adaptive particle filter. Appl. Energy 2017, 190, 740–748. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An Enhanced Mutated Particle Filter Technique for System State Estimation and Battery Life Prediction. IEEE Trans. Instrum. Meas. 2019, 68, 923–935. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Courier Corporation: Mineola, NY, USA, 2007. [Google Scholar]
- Zhang, D.; Couto, L.D.; Gill, P.; Benjamin, S.; Zeng, W.; Moura, S.J. Interval Observer for SOC Estimation in Parallel-Connected Lithium-ion Batteries. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 1149–1154. [Google Scholar]
- Zhang, D.; Couto, L.D.; Gill, P.S.; Benjamin, S.; Zeng, W.; Moura, S.J. Thermal-Enhanced Adaptive Interval Estimation in Battery Packs With Heterogeneous Cells. IEEE Trans. Control Syst. Technol. 2022, 30, 1102–1115. [Google Scholar] [CrossRef]
- Hildebrandt, E.; Kersten, J.; Rauh, A.; Aschemann, H. Robust Interval Observer Design for Fractional-Order Models with Applications to State Estimation of Batteries. IFAC-Pap. 2020, 53, 3683–3688. [Google Scholar] [CrossRef]
- Gouzé, J.; Rapaport, A.; Hadj-Sadok, M. Interval observers for uncertain biological systems. Ecol. Model. 2000, 133, 45–56. [Google Scholar] [CrossRef]
- Lin, H.; Zhai, G.; Antsaklis, P.J. Set-valued observer design for a class of uncertain linear systems with persistent disturbance and measurement noise. Int. J. Control 2003, 76, 1644–1653. [Google Scholar] [CrossRef]
- Zimmer, G. State observation by on-line minimization. Int. J. Control 1994, 60, 595–606. [Google Scholar] [CrossRef]
- Alamir, M. Nonlinear Moving Horizon Observers: Theory and Real-Time Implementation. In Nonlinear Observers and Applications; Springer: Berlin/Heidelberg, Germany, 2007; pp. 139–179. [Google Scholar]
- Schiller, J.D.; Muntwiler, S.; Köhler, J.; Zeilinger, M.N.; Müller, M.A. A Lyapunov function for robust stability of moving horizon estimation. IEEE Trans. Autom. Control 2023, 1–16. [Google Scholar] [CrossRef]
- Krener, A.J. Minimum Energy Estimation and Moving Horizon Estimation. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 4952–4957. [Google Scholar]
- Shen, J.; Wang, Q.; Zhao, G.; Ma, Z.; He, Y. A joint moving horizon strategy for state-of-charge estimation of lithium-ion batteries under combined measurement uncertainty. J. Energy Storage 2021, 44, 103316. [Google Scholar] [CrossRef]
- Morabito, B.; Klein, R.; Findeisen, R. Real time feasibility and performance of moving horizon estimation for Li-ion batteries based on first principles electrochemical models. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 3457–3462. [Google Scholar]
- Shen, J.N.; Shen, J.J.; He, Y.J.; Ma, Z.F. Accurate State of Charge Estimation With Model Mismatch for Li-Ion Batteries: A Joint Moving Horizon Estimation Approach. IEEE Trans. Power Electron. 2019, 34, 4329–4342. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.; Chen, S.; Ren, H.; Gao, Z. A combined robust approach based on auto-regressive long short-term memory network and moving horizon estimation for state-of-charge estimation of lithium-ion batteries. Int. J. Energy Res. 2021, 45, 12838–12853. [Google Scholar] [CrossRef]
- Shen, J.N.; He, Y.J.; Ma, Z.F.; Luo, H.B.; Zhang, Z.F. Online state of charge estimation of lithium-ion batteries: A moving horizon estimation approach. Chem. Eng. Sci. 2016, 154, 42–53. [Google Scholar] [CrossRef]
- Hu, X.; Cao, D.; Egardt, B. Condition Monitoring in Advanced Battery Management Systems: Moving Horizon Estimation Using a Reduced Electrochemical Model. IEEE/ASME Trans. Mechatron. 2018, 23, 167–178. [Google Scholar] [CrossRef]
- Bernard, P.; Andrieu, V.; Astolfi, D. Observer design for continuous-time dynamical systems. Annu. Rev. Control 2022, 53, 224–248. [Google Scholar] [CrossRef]
- Bernard, P. Observer Design for Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 2019; Volume 479. [Google Scholar]
- Besançon, G. Nonlinear Observers and Applications; Springer: Berlin/Heidelberg, Germany, 2007; Volume 363. [Google Scholar]
- Cecilia, A. Nonlinear Observer Design. In Advances in Nonlinear Observer Design for State and Parameter Estimation in Energy Systems; Springer Nature: Cham, Switzerland, 2023; pp. 17–54. [Google Scholar]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Lee, J.; Nam, O.; Cho, B. Li-ion battery SOC estimation method based on the reduced order extended Kalman filtering. J. Power Sources 2007, 174, 9–15. [Google Scholar] [CrossRef]
- Yuan, S.; Wu, H.; Yin, C. State of Charge Estimation Using the Extended Kalman Filter for Battery Management Systems Based on the ARX Battery Model. Energies 2013, 6, 444–470. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Improved extended Kalman filter for state of charge estimation of battery pack. J. Power Sources 2014, 255, 368–376. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N.E.B. Improved OCV Model of a Li-Ion NMC Battery for Online SOC Estimation Using the Extended Kalman Filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge Estimation of Batteries With Adaptive Extended Kalman Filter by Experiment Approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Liu, C.z.; Zhu, Q.; Li, L.; Liu, W.q.; Wang, L.Y.; Xiong, N.; Wang, X.y. A State of Charge Estimation Method Based on H∞ Observer for Switched Systems of Lithium-Ion Nickel–Manganese–Cobalt Batteries. IEEE Trans. Ind. Electron. 2017, 64, 8128–8137. [Google Scholar] [CrossRef]
- Aung, H.; Low, K.S. Temperature dependent state-of-charge estimation of lithium ion battery using dual spherical unscented Kalman filter. IET Power Electron. 2015, 8, 2026–2033. [Google Scholar] [CrossRef]
- Gholizade-Narm, H.; Charkhgard, M. Lithium-ion battery state of charge estimation based on square-root unscented Kalman filter. IET Power Electron. 2013, 6, 1833–1841. [Google Scholar] [CrossRef]
- Aung, H.; Soon Low, K.; Ting Goh, S. State-of-Charge Estimation of Lithium-Ion Battery Using Square Root Spherical Unscented Kalman Filter (Sqrt-UKFST) in Nanosatellite. IEEE Trans. Power Electron. 2015, 30, 4774–4783. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, P.; Yang, Y.; Xie, C.; Shi, Y. SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm. Energies 2019, 12, 3122. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, G.; Fang, L. Battery state estimation using Unscented Kalman Filter. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1863–1868. [Google Scholar]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Du, J.; Liu, Z.; Wang, Y. State of charge estimation for Li-ion battery based on model from extreme learning machine. Control Eng. Pract. 2014, 26, 11–19. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of Charge Estimation of Battery Energy Storage Systems Based on Adaptive Unscented Kalman Filter With a Noise Statistics Estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Li, J.; Klee Barillas, J.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Bi, Y.; Choe, S.Y. An adaptive sigma-point Kalman filter with state equality constraints for online state-of-charge estimation of a Li(NiMnCo)O2/Carbon battery using a reduced-order electrochemical model. Appl. Energy 2020, 258, 113925. [Google Scholar] [CrossRef]
- He, L.; Wang, Y.; Wei, Y.; Wang, M.; Hu, X.; Shi, Q. An adaptive central difference Kalman filter approach for state of charge estimation by fractional order model of lithium-ion battery. Energy 2022, 244, 122627. [Google Scholar] [CrossRef]
- Sangwan, V.; Kumar, R.; Rathore, A.K. State-of-charge estimation for li-ion battery using extended Kalman filter (EKF) and central difference Kalman filter (CDKF). In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–6. [Google Scholar]
- Xuan, D.J.; Shi, Z.; Chen, J.; Zhang, C.; Wang, Y.X. Real-time estimation of state-of-charge in lithium-ion batteries using improved central difference transform method. J. Clean. Prod. 2020, 252, 119787. [Google Scholar] [CrossRef]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Linghu, J.; Kang, L.; Liu, M.; Luo, X.; Feng, Y.; Lu, C. Estimation for state-of-charge of lithium-ion battery based on an adaptive high-degree cubature Kalman filter. Energy 2019, 189, 116204. [Google Scholar] [CrossRef]
- Liu, Z.; Dang, X.; Jing, B.; Ji, J. A novel model-based state of charge estimation for lithium-ion battery using adaptive robust iterative cubature Kalman filter. Electr. Power Syst. Res. 2019, 177, 105951. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Kim, D.; Goh, T.; Park, M.; Kim, S.W. Fuzzy Sliding Mode Observer with Grey Prediction for the Estimation of the State-of-Charge of a Lithium-Ion Battery. Energies 2015, 8, 12409–12428. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Dai, M.; Cao, Z.; Jin, J.; Kapoor, A. Robust adaptive sliding-mode observer using RBF neural network for lithium-ion battery state of charge estimation in electric vehicles. IEEE Trans. Veh. Technol. 2015, 65, 1936–1947. [Google Scholar] [CrossRef]
- Huangfu, Y.; Xu, J.; Zhao, D.; Liu, Y.; Gao, F. A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer. Energies 2018, 11, 1211. [Google Scholar] [CrossRef]
- Kim, I.S. The novel state of charge estimation method for lithium battery using sliding mode observer. J. Power Sources 2006, 163, 584–590. [Google Scholar] [CrossRef]
- Kim, I.S. A Technique for Estimating the State of Health of Lithium Batteries Through a Dual-Sliding-Mode Observer. IEEE Trans. Power Electron. 2010, 25, 1013–1022. [Google Scholar]
- Chen, Q.; Jiang, J.; Ruan, H.; Zhang, C. Simply designed and universal sliding mode observer for the SOC estimation of lithium-ion batteries. IET Power Electron. 2017, 10, 697–705. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. Adaptive gain sliding mode observer for state of charge estimation based on combined battery equivalent circuit model. Comput. Chem. Eng. 2014, 64, 114–123. [Google Scholar] [CrossRef]
- Anderson, J.L.; Moré, J.J.; Puleston, P.F.; Roda, V.; Costa-Castelló, R. Control Super-Twisting con adaptación basada en cruce por cero. Análisis de estabilidad y validación. RIAI—Rev. Iberoam. Autom. Inform. Ind. 2022, 20, 104–114. [Google Scholar] [CrossRef]
- Carnevale, D.; Possieri, C.; Sassano, M. State-of-charge estimation for lead–acid batteries via embeddings and observers. Control Eng. Pract. 2019, 85, 132–137. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Zhang, F. A high-gain adaptive observer for detecting Li-ion battery terminal voltage collapse. Automatica 2014, 50, 896–902. [Google Scholar] [CrossRef]
- Cecilia, A.; Serra, M.; Costa-Castelló, R. Nonlinear adaptive observation of the liquid water saturation in polymer electrolyte membrane fuel cells. J. Power Sources 2021, 492, 229641. [Google Scholar] [CrossRef]
- Cecilia, A.; Costa-Castelló, R. Estimation of the liquid water saturation in PEM fuel cells: A low-power peaking-free dead-zone observer approach. ISA Trans. 2023, 140, 368–384. [Google Scholar] [CrossRef]
- Dey, S.; Ayalew, B.; Pisu, P. Nonlinear adaptive observer for a lithium-ion battery cell based on coupled electrochemical–thermal model. J. Dyn. Syst. Meas. Control 2015, 137, 111005. [Google Scholar] [CrossRef]
- Jenkins, B.; Krupadanam, A.; Annaswamy, A.M. Fast Adaptive Observers for Battery Management Systems. IEEE Trans. Control Syst. Technol. 2020, 28, 776–789. [Google Scholar] [CrossRef]
- Chiang, Y.H.; Sean, W.Y. Dynamical estimation of State-of-Health of batteries by using adaptive observer. In Proceedings of the 2009 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 19–20 December 2009; Volume 1, pp. 110–115. [Google Scholar]
- Limoge, D.W.; Annaswamy, A.M. An Adaptive Observer Design for Real-Time Parameter Estimation in Lithium-Ion Batteries. IEEE Trans. Control Syst. Technol. 2020, 28, 505–520. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Lyapunov-based state of charge diagnosis and health prognosis for lithium-ion batteries. J. Power Sources 2018, 397, 352–360. [Google Scholar] [CrossRef]
- Zhang, D.; Dey, S.; Couto, L.D.; Moura, S.J. Battery Adaptive Observer for a Single-Particle Model With Intercalation-Induced Stress. IEEE Trans. Control Syst. Technol. 2020, 28, 1363–1377. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Blondel, P.; Postoyan, R.; Raël, S.; Benjamin, S.; Desprez, P. Nonlinear Circle-Criterion Observer Design for an Electrochemical Battery Model. IEEE Trans. Control Syst. Technol. 2019, 27, 889–897. [Google Scholar] [CrossRef]
- Movahedi, H.; Figueroa-Santos, M.A.; Siegel, J.B.; Stefanopoulou, A.G.; Rajamani, R. Hybrid nonlinear observer for battery state-of-charge estimation using nonmonotonic force measurements. Adv. Control Appl. Eng. 2020, 2, e38. [Google Scholar] [CrossRef]
- Ortega, R.; Bobtsov, A.; Nikolaev, N.; Schiffer, J.; Dochain, D. Generalized parameter estimation-based observers: Application to power systems and chemical–biological reactors. Automatica 2021, 129, 109635. [Google Scholar] [CrossRef]
- Brivadis, L.; Andrieu, V.; Bernard, P.; Serres, U. Further remarks on KKL observers. Syst. Control Lett. 2023, 172, 105429. [Google Scholar] [CrossRef]
- Peralez, J.; Nadri, M. Deep Learning-based Luenberger observer design for discrete-time nonlinear systems. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021; pp. 4370–4375. [Google Scholar]
- Lejarza, F.; Baldea, M. Data-driven discovery of the governing equations of dynamical systems via moving horizon optimization. Sci. Rep. 2022, 12, 11836. [Google Scholar] [CrossRef]
- Petri, E.; Reynaudo, T.; Postoyan, R.; Astolfi, D.; Nešić, D.; Raël, S. State estimation of an electrochemical lithium-ion battery model: Improved observer performance by hybrid redesign. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar]
- Astolfi, D.; Alessandri, A.; Zaccarian, L. Stubborn and Dead-Zone Redesign for Nonlinear Observers and Filters. IEEE Trans. Autom. Control 2021, 66, 667–682. [Google Scholar] [CrossRef]
- Samad, T.; Bauer, M.; Bortoff, S.; Di Cairano, S.; Fagiano, L.; Odgaard, P.F.; Rhinehart, R.R.; Sánchez-Peña, R.; Serbezov, A.; Ankersen, F.; et al. Industry engagement with control research: Perspective and messages. Annu. Rev. Control 2020, 49, 1–14. [Google Scholar] [CrossRef]



| Region | Overvoltage | Undervoltage | High Currents |
|---|---|---|---|
| Negative electrode | Lithium plating | Solid electrolyte interphase | Particle fracture |
| Positive electrode | Oxidation of electrolyte | Solid electrolyte interphase | - |
| Chemistry Family | Capacity | Specific Power | Safety | Performance | Lifespan | Cost |
|---|---|---|---|---|---|---|
| LCO | 4 | 2 | 2 | 3 | 2 | 3 |
| LMO | 3 | 3 | 3 | 2 | 2 | 3 |
| LFP | 2 | 4 | 4 | 3 | 4 | 3 |
| NMC | 4 | 3 | 3 | 3 | 3 | 3 |
| NCA | 4 | 3 | 2 | 3 | 3 | 2 |
| LTO | 2 | 3 | 4 | 4 | 4 | 1 |
| Symbol | Definition | Unit |
|---|---|---|
| Parameter/variable related to solid | - | |
| Parameter/variable related to electrolyte | - | |
| Concentration of x | ||
| Diffusion of x | ||
| r | Radial coordinate | m |
| Radius of particle x | m | |
| F | Faraday constant | |
| Electroactive surface area of x | ||
| A | Cell cross-sectional area | |
| L | Thickness | m |
| Porosity | - | |
| Volume fraction of the solid electrode material in the porous electrode | - | |
| j | Molar flux | |
| Transference number | - | |
| Current density | ||
| I | Current | A |
| Transport coefficient | - | |
| Exchange current density | ||
| Effective electrolyte conductivity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martí-Florences, M.; Cecilia, A.; Costa-Castelló, R. Modelling and Estimation in Lithium-Ion Batteries: A Literature Review. Energies 2023, 16, 6846. https://doi.org/10.3390/en16196846
Martí-Florences M, Cecilia A, Costa-Castelló R. Modelling and Estimation in Lithium-Ion Batteries: A Literature Review. Energies. 2023; 16(19):6846. https://doi.org/10.3390/en16196846
Chicago/Turabian StyleMartí-Florences, Miquel, Andreu Cecilia, and Ramon Costa-Castelló. 2023. "Modelling and Estimation in Lithium-Ion Batteries: A Literature Review" Energies 16, no. 19: 6846. https://doi.org/10.3390/en16196846
APA StyleMartí-Florences, M., Cecilia, A., & Costa-Castelló, R. (2023). Modelling and Estimation in Lithium-Ion Batteries: A Literature Review. Energies, 16(19), 6846. https://doi.org/10.3390/en16196846






