Integrated Multi-Criteria Planning for Resilient Renewable Energy-Based Microgrid Considering Advanced Demand Response and Uncertainty
Abstract
:1. Introduction
- A comprehensive and integrated method for planning community microgrids based on VREs is proposed and examined. This approach incorporates DRPs strategies, precise forecasting, and combined sizing and operational planning, all under uncertain conditions.
- The techno-economic advantages of implementing a combined DRP approach, integrating DRP strategies based on shortage/surplus adaptive pricing (SSAP) alongside variable peak critical peak pricing (VP-CPP) DRPs, have been proposed and thoroughly investigated. These are compared with a combination of time of use (TOU) and VP-CPP strategies. These two ensemble DRP approaches have been demonstrated to provide a more robust and dynamic response, significantly enhancing the resilience and reliability of microgrids under severe conditions, such as extreme weather events, compared to traditional DRP strategies.
- To ascertain the role of accurate forecasting in conjunction with SSAP VP-CPP DRP strategies, the LSTM approach has been investigated for VRE generation and load demand forecasting to enable optimal preparation and reduce the need for load curtailment or generation curtailment, thereby bolstering the resilience of microgrids against sudden power generation fluctuations.
- To address the inherent variability and resulting uncertainty introduced by VREs and load variation, which could potentially undermine the reliability and operability of isolated community microgrids, Monte Carlo simulations have been employed to generate uncertainty scenarios. This ensures the robustness of the system against extreme weather fluctuations.
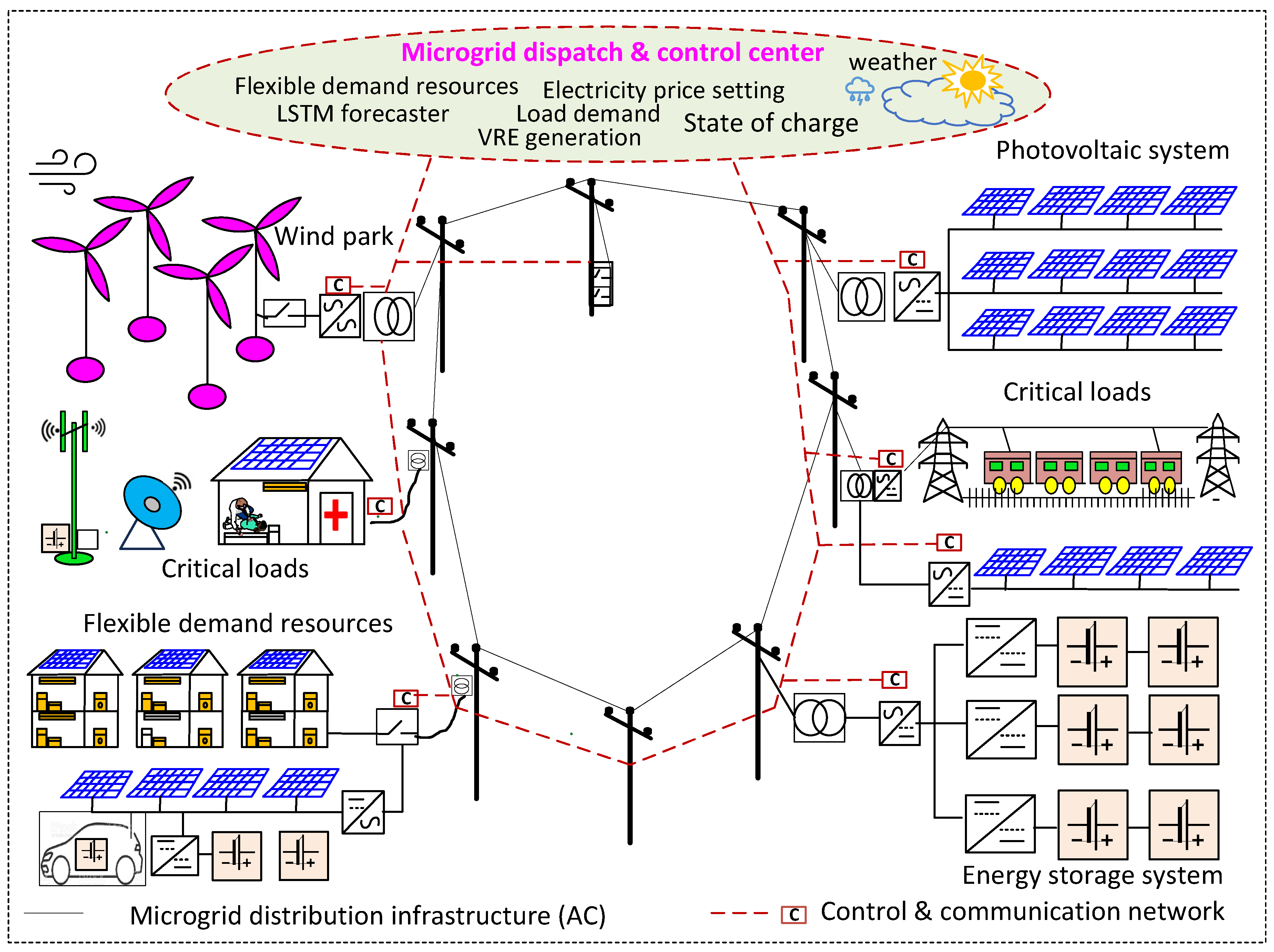
2. System Configuration and Mathematical Modelling
2.1. Wind Turbine ()
2.2. Photovoltaic ()
2.3. Battery Energy Storage System ()
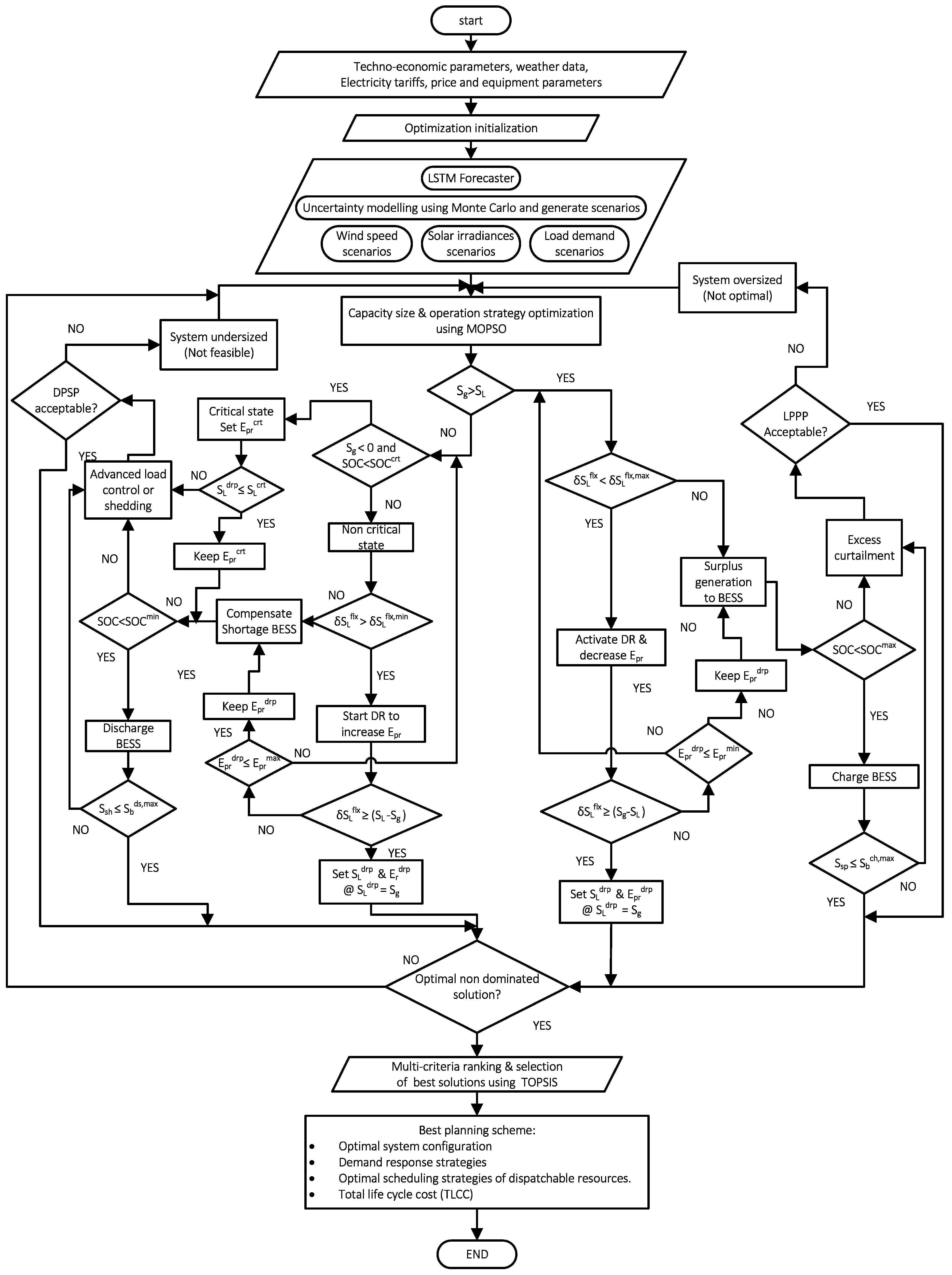
3. Proposed Integrated Planning Framework
3.1. Demand Response Programs, Load Modeling Concept, and Flexible Demand Resources
3.1.1. Flexible Demand Resource Modeling and Economic Load Model
3.1.2. Price Elasticity of Demand
3.2. Combined Time-of-Use and Variable Peak Critical Peak Pricing (DRP)
3.3. Shortage/Suplus-Based Adaptive Pricing and Variable Peak Critical Peak Pricing DRP
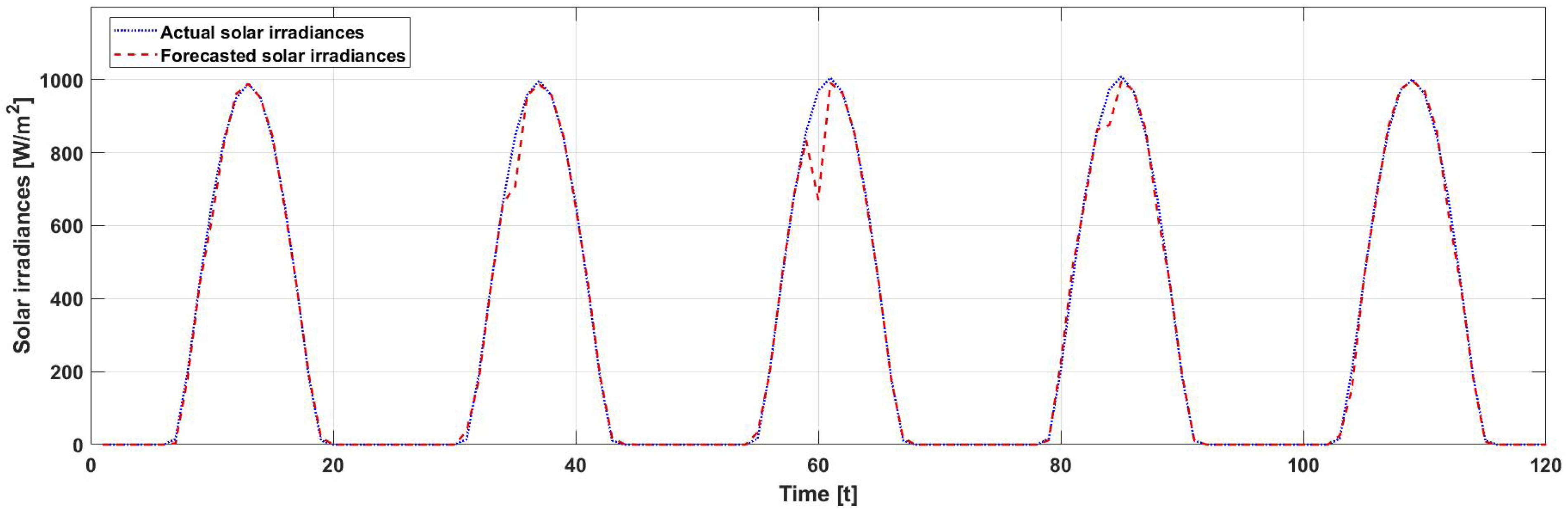
3.4. Point Forecasting Using LSTM and Uncertainty Modeling Using Monte Carlo Simulations
3.4.1. LSTM-Based Point Forecasting
3.4.2. Uncertainty Modeling with Monte Carlo
3.5. MOPSO Algorithm and TOPSIS Ranking Technique
3.5.1. Multi-Objective Particle Swarm Optimization
3.5.2. Technique for Order Preference by Similarity to Ideal Solution
4. Multi-Objective Optimization Problems Formulation and Simulation Setup
4.1. Objective Functions
- Objective 1—Total Life-Cycle Cost (TLCC) minimization (Economic criteria): The first objective function is formulated as a total life-cycle cost () minimization problem, as elaborated in Equation (26), which aims to optimize the net present value () of all costs associated with the system components incurred throughout the system’s lifetime. The is composed of the investment costs (), annual operation and maintenance costs (), replacement costs (), and salvage value ().where in Equation (26), z is used as an index to identify each specific component within the system. The decision variables, denoted as , signify the most efficient capacities for the individual system components, namely PV (photovoltaic), ESS (energy storage system), and WT (wind turbine). The project lifetime and the yearly time step are denoted as N and n, respectively. The decision variables are the capacities of the WT, denoted as ; the photovoltaic panels (PV), denoted as ; and the BESS, denoted as ().
- Objective 2—Deficiency of power supply probability (Reliability criteria): DPSP is the ratio of the total curtailed load demand (the unserved energy demands) () to the total load demand over an entire operation planning period (T).
- Objective 3—Loss of Produced Power Probability (LPPP): LPPP is the proportion of total curtailed power (wasted/unused) from VREs () to the total power that all the VRE sources could potentially generate () during the entire operation period (T). LPPP is a metric that signifies the likelihood of non-utilization of available variable renewable energy (VRE) due to factors such as BESS restrictions, demand–supply imbalances, or operational constraints [42].A high LPPP indicates a substantial waste of potential renewable energy, signaling suboptimality in the power system’s operation and design.
4.2. Constraints
- Demand-generation power balance constraints: At any given time (t), the combined power from VREs and the BESS should meet the load demand, regardless of the DRP or uncertainty considerations:Cases 1 through 3 are deterministic, while Cases 4 through 6 incorporate load and VREs uncertainties.
- BESS constraints:Equation (30) represents the upper bounds for both the discharging () and charging power () of the BESS, which are determined by the C-Rate of the BESS, which is the rate at which the BESS is being charged or discharged relative to its total capacity.
- FDR constraint:where () and () correspond to the minimum and maximum allowable capacities for an FDR, respectively, at any given time (t).
- Set electricity price limits:where () and () represent the maximum and minimum electricity price limits, respectively, at any given time (t).
- VREs power output limits:
4.3. Optimization Parameters, Case Study, and Simulation Cases
4.3.1. Techno-Economic Parameter and Case Study
4.3.2. Simulation Cases
- Case 1—Deterministic-based Planning (base case): This case focuses on capacity sizing and operation planning without considering DRP and forecasting. A flat reference pricing scheme is adopted in this case.
- Case 2—Deterministic-based planning considering TOU-VP-CPP DRP: This case integrates the time-of-use (TOU) with variable peak critical pricing (TOU-VP-CPP DRP). In this case, a TOU pricing model is merged with a VP-CPP DRP overlay for exceptional events. During a normal state, the load profile is categorized into three pricing periods: peak demand from 7 p.m. to 11 p.m. at 150% of the flat rate, off-peak from 8 a.m. to 7 p.m. at the reference price, and low peak at 50% of the flat rate. During an extreme event or critical microgrid state, the pricing is set to 200% of the reference price.
- Case 3—Deterministic-based planning considering SSAP DRP: A shortage/surplus-based adaptive pricing (SSAP) DRP is introduced. The pricing setup is dynamic, with the maximum and minimum price limits set to 150% and 50% of the reference price, respectively, during the normal microgrid state. During extreme events, the price is set to an extreme rate of 200% of the reference price.
- Case 4—Stochastic-based planning considering uncertainty: This case accounts for the uncertainty in VREs and the load demand using MCSs without incorporating any DRPs or forecasting in the operation strategy. The pricing scheme is similar to that of Case 1.
- Case 5—Stochastic-based planning considering uncertainty, TOU DRP, and LSTM forecasting: This case employs stochastic optimization with MCSs to account for the uncertainty in VREs and the load demand. It optimizes operation planning using time-of-use variable peak critical peak pricing (TOU-VP-CPP DRP). The pricing structure is similar to that of Case 2.
- Case 6—Stochastic planning considering uncertainty, LSTM forecasting, and SSAP DRP: The system incorporates SSAP DRP and employs forecasting for VREs and the load demand to devise a flexible and responsive microgrid system. While the pricing scheme is similar to that of Case 3, electricity prices for the upcoming hour are announced one hour in advance based on the forecasted power imbalances in the system.
4.3.3. Demand Response Structure and Flexible Demand Capacity
5. Results, Analysis, and Discussions
5.1. LSTM-Based Point Forecasts for Wind Speed, Solar Irradiances, and Load Demand
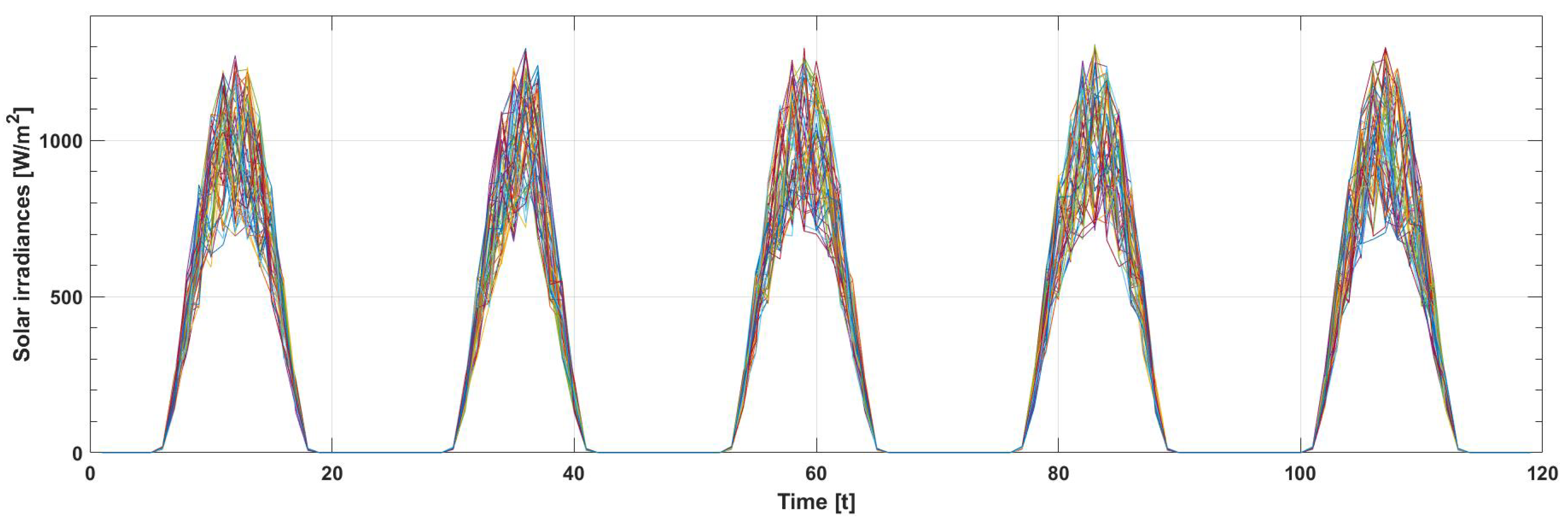
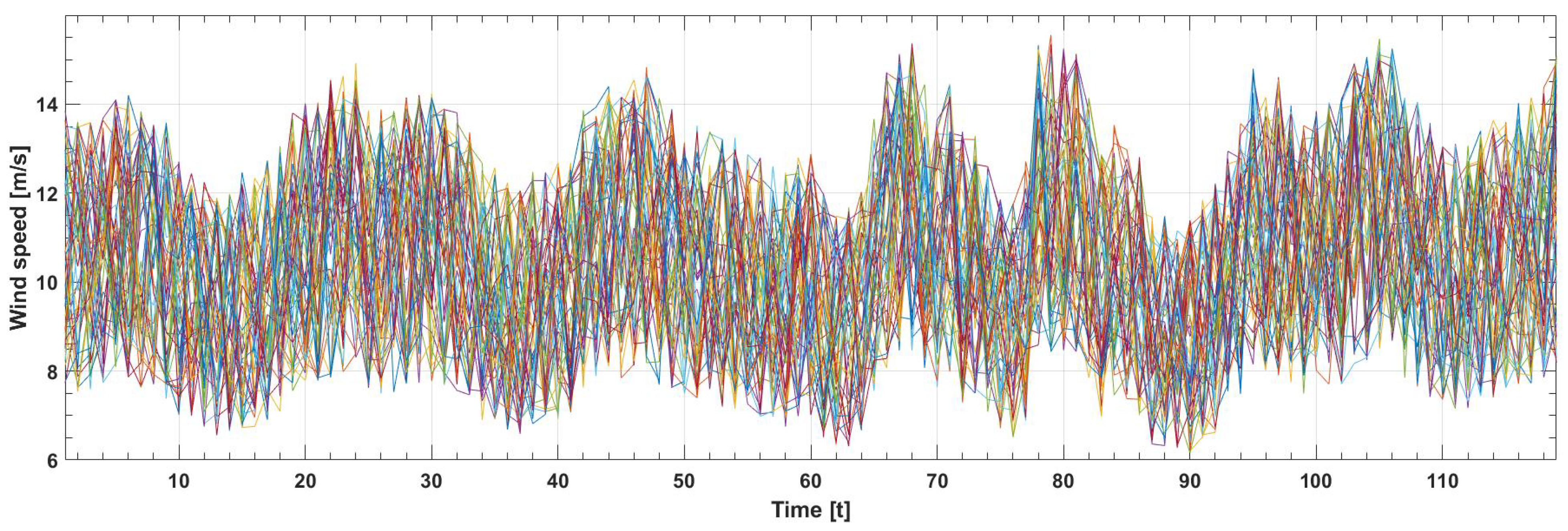
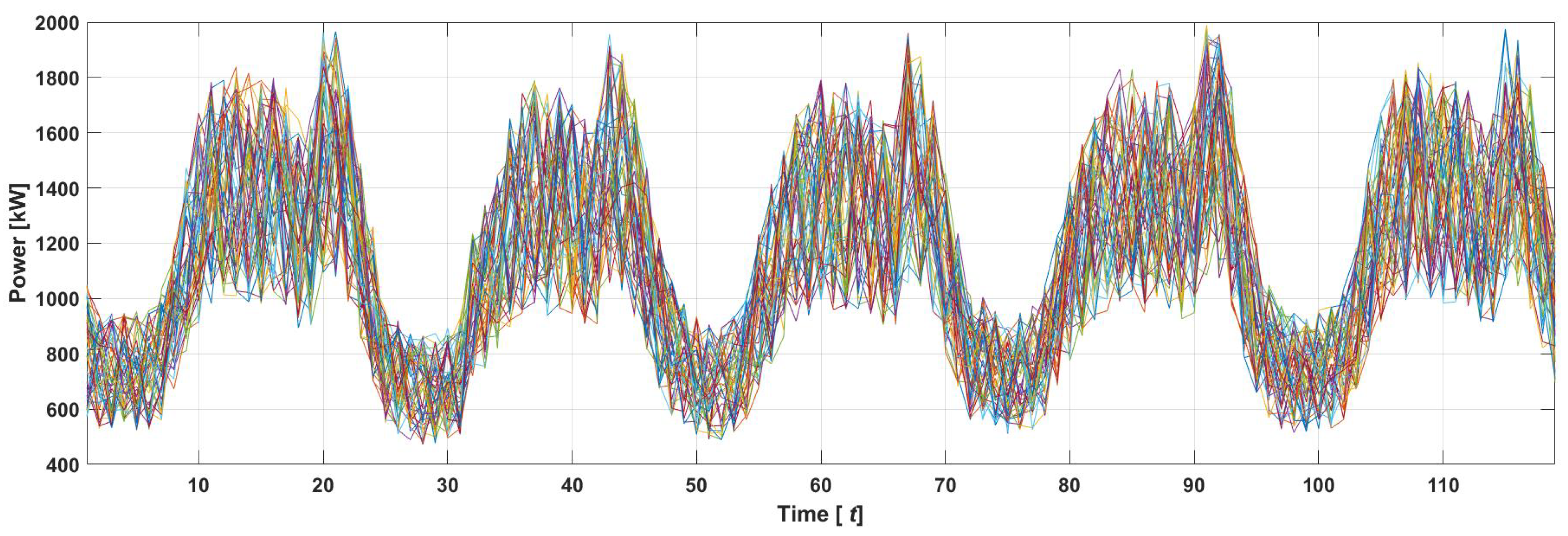
5.2. Case 1: Optimal System Component Capacities and Operation Planning without Considering Demand Response
5.3. Case 2: Optimal System Component Sizing and Operation Planning Considering TOU VP-CPP DRP
5.4. Case 3: Optimal System Component Sizing and Operation Planning Considering SSAP VP-CPP DRP
5.5. Case 4: Optimal System Component Capacities and Operation Planning Considering Uncertainty
5.6. Case 5: Optimal System Component Sizing and Operation Planning Considering LSTM-Based Forecasting, TOU VP-CPP DRP, and Uncertainty
5.7. Case 6: Optimal System Component Sizing and Operation Planning Considering LSTM-Based Forecasting, SSAP VP-CPP DRP, and Uncertainty
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| variable renewable energy | |
| battery energy storage system | |
| deficiency of power supply probability (%) | |
| photovoltaic system | |
| wind turbine | |
| T | planning horizon (8760 h) |
| t | hour index (hour) |
| penalty rates DRP (US cents/kWh) | |
| incentive rates for DRP (US cents/kWh) | |
| wind turbine’s power capacity (kW) | |
| wind turbine’s power capacity (kW) | |
| instantaneous total VREs output power (kW) | |
| instantaneous power output of PV (kW) | |
| instantaneous power output of WT (kW) | |
| BESS installed capacity (kWh) | |
| BESS maximum state of charge (kWh) | |
| BESS minimum state of charge (kWh) | |
| BESS critical state of charge (kWh) | |
| instantaneous capacity of FDR (kW) | |
| maximum allowable FDR capacity (kW) | |
| minimum allowable FDR capacity (kW) | |
| flexible demand resource | |
| demand response program | |
| variable peak critical peak pricing DRP | |
| time-of-use DRP | |
| TOU with VP-CPP DRP | |
| shortage/surplus-based adaptive pricing DRP | |
| shortage/surplus-based adaptive pricing with VP-CPP DRP | |
| load demand (kW) | |
| reference price of electricity (US cents/kWh) | |
| TOU-VP-CPP DRP electricity price (US cents/kWh) | |
| SSAP-VP-CPP DRP electricity price (US cents/kWh) | |
| N | project lifetime (years) |
| curtailed load demand | |
| curtailed power from VREs | |
| f | inflation rate (%) |
| i | annual interest rate (%) |
| d | discount rate (%) |
| operation and maintenance | |
| incident solar irradiance (W/m2) | |
| temperature of the PV module | |
| temperature coefficient of the PV module | |
| derating factor of PV (%) | |
| demand response |
References
- Salehi, N.; Martínez-García, H.; Velasco-Quesada, G.; Guerrero, J.M. A Comprehensive Review of Control Strategies and Optimization Methods for Individual and Community Microgrids. IEEE Access 2022, 10, 15935–15955. [Google Scholar] [CrossRef]
- Yang, J.; Su, C. Robust optimization of microgrid based on renewable distributed power generation and load demand uncertainty. Energy 2021, 223, 120043. [Google Scholar] [CrossRef]
- Rekioua, D. Energy Storage Systems for Photovoltaic and Wind Systems: A Review. Energies 2023, 16, 3893. [Google Scholar] [CrossRef]
- Sahri, Y.; Belkhier, Y.; Tamalouzt, S.; Ullah, N.; Shaw, R.N.; Chowdhury, M.S.; Techato, K. Energy management system for hybrid PV/wind/battery/fuel cell in microgrid-based hydrogen and economical hybrid battery/super capacitor energy storage. Energies 2021, 14, 5722. [Google Scholar] [CrossRef]
- Khalid, M. A review on the selected applications of battery-supercapacitor hybrid energy storage systems for microgrids. Energies 2019, 12, 4559. [Google Scholar] [CrossRef]
- Kiptoo, M.K.; Adewuyi, O.B.; Howlader, H.O.R.; Nakadomari, A.; Senjyu, T. Optimal Capacity and Operational Planning for Renewable Energy-Based Microgrid Considering Different Demand-Side Management Strategies. Energies 2023, 16, 4147. [Google Scholar] [CrossRef]
- Kamwa, I.; Bagherzadeh, L.; Delavari, A. Integrated Demand Response Programs in Energy Hubs: A Review of Applications, Classifications, Models and Future Directions. Energies 2023, 16, 4443. [Google Scholar] [CrossRef]
- Shariatzadeh, F.; Mandal, P.; Srivastava, A.K. Demand response for sustainable energy systems: A review, application and implementation strategy. Renew. Sustain. Energy Rev. 2015, 45, 343–350. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Folly, K.A.; Oyedokun, D.T.; Sun, Y. Artificial Intelligence Application to Flexibility Provision in Energy Management System: A Survey. In Advances in Artificial Intelligence for Renewable Energy Systems and Energy Autonomy; Springer: Berlin/Heidelberg, Germany, 2023; pp. 55–78. [Google Scholar]
- Kiptoo, M.K.; Adewuyi, O.B.; Lotfy, M.E.; Amara, T.; Konneh, K.V.; Senjyu, T. Assessing the techno-economic benefits of flexible demand resources scheduling for renewable energy–based smart microgrid planning. Future Internet 2019, 11, 219. [Google Scholar] [CrossRef]
- Conteh, A.; Lotfy, M.E.; Adewuyi, O.B.; Mandal, P.; Takahashi, H.; Senjyu, T. Demand response economic assessment with the integration of renewable energy for developing electricity markets. Sustainability 2020, 12, 2653. [Google Scholar] [CrossRef]
- Kaluthanthrige, R.; Rajapakse, A.D. Demand response integrated day-ahead energy management strategy for remote off-grid hybrid renewable energy systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106731. [Google Scholar] [CrossRef]
- Kharrich, M.; Akherraz, M.; Sayouti, Y. Optimal sizing and cost of a Microgrid based in PV, WIND and BESS for a School of Engineering. In Proceedings of the 2017 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS), Fez, Morocco, 19–20 April 2017; pp. 1–5. [Google Scholar]
- Gamil, M.M.; Senjyu, T.; Masrur, H.; Takahashi, H.; Lotfy, M.E. Controlled V2Gs and battery integration into residential microgrids: Economic and environmental impacts. Energy Convers. Manag. 2022, 253, 115171. [Google Scholar] [CrossRef]
- Cai, Q.; Xu, Q.; Qing, J.; Shi, G.; Liang, Q.M. Promoting wind and photovoltaics renewable energy integration through demand response: Dynamic pricing mechanism design and economic analysis for smart residential communities. Energy 2022, 261, 125293. [Google Scholar] [CrossRef]
- Luo, Z.; Peng, J.; Cao, J.; Yin, R.; Zou, B.; Tan, Y.; Yan, J. Demand flexibility of residential buildings: Definitions, flexible loads, and quantification methods. Engineering 2022, 16, 123–140. [Google Scholar] [CrossRef]
- Panda, S.; Mohanty, S.; Rout, P.K.; Sahu, B.K.; Bajaj, M.; Zawbaa, H.M.; Kamel, S. Residential Demand Side Management model, optimization and future perspective: A review. Energy Rep. 2022, 8, 3727–3766. [Google Scholar] [CrossRef]
- Yousefi, S.; Moghaddam, M.P.; Majd, V.J. Optimal real time pricing in an agent-based retail market using a comprehensive demand response model. Energy 2011, 36, 5716–5727. [Google Scholar] [CrossRef]
- Park, M.J.; Ham, A. Energy-aware flexible job shop scheduling under time-of-use pricing. Int. J. Prod. Econ. 2022, 248, 108507. [Google Scholar] [CrossRef]
- Yelisetti, S.; Saini, V.K.; Kumar, R.; Lamba, R.; Saxena, A. Optimal energy management system for residential buildings considering the time of use price with swarm intelligence algorithms. J. Build. Eng. 2022, 59, 105062. [Google Scholar] [CrossRef]
- Schittekatte, T.; Mallapragada, D.S.; Joskow, P.L.; Schmalensee, R. Electricity Retail Rate Design in a Decarbonized Economy: An Analysis of Time-of-Use and Critical Peak Pricing; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2022. [Google Scholar]
- Yusuf, J.; Hasan, A.S.M.J.; Ula, S. Impacts Analysis & Field Implementation of Plug-in Electric Vehicles Participation in Demand Response and Critical Peak Pricing for Commercial Buildings. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, X.; Ma, Y.; Zhang, D. Critical peak rebate strategy and application to demand response. Prot. Control Mod. Power Syst. 2021, 6, 28. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, J.; Chai, Q. Customized Critical Peak Rebate Pricing Mechanism for Virtual Power Plants. IEEE Trans. Sustain. Energy 2021, 12, 2169–2183. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Unsupervised pre-training of a deep LSTM-based stacked autoencoder for multivariate time series forecasting problems. Sci. Rep. 2019, 9, 19038. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, V.; Abdollahi, A.; Rashidinejad, M.; Heydarian-Forushani, E.; Alhelou, H.H. Integrated electricity and natural gas demand response in flexibility-based generation maintenance scheduling. IEEE Access 2022, 10, 76021–76030. [Google Scholar] [CrossRef]
- Gu, B.; Zhang, T.; Meng, H.; Zhang, J. Short-term forecasting and uncertainty analysis of wind power based on long short-term memory, cloud model and non-parametric kernel density estimation. Renew. Energy 2021, 164, 687–708. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Paki, R. Improving time series forecasting using LSTM and attention models. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 673–691. [Google Scholar] [CrossRef]
- Kumar, G.; Singh, U.P.; Jain, S. An adaptive particle swarm optimization-based hybrid long short-term memory model for stock price time series forecasting. Soft Comput. 2022, 26, 12115–12135. [Google Scholar] [CrossRef]
- Tavakoli, A.; Karimi, A. Development of Monte-Carlo-based stochastic scenarios to improve uncertainty modelling for optimal energy management of a renewable energy hub. IET Renew. Power Gener. 2023, 17, 1139–1164. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Shen, X.; Zhang, J. A comprehensive wind speed prediction system based on Monte Carlo and artificial intelligence algorithms. Appl. Energy 2022, 305, 117815. [Google Scholar] [CrossRef]
- Vaka, S.S.K.R.; Matam, S.K. Optimal sizing of hybrid renewable energy systems for reliability enhancement and cost minimization using multiobjective technique in microgrids. Energy Storage 2022, 5, e419. [Google Scholar] [CrossRef]
- Konneh, D.A.; Howlader, H.O.R.; Shigenobu, R.; Senjyu, T.; Chakraborty, S.; Krishna, N. A multi-criteria decision maker for grid-connected hybrid renewable energy systems selection using multi-objective particle swarm optimization. Sustainability 2019, 11, 1188. [Google Scholar] [CrossRef]
- Yoon, K.P.; Kim, W.K. The behavioral TOPSIS. Expert Syst. Appl. 2017, 89, 266–272. [Google Scholar] [CrossRef]
- Tsou, C.S. Multi-objective inventory planning using MOPSO and TOPSIS. Expert Syst. Appl. 2008, 35, 136–142. [Google Scholar] [CrossRef]
- Fu, G.; Li, B.; Yang, Y.; Li, C. Re-ranking and TOPSIS-based ensemble feature selection with multi-stage aggregation for text categorization. Pattern Recognit. Lett. 2023, 168, 47–56. [Google Scholar] [CrossRef]
- Méndez, M.; Frutos, M.; Miguel, F.; Aguasca-Colomo, R. Topsis decision on approximate pareto fronts by using evolutionary algorithms: Application to an engineering design problem. Mathematics 2020, 8, 2072. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, H.; Gao, Y. Security constrained economic dispatch: Considering contractual performance ability evaluating of power producers using TOPSIS method in spot market environment. Energy Rep. 2023, 9, 343–352. [Google Scholar] [CrossRef]
- Amara, S.; Toumi, S.; Salah, C.B. A comparison of optimal sizing methods for Microgrid applications and description of a proposed iterative algorithm. In Proceedings of the 2022 IEEE 21st international Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2022; pp. 654–659. [Google Scholar]
- Zhao, G.; Cao, T.; Wang, Y.; Zhou, H.; Zhang, C.; Wan, C. Optimal Sizing of Isolated Microgrid Containing Photovoltaic/Photothermal/Wind/Diesel/Battery. Int. J. Photoenergy 2021, 2021, 5566597. [Google Scholar] [CrossRef]
- Li, B.; Wang, H.; Tan, Z. Capacity optimization of hybrid energy storage system for flexible islanded microgrid based on real-time price-based demand response. Int. J. Electr. Power Energy Syst. 2022, 136, 107581. [Google Scholar] [CrossRef]
- Furukakoi, M.; Adewuyi, O.B.; Matayoshi, H.; Howlader, A.M.; Senjyu, T. Multi objective unit commitment with voltage stability and PV uncertainty. Appl. Energy 2018, 228, 618–623. [Google Scholar] [CrossRef]
- Mo, M.; Lotfy, M.; Ibrahimi, A.M.; Senjyu, T.; Krishnan, N. Stochastic Unit Commitment and Optimal Power Trading Incorporating PV Uncertainty. Sustainability 2019, 11, 4504. [Google Scholar] [CrossRef]
- Weather Mount Marsabit. 2019. Available online: https://www.meteoblue.com (accessed on 30 March 2023).
- Photovoltaic Geographical Information System. 2019. Available online: https://joint-research-centre.ec.europa.eu/photovoltaic-geographical-information-system-pvgis_en (accessed on 30 March 2023).
- The Presidency, Republic of Kenya. Power Generation and Transmission Master Plan, Kenya Medium Term Plan 2015–2020—Vol. I. 2016. Available online: https://www.epra.go.ke/download/power-generation-and-transmission-master-plan-kenya-medium-term-plan-2015-2020-3/ (accessed on 16 May 2023).
- Ministry of Energy and Petroleum, Republic of Kenya. Updated Least Cost Power Development Plan 2017–2037. 2018. Available online: https://www.climatepolicydatabase.org/policies/least-cost-power-development-plans-lcpdp-2017-2037 (accessed on 1 April 2023).
- Dhundhara, S.; Verma, Y.P.; Williams, A. Techno-economic analysis of the lithium-ion and lead-acid battery in microgrid systems. Energy Convers. Manag. 2018, 177, 122–142. [Google Scholar] [CrossRef]
- Perkins, G. Techno-economic comparison of the levelised cost of electricity generation from solar PV and battery storage with solar PV and combustion of bio-crude using fast pyrolysis of biomass. Energy Convers. Manag. 2018, 171, 1573–1588. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, A. Optimal energy management and feasibility analysis of hybrid renewable energy sources with BESS and impact of electric vehicle load with demand response program. Energy 2023, 278, 127867. [Google Scholar] [CrossRef]
- Tarrif Setting: Electricity. 2019. Available online: https://www.epra.go.ke/services/economic-regulation/tarrif-setting/tarrif-setting-electricity/ (accessed on 1 April 2023).
- Nayak, A.; Maulik, A.; Das, D. An integrated optimal operating strategy for a grid-connected AC microgrid under load and renewable generation uncertainty considering demand response. Sustain. Energy Technol. Assess. 2021, 45, 101169. [Google Scholar] [CrossRef]



| Economics | [47] | |
| Inflation rate | 4 (%) | |
| Discount rate | 4 (%) | |
| System lifetime | 20 (years) | |
| Scheduling horizon | 8760 (h) | |
| PV system | [48] | |
| Investment cost | 1695 ($/kW) | |
| O and M cost | 26 ($/kW/yr) | |
| Derating factor of PV | 90 (%) | |
| Lifetime | 20 (years) | |
| WT specifications | [47] | |
| Investment cost | 2030 ($/kW) | |
| O and M cost | 76 ($/kW/yr) | |
| Lifetime | 20 (years) | |
| Cut-in wind speed | 4 (m/s) | |
| Rated wind speed | 14.5 (m/s) | |
| Cut-out speed | 25 (m/s) | |
| Survival wind speed | 60 (m/s) | |
| Wind shear coefficient | 0.143 | |
| BESS | [49,50,51] | |
| Investment costs | 330 ($/kWh) | |
| Replacement cost | 330 ($/kWh) | |
| Round-trip efficiency | 90 (%) | |
| Lifetime | 10 (years) |
| Peak | Mid-Peak | Off-Peak | |
|---|---|---|---|
| Mid-peak | 0.016 | 0.01 | −0.1 |
| Peak | −0.1 | 0.012 | 0.016 |
| Valley | 0.012 | −0.1 | 0.01 |
| Case | DPSP (%) | TLCC (US $) | LPPP (%) | PV (kW) | WT (kW) | BESS (kWh) | TOPSIS Rank |
|---|---|---|---|---|---|---|---|
| #1 | 0.48 | 10,377,384.54 | 6.26 | 1440 | 1850 | 4800 | 1 |
| 0.41 | 10,494,044.60 | 3.22 | 1300 | 1990 | 4400 | 2 | |
| 0.00 | 11,019,716.78 | 1.21 | 1230 | 1990 | 6500 | 3 | |
| 1.81 | 10,340,568.33 | 8.35 | 1690 | 1790 | 3800 | 4 | |
| #2 | 0.57 | 10,314,687.16 | 4.35 | 1530 | 1830 | 4200 | 1 |
| 0.76 | 10,362,979.42 | 1.30 | 1050 | 2130 | 4000 | 2 | |
| 0.83 | 10,529,262.01 | 0.60 | 1120 | 2040 | 5100 | 3 | |
| 0.03 | 10,899,321.22 | 5.22 | 1540 | 1960 | 4600 | 4 | |
| #3 | 0.06 | 9,649,293.00 | 1.33 | 1270 | 1840 | 3500 | 1 |
| 0.09 | 9,814,061.64 | 1.24 | 1090 | 1920 | 4200 | 2 | |
| 0.01 | 9,893,660.45 | 1.95 | 1610 | 1670 | 3700 | 3 | |
| 0.00 | 9,952,736.65 | 2.16 | 1280 | 1790 | 4900 | 4 | |
| #4 | 0.12 | 10,576,185.15 | 10.31 | 1480 | 2000 | 4900 | 1 |
| 0.00 | 11,157,231.69 | 4.32 | 1200 | 2260 | 4400 | 2 | |
| 1.55 | 10,318,166.83 | 6.28 | 1290 | 2000 | 3700 | 3 | |
| 3.52 | 9,718,020.35 | 3.09 | 1150 | 1960 | 3100 | 4 | |
| #5 | 0.36 | 10,378,836.97 | 5.05 | 1430 | 1930 | 3600 | 1 |
| 0.23 | 10,400,379.64 | 3.50 | 1710 | 1680 | 5100 | 2 | |
| 0.00 | 10,570,027.75 | 1.56 | 1310 | 1960 | 4700 | 3 | |
| 0.58 | 10,157,349.44 | 2.86 | 1480 | 1840 | 3900 | 4 | |
| #6 | 0.04 | 10,066,405.65 | 2.05 | 1420 | 1920 | 3200 | 1 |
| 0.00 | 10,093,575.32 | 3.23 | 1390 | 2050 | 4100 | 2 | |
| 0.19 | 9,371,605.78 | 1.10 | 1580 | 1550 | 3800 | 3 | |
| 0.11 | 9,319,214.79 | 0.73 | 1210 | 1850 | 2600 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiptoo, M.K.; Adewuyi, O.B.; Furukakoi, M.; Mandal, P.; Senjyu, T. Integrated Multi-Criteria Planning for Resilient Renewable Energy-Based Microgrid Considering Advanced Demand Response and Uncertainty. Energies 2023, 16, 6838. https://doi.org/10.3390/en16196838
Kiptoo MK, Adewuyi OB, Furukakoi M, Mandal P, Senjyu T. Integrated Multi-Criteria Planning for Resilient Renewable Energy-Based Microgrid Considering Advanced Demand Response and Uncertainty. Energies. 2023; 16(19):6838. https://doi.org/10.3390/en16196838
Chicago/Turabian StyleKiptoo, Mark Kipngetich, Oludamilare Bode Adewuyi, Masahiro Furukakoi, Paras Mandal, and Tomonobu Senjyu. 2023. "Integrated Multi-Criteria Planning for Resilient Renewable Energy-Based Microgrid Considering Advanced Demand Response and Uncertainty" Energies 16, no. 19: 6838. https://doi.org/10.3390/en16196838
APA StyleKiptoo, M. K., Adewuyi, O. B., Furukakoi, M., Mandal, P., & Senjyu, T. (2023). Integrated Multi-Criteria Planning for Resilient Renewable Energy-Based Microgrid Considering Advanced Demand Response and Uncertainty. Energies, 16(19), 6838. https://doi.org/10.3390/en16196838










