Maximizing Returns and Minimizing Risks in Hybrid Renewable Energy Systems: A Stochastic Discounted Cash Flow Analysis of Wind and Photovoltaic Systems in Brazil

Abstract

The use of renewable energy sources has become strategic in the production of electricity worldwide due to global efforts to increase energy efficiency and achieve a net zero carbon footprint. Hybrid systems can maximize stability and reduce costs by combining multiple energy sources. A conventional metric, such as the levelized cost of energy (LCOE), that is appropriate for assessing the cost-effectiveness of an option may not be appropriate when evaluating the economic feasibility of hybrid systems. This study proposes a stochastic discounted cash flow model (DCF) to assess the economic viability of a hybrid renewable energy system (HRES) in Brazil. The objective is to determine the combinations that will provide the highest 50th percentile internal rate of return (IRR) and the lowest coefficient of variation (CV). Model variables include capital expenditures (CAPEX), operation and maintenance (O&M) costs, sectoral charges, taxes, and long-term energy production metrics. The results demonstrate that the synergies modeled contributed to the higher economic outcomes for the HRES obtained by combining both energy sources rather than opting for a stand-alone configuration. A wind-dominant combination of 60% wind was able to increase the 50th percentile of the IRR, while a solar-dominant combination of 65% solar minimized the CV.

1. Introduction

1.1. Motivation and Background

As the world moves toward a cleaner energy matrix, renewable energy technologies have gained increasing importance. According to the World Energy Investment 2023 report, global investments in clean energy reached record levels in 2022, surpassing USD 1.7 trillion, and are expected to reach USD 1.9 trillion in 2023, where solar PV (photovoltaic) is expected to contribute more than USD 1 billion per day, surpassing upstream oil and gas investments for the first time in history. Global wind power investment is expected to grow by approximately 10% in 2023 and by approximately 25% from 2024 to 2030 [1].

In recent years, the Brazilian renewable energy sector has experienced steady growth. In 2023, there will be two major transmission auctions scheduled, including the largest in terms of investment [1]. Although hydropower still accounts for the majority of Brazil’s renewable energy capacity, wind and solar have grown rapidly. According to IRENA statistics [2], wind and solar energy capacities in Brazil have increased by 11-fold (from 2202 MW to 24,163 MW) and over 1800-fold (from 13 MW to 24,079 MW), respectively, which paves the way for HRES growth in the future.

The Brazilian Electricity Regulatory Agency (ANEEL) established a favorable regulatory framework for the HRES, resulting in increased popularity of the technology due to the possibility of cost reduction, market opportunities, and complementarity between energy sources, which can result in more advantageous economic outcomes than stand-alone energy systems. However, the complexity of combining multiple sources of energy may influence the decision to invest in this technology [3].

Brazil’s Decennial Energy Expansion Plan 2031 [4] forecasts a significant rise in renewable energy capacity, escalating from 151 GW in 2022 to 267 GW by 2031. It is acknowledged by the government that the HRES plays a pivotal role in the energy sector; however, the energy sources are considered separately in their analysis, resulting in an important gap. Moreover, an extensive body of academic literature relies heavily on metrics such as the traditional (deterministic) DCF or the levelized cost of energy (LCOE) [5]. Despite this, this approach has significant gaps from a variety of perspectives [6], as well as ignoring important aspects of evaluating the economic attractiveness of energy projects, such as the time value of money and the unpredictable nature of renewable energy.

In order to transcend the limitations of the LCOE, a more comprehensive analytical framework may be required, offering a nuanced understanding of HRESs and providing a more cohesive and synergistic approach to energy planning and analysis. As indicated by [5], approximately 85% of the reviewed papers used either discounted cash flow (DCF) or LCOE techniques. According to the authors, traditional project evaluation methods (TPEM), which refers to net present value (NPV), IRR, and payback period (PBP), were the largest category with 921 papers.

The DCF technique traditionally relies on deterministic forecasts of cash flows, whereas probabilistic cash flow analysis is associated with simulations and scenarios. However, when assessing the HRES, a probabilistic approach must not only be able to account for the energy intermittency but also consider the synergies’ impact on the decision metrics.

This study assumes that dynamic (probabilistic) DCF models can contribute significantly to the development of a more comprehensive analysis. A DCF model, unlike a LCOE, is designed to incorporate the time value of money into the long-term financial projections of a project. A probabilistic model can encompass various uncertainties, such as fluctuating market dynamics and long-term energy production, offering a robust platform for sensitivity and scenario analysis.

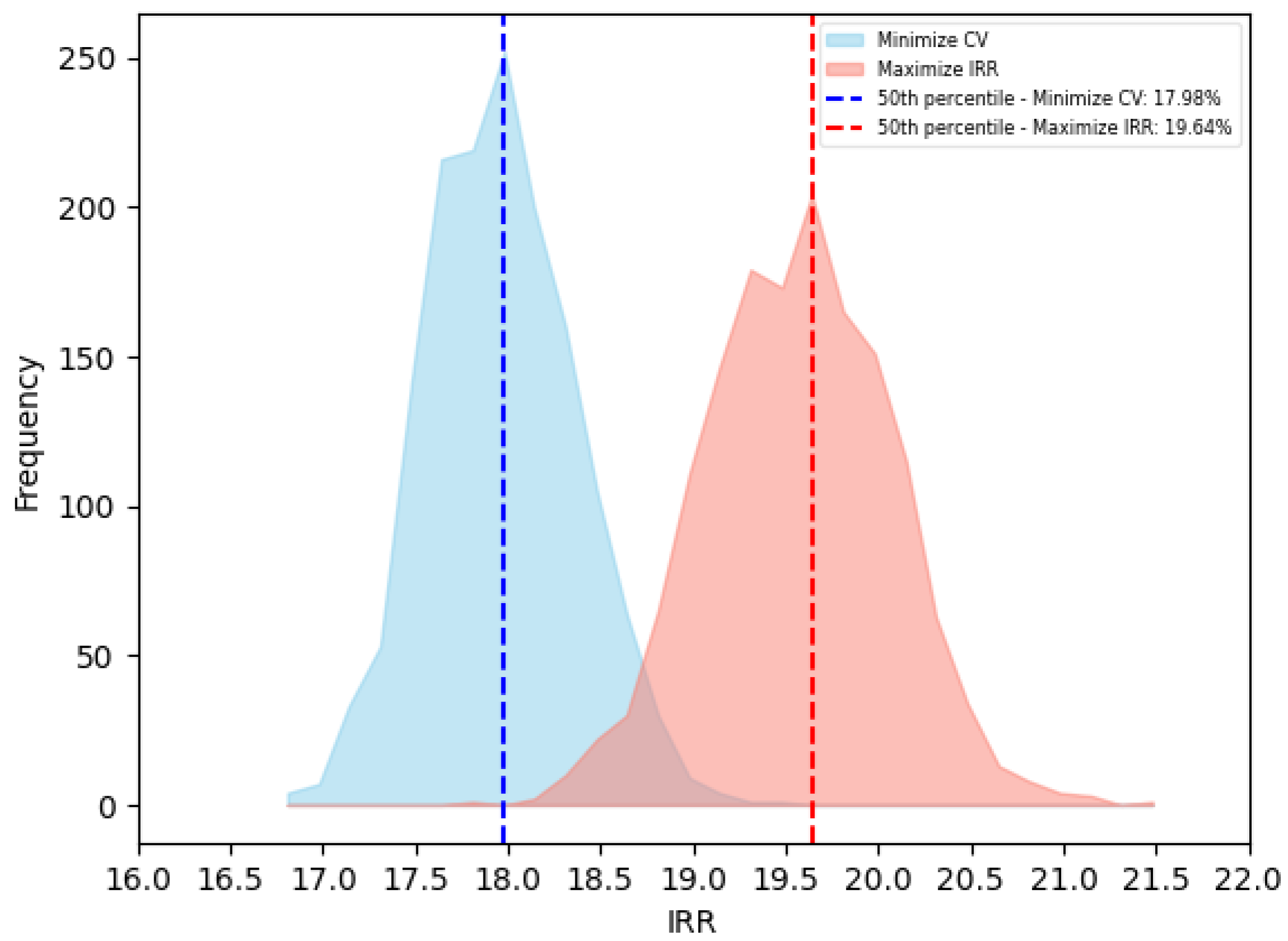
The purpose of this study is to present a new dynamic DCF approach that considers both the intermittency of the energy sources, as well as the synergies of the HRES, to assess the combination of wind and solar to maximize the 50th percentile of the HRES IRR and minimize its CV. Throughout this study, these combinations will be referred to as “optimal”.

Achieving both the maximization of IRR and the minimization of the CV is an indication that a wind–solar combination can be not only lucrative but can also demonstrate a certain degree of predictability in its returns, making it a useful metric for evaluating the feasibility of expanding the HRES. As a result, this new approach can facilitate informed investment decisions by incorporating dynamic financial structuring and incentives, as well as providing insights into the project’s IRR, thereby serving as a tool for navigating the complex renewable energy industry with a refined analytical perspective.

1.2. Literature Review

In Europe, the levelized cost of energy (LCOE) for renewable energy increased significantly between 2021 and 2022 due to higher financing costs and input costs for turbines and modules. Based on the data presented in [1], the cost per MWh has increased from 50–55 USD/MWh in Q1 2021 to 70–75 USD/MWh in Q4 2022. Although the LCOEs for onshore wind and solar PV increased by 15% and 30%, respectively, their appeal remained unchanged due to their cost-effectiveness. Conversely, combining wind, solar PV, and batteries into hybrid systems can reduce the LCOE compared to isolated systems [1].

According to [7], the capital expenditures per megawatts (CAPEX/MW) of photovoltaics may decline by up to 75% by 2050. Onshore and offshore wind are expected to experience a decline of 40% and 50%, respectively, for the same period. A reduced CAPEX will result in a lower future LCOE, thereby increasing the competitiveness of HRESs. Complementarity between energy sources provides a basis for designing hybrid energy systems that combine multiple energy sources or technologies to achieve better results. Complementary energy sources can enhance system reliability and optimize hybrid renewable energy systems [8]. According to [9], wind and solar resources are more effectively matched in terms of load than individual resources.

In other studies [10,11,12], the complementarity of wind and solar energy was examined in different countries, including Algeria, Brazil, and China. In Algeria [10], high complementarity was found in coastal and highland regions and moderate complementarity along the coast. In Brazil [11], the Northeast region displayed the strongest complementarity between wind and solar energy. Based on the specific study site in China [12], the authors determined that a solar–wind ratio of 1:0.27 resulted in the most stable total renewable energy production.

A detailed analysis of optimum sizing approaches for HRESs has been presented in [13], which reviews several optimization techniques in combination with HOMER (Hybrid Optimization of Multiple Energy Sources), a software developed by the National Renewable Energy Laboratory (NREL) which is current in version 3.16.2. As a result of the lack of open-source code, HOMER is described by the authors as a “black box” in terms of its internal operations.

HOMER has been widely used for analyzing hybrid energy system applications for a variety of purposes [14,15,16,17,18]. A hydrogen energy storage vector was used in [13] to overcome some limitations of solar and PV energy sources, such as variability and intermittency. Hybrid configurations have been found to be more economical and cost-effective than stand-alone configurations [14,15,16,17]. As a critical factor for economic viability, the regulatory framework has been mentioned in [18]. The expansion of HRES is currently hindered by the lack of clear regulations in many countries, which creates an uncertainty environment.

It has been found, despite differences in methodology, that hybrid designs often lead to optimal and cost-effective solutions [19,20,21,22,23,24]. As part of the effort to provide electricity to rural areas in remote locations, a techno-economic feasibility study was conducted [20]. According to the authors, a hybrid system provides more reliable and affordable electricity than grid extensions. A feasibility study on a HRES in Italy was conducted in [21]. The hybrid system was found to be technically and economically feasible under a scenario where PV and wind are complementary throughout the year.

The lowest net present cost (NPC) was obtained with PV–wind–diesel–biomass [22], PV–wind–battery [23], and PV–battery [24]. In [22], PV was identified as the most suitable primary energy source. In a similar study conducted in [24], PV coupled with battery storage was found to provide the greatest economic benefits. Although the PV–wind–battery combination in [23] had the lowest NPC, the high investment in renewables resulted in a higher LCOE for households and corporations.

Approaches based on hybrid solutions have also been proven to be effective to improve grid stability and competitiveness of renewable sources [25], overcome challenges like constrained energy transmission [26], and to reduce power fluctuations from intermittent renewable sources [27]. The introduction of a wind, solar, pumped-storage cooperative (WSPC) model by [25] successfully enhanced the wind–solar competitiveness and led to better revenue distribution. The study presented in [28] proposed an event-triggered distributed hybrid control (DHC) that optimized the energy hub device operation for minimum cost. A wider expansion in renewable energy can also benefit the entire market through energy price reduction [29].

In [6], it has been demonstrated that metrics such as the LCOE are insufficient for evaluating renewable energy sources. According to the authors, the LCOE ignores the time-dependent value of energy generation, overvalues variable renewable sources of energy, and does not adequately address the devaluation of renewable energy sources (RES) as they are generated. To provide a solution, the cost of valued energy (COVE) metric has been proposed, which weighs energy based on real-time market prices. As a result, the COVE was 25% higher than the LCOE for solar in California and 129% higher for wind in Texas. According to the authors, RES should be designed to minimize the COVE rather than the LCOE.

In this study, a stochastic discounted cash flow (DCF) model based on long-term expectations of wind and solar energy production is used to evaluate an optimal HRES configuration. The objective of this study is to identify the optimal combinations of wind–solar in relation to the total HRES installed capacity to maximize the 50th percentile of the IRR, which will be referred to as ${IRR}_{P50}$ for brevity, and to minimize the coefficient of variation (CV) of the estimated IRR. Although maximizing ${IRR}_{P50}$ may result in higher potential returns, minimizing the CV may indicate a more reliable and consistent IRR. Several metrics can be used by decision-makers when evaluating investments, and the metric chosen will be dependent on the risk management strategy. Based on the results of the study, the hybrid system in Brazil achieves the best scale gains in every scenario; however, the optimal wind–solar ratio varies based on the objective.

1.3. Paper Organization

This paper is organized as follows: Materials and Methods (Section 2) presents the model. The variables and equations of the cash flow model are described in Section 2.1 (Cash Flow Model). In segments 2.1.1 and 2.1.2, gross revenue and costs/expenses are discussed, respectively. Segment 2.1.3 describes the investment decision. In Section 2.2, the data and variables modeled are outlined. Results are presented in Section 3. 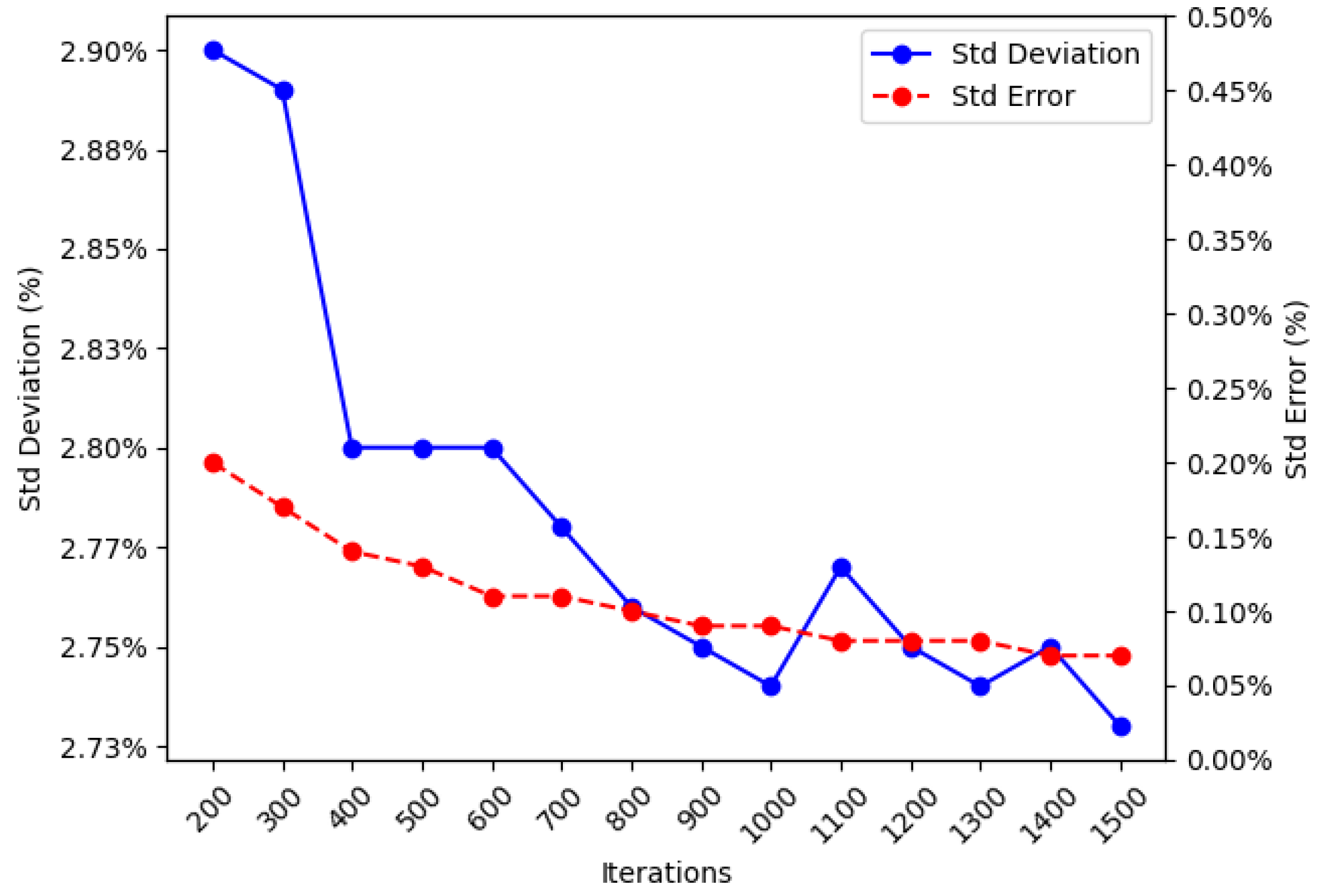In Section 3.1, the Convergence Test is presented. 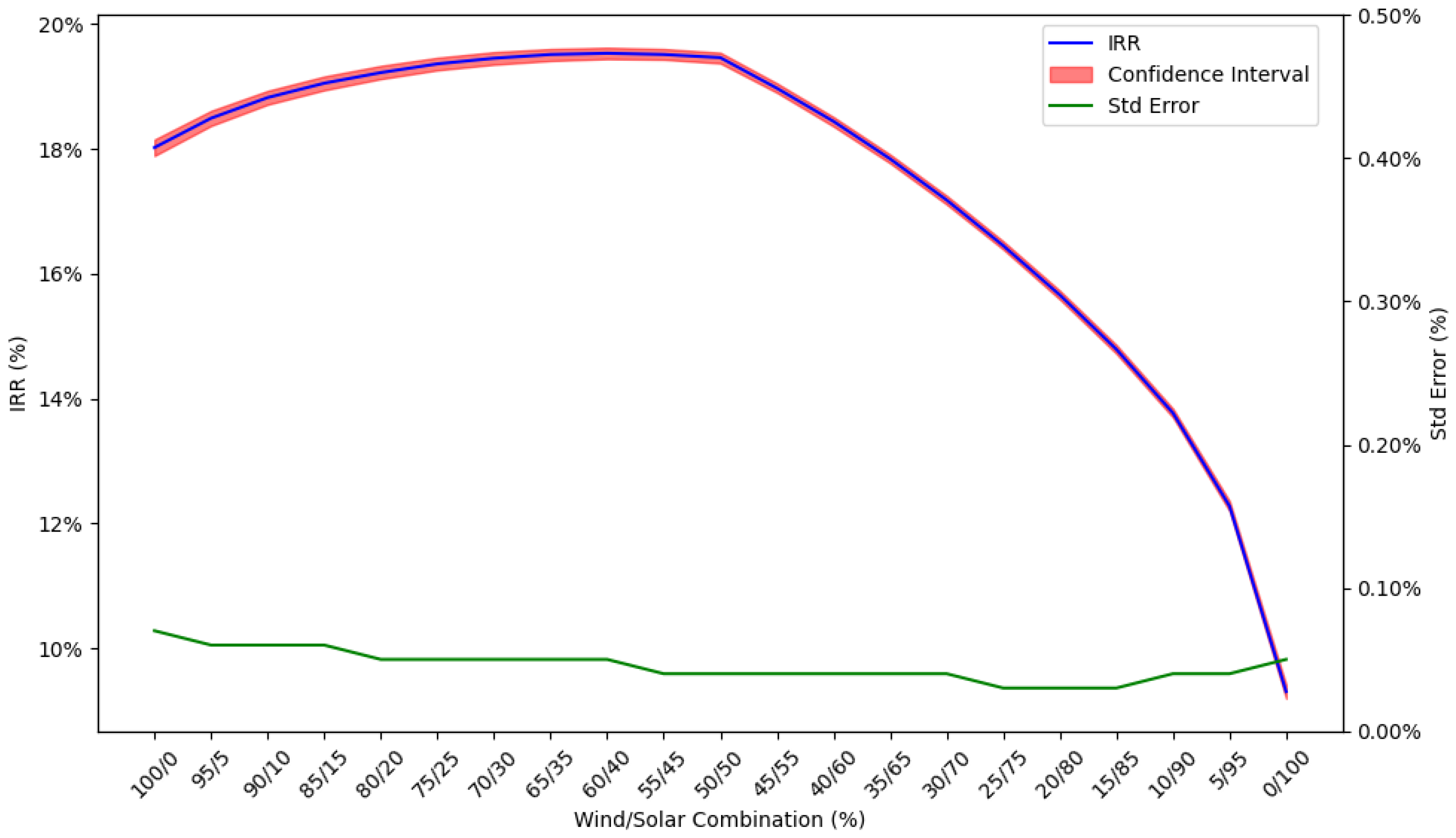Section 3.2 presents the IRR and CV results along with specific statistical measures such as standard error lower and upper bounds. Section 3.3 presents the confidence intervals, Section 3.4 presents the probability distributions, and Section 3.5 presents the synergies of costs and revenues. Section 3.6 presents the sensitivity analysis. The results and their implications are discussed in Section 4, as well as future research directions. Section 5 presents the conclusions.

2. Materials and Methods

This section provides a detailed description of the components of the proposed cash flow model, as well as the equations required to replicate its results. In this case, the investment decision involves identifying the optimal wind–solar configuration that maximizes ${IRR}_{P50}$ and minimizes the CV (coefficient of variation). It is important to recognize that every country has its own set of economic laws and tributaries, which may lead to variations in cash flow models. A Brazilian-specific model is presented in this study.

2.1. Cash Flow Model

In each country, regulations, costs, synergies, and tributes may vary, resulting in different outcomes. The expected annual long-term production of wind and solar energy is treated as a stochastic variable in the model. This study uses a monthly cash flow model to track financial movements and identify possible cash shortages more accurately.

Table 1. Cash flow.

Financial Analysis Parameters 1	Variable	Variable Type
Gross Revenue	(A)	Stochastic
Tributes (Tax Deductions)	(B)	Deterministic
Net Revenue	(C) = (A) − (B)	Stochastic
Sectoral Charges and Fees	(D)	Deterministic
Transmission System Use Expense	(E)	Deterministic
Operating Expenses	(F)	Deterministic
Energy purchase costs	(G)	Deterministic
Income Tax	(H)	Deterministic
Social Contribution on Net Profit	(I)	Deterministic
Operational Cash Flow	(J) = (C) − (D) − (E) − (F) − (G) − (H) − (I)	Stochastic
Investing Cash Flow	(K)	Deterministic
Financial Cash Flow	(L)	Deterministic
Free Cash Flow	(X) = (J) − (K) − (L)	Stochastic

¹: Millions of Brazilian reais, where M stands for millions and BRL is the ISO (International Organization for Standardization) code for the Brazilian real currency.

categorizes the financial metrics variables and specifies whether they are stochastic (probabilistic) or deterministic (fixed).

In the following subsections, a detailed analysis of the interactions between these financial metrics is presented. In cash flow modeling, a positive sign indicates an inflow or receipt of funds, while a negative sign indicates an outflow or disbursement.

2.1.1. Gross Revenue—Variable A

Energy production can either be allocated through a long-term contract, a power purchase agreement (PPA), or on the spot market (SM). Under a PPA, the seller is obligated to deliver a predetermined quantity of energy over a specified period at an agreed-upon price. In contrast, SM prices are more volatile and are influenced by supply and demand on an hourly basis. In Equation (1), gross revenue is calculated by adding the energy sold in both markets:

$$A_n=(\overline{Q_{PPA}}\times {PC}_n+Q_{{SM}_n}\times {PS}_n)\times T_n$$

(1)

where n represents the period (month), $A_n$ is the gross revenue in BRL (Brazilian reais), $Q_{PPA}$ represents the contracted amount of energy to be delivered, in megawatts (MW), upon the HRES COD (commercial operation date) which will remain constant throughout the project’s lifetime, ${PC}_n$ is the inflation-adjusted PPA price, ${PS}_n$ is the inflation-adjusted spot price, and $T_n$ is the difference in the total of hours between n + 1, and n. $Q_{{SM}_n}$ is the amount of energy liquidated, in MW, in the spot market according to Equation (2):

$$Q_{{SM}_n}=\max (0,{EG}_n-\overline{Q_{PPA}})$$

(2)

where ${EG}_n$ represents the amount of energy expected to be generated by the HRES. This study assumes that the energy to be liquidated on the spot market can only be greater than zero if, and only if, the energy generation exceeds $\overline{Q_{PPA}}$. Otherwise, there will be no gross revenue on the spot market. In cases where $\overline{Q_{PPA}}$ exceeds ${EG}_n$, the difference must be acquired on the spot market and accounted for as an energy purchase cost (G) valued on the ${PS}_n$. In this study, it is assumed that the $\overline{Q_{PPA}}$ represents the generation capacity of each source with a 90% probability of exceeding it.

It is important to note that despite the numerous possibilities for representing wind and solar uncertainties [30,31,32], this study assumes a Gaussian probability distribution function with different parameters for each source. In Equation (3), the expected energy generation of the hybrid system is shown:

$${EG}_n={IC}_{HRES}\times [\mathrm{W}\times \mathrm{f}(\mathrm{w})+\mathrm{S}\times \mathrm{f}(\mathrm{s})\times (1-\mathrm{\nu }\times \mathrm{p}\left)\right]$$

(3)

where $\mathrm{W}$ and S represent, respectively, the percentage of wind and solar energy in the HRES’ total installed capacity (power), ${IC}_{HRES}$ is the installed capacity (IC) of the HRES, in MW, ν is the annual degradation factor considered for the solar panels, p is the number of years that the HRES has been in operation, and f(w), f(s) represent Gaussian distributions as shown in Equations (4) and (5):

$$\mathrm{f}\left(\mathrm{w}\right)~\mathrm{N}({P50}_w,{\mathsf{\sigma }}_w^2)$$

(4)

$$\mathrm{f}\left(\mathrm{s}\right)~\mathrm{N}({P50}_s,{\mathsf{\sigma }}_s^2)$$

(5)

where P50 is the 50th percentile of the expected annual long-term energy production, w and s refer to, respectively, wind and sun, and ${\mathsf{\sigma }}^2$ is the variance of each distribution.

2.1.2. Costs and Expenses—Variables B to X

The Social Integration Program (PIS) and the Contribution for Financing Social Security (COFINS) are taxes imposed on revenue. The tax rate can be influenced by the tax regime and government subsidies. Equation (6) illustrates its calculation as follows:

$$B_n=\mathrm{t}\times A_n$$

(6)

where t is the effective total tax rate and $B_n$ is the total tribute cost.

The sectoral charges and fees (D) are applied to the use of energy resources. Brazilian market examples include R&D (research and development), inspection fees for electricity services, and national system operator fees. Equation (7) illustrates the calculation:

$$D_n=\mathrm{d}\times C_n$$

(7)

where d is the effective rate, $D_n$ is the total sectorial charges and fees incurred, and $C_n$ is the net revenue ($A_n+B_n)$.

A transmission system use expense (TSUE) represents the charges associated with the use of the electric transmission and distribution network. This is a substantial expense incurred by generators, traders, and consumers of energy for the purpose of providing the necessary infrastructure to the transmission and distribution companies. The HRES may benefit from scale gains and a lower TSUE than stand-alone configurations due to the complementarity of the energy sources, as shown in Equation (8):

$$E_n=\mathrm{T}\mathrm{S}\mathrm{U}\mathrm{T}\times \beta \times \mathrm{m}\mathrm{a}\mathrm{x}[\mathrm{W}\times {IC}_{HRES},S\times {IC}_{HRES}]$$

(8)

where $E_n$ is the TSUE total, TSUT is the effective tariff and $\beta$ is the inflation adjustment. This study assumes that the energy sources have perfect hourly complementarity, under which the scale gains obtained from this variable will be maximized. The HRES may achieve lower-scale gains in different scenarios with lower complementarity.

In the cash flow model, expenses associated with operations and maintenance (O&M) are classified as operating expenses (F). It, therefore, plays a crucial role in the energy sector as it ensures that energy facilities operate at maximum efficiency. Even though the combined energy sources may result in lower costs for the HRES than if they were configured separately, this study assumes that the effective HRES O&M equates to the weighted stand-alone O&Ms.

Equation (9) indicates that this expense will be adjusted for inflation throughout the investment life cycle:

$$F_n=\beta \times {IC}_{HRES}\times [-{O\&M}_w\times \mathrm{W}-{O\&M}_s\times \mathrm{S}]$$

(9)

where $F_n$ is the O&M total, ${O\&M}_w$ and ${O\&M}_s$ refer to, respectively, the O&M of wind and solar.

Companies in Brazil are subject to income tax (H) and the social contribution on net profit (I). The calculation is based on a company’s profits, which differ depending on its taxation regime, as shown in Equation (10):

$$H_n+I_n=-A_{n+p\left(r\right)}\times (\mathsf{\alpha }+\mathsf{\gamma })$$

(10)

where $H_n$ and $I_n$ represent the amount to be paid in income tax and the social contribution on net profits, respectively, $\mathsf{\alpha }$ and $\mathsf{\gamma }$ refer to the respective taxes, r represents the company’s tax regime, and p is a function of r that is used to represent the specific periods during which income taxes are assessed and paid. Quarterly payment is assumed in this study under the presumed profit regime.

An operational cash flow forecast (J) provides an indication of future cash generation. The amount spent on investing activities is represented by investing cash flow (K). As part of the investment cash flow modeling, CAPEX (capital expenditures) is taken into consideration since these expenses are incurred by the company to acquire physical assets that will generate future income and cash flow. Scale gains are also represented by this variable as technology advances. Equation (11) shows the total HRES CAPEX:

$${HRES\text{\_}CAPEX}_n=\frac{1}{z}\times {{IC}_{HRES}[CAPEX}_w\times W+{CAPEX}_s\times \mathrm{S}]$$

(11)

where ${HRES\text{\_}CAPEX}_n$ is the HRES CAPEX, z is the total period of disbursement, and ${CAPEX}_w,{CAPEX}_s$ are the respective CAPEX of wind and solar.

The financial cash flow (L) includes financing activities such as debt issuance and repayment. Long-term debt fundraising may contribute to the investment decision if the interest rate and payment conditions are favorable.

Free cash flow (X) is a financial performance measure widely used by investors to assess a company’s ability to generate value. Discounted cash flow (DCF) is a technique used in financial valuation to estimate the present values of future cash flows based on the investors’ expected rate of return ($K_e)$.

2.1.3. Investment Decision

In addition to the LCOE metric used to assess the cost-effectiveness of different energy systems, the IRR is used to determine the rate at which the investment cost equals the present value of future cash flows. Projects are considered desirable when the IRR exceeds the investor’s desired return rate. The investment decision is positive if the IRR exceeds $K_e$, where the net present value (NPV) is positive, and negative otherwise [33]. The IRR calculation is shown in Equation (12):

$$-X_0+\frac{X_1}{{\left(1+\mathrm{I}\mathrm{R}\mathrm{R}\right)}^1}+\cdots +\frac{X_n}{{\left(1+\mathrm{I}\mathrm{R}\mathrm{R}\right)}^n}=0$$

(12)

where $X$ is the forecasted free cash flow.

The investment decision is given by Equation (13) [33]. The decision to invest occurs if, and only if, the DCF is positive, which indicates that value has been generated:

$$\left\{\begin{array}{c}\mathrm{invest}⟺{-\mathrm{H}\mathrm{R}\mathrm{E}\mathrm{S}\text{\_}\mathrm{C}\mathrm{A}\mathrm{P}\mathrm{E}\mathrm{X}}_0+{\displaystyle \sum _{t=1}^N}\frac{X_t}{{\left(1+K_e\right)}^t}>0\\ \mathrm{Do}\mathrm{not}\mathrm{invest}\mathrm{otherwise}.\end{array}\right.$$

(13)

Alternatively, the minimization of the CV contributes to reduce the variability of uncertain returns and can suggest the investor’s preference for a lower variability around the expected IRR. The objective functions proposed in this study aim to identify the optimal combinations of wind and solar, which maximizes the ${IRR}_{P50}$ and minimizes its CV. Equation (14) represents the CV:

$$\mathrm{C}\mathrm{V}=\frac{{\sigma }_{IRR}}{Q_{0.5}\left(IRR\right)}$$

(14)

where ${\sigma }_{IRR}$ is the standard deviation of the IRR and $Q_{0.5}$ is its 50th percentile.

Equations (15) and (16) present, respectively, the objective functions proposed in this study to maximize the ${IRR}_{P50}$ and minimize CV:

$$\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}:\mathrm{E}\left[\mathrm{I}\mathrm{R}\mathrm{R}\right(\mathrm{O}\&\mathrm{M}\mathrm{w},\mathrm{O}\&\mathrm{M}\mathrm{s},\mathrm{C}\mathrm{A}\mathrm{P}\mathrm{E}\mathrm{X}\mathrm{w},\mathrm{C}\mathrm{A}\mathrm{P}\mathrm{E}\mathrm{X}\mathrm{s},\mathrm{W},\mathrm{S},\mathrm{f}\left(\mathrm{w}\right),\mathrm{f}\left(\mathrm{s}\right),\mathrm{S}\mathrm{T}\mathrm{U}\mathrm{T}\left)\right]$$

(15)

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}:\mathrm{C}\mathrm{V}\left[\mathrm{I}\mathrm{R}\mathrm{R}\right(\mathrm{O}\&\mathrm{M}\mathrm{w},\mathrm{O}\&\mathrm{M}\mathrm{s},\mathrm{C}\mathrm{A}\mathrm{P}\mathrm{E}\mathrm{X}\mathrm{w},\mathrm{C}\mathrm{A}\mathrm{P}\mathrm{E}\mathrm{X}\mathrm{s},\mathrm{W},\mathrm{S},\mathrm{f}\left(\mathrm{w}\right),\mathrm{f}\left(\mathrm{s}\right),\mathrm{S}\mathrm{T}\mathrm{U}\mathrm{T}\left)\right]$$

(16)

Both are subject to the same constraints, as shown in Equation (17):

$$\begin{gathered} \mathrm{W}+\mathrm{S}=1 \\ \mathrm{W}\in \{0,0.05,0.10,\dots ,1\} \\ \mathrm{f}\left(\mathrm{w}\right)~\mathrm{N}({P50}_w,{\mathsf{\sigma }}_w^2) \\ \mathrm{f}\left(\mathrm{s}\right)~\mathrm{N}({P50}_s,{\mathsf{\sigma }}_s^2) \end{gathered}$$

(17)

Considering that the sum of W and S must equal one unity, the constraints guarantee that the installed capacity of the HRES will be completely distributed among wind and solar sources. The simulation has been conducted in steps of 5% ranging from 0% to 100% of wind. It has been assumed that the long-term production uncertainty of energy follows a Gaussian distribution.

2.2. Data and Variables Modeled

Empirical and hypothetical data were used to evaluate the model. Observable data is based on real case studies in Brazil, while hypothetical data is based on plausible but not necessarily observed conditions. This study considered the Cost Parameters Notebook for Generation and Transmission [34] to estimate CAPEX, disbursement, 50th percentile, tributes, and O&M, while the results from the 37th Brazilian Energy Auction [26] were used to estimate the PPA price. Due to its highly unpredictable nature, the spot market has been considered a theoretical variable.

The values for TSUT are defined by the Brazilian Electricity Regulatory Agency (ANEEL) on each regulatory cycle. The values vary according to the location. Geographical, technological, and economic factors influence the costs of infrastructure in different regions, which makes it difficult to predict. As a result of the requirement for robust equipment or specialized technologies, areas with a high energy demand may face higher costs, which will affect the tariff. In addition, regions with more complex or extensive transmission networks may have experienced an increase in TSUT because of the greater costs associated with their management and maintenance. In order to simplify the modeling process, it has been assumed that TSUT starts on a flat value that will be adjusted for inflation throughout the lifecycle of the project.

Depending on the complexity of the project, the disbursement schedule may vary. A specific payment condition may affect the monthly disbursement rate, which is the percentage of total CAPEX to be disbursed each month. Based on [35], the average disbursement period for onshore wind and solar is 24 months and 12 months, respectively. In terms of stand-alone setups, the O&M expenses for wind power are 80% higher than those for solar power. As for onshore wind, CAPEX varies from 3.8 to 5.0 M BRL/MW (millions of Brazilian reals per megawatt), and as for solar, it varies from 2.8 to 4.5 M BRL/MW.

The variables were considered theoretical for the long-term debt modeling. The credit rating of a borrower, financing terms, and availability may differ significantly. According to a corporation’s financial health and market standing, it may be possible to secure financing at a more favorable rate, which will impact the IRR.

Constant amortization service, or CAS, is a loan repayment method in which the principal amount is repaid in consistent, equal payments over the course of the loan. Consequently, the total payment is reduced over time due to a decrease in interest payments and a decrease in outstanding principal.

Variables such as the price PPA, price spot market, CAPEX, sectorial charges, O&M, and TSUT are adjusted annually for inflation. The projected inflation may vary depending on macroeconomic conditions but has been considered flat throughout the life of the project. Although $K_e$ is a strategic and non-observable variable, this study considered the estimated regulatory $K_e$ for energy generation published by ANEEL [36].

Table 2. General modeling variables.

Variable	Value	Unit of Measurement	Data Type	Data Source
Price_PPA	175	BRL/MWh	Empirical	[35]
Price_Spot_Market	200	BRL/MWh	Assumption	AA
CAPEX_Wind	5.50	M BRL/MW	Empirical	[34]
CAPEX_Solar	4.00	M BRL/MW	Empirical	[34]
Initial period of the cash flow	1	Month	Assumption	AA
Disbursement Schedule	24	Months	Empirical	[34]
Monthly Disbursement Rate	1/24	Percentage	Assumption	AA
Project lifetime	420	Months	Assumption	AA
P50_Wind	47.00%	Percentage	Empirical	[34]
P90_Wind	35.29%	Percentage	Assumption	AA
Standard_Deviation Wind	10.00%	Percentage	Assumption	AA
P50_Solar	31.94%	Percentage	Empirical	[34]
P90_Solar	29.65%	Percentage	Assumption	AA
Standard_Deviation_Solar	5.00%	Percentage	Assumption	AA
Degradation_Factor_Solar	0.40% p.a.	Percentage	Assumption	AA
Installed_Capacity	100	Megawatts (MW)	Assumption	AA
Sectorial_Charges	150	BRL/kW/year	Empirical	[34]
O&M_Expenses_Wind	90	BRL/kW/year	Empirical	[34]
O&M_Expenses_Solar	50	BRL/kW/year	Empirical	[34]
Taxation_Regime	Presumed Profit Regime	-	Assumption	AA
Tributes	3.65%	Percentage	Assumption	[34]
TSUT	65.40	BRL/kW/year	Assumption	AA
$K_e$	9.67%	Percentage p.a.—real terms	Empirical	[36]
Projected_inflation	4.00%	Percentage p.a.	Assumption	AA

presents the variables grouped in the “General” category, where “AA” stands for authors’ assumptions.

The assumption of some variables has been made for a variety of reasons. Due to the hydrological regime in Brazil, the spot market price is highly uncertain. This description also applies to TSUT for the reasons discussed in Section 2.1.2. The initial period of the cash flow is used for modeling purposes, as well as the installed capacity. Monthly disbursement rates represent the CAPEX disbursement schedule and are determined by the contract with third parties.

Depending on the regulatory framework, the project lifetime may vary. Although a P50 interval can be obtained for wind and solar in [34], the P90 and standard deviation for each source depend on specific wind and solar characteristics that also consider degradation. The taxation regime has been assumed based on the current Brazilian legislation. The projected inflation rate has been set at 4.0% in light of the country’s macroeconomic uncertainties.

Table 3. Long-term debt.

Variable	Value	Unit of Measurement	Data Type	Data Source
Financed_amount	80%	Percentage of CAPEX	Assumption	[37]
Interest	7.49%	Percentage per year	Assumption	AA
Release_date	13th	Month of the cash flow	Assumption	AA
Grace_period	13th–30st	Months	Assumption	AA
Amortization_start_period	31st	Month of the cash flow	Assumption	AA
Amortization_end_period	318th	Month of the cash flow	Assumption	AA
Amortization_type	CAS	-	Assumption	AA

presents the financing assumptions considered in this study.

A company’s debt issuance conditions, specifically the amount financed, can vary according to its credit score and can be influenced by macroeconomic factors. The financed amount has been considered as the maximum possible [37], which may not be appropriate for every company. The other variables have been assumed for modeling purposes.

CAS (constant amortization system) refers to a method of repaying loans in Brazil in which the borrower pays off a fixed amount of principal at regular intervals while interest rates decline, amortization remains constant, and overall payments decrease.

3. Results

The findings of the HRES assessment are summarized in this section by presenting the optimal combinations, results of the statistical tests, sensitivity analysis, and synergies between costs and revenues.

3.1. Convergence Test

The purpose of this test is to confirm the validity of the outputs and to ensure that the simulations performed are sufficient to produce accurate results. Several simulations have been performed to determine the number of simulations required to obtain a reliable estimate. The results are presented in

Table 4. Convergence results.

Iterations	Std Deviation	Std Error
200	2.90%	0.20%
300	2.89%	0.17%
400	2.80%	0.14%
500	2.80%	0.13%
600	2.80%	0.11%
700	2.78%	0.11%
800	2.76%	0.10%
900	2.75%	0.09%
1000	2.74%	0.09%
1100	2.77%	0.08%
1200	2.75%	0.08%
1300	2.74%	0.08%
1400	2.75%	0.07%
1500	2.73%	0.07%

:

A decreasing standard error indicates that there is an increase in precision as interactions are increased. Stabilized standard deviations are indicative of a steady process.

In Figure 1, the values in Table 4 are represented visually.

As a result, adding more iterations is unlikely to make a significant difference in the outcome since the gain in precision may be minor.

3.2. IRR and CV Results

The results of the simulations are presented in

Table 5. HRES economic results.

Wind–Solar Combinations	IRR P50	CV	Std Error	Lower Bound	Upper Bound	Optimal Combination?
100–0%	18.02%	14.27%	0.066%	17.89%	18.15%	No
95–5%	18.49%	12.90%	0.062%	18.37%	18.61%	No
90–10%	18.82%	11.94%	0.058%	18.71%	18.93%	No
85–15%	19.05%	11.23%	0.055%	18.94%	19.16%	No
80–20%	19.22%	10.68%	0.053%	19.12%	19.33%	No
75–25%	19.36%	10.20%	0.051%	19.26%	19.46%	No
70–30%	19.45%	9.76%	0.049%	19.35%	19.55%	No
65–35%	19.51%	9.34%	0.047%	19.41%	19.60%	No
60–40%	19.53%	8.96%	0.045%	19.44%	19.62%	Yes, highest IRR.
55–45%	19.51%	8.60%	0.043%	19.43%	19.60%	No
50–50%	19.46%	8.29%	0.042%	19.37%	19.54%	No
45–55%	18.97%	8.10%	0.040%	18.90%	19.05%	No
40–60%	18.44%	7.97%	0.038%	18.36%	18.51%	No
35–65%	17.84%	7.92%	0.036%	17.77%	17.91%	Yes, lowest CV.
30–70%	17.18%	7.97%	0.035%	17.11%	17.25%	No
25–75%	16.45%	8.15%	0.035%	16.39%	16.52%	No
20–80%	15.66%	8.47%	0.034%	15.59%	15.73%	No
15–85%	14.79%	9.00%	0.034%	14.72%	14.86%	No
10–90%	13.77%	10.09%	0.036%	13.70%	13.84%	No
5–95%	12.28%	13.14%	0.042%	12.20%	12.36%	No
0–100%	9.31%	22.38%	0.054%	9.20%	9.42%	No

. For each wind–solar combination, the 50th percentile of the IRR, CV, and standard error of the IRR have been calculated. Lower and upper bounds have been calculated using 95% confidence intervals. The wind–solar combinations indicate the percentage of each source relative to the HRES installed capacity.

The standard error measures the uncertainty associated with predicted values. The optimal wind–solar combination is found to occur at 60–40% (maximize the IRR) and 35–65% (minimize the CV).

Figure 2 illustrates the visual representation of the IRR.

Moving from a position based solely on wind to a position based on 60% wind and 40% solar produces the highest IRR of 19.53 percent. Figure 3 presents a visual representation of the CV.

A stand-alone configuration based exclusively on solar exhibits the highest CV. The lowest CV of 7.92% was achieved by a solar-dominant combination of 65% solar and 35% wind.

3.3. Confidence Intervals

Confidence intervals can be used to quantify the uncertainty associated with the outputs, improving the accuracy of the model. Figure 4 illustrates the IRR, confidence interval, and standard error presented in Table 5.

The lower and upper bounds represent conservative estimates of the IRR. Based on a 95% confidence interval, the lower bound represents the 2.5th percentile, and the upper bound represents the 97.5th percentile of the IRR. Values assure the reliability of estimates.

3.4. Probability Distributions

Figure 5 illustrates the probability distributions for the HRES combinations wind-solar of 60–40% (maximize IRR) and 35–65% (minimize CV). For risk analysis, this analysis is useful since it compares the different IRR behavior between the two strategies.

A change from a Minimize CV distribution (blue) to a Maximize IRR distribution (red) increases the IRR at the cost of a higher degree of uncertainty.

3.5. Synergies

The combination of solar and wind energy in an HRES configuration results in synergies that contribute to maximizing the economic results presented in the following sections. Presented below is an analysis of the synergies from a cost and revenue perspective.

3.5.1. Costs

Figure 6 shows, in nominal terms, the sum of selected variables impacted by synergy gains, such as CAPEX, O&M, and TSUE. The secondary y-axis presents the IRR and CV results, as well as the HRES combinations of wind and solar.

A reduction in CAPEX and O&M can be noted from a stand-alone wind to a stand-alone solar configuration. However, TSUE exhibits a different pattern of behavior. At 50% wind, its value decreases to its minimum and, therefore, increases.

3.5.2. Revenues

Similar to Figure 6, the PPA and SM revenues are presented in nominal terms in Figure 7. Revenue patterns differ from those found in costs.

From a stand-alone wind to a stand-alone solar configuration, the total revenue (TOTAL) decreases linearly. In relation to the wind–solar combinations, the revenue PPA and revenue SM exhibit convex behavior.

3.6. Sensitivity Analysis

The variables have been analyzed based on their most influential sources of uncertainty through a sensitivity analysis.

Table 6. Sensitivity analysis results–highest IRR HRES combination.

Variable	Disadvantage	Advantage	Interval	Explained Variation	Elasticity
Financed_amount	18.94%	24.51%	5.57%	63.48%	1.62
CAPEX_Wind	22.93%	19.59%	3.34%	86.34%	−0.98
Price_PPA	20.19%	22.16%	1.97%	94.24%	0.58
CAPEX_Solar	22.01%	20.39%	1.62%	99.60%	−0.48
O&M_Expenses_Wind	21.33%	21.02%	0.31%	99.79%	−0.09
TSUT	21.33%	21.03%	0.30%	99.97%	−0.09
O&M_Expenses_Solar	21.23%	21.12%	0.11%	100.00%	−0.03
P50_Solar	21.18%	21.18%	0.00%	100.00%	0.00
P50_Wind	21.18%	21.18%	0.00%	100.00%	0.00

presents the results of the 60% wind HRES combination for selected variables.

Both disadvantages and advantages are related to changes in the outcome variable per unit change in the predictor variable. With 63.48% of its variation explained by the financed amount, which represents the percentage of borrowed capital in relation to CAPEX, the variable exhibited the greatest impact on IRR.

As a measure of a relatively sensitive relationship, elasticity refers to the responsiveness of the outcome (IRR) to a change in an input variable. The sign of the elasticity value indicates the direction of the relationship between the input and the output. Positive results indicate a direct relationship. An inverse relationship is perceived if the relationship is negative.

Table 7. Sensitivity analysis results—lowest CV HRES combination.

Variable	Disadvantage	Advantage	Interval	Explained Variation	Elasticity
Financed_amount	16.63%	21.17%	4.54%	57.13%	1.52
CAPEX_Solar	19.85%	17.20%	2.65%	76.60%	−0.90
Price_PPA	17.42%	19.51%	2.09%	88.76%	0.71
CAPEX_Wind	19.48%	17.52%	1.96%	99.42%	−0.66
TSUT	18.64%	18.28%	0.36%	99.78%	−0.12
O&M_Expenses_Solar	18.56%	18.36%	0.20%	99.89%	−0.07
O&M_Expenses_Wind	18.56%	18.37%	0.20%	100.00%	−0.07
P50_Solar	21.18%	21.18%	0.00%	100.00%	0.00
P50_Wind	21.18%	21.18%	0.00%	100.00%	0.00

shows the results of the 35% wind HRES combination.

Similar to Table 6, the variable financed amount represents the highest explained variation and elasticity, suggesting that access to resources (securing debt) is essential to the viability of the HRES.

4. Discussion

The results indicate that specific HRES configurations provide higher IRRs and lower CVs than stand-alone configurations, resulting in greater economic benefits from expanding the energy supply through HRESs rather than stand-alone configurations. Even though this study is based on a different perspective than the LCOE, the findings regarding HRES preference are similar to those reported in [14,15,16,17,18,19,20,21,22,24].

Results from 1.500 iterations indicate that the IRR predictor is statistically reliable with low standard errors and deviations. For every wind–solar combination, the lower and upper bounds provided a range of possible values for the IRR, which lay between the thresholds. According to the assumptions considered in this study, the optimal combinations to maximize the IRR and minimize the CV were 60/40 and 35/65, respectively. Synergies modeled contributed to making the HRES preferable for maximizing the IRR and minimizing the CV. The use of a hybrid approach has been found to be superior to achieve better economic results in this study, similar to those reported in [25,26,27,28] while applying other hybrid approaches to overcome different challenges.

According to the sensitivity analysis, the financed amount of CAPEX is vital to the attractiveness of the HRES. As can be seen from the elasticities found for the highest IRR (1.62) and the lowest CV (1.52), both outcomes are highly sensitive to changes in the amount of debt. Although the positive sign of elasticity for the IRR indicates a desirable outcome (more debt, higher IRR), the same cannot be said for the CV (more debt, higher CV). It is important to note that the annual interest rate assumed for the long-term debt is lower than the internal rate of return. In this situation, an increased amount of debt at a lower cost than the IRR will increase the effective IRR. Energy system expansion may be compromised if there is no external funding available at a competitive cost for both HRES and stand-alone configurations.

Based on the probability distributions of the optimal HRES combinations, shifting from a set-up that minimizes the CV to a set-up that maximizes the IRR increases the expected return at the cost of increased volatility. The CV provides valuable information regarding risk factors. Generally, wind energy has a higher capacity factor. However, it also has a higher standard deviation meaning a wind-dominant combination maximized CV and a solar-dominant combination minimized CV.

In terms of cost synergy, the CAPEX and O&M decreased linearly from the stand-alone wind configuration to the stand-alone solar configuration, contributing to an increase in the IRR. Both the operating and capital expenses associated with the HRES have decreased. Although solar has been considered to be less costly with regard to CAPEX (BRL 4 million for solar versus BRL 5.5 million for wind), its capacity factors are lower, and a degradation factor has been included. There is a possibility that CAPEX may change in the future, as suggested in [7], or that CAPEX ratios would differ between the various energy sources, which could adversely affect the results and undermine the HRES’ economic superiority. A linear decrease in total costs was observed until TSUE reached its minimum (50% wind and 50% solar). As a result, if wind and solar complement each other, as assumed in the study, then the HRES’ total dispatched energy is at its lowest at this point.

Analysis of revenue synergies can help determine why 50/50 failed to maximize the IRR or minimize the CV. TSUE, CAPEX, and O&M decreased linearly until the 50/50 combination; however, TOTAL revenue decreased linearly from a stand-alone wind configuration to a stand-alone solar configuration. Adding solar energy to a stand-alone wind set-up reduces the TOTAL revenue due to the lower P50 of solar energy.

As a result of adding solar to a stand-alone wind system, revenues intersected twice. In contrast to stand-alone wind configurations, stand-alone solar configurations have a negative revenue SM and a lower revenue PPA. As there is no retrofit investment in this study, the degradation factor reduces solar generation, resulting in late requirements to purchase electricity on the spot market in order to meet PPA obligations.

For future research, it would be desirable to address critical factors such as hourly energy prices on the spot market, complementarity between sources, the use of a battery energy storage system (BESS), optimal trading strategies, financing advantages for hybrid configurations, real options to the cash flow analysis, and a comprehensive analysis of synergies.

5. Conclusions

A dynamic cash flow analysis using stochastic and deterministic variables was used to estimate the optimal combination of wind and solar to maximize the 50th percentile IRR and minimize the CV for hypothetical HRES. Based on the results, a wind-dominant combination maximized the IRR, while a solar-dominant combination minimized the CV. Modeled synergies indicated that certain combinations of HRESs were more effective than stand-alone arrangements.

The IRR and CV may be affected differently by factors such as capacity factors, the amount financed, CAPEX, and the market price. When assessing the economic viability of a project, financing is an important factor to consider. Although the dynamic cash flow model was applied to a hypothetical premise, the results indicate that HRES combinations may provide better economic outcomes than stand-alone configurations depending on their synergies.

The HRES combinations presented in this study may not be appropriate for all situations. Combined wind and solar energy can result in higher IRRs and lower CVs; however, this behavior is dependent both on the complementary nature of the two energy sources as well as on the synergies that exist between the regulatory frameworks of the various countries. A HRES may be a more cost-effective alternative, but it may not be economically feasible and desirable if the sources do not complement each other and do not share any synergies.

The findings of this study have practical applications and can be used as a foundation tool in the strategic planning and development of HRESs. Further development can be made to the model to create a more accurate dynamic cash flow model capable of analyzing more accurately HRES configurations and synergies. Adapting this model, practitioners and policymakers can conduct feasibility studies and evaluate the economic and environmental benefits of integrating wind and solar energy systems, aligning with global efforts to achieve a more sustainable world with a zero-carbon footprint.