Cooperative Voltage and Frequency Regulation with Wind Farm: A Model-Based Offline Optimal Control Approach
Abstract
:1. Introduction
- The EMPC controllers enable cooperative and optimal control of frequency and voltage, facilitating simultaneous regulation of both parameters.
- The proposed control strategy addresses constraints using the Karush–Kuhn–Tucker (KKT) condition and effectively handles the multiparametric quadratic programming problem [22]. The controllers ensure that the power output of the wind farm remains within the specified limits.
- The simulation allows for adaptable modifications to the control magnitude. By adjusting the prediction horizons of the EMPC controller, the amplitude of the active and reactive power output from the wind farm can be customized.
2. System Description and Modeling
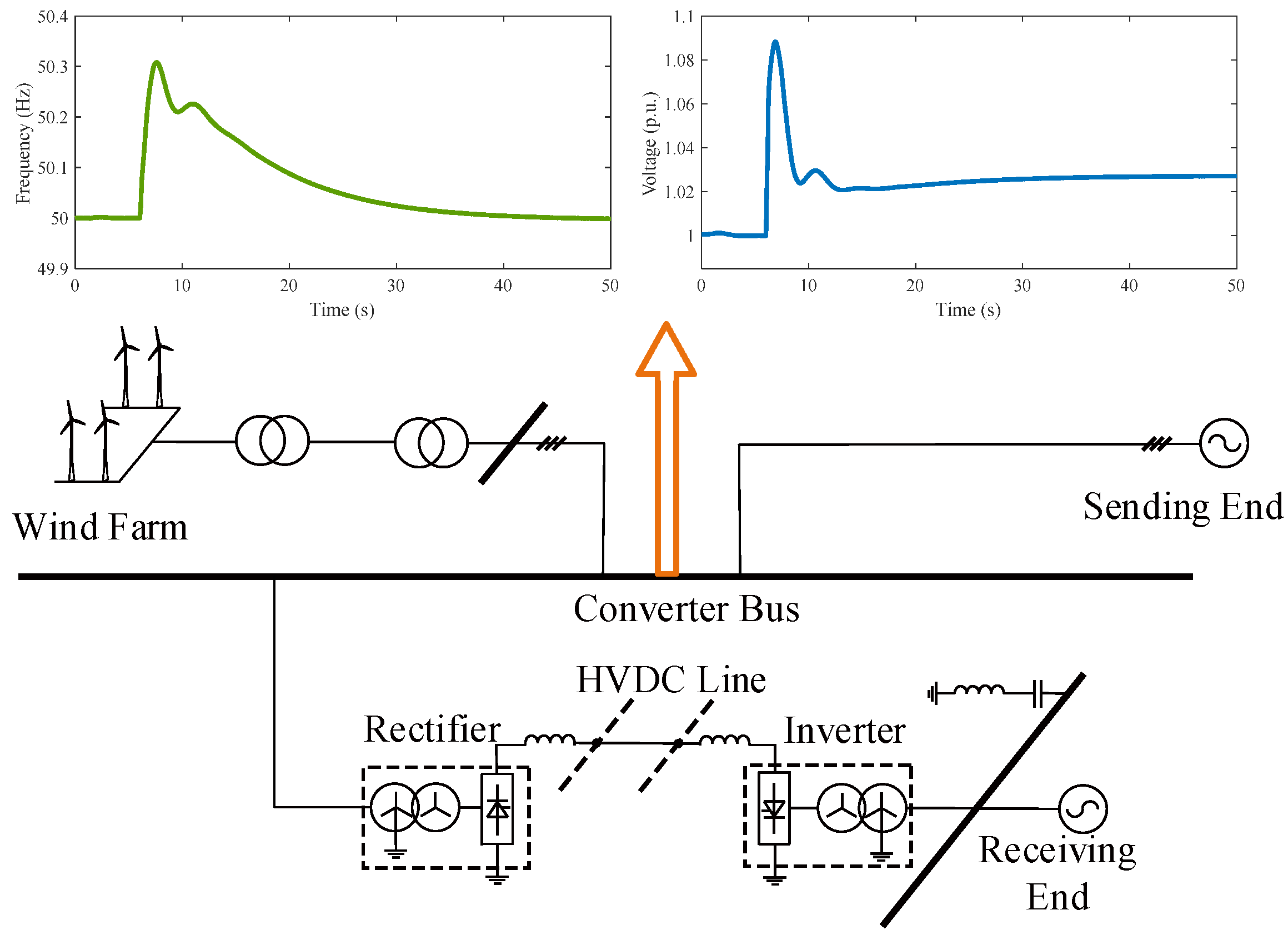
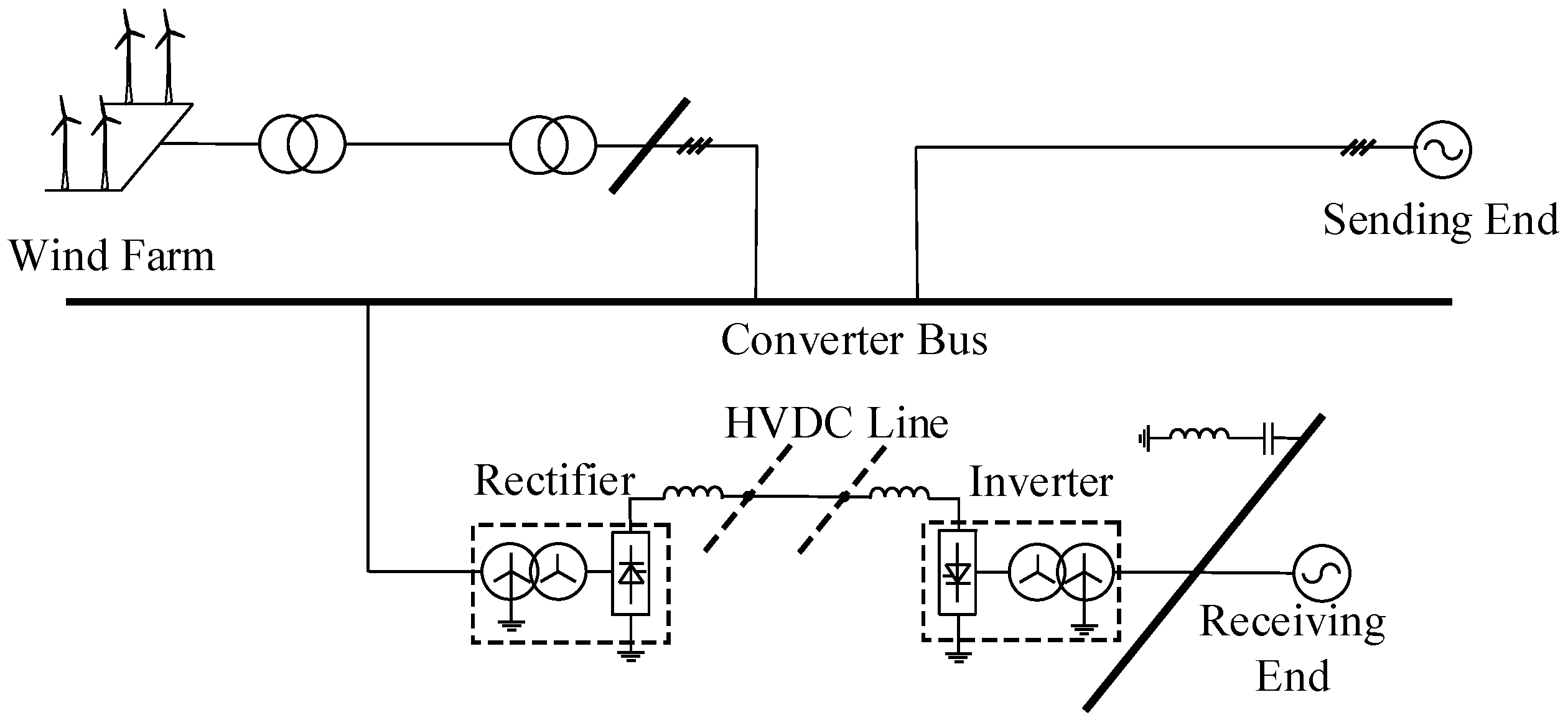
2.1. System Description
2.2. Frequency Dynamics Model
2.3. Voltage Dynamics Model
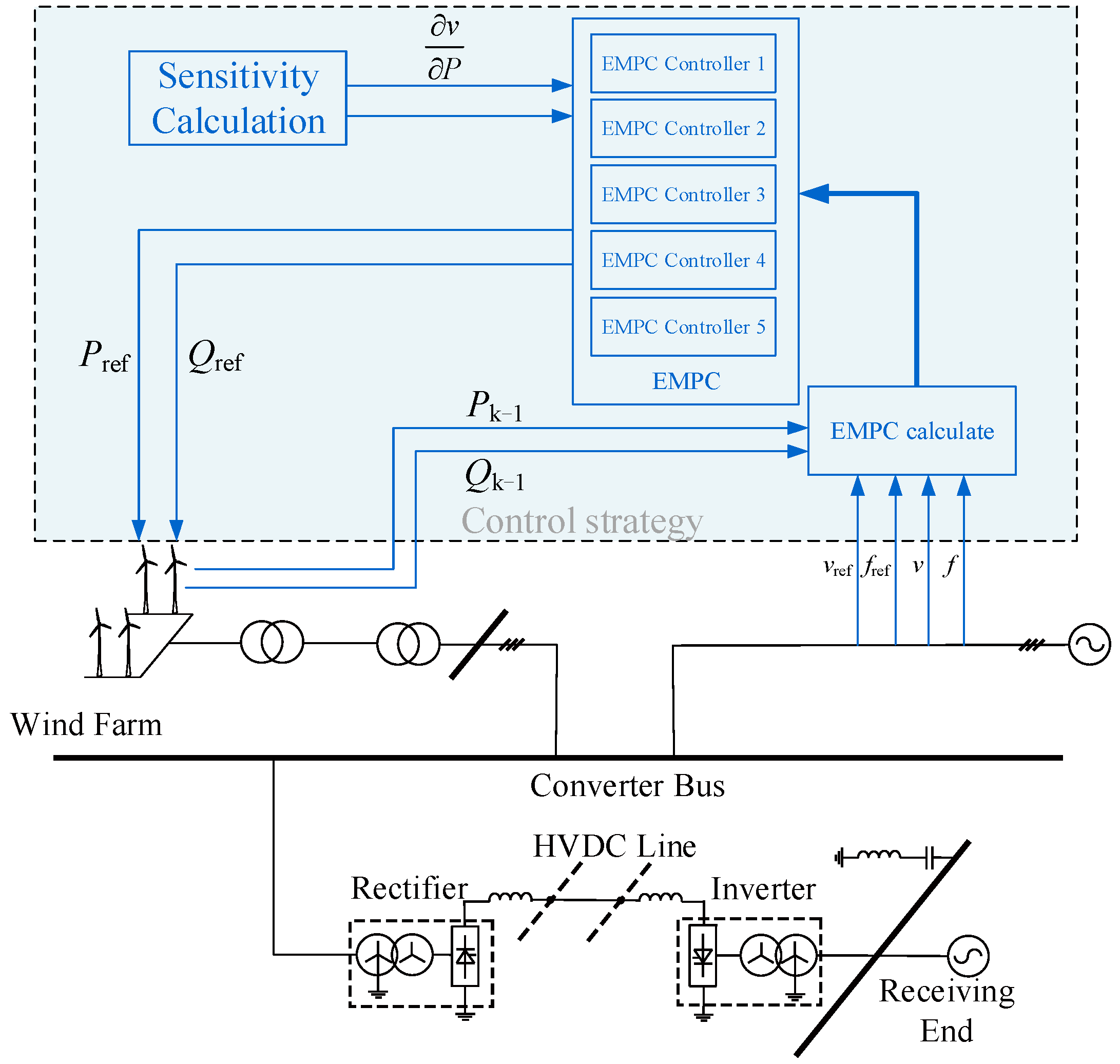
3. Control Strategy
3.1. Control Principle
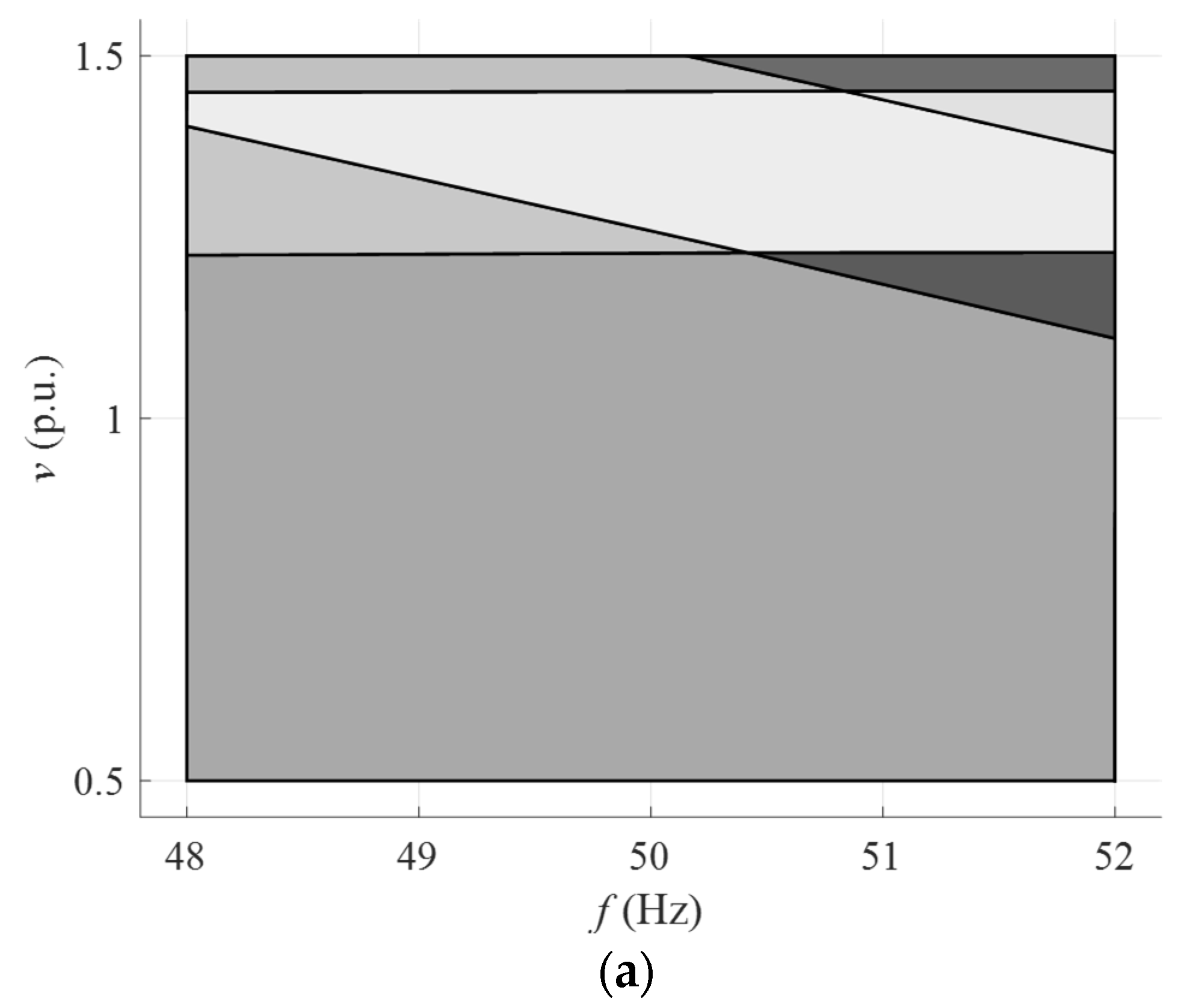
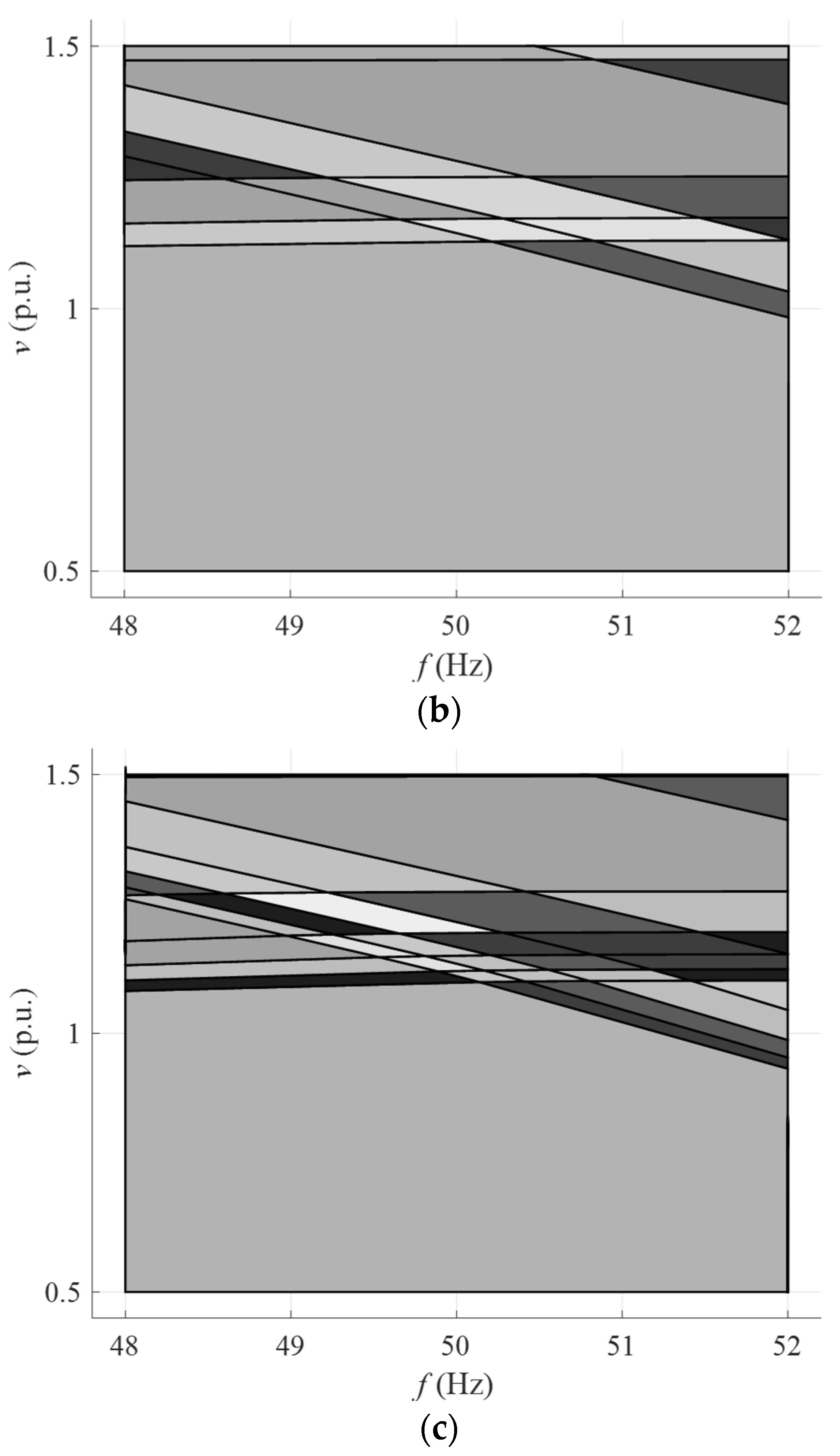
3.2. EMPC Controller Design
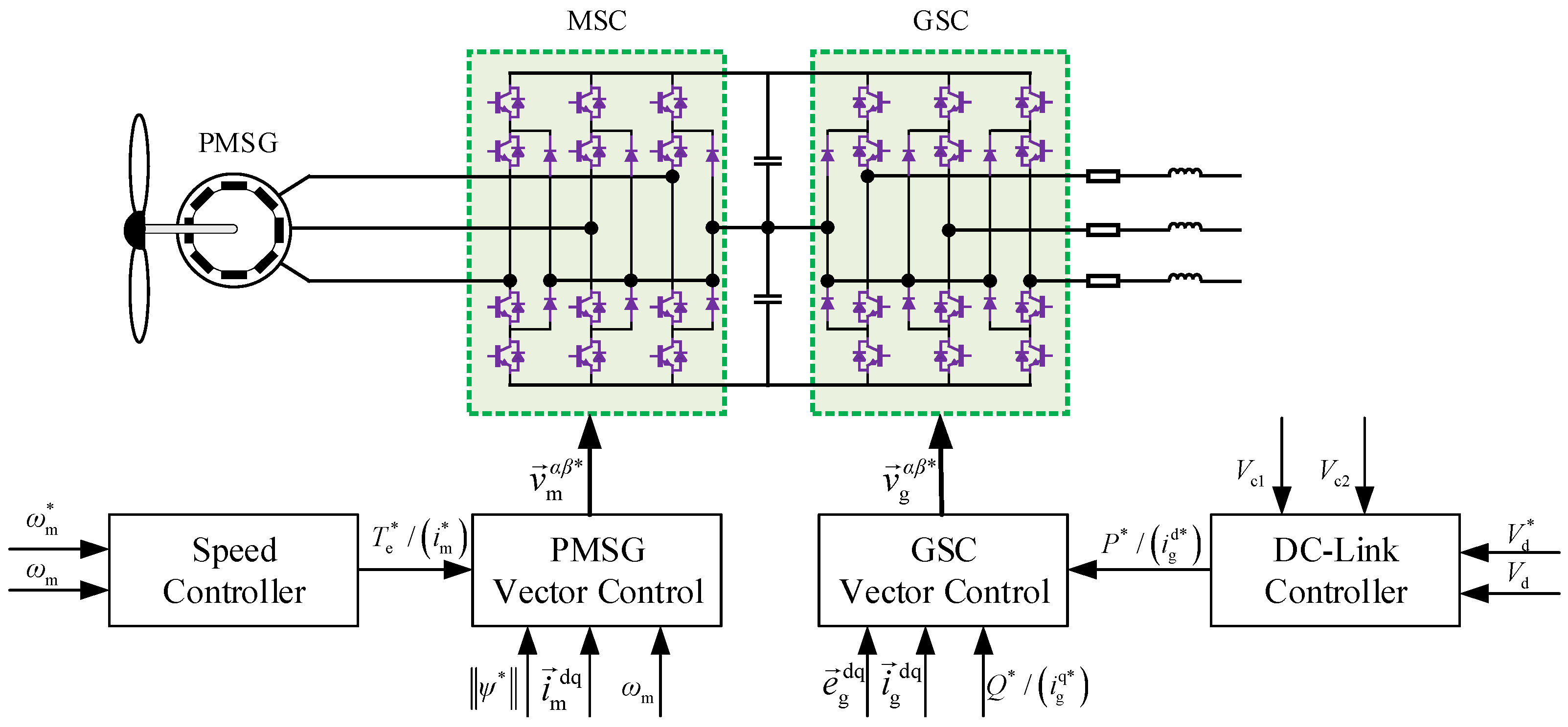
3.3. Wind Farm Local Controller Design
4. Simulation Studies
4.1. Simulation Setup
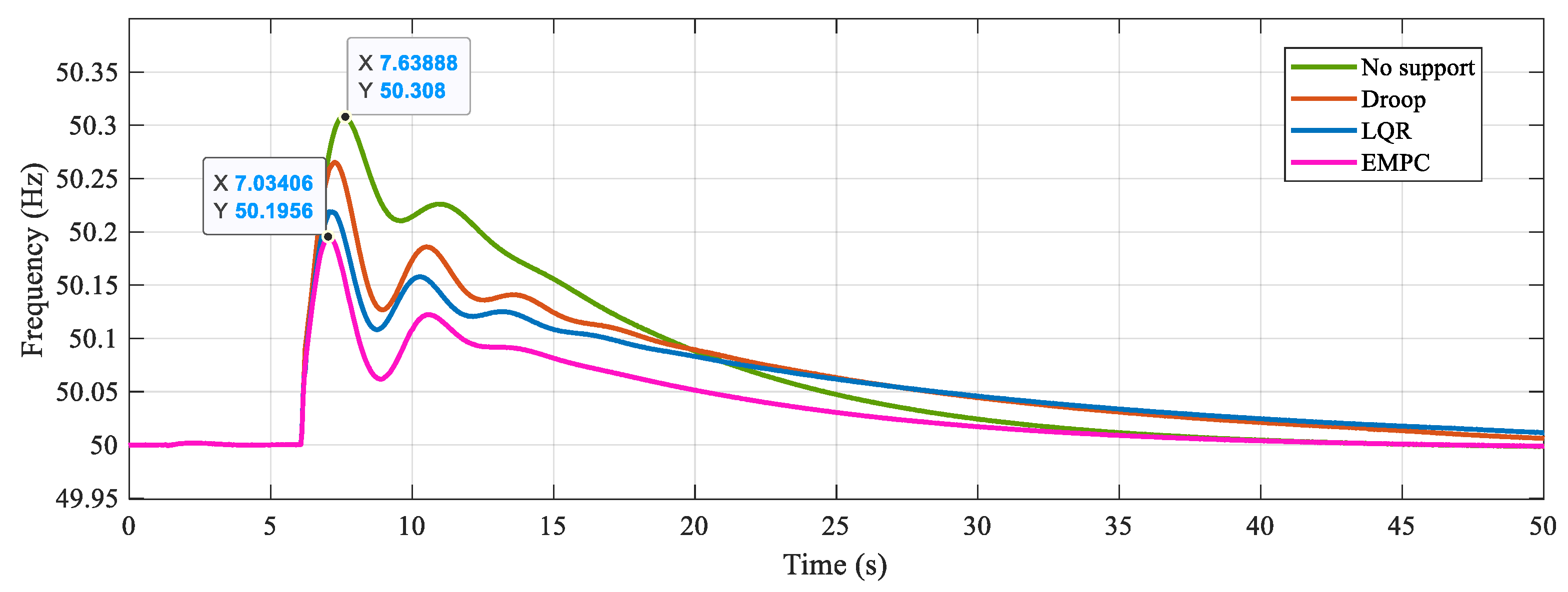
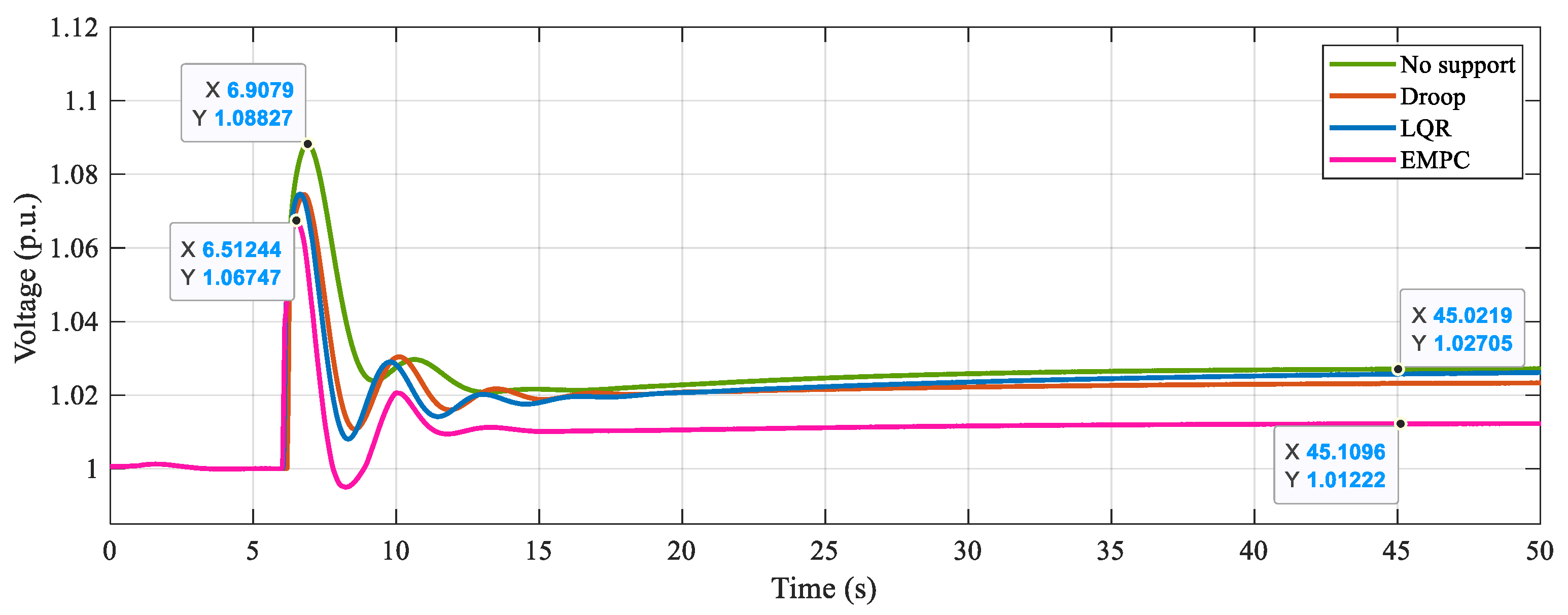
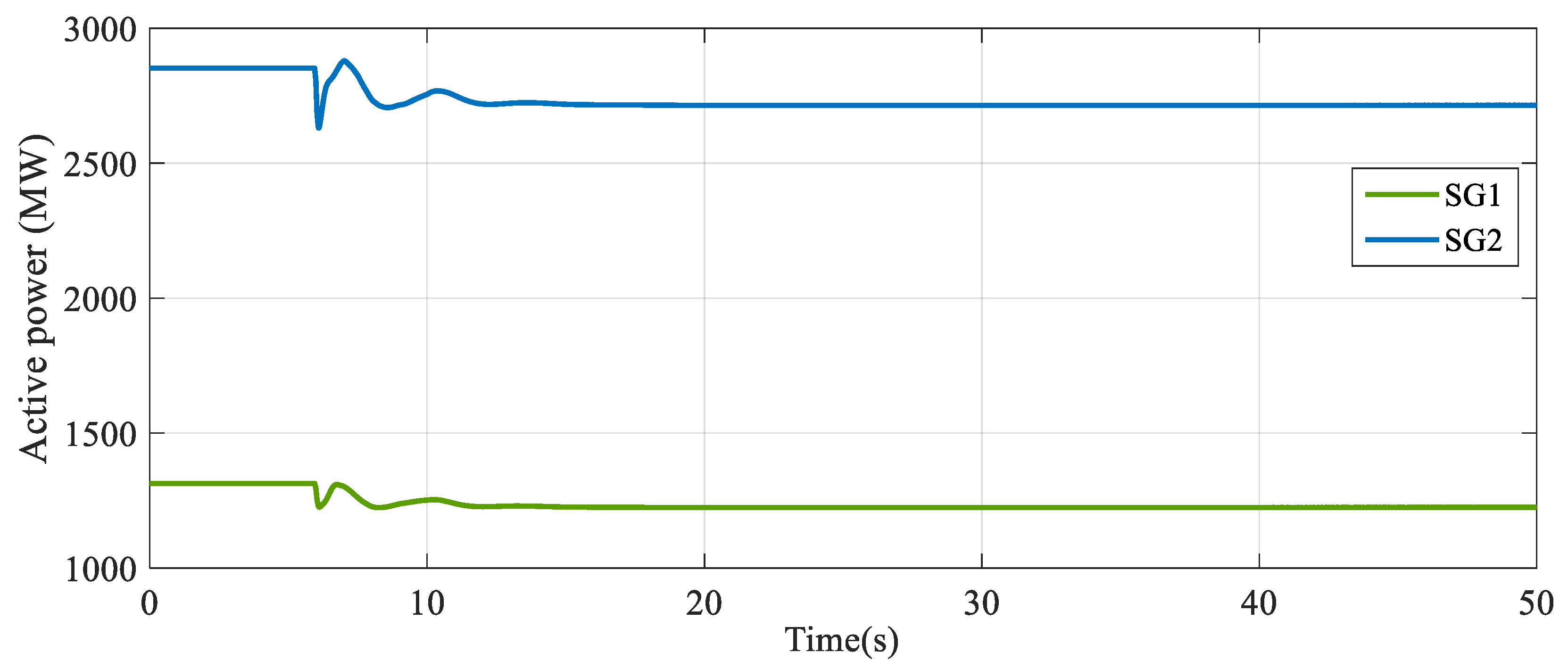
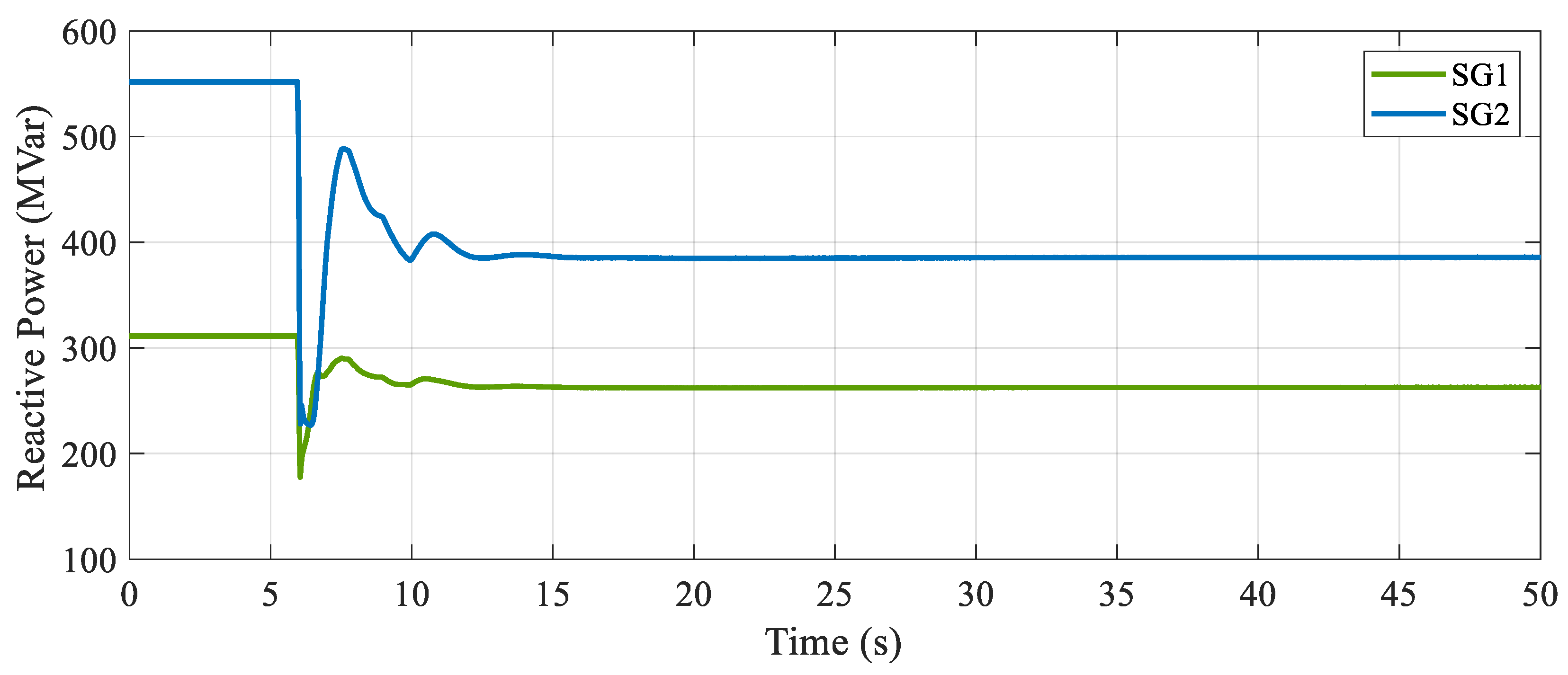
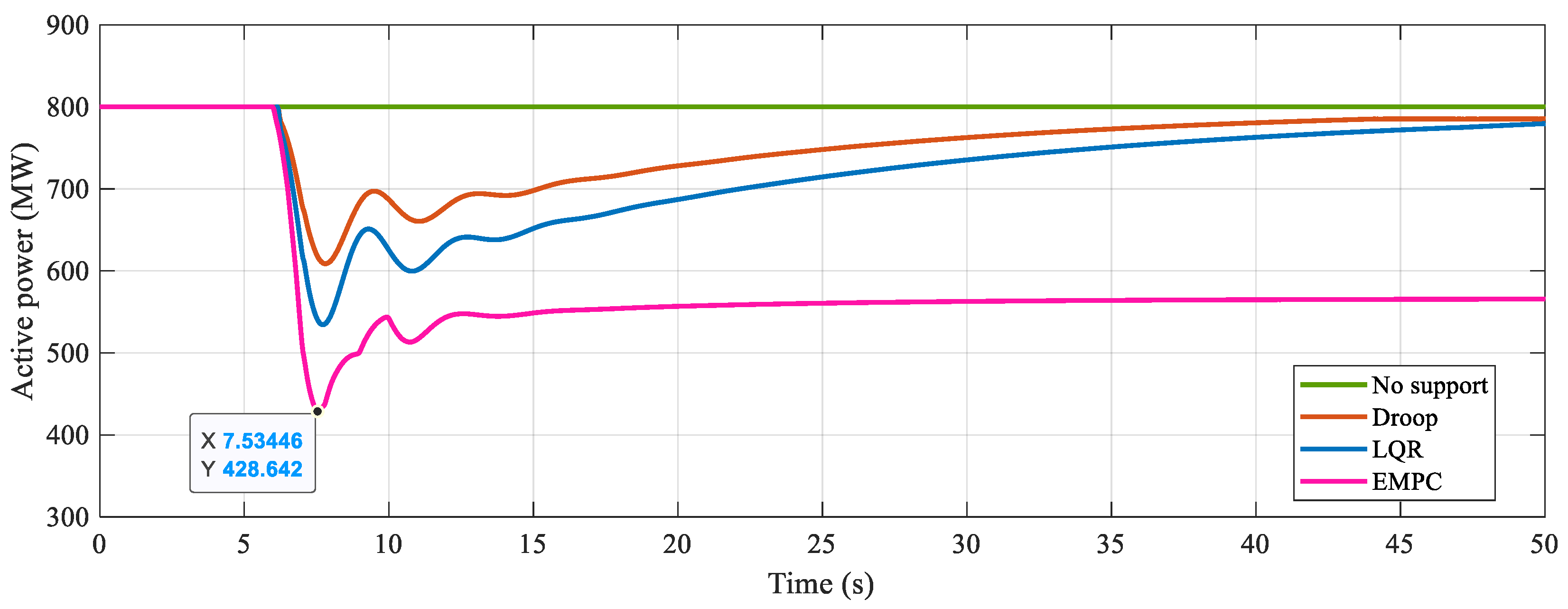
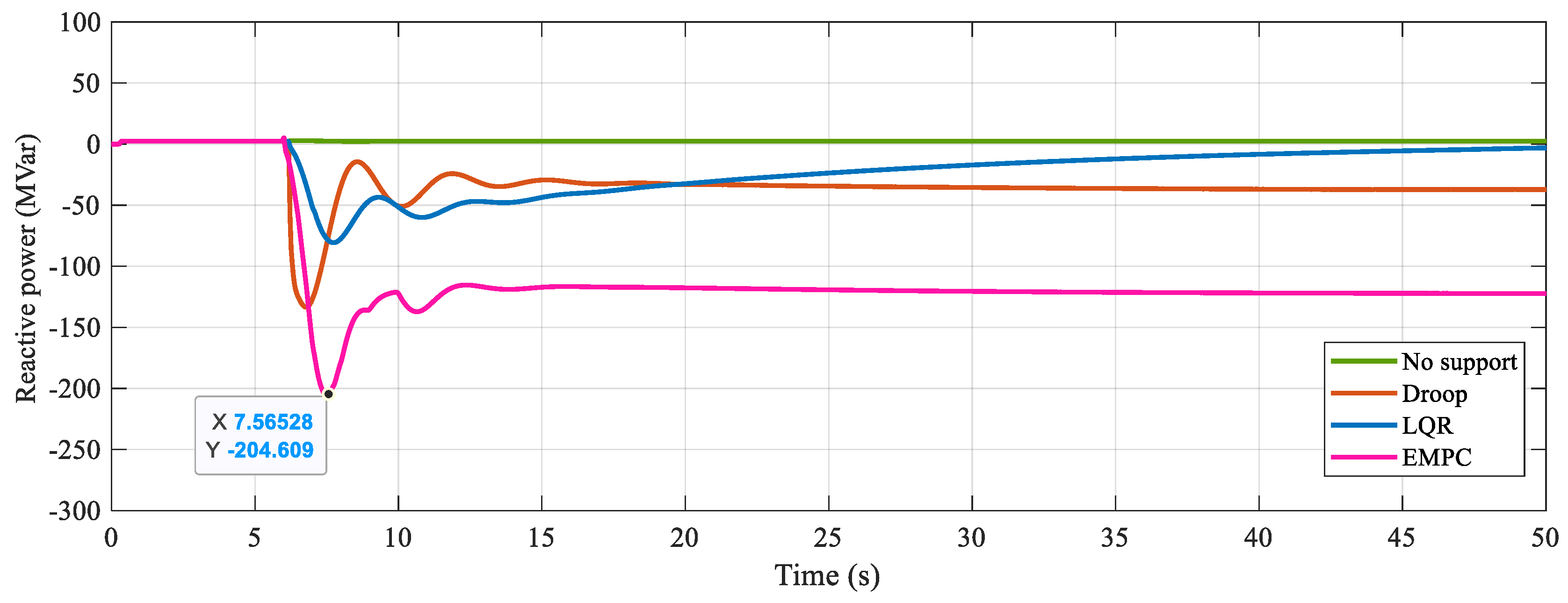
4.2. EMPC Control Performance
4.3. EMPC Controller Adjustment
4.4. Simulation Scenario Adjustment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pradhan, C.; Bhende, C.N.; Samanta, A.K. Adaptive virtual inertia-based frequency regulation in wind power systems. Renew. Energy 2018, 115, 558–574. [Google Scholar] [CrossRef]
- Toolabi Moghadam, A.; Sarani, E.; Rezaie, M.; Sheykhi, E.; Azimian, M.; Mohammed, A.H. Optimal Planning and Bidding Strategy for Wind Farms in Joint Balancing and Day-Ahead Energy Markets. IET Renew. Power Gener. 2022, 16, 3299–3310. [Google Scholar] [CrossRef]
- Wan, Y.; Mao, M.; Zhou, L.; Xi, X.; Xie, B.; Zhou, S. Review on topology-based dc short-circuit fault ride-through strategies for MMC-based HVDC system. IET Power Electron. 2020, 13, 203–220. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, C.; Fan, L.; Bo, R. Distributionally robust unit commitment with flexible generation resources considering renewable energy uncertainty. IEEE Trans. Power Syst. 2022, 37, 4179–4190. [Google Scholar] [CrossRef]
- Wang, W.; Xiong, X.; Li, M.; Yu, R. A flexible control strategy to prevent sending-end power system from transient instability under HVDC repetitive commutation failures. IEEE Trans. Power Syst. 2020, 35, 4445–4458. [Google Scholar] [CrossRef]
- Taylor, C.W.; Lefebvre, S. HVDC controls for system dynamic performance. IEEE Trans. Power Syst. 1991, 6, 743–752. [Google Scholar] [CrossRef]
- Shangguan, X.C.; He, Y.; Zhang, C.K.; Jin, L.; Yao, W.; Jiang, L.; Wu, M. Control performance standards-oriented event-triggered load frequency control for power systems under limited communication bandwidth. IEEE Trans. Control Syst. Technol. 2021, 30, 860–868. [Google Scholar] [CrossRef]
- Kumar, M.; Hote, Y.V. Robust PIDD2 controller design for perturbed load frequency control of an interconnected time-delayed power systems. IEEE Trans. Control Syst. Technol. 2020, 29, 2662–2669. [Google Scholar] [CrossRef]
- Lin, C.; Hu, B.; Shao, C.; Li, W.; Li, C.; Xie, K. Delay-dependent optimal load frequency control for sampling systems with demand response. IEEE Trans. Power Syst. 2022, 37, 4310–4324. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y.; Jia, H.; He, H. Energy-storage-based intelligent frequency control of microgrid with stochastic model uncertainties. IEEE Trans. Smart Grid 2020, 11, 1748–1758. [Google Scholar] [CrossRef]
- Liu, K.; Liu, T.; Tang, Z.; Hill, D.J. Distributed MPC-based frequency control in networked microgrids with voltage constraints. IEEE Trans. Smart Grid 2019, 10, 6343–6354. [Google Scholar] [CrossRef]
- de Oliveira, J.D.A.; de Araújo Lima, F.K.; Tofoli, F.L.; Branco, C.G.C. Synchronverter-based frequency control technique applied in wind energy conversion systems based on the doubly-fed induction generator. Electr. Power Syst. Res. 2023, 214, 108820. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Z.; Du, L.; Liu, Y.; Ding, Z. Coordination strategy of large-scale DFIG-based wind farm for voltage support with high converter capacity utilization. IEEE Trans. Sustain. Energy 2020, 12, 1416–1425. [Google Scholar] [CrossRef]
- Shaikh, U.A.; AlGhamdi, M.K.; AlZaher, H.A. Novel product ANFIS-PID hybrid controller for buck converters. J. Eng. 2018, 2018, 730–734. [Google Scholar] [CrossRef]
- Yadav, O.; Prasad, S.; Kishor, N.; Negi, R.; Purwar, S. Controller design for MTDC grid to enhance power sharing and stability. IET Gener. Transm. Distrib. 2020, 14, 2323–2332. [Google Scholar] [CrossRef]
- Xu, J.; Jia, Y.; Liao, S.; Lei, X.; Yu, J.; Gao, W.; Yao, L.; Ke, D.; Li, X.; Yang, J.; et al. Phasor measurement units-based fast voltage control strategy for distribution network with high-penetration distributed photovoltaic. IET Renew. Power Gener. 2023, 17, 1165–1179. [Google Scholar] [CrossRef]
- Debouza, M.; Ahmed, A. Grid ancillary services from doubly fed induction generator-based wind energy conversion system: A review. IEEE Access 2018, 7, 7067–7081. [Google Scholar] [CrossRef]
- Okyere, E.; Bousbaine, A.; Poyi, G.T.; Joseph, A.K.; Andrade, J.M. LQR controller design for quad-rotor helicopters. J. Eng. 2019, 2019, 4003–4007. [Google Scholar] [CrossRef]
- Beccuti, A.G.; Mariéthoz, S.; Cliquennois, S.; Wang, S.; Morari, M. Explicit model predictive control of DC–DC switched-mode power supplies with extended Kalman filtering. IEEE Trans. Ind. Electron. 2009, 56, 1864–1874. [Google Scholar] [CrossRef]
- Tian, N.; Fang, H.; Wang, Y. Real-time optimal lithiumion battery charging based on explicit model predictive control. IEEE Trans. Ind. Inform. 2020, 17, 1318–1330. [Google Scholar] [CrossRef]
- Lee, J.; Chang, H.J.; Ahn, H.S. Explicit MPC for column-type EPS systems. IET Electr. Power Appl. 2020, 14, 91–100. [Google Scholar] [CrossRef]
- Qiu, Y.; Lin, J.; Liu, F.; Song, Y. Explicit MPC based on the Galerkin method for AGC considering volatile generations. IEEE Trans. Power Syst. 2019, 35, 462–473. [Google Scholar] [CrossRef]
- Zhang, Y.; Kou, P.; Yu, L.; Liang, D. Coordinated voltage and frequency control for HVDC sending end under pole-block fault: Using model predictive control. Int. J. Electr. Power Energy Syst. 2022, 136, 107655. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Yu, L.; Gao, L. Nonlinear model predictive control of wind farm for system frequency support. IEEE Trans. Power Syst. 2019, 34, 3547–3561. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Bemporad, A.; Borrelli, F.; Morari, M. Model predictive control based on linear programming—The explicit solution. IEEE Trans. Autom. Control 2002, 47, 1974–1985. [Google Scholar] [CrossRef]
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of permanent-magnet generators applied to variable-speed wind-energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]
- Baccino, F.; Conte, F.; Grillo, S.; Massucco, S.; Silvestro, F. An optimal model-based control technique to improve wind farm participation to frequency regulation. IEEE Trans. Sustain. Energy 2015, 6, 993–1003. [Google Scholar] [CrossRef]
- Zhang, Z. On Control of Grid-Tied Back-to-Back Power Converters and Permanent Magnet Synchronous Generator Wind Turbine Systems. Ph.D. Thesis, Technische Universität München, München, Germany, 19 October 2016. [Google Scholar]
- Li, X.; Li, H.; Yan, Y.; Kou, P. Combined Frequency and Volt-age Support by Wind Farm with Linear Quadratic Regulator under Converter Blocking. In Proceedings of the 2022 12th International Conference on Power and Energy Systems (ICPES), Guangzhou, China, 23–25 December 2022; pp. 35–39. [Google Scholar]
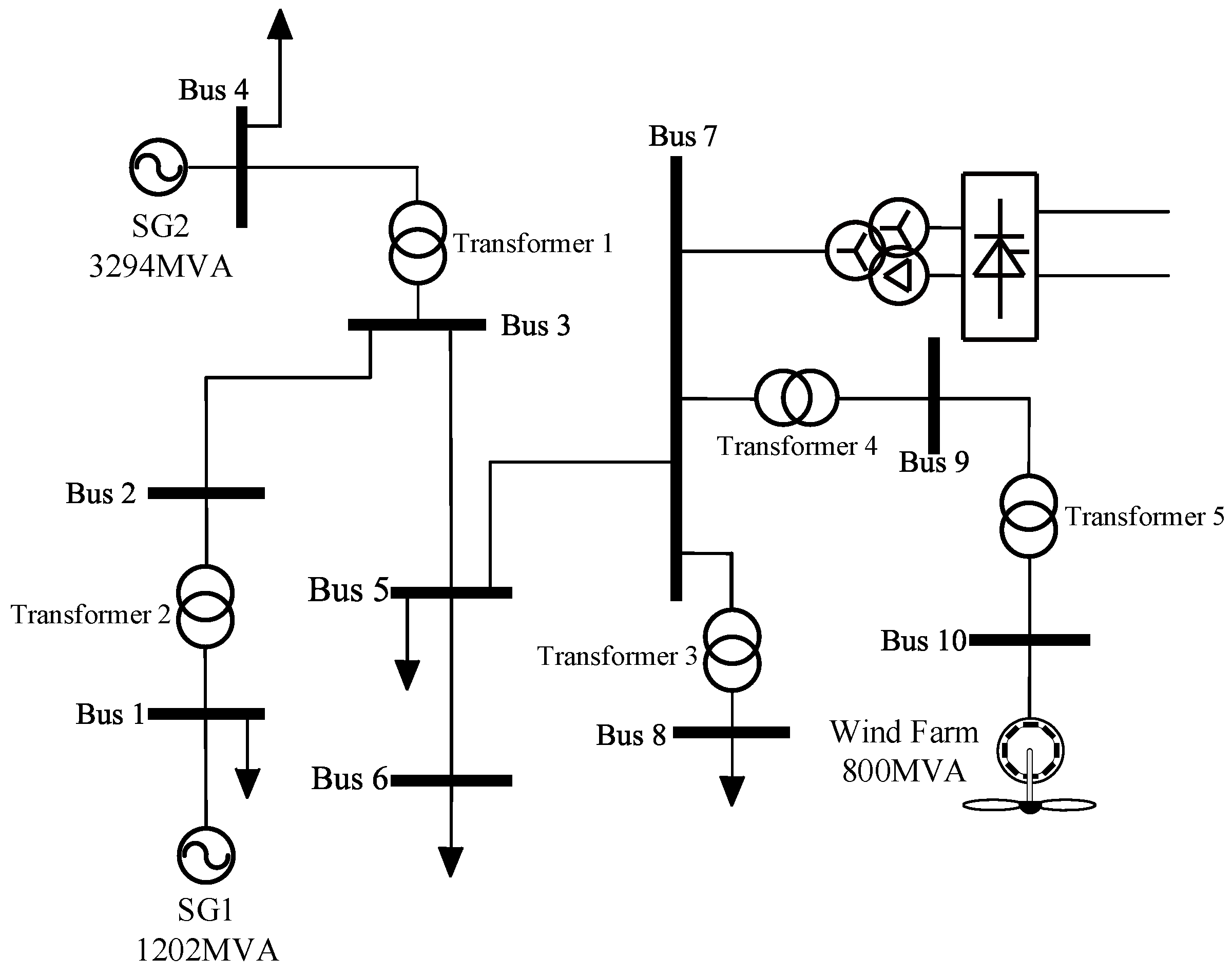
| The Three-Phase Transformer | Power (MVA) | V1/V2 (kV) |
|---|---|---|
| Transformer 1 | 2200 | 13.8/500 |
| Transformer 2 | 2200 | 13.8/500 |
| Transformer 3 | 1000 | 13.8/500 |
| Transformer 4 | 1000 | 13.8/500 |
| Transformer 5 | 1000 | 2.4/13.8 |
| AC Line | Resistance (Ohms) | Inductance (H) |
|---|---|---|
| Bus 2–Bus 3 | 1.067 | 0.078 |
| Bus 3–Bus 5 | 0.304 | 0.022 |
| Bus 5–Bus 6 | 0.14 | 0.010 |
| Bus 5–Bus 7 | 0.297 | 0.022 |
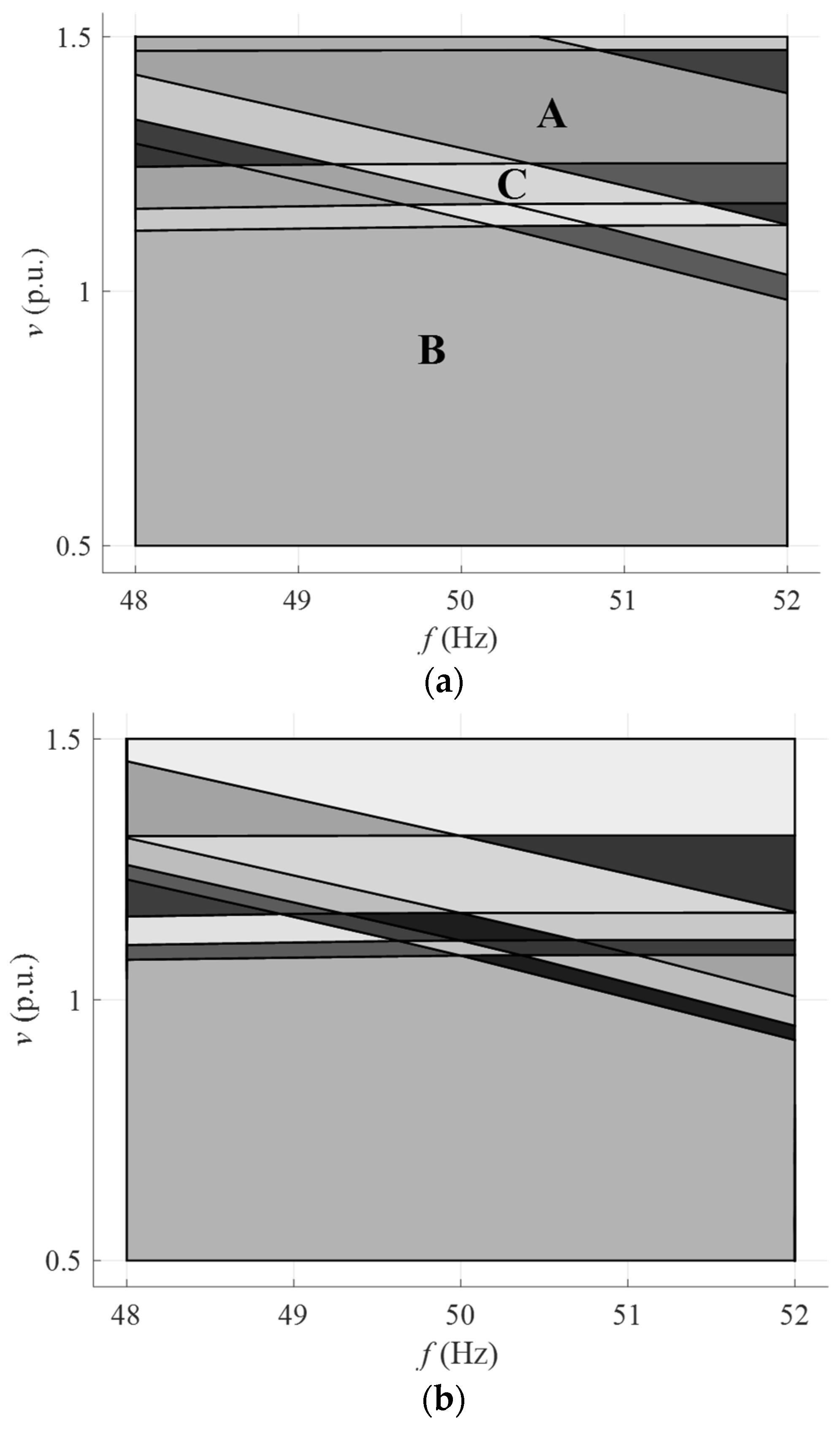
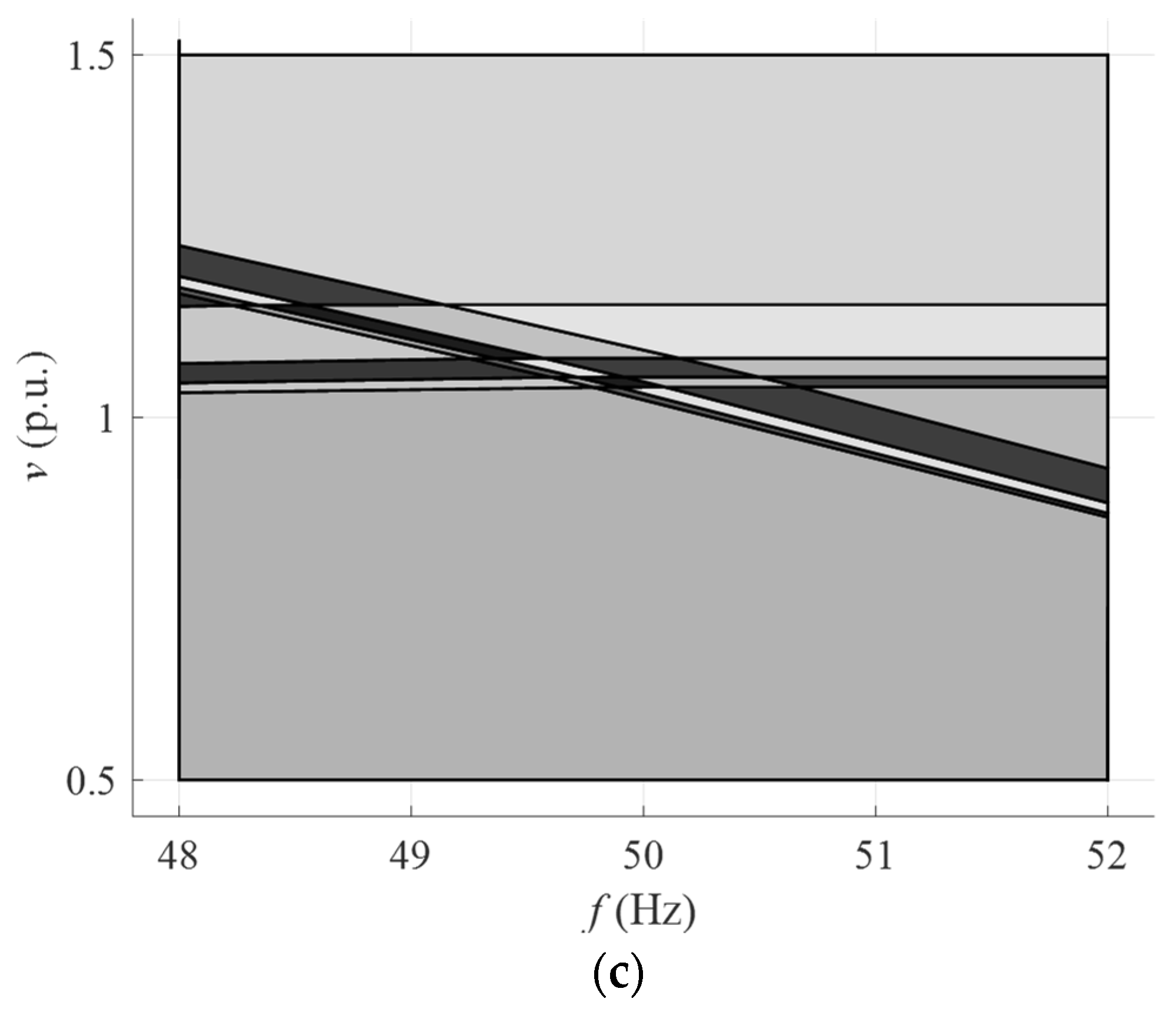
| Critical Region | F | g | A | b |
|---|---|---|---|---|
| A | ||||
| B | ||||
| C |
| Frequency Reduction (Hz) | Voltage Reduction (V) | Cost | Implementation Complexity | Advantages | Shortcomings | |
|---|---|---|---|---|---|---|
| Droop control | 0.043 | 0.014 | low | low | Simple implementation | No coordinated control |
| LQR control | 0.093 | 0.014 | moderate | high | Cooperative control | Cannot handle constraints |
| EMPC control | 0.112 | 0.021 | high | high | Cooperative control can be performed under constraints | Takes up more storage resources |
| Prediction Horizons | The Peak Value of Frequency (Hz) | The Peak Value of Voltage (p.u.) |
|---|---|---|
| 3 | 50.233 | 1.074 |
| 4 | 50.218 | 1.070 |
| 5 | 50.196 | 1.067 |
| 6 | 50.188 | 1.064 |
| 7 | 50.182 | 1.062 |
| Different Model | No Support | Droop Control | LQR Control | EMPC Control | |
|---|---|---|---|---|---|
| 600 MW | Peak frequency (Hz) | 50.339 | 5.290 | 50.241 | 50.232 |
| Peak voltage (V) | 1.093 | 1.078 | 1.078 | 1.069 | |
| 700 MW | Peak frequency (Hz) | 50.327 | 5.282 | 50.235 | 50.210 |
| Peak voltage (V) | 1.090 | 1.076 | 1.076 | 1.068 | |
| 800 MW | Peak frequency (Hz) | 50.308 | 50.265 | 50.219 | 50.196 |
| Peak voltage (V) | 1.088 | 1.075 | 1.075 | 1.067 | |
| Different Model | No Support | Droop Control | LQR Control | EMPC Control | |
|---|---|---|---|---|---|
| 400 MW/ 160 MVar | Peak frequency (Hz) | 50.250 | 50.226 | 50.181 | 50.163 |
| Peak voltage (V) | 1.068 | 1.058 | 1.058 | 1.052 | |
| 450 MW/ 180 MVar | Peak frequency (Hz) | 50.281 | 50.245 | 50.202 | 50.183 |
| Peak voltage (V) | 1.078 | 1.066 | 1.066 | 1.060 | |
| 500 MW/ 200 MVar | Peak frequency (Hz) | 50.308 | 50.265 | 50.219 | 50.196 |
| Peak voltage (V) | 1.088 | 1.075 | 1.075 | 1.067 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, X.; Xiong, W.; Yan, Y.; Zhang, Y.; Kou, P. Cooperative Voltage and Frequency Regulation with Wind Farm: A Model-Based Offline Optimal Control Approach. Energies 2023, 16, 6307. https://doi.org/10.3390/en16176307
Li H, Li X, Xiong W, Yan Y, Zhang Y, Kou P. Cooperative Voltage and Frequency Regulation with Wind Farm: A Model-Based Offline Optimal Control Approach. Energies. 2023; 16(17):6307. https://doi.org/10.3390/en16176307
Chicago/Turabian StyleLi, Hua, Xudong Li, Weichen Xiong, Yichen Yan, Yuanhang Zhang, and Peng Kou. 2023. "Cooperative Voltage and Frequency Regulation with Wind Farm: A Model-Based Offline Optimal Control Approach" Energies 16, no. 17: 6307. https://doi.org/10.3390/en16176307
APA StyleLi, H., Li, X., Xiong, W., Yan, Y., Zhang, Y., & Kou, P. (2023). Cooperative Voltage and Frequency Regulation with Wind Farm: A Model-Based Offline Optimal Control Approach. Energies, 16(17), 6307. https://doi.org/10.3390/en16176307





