Proof of Concept of a Novel Solid–Solid Heat Exchanger Based on a Double L-Valve Concept

Abstract

A proof of concept of a novel parallel-flow solid–solid heat exchanger consisting of two L-Valves with concentric vertical tubes, named as Double L-Valve, is presented for the case of the Carbonate Looping process, as a CO₂ capture technology. The operational objective of the solid–solid heat exchanger is to heat up the relatively cold solid stream coming from the carbonator reactor by absorbing heat from the hotter stream coming from the calciner. This novel solid–solid heat exchanger concept has been constructed on a small scale to study the hydrodynamic response of the system experimentally at different designs and airflow rates in its cold state. Based on the experimental data from the small prototype, a scaled-up hydrodynamic model is proposed that provides estimations for the operational requirements at an industrial scale. Apart from the cold flow pilot model, the heat exchanger is being assessed in the current work for an industrial case study in terms of the following: (a) the heat transfer via rigorous one-dimensional thermal modelling, (b) the structural integrity of the design through Finite Element Method (FEM) analysis, and (c) a parametric study for its expected cost. The purpose of this work is to provide a holistic approach of this novel solid–solid heat exchanger concept, the main advantage of which is its simple design and relatively low cost.

1. Introduction

The reversible reaction between calcium oxide (CaO) and carbon dioxide (CO₂) shows great potential as a method for Carbon Capture and Storage (CCS) applications [1,2]. This process is known as Carbonate Looping (CaL). The overall reaction can be represented as follows [3]:

CaO + CO₂ ⇌ CaCO₃

The reaction involves two steps:

• Carbonation, which is the forward reaction, where Calcium oxide (CaO) reacts with carbon dioxide (CO₂) to form calcium carbonate (CaCO₃). This reaction is exothermic, releasing heat.
• Calcination, which is the reverse reaction, where the calcium carbonate (CaCO₃) is heated to a high temperature, which decomposes it back into calcium oxide (CaO) and carbon dioxide (CO₂). This reaction is endothermic and requires an external heat source (e.g., in situ combustion of a fossil fuel inside the calciner, indirect heating of the calciner through the side walls or heat pipes, etc.).

By looping between these two steps, the process facilitates the continuous removal and capture of CO₂ from the exhaust gases of a power station or any other CO₂ emitting industry, such as cement, steel or lime. The captured CO₂ can then be separated and stored for geological sequestration or utilized for other purposes such as enhanced oil recovery or the production of chemicals and materials [4,5].

Typically, the flue gases from the source are directed into the carbonator. Within the carbonator, CO₂ reacts with the CaO obtained from the return stream of the sorbent loop, resulting in the formation of CaCO₃. The resulting mixture of solid and gas exits the carbonator through the top and it is then separated using a cyclone. The gas phase, consisting of a CO₂-lean flue gas, exits through the top of the cyclone, while the solids exit through the bottom. The solids from the carbonator move into the calciner, where they undergo calcination due to the high temperatures.

The advantages of using CaL for CO₂ capture include the abundance of calcium oxide (CaO) and the relatively low cost compared to other capture technologies. Additionally, the captured CO₂ is obtained in a concentrated form, making it easier to handle for storage or utilization [6]. However, it is important to note that CaL is still an emerging technology and has some challenges to overcome, such as the energy requirements for the calcination step and the long-term stability of the calcium-based sorbent [7,8]. Further research and development are ongoing to optimize and scale up this process for practical implementation in large-scale industrial applications [7,9].

A significant challenge lies in the high heat demand of the calciner, especially in the case of indirect heating [10], which requires a considerable number of heat pipes to transfer the heat from the external combustor, something that increases the size of the calciner. Part of the necessary thermal load is needed to heat-up the solid stream coming from the carbonator to the calcination temperature. To reduce the heat demand of the calciner, the integration of an external heat exchanger to preheat the calcium oxide [11] has been suggested. Another novel option recently proposed in the ANICA project [12] is the integration of a solid–solid heat exchanger between the carbonator and the calciner, as illustrated in Figure 1 [13]. This heat exchanger facilitates the transfer of heat from the “hot” solids exiting the calciner to the “cold” solids entering from the carbonator. As a result, the calciner requires less heat to raise the incoming solids’ temperature to 900 °C, establishing the solid–solid heat exchanger as a critical point for integration [14]. Also, the indirect heating from a combustor through many heat pipes connecting the calciner with the combustor is very promising [15] and thoroughly investigated [16,17,18].

It is evident from the literature that limited research has been conducted on developing the technology of solid–solid heat exchangers, which still remains more conceptual in design than being fully developed and operational. The advantages of this design compared to other developing options for heat exchange between the calciner and the carbonator [12] are its rather simple design and low cost, the latter of which is examined in the current work. In this study the solid–solid heat exchanger concept named as “Double L-Valve” [19] is presented and analyzed. The L-Valve and down-comer system for the carbonator and calciner streams are arranged in a concentric configuration, with one placed inside the other. Figure 2 reveals the fundamental principle of the Double L-Valve type solid–solid heat exchanger.

The single L-Valve principle of operation is based on a pneumatic valve invented by Knowlton [20]. The flow of solids through the valve is controlled by aeration and the geometry of the pipe [21], thus avoiding any moving parts that are prone to wear. It is a simple construction because it consists only of a vertical and a horizontal pipe and an aeration point placed at the vertical pipe, close to the elbow (bend) of the L-Valve. The angle of the two pipes is 90 degrees [22], and the vertical part is parallel to gravity. It is often used in Circulating Fluidized Beds (CFBs) as a device that returns the solids from the cyclone to the Fluidized bed and for the interconnection of two FBs in a dual Fluidized Bed system [23,24,25].

The Double L-Valve concept works hydrodynamically with the same principle. The two L-Valves work independently one from another. Their vertical tubes are concentric, but without any mixing of their gas–solid streams. Owing to this concentric arrangement, heat transfer, mostly through radiation, can be achieved from one hot stream to another colder, both of them flowing independently into the two pipes.

The case of a parallel Double L-Valve with two concentric vertical packed vertical tube offers several advantages for the CaL application [26]:

• It has no moving mechanical parts, which can be subject to wear and/or seizure. This feature is especially beneficial when operating at elevated temperatures as in the Calcium Looping Process.
• It has a rather low construction cost, because this type of heat exchanger is constructed from ordinary pipes and fittings, and low operating expenditures, since the absence of moving parts reduces the number of breakdowns and hence the downtime and maintenance costs.

Junhyung Park et al. [27] introduced an one-dimensional model of a turbulent fluidized bed for CO₂ capture using 37 EB-PEI/SiO₂ sorbent, where the absorber and desorber have significant temperature variation in beds, unlike CaL. In the CaL process, the outlet flow temperature is considered 900 °C, as the calciner walls are considered adiabatic and only transfer heat through heat pipes. The calciner’s operating temperature is ~900 °C to ensure complete calcination within a nearly pure CO₂ atmosphere, based on the models proposed by Baker and García [28]. A heat transfer model along the vertical tubes under hot conditions is a necessity to reveal several aspects, i.e., heat transfer efficiency, radiation effect on heat transfer, vertical tube length and diameter for an optimum heat transfer.

To the best of the authors’ knowledge, this is the first time that a solid–solid HE has been investigated. Experiments in a cold model are carried out in order to investigate the hydrodynamic response of the system, such as the solid mass flux-aeration requirements, the diameter as well as the length of the pipes. Based on the experimental results, a scale-up model is constructed in order to draw some useful conclusions about an industrial-scale model. In principle, the Double L-Valve arrangement is a trade-off between heat transfer efficiency and cost. Thus, a heat transfer analysis is performed in parallel with a cost analysis to find the optimum solution. The design process of the Double L-Valve system requires structural modelling to assess the manufacturability of the design. The purpose of this work is to provide a holistic approach to evaluate this novel concept focusing more on the many aspects of it, namely experimental aspects, heat transfer model, FEM and cost, rather than going deep into every single one of them.

2. Experimental Setup

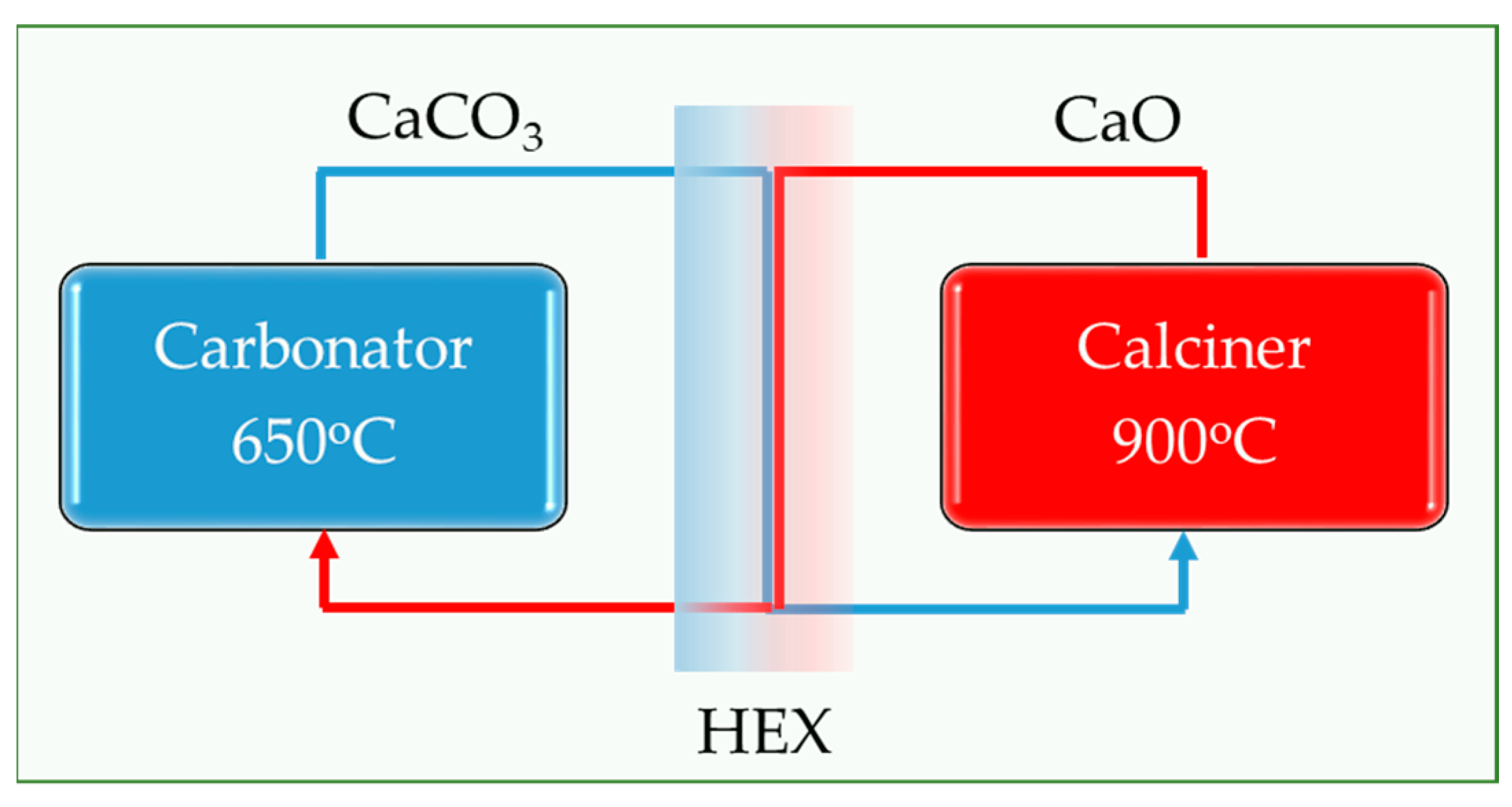
2.1. Test Rig Design and Construction

The construction of a suitable apparatus for investigating the hydrodynamic response of the Double L-Valve under cold conditions required the design of the following three different subsystems:

• A piping system of granular material;
• A pneumatic system of inlet air;
• An electronic system of measuring instruments.

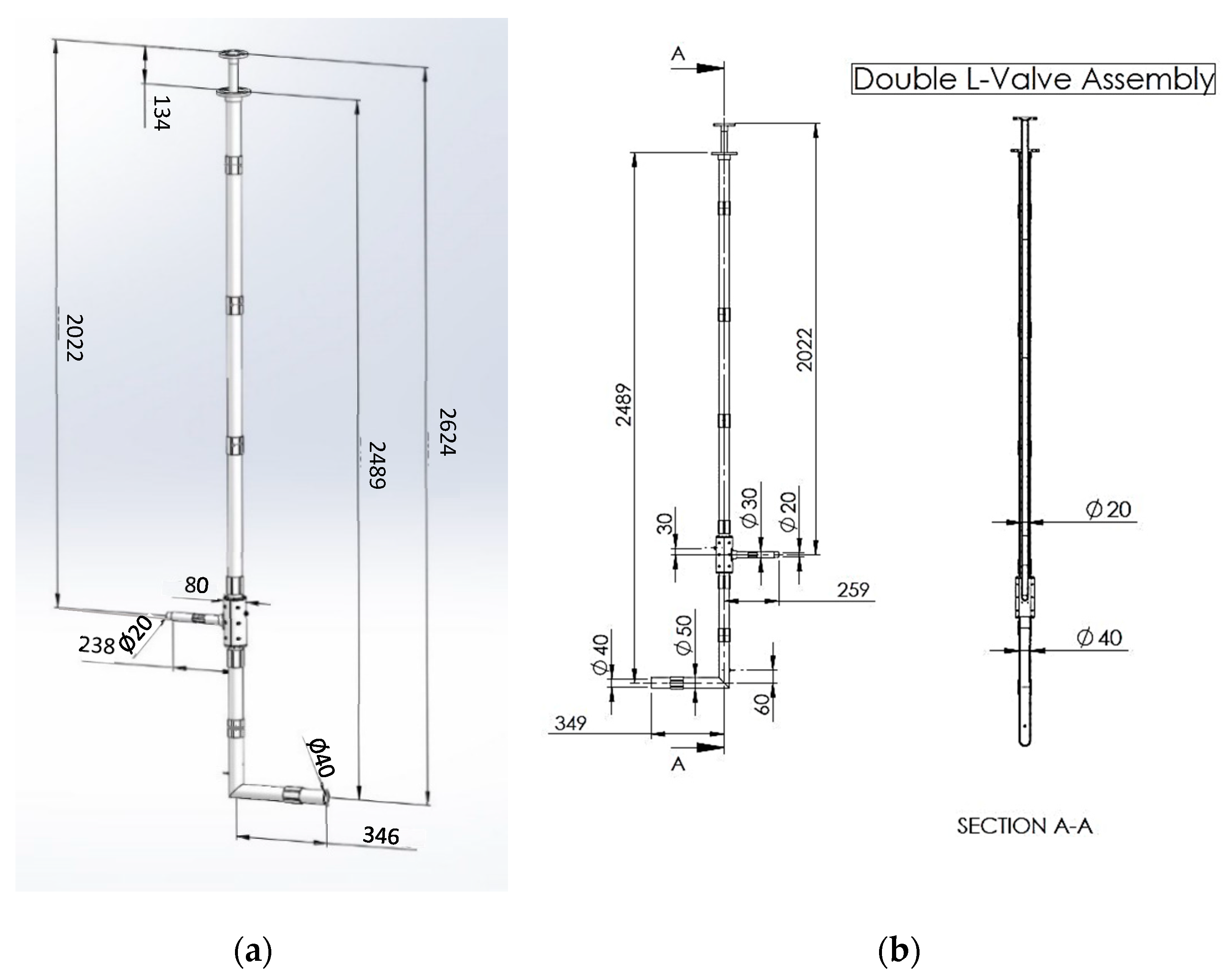
The piping system for the circulation of the granular material has the geometry of the Double L-Valve, and it consists of transparent Plexiglass tubes and appropriate sealed fittings. The system was designed as shown in Figure 3a,b and constructed as Figure 4 presents. The system was designed to be transparent, allowing the flow of granular material to be visually observed. It was also designed to be inexpensive, enabling the testing of various L-Valve diameters that can be purchased and evaluated. Moreover, the system is modular, facilitating the testing of different arrangements by easily changing the length of the horizontal and vertical tubes.

The pneumatic system of air supply at the inlets of the Double L-Valve consists of an air compressor and the air piping system from plastic pipes and fittings. The electronic system for the measurement of the airflow rate and the granular mass flux at the outlet of the cold model, consists of two custom measuring devices, their wiring system, one Arduino board and a computer. The weighing device (Figure 5a) has a wooden frame and a metal surface to place the weight, which is connected to the frame by two load cells capable of measuring up to 10 kg each. Therefore, the total load capacity of the weighing device is 20 kg, and its accuracy is 1 g. On the metallic surface of the weighing device a container is placed into which the outgoing granular material falls. Using the weighing sensors, the increase in the weight of the sand as a function of time is recorded.

To accomplish the measurement of the airflow rate, another custom device was constructed, which consists of a 3D-printed venturi tube and two pressure–temperature sensors placed at the two cross sections of the venturi tube. More specifically, the sensors are “BMP388” by DFRobot based at Zhangjiang Hi-Tech Park, Shanghai, China and can measure both the temperature and the static pressure at a given point. Hence, by measuring the static pressure at the greater and the smaller cross section of the venturi, the volumetric airflow can be obtained by Equation (1):

$$Q=A_1\sqrt{\frac{2}{{\rho }_{air}}\frac{p_1-p_2}{1-{\left(\frac{A_1}{A_2}\right)}^2}}$$

(1)

The set-up of the venturi tube and the sensors is presented in Figure 5b. All the sensors are connected to an Arduino board, and all the measurements are saved to a computer. The loadcells are connected to the analog pins of the Arduino. This is also the case for the pressure sensors; however, they use the I2C protocol, so the use of a multiplexer was necessary in order to address every sensor separately. All the sensors are carefully calibrated and programmed in the Arduino environment.

2.2. Experimental Results

The hydrodynamic response of the system was studied by simultaneously measuring the airflow and the granular mass flux. Several experiments were made under different airflow rates and different Double L-Valve designs, as shown in

Table 1. Cold model parameters at experimental data in Figure 7 and Figure 8.

Parameter	Symbol	Unit	Value
Tube hydraulic diameter	$D_h$	m	0.02–0.04
Granular material apparent viscosity	$\mu$	Pa s	0.3
Area of tube cross section	$A$	m2	3.14·10−4
Granular material apparent density	$\rho$	kg/m3	1100
Vertical length of L-Valve	$L_1$	m	0.4–0.7–1–1.3
Horizontal length of L-Valve	$L_2$	m	0.2–0.3–0.4

. More specifically, the lengths of the horizontal tube parts tested were 20 cm, 30 cm and 40 cm. Several experiments were conducted on the internal L-Valve for different aeration rates, for every design, and the mass flux at the weighing device is measured. In Figure 6a,b the raw data set of an indicative experiment is presented. Figure 6a presents the airflow rate, while Figure 6b presents the granular mass increase at the weighing device as a function of time. Every experiment has the same initial conditions for the consistency of the experimental data. Initially, the vertical tube is always filled with granular material, while the horizontal tube is always empty, in order to avoid the stick-slip effect of the granules in the horizontal tube at the beginning of every experiment. At the beginning, it can be observed that the airflow is negligible, and hence, there is no mass flux. When the airflow increases, the granular material starts to drop inside the weighing device until the inner tube is empty. From a practical point of view, it was not possible to ensure a continuous mass supply at the inlet of the vertical tube consistently. Therefore, it was decided to not add a new amount of granular material during the experiment, thus introducing randomness in each experiment, so that we could compare the experimental data.

During the hydrodynamic tests, a steady state is not attained because the mass leaving the L-Valve is not replenished at the inlet of the L-Valve. Nevertheless, the height of the granular material is calculated every moment, representing the equivalent height of the vertical tube at that specific time. With this consideration, the experimental data are used to develop a novel methodology that provides initial estimations. The experimental conditions described above do not exactly match real conditions of carbonate cycles, in which there are interconnected reactors under hot state. For each specific plant and L-Valve design configuration, the particles flow rate should be determined by the parameters of fluidization in the reactors, using other type of numerical tools or experimental data, which can also account for the capture efficiency of cyclones. The goal of the current work was to conduct a parametric investigation using indicative conditions, in order to estimate the required power for granular circulation utilizing only the main geometrical parameters of the L-Valve.

Prior studies have successfully formulated mathematically physical relationships in L-Valves, i.e., between the airflow rate and the flow of granular material [29]. The goal of this work is to construct a reduced scale-up model in order to provide easily insight and preliminary rough estimations about the energy consumption of the system during operation in industrial-scale models. Thus, instead of re-exploring the physical relationships in L-Valves with highly complex models, the following methodology has been developed based on a simple energy method.

The following equations are applicable for a Newtonian fluid. For a given air flow (Q), the mass flow ($\dot{m}$) on the weighing device is measured. From the $\dot{m}$, the Reynolds number of the flow is calculated depending on the viscosity of the granular.

$$Re=\frac{\dot{m}{D}_h }{\mu A},$$

(2)

where $\mu$ is the equivalent viscosity of the granular flow, and $D_h$ is the hydraulic diameter of the tube and the area of the tube’s cross section.

From the Reynolds number, using the Jain formula, the coefficient λ, which determines the pressure drop in the pipes, is calculated. For laminar flow, we can use the following expression:

$$\lambda =\frac{64}{Re}$$

(3)

Given the λ coefficient, the linear losses at the horizontal tube, $\mathsf{\Delta }p$, are calculated depending on its length and diameter. Hence, using Equation (4), the pressure drop $\mathsf{\Delta }p$ is calculated.

$$\mathsf{\Delta }p=\frac{\lambda L_2}{D_h}\frac{\rho }{2}{u}^2,$$

(4)

where the velocity $u$ of the granular medium is calculated as:

$$u=\frac{\dot{m}}{\rho A},$$

(5)

where ρ is the apparent density of the granular material, $D_h$ is the hydraulic diameter of the tube, and $A$ is the area of the tube’s cross section.

Thus, the theoretical required power from the compressor is equal to:

$$\dot{W}=\mathsf{\Delta }pAu$$

(6)

Measuring the actual mass flux from every experiment, it is possible to calculate the theoretical required power supply from the air compressor using Equations (2)–(6). In reality, however, the working medium is a granular material. That means that a fraction of the supplied airflow is passing through the porosity of the packed granular without transferring energy to it. The real power of the aeration at every experiment is calculated by Equation (7) at the narrow part of the venturi tube, where the total pressure ($P_{tot}$) is given by Equation (8).

$$N=P_{tot}Q$$

(7)

$$P_{tot}=P+\frac{1}{2}\rho u^2,$$

(8)

where P is the measured static pressure at the point, and Q is the calculated airflow.

It has been observed that the measured power of air supply ($N)$ from the compressor is greater than the calculated power $(\dot{W})$ for the equivalent Newtonian fluid, since in the case of the granular material, there are additional power losses exerted, due to its porosity. Hence, it is necessary for a hydrodynamic effectiveness $\left(ef\right)$ to be introduced by Formula (9), which will be used as a correction factor to model the granular material as a Newtonian fluid.

$$ef=\frac{\dot{W}}{N}$$

(9)

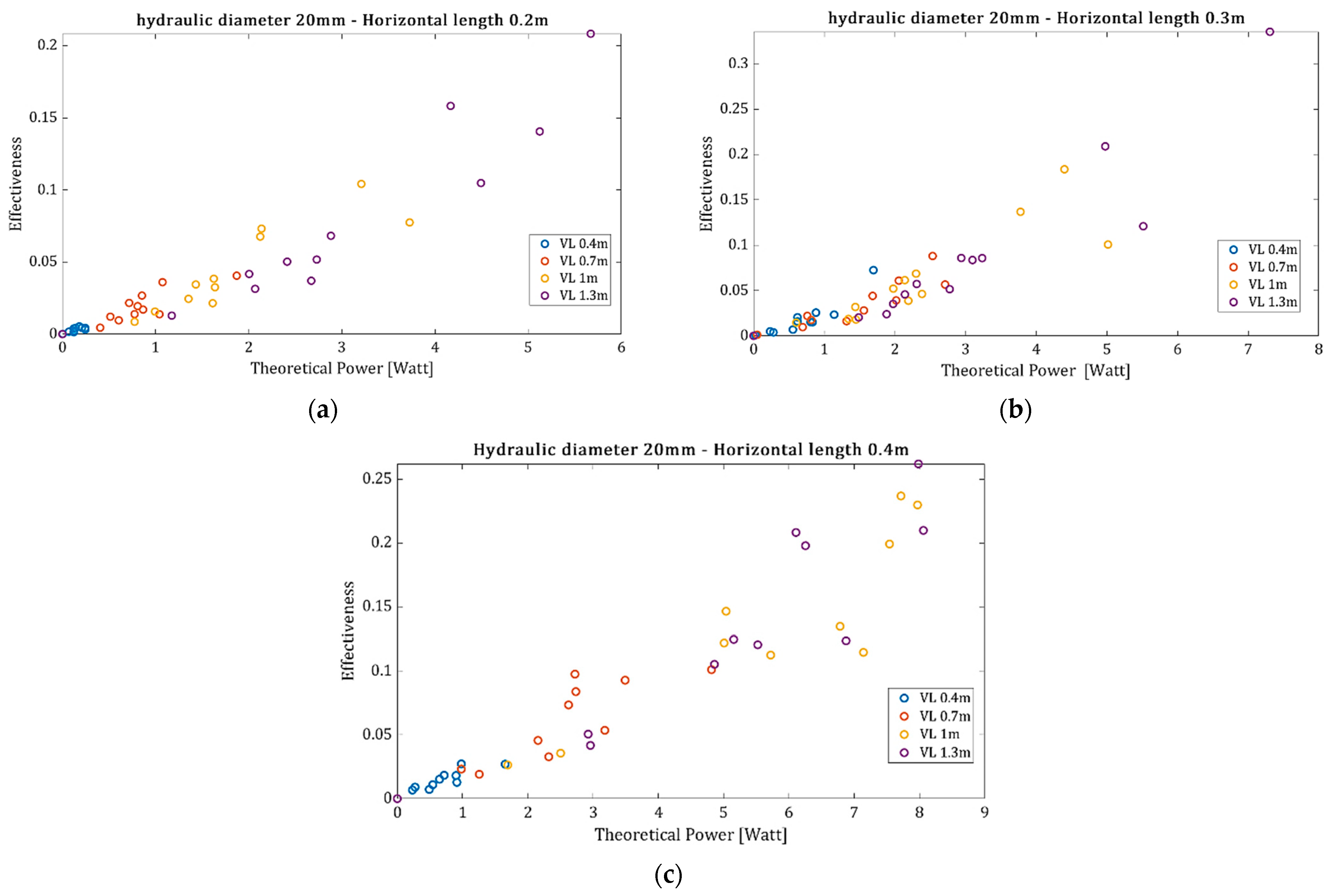
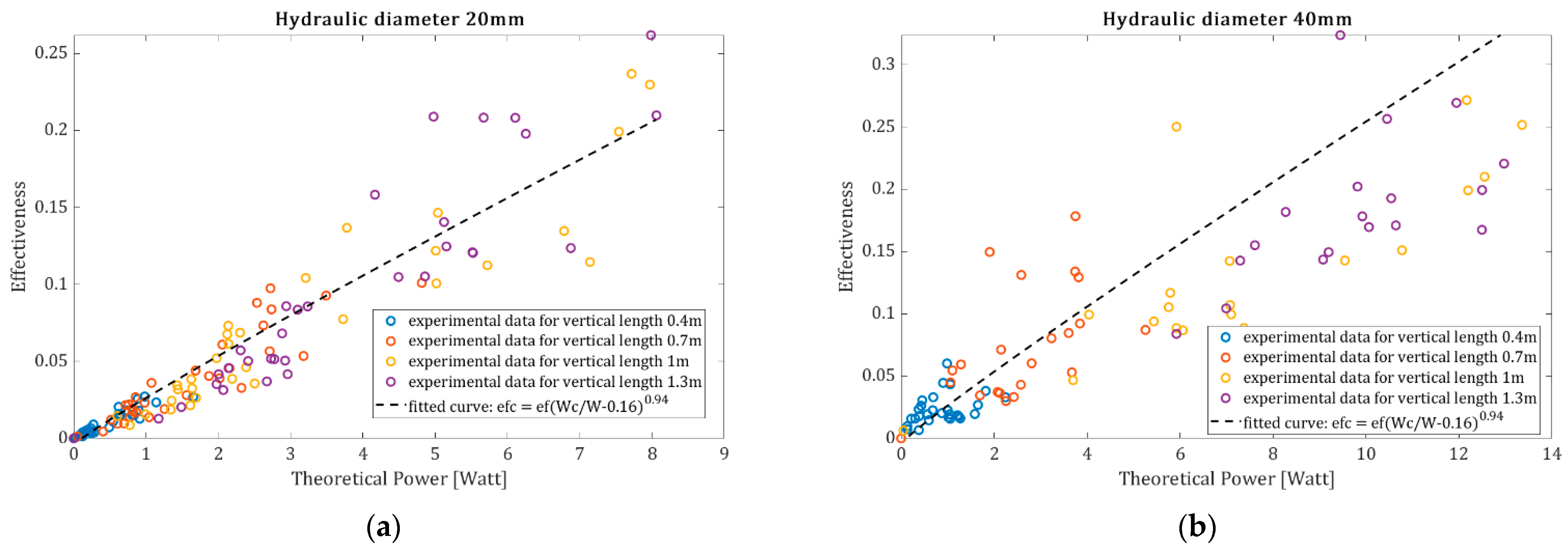
The effectiveness, as defined by Equation (9), for every conducted experiment in comparison to the theoretical required power from the air compressor is presented in Figure 7 for a hydraulic diameter equal to 20 mm, and the rest of the parameters are summarized in Table 1. The values of mass flux and aeration are calculated at four different heights of the vertical tube to observe the effect of the upstream pressure, while the horizontal tube is always filled by granular material. The apparent density ρ of the stacked solids has been measured, and the viscosity μ is calculated via the Hagen Poiseuille formula (Equation (35)) using the mass flux from an experiment with high aeration rate. The curves of mass and airflow obtained from the sensors are filtered with a moving average filter to reduce the measuring errors.

Figure 7a–c indicate that as the power supply from the air compressor increases, the effectiveness increases. When the level of the granular at the vertical tube is higher, the upstream pressure is greater, and thus, the resulting mass flux is also increased. Higher mass flux means higher pressure drop at the horizontal tube (Equations (2)–(6)).

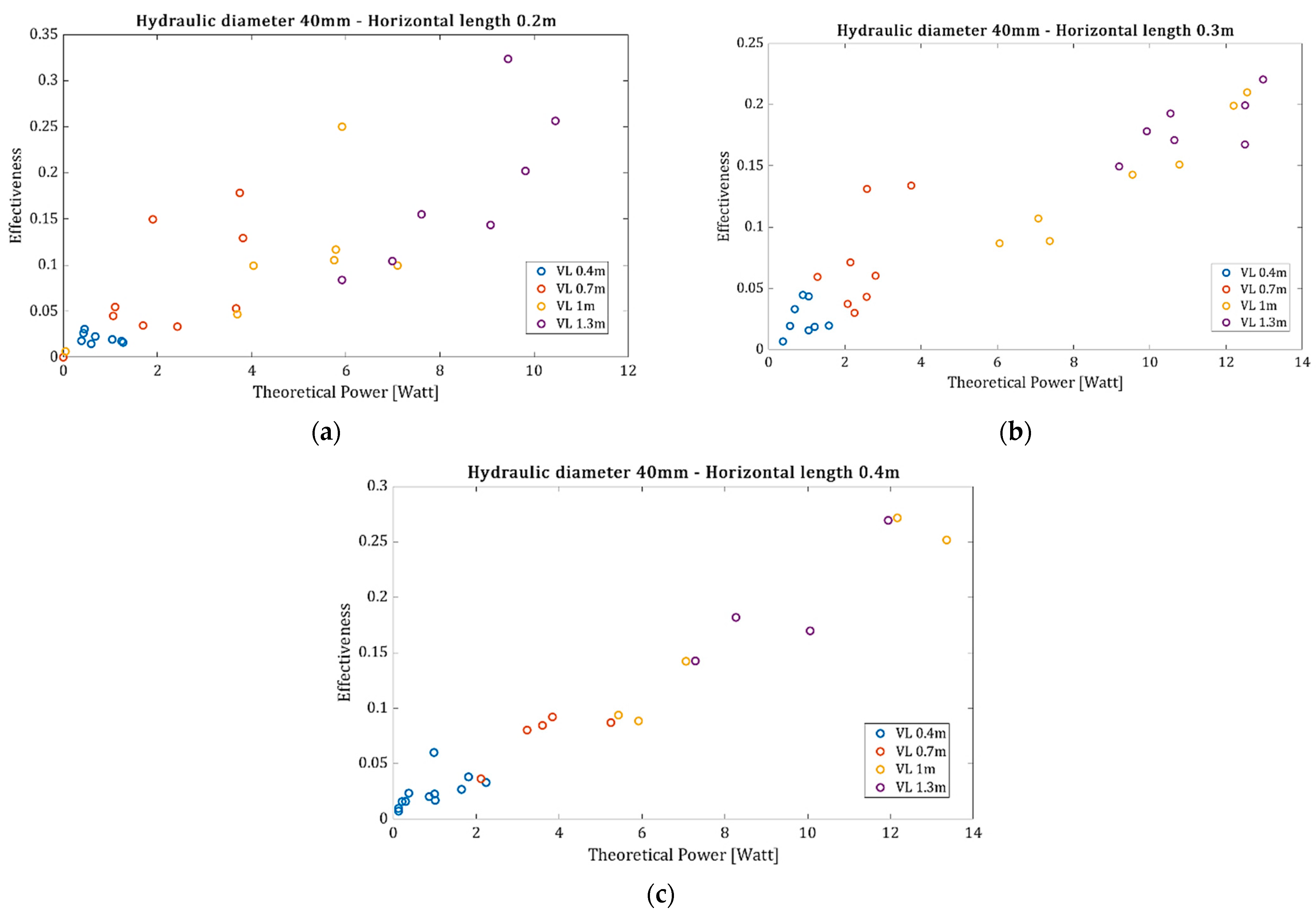
In addition, the experiments were conducted with the parameters of Table 1, but for a hydraulic diameter equal to 40 mm. The data obtained are presented in Figure 8a–c, where it can be observed that as the mass flux increases, the resulting effectiveness also increases but with a higher dispersion.

From the experimental data, it is clear that the lower the theoretical power requirement to overcome the linear pressure drop in a horizontal tube arrangement, the lower the resulting effectiveness. In fact, for a very small theoretical power, where the air supply is very small, the effectiveness is zero as the entire airflow passes through the porosity of the granular material without moving particles. From the experimental data, it is clear that longer horizontal pipes result in lower mass fluxes due to the increased linear pressure drop, while pipes with larger diameters result in higher mass fluxes due to the lower linear pressure drop.

2.3. Scale-Up Model

The aeration needs of every industrial-scale model can be calculated using a single formula. Equation (13) gives the necessary power supply for a case study with operating parameters given by Equation (10) as function of the equivalent parameters at a small scale:

$$\begin{gathered} {\dot{m}}_c=a\dot{m} \\ {D_h}_c=b{D}_h \\ {\mu }_c=c\mu \\ {\rho }_c=d\rho \\ {L_2}_c=e{L}_2 \end{gathered}$$

(10)

$${\dot{W}}_c=\frac{a^{2}ec}{d^2{b}^4}\dot{W}$$

(11)

$${ef}_c=ef{\left(\frac{{\dot{W}}_c}{\dot{W}}+C\right)}^m{\left(\frac{{L_1}_c}{L_1}\right)}^n$$

(12)

$$N_c=\frac{{\dot{W}}_c}{{ef}_c}$$

(13)

The theoretical power losses at the horizontal tube $\dot{W}$ can be easily scaled using the Formulas (2)–(6), reaching Equation (11). However, to calculate the real required power, the effectiveness has to be scaled as well. The scaling of the effectiveness will be accomplished via dimensional analysis to assess the effect of the theoretical required power and the height of the vertical tube. Hence, Equation (12) was introduced, for which the exponents m, n and the constant C will be fitted using the experimental data.

The best fit of the parameters m, n and C was accomplished using some sets of experimental data and validated to other sets. First of all, the theoretical power ($\dot{W}$), the vertical length ($L_1$) and the effectiveness ($ef$) of an experiment were selected. The selected values are entered into Equation (12), which must have the appropriate parameters to give the scaled effectiveness. The best fit of the parameters m and C in Equation (12) was conducted using experiments where the vertical length of the tube was the same as that in the selected experiment in order to remove the unknown n exponent from the equation. The best fit was performed against experimental data, where the hydraulic diameter was equal to 20 mm, and the vertical tube length was 0.7 m. The fitted curve is presented in Equation (14).

$${ef}_c=0.022 {\left(\frac{{\dot{W}}_c}{0.72}-0.016\right)}^{0.94}{\left(\frac{{L_1}_c}{0.7}\right)}^n$$

(14)

The n exponent was calculated with a value close to zero via Equation (15) using experimental data from L-Valves with a vertical tube length of 1 m, and the results were validated for the series of available experimental data from the experiments conducted for tube heights of 0.4 m and 1.3 m.

$$\frac{\partial }{\partial n}\left(\frac{1}{p_1}\sum _{i=1}^{p_1}\left|0.022 {\left(\frac{{\dot{W}}_c}{0.72}-0.016\right)}^{0.94}{\left(\frac{{L_1}_c}{0.7}\right)}^n-{ef}_i\right|\right)=0,$$

(15)

where $p_1$ is the amount of the experimental datapoints from L-Valves with a hydraulic diameter of 20 mm and a vertical length of 1 m, and ${ef}_i$ is the experimental effectiveness.

Since the exponent n is equal to zero, the scaling of effectiveness is given by the simple equation:

$${ef}_c=0.022 {\left(\frac{{\dot{W}}_c}{0.72}-0.016\right)}^{0.94}$$

(16)

Figure 9a,b present the experimental data along with the fitted curve. Since the Double L-Valve does not have any moving parts, the energy consumption during operation is exclusively due to the air consumption provided by air-compressors and blowers, which can be estimated for a specific industrial application using Equation (16). It is important to note that the scale-up model can be used only for rough preliminary estimations. After all, conducting accurate estimations is very difficult due to the stochastic nature of this phenomenon, which exhibits a significant inherent variation, as shown in the scatterplots.

To conclude, based on the experimental data from the small prototype, a scaled-up hydrodynamic model is proposed (Equation (16)) that provides estimations for the operational requirements at an industrial scale. By using this model, initial conclusions can be drawn about the operating expenditures (OPEX) of the system and its requirements in pneumatic equipment. Consequently, the scale-up model may serve the industry as a useful tool for conducting preliminary feasibility studies about a Double L-Valve arrangement.

3. Thermal Analysis

3.1. Governing Equations

A reduced analytical transient thermal model is introduced for the thermal simulation of an industrial-scale Double L-Valve type solid–solid heat exchanger (HE), with low computational cost. The required input for the model are as follows: (i) the geometry of the HE, (ii) the tube material and granular parameters, (iii) the boundary conditions of granular materials and (iv) the initial conditions. Given all these parameters, the temperature distribution on granular materials and walls are calculated at transient and steady state. In

Table 2. Inputs to transient thermal model.

Parameter	Symbol	Parameter	Symbol
Inner tube radius	$R_{i1}$	Granular material density	${\rho }_{si}$
Outer tube radius	$R_{i2}$	Granular average voidage	$e_s$
Length of HE	$L$	Radiation coefficient	$\sigma$
Mass flux through tube	${\dot{m}}_i$	Granular material emissivity	$e_i$
Input granular temperature	${T_i}_0$	Tube material emissivity	$e_m$
Initial tube temperature	${T_{mi}}_0$	Tube material density	${\rho }_m$
Thermal conductivity of granular	$k_{{gr}_i}$	Tube material heat capacity	$C_{pm}$
Thermal conductivity of gas	$k_{{gas}_i}$	Tube material thermal conductivity	$k_m$
Granular apparent heat capacity	$C_{pi}$	Mean granular particle diameter	$d_p$

and

Table 3. Outputs of transient thermal model.

Parameter	Symbol
Granular temperature distribution as a function of time	${T_i}_j\left(t\right)$
Temperature distribution to tube material as a function of time	${T_{mi}}_j\left(t\right)$

, inputs and outputs are presented analytically, where subscript i takes the value of 1 when referring to the inner tube and the value of 2 when referring to the outer, and subscript j indicates the finite element number.

The Double L-Valve consists of two concentric tubes, i.e., the inner tube and the outer one with radiuses as shown in Figure 10a. The granular materials, referred to also as “fluids”, flow from top to bottom into these tubes. It is considered that all the heat transfer is taking place at the vertical tubes of the Double L-Valve axisymmetrically. The following assumptions have been made:

• Uniform temperature distribution at each circular cross section, since the radius of the tubes is significantly smaller than their length.
• Constant temperature along wall thickness, since the resulting Biot numbers are much smaller than 0.1 [30].
• Adiabatic insulated outer walls, so that there are no heat losses to the environment.

Both the tubes and the fluids are divided into finite elements along the length of the tube, so that the temperature distribution along can be obtained.

For the case of evenly distributed granular material, Equations (17) and (18) apply to the j^th finite element of fluid in the j^th finite element of inner tube:

$$q2\pi R_{11}={\dot{m}}_1{C}_{p1}\frac{d{T_1}_j}{dx}$$

(17)

$$q=h_{1j}\left({T_{m1}}_j-{T_1}_j\right),$$

(18)

where $dx$ is the length of finite element, $h_{1j}$ is the equivalent convective heat coefficient of the fluid in inner cylinder, $C_{p1}$ is the heat capacity of the inner fluid, and ${\dot{m}}_1$ is its mass flux.

Hence, combining Equations (17) and (18), the temperature of the inner fluid ${T_1}_j$ at every element is calculated from the differential Equation (19), which can be solved analytically (20):

$$\frac{d{T_1}_j}{dx}+\frac{2\pi R_{11}{h}_{1j}}{{\dot{m}}_1{C}_{p1}}{T_1}_j=\frac{2\pi R_{11}{h}_{1j}}{{\dot{m}}_1{C}_{p1}}{T_{m1}}_j$$

(19)

$${T_1}_j={T_{m1}}_j+({T_1}_{j-1}-{T_{m1}}_j)e^{\frac{-2\pi R_{11}{h}_{1j}dx}{{\dot{m}}_1{C}_{p1}}}$$

(20)

Similarly, for the fluid in the outer cylinder the following applies:

$$h_{21j}\left({T_{m1}}_j-{T_2}_j\right)2\pi R_{12}+h_{22j}\left({T_{m2}}_j-{T_2}_j\right)2\pi R_{21}={\dot{m}}_2{C}_{p2}\frac{d{T_2}_j}{dx}$$

(21)

$$\frac{d{T_2}_j}{dx}+\frac{2\pi R_{12}{h}_{21j}+2\pi R_{22}{h}_{22j}}{{\dot{m}}_2{C}_{p2}}{T_2}_j=\frac{2\pi R_{12}{h}_{21j}{T_{m1}}_j+2\pi R_{22}{h}_{22j}{T_{m2}}_j}{{\dot{m}}_2{C}_{p2}}$$

(22)

$${T_2}_j=\frac{{h_{21j}2\pi R_{12}{T}_{m1}}_j+{h_{22j}2\pi R_{22}{T}_{m2}}_j}{h_{21j}2\pi R_{12}+h_{22j}2\pi R_{21}}+({T_2}_{j-1}-\frac{{h_{21j}2\pi R_{12}{T}_{m1}}_j+{h_{22j}2\pi R_{22}{T}_{m2}}_j}{h_{21j}2\pi R_{12}+h_{22j}2\pi R_{21}}){ e}^{-\frac{(h_{21j}2\pi R_{12}+h_{22j}2\pi R_{21})dx}{{\dot{m}}_2{C}_{p2}}},$$

(23)

where $h_{2j}$ is the convective heat coefficient of the fluid in outer cylinder, $C_{p2}$ is the heat capacity of the fluid, and ${\dot{m}}_2$ is its mass flux.

Due to the fact that every finite element of tube has a different temperature, there are conductive thermal currents between adjacent elements, as shown in Figure 10b with green color. These are calculated from Equation (24).

$$\begin{gathered} Q_{1j}=\frac{k_m\pi \left(R_{12}^2-R_{11}^2\right)}{dx}({T_{m1}}_{j-1}-{T_{m1}}_j) \\ {Q}_{2j}=\frac{k_m\pi \left(R_{12}^2-R_{11}^2\right)}{dx}({T_{m1}}_{j+1}-{T_{m1}}_j) \\ {Q}_{3j}=\frac{k_m\pi \left(R_{22}^2-R_{21}^2\right)}{dx}\left({T_{m2}}_{j-1}-{T_{m2}}_j\right) \\ {Q}_{4j}=\frac{k_m\pi \left(R_{22}^2-R_{21}^2\right)}{dx}\left({T_{m2}}_{j+1}-{T_{m2}}_j\right), \end{gathered}$$

(24)

where $k_m$ is the thermal conductivity of the metal.

The convective thermal currents between the fluids and the tubes are presented with orange color in Figure 10b and are calculated from Equation (25):

$$\begin{gathered} Q_{5j}=h_{1j}2\pi R_{11}dx({T_{m1}}_j-{T_1}_j) \\ {Q}_{6j}=h_{21j}2\pi R_{12}dx({T_2}_j-{T_{m1}}_j) \\ {Q}_{7j}=h_{22j}2\pi R_{21}dx({T_2}_j-{T_{m2}}_j) \end{gathered}$$

(25)

Hence, the temperature of the tube material at the next time step Dt is given by Equations (26) and (27) for the inner and the outer tube, respectively.

$${T_{m1}}_{j new}={T_{m1}}_{j old}+\frac{Q_{1j}+Q_{2j}+Q_{5j}+Q_{6j}}{m_{m1j}{C}_{pm}}Dt$$

(26)

$${T_{m2}}_{j new}={T_{m2}}_{j old}+\frac{Q_{3j}+Q_{4j}+Q_{7j}}{m_{m2j}{C}_{pm}}Dt,$$

(27)

where $m_{m1j}$ is the mass of a finite element of the inner tube, and $m_{m2j}$ is the mass of a finite element of the outer tube.

3.2. Heat Transfer Coefficients

The convective heat transfer coefficient can be calculated considering the solids and the interstitial gas as a continuum fluid flowing through the heat transfer surface with a uniform velocity. Both gas and solids have the same velocity. It is considered that the granular material volume ratio inside the tubes is high, and the granular material, depending on the mass flux, descends at a relatively constant speed. Considering the particles are spherical, the maximum theoretical packing limit is 65%, so the volume ratio cannot be higher than that. According to Dutta and Basu [31] the convective heat transfer coefficient to a certain surface, for the dense section, is:

$$h_{ci}=\frac{1}{R_{ci}+R_{ei}},$$

(28)

where $R_c$ is the contact resistance given by:

$$R_{ci}=\frac{\delta d_p}{k_{gi}},$$

(29)

where δ is the non-dimensional gas layer thickness between the wall and moving solids, which can be approximated as:

$$\delta =0.0282{(1-e_s)}^{-0.59},$$

(30)

and $R_e$ is the thermal resistance of solids given by:

$$R_{ei}=\sqrt{\frac{\pi L}{k_i{\rho }_i{C}_i{U}_s}},$$

(31)

where $U_s$ is the downward velocity of granular materials, and $k_i$ is the conductivity of the fixed bed with static fluid, which is given by Equation (32):

$$k_i=k_{gri}{(\frac{k_{gi1}}{k_{gas}})}^{(0.28-0.757{ log}_{10}(\frac{k_{gi1}}{k_{gas}}))},$$

(32)

In addition, the contribution of radiation to the heat transfer is taken into consideration. The radiation coefficients are calculated by Equation (33) [32].

$$\begin{gathered} h_{r1j}=\frac{\sigma (T_{m1j}^2+T_{1j}^2)({T_{m1}}_j+{T_1}_j)}{\frac{1}{e_{gr1}}+\frac{1}{e_m}-1} \\ {h}_{r21j}=\frac{\sigma (T_{2j}^2+T_{m1j}^2){(T_2}_j+{T_{m1}}_j)}{\frac{1}{e_{gr2}}+\frac{1}{e_m}-1} \\ {h}_{r22j}=\frac{\sigma (T_{2j}^2+T_{m2j}^2)({T_2}_j+{T_{m2}}_j)}{\frac{1}{e_{gr2}}+\frac{1}{e_m}-1}, \end{gathered}$$

(33)

where $\sigma$ is the Stefan–Boltzmann constant, and $e_{gr1}$,$e_{gr2}$ and $e_m$ are the emissivity of inner granular, outer granular and tube material, respectively.

Hence, three coefficients are derived at every cross section, taking into consideration both convection and radiation.

$$\begin{gathered} h_{1j}=h_{c1}+h_{r1j} \\ {h}_{21j}=h_{c2}+h_{r21j} \\ {h}_{22j}=h_{c2}+h_{r22j}, \end{gathered}$$

(34)

3.3. Critical Mass Flow

A solid–solid heat exchanger (HE) is responsible for circulating a specific granular mass flow, and it may consist of several Double L-Valve units. Each Double L-Valve has the capacity to transfer a maximum granular mass flow through its inner and outer vertical tubes. Therefore, for the total mass flow (${\dot{m}}_i$) of a specific case study, a minimum number of Double L-Valves can be calculated. This depends on the hydraulic diameter of the pipes and the equivalent viscosity of the fluids and can be calculated from the Hagen Poiseuille law. Utilizing Equation (35), the average downward velocity of the fluid can be calculated as:

$$u_{ci}=\frac{{\rho }_{i}g}{8{\mu }_i}{R_{hi}}^2,$$

(35)

where $R_{hi}$ is the hydraulic radius of the tube, ${\rho }_i$ is the apparent density of the fluid (${\rho }_i\cong a_{si}{\rho }_{si}$), and ${\mu }_i$ is its viscosity, which is calculated using Equations (36)–(38) [33]:

$${\mu }_{s,col}=\frac{4}{5}{a}_{si}{\rho }_{si}{d}_{si}{g}_{0ssi}(1+e_{ssi})({\frac{{\Theta }_{si}}{\pi })}^{1/2}$$

(36)

$${\mu }_{s,kin}=\frac{{\rho }_{si}{d}_{si}\sqrt{{\Theta }_{si}\pi }}{6(3-e_{ssi})}[1+\frac{2}{5}\left(1+e_{ssi}\right)\left(3e_{ssi}-1\right)a_{si}{g}_{0ssi}]$$

(37)

$${\mu }_i={\mu }_{si,col}+{\mu }_{si,kin},$$

(38)

where $a_{si}$ is the volume fraction ($a_{si}=1-e_{si}$), ${\rho }_{si}$ is the density of particles, $d_{si}$ is the mean particle diameter, $g_{0ss}$ is the radial distribution coefficient, $e_{ssi}$ is the restitution coefficient, and ${\Theta }_{si}$ is the granular temperature [m²/s²].

The number of the Double L-Valves ($N$) for every HE design is $N\ge N_{min}$, where $N_{min}$ is given by Equation (39)

$$N_{min}=\frac{{\rho }_2\pi {R_{hi}}^2}{{\dot{m}}_i}{u}_{ci}$$

(39)

3.4. Inputs and Boundary Conditions

The boundary conditions considered, are taken from an industrial case study in ANICA research project [12], which is focused on developing a novel indirectly heated carbonate lopping process. In this case study, the total granular mass flux from carbonator is 35.91 kg/s with a temperature of 650 °C, and the total granular mass flux from calciner is 31.54 kg/s with a temperature of 900 °C (

Table 4. Case study boundary conditions.

Symbol	Unit	Value
${T_1}_0$	°C	900
${T_2}_0$	°C	650
${\dot{m}}_1$	kg/s	31.54
${\dot{m}}_2$	kg/s	35.91

).

The optimal arrangement of the heat exchanger is calculated according to the specific industrial application, and it includes the selection of vertical tube dimensions and the number of Double L-Valves, relating the heat recovery of the Double L-Valve with its required CAPEX. The main parameters influencing the HE CAPEX is the cost of tube material and its required insulation at the outer surface. The main constraint for every Double L-Valve design is the maximum mass flux that can be transferred through its vertical tubes.

The optimization procedure, including all assumptions, constraints and the costing of the heat exchanger, is presented in Section 5. It should be mentioned that the optimization procedure does not take into account strict restrictions regarding the size and construction of the system, since this is outside the scope of this study, and also, imposing restrictions on the algorithm might obscure the trends of the optimal solutions. The result of the optimization was a heat exchanger with 11 Double L-Valves with the length and radii listed in

Table 5. Case study input parameters.

Parameter	Symbol	Unit	Value
Inner radius of inner tube	$R_{11}$	mm	280
Outer radius of inner tube	$R_{12}$	mm	282
Inner radius of outer tube	$R_{21}$	mm	391
Outer radius of outer tube	$R_{22}$	mm	393
Length of HE	$L$	m	50
Mass flux in inner tube	${\dot{m}}_1$	kg/s	3.26
Mass flux in outer tube	${\dot{m}}_2$	kg/s	2.87
Inner granular material density	${\rho }_{s1}$	kg/m3	1478
Outer granular material density	${\rho }_{s2}$	kg/m3	1734
Input temperature of inner granular	${T_1}_0$	°C	900
Input temperature of outer granular	${T_2}_0$	°C	650
Initial temperature of inner tube	${T_{m1}}_0$	°C	22
Initial temperature of outer tube	${T_{m2}}_0$	°C	22
Thermal conductivity of granulates	$k_{gr}$	W/m/K	2.6
Thermal conductivity of gas	$k_{gas}$	W/m/K	0.026
Inner fluid average voidage	$e_{s1}$	-	0.4
Outer fluid average voidage	$e_{s2}$	-	0.4
Inner granular heat capacity	$C_{p1}$	J/kg/K	996.7
Outer granular heat capacity	$C_{p2}$	J/kg/K	920.2
Inner granular emissivity	$e_{gr1}$	-	0.9
Outer granular emissivity	$e_{gr2}$	-	0.35
Tube material emissivity	$e_m$	-	0.9
Tube material density	${\rho }_m$	kg/m3	8000

along with the rest input parameters of the thermal model. Since there are 11 Double L-Valves, the mass fluxes of calcium carbonate and calcium oxide through a single Double L-Valve are 3.26 kg/s and 2.87 kg/s, respectively. The thermomechanical properties of the HE material are those of AISI 310s, which is a stainless steel suitable for high working temperatures and has high strength at corrosion, fatigue and creep.

3.5. Thermal Simulation Results

In Figure 11a, the temperature change of the fluids and tube walls, at steady state, are presented. More specifically, the length of the vertical tubes is 50 m, and the temperature of granular from carbonator is increased by 110 °C, from 650 °C to 760 °C. The temperature distribution at the outer tube wall is equal to the temperature of the solids from the carbonator, which are transferred through the outer tube due to insulation. The inner tube wall obtains a temperature between that of the hot and cold solids at steady state. In addition, in Figure 11b, the temperature of the upper and the lower elements of vertical tubes and the outlet temperature of fluids are presented as a function of time. The initial temperature of the tubes is considered 22 °C. When the temperature of the tube material is stabilized, the system reaches its thermal steady state. Finally, Figure 11c presents the percentage of radiation at the heat currents $Q_5$, $Q_6$ and $Q_7$ (see Figure 10b), for the first and the last elements of fluids. It can be observed that the radiation is the dominant phenomenon of heat transfer since 94% of the total heat transfer occurs via radiation. This observation depends on the temperature levels of the tube and solids and holds true for the specific case examined. The resulting convection is very low since the granular material is fully packed in the tubes, and its resulting downward velocity is very low.

4. Structural Analysis

In Figure 12, there is a schematic representation of the Double L-Valve’s mounting. The mounting flange is responsible for carrying the weight of the structure, thus allowing the radial thermal expansion of the cross section. The suspensions and axial expansion joint (see Figure 12) are responsible for receiving the axial expansion of the vertical tubes as they are not prone to buckling. However, additional thermally induced stresses emerge in the HE, and therefore, a Finite Element Analysis (FEA) model was constructed in ANSYS Mechanical (v22.1) [34] in order to check the structural integrity of the structure.

4.1. Tube Material Parameters

The selected material for the construction is AISI 310s, its structural parameters are obtained from the ANSYS material database, and they are presented in

Table 6. AISI 310s structural parameters.

Temperature (°C)	Young’s Modulus (Pa)	Poisson’s Ratio	Bulk Modulus (Pa)	Shear Modulus (Pa)
20	1.95 × 1011	0.25	1.3 × 1011	7.8 × 1010
100	1.91 × 1011	0.26	1.33 × 1011	7.58 × 1010
200	1.86 × 1011	0.275	1.38 × 1011	7.29 × 1010
300	1.8 × 1011	0.315	1.62 × 1011	6.84 × 1010
400	1.73 × 1011	0.33	1.7 × 1011	6.5 × 1010
500	1.64 × 1011	0.3	1.37 × 1011	6.31 × 1010
600	1.55 × 1011	0.32	1.44 × 1011	5.87 × 1010
700	1.44 × 1011	0.31	1.26 × 1011	5.5 × 1010
800	1.31 × 1011	0.24	8.4 × 1010	5.28 × 1010
900	1.17 × 1011	0.24	7.5 × 1010	4.72 × 1010
1000	1 × 1011	0.24	6.41 × 1010	4.03 × 1010
1100	8.1 × 1010	0.24	5.19 × 1010	3.27 × 1010
1200	5.1 × 1010	0.24	3.27 × 1010	2.06 × 1010

and Figure 13. It can be observed that as the temperature increases, the Young’s modulus and the yield strength of the material decrease, while the thermal expansion coefficient increases.

4.2. FEM Model Setup

Since the Double L-Valve has a bilateral symmetry, only half the model was simulated structurally, and roller supports were added to the catted cross section, which also restrict the movement of the model along the z axis (Displacement2 in Figure 14a). The vertical movement of the Double L-Valve is restricted by a flange between the two horizontal tubes. For the sake of simplification, the flange is not added to the model, but an edge restricts the movement at the y axis instead (Displacement in Figure 14a). The concentricity of the tubes and the restriction at the x axis is accomplished by restricting the movement at the x axis of the central tube axial line (Displacement3 in Figure 14a). In order to reduce the computational cost and increase the accuracy of the model, hexahedral elements were used, as shown in Figure 14b, resulting in 110,531 elements total.

In order to reduce the computational cost of the simulation, the long vertical tubes are considered ten times shorter, and the temperature distribution is compacted along the tube length by a factor of ten times. Since this simulation does not study the structure to buckling, it is possible to make this assumption because the more compact the temperature distribution along the length of the tubes, the higher the temperature gradients; therefore, the emerging shear stresses are overestimated. Figure 15 presents the imported temperature distribution at both tubes, which was calculated from the thermal model of Section 3.

4.3. FEA Simulation Results

Figure 16 presents the thermal (a) as well as the Von-Misses (b) stresses as calculated by the FEA simulations. As can be seen, the emerged Von-Misses stresses due to the thermal loads are at maximum equal to ~12MPa, which is much lower than the yield strength of the material. Since the resulting stresses on this preliminary concept of the structure are so low, it can be concluded that the Double L-Valve concept can be constructed and operate reliably, in terms of mechanical failure.

5. Cost Analysis

An approximate CAPEX analysis of a Double L-Valve is presented hereunder according to its geometrical parameters. The cost of the tube material (5 EUR/kg) represents the highest portion of the associated CAPEX. The cost of the insulation blankets, which is considered as 500 EUR/m², is proportional to the outer surface of the outer tube. Hence, designs of tubes with small diameters will be preferred by the algorithm because they result in low material and insulation costs. However, the narrower the Double L-Valve, the more Double L-Valves will be needed to circulate the required flux. Hence, these designs are going to have increased assembly costs.

Regarding the assembly costs, the cutting, welding and mounting costs of the Double L-Valves are included, which are proportional to their number and their tube length. More specifically, cutting and welding processes are required for the machining of the 90 degrees elbows to a single Double L-Valve with an estimated cost of 2000 EUR/piece. The mounting costs include the Double L-Valve mounting with a flange at the lower end, which is estimated to cost EUR 2000 for every Double L-Valve, and all the necessary elastic parts responsible to receive the axial deformations from the expansion of the tubes. The cost of the axial suspension, which prevents the tubes from buckling, estimated to cost only EUR 500 thanks to its simple design (a simple spring).

Furthermore, it is considered necessary to add a custom spacer along the tubes every five meters in length in order to dictate the concentricity of the tubes. The slim profile spacer design is presented in Figure 17a. The cost of every spacer is dependent on the tube diameters, but it is estimated to be about EUR 100. The long tubes that make up the L-Valve consist of sections of pipes of 5 m that are connected to each other as they have suitable machined geometries as Figure 17b presents. This machine costs EUR 500 for each pipe section.

Table 7. Equipment parametric costs.

Material Costs		Value	Unit
Tube material	Total mass	5	EUR/kg
Insulation	Outer surface	500	EUR/m2
Assembly costs		Value	Unit
Tube cutting and welding	Number of Double L-Valves	2000	EUR/piece
Upper suspensions	Number of Double L-Valves	500	EUR/piece
Axial expansion joint	Number of Double L-Valves	300	EUR/piece
Flange mounting	Number of Double L-Valves	2000	EUR/piece
Tube spacers	Heat exchange total length	100	EUR/m
Machining of tubes	Heat exchange total length	500	EUR/m

summarizes the aforementioned parameters of the equipment costs. This parametric costing was included in the optimization process presented below.

The thermal response was examined in relation to the CAPEX of several different HE designs for the case study presented in Table 4. The results of all the simulations are summarized in a Pareto diagram presented in Figure 18, where every point represents an HE arrangement, whereas on the x axis, there is the equipment cost, and on the y axis, there is the achieved temperature at the calciner inlet. For every simulation conducted, the simulation time is set equal to two hours with a time step of 2 s. Also, every finite element has a length of 10 mm.

The range of Double L-Valve design parameters investigated is presented by Equation (40), where the independent parameters are the inner radius of the inner tube and the length of the tubes, while the corresponding radius of the outer tube is such that the velocity of the granular materials inside and outside is equal.

$$\begin{gathered} 20 \mathrm{mm}<R_{11}<300 \mathrm{mm} \\ 5 \mathrm{m}<L<60 \mathrm{m} \\ {R}_{12}=R_{11}+2 \mathrm{mm} \\ {R}_{21}=\sqrt{\frac{{\dot{m}}_2}{{\dot{m}}_1}\frac{{\rho }_1}{{\rho }_2}{R}_{11}^2+R_{12}^2} \\ {R}_{22}=R_{21}+2 \mathrm{mm} \end{gathered}$$

(40)

The minimum number of L-Valves according to Equation (41) is calculated as follows:

$$N_{min}=\frac{{\rho }_2\pi (R_{12}^2-R_{21}^2)}{{\dot{m}}_2}{u}_{c2},$$

(41)

where $u_{c2}$ is the critical velocity calculated by Equation (35).

The proposed optimal arrangement from the Pareto front is presented in

Table 8. Basic design parameters and CAPEX.

HE Thermal Parameters	Unit	Value
${T_1}_0$	°C	900
${T_2}_0$	°C	650
${\rho }_{s1}$	kg/m3	1478
${\rho }_{s2}$	kg/m3	1794
$a_s$	-	0.6
${C_p}_1$	J/kg/K	920.2
${C_p}_2$	J/kg/K	996.7
${\dot{m}}_1$	kg/s	31.54
${\dot{m}}_2$	kg/s	35.91
Temperature at the calciner inlet	°C	760
Heat recovery	MW	3.93
Design parameters of Double L-Valves	Unit	Value
Inner tube diameter	mm	560
Outer tube diameter	mm	728.5
Length of tubes	m	50
Number of Double L-Valves	-	11
Costs	Unit	Value
Material costs	EUR	875,800
Assembly costs	EUR	221,800
Total CAPEX	EUR	1,097,600

.

6. Conclusions

In the framework of this work, a holistic approach for the design and assessment of parallel flow L-Valve solid–solid heat exchangers has been developed and presented for the operation in a CaL concept. This holistic approach includes, initially, hydrodynamic measurements supporting the development of a scale-up model for the modelling and dimensioning of industrial-scale HEs. In addition, an analytical transient thermal model has been introduced to evaluate the performance of the heat exchanger in terms of heat transfer. Finally, FEA and cost models have been developed to enhance the structural integrity of the proposed designs as well as to optimize the costs. The main conclusions of the current work are as follows:

• The experimental data indicated that a smaller air supply leads to less effective transfer of granular material.
• The thermal model results showed that the heat exchange that takes place is due approximately 94% to radiation and 6% to convection, resulting in a 110 °C temperature increase for the studied case ($T_{hot}=900 °\mathrm{C}, T_{cold}=650 °\mathrm{C}, {\dot{m}}_{hot}=31.54 \frac{\mathrm{kg}}{\mathrm{s}}, {\dot{m}}_{cold}=35.91 \mathrm{kg}/\mathrm{s}$).
• The structural integrity of the proposed design under the resulting thermal loads has been checked via FEA models, proving the manufacturability of the concept at an industrial scale. In this design, each HE is mounted at the bottom by a flange and at the top by a suspension so that it does not buckle.
• All these features were costed parametrically, but the main costs are the tube material and insulation. The resulting CAPEX of the industrial case studied is 0.279 EUR/Watt.

All in all, the proposed HE concept offers several advantages including design flexibility, a simple construction, a rather sufficient heat transfer efficiency, durability and a rather low cost. Finally, the developed methodology can be utilized for the assessment of other solid–solid HEs in the future.