Large Eddy Simulation of Externally Induced Ingress about an Axial Seal by Stator Vanes
Abstract
:1. Introduction
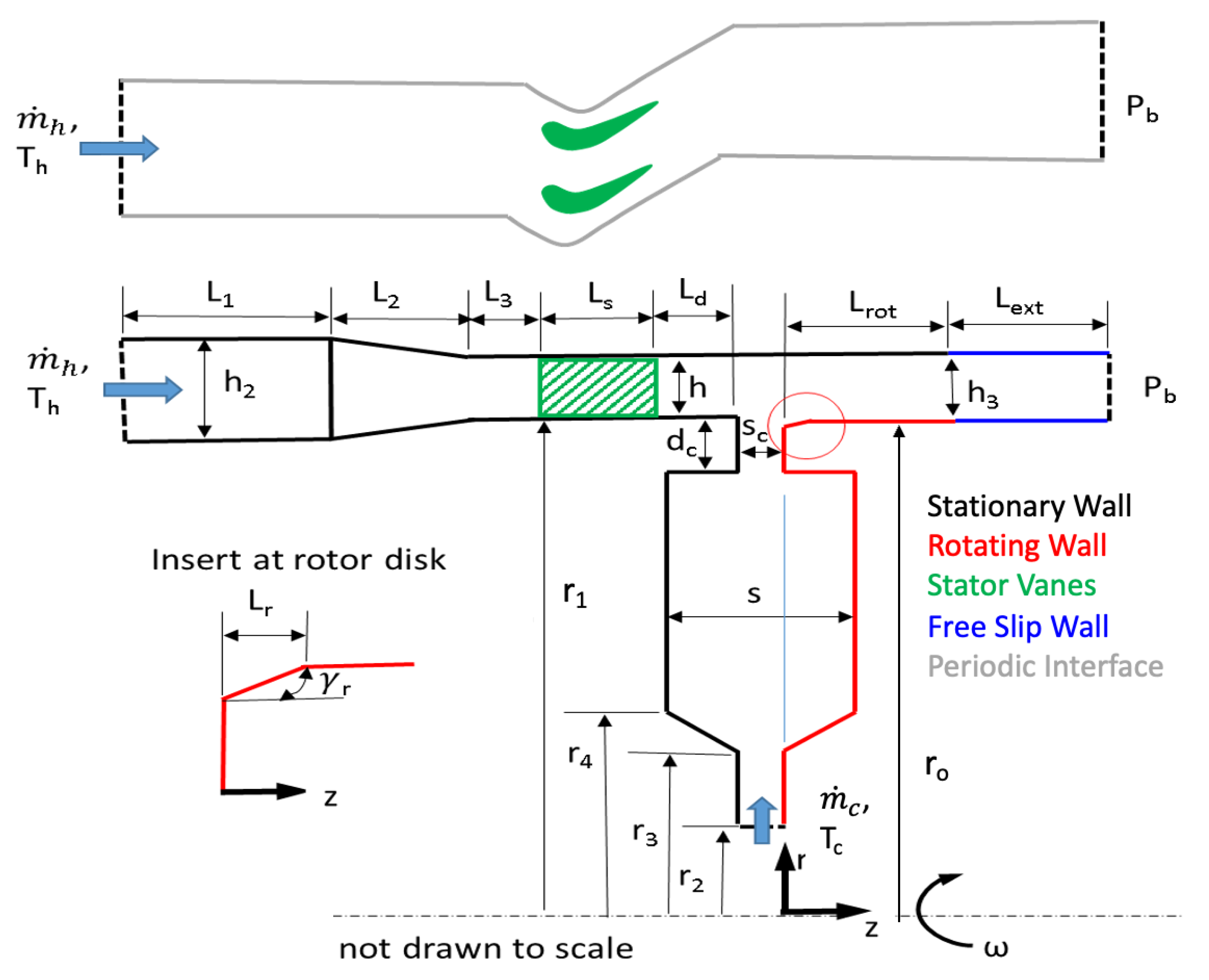
2. Problem Description
3. Problem Formulation
4. Numerical Method of Solution
5. Results and Discussion
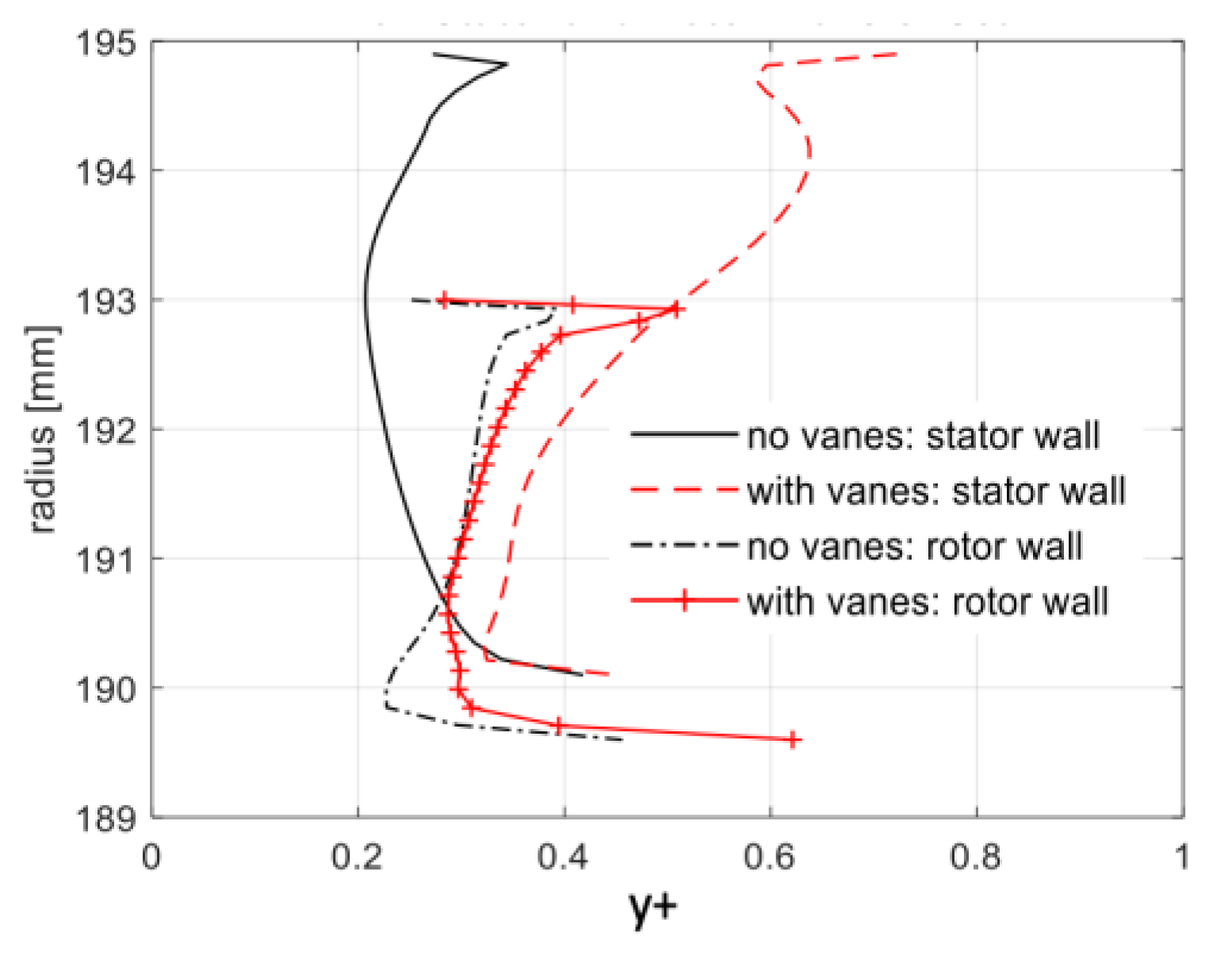
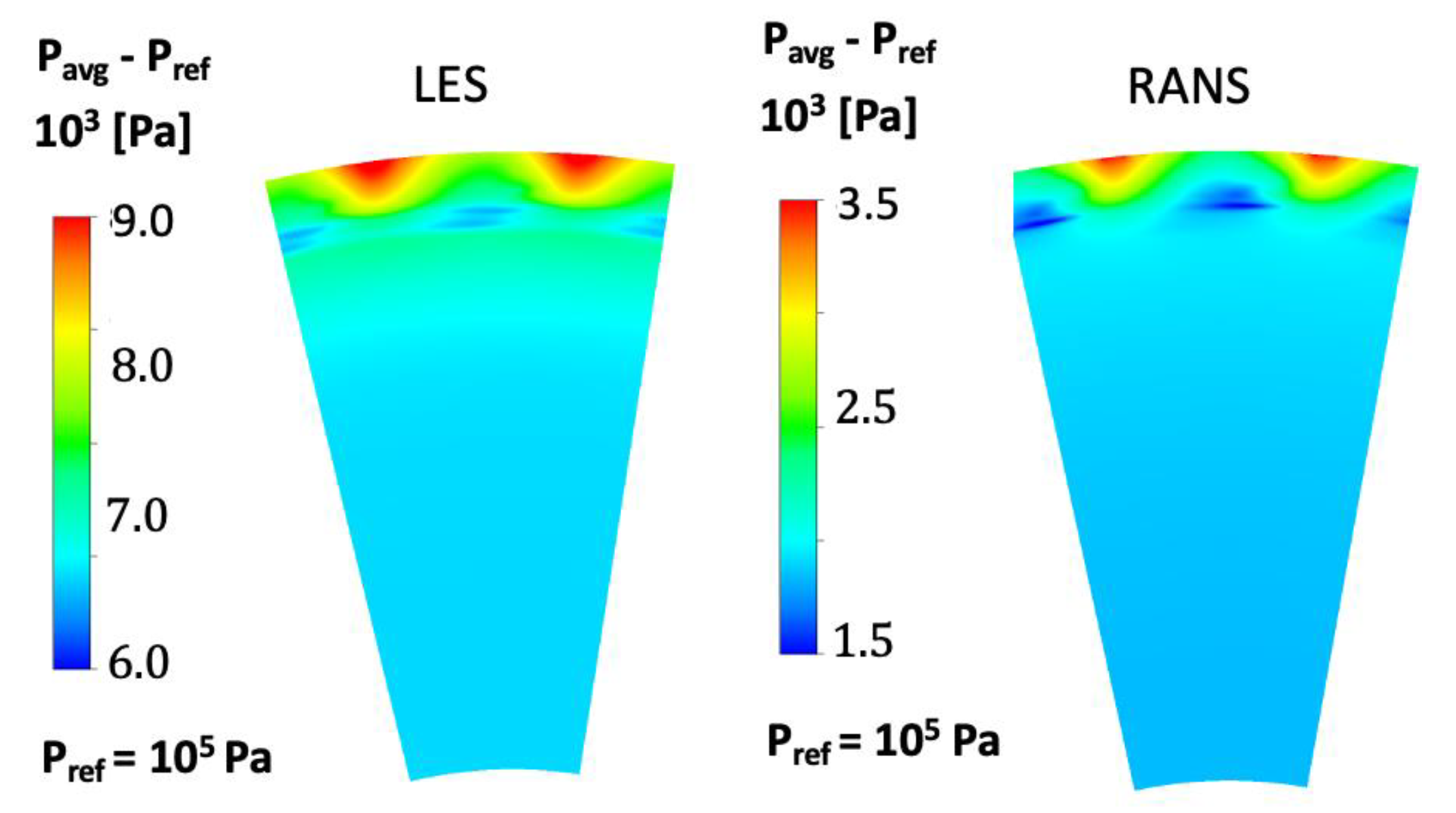
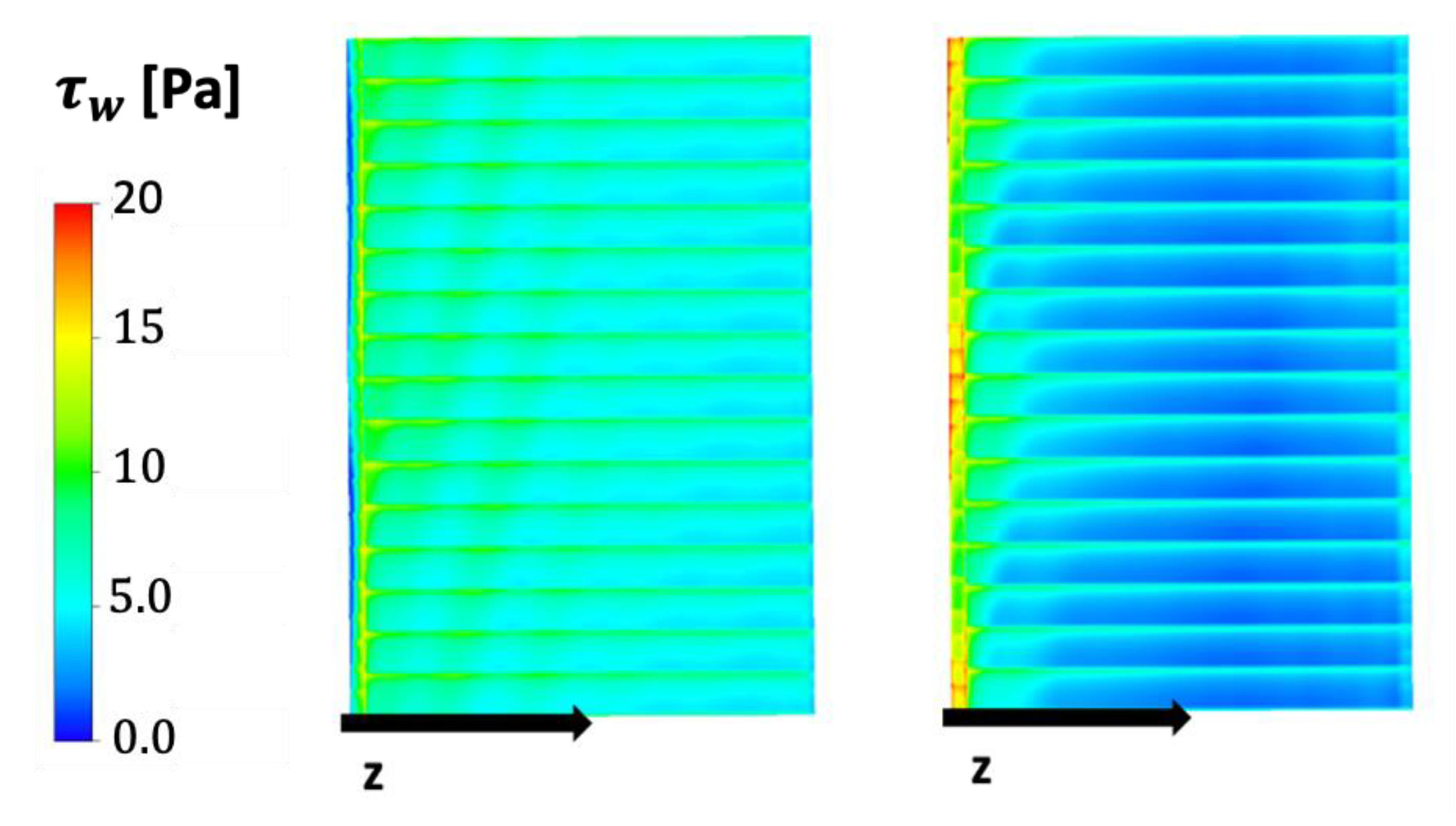
5.1. Verification and Validation
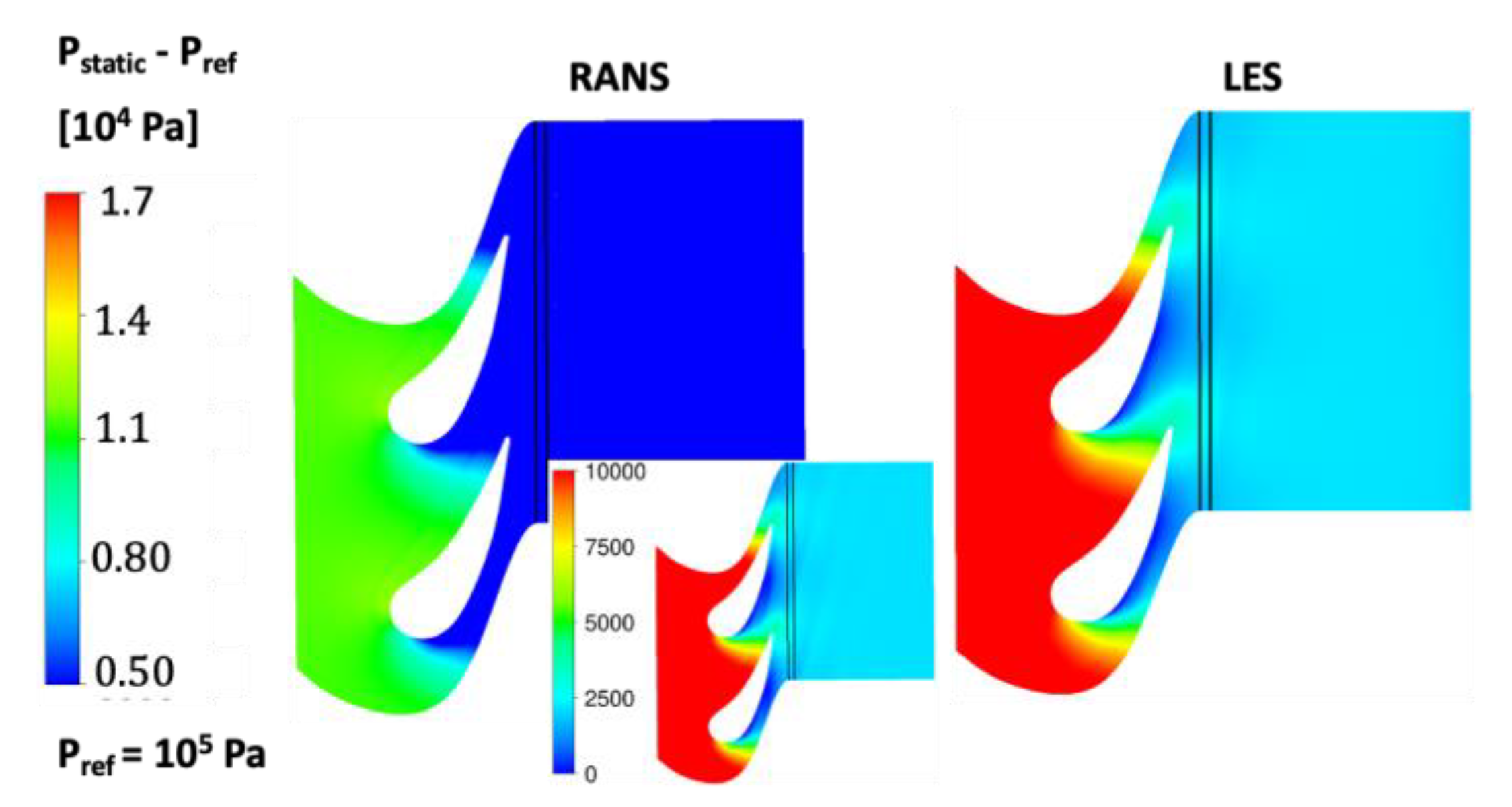
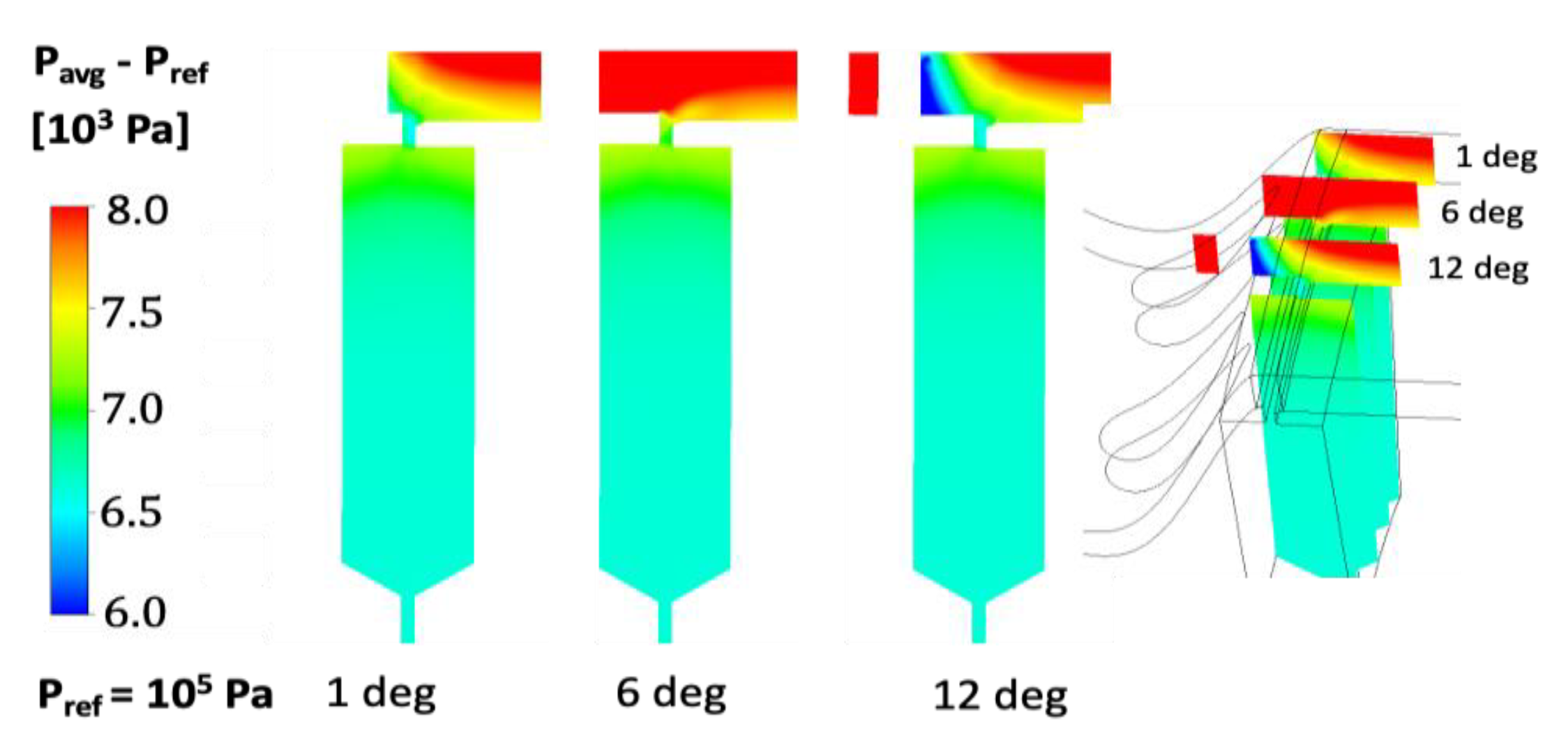
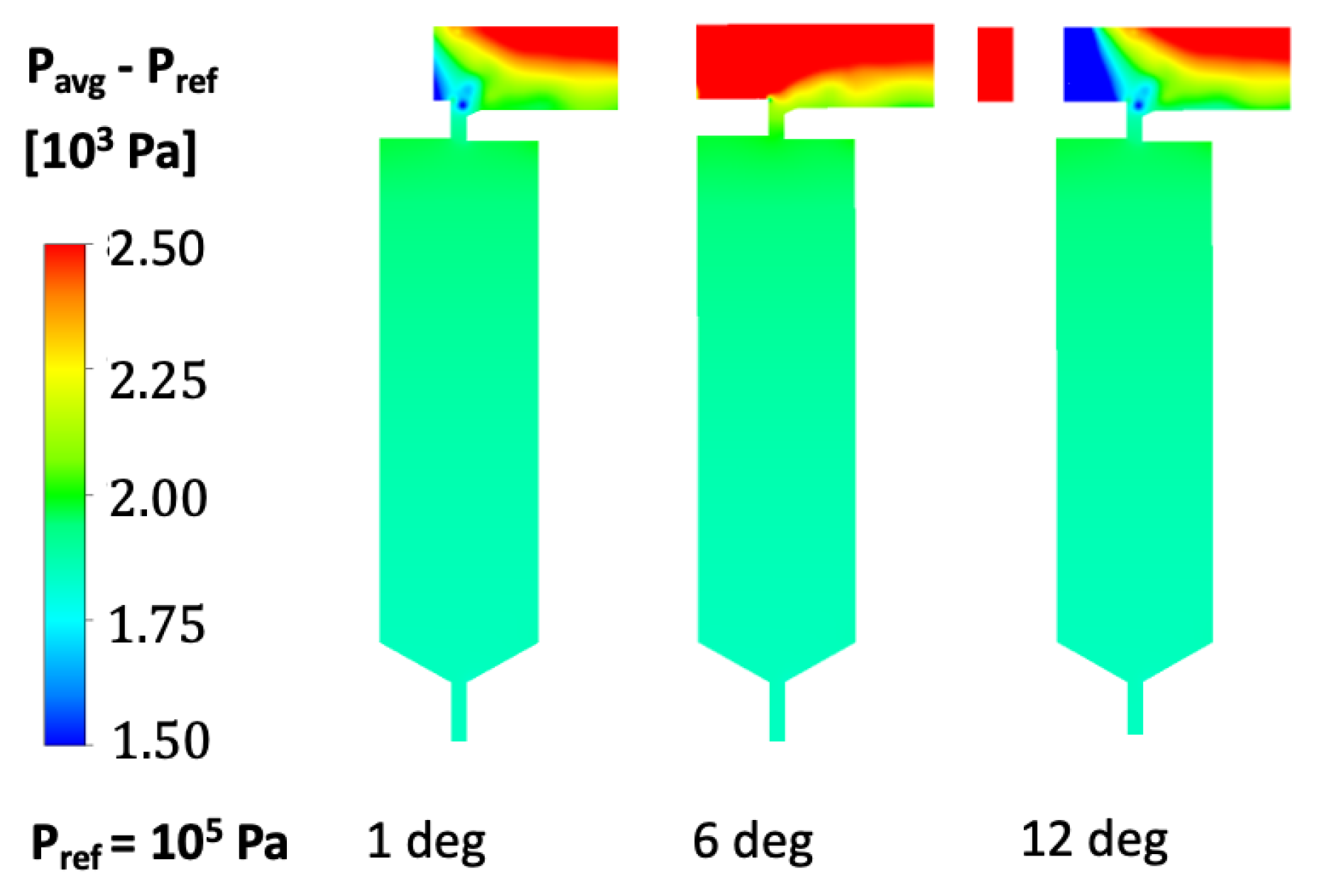
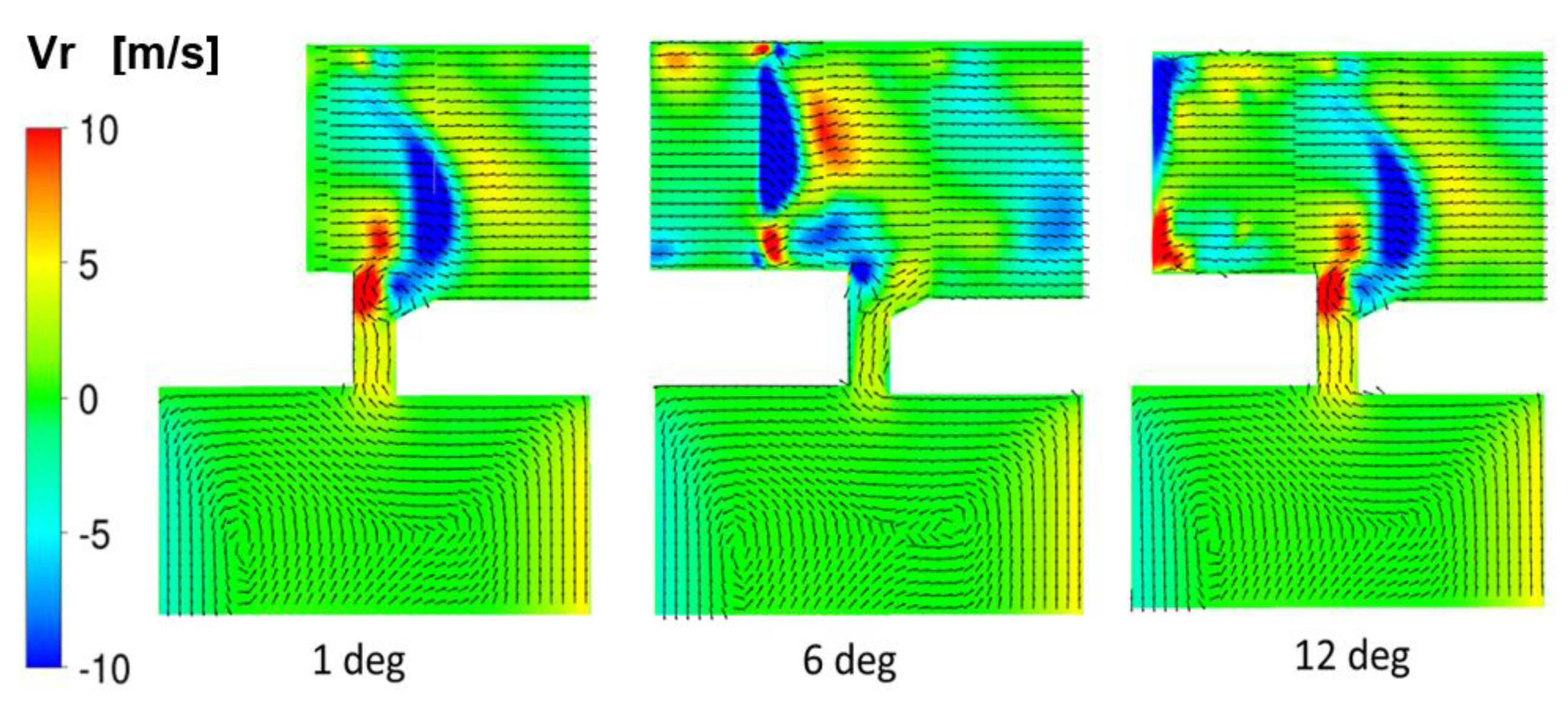
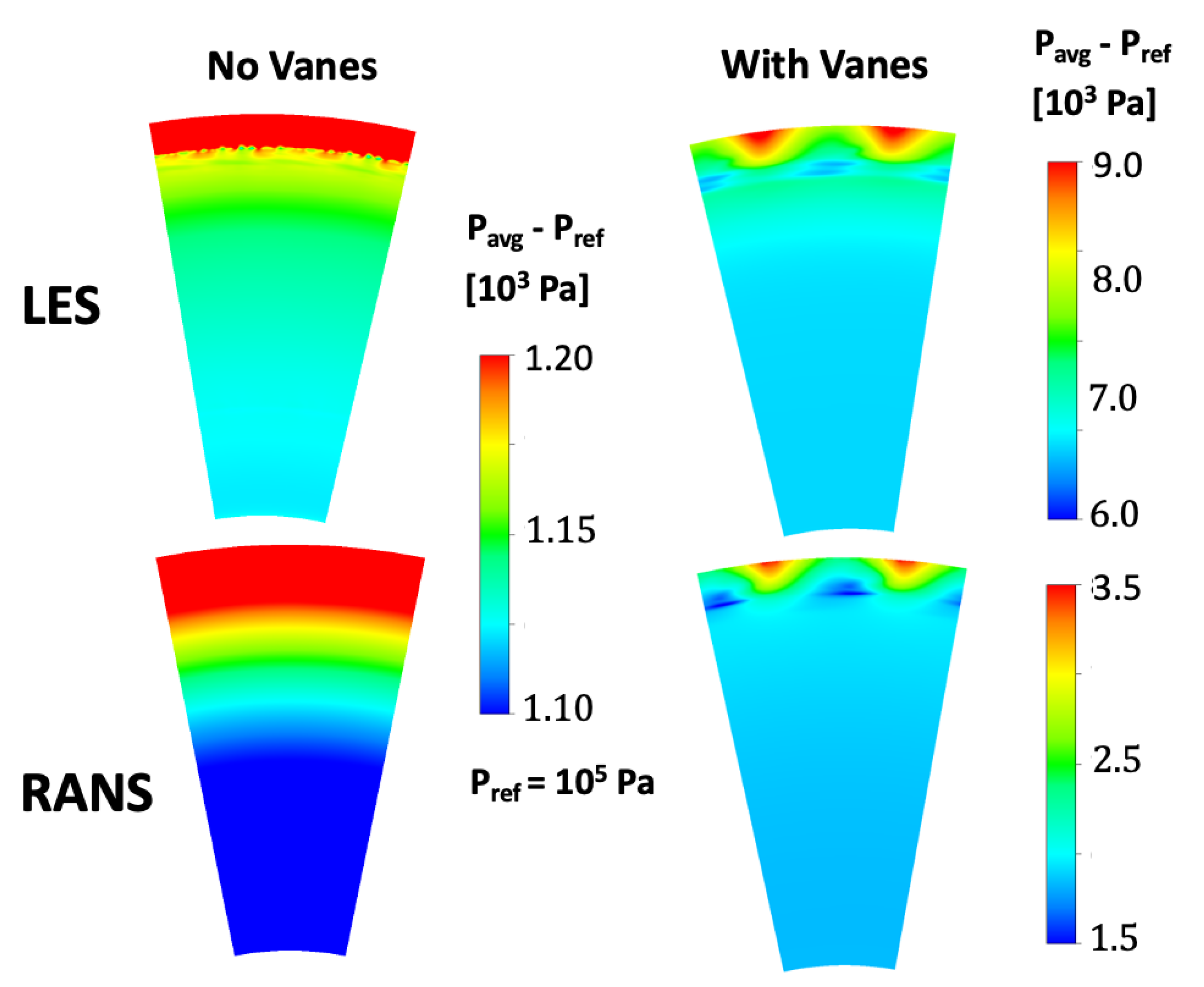
5.2. Flow Field with Stator Vanes
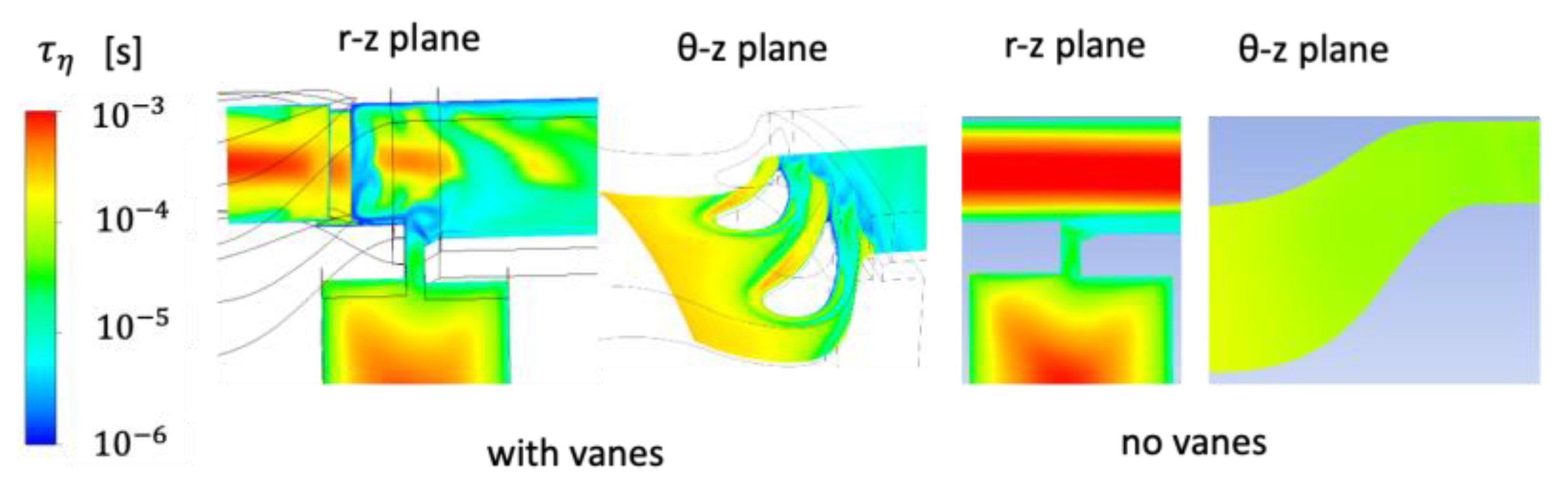
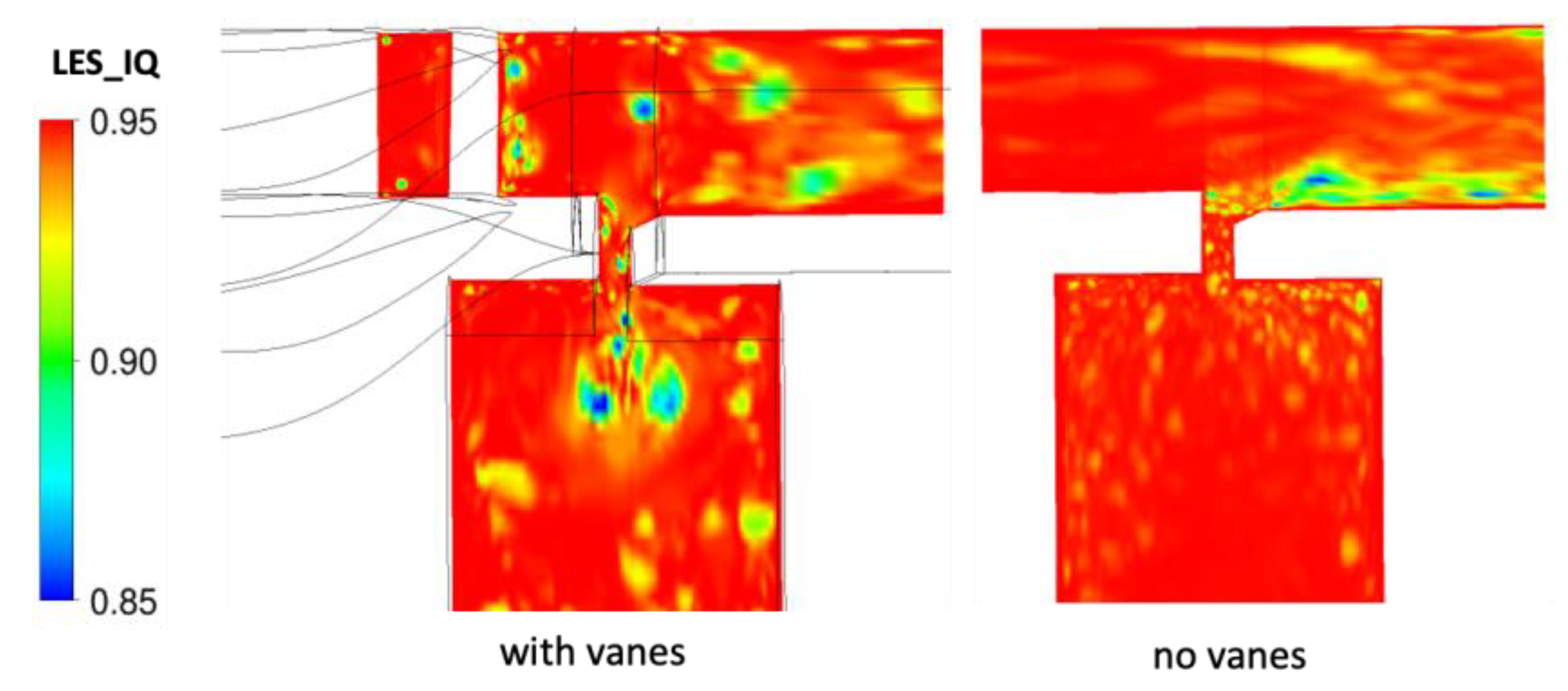
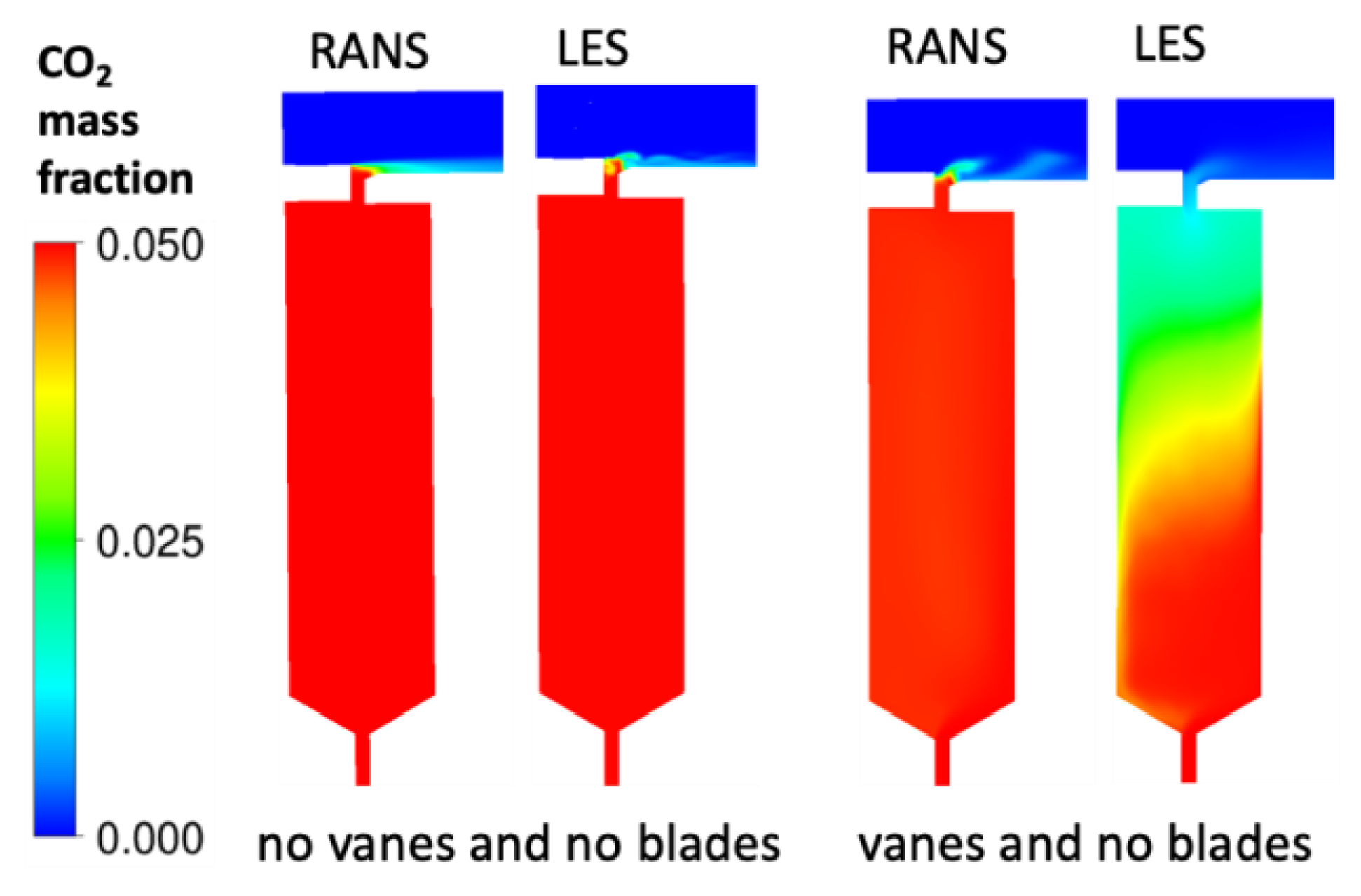
5.3. Flow Field with and without Stator Vanes
6. Conclusions
- Both LES and RANS could predict the normalized pressure coefficient, Cp, on the stator platform downstream of the stator vanes and upstream of the seal with reasonable accuracy.
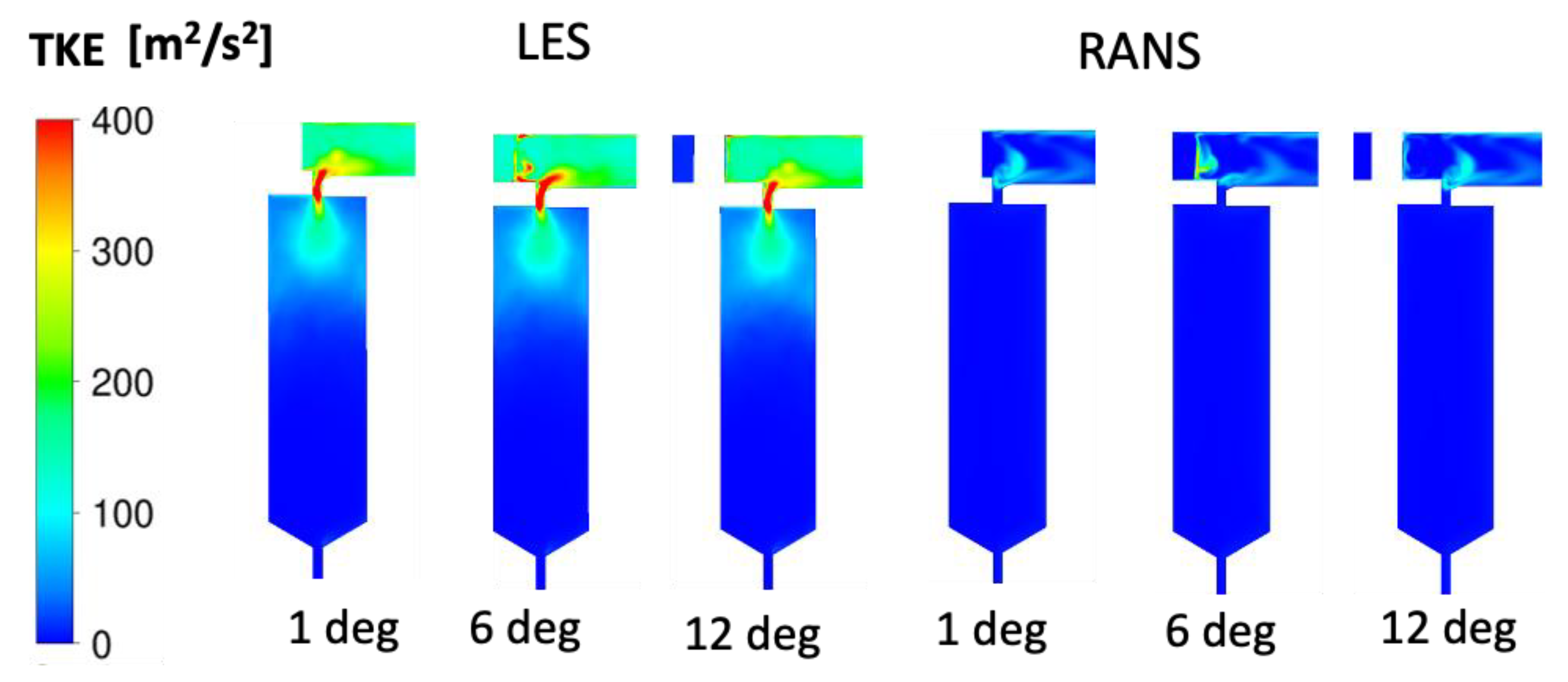
- LES could predict ingress and the correct sealing effectiveness for the configuration and operating condition studied.
- Steady RANS could not predict ingress and predicted a grossly incorrect sealing effectiveness.
- Since steady RANS could predict Cp with reasonable accuracy but could not predict ingress or the correct sealing effectiveness, Cp by itself is inadequate in quantifying ingress.
- LES predicted a much higher pressure drop in the axial direction about the seal region than RANS, and this produced a much higher pressure drop across the seal in the radial direction to drive ingress into the wheelspace.
- For LES to correctly predict ingress, the grid size and time-step size must be small enough to resolve the small-scale structures created by the interaction between the hot gas flow in the axial direction, the boundary layer flow induced by rotation in the azimuthal direction, and the shedding of vortices in the seal clearance.
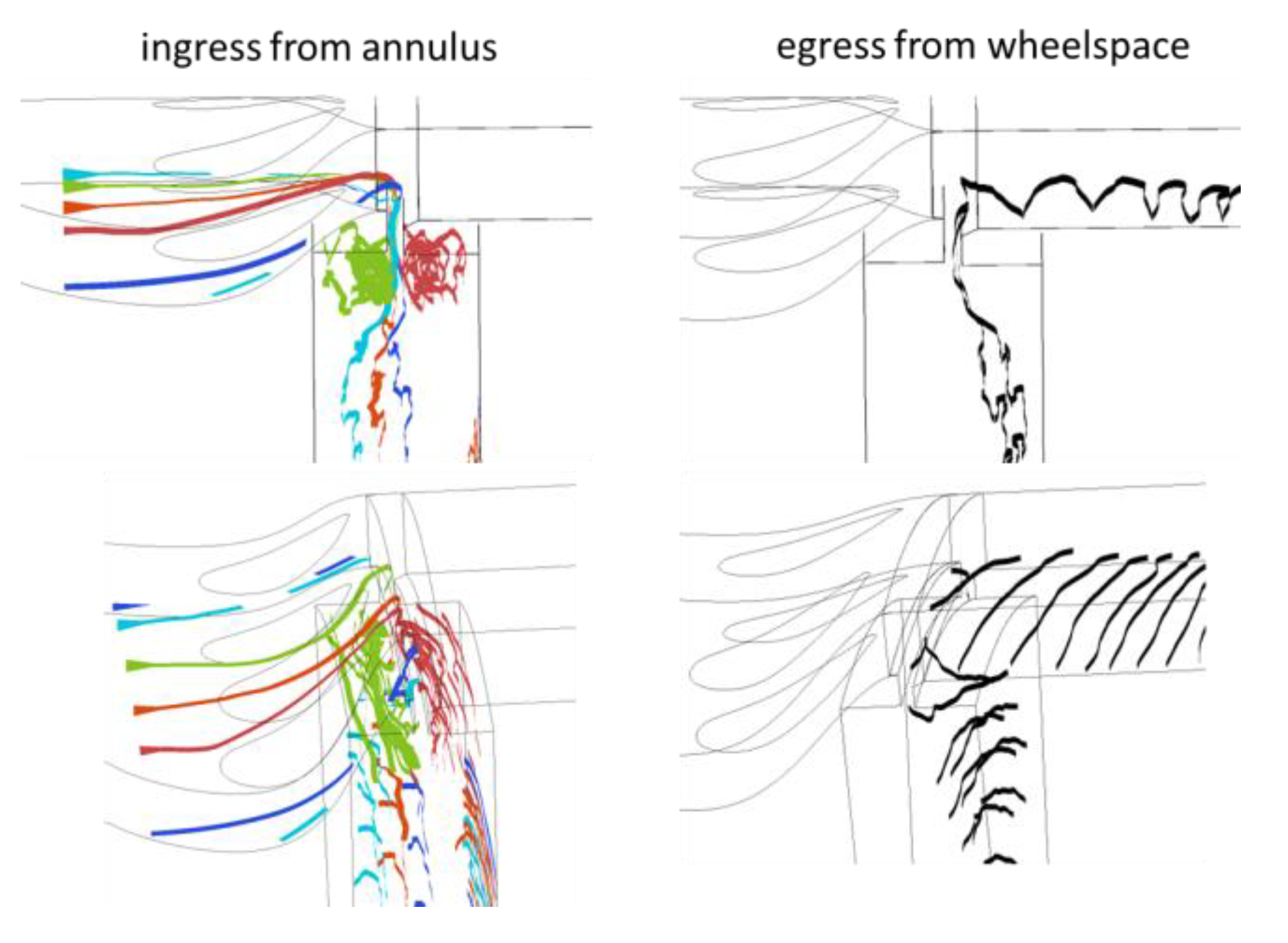
- On ingress induced by the stator vanes, it starts in the middle of the seal and later deflects onto the stator side. Once in the wheelspace, the flow is entrained by the vortical structures there.
- On egress, it flows along the rotor side of the wheelspace and exits on the rotor side of the seal.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ca | concentration of CO2 in annulus |
| co | concentration of CO2 in sealing flow |
| cs | concentration of CO2 in the wheelspace |
| Cp | pressure coefficient: |
| nondimensional coolant flow rate: | |
| h | height of annulus (see Figure 1) |
| I | turbulence intensity |
| Li | length (i = 1, 2; see Figure 1) |
| ṁ | mass flow rate |
| P | static pressure |
| mean static pressure | |
| Pb | back pressure |
| r | radial coordinate |
| ro | radius of hub/inner radius of annulus |
| r1 | outer radius of annulus |
| external flow Reynolds number: | |
| rotational Reynolds number: | |
| s | axial distance between rotor and stator (gap) |
| sc | axial distance in seal opening (clearance) |
| Tw | wall temperature |
| local friction velocity: , where is the averaged wall shear stress | |
| V | velocity |
| y+ | nondimensional turbulent distance |
| z | axial coordinate |
| normalized grid spacing: where | |
| sealing effectiveness based on CO2 concentration: | |
| ε | rate of turbulence dissipation |
| θ | azimuthal coordinate |
| θo | sector size of configuration |
| dynamic viscosity | |
| kinematic viscosity | |
| effective kinematic viscosity (laminar + turbulent) | |
| ρ | density |
| Kolmogorov time scale: | |
| angular speed of rotor disk | |
| Subscripts | |
| c | coolant flow |
| h | mainstream flow |
References
- Johnson, B.V.; Mack, G.J.; Paolillo, R.E.; Daniels, W.A. Turbine Rim Seal Gas Path Flow Ingestion Mechanisms; Paper No. 94-2703; AIAA: Reston, VA, USA, 1994. [Google Scholar]
- Chew, J.W.; Gao, F.; Palermo, D.M. Flow Mechanisms in Axial Turbine Rim Sealing. J. Mech. Eng. Sci. 2019, 233, 7637–7657. [Google Scholar] [CrossRef] [Green Version]
- Bohn, D.; Johann, E.; Krüger, U. Experimental and Numerical Investigations of Aerodynamic Aspects of Hot Gas Ingestion in Rotor-Stator Systems with Superimposed Cooling Mass Flow. In Proceedings of the SME 1995 International Gas Turbine and Aeroengine Congress and Exposition, Houston, TX, USA, 5 June 1995; Volume 1: Turbomachinery. p. V001T01A034. [Google Scholar] [CrossRef] [Green Version]
- Bohn, D.; Rudzinski, B.; Sürken, N.; Gärtner, W. Influence of Rim Seal Geometry on Hot Gas Ingestion into the Upstream Cavity of an Axial Turbine Stage, 1999. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999; Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration. p. V003T01A066. [Google Scholar] [CrossRef] [Green Version]
- Bohn, D.; Rudzinski, B.; Sürken, N.; Gärtner, W. Experimental and Numerical Investigation of the Influence of Rotor Blades on Hot Gas Ingestion into the Upstream Cavity of an Axial Turbine Stage. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000; Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration. p. V003T01A088. [Google Scholar] [CrossRef]
- Green, T.; Turner, A.B. Ingestion into the Upstream Wheelspace of an Axial Turbine Stage. J. Turbomach. 1994, 116, 327–332. [Google Scholar] [CrossRef]
- Sangan, C.M.; Pountney, O.J.; Zhou, K.; Wilson, M.; Owen, J.M.; Lock, G.D. Experimental Measurements of Ingestion Through Turbine Rim Seals—Part I: Externally Induced Ingress. J. Turbomach. 2013, 135, 021012. [Google Scholar] [CrossRef]
- Sangan, C.M.; Pountney, O.J.; Zhou, K.; Owen, J.M.; Wilson, M.; Lock, G.D. Experimental Measurements of Ingestion through Turbine Rim Seals—Part II: Rotationally Induced Ingress. J. Turbomach. 2013, 135, 021013. [Google Scholar] [CrossRef]
- Roy, R.P.; Feng, J.; Narzary, D.; Paolillo, R.E. Experiment on Gas Ingestion Through Axial-Flow Turbine Rim Seals. ASME J. Eng. Gas Turbines Power. 2005, 127, 573–582. [Google Scholar] [CrossRef]
- Laskowski, G.M.; Bunker, R.S.; Bailey, J.C.; Kapetanovic, S.; Itzel, G.M.; Sullivan, M.A.; Farrell, T.R. An Investigation of Turbine Wheelspace Cooling Flow Interactions with a Transonic Hot Gas Path—Part II: CFD Simulations. J. Turbomach. 2009, 133, 041020. [Google Scholar] [CrossRef]
- Zhou, D.W.; Roy, R.P.; Wang, C.; Glahn, J.A. Main Gas Ingestion in a Turbine Stage for Three Rim Cavity Configurations. ASME J. Turbomach. 2011, 133, 031023. [Google Scholar] [CrossRef]
- Mahoney, T.; Hills, N.; Chew, J.; Scanlon, T. Large-Eddy Simulation of Rim Seal Ingestion. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2011, 225, 2881–2891. [Google Scholar] [CrossRef]
- Liu, J.; Weaver, A.; Shih, T.I.-P.; Sangan, C.M.; Lock, G.D. Modelling and Simulation of Ingress into the Rim Seal and Wheelspace of a Gas-Turbine Rotor-Stator Configuration. In Proceedings of the AIAA SciTech Forum, 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Nketia, S.; Shih, T.I.-P.; Bryden, K.; Dalton, R.; Dennis, R.A. Large Eddy Simulation of Rotationally Induced Ingress and Egress around an Axial Seal between Rotor and Stator Disks. Energies 2023, 16, 4354. [Google Scholar] [CrossRef]
- Pehle, L.; Wirsum, M.; Stotz, S. Unsteady Flow Phenomena in a 1.5-Stage Test Turbine with an Axial Rim Seal, GT2023-103434. In Proceedings of the ASME Turbo Expo, Boston, MA, USA, 26–30 June 2023. [Google Scholar]
- Vella, S.; Darby, P.; Carnevale, M.; Scobie, J.A.; Lock, G.D.; Jarrossay, C.; Salvatori, F.; Bonneau, D.; Sangan, C.M. A Combined Experimental and Turbulence-Resolved Modelling Approach for Aeroengine Turbine Rim Seals. GT2023-103895. In Proceedings of the ASME Turbo Expo, Boston, MA, USA, 26–30 June 2023. [Google Scholar]
- Burden, S.; Chew, J.W.; Gao, F.; Marxen, O. Effect of Rim Seal Geometry on Rotationally-Driven Ingestion. GT2023-103041. In Proceedings of the ASME Turbo Expo, Boston, MA, USA, 26–30 June 2023. [Google Scholar]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Dhamankar, N.; Blaisdell, G.; Lyrintzis, A. Overview of Turbulent Inflow Boundary Conditions for Large-Eddy Simulations. AIAA J. 2018, 56, 1317–1334. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal Two-Equation k-ω Turbulence Models for Aerodynamic Flows; AIAA Paper 93-2906. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Ansys Fluent Fluid Simulation Software. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 30 June 2023).
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corp.: Washington, DC, USA, 1980. [Google Scholar]
- Celik, I.B.; Cehreli, Z.N.; Yavuz, I. Index of Resolution Quality for Large Eddy Simulations. J. Fluids Eng. 2005, 127, 949–958. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nketia, S.; Bryden, K.M.; Dalton, R.; Shih, T.I.-P. Large Eddy Simulation of Externally Induced Ingress about an Axial Seal by Stator Vanes. Energies 2023, 16, 5985. https://doi.org/10.3390/en16165985
Nketia S, Bryden KM, Dalton R, Shih TI-P. Large Eddy Simulation of Externally Induced Ingress about an Axial Seal by Stator Vanes. Energies. 2023; 16(16):5985. https://doi.org/10.3390/en16165985
Chicago/Turabian StyleNketia, Sabina, Kenneth Mark Bryden, Richard Dalton, and Tom I-P. Shih. 2023. "Large Eddy Simulation of Externally Induced Ingress about an Axial Seal by Stator Vanes" Energies 16, no. 16: 5985. https://doi.org/10.3390/en16165985
APA StyleNketia, S., Bryden, K. M., Dalton, R., & Shih, T. I.-P. (2023). Large Eddy Simulation of Externally Induced Ingress about an Axial Seal by Stator Vanes. Energies, 16(16), 5985. https://doi.org/10.3390/en16165985




