Research on an Error Compensation Method of SINS of a Mine Monorail Crane
Abstract
:1. Introduction
2. Dynamic Analysis of Monorail Crane
2.1. Analysis of Monorail Crane Motion
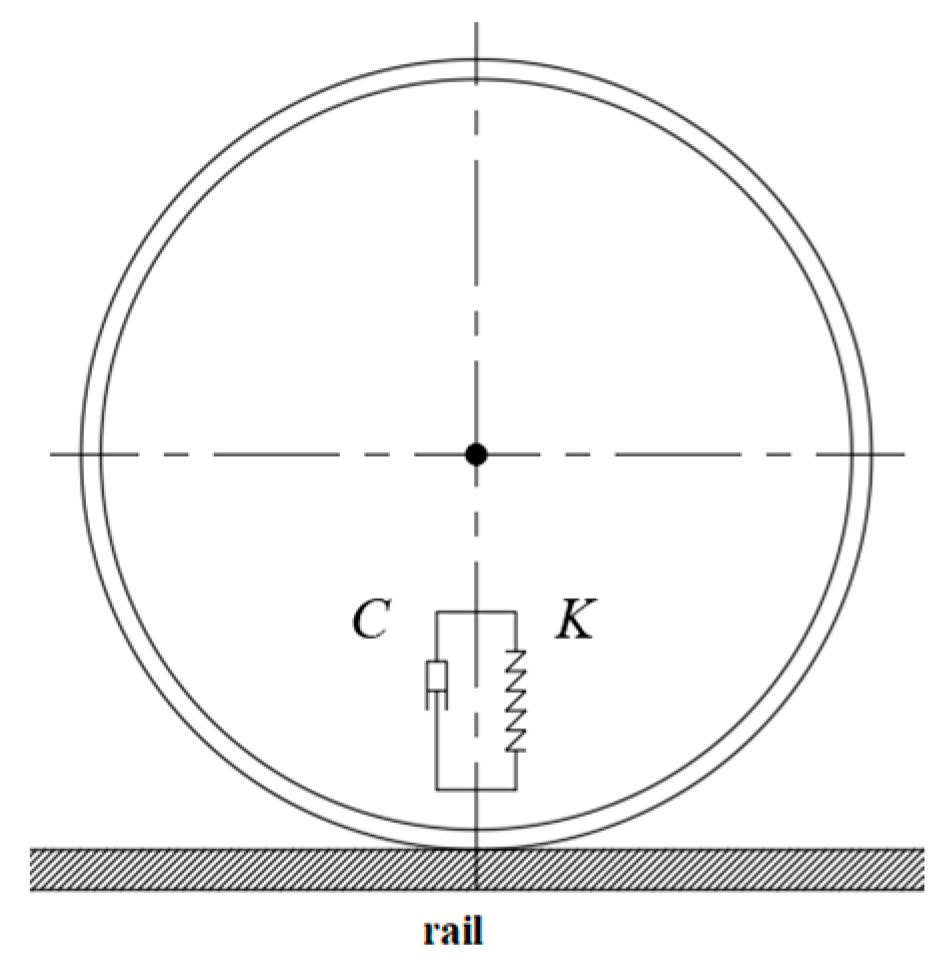
2.2. Force Analysis of Monorail Crane Wheel Set
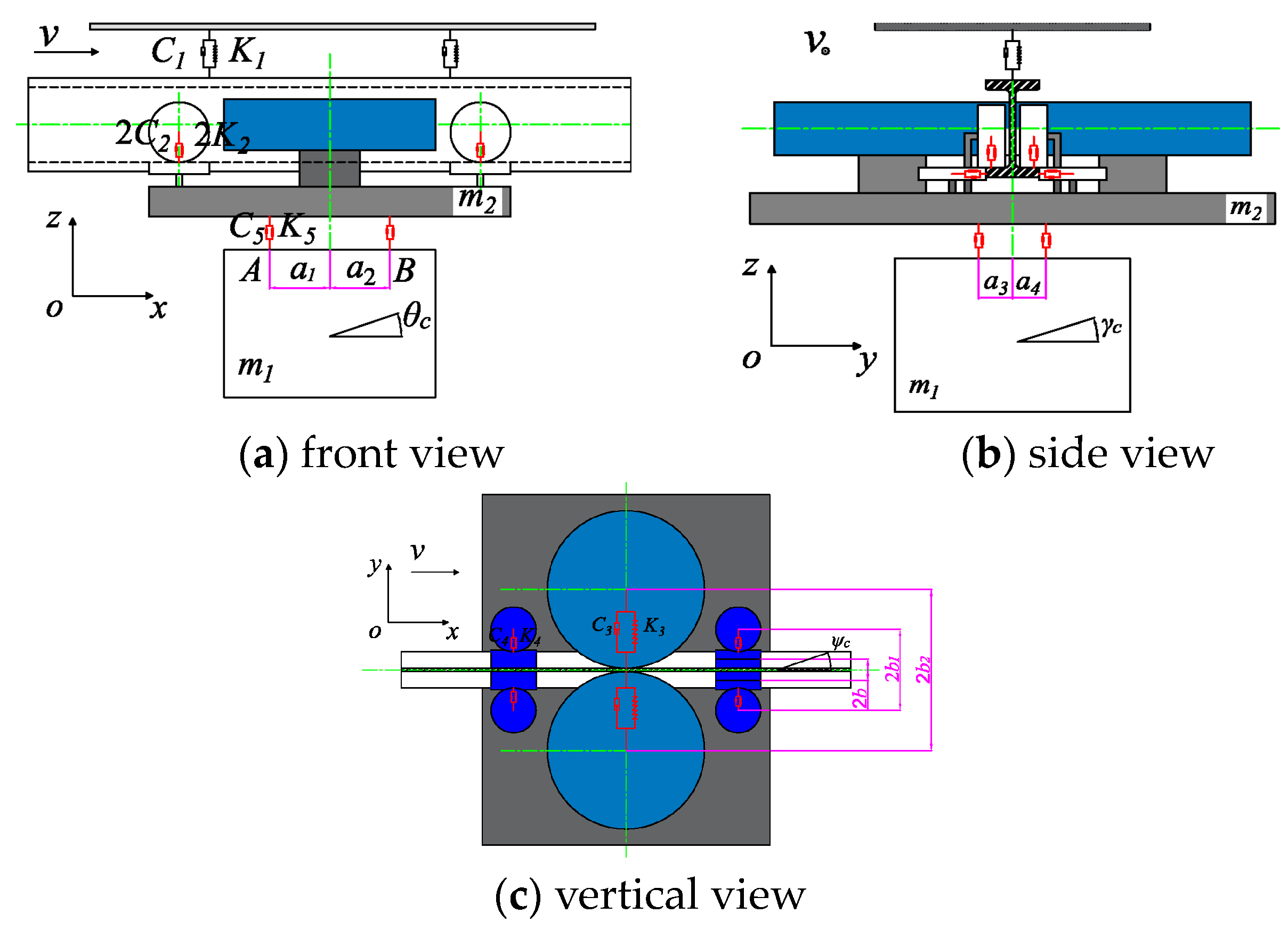
2.3. Establishment of Dynamic Model for the Driving Part of Monorail Crane
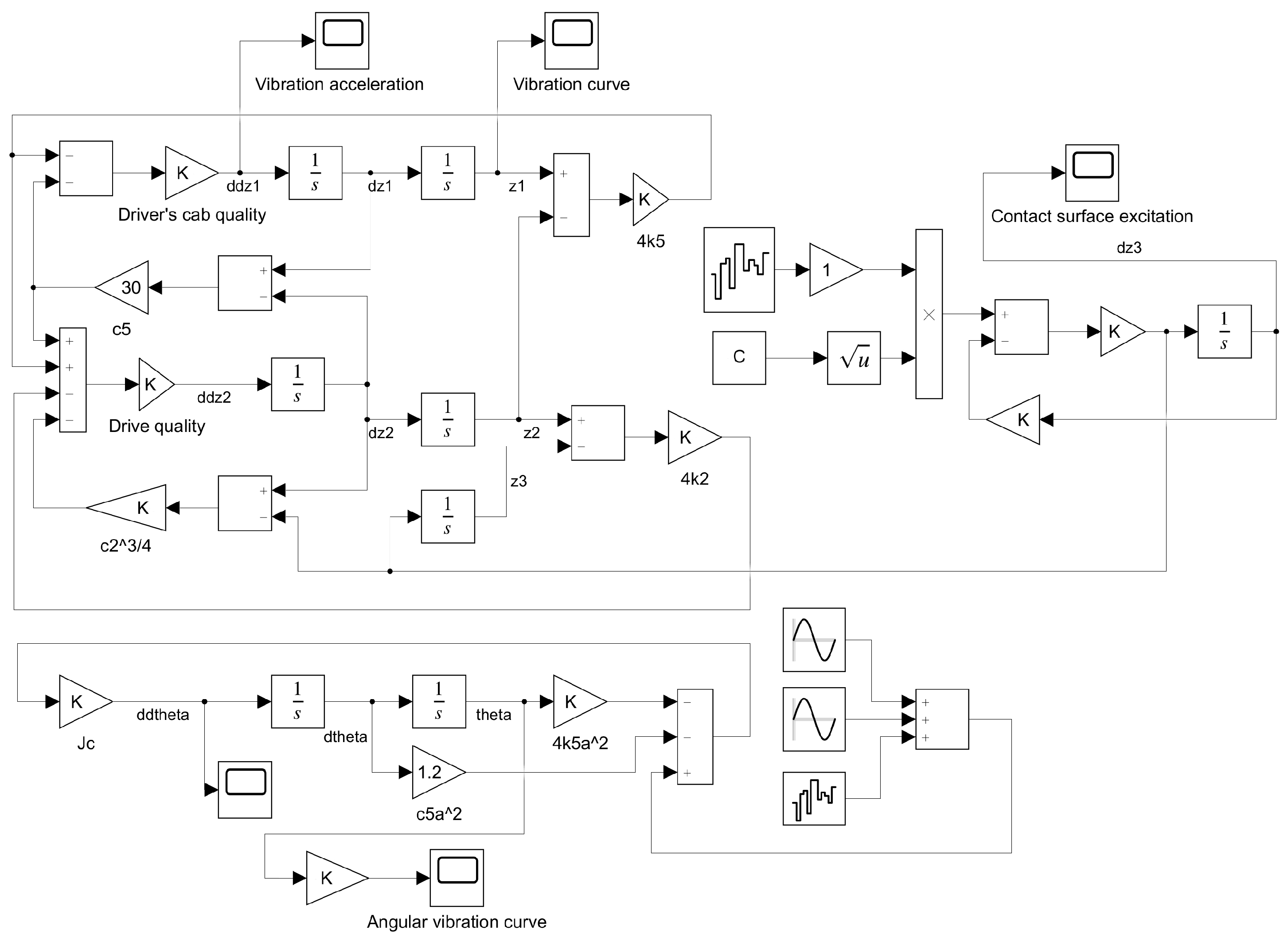
2.4. Solving the Dynamic Model of Monorail Crane
3. Compensation for Calculation Error of Monorail Crane SINS
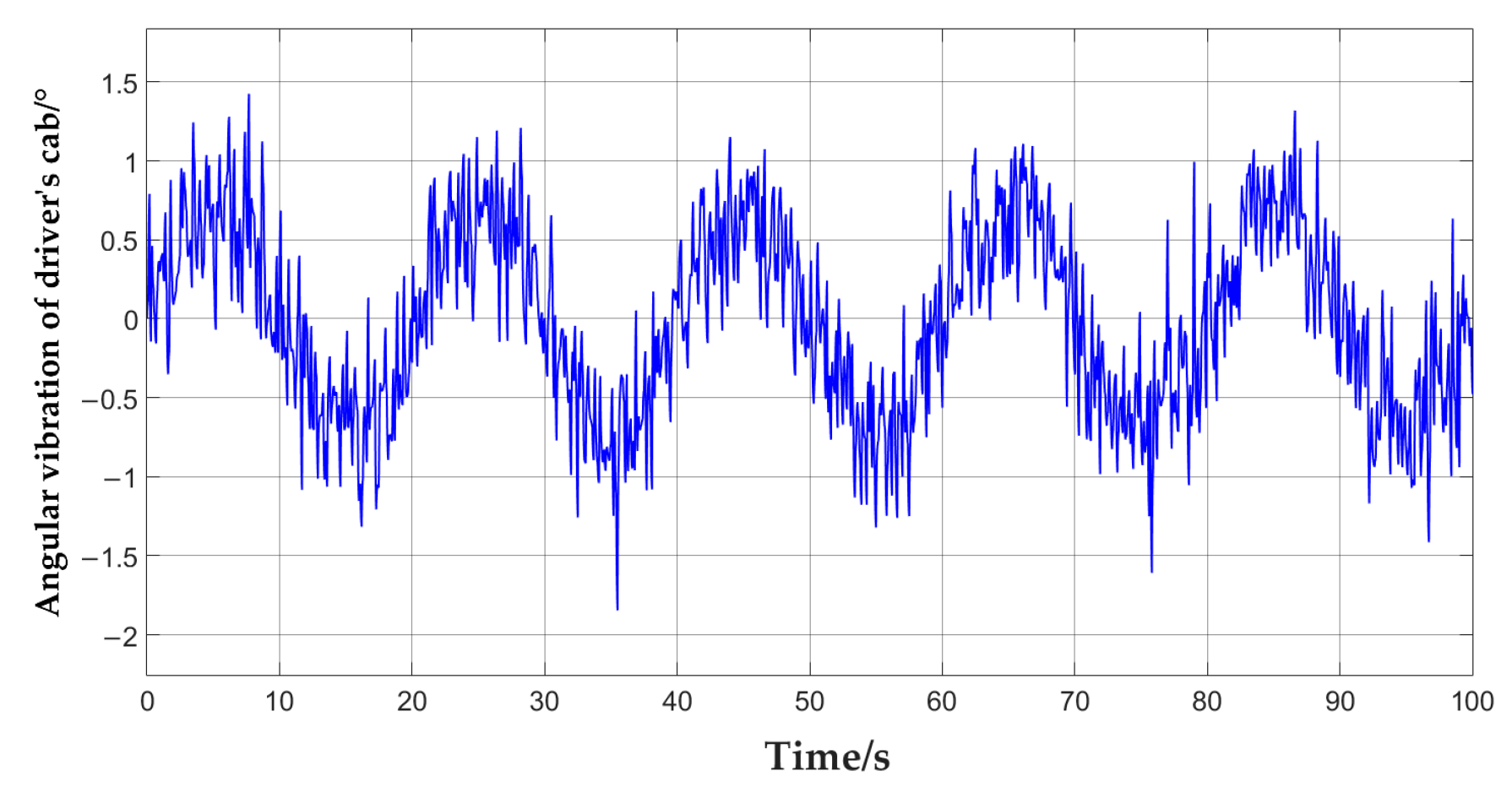
3.1. Compensation Algorithm for Angular Vibration
3.2. Linear Vibration Compensation Algorithm
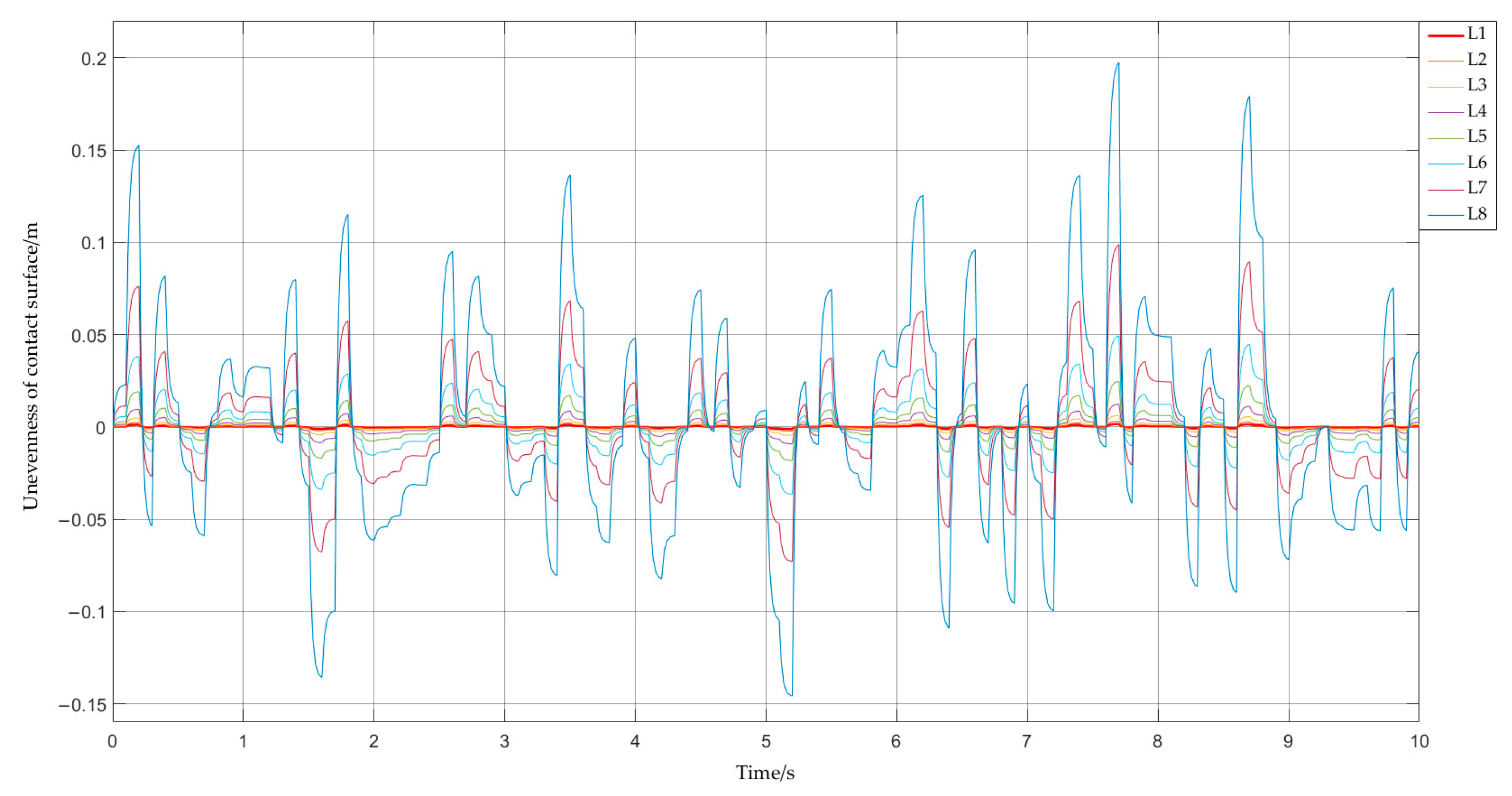
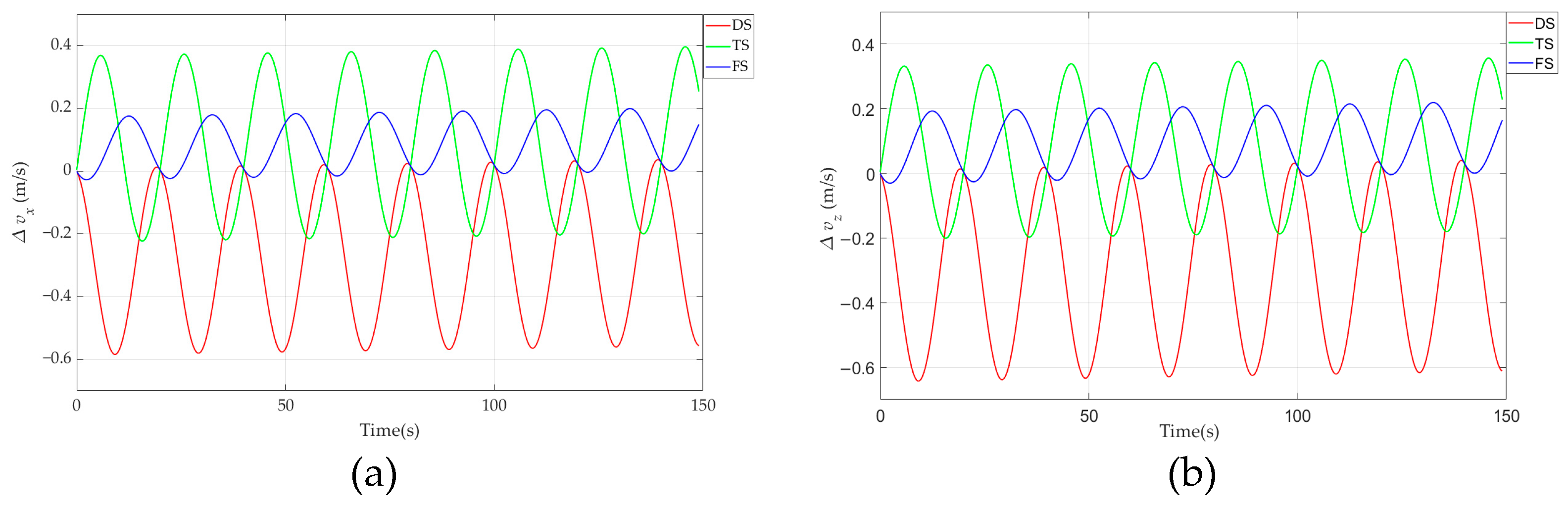
4. Simulation Analysis of Multiple Subsample Compensation Algorithm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Sun, J.; Li, Q. Status and Prospect of Research on China’s Energy Structure Optimization. Coal Eng. 2019, 51, 149–153. [Google Scholar]
- Gao, F. Discussion on the Present Situation and Development Trend of Auxiliary Transportation in Coal Mine. Mod. Chem. Res. 2021, 4, 14–15. [Google Scholar]
- Guo, K. Study on the Present Situation and Development of Auxiliary Haulage in Coal Mine. Mech. Manag. Dev. 2017, 32, 151–152+178. [Google Scholar]
- Li, Q. Brif Analysis of the Present Situation and Development Trend of Auxiliary Transportation in Coal Mine. Mod. Chem. Res. 2021, 13, 13–14. [Google Scholar]
- Yang, Y.; Wang, F.; Zhou, S. Design of Mine Locomotive Positioning System Based on RFID and ZigBee Technology. Coal Technol. 2017, 36, 245–247. [Google Scholar]
- Song, B.; Jiang, H.; Li, S.; Ji, W. Missed Event Processing for RFID Composite-events Based on the Logical Area Event Relationship Model. J. Chin. Comput. Syst. 2015, 36, 2224–2228. [Google Scholar]
- Zhang, J. Design and Research of Remote Monitoring and Positioning System of Underground Motor Vehicles in a Coal Mine. Mech. Manag. Dev. 2022, 37, 246–248. [Google Scholar]
- Li, X.; Qiao, H.; Ge, A. Precise Positioning System of Mining Locomotive Based on Inertial Navigation Technology. Comput. Syst. Appl. 2012, 21, 43–46. [Google Scholar]
- Titterton, D.; Weston, J. Basic Principles of Strapdown Inertial Navigation Systems. In Strapdown Inertial Navigation Technology; The Institution of Engineering and Technology: Hong Kong, China, 2004. [Google Scholar]
- Shen, Y.; Wang, P.; Zheng, W.; Ji, X.; Jiang, H.; Wu, M. Error Compensation of Strapdown Inertial Navigation System for the Boom-Type Roadheader under Complex Vibration. Axioms 2021, 10, 224. [Google Scholar] [CrossRef]
- Miller, R.B. A new strapdown attitude algorithm. J. Guid. Control. Dyn. 1983, 6, 287–291. [Google Scholar] [CrossRef]
- Musoff, H.; Murphy, J.H. Study of strapdown navigation attitude algorithms. J. Guid. Control. Dyn. 1995, 18, 287–290. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown Inertial Navigation Integration Algorithm Design Part 1: Attitude Algorithms. J. Guid. Control. Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown Inertial Navigation Integration Algorithm Design Part 2: Velocity and Position Algorithms. J. Guid. Control. Dyn. 1998, 21, 208–221. [Google Scholar] [CrossRef]
- Park, C.G.; Kim, K.J.; Lee, J.G.; Chung, D. Formalized Approach to Obtaining Optimal Coefficients for Coning Algorithms. J. Guid. Control. Dyn. 1999, 22, 165–168. [Google Scholar] [CrossRef]
- Yang, H. Research on Accurate Position and Pose Perception Theory and Technology for Shearer with SINS/WSN Integrated Localization. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2016. [Google Scholar]
- Quan, F. Research on Dynamic Characteristics of Electric Traction Monorail Drive System. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2016. [Google Scholar]
- Huang, H. Research on Dynamics Simulation of Suspended Monorail Single Motor Dual-Axle Drive Bogie Vehicle. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2021. [Google Scholar]
- Wang, L.; Liu, J.; Lu, J. Coning Error Compensation Algorithm of SINS Self-Alignment on Swaying Base. Acta Armamentarii 2012, 33, 826–830. [Google Scholar]
- Chang, C. A Study on Wheel/Rail Rolling Contact Theory Based on Finite Element Method and Its Applying. Ph.D. Thesis, China Academy of Railway Sciences, Beijing, China, 2010. [Google Scholar]
- Zhao, X.; Wen, Z.; Wang, H.; Jin, X. 3D Transient Finite Element Model for High-speed Wheel-rail Rolling Contact and Its Application. J. Mech. Eng. 2013, 49, 18. [Google Scholar] [CrossRef]
- Feng, S. Study on the Influence of the Imperfect State Wheel on Metro Vehicle Dynamics Performance. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2014. [Google Scholar]
- Zhao, X.; Li, Z. A three-dimensional finite element solution of frictional wheel–rail rolling contact in elasto-plasticity. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 86–100. [Google Scholar] [CrossRef]
- Wang, H. Force Analysis and Structural Optimization of Mine Monorail Crane Auxiliary Carrier Vehicle. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2021. [Google Scholar]
- Gao, W.; Ben, Y.; Li, Q. Initial Alignment for Strapdown Inertial Navigation System, 1st ed.; National Defense Industry Press: Beijing, China, 2014. [Google Scholar]
- Qin, Y.Y. Strapdown Inertial Navigation System. In Inertial Navigation, 2nd ed.; Science Press: Beijing, China, 2014; Chapter 7; pp. 259–298. [Google Scholar]




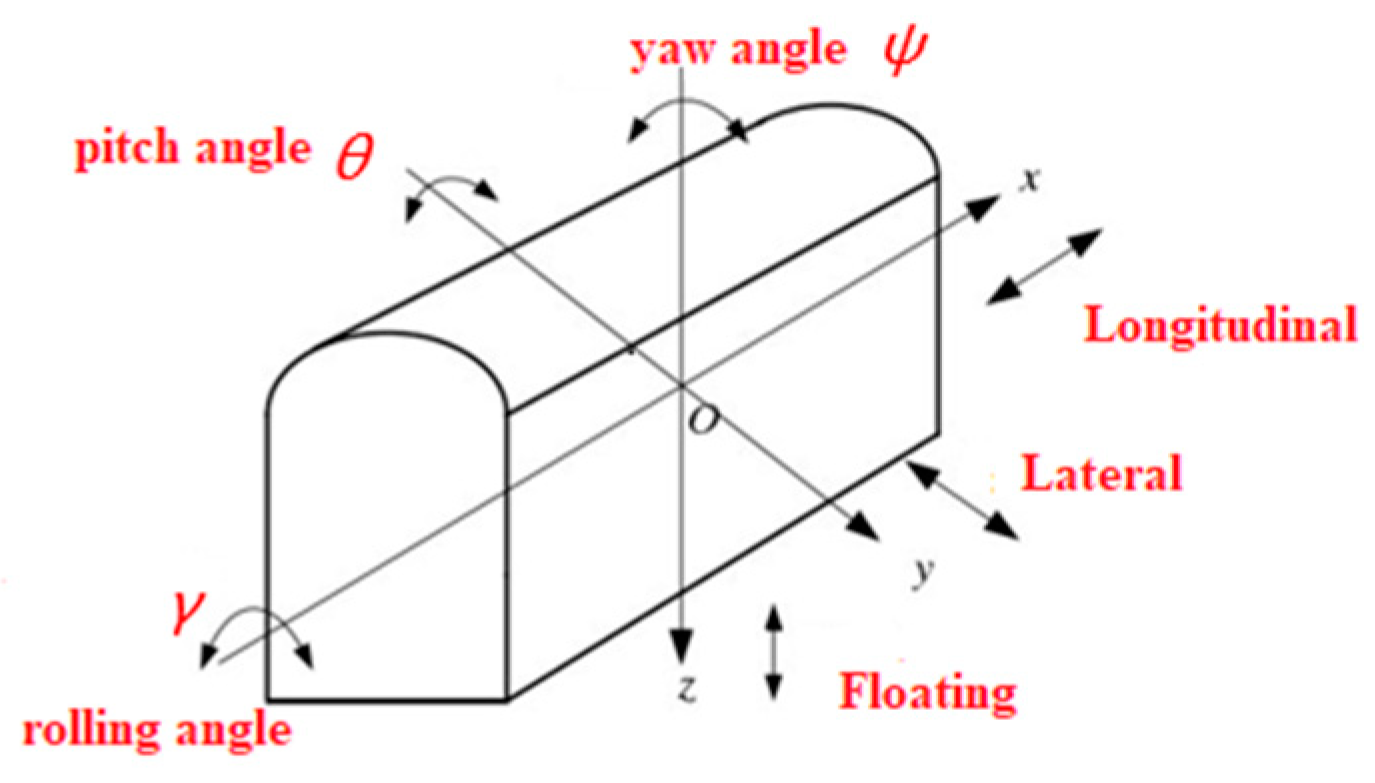





| Movement | Longitudinal | Lateral | Floating | Roll | Pitch | Yaw |
|---|---|---|---|---|---|---|
| Degree of freedom parameters | ||||||
| Degree of freedom | Parallel motion along the x-axis | Parallel motion along the y-axis | Parallel motion along the z-axis | Rotation around the x-axis | Rotation around the y-axis | Rotation around the z-axis |
| Level | Mean | Level | Mean |
|---|---|---|---|
| 1 | 16 | 5 | 4096 |
| 2 | 64 | 6 | 16,384 |
| 3 | 256 | 7 | 65,536 |
| 4 | 1024 | 8 | 262,144 |
| 1 | - | ||||
| 2 | 2/3 | ||||
| 3 | 27/20 | 9/20 | |||
| 4 | 214/105 | 92/105 | 54/105 | ||
| 5 | 1375/504 | 650/504 | 525/504 | 250/504 | |
| 6 | 15,797/4620 | 7834/4620 | 7296/4620 | 4558/4620 | 2315/4620 |
| Subsample Number | Statistical Characteristics | Coning Error (10−3) | ||
|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | ||
| DS | Mean | −4.684 | −4.409 | 4.133 |
| Std | 3.571 | 3.361 | 3.151 | |
| Max/° | −9.932 | −9.348 | −8.764 | |
| TS | Mean | 1.072 | 1.169 | 0.974 |
| Std | 2.313 | 2.524 | 2.103 | |
| Max/° | 4.358 | 4.755 | 3.962 | |
| FS | Mean | 0.839 | 0.840 | 0.840 |
| Std | 0.715 | 0.715 | 0.7151 | |
| Max/° | 1.993 | 1.993 | 1.993 | |
| Subsample Number | Statistical Characteristics | Sculling Error | ||
|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | ||
| DS | Mean | −0.2756 | −0.248 | −0.3031 |
| Std | 0.2101 | 0.1891 | 0.2311 | |
| Max/m/s | −0.5843 | −0.5258 | −0.6427 | |
| TS | Mean | 0.0974 | 1.072 | 0.0877 |
| Std | 0.2103 | 0.2313 | 0.1893 | |
| Max/m/s | 0.3962 | 0.4358 | 0.3566 | |
| FS | Mean | 0.0671 | 0.1007 | 0.0923 |
| Std | 0.0572 | 0.0858 | 0.07866 | |
| Max/m/s | 0.1594 | 0.2392 | 0.2192 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Ji, X.; Yang, Y.; Du, J.; Wu, M. Research on an Error Compensation Method of SINS of a Mine Monorail Crane. Energies 2023, 16, 5969. https://doi.org/10.3390/en16165969
Jiang H, Ji X, Yang Y, Du J, Wu M. Research on an Error Compensation Method of SINS of a Mine Monorail Crane. Energies. 2023; 16(16):5969. https://doi.org/10.3390/en16165969
Chicago/Turabian StyleJiang, Hai, Xiaodong Ji, Yang Yang, Jialu Du, and Miao Wu. 2023. "Research on an Error Compensation Method of SINS of a Mine Monorail Crane" Energies 16, no. 16: 5969. https://doi.org/10.3390/en16165969
APA StyleJiang, H., Ji, X., Yang, Y., Du, J., & Wu, M. (2023). Research on an Error Compensation Method of SINS of a Mine Monorail Crane. Energies, 16(16), 5969. https://doi.org/10.3390/en16165969






