A J-Type Air-Cooled Battery Thermal Management System Design and Optimization Based on the Electro-Thermal Coupled Model
Abstract
1. Introduction
2. Model Development
2.1. Computational Fluid Method
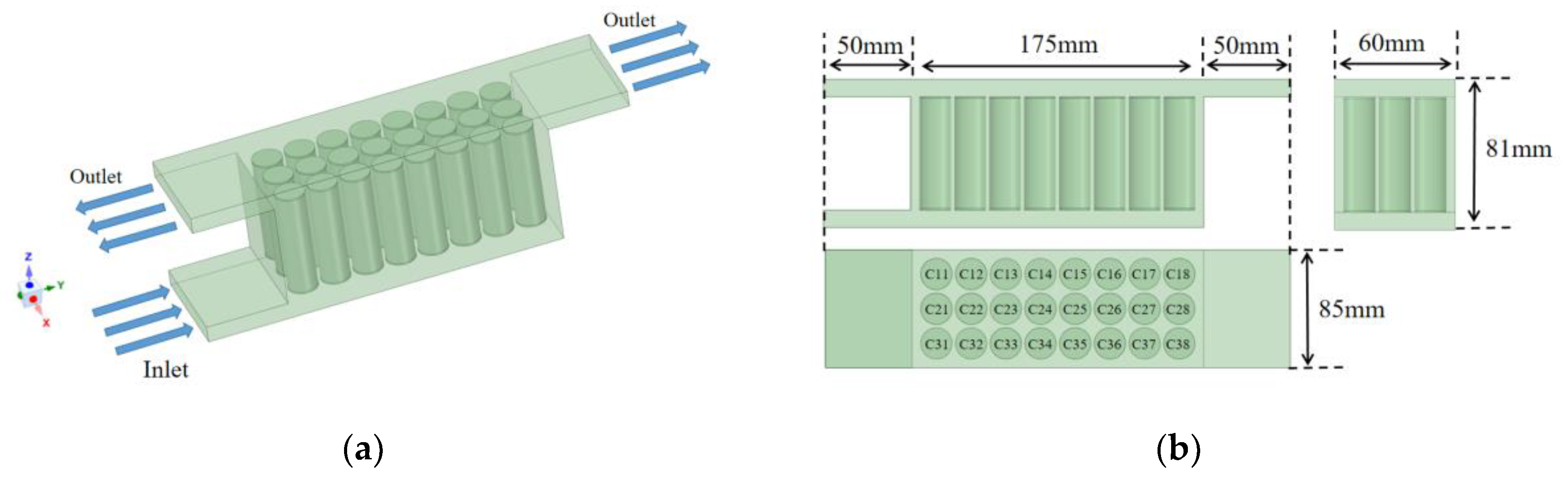
2.2. Model and Boundary Conditions Setup
2.3. Experimental Setup and Procedure
2.4. Grid Independence Analysis
2.5. Thermal Model Verification
3. Simulation Results and Optimization of Air-Cooled BTMS
3.1. Analysis of Simulation Results for Air-Cooled BTMS
3.2. Optimization of Air Duct Size for Air-Cooled BTMS
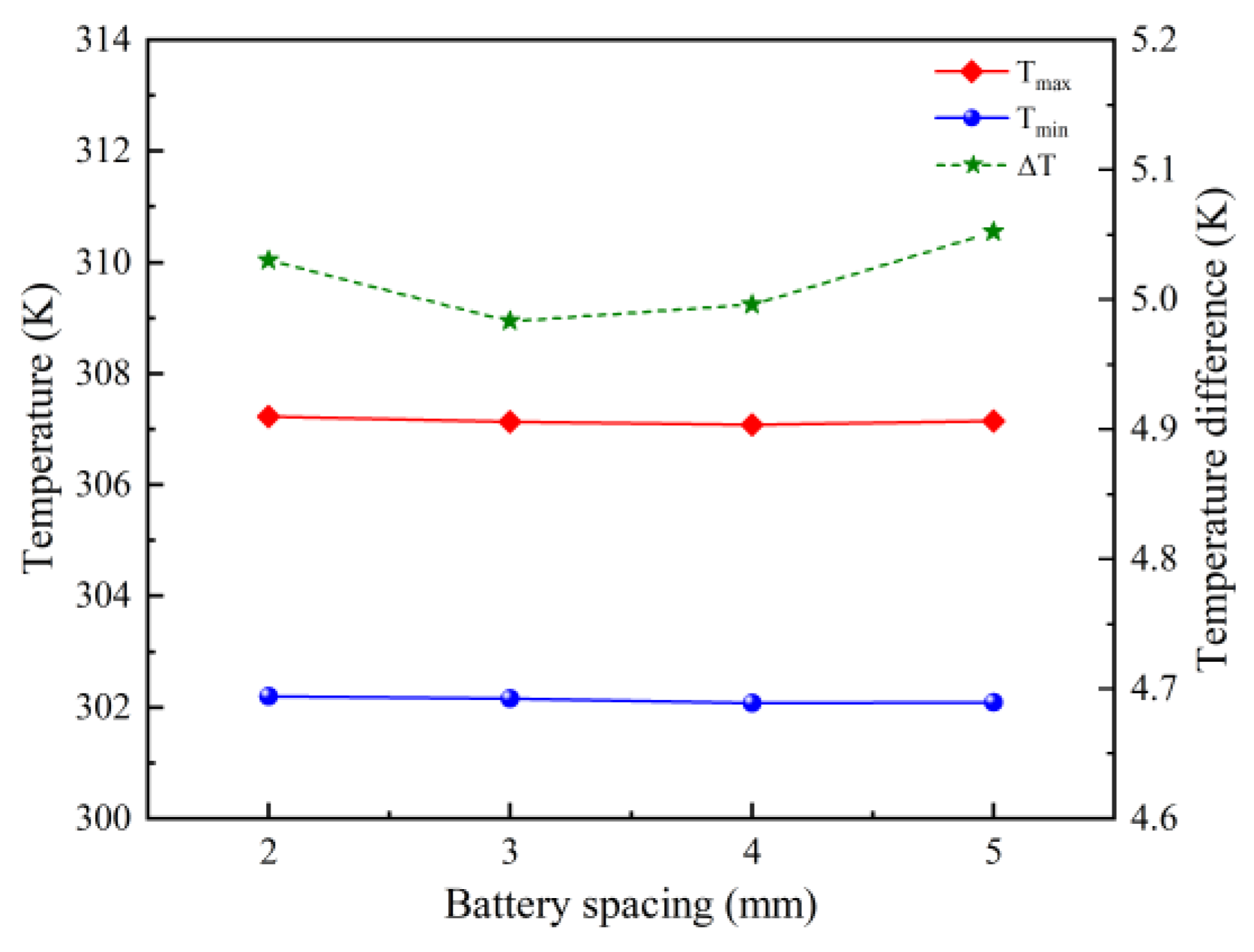
3.3. Optimization of Battery Spacing for Air-Cooled BTMS
3.4. Optimization of Battery Arrangement for Air-Cooled BTMS
3.5. Impact of Air Velocity on Air-Cooled BTMS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tiwari, N.; Verma, P.; Kumar, S.; Kumar, S.; Dutt, H.; Ahmad, S.; Chauhan, S.S. Converting gasoline vehicle into an electric vehicle (EV)—A review. Mater. Today Proc. 2023, 79, 379–388. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Liu, Y.G.; You, M.X. Two-stage aging trajectory prediction of LFP lithium-ion battery based on transfer learning with the cycle life prediction. Green Energy Intell. Transp. 2022, 1, 100008. [Google Scholar] [CrossRef]
- Li, W.Z.; Zhou, Y.H.; Zhang, H.N.; Tang, X. A Review on Battery Thermal Management for New Energy Vehicles. Energies 2023, 16, 4845. [Google Scholar] [CrossRef]
- Tan, X.; Lyu, P.; Fan, Y.; Rao, J.; Ouyang, K. Numerical investigation of the direct liquid cooling of a fast-charging lithium-ion battery pack in hydrofluoroether. Appl. Therm. Eng. 2021, 196, 117279. [Google Scholar] [CrossRef]
- Fang, Q.H.; Wei, X.Z.; Lu, T.Y.; Dai, H.F.; Zhu, J.G. A State of Health Estimation Method for Lithium-Ion Batteries Based on Voltage Relaxation Model. Energies 2019, 12, 1349. [Google Scholar] [CrossRef]
- Sikarwar, S.; Kumar, R.; Yadav, A.; Gwalwanshi, M. Battery thermal management system for the cooling of Li-Ion batteries, used in electric vehicles. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Li, D.; Yang, L.; Li, C. Control-oriented thermal-electrochemical modeling and validation of large size prismatic lithium battery for commercial applications. Energy 2021, 214, 119057. [Google Scholar] [CrossRef]
- Perez Estevez, M.A.; Calligaro, S.; Bottesi, O.; Caligiuri, C.; Renzi, M. An electro-thermal model and its electrical parameters estimation procedure in a lithium-ion battery cell. Energy 2021, 234, 121296. [Google Scholar] [CrossRef]
- Kumaresan, K.; Sikha, G.; White, R.E. Thermal Model for a Li-Ion Cell. J. Electrochem. Soc. 2008, 155, A164–A171. [Google Scholar] [CrossRef]
- Mastali, M.; Foreman, E.; Modjtahedi, A.; Samadani, E.; Amirfazli, A.; Farhad, S.; Fraser, R.A. Electrochemical-thermal modeling and experimental validation of commercial graphite/LiFePO4 pouch lithium-ion batteries. Int. J. Therm. Sci. 2018, 129, 218–230. [Google Scholar] [CrossRef]
- Li, H.H.; Saini, A.; Liu, C.Y.; Yang, J.F.; Wang, Y.P.; Yang, T.; Pan, C.F.; Chen, L.; Jiang, H.B. Electrochemical and thermal characteristics of prismatic lithium-ion battery based on a three-dimensional electrochemical-thermal coupled model. J. Energy Storage 2021, 42, 102976. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Li, C.S.; Zhang, R.J.; Lin, Y.X.; Fang, H.S. Thermal analysis of a 6s4p Lithium-ion battery pack cooled by cold plates based on a multi-domain modeling framework. Appl. Therm. Eng. 2020, 173, 115216. [Google Scholar] [CrossRef]
- Huang, W.N.; Zhang, W.G.; Chen, A.; Zhang, Y.R.; Li, M. A Co-Simulation Method Based on Coupled Thermoelectric Model for Electrical and Thermal Behavior of the Lithium-ion Battery. IEEE Access 2019, 7, 180727–180737. [Google Scholar] [CrossRef]
- Chen, L.G.; Hu, M.H.; Cao, K.B.; Li, S.X.; Su, Z.; Jin, G.Q.; Fu, C.Y. Core temperature estimation based on electro-thermal model of lithium-ion batteries. Int. J. Energy Res. 2020, 44, 5320–5333. [Google Scholar] [CrossRef]
- Chen, W.; Hou, S.B.; Shi, J.L.; Han, P.; Liu, B.; Wu, B.P.; Lin, X.X. Numerical Analysis of Novel Air-Based Li-Ion Battery Thermal Management. Batteries 2022, 8, 128. [Google Scholar] [CrossRef]
- Falcone, M.; Palka, B.D.; Hellany, A.; Rossi, C.; Pulvirenti, B. Lithium-Ion Battery Thermal Management Systems: A Survey and New CFD Results. Batteries 2021, 7, 86. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liu, B.; Han, P.; Hao, C.S.; Li, S.H.; You, Z.P.; Wang, M.Q. Optimization of an air-based thermal management system for lithium-ion battery packs. J. Energy Storage 2021, 44, 103314. [Google Scholar] [CrossRef]
- Habib, A.K.; Hasan, M.K.; Issa, G.F.; Singh, D.; Islam, S.; Ghazal, T. Lithium-Ion Battery Management System for Electric Vehicles: Constraints, Challenges, and Recommendations. Batteries 2023, 9, 152. [Google Scholar] [CrossRef]
- Mahek, M.K.; Alkhedher, M.; Ghazal, M.; Abdelkareem, M.A. Effects of control volume outlet variation on axial air cooling of lithium-ion batteries. Int. J. Thermofluids 2023, 19, 100373. [Google Scholar] [CrossRef]
- Kirad, K.; Chaudhari, M. Design of cell spacing in lithium-ion battery module for improvement in cooling performance of the battery thermal management system. J. Power Sources 2021, 481, 229016. [Google Scholar] [CrossRef]
- Park, H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles. J. Power Sources 2013, 239, 30–36. [Google Scholar] [CrossRef]
- Xie, J.H.; Ge, Z.J.; Zang, M.Y.; Wang, S.F. Structural optimization of lithium-ion battery pack with forced air cooling system. Appl. Therm. Eng. 2017, 126, 583–593. [Google Scholar] [CrossRef]
- Hai, T.; Abidi, A.; Abed, A.M.; Zhou, J.C.; Malekshah, E.H.; Aybar, H. Three-dimensional numerical study of the effect of an air-cooled system on thermal management of a cylindrical lithium-ion battery pack with two different arrangements of battery cells. J. Power Sources 2022, 550, 232117. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J. Design a J-type air-based battery thermal management system through surrogate-based optimization. Appl. Energy 2019, 252, 113426. [Google Scholar] [CrossRef]
- Jeon, D.H.; Baek, S.M. Thermal modeling of cylindrical lithium ion battery during discharge cycle. Energy Convers. Manag. 2011, 52, 2973–2981. [Google Scholar] [CrossRef]
- Chen, K.; Wu, W.X.; Yuan, F.; Chen, L.; Wang, S.F. Cooling efficiency improvement of air-cooled battery thermal management system through designing the flow pattern. Energy 2019, 167, 781–790. [Google Scholar] [CrossRef]
- Kiša, M.; Jelemenský, Ľ. CFD dispersion modelling for emergency preparadnes. J. Loss Prev. Process Ind. 2009, 22, 97–104. [Google Scholar] [CrossRef]
- Xing, J.; Liu, Z.Y.; Huang, P.; Feng, C.G.; Zhou, Y.; Zhang, D.P.; Wang, F. Experimental and numerical study of the dispersion of carbon dioxide plume. J. Hazard. Mater. 2013, 256–257, 40–48. [Google Scholar] [CrossRef]
- Zhang, F.R.; Lin, A.Z.; Wang, P.W.; Liu, P.W. Optimization design of a parallel air-cooled battery thermal management system with spoilers. Appl. Therm. Eng. 2021, 182, 116062. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J. Self-adapting J-type air-based battery thermal management system via model predictive control. Appl. Energy 2020, 263, 114640. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Behi, M.; Ghanbarpour, M.; Jaguemont, J.; Sokkeh, M.A.; Gandoman, F.H.; Berecibar, M.; Van Mierlo, J. A new concept of thermal management system in Li-ion battery using air cooling and heat pipe for electric vehicles. Appl. Therm. Eng. 2020, 174, 115280. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Wang, T.T.; Liu, X.; Qin, D.C.; Duan, Y.C. Thermal Modeling and Prediction of The Lithium-ion Battery Based on Driving Behavior. Energies 2022, 15, 9088. [Google Scholar] [CrossRef]
- Spinner, N.S.; Hinnant, K.M.; Mazurick, R.; Brandon, A.; Rose-Pehrsson, S.; Tuttle, S. Novel 18650 lithium-ion battery surrogate cell design with anisotropic thermophysical properties for studying failure events. J. Power Sources 2016, 312, 1–11. [Google Scholar] [CrossRef]



















(kg/m3) | Specific Heat Capacity Cp (J/kg/K) | Thermal Conductivity k (W/m/K) | (kg/m/s) | |
|---|---|---|---|---|
| Air | 1.225 | 1006.43 | 0.0242 | |
| Cathode | 1347.3 | 1437.4 | 1.04 | — |
| Anode | 2328.5 | 1269.2 | 1.58 | — |
| Cell | 2722 | 1200 | Radial thermal conductivity: kx = 1.27 Axial thermal conductivity: kz = 27.58 | — |
| Region | Inlet | Outlet | Top, Side and Bottom | Interfaces between Batteries and Fluid | Initial Temperature | Ambient Temperature |
|---|---|---|---|---|---|---|
| Boundary conditions | Velocity inlet (1–5 m/s) | Pressure Outlet (1.013 × 105 Pa) | Adiabatic non-slip walls | Coupled walls | 300 K | 300 K |
| Specifications | Value |
|---|---|
| Battery brand | Samsung ICR18650 |
| Battery size | Diameter of 18.06 mm, height of 65.02 mm |
| Charge cut-off voltage Discharge cut-off voltage | 4.3 V 2.6 V |
| Nominal voltage | 3.7 V |
| Nominal capacity | 2 600 mAh |
| Battery temperature | Charge (283–318 K); discharge (253–333 K) |
| Anode material | Lithium cobaltate |
| Cathode material | Graphite |
| Air Velocity (m/s) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Mass flow rate (kg/s) | 0.819 | 1.638 | 2.457 | 3.276 | 4.095 |
| Inlet and outlet pressure difference (Pa) | 0.9414 | 2.3885 | 4.1943 | 6.3947 | 9.0499 |
| Cooling power (W) | 1.7124 | 6.3009 | 14.4996 | 27.3439 | 46.1092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Wang, L.; Chen, W.; Liu, B.; Wang, P. A J-Type Air-Cooled Battery Thermal Management System Design and Optimization Based on the Electro-Thermal Coupled Model. Energies 2023, 16, 5962. https://doi.org/10.3390/en16165962
Fan H, Wang L, Chen W, Liu B, Wang P. A J-Type Air-Cooled Battery Thermal Management System Design and Optimization Based on the Electro-Thermal Coupled Model. Energies. 2023; 16(16):5962. https://doi.org/10.3390/en16165962
Chicago/Turabian StyleFan, Hao, Lan Wang, Wei Chen, Bin Liu, and Pengxin Wang. 2023. "A J-Type Air-Cooled Battery Thermal Management System Design and Optimization Based on the Electro-Thermal Coupled Model" Energies 16, no. 16: 5962. https://doi.org/10.3390/en16165962
APA StyleFan, H., Wang, L., Chen, W., Liu, B., & Wang, P. (2023). A J-Type Air-Cooled Battery Thermal Management System Design and Optimization Based on the Electro-Thermal Coupled Model. Energies, 16(16), 5962. https://doi.org/10.3390/en16165962




