Electricity Load Lost in the Largest Windstorms—Is the Fragility-Based Model up to the Task?
Abstract
1. Introduction
- Meteorological factors—review the wind impact driving factors, and the most impactful windstorms.
- Electricity system resilience—analyze the available data on the electricity system structure, and their changes with time, and electricity system interruptions, and how their duration depends on the storm severity.
- Modeling cases—test the fragility-based impact model’s ability to recreate the spatiotemporal LL profile for the most recent, and the most impactful windstorm cases to which the model is not fitted.
2. Impact of Extreme Wind in Finland
2.1. Impact Driving Factors
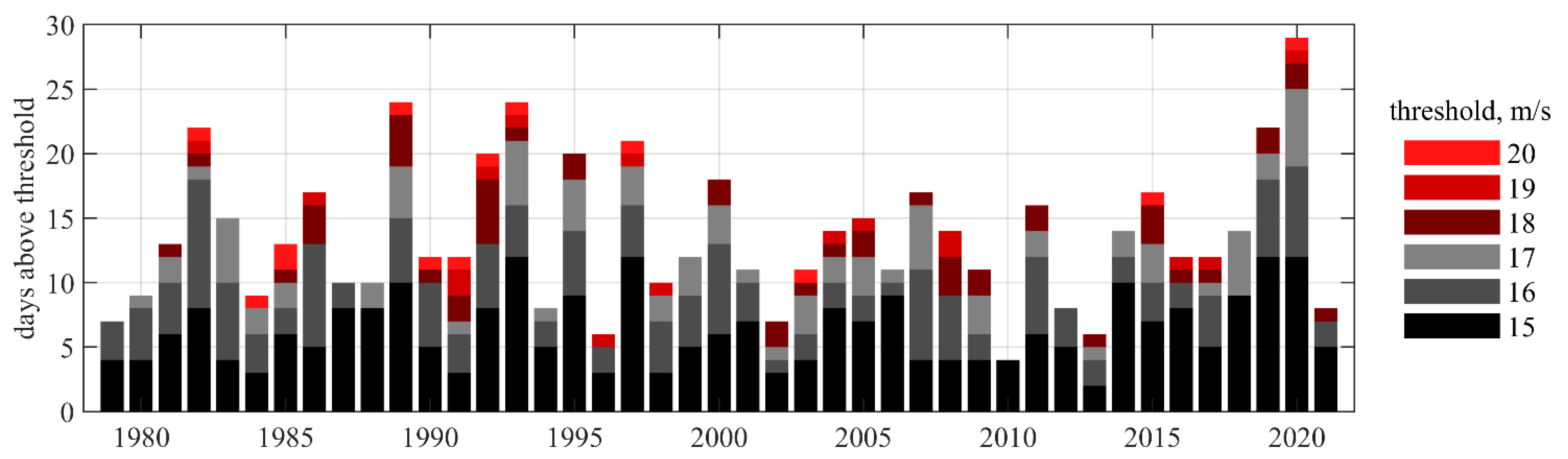
2.2. Seasons, Annual, and Decadal Trends
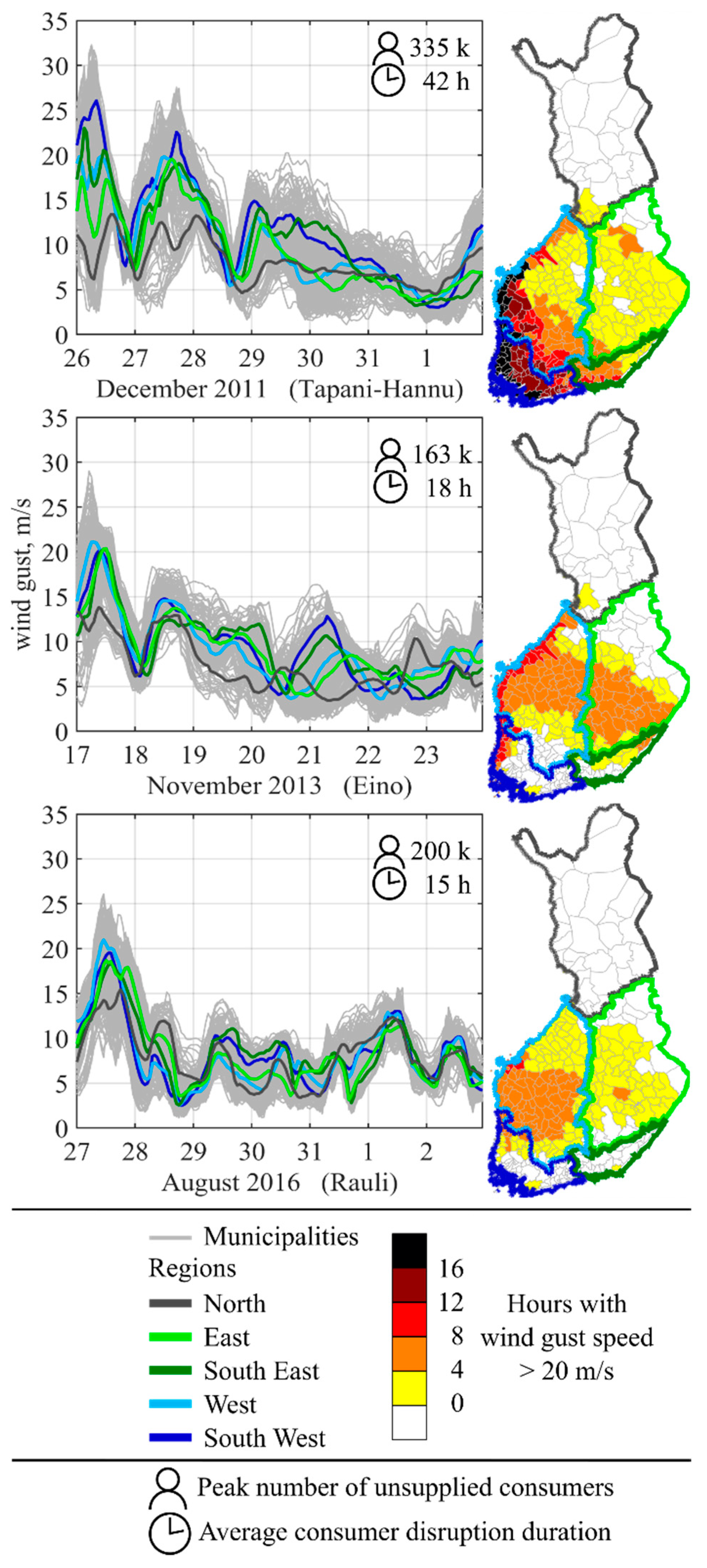
2.3. The Most Impactful and Recent Windstorms
3. Electricity System Resilience
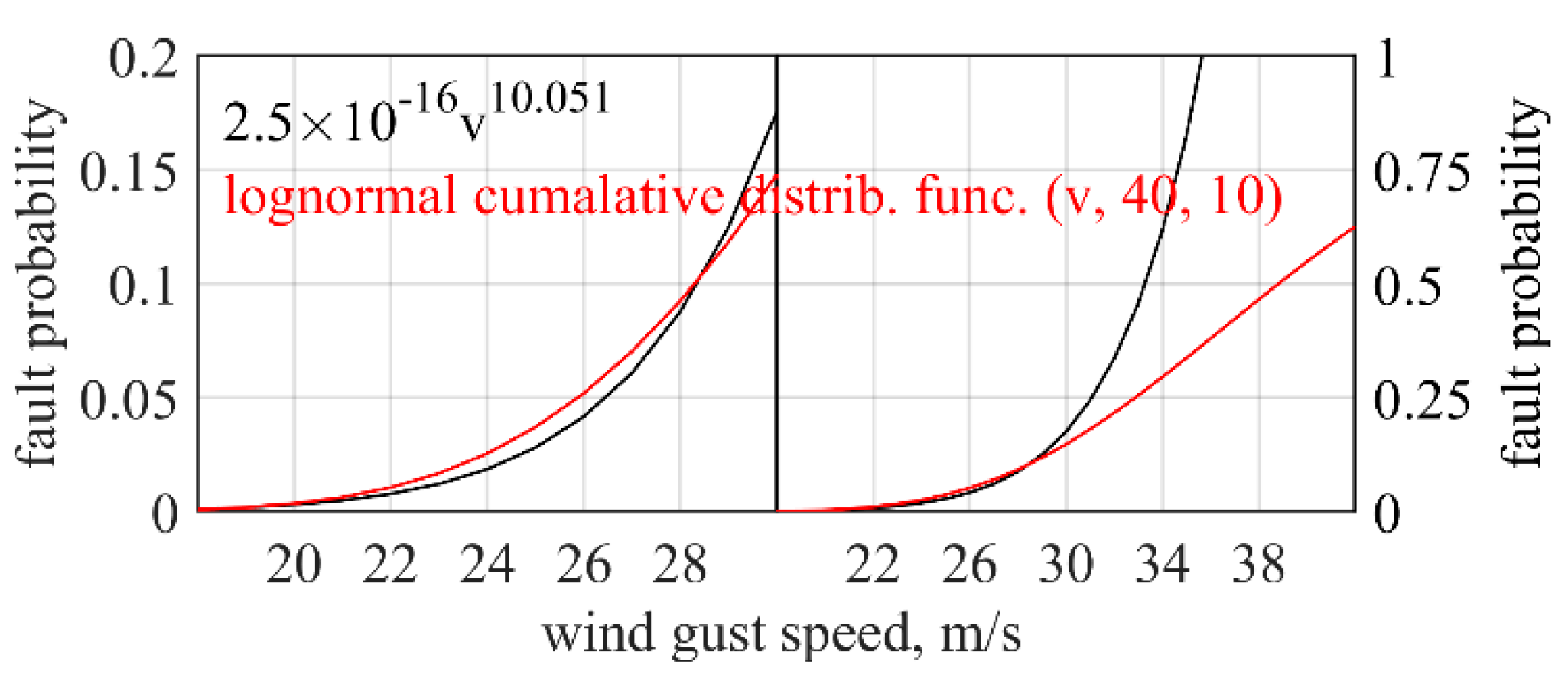
3.1. Modeling Framework
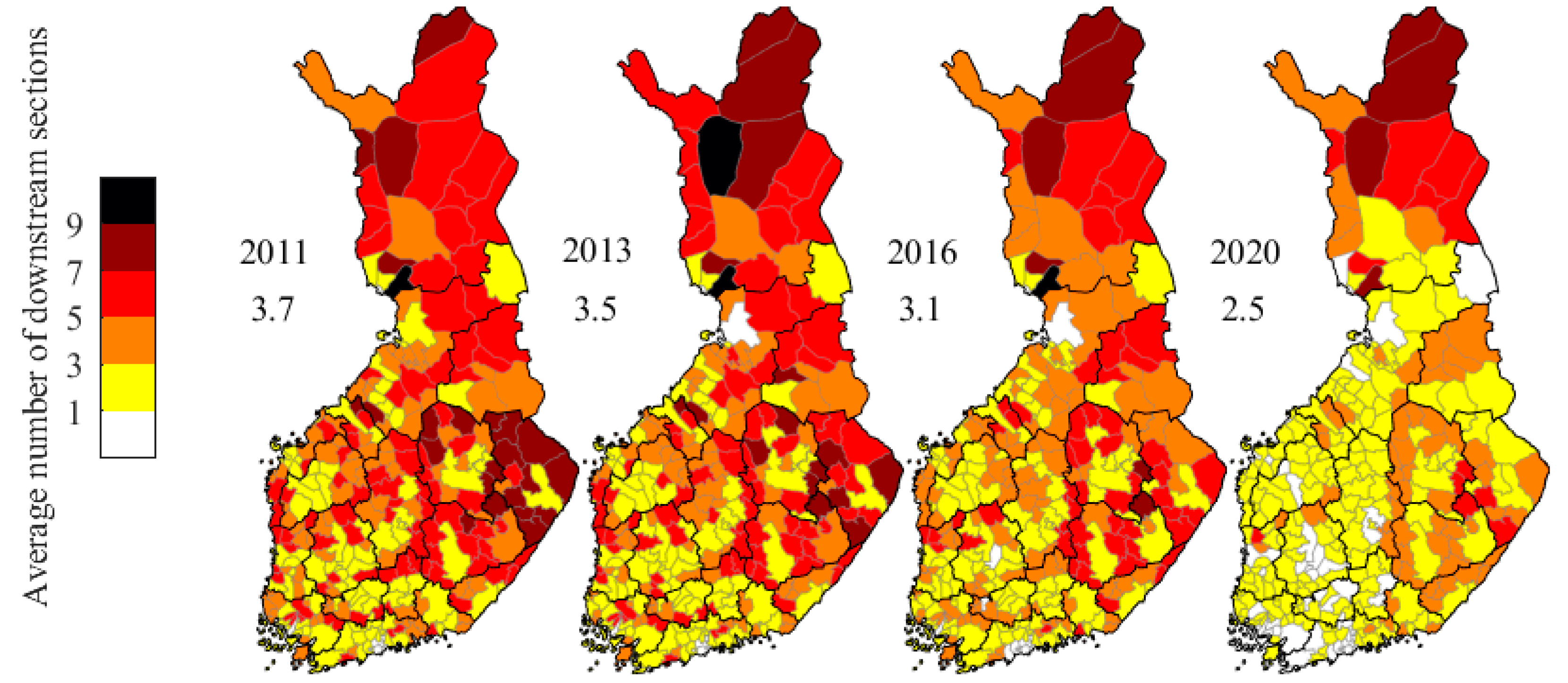
3.2. Electricity System Vulnerability
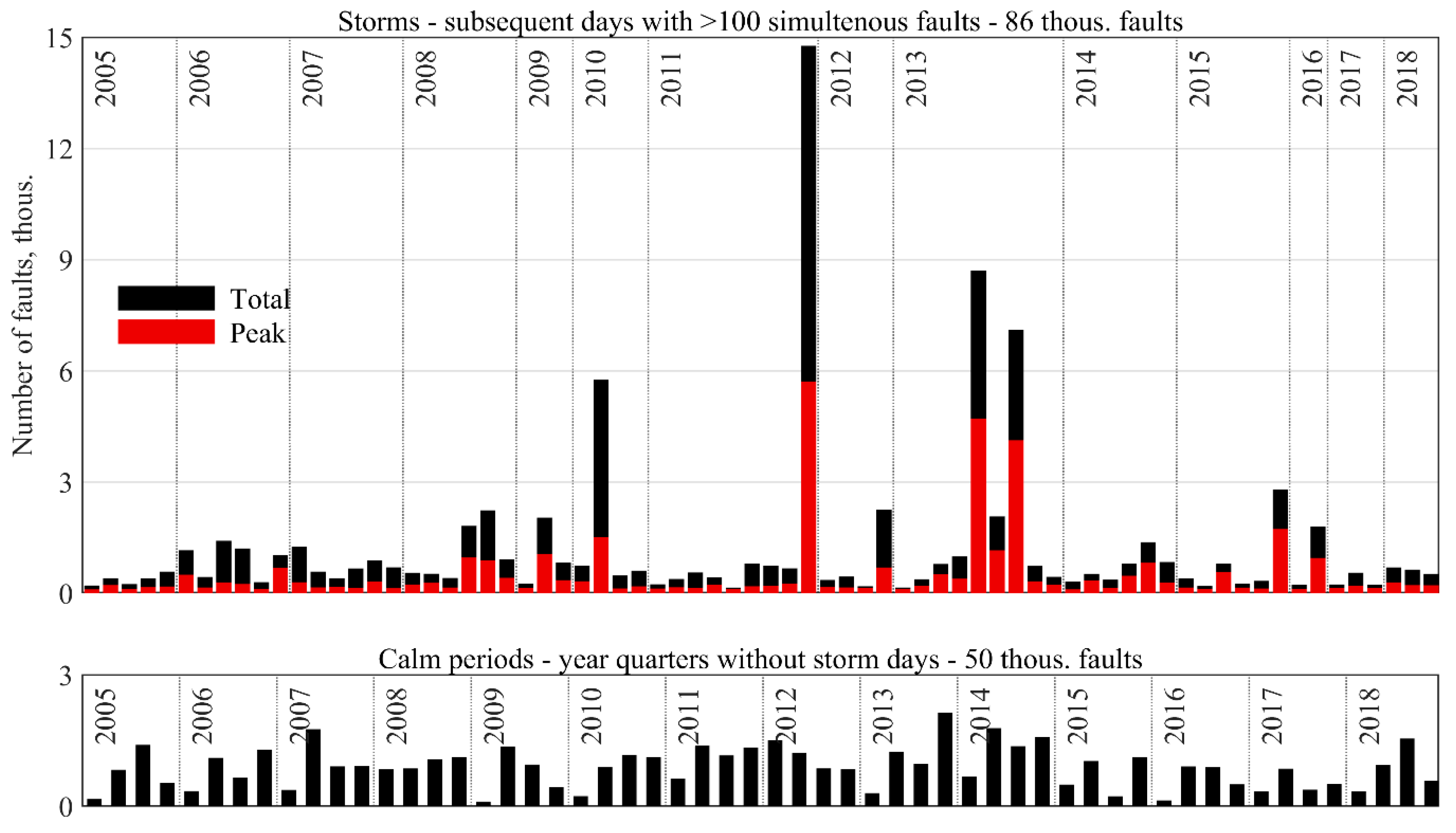
3.3. Interruption Data Analysis
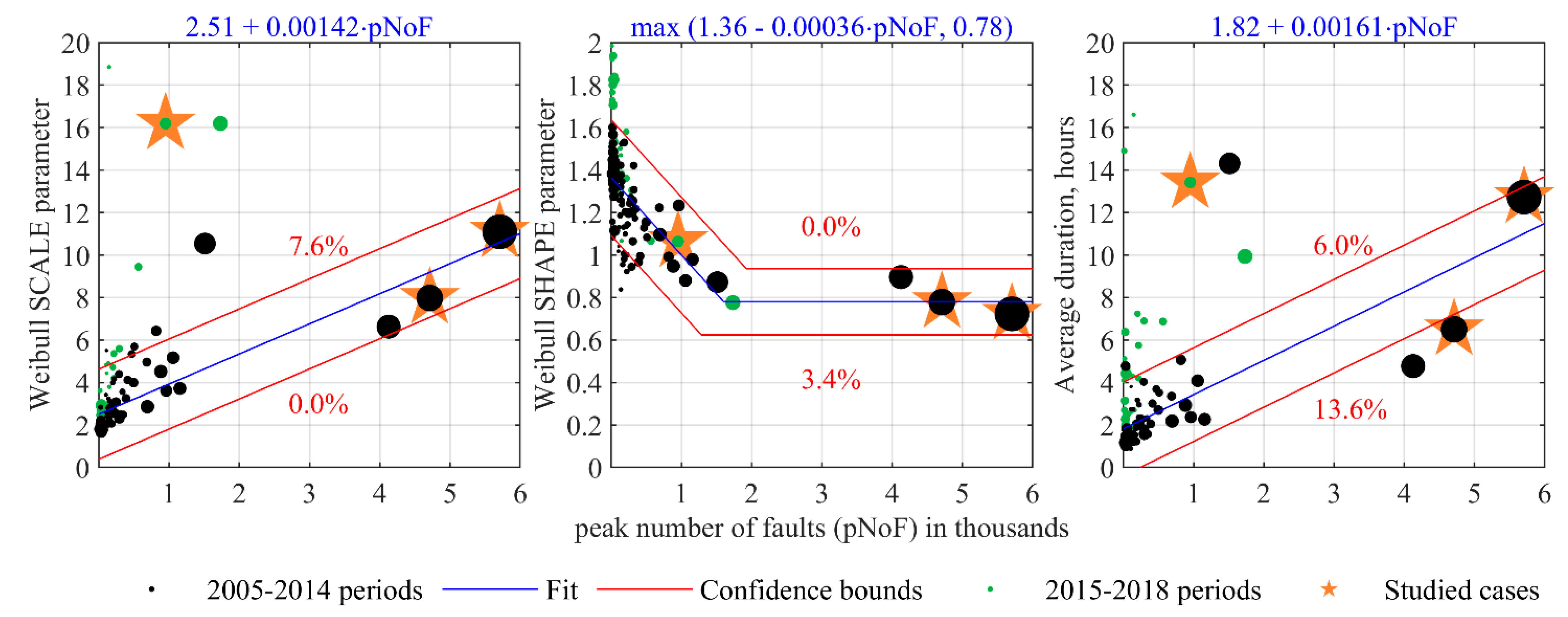
3.4. Fixing Times
4. Replicating Historic Impacts
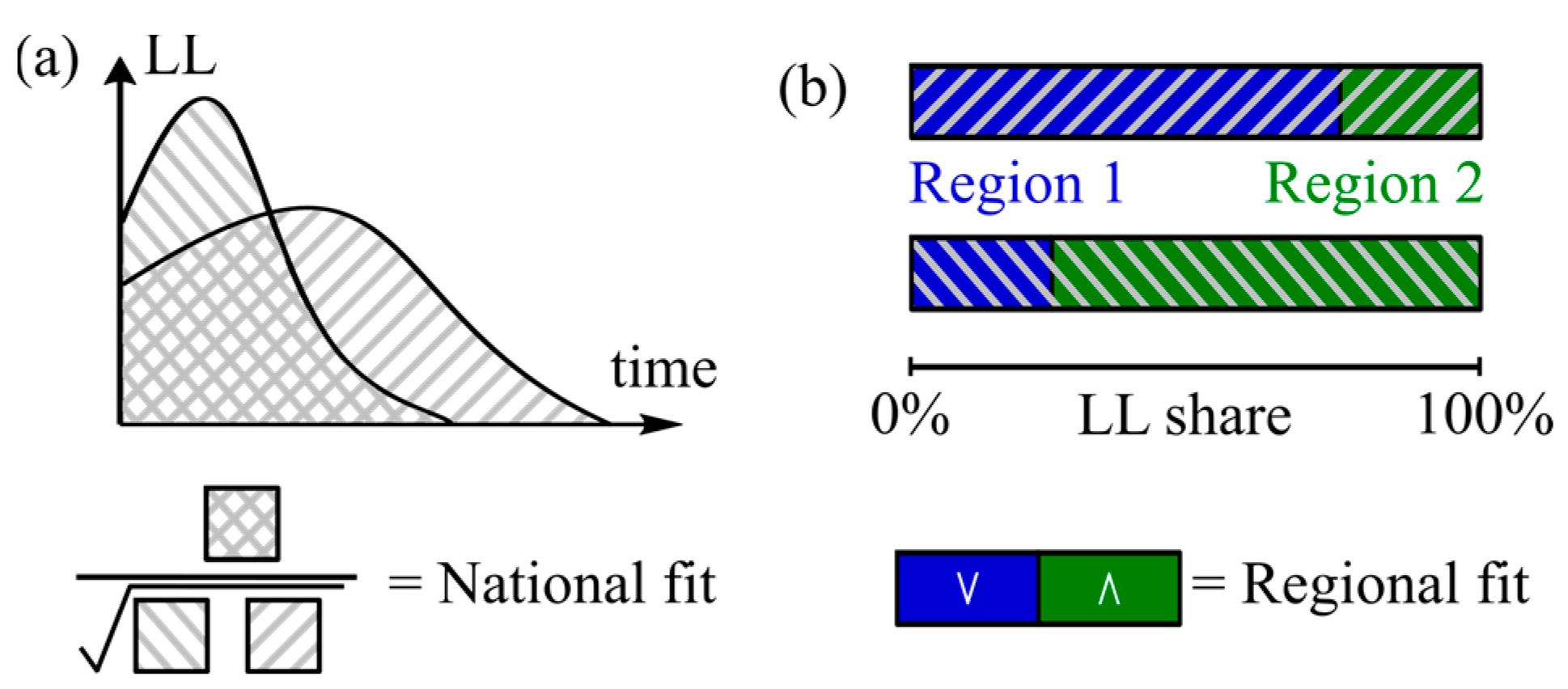
4.1. Means for Result Evaluation
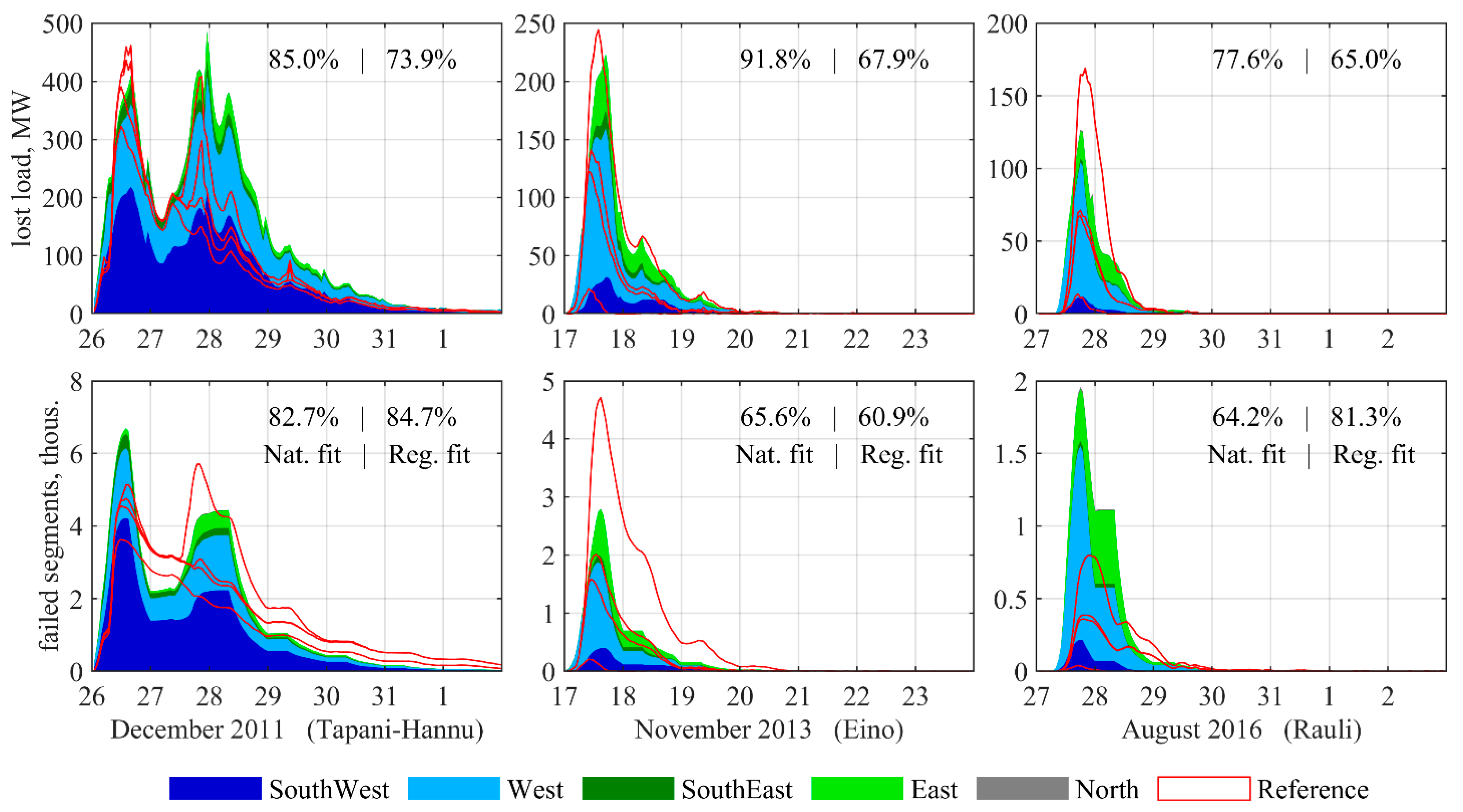
4.2. Model Results vs. Reference Profiles
5. Conclusions
- The impacts of windstorms on the electricity system are driven by a multitude of region-specific environmental, infrastructural, and organizational factors.
- The account of the significance of these factors, let alone the representation in a fragility-based impact model, is difficult.
- Attempts to quantify these factors have been few, especially in the Finnish environment.
- Most impactful windstorms share some similarities, which are expected to remain present in the most impactful future windstorms.
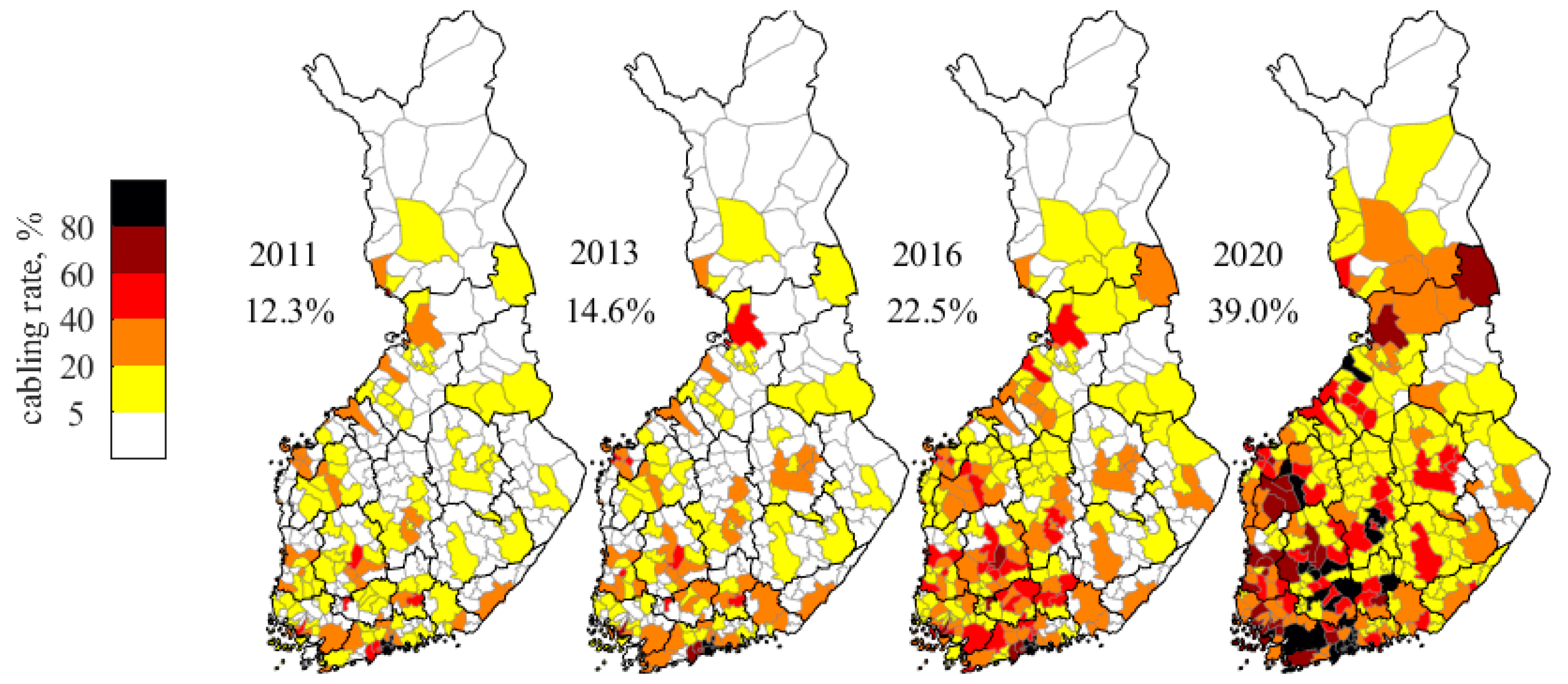
- Grid-cabling efforts in the last decade have significantly reduced Finnish electricity grid vulnerability to wind hazards.
- Storm and calm periods provide an optimal grouping basis for interruption data analysis, as they can be considered to present individual meteorological events.
- The two-level fitting of fixing times with such grouping provides a strong statistical basis for the resulting severity-dependent distribution and indication of the associated uncertainties (around 20%) that are difficult to capture through analytical means.
- The fragility functions and fixing-time distributions are designed to be applicable beyond the historical windstorm severity range, even though there are no direct means to validate the model ability there.
- A fragility-based model accounting for only a few factors can reproduce major windstorm impact profiles for different windstorm and grid cases, without recalibration.
- The collective evidence indicates that the presented model can generate realistic national LL profiles for the most impactful windstorms in Finland, with uncertainties in the order of 20%.
- The obtained level of accuracy is expected to be sufficient for the intended model use in studies on strategic electricity system development, and broader emergency preparedness questions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bompard, E.; Huang, T.; Wu, Y.; Cremenescu, M. Classification and Trend Analysis of Threats Origins to the Security of Power Systems. Int. J. Electr. Power Energy Syst. 2013, 50, 50–64. [Google Scholar] [CrossRef]
- Gregow, H.; Laurila, T.K.; Mäkelä, A.; Rantanen, M. Review on Winds, Extratropical Cyclones and Their Impacts in Northern Europe and Finland; Finnish Meteorological Institute: Helsinki, Finland, 2020.
- Jasiūnas, J.; Heikkinen, T.; Lund, P.D.; Láng-Ritter, I. Resilience of Electric Grid to Extreme Wind: Considering Local Details at National Scale. Reliab. Eng. Syst. Saf. 2023, 232, 109070. [Google Scholar] [CrossRef]
- Forssén, K. Resilience of Finnish Electricity Distribution Networks against Extreme Weather Conditions. Master’s Thesis, Aalto University, Espoo, Finland, 2016. [Google Scholar]
- Nurmi, V.; Pilli-Sihvola, K.; Gregow, H.; Perrels, A. Overadaptation to Climate Change? The Case of the 2013 Finnish Electricity Market Act. EconDisCliCha 2019, 3, 161–190. [Google Scholar] [CrossRef]
- Tervo, R.; Láng, I.; Jung, A.; Mäkelä, A. Predicting Power Outages Caused by Extratropical Storms. Nat. Hazards Earth Syst. Sci. 2021, 21, 607–627. [Google Scholar] [CrossRef]
- McRoberts, D.B.; Quiring, S.M.; Guikema, S.D. Improving Hurricane Power Outage Prediction Models Through the Inclusion of Local Environmental Factors. Risk Anal. 2018, 38, 2722–2737. [Google Scholar] [CrossRef]
- Watson, P.L.; Spaulding, A.; Koukoula, M.; Anagnostou, E. Improved Quantitative Prediction of Power Outages Caused by Extreme Weather Events. Weather Clim. Extrem. 2022, 37, 100487. [Google Scholar] [CrossRef]
- Nateghi, R.; Guikema, S.; Quiring, S.M. Power Outage Estimation for Tropical Cyclones: Improved Accuracy with Simpler Models. Risk Anal. 2014, 34, 1069–1078. [Google Scholar] [CrossRef]
- Popović, Ž.N.; Kovački, N.V.; Popović, D.S. Resilient Distribution Network Planning under the Severe Windstorms Using a Risk-Based Approach. Reliab. Eng. Syst. Saf. 2020, 204, 107114. [Google Scholar] [CrossRef]
- Xue, J.; Mohammadi, F.; Li, X.; Sahraei-Ardakani, M.; Ou, G.; Pu, Z. Impact of Transmission Tower-Line Interaction to the Bulk Power System during Hurricane. Reliab. Eng. Syst. Saf. 2020, 203, 107079. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, T.Y.; White, A.G.; Guikema, S.D. Power Outage Prediction for Natural Hazards Using Synthetic Power Distribution Systems. Reliab. Eng. Syst. Saf. 2021, 208, 107348. [Google Scholar] [CrossRef]
- Prettico, G.; Gangale, F.; Mengolini, A.; Lucas, A.; Fulli, G. Distribution System Operators Observatory: From European Electricity Distribution Systems to Reference Network; EU JRC Institute for Energy and Transport: Luxembourg, 2016. [Google Scholar]
- Panteli, M.; Pickering, C.; Wilkinson, S.; Dawson, R.; Mancarella, P. Power System Resilience to Extreme Weather: Fragility Modeling, Probabilistic Impact Assessment, and Adaptation Measures. IEEE Trans. Power Syst. 2017, 32, 3747–3757. [Google Scholar] [CrossRef]
- Clements, D.; Mancarella, P. Fragility Curve Based Storm Modelling of Distribution Networks with Staff Constraints. In Proceedings of the IET International Conference on Resilience of Transmission and Distribution Networks (RTDN 2017), Birmingham, UK, 26–28 September 2017; pp. 1–5. [Google Scholar]
- Jamieson, M.R.; Strbac, G.; Bell, K.R.W. Quantification and Visualisation of Extreme Wind Effects on Transmission Network Outage Probability and Wind Generation Output. IET Smart Grid 2020, 3, 112–122. [Google Scholar] [CrossRef]
- Scherb, A.; Garrè, L.; Straub, D. Evaluating Component Importance and Reliability of Power Transmission Networks Subject to Windstorms: Methodology and Application to the Nordic Grid. Reliab. Eng. Syst. Saf. 2019, 191, 106517. [Google Scholar] [CrossRef]
- Fu, G.; Wilkinson, S.; Dawson, R.J.; Fowler, H.J.; Kilsby, C.; Panteli, M.; Mancarella, P. Integrated Approach to Assess the Resilience of Future Electricity Infrastructure Networks to Climate Hazards. IEEE Syst. J. 2018, 12, 12. [Google Scholar] [CrossRef]
- Mutanen, A. Improving Electricity Distribution System State Estimation with AMR-Based Load Profiles. Ph.D. Thesis, Tampere University of Technology, Tampere, Finland, 2018. [Google Scholar]
- Perrels, A.; Haakana, J.; Hakala, O.; Kujala, S.; Láng-Ritter, I.; Lehtonen, H.; Lintunen, J.; Pohjola, J.; Sane, M.; Fronzek, S.; et al. Kustannusarviointi Ilmastonmuutokseen Liittyvästä Toimimattomuudesta (KUITTI) (Assessment of the Cost of Inaction Regarding Climate Change (KUITTI)); Publications of the Government’s Analysis, Assessment and Research Activities 2022:37; Valtioneuvoston Kanslia: Helsinki, Finland, 2022. [Google Scholar]
- Ouyang, M.; Dueñas-Osorio, L. Multi-Dimensional Hurricane Resilience Assessment of Electric Power Systems. Struct. Saf. 2014, 48, 15–24. [Google Scholar] [CrossRef]
- Räisänen, O.; Haapaniemi, J.; Haakana, J.; Lassila, J.; Partanen, J.; Ahonen, J.; Kurki, L. Assessing Overhead Line’s Susceptability to Storm Wind Damage Using Open Data. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Online, 20–23 September 2021; Volume 2021, pp. 2794–2798. [Google Scholar]
- Noebels, M.; Quirós-Tortós, J.; Panteli, M. Decision-Making Under Uncertainty on Preventive Actions Boosting Power Grid Resilience. IEEE Syst. J. 2022, 16, 2614–2625. [Google Scholar] [CrossRef]
- Valta, H.; Lehtonen, I.; Laurila, T.K.; Venäläinen, A.; Laapas, M.; Gregow, H. Communicating the Amount of Windstorm Induced Forest Damage by the Maximum Wind Gust Speed in Finland. Adv. Sci. Res. 2019, 16, 31–37. [Google Scholar] [CrossRef]
- Roberts, J.F.; Champion, A.J.; Dawkins, L.C.; Hodges, K.I.; Shaffrey, L.C.; Stephenson, D.B.; Stringer, M.A.; Thornton, H.E.; Youngman, B.D. The XWS Open Access Catalogue of Extreme European Windstorms from 1979 to 2012. Nat. Hazards Earth Syst. Sci. 2014, 14, 2487–2501. [Google Scholar] [CrossRef]
- Gardiner, B.; Byrne, K.; Hale, S.; Kamimura, K.; Mitchell, S.J.; Peltola, H.; Ruel, J.-C. A Review of Mechanistic Modelling of Wind Damage Risk to Forests. For. Int. J. For. Res. 2008, 81, 447–463. [Google Scholar] [CrossRef]
- Safety Investigation Authority. July-August 2010 Fierce Weather (Heinä-Elokuun 2010 Rajuilmat); Safety Investigation Authority: Helsinki, Finland, 2010. [Google Scholar]
- Gregow, H.; Peltola, H.; Laapas, M.; Saku, S.; Venäläinen, A.; Laapas, H. Combined Occurrence of Wind, Snow Loading and Soil Frost with Implications for Risks to Forestry in Finland under the Current and Changing Climatic Conditions. Silva Fenn. 2011, 45, 35–54. [Google Scholar] [CrossRef]
- Kilpeläinen, A.; Gregow, H.; Strandman, H.; Kellomäki, S.; Venäläinen, A.; Peltola, H. Impacts of Climate Change on the Risk of Snow-Induced Forest Damage in Finland. Clim. Chang. 2010, 99, 193–209. [Google Scholar] [CrossRef]
- Venäläinen, A.; Tuomenvirta, H.; Heikinheimo, M.; Kellomäki, S.; Peltola, H.; Strandman, H.; Väisänen, H. Impact of Climate Change on Soil Frost under Snow Cover in a Forested Landscape. Clim. Res. 2001, 17, 63–72. [Google Scholar] [CrossRef]
- Gardiner, B.; Blennow, K.; Carnus, J.-M.; Fleischer, P.; Ingemarson, F.; Landmann, G.; Lindner, M.; Marzano, M.; Nicoll, B.; Orazio, C.; et al. Destructive Storms in European Forests: Past and Forthcoming Impacts; European Forest Institute: Joensuu, Finland, 2010. [Google Scholar]
- Gardiner, B. Wind Damage to Forests and Trees: A Review with an Emphasis on Planted and Managed Forests. J. For. Res. 2021, 26, 248–266. [Google Scholar] [CrossRef]
- Liu, S.; Ji, X.; Zhang, X. Effects of Soil Properties and Tree Species on Root–Soil Anchorage Characteristics. Sustainability 2022, 14, 7770. [Google Scholar] [CrossRef]
- Haakana, J.; Räisänen, O.; Karhunen, M.; Láng-Ritter, I. Impact of Wind Speed and Ground Frost on Electricity Distribution System Interruptions. Reliab. Eng. Syst. Saf. 2023, in press.
- Laurila, T.K.; Gregow, H.; Cornér, J.; Sinclair, V.A. Characteristics of Extratropical Cyclones and Precursors to Windstorms in Northern Europe. Weather Clim. Dyn. 2021, 2, 1111–1130. [Google Scholar] [CrossRef]
- Laurila, T.K. Winds and Windstorms in Northern Europe and Finland. Ph.D. Thesis, Ilmatieteen laitos-Finnish Meteorological Institute, Helsinki, Finland, 2022. [Google Scholar]
- Rimali, A. Analysis of Frozen Ground in Finland: Affecting Environmental Factors, Trends in Northern Finland and Applicability of Satellite Data. Master’s Thesis, University of Oulu, Oulu, Finland, 2019. [Google Scholar]
- Gregow, H. Impact of Strong Winds, Heavy Snow Loads and Soil Frost Conditions on the Risks to Forests in Northern Europe. Ph.D. Thesis, University of Eastern Finland, Joensuu, Finland, 2013. [Google Scholar]
- Lehtonen, I.; Venäläinen, A.; Kämäräinen, M.; Asikainen, A.; Laitila, J.; Anttila, P.; Peltola, H. Projected Decrease in Wintertime Bearing Capacity on Different Forest and Soil Types in Finland under a Warming Climate. Hydrol. Earth Syst. Sci. 2019, 23, 1611–1631. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- ERA5 Hourly Data on Single Levels from 1979 to Present. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form (accessed on 3 December 2021).
- Jeppesen, J. Fact Sheet: Reanalysis. Available online: https://www.ecmwf.int/en/about/media-centre/focus/2020/fact-sheet-reanalysis (accessed on 28 December 2022).
- Gryning, S.-E.; Floors, R. Investigating Predictability of Offshore Winds Using a Mesoscale Model Driven by Forecast and Reanalysis Data. Metz 2020, 29, 117–130. [Google Scholar] [CrossRef]
- Finnish Meteorological Institute Merkittäviä Myrskyjä Suomessa-Significant Storms in Finland. Available online: https://www.ilmatieteenlaitos.fi/merkittavia-myrskyja-suomessa (accessed on 2 January 2023).
- Kufeoglu, S.; Lehtonen, M. Cyclone Dagmar of 2011 and Its Impacts in Finland. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Krohns-Välimäki, H. Development of a Situation Awareness System for Disturbance Management of Electricity Networks. Ph.D. Thesis, Tampere University of Technology, Tampere, Finland, 2018. [Google Scholar]
- Finnish Meteorological Institute. Monthly Climate Review. December 2011 (Ilmastokatsaus. Joulukku 2011); Finnish Meteorological Institute: Helsinki, Finland, 2011.
- Storms over Scandinavia. Available online: https://www.eumetsat.int/storms-over-scandinavia (accessed on 22 December 2022).
- Finnish Meteorological Institute. Monthly Climate Review. November 2013 (Ilmastokatsaus. Marraskuu 2013); Finnish Meteorological Institute: Helsinki, Finland, 2013.
- Storm History Blog: 2013 Eino Ja Seija, Reima Ja Oskari, “Elviira”-Ukkosmyrsky (Thunderstorms). Available online: https://myrskyvaroitus.com/index.php/myrskytieto/myrskyhistoria/37-2013 (accessed on 22 December 2022).
- Finnish Meteorological Institute. Monthly Climate Review. Rauli Rose to the Heavyweight of the Storms (Ilmastokatsaus. Rauli Nousi Myrskyjen Raskaaseen Sarjaan); Finnish Meteorological Institute: Helsinki, Finland, 2016.
- Enease Oy. Interruptions 2005–2014 (Keskeytykset 2005–2014). Received via Personal Communication with Anssi Seppälä; Enease Oy: Helsinki, Finland, 2017. [Google Scholar]
- Enease Oy. Interruptions 2015–2018 (Keskeytykset 2015–2018). Received via Personal Communication with Anssi Seppälä; Enease Oy: Helsinki, Filand, 2019. [Google Scholar]
- Priestley, M.D.K.; Catto, J.L. Future Changes in the Extratropical Storm Tracks and Cyclone Intensity, Wind Speed, and Structure. Weather Clim. Dyn. 2022, 3, 337–360. [Google Scholar] [CrossRef]
- Sinclair, V.A.; Rantanen, M.; Haapanala, P.; Räisänen, J.; Järvinen, H. The Characteristics and Structure of Extra-Tropical Cyclones in a Warmer Climate. Weather Clim. Dyn. 2020, 1, 1–25. [Google Scholar] [CrossRef]
- Jasiūnas, J.; Lund, P.D.; Mikkola, J. Energy System Resilience—A Review. Renew. Sustain. Energy Rev. 2021, 150, 111476. [Google Scholar] [CrossRef]
- Energy Authority. Technical Indicators for Electricity Network Operation 2005–2015 (Sähköverkkotoiminnan Tekniset Tunnusluvut 2005–2015), Received upon Personal Request from Energy Authority; Energy Authority: Helsinki, Finland, 2021. [Google Scholar]
- Energy Authority Technical Indicators for Electricity Network Operation 2016–2020 (Sähköverkkotoiminnan Tekniset Tunnusluvut 2016–2020). Available online: https://energiavirasto.fi/verkkotoiminnan-julkaisut (accessed on 4 July 2022).
- Adato Energia Oy. DSO Service Area Responsibility Map 2015 Shapefile (Vastuual). Received via Personal Communication with Risto Heliö; Adato Energia Oy: Helsinki, Finland, 2020. [Google Scholar]
- National Land Survey of Finland File Service of Open Data. Available online: https://tiedostopalvelu.maanmittauslaitos.fi/tp/kartta?lang=en (accessed on 18 November 2021).
- Statistics Finland Population Grid Data 1 km × 1 km. Available online: https://stat.fi/org/avoindata/paikkatietoaineistot/vaestoruutuaineisto_1km_en.html (accessed on 18 November 2021).
- Finnish Energy Electricity Use by Municipality in 2007 to 2020 (Sähkönkäyttö Kunnittain 2007–2020). Available online: https://energia.fi/uutishuone/materiaalipankki/sahkonkaytto_kunnittain_2007-2020.html (accessed on 18 November 2021).
- Energy Authority Load Profiles (Kuormitusprofiilit). Available online: https://energiavirasto.fi/hinnoittelun-valvonta (accessed on 3 December 2021).
- Statistics Finland Household-Dwelling Units by Tenure Status, Type of Building, Number of Persons, 2005–2020. Available online: https://pxdata.stat.fi/PxWeb/pxweb/en/StatFin/StatFin__asas/statfin_asas_pxt_115y.px/ (accessed on 3 December 2021).
- Finnish Energy Hourly Data on Electricity (Sähkön Tuntidata). Available online: https://energia.fi/uutishuone/materiaalipankki/sahkon_tuntidata.html (accessed on 27 July 2022).
- Finnish Environment Institute Land cover by Municipality at the 2nd Classification Level (Maanpeite Kunnittain 2. Luokit-telutasolla). Available online: https://www.syke.fi/fi-FI/Avoin_tieto/Paikkatietoaineistot/Paikkatietoanalyysien_tuloksia(37720) (accessed on 8 December 2021).
- Partanen, J.; Lassila, J.; Haakana, J. Regulation and Development of Electricity Distribution Network Business (Sähkönjakeluverkkoliiketoiminnan Sääntely ja Kehittäminen); Lappeenranta University of Technology: Lappeenranta, Finland, 2020. [Google Scholar]
- Jufri, F.H.; Widiputra, V.; Jung, J. State-of-the-Art Review on Power Grid Resilience to Extreme Weather Events: Definitions, Frameworks, Quantitative Assessment Methodologies, and Enhancement Strategies. Appl. Energy 2019, 239, 1049–1065. [Google Scholar] [CrossRef]
- Hughes, W.; Zhang, W.; Cerrai, D.; Bagtzoglou, A.; Wanik, D.; Anagnostou, E. A Hybrid Physics-Based and Data-Driven Model for Power Distribution System Infrastructure Hardening and Outage Simulation. Reliab. Eng. Syst. Saf. 2022, 225, 108628. [Google Scholar] [CrossRef]
- Power Outage Statistics 2010–2019 (Keskeytystilasto). Available online: https://energia.fi/tilastot/sahkotilastot/keskeytystilasto (accessed on 10 January 2023).
- Finnish Energy. Interruption Statistics 2015 (Keskeytystilasto 2015); Finnish Energy: Helsinki, Finland, 2016. [Google Scholar]
- Storm History Blog: 2016 Salomo ja Rauli kesämyrskyt (Summer storms). Available online: https://myrskyvaroitus.com/index.php/myrskytieto/myrskyhistoria/156-2016-salomo-ja-rauli-kesaemyrskyt (accessed on 10 February 2023).
- Dunn, S.; Wilkinson, S.; Alderson, D.; Fowler, H.; Galasso, C. Fragility Curves for Assessing the Resilience of Electricity Networks Constructed from an Extensive Fault Database. Nat. Hazards Rev. 2018, 19, 04017019. [Google Scholar] [CrossRef]
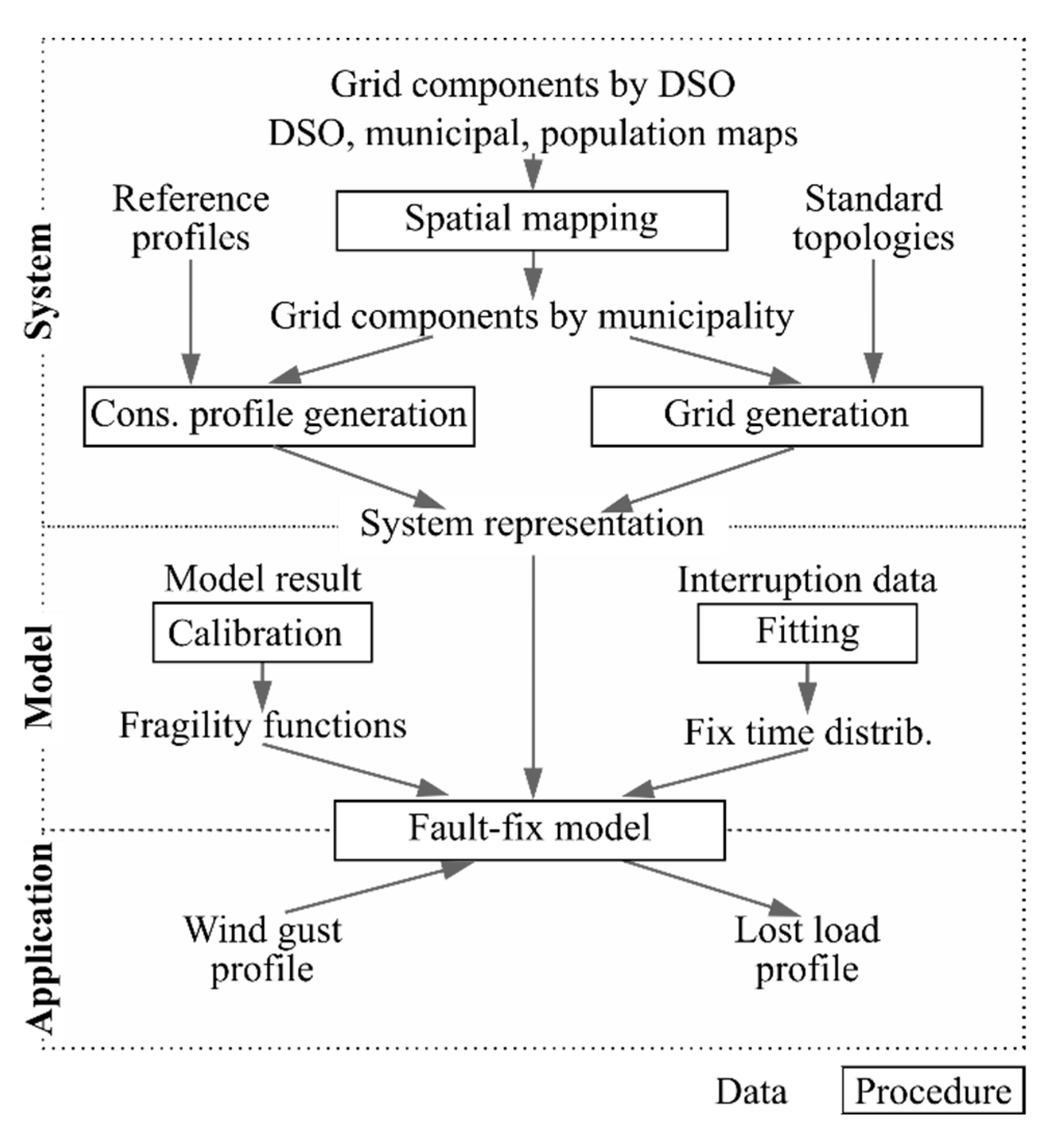
| Variable | Resolution | Source | Used in | ||
|---|---|---|---|---|---|
| Spatial | Temporal | ||||
| Number of transformers (MV, HV) | DSO service area | Year | Energy Authority (regulator) | [57,58] | Spatial mapping |
| Length of powerlines (MV) | |||||
| Cabling rate (MV) | |||||
| Number of consumers (MV) | |||||
| Consumption (LV, MV) | |||||
| DSO service area shapefiles | DSO service area | Year | Adato Energy (consultancy) | [59] | Spatial mapping |
| Municipality shapefiles | Municipality | Year | National Land Survey | [60] | Spatial mapping |
| Population data shapefiles | 1 km × 1 km | Year | Statistics Finland | [61] | Spatial mapping |
| Consumption by sector | Municipality | Year | Finnish Energy (industry association) | [62] | Spatial mapping |
| Reference consumption profiles | Country | Hour | Energy Authority (regulator) | [63] | Profile generation |
| Dwelling units by building type | Municipality | Year | Statistics Finland | [64] | Profile generation |
| Consumption | Country | Hour | Finnish Energy (industry association) | [65] | Profile generation |
| Temperature | 31 km × 31 km | Hour | ERA5 reanalysis | [40,41] | Profile generation |
| Wind gust speed | Application | ||||
| Forested area share | Municipality | Year | Finnish Environmental Institute | [66] | Application |
| Interruption | Aggregated region | Second | Enease (consultancy) | [52,53] | Model and application |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiūnas, J.; Láng-Ritter, I.; Heikkinen, T.; Lund, P.D. Electricity Load Lost in the Largest Windstorms—Is the Fragility-Based Model up to the Task? Energies 2023, 16, 5678. https://doi.org/10.3390/en16155678
Jasiūnas J, Láng-Ritter I, Heikkinen T, Lund PD. Electricity Load Lost in the Largest Windstorms—Is the Fragility-Based Model up to the Task? Energies. 2023; 16(15):5678. https://doi.org/10.3390/en16155678
Chicago/Turabian StyleJasiūnas, Justinas, Ilona Láng-Ritter, Tatu Heikkinen, and Peter D. Lund. 2023. "Electricity Load Lost in the Largest Windstorms—Is the Fragility-Based Model up to the Task?" Energies 16, no. 15: 5678. https://doi.org/10.3390/en16155678
APA StyleJasiūnas, J., Láng-Ritter, I., Heikkinen, T., & Lund, P. D. (2023). Electricity Load Lost in the Largest Windstorms—Is the Fragility-Based Model up to the Task? Energies, 16(15), 5678. https://doi.org/10.3390/en16155678







