A Peer-to-Peer Energy Trading Model for Optimizing Both Efficiency and Fairness
Abstract
1. Introduction
1.1. Research Background
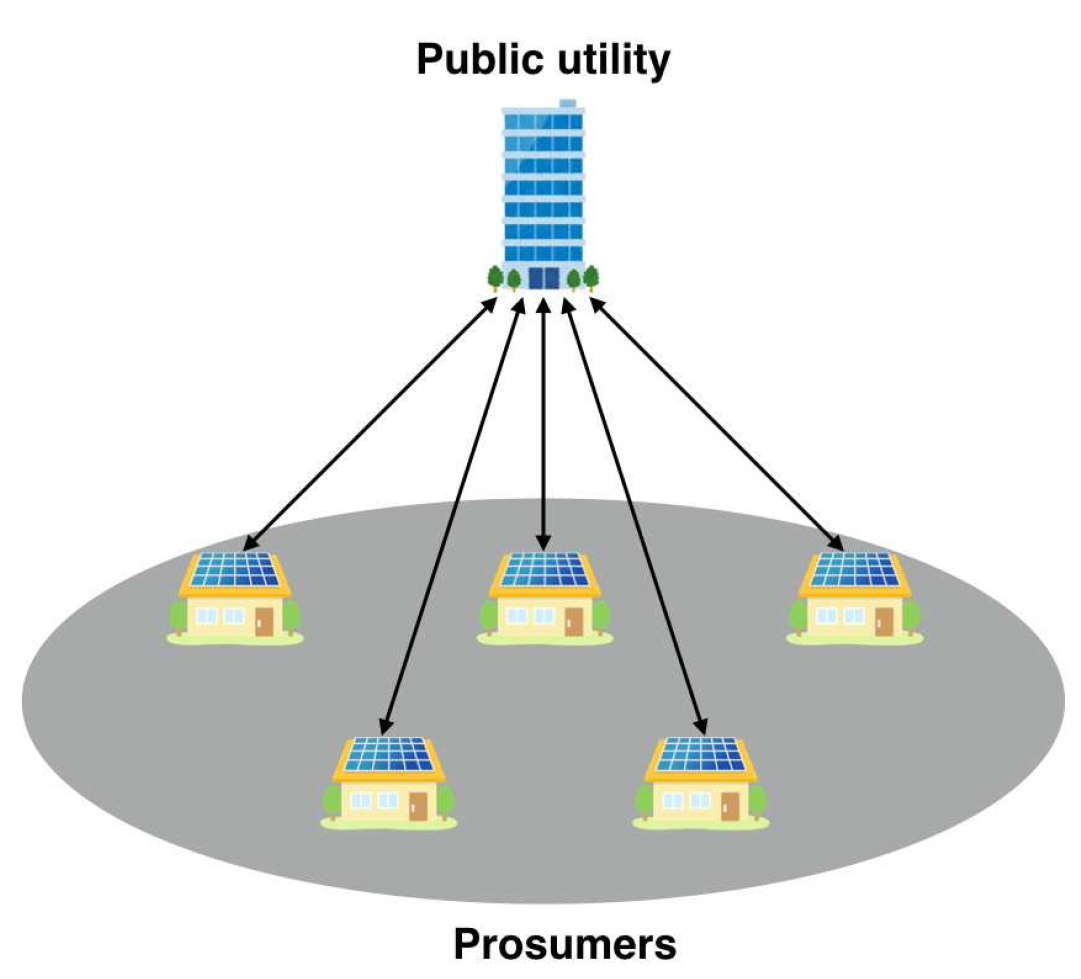
1.2. Peer-to-Peer Energy Trading
1.3. Related Work
1.4. Contribution
- It envisions a decline in the economic strain exerted upon standard households that necessitate electricity. FIT and FIP, which are invariably shouldered by these households, are encompassed within the realm of renewable energy surcharges. The number of prosumers is undeniably escalating. Consequently, it is indisputable that the quantity of surplus electricity, which public utilities are obliged to procure, is consistently on the rise. However, if this surplus electricity is judiciously employed within a localized energy network, the need for public utilities to purchase it diminishes, thereby stimulating transactions amongst prosumers. As a result, this precipitates a decline in the renewable energy surcharges that typical households are burdened with.
- Secondly, the proposed method lends assistance to typical households in their pursuit of identifying suitable trading partners. Each prosumer is confronted with the decision to elect a supplier or purchaser during every transaction within the peer-to-peer energy trading domain. Given the overwhelming myriad of options, this process is often complex for individuals. However, the proposed method, when implemented in distributed power apparatuses such as smart meters, facilitates the automatic determination of trading partners.
1.5. Paper Structure
2. Definitions
2.1. Model Illustration
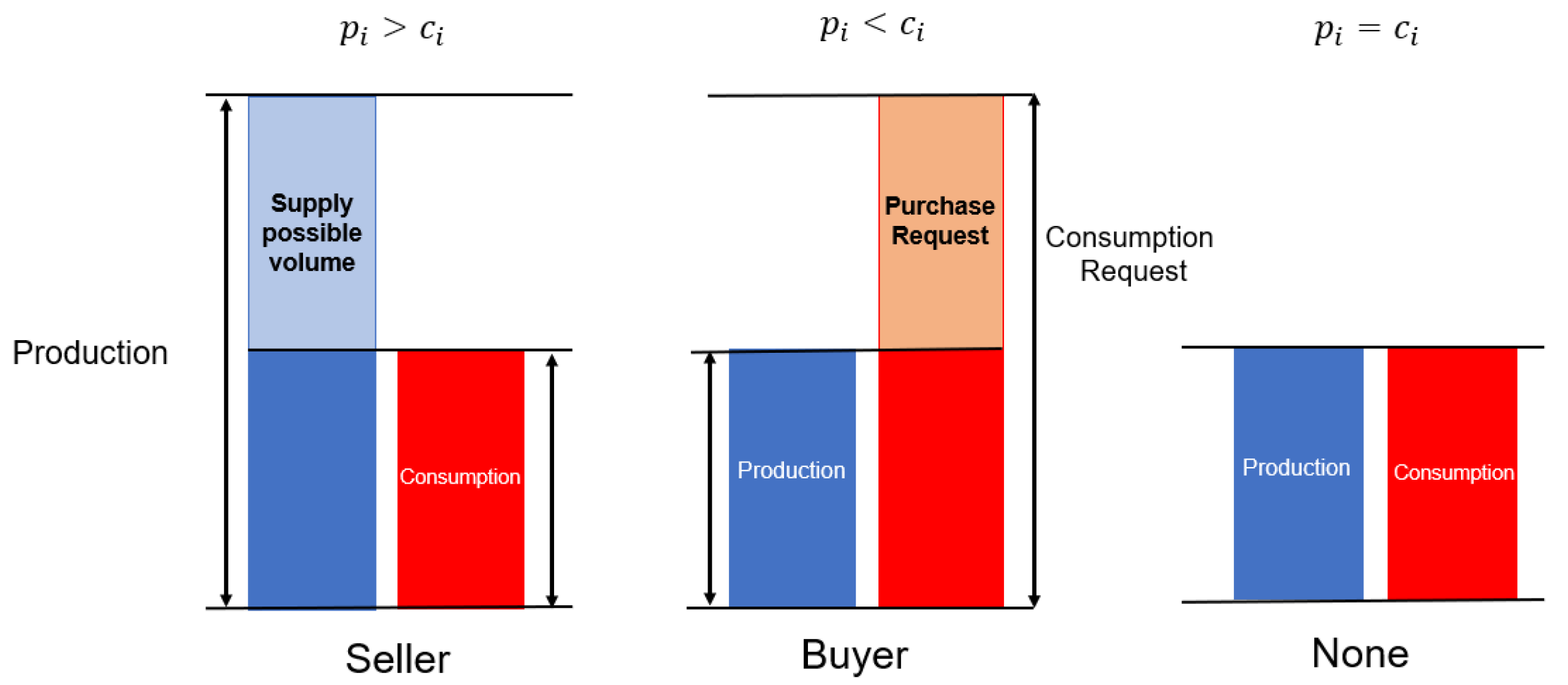
2.2. Restrictions on the Volume of Trades
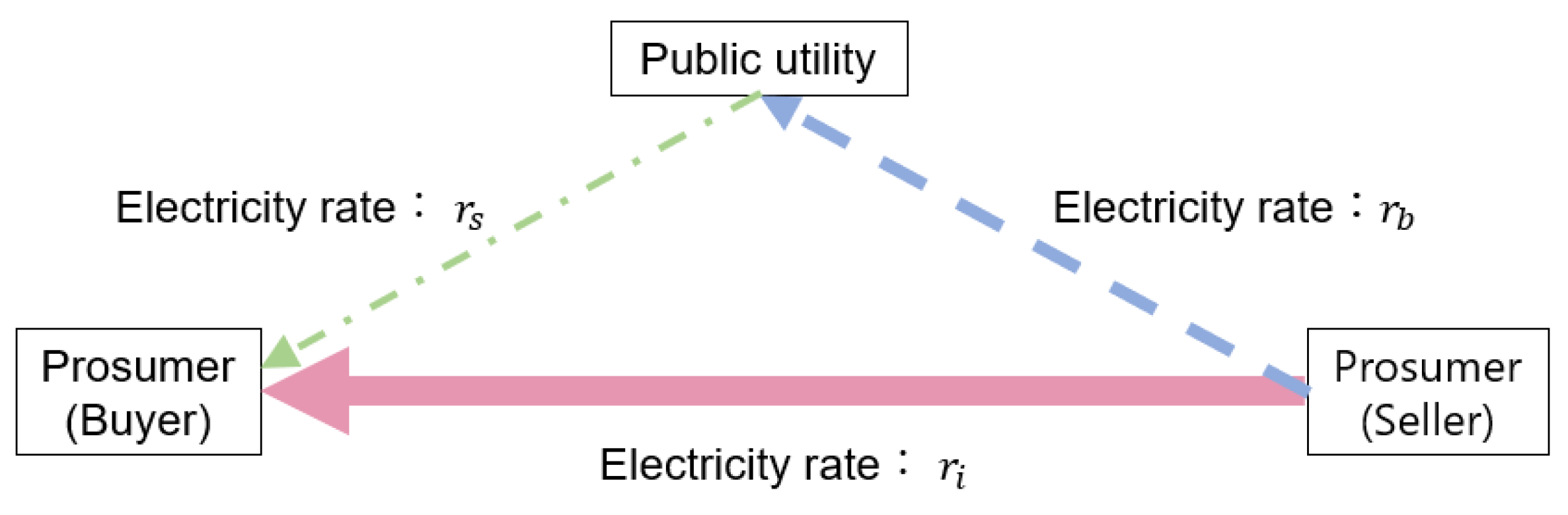
2.3. Rate
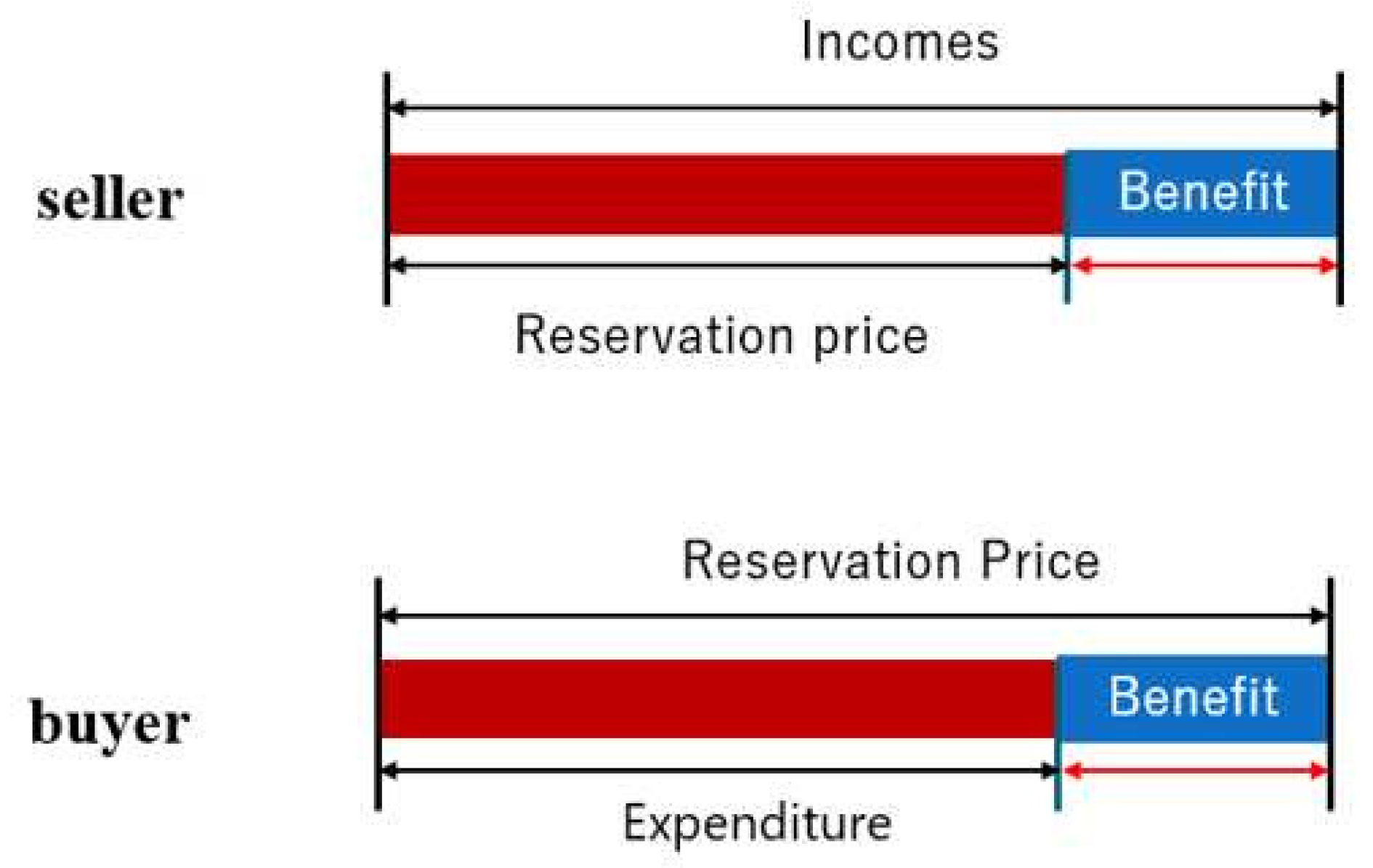
2.4. Reservation Price
2.5. Prosumer’s Benefit
3. Problem Formulation
3.1. Prosumer’s Benefit Maximization
3.2. Minimum Prosumer’s Benefit Maximization
3.3. Multi-Objective Optimization
4. Simulation Results
4.1. Conditions
4.2. Simulators
4.2.1. For Single-Objective Optimization
4.2.2. For Multi-Objective Optimization
- Non-dominated sorting genetic algorithms-II (NSGA-II)
- Generalized differential evolution-III (GDE3)
- Optimized multi-objective particle swarm optimization (OMOPSO)
- Speed-constrained multi-objective particle swarm optimization (SMPSO)
- Strength Pareto evolutionary algorithm-II (SPEA2)
- -multi-objective evolutionary algorithm (-MOEA)
4.3. Evolutionary Algorithms
4.3.1. NSGA-II
4.3.2. GDE3
4.3.3. OMOPSO
4.3.4. SMPSO
4.3.5. SPEA2
4.3.6. -MOEA
4.4. Evaluation Metrics
4.5. Results and Discussion
4.5.1. Prosumer’s Benefit Maximization Results
4.5.2. Minimum Prosumer’s Benefit Maximization Results
4.5.3. Multi-Objective Optimization Results
4.5.4. Discussions
4.5.5. Computational Time
5. Conclusions and Future Works
5.1. Conclusions
5.2. Future Work
- Considering the environmental impact of prosumersRenewable energy generation is inherently variable due to factors such as seasonal changes and weather conditions. Moreover, prosumers’ consumption patterns fluctuate based on their individual lifestyles. However, this paper does not consider the specific dynamics of prosumer’s production and consumption. We believe that one approach to consider to take lifestyle into account is using a weighted multi-objective method [25]. This approach allows for considering multiple factors and assigning different weights based on their importance. Furthermore, forecasting the real-time production and consumption of prosumers based on predefined measured values can be a direction to consider.
- Considering the introduction of fluctuating electricity pricesThe electricity rate is fixed in this paper; however, prices fluctuate in a realistic trading system due to different demand levels during peak and off-peak periods. Therefore, by setting electricity rates that fluctuate based on demand, we can make the trading system more realistic.
- Considering other factors of prosumer’s benefit in addition to priceThe EAs are used as meta-heuristics methods in this paper. Since our definitions of prosumer’s benefit considered only monetary gain, other factors of prosumer’s benefit should be considered to explain more real behavior of prosumers.
- Considering the security aspectAlthough we have not considered security aspects at this stage, we believe it would be appropriate to incorporate the STRIDE methodology, a vulnerability assessment method, into the process for conducting a comparison between the conventional transaction model and the new approach [26].
- Considering the pursuit of speed for optimizationThis paper can be led to an optimized solution; however, it is taking too long to reach a solution. We need to revise these codes and, at this stage, should consider implementing machine learning.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EA | Evolutionary Algorithm |
| TEPCO | Tokyo Electric Power Company |
| PBMP | Prosumer’s Benefit Maximization Problem |
| MPMP | Minimum Prosumer’s Benefit Maximization Problem |
| MOP | Multi-objective Optimization Problem |
References
- Koyama, K. The Role and Future of Fossil Fuel. IEEJ Energy J. Spec. Issue 2017, 3, 80–84. [Google Scholar]
- Japan’s Roadmap to ’Beyond-Zero’ Carbon. Available online: https://www.meti.go.jp/english/policy/energy_environment/global_warming/roadmap/ (accessed on 15 December 2021).
- Toffler, A.; Toffler, H. Revolutionary Wealth; Knopf: New York, NY, USA, 2006. [Google Scholar]
- Japan’s FiP Renewables System Likely to Exclude Biomass. Available online: https://www.argusmedia.com/en/news/2112632-japans-fip-renewables-system-likely-to-exclude-biomass (accessed on 20 December 2021).
- Lampropoulos, I.; van den Broek, M.; van der Hoofd, E.; Hommes, K.; van Sark, W. A system perspective to the deployment of flexibility through aggregator companies in the Netherlands. Energy Policy 2018, 118, 534–551. [Google Scholar] [CrossRef]
- Suthar, S.; Cherukuri, S.; Pindoriya, N. Peer-to-peer energy trading in smart grid: Frameworks, implementation methodologies, and demonstration projects. Electr. Power Syst. Res. 2023, 214 Pt A, 1–20. [Google Scholar] [CrossRef]
- Park, C.; Yong, T. Comparative review and discussion on P2P electricity trading. Energy Procedia 2017, 128, 3–9. [Google Scholar] [CrossRef]
- Argyris, N.; Karsu, O.; Yavuz, M. Fair resource allocation: Using welfare-based dominance constraints. Eur. J. Oper. Res. 2022, 297, 560–578. [Google Scholar] [CrossRef]
- Tan, M.; Zhou, Y.; Wang, L.; Su, Y.; Duan, B.; Wang, R. Fair-efficient energy trading for microgrid cluster in an active distribution network. Sustain. Energy Grids Netw. 2021, 26, 100453–100461. [Google Scholar] [CrossRef]
- Jing, R.; Xie, M.N.; Wang, F.X.; Chen, L.X. Fair P2P energy trading between residential and commercial multi-energy systems enabling integrated demand-side management. Appl. Energy 2020, 262, 114551–114567. [Google Scholar] [CrossRef]
- Regener, V.; Rommelt, G.; Zeiselmair, A.; Wasmeier, L.; Bogensperger, A. Design choices in peer-to-peer energy markets with active network management. IET Smart Grid. Spec. Issue Peak Load Forecast. Appl. 2022, 5, 281–296. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Z.; Yu, M.; Gao, H.; Wang, W. Optimal peer-to-peer energy trading for building based on data envelopment analysis. Energy Rep. 2023, 9, 4604–4616. [Google Scholar] [CrossRef]
- Kong, K.G.H.; Lim, J.Y.; Leong, W.D.; Ng, W.P.Q.; Teng, S.Y.; Sunarso, J.; How, B.S. Fuzzy optimization for peer-to-peer (P2P) multi-period renewable energy trading planning. J. Clean. Prod. 2022, 368, 133122. [Google Scholar] [CrossRef]
- Renewable Energy Purchase Prices, Surcharge Rate, and Other Details Related to FIT and FIP Schemes from FY2022 Onward to Be Determined. Available online: https://www.meti.go.jp/english/press/2022/0325_004.html (accessed on 25 December 2021).
- Saunders, A.; Cornett, M.M. Financial Markets and Institutions, 8th ed.; McGraw Hill: New York, NY, USA, 2022; Chapter 5 Appendix 5A. [Google Scholar]
- JUNG. Available online: http://jung.sourceforge.net (accessed on 18 December 2021).
- Introduction to lp_solve 5.5.2.11. Available online: https://lpsolve.sourceforge.net/5.5/ (accessed on 15 June 2021).
- Platypus—Multiobjective Optimization in Python. Available online: https://platypus.readthedocs.io/en/latest/ (accessed on 10 December 2021).
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist non-dominated sorting genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. GDE3: The third evolution step of generalized differential evolution. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 1, pp. 443–450. [Google Scholar]
- Sierra, M.R.; Coello, C.A.C. Improving PSO-Based multi-objective optimization using crowding, mutation and ϵ-dominance. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; pp. 505–519. [Google Scholar]
- Nebro, A.J.; Durillo, J.J.; Garcia-Nieto, J.; Coello, C.C.; Luna, F.; Alba, E. SMPSO: A new pso-based metaheuristic for multi-objective optimization. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making (MCDM), Nashville, TN, USA, 30 March–2 April 2009; pp. 66–73. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm. TIK Rep. 2001, 103, 1–21. [Google Scholar]
- Deb, K.; Mohan, M.; Mishra, S. A Fast Multi-Objective Evolutionary Algorithm for Finding Well-Spread Pareto-Optimal Solutions; Technical Report 2003002; Indian Institute of Technology, (KanGAL): Kanpur City, India, 2003. [Google Scholar]
- Qu, H.; Ye, Z. Multi-objective optimization operation of micro energy network with energy storage system based on improved weighted fuzzy method. In Proceedings of the International Conference on Frontiers of Energy and Environment Engineering (CFEEE), Beihai, China, 16–18 December 2022; Energy Reports. Volume 9, pp. 1995–2003. [Google Scholar]
- Sahay, R.; Estay, D.S.; Meng, W.; Jensen, C.D.; Barfod, M.B. A comparative risk analysis on CyberShip system with STPA-Sec, STRIDE and CORAS. Comput. Secur. 2023, 128, 103179. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| # of prosumers | 10 |
| [Wh] | Randomly decided between 349 Wh and 749 Wh |
| [Wh] | Randomly decided between 302 Wh and 702 Wh |
| [yen/kWh] | 29.05 |
| [yen/kWh] | 8.05 |
| [yen/kWh] | 18.55 |
| 1000 |
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| PBMP | 0.0021 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MPMP | 0.001155 | |||||||||
| EPsMOEA | ||||||||||
| GDE3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NSGAII | ||||||||||
| OMOPSO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SMPSO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SPEA2 |
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| capacity | 804.8463 | 792.5969 | 527.1893 | 739.5148 | 506.7915 | 694.2612 | 653.2675 | 749.6945 | 635.1398 | 690.4667 |
| demand | 562.647 | 607.578 | 696.4479 | 753.1572 | 844.3062 | 665.5017 | 886.1528 | 704.568 | 676.5624 | 785.0377 |
| PBMP | 2.5431 | 1.94271 | 1.77723 | 0.143325 | 3.340995 | 0.30198 | 0 | 0.47376 | 0 | 0 |
| MPMP | 2.5431 | 1.94271 | 0.143325 | 0.143325 | 1.101765 | 0.30198 | 2.44524 | 0.47376 | 0.43491 | 0.992985 |
| EPsMOEA | 0.445365 | 0.390073 | 0.066981 | 0.011476 | 0.094538 | 0.115392 | 0.080478 | 0.154343 | 0.022629 | 0.042448 |
| GDE3 | 1.71181 | 1.154414 | 0.003779 | 0 | 0.579017 | 0.114801 | 0.275869 | 0.155032 | 0 | 0.005253 |
| NSGAII | 0.456026 | 0.509109 | 0.068836 | 0.016035 | 0.108889 | 0.081164 | 0.055153 | 0.17269 | 0.029628 | 0.053791 |
| OMOPSO | 0.008554 | 0.024892 | 0.003203 | 0.007332 | 4.67 × 10 | |||||
| SMPSO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| SPEA2 | 0.599343 | 0.895141 | 0.137731 | 0.015724 | 0.242896 | 0.107725 | 0.127837 | 0.189232 | 0.053723 | 0.117297 |
| Problem (Algorithm) | Time [s] |
|---|---|
| PBMP | 5.401 |
| MPMP | 4.956 |
| Weighted (average) | 4.263 |
| MOP(NSGA-II) | 3519 |
| MOP(GDE3) | 2972 |
| MOP(OMOPSO) | 3036 |
| MOP(SMPSO) | 2883 |
| MOP(SPEA2) | 4065 |
| MOP(-MOEA) | 3508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusatake, E.; Imahori, M.; Shinomiya, N. A Peer-to-Peer Energy Trading Model for Optimizing Both Efficiency and Fairness. Energies 2023, 16, 5501. https://doi.org/10.3390/en16145501
Kusatake E, Imahori M, Shinomiya N. A Peer-to-Peer Energy Trading Model for Optimizing Both Efficiency and Fairness. Energies. 2023; 16(14):5501. https://doi.org/10.3390/en16145501
Chicago/Turabian StyleKusatake, Eiichi, Mitsue Imahori, and Norihiko Shinomiya. 2023. "A Peer-to-Peer Energy Trading Model for Optimizing Both Efficiency and Fairness" Energies 16, no. 14: 5501. https://doi.org/10.3390/en16145501
APA StyleKusatake, E., Imahori, M., & Shinomiya, N. (2023). A Peer-to-Peer Energy Trading Model for Optimizing Both Efficiency and Fairness. Energies, 16(14), 5501. https://doi.org/10.3390/en16145501






