Abstract
Corroded transmission towers, whose load-bearing capacities are lowered, are suffering from wind-induced damage. By simulating the member corrosion through section thinning, the structural dynamic finite element model of an angle-steel transmission tower with a corrosion depth of 0 mm to 1.4 mm was established using ANSYS/LS-DYNA software. The incremental dynamic analysis method was used to study the collapse mode of the tower under different degrees of corrosion, as well as the effects of corrosion on structural self-vibration characteristics, wind-induced member stress, and tower-top displacement. The results show that with the corrosion deepening, the first three vibration frequencies decrease, and the torsional mode becomes the first mode. When the corrosion depth is smaller, the overall structure failure occurs under strong wind. The failure starts at the most unfavorable oblique rod between the upper and middle cross arm, then expands to the rods under the lower cross arm. When the corrosion depth is larger, the overall structure failure occurs restrictedly between the upper and middle cross arm. Internal axial force and bending moment redistribution happen when corrosion deepens. Under the critical failure state, the oblique rods are always at a high stress level, while the stresses of the main rods decrease. Corrosion has a stronger impact on component strength and stability than on structural stiffness.
1. Introduction
The transmission tower-line system, as the most important carrier of electric power, plays a crucial role in modern life. In China, the transmission tower-line systems of over 220 kV were constructed since the 1950s and have been in service for several decades. As transmission tower-line systems are usually placed in direct contact with industrial pollution, acid rain, and saline water vapor, the angle-steel components of transmission towers experience severe corrosion, resulting in serious issues, such as cross-section thinning, rusting, and even breaking. A survey [1] showed that there were as many as 793 cases of transmission-tower corrosion in 25 provinces of China. Components at the segments of cross arm, tower body, and tower foot suffered from corrosion and the corrosion of transmission towers in coastal areas has no significant difference from inland in quantity. Since the cross-section area and moment of inertial of steel components decrease due to the thinning of their thickness, weakening the structure’s load-bearing capacity, and causing the redistribution of load-induced internal forces, collapses of transmission towers are more likely to happen under the action of strong wind, ice, and other working conditions, and in severe cases, it may cause the failure of the entire transmission tower-line system [1,2].
The previous literature has elaborated on the harm of corrosion to the safety of transmission towers from the perspectives of local components and structural systems. From the perspective of local components, Zu et al. [3] studied the corrosion-fatigue performances of 43 equal angles in the simulated acid-rain atmospheric environment and obtained their stress-fatigue life curves and surfaces with different guarantee ratios. It was found that the acid-rain atmospheric environment can dramatically shorten the medium-term and long-term fatigue lives of angle steel under medium or low load levels, while the influence is slight on the short-term fatigue lives under high load levels. Zhang et al. [4] tested the corrosion fatigue of three types of 18 Q345 equal angles in different corrosion times and demonstrated that the fatigue life decreases sharply with the increase of corrosion time under the same load; the effect of corrosion on fatigue life became more and more serious with the decrease of load in the same corrosion time. Zhang [5] found that with the increase of corrosion, the high-strength bolted slip resistance coefficient of a specimen increased within a certain range. Chen et al. [6] conducted field measurements on the corrosion of some angle-steel transmission towers in Guangxi and found that the average corrosion depth of severely corroded components reached 2.1 mm, resulting in a 40% decrease in the flexural and torsional buckling bearing capacity of the components due to section loss. Zheng et al. [7] simulated the effect of corrosion on the load-bearing capacity of diagonal components of an angle-steel tower using section thinning and found that, when the thickness of components halved, the maximum stress of the cross-section increased sharply; and further thinning of the cross-section would result in component failure.
From the perspective of a structure system, Li et al. [8] divided transmission towers into four layers based on the analytic hierarchy process (AHP) and classified the components in each layer into different species according to the cross-section stress and importance. Safety margins were used in this study to define the components to solve the safety of each layer and the overall structure. Huang [9] considered the corrosion-induced decrease in the nominal yield strength of steel and investigated the critical and ultimate corrosion rates of the main components of the tower and each segment, such as the tower leg, body, head, and cross arm. In order to evaluate the health of a transmission tower and its components, Qian et al. [10] proposed the allowable corrosion thickness of each component based on the functional relationship between steel corrosion degree and nominal yield strength, nominal ultimate strength, as well as the calculated stress ratio under typical working conditions. Wang [11] studied the wind-induced response of corroded transmission towers in Ningbo, China based on long-term prediction models for carbon-steel corrosion depth in different atmospheric environments. It was found that with the increase in service life, the wind-induced vibration response of transmission towers in various atmospheric environments increased and the fastest increase was observed in marine industrial mixed atmospheric environments. Guo [12] proposed the S-N curve and P-S-N surface of bolted and welded connections under the combined action of fatigue and corrosion, analyzed the dynamic response of the tower under wind load, and analyzed its corrosion fatigue reliability using node failure as the structural failure criterion. Deng et al. [13] simulated the corrosion depth by changing the thickness of the angle steel of components at the lower leg and found that the internal force of the surrounding diagonal material significantly increased as the thickness decreased, resulting in an unfavorable state where the stress extreme exceeded the yield strength of carbon steel. Liu et al. [14] conducted field measurements on critical corrosion components of a transmission tower, obtained the critical and ultimate corrosion rates of main components at the tower leg, body, head, and cross arm, and proposed replacement suggestions for these components. Salazar et al. [15] calculated the service life of a transmission tower in Venezuela based on the thickness of the galvanized layer, components, and the annual corrosion rate of steel in the marine atmospheric environment. However, the load-bearing capacity of different components is weakened in various degrees when the corrosion depths are the same, and different component corrosions have different impacts on the structural load-bearing capacity. The collapse mode of corroded transmission towers under strong wind is likely to change with the deepening of component corrosion. However, the components of a transmission tower, with different cross-section sizes and design stress ratios, are not equally sensitive to corrosion depth. In other words, the effect of corrosion on each component is different. With the same corrosion depth, the strong wind-induced stresses increase a little in some components, while increasing a lot in other components. Therefore, it is necessary to analyze the stress level of corroded components of transmission towers starting from the collapse mode, explore the wind-resistance bearing capacity of the structure, and find out the key components which are sensitive to steel corrosion the most.
In this study, the corrosion depth of angle steel is simulated by thinning its thickness. First, finite element models (FEMs) of an angle-steel transmission tower with different corrosion depths were constructed by ANSYS/LS-DYNA software (version 19.2), and the structural natural frequencies and vibration modes of corroded towers were analyzed. Second, the failure criteria for an angle-steel component were established according to the permissible stress (PS); the failure modes of corroded towers with different corrosion depths were investigated by an incremental dynamic analysis (IDA) approach and the associated failure wind speed was estimated. Third, the stresses of main and oblique components, wind-induced responses of the corroded tower, and the impact of corrosion depth on whole and local structure stability were analyzed.
2. Materials and Methods
The objective of this study was a typical angle-steel tower in a 220 kV transmission tower-line system located in Zhoushan, China, as shown in Figure 1. The tower has a pinnacle of 64.3 m and a foundation of 12.27 m × 12.27 m. The main, oblique, diaphragm, and auxiliary components are made by three types of equilateral angle steels, i.e., Q420, Q345, and Q235. The mechanical parameters of the three kinds of steel are shown in Table 1, in which is yield stress, is the Young’s modulus, μ is the Poisson’s ratio, and ρ is the material density.

Figure 1.
Configuration of an angle-steel transmission tower.

Table 1.
Mechanical parameters of steel.
The FEM model of this tower was established by ANSYS/LS-DYNA software (version 19.2), as shown in Figure 2. The origin of the coordinated system of the tower was located at the geometric center of the foundation of the tower, where axis X was perpendicular to the transmission line, axis Y was along with the transmission line, and axis Z was vertical. The main, oblique, and diaphragm components of the tower were modeled via beam element, namely the Hughes–Liu beam of BEAM161 in the LS-DYNA element library, and the auxiliary components were modeled via link element, i.e., LINK160. In order to simulate the mass property of bolts and node plates, i.e., meet the mass property consistency between the model and prototype, the material density was amplified by 1.2 times in FEM. Conductors and ground wires were simplified as particles located at hang points and modeled via mass element, i.e., MASS166. There were 12 particles of conductors and each of them had a weight of 4884.7 kg. There were 4 particles of ground wire and each of them had a weight of 1265.3 kg.

Figure 2.
Finite element model of transmission tower.
The beam element with the material model of PLASTIC_KINEMATIC (MAT_003) in ANSYS/LS-DYNA was used to model the main, oblique, and diaphragm components. Since the strain rate had little impact on the collapse routine and bearing capacity, it is comparatively insignificant [16], the bilinear model defined as follows was adopted for the stress–strain relation.
where is the stress, is the yield stress, is the strain, is the yield strain, = 0.02 is the ultimate strain, and = 2100 MPa is the tangent modulus.
3. Simulation of Random Wind Loads
3.1. Simulation of Random Wind Field
The tower was located in an open-country terrain, defined as category B in Chinese load code GB 50009-2012 [16]. The harmonic synthesis method was used to simulate the fluctuating wind field around the tower and the mean wind speed profile, fluctuating wind power spectrum, and spatial coherence of the fluctuating wind speed are expressed as follows.
where is the basic wind speed, is the mean wind speed at the height of ,= 0.15 is the power exponent of the mean wind speed profile, is the fluctuating wind power spectrum, n and are frequency and circular frequency, respectively, k = 0.004 is ground roughness, , is spatial coherence of fluctuating wind speed, are the 3D coordinates of simulated points, = 16, = 18, and = 10 are attenuation coefficients. The design basic wind speed of the tower with a return period of 50 years was = 39 m/s. The simulated fluctuating wind-speed time history and wind-power spectrum at the top of the tower are shown in Figure 3. It can be concluded in Figure 3 that the time history of simulated fluctuating wind speed is a stationary Gaussian process and the power spectrum of simulated fluctuating wind is highly consistent with the Davenport spectrum, which indicates that the simulated fluctuating wind field can reasonably reflect the characteristics of the natural wind field and can be used as the input wind field of the tower.

Figure 3.
(a) Time history and (b) power spectrum of simulated fluctuating wind speed at the tower top.
3.2. Wind Loads on Tower
According to Chinese order (DL/T 5154-2012), the instantaneous wind loads perpendicular to the transmission line acting on components at a height of z can be calculated as
where = 1.25 kg/m is the air density, is the fluctuating wind speed at the height of z, is the shape factor, is the wind-load reduction coefficient on the leeward side of the tower, is the projected area of the windward component.
3.3. Wind Loads on Conductors and Ground Wires
The wind loads on conductors and ground wires were applied as equivalent static wind loads (ESWLs) [17]. According to the design document, the ESWLs, acting on the upper, middle, and lower particles of conductors and ground wires, are shown in Table 2. In the collapse analysis of this tower, the applied wind loads should be gradually increased or decreased. When the basic wind speed increases from to , ESWLs acting on the upper, middle, and lower particles of conductors and ground wires can be calculated as

Table 2.
Equivalent static wind load of conductors and ground wire.
4. Collapse Analysis Methodologies of Transmission Tower
4.1. Explicit Integration Method
The collapse analysis of transmission towers involved nonlinear problems such as large deformation and removal of the components. Hence, the explicit algorithm instead of the implicit algorithm in performing the progressive collapse analysis of the transmission tower was applied. The central difference method was used to perform the explicit integration and the solution converges while the time interval fulfills
in which is the maximum frequency of the individual element in the FEM.
4.2. Failure Criterion of the Component
The allowable stress criterion was used to judge whether a component failed or not. The components of a transmission tower may suffer tension-bending or compression-bending under the action of strong wind. According to Chinese order (DL/T 5154-2012), the failure of tension-bending components is controlled by strength and the control equation is
The failure of compression-bending components is controlled by stability and the control equation is
in which is the demand to capacity ratio, , are the axial force and bending moment, , , and are cross-section gross area, net area, and modulus, respectively, , , and are strength reduction factor, stability reduction factor, and stability factor, respectively, is the design yield strength and equals to , is the corrected Euler buckling load, and is the slenderness. The demand-to-capacity ratio history of a component was derived from the wind-induced dynamic response analysis of the transmission tower. When the peak of of a component, defined as , is larger than 1, the component fails. and are the mean and standard deviation of , respectively.
4.3. Effects of Failure Members
The birth–death element technique is used to simulate the component which loses its load-bearing capacity in the progressive collapse of the tower [18,19]. When a component is killed, its contribution to the mass and stiffness matrix does not exist anymore. However, the failure of a component has an impact on the stiffness matrix but no impact on the mass matrix in practice. Hence, simply removing the failure component is inappropriate and may result in an inaccurate simulation of continuous collapse paths. In order to reduce the impact of the failure component on the mass matrix, each component of the tower was divided into three elements and only the middle element was killed and the rest of the component is retained when the failure component appears. Li et al. (2021) confirmed that no matter which element is killed, the progressive collapse process of the tower will not be affected.
4.4. Case of Progressive Collapse Analysis
The progressive collapse of a tower experiencing uniform corrosion over the tower body and cross arm were simulated in this study. There are eight cases simulated here. The corrosion depth gradually increased from 0 to 1.4 mm with an interval of 0.2 mm, as shown in Table 3. Corrosion resulted in thinning of the component cross section; the associated parameters such as section area, modulus, and inertia radius decreased accordingly.

Table 3.
Collapse simulation cases.
The IDA [20] was used to obtain the critical wind speed resulting in structure failure and the mode of collapse of the tower with different corrosion depths. The process is as follows: when the corrosion depth is 0 mm (i.e., Gk1), the inflow wind speed is gradually increased at an interval of 1 m/s from the design basic wind speed to obtain the critical wind speed and collapse mode. In the cases of Gk2~Gk6, the incoming wind speed is gradually reduced at an interval of −1 m/s from the critical wind speed of the previous case until the critical wind speed has been found and the associated collapse mode has been analyzed.
5. Natural Vibration Characteristics of Corroded Towers
The modal analyses of the angle-steel tower with different corrosion depths were conducted on the FEM models using the block Lanczos method by the software ANSYS (version 19.2). According to the results, the first three natural frequencies (, , ) and modes of the angle-steel tower with different corrosion depths are taken and shown in Table 4 and Table 5. Figure 4 shows the definition of the first three modes: first-order X bending mode, first-order Y bending mode, and first torsional mode. It can be concluded that the natural frequencies decreased with the corrosion depth, and the torsional mode gradually became the first-order mode of the tower. When the corrosion depth ranged from 0 mm to 0.8 mm, the first three modes of the tower were first-order X bending mode, first-order Y bending mode, and first torsional mode, respectively. When the corrosion depth was 1.0 mm, the first three modes were first-order X bending mode, first torsional mode, and first-order Y bending mode, respectively. Compared with the uncorroded structure, the frequency decreased by 2.06%, 7.62%, and 2.00%, respectively. When the corrosion depth ranged from 1.2 mm to 1.4 mm, the first three modes were first torsional mode, first-order X bending mode, and first-order Y bending mode. Compared with the uncorroded structure, the frequency with a corrosion depth of 1.4 mm decreased by 2.06%, 7.62%, and 2.00%, respectively.

Table 4.
First 3 frequencies of corrosive towers.

Table 5.
First 3 modes of the tower with different corrosion depths.

Figure 4.
First three modes of the tower with different corrosion depths: (a) first-order X bending mode, (b) first-order Y bending mode, (c) first torsional mode.
6. Wind-Induced Collapse Modes of Corroded Angle-Steel Towers
6.1. Loading Procedure
In order to eliminate the dynamic impact of three kinds of loads, namely the gravity of the tower body, gravity of conductors and ground wires, and wind loads on the tower, a step-by-step loading strategy is adopted to apply the load [21]. First, set the structural damping ratio to 1.00 and apply the gravity of the tower body, conductors, and ground wires. Second, apply the ESWLs of conductors and ground wires linearly at t = 3~7 s. The sudden action of ESWLs of conductors and ground wires decayed rapidly due to the large damping ratio. Finally, adjust the damping ratio to 0.02 at t = 10 s and apply the fluctuating wind-load time histories of the tower body. Figure 5 shows the wind-induced axial force time history of a main component at 1/2 height of the tower body. It can be seen that the oscillation of axial force caused by sudden gravity decays rapidly within 3 s and tends to stabilize. The axial force caused by ESWLs, which is applied at t = 3~7 s, oscillates slightly and, then, tends to stabilize. The impact of sudden action of wind loads on the tower body disappears at t = 15 s. It indicates that the adopted loading procedure can eliminate the impulsive effect of the three kinds of loads effectively.
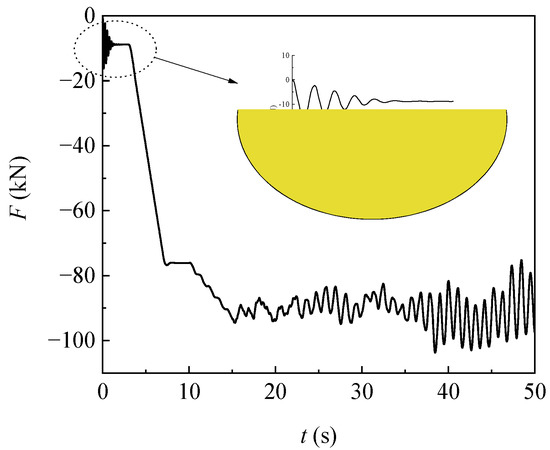
Figure 5.
Time history of axial force of a main component.
6.2. Collapse Modes
The time history of the wind displacement at the tower top with a corrosion depth of 0 mm is displayed in Figure 6. Figure 7, Figure 8 and Figure 9 show the progressive collapse processes of the towers under strong wind with corrosion depths of 0 mm (Gk1), 1.0 mm (Gk6), and 1.4 mm (Gk8). The tower without corrosion collapsed at the basic wind speed of 42 m/s, which increased by 7.7% compared to the design basic wind speed of 39 m/s. In Figure 7, the oblique component (named XC-1) at the tower body between the lower and middle cross arm failed firstly due to instability, resulting in an increase of internal forces and consequence failure of neighbor components and a sudden increase of displacement at the tower top (in Figure 6). The failed components were located within the height of 31.1 m to 52.8 m of the tower body, including the main, oblique, and auxiliary components. The tower with a corrosion depth of 1.0 mm collapsed at the basic wind speed of 38 m/s. It is shown in Figure 8 that the first failure component and collapse mode were consistent with the tower without corrosion but, since the weakening of the load-bearing capacity of different components varied even if the corrosion depth is consistent, the redistribution of internal force occurred in the overall structure; the failure components were limited between the lower and middle cross arm (47.0~52.8 m). The tower with a corrosion depth of 1.4 mm collapsed at the basic wind speed of 34 m/s, reducing by 12.8% compared to the design basic wind speed. In Figure 9, in addition to the failure of the tower body, the auxiliary component (named FC-1) at the upper cross arm failed due to instability (in Figure 6). However, the local failure did not result in the failure of the upper cross arm. It should be noted that in the process of collapse, time is only used to record the sequence of component failures.
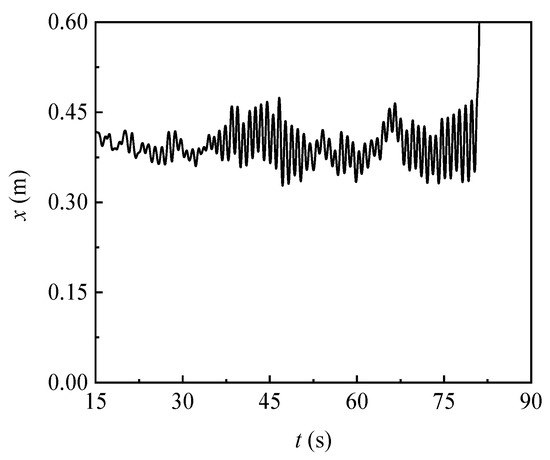
Figure 6.
Time history of displacement at tower top without corrosion (Gk1) ().

Figure 7.
Progressive collapse of the uncorroded tower ().

Figure 8.
Progressive collapse of the tower with corrosion depth of 1.0 mm ().
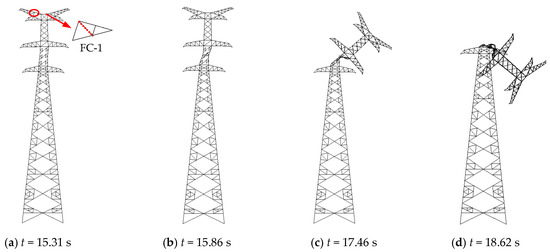
Figure 9.
Progressive collapse of the tower with corrosion depth of 1.4 mm ().
6.3. Wind-Induced Stress
Figure 10 shows the time history and power spectrum of the demand-to-capacity ratio of the first failed oblique component (XC-1) of the tower without corrosion at the critical basic wind speed of 42 m/s. Figure 11 shows the time history and power spectrum of of the first failed auxiliary component (FC-1) of the tower with a corrosion depth of 1.4 mm at the critical basic wind speed of 34 m/s. For XC-1, the mean of induced by critical basic wind speed was about 0.86 and the standard deviation of is about 0.04. For FC-1, the mean of induced by critical basic wind speed was about 0.98 and the standard deviation of is about 0.006. The three peaks of the power spectrum in Figure 10 and Figure 11 both occurred at the frequencies of 0.97 Hz, 1.11 Hz, and 1.45 Hz, which is consistent with the first three orders of X bending mode. Figure 12 shows the peak demand-to-capacity ratio of XC-1 and FC-1 along with basic wind speed. It can be concluded that XC-1 failed with different corrosion depths, which was the beginning of the overall failure of the tower, while FC-1 only experienced localized failure when the corrosion depth was large.

Figure 10.
(a) Time history and (b) power spectrum of demand to capacity ratio of oblique component XC-1 without corrosion (Gk1).

Figure 11.
(a) Time history and (b) power spectrum of demand to capacity ratio of auxiliary component FC-1 without corrosion (Gk1).

Figure 12.
Peak demand-to-capacity ratio of XC-1 and FC-1 varies with basic wind speeds.
The failure of the main and diagonal components caused by wind is the fundamental cause of the overall failure of the corroded tower. Figure 13 shows the critical basic wind speed corresponding to the overall failure of the tower with a corrosion depth of 0~1.4 mm. Generally, the critical wind speed decreased linearly along with the corrosion depth. When the corrosion depth was less than 0.6 mm, the critical basic wind speed of the tower was larger than the design basic wind speed. Due to the wind resistance design redundancy, the tower can still resist the design basic wind speed even when slightly corroded. Figure 14 and Figure 15 show the main and oblique components at the critical basic wind speed. It can be seen that (1) the most unfavorable main component was located at the tower foot and the height of 37 m of the tower body; and the most unfavorable oblique component was located at the height of 50 m of the tower body. (2) of the most unfavorable oblique component with different corrosion depths are maintained at a high level, and greater than the most unfavorable main component, indicating that overall failure of the structure began at the oblique component; and the oblique component was the key component in the corrosion resistance design of the angle-steel tower. (3) When the corrosion depth was small, the of the most unfavorable main component was larger and the overall failure starting from the failure of the oblique component gradually spread below the lower cross arm (Figure 7). When the corrosion depth was large, due to the redistribution of internal forces in the structure, the of the most unfavorable main component gradually decreased and the overall failure starting from the oblique component was only limited between the lower and middle cross arms (Figure 8 and Figure 9), reducing the range of failed components.

Figure 13.
Critical basic wind speed of towers with different corrosions.
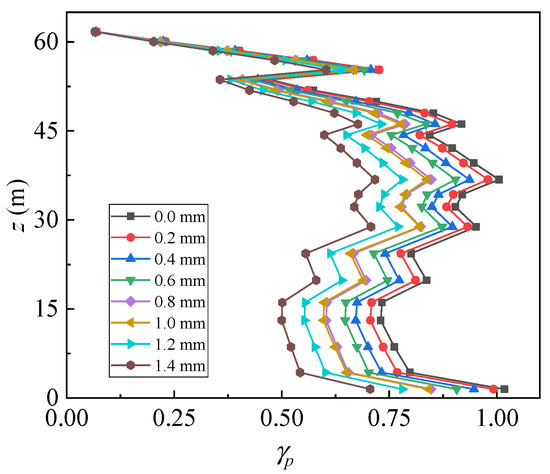
Figure 14.
Peak demand-to-capacity ratio of main components when tower collapses in Gk1~8.

Figure 15.
Peak demand-to-capacity ratio of oblique components when tower collapses in Gk1~8.
7. Conclusions
In this study, the corrosion depth of angle steel was simulated by thinning its thickness. The FEM of an angle-steel tower with different corrosion depths was constructed by ANSYS/LS-DYNA software (version 19.2) and the structural natural frequencies and vibration modes of corroded towers were analyzed. The failure criteria for the angle-steel component were established according to the permissible stress (PS); failure modes of corroded towers with different corrosion depths were investigated by incremental dynamic analysis (IDA) approach. Then, the natural vibration, failure modes and components, wind-induced response, and redistribution of internal forces were analyzed. The following conclusion can be obtained.
- (1)
- The natural frequency of the structure decreased along with the increase of corrosion depth. When the corrosion depth was larger than 1.2 mm, the first-order mode of the structure changed from first-order X bending mode to first torsional mode;
- (2)
- When the corrosion depth was small, the overall failure of the structure occurred under the action of strong wind. The most unfavorable diagonal component between the lower and middle cross arms failed first and, then, failure gradually spread to the components below the lower cross arm. When the corrosion depth was large, the overall failure was limited between the lower and middle cross arms and did not spread to other components. Local failure of the auxiliary component at the upper cross arm did not cause overall structural failure;
- (3)
- The oblique component components located between the lower and middle cross arms, which resulted in the largest capacity ratio and failed first under the action of strong wind, were the key components. In the wind-resistant design of a transmission tower at the highly corrosive areas, these components should be reinforced.
Author Contributions
Conceptualization, L.Z. and Y.R.; methodology, X.Z.; investigation, X.Z.; writing—original draft preparation, Z.T.; writing—review and editing, G.S. and J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant No. 52178511.
Data Availability Statement
Not applicable.
Acknowledgments
The authors greatly appreciate the support from the National Natural Science Foundation of China under Grant No. 52178511. The opinions and statements do not necessarily represent those of the sponsors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shan, K.Y.; Li, T. Influence of Tower Feet orrosion on Safety Performance of Power Transmission Tower. Corros. Prot. 2021, 42, 28–33+63. [Google Scholar]
- Cheng, L.; Ma, G. Corrosion and Protection of Steel Structures for Transmission and Distribution Project. Steel Struct. 2014, 29, 76–79. [Google Scholar]
- Zu, Y.F.; Li, Z.L. Experimental study on corrosion fatigue behavior of Q420Bangle in simulated acid rain atmospheric environment. J. Build. Struct. 2020, 41, 105–115. [Google Scholar]
- Zhang, C.T.; Fan, W.L. Experimental research on the corrosion fatigue properties of Q345 equal angles. J. Vib. Shock 2014, 33, 193–198. [Google Scholar]
- Zhang, M. Corrosion of High Strength Steel Bolt Friction Type Connection Test of Performance Degradation. Master’s Thesis, Xi an University of Architecture and Technology, Xi’an, China, 2011. [Google Scholar]
- Chen, L.; Xu, S.H. Application of Finite Element Method to Safety Assessment on Corroded Transmission Towers. Steel Struct. 2010, 25, 76–78+10. [Google Scholar]
- Zheng, H.W.; Yu, J.F. Influence of Corrosion on Mechanical Properties of Cross Inclined Materials of Transmission Tower. In Proceedings of the 2022 Industrial Architecture Academic Exchange, Beijing, China, 14 October 2022; Volume 5. [Google Scholar]
- Li, J.; Wu, S.J. Safety Analysis and Evaluation of Corroded Transmission Tower Structure. Water Resour. Power 2016, 34, 176–178. [Google Scholar]
- Huang, X.L. Study on the Natural Vibration Period of the Bucket Transmission Tower and the Overall Safety Performance While Corrosive. Master’s Thesis, South China University of Technology, Guangzhou, China, 2017. [Google Scholar]
- Qian, X.H.; Liang, H. Corroded Component Durability Evaluation for Service Tower of Transmission Line. East China Electr. Power 2013, 41, 1695–1698. [Google Scholar]
- Wang, Y.M. Evaluation of Wind Resistance Performance of Steel Transmission Tower Considering the Influence of Corrosion. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2021. [Google Scholar]
- Guo, H.R. Reliability Analysis of the Transmission Tower considering Corrosion Fatigue of Joints. Master’s Thesis, Chongqing University, Chongqing, China, 2019. [Google Scholar]
- Deng, C.Z.; Guo, Y.L.; Zhang, K.; Zhao, X.; Niu, H.R. Reinforcenment Measures and Simulation Calculation of Corrosion Tower Leg of Transmission Line Tower. J. China Three Gorges Univ. (Nat. Sci.) 2019, 41, 76–80. [Google Scholar]
- Liu, J.; Huang, Q.D. Research of the Natural Vibration Period of the Transmission Tower and the Overall Safety Performance in Corrosive Environment. Steel Struct. 2018, 41, 113–117. [Google Scholar]
- Salazar, J.E.; Mendoza, J.A. Life Prediction of Electrical Power Transmission Towers. In Proceedings of the ASME 2008 9th Biennial Conference on Engineering Systems Design and Analysis, Haifa, Israel, 7–9 July 2008; pp. 313–323. [Google Scholar]
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Department of the People’s Republic of China; China Architecture and Building Press: Beijing, China, 2012.
- DLT 5154-2012; Technical Regulation for Structural Design of Overhead Transmission Line Poles and Towers. Ministry of Housing and Urban-Rural Department of the People’s Republic of China; China Architecture and Building Press: Beijing, China, 2012.
- Tian, L.; Yu, Q. The collapse analysis of a transmission tower under wind excitation. Open Civ. Eng. J. 2014, 8, 136–142. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H. The Numerical Analysis of Transmission Tower-Line System Wind-Induced Collapsed Performance. Math. Probl. Eng. 2013, 2013 Pt 6, 413275. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y. Member capacity-based progressive collapse analysis of transmission towers under wind load. Wind Struct. 2021, 33, 317–329. [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).