The Solar Energy Potential of Greece for Flat-Plate Solar Panels Mounted on Double-Axis Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Data Processing and Analysis
3. Results
3.1. Annual Solar Energy Potential
3.2. Monthly Solar Energy Potential
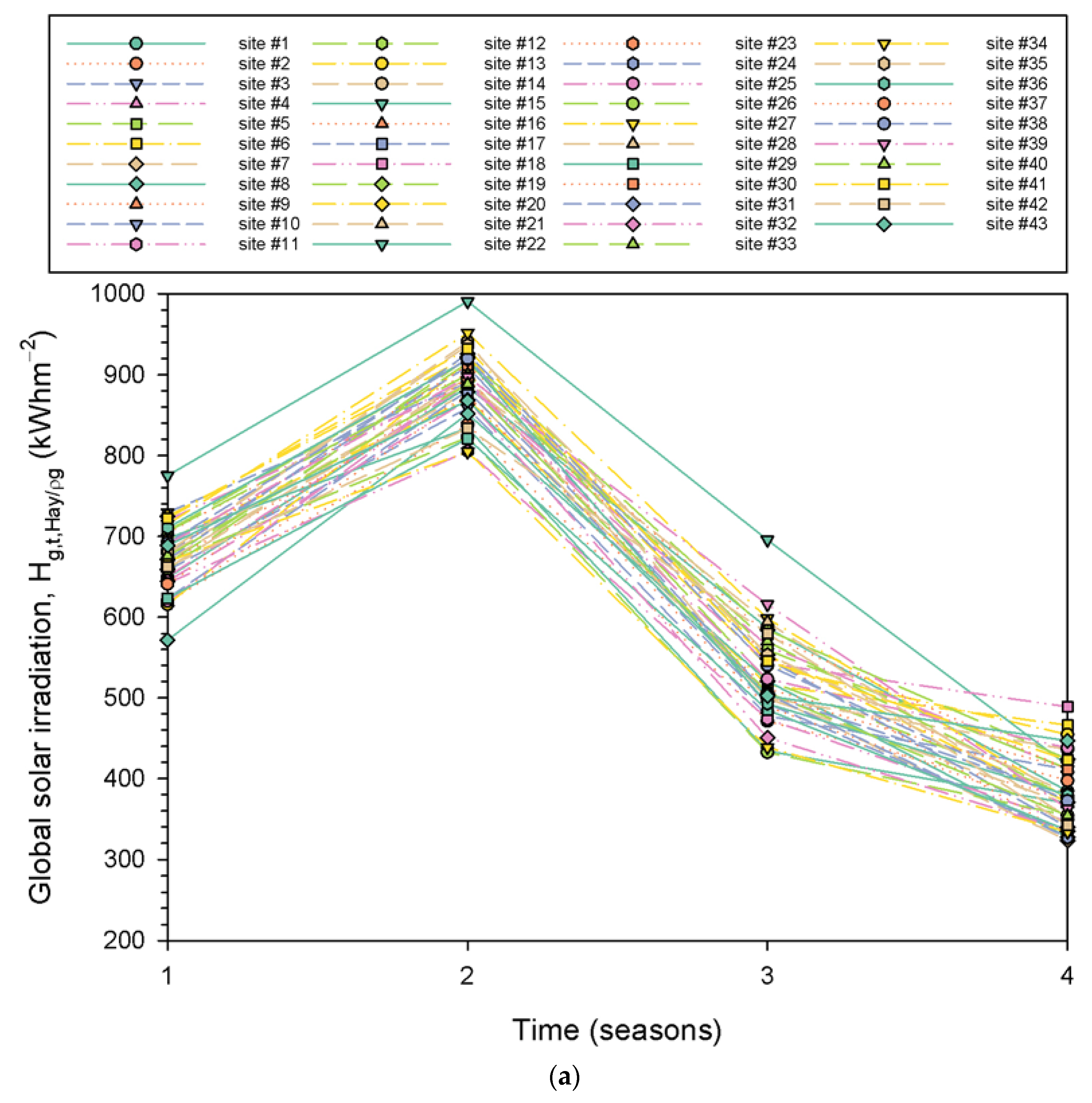
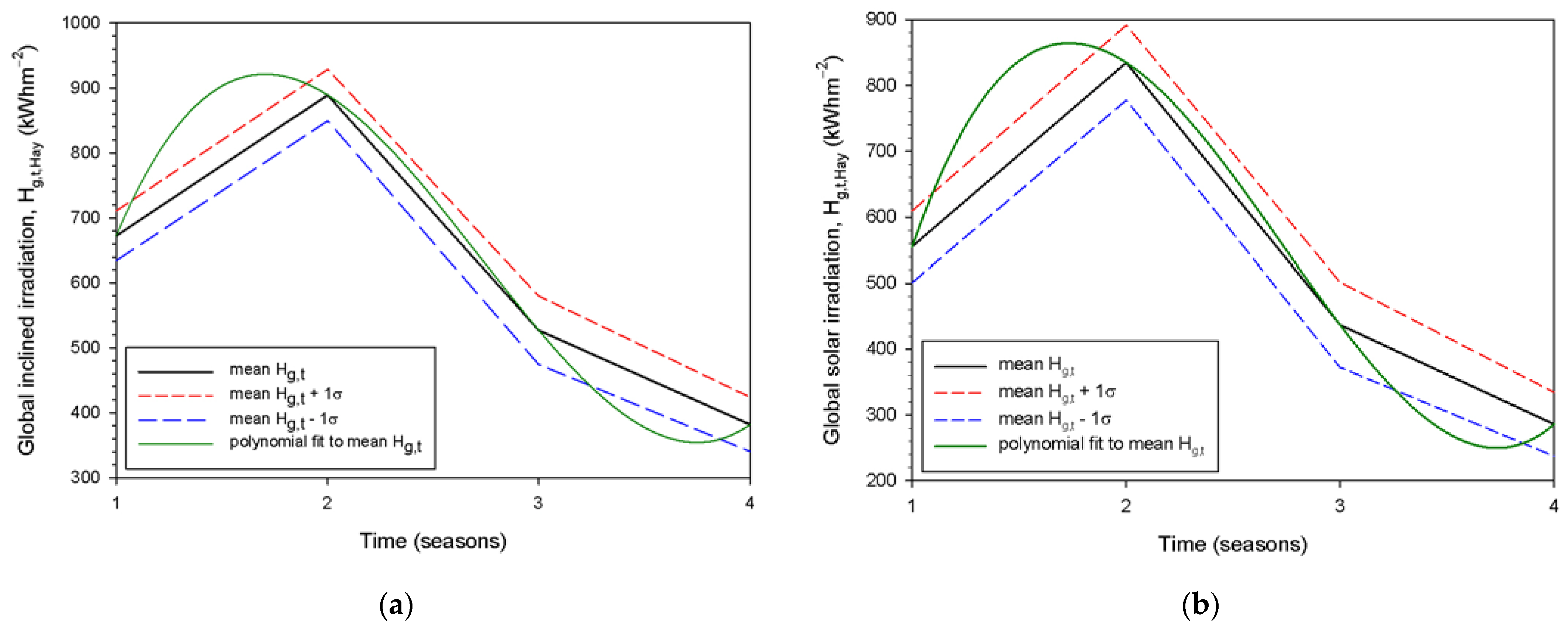
3.3. Seasonal Solar Energy Potential
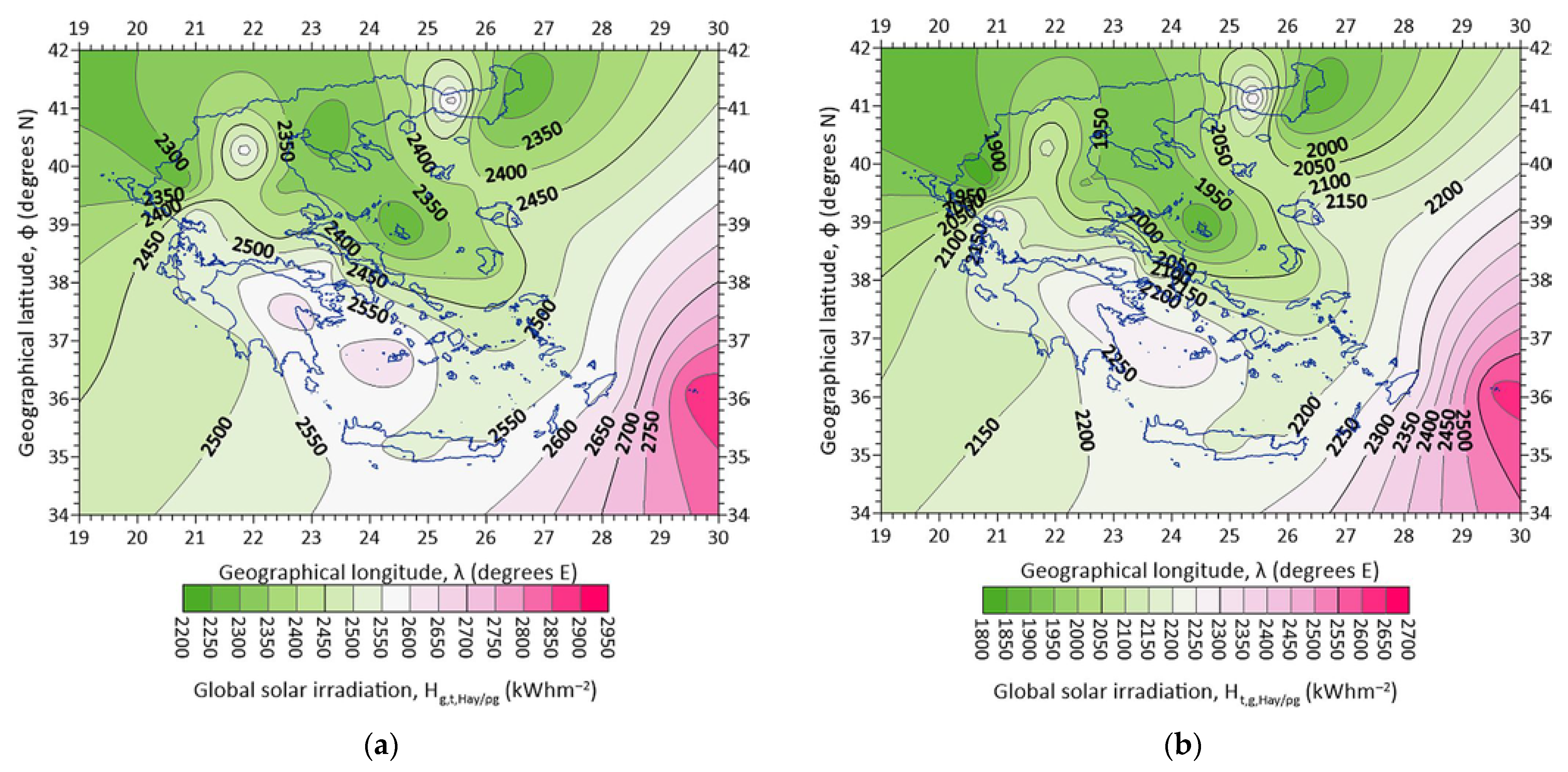
3.4. Maps of Annual Solar Energy Potential
3.5. Specialized Analysis
- (i)
- Various researchers [33,34,59,60] have shown that the PVGIS tool simulates values for a solar horizontal radiation with an accuracy between −14% and +11% (a median value of −1.5% is, therefore, very comparable to the ±3% accuracy of most pyranometers). This was done by comparing the PVGIS-simulated solar radiation values with real measurements. Thus, no new evaluation was required for the PVGIS tool. As far as the interdependence of the Hg,t,Hay/ρg- and Hg,t,L-J/ρg-estimated values is concerned, this is shown in Figure 11a for all- and Figure 11b for clear-sky conditions. In both cases, the interdependence is linear, as anticipated.
- (ii)
- Figure 12a shows the dependence of Hg,t,Hay/ρg on ke. A linear fit to the data points was derived with a negative slope, which implies decreasing solar irradiation values with an increasing atmospheric extinction index. In other words, a 0.1 increase in ke results in an almost 1273 kWhm−2 decrease in Hg,t,Hay/ρg (calculated by applying the linear expression in Figure 12a twice for ke1 = 0.38 and ke2 = 0.48, computing the Hg,t,Hay/ρg1 and Hg,t,Hay/ρg2 values, and taking their difference (Hg,t,Hay/ρg2 − Hg,t,Hay/ρg1). As these energy values concern the entire Greek territory (i.e., the average value for all 43 sites), then a decrease of about 30 kWhm−2 (=1273/43) per site in a year-round is calculated or a decrease of ≈2.5 kWhm−2 (=30/12) per site and per month. From Figure 7a, one sees that the average energy yield for January (worst case) is about 130 kWhm−2 for all 43 sites or about 3.0 kWhm−2 (=130/43) per site, and 330 kWhm−2 in July (best case) for all 43 sites or 7.8 kWhm−2 (=330/43) per site. The site-month values of 3.0 (or 7.8) kWhm−2 are comparable to (or 3 times higher than) the 2.5 kWhm−2 decrease in Hg,t,Hay/ρg due to a 0.1 increase in ke. Since ke = Hd/Hb (consider Hb = constant), a 0.1 increase in ke means a 10% increase in Hd and a subsequent decrease in Hg,t,Hay/ρg equal to 1273 kWhm−2 (or 14% equivalently). Therefore, any solar energy investor in Greece should consult not only the solar energy potential map of Greece (Figure 10a) but also the corresponding map of ke in Figure 12b. In the latter map, higher ke values occur over the northern Aegean Sea, Macedonia, and Thrace regions and lower ones over Peloponnese, Crete, and Rhodes. Considering that a constant Hb value indicates that favorable areas for solar harvesting in Greece are those of Peloponnese, Crete, and Rhodes because the contribution of the diffuse solar component is less important than in the northern areas, no extra cost in the solar panel material is anticipated to exploit the higher diffuse radiation in northern Greece with respect to the Hb component.
- (iii)
- Now that the importance of the ke index in solar harvesting has been established, it is useful to derive and present the monthly and seasonal mean variation in the index for Greece. Figure 13 shows the intra-annual variations in the ke. It is interesting to observe that minimum values occur in the summertime due to lower Hd/Hb values; this is also because, on the one hand, the Hd levels are lower than in the other seasons (less frequent cloudiness), and, on the other hand, the Hb levels are higher in this season. The above observations are also confirmed by Figure 14, which presents the seasonal variation in ke under all-sky conditions in Greece. The spring and summer ke patterns are remarkably similar, with higher values in the northern part of Greece and lower values in the south. The lower ke values imply lower diffuse radiation in comparison to the direct one; therefore, solar panels need to exploit the direct solar component without paying attention to the diffuse component in southern Greece. In contrast, diffuse radiation becomes more dominant in northern Greece, and this must be considered in PV installations. This outcome indicates a preference for solar harvesting below the latitude of φ ≈ 39° N (same conclusion in Section 3.4 for the annual values of Hg,t,Hay/ρg) during spring and summer. In contrast, the autumn and winter patterns differ; some relatively high values are observed over the northern Aegean Sea, Macedonia, Thrace, and south of Peloponnese (autumn), Crete, and almost all of the Aegean Sea (winter). In these two seasons, the rule of an imaginary dividing line at φ ≈ 39° N is not obeyed.
- (iv)
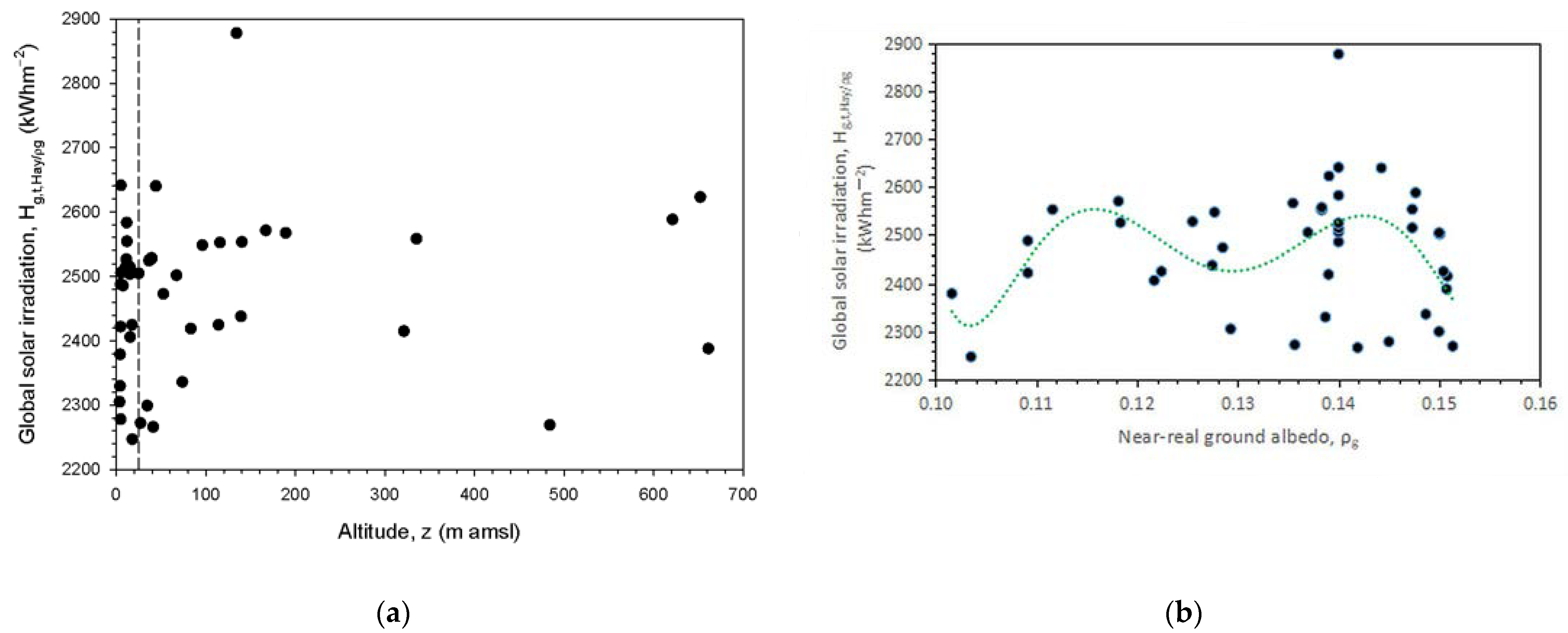
- The variations in the annual Hg,t,Hay/ρg values versus φ were presented in Figure 4. Here, analogous plots were derived with respect to z and ρg. The variation in the annual Hg,t,Hay/ρg values versus z is shown in Figure 15a, while the variation in Hg,t,Hay/ρg versus ρg is shown in Figure 15b. In both figures, a wide dispersion of the Hg,t,Hay values versus z or ρg is observed; moreover, many Hg,t,Hay values occur at lower elevations (below 25 m amsl, vertical dashed line in Figure 15a), which shows that the global solar irradiation is not strictly related to the altitude of the site (at least in the range of 0–700 m amsl). Indeed, 16 of 43 sites (37.2%) are at altitudes lower than 25 m amsl. A similar conclusion is drawn from Figure 15b; here, the sixth-order polynomial fit is shown to form two peaks at ρg ≈ 0.116 and ≈ 0.144. The very loose dependence of solar irradiation (for flat-plate solar panels fixed on dual-axis systems in Greece) either on the site location (i.e., geographical latitude) or the type of ground (i.e., ground albedo) concludes that the general rule for solar energy system installation is only the region (northern or southern Greece, see Figure 10 and Figure 16).
- (v)
- Four seasonal maps of Hg,t,Hay/ρg over Greece under all-sky conditions are presented in Figure 16. The Hg,t,Hay/ρg patterns are the opposite of those for ke in the corresponding seasons. This is quite logical because high global solar radiation consists mainly of direct solar component and less of diffuse solar radiation; this is equivalent to low ke (i.e., Hd/Hb) values and vice versa.
- (vi)
- A 3D graph of Hg,t,Hay/ρg versus φ is presented in Figure 17a, and a scatter plot of ρg versus φ in Figure 17b, both under all-sky conditions. The Hg,t,Hay/ρg pattern has a wave-like shape, as confirmed by the 2D plot, in which the green line is a sixth-order polynomial fit to the data points. This is an interesting result and shows that reflections from the ground play a role in the performance of a double-axis solar system. The large scatter in the data points of Figure 17b implies that the ground reflections do not depend directly on the geographical latitude; however, two peaks in the ρg values can be observed for φ ≈ 38° N and φ ≈ 41° N, which correspond to sites located in central and northern Greece, where green lands (forests or cultivated areas) exist that reflect more radiation than the bare soil in most parts of the southern territories of the country (for φ < 38° N). Apart from the general territory rule of φ ≈ 39° N (see Figure 10 and Figure 16) in investing solar energy systems in Greece formulated in (iv) above, one should also consider that a system installed at a site with φ = 38° N or φ = 41° N may receive almost 1.4 times higher ground reflection than other sites at φ ≈ 36° N or φ ≈ 39° N. However, a combination of Figure 15b and Figure 17b results in Figure 17a, in which the solar irradiation levels over Greece take a waveform pattern.
- (vii)
- Figure 18 presents the intra-annual (i.e., monthly) variation in the near-real ground albedo over Greece. The mean ρg ± 1σ band is also shown, which implies a ρg variation in the range of 0.108–0.155. This broad ±1σ band is justified by the wide dispersion of the annual ρg values in relation to φ shown in Figure 17b. Nevertheless, the annual mean ρg value for Greece was estimated to be 0.135. Psiloglou and Kambezidis [61] estimated an annual ground albedo value for Athens of 0.145 from solar radiation measurements performed at the Actinometric Station, National Observatory of Athens, Greece, in the period 1999–2008.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kambezidis, H.D.; Psiloglou, B.E. Estimation of the Optimum Energy Received by Solar Energy Flat-Plate Convertors in Greece Using Typical Meteorological Years. Part I: South-Oriented Tilt Angles. Appl. Sci. 2021, 11, 1547. [Google Scholar] [CrossRef]
- Demain, C.; Journée, M.; Bertrand, C. Evaluation of Different Models to Estimate the Global Solar Radiation on Inclined Surfaces. Renew. Energy 2013, 50, 710–721. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón, L.; Díaz, G.; Silva, C.A. Investigation of the Effect of Albedo in Photovoltaic Systems for Urban Applications: Case Study for Spain. Energies 2022, 15, 7905. [Google Scholar] [CrossRef]
- Akbar, H.S.; Fathallah, M.N.; Raoof, O.O. Efficient Single Axis Sun Tracker Design for Photovoltaic System Applications. IOSR J. Appl. Phys. 2017, 09, 53–60. [Google Scholar] [CrossRef]
- Heslop, S.; MacGill, I. Comparative Analysis of the Variability of Fixed and Tracking Photovoltaic Systems. Sol. Energy 2014, 107, 351–364. [Google Scholar] [CrossRef]
- Abdallah, S.; Nijmeh, S. Two Axes Sun Tracking System with PLC Control. Energy Convers. Manag. 2004, 45, 1931–1939. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Al-Hazmi, F.S.; Al-Ghamdi, A.A.; Yaghmour, S.J. Global, Direct and Diffuse Solar Radiation on Horizontal and Tilted Surfaces in Jeddah, Saudi Arabia. Appl. Energy 2010, 87, 568–576. [Google Scholar] [CrossRef]
- Akbar, H.S. Design of Sun Tracker System for Solar Energy Applications. J. Phys. Res. 2015, 1, 29–34. [Google Scholar]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar Tracking Systems: Technologies and Trackers Drive Types—A Review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Altarawneh, I.S.; Rawadieh, S.I.; Tarawneh, M.S.; Alrowwad, S.M.; Rimawi, F. Optimal Tilt Angle Trajectory for Maximizing Solar Energy Potential in Ma’an Area in Jordan. J. Renew. Sustain. Energy 2016, 8, 033701. [Google Scholar] [CrossRef]
- Talebizadeh, P.; Mehrabian, M.A.; Abdolzadeh, M. Prediction of the Optimum Slope and Surface Azimuth Angles Using the Genetic Algorithm. Energy Build. 2011, 43, 2998–3005. [Google Scholar] [CrossRef]
- Evseev, E.G.; Kudish, A.I. The Assessment of Different Models to Predict the Global Solar Radiation on a Surface Tilted to the South. Sol. Energy 2009, 83, 377–388. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kampezidou, S.I.; Kampezidou, D. Mathematical Determination of the Upper and Lower Limits of the Diffuse Fraction at Any Site. Appl. Sci. 2021, 11, 8654. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The Solar Radiation Climate of Greece. Climate 2021, 9, 183. [Google Scholar] [CrossRef]
- Kaddoura, T.O.; Ramli, M.A.M.; Al-Turki, Y.A. On the Estimation of the Optimum Tilt Angle of PV Panel in Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 65, 626–634. [Google Scholar] [CrossRef]
- Ohtake, H.; Uno, F.; Oozeki, T.; Yamada, Y.; Takenaka, H.; Nakajima, T.Y. Estimation of Satellite-Derived Regional Photovoltaic Power Generation Using a Satellite-Estimated Solar Radiation Data. Energy Sci. Eng. 2018, 6, 570–583. [Google Scholar] [CrossRef]
- Tsalides, P.; Thanailakis, A. Direct Computation of the Array Optimum Tilt Angle in Constant-Tilt Photovoltaic Systems. Sol. Cells 1985, 14, 83–94. [Google Scholar] [CrossRef]
- Koronakis, P.S. On the Choice of the Angle of Tilt for South Facing Solar Collectors in the Athens Basin Area. Sol. Energy 1986, 36, 217–225. [Google Scholar] [CrossRef]
- Balouktsis, A.; Tsanakas, D.; Vachtevanos, G. On the Optimum Tilt Angle of a Photovoltaic Array. Int. J. Sol. Energy 1987, 5, 153–169. [Google Scholar] [CrossRef]
- Synodinou, B.M.; Katsoulis, B.D. A Comparison of Three Models for Estimation of Global Solar Irradiation on Tilted and Oriented Surfaces in Athens. Int. J. Sol. Energy 1996, 18, 83–102. [Google Scholar] [CrossRef]
- Darhmaoui, H.; Lahjouji, D. Latitude Based Model for Tilt Angle Optimization for Solar Collectors in the Mediterranean Region. Energy Procedia 2013, 42, 426–435. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Kapsali, M.; Kavadias, K.A. Temperature and Wind Speed Impact on the Efficiency of PV Installations. Experience Obtained from Outdoor Measurements in Greece. Renew. Energy 2014, 66, 612–624. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Jadhav, V. World Estimates of PV Optimal Tilt Angles and Ratios of Sunlight Incident upon Tilted and Tracked PV Panels Relative to Horizontal Panels. Sol. Energy 2018, 169, 55–66. [Google Scholar] [CrossRef]
- Raptis, I.-P.; Moustaka, A.; Kosmopoulos, P.; Kazadzis, S. Selecting Surface Inclination for Maximum Solar Power. Energies 2022, 15, 4784. [Google Scholar] [CrossRef]
- Palz, W.; Greif, J. Introduction to the Tables for Daily Global and Diffuse Radiation Incident on Slopes. In European Solar Radiation Atlas; Springer: Berlin/Heidelberg, Germany, 1996; pp. 25–27. [Google Scholar] [CrossRef]
- Page, J.; Albuisson, M.; Wald, L. The European Solar Radiation Atlas: A Valuable Digital Tool. Sol. Energy 2001, 71, 81–83. [Google Scholar] [CrossRef]
- ESMAP. Global Solar Atlas 2.0; ESMAP: Washington, DC, USA, 2019; Available online: www.solargis.com (accessed on 12 June 2021).
- Kambezidis, H.D.; Psiloglou, B.E.; Kavadias, K.A.; Paliatsos, A.G.; Bartzokas, A. Development of a Greek Solar Map Based on Solar Model Estimations. Sun Geosph. 2016, 11, 137–141. [Google Scholar]
- Katopodis, T.; Markantonis, I.; Politi, N.; Vlachogiannis, D.; Sfetsos, A. High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model. Atmosphere 2020, 11, 761. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A New Solar Radiation Database for Estimating PV Performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Koubli, E.; Huld, T.; Trentmann, J.; Riihelä, A.; Lindfors, A.V.; Palmer, D.; Gottschalg, R.; Antonanzas-Torres, F. Extensive Validation of CM SAF Surface Radiation Products over Europe. Remote Sens. Environ. 2017, 199, 171–186. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of Global Horizontal Irradiance Estimates from ERA5 and COSMO-REA6 Reanalyses Using Ground and Satellite-Based Data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Mueller, R.W.; Matsoukas, C.; Gratzki, A.; Behr, H.D.; Hollmann, R. The CM-SAF Operational Scheme for the Satellite Based Retrieval of Solar Surface Irradiance—A LUT Based Eigenvector Hybrid Approach. Remote Sens. Environ. 2009, 113, 1012–1024. [Google Scholar] [CrossRef]
- Amillo, A.G.; Huld, T.; Müller, R. A New Database of Global and Direct Solar Radiation Using the Eastern Meteosat Satellite, Models and Validation. Remote Sens. 2014, 6, 8165–8189. [Google Scholar] [CrossRef]
- Walraven, R. Calculating the Position of the Sun. Sol. Energy 1978, 20, 393–397. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Papanikolaou, N.S. Solar Position and Atmospheric Refraction. Sol. Energy 1990, 44, 143–144. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Tsangrassoulis, A.E. Solar Position and Right Ascension. Sol. Energy 1993, 50, 415–416. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Mimidis, K.; Kavadias, K.A. Correction of the Solar Azimuth Discontinuity at Sunrise and Sunset. Sun Geosph. 2022, 15, 19–34. [Google Scholar] [CrossRef]
- Liu, B.; Jordan, R.C. The Long-Term Average Performance of Flat-Plate Solar-Energy Collectors. Sol. Energy 1963, 7, 53–74. [Google Scholar] [CrossRef]
- Hay, J.E. Calculation of Monthly Mean Solar Radiation for Horizontal and Inclined Surfaces. Sol. Energy 1979, 23, 301–307. [Google Scholar] [CrossRef]
- Hay, J.E. Calculating Solar Radiation for Inclined Surfaces: Practical Approaches. Renew. Energy 1993, 3, 373–380. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E.; Gueymard, C. Measurements and Models for Total Solar Irradiance on Inclined Surface in Athens, Greece. Sol. Energy 1994, 53, 177–185. [Google Scholar] [CrossRef]
- Pandey, C.K.; Katiyar, A.K. Hourly Solar Radiation on Inclined Surfaces. Sustain. Energy Technol. Assess. 2014, 6, 86–92. [Google Scholar] [CrossRef]
- Acker, J.G.; Leptoukh, G. Online Analysis Enhances Use of NASA Earth Science Data. Eos Trans. Am. Geophys. Union 2007, 88, 14–17. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E. Climatology of the Linke and Unsworth-Monteith Turbidity Parameters for Greece: Introduction to the Notion of a Typical Atmospheric Turbidity Year. Appl. Sci. 2020, 10, 4043. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Zelenka, A. Making Full Use of the Clearness Index for Parameterizing Hourly Insolation Conditions. Sol. Energy 1990, 45, 111–114. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Labban, A. The Solar Radiation Climate of Saudi Arabia. Climate 2023, 11, 75. [Google Scholar] [CrossRef]
- Kafka, J.L.; Miller, M.A. A Climatology of Solar Irradiance and Its Controls across the United States: Implications for Solar Panel Orientation. Renew. Energy 2019, 135, 897–907. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Kambezidis, H.D. The Solar Resource. In Comprehensive Renewable Energy; Letcher, T.M., Ed.; Elsevier: Oxford, UK, 2022; Volume 3, pp. 26–117. [Google Scholar] [CrossRef]
- Gueymard, C.A. A Reevaluation of the Solar Constant Based on a 42-Year Total Solar Irradiance Time Series and a Reconciliation of Spaceborne Observations. Sol. Energy 2018, 168, 2–9. [Google Scholar] [CrossRef]
- Spencer, J.W. Fourier Series Representation of the Position of the Sun. Search 1971, 2, 172. [Google Scholar]
- Kasten, F. A New Table and Approximation Formula for the Relative Optial Air Mass. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1965, 14, 206–223. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Ramadan, E. Solar Energy Potential on Surfaces with Various Inclination Modes in Saudi Arabia: Performance of an Isotropic and an Anisotropic Model. Appl. Sci. 2022, 12, 5356. [Google Scholar] [CrossRef]
- Esbond, G.I.; Funmilayo, S.W.O. Solar Energy Potential in Yola, Adamawa State, Nigeria 2 The Problem 3 Literature Review. Int. J. Renew. Energy Sources 2019, 4, 48–55. [Google Scholar]
- Raisz, E. The Analemma. J. Geogr. 1941, 40, 90–97. [Google Scholar] [CrossRef]
- Lynch, P. The Equation of Time and the Analemma. Ir. Math. Soc. Bull. 2021, 69, 47–56. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Larissi, I.K.; Nastos, P.T.; Paliatsos, A.G. Spatial Variability and Trends of the Rain Intensity over Greece. Adv. Geosci. 2010, 26, 65–69. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Ramadan, E. Solar Potential in Saudi Arabia for Southward-Inclined Flat-Plate Surfaces. Appl. Sci. 2021, 11, 4101. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Al Otaibi, M. Solar Potential in Saudi Arabia for Inclined Flat-Plate Surfaces of Constant Tilt Tracking the Sun. Appl. Sci. 2021, 11, 7105. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Kambezidis, H.D. Estimation of the Ground Albedo for the Athens Area, Greece. J. Atmos. Sol.-Terr. Phys. 2009, 71, 943–954. [Google Scholar] [CrossRef]
- Hammad, B.; Al-Sardeah, A.; Al-Abed, M.; Nijmeh, S.; Al-Ghandoor, A. Performance and Economic Comparison of Fixed and Tracking Photovoltaic Systems in Jordan. Renew. Sustain. Energy Rev. 2017, 80, 827–839. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Longo, M.; Roscia, M.; Pagano, M. Comparative Analysis of Fixed and Sun Tracking Low Power PV Systems Considering Energy Consumption. Energy Convers. Manag. 2015, 92, 143–148. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Farahat, A.; Almazroui, M.; Ramadan, E. Solar Potential in Saudi Arabia for Flat-Plate Surfaces of Varying Tilt Tracking the Sun. Appl. Sci. 2021, 11, 11564. [Google Scholar] [CrossRef]
- Drury, E.; Lopez, A.; Denholm, P.; Margolis, R. Relative Performance of Tracking versus Fixed Tilt Photovoltaic Systems in the USA. Prog. Photovolt. Res. Appl. 2014, 22, 1302–1315. [Google Scholar] [CrossRef]
- Eke, R.; Senturk, A. Performance Comparison of a Double-Axis Sun Tracking versus Fixed PV System. Sol. Energy 2012, 86, 2665–2672. [Google Scholar] [CrossRef]
- Vaziri Rad, M.A.; Toopshekan, A.; Rahdan, P.; Kasaeian, A.; Mahian, O. A Comprehensive Study of Techno-Economic and Environmental Features of Different Solar Tracking Systems for Residential Photovoltaic Installations. Renew. Sustain. Energy Rev. 2020, 129, 109923. [Google Scholar] [CrossRef]

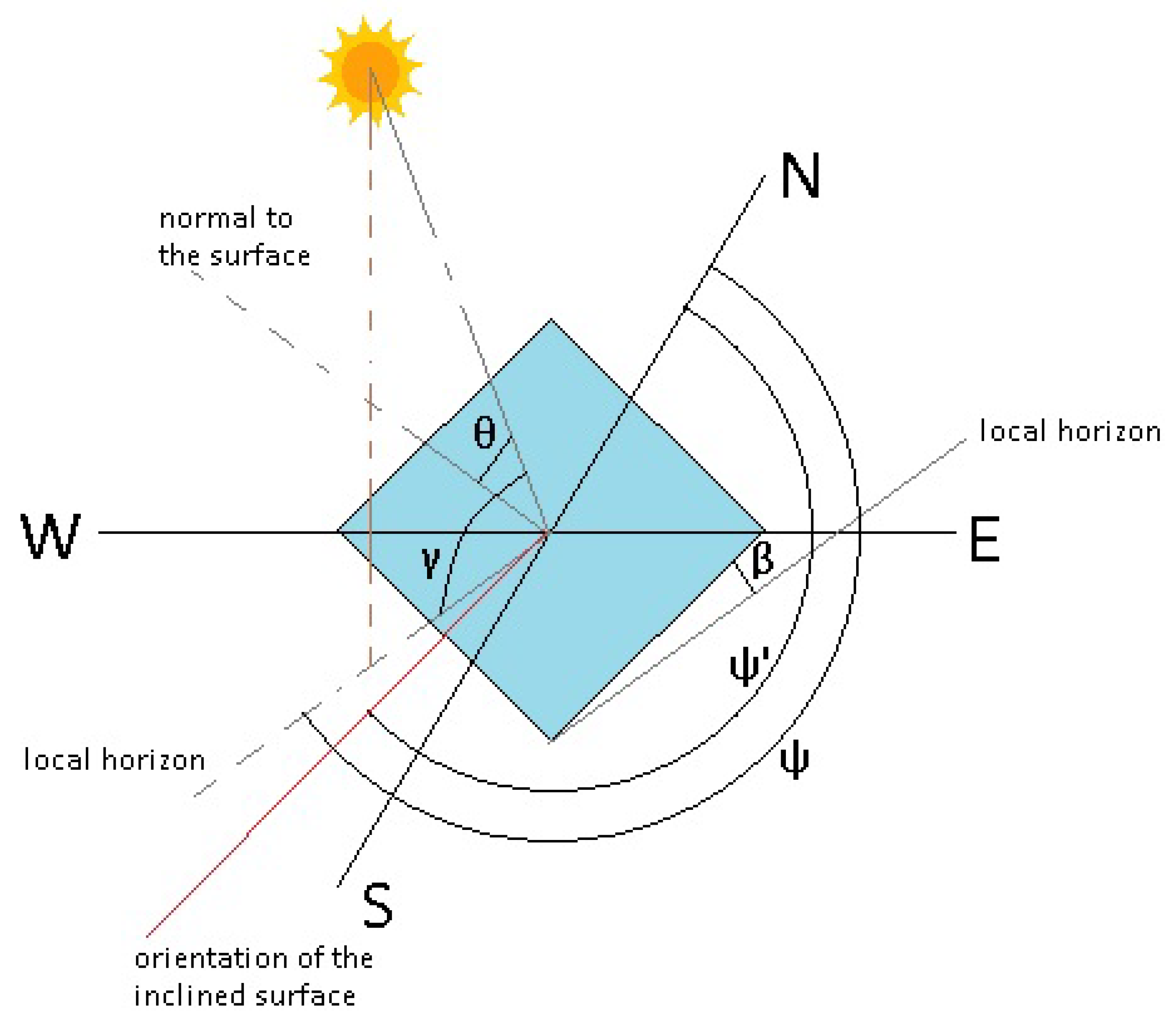



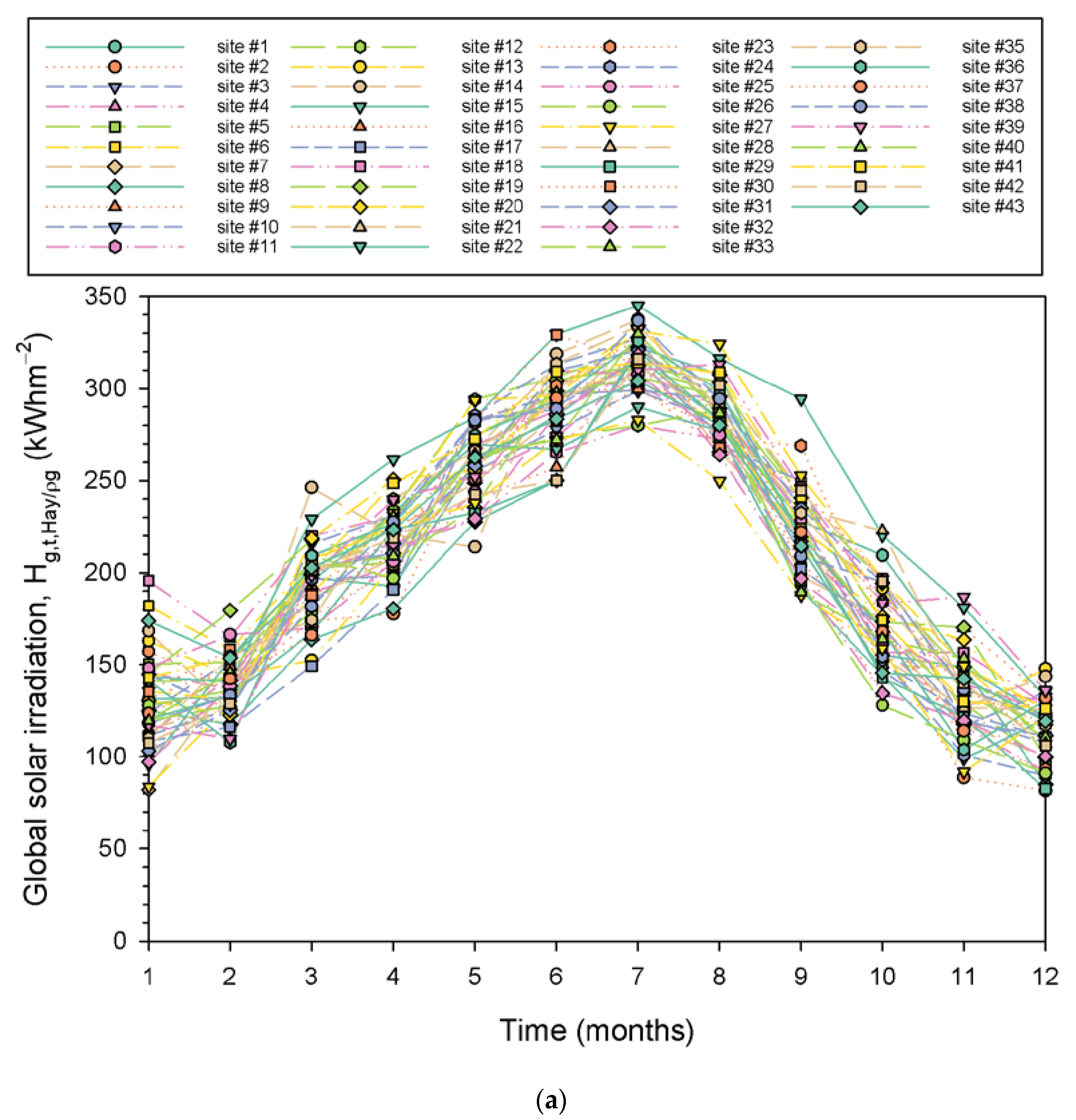
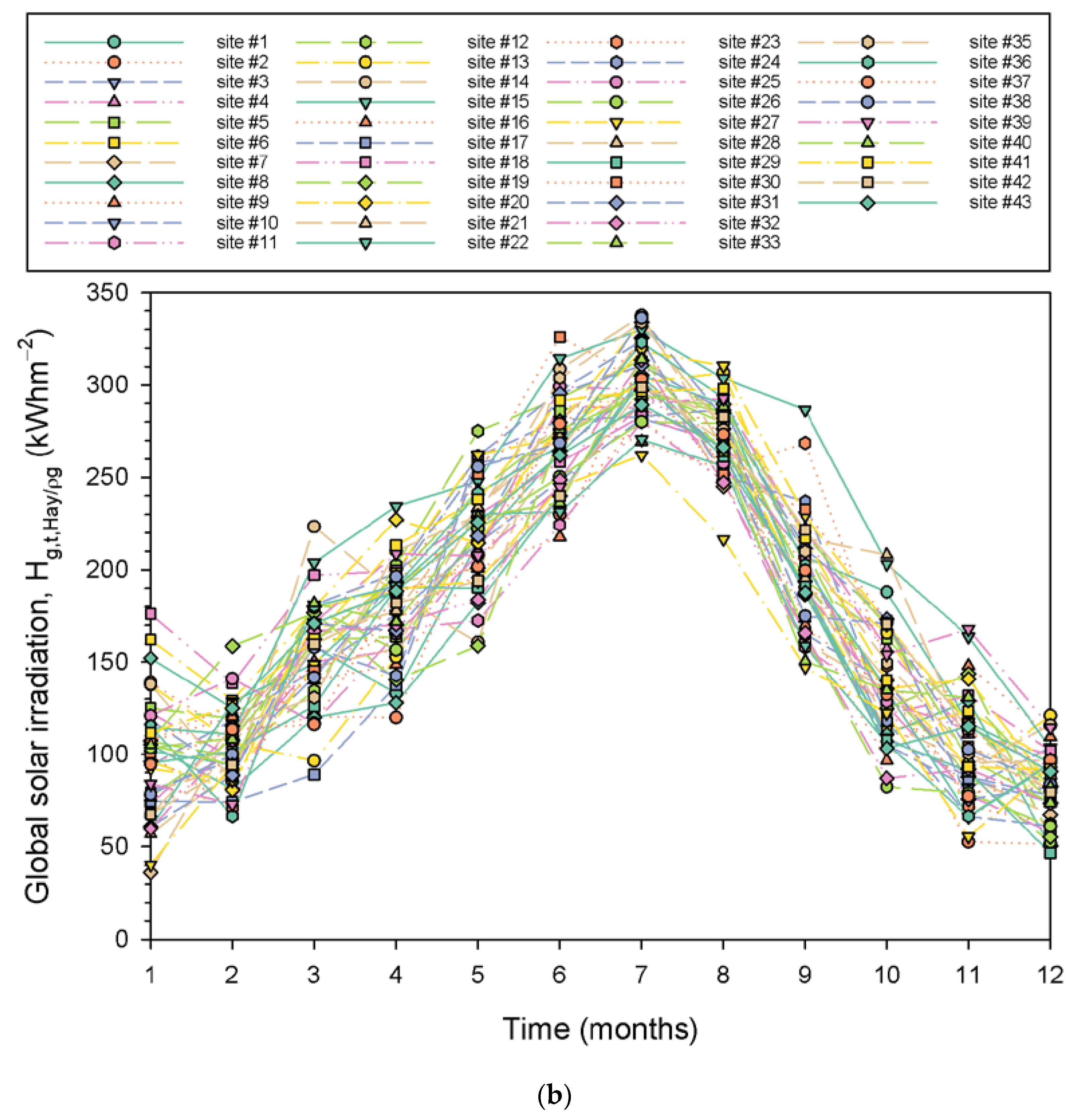
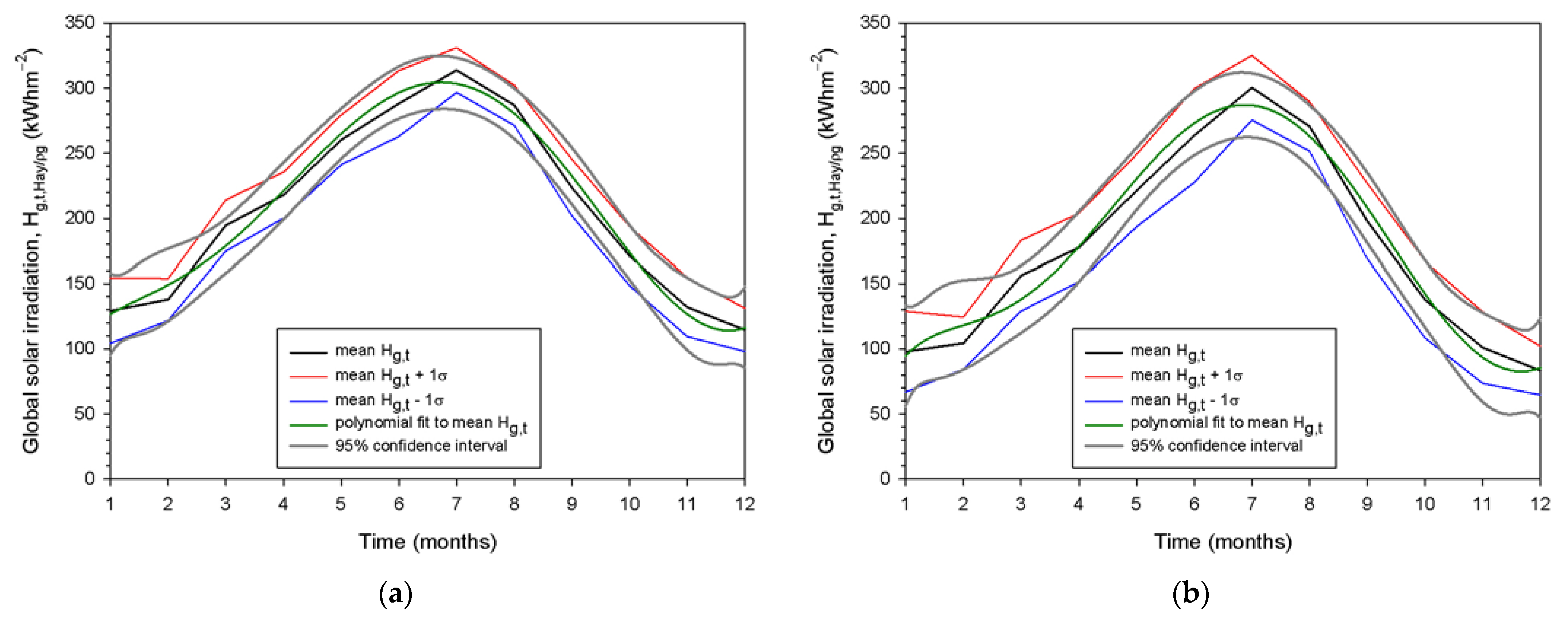






| Site Number | Site Name/Region/z (in m amsl) | λ (° East) | φ (° North) |
|---|---|---|---|
| 1 | Agrinio/western Greece/25 | 21.383 | 38.617 |
| 2 | Alexandroupoli/eastern Macedonia and Thrace/3.5 | 25.933 | 40.850 |
| 3 | Anchialos/Thessaly/15.3 | 22.800 | 39.067 |
| 4 | Andravida/western Greece/15.1 | 21.283 | 37.917 |
| 5 | Araxos/western Greece/11.7 | 21.417 | 38.133 |
| 6 | Arta/Epirus/96 | 20.988 | 39.158 |
| 7 | Chios/northern Aegean/4 | 26.150 | 38.350 |
| 8 | Didymoteicho/eastern Macedonia and Thrace/27 | 26.496 | 41.348 |
| 9 | Edessa/western Macedonia/321 | 22.044 | 40.802 |
| 10 | Elliniko/Attica/15 | 23.750 | 37.900 |
| 11 | Ioannina/Epirus/484 | 20.817 | 39.700 |
| 12 | Irakleio/Crete/39.3 (also written as Heraklion) | 25.183 | 35.333 |
| 13 | Kalamata/Peloponnese/11.1 | 22.000 | 37.067 |
| 14 | Kastelli/Crete/335 | 25.333 | 35.120 |
| 15 | Kastellorizo/southern Aegean/134 | 29.576 | 36.142 |
| 16 | Kastoria/western Macedonia/660.9 | 21.283 | 40.450 |
| 17 | Kerkyra/Ionian Islands/4 (also known as Corfu) | 19.917 | 39.617 |
| 18 | Komotini/eastern Macedonia and Thrace/44 | 25.407 | 41.122 |
| 19 | Kozani/western Macedonia/625 | 21.783 | 40.283 |
| 20 | Kythira/Attica/166.8 | 23.017 | 36.133 |
| 21 | Lamia/Sterea Ellada/17.4 | 22.400 | 38.850 |
| 22 | Larissa/Thessaly/73.6 | 22.450 | 39.650 |
| 23 | Lesvos/northern Aegean/4.8 | 26.600 | 39.067 |
| 24 | Limnos/northern Aegean/4.6 | 25.233 | 39.917 |
| 25 | Methoni/Peloponnese/52.4 | 21.700 | 36.833 |
| 26 | Mikra/central Macedonia/4.8 | 22.967 | 40.517 |
| 27 | Milos/southern Aegean/5 | 24.475 | 36.697 |
| 28 | Naxos/southern Aegean/9.8 | 25.533 | 37.100 |
| 29 | Orestiada/eastern Macedonia and Thrace/41 | 26.531 | 41.501 |
| 30 | Rodos/southern Aegean/11.5 (also written as Rhodes) | 28.117 | 36.400 |
| 31 | Samos/northern Aegean/7.3 | 26.917 | 37.700 |
| 32 | Serres/central Macedonia/34.5 | 23.567 | 41.083 |
| 33 | Siteia/Crete/115.6 | 26.100 | 35.120 |
| 34 | Skyros/Sterea Ellada/17.9 | 24.550 | 38.900 |
| 35 | Souda/Crete/140 | 21.117 | 35.550 |
| 36 | Spata/Attica/67 | 23.917 | 37.967 |
| 37 | Tanagra/Sterea Ellada/139 | 23.550 | 38.317 |
| 38 | Thira/southern Aegean/36.5 | 25.433 | 36.417 |
| 39 | Thiva/Sterea Ellada/189 | 23.320 | 38.322 |
| 40 | Trikala/Thessaly/114 | 21.768 | 39.556 |
| 41 | Tripoli/Peloponnese/652 | 22.400 | 37.533 |
| 42 | Xanthi/Eastern Macedonia and Thrace/83 | 24.886 | 41.130 |
| 43 | Zakynthos/Ionian Islands/7.9 (also known as Zante) | 20.900 | 37.783 |
| Site Number | Hg,t,Hay/ρg,all skies | Hg,t,Hay/ρg,clear skies |
|---|---|---|
| 1 | 2505 | 2141 |
| 2 | 2305 | 1906 |
| 3 | 2406 | 2027 |
| 4 | 2515 | 2171 |
| 5 | 2554 | 2202 |
| 6 | 2548 | 2228 |
| 7 | 2379 | 2032 |
| 8 | 2272 | 1856 |
| 9 | 2415 | 2039 |
| 10 | 2504 | 2181 |
| 11 | 2269 | 1806 |
| 12 | 2528 | 2177 |
| 13 | 2526 | 2175 |
| 14 | 2558 | 2211 |
| 15 | 2878 | 2617 |
| 16 | 2388 | 1963 |
| 17 | 2330 | 1927 |
| 18 | 2640 | 2311 |
| 19 | 2588 | 2130 |
| 20 | 2571 | 2235 |
| 21 | 2425 | 2070 |
| 22 | 2336 | 1941 |
| 23 | 2488 | 2194 |
| 24 | 2422 | 2094 |
| 25 | 2473 | 2131 |
| 26 | 2278 | 1921 |
| 27 | 2641 | 2288 |
| 28 | 2514 | 2182 |
| 29 | 2266 | 1868 |
| 30 | 2583 | 2274 |
| 31 | 2486 | 2141 |
| 32 | 2299 | 1916 |
| 33 | 2552 | 2203 |
| 34 | 2247 | 1831 |
| 35 | 2553 | 2207 |
| 36 | 2502 | 2177 |
| 37 | 2438 | 2075 |
| 38 | 2525 | 2191 |
| 39 | 2567 | 2227 |
| 40 | 2425 | 2093 |
| 41 | 2623 | 2280 |
| 42 | 2419 | 2031 |
| 43 | 2506 | 2177 |
| Sum | 106,245 | 90,848 |
| Average | 2471 | 2113 |
| Standard deviation (σ) | 127 | 157 |
| Average + 1σ | 2598 | 2270 |
| Average − 1σ | 2344 | 1956 |
| R2 | Regression Equation | Time Scale, Sky Conditions |
|---|---|---|
| 0.9863 | Hg,t,Hay/ρg = −0.0033t6 + 0.1485t5 − 2.3671t4 + 15.9147t3 − 44.9313t2 + 76.8700t + 81.1407 | months, all |
| 1 | Hg,t,Hay/ρg = −917.6945t3 + 2542.8111t2 − 1084.9270t + 132.6128 | seasons, all |
| 0.9818 | Hg,t,Hay/ρg = −0.0072t6 + 0.3158t5 − 5.0788t4 + 36.7942t3 − 121.8914t2 + 198.4854t − 13.8347 | months, clear |
| 1 | Hg,t,Hay/ρg = −1325.2487t3 + 2988.9232t2 − 1262.3960t + 153.9639 | seasons, clear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kambezidis, H.D.; Mimidis, K.; Kavadias, K.A. The Solar Energy Potential of Greece for Flat-Plate Solar Panels Mounted on Double-Axis Systems. Energies 2023, 16, 5067. https://doi.org/10.3390/en16135067
Kambezidis HD, Mimidis K, Kavadias KA. The Solar Energy Potential of Greece for Flat-Plate Solar Panels Mounted on Double-Axis Systems. Energies. 2023; 16(13):5067. https://doi.org/10.3390/en16135067
Chicago/Turabian StyleKambezidis, Harry D., Konstantinos Mimidis, and Kosmas A. Kavadias. 2023. "The Solar Energy Potential of Greece for Flat-Plate Solar Panels Mounted on Double-Axis Systems" Energies 16, no. 13: 5067. https://doi.org/10.3390/en16135067
APA StyleKambezidis, H. D., Mimidis, K., & Kavadias, K. A. (2023). The Solar Energy Potential of Greece for Flat-Plate Solar Panels Mounted on Double-Axis Systems. Energies, 16(13), 5067. https://doi.org/10.3390/en16135067









