Non-Intrusive Load Identification Method Based on KPCA-IGWO-RF
Abstract
1. Introduction
2. Load Identification Model
2.1. Kernel Principal Component Analysis
2.2. Improved Grey Wolf Optimizer
2.3. Random Forest
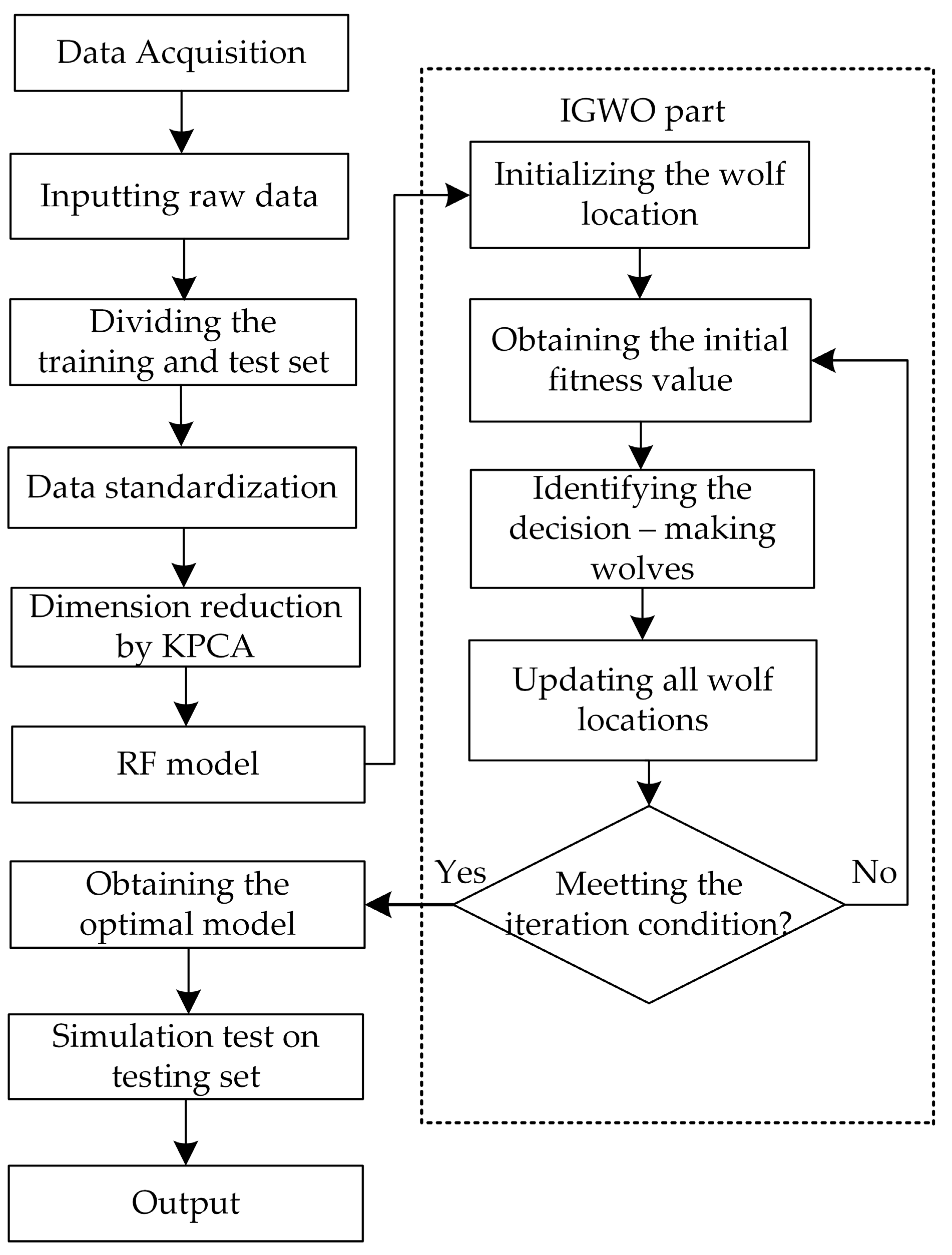
2.4. KPCA-IGWO-RF Load Identification Model Flow
3. Experimental Verification
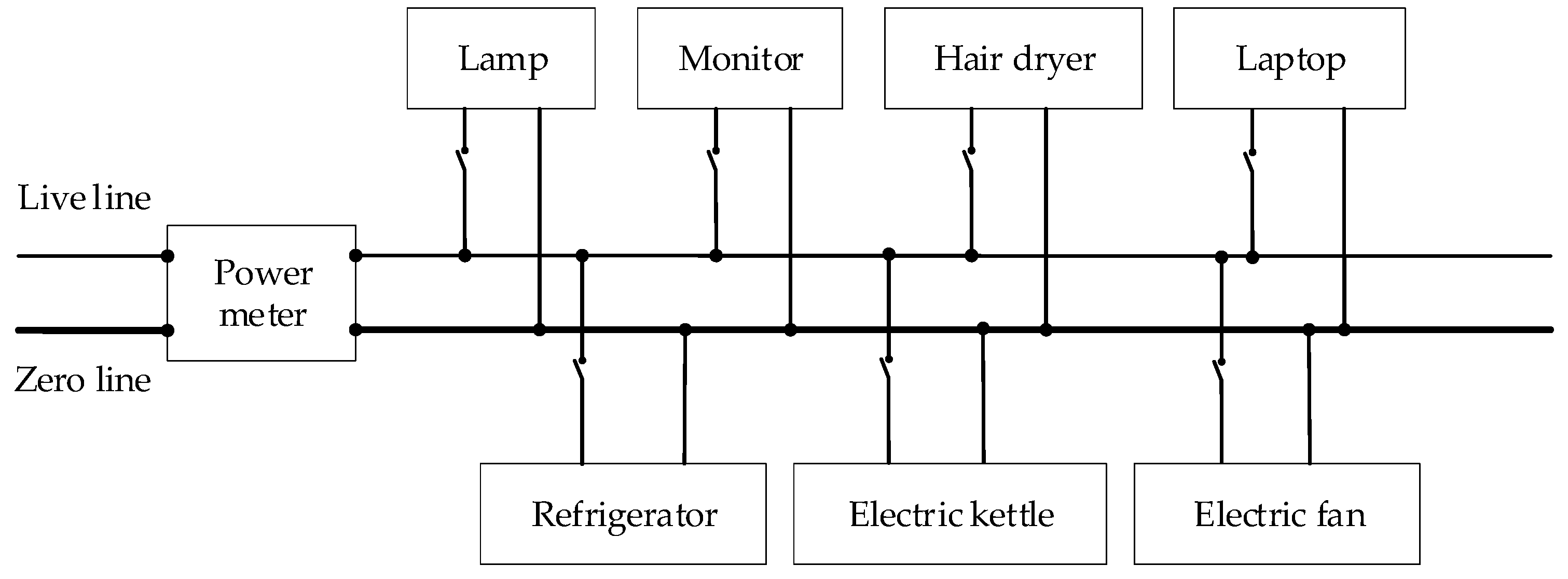
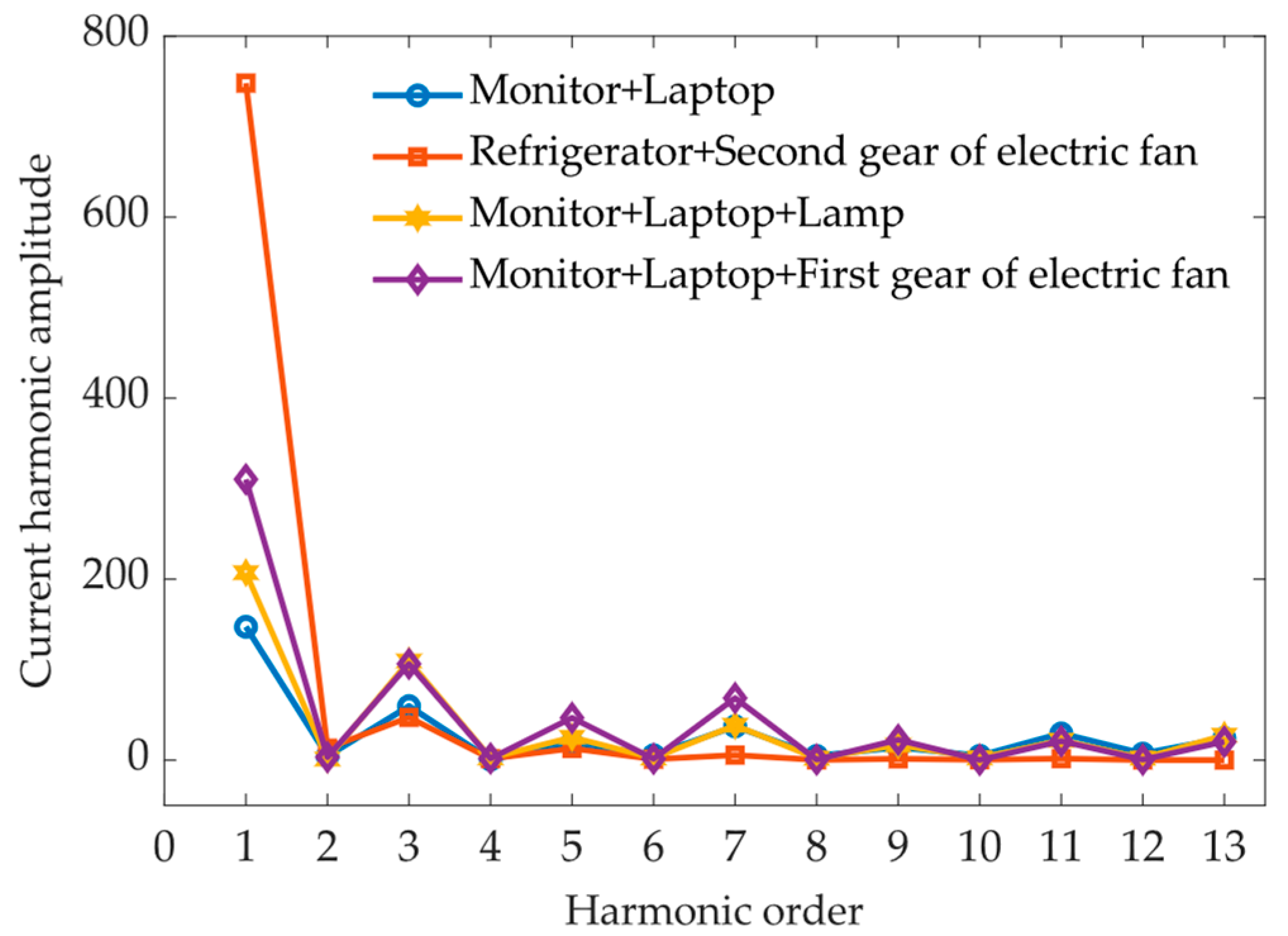
3.1. Data Acquisition and Identification Feature Selection
3.2. Principal Component Extraction Based on KPCA
3.3. Load Identification Evaluation Index
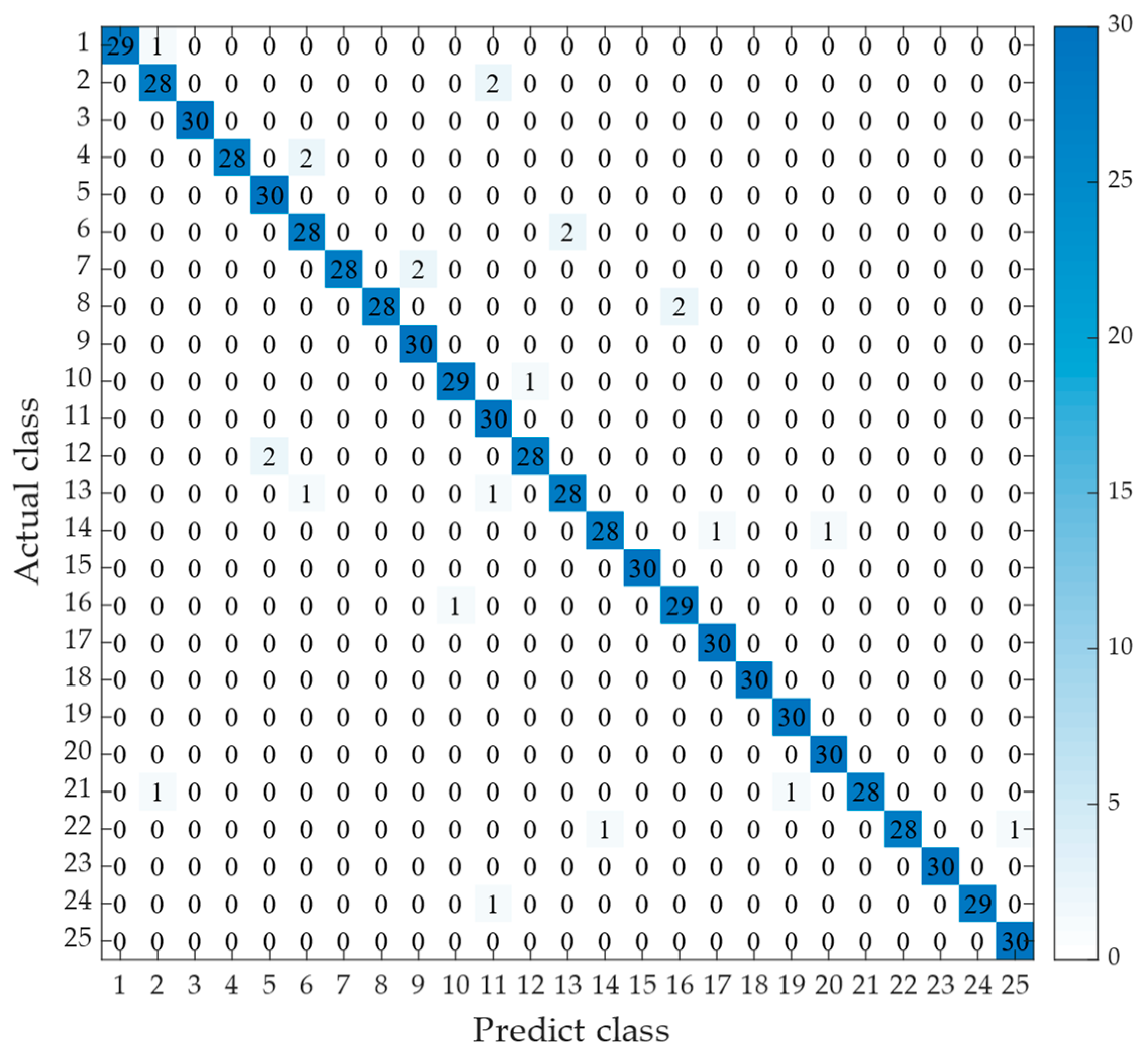
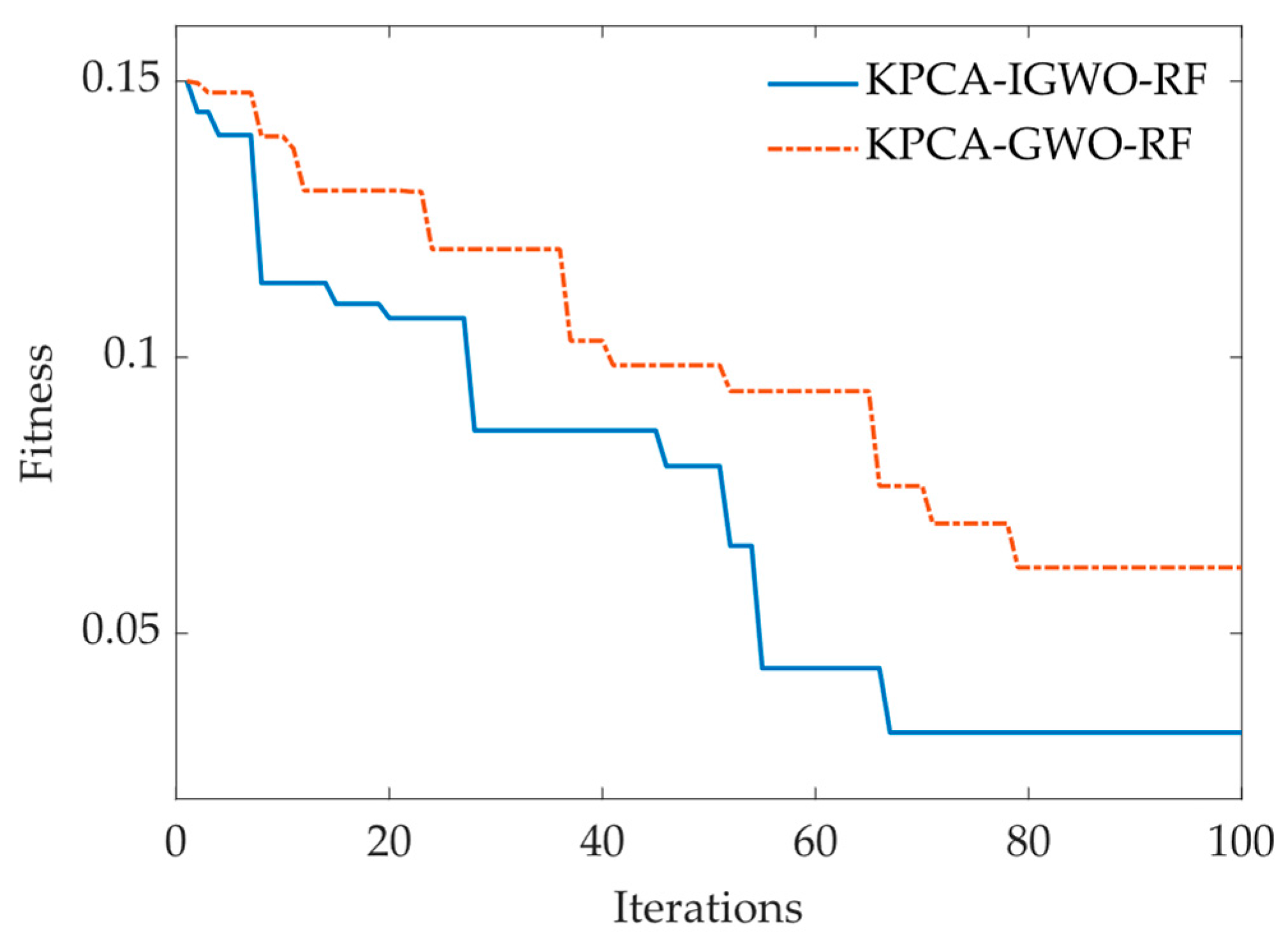
3.4. Test of KPCA-IGWO-RF Load Identification Model
3.5. In Comparison to Other Existing Approaches
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhuang, D.; Gan, V.J.; Tekler, Z.D.; Chong, A.; Tian, S.; Shi, X. Data-driven predictive control for smart HVAC system in IoT-integrated buildings with time-series forecasting and reinforcement learning. Appl. Energy 2023, 338, 120936. [Google Scholar] [CrossRef]
- Tekler, Z.D.; Low, R.; Yuen, C.; Blessing, L. Plug-Mate: An IoT-based occupancy-driven plug load management system in smart buildings. Build. Environ. 2022, 223, 109472. [Google Scholar] [CrossRef]
- Schrenk, M.; Wasserburger, W.W.; Mušič, B.; Dörrzapf, L. SUNSHINE: Smart UrbaN ServIces for Higher eNergy Efficiency. In Proceedings of the GI_Forum, Rome, Italy, 20–23 May 2013; pp. 18–24. [Google Scholar]
- Athanasiadis, C.; Doukas, D.; Papadopoulos, T.; Chrysopoulos, A. A scalable real-time non-intrusive load monitoring system for the estimation of household appliance power consumption. Energies 2021, 14, 767. [Google Scholar] [CrossRef]
- Tekler, Z.D.; Low, R.; Zhou, Y.; Yuen, C.; Blessing, L.; Spanos, C. Near-real-time plug load identification using low-frequency power data in office spaces: Experiments and applications. Appl. Energy 2020, 275, 115391. [Google Scholar] [CrossRef]
- Hart, G.W. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Kamat, S.P. Fuzzy logic based pattern recognition technique for non-intrusive load monitoring. In Proceedings of the 2004 IEEE Region 10 Conference TENCON 2004, Chiang Mai, Thailand, 24 November 2004; pp. 528–530. [Google Scholar]
- Bonfigli, R.; Principi, E.; Fagiani, M.; Severini, M.; Squartini, S.; Piazza, F. Non-intrusive load monitoring by using active and reactive power in additive Factorial Hidden Markov Models. Appl. Energy 2017, 208, 1590–1607. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, C.; Peng, W.; Liu, W.; Zhang, H. Non-intrusive load monitoring using factorial hidden markov model based on adaptive density peak clustering. Energy Build. 2021, 244, 111025. [Google Scholar] [CrossRef]
- Kosuke, S.; Shinkichi, I.; Tatsuya, S.; Hisahide, N.; Koichi, I. Nonintrusive appliance load monitoring based on integer programming. In Proceedings of the 2008 SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; pp. 2742–2747. [Google Scholar]
- Hassan, T.; Javed, F.; Arshad, N. An empirical investigation of VI trajectory based load signatures for non-intrusive load monitoring. IEEE Trans. Smart Grid 2013, 5, 870–878. [Google Scholar] [CrossRef]
- Gillis, J.M.; Morsi, W.G. Non-intrusive load monitoring using semi-supervised machine learning and wavelet design. IEEE Trans. Smart Grid 2016, 8, 2648–2655. [Google Scholar] [CrossRef]
- Huang, L.; Chen, S.; Ling, Z.; Cui, Y.; Wang, Q. Non-invasive load identification based on LSTM-BP neural network. Energy Rep. 2021, 7, 485–492. [Google Scholar] [CrossRef]
- Fang, Y.; Jiang, S.; Fang, S.; Gong, Z.; Xia, M.; Zhang, X. Non-Intrusive Load Disaggregation Based on a Feature Reused Long Short-Term Memory Multiple Output Network. Buildings 2022, 12, 1048. [Google Scholar] [CrossRef]
- Popescu, F.; Enache, F.; Vizitiu, I.; Ciotîrnae, P. Recurrence Plot Analysis for characterization of appliance load signature. In Proceedings of the 2014 10th International Conference on Communications (COMM), Bucharest, Romania, 29–31 May 2014; pp. 1–4. [Google Scholar]
- Zhou, Y.; Sun, M.; Li, P.; Cui, W.; Liu, R.; Zheng, Z.; Jing, Z.; Zhu, H. Research on non-invasive load monitoring based on convolutional neural network. In Proceedings of the 2022 4th International Conference on Communications, Information System and Computer Engineering (CISCE), Shenzhen, China, 27–29 May 2022; pp. 472–477. [Google Scholar]
- Dufour, L.; Genoud, D.; Jara, A.; Treboux, J.; Ladevie, B.; Bezian, J. A non-intrusive model to predict the exible energy in a residential building. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), New Orleans, LA, USA, 9–12 March 2015; pp. 69–74. [Google Scholar]
- Blanchard, G.; Bousquet, O.; Zwald, L. Statistical properties of kernel principal component analysis. Mach. Learn. 2007, 66, 259–294. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Tekler, Z.D.; Chong, A. Occupancy prediction using deep learning approaches across multiple space types: A minimum sensing strategy. Build. Environ. 2022, 226, 109689. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Guo, Q. Modified whale optimization algorithm based on tent chaotic mapping and its application in structural optimization. KSCE J. Civ. Eng. 2020, 24, 3703–3713. [Google Scholar] [CrossRef]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef]
- Paul, A.; Mukherjee, D.P.; Das, P.; Gangopadhyay, A.; Chintha, A.R.; Kundu, S. Improved random forest for classification. IEEE Trans. Image Process. 2018, 27, 4012–4024. [Google Scholar] [CrossRef]
- Wan, T.; Jun, H.U.; Zhang, H.; Pan, W.U.; Hua, H.E. Kappa coefficient: A popular measure of rater agreement. Shanghai Arch. Psychiatry 2015, 27, 62–67. [Google Scholar]
- Tao, P.; Liu, X.; Zhang, Y.; Li, C.; Ding, J. Multi-level non-intrusive load identification based on k-NN. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 1905–1910. [Google Scholar]
- Low, R.; Tekler, Z.D.; Cheah, L. An end-to-end point of interest (POI) conflation framework. ISPRS Int. J. Geo-Inf. 2021, 10, 779. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]



| One Load | Two Loads | Three Loads | |||
|---|---|---|---|---|---|
| Condition | Label | Condition | Label | Condition | Label |
| L1 | 1 | L1 + L2 | 11 | L1 + L2 + L3 | 19 |
| L2 | 2 | L2 + L5 | 12 | L1 + L2 + L5 | 20 |
| L3 | 3 | L5 + L2 | 13 | L1 + L2 + L9 | 21 |
| L4 | 4 | L3 + L8 | 14 | L2 + L3 + L4 | 22 |
| L5 | 5 | L5 + L7 | 15 | L3 + L4 + L8 | 23 |
| L6 | 6 | L6 + L9 | 16 | L4 + L2 + L9 | 24 |
| L7 | 7 | L8 + L10 | 17 | L2 + L5 + L7 | 25 |
| L8 | 8 | L8 + L9 | 18 | ||
| L9 | 9 | ||||
| L10 | 10 | ||||
| Model | Accuracy/% | ||||
|---|---|---|---|---|---|
| One Load | Two Loads | Three Loads | Overall | Kappa | |
| RF | 73.6667 | 76.6667 | 78.5714 | 76 | 0.75 |
| KPCA-RF | 85 | 95.8333 | 80.4762 | 85 | 0.8667 |
| KPCA-GWO-RF | 90.3333 | 95 | 94.2857 | 93.8095 | 0.925 |
| KPCA-IGWO-RF | 96 | 97.0833 | 97.6190 | 96.8 | 0.9667 |
| Model | Accuracy/% | ||||
|---|---|---|---|---|---|
| One Load | Two Loads | Three Loads | Overall | Kappa | |
| LSTM-BP | 94 | 96.6667 | 90.9524 | 94 | 0.9375 |
| SVM | 93.6667 | 96.6667 | 81.4286 | 91.2 | 0.9083 |
| k-NN | 90.3333 | 93.75 | 88.5714 | 92.1333 | 0.9181 |
| KPCA-IGWO-RF | 96 | 97.0833 | 97.6190 | 96.8 | 0.9667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Yuan, G.; Hu, K.; Liu, C.; Wu, M. Non-Intrusive Load Identification Method Based on KPCA-IGWO-RF. Energies 2023, 16, 4805. https://doi.org/10.3390/en16124805
Hu S, Yuan G, Hu K, Liu C, Wu M. Non-Intrusive Load Identification Method Based on KPCA-IGWO-RF. Energies. 2023; 16(12):4805. https://doi.org/10.3390/en16124805
Chicago/Turabian StyleHu, Sheng, Gongjin Yuan, Kaifeng Hu, Cong Liu, and Minghu Wu. 2023. "Non-Intrusive Load Identification Method Based on KPCA-IGWO-RF" Energies 16, no. 12: 4805. https://doi.org/10.3390/en16124805
APA StyleHu, S., Yuan, G., Hu, K., Liu, C., & Wu, M. (2023). Non-Intrusive Load Identification Method Based on KPCA-IGWO-RF. Energies, 16(12), 4805. https://doi.org/10.3390/en16124805






