Passivity-Based Control and Current Balance Control of a Current-Source Pulse-Width-Modulation Rectifier
Abstract
1. Introduction
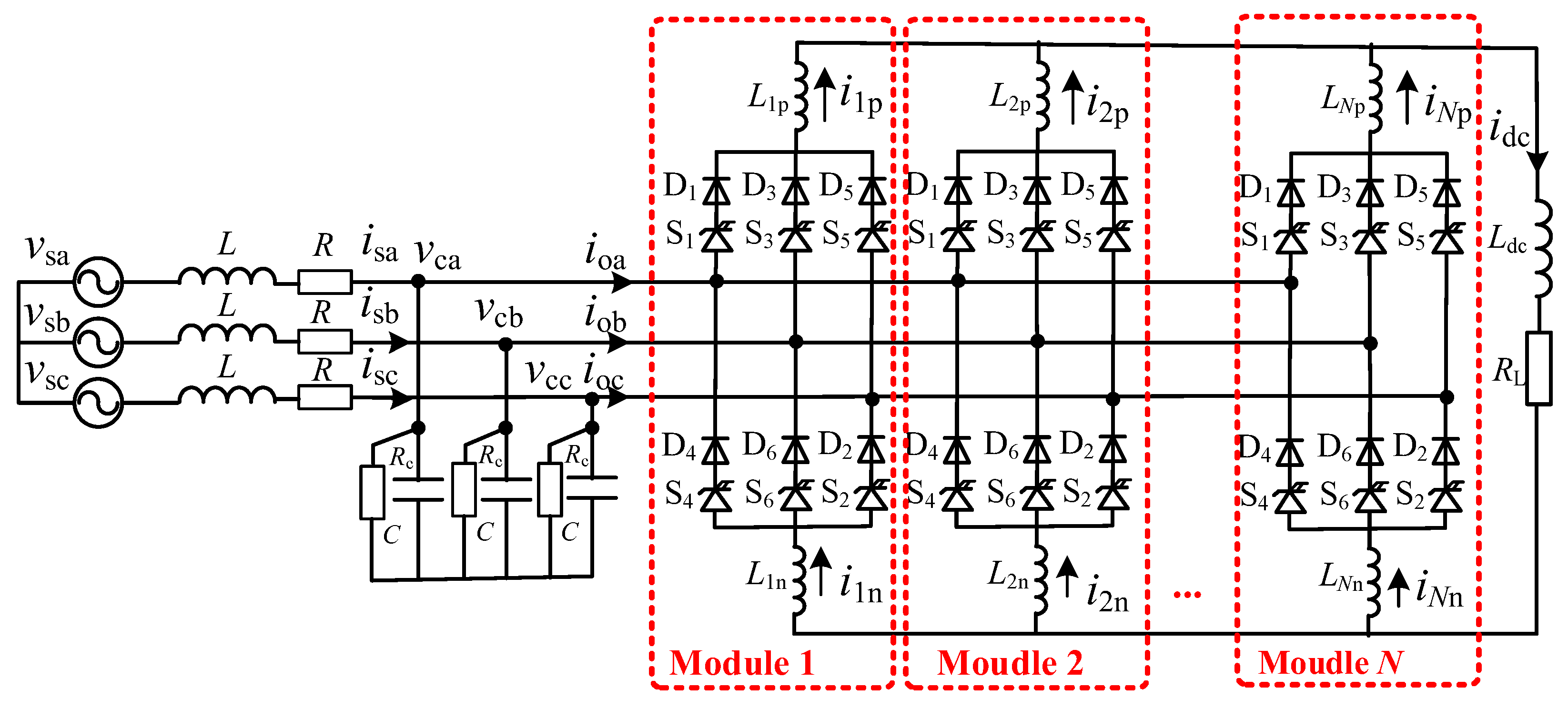
2. Current-Source PWM Rectifier with Multiple Modules
3. Mathematical Model and Controller Design
3.1. EL Mathematical Model
3.2. Passive Analysis
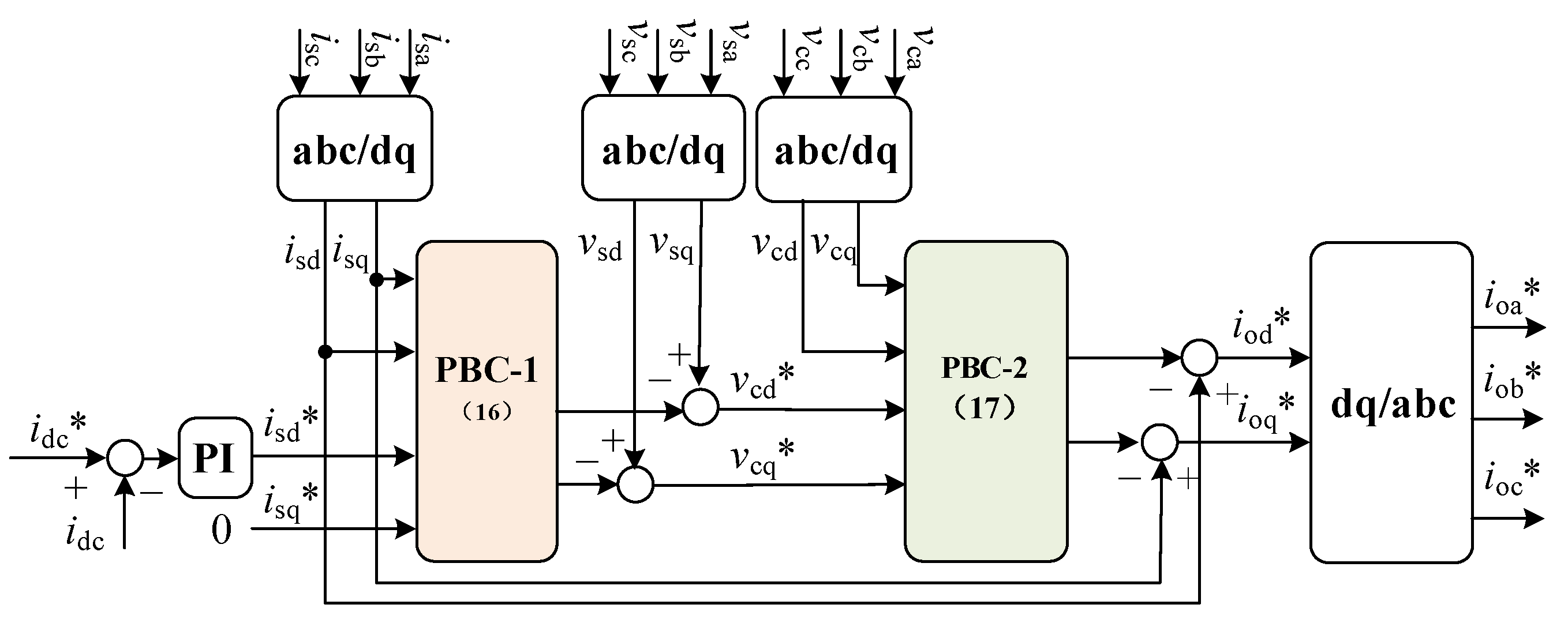
3.3. Passivity-Based Controller Design
4. Current Balance Control
- (1)
- Generate module current references:
- (2)
- Obtain the sector of the current reference vector:
- (3)
- Select the current subvector combination:
- (4)
- Calculate the number of subvectors:
- (5)
- Assign current subvectors to the odd sector:
- (6)
- Assign current subvectors to the even sector:
5. Simulation Verification
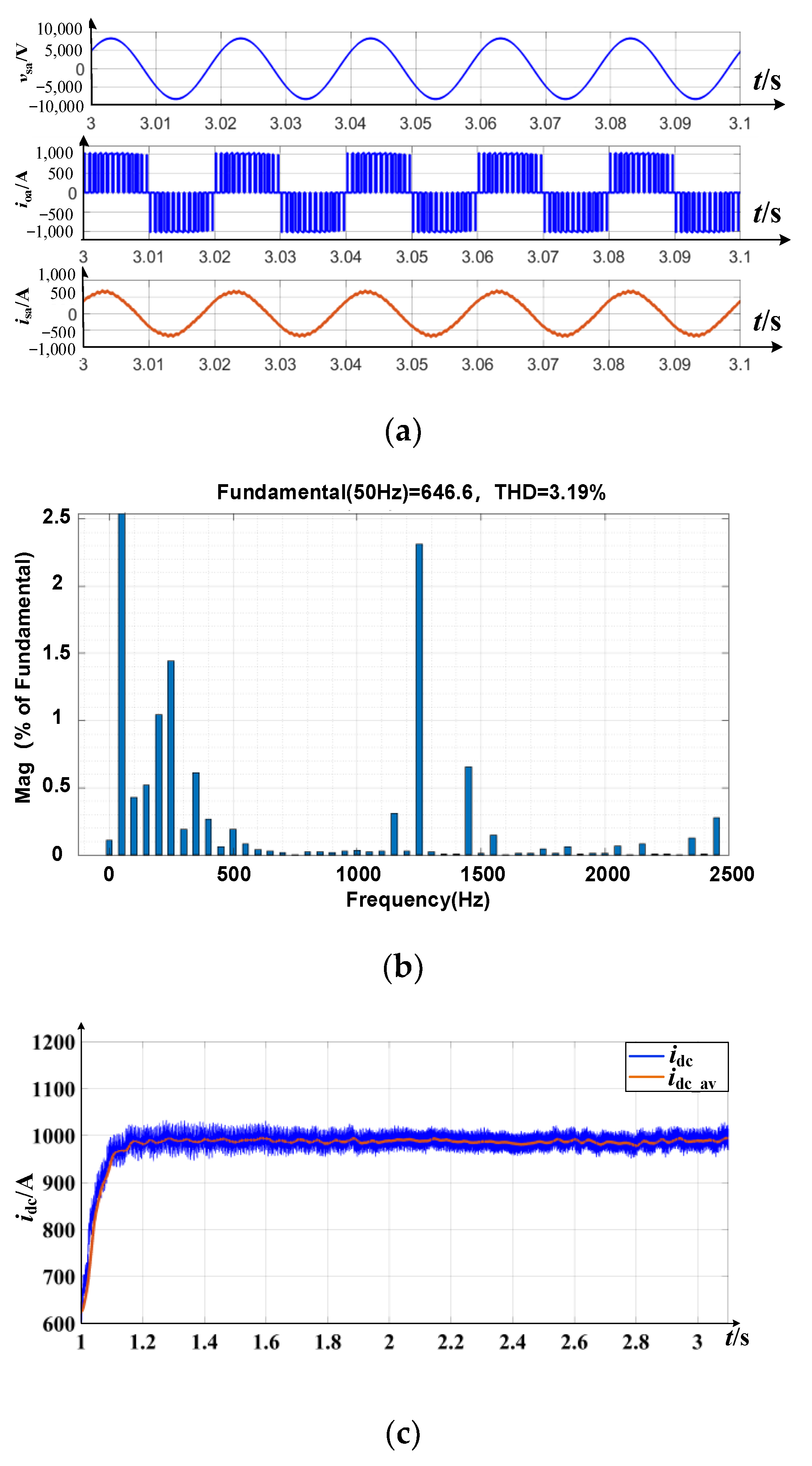
5.1. PBC Control Simulation
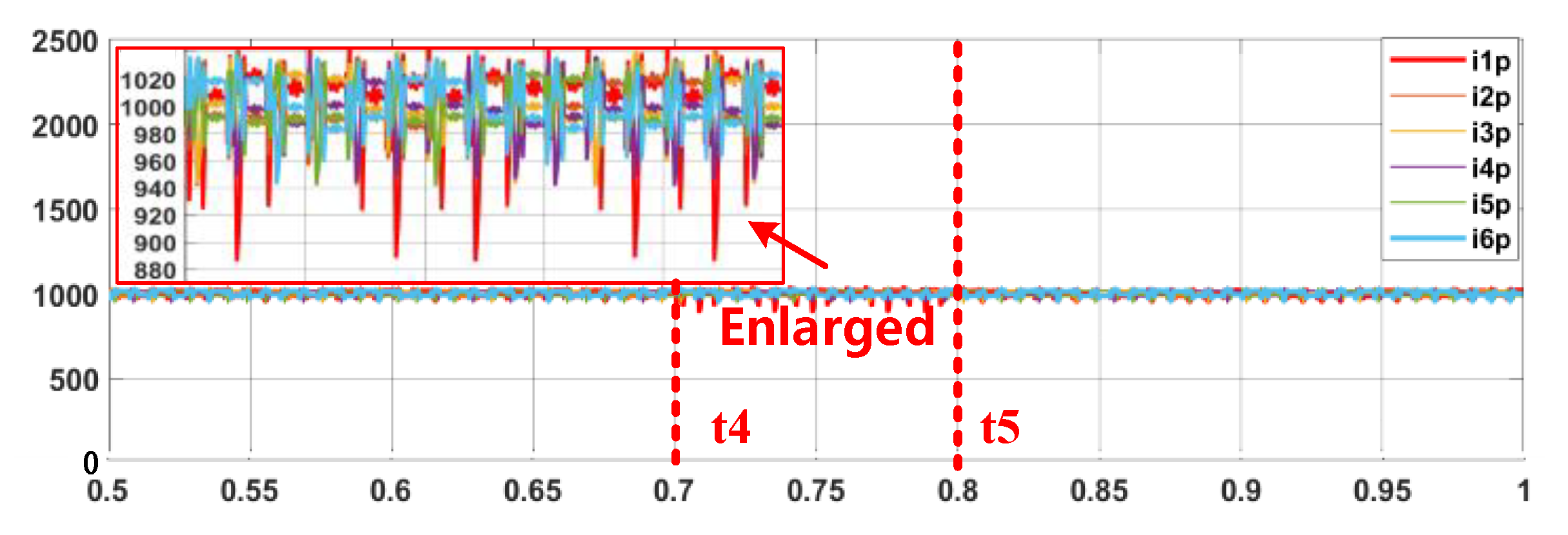
5.2. Current Balance Control Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, W.; Jiang, Q.; Hu, M.; Tang, G.Q.; Jiang, P. Mathematical model and main circuit design of three-phase voltage-source PWM rectifier. J. Southeast Univ. (Nat. Sci. Ed.) 2002, 32, 50–55. [Google Scholar]
- Xianping, Z.; Yaxi, L.; Lei, P. Analysis and design of LCL type filter for three-phase voltage source rectifier. Electrotech. Appl. 2007, 26, 65–68. [Google Scholar]
- Yao, W.Z.; Wang, Z.A. Research on three-phase large capacity PWM rectifier. J. Hunan Inst. Eng. 2001, 11, 1–4. [Google Scholar]
- Xu, K.; Ma, X.; Rao, C. Research and comparison of DC deicing technologies based on full bridge MMC and thyristor rectifier. South. Power Syst. Technol. 2020, 14, 45–53. [Google Scholar]
- Zhang, W.J. Current Source PWM Rectifier and Its Application in Induction Heating. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2007. [Google Scholar]
- Popat, M.; Wu, B.; Zargari, N.R. A novel decoupled interconnecting method for current-source converter-based offshore wind farms. IEEE Trans. Power Electron. 2012, 27, 4224–4233. [Google Scholar] [CrossRef]
- Zhu, N.; Xu, D.; Wu, B.; Zargari, N.R.; Kazerani, M.; Liu, F. Common-mode voltage reduction methods for current-source converters in medium-voltage drives. IEEE Trans. Power Electron. 2013, 28, 995–1006. [Google Scholar] [CrossRef]
- Burgos, R.P.; Wiechmann, E.P.; Holtz, J. Complex state-space modeling and nonlinear control of active front-end converters. IEEE Trans. Ind. Electron. 2005, 52, 363–377. [Google Scholar] [CrossRef]
- Liu, W.H.; Hu, Y.C.; Liu, B.; Wang, Z.H. IGCT and IEGT- new high power silicon switches suitable for STATCOM. Autom. Electr. Power Syst. 2000, 23, 66–70. [Google Scholar]
- Liu, W.H.; Song, Q.; Yan, G.G. Medium voltage drive with NPC three-level inverter using IGCTs. Autom. Electr. Power Syst. 2002, 26, 61–65. [Google Scholar]
- Espinoza, J.R.; Joos, G. State variable decoupling and power flow control in PWM current-source rectifiers. IEEE Trans. Ind. Electron. 1998, 45, 78–87. [Google Scholar] [CrossRef]
- Liu, Y.H.; Watson, N.R.; Zhou, K.L.; Yang, B.F. Converter system nonlinear modelling and control for transmission applications-Part II: CSC systems. IEEE Trans. Power Deliv. 2013, 28, 1391–1401. [Google Scholar] [CrossRef]
- Zhu, X.R. Research on Current Source PWM Rectifier and Its Nonlinear Control Strategy. Ph.D. Thesis, North China Electric Power University, Baoding, China, 2009. [Google Scholar]
- Wu, K.; Li, Y.; Lin, P.; Wu, K.Z.; Zhang, W.J. Current source PWM rectifier based on indirect current control. Proc. CSU-EPSA 2008, 20, 62–65. [Google Scholar]
- Hiti, S.; Vlatkovic, V.; Borojevic, D.; Lee, F. A new control algorithm for three-phase PWM buck rectifier with input displacement factor compensation. IEEE Trans. Power Electron. 1994, 9, 173–180. [Google Scholar] [CrossRef]
- Liu, H.P.; Qiu, B.B.; Peng, D.L.; Ren, F.; Guo, Q.; Zheng, Q. Improvement strategy for indirect current control of current source pulse width modulation rectifier. Power Syst. Technol. 2012, 36, 182–187. [Google Scholar]
- Sato, Y.; Kataoka, T. State feedback control of current type PWM AC-to-DC converters. IEEE Trans. Ind. Appl. 1993, 29, 1090–1097. [Google Scholar] [CrossRef]
- Wang, X.; Ooi, B. Real-time multi-DSP control of three-phase current-source unity power factor PWM rectifier. IEEE Trans. Power Electron. 1993, 8, 295–300. [Google Scholar] [CrossRef]
- Zargari, N.; Joos, G. An on-line operated near unity power factor PWM rectifier with minimum control requirements. In Proceedings of the 20th Annual Conference of IEEE Industrial Electronics, Bologna, Italy, 5–9 September 1994; pp. 593–598. [Google Scholar]
- Jin, T.; Guo, J.; Mohamed, M.A.; Wang, M. A novel model predictive control via optimized vector selection method for common-mode voltage reduction of three-phase inverters. IEEE Access 2019, 7, 95351–95363. [Google Scholar] [CrossRef]
- Jin, T.; Guo, J.; Mohamed, M.A.; Wang, M. An improved three-stages cascading passivity-based control of grid-connected LCL converter in unbalanced weak grid condition. IEEE Access 2021, 9, 89497–89506. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Bai, Z.; Ma, H.; Xu, D.; Wu, B. Control strategy with a generalized DC current balancing method for multimodule current-source converter. IEEE Trans. Power Electron. 2014, 29, 366–373. [Google Scholar] [CrossRef]
- Alakran, F.; Simoes, M.G. Multilevel current source converter-based STATCOM suitable for medium-voltage applications. IEEE Trans. Power Deliv. 2021, 36, 1222–1232. [Google Scholar] [CrossRef]
- Corti, F.; Reatti, A.; Lozito, G.M.; Cardelli, E.; Laudani, A. Influence of non-linearity in losses estimation of magnetic components for DC-DC converters. Energies 2021, 14, 6498. [Google Scholar] [CrossRef]
- Boteler, D.H. Characteristics of time-varying inductance. IEEE Trans. Magn. 1994, 30, 172–176. [Google Scholar] [CrossRef]
- Akbari, M.; Rezaei-Zare, A.; Cheema, M.A.M.; Kalicki, T. Air gap inductance calculation for transformer transient model. IEEE Trans. Power Deliv. 2021, 36, 492–494. [Google Scholar] [CrossRef]
- Corti, F.; Laudani, A.; Lozito, G.M.; Reatti, A. Computationally Efficient Modeling of DC-DC Converters for PV Applications. Energies 2020, 13, 5100. [Google Scholar] [CrossRef]
- Reatti, A.; Balzani, M. PWM switch model of a buck-boost converter operated under discontinuous conduction mode. In Proceedings of the 48th Midwest Symposium on Circuits and Systems, Cincinnati, OH, USA, 7–10 August 2005; pp. 667–670. [Google Scholar]



| Parameter | Value |
|---|---|
| AC voltage Vs/kV | 10 |
| DC current Idc/A | 0–1000 |
| filter inductance L/mH | 3 |
| filter capacitance C/uF | 160 |
| DC inductance Ldc/mH | 40 |
| damping coefficient r11 | 3.00 |
| damping coefficient g11 | 0.11 |
| Number of parallel modules | 6 |
| Positive and negative inductance Lp, Ln/mH | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, H.; Li, J.; Yang, Q.; Xu, K.; Ma, X.; Zhao, B. Passivity-Based Control and Current Balance Control of a Current-Source Pulse-Width-Modulation Rectifier. Energies 2023, 16, 4682. https://doi.org/10.3390/en16124682
Zeng H, Li J, Yang Q, Xu K, Ma X, Zhao B. Passivity-Based Control and Current Balance Control of a Current-Source Pulse-Width-Modulation Rectifier. Energies. 2023; 16(12):4682. https://doi.org/10.3390/en16124682
Chicago/Turabian StyleZeng, Huarong, Jianguo Li, Qi Yang, Kui Xu, Xiaohong Ma, and Biao Zhao. 2023. "Passivity-Based Control and Current Balance Control of a Current-Source Pulse-Width-Modulation Rectifier" Energies 16, no. 12: 4682. https://doi.org/10.3390/en16124682
APA StyleZeng, H., Li, J., Yang, Q., Xu, K., Ma, X., & Zhao, B. (2023). Passivity-Based Control and Current Balance Control of a Current-Source Pulse-Width-Modulation Rectifier. Energies, 16(12), 4682. https://doi.org/10.3390/en16124682






