A Hybrid Chaotic-Based Multiobjective Differential Evolution Technique for Economic Emission Dispatch Problem
Abstract
1. Introduction
1.1. Research Background
1.2. Related Works
1.3. Main Contributions
- In the EEDP modeling, all operating constraints, such as total system losses and VPLE, POZ, and power balance constraints, are considered. To overcome difficulties caused by the equality constraint describing the power balance constraint, the optimal generation of all thermal units except the slack unit is determined by the suggested optimization technique. The slack unit output will be the gap between the total generation of the other TGUs and the sum of the system load and total power losses. Therefore, more accurate optimal generation can be provided.
- To solve this discontinuous and nonconvex EEDP, an enhanced multiobjective DE algorithm is proposed where both total operating cost and total emissions are simultaneously minimized. In the proposed optimization technique named chaotic map-based multiobjective DE (ChMODE), two different chaotic maps are integrated with the initialization, crossover, and mutation phases of the classical DE to generate chaotic sequences instead of random numbers. Moreover, a nondomination sorting process and crowding distance calculation are added to the proposed algorithm to generate an accurate and well-distributed Pareto front. Unlike weighted sum-based approaches, the proposed multiobjective algorithm can provide the optimal PF in a single run.
- The applicability and robustness of the ChMODE algorithm for solving this problem are tested on various case studies and obtained results are compared with other single-objective and multiobjective techniques recently reported in the literature. The case studies are the six-unit system with quadratic cost and emission functions without considering system losses, the ten-unit system including system losses and VPLE constraints, and the ten-unit system with all operating constraints including system losses, VPLEs, and POZs.
- By investigating the simulation results, it was shown that the proposed method outperformed the other comparison algorithms in terms of stability and accuracy of the results. Moreover, it was shown that using chaotic sequences in the population initialization helped the ChMODE to start from the lowest values for both cost and emission functions compared to the other studied methods. Additionally, statistical results comprising various performance indicators showed that the nondominated solutions obtained by ChMODE are well distributed in the objective space, and its compromise solution has the highest average satisfactory degree of the decision-maker.
1.4. Paper Organization
2. Theoretical Foundation
2.1. Production Cost and Emission Functions
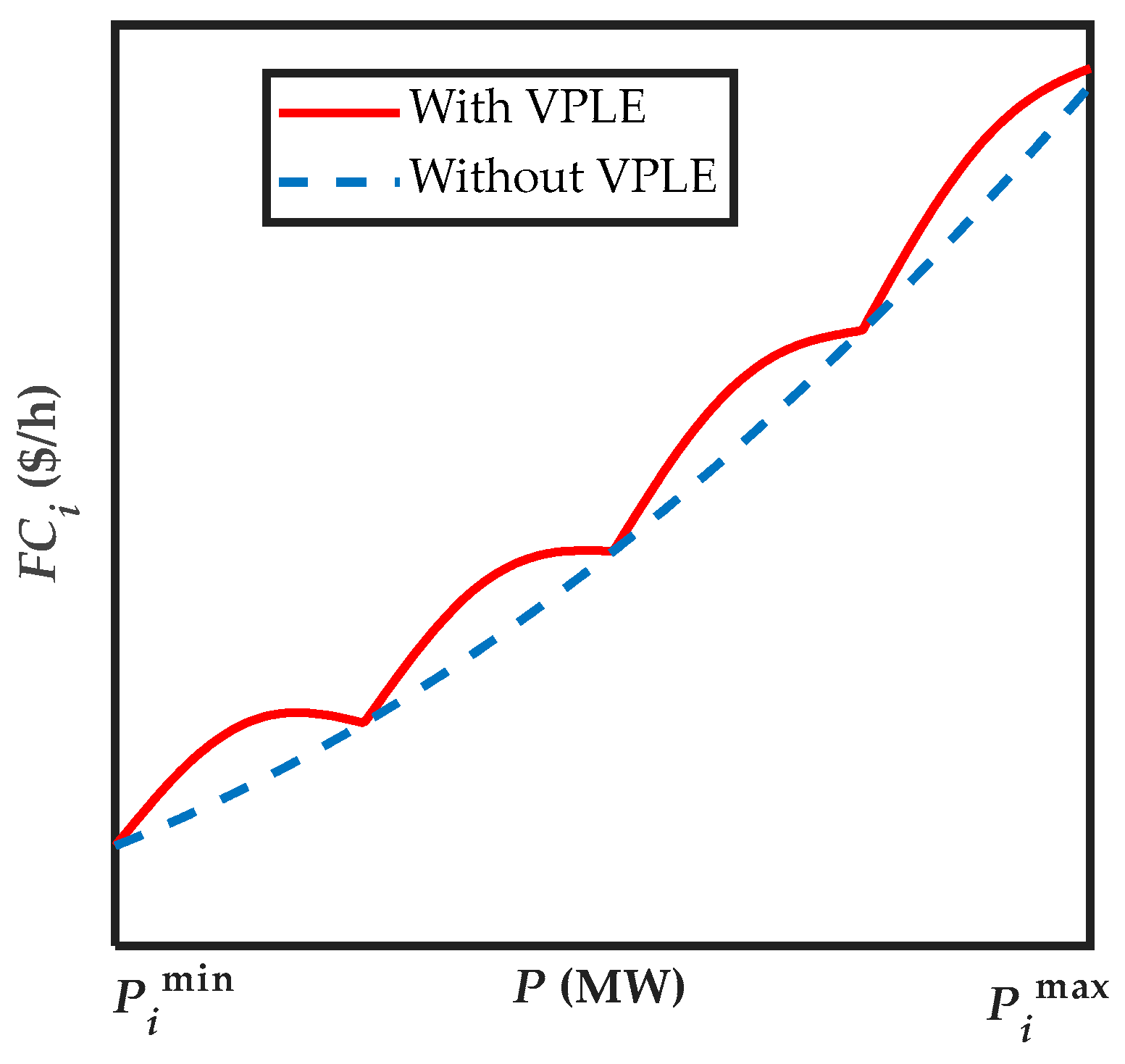
2.2. EEDP Constraints
2.2.1. Power Balance Constraint
| Algorithm 1: Pseudocode for calculation of , and objective functions. |
| 1. Inputs: Power network data Set of optimal solutions (OS) 2. Outputs: Power output of the slack generator (Ps) Transmission power losses (Ptl) Total fuel cost values (TC) Total Emission values (TE) 3. For i = 1 to |OS| do 3.1. Solve Equation (7) 3.2. Find and 3.3. Evaluation of fitness function 3.3.1. If or or then 3.3.2. Else Calculate TC using Equation (1) Calculate TE using Equation (2) 3.3.3. End If 4. End For |
2.2.2. Power Generation Capacity
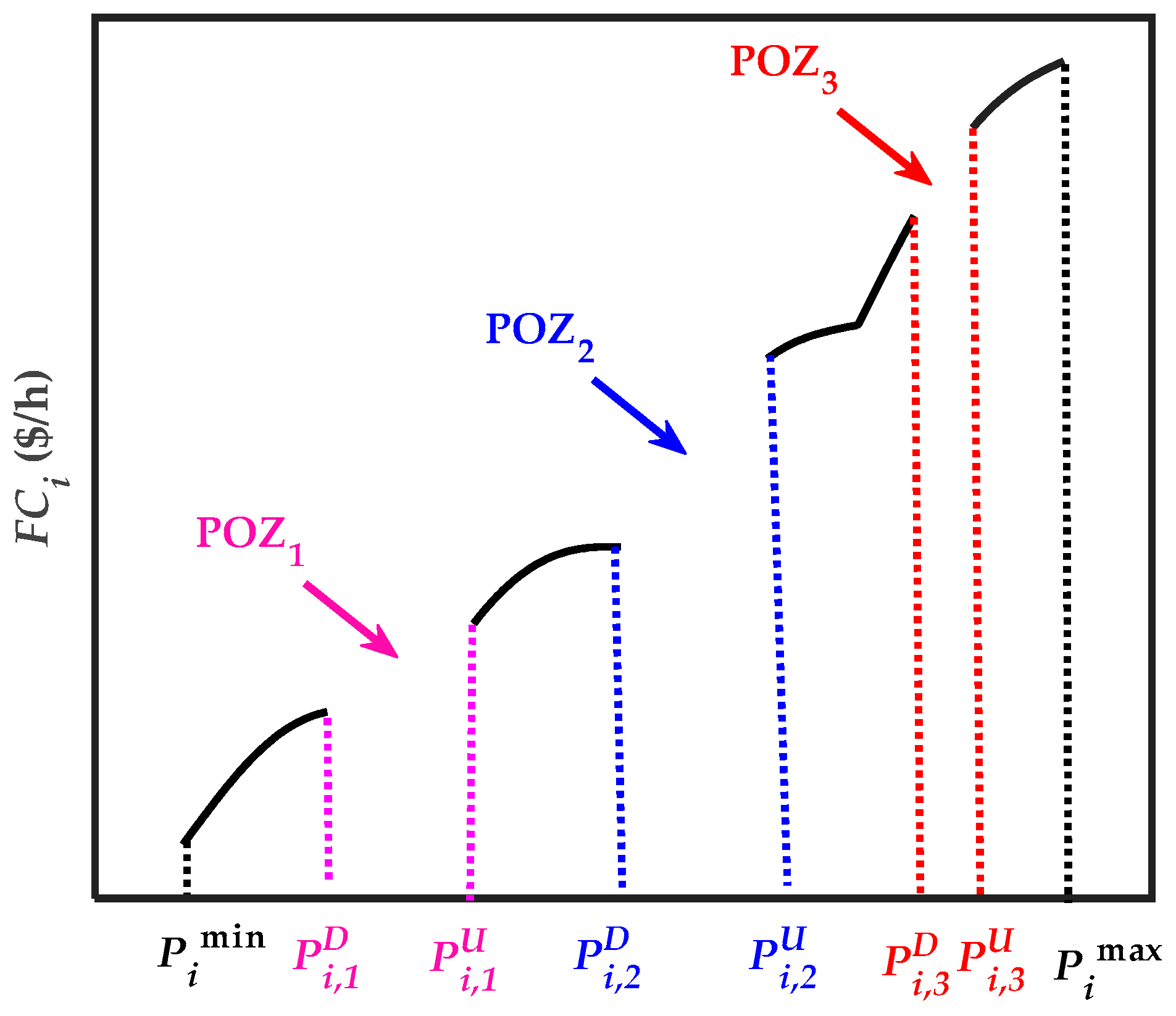
2.2.3. POZ Constraints
3. Proposed Optimization Technique
3.1. The Original DE Algorithm
3.2. Proposed ChMODE Algorithm
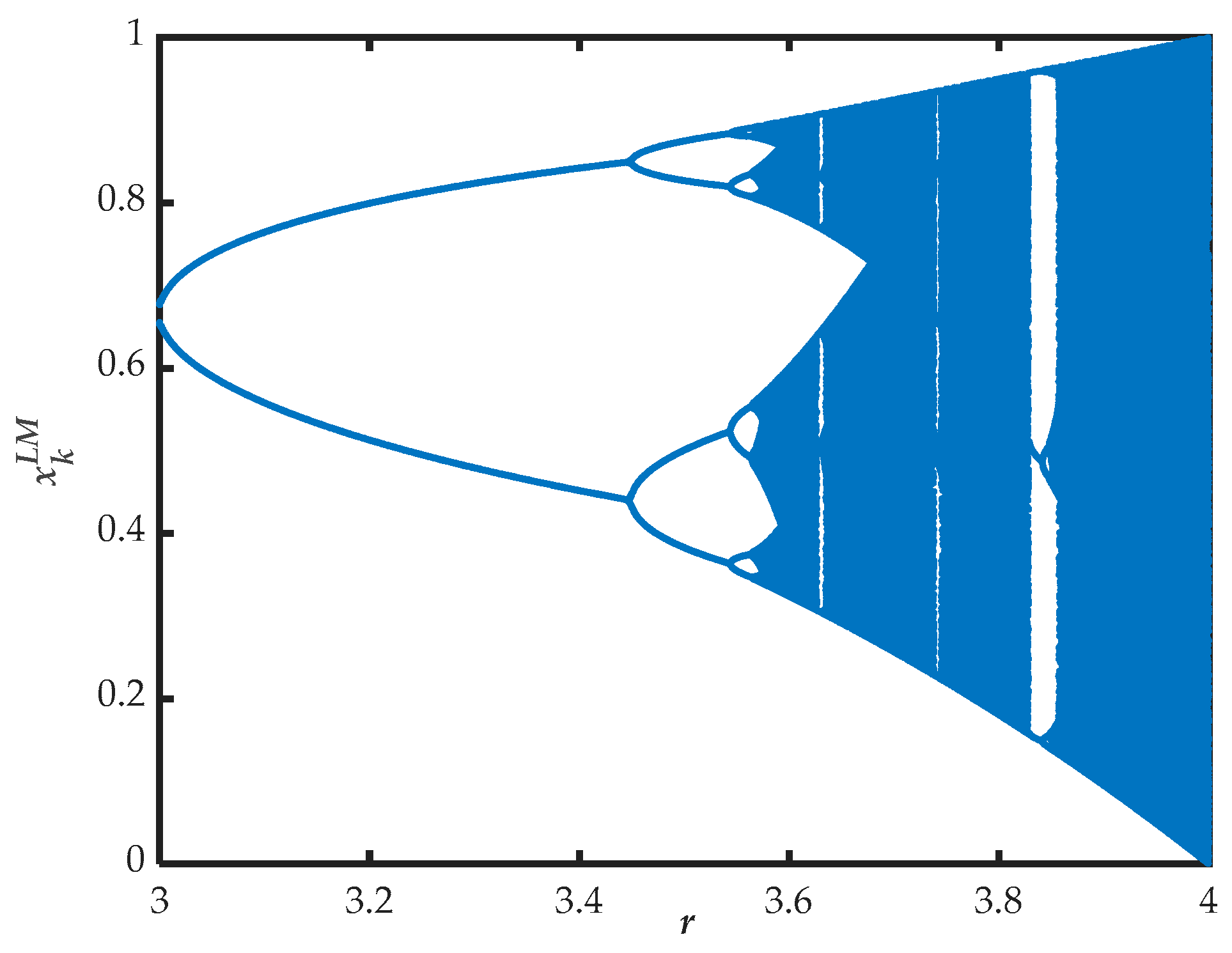
3.2.1. Logistic Map
3.2.2. Lorenz Attractor
3.2.3. NonDomination Sorting
| Algorithm 2: Pseudocode of the generation of a new population. |
| 1. Inputs: Parent population Offspring population 2. Outputs: New population 3. Combine and 4. Apply nondomination sorting of 4.1. 4.2. 4.3. 4.4. While do 4.4.1. 4.4.2. 4.4.3. 4.5. End 5. If do 5.1. Calculate crowding distance of all members of 5.2. Sort according to the crowding distances of its members in ascending order 5.3. 5.4. While do ; is the j-th member of the sorted set 5.5. End While 6. End If |
| Algorithm 3: Pseudocode of the ChMODE for solving the EEDP. |
| 1. Inputs: Power network data DE parameters Chaotic maps parameters 2. Outputs: Optimal power output of thermal units Optimal operating cost Optimal emissions 3. Generation of chaotic sequences 3.1. Generate logistic map sequences 3.2. Generate Lorenz attractor sequences , , and 3.3. Construct matrices , , , and, 4. Population initialization 4.1. For i = 1 to NS do 4.1.1. For k = 1 to D do 4.1.2. End For 4.2. End For 5. Application of mutation, crossover, and selection operators 5.1. While do 5.1.1. 5.1.2. 5.1.3. For i = 1 to do 5.1.3.1. For k = 1 to D do Generate random number 5.1.2.1.1. If do 5.1.2.1.2. Else 5.1.2.1.3. End If 5.1.3.2. End For Evaluate and according to Algorithm 1 5.1.4. End For 5.1.5. Generation of the new population according to Algorithm 2 5.2. End While 6. Print the optimal generation of thermal units |
4. Case Studies and Simulation Results
4.1. Case 1: Six-Unit System
4.2. Case 2: Ten-Unit System without POZs
4.3. Case 3: Test System 2 with POZ Constraints
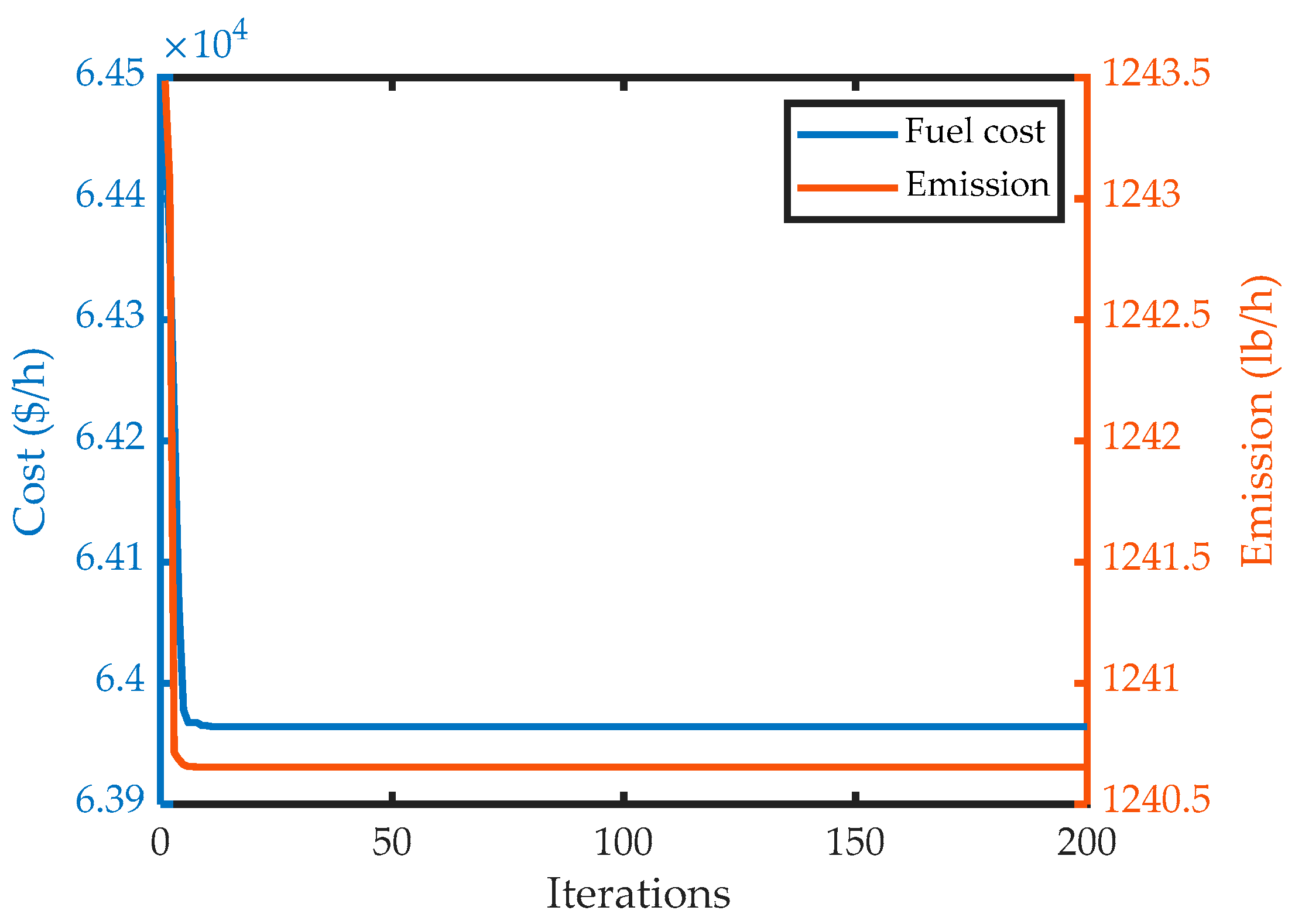
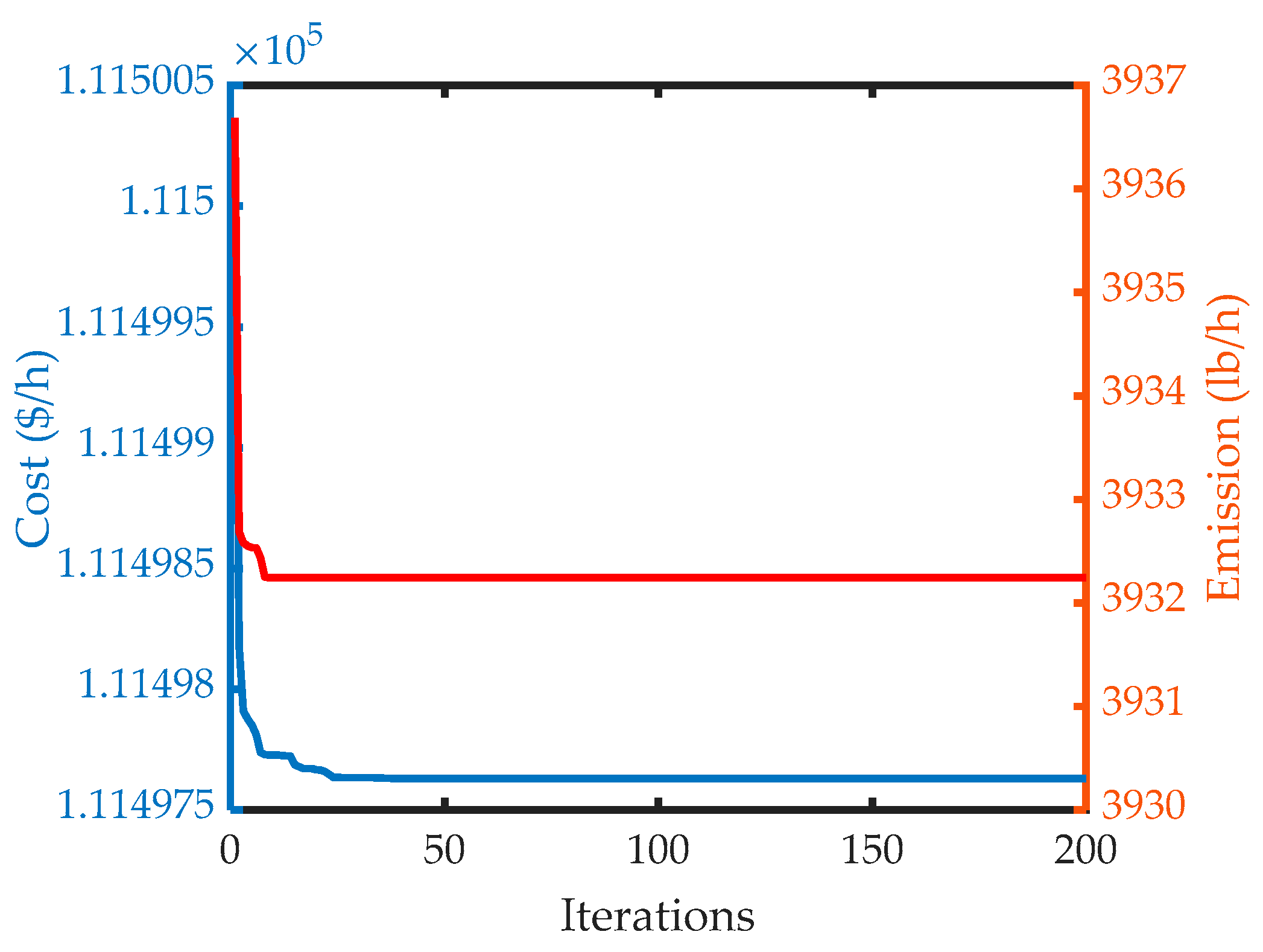
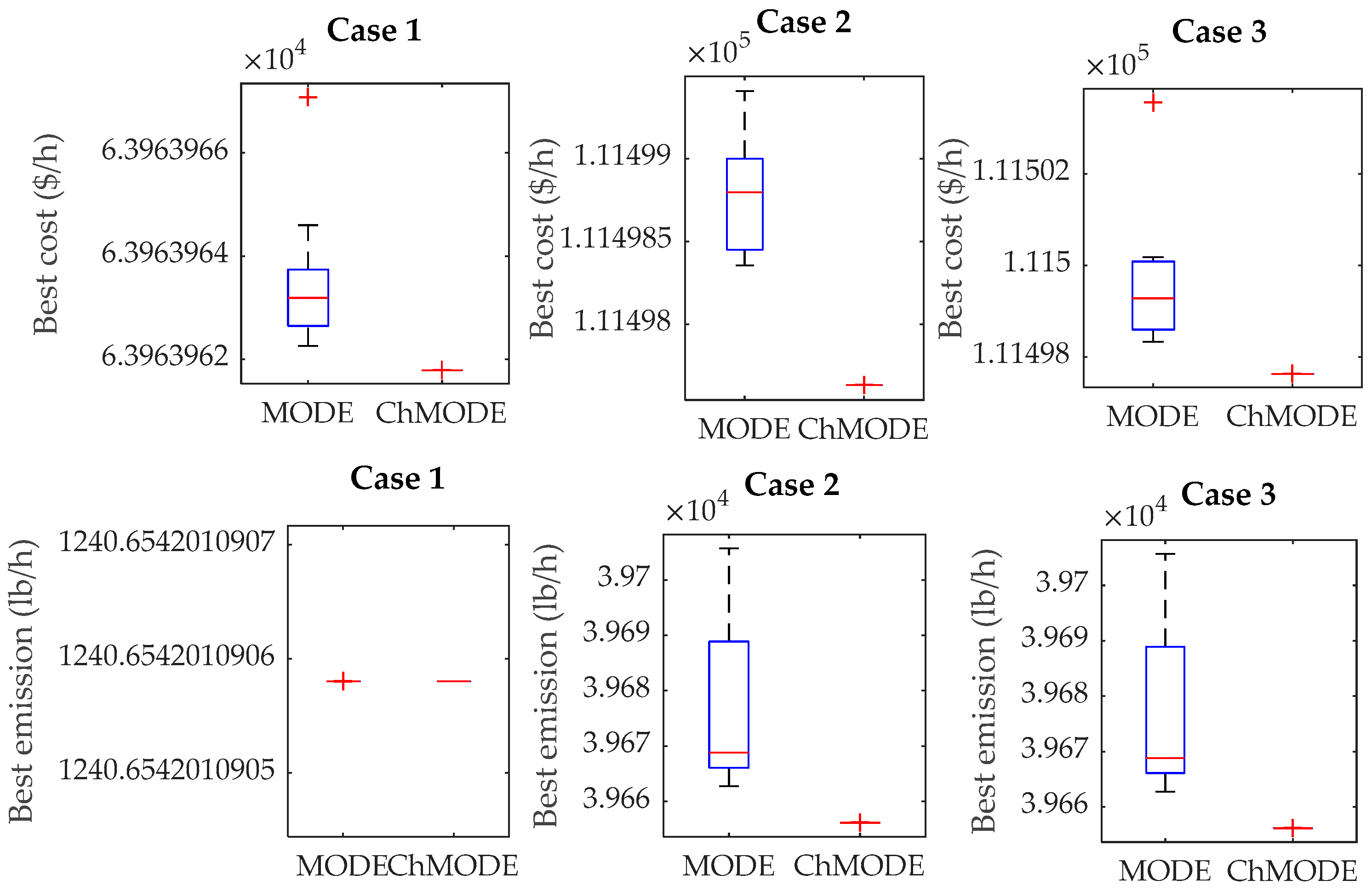
4.4. Robustness Analysis
4.5. Results Discussion and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| TC | Total fuel cost in $/h |
| TE | Total emissions in lb/h |
| Total fuel cost corresponding to the maximum generation | |
| Total emissions corresponding to the maximum generation | |
| Fuel cost of the i-th unit in $/h | |
| Emissions of the i-th unit in lb/h | |
| Generation of the i-th unit in MW | |
| Number of TGUs | |
| Lower and upper limits of generation in MW for the i-th unit, respectively | |
| Total load demand in MW | |
| Total real power losses in MW | |
| The ij-th element of the matrix of the loss coefficients | |
| Down and up limits of the z-th POZ of the i-th TGU | |
| Number of POZs of the i-th TGU | |
| POZi | The i-th POZ of a TGU |
| NS | Population size |
| D | Number of decision variables |
| The i-th solution at the t-th iteration | |
| k-th decision variable of the i-th solution in the initial population | |
| Length of the chaotic sequences generated by the logistic map | |
| Length of the chaotic sequences generated by the Lorenz attractor | |
| Parent population at the t-th iteration | |
| Offspring population at the t-th iteration | |
| Logistic map sequences | |
| Lorenz attractor sequences |
Appendix A
| Units | ai | bi | ci | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 756.80 | 38.5390 | 0.15247 | 13.8593 | 0.32767 | 0.00419 | 125 | 10 |
| 2 | 451.33 | 46.1591 | 0.10587 | 13.8593 | 0.32767 | 0.00419 | 150 | 10 |
| 3 | 1050.00 | 40.3965 | 0.02803 | 40.2669 | −0.54551 | 0.00683 | 225 | 35 |
| 4 | 1243.53 | 38.3055 | 0.03546 | 40.2669 | −0.54551 | 0.00683 | 210 | 35 |
| 5 | 1658.57 | 36.3278 | 0.02111 | 42.8955 | −0.51116 | 0.00461 | 325 | 130 |
| 6 | 1356.66 | 38.2704 | 0.01799 | 42.8955 | −0.51116 | 0.00461 | 325 | 125 |
| Unit | ai | bi | ci | di | ei | (MW) | (MW) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1000.403 | 40.5407 | 0.12951 | 33 | 0.0174 | 360.0012 | −3.9864 | 0.04702 | 0.25475 | 0.01234 | 55 | 10 |
| 2 | 950.606 | 39.5804 | 0.10908 | 25 | 0.0178 | 350.0056 | −3.9524 | 0.04652 | 0.25475 | 0.01234 | 80 | 20 |
| 3 | 900.705 | 36.5104 | 0.12511 | 32 | 0.0162 | 330.0056 | −3.9023 | 0.04652 | 0.25163 | 0.01215 | 120 | 47 |
| 4 | 800.705 | 39.5104 | 0.12111 | 30 | 0.0168 | 330.0056 | −3.9023 | 0.04652 | 0.25163 | 0.01215 | 130 | 20 |
| 5 | 756.799 | 38.539 | 0.15247 | 30 | 0.0148 | 13.8593 | 0.3277 | 0.0042 | 0.24970 | 0.01200 | 160 | 50 |
| 6 | 451.325 | 46.1592 | 0.10587 | 20 | 0.0163 | 13.8593 | 0.3277 | 0.0042 | 0.24970 | 0.01200 | 240 | 70 |
| 7 | 1243.531 | 38.3055 | 0.03546 | 20 | 0.0152 | 40.2669 | −0.5455 | 0.0068 | 0.24800 | 0.01290 | 300 | 60 |
| 8 | 1049.998 | 40.3965 | 0.02803 | 30 | 0.0128 | 40.2669 | −0.5455 | 0.0068 | 0.24990 | 0.01203 | 340 | 70 |
| 9 | 1658.569 | 36.3278 | 0.02111 | 60 | 0.0136 | 42.8955 | −0.5112 | 0.0046 | 0.25470 | 0.01234 | 470 | 135 |
| 10 | 1356.659 | 38.2704 | 0.01799 | 40 | 0.0141 | 42.8955 | −0.5112 | 0.0046 | 0.25470 | 0.01234 | 470 | 150 |
References
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Tang, X.; Li, Z.; Xu, X.; Zeng, Z.; Jiang, T.; Fang, W.; Meng, A. Multi-objective economic emission dispatch based on an extended crisscross search optimization algorithm. Energy 2022, 244, 122715. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.; El-Sehiemy, R.; Gafar, M. A multi-objective teaching–learning studying-based algorithm for large-scale dispatching of combined electrical power and heat energies. Mathematics 2022, 10, 2278. [Google Scholar] [CrossRef]
- Marouani, I.; Guesmi, T.; Hadj Abdallah, H.; Alshammari, B.M.; Alqunun, K.; Alshammari, A.S.; Rahmani, S. combined economic emission dispatch with and without consideration of PV and wind energy by using various optimization techniques: A review. Energies 2022, 15, 4472. [Google Scholar] [CrossRef]
- Guesmi, T.; Farah, A.; Marouani, I.; Alshammari, B.M.; Hadj Abdallah, H. Chaotic sine–cosine algorithm for chance–constrained economic emission dispatch problem including wind energy. IET Renew. Power Gener. 2020, 14, 1808–1821. [Google Scholar] [CrossRef]
- Bai, C.; Li, Q.; Zhou, W.; Li, B.; Zhang, L. Fast distributed gradient descent method for economic dispatch of microgrids via upper bounds of second derivatives. Energy Rep. 2022, 8, 1051–1060. [Google Scholar] [CrossRef]
- Qin, J.; Wan, Y.; Yu, X.; Kang, Y. A Newton method-based distributed algorithm for multi-area economic dispatch. IEEE Trans. Power Syst. 2020, 35, 986–996. [Google Scholar] [CrossRef]
- Singhal, P.K.; Naresh, R.; Sharma, V.; Goutham, K.N. Enhanced lambda iteration algorithm for the solution of large scale economic dispatch problem. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; pp. 1–6. [Google Scholar]
- Jacobo, J.C.; Cira Perez, N.P.; Flores Romero, J.J. A Graph-based method to solve the economical dispatch problem disregarding slack variables. Proc. Technol. 2012, 3, 304–315. [Google Scholar] [CrossRef]
- Liang, Z.-X.; Glover, J.D. A zoom feature for a dynamic programming solution to economic dispatch including transmission losses. IEEE Trans. Power Syst. 1992, 7, 544–550. [Google Scholar] [CrossRef]
- Basu, M. Dynamic economic emission dispatch using nondominated sorting genetic algorithm-II. Int. J. Electr. Power Energy Syst. 2008, 30, 140–149. [Google Scholar] [CrossRef]
- Cheng, Y.S.; Chuang, M.T.; Liu, Y.H.; Wang, S.C.; Yang, Z.Z. A particle swarm optimization based power dispatch algorithm with roulette wheel re-distribution mechanism for equality constraint. Renew. Energy 2016, 88, 58–72. [Google Scholar] [CrossRef]
- Prasad, D.; Banerjee, A.; Singh, R.P. Optimal reactive power dispatch using modified differential evolution algorithm. Adv. Comput. Commun. Control. 2019, 41, 275–283. [Google Scholar]
- Arul, R.; Ravi, G.; Velusami, S. An improved harmony search algorithm to solve economic load dispatch problems with generator constraints. Electr. Eng. 2014, 96, 55–63. [Google Scholar] [CrossRef]
- Jadhav, H.T.; Roy, R. Gbest guided artificial bee colony algorithm for environmental/economic dispatch considering wind power. Expert Syst. Appl. 2013, 40, 6385–6399. [Google Scholar] [CrossRef]
- Vennila, H.; Giri, N.C.; Nallapaneni, M.K.; Sinha, P.; Bajaj, M.; Abou Houran, M.; Kamel, S. Static and dynamic environmental economic dispatch using tournament selection based ant lion optimization algorithm. Front. Energy Res. 2022, 10, 972069. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S.; Abd Elazim, S.M. Flower pollination algorithm to solve combined economic and emission dispatch problems. Eng. Sci. Technol. Int. J. 2016, 19, 980–990. [Google Scholar] [CrossRef]
- Alghamdi, A.S. A new self-adaptive teaching–learning-based optimization with different distributions for optimal reactive power control in power networks. Energies 2022, 15, 2759. [Google Scholar] [CrossRef]
- Abdullah, M.N.; Abdullah, N.A.; Aswan, N.F.; Jumaat, S.A.; Radzi, N.H.; Nor, A.F.M. Combined economic-emission load dispatch solution using firefly algorithm and fuzzy approach. Indones. J. Electr. Eng. Comput. Sci. 2019, 16, 127–135. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, B.; Dong, Y.; Qu, B.; Wu, D. Multiobjective dynamic economic emission dispatch using evolutionary algorithm based on decomposition. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1323–1333. [Google Scholar] [CrossRef]
- Hadji, B.; Mahdad, B.; Srairi, K.; Mancer, N. Multi-objective economic emission dispatch solution using dance bee colony with dynamic step size. Energy Procedia 2015, 74, 65–76. [Google Scholar] [CrossRef]
- Xia, A.; Wu, X. A Hybrid Multi-Objective Optimization Algorithm for Economic Emission Dispatch Considering Wind Power Uncertainty. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 1277–1293. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Z.; Dai, C.; Xu, X.; Xiong, Z.; Su, Q. Multiobjective Grey prediction evolution algorithm for environmental/economic dispatch problem. IEEE Access 2020, 8, 84162–84176. [Google Scholar] [CrossRef]
- Bhesdadiya, R.H.; Trivedi, I.N.; Jangir, P.; Jangir, N.; Kumar, A. An NSGA-III algorithm for solving multi-objective economic/environmental dispatch problem. Cogent Eng. 2016, 3, 1269383. [Google Scholar] [CrossRef]
- Alatas, B.; Bingol, H. Comparative Assessment of Light-based Intelligent Search and Optimization Algorithms. Light Eng. 2020, 28, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Akyol, S.; Alatas, B. Plant intelligence based metaheuristic optimization algorithms. Artif. Intell. Rev. 2017, 47, 417–462. [Google Scholar] [CrossRef]
- Hazra, S.; Roy, P.K. Quasi-oppositional chemical reaction optimization for combined economic emission dispatch in power system considering wind power uncertainties. Renew. Energy Focus 2019, 31, 45–62. [Google Scholar] [CrossRef]
- Younes, Z.; Alhamrouni, I.; Mekhilef, S.; Reyasudin, M. A memory-based gravitational search algorithm for solving economic dispatch problem in micro-grid. Ain Shams Eng. J. 2012, 12, 1985–1994. [Google Scholar] [CrossRef]
- Bouchekara, H.; Abido, M.; Chaib, A.; Mehasni, R. Optimal power flow using the league championship algorithm: A case study of the Algerian power system. Energy Convers. Manag. 2014, 87, 58–70. [Google Scholar] [CrossRef]
- Zaoui, S.; Belmadani, A. Solution of combined economic and emission dispatch problems of power systems without penalty. Appl. Artif. Intell. 2022, 36, 1976092. [Google Scholar] [CrossRef]
- Xu, X.; Hu, Z.; Su, Q.; Xiong, Z. Multiobjective collective decision optimization algorithm for economic emission dispatch problem. Complexity 2018, 2018, 1027193. [Google Scholar] [CrossRef]
- Sharifi, S.; Sedaghat, M.; Farhadi, P.; Ghadimi, N.; Taheri, B. Environmental economic dispatch using improved artificial bee colony algorithm. Evol. Syst. 2017, 8, 233–242. [Google Scholar] [CrossRef]
- Sen, T.; Mathur, H.D. A new approach to solve economic dispatch problem using a hybrid ACO–ABC–HS optimization algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 735–744. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Nor Ashidi, M.I.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Ezugwu, A.E.; Agushaka, J.O.; Abu Zitar, R.; Abualigah, L. Differential evolution and its applications in image processing problems: A comprehensive review. Arch. Computat. Methods Eng. 2022, 30, 985–1040. [Google Scholar] [CrossRef] [PubMed]
- Huy Anh, H.P.; Son, N.N.; Kien, C.V.; Ho-Huu, V. Parameter identification using adaptive differential evolution algorithm applied to robust control of uncertain nonlinear systems. Appl. Soft Comput. 2018, 71, 672–684. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Xiao, J. Differential evolution-based load frequency robust control for micro-grids with energy storage systems. Energies 2018, 11, 1686. [Google Scholar] [CrossRef]
- Liu, X.; Xu, W. Economic load dispatch constrained by wind power availability: A here-and-now approach. IEEE Trans. Sustain. Energy 2010, 1, 2–9. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, H. A dynamic economic dispatch model incorporating wind power based on chance constrained programming. Energies 2015, 8, 233–256. [Google Scholar] [CrossRef]
- Noman, N.; Iba, H. Differential evolution for economic load dispatch problems. Electr. Power Syst. Res. 2008, 78, 1322–1331. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Gupta, N.; Niazi, K.R.; Swarnkar, A.; Bansal, R.C. Multi-area economic dispatch using improved particle swarm optimization. Energy Procedia 2015, 75, 1087–1092. [Google Scholar] [CrossRef]
- Afandi, A.N.; Miyauchi, H. Improved artificial bee colony algorithm considering harvest season for computing economic dispatch on power system. IEEJ Trans. 2014, 9, 251–257. [Google Scholar] [CrossRef]
- Zou, D.; Li, S.; Wang, G.G.; Li, Z.; Ouyang, H. An improved differential evolution algorithm for the economic load dispatch problems with or without valve-point effects. Appl. Energy 2016, 181, 375–390. [Google Scholar] [CrossRef]
- Hongfeng, Z. Dynamic economic dispatch based on improved differential evolution algorithm. Clust. Comput. 2019, 22, 8241–8248. [Google Scholar] [CrossRef]
- Gherbi, Y.A.; Bouzeboudja, H.; Gherbi, F.Z. The combined economic environmental dispatch using new hybrid metaheuristic. Energy 2016, 115, 468–477. [Google Scholar] [CrossRef]
- Ghasemi, M.; Aghaei, J.; Akbari, E.; Sahand, G.; Li, L. A differential evolution particle swarm optimizer for various types of multi-area economic dispatch problems. Energy 2016, 107, 182–195. [Google Scholar] [CrossRef]
- Edwin, C.R.; Selva, R.; Marsaline Beno, M.; Annrose, J. A solution for combined economic and emission dispatch problem using hybrid optimization techniques. J. Electr. Eng. Technol. 2019, 2019, 1–10. [Google Scholar]
- Mohammad, J.M.; Taher, N.; Jamshid, A.; Miadreza, S.K.; Joao, P.S.; Catal, A. Hybrid optimization algorithm to solve the nonconvex multiarea economic dispatch problem. IEEE Syst. J. 2018, 13, 3400–3409. [Google Scholar]
- Nourianfar, H.; Abdi, H. Environmental/economic dispatch using a new hybridizing algorithm integrated with an effective constraint handling technique. Sustainability 2022, 14, 3173. [Google Scholar] [CrossRef]
- Marek, M.; Kadlec, P. Another evolution of generalized differential evolution: Variable number of dimensions. Eng. Optim. 2022, 54, 61–80. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Liu, B.; Fernández, F.V.; Zhang, Q.; Pak, M.; Sipahi, S.; Gielen, G. An enhanced MOEA/D-DE and its application to multiobjective analog cell sizing. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Z.; Zhou, J. Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1229–1246. [Google Scholar] [CrossRef]
- Gao, S.; Yu, Y.; Wang, Y.; Wang, J.; Cheng, J.; Zhou, M. Chaotic local search-based differential evolution algorithms for optimization. IEEE Trans. Syst. Man Cybern. 2021, 51, 3954–3967. [Google Scholar] [CrossRef]
- Shukla, A.K. Chaos teaching learning based algorithm for large-scale global optimization problem and its application. Concurr. Computat. Pract. Exper. 2021, 34, e6514. [Google Scholar] [CrossRef]
- Pandey, V.C.; Jadoun, V.K.; Gupta, N.; Niazi, K.R.; Swarnkar, A. Improved fireworks algorithm with chaotic sequence operator for large-scale non-convex economic load dispatch problem. Arab. J. Sci. Eng. 2018, 43, 2919–2929. [Google Scholar] [CrossRef]
- Singh, N.J.; Singh, S.; Chopra, V.; Aftab, M.A.; Hussain, S.M.S.; Ustun, T.S. Chaotic evolutionary programming for an engineering optimization problem. Appl. Sci. 2021, 11, 2717. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hagag, E.A.; El-Fergany, A.A. Chaos-enhanced multi-objective tunicate swarm algorithm for economic-emission load dispatch problem. Soft Comput. 2022, 27, 5721–5739. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Eldesoky, I.M.; Basyouni, M.M.; Nassar, I.; El-Refaey, A.M. Chaotic search-based salp swarm algorithm for dealing with system of nonlinear equations and power system applications. Mathematics 2022, 10, 1368. [Google Scholar] [CrossRef]
- Singh, N.J.; Dhillon, J.S.; Kothari, D.P. Multi-objective thermal power load dispatch using chaotic differential evolutionary algorithm and Powell’s method. Soft Comput. 2018, 22, 2159–2174. [Google Scholar] [CrossRef]
- Daqaq, F.; Ouassaid, M.; Kamel, S.; Ellaia, R.; El-Naggar, M.F. A novel chaotic flower pollination algorithm for function optimization and constrained optimal power flow considering renewable energy sources. Front. Energy Res. 2022, 10, 941705. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Dou, Z.; Qiao, M.; Zhao, Y.; Xie, R.; Liu, L. Decentralized Coordination Dispatch Model Based on Chaotic Mutation Harris Hawks Optimization Algorithm. Energies 2022, 15, 3815. [Google Scholar] [CrossRef]
- Varol Altay, E.; Alatas, B. Bird swarm algorithms with chaotic mapping. Artif. Intell. Rev. 2020, 53, 1373–1414. [Google Scholar] [CrossRef]
- May, R. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Du, B.; Liang, X. Image encryption algorithm based on logistic and two-dimensional Lorenz. IEEE Access 2020, 8, 13792–13805. [Google Scholar] [CrossRef]
- Moon, S.; Mango Seo, j.; Han, B.-S.; Park, J.; Baik, J.J. A physically extended Lorenz system. Chaos 2019, 29, 0631. [Google Scholar] [CrossRef]
- Zainel, Q.M.; Darwish, S.M.; Khorsheed, M.B. Employing quantum fruit fly optimization algorithm for solving three-dimensional chaotic equations. Mathematics 2022, 10, 4147. [Google Scholar] [CrossRef]
- Basu, M. Economic environmental dispatch using multi-objective differential evolution. Appl. Soft Comput. 2011, 11, 2845–2853. [Google Scholar] [CrossRef]
- Roy, P.K.; Bhui, S. Multi-objective quasi-oppositional teaching learning based optimization for economic emission load dispatch problem. Int. J. Elect. Power Energy Syst. 2013, 53, 937–948. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Suman, M.; Sathya, P.D. Combined economic and emission power dispatch problems through multi-objective squirrel search algorithm. Appl. Soft Comput. 2021, 100, 106950. [Google Scholar] [CrossRef]
- Bhattacharjee, K.; Bhattacharya, A.; Halder nee Dey, S. Backtracking search optimization based economic environmental power dispatch problems. Int. J. Electr. Power Energy Syst. 2015, 73, 830–842. [Google Scholar] [CrossRef]
- Dong, R.; Wang, S. New optimization algorithm inspired by Kernel tricks for the economic emission dispatch problem with valve point. IEEE Access 2020, 8, 16584–16594. [Google Scholar] [CrossRef]
- Taherkhani, M.; Safabakhsh, R. Anovel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281295. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Goh, H.H.; Srikrishna, S.; Sathya, P.D.; Abdul Rahim, S.K. Multi-objective squirrel search algorithm for multi-area economic environmental dispatch with multiple fuels and valve point effects. IEEE Access 2021, 9, 3988–4007. [Google Scholar] [CrossRef]
- Alshammari, B.M. Dynamic Environmental/Economic Power Dispatch with Prohibited Zones Using Improved Multi-Objective PSO Algorithm. Int. Rev. Electr. Eng. 2016, 11, 411–419. [Google Scholar] [CrossRef]
- Audet, C.; Bigeon, J.; Cartier, D.; Le Digabel, S.; Salomon, L. Performance indicators in multiobjective optimization. Eur. J. Oper. Res. 2021, 292, 397–422. [Google Scholar] [CrossRef]


| Method | Swarm Based | Social Based | Biology Based | Physics Based | Math Based | Chemistry Based | Music Based | Sports Based | Hybrid | Sigle Objective | Multi Objective |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSO [12] | ✓ | ✓ | |||||||||
| IHS [14] | ✓ | ✓ | |||||||||
| QOCRO [27] | ✓ | ✓ | |||||||||
| MBGSA [28] | ✓ | ✓ | |||||||||
| LCA [29] | ✓ | ✓ | |||||||||
| NSGA-III [24] | ✓ | ✓ | |||||||||
| OWP-based OMF [30] | ✓ | ✓ | |||||||||
| MOPSO [31] | ✓ | ✓ | |||||||||
| IABC [32] | ✓ | ✓ | |||||||||
| CSCA [5] | ✓ | ✓ | |||||||||
| ACO-ABC-HS [33] | ✓ | ✓ | |||||||||
| MTLSBA [3] | ✓ | ✓ | |||||||||
| NSGAII [11] | ✓ | ✓ |
| ChMODE and DE Parameters | |
|---|---|
| Population size | 300 |
| Maximum number of iterations | 200 |
| CR | 0.75 |
| F | 0.75 |
| Mutation operator | DE/rand/1 |
| Crossover operator | Binomial crossover |
| ABC parameters | |
| Number of bees | 300 |
| Number of food sources | 150 |
| Maximum number of iterations | 200 |
| Trial limit | 30 |
| IWO parameters | |
| Population size | 300 |
| Maximum number of iterations | 200 |
| Maximum number of seeds | 5 |
| Minimum number of seeds | 0 |
| Initial value of standard deviation | 2 |
| Final value of standard deviation | 0.01 |
| Unit Output (MW) | QOTLBO [70] | EMOCA [71] | BSA [72] | NSGA-III [29] | DE [69] | ChMODE |
|---|---|---|---|---|---|---|
| P1 (MW) | 79.5547 | 90.00 | 79.6762 | 84.6285 | 84.4354 | 80.6856 |
| P2 (MW) | 88.8977 | 88.08 | 88.7507 | 93.4213 | 93.3638 | 87.5760 |
| P3 (MW) | 210.0000 | 210.00 | 210.0000 | 210.0000 | 225.0000 | 225.0000 |
| P4 (MW) | 224.9944 | 225.00 | 225.0000 | 225.0000 | 209.9995 | 210.0000 |
| P5 (MW) | 324.9708 | 315.00 | 325.0000 | 315.0000 | 325.0000 | 325.0000 |
| P6 (MW) | 324.9977 | 325.00 | 324.9927 | 325.0000 | 314.9998 | 325.0000 |
| TC ($/h) | 63,977 | 64,100.3 | 63,976 | 64,099 | 64,083 | 63,963.96 |
| TE (lb/h) | 1360.1 | 1345.73 | 1360.1 | 1345.9 | 1345.6 | 1359.87 |
| Ptl (MW) | 53.42 | 53.08 | 53.42 | 53.0498 | 52.7985 | 53.26 |
| Unit Output (MW) | QOTLBO [70] | EMOCA [71] | BSA [72] | NSGA-III [29] | DE [69] | ChMODE |
|---|---|---|---|---|---|---|
| P1 (MW) | 125.0000 | 125.00 | 125.0000 | 125.0000 | 125.0000 | 125.0000 |
| P2 (MW) | 150.0000 | 150.00 | 150.0000 | 150.0000 | 150.0000 | 150.0000 |
| P3 (MW) | 201.2679 | 201.26 | 201.2684 | 201.4824 | 201.1816 | 201.2684 |
| P4 (MW) | 199.3701 | 197.63 | 199.369 | 198.8723 | 199.5454 | 199.3690 |
| P5 (MW) | 287.9708 | 290.40 | 287.9713 | 288.5129 | 287.6191 | 287.9713 |
| P6 (MW) | 286.5498 | 285.83 | 286.5499 | 286.2913 | 286.8137 | 286.5499 |
| TC ($/h) | 65,992 | 65,985.6 | 65,992 | 65,992 | 65,991 | 65,990.4 |
| TE (lb/h) | 1240.6 | 1240.57 | 1240.6 | 1240.7 | 1240.7 | 1240.6 |
| Ptl (MW) | 50.1586 | 50.12 | 50.1586 | 50.1589 | 50.1598 | 50.1586 |
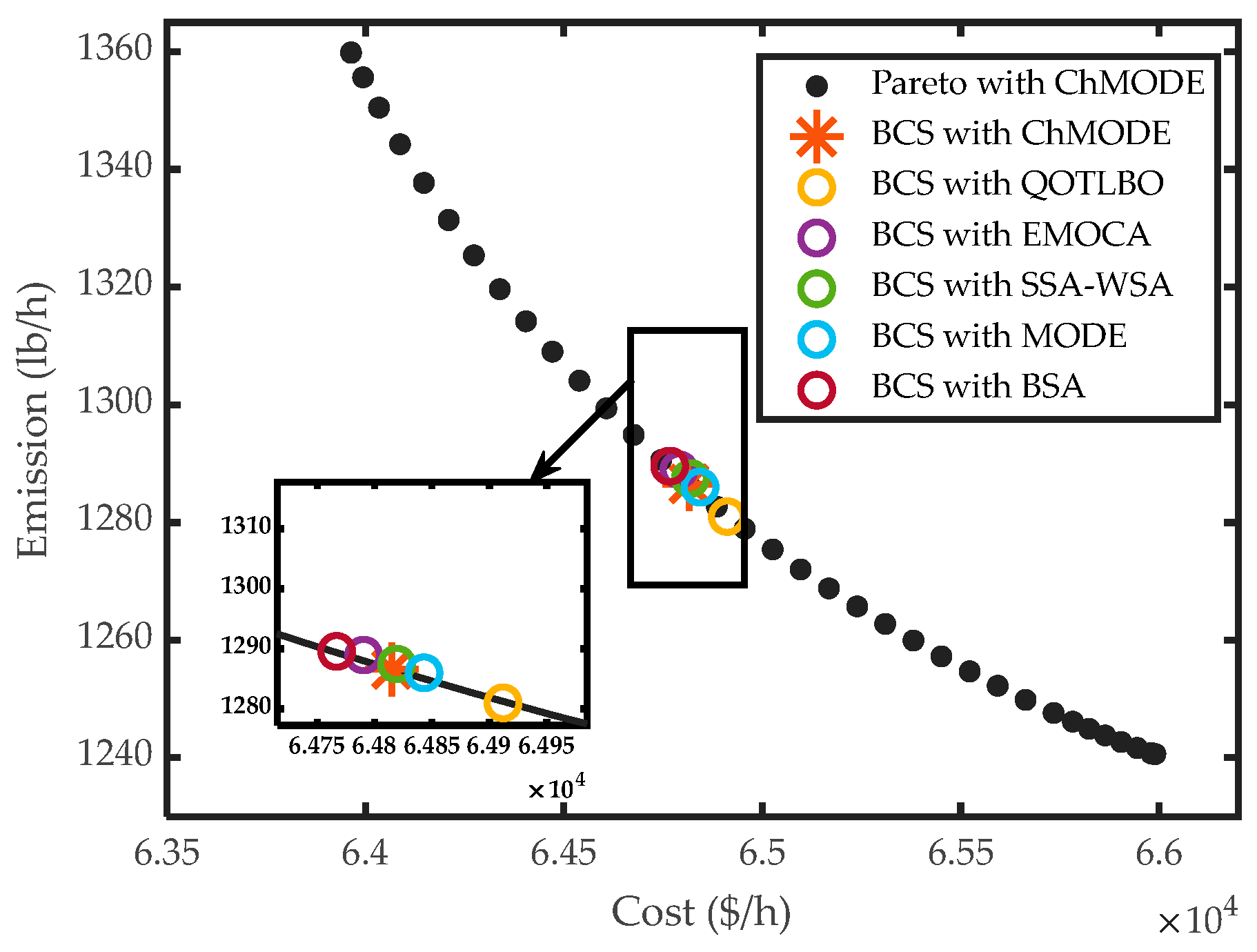
| Unit | QOTLBO [70] | EMOCA [71] | SSA-WSA [71] | MODE [69] | BSA [72] | NSGA-III [29] | ChMODE |
|---|---|---|---|---|---|---|---|
| P1 (MW) | 107.3101 | 106.693 | 107.0054 | 108.6284 | 104.0109 | 107.9932 | 105.4536 |
| P2 (MW) | 121.4970 | 115.6497 | 116.6309 | 115.9456 | 117.4296 | 118.3631 | 118.7674 |
| P3 (MW) | 206.5010 | 210.0000 | 206.8649 | 206.7969 | 207.5811 | 210.0000 | 210.0413 |
| P4 (MW) | 206.5826 | 203.3266 | 205.7633 | 210.0000 | 206.6238 | 204.6500 | 203.2925 |
| P5 (MW) | 304.9838 | 303.0506 | 309.3058 | 301.8884 | 309.0648 | 306.6592 | 308.5158 |
| P6 (MW) | 304.6036 | 313.0506 | 305.2939 | 308.4127 | 306.9983 | 303.8712 | 305.5247 |
| TC ($/h) | 64,912 | 64,790.370 | 64,819.163 | 64,843 | 64,766.823 | 64,830 | 64,815.143 |
| TE (lb/h) | 1281 | 1288.970 | 1287.475 | 1286 | 1289.586 | 1285 | 1286.563 |
| Ptl (MW) | 51.50 | 51.77 | 50.86 | 51.67 | 51.71 | 51.5367 | 51.60 |
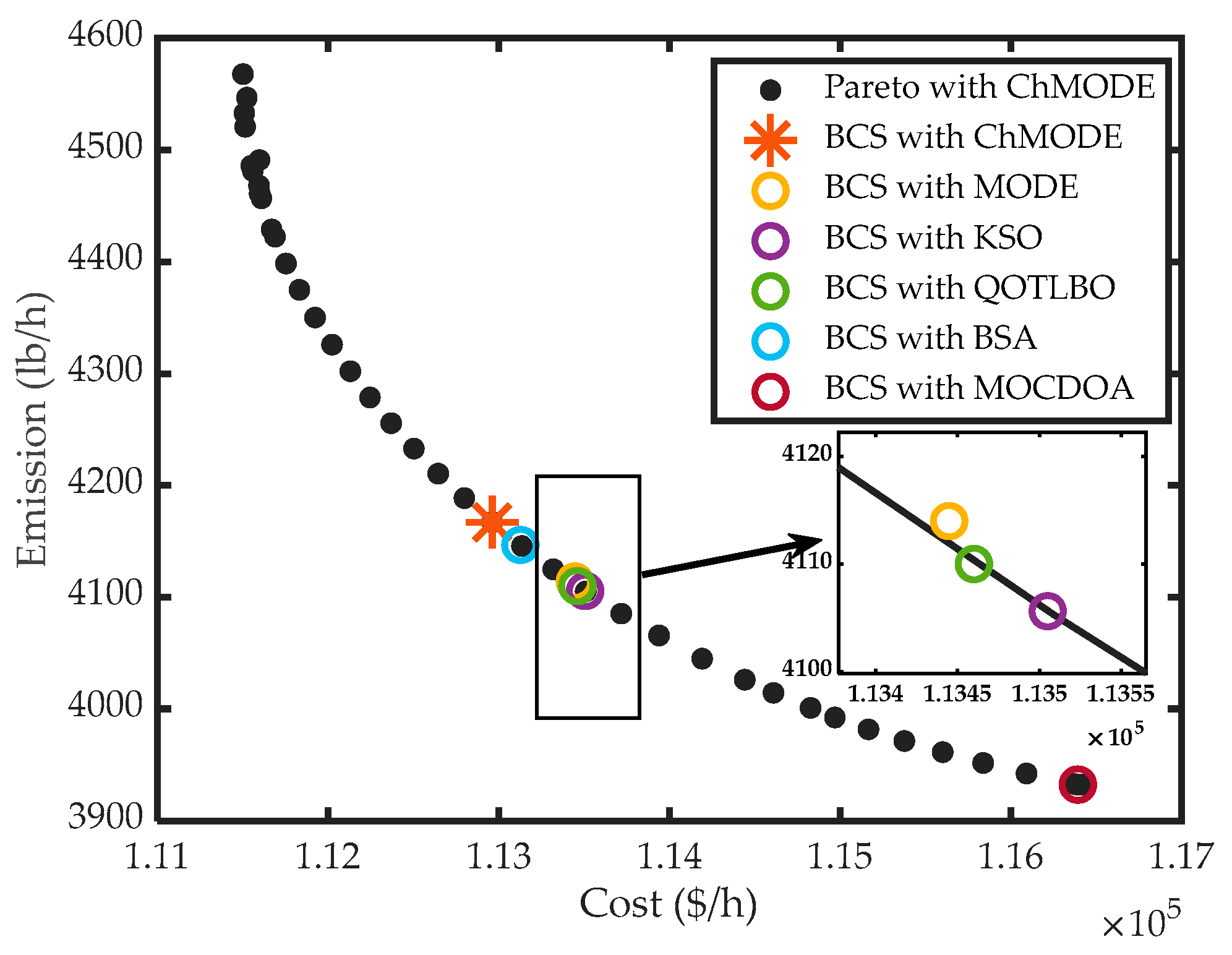
| Unit | DE [69] | QOTLBO [70] | OWP-Based OMF [30] | MOCDOA [31] | NSGA-III [29] | KSO [73] | ChMODE |
|---|---|---|---|---|---|---|---|
| P1 (MW) | 55.0000 | 55.0000 | 55.0000 | 54.1271 | 55.0000 | 55.0000 | 55.0000 |
| P2 (MW) | 79.8063 | 79.9991 | 80.0000 | 79.2076 | 80.0000 | 80.0000 | 80.0000 |
| P3 (MW) | 106.8253 | 107.9231 | 106.8771 | 94.9232 | 106.0514 | 106.8407 | 106.9399 |
| P4 (MW) | 102.8307 | 98.6479 | 100.7023 | 92.9628 | 99.2176 | 100.9243 | 100.5760 |
| P5 (MW) | 82.2418 | 82.0180 | 81.537 | 81.7613 | 81.5808 | 81.3210 | 81.5017 |
| P6 (MW) | 80.4352 | 83.4878 | 82.9221 | 110.9617 | 85.1964 | 82.9457 | 83.0212 |
| P7 (MW) | 300.0000 | 300.0000 | 300.0000 | 299.2531 | 299.9843 | 300.0000 | 300.0000 |
| P8 (MW) | 340.0000 | 340.0000 | 340.0000 | 336.9639 | 340.0000 | 340.0000 | 340.0000 |
| P9 (MW) | 470.0000 | 469.9706 | 470.0000 | 467.1387 | 470.0000 | 470.0000 | 470.0000 |
| P10 (MW) | 469.8975 | 469.9988 | 470.0000 | 469.4260 | 470.0000 | 470.0000 | 470.0000 |
| TC ($/h) | 111,500 | 111,498 | 111,497.6407 | 111,647.2433 | 111,500 | 111,497.27 | 111,497.6308 |
| TE (lb/h) | 4581.0 | 4568.7 | 4572.4396 | 4463.7355 | 4562 | 4573.24 | 4572.1944 |
| Ptl (MW) | 87.0368 | 87.0453 | 87.0386 | 86.7254 | 87.0305 | 87.0374 | 87.0388 |
| (MW) | 3.05 × 10−6 | 2.57 × 10−5 | NA | NA | NA | 5.68 × 10−3 | 0 |
| Unit | DE [69] | QOTLBO [70] | OWP-Based OMF [30] | MOCDOA [31] | NSGA-III [29] | KSO [73] | ChMODE |
|---|---|---|---|---|---|---|---|
| P1 (MW) | 55.0000 | 55.0000 | 55.0000 | 53.9676 | 55.0000 | 55.0000 | 55.0000 |
| P2 (MW) | 80.0000 | 80.0000 | 80.0000 | 72.9059 | 79.9782 | 80.0000 | 80.0000 |
| P3 (MW) | 80.5924 | 81.1342 | 80.9248 | 91.0182 | 82.1289 | 81.1342 | 81.1342 |
| P4 (MW) | 81.0233 | 81.3637 | 81.1019 | 86.6490 | 82.3506 | 81.3637 | 81.3637 |
| P5 (MW) | 160.0000 | 160.0000 | 160.0000 | 159.9516 | 160.0000 | 160.0000 | 160.0000 |
| P6 (MW) | 240.0000 | 240.0000 | 240.0000 | 238.7233 | 240.0000 | 240.0000 | 240.0000 |
| P7 (MW) | 292.7434 | 294.4843 | 294.5495 | 276.9106 | 296.1872 | 294.4851 | 294.4851 |
| P8 (MW) | 299.1214 | 297.2710 | 297.6624 | 298.1337 | 296.2329 | 297.2701 | 297.2701 |
| P9 (MW) | 394.5147 | 396.7645 | 396.3406 | 389.5693 | 397.4092 | 396.7657 | 396.7657 |
| P10 (MW) | 398.6383 | 395.5775 | 396.0266 | 413.7970 | 392.2266 | 395.5763 | 395.5763 |
| TC ($/h) | 116,400 | 116,412.44 | 116,411.9936 | 116,322.8936 | 116,430 | 116,412.44 | 116,412.4441 |
| TE (lb/h) | 3932.4 | 3932.24 | 3932.2538 | 3950.7644 | 3932.5 | 3932.24 | 3932.2433 |
| Ptl (MW) | 81.6335 | 81.5952 | 81.6057 | 81.6262 | 81.5136 | 81.5951 | 81.5952 |
| (MW) | 9.04 × 10−5 | 4.07 × 10−5 | NA | NA | NA | 4.69 × 10−5 | 0 |
| TC ($/h) | 116,393.2399 | 114,826.3280 | 115,599.7082 | 112,797.543 | 111,557.6631 | 111,831.5004 |
| TE (lb/h) | 3932.3950 | 4000.9918 | 3961.3745 | 4188.6816 | 4481.5675 | 4375.0299 |
| Unit | MODE [69] | KSO [73] | QOTLBO [70] | BSA [72] | OWP-Based OMF [30] | MOCDOA [31] | NSGA-III [29] | ChMODE |
|---|---|---|---|---|---|---|---|---|
| P1 (MW) | 54.9487 | 55.0000 | 55.0000 | 55.0000 | 55.0000 | 53.0198 | 54.9324 | 55.0000 |
| P2 (MW) | 74.5821 | 80.0000 | 80.0000 | 80.0000 | 80.0000 | 75.4397 | 80.0000 | 80.0000 |
| P3 (MW) | 79.4294 | 84.7412 | 84.8457 | 85.6466 | 81.1085 | 89.5564 | 82.8893 | 86.0167 |
| P4 (MW) | 80.6875 | 83.4185 | 83.4993 | 84.1270 | 80.7725 | 86.9663 | 83.7835 | 84.3972 |
| P5 (MW) | 136.8551 | 143.7777 | 142.9210 | 136.4905 | 160.0000 | 137.3076 | 149.0664 | 133.0681 |
| P6 (MW) | 172.6393 | 164.2877 | 163.2711 | 155.5642 | 240.0000 | 147.6495 | 153.8082 | 151.3739 |
| P7 (MW) | 283.8233 | 299.5076 | 299.8066 | 300.0000 | 291.5934 | 289.5841 | 299.6631 | 300.0000 |
| P8 (MW) | 316.3407 | 315.4369 | 315.4388 | 316.6807 | 296.0321 | 322.6523 | 317.0490 | 318.2507 |
| P9 (MW) | 448.5923 | 427.8255 | 428.5084 | 434.1352 | 398.8523 | 442.612 | 435.7486 | 436.8178 |
| P10(MW) | 436.4287 | 429.7994 | 430.5524 | 436.5834 | 398.3150 | 439.6483 | 427.0254 | 439.5055 |
| TC ($/h) | 113,444.85 | 113,505 | 113,460 | 113,126.7515 | 116,391.8270 | 112,729.353799 | 113,410 | 112,960.6297 |
| TE (lb/h) | 4113.98 | 4105.62 | 4110 | 4146.7286 | 3932.4035 | 4180.868813 | 4118.6 | 4167.0660 |
| Ptl (MW) | 83.56 | 84.8563 | 83.8433 | 84.2276 | 81.6790 | 84.4360 | 83.9659 | 84.4299 |
| Methods | Economic Dispatch | Emission Dispatch | ||||||
|---|---|---|---|---|---|---|---|---|
| Best | Mean | Worst | Std | Best | Mean | Worst | Std | |
| ChMODE | 111,497.63 | 111,497.63 | 111,497.63 | 5.51 × 10−9 | 3932.24 | 3932.24 | 3932.24 | 9.39 × 10−12 |
| SAIWPSO [63] | 111,497.63 | 111,497.64 | 111,497.64 | 1.81 × 10−4 | 3932.24 | 3932.25 | 3932.25 | 2.33 × 10−3 |
| OWP-OMF [61] | 111,497.640 | 111,497.64 | 111,497.642 | 3.9 × 10−4 | 3932.25 | 3932.2542 | 3932.255 | 3.2 × 10−4 |
| GQPSO [60] | 112,429.74 | 113,102.46 | 113,327.07 | 2.56 × 102 | 4011.92 | 4032.93 | 4042.19 | 7.55 × 100 |
| Unit | POZ1 | POZ2 | ||
|---|---|---|---|---|
| 1 | 12 | 17 | 35 | 45 |
| 2 | 20 | 30 | 40 | 45 |
| 9 | 90 | 110 | 240 | 250 |
| 10 | 150 | 165 | 448 | 453 |
| EcDP | EmDP | |||||||
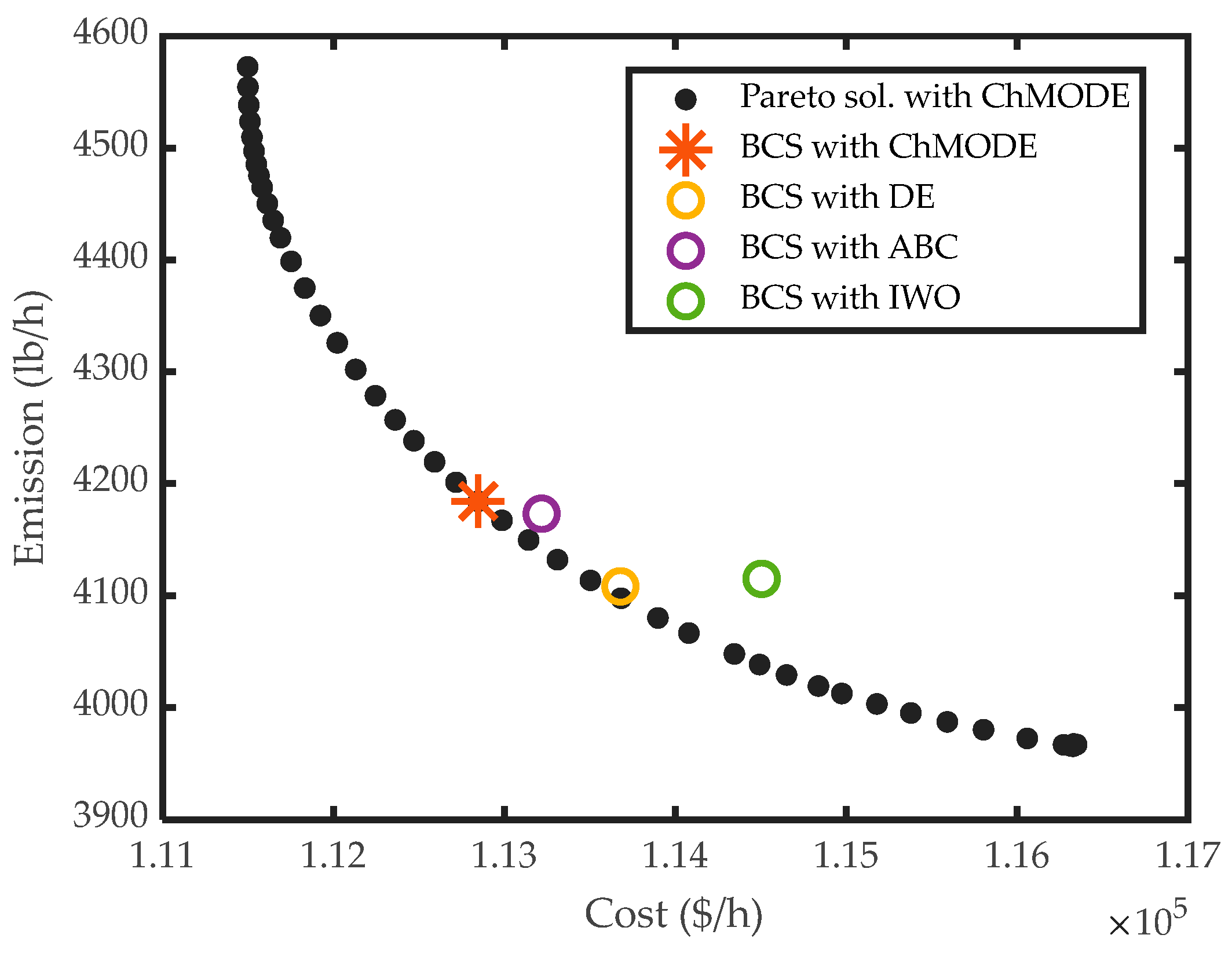
|---|---|---|---|---|---|---|---|---|
| Unit | IWO | ABC | DE | ChMODE | IWO | ABC | DE | ChMODE |
| P1 (MW) | 54.9644 | 55.000 | 54.9726 | 55.0000 | 54.9367 | 55.0000 | 55.0000 | 55.0000 |
| P2 (MW) | 69.7777 | 77.1955 | 80.0000 | 80.0000 | 79.4097 | 80.0000 | 80.0000 | 78.6128 |
| P3 (MW) | 111.0655 | 113.1760 | 107.7073 | 106.9400 | 79.1616 | 91.8763 | 80.4568 | 78.4628 |
| P4 (MW) | 92.7977 | 102.3596 | 100.2584 | 100.5763 | 78.6398 | 91.6537 | 79.5042 | 78.6725 |
| P5 (MW) | 129.4502 | 144.1178 | 81.0816 | 81.5017 | 159.9894 | 152.2381 | 160.0000 | 160.0000 |
| P6 (MW) | 162.1251 | 112.1123 | 83.3263 | 83.0209 | 239.9808 | 223.2139 | 240.0000 | 240.0000 |
| P7 (MW) | 276.9582 | 260.6269 | 300.0000 | 300.0000 | 279.8024 | 263.5496 | 272.1162 | 278.5313 |
| P8 (MW) | 323.0147 | 293.9795 | 339.8291 | 340.0000 | 283.7445 | 249.5820 | 284.8455 | 280.8442 |
| P9 (MW) | 393.7317 | 457.9211 | 470.0000 | 470.0000 | 373.7658 | 422.8764 | 377.5210 | 379.4409 |
| P10 (MW) | 469.9996 | 468.7058 | 469.8573 | 470.0000 | 453.0547 | 453.0631 | 453.0478 | 453.0000 |
| TC ($/h) | 113,252.3886 | 112,662.9052 | 111,499.3218 | 111,497.6308 | 116,344.5128 | 115,476.9771 | 116,322.3313 | 116,329.3508 |
| TE (lb/h) | 4228.1994 | 4350.2047 | 4573.5753 | 4572.1958 | 3966.19708 | 4036.1652 | 3966.4347 | 3965.61212 |
| Ptl (MW) | 83.8848 | 85.1946 | 87.0325 | 87.0388 | 82.4854 | 83.0532 | 82.4915 | 82.5644 |
| (MW) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Methods | Economic Dispatch | Emission Dispatch | ||||||
|---|---|---|---|---|---|---|---|---|
| Best | Mean | Worst | Std | Best | Mean | Worst | Std | |
| ChMODE | 111,497.63 | 111,497.63 | 111,497.63 | 4.27 × 10−5 | 3965.61 | 3965.61 | 3965.61 | 2.96 × 10−9 |
| DE | 111,499.32 | 111,507.60 | 111,518.59 | 6.90 × 100 | 3966.43 | 3977.57 | 4061.78 | 2.96 × 102 |
| ABC | 112,662.91 | 113,856.98 | 114,851.36 | 8.82 × 102 | 4036.17 | 4103.98 | 4200.68 | 7.02 × 102 |
| IWO | 113,252.39 | 113,426.98 | 113,60 | 2.45 × 102 | 3966.20 | 3967.26 | 3968.85 | 1.4 × 101 |
| Unit | IWO | ABC | DE | ChMODE |
|---|---|---|---|---|
| P1 (MW) | 55.0000 | 53.4051 | 55.0000 | 54.9645 |
| P2 (MW) | 70.3616 | 77.3177 | 80.0000 | 79.9985 |
| P3 (MW) | 83.6639 | 74.3529 | 83.8312 | 85.3545 |
| P4 (MW) | 99.9302 | 69.5748 | 81.0322 | 83.9675 |
| P5 (MW) | 123.7151 | 132.0192 | 147.3838 | 130.8185 |
| P6 (MW) | 214.5914 | 164.1634 | 169.8290 | 149.2222 |
| P7 (MW) | 276.0150 | 291.2655 | 289.6293 | 298.5015 |
| P8 (MW) | 268.1567 | 333.5401 | 307.7289 | 315.4726 |
| P9 (MW) | 438.8978 | 435.9634 | 416.4693 | 433.4295 |
| P10 (MW) | 453.3848 | 453.3839 | 453.1049 | 453.0000 |
| TC ($/h) | 114,505.3639 | 113,217.4619 | 113,678.6333 | 112,846.3343 |
| TE (lb/h) | 4115.1328 | 4173.3020 | 4098.3634 | 4184.4041 |
| Ptl (MW) | 83.7165 | 84.9860 | 84.0087 | 84.7294 |
| (MW) | 0 | 0 | 0 | 0 |
| ChMODE | MODE | NSPSO | MOCDOA | MOPSO | NSGA-II | PESA-II | MOSSA | |
|---|---|---|---|---|---|---|---|---|
| ASD | 0.6823 | 0.6756 | 0.6790 | 0.6802 | 0.6566 | 0.5730 | 0.6471 | NR |
| IGD | 0.4507 | 0.4725 | 0.4551 | NR | NR | NR | NR | NR |
| HV | 0.033 | 0.026 | 0.032 | NR | NR | NR | NR | Between 0.024 and 0.027 |
| SM | 0.9568 | 1.1266 | NR | NR | NR | NR | NR | NR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almalaq, A.; Guesmi, T.; Albadran, S. A Hybrid Chaotic-Based Multiobjective Differential Evolution Technique for Economic Emission Dispatch Problem. Energies 2023, 16, 4554. https://doi.org/10.3390/en16124554
Almalaq A, Guesmi T, Albadran S. A Hybrid Chaotic-Based Multiobjective Differential Evolution Technique for Economic Emission Dispatch Problem. Energies. 2023; 16(12):4554. https://doi.org/10.3390/en16124554
Chicago/Turabian StyleAlmalaq, Abdulaziz, Tawfik Guesmi, and Saleh Albadran. 2023. "A Hybrid Chaotic-Based Multiobjective Differential Evolution Technique for Economic Emission Dispatch Problem" Energies 16, no. 12: 4554. https://doi.org/10.3390/en16124554
APA StyleAlmalaq, A., Guesmi, T., & Albadran, S. (2023). A Hybrid Chaotic-Based Multiobjective Differential Evolution Technique for Economic Emission Dispatch Problem. Energies, 16(12), 4554. https://doi.org/10.3390/en16124554






