Short-Term Wind Power Prediction Based on a Hybrid Markov-Based PSO-BP Neural Network
Abstract
1. Introduction
- State classification of higher-order Markov models: If the interval of the model is divided into too many parts, a huge TPM is generated, which leads to an increase in computational complexity. If the division is too small, prediction accuracy will be affected. In addition, higher-order models that produce TPMs may be difficult to even store.
- The point forecast model needs further improvement: In the literature authored by Carpinone et al., some Markov models use probability intervals for prediction [28], some base the final prediction on weighting [11,13], and some use the mean of the maximum probability interval for prediction [29]. How to determine the state interval at the next moment and estimate its final point prediction value still need further research.
- For the first problem, we study the idea of building a Markov model and using a real-time calculation to obtain the state probability interval of the next moment of the model, which can be applied to both wind power prediction and generate wind speed data.
- For the second problem, we propose a combined model that combines the Markov model with a Particle Swarm Algorithm (PSO) and Back Propagation (BP) neural network for short-term wind power prediction. In addition, we compared the first-order Markov model, the second-order Markov model, the third-order Markov model, and the weighted Markov model for point prediction.
2. Markov-Based Prediction Approach
2.1. Single-Order and Multi-Order Markov Models
- Acquisition of operational data from actual wind farms and pre-processing of the selected data;
- Slice the preprocessed data into m intervals;
- Statistical calculation of the state sequence to obtain the transfer frequency matrix and the one-step transfer probability matrix;
- The initial probability vector is calculated from the initial data and combined with the calculated one-step transfer probability matrix, and thus the probability distribution for the moment to be predicted can be derived;
- The average of the probability interval with the highest probability in the probability distribution is taken as the state of the next moment.
2.2. Improved Multi-Order Markov-Based Real-Time Algorithm
- Enter the pre-processed wind power time series , number of segments , training points , prediction points , and Markov model order ();
- The pre-processed data is sliced into m intervals with interval sizes of ;
- Assign to the corresponding interval and obtain the sequence of the wind power state interval ;
- The sequences of Markov state transfers satisfying order k in the sequence of wind power intervals are found via retrieval and the values of their next positions are counted;
- The value with the highest frequency in the statistics is used as the predicted value. Let be the initial state at the next moment and repeat step 4 times;
- Satisfy to end the loop and return the final prediction sequence.
| Algorithm 1 Improved k-order Markov-based real-time algorithm. |
| Input: After pre-processing, the wind power time series , number of segments , training points , prediction Points , and Markov model order ). Output: Markov Model Predicted Power . 1: 2: for do 3: where [] is the rounding function 4: end for 5: for do 6: 7: for do 8: 9: 10: end for 11: 12: end for |
2.3. Weighted Markov-Based Prediction Model
- Set the criteria for grading;
- Distinguish the state corresponding to each data point;
- Calculate the autocorrelation coefficients of different orders according to the following Equation:
- 4.
- Normalize the autocorrelation coefficients of the different orders according to the following Equation:
- 5.
- The results of the previous step are counted to obtain the transfer probability matrix at different step sizes;
- 6.
- Assuming that the previous data are the initial states, the state probabilities can be found using the corresponding transfer probability matrix;
- 7.
- Let the weighted sum of the probabilities of each state in the same state be the predicted probability; repeat steps 1 through 6 to perform the next round of prediction.
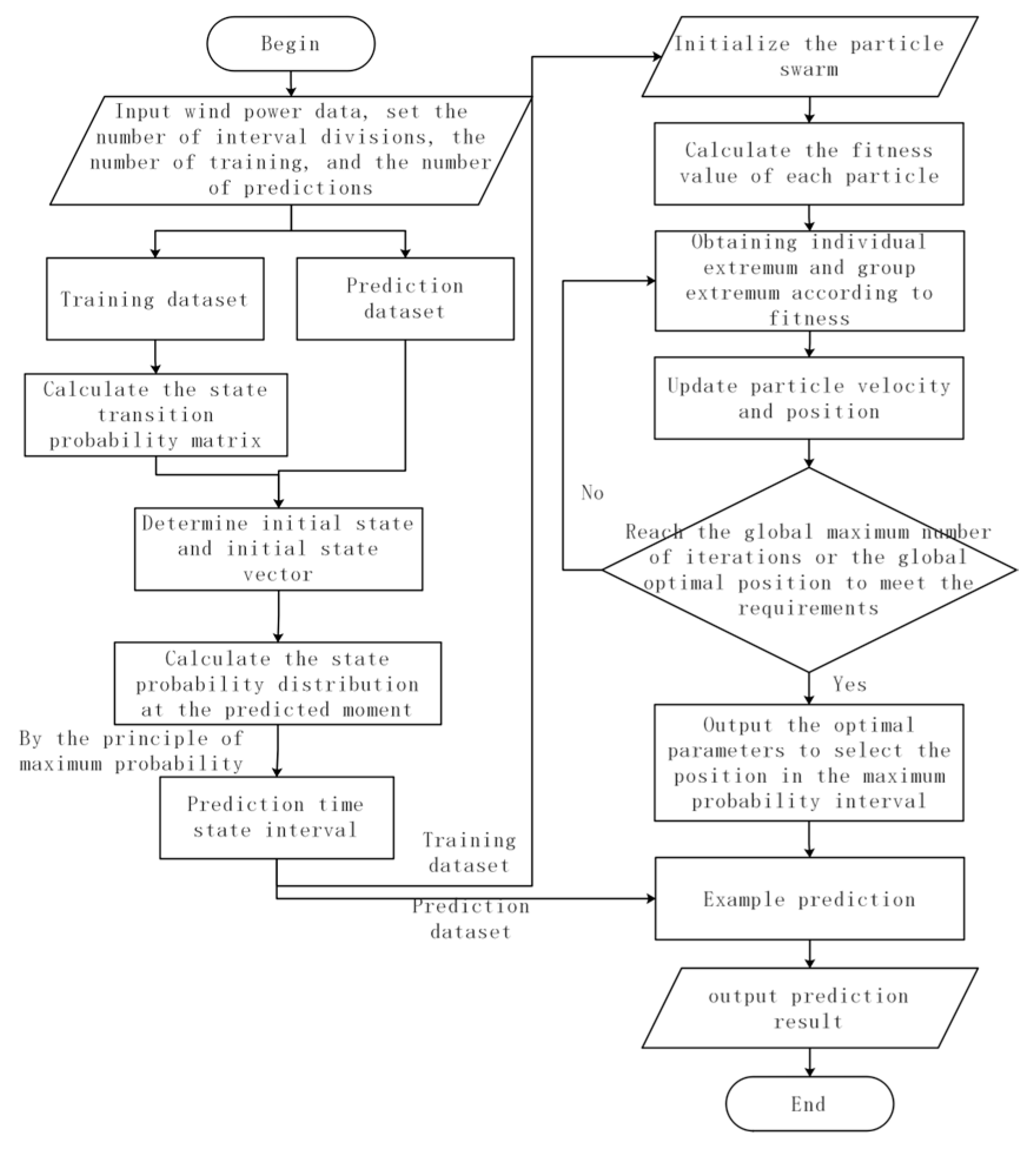
3. Markov-Based Prediction Approach Combined with the PSO-BP Neural Network
3.1. Hybrid Model
3.1.1. Markov and BP Neural Networks
3.1.2. Markov and PSO
3.1.3. Markov Combined with PSO and BP Neural Network
3.2. Evaluation Indicators
4. Numerical Experiments and Sensitivity Analysis
4.1. Data
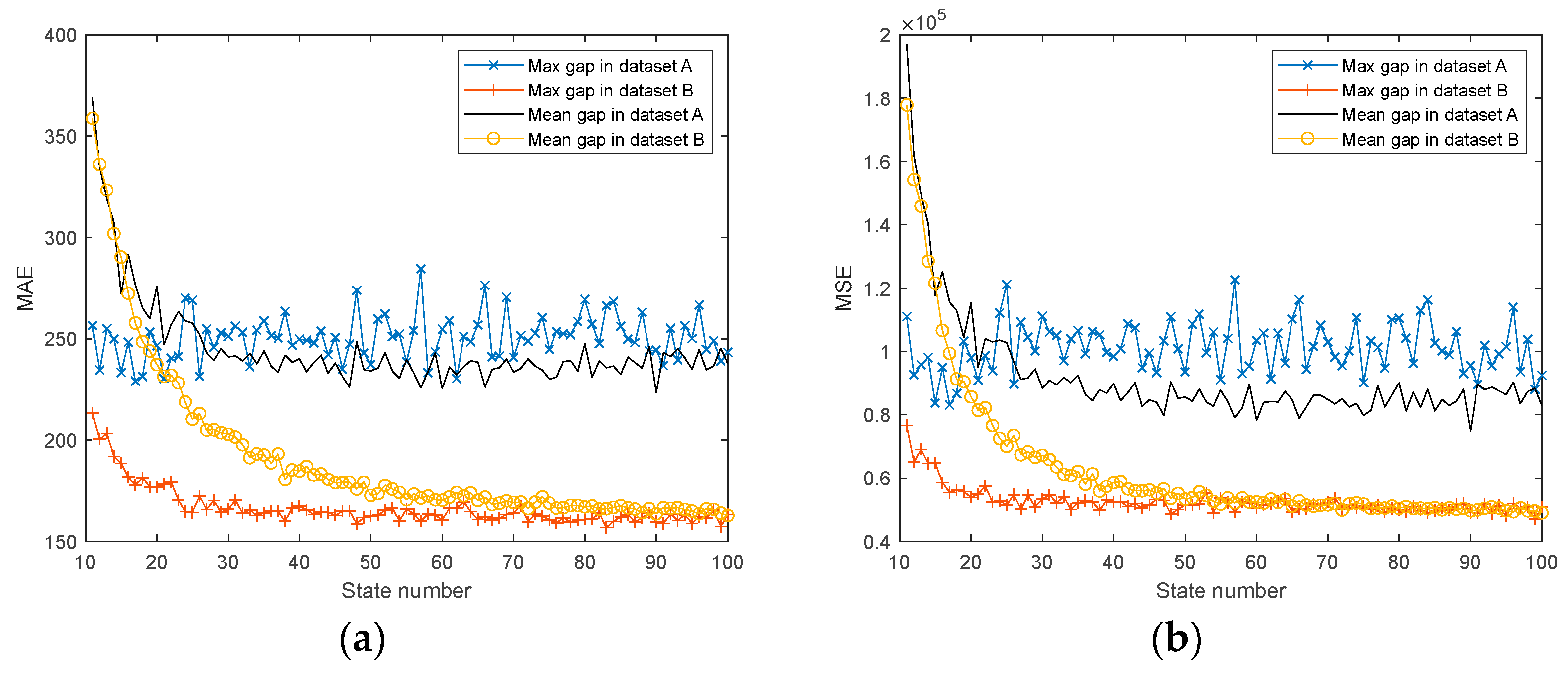
4.2. CPU Time Comparison for the Improved Higher-Order Markov
4.3. Comparison of Multiple Markov-Based Prediction Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | Parameter Meaning |
| Markov model order | |
| Number of interval splits | |
| Current moment | |
| Predicted steps | |
| Probability of state from i to j | |
| State Space | |
| The state at moment i | |
| MAE | Mean Absolute Error |
| MSE | Mean Square Error |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
| SMAPE | Symmetric Mean Absolute Percentage Error |
| Coefficient of Determination | |
| Actual value at moment i | |
| Predicted value at moment i | |
| Predicting the actual mean value of the data set | |
| Transfer probability matrix | |
| The distribution vector in the initial state | |
| Markov model interval split interval size | |
| Training Points | |
| Prediction Points | |
| The state interval to which wind power is attributed at moment i | |
| Wind power at predicted data points at time t | |
| The state corresponding to the largest probability interval in the probability interval at the next moment | |
| The final predicted power value at moment t | |
| Autocorrelation coefficient | |
| Normalized autocorrelation coefficient |
References
- Lu, X.; Chen, S.; Nielsen, C.P.; Zhang, C.; Li, J.; Xu, H.; Wu, Y.; Wang, S.; Song, F.; Wei, C.; et al. Combined Solar Power and Storage as Cost-Competitive and Grid-Compatible Supply for China’s Future Carbon-Neutral Electricity System. Proc. Natl. Acad. Sci. USA 2021, 118, e2103471118. [Google Scholar] [CrossRef]
- Batrancea, L.M.; Rathnaswamy, M.M.; Rus, M.-I.; Tulai, H. Determinants of Economic Growth for the Last Half of Century: A Panel Data Analysis on 50 Countries. J. Knowl. Econ. 2022, 13, 1–25. [Google Scholar] [CrossRef]
- Batrancea, L.; Pop, M.C.; Rathnaswamy, M.M.; Batrancea, I.; Rus, M.-I. An Empirical Investigation on the Transition Process toward a Green Economy. Sustainability 2021, 13, 13151. [Google Scholar] [CrossRef]
- Global Wind Report 2022; Global Wind Energy Council: Brussels, Belgium, 2022; Available online: https://gwec.net/global-wind-report-2022/ (accessed on 23 February 2023).
- Shamshad, A.; Bawadi, M.; Wanhussin, W.; Majid, T.; Sanusi, S. First and Second Order Markov Chain Models for Synthetic Generation of Wind Speed Time Series. Energy 2005, 30, 693–708. [Google Scholar] [CrossRef]
- Nfaoui, H.; Essiarab, H.; Sayigh, A.A.M. A Stochastic Markov Chain Model for Simulating Wind Speed Time Series at Tangiers, Morocco. Renew. Energy 2004, 29, 1407–1418. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Klockl, B. MCMC for Wind Power Simulation. IEEE Trans. Energy Convers. 2008, 23, 234–240. [Google Scholar] [CrossRef]
- Xie, K.; Liao, Q.; Tai, H.-M.; Hu, B. Non-Homogeneous Markov Wind Speed Time Series Model Considering Daily and Seasonal Variation Characteristics. IEEE Trans. Sustain. Energy 2017, 8, 1281–1290. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. First and Second Order Semi-Markov Chains for Wind Speed Modeling. Phys. Stat. Mech. Its Appl. 2013, 392, 1194–1201. [Google Scholar] [CrossRef]
- Yousuf, M.U.; Al-Bahadly, I.; Avci, E. Short-Term Wind Speed Forecasting Based on Hybrid MODWT-ARIMA-Markov Model. IEEE Access 2021, 9, 79695–79711. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Wang, Z.; Wu, L.; Zhai, B.; Lan, H.; Yang, S. Spatio-temporal Markov Chain Model for Very-short-term Wind Power Forecasting. J. Eng. 2019, 2019, 5018–5022. [Google Scholar] [CrossRef]
- Poncela-Blanco, M.; Poncela, P. Improving Wind Power Forecasts: Combination through Multivariate Dimension Reduction Techniques. Energies 2021, 14, 1446. [Google Scholar] [CrossRef]
- Yang, X.; Ma, X.; Kang, N.; Maihemuti, M. Probability Interval Prediction of Wind Power Based on KDE Method With Rough Sets and Weighted Markov Chain. IEEE Access 2018, 6, 51556–51565. [Google Scholar] [CrossRef]
- Munkhammar, J.; van der Meer, D.; Widén, J. Very Short Term Load Forecasting of Residential Electricity Consumption Using the Markov-Chain Mixture Distribution (MCM) Model. Appl. Energy 2021, 282, 116180. [Google Scholar] [CrossRef]
- Munkhammar, J.; van der Meer, D.; Widén, J. Probabilistic Forecasting of High-Resolution Clear-Sky Index Time-Series Using a Markov-Chain Mixture Distribution Model. Sol. Energy 2019, 184, 688–695. [Google Scholar] [CrossRef]
- Yang, D.; van der Meer, D.; Munkhammar, J. Probabilistic Solar Forecasting Benchmarks on a Standardized Dataset at Folsom, California. Sol. Energy 2020, 206, 628–639. [Google Scholar] [CrossRef]
- Guan, H.; Jie, H.; Guan, S.; Zhao, A. A Novel Fuzzy-Markov Forecasting Model for Stock Fluctuation Time Series. Evol. Intell. 2020, 13, 133–145. [Google Scholar] [CrossRef]
- Li, W.; Jia, X.; Li, X.; Wang, Y.; Lee, J. A Markov Model for Short Term Wind Speed Prediction by Integrating the Wind Acceleration Information. Renew. Energy 2021, 164, 242–253. [Google Scholar] [CrossRef]
- Chen, B.; Li, J. Combined Probabilistic Forecasting Method for Photovoltaic Power Using an Improved Markov Chain. IET Gener. Transm. Distrib. 2019, 13, 4364–4373. [Google Scholar] [CrossRef]
- Wang, C.-H.; Chen, Y.-T.; Wu, X. A Multi-Tier Inspection Queueing System with Finite Capacity for Differentiated Border Control Measures. IEEE Access 2021, 9, 60489–60502. [Google Scholar] [CrossRef]
- Liu, Q.; Li, D.; Liu, W.; Xia, T.; Li, J. A Novel Health Prognosis Method for a Power System Based on a High-Order Hidden Semi-Markov Model. Energies 2021, 14, 8208. [Google Scholar] [CrossRef]
- Wang, C.-H. A Three-Level Health Inspection Queue Based on Risk Screening Management Mechanism for Post-COVID Global Economic Recovery. IEEE Access 2020, 8, 177604–177614. [Google Scholar] [CrossRef] [PubMed]
- Nunez Segura, G.A.; Borges Margi, C. Centralized Energy Prediction in Wireless Sensor Networks Leveraged by Software-Defined Networking. Energies 2021, 14, 5379. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.-H.; Dong, Z.; Chen, S.; Yang, Q.; Wei, Y. A Matrix-Analytic Solution to Three-Level Multi-Server Queueing Model with a Shared Finite Buffer. In Genetic and Evolutionary Computing; Chu, S.-C., Lin, J.C.-W., Li, J., Pan, J.-S., Eds.; Springer Nature: Singapore, 2022; pp. 690–699. [Google Scholar]
- Wang, C.-H.; Luh, H.P. Estimating the Loss Probability under Heavy Traffic Conditions. Comput. Math. Appl. 2012, 64, 1352–1363. [Google Scholar] [CrossRef]
- Yoder, M.; Hering, A.S.; Navidi, W.C.; Larson, K. Short-Term Forecasting of Categorical Changes in Wind Power with Markov Chain Models: Forecasting Categorical Changes in Wind Power. Wind Energy 2013, 17, 1425–1439. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.; Lu, L.; Qi, R. First Order Multivariate Markov Chain Model for Generating Annual Weather Data for Hong Kong. Energy Build. 2011, 43, 2371–2377. [Google Scholar] [CrossRef]
- Carpinon, A.; Langella, R.; Testa, A.; Giorgio, M. Very Short-Term Probabilistic Wind Power Forecasting Based on Markov Chain Models. In Proceedings of the 2010 IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems, Singapore, 14–17 June 2010; pp. 107–112. [Google Scholar]
- Yun, P.; Ren, Y.; Xue, Y. Energy-Storage Optimization Strategy for Reducing Wind Power Fluctuation via Markov Prediction and PSO Method. Energies 2018, 11, 3393. [Google Scholar] [CrossRef]
- Carpinone, A.; Giorgio, M.; Langella, R.; Testa, A. Markov Chain Modeling for Very-Short-Term Wind Power Forecasting. Electr. Power Syst. Res. 2015, 122, 152–158. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Zhu, J. Residual Life Prediction Based on Dynamic Weighted Markov Model and Particle Filtering. J. Intell. Manuf. 2018, 29, 753–761. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S. Neural Networks and Statistical Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 978-1-4471-5571-3. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- PJM Electricity Market. Available online: https://dataminer2.pjm.com/feed/hrl_load_metered (accessed on 23 February 2023).
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Olarewaju, R.O.; Munda, J.L. Comparative Assessment of Wind Speed Predictive Capability of First-and Second-Order Markov Chain at Different Time Horizons for Wind Power Application. Energy Eng. 2019, 116, 54–80. [Google Scholar] [CrossRef]
- Wang, C.-H.; Chen, S.; Zhao, Q.; Suo, Y. An Efficient End-to-End Obstacle Avoidance Path Planning Algorithm for Intelligent Vehicles Based on Improved Whale Optimization Algorithm. Mathematics 2023, 11, 1800. [Google Scholar] [CrossRef]
- Chen, S.; Wang, C.-H.; Dong, Z.; Zhao, Q.; Yang, Q.; Wei, Y.; Huang, G. Performance Evaluation of Three Intelligent Optimization Algorithms for Obstacle Avoidance Path Planning. In Genetic and Evolutionary Computing; Chu, S.-C., Lin, J.C.-W., Li, J., Pan, J.-S., Eds.; Springer Nature: Singapore, 2022; pp. 60–69. [Google Scholar]
- Vancea, D.; Kamer-Ainur, A.; Simion, L.; Vanghele, D. Export Expansion Policies. An Analysis of Romanian Exports Between 2005–2020 Using the Principal Component Analysis Method and Short Recommandations for Increasing This Activity. Struct. Transf. Bus. Dev. 2021, 20, 614–634. [Google Scholar]
- Aivaz, K.-A.; Munteanu, I.F.; Stan, M.-I.; Chiriac, A. A Multivariate Analysis of the Links between Transport Noncompliance and Financial Uncertainty in Times of COVID-19 Pandemics and War. Sustainability 2022, 14, 10040. [Google Scholar] [CrossRef]

















| Parameter Setting | Value |
|---|---|
| Number of input layer nodes | 3 |
| Number of hidden layer nodes | 5 |
| Number of output layer nodes | 1 |
| Number of training sessions | 1000 |
| Learning Rate | 0.01 |
| Minimum error of training target | 0.001 |
| Hidden layer transfer function | tansig |
| Hidden layer transfer function | purelin |
| Parameter Setting | Value |
|---|---|
| Group size | 50 |
| Dimensionality | 60 |
| Number of evolutions | 100 |
| Acceleration constant c1 | 1.3 |
| Acceleration constant c2 | 1.3 |
| Maximum speed | 0.1 |
| Inertia weights | 1.8 |
| Models | Number of Interval Splits | Prediction Points | Training Points | Transfer Probability Matrix Memory Space Size | Time Complexity |
|---|---|---|---|---|---|
| 3rd-order Markov model | |||||
| 4th-order Markov model | |||||
| 5th-order Markov model | |||||
| k-order Markov model | |||||
| 3rd-order improved Markov model | N/A | ||||
| 4th-order improved Markov model | N/A | ||||
| 5th-order improved Markov model | N/A | ||||
| k-order improved Markov model | N/A |
| Prediction Algorithms | MAE | MSE | RMSE | MAPE | R-squared | SMAPE | CPU Time |
|---|---|---|---|---|---|---|---|
| first-order Markov | 238.51 | 97,269.98 | 311.88 | 17.81% | 0.846 | 6.57% | 0.359 |
| second-order Markov | 210.35 | 81,186.05 | 284.93 | 16.58% | 0.871 | 5.31% | 1.297 |
| Markov-PSO-BP | 179.26 | 64,441.47 | 253.85 | 12.7% | 0.9005 | 4.44% | 85.312 |
| Markov-PSO | 237.28 | 94,774.67 | 307.85 | 17.76% | 0.8537 | 6.49% | 4.312 |
| ARIMA(2,0,2) | 183.34 | 65,783.07 | 256.48 | 13.58% | 0.9116 | 4.56% | 9.203 |
| BPNN | 185.01 | 67,882.95 | 260.54 | 13.12% | 0.8952 | 4.63% | 0.515 |
| Markov-BP | 183.62 | 66,599.47 | 258.06 | 12.96% | 0.8972 | 4.61% | 0.687 |
| two-step weighted Markov | 279 | 135,322.8 | 367.85 | 20.91% | 0.7911 | 7.21% | 0.562 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-H.; Zhao, Q.; Tian, R. Short-Term Wind Power Prediction Based on a Hybrid Markov-Based PSO-BP Neural Network. Energies 2023, 16, 4282. https://doi.org/10.3390/en16114282
Wang C-H, Zhao Q, Tian R. Short-Term Wind Power Prediction Based on a Hybrid Markov-Based PSO-BP Neural Network. Energies. 2023; 16(11):4282. https://doi.org/10.3390/en16114282
Chicago/Turabian StyleWang, Chia-Hung, Qigen Zhao, and Rong Tian. 2023. "Short-Term Wind Power Prediction Based on a Hybrid Markov-Based PSO-BP Neural Network" Energies 16, no. 11: 4282. https://doi.org/10.3390/en16114282
APA StyleWang, C.-H., Zhao, Q., & Tian, R. (2023). Short-Term Wind Power Prediction Based on a Hybrid Markov-Based PSO-BP Neural Network. Energies, 16(11), 4282. https://doi.org/10.3390/en16114282







