On the Optimal Shape and Efficiency Improvement of Fin Heat Sinks
Abstract
1. Introduction
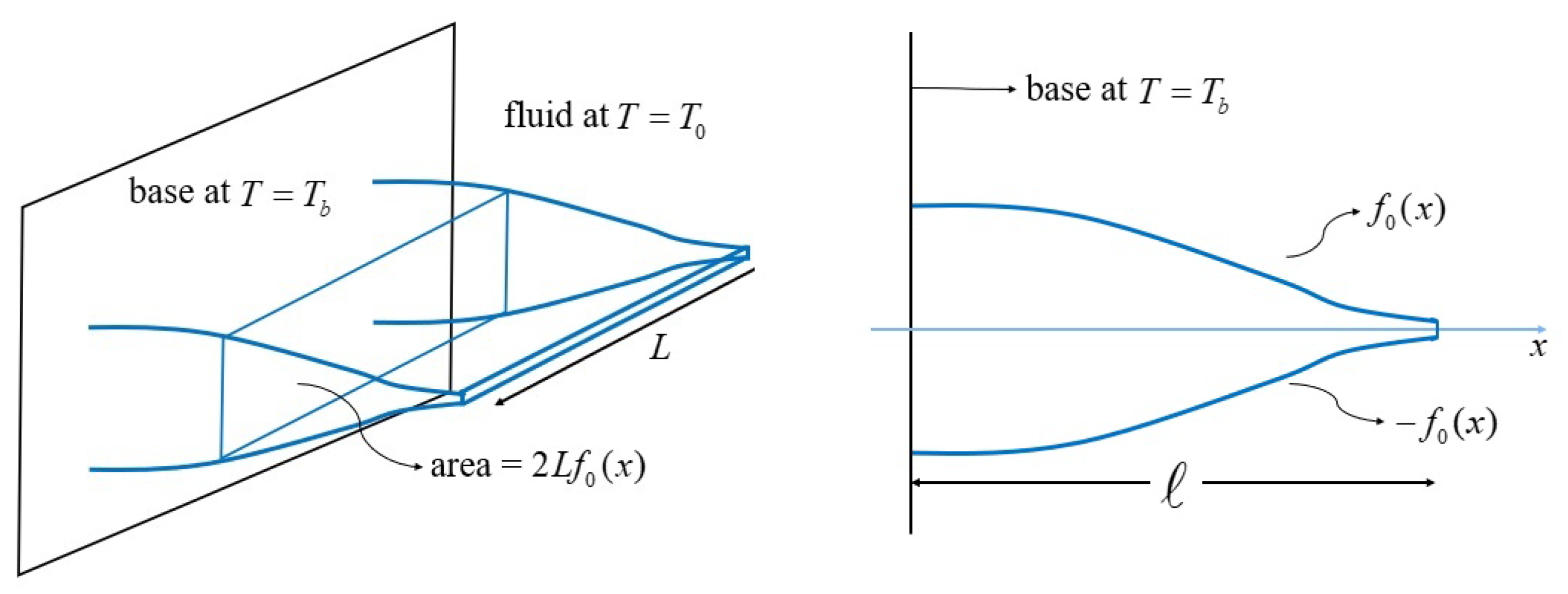
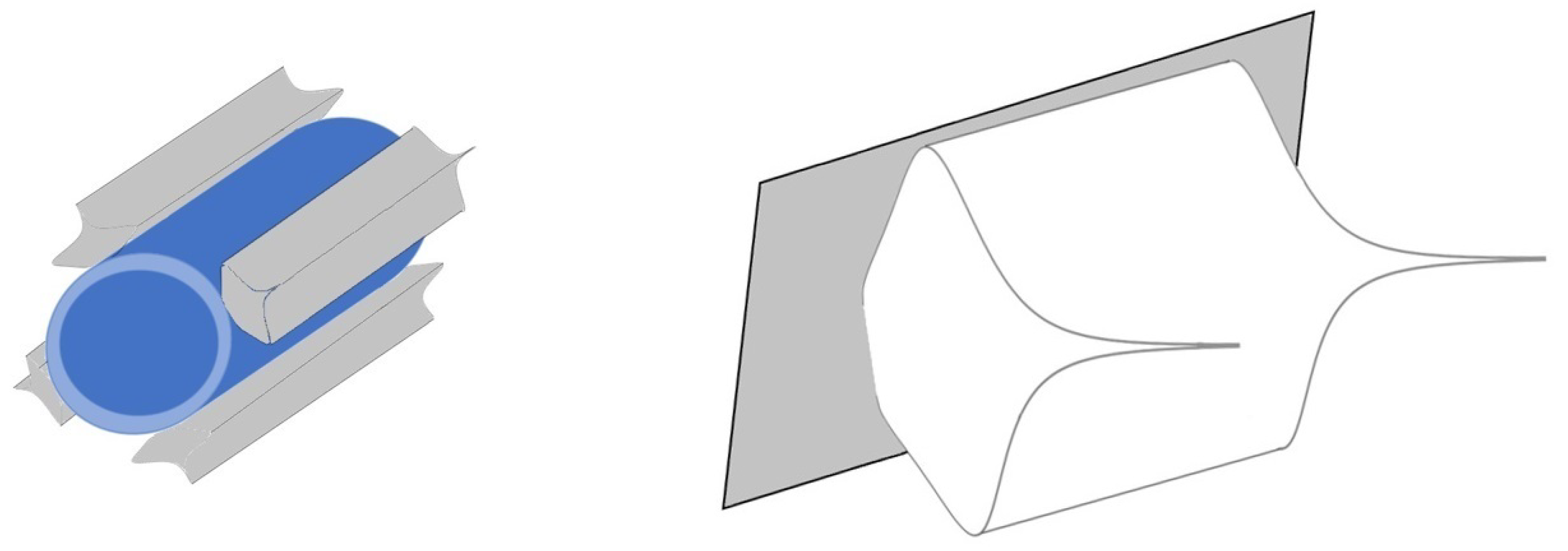
2. Description of the Physical Model
3. The Entropic Efficiency
4. The Case of Non-Radiating Fins
4.1. Tip at
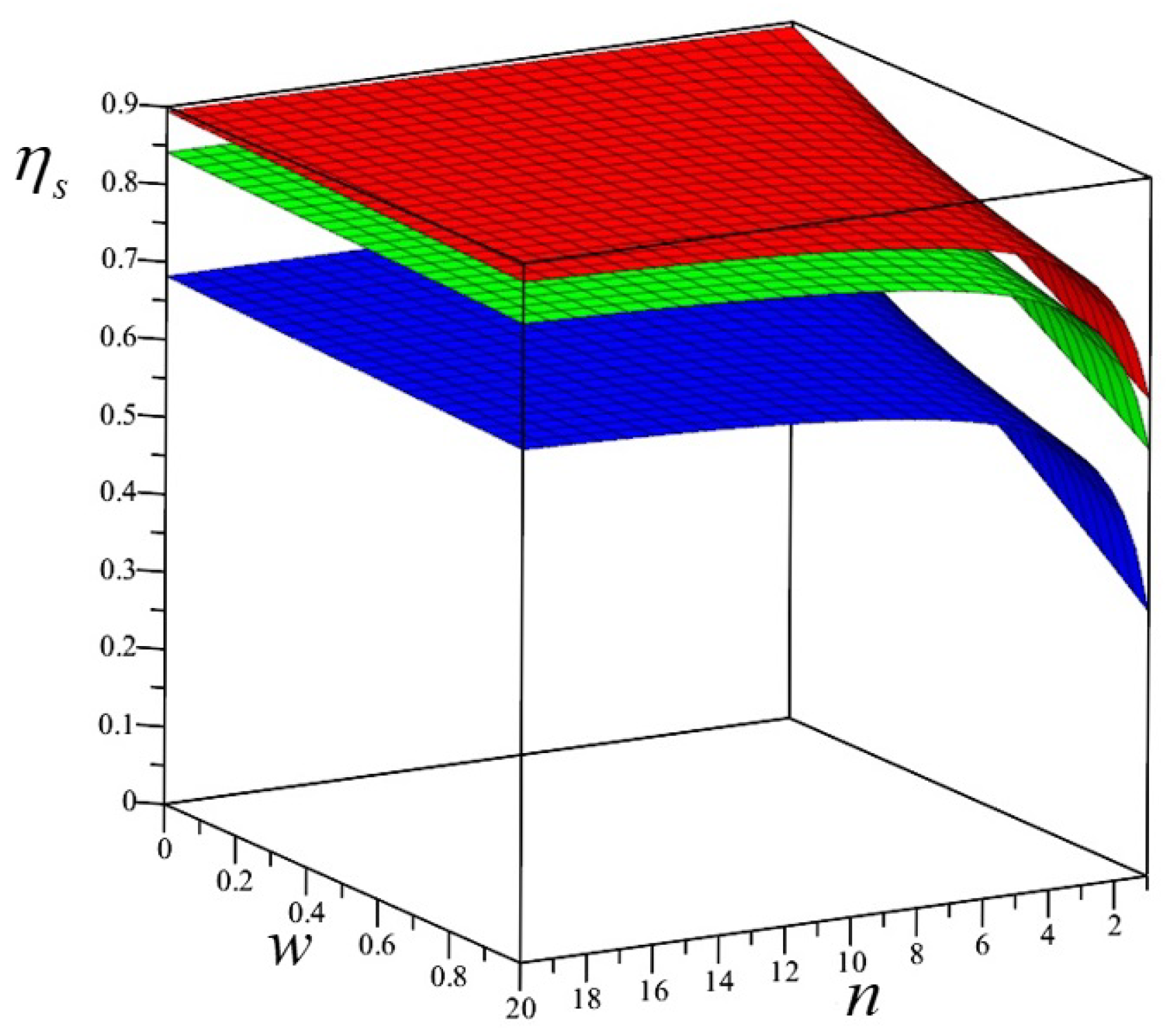
- . For small of w and large n the value of the efficiency (11) is ∼ 0.68. Numerically we see that only if , where is a certain value of w that depends also on n. A plot of as a function of n is reported in Figure 6. It is possible to show that for n large and for the given values of and m, is asymptotic to 0.3174…
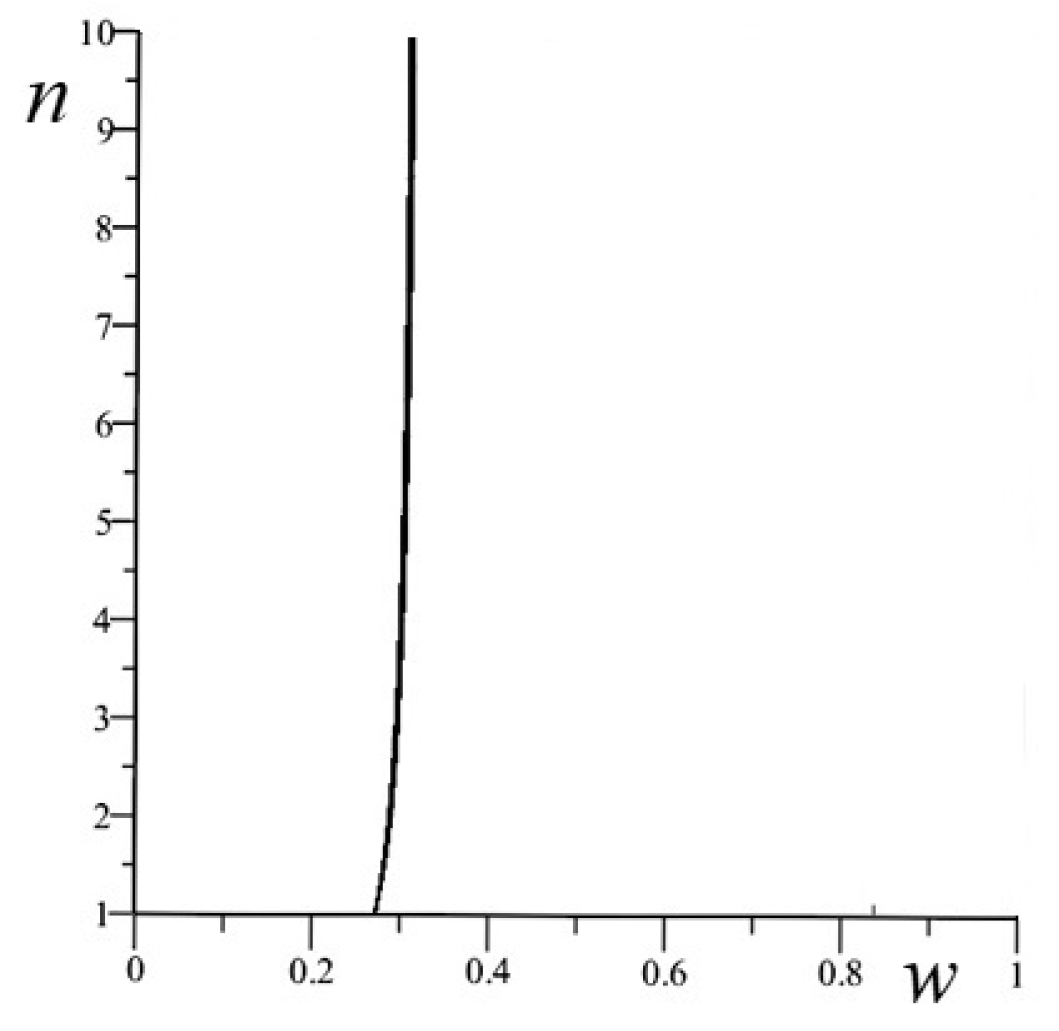
- . Again, we have a threshold such that only if . For n large is asymptotic to 0.361... We take . The asymptotic maximum value of the efficiency, if , is given by . This is the maximum value for the given parameters m, , k and w, obtained for large n. However, for large values of n, the maximum of becomes greater than four. There is another threshold value, this time for n, given by , such that the maximum of is not greater than four. Therefore, we take . The corresponding value of the efficiency is . The fin profile is reported in (Figure 8).
- . We have a threshold such that only if . For n large is asymptotic to 0.389... We take . The asymptotic maximum value of the efficiency is given by . However, for large values of n, the maximum of becomes greater than four. The threshold value for n (such that the maximum of is not greater than 4) is now given by . Therefore, we take . The value of the efficiency is .
- . We have a threshold such that only if . For n large is asymptotic to 0.407... We take . The asymptotic maximum value of the efficiency in this case is given by . There is a threshold value for n, given by , such that the maximum of is not greater than four. Therefore, we take . The value of the efficiency is . Actually, for small values of n, it would be possible to take some smaller values of w with respect to (since actually depends on n). But the difference in the efficiencies is not really large. The fin profile is reported in Figure 9.
- . We have a threshold such that only if . For n large is asymptotic to 0.420... We take . The asymptotic maximum value of the efficiency in this case is given by . The threshold value for n is now given by . Therefore, we take . The corresponding value of the efficiency is .
4.2. The Insulated Tip
- . All the parameters are fixed apart n. As a function of n the efficiency is an increasing function, with an asymptotic value equal to 0.870.... However, for n greater than 7.26 the function has a maximum greater than 4. Therefore, we take . The corresponding value of the efficiency is 0.863.
- . As a function of n now the efficiency is asymptotic to ∼0.9. However, the threshold on n giving a maximum of greater than four is very small: it is given by . We take . The corresponding value of the efficiency is ∼ 0.874.
- . The efficiency is asymptotic to ∼0.92. For this value of k the threshold value of n is smaller than 1: the corresponding value of the efficiency is smaller than the previous, giving an optimal value of k equal to 3.
4.3. Comparison with the Classical Definition of the Efficiency for Non-Radiating Fins
5. Profile Optimization of the Convecting–Radiating Fin
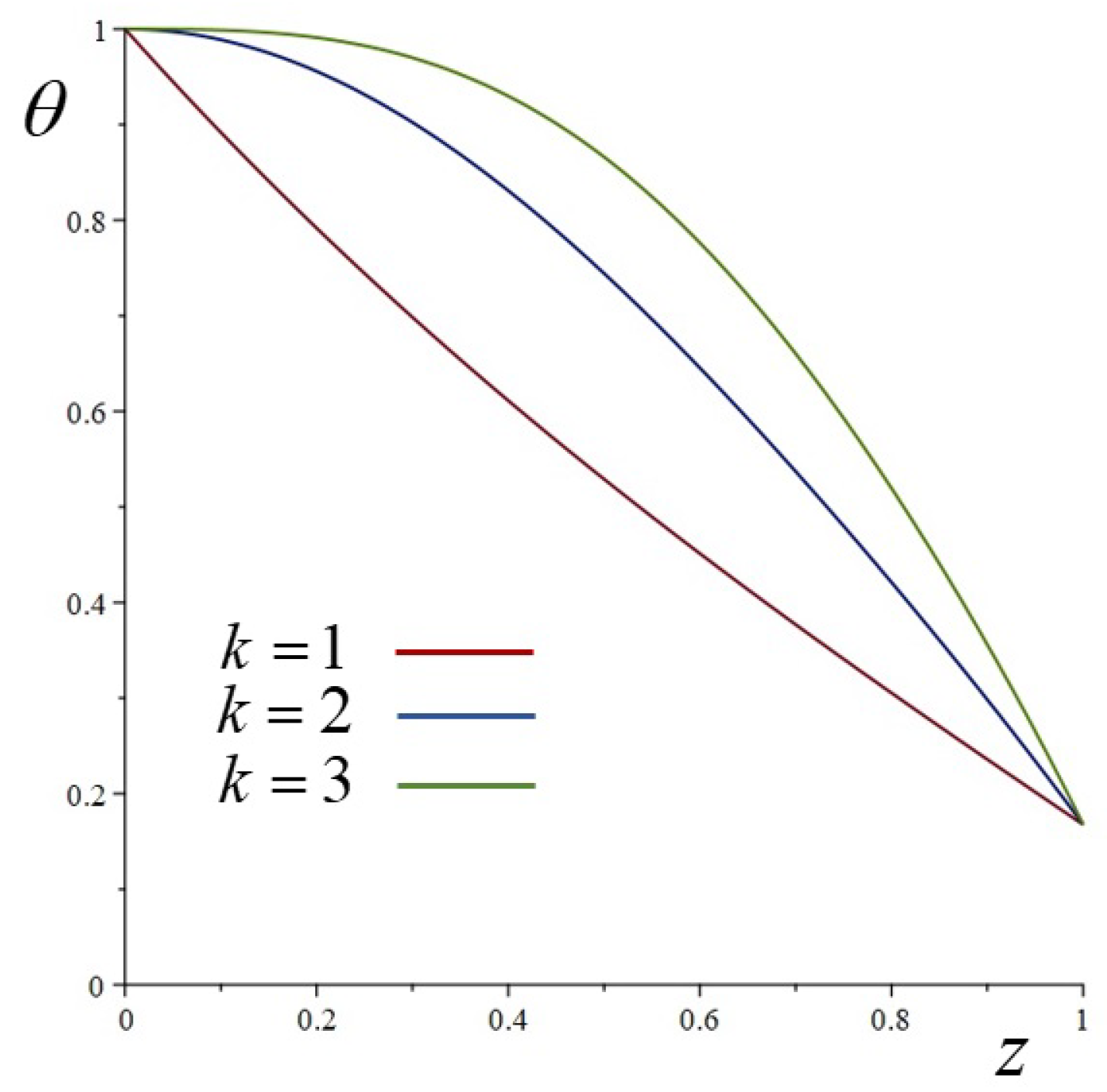
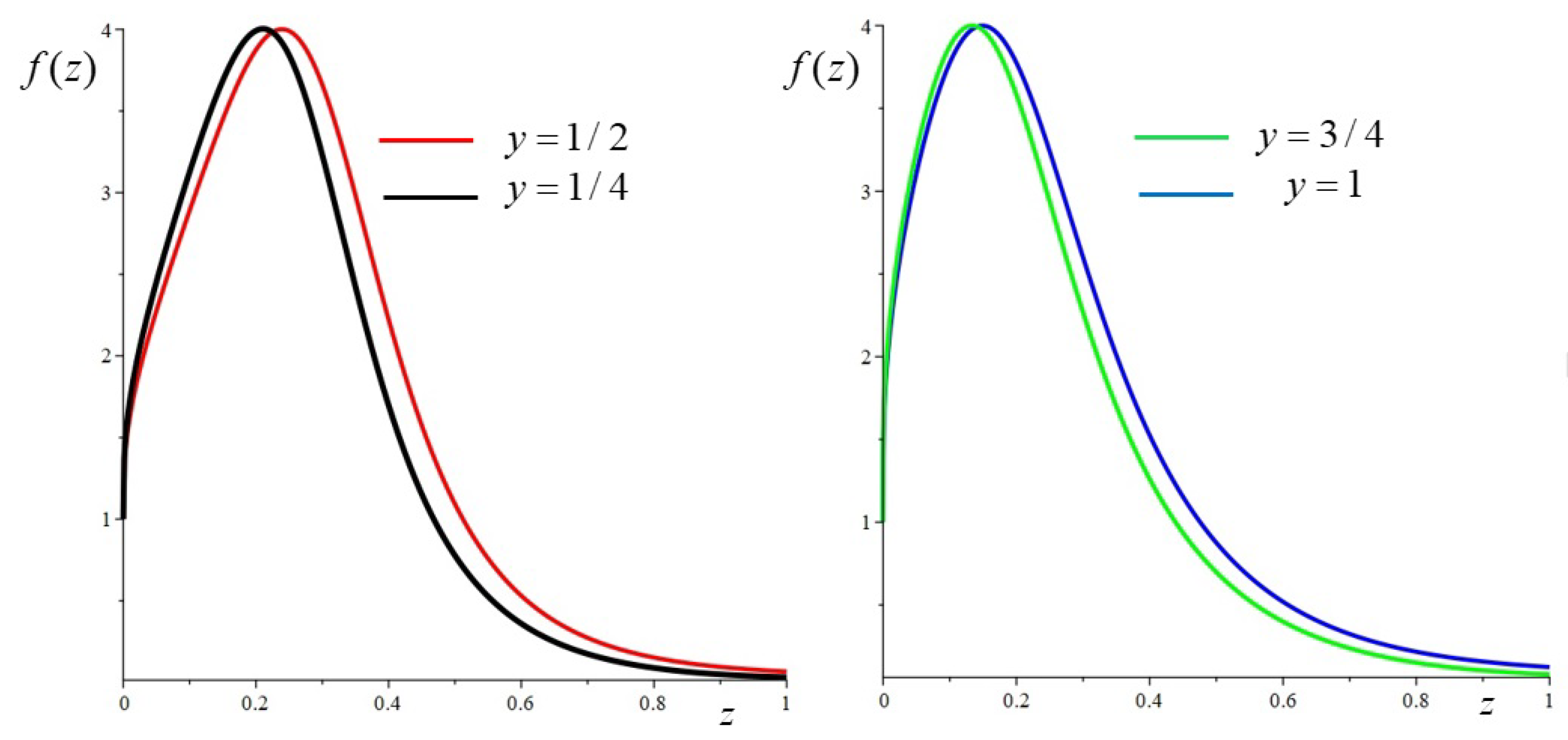
- . For fixed values of w and n the value of the efficiency (28) is a function of y. For small w and large n this function is asymptotic, say, to . is decreasing with y: it goes from for to for . Numerically we see that only if , where is a certain value of w that depends on n and y. It is possible to show that for n large and for the given values of and m, is asymptotic to , so we take . The corresponding profiles for and four values of y are given in Figure 12. The efficiency, with these values of the parameters, is a decreasing function of y from for to for . A plot of as a function of y is given in Figure 13.
- . Again, we see that only if , where is a certain value of w that depends on n and y. It is possible to show that for n large and for the given values of and m, is asymptotic to , so we take . For any fixed value of there is a threshold value of n, such that the maximum of is greater than four for . For , , and 1, the values of are, respectively, given by , , and . By taking values of n just below these thresholds, one obtains the following values of the efficiencies (in order from to ): , , and .
- . The threshold value of w, is asymptotic, for n large, to , so we take . For any fixed value of there is a threshold value of n, such that the maximum of is greater than four for . For , , and 1, the values of are, respectively, given by , , and . The corresponding efficiencies are given by 0.641, 0.607, 0.571 and 0.528.
- . The threshold value of w, is now asymptotic, for large n, to : let us take . The threshold values of n, say , such that the maximum of is greater than four for , are the following: in , in , in and in . The corresponding efficiencies are given by , , and .
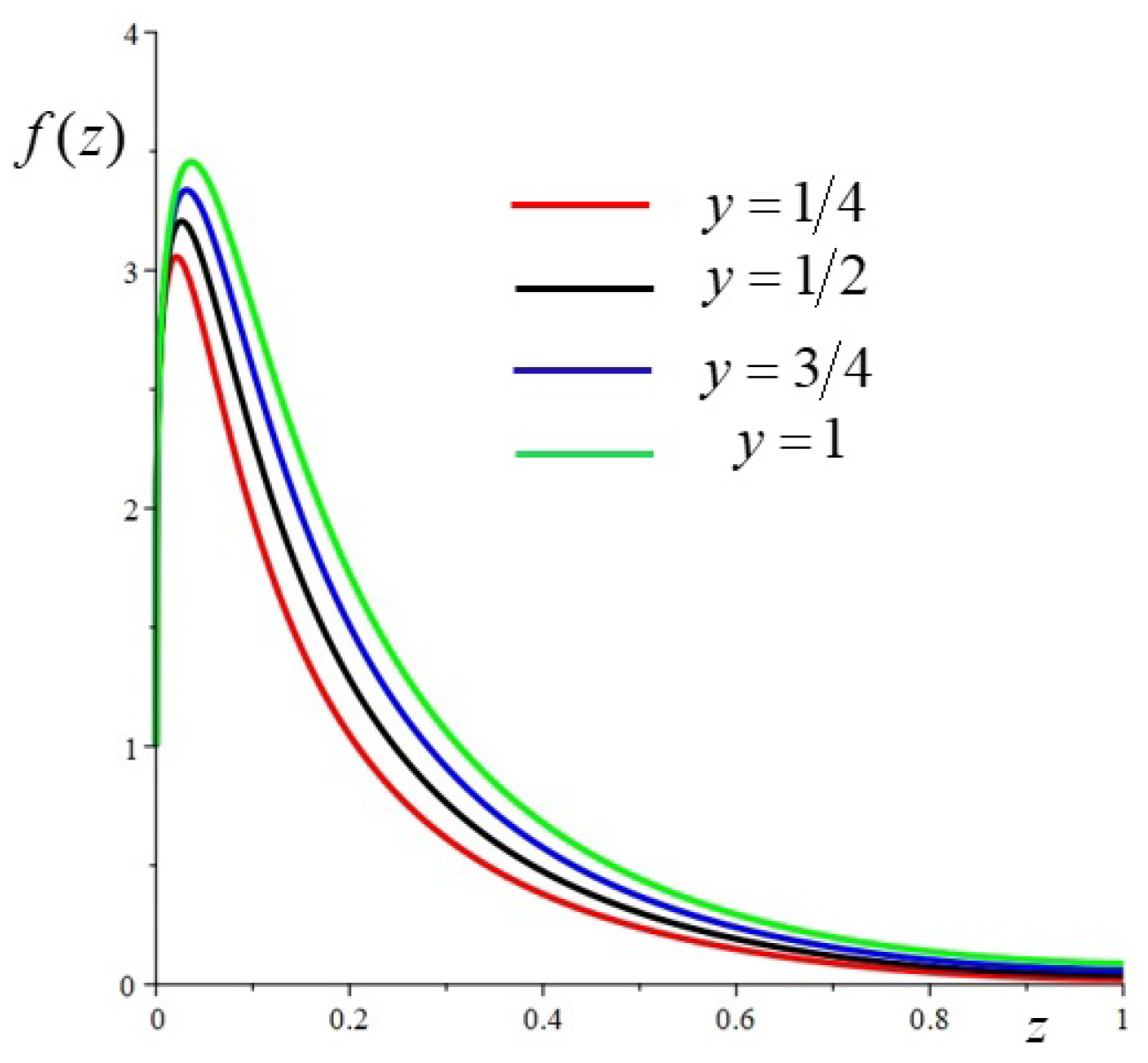
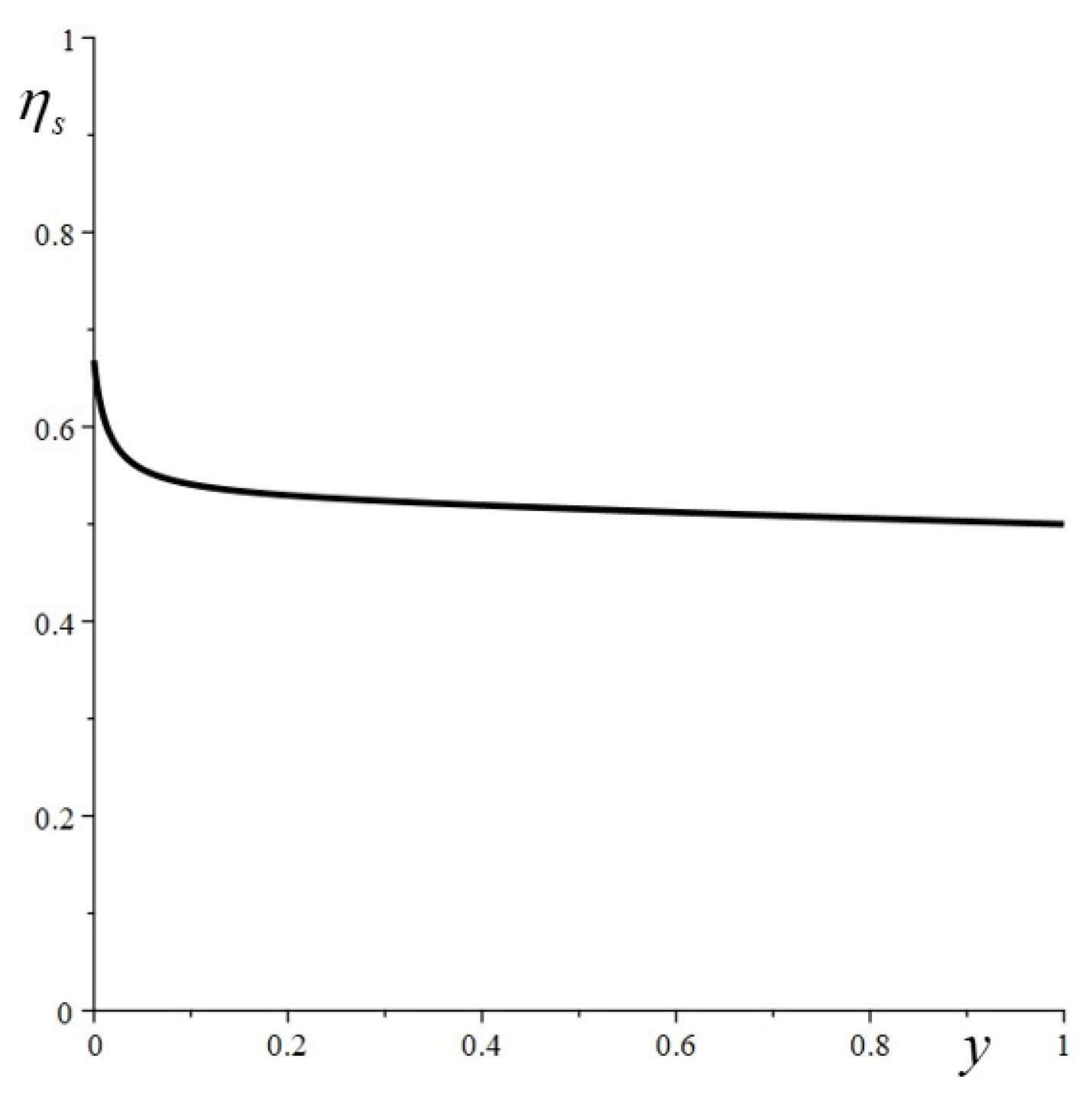
6. Analysis of the Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kraus, A.D.; Aziz, A.; Welty, J.R. Extended Surface Heat Transfer; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Howell, J.R.; Mengüç, M.P.; Siegel, R. Thermal Radiation Heat Transfer, 6th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Nguyen, H.; Aziz, A. Heat transfer from convecting-radiating fins of different profile shapes. Heat Mass Transf. 1992, 27, 67–72. [Google Scholar] [CrossRef]
- Bochicchio, I.; Naso, M.G.; Vuk, E.; Zullo, F. Convecting-radiating fins: Explicit solutions, efficiency and optimization. Appl. Math. Model. 2021, 89, 171–187. [Google Scholar] [CrossRef]
- Giorgi, C.; Zullo, F. Entropy Production and Efficiency in Longitudinal Convecting-Radiating Fins. Proceedings 2020, 58, 13. [Google Scholar]
- Giorgi, C.; Zullo, F. Entropy Rates and Efficiency of Convecting-Radiating Fins. Energies 2021, 14, 1643. [Google Scholar] [CrossRef]
- Mosayebidorcheh, S.; Hatami, M.; Mosayebidorcheh, T.; Ganji, D.D. Optimization analysis of convective-radiative longitudinal fins with temperature-dependent properties and different section shapes and materials. Energy Convers. Manag. 2015, 106, 1286–1294. [Google Scholar] [CrossRef]
- Mao, Q.; Hu, X.; Zhu, Y. Numerical Investigation of Heat Transfer Performance and Structural Optimization of Fan-Shaped Finned Tube Heat Exchanger. Energies 2022, 15, 5682. [Google Scholar] [CrossRef]
- Gardner, K.A. Efficiency of Extended Surface. Trans. ASME 1945, 67, 621. [Google Scholar]
- Marck, G.; Nadin, G.; Privat, Y. What is the optimal shape of a fin for one-dimensional heat conduction? SIAM J. Appl. Math. 2014, 74, 1194–1218. [Google Scholar] [CrossRef]
- Basavarajappa, S.; Manavendra, G.; Prakash, S.B. A review on performance study of finned tube heat exchanger. J. Phys. Conf. Ser. 2020, 1473, 012030. [Google Scholar] [CrossRef]
- Abdulateef, A.M.; Mat, S.; Abdulateef, J.; Sopian, K.; Al-Abidi, A.A. Geometric and design parameters of fins employed for enhancing thermal energy storage systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 1620–1635. [Google Scholar] [CrossRef]
- Cuce, P.M.; Cuce, E. Optimization of configurations to enhance heat transfer from a longitudinal fin exposed to natural convection and radiation. Int. J.-Low-Carbon Technol. 2014, 9, 305–310. [Google Scholar] [CrossRef]
- del Rio, F.; de la Selva, S.M.T. Reversible and irreversible heat transfer by radiation. Eur. J. Phys. 2015, 36, 035001. [Google Scholar] [CrossRef]
- Schwabl, F. Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 13 978-3-540-32343-3. [Google Scholar]
- Saha, S.K.; Ranjan, H.; Emani, M.S.; Bharti, A.K. Heat Transfer Enhancement in Externally Finned Tubes and Internally Finned Tubes and Annuli; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]





| 0.462 | 0.520 | |
| 0.619 | 0.668 | |
| 0.701 | 0.743 | |
| 0.740 | 0.779 | |
| 0.758 | 0.797 | |
| 0.758 | 0.799 | |
| 0.761 | 0.814 | |
| 0.823 | 0.863 | |
| 0.836 | 0.875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zullo, F.; Giorgi, C. On the Optimal Shape and Efficiency Improvement of Fin Heat Sinks. Energies 2023, 16, 316. https://doi.org/10.3390/en16010316
Zullo F, Giorgi C. On the Optimal Shape and Efficiency Improvement of Fin Heat Sinks. Energies. 2023; 16(1):316. https://doi.org/10.3390/en16010316
Chicago/Turabian StyleZullo, Federico, and Claudio Giorgi. 2023. "On the Optimal Shape and Efficiency Improvement of Fin Heat Sinks" Energies 16, no. 1: 316. https://doi.org/10.3390/en16010316
APA StyleZullo, F., & Giorgi, C. (2023). On the Optimal Shape and Efficiency Improvement of Fin Heat Sinks. Energies, 16(1), 316. https://doi.org/10.3390/en16010316







