Transient Calculation Studies of Liquid–Solid Collision in Jet Descaling
Abstract
1. Introduction
2. Droplet–Scale Impact Model
2.1. Physical Analysis
2.2. Coupling of 2D Droplet–Scale Impact Model
2.3. Solving Droplet–Scale Impact Model
3. Simulation Results, Analysis, and Conclusions
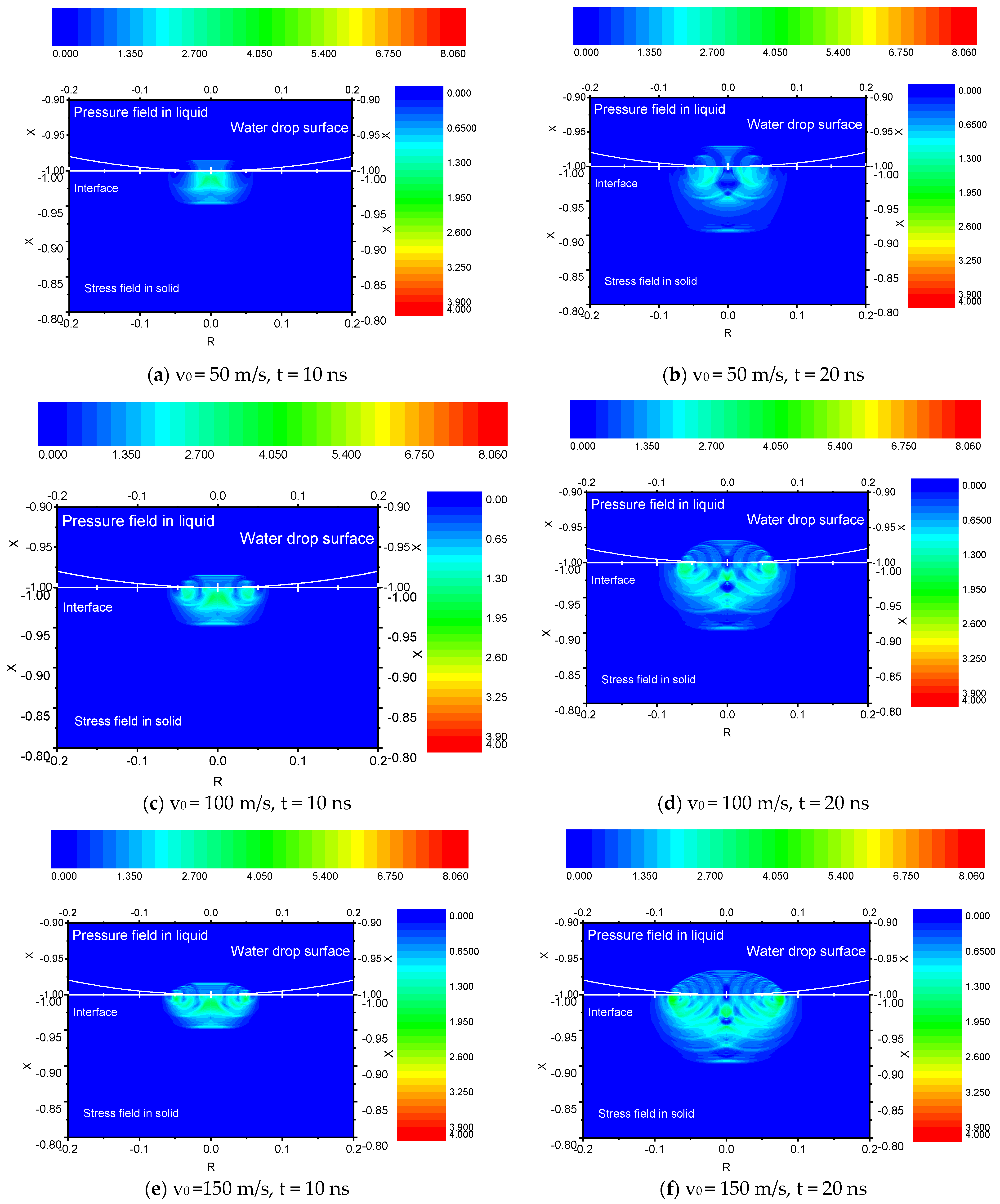
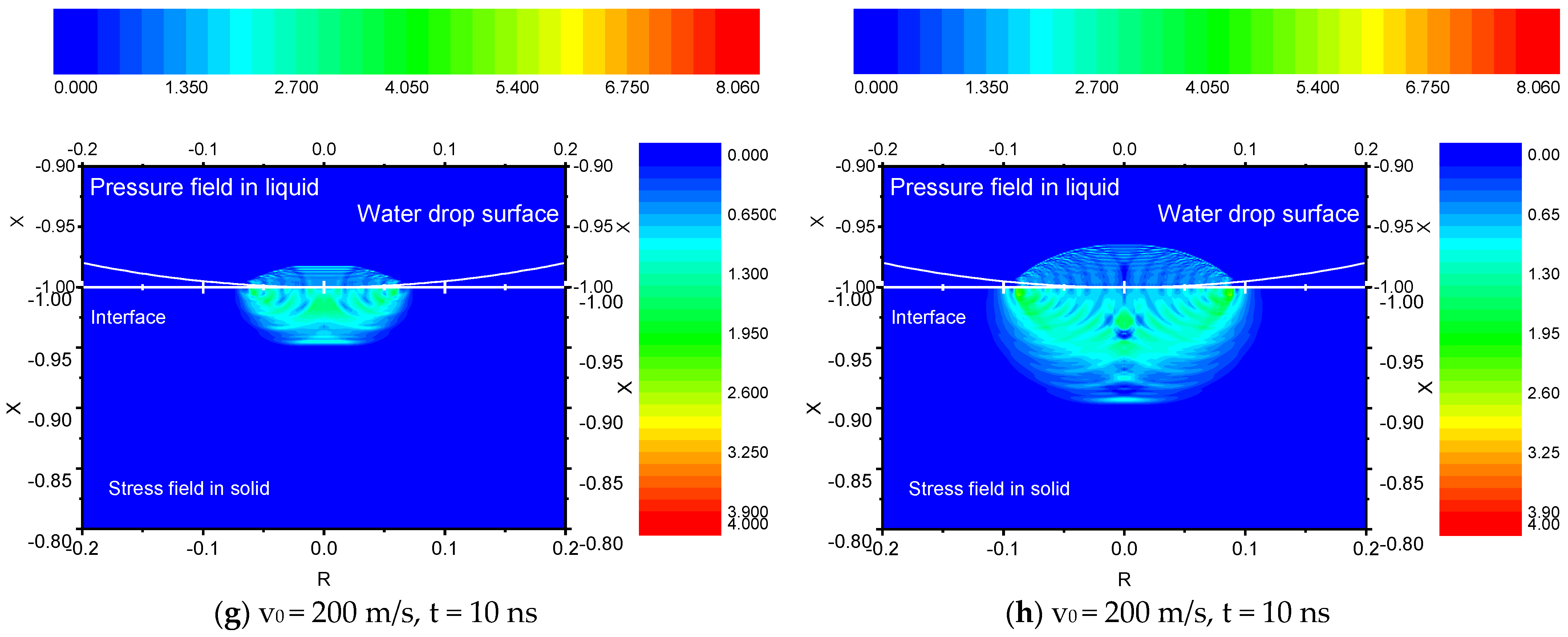
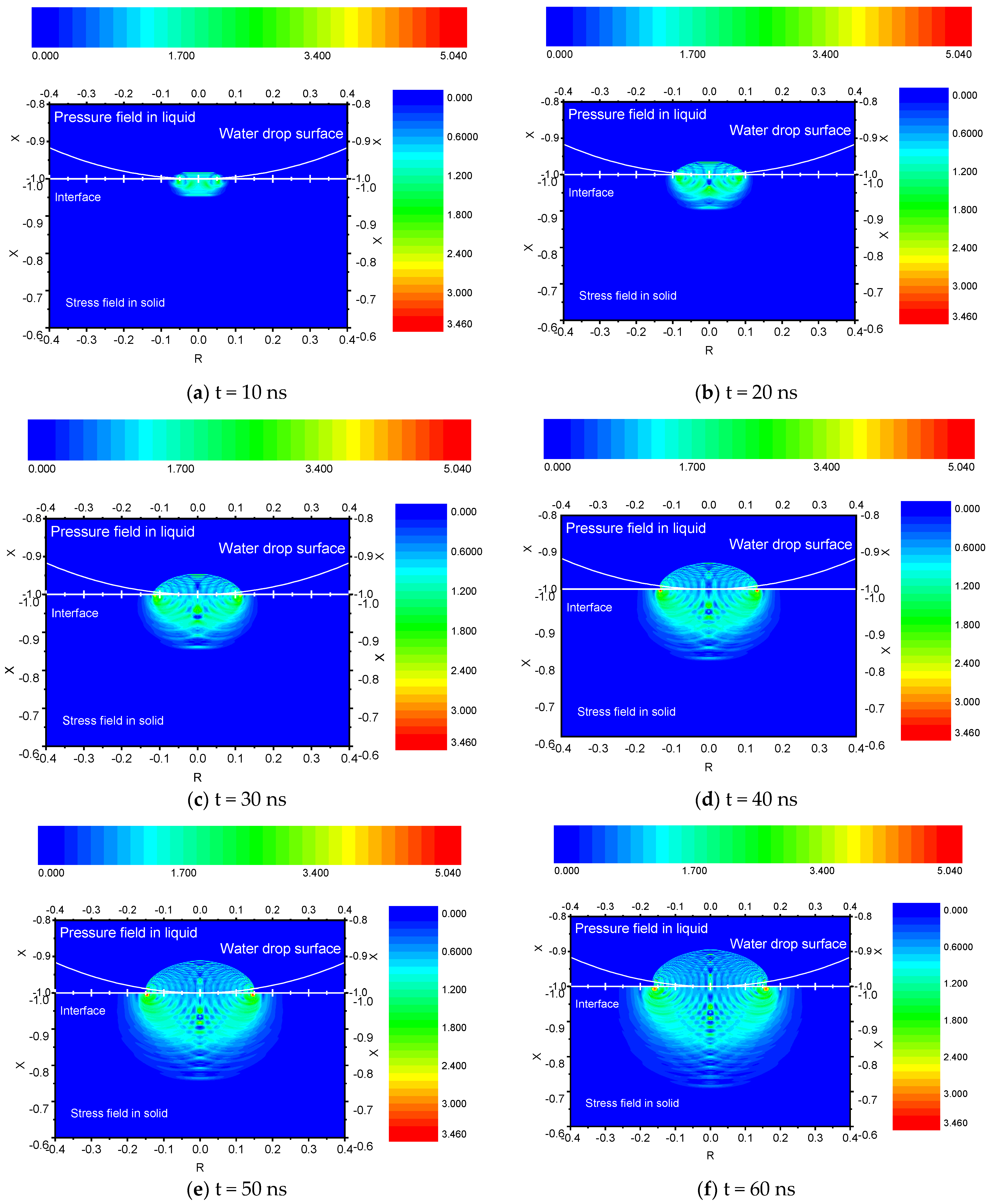
Impact of the Droplet on the Scale
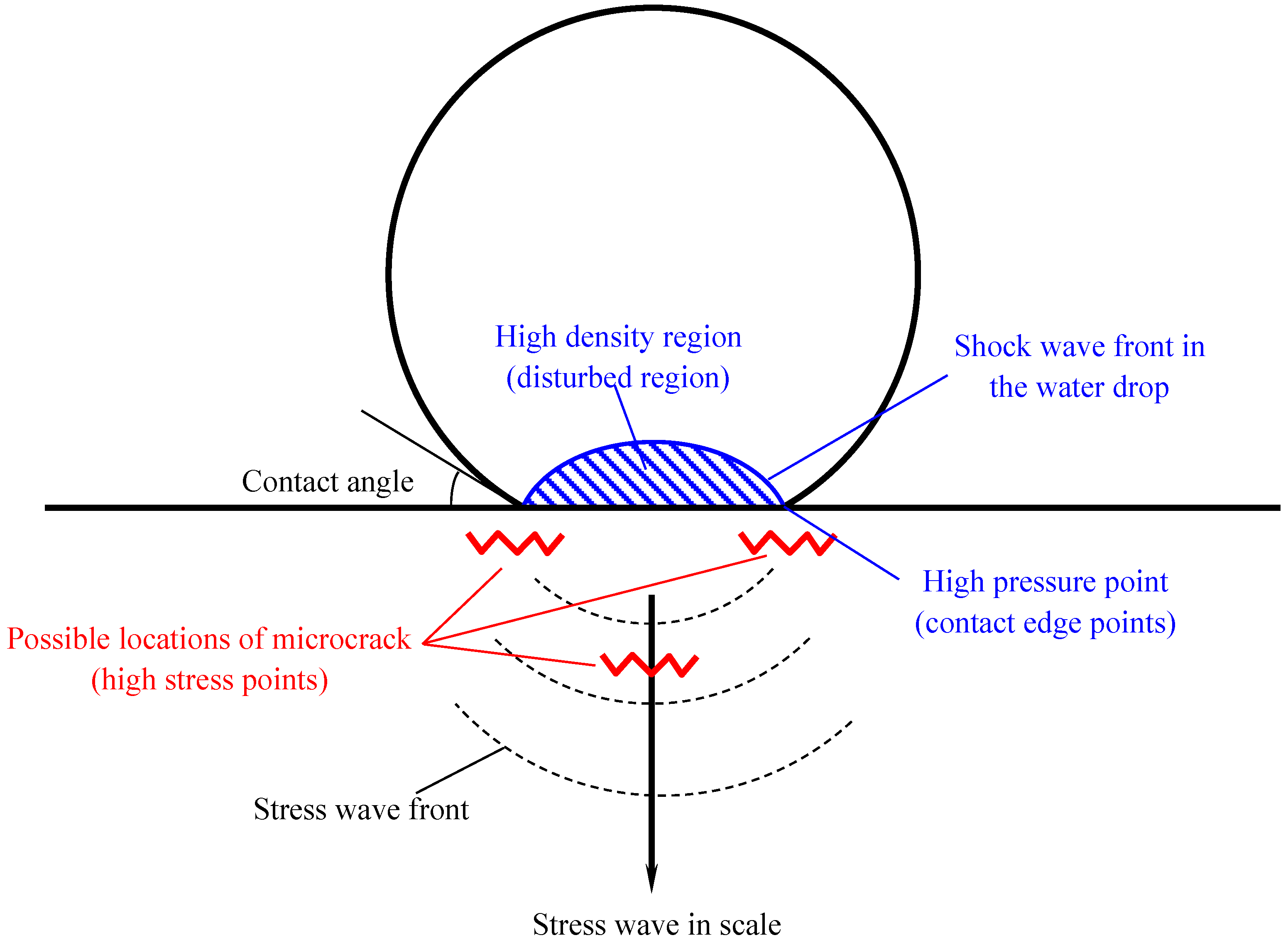
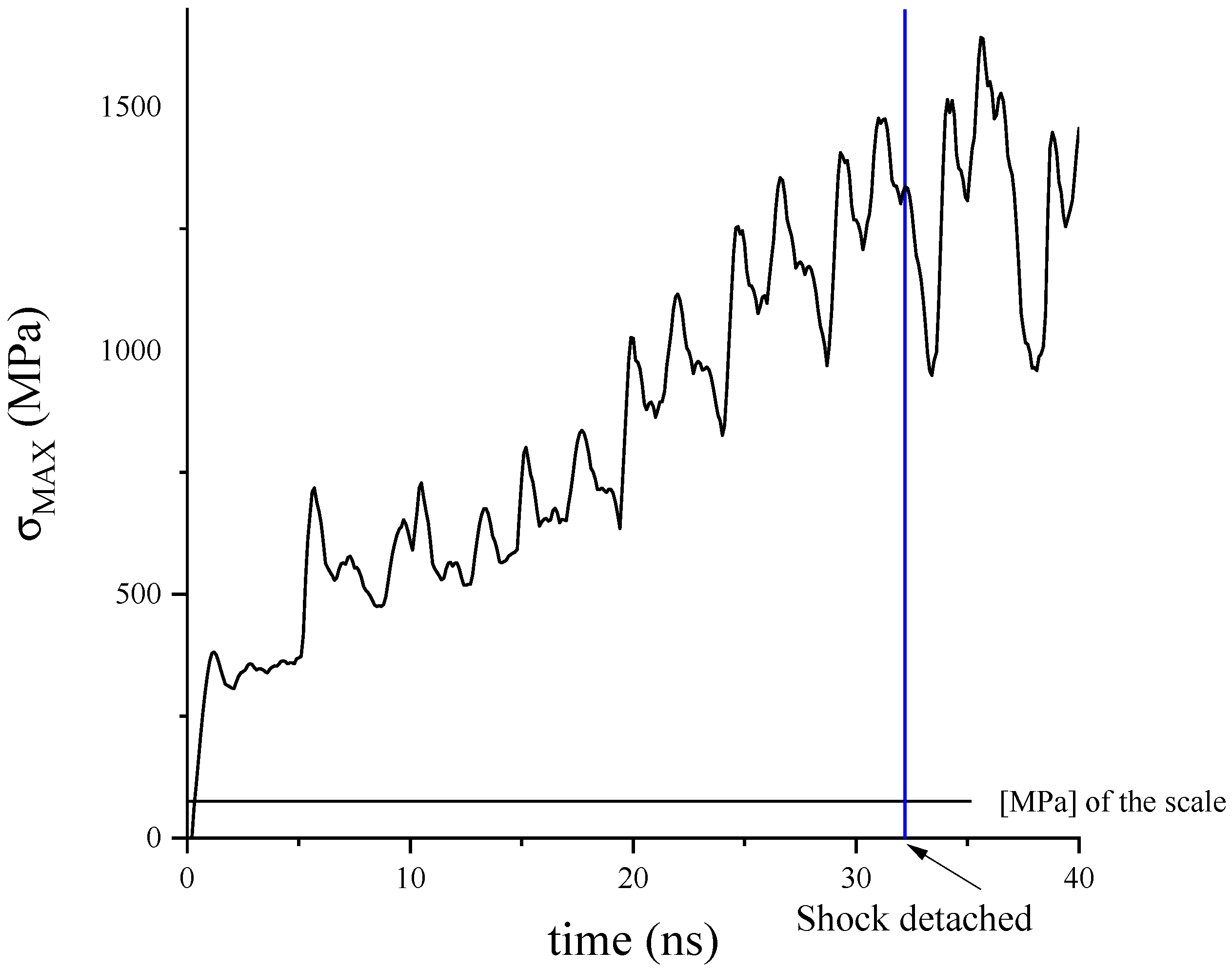
- The pressure value in the droplet keeps increasing. On the contact surface of the water droplet and the scale, the point of highest pressure always occurs at the edge of the interface (the shock front). Figure 3a–f clearly shows that the internal shock wavefront of the droplet forms a flat crown in the disturbance area. Because the density of water increases and the elastic modulus increases in the disturbed area, the speed of sound in the disturbed area is greater than that in the undisturbed area. Therefore, the pressure wave in the disturbed area can catch up with the initial pressure wavefront to form a superposition of the wavefront, thereby forming a shock wave.
- The pressure wave is transmitted faster in the radial direction than in the axial direction. Assuming a contact angle of θ, for a first-order approximation, the speed of motion at the contact edge point of the droplet with the scale is:For the collision process at the nanosecond level, if the impact velocity is considered constant, the equation is as follows:For r0 = 1 mm, v0 = 210 m/s, and t = 10 ns, the estimated moving speed of the edge point is ve = 3235 m/s, but the speed of sound in water is about 1430 m/s. At this time, the moving speed of the edge point is not only much greater than the impact speed but also greater than the speed of sound. Therefore, in the radial direction, the disturbance source moves faster than the speed of sound, but the pressure wave can only travel at the speed of sound. At this time, the maximum pressure point in the droplet appears inside the droplet. However, due to the lack of contact with the scale, it is not our main concern.
- Since the speed of sound in the scale (4268 m/s) is higher than the moving speed of the edge point, the propagation of the stress wave in the scale is less affected by the disturbance source, so the stress-wave influence area in the solid is spherical. There are two areas with high-stress values. The first is located near the edge of the water-droplet contact with the scale, which is where the peak pressure in the water droplet occurs. The second is located at a certain depth on the axis and is superimposed by the axially symmetrically distributed stress waves. This area is the source of stress at which scale erosion occurs at a certain depth.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, H.; Huang, Y.; Deng, S.; Wang, L.; Peng, H.; Shen, X.; Ling, D.; Liu, L.; Liu, Y. Research progress on scaling mechanism and anti-scaling technology of geothermal well system. J. Dispers. Sci. Technol. 2022, 1–14. [Google Scholar] [CrossRef]
- Jamero, J.; Zarrouk, S.J.; Mroczek, E. Mineral scaling in two-phase geothermal pipelines: Two case studies. Geothermics 2018, 72, 1–14. [Google Scholar] [CrossRef]
- Haklıdır, F.S.T.; Balaban, T.Ö. A review of mineral precipitation and effective scale inhibition methods at geothermal power plants in West Anatolia (Turkey). Geothermics 2019, 80, 103–118. [Google Scholar] [CrossRef]
- Zhou, Q.; Luo, N.; Li, J.; Lei, Y.; Gao, Y.; Liu, J.; Dou, H.; Wang, J.; Wang, X.; Yu, C. A Plug Removal Technique with Rotary Water Jet: Equipment Design, Simulation Study and Experiments. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 26–28 April 2022; p. D011S006R001. [Google Scholar]
- Li, G.; Huang, Z.; Tian, S.; Shen, Z. Research and application of water jet technology in well completion and stimulation in China. Pet. Sci. 2010, 7, 239–244. [Google Scholar] [CrossRef]
- Guo, R.; Zhou, C.; Yuan, S. Influence of abrasive water jet parameters on steel surface. JOM 2020, 72, 4273–4280. [Google Scholar] [CrossRef]
- Ning, D.; Wang, Q.; Tian, J.; Gong, Y.; Du, H.; Chen, S.; Hou, J. Experimental study on the coating removing characteristics of high-pressure water jet by micro jet flow. Micromachines 2021, 12, 173. [Google Scholar] [CrossRef] [PubMed]
- Yar’adua, K.H.; John, I.J.; Abbas, A.J.; Lawal, K.A.; Kabir, A. An experimental study on high-pressure water jets for paraffin scale removal in partially blocked production tubings. J. Pet. Explor. Prod. 2021, 11, 973–988. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Z.; Wang, B.; Li, L.; Zhu, X. Numerical Simulation and Test Study on Mechanical Properties Evolution of High-Pressure Water Injection Coal Seam. Chin. J. Rock Mech. Eng. 2009, 28, 3371–3375. [Google Scholar]
- Zhang, Z.W.; Meng, G.Y.; Wang, A.M.; Wang, S. Parametric optimization for jet descaling nozzle of mine main drainage pipeline. Coal Eng. 2017, 49, 110–113. [Google Scholar]
- Tamura, Y.; Ueoka, S.; Kimura, Y.; Kabeya, K. Influence of Injection Distance on Water Droplet Behavior in High Pressure Descaling. ISIJ Int. 2020, 60, 128–135. [Google Scholar] [CrossRef]
- Wang, A.; Sun, P.; Zhang, Z.; He, B.; Meng, G.; Yang, J.; Cheng, X. Numerical Simulation and Experimental Study on High-Pressure Water Jet Descaling in Coal Mine Drainage Pipeline. Iran. J. Sci. Technol. Trans. Mech. Eng. 2022, 46, 113–130. [Google Scholar] [CrossRef]
- Staniša, B.; Schauperl, Z.; Grilec, K. Erosion behaviour of turbine rotor blades installed in the Krsko nuclear power plant. Wear 2003, 254, 735–741. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, N.; Chen, X.; Xu, T.; Hui, S.; Zhang, D. Liquid drop impact on solid surface with application to water drop erosion on turbine blades, Part II: Axisymmetric solution and erosion analysis. Int. J. Mech. Sci. 2008, 50, 1543–1558. [Google Scholar] [CrossRef]
- Li, N.; Zhou, Q.; Chen, X.; Xu, T.; Hui, S.; Zhang, D. Liquid drop impact on solid surface with application to water drop erosion on turbine blades, Part I: Nonlinear wave model and solution of one-dimensional impact. Int. J. Mech. Sci. 2008, 50, 1526–1542. [Google Scholar] [CrossRef]
- Renger, A.; Johnson, K. Contact Mechanics; Cambridge University Press: Cambridg, UK, 1985. [Google Scholar]
- Eberhard, P.; Hu, B. Advanced Contact Dynamics; South-East University: Nanjing, China, 2003. [Google Scholar]
- Xi, C.; Hutchinson, J.W. Particle impact on metal substrates with application to foreign object damage to aircraft engines. J. Mech. Phys. Solids 2002, 50, 2669–2690. [Google Scholar]
- Honegger, E. Tests on erosion caused by jets. Brown Boveri Rev. 1927, 14, 95–104. [Google Scholar]
- Cook, S.S. Erosion by Water-Hammer. Proc. R. Soc. Lond. 1928, 119, 481–488. [Google Scholar]
- Engel, O.G. Waterdrop collisions with solid surfaces. J. Res. Natl. Bur. Stand. 1955, 54, 281–298. [Google Scholar] [CrossRef]
- Heymann, F.J. High-speed Impact between a Liquid Drop and a Solid Surface. J. Appl. Phys. 1970, 40, 5113–5122. [Google Scholar] [CrossRef]
- Dear, J.P.; Field, J.E. High-speed photography of surface geometry effects in liquid/solid impact. J. Appl. Phys. 1988, 63, 1015–1021. [Google Scholar] [CrossRef]
- Field, J.E.; Dear, J.P.; Ogren, J.E. The effects of target compliance on liquid drop impact. J. Appl. Phys. 1989, 65, 533–540. [Google Scholar] [CrossRef]
- Crooks, R.; Boger, D.V. Influence of fluid elasticity on drops impacting on dry surfaces. J. Rheol. 2000, 44, 973–996. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Park, S.-Y.; Min, K. Imaging the high-speed impact of microdrop on solid surface. Rev. Sci. Instrum. 2003, 74, 4930–4937. [Google Scholar] [CrossRef]
- Bartolo, D.; Josserand, C.; Bonn, D. Singular jets and bubbles in drop impact. Phys. Rev. Lett. 2006, 96, 124501. [Google Scholar] [CrossRef]
- Shi, H.H.; Takayama, K.; Nagayasu, N. The measurement of impact pressure and solid surface response in liquid-solid impact up to hypersonic range. Wear 1995, 186, 352–359. [Google Scholar] [CrossRef]
- Blowers, R. On the response of an elastic solid to droplet impact. IMA J. Appl. Math. 1969, 5, 167–193. [Google Scholar] [CrossRef]
- Lee, M.-K.; Kim, W.-W.; Rhee, C.-K.; Lee, W.J. An analysis of stress waves in 12Cr steel, Stellite 6B and TiN by liquid impact loading. Nucl. Eng. Des. 2002, 214, 183–193. [Google Scholar] [CrossRef]
- Fedorchenko, A.I.; Wang, A.-B.; Wang, Y.-H. Effect of capillary and viscous forces on spreading of a liquid drop impinging on a solid surface. Phys. Fluids 2005, 17, 093104. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kim, J.-S.; Kang, H.-J.; Kim, S.R. Stress wave propagation in a coated elastic half-space due to water drop impact. J. Appl. Mech. 2001, 68, 346–348. [Google Scholar] [CrossRef]
- Haller, K.; Ventikos, Y.; Poulikakos, D.; Monkewitz, P. Computational study of high-speed liquid droplet impact. J. Appl. Phys. 2002, 92, 2821–2828. [Google Scholar] [CrossRef]
- Huang, S.; Li, N.; Zhou, Q. The protection of solid in liquid-solid impact by microstructure. J. Engin. Thermophys. 2018, 39, 1279–1284. [Google Scholar]
- Grant, M.M.; Lush, P. Liquid impact on a bilinear elastic-plastic solid and its role in cavitation erosion. J. Fluid Mech. 1987, 176, 237–252. [Google Scholar] [CrossRef]
- Lush, P. Comparison between analytical and numerical calculations of liquid impact on elastic-plastic solid. J. Mech. Phys. Solids 1991, 39, 145–155. [Google Scholar] [CrossRef]
- Teng, Z.; Li, N.; Zhou, Q.; Chen, X. A study of the effect of microstructure on liquid-solid impact. In Proceedings of the Lcope International Conference on Power Engineering, Yokohama, Japan, 30 November–4 December 2015. [Google Scholar]
- Huang, S.; Zhou, Q.; Li, N.; Teng, Z.; Yin, H. The effect of coating layer in liquid–solid impact problem. Int. J. Mech. Sci. 2017, 128, 583–592. [Google Scholar] [CrossRef]
- Cheng, L. Dynamic spreading of drops impacting onto a solid surface. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 192–197. [Google Scholar] [CrossRef]
- Vala, M. The measurement of the non-setting parameters of the high pressure water jets. In Geomechanics 93; Routledge: Abingdon, UK, 2018; pp. 333–336. [Google Scholar]
- Yang, H.T.; Zhang, W.; Chen, B.; Cai, C.M.; Zhang, J. Parameter optimization of high pressure water-jet target detection. In Advanced Materials Research; Trans Tech Publications: Wollerau, Switzerland, 2012. [Google Scholar]
| Scale | Droplet | |
|---|---|---|
| Density (m3/kg) | 4090 | 1000 |
| Sonic speed (m/s) | 4268 | 1430 |
| Acoustic impedance (kg/m2s) | 1.746 × 107 | 1.430 × 106 |
| Young’s modulus (Pa) | 74.5 × 109 | |
| Poisson’s ratio | 0.28 | |
| Flexure (tensile) strength (MPa) | 75.4 | |
| Compressive strength (MPa) | 1300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Teng, Z.; Huang, S.; Li, N.; Zhou, Q. Transient Calculation Studies of Liquid–Solid Collision in Jet Descaling. Energies 2023, 16, 292. https://doi.org/10.3390/en16010292
Hu S, Teng Z, Huang S, Li N, Zhou Q. Transient Calculation Studies of Liquid–Solid Collision in Jet Descaling. Energies. 2023; 16(1):292. https://doi.org/10.3390/en16010292
Chicago/Turabian StyleHu, Shu, Zhaohui Teng, Shan Huang, Na Li, and Qulan Zhou. 2023. "Transient Calculation Studies of Liquid–Solid Collision in Jet Descaling" Energies 16, no. 1: 292. https://doi.org/10.3390/en16010292
APA StyleHu, S., Teng, Z., Huang, S., Li, N., & Zhou, Q. (2023). Transient Calculation Studies of Liquid–Solid Collision in Jet Descaling. Energies, 16(1), 292. https://doi.org/10.3390/en16010292






