E-Bike Motor Drive: A Review of Configurations and Capabilities

Abstract

In recent years, the mobility sector is undergoing a revolution, which is resulting also into a worldwide spread of light electric vehicles, such as electric scooters and bicycles. The increasing public concern about environmental problems further feeds this revolution. Electric-bicycles (or e-bikes) are a new trend which fits different riders’ needs. In fact, they offer extended range and ease of use, allowing riders to travel in urban centres, but also to take longer trips. E–bikes are reliable, easy to ride, affordable, and they help people live and travel a little greener, with a great benefit for their health. Many Companies (such as Brose, Bafang, Bosch and Shimano) developed performing e-bike motor drives. However, there is not a detailed general procedure to help the choice and design of electric bikes, in particular concerning the electric machine. This review focuses on the analysis of different motors for e-bike application. First, the e-bike system state of art is presented. The pedal-assist and power-on-demand e-bike system typologies are presented, together with the most popular parallel configuration and the less common series configuration. Further on, the environmental resistances are analysed for a traditional bicycle system and then the force balance is extended to the electric vehicle example. The most common Lithium-ion battery and the battery management system state of art is discussed, presenting design schemes and typical performances. Concerning the electrical machine, some electromagnetic design approaches are described, together with some data on commercial motors. Finite element analysis of a common motor model is carried out and some experimental tests are presented to highlight their capabilities. Different control strategies are compared, including innovative solutions and new trends.

1. Introduction

Recently, owing to the increasing public concern about environmental problems, such as global climate change, various technologies have begun to spread. Particularly, eco-friendly mobility has attracted increasing attention because it contributes to reducing global warming. In particular, Electric Vehicles (EVs) are rapidly spreading worldwide. Such a revolution in mobility also extends to light EVs, such as electric scooters and bicycles.

Electric motor powered bicycles, called electric-bicycles (or e-bikes) [1], are a new trend which fits different riders needs. They offer greater range and ease of use, allowing travel in urban centres and longer trips. E-bikes are reliable, easy to ride, affordable, and they help people live and travel a little greener, with a great benefit for their health [2,3,4]. Considering a urban environment, e-bikes allow for a faster travel and reduce parking issues compared to cars. More importantly, they cut down on fuels consumption and pollution, helping to improve air quality and the environment. Moreover, people can switch to a healthier travel solution with the comfort of a reduced physical effort [5]. Electric bicycles also offer the boost needed to ride much longer or challenging bicycle routes. The assistance of the electric motor helps overcome hills, slopes and rough terrain, allowing for a smoother ride. As a result, the young generation of cyclists is embracing this technology, thus making climbs less difficult and going farther and faster than they could have done with their own pedal power. Moreover, this new technology helps to get people cycling who could not ride a traditional bike because of physical aches and pains [6].

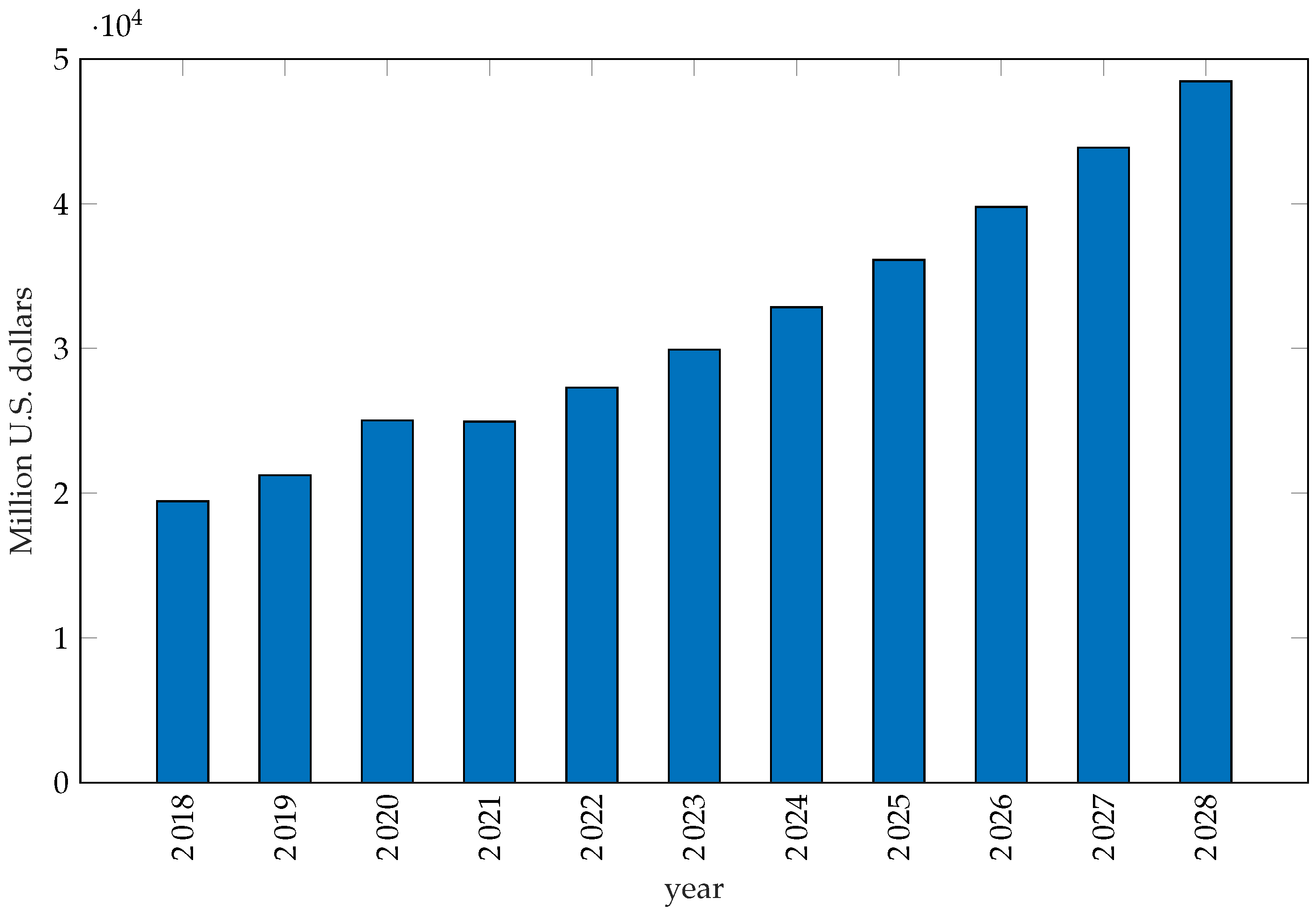
E-bikes are currently the most popular bikes on the market and their popularity is constantly rising. Figure 1 shows the e-bike global market trend, from 2018 to 2028. In 2021, market reached about USD 25 billion. The annual growth rate forecasted is equal to about 10 percent between 2021 and 2028, reaching USD 48.5 billion in 2028, almost twice the 2021 market size [7]. Europe accounts for approximately 30% of the e-bike market [8], dominated by Germany and followed by Netherlands and France [9].

This paper deals with e-bike system configurations and capabilities. The design of an electric bicycle can be divided into three different domains: system level, mechanical and electrical design [10]. The overall system design includes the choice of the e-bike topology (series or parallel), the type of electric energy assistance (pedelec or power-on-demand) and a possible energy regeneration. All these aspects are deepened in Section 2. The mechanical domain consists in choosing the motor placement and the gear type. Such a topic will be deepened in Section 3. Finally, the electrical domain includes the energy storage type choice, discussed in Section 4, and the electrical machine configuration.

For the dissemination of a more eco-friendly mobility, high-performance electrical motors are required. In particular, motors that exhibit high torque at low speed, and constant output characteristics over a wide range. Considering this, Permanent Magnet Synchronous Motors (PMSMs) are the most suitable traction motors. In Section 5 the most recent technologies about electric motor design are presented, together with some simulation and experimental results on a PMSM motor.

Many control strategies have been developed over time. Some of them are presented from Section 6, Section 7, Section 8, Section 9 and Section 10. Other e-bike applications are discussed in Section 12, while conclusions are drawn in Section 13.

2. E-Bike System

An e-bike can be seen as a light hybrid electric vehicle that combines human and electric power. The overall e-bike drive system consists of four blocks, as represented in Figure 2:

• a battery, currently the most popular are low-voltage Lithium-ion batteries;
• a power converter, which connects the battery to the motor, regulating the current supplied;
• a controller, which controls the switching based on the duty cycle, according to the user demand and the battery voltage;
• an electric motor.

E-bikes are classified according to the power that the electric motor can deliver and the control system. Two categories are defined: the pedal-assist and the power-on-demand electric bicycle.

The pedal-assist e-bike, also called pedelec, is characterized by an electric motor that assists the rider while pedalling. The additional torque value depends on the driver effort and this assistance can be provided up to a maximum speed and a maximum power, depending on specific regulations of the country. Over short periods of time, higher power output is allowed. This type of system requires pedalling speed sensors and/or force sensors.

The power-on-demand e-bike has an electric motor activated by a throttle. Thus, there is no need to pedal to benefit from the electric motor propulsion.

Considering the overall system, there are two ways to design such a light EV [10]: as a serial or parallel way.

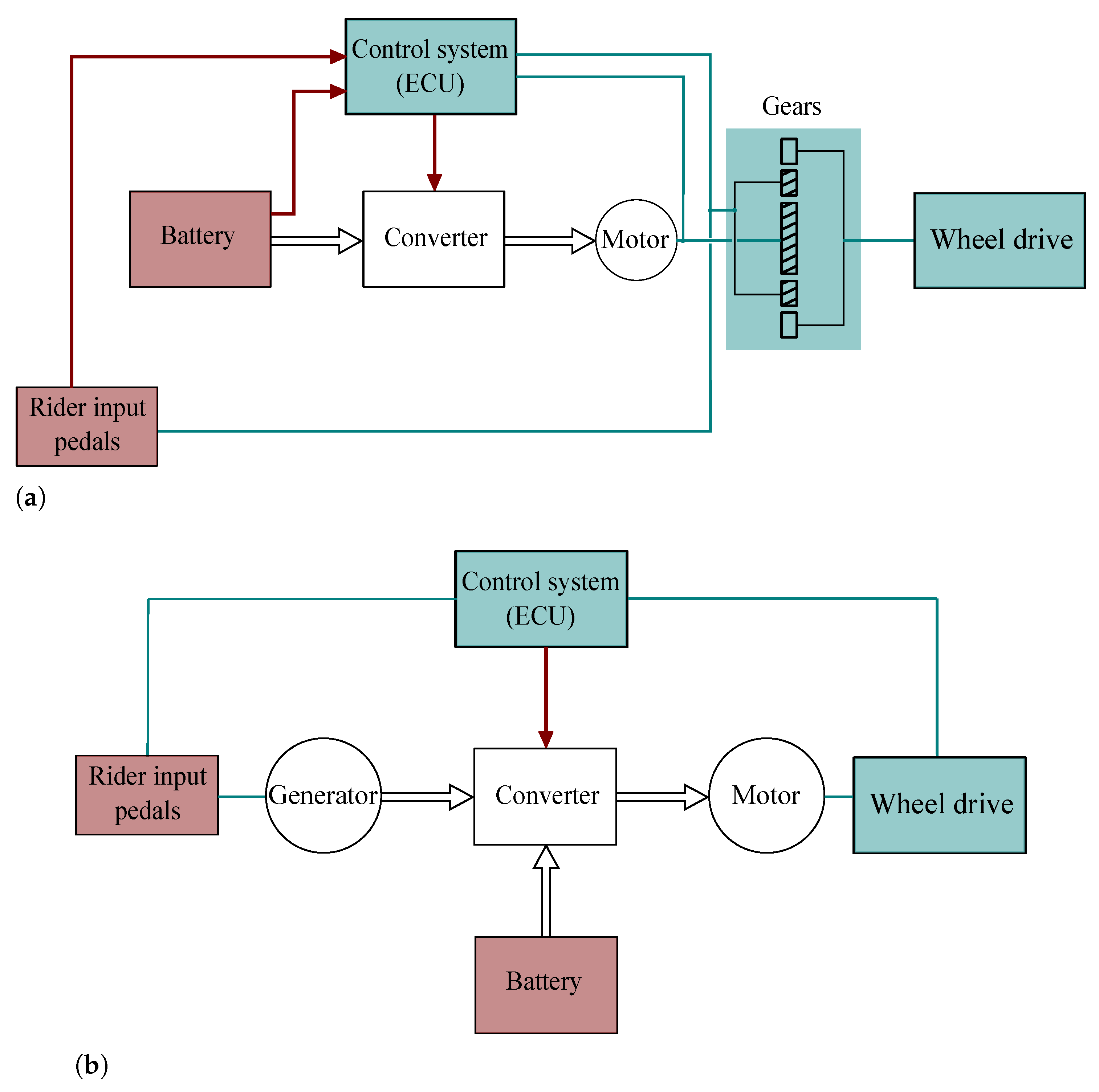
The parallel case [11], shown in Figure 3a, is the most popular configuration adopted. The human torque and the motor torque are combined in the mechanical domain via gears.

In the series configuration [12], shown in Figure 3b, the human and electrical machine torque are coupled in the electrical domain. Thus, the series vehicle is characterized by the absence of a mechanical transmission: the pedals are connected to a generator electrically coupled to a battery pack and an electric motor. The double conversion of human power has the positive effect that optimal cadence can be achieved at all slopes. A high efficiency can be achieved by keeping the rider operation in its optimal efficiency point all the time, as a typical series electrical-internal combustion engine hybrid machine.

Besides the assist type classification, e-bikes can be categorized [2,3] on the basis of motor type, motor assembly (gear, hub, friction), throttle type (thumb throttle, twist throttle, push button) and motor placement (front or rear wheel), as examinated in the following.

3. Mechanical Fundamentals

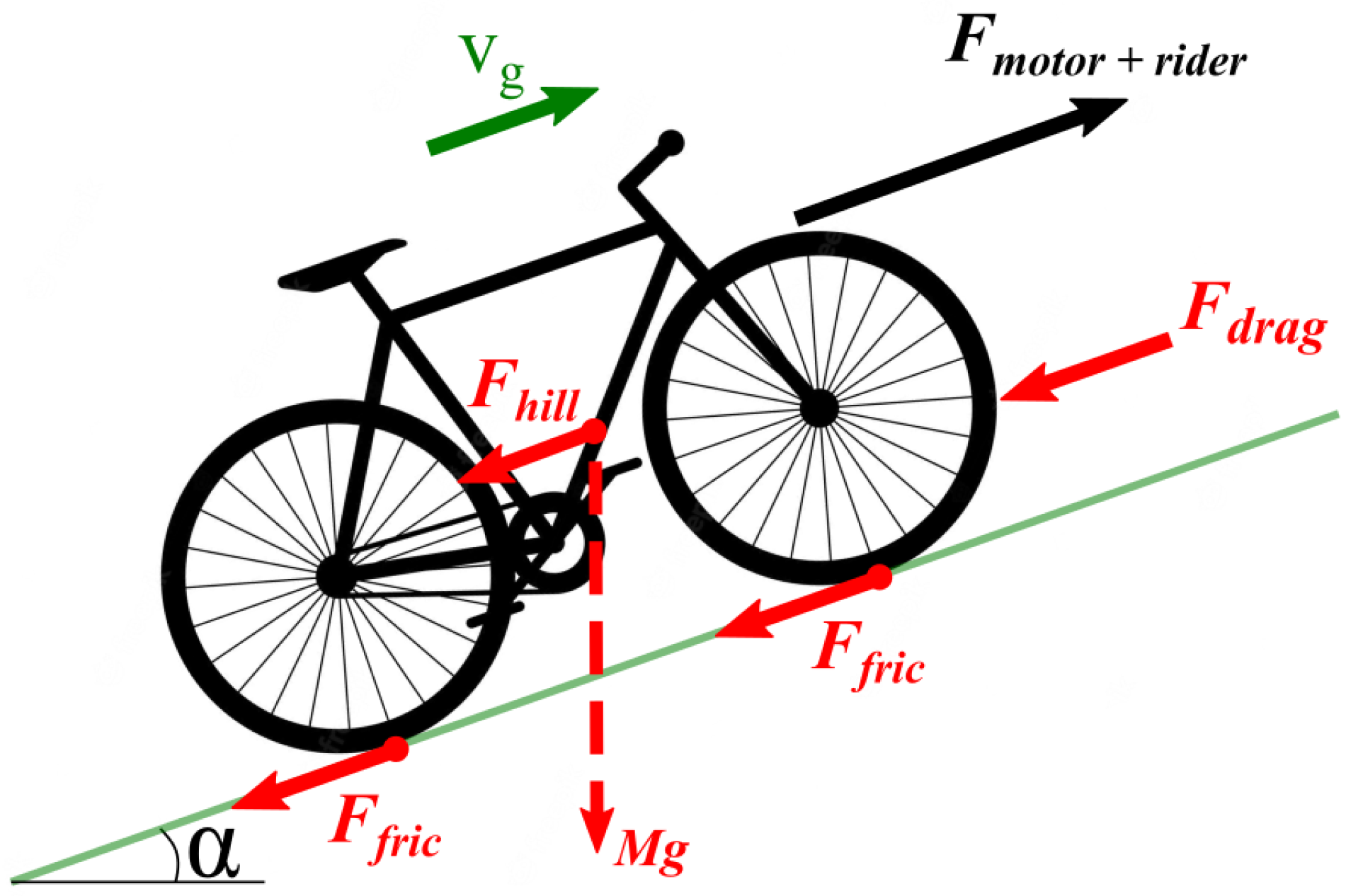
3.1. General Mechanics of a Bicycle

This Section deals with the mechanics and aerodynamics of e-bike [1,2,3], and in general, bicycles (powered by human torque). Considering a ride along a tilted surface, the bicycle is subject to forces represented in Figure 4.

The power consumed to drive the bike $P_{tot}$ is due to overcoming wind resistance $P_{drag}$, lifting mass up hills $P_{hill}$ and to overcoming frictions $P_{friction}$:

$$P_{tot}=P_{drag}+P_{hill}+P_{friction}$$

(1)

When the riding speed is high (greater than 3 $\mathrm{m}/\mathrm{s}$), most of the power is consumed to overcome wind resistance $P_{drag}$. When the riding speed is low, frictions are predominant over drag resistance. Differently, on step hills the majority of the power is delivered to overcome the slope.

Considering the wind drag, its force can be expressed as:

$$F_{drag}=\frac{1}{2}·C_d·{\rho }_{air}·A·{(v_g+v_w)}^2$$

(2)

where $C_d$ is the drag coefficient (between 0.12 and 1.1 depending on the bicycle and rider system shape), ${\rho }_{air}$ is the air density (1.225 $\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$) and A is the frontal area of the mass. To compute the drag force the relative speed in air is computed as the sum between ground speed $v_g$ and wind vector $v_w$. The power consumed to overcome the wind drag resistance travelling at a ground speed $v_g$ is:

$$P_{drag}=\frac{1}{2}·C_d·{\rho }_{air}·A·{(v_g+v_w)}^2·v_g$$

(3)

The power consumed to carry the total mass M (bicycle and rider) along a hill with tilt $\alpha$, considering the weight force component parallel to the ground $F_{hill}=M·g·sin\alpha$, is computed as:

$$P_{hill}=M·g·sin\alpha ·v_g$$

(4)

where $v_g$ is the vertical speed of the system.

At a very low speed on a level route, power consumption is mainly due to the rolling resistance. Such a friction depends on the vehicle weight, the type of bearings used and the type of tires. The friction force on bicycle wheels is $F_{fric}=M·g·C_r$, thus the power consumed to overcome rolling resistance when travelling at a ground speed $v_g$ is computed as:

$$P_{fric}=M·g·C_r·v_g$$

(5)

where $C_r$ is the rolling resistance coefficient, which depends on friction effects, for example ground conformation, mass variation or tire pressure (between 0.002 and 0.012). An approximated computation of the rolling coefficient applied to e-bikes is presented in Figure 2.1 of [1].

All forces presented describe the resistances to overcome for bicycles in general. Considering electric bicycles, the sum of the rider pedal power and the power provided by the electric motor has to satisfy:

$$P_{rider}+P_{motor}\ge P_{tot}$$

(6)

A full dynamic model of the bike, including kinematics, tilt and roll dynamics is reported in [13]. The model equations are then linearized to achieve the transfer functions and to design the control system.

3.2. Electric Bicycle Solution

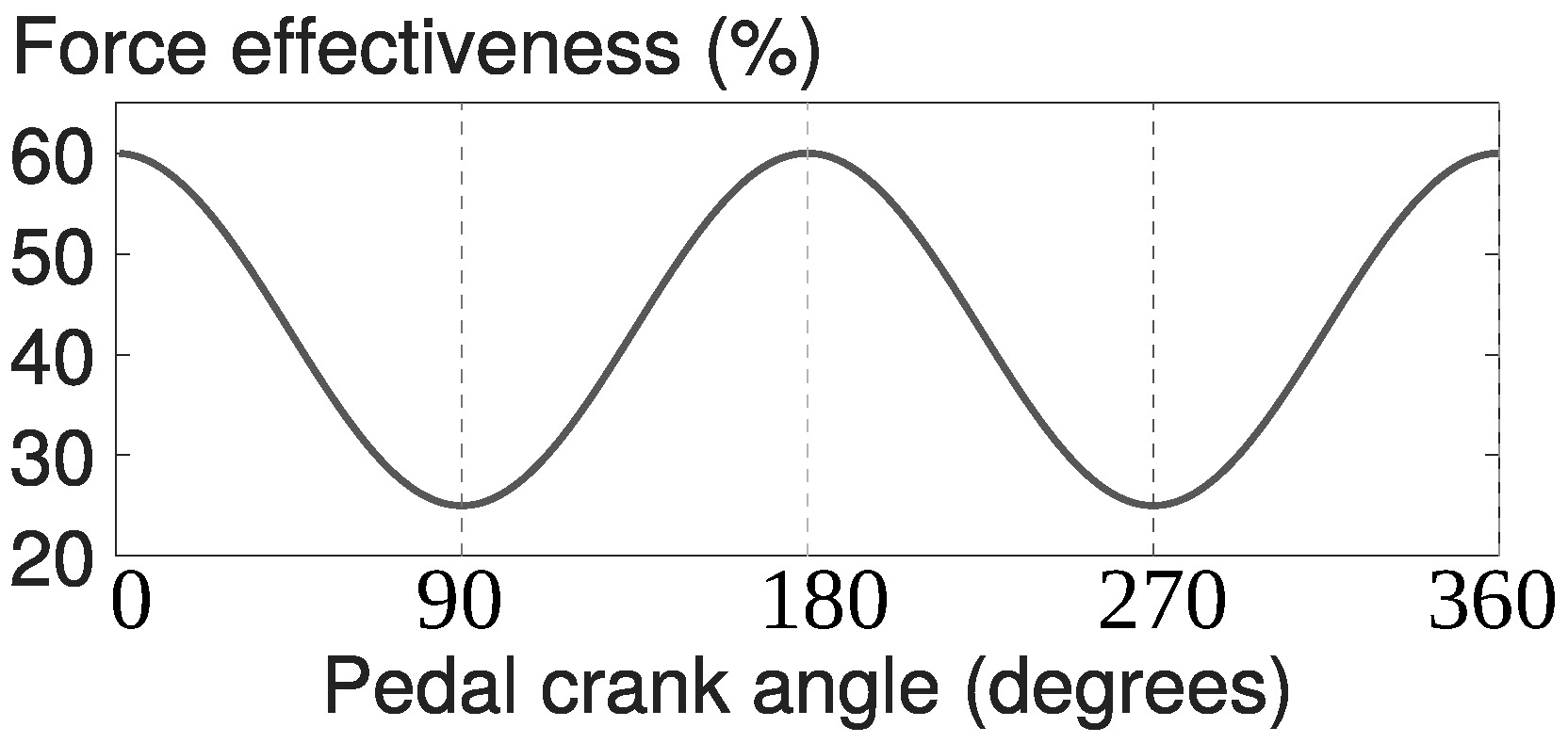
The torque produced by a human at the pedal cranks of a bicycle varies through the complete crank revolution. The pedalling torque peaks reach maximum value at particular crank angles. This variable cycling torque is not an issue when pedalling at a constant speed or even during modest acceleration on a flat road, but it becomes significant when pedalling up a steep hill: the cycling effort and thus the cyclist’s energy consumption becomes considerable. Difficulties are also observed when starting to cycle from a complete standstill, situation faced by using a lower gear to increase torque. However, the uneven production of torque by the cyclist cannot be smoothed completely by cyclist effort or cycling techniques alone. Figure 5 shows the human force effectiveness (both legs), as reported in [14,15].

In addition to the several advantages of electric bicycles, there are also some disadvantages. Among the others, the added weight to the bicycle due to the additional electric motor and battery pack and the need to recharge the battery every time after cycling. Several solutions have been developed to mitigate these drawbacks. In [11] an algorithm is designed to recover energy from the cyclist during high-efficiency pedalling and return it during low-efficiency pedalling. By this way, the battery charge is improved up to 25% in equivalent cycling efficiency.

Power saving concepts to take into account limited available energy in e-bikes have been also proposed in [16].

In [15], the authors deals with the design of a switched reluctance motor for an electric bicycle. The typical cycling operations are computed as torque-speed requirement to the motor and these operating points are plotted in the efficiency map of the motor. Since the human propulsive torque models is varies as a sine wave (Figure 5), the motor torque is instantaneously controlled so that the combined total propulsive torque is smooth. The cyclist’s cadence is measured to vary the motor torque so that the motor provides the torque difference to achieve a smooth propulsion torque profile. The sinusoidal reference of the motor torque is in phase offset from the cyclist torque signal, according to the pedal crank angle.

The switched reluctance motor is also considered for an electric bicycle in [17]. The authors focus on methods to effectively reduce torque ripple and acoustic noise, which are the major drawbacks of such a motor, limiting its widespread use. The torque ripple is reduced defining the phase current waveform to achieve constant torque in the commutation region. This is accomplished by use of a torque sharing function, which divides a constant torque reference among different phases by defining a reference current profile for each phase. The total torque is the combination of the torque produced by all active phases, with the target of obtain a constant torque.

3.3. Load Diagrams

Considering the e-bike electric motor, its torque versus speed diagram has to satisfy some standard requirements. The maximum rated torque delivered (during over-load operation) is equal to 100 $\mathrm{N}\mathrm{m}$ up to the rated speed, about 40 $\mathrm{r}/\min$ (4.2 $\mathrm{rad}/\mathrm{s}$). The maximum speed that the electric motor reaches is 120 $\mathrm{r}/\min$ (12.6 $\mathrm{rad}/\mathrm{s}$). Such values refer to the torque and speed delivered to the wheel, i.e., including the gear transmission ratio. Such a torque-speed characteristic has to interact with the load resistant torque plot.

Load curve represents the resistant torque variation with the speed. Considering the previously analysed Equations (3)–(5), the resistant torque is equal to:

$${\tau }_{load}={\tau }_{drag}+{\tau }_{hill}+{\tau }_{fric}$$

(7)

where the drag torque depends quadratically on the speed, considering a zero wind velocity ($v_w=0\mathrm{m}/\mathrm{s}$):

$${\tau }_{drag}=\frac{1}{2}·C_d·{\rho }_{air}·A·v_g^2$$

(8)

Differently, the torque resistance related to the hill does not depend on the speed, but only on the ground slope:

$${\tau }_{hill}=M·g·sin\alpha ·v_g$$

(9)

Finally, the rolling resistance torque is a constant term that does not depend on either speed or slope:

$${\tau }_{fric}=M·g·C_r$$

(10)

Figure 6 shows the load diagram together with the torque versus speed capability of the electric motor. The human muscular torque is not presented. The drag coefficient is $C_d=0.6$, the frontal area is considered equal to $1{\mathrm{m}}^2$, the total mass is $M=100\mathrm{k}\mathrm{g}$ and the rolling resistance coefficient is $C_r=0.01$. The ground slope varies from $0^{°}$ to $8^{°}$. With just the torque of the electric motor to the wheel, the vehicle can overcome a tilt of 8 degrees. For a specific ground slope, the difference between the motor torque and the load resistant torque represents the acceleration torque.

In literature the study of [18] presents the analysis of the human torque delivered during the e-bike motion, considering different resistance components. Such a torque is related to the vehicle speed, in order to develop some possible torque control strategies. The proposed strategies are manual control, proportional control, and assistant control, respectively.

In [19] operating cycle profiles are measured during actual road tests.

4. Battery and Charging

4.1. Lithium Batteries

Originally, most of the commercial light EVs were powered by Lead-acid batteries, that have both low specific energy (low energy density) and low charging current, resulting in a short range and a long recharging time. Then, Nickel-metal hydride and later Lithium-ion batteries have come into the market, outperforming the Lead batteries in the specific energy that is up to five times higher and in the recharging time that is up to three times shorter [20].

Besides the very high specific energy, any Lithium-ion cell has the merit of generating a relatively high voltage (3.7 V for Lithium-ion versus 1.2 V for Nickel-metal hydride or Nickel-Cadmium). It is a comparatively high value that helps lowering the number of cells to be connected in series to get the required voltage. In addition, Lithium-ion batteries are widely used in e-bike applications also due to their high power density, high efficiency, low self-discharge and long life cycle [21].

In a charged battery, an electromotive force (emf) of electrochemical type arises due to the different polarities of the reactants (polarization emf). When connecting a load, the battery acts as an energy generator. The polarization emf produces a flow of electrons (current) in the load connected to the battery terminals and is responsible for the conversion of chemical energy into electric energy, with the corresponding delivery of the stored chemical energy and the discharge of the battery. When connecting an electric energy source, the battery acts as an user. The polarization emf opposes the flow of electrons (current) produced by the external source into the battery and is responsible for the conversion of electric energy into chemical energy, with the corresponding storage of chemical energy and the charge of the battery.

From the chemical point of view, operation of the batteries is based on a redox reaction, i.e., a chemical reaction that takes place when a substance undergoes reduction (gain of an electron), while another element undergoes oxidation (loss of an electron). Redox reactions of opposite type occur when connecting the battery to an electric load or to an electric energy source (generator). The redox reaction occurs between two electrodes: the cathode and the anode. The anode is the electrode where oxidation occurs, the cathode where reduction occurs.

The charging mechanism of a Lithium-ion battery consists in ions flowing from the crystal lattice of the anode to the cathode. During discharge, the dissociation of Lithium ions creates free electrons in the anode, which generates a charge at the positive current collector. The electrical current generated then flows from the current collector through a load to the negative current collector (i.e., the cathode). While the battery is discharging and providing an electric current through the external electric circuit, the anode releases positively charged Lithium ions to the cathode, generating an ion flow inside of the battery. Between cathode and anode, an electrolyte favours the Lithium positive ions movement, while a separator blocks the flow of electrons inside the battery. When plugging in the device, the opposite reaction happens. Figure 7 shows the simplified schematic of Lithium-ion cell operation [22].

There is a wide variability in the choice of materials to be used in positive electrodes for Lithium-ion cells. For automotive applications Cobalt compounds are commonly used, due to the good electrochemical performances, the high energy density obtained, and the high thermal stability. However, the main problem is that Cobalt is rare, toxic, and expensive. Performances with different cathodic and anodic materials are exposed in [23].

Considering the e-bike application, several Lithium-ion cells are series connected to built the battery pack with the required voltage. The battery voltage is quite low, typically 36 $\mathrm{V}$ or 48 $\mathrm{V}$). The resulting current is around 10–20 A in rated condition, reaching 40–50 A during overload operations, for a limited time. The actual trend is to mount an integrated battery pack in frame of the bicycle, as represented in the sketch of Figure 8. Integrated batteries have the great advantage of an enhanced durability, since they are not exposed to harsh weather conditions and dust, wetness or dirt of the environment. Some typical e-bike integrated battery specifications are presented in

Table 1. Integrated battery specifications for e-bike application.

Parameter	Value	Unit
Battery voltage	36/48	$\mathrm{V}$
Capacity	11–20	$\mathrm{A}\mathrm{h}$
Energy	400–750	$\mathrm{W}\mathrm{h}$
Cycle life	800–1000	cycles
Charging time
w/compact charger	50% of the capacity	2.5–4.2 $\mathrm{h}$
	100% of the capacity	6.5–8.8 $\mathrm{h}$
Charging time
w/standard charger	50% of the capacity	1.5–2.1 $\mathrm{h}$
	100% of the capacity	3.5–5.4 $\mathrm{h}$
Charging time
w/fast charger	50% of the capacity	1–1.4 $\mathrm{h}$
	100% of the capacity	2.5–3.7 $\mathrm{h}$
Operation temperature	−20–60	${}^{°}\mathrm{C}$
Weight	2.9–4.3	$\mathrm{k}\mathrm{g}$

.

4.2. Battery Management System

Besides the very high specific energy, Lithium cells are very sensitive to temperature, and a cell can be ruined when overcharged, thus they need some management during their operation. To this purpose, a Battery Management System (BMS) is usually employed to control battery operation, charge, and discharge [24,25,26,27]. This system solves many safety problems such as overloading, heating in the battery and possible pack explosion. Since it makes the working system of the battery efficient, it also increases its life.

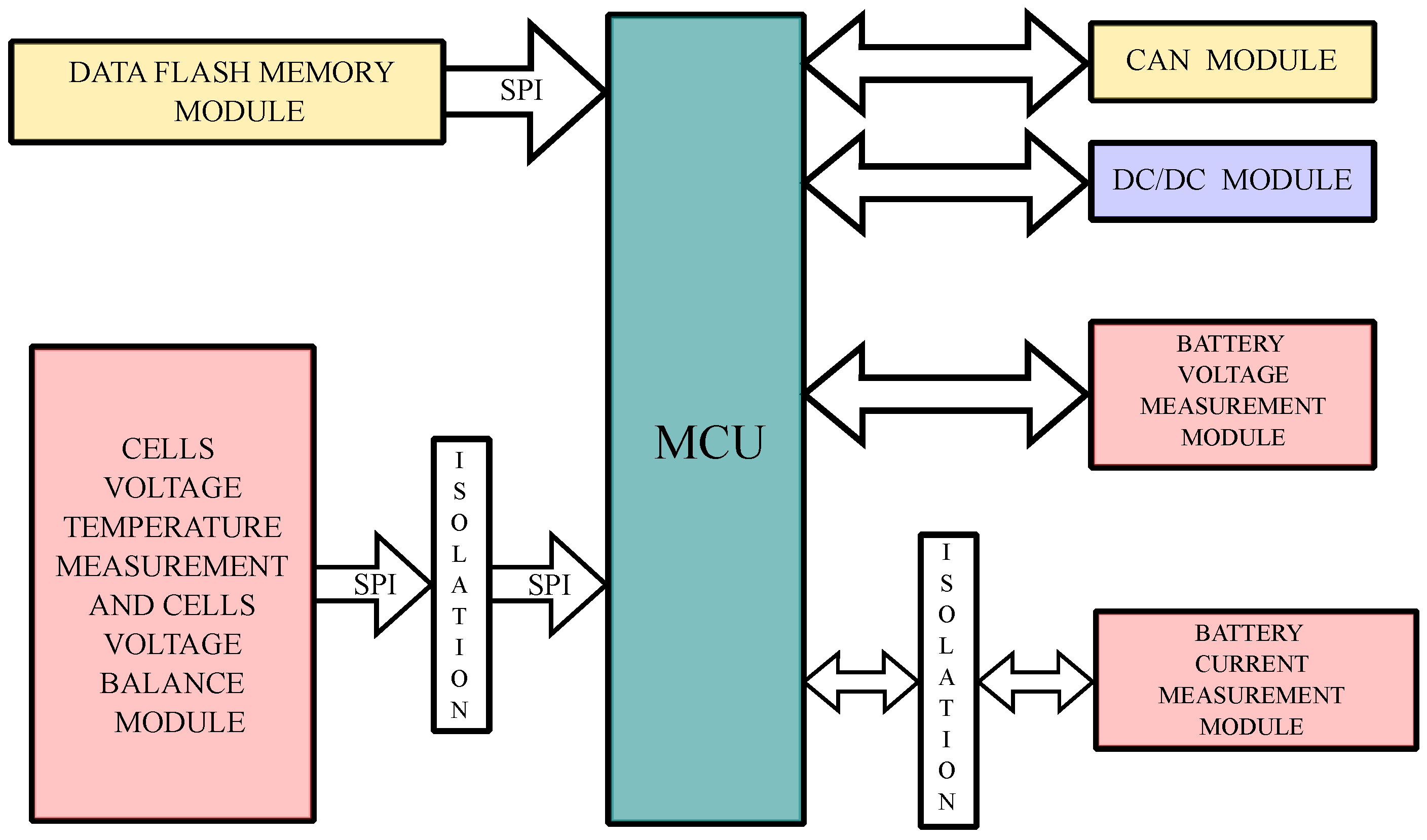
Figure 9 represents the block scheme of battery pack interfacing the BMS system.

The BMS structure is represented in Figure 10 [25]. It consists of one central Microcontroller Control Unit (MCU) and several local Electronic Control Units (ECUs). Each module must communicate with the main controller that manages all modules work correctly. CAN-bus module is used for communication. Data FLASH memory module is used for storage data of measurement. The measurement data can be preserved up to one month. A DC/DC module is used for transform the 12 V power source into 5 V power supply. In order to improve the rejection of disturbs, the DC/DC module is an isolated power supply. The battery current measurement module is used for measuring charge and discharge current of battery. The battery voltage measurement module is used for measuring voltage of all cells in series and evaluate the SOC. Temperature measurement module is used for inspecting surface of all cells. In addition, as a too high temperature on the surface of Li-ion battery would result in safety problems, the temperature measurement is essential. The central ECU constantly monitors voltage and temperature of the cells and, when an alarm situation is detected, it reacts in order to protect the overall system.

Lithium-ion battery system has a high requirement on cell voltage balance. In fact, even two cells of the same model and from the same manufacturer are not identical. There are always slight differences in SOC, voltage, current, impedance, and temperature characteristics. If the SOC of each cells is not periodically equalized, or balanced, such cells will undergo over-charge or over-discharge, leading to damage, and eventually complete battery stack failure. BMS will monitor the parameters and determine battery SOC, state of health and maintains the system in accurate, reliable and balanced state and also determines the life span of a battery [26]. In particular battery cell balancing is carried out by two methods, passive and active [27,28].

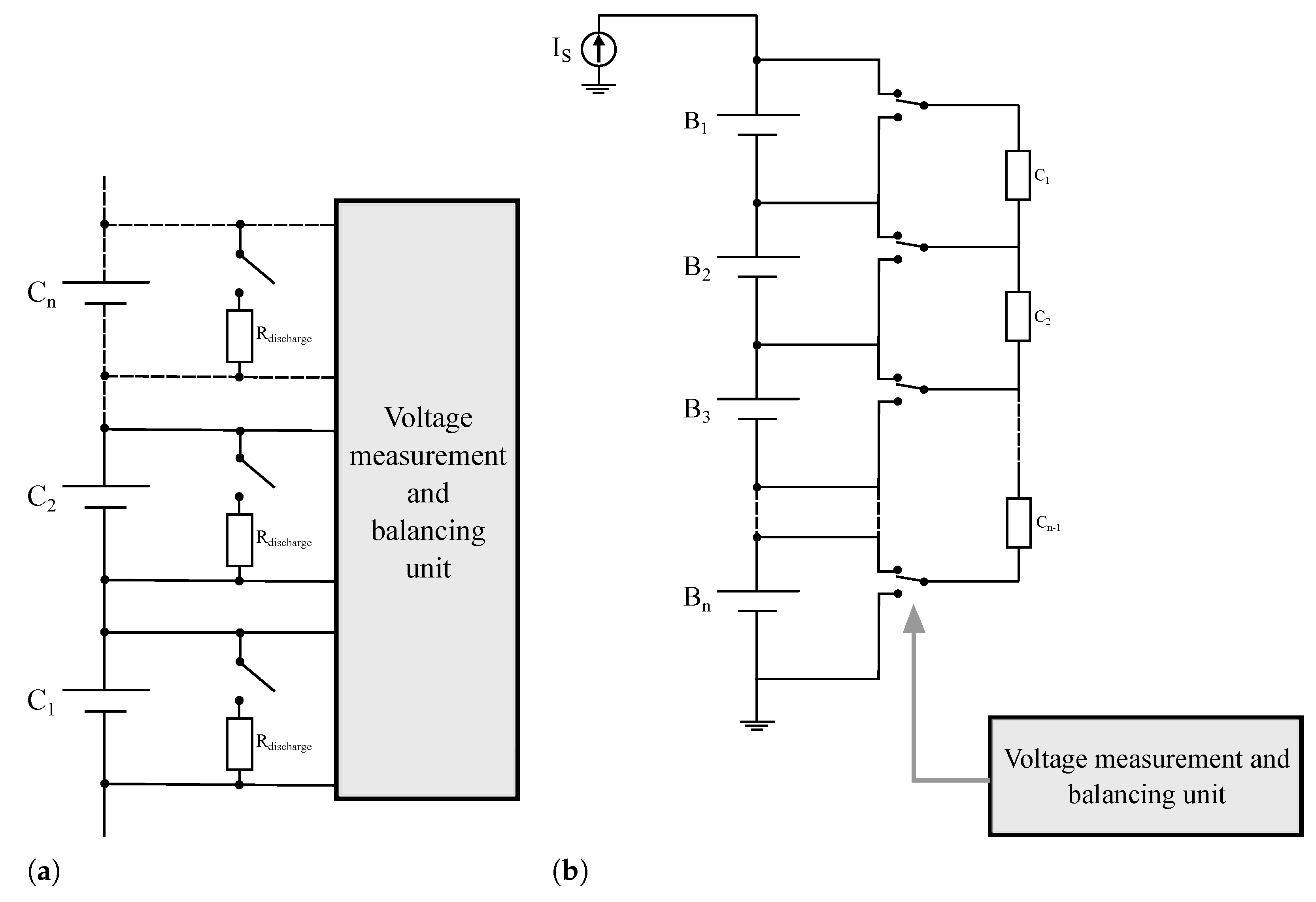
With the passive cell balancing approach, the cell energy in excess is dissipated through resistors (in form of heat), as represented in Figure 11a. Passive cell balancing technique is easy to execute, but less effective and should not be used during discharging. It is possible to adopt a fixed shunt resistor, continuously bypassing the current and limiting the voltage by varying the resistor. This is a simple and cheap approach, but it is suitable only for a small number of cells, it does not allow for a controlled operation and the continuous energy dissipation increases the heat generation and reduces the battery pack life. Alternatively, a controlled shunt resistor can be adopted, as in the example of Figure 11a. Controlled switches/relays are used instead of continuously discharging higher charged cells. This is a simple, more efficient and reliable approach, yet still implies energy dissipation in heat, thus lifetime reduction, and it is useful only during charging.

The active cell balancing approach uses capacitive or inductive charge storage in order to transfer the excessive energy from a high-charge cell to a low-charge cell. By this way, imbalance between cells is regulated: more crucial SOC cells electric energy is transferred to lower SOC cells, with no damage and no energy dissipation in heat. This method maximizes the battery available power and is more effective and efficient than the passive balancing technique.

Active cell balancing topologies include cell bypass, cell-to-cell, cell-to-pack, and pack-to-cell methods.

• The cell bypass method consists in making the current bypassing the cells that have reached a crucial SOC value. The bypassed current continues flowing through the remaining cells until they reach the maximum SOC as well. Cell bypass techniques are easy to implement and relatively low in cost. However, they are effective only toward the end of the charging process when one or more cells have reached maximum SOC.
• Cell-to-cell methods consist in transferring the extra energy stored in a cell to adjacent cells, if they have lower stored energy. Even if this method is more efficient than cell bypass, it is complex to implement and slow.
• In cell-to-pack equalization, the most-charged cell energy is equally subdivided between the remaining cells in the pack.
• Pack-to-cell method is the complementary technology of cell-to-pack. Energy is transferred from the entire pack to the least charged cell. Both cell-to-pack and pack-to-cell are lower in efficiency than cell bypass and cell-to-cell, and their complexity is relatively high.

Figure 11b shows an example of cell-to-cell active balancing realized by means of flying capacitors ($C_1,C_2\dots C_{n-1}$). A switch structure allows for various capacitors-to-batteries connections, depending on the balancing conditions. At the beginning, the capacitor is connected to charge the cell with the higher voltage. Then, the capacitor is connected to discharge the lower voltage cell. Besides the good charge balancing, this method allows energy transfer only between adjacent cells and it causes losses during charging and discharging of the capacitor.

4.3. Charge

Battery charging is playing an important role in the BMS, since charging profiles have a strong influence on the battery performance and life cycles. Many charging algorithms have been developed and implemented. Some popular charging algorithms include the Constant Current and Constant Voltage (CC-CV) [29,30,31], the pulse charging [32], and the Sinusoidal Ripple-Current (SRC) charging algorithms [33,34] have been used to charge the Lithium-ion batteries.

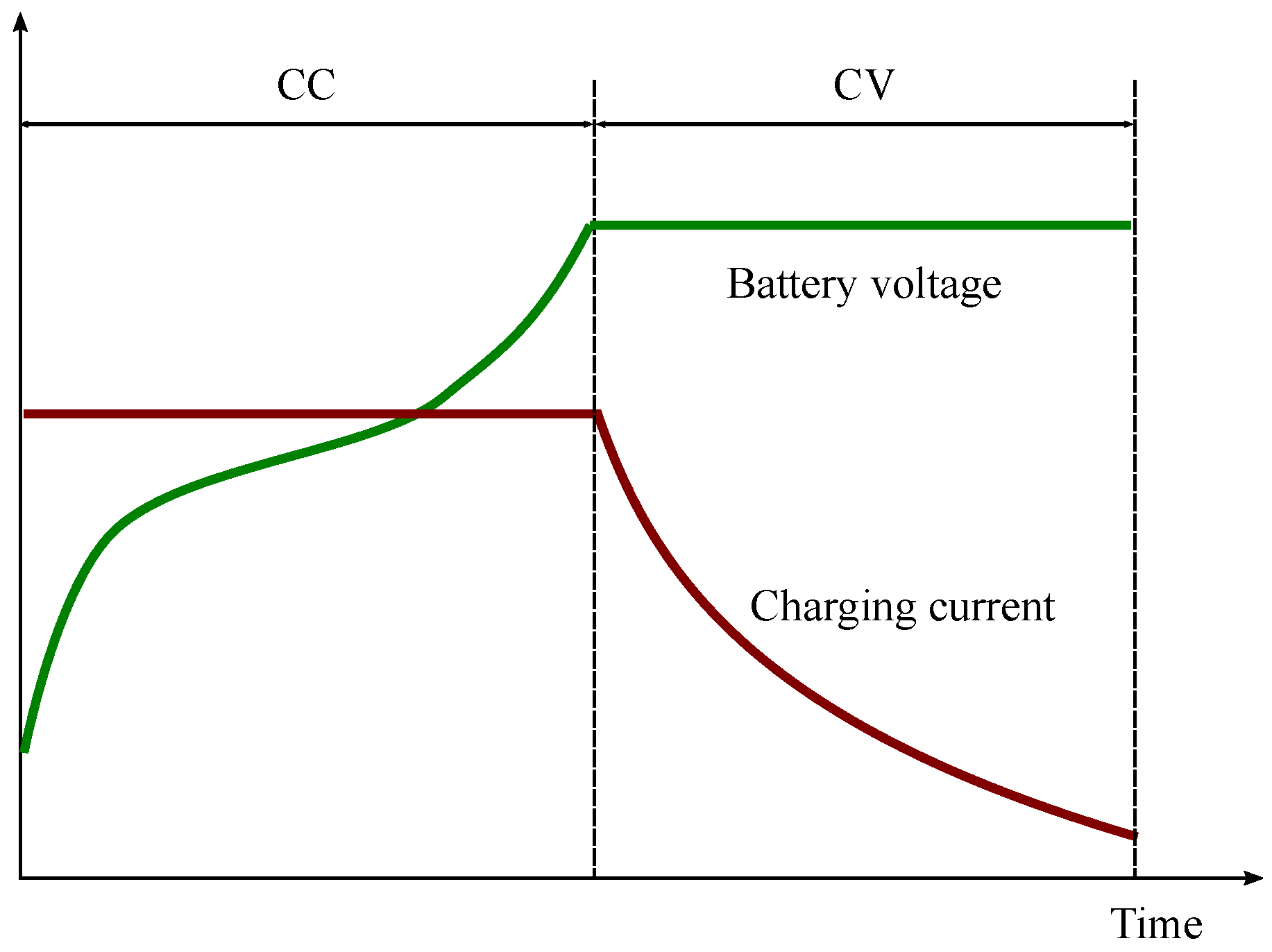
Under the CC-CV charging algorithm, a constant controlled current is applied to charge the battery until the battery voltage reaches a predefined maximum value. Then, the charging voltage is maintained constant at this level, and the charging current is reduced exponentially. When the charging current drops to a cut-off current limit, the charging process is terminated. Figure 12 shows the voltage and current evolution in time when CC-CV charging is carried out. Based on the charging current in the CC mode, the total charging time is varied from 1 h to 2.5 h. In general, the lower the charging current of the CC mode, the higher the charging efficiency and longer the charging time and the battery life. Such a charging algorithm is widely used to charge Li-ion batteries due to its simplicity and easy implementation, even if it requires a long charging time and it causes a large thermal rising while applying a high charging current, reducing the life cycle of the battery.

When the pulse charge is carried out, the battery voltage is kept constant for the entire charging process while the frequency or duty cycle of the pulse charging current is changed. Such a method is faster and more efficient than CC-CV charging for Li-ion batteries.

Recently, the SRC charging algorithm has also been paid attention to increase the battery lifetime. The charging current consisting of two components: a DC component and an AC ripple one. The magnitude and frequency of the ripple component are optimized timely to minimize the internal impedance of Li-ion batteries. Under the minimal internal impedance condition, the battery temperature during charge is reduced, so both power and energy efficiencies of the charging process are improved.

However, both pulse charging and SRC charging algorithms have some disadvantages including complicated implementation, bulky size, and high cost. This makes the CC-CV method more popular in actual applications.

5. Electric Motors for E-Bike Application

This Section deals with the state of art of the electric motor for e-bike application. Figure 13 shows possible motor locations on the e-bike structure.

Front wheel hub motors are convenient for maintenance because they can be easily installed and removed and it creates a better weight balance in the bike with respect to rear wheel motor. However, some disadvantages of such a configuration are the possible front wheel slippage, the difficulty in e-bike controlling and steering, and generally a lower power than that of a rear wheel hub motor.

Unlike a front wheel hub motor, a rear wheel hub motor does not seem to cause wheel slippage because its weight is distributed at the rear of the e-bike. However, locating the motor on the rear wheel hub causes an imbalance between the rear and front of the bike.

A mid-drive motor is located in a low and centred position of the e-bike, creating a better weight balance than front and rear wheel hub motors. Compared with hub motors of the same power, mid-drive motors are generally smaller and can be directly integrated into the frame of the bike. Furthermore, mid-drive motors have better hill-climbing characteristics than hub motors with a similar power, even though they require custom designed frames when integrated, and they are usually more expensive.

Concerning the electrical machine, main technologies include brushless dc or brushless ac motors, that will be described in the next Subsections.

5.1. Brushless DC Motors

In the past e-bikes were typically equipped with brushed dc or brushless dc (BLDC) electric motors [3,20,35,36]. The brushed dc motor, even if very popular in early e-bike models, has been gradually replaced by the BLDC motor. Brushed dc motors are more robust and relatively cheap compared with BLDC motors. However, the BLDC motor has higher reliability and power density, thus smaller dimensions. In addition, brushed dc motors produce higher noise, they are heavier, and require relatively frequent maintenance service.

Brushless motors are synchronous motors characterized by a magnetization field produced by Permanent Magnets (PMs) on the rotor. The armature windings are positioned on the stator to avoid using of any sliding connection. Torque originates from the interaction of the magnetization field with the (armature) field produced by the current flowing into the stator windings. When the armature current supplied is a dc current, the brushless machine is called BLDC motor. Figure 14 shows the fundamental block scheme of a BLDC motor.

BLDC motor merits are its simple and robust electromagnetic structure, its easy control, its great power ratio and that it requires a position transducer set with a resolution of 120${}^{°}$. However, BLDC motor drawbacks include the phase current commutation process, the high torque ripple and the torque-speed characteristic drop at high speeds.

5.2. Permanent Magnet Synchronous Motors

The actual trend is to develop high-performance e-bike traction motors that exhibit high torque density, especially at low speeds. Thus Permanent Magnet Synchronous Motors (PMSMs) are spreading worldwide. The PMSM is an AC electric motor characterized by a rotation of the shaft synchronized with the frequency of the field associated to the stator winding (armature field), generated by the current supplied. The rotor magnetizing flux interacts with the stator armature field, which is generated by an AC winding. To satisfy the high power density constraint, high-energy rare-earth PMs, such as NdFeB or SmCo [37], represent a key technology for the rotor field design.

5.2.1. Rotor Geometry

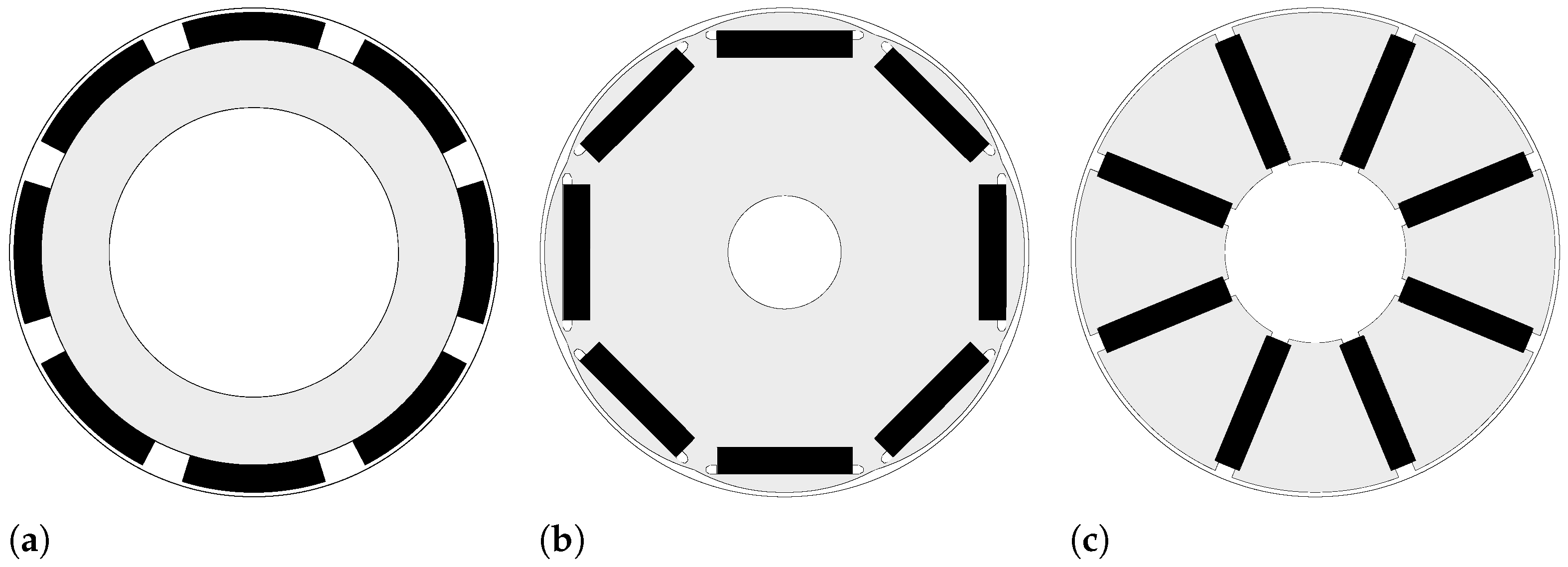
Different rotor design solutions can be adopted: the Surface-mounted PM (SPM) motor of Figure 15a, the Interior PM (IPM) motor of Figure 15b and the IPM spoke motor of Figure 15c.

The SPM geometry is mainly adopted when the motor is designed with an outer rotor, as shown in Figure 16. This is due to the limited space available in the rotating part. Such a solution is adopted in light electric vehicles with a wheel hub motor, that can be characterized by IPM geometry as well [38]. A single planetary gearbox connects the rotor to the wheel.

In inner rotor motors the IPM configuration is preferred. Such a solution is adopted with crank motor drives, connected to the chain ring by using a two-stage gearbox.

Comparing the torque density, IPM machines theoretically exhibit a higher torque than SPM machines [39,40,41,42]. In fact, the torque has two components: one due to the interaction between PM flux and stator current, another due to rotor anisotropy, that is, the difference between the direct- and quadrature-axis inductances (due to the changing reluctance value along the rotor, from the stator point of view). The SPM machines are characterised by an isotropic rotor (PMs are located on the rotor surface, i.e., the reluctance from the stator point of view does not change), so that only the first torque term is produced. In the IPM machines, the rotor is anisotropic (PMs are buried in the rotor core, i.e., the reluctance from the stator point of view varies), thus also the reluctance torque component is expected. However, the rotor anisotropy is low in IPM motors for e-bike application, thus the second term is almost negligible. This is due to the following reasons:

• the typical high number of poles: the higher the number of poles, the lower the saliency [43];
• the small size of the motor: the air gap and the leakage fluxes are high in relative terms;
• if the fractional-slot winding solution is adopted to reduce the copper, the rotor saliency decreases [44].

Furthermore, a PM mechanically inserted in the rotor prevents magnet scattering at high speeds and exhibits equal mechanical and electrical air-gap length.

5.2.2. Fractional-Slot Stator Winding

In the majority of e-bike applications, fractional-slot stator windings with non- overlapped coils are adopted [45,46,47]. They are characterized by a non-integral number of slots per poles and per phase. Fractional-slot motors are usually characterized by a high number of parallel paths, according to the high currents required, and they are suitable for machines with high number of poles [48]. In addition, the non-overlapped coil windings are characterized by reduced end-winding lengths, thus lower copper weight and Joule losses [49]. Moreover, fractional-slot machines have a phase inductance higher than the corresponding integral-slot machine. As a result, the flux-weakening capability of the machine is increased [50] and the short-circuit current in the event of fault is reduced. Since winding phases are physically and magnetically separated the fault in one phase is not propagated to other phases. Thus, the fault-tolerance of fractional-slot windings is improved [51]. However, the torque ripple is higher and some solutions exhibit low winding factor [49] or Magneto Motive Forces (MMF) sub-harmonics which cause additional rotor losses and torque ripple [52].

Table 2. Motor typology of different commercial PM machines.

Parameter	Bosch	Bafang	Brose	Shimano
Type of motor	spoke IPM	radial IPM	radial IPM	spoke IPM
Number of slots $Q_s$	48	12	12	12
Number of poles $2p$	16	8	10	14
Winding typology	hairpin	concentrated	concentrated	concentrated
	distributed	fractional-slot	fractional-slot	fractional-slot

compares different commercial motors typologies, including Bosch, Bafang, Brose and Shimano e-bike electric motors. They are all PM motors, in particular IPM motors, some with the radial flux density (radial IPM) and others with the spoke-type geometry (spoke IPM). Only Bosch motor is characterized by a distributed hairpin winding that is not a fractional-slot type. Such a typology will be discussed in the next Subsection.

The majority of companies employ fractional-slot machines, i.e., the number of slots per pole per phase is not an integer number. In particular the number of slots per pole per phase of Bafang motor is $1/2$, Brose motor is a $2/5$ configuration and Shimano motor a $2/7$ typology.

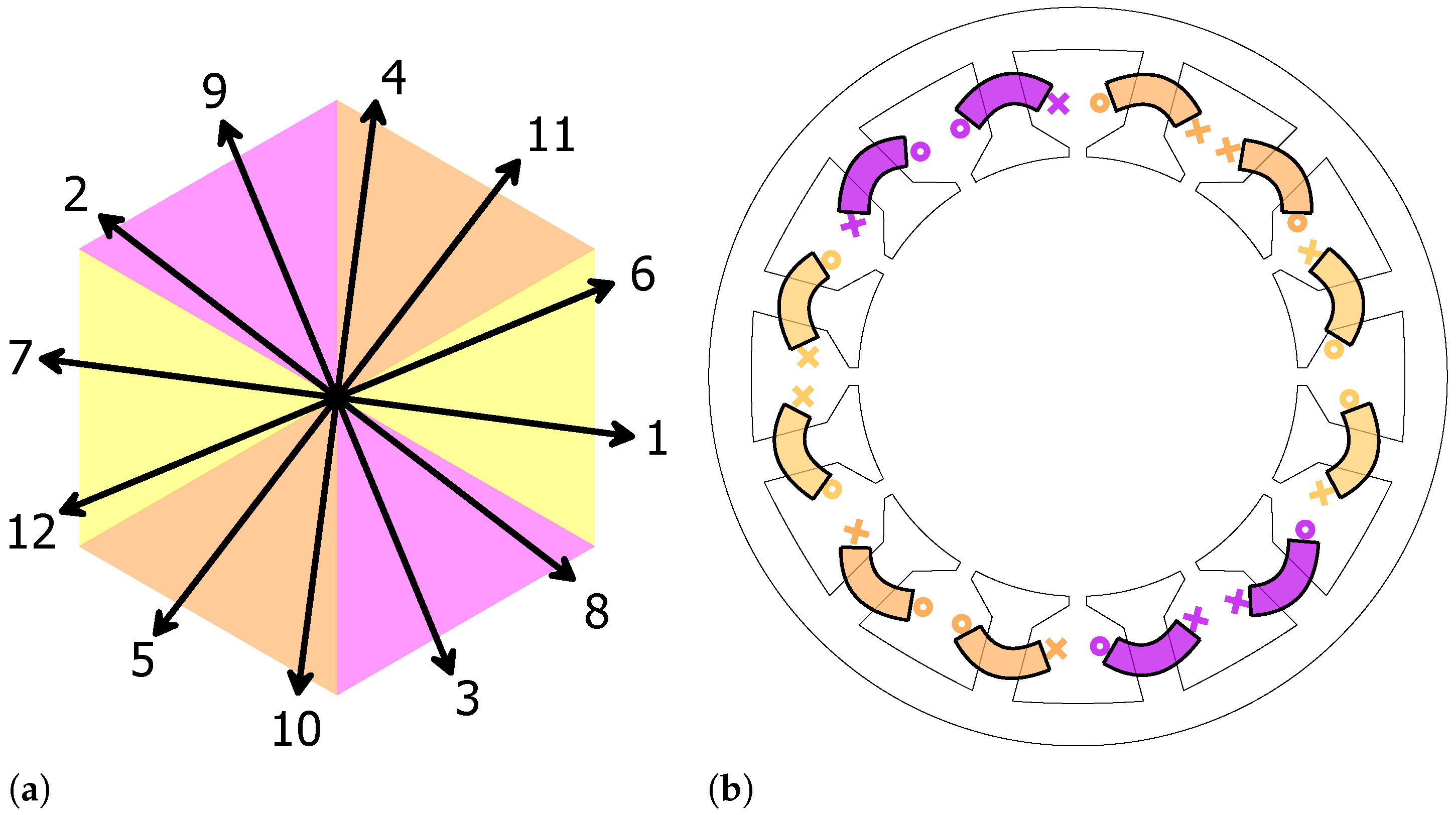
Since the $12-$slots / $10-$poles and the $12-$slots / $14-$poles configuration are equivalent in terms of field waveform, the $12-$slots / $10-$poles configuration is analysed hereafter as an example. The star of slots and winding connections are represented in Figure 17. Phase A is identified with the yellow colour, phase B with the pink colour and phase C with the orange colour.

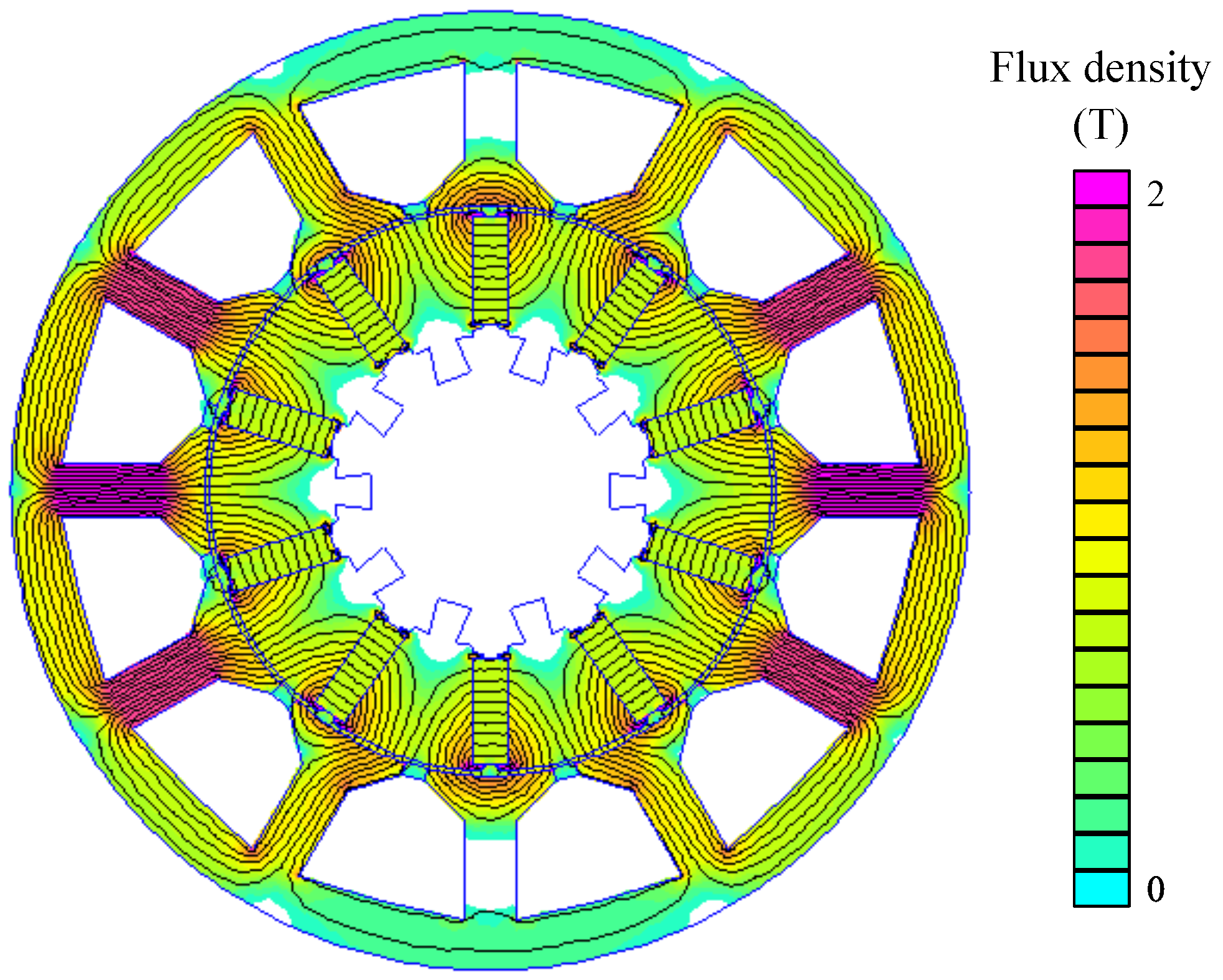
A two-dimensional finite element analysis is carried out through $FEMM4.2$ software. The $12-$slots / $10-$poles motor model analysed is characterized by an IPM spoke-type rotor. Figure 18 shows the no-load flux lines and flux density of the motor. It is worth noting that the radial force on the rotor remains balanced.

Figure 19a shows the flux linked by phase A and the d-axis flux-linkage in a mechanical period (which corresponds to 360 electrical degrees, as the electrical angle is equal to p times the mechanical angle). The waveform of phase A flux-linkage is almost sinusoidal, as confirmed by the constant value of the d-axis flux-linkage and the Fourier analysis of Figure 19b. A very low third harmonic is present.

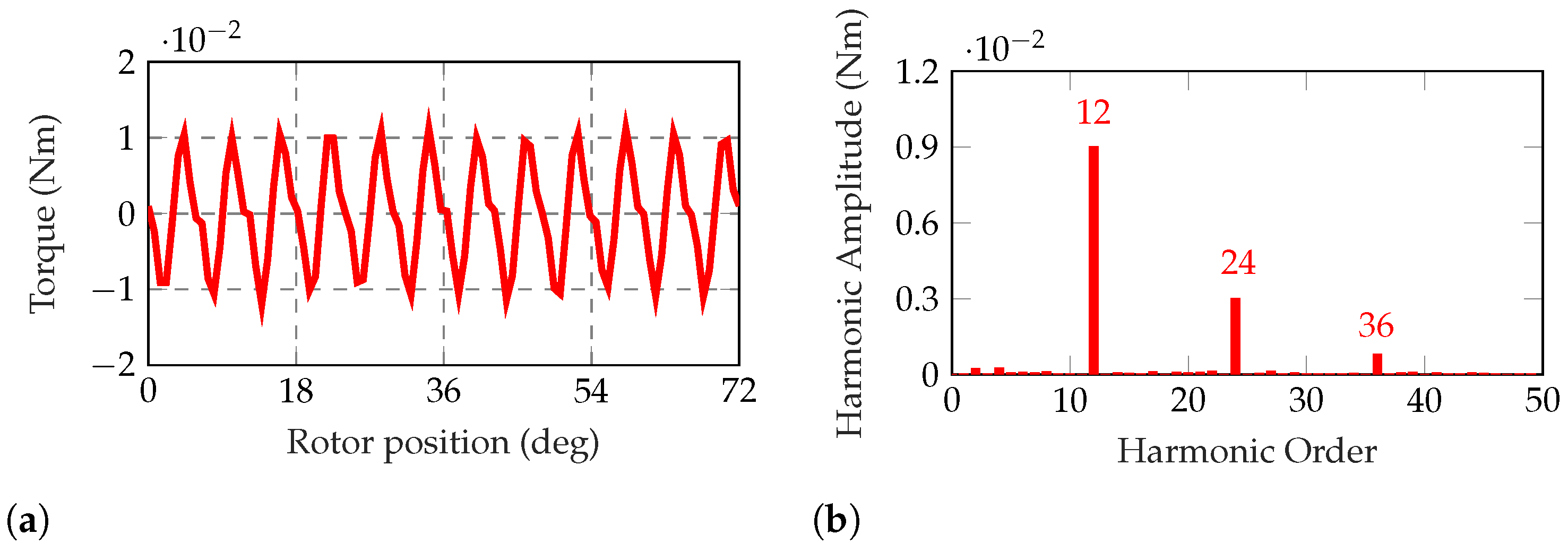
Figure 20 shows the no-load torque of the configuration along a mechanical period rotation together with its Fourier analysis. Such a torque is defined as cogging torque, since it is related to the interaction between the rotor and stator slots when no current is supplied, i.e., the motor cogging. The maximum torque value is very low, thus the on-load torque delivered is expected to have a smooth waveform. The fundamental harmonic is equal to 12 and harmonics of second and third order are present.

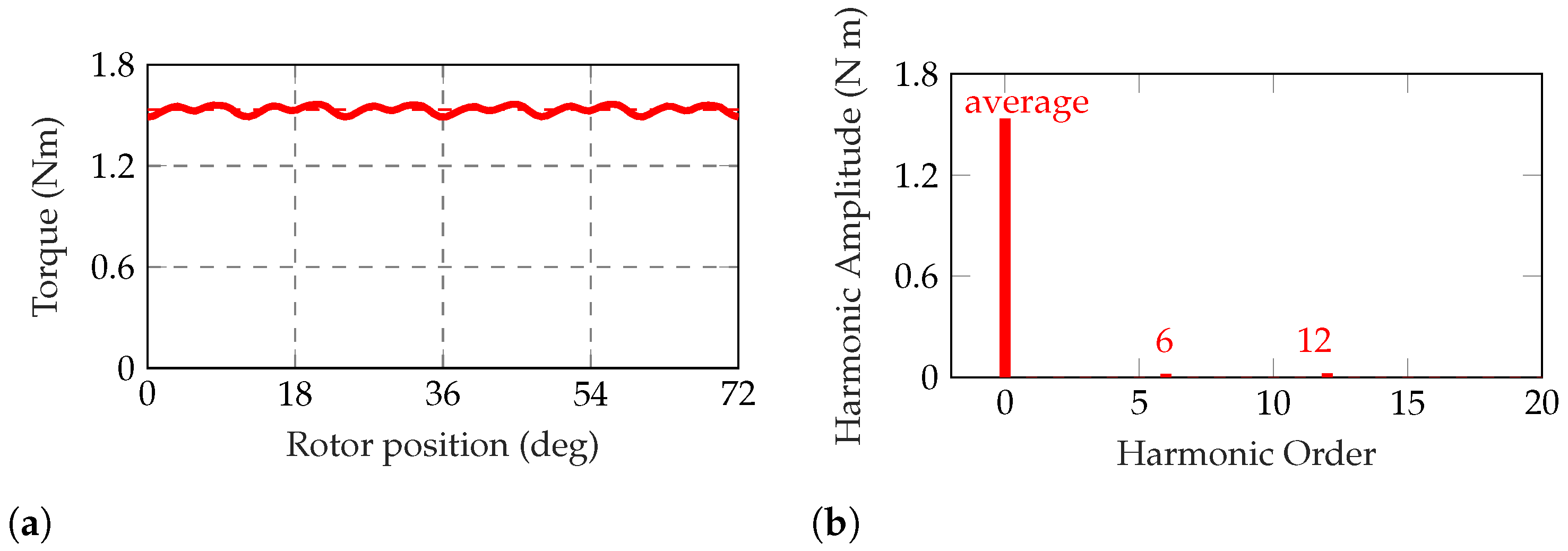
Figure 21 shows the on-load torque computed. As expected it is very smooth, having a dominant average value. The higher harmonics are of order 6 and 12.

A $12/10$ commercial motor has been tested to verify the preliminary theoretical analysis on such a configuration. The test bench arrangement is reported in Figure 22.

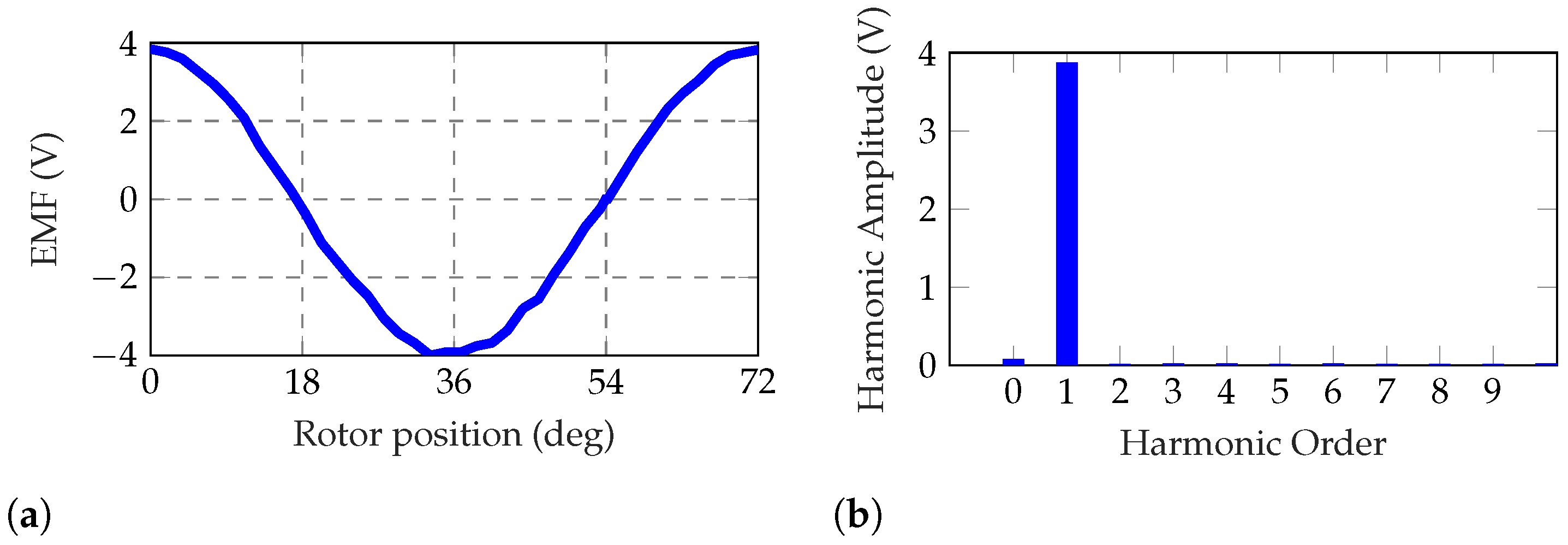
When the motor is dragged at high speed without any current supply, the phase-to-phase Electro-Motive Force (EMF) is measured. Figure 23a shows the measured EMF waveform, which is almost sinusoidal, as verified by the Fourier analysis of Figure 23b. This experimental result confirms the flux-linkage analysis of the $12/10$ configuration ( Figure 19).

When the motor is supplied by the Maximum Torque Per Ampere (MTPA) current the torque versus rotor position is measured. Figure 24 shows the very smooth torque waveform, which is almost constant.

Varying the direct- and quadrature-axis currents $I_d$ and $I_q$ the motor performance can be defined in the whole $(I_d,I_q)$ plane. Figure 25 shows the torque, current and speed limit curves obtained for the $12/10$ motor.

Considering the theoretical definition of the output torque:

$$\tau =3/2·p·[{\mathsf{\Lambda }}_m·I_q+(L_d-L_q)·I_d]$$

(11)

it represents a family of hyperbolae in the $(I_d,I_q)$ plane. However, the resulting torque curves of Figure 25 (black bold lines) are almost straight lines, similar to those obtained with a SPM motor. This is a further confirmation that the rotor saliency and the reluctance torque term are negligible, as remarked in Section 5.2.1.

The current limits are represented by circumferences with radius $\widehat{I}$:

$$I_d^2+I_q^2={\widehat{I}}^2$$

(12)

Different current circles can be represented. The maximum torque generated for a given current amplitude can be identified as the torque contour line tangent to such a current limit circumference. The red curve represents the MTPA trajectory (i.e., MTPA computed for different current amplitudes). All motors exhibit an MTPA trajectory very similar to the SPM motor. Thus, the control can be simplified imposing only q-axis current supply (i.e., $I_d=0,I_q=\widehat{I}$).

Flux-linkage limit curves are represented by a family of ellipses with equation:

$${\lambda }_d^2+{\lambda }_q^2={(V_N/{\omega }_m^e)}^2$$

(13)

where $V_N$ is the voltage supplied and ${\omega }_m^e$ is the electrical speed. For a specific operating point, the speed is computed in the crossing point between the torque curves and current circles.

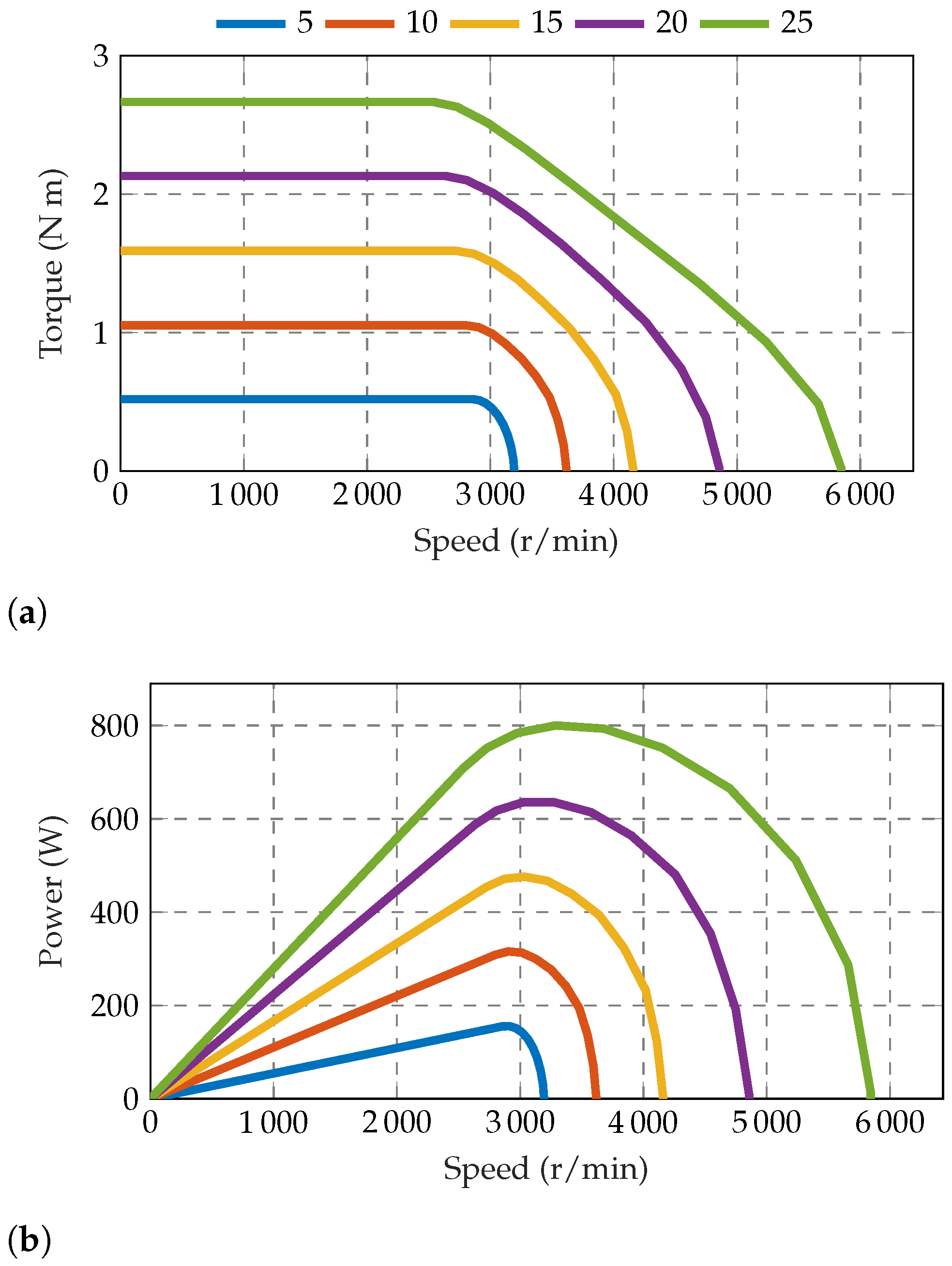
Considering the maps presented above, the torque versus speed and power versus speed characteristics can be computed. The torque remains constant up to the base speed, then the Flux Weakening (FW) operation is achieved. The FW strategy consists in supplying an increasing demagnetizing current, weakening the motor flux, thus reducing the torque delivered and increasing the speed. Figure 26 shows torque versus speed and power versus speed results when different current amplitudes are supplied.

As the current supplied increases both the torque delivered and the operating speed range increase.

5.2.3. Distributed Hairpin Windings

In applications as e-bikes, one of the most important requirements is the high torque density of the electric motor. For a given motor volume, the motor torque increases proportionally to the air gap flux density (as discussed above) and the operating current. However, due to constraints on the motor cooling system, a simple increase of the current, or the current density in the wires, is not feasible.

Following the actual trend in designing traction motors for automotive applications, a solution is the adoption of hairpin windings, which yields to higher slot fill factor (i.e., the ratio between the total copper in slot and the slot area), adopting conductors with higher cross section area. Hairpin technology allows having a slot fill factor even higher than 50% with respect to traditional round wire windings. Figure 27 shows a commercial e-bike motor adopting hairpin coils in the stator winding.

For given Joule losses, a higher fill factor leads to a higher torque density. The hairpin technology is gaining attention not only for its high slot fill factor, but also for its good heat dissipation. Figure 28 shows the comparison between the heat transfer of a winding with non-overlapped coil and the hairpin winding. In this map, the same Joule losses are imposed. The higher temperature rise in the first stator winding is evident.

Despite all advantages described above, hairpin winding losses may be higher at high speed, due to non-uniform distribution of currents [54]. However, the conductor cross section area is quite reduced in this small-size motor so that the additional losses are moderate. To the aim of their reduction, particular care is given to the winding design, with proper parallel paths and wires transposition [55].

5.3. Other Motor Typologies

Other types of ac motors, namely the induction machine, switched reluctance and other synchronous motors have not gained popularity yet.

The induction machine, although cheaper and more reliable, has the disadvantages of lower torque density and lower efficiency. Thus its application in small electric vehicles, such as an e-bike, is not very popular. One example using induction machine is shown in [56].

Another possibility is to employ a switched reluctance motor [57]. In its classical form it offers better fault tolerance, cost and easier sensorless control, while its disadvantages are lower efficiency, torque density, noise and larger torque ripple in comparison to the brushless motor.

Among synchronous motors, also the reluctance machine has been considered for light EV applications [58,59]. However, such a machine is characterized by a lower power density than PM synchronous motors, thus its volume has to be higher to achieve the required performance. The actual trend is to enhance the light EV performance adopting PMs.

A comparative study of different motor geometries is presented in [60]. The double-stator switched reluctance machine analysed is able to meet and exceed the high torque (power) performance of an IPM motor at a very competitive cost, using a feasible thermal management system.

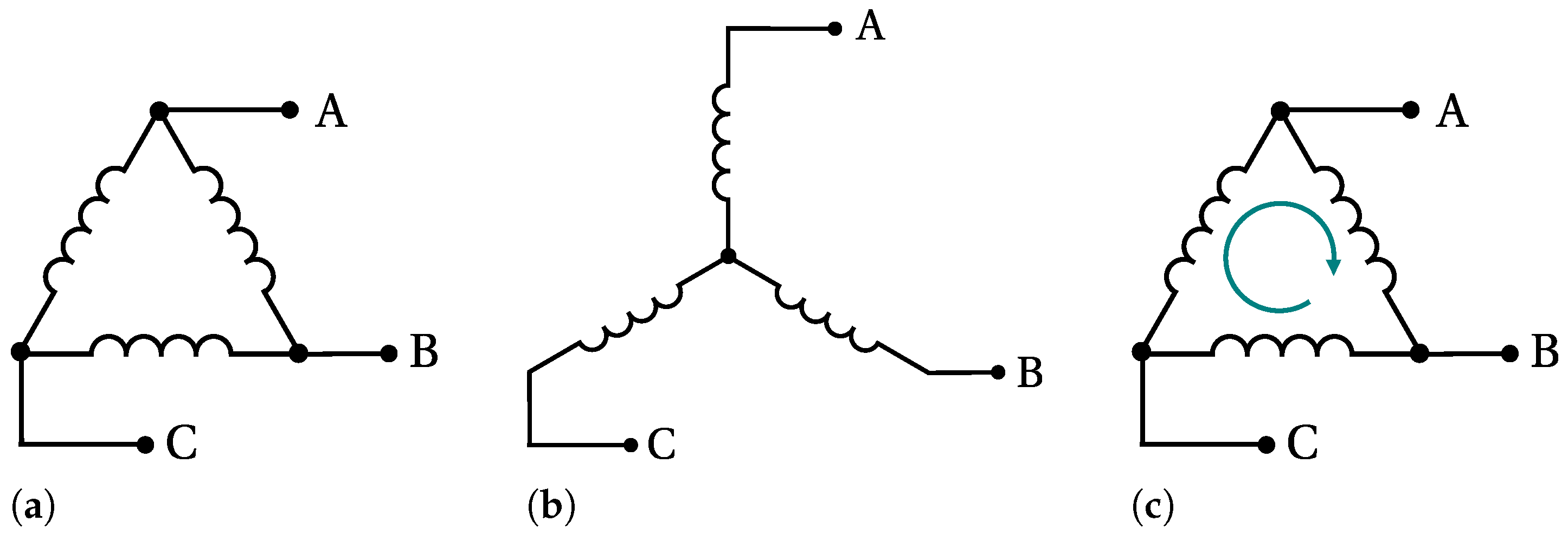
5.4. Stator Terminals Connection

Concerning the stator winding terminals connection, there are two possibilities: the delta-connection and the star-connection, represented in Figure 29.

Delta-connected stator windings are often used in mass production of small PMSMs. In comparison to star-connected stator windings, a delta-connected system has the advantage of a cheaper manufacturing. However, motors with such a winding system have additional losses caused by the zero-sequence current component circulating in the circuit, as represented in Figure 29c.

In [61] losses of a delta-connected PMSM for pedelec application are analysed and compared with the same motor with a star connection. In delta-connected machine the additional copper losses are around 6% compared to those generated by the first order current harmonic. In the nominal operating point the efficiency of the delta-connected machine is 0.6% smaller, while it is up to 4% smaller in other operating points.

6. Standard Control Methods

Considering commercial pedelec, conventional assisted power methods can be classified in two groups [62].

The first one is the constant-assisted power method. The rider is assisted by the motor with a predetermined constant power. A predefined paddle torque is sensed, i.e., the rider needs assisted power to move the pedelec forward. This method is simple to implement. However, the same predefined assisted power is provided without considering the riding environment and the rider physical condition. Therefore the comfort and the safety of the rider might not be guaranteed.

The second group is the proportion-assisted power method. According to the bike velocity v, the assisted power ratio ($P_R$) can be expressed as follows

$$P_R=\left\{\begin{array}{ccc}1,\hfill & \hfill & v\le v^{\prime }\hfill \\ 1-k·(v-v^{\prime }),\hfill & \hfill & v^{\prime }<v<v_{max}\hfill \\ 0,\hfill & \hfill & v\ge v_{max}\hfill \end{array}\right.$$

(14)

If the vehicle velocity v is lower than a predefined velocity $v^{\prime }$, the assisted power provides the same power as the rider power. Over such a speed, $P_R$ gradually decreases according to the parameter k which is chosen to attenuate the assisted power ratio. It is defined as the inverse of $v_{max}-v^{\prime }$. The motor assisted power is $P_R$ multiplied by the rider power. At last, if the vehicle velocity v is higher than the maximum allowed velocity $v_{max}$, the assisted power is zero. Typical values are $v_{max}$ = 25 km/h, $v^{\prime }$ = 15 km/h, and k = 0.1. Figure 30 shows the behaviours of the assisted power ratio $P_R$ as a function of the bike velocity.

A control technique based on disturbance observers is described in [63]. It is able to adapt to load and road slope.

A control system for a 350 W 3-phase brushless DC motor supplied by a 36 V 5.5 Ah Li-Ion battery pack is described in [64].

Similarly, model, simulations and measurements are reported in [65].

7. Standard Control Implementations

In [66] an integrated driving-braking control is presented. It is essentially based on the proportional-integral-derivative (PID) control. A brushless DC hub motor is controlled by means of the field oriented control for both driving and braking actions.

Using a DC motor, some simulation results are reported in [67]. An ATMEGA-32 microcontroller is used to regulate the analog input from the throttle in an e-bike in [15]. Similarly, a control drive for a brushless DC hub motor is also described in [68], based on an Arduino board. Simulations and description of the full system are reported in [69]. Similar studies have been carried out on scooter, as in [70].

8. Advanced Control Strategies

8.1. Reinforcement-Learning

In [62] a reinforcement learning is proposed to provide assisted power with comfort of ride. The agent of the RL takes a sequence of action, i.e., different levels of assisted power, in the nondeterministic environment of pedelec riding and receives rewards for its actions in trying to solve the comfort-of-ride problem. After a set of trial-and-error steps, the RL agent learns the best sequence of action that achieves the comfort of ride for rider. The first purpose is to satisfy the predetermined quality-of-riding. In the situation of pedelec it is often complex, since the rider pedal force varies with different road types and the rider physical conditions in a non deterministic way. Therefore a correct input/output mapping for electric-assisted power is hard to provide.

A second purpose of the algorithm is to maximize the energy utilization of the battery.

8.2. Fault Diagnosis

As for other electric devices, different techniques to detect faults can be adopted. In [71] a fault diagnosis approach is described for pedelec drive units. A data-driven approach for the detection of faults in mechanical components maximizes the information content of the signals that are already available in the drive unit, avoiding the addition of other sensors. Support Vector Machine is adopted by the authors, which is a supervised learning algorithm. The key objective is to construct a hyperplane that separates two classes, so that the margin is maximum between the hyperplane and the closest data points of the training set, which are called support vectors. N input vectors $x_n\in {\Re }^N$ form the training set, with target values $y_n\in \{-1,1\}$. Defining a fixed feature-space transformation, $\varphi \left(x\right)$, the hyperplane that separates the two classes is given by

$$y\left(x\right)=w^T\varphi \left(x\right)+b=0$$

(15)

where $w\in {\Re }^N$ is a weight vector and b is the bias. The optimal solution requires to minimize ${\left|\right|w\left|\right|}^2$. The authors proved that the algorithm is able to identify malfunctions on systems after a training stage.

8.3. Fuzzy Logic Control

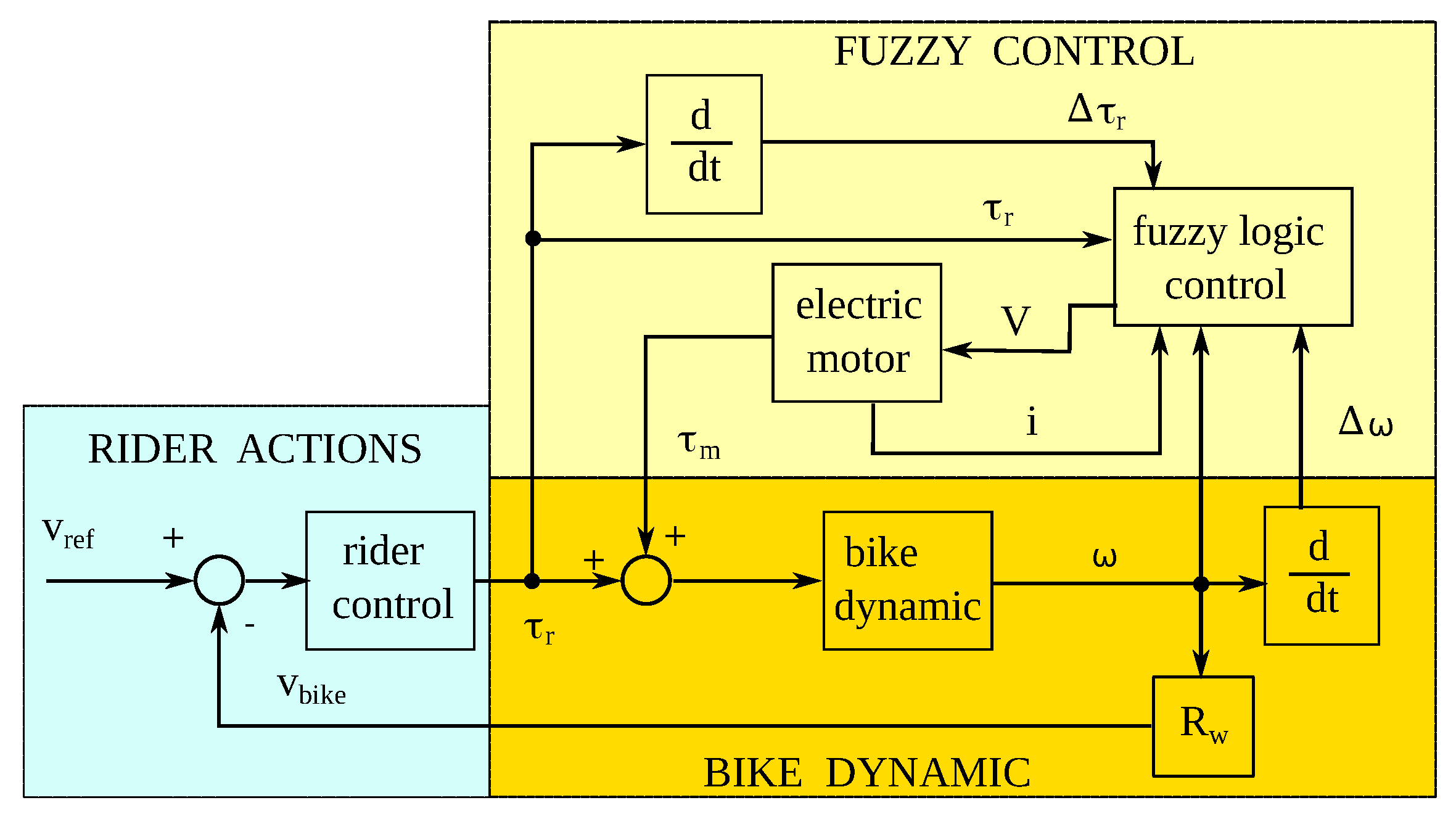
Some authors deal with the control of the electric bike by means of a fuzzy logic approach.

Figure 31 reports the scheme proposed in [72], where the expected velocity $v\ast$ is compared to the actual bike velocity $v_{bike}$ (which is linked to the angular speed ${\omega }_m$ by means of the wheel radius $R_w$). The input to the fuzzy logic system are the angular speed and its rate of change, the rider torque and its rate of change, the motor current (which is proportional to the motor torque) and its rate of change.

Typical membership functions, as sketched in Figure 32, are adopted to manage the inputs and obtain the output. The latter corresponds to the voltage command to the motor.

A fuzzy logic approach is also adopted for an autonomous dynamic balance of a running electrical bicycle in [73]. To deal with the huge uncertainties of the bicycle system caused by different ground conditions and gusts of wind a fuzzy sliding-mode under actuated control is proposed. The purpose of the strategy employed is twofold: (i) to control the bike centre of gravity (as a pendulum), (ii) to control the angle of the bike steering handle. An additional variable is the lean angle. The proposed system produces three outputs affecting the dynamic balance of the electrical bicycle: the bike pendulum angle, the steering angle and the lean angle with respect to the gravity direction of the bicycle in motion.

Fuzzy logic control is used for an electric bike derived reproducing a normal pedal powered bicycle is also given in [74]. Fuzzy control is also used in [75] where a kid cycling is described by means of illustrative rules. Again, a soft-starting method brushless DC motor in an electric bicycle is reported in [76].

9. Control Interacting with the Rider

There are many studies dealing with the interaction between the power motor assistance and the cyclist, that can be defined as a human rider synergic control.

For this purpose a particular control strategy is proposed in [11], which is based three parameters: (a) an equivalent cycling efficiency based on oxygen consumption, that is ad hoc-defined, (b) a dynamic model for the state of fatigue, including the maximum isometric force (static force without movement of the muscles), i.e., maximum voluntary contraction, and (c) heart rate measurements. A control-oriented analysis of the rider metabolic efficiency is carried out to guide the design of the control algorithm. The idea is to recover energy from the cyclist during high-efficiency pedalling and return it during low-efficiency pedalling. It reaches an improvement up to 25% in equivalent cycling efficiency and a reduction in peak heart rate and state of fatigue during a urban cycling.

In [13] the authors focus on the control of high speed bicycles, based on the bike shapes designed by Weaver. The peak speed was 112 km/h during a race in Nevada. An automated steering controllers for these high-speed bikes is studied. Because of limitations in human capability, roll control of the bike was getting difficult at higher speeds. They observed that unexpected wind gusts tends to flip the bike over.

10. Chain-Less Bike Solutions

A series hybrid electric bicycle is proposed in [12]. The cyclist powers an electric generator that in turn supplies the electric motor and a battery pack. The authors claim that this e-bike achieve a high efficiency by keeping the rider in its optimal efficiency point all the time regardless of the bicycle velocity. However, they highlight some challenging items: (i) how to provide a natural pedalling feeling (especially at low cadence or when starting) and (ii) how really optimize the vehicle efficiency.

A bilateral control is proposed to the aim of managing the level of assistance while providing a natural feeling in a systematic way. The generator has to be controlled to emulate the desired inertia, so as to give satisfactory feeling at the pedal and also for the vehicle dynamics. The objective is to replicate at the generator, the behaviour of the motor, and vice versa. An algorithm is studied to control the bike and to provide a natural pedalling.

The rider torque and speed have to be linked to the load torque and speed by a relationship as

$$\left[\begin{array}{c}{\tau }_{ped}\hfill \\ {\omega }_{ped}\hfill \end{array}\right]=\left[\begin{array}{cc}{K}_1\hfill & 0\hfill \\ 0\hfill & \rho /K_1\hfill \end{array}\right]·\left[\begin{array}{c}{\tau }_{load}\hfill \\ {\omega }_{load}\hfill \end{array}\right]$$

(16)

where $K_1$ corresponds to the traditional transmission ratio between the pedal and the traction wheel, and $\rho$ is an assistance factor operating as a torque scaling factor.

Bike Emulator

A pedalling experience can be dynamically simulated by means of a bike emulator [77]. A chain-less series bicycle is considered, controlling the electric generator connected to the pedals. The electric machine is connected to the pedals to enhance a virtual bike driveline emulation. The authors focus on reproducing the effect of the freewheel mechanism, which makes the torque transmission unidirectional: the transmission disengages when the pedals rotate at a lower rate than the wheel (reduced to the pedal shaft). The proposed motor control strategy is based on two concurrent controllers that simultaneously operate: cadence and torque. An integration strategy selects which controller is active, because of the single controllable input that is the motor voltage. The designed integration strategy guarantees a smooth interchange between the two controllers and copes with the wind-up phenomenon that affects the deactivated controller.

The controller integration law is achieved taking the minimum between the two control variables, thus selecting the correct control action automatically:

$$u\left(t\right)=min\{u_1\left(t\right),u_2\left(t\right)\}$$

(17)

without needs of additional switching and guaranteeing bump-less transitions between the two control actions.

An ad-hoc anti-wind-up strategy is designed to manage the wind-up phenomenon occurring with the controllers integration. The output of the active controller acts as a dynamic upper saturation for the other controllers. A non-zero threshold $U_{th}$ value is added to the control variable $u\left(t\right)$ which causes a certain drift of the control variable of the inactive regulator but prevents too frequent interchanges between the controllers. An admissibility region is implemented:

$$R\left(t\right)=\{U_{min},min\{U_{max},u\left(t\right)+U_{th}\}\}$$

(18)

where $U_{min}$ and $U_{max}$ are the actuator limits.

11. Remarks on Costs

As the e-bike technology requires several additional advanced components compared to traditional muscular bicycles, such a vehicle is characterised by high costs. This Section deals with a simple cost analysis for such technology.

Considering the commercial cost of an e-bike, several factors influence the final price. First of all, the brand name plays an important role on the final price proposed to costumers. In fact, brands that have been in the bike industry for years have established a reputation for design, reliability, and performance. Customers are comforted by the robustness of the companies and the quality of their products, allowing them to charge a higher price.

Second, the price varies depending on the quality of each part that compose the e-bike. Advanced technologies and fine components will rise exponentially the overall e-bike value. Finally, a different price is defined based on the customized part of the vehicle, from a simple custom detail to a fully customized e-bike.

The e-bike market can be subdivided into the low-cost and the high-cost e-bikes categories. Different cost analysis can be carried out depending on the category considered. For the low-cost e-bikes, the highest impact on the final cost is given by:

• battery cost (about $23\%$);
• shipping cost (about $19\%$), as many components come from Asia;
• electric motor cost (about $15\%$);
• controller and display cost (about $8\%$).

Therefore, the electronics (battery, motor, controller and display) and shipping make the biggest impact on the final price of a low-cost e-bike.

For the high-cost e-bikes, the highest impact on the final cost is given by:

• battery cost (about $20\%$);
• suspension cost (about $17\%$);
• electric motor cost (about $14\%$);
• frame cost (about $9\%$);
• shipping cost (about $9\%$);
• rims and tires cost (about $7\%$);
• drivetrain cost (about $7\%$).

Therefore, the electronics (battery, motor, controller and display), the suspension and frame, brakes and groupset make the biggest impact on the final price of a low-cost e-bike. The electronics of a high-cost e-bike is not much different than the low-cost e-bike. Some improvements can concern battery size, motor power, LCD/Color display, controller amperage, etc. What makes the difference between a low-cost and a high-cost e-bike is the quality of other mechanic components. For example lighter carbon or titanium frames or hydraulic brakes contribute to increase the cost.

Since the power storage of an electric bicycle is the battery and its cost has a high impact on the final price, some data of battery costs are presented hereafter. Top battery suppliers (Bosch, Shimano and Yamaha for specific e-bike batteries, Panasonic, Samsung, LG, and Sony for high quality batteries) charge $550–950 for a typical $500\mathrm{W}\mathrm{h}$ battery. The price increases when customized battery packs are designed.

Table 3. E-bike battery cost.

Battery Pack	Energy	Price	Relative Price
	${W}{h}$	$	$$/{W}{h}$
Bosch Power Pack 500	500	≈900	≈1.8
Bosch Power Tube 400	400	≈700	≈1.75
Shimano STEPS BT-E8020	504	≈750	≈1.5
Yamaha	500	≈700	≈1.6

shows battery cost comparison for some famous companies. The reference parameter is the energy in $\mathrm{W}\mathrm{h}$, thus costs are related to the energy, resulting measured in $\$/\mathrm{W}\mathrm{h}$. Other battery suppliers such as Panasonic, Samsung, LG, and Sony offer lower relative prices (around 0.7 $\$/\mathrm{W}\mathrm{h}$), since they do not produce specifically e-bike battery packs.

12. Other Applications

12.1. Autonomous Bike

In [78] an autonomous bike is presented, adoptong a flywheel balancer to be stabilized and it is able to performs a wheelie movement and quick turns. A model predictive control is implemented for the prediction of the future behaviors. The control input is obtained by solving an optimization problem at each time, given by the form

$$J=\varphi \left(x\right)+{\int }_t^{t+T}L(x,u)d\tau$$

(19)

with $x\left(t\right)$ the state vector and $u\left(t\right)$ the input vector. Both the functions $\varphi \left(x\right)$ and $L(x,u)$ manage the actual state in comparison to the desired (target) state of the bike.

12.2. Adaptive Assistance

Electrical assistance can indirectly control the ventilation rate of a cyclist, which is particularly important to reduce the air intake of cyclists in polluted areas. In [79] a cyber-physical control system is designed to manage the interaction of the cyclist and electric motor of the bike, showing that the air ventilation rate of the cyclist can be indirectly controlled. The control is organised as follows.

(1) A route prediction module: historical data from the cyclist is used to model both the intent of the cyclist and likely energy consumption along predicted routes.

(2) An energy management module: the battery state-of-charge is monitored and this information is used to calculate the allowed energy consumption along the expected route.

(3) A control module: such a module manages the interaction between the cyclist and the electric motor.

Many measurements of ventilation rate are reported in [79] referring to people with various fitness level, gender and age.

An e-bike able to help people with limited physical capabilities to safely engage in physical activity is described in [80]. The purpose is to use an control to regulate the heart rate of the cyclist and to manage the motor assistance incorporating trip information. The proposed system consists of two parts. (A) a control part, based on a model predictive controller, which regulates the heart rate by changing the motor power and gear ratio to maintain a user-defined physical effort. The optimal control input of the predictive control includes (i) the tracking of the reference heart rate, (ii) the achievement of a riding velocity as fast as possible, (iii) the prevent of fast switching of the gears so as to avoid uncomfortable cycling experience, (iv) the keeping a given physical strain of the cyclist. (B) A planning stage, which processes a priori information to estimate the power demand during different parts of the route. The optimal motor power is computed for each part of the route, also aiming to limit the energy consumption and to save energy. In addition, including a trip information helps to manage the energy consumption over the entire trip, reducing the battery energy discharge. The authors highlight that a combined control of motor power and transmission ratio gives higher performance than using each control variable separately.

12.3. Driving Assistance System

A driving assistance system for pedelecs is described in [16]. Such a system focuses on sensor fusion of radar and camera. The radar allows a precise position and velocity measurement, and the camera provides additional object information including classification in the proximity of the bike. The authors implemented an optimization of sensor fusion parameters, an identification of the most important object and an optimization of the human machine interface to warn against this most important object. The radar provides an object list with position and velocity. A front-facing 180${}^{°}$ camera and a rear-facing 80${}^{°}$ camera are used to detect traffic participants.

Similarly, in [81] an architecture for pedestrian recognition in urban environment. The models are generated by a synthetic human walking model. The detection is based on the integration of texture information and template matching using the Hausdorff distance. Motion actions are extracted by utilizing robust trackers. Additionally the motion cues are used in combination with the contour model-features for a complete recognition.

According to the slope of the road, a self-adjusting of the seat is proposed in [82]. A sensor in the bike detects the inclination with respect the gravity direction and the seat angle is adjusted improving the biker posture and the bike stability.

12.4. Rehabilitation Use

Among the others, an interesting utilization of the electric bike is for rehabilitation. There are several studies dealing with the positive impact of cycling for people suffering from physical diseases.

In [83] the focus is on rehabilitation in individuals with Parkinson’s disease. An exercise bike controls accurately the rider experience at an accelerated pedalling rate, while capturing real-time test data. well as the software and control algorithms are presented.

A first control algorithm is developed for the bike implementing an inertia load (static mode): the bike operates as a regular exercise bike with programmable resistance (load) and captures and records signals as heart rate, cadence, power. A second control algorithm implements a speed reference (dynamic mode): the bike operates at a user-selected speed (cadence) with programmable variability in speed. This seems to achieve the desired benefits for patients. session parameters such as cadence set point and load. Clinical trials of riders Parkinson’s disease are conducted since 2012, confirming the proper operation of the bike and the validity of the data acquisition system.

The author in [84] deals with functional electrical stimulation (FES) cycling, done to regain mobility and for health benefits. Many physiological effects of FES-cycling are remarked, as increase of muscles, better blood flow, reduction of pressure ulcers, reduction of bone mineral density. FES cycling may be for home use, much saver and easier than FES walking, or coupled to a wheelchair, combining arm cranking and FES cycling.

The approach for FES cycling described in [85] uses the crank angle to generate the stimulation pattern for inducing a pedalling motion. For the majority of available systems, the patient sits with his wheelchair in front of anemometer for the training period while the mobile cycling is performed on recumbent tricycles. A crank angle measurement system is needed, and the muscle stimulation phases with positive torque regarding the crank angle is determined according to the seating position and the seat-to-crank distance.

A tricycle for enabling paraplegic riders (people with spinal cord lesion) to compete in races is described in [86]. An accurate study of the various phases during one cycle for the knee joint is presented, determining (a) a start of the extension phase, (b) an extension phase, (c) a start of the flexion phase, and (d) a flexion phase. Angles and generating stimulation timing. The seat position of the model is varied in distance and height with respect to the crank as well as the inclination angle of the back of the cyclist. A proportional-integral controller is used to control the mean cycling speed to 50 round/minute by controlling the pulse width and keeping constant the stimulation frequency. The muscles are stimulated in advance during cycling to guarantee that extension and flexion torques occur exactly at the extension and flexion phases of the legs, respectively. The athlete training, preparation and rate are described in the paper.

12.5. Measuring Performance of E-Bike

In order to measure the performance of the electric bicycle, a proper test bench has to be designed, able to emulate the cyclist in different exercise conditions and to extract the torque and power of the electric motor. In [87,88] the description of a test bench for measuring and charactering a pedal electric bicycle drivetrain is reported. The torque on the pedal cranks is simulated by means of two motors that produce a variable torque, to achieve a total torque behaviour similar to that shown in Figure 5. The torque amplitude and cadence frequency can be regulated, to simulate the effort of various cyclists. The terrain is reproduced by an output drive directly coupled to the rear hub or pressing the rear wheel on rolls. Additional weights are used to adjust the pressure from the rear wheel to the roll. Force sensors are used to measure the strains, or to adjust the pressure from the rear wheel to the roll.

13. Conclusions

In recent years, electric bicycles began to play a more important role because they were an economic and simple option for urban transport problems and had environmental advantages, especially in highly populated cities. In this study, the various elements that make up the electric bicycle system are described. The objective of this manuscript is to detect the main trends in this field, exploring the main features of the actual state of art for main subsystems of the electric bicycle.

Some mechanics fundamentals are presented to investigate the resistant forces to overcome through either muscular power or electric power. The advantage of a pedal-assisted bicycle is emphasized, as the additional power of the electric machine boosts the cyclist’s performance, allowing for much more challenging routes.

The state of art of the energy storage employed in e-bike application is presented, together with some typical commercial battery data. The study focuses on Lithium-ion batteries, as they are the most performing and they allow for an enhanced power-assisted operation of the e-bike. In particular, the main advantage of such batteries is their high power density, which allows to minimize the overall volume and weight of the vehicle.

Then the electrical machine features are presented and deeply analysed. The motor location and typology are discussed, comparing simulation results with experimental tests. The best motor location is the mid-drive one, since weights are balanced. The best motor typology is the PM synchronous motor, which replaced the BLDC motor for e-bike application, moving towards configurations more similar to automotive application electrical machines (with lower power). As far as the authors know, in e-bike literature only BLDC electric motors are considered. Besides some particular solutions (for example reluctance machines), PM synchronous motors designed for e-bike application have never been deeply described.

In addition, many control strategies are presented, to give an overview of the state of art and to present some innovative implementations. No dominant control technique is currently widespread among the others. In general the control system has to take into account several inputs, including cyclist requirement, energy consumption, torque oscillation, overload, laws limits, etc.

They can be divided in two categories: standard and advanced control methods. Standard methods are simple to implement and require fewer sensors or data exchange. However, they do not always guarantee safety and comfort. Differently, advanced control methods represent an high technology tool, satisfying safety and rider comfort requirements. They allow adapting to the rider effort, controlling the electrical power delivered on the basis of the muscular power, exploiting the battery efficiently and detecting faults. Finally, some remarks on costs and other applications of similar light electric vehicles conclude the review.