An Explicable Neighboring-Pixel Reconstruction Algorithm for Temperature Distribution by Acoustic Tomography

Abstract

Acoustic process tomography is a powerful tool for monitoring multiphase flow and combustion. However, its capability of revealing details of the interrogation zone is restricted by the ill-posed and rank deficiency problems. In each projection, a probing sound beam only passes the pixels along its propagation path, resulting in a large number of zero-valued elements in the measurement matrix. This is more pronounced as the resolution of the imaging zone becomes gradually finer, which is detrimental to image reconstruction. In this study, a mathematically explicable reconstruction algorithm of regularization is proposed by assigning each zero-valued pixel with a combination of the values of the neighboring pixels, ruled by the appropriate regularization factors. The formula to determine the regularization factors is also derived. Simulations are carried out to verify this new approach, and some representative cases are presented. As a result, the ambiguity of the inverse process is removed, and the accuracy of the image reconstruction is significantly improved. The results show the robustness of the algorithm and certain advantages over the standard Tikhonov regularization formula.

1. Introduction

In industrial operations, the online monitoring of the operation parameters plays a vital role in securing the quality of the products. The temperature distribution is one of the most important parameters to be monitored. The operation safety, process efficiency, pollution control, etc., are very often closely related to the temperature distributions. With the advantages of a nonintrusive technique, acoustic tomography is one of the modern techniques in reconstructing temperature distribution in various devices.

For a time-of-flight method, the reconstruction of temperature distributions needs the measurement of time as the acoustic wave propagates through the interrogation section, and certain algorithms to calculate the temperature in the sections [1,2,3,4]. Some frequently used algorithms include Linear Back Projection (LBP) [5], Landweber iteration [6], Algebraic Reconstruction Algorithms [7,8,9,10], Singular Value Decomposition (SVD) [11], etc. Zhang [12] proposed a meshless Radial Basis Function (RBF) method combined with the modified Tikhonov regularization to reconstruct the two-dimensional velocity field. The impacts of shape parameters, types of RBF, and the collocation of central points on the reconstruction are analyzed. The feasibility and effectiveness of the proposed method show that the proposed method is appropriate to solve severely ill-posed and underdetermined acoustic tomography problems. Kong [13] put forward a new 3D temperature field reconstruction method based on radial basis function approximation with polynomial reproduction (RBF-PR) and truncated generalized singular value decomposition (TGSVD). The experimental and simulation results both showed the effectiveness of the proposed method. He also studied the anti-noise ability of the proposed method, and the results indicated that model could reconstruct the temperature distribution with higher accuracy and better anti-noise ability compared with TGSVD [14]. Yu [15] developed a novel nonlinear acoustic tomography to reconstruct both temperature and the velocity field simultaneously, which was confirmed by the simulation. Otero [16] also described a novel acoustic tomography method for simultaneous velocity and static temperature distributions in high subsonic Mach number flows and presented the proof by the laboratory experiment. Li J. [17] combined the integral equation (IE) in the forward process and the contrast source inversion (CSI) in the inverse process in monitoring the properties of concrete quality defects. The method was validated by the numerical cases. Rao [18] developed an ultrasonic tomography method based on acoustic multiparameter full waveform inversion (FWI) for high-resolution reconstructions of velocity and density in metal components. In his study, the inverse Hessian was applied to mitigate the coupling effects of multiparameters. The method could effectively alleviate the tradeoff effects between velocity and density.

In recent years, some scholars have also proposed some reconstruction algorithms of two-dimensional temperature distribution, which represent the research state-of-the-art in this field. Liu [19] studied a new reconstruction method that integrated the advantages of the Tikhonov regularization method and the Least Squares Support Vector Machine (LSSVM). The reconstruction quality was improved. Wu [20] proposed a new reconstruction algorithm based on the Radial Basis Function (RBF) interpolation method optimized by the evaluation function (EF-RBFI). The reconstruction results also verified the feasibility of the proposed algorithm. Chen [21] put forward an improved Tikhonov regularization reconstruction algorithm and reconstruction errors of temperature fields were reduced based on simulation and experiment. Liu [22] presented a two-phase reconstruction method to ameliorate the reconstruction accuracy, and the superiority of the robustness and reconstruction accuracy was validated by numerical simulations and experiment measurement. Wang [23] proposed a new reconstruction algorithm based on the logarithmic–quadratic (LQ) Radial Basis Function (RBF) and Singular Value Decomposition (LQ-SVD). The reconstruction results revealed the stronger robustness and better anti-interference ability.

However, currently, it is difficult to find an algorithm to effectively deal with the severe rank deficient problems. As the number of the paths of the acoustic waves is limited by the number of the transducers, the waves may not be able to pass all the pixels in the interrogation zone, if there are a large number of pixels. There may even be questions as whether the results of the reconstructions are the solutions of the real problems. Although a definite solution may be acquired by reducing the number of pixels to a number smaller than the probing paths of the waves, this will tend to cause to coarse pixels that will largely reduce the quality of the reconstructed images.

In this study, we propose an explicable neighboring-pixel reconstruction algorithm for the regularization terms to remove the ambiguity of the reconstruction results and to enable the inverse process to generate a solution. By doing so, the reconstructed images will less severely suffer from the ill-posed problems in acoustic tomography. Firstly, it is feasible to increase the number of pixels, which is limited by the probing paths of the waves in the reported literature. This contributes to improving the accuracy of the image reconstruction substantially. Secondly, the formula solution directly generates optimal results instead of the common iterative method, facilitating error calculation. Thirdly, a majority of the calculations can be performed beforehand, which obviously boosts the speed and reduces the calculation burden. Numerical simulations in four cases, including centrally symmetrical, stratified distribution, multipeak distribution, and mixed distribution, were carried out to verify the effectiveness of our method. In summary, the main contributions of our algorithm are as follows.

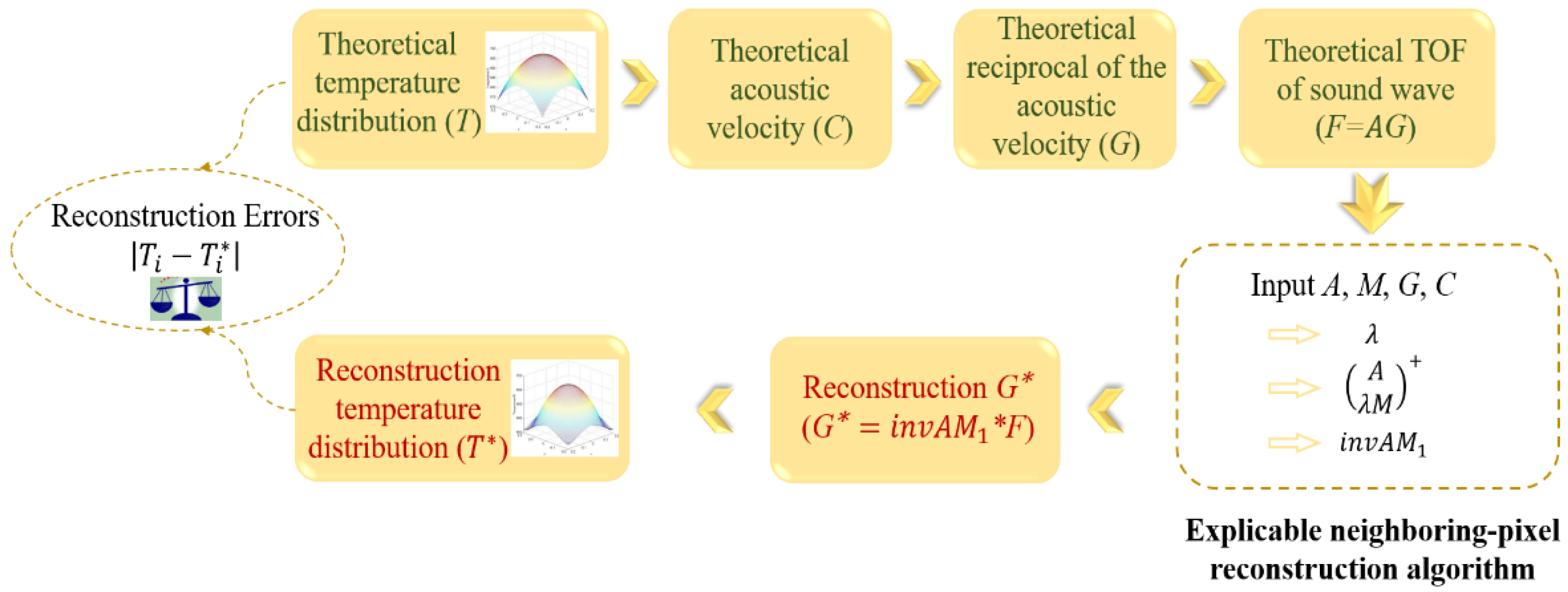
• The proposed explicable neighboring-pixel reconstruction algorithm prominently increases the accuracy of image reconstruction. The number of pixels can be much larger than the number of paths, which is limited in the existing studies.
• Our method is explicable because it gives the formula solution for the first time. In addition, it helps calculate the error.
• The fast speed and the light weight are remarkable resulting from the prior calculation of the most parameters.
• It can be universally applied to sound velocity tomography, acoustic relaxation attenuation tomography, and optical tomography, which is of great significance.

2. Principles of Acoustic Tomography for Temperature Field Reconstruction

Acoustic measurement inverts the physical characteristics of the medium by measuring the change in the propagation parameters of the sound wave. The principle of Acoustic Tomography for temperature field reconstruction is to invert the reciprocal of the sound speed, which is related to the temperature, according to time of flight (TOF) of the sound wave. As shown in Figure 1, given the theoretical temperature distribution, the theoretical time of flight, i.e., $\mathit{F}$, could be calculated. The acoustic tomography reconstructs $G^{\ast }$ using the proposed reconstruction algorithm, according to the TOF.

It is well known that the propagation of a sound wave in air will vary with temperature, assuming that there is no heat transfer associated with the acoustic wave propagation, as described by [24]:

$$c=\sqrt{\frac{1.4RT}{M}}$$

(1)

where $c$ is the sound wave velocity in air, m/s; R is the molar gas constant, 8.31451 J/(mol·K); T is temperature in K; and M is the relative molecular mass, kg/kmol. Equation (1) is the basis for the acoustic measurement of temperature distributions in a gaseous medium.

It can be supposed that the mixed gases would not produce a chemical reaction, and there is no heat transfer in the measured area. Moreover, a cross-section is considered to describe the coordinates of the emitter or receiver via the cartesian coordinate system, which are $P_{pro}\left(x_{pro},y_{pro}\right)$ and $P_{rec}\left(x_{rec},y_{rec}\right)$ respectively. Then, the time of flight from emitter to receiver $T_{PR}$ is as follows [24],

$$T_{PR}={{\displaystyle \int }}_{L_{PR}}g\left(x,y\right)dl$$

(2)

where $L_{PR}$ indicates the path of the sound wave between $P_{pro}$ and $P_{rec}$, $g\left(x,y\right)$ is the reciprocal of the sound velocity at the position of $\left(x, y\right)$, and $dl$ is the differential length in the path of the soundwave. It is notable that $g\left(x,y\right)$ is an unknown function to be solved. Since the line connecting $P_{pro}$ and $P_{rec}$ can be expressed by

$$y\left(x\right)=\frac{y_{rec}-y_{pro}}{x_{rec}-x_{pro}}\left(x-x_{pro}\right)+y_{pro}$$

(3)

then, $dl$ is converted as follows,

$$dl=\sqrt{1+{\left(\frac{y_{rec}-y_{pro}}{x_{rec}-x_{pro}}\right)}^2}dx$$

(4)

So, $T_{PR}$ can be derived as

$$T_{PR}={{\displaystyle \int }}_{x_{pro}}^{x_{rec}}g\left(x,y\left(x\right)\right)\sqrt{1+{\left(\frac{y_{rec}-y_{pro}}{x_{rec}-x_{pro}}\right)}^2}dx$$

(5)

where we assume $x_{rec}>x_{pro}$.

The $T_{PR}$ is the theoretical value of TOF. It is an integral form in Equation (5), which is difficult to solve. Therefore, the approximate calculation is performed for each path in Equation (6). If $\tilde{m}$ transducers, each with a two-fold capability of being an emitter or a receiver, are arranged around the periphery of a circular region, then a number of $m=\tilde{m}\left(\tilde{m}-1\right)/2$ sound paths can be attained. If the measurement region is divided into n cells, or pixels, and we assume the temperature in the region varies continuously, then the time of flight (TOF) of the sound wave along the i-th path $f_i$ can be expressed by

$$f_i\approx {\displaystyle \sum }_{j=1}^n{g}_j{l}_{ij}$$

(6)

where $g_j$ is the reciprocal of the sound speed in the j-th cell, and $l_{ij}$ is the length of the i-th path inside cell j. The $f_i$ is the experimental value of TOF in the i-th path. Let

$$\mathit{A}=\left(\begin{array}{cccc}{l}_{11}& l_{12}& \cdots & l_{1n}\\ l_{21}& l_{22}& \cdots & l_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ l_{m1}& l_{m2}& \cdots & l_{mn}\end{array}\right),\mathit{G}=\left(\begin{array}{c}{g}_1\\ g_2\\ ⋮\\ g_n\end{array}\right),\mathit{F}=\left(\begin{array}{c}{f}_1\\ f_2\\ ⋮\\ f_m\end{array}\right)$$

(7)

Then, the matrix form in all paths is expressed as,

$$\mathit{A}\mathit{G}=\mathit{F}$$

(8)

It should be noted that $\mathit{A}\mathit{G}$ is approximately equal to the measurements $\mathit{F}$. The specific optimization problem is to determine $\mathit{G}$ so as to minimize $||\mathit{A}\mathit{G}-\mathit{F}{||}_2$. Generally, the determination of $\mathit{G}$, which minimizes the least squares error, is presented as the solution of $\mathit{A}\mathit{G}=\mathit{F}$ in matrix theory. So, Equation (8) is expressed as an equality. If the least square solution of $\mathit{A}\mathit{G}=\mathit{F}$ is unique, then $\mathit{G}$ can be taken as the distribution of the reciprocal of the sound speed.

As indicated in Figure 2, there are a set of 12 transducers arranged evenly in a circle, which are named as transducer_1 to transducer_12. For the extensibility of the method, the center of the circle is defined as the origin, and the radius of the circle is 0.2. The lines show the paths of sound waves that are generated by transducer_1 and received by the other eleven transducers. Each transducer can be considered as an emitter or a receiver. So, there will be a combination of sixty−six effective paths of sound waves attainable from twelve transducers.

According to [25], there are mainly three factors that influence the resolution and accuracy of the reconstruction of the temperature field by acoustic CT.

(1)

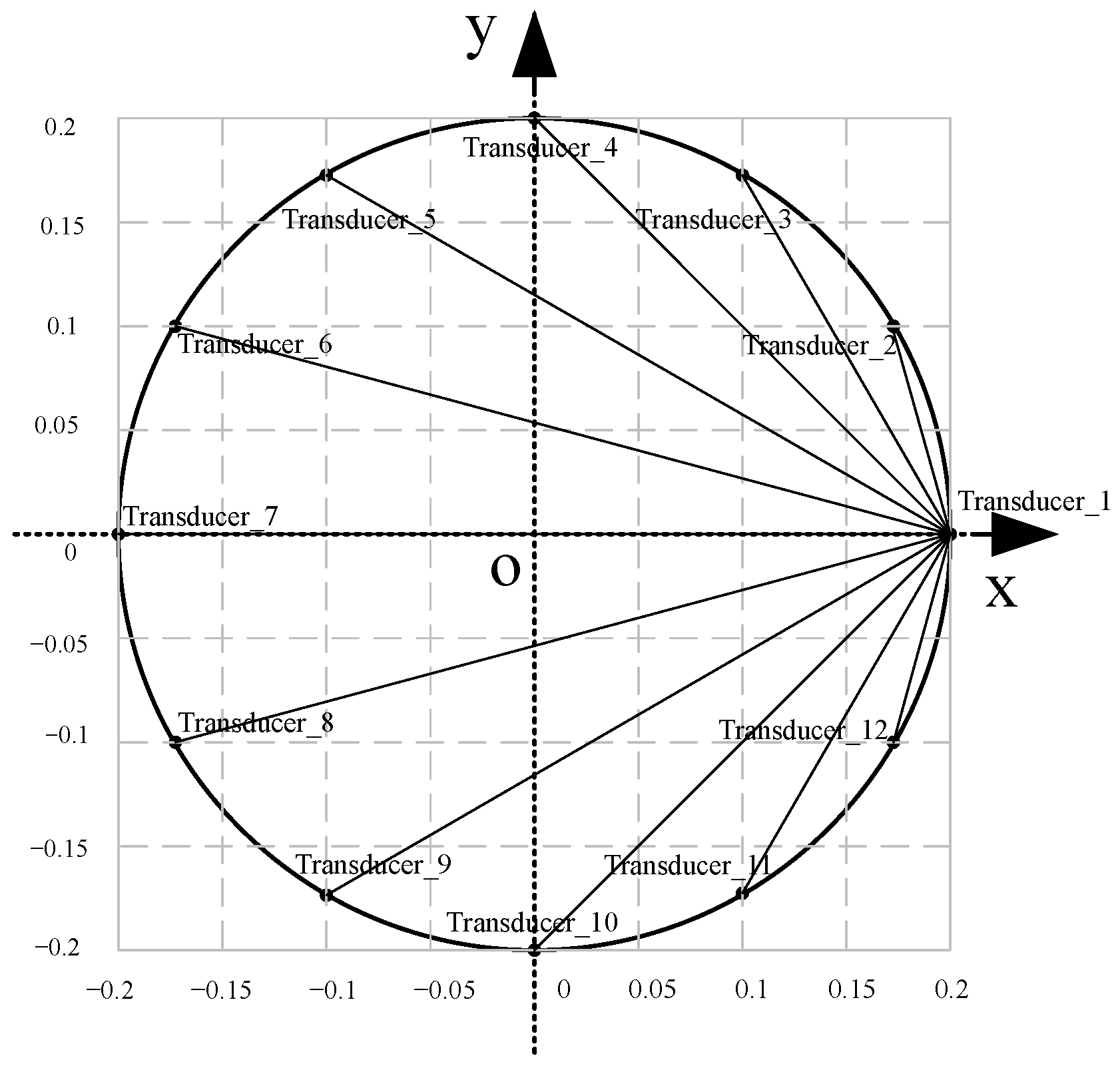
The number and positions of the transducers.

Generally speaking, more transmitters can provide more information for image reconstruction, resulting in more accurate images but possibly with a higher cost of the device and elongated measurement time. As for the transmitters, normally, they are evenly distributed around the periphery of the measurement boundaries to have a balanced interrogation beam coverage over the sensing zone.

(2)

The accuracy of the TOF measurement.

The relative error of the TOF measurement will lead to the relative error of the temperature measurement.

(3)

The state-of-the-art model and algorithm employed in the reconstruction.

The model and algorithm should reconstruct the complex temperature field accurately and be robust.

3. A Neighboring Cells Regularization Model

3.1. An Analysis of the Conventional Method

According to the mean value theorem for integration [26], the errors of Equation (6) are affected not only by the distribution of the temperature but also by the maximum size of the differential element or the pixel in the context of image reconstruction, $d_{max}$, as well as by how the characteristic parameter for a pixel is defined. According to the matrix theory [27], for a linear system of equations $\mathit{A}\mathit{G}=\mathit{F}$ to have a unique least squares solution, the coefficient matrix $\mathit{A}$ must have full column rank. In particular, there should be no column(s) with all zero members.

It has been a widely adopted practice to virtually divide the measurement zone into small pixels by equally spaced horizontal lines and vertical lines. If a square interrogation area is divided by $\tilde{n}$ horizontal lines and $\tilde{n}$ vertical lines, then ${\tilde{n}}^2$ pixels will be counted within this area, named as n. Accordingly, there will be ${\tilde{n}}^2$ columns in matrix $\mathit{A}$. For a circular interrogation area, however, the interrogation area may not contain all the pixels thus generated, some pixels in the corners will stay outside the circular area. This will be case if the division $\tilde{n}$ exceeds a certain value, since the smaller the pixels, the more the pixels that can be contained between the circle and the square area in the corners. If this happens, there will be zero column(s) in matrix $\mathit{A}$, implying that there will not be a unique solution for $\mathit{A}\mathit{G}=\mathit{F}$. Therefore, we name this value the limit of divisions for a unique solution, LDUS for short. It is not difficult to work out the number of the outsider pixels for a given division $\tilde{\mathrm{n}}$. The number of the pixels inside the circular area represented by matrix $\mathit{A}$ corresponding to each $\tilde{n}$ can be given by the

Table 1. Number of pixels inside the circular zone for each number of $\tilde{n}$.

Parameter	Number
$\tilde{n}$	4	5	6	7	8	9	10	11	12
Number of pixels inside the circular zone	12	21	32	37	52	69	80	97	112

.

For example, for $\tilde{m}=12$, where the number of measurements is 66, $\tilde{n}$ must be smaller than 9 to limit the number of pixels inside the measurement zone to a valve smaller than the number of data acquired from the measurement, if a unique least squares solution is required for $\mathit{A}\mathit{G}=\mathit{F}$.

If $\tilde{n}$ is chosen to be small to meet the requirement for a unique square solution, then the errors of the solution will be inevitably large, due to the large size of the pixels. However, if $\tilde{n}$ is too large, the requirement on $\tilde{n}$ for a unique least squares solution for $\mathit{A}\mathit{G}=\mathit{F}$ will not be satisfied, resulting in underdetermined problems. The Tikhonov regularization method very often is an effective method to alleviate the underdetermined problems. The essence of the Tikhonov method is to acquire an optimized solution for the following problem:

$$\mathit{min}\{||\mathit{AG}-\mathit{F}{||}_2+\lambda {||\mathit{G}||}_2\}$$

(9)

where λ ≥ 0 is the regularization parameter. The above model first minimizes the error $||\mathit{A}\mathit{G}-\mathit{F}{||}_2$, while the penalty term $\lambda {||\mathit{G}||}_2$ will force a unique solution.

As shown in Figure 3, a circular measurement zone of a diameter d can be evenly divided into $\tilde{n}$ by $\tilde{n}$ squares. According to the presence of the sound beams, the pixels can be categorized into two sets of indexes, $\mathit{Index}\_1=\left\{i: \mathit{at} \mathit{least} \mathit{one} \mathit{probing} \mathit{beam} \mathit{passing} \mathit{pixel} i \right\}$, and $\mathit{Index}\_2=\left\{i: \mathit{no} \mathit{probing} \mathit{beam} \mathit{passing} \mathit{pixiel} i \right\}$. For a conventional 12-electrode sensor, the index-set, namely $\mathrm{Index}\_2$, will be a nonempty set when $\tilde{n}\ge 23$. The number of elements in $\mathrm{Index}\_2$ will increase with $\tilde{n}$. For example, $\mathrm{Index}\_2$ will have 2 elements for $\tilde{n}=23$ and 18 elements when $\tilde{n}=32$.

Theorem 1.

If $\mathit{Index}\_\mathit{2}$is not an empty set, then the solution of the optimization model is not the solution of the original problem.

Proof of Theorem 1.

If Index_2 is not an empty set, then at least one column in matrix $\mathit{A}$ will have all-zero members, if this column’s index corresponds to a pixel indexed in $\mathrm{Index}\_2$. Let vector $\tilde{\mathit{G}}$ be the same as $\mathit{G}$ except setting all the pixel values to zero if the pixels belong to $\mathrm{Index}\_2$. Then, using the definitions of the terms in Equation (9), we have $||\mathit{A}\mathit{G}-\mathit{F}{||}_2=||\mathit{A}\tilde{\mathit{G}}-\mathit{F}{||}_2$, and $||\mathit{G}{||}_2\ge ||\tilde{\mathit{G}}{||}_2$. Consequently, for any regularization factor $\lambda \ge 0$, the value of a pixel in the solution of Equation (9) must be zero if the pixel belongs to $\mathrm{Index}\_2$. This implies that, if $\mathrm{Index}\_2$ is not an empty set, the solution of the optimization problem, i.e., Equation, will not be the solution of the original problem. Therefore, when using Equation (9) for an optimized solution, the size of each pixel must not be smaller than $d/23$, i.e., $\tilde{\mathrm{n}}$ must be smaller than 23. □

$$\min \left\{||\mathit{A}\mathit{G}-\mathit{F}{||}_{\mathrm{p}}+{\mathsf{\lambda }}^2{||\mathit{G}||}_{\mathrm{p}}\right\}$$

(10)

For the same reason, if $\mathrm{Index}\_2$ is not an empty set, solutions using $\lambda {||\mathit{G}||}_p$, $p\ge 1$ in the Equation as the regularization term will not be the solution to the original problem.

3.2. The Neighboring Cells Regularization Model and Solution Scheme

For more refined images, $\tilde{n}$ needs to be increased for more pixels. However, as has been discussed above, a large number of $\tilde{n}$ will make $\mathrm{Index}\_2$ nonempty, thus exceeding the critical limit for a true solution to the original problem. To solve this problem, we propose a method to maintain $\mathrm{Index}\_2$ as an empty set even when $\tilde{n}$ is increased beyond the aforementioned critical limit.

Without loss of generality, suppose the distribution of the medium presents a continuous 2D function inside the measurement area, in which a pixel $P_{i,j}$ is located at $\left(x_i,y_j\right)$, as described in Figure 4.

Assuming $g\left(x,y\right)$ has a continuous first derivative, an approximation function can be established using the first-order Taylor expansion as follows.

$$\begin{gathered} g\left(x_i,y_j\right)\approx {\displaystyle \sum }_{k=i-1}^{i+1}{d}_{k,j-1} g\left(x_k,y_{j-1}\right)+{\displaystyle \sum }_{k=i-1}^{i+1}{d}_{k,j+1} g\left(x_k,y_{j+1}\right)+d_{i-1,j}g\left(x_{i-1},y_j\right) \\ +d_{i+1,j}g\left(x_{i+1},y_j\right)i\ne 1,\tilde{n},j\ne 1,\tilde{n} \end{gathered}$$

(11)

in which:

$$d_{k,j-1}=d_{k,j+1}=d_{k-1,j}=d_{k+1,j}=\frac{\sqrt{2}}{4\left(1+\sqrt{2}\right)}$$

(12)

$$d_{k-1,j-1}=d_{k-1,j+1}=d_{k+1,j-1}=d_{k+1,j+1}=\frac{1}{4\left(1+\sqrt{2}\right)}$$

(13)

The sum of all the $d_{k,j}$ is 1. The values of the coefficients are determined because the distances between $P_{i,j-1},P_{i,j+1},P_{i-1,j}, \mathrm{and} P_{i+1,j}$ are unity (or can be normalized to unity), and between $P_{i,j-1},P_{i,j+1},P_{i-1,j},P_{i+1,j}, \mathrm{and} P_{i,j}$, they are $\sqrt{2}$. The smaller the distance between two points, the smaller the difference between their function values. When expressed by the function value of adjacent points, if the distance is large, the weight coefficient is small; if the distance is small, the weight coefficient is large.

For cells on the lower boundary,

$$\begin{gathered} g\left(x_1,y_j\right)\approx {\displaystyle \sum }_{k=j-1}^{j+1}{d}_{2,k} g\left(x_2,y_k\right)+d_{1,j-1}g\left(x_1,y_{j-1}\right) \\ +d_{1,j+1}g\left(x_1,y_{j+1}\right) j\ne 1,\tilde{n} \end{gathered}$$

(14)

in which:

$$d_{1,j-1}=d_{1,j+1}=d_{2,j}=\frac{1}{3+\sqrt{2}}$$

(15)

$$d_{2,j-1}=d_{2,j+1}=\frac{1}{3\sqrt{2}+2}$$

(16)

For cells on the upper boundary,

$$\begin{gathered} g\left(x_{\tilde{n}},y_j\right)={\displaystyle \sum }_{k=j-1}^{j+1}{d}_{\tilde{n}-1,k} g\left(x_{\tilde{n}-1},y_k\right)+d_{\tilde{n},j-1}g\left(x_{\tilde{n}},y_{j-1}\right) \\ +d_{\tilde{n},j+1}g\left(x_{\tilde{n}},y_{j+1}\right)j\ne 1,\tilde{n} \end{gathered}$$

(17)

in which:

$$d_{\tilde{n},j-1}=d_{\tilde{n},j+1}=d_{\tilde{n}-1,j}=\frac{1}{3+\sqrt{2}}$$

(18)

$$d_{\tilde{n}-1,j-1}=d_{\tilde{n}-1,j+1}=\frac{1}{3\sqrt{2}+2}$$

(19)

For cells on the left boundary,

$$\begin{gathered} g\left(x_j,y_1\right)\approx {\displaystyle \sum }_{k=j-1}^{j+1}{d}_{k,2} g\left(x_k,y_2\right)+d_{j-1,1}g\left(x_{j-1},y_1\right) \\ +d_{j+1,1}g\left(x_{j+1},y_1\right)\hspace{1em}j\ne 1,\tilde{n} \end{gathered}$$

(20)

in which:

$$d_{j-1,1}=d_{j+1,1}=d_{j,2}=\frac{1}{3+\sqrt{2}}$$

(21)

$$d_{j-1,2}=d_{j+1,2}=\frac{1}{3\sqrt{2}+2}$$

(22)

For cells on the right boundary,

$$\begin{gathered} g\left(x_j,y_{\tilde{n}}\right)={\displaystyle \sum }_{k=j-1}^{j+1}{d}_{k,\tilde{n}-1} g\left(x_k,y_{\tilde{n}-1}\right)+d_{j-1,\tilde{n}}g\left(x_{j-1},y_{\tilde{n}}\right) \\ +d_{j+1,\tilde{n}}g\left(x_{j+1},y_{\tilde{n}}\right)j\ne 1,\tilde{n} \end{gathered}$$

(23)

in which:

$$d_{j-1,\tilde{n}}=d_{j+1,\tilde{n}}=d_{j,\tilde{n}-1}=\frac{1}{3+\sqrt{2}}$$

(24)

$$d_{j-1,\tilde{n}-1}=d_{j+1,\tilde{n}-1}=\frac{1}{3\sqrt{2}+2}$$

(25)

We express $g\left(x_1,y_1\right),g\left(x_1,y_2\right),\cdots ,g\left(x_1,y_{\tilde{n}}\right),\cdots ,g\left(x_{\tilde{n}},y_1\right), g\left(x_{\tilde{n}},y_2\right),\cdots ,g\left(x_{\tilde{n}},y_{\tilde{n}}\right)$ as a column vector, i.e., $\left\{g\left(x_i,y_j\right)|i,j=1,2,\cdots ,\tilde{n}\right\}$. That means there will be n equations for $g\left(x_i,y_j\right)$ which are expressed above by the function value of its neighbor. Then, the left part of the Equation (11) (or 14, 17, 20, 23) could be moved to the right part. These n equations can be expressed as $\mathit{M}·\mathit{G}\approx {\mathbf{0}}_{\mathit{n}\times \mathbf{1}}$, where $\mathit{M}$ is the constructed matrix. Here, the elements in the $i+\left(j-1\right)\times \tilde{n}$ row of $\mathit{M}$ in each column are

(1)

$\frac{\sqrt{2}}{4\left(1+\sqrt{2}\right)}$ at the position of $P_{i,j-1},P_{i,j+1},P_{i-1,j},P_{i+1,j}$,

(2)

$\frac{1}{4\left(1+\sqrt{2}\right)}$ at the position of $P_{i-1,j-1},P_{i-1,j+1},P_{i+1,j-1},P_{i+1,j+1}$,

(3)

$-1$-in the $i+\left(j-1\right)\times \tilde{n}$ column, which is also the diagonal element of $\mathit{M}$,

(4)

0 at the other positions.

Therefore, we can build the following optimization model to solve the problem ($\mathit{A}$ neighboring cells regularization model)

$$\mathit{min}\left\{||\mathit{A}\mathit{G}-\mathit{F}{||}_2^2+{\lambda }^2||\mathit{M}\mathit{G}{||}_2^2\right\}$$

(26)

Since $\left(\begin{array}{c}\mathit{A}\\ \mathit{M}\end{array}\right)$ is column full rank, the equation has a unique solution. In other words, by adding the regularization term $||\mathit{M}\mathit{G}{||}_2^2$, Equation (26) has a unique solution, and an approximation of the original problem is consequently guaranteed.

As an example, we applied the above method to the reconstruction of a temperature field. The case is a common one—a 2D continuous temperature distribution, for which a minimum solution with a regularization term $||\mathit{M}\mathit{G}{||}_2^2$ can be expected. In this new model, the distances among the pixel $P_{i,j}$ and neighboring pixels $P_{i,j-1},P_{i,j+1},P_{i-1,j},P_{i+1,j}$, $P_{i-1,j-1},P_{i-1,j+1},P_{i+1,j-1},P_{i+1,j+1}$ were taken into account when constructing matrix $\mathit{M}$, which effectively removed the ambiguity of the element values, caused by the all-zero-element in certain columns due to the absence of the probing beam passing the pixels, as described above.

3.3. Solution of the Model

Here, $A\in R^{m\times n}$ and $G\in R^{n\times m}$ are called the plus inverse of $A$ and denoted by $A^{+}$ if $G$ satisfies the following Penrose—Moore equations

$$AGA=A$$

(27)

$$GAG=G$$

(28)

$${\left(AG\right)}^T=AG$$

(29)

$${\left(GA\right)}^T=GA$$

(30)

where $A^{+}$ is also called the Penrose—Moore inverse. For the system of linear equations Ax = b, $x_0\in R^n$ is called the the least squares solution if it satisfies the following equation

$$||A{x}_0-b{||}_2=\underset{x\in R^n}{min}||Ax-b{||}_2$$

(31)

According to the following theorem [28], let $A\in R^{m\times n}$ and $b\in R^m$; then,

(1)

$A^{+}$ exists as unique,

(2)

If $A$ is full-rank, then $x=A^{+}b$ is the only least square solution of the linear equation $Ax=b$.

The model (26) is a linear least square problem, as

$$||\mathit{A}\mathit{G}-\mathit{F}{||}_2^2+{\lambda }^2||\mathit{M}\mathit{G}{||}_2^2=||\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)\mathit{G}-\left(\begin{array}{c}\mathit{F}\\ {\mathbf{0}}_{\mathit{n}\times \mathbf{1}}\end{array}\right){||}_2^2$$

(32)

In addition, the model (26) is equivalent to the following formula

$$min||\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)\mathit{G}-\left(\begin{array}{c}\mathit{F}\\ {\mathbf{0}}_{\mathit{n}\times \mathbf{1}}\end{array}\right){||}_2^2$$

(33)

As $\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)$ is full-rank, by the above theorem, the models (33) can be solved by the generalized inverse; that is,

$$\mathit{G}={\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)}^{+}\left(\begin{array}{c}\mathit{F}\\ {\mathbf{0}}_{\mathbf{n}\times \mathbf{1}}\end{array}\right)$$

(34)

Suppose ${\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)}^{+}=\left(inv\mathit{A}{\mathit{M}}_{\mathbf{1}},inv\mathit{A}{\mathit{M}}_{\mathbf{2}}\right)$, where $inv\mathit{A}{\mathit{M}}_{\mathbf{1}}$ is the first m columns in ${\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)}^{+}$; then,

$${\mathit{G}}^{\ast }=inv\mathit{A}{\mathit{M}}_{\mathbf{1}}·\mathit{F}$$

(35)

In summary, we provide the following algorithm steps:

(1)

Input $\mathit{A}$, $\mathit{M}$, $\mathit{G}$, and C and assign a value for the regularization parameter $\mathsf{\lambda }$.

(2)

Calculate ${\left(\begin{array}{c}\mathit{A}\\ \lambda \mathit{M}\end{array}\right)}^{+}$, and select its first m raw as $inv\mathit{A}{\mathit{M}}_{\mathbf{1}}$.

(3)

Calculate the optimal solution ${\mathit{G}}^{\ast }=inv\mathit{A}{\mathit{M}}_{\mathbf{1}}·\mathit{F}$.

The above procedure has the following advantages:

(1)

Equation (35) is used to obtain ${\mathit{G}}^{\ast }$ instead of the commonly used iterative method. Therefore, $\mathit{G}$ does not need a particular initialization. This yields a faster speed.

(2)

After the size and the positions of the pixels are defined, Matrix $\mathit{M}$ is then determined. Similarly, if the setup of the transducers is known, then matrix $\mathit{A}$ is also decided. In addition, the value of $\lambda$ can be assigned beforehand. Consequently, $inv\mathit{A}{\mathit{M}}_{\mathbf{1}}$ can also be determined. Because the above can all be precalculated, the solution of the problem can be acquired very quickly.

4. Further Analyses and Simulations

4.1. Error Analysis

As compared to the common iterative methods to generate optimal results, our method gives the formula solution, for which it is easy to calculate the error.

From Equations (35) and (36) could be obtained as follows

$$||\mathit{\Delta }{\mathit{G}}^{\ast }||{}_2\le ||inv\mathit{A}{\mathit{M}}_{\mathbf{1}}||{}_2·||\mathit{\Delta }\mathit{F}{||}_2$$

(36)

Suppose:

$$inv\mathit{A}{\mathit{M}}_{\mathbf{1}}=\left(\begin{array}{cccc}a{m}_{11}& a{m}_{12}& \cdots & a{m}_{1m}\\ a{m}_{21}& a{m}_{22}& \cdots & a{m}_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ a{m}_{n1}& a{m}_{n2}& \cdots & a{m}_{nm}\end{array}\right),\mathit{\Delta }{\mathit{G}}^{\ast }=\left(\begin{array}{c}\mathit{\Delta }{\mathit{G}}_{\mathbf{1}}^{\ast }\\ \mathit{\Delta }{\mathit{G}}_{\mathbf{2}}^{\ast }\\ ⋮\\ \mathit{\Delta }{\mathit{G}}_{\mathit{n}}^{\ast }\end{array}\right),\mathit{\Delta }\mathit{F}=\left(\begin{array}{c}\mathit{\Delta }{\mathit{F}}_{\mathbf{1}}\\ \mathit{\Delta }{\mathit{F}}_{\mathbf{2}}\\ ⋮\\ \mathit{\Delta }{\mathit{F}}_{\mathit{m}}\end{array}\right)$$

Then,

$$\left|\mathit{\Delta }{\mathit{G}}_{\mathit{i}}^{\ast }\right|=\left|{\displaystyle \sum }_{j=1}^{m}a{m}_{ij}\mathit{\Delta }{\mathit{F}}_{\mathit{i}}\right|\le {\displaystyle \sum }_{j=1}^m\left|a{m}_{ij}\right|·\left|\mathit{\Delta }{\mathit{F}}_{\mathit{i}}\right|\le ||\mathit{\Delta }\mathit{F}{||}_{\infty }{\displaystyle \sum }_{j=1}^m\left|a{m}_{ij}\right|$$

(37)

Equation (36) gives an upper bound of the variation of $||\mathit{\Delta }{\mathit{G}}^{\ast }||{}_2$ when $\mathit{F}$ changes by an increment $\mathit{\Delta }\mathit{F}$. Equation (37) also offers the upper bound of the changes in $\left|\mathit{\Delta }{\mathit{G}}_{\mathit{i}}^{\ast }\right|$ when $\mathit{F}$ changes by an increment $\mathit{\Delta }\mathit{F}$. As described previously, $inv\mathit{A}{\mathit{M}}_{\mathbf{1}}$ is determined once the pixels are defined, the transducers are located, and $\mathsf{\lambda }$ is chosen. Therefore, when the upper bound of $\left|\mathit{\Delta }{\mathit{F}}_{\mathit{j}}\right|,j=1,2,\cdots ,m$ is available, then the upper bounds of $||\mathit{\Delta }{\mathit{G}}^{\ast }||{}_2$ and $\left|\mathit{\Delta }{\mathit{G}}_{\mathit{i}}^{\ast }\right|$ can be evaluated.

4.2. Effect of Parameter $\lambda$

It can be seen that Equation (36) does play a role in the error estimation. To have an initial understanding of such an effect,

Table 2. Values of $||inv\mathit{A}{\mathit{M}}_{\mathbf{1}}||{}_2$.

Parameter	Value
$\lambda$	0.05	0.02	0.01	0.008	0.005	0.001
$||inv\mathit{A}{\mathit{M}}_{\mathbf{1}}||{}_2$	346.31	375.3226	380.0822	380.6652	381.2999	381.6919

below lists a series of values of $||inv\mathit{A}{\mathit{M}}_{\mathbf{1}}||{}_2$ in relation to $\lambda$, when $\tilde{m}=12$ and $\tilde{n}=64$.

Table 2 shows the trend that when $\mathsf{\lambda }$ falls below certain value, say 0.01, the variation of $||inv\mathit{A}{\mathit{M}}_{\mathbf{1}}||{}_2$ will tend to level off. This phenomenon may be used to assist in the selection of $\lambda$. After determining the position of the sensor and the method of partitioning, matrix $\mathit{A}$ and $\mathit{M}$ are determined. At this point, we can calculate the corresponding $||inv\mathit{A}{\mathit{M}}_{\mathbf{1}}||{}_2$ for different λ and select a suitable λ. Take for example, $\tilde{m}=12$, $\tilde{n}=64$, $\mathsf{\lambda }$ can be selected in the interval [0.001, 0.01].

4.3. Simulation

As shown in Figure 3, in the simulation, a circular area with d = 0.4 was evenly divided by parallel lines at an interval of $d/\tilde{n}$. Twelve transmitters were placed at equal distances around the periphery of the circular area, with one of them located at $(0.2 0)$. Under such an arrangement the dimensions of matrix $\mathit{A}$ were $66 \times 3228$. To cover a range of simulation conditions, we focused on four different conditions in this study, and the distribution models were as follows,

(1)

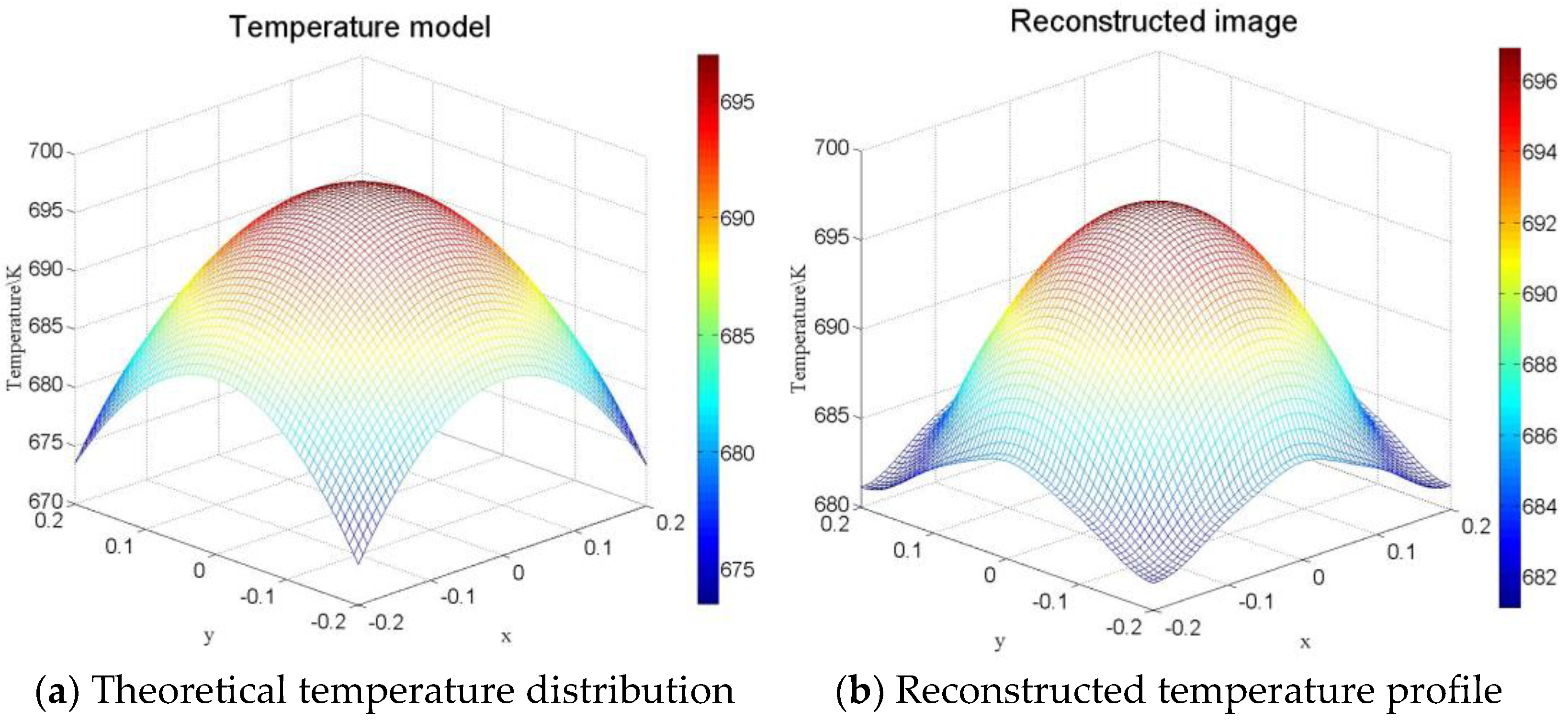
Model I, Central–symmetric temperature distribution,

$$T_1\left(x,y\right)=297+400ex{p}^{-78.125\left(x^2+y^2\right)}$$

(38)

(2)

Model II, Stratified temperature distribution,

$$T_2\left(x,y\right)=297+400ex{p}^{-\frac{ 625{(x-0.1)}^2}{2}-\frac{5000{(y-0.12)}^2}{49}}$$

(39)

(3)

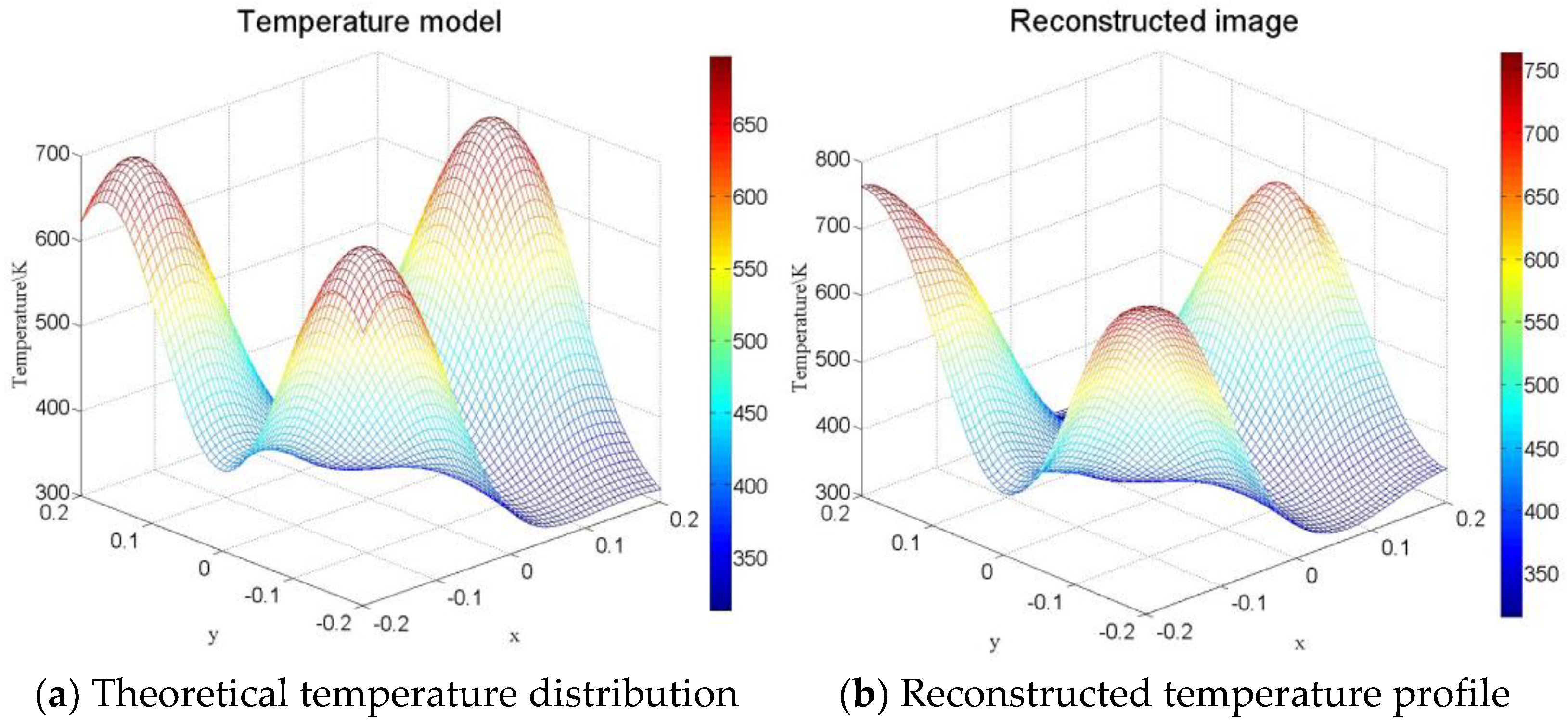
Model III, Multipeak temperature distribution,

$$\begin{gathered} T_3\left(x,y\right)=297+400\left[ex{p}^{- 78.125\left[{(x+0.16)}^2+{(y-0.16)}^2\right]}+ex{p}^{- 78.125\left[{(x-0.16)}^2+{(y+0.16)}^2\right]} \\ +ex{p}^{- 78.125\left[x^2+{(y-0.16)}^2\right]}\right] \end{gathered}$$

(40)

(4)

Model IV, Mixed temperature distribution,

$$\begin{gathered} T_4\left(x,y\right)=297+400ex{p}^{- \frac{625{(x-0.1)}^2}{2}-\frac{5000{(y-0.12)}^2}{49}} \\ +100\left(3.5-\mathit{cos}\frac{76\pi }{195}x\right)\left(2-\mathit{cos}\frac{3.125\pi }{13}y\right) \end{gathered}$$

(41)

The imaging area was divided into 64 by 64 pixels. For each of the above models, acoustic velocity $\mathit{C}$ was calculated according to the distribution of temperature for each pixel. Numerical calculations were carried out to obtain the TOF between the transmitters, i.e., the measurement data $\mathit{F}$. Then, based on the simulated $\mathit{F}$, the temperature distribution was reconstructed via the above-described method.

Figure 5, Figure 6, Figure 7 and Figure 8 represent the above four models sequentially. In the figures, the left column shows the images of the original setups, and in the right column are the reconstructed temperature distributions. Judging visually, the agreement was good. Small but visible differences occurred at the corners. However, the corner parts had no effect on the results, since they were outside the sensing area. For more subjective assessments,

Table 3. Comparison of the errors in four models.

Items	Equations	Model Ⅰ	Model Ⅱ	Model Ⅲ	Model Ⅳ
Maximum absolute error	$\underset{1\le i\le n}{max}\left|{\mathit{T}}_{\mathit{i}}-{\mathit{T}}_{\mathit{i}}^{\ast }\right|$	0.4323	13.1568	7.1706	9.4499
Average absolute error	$\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|{\mathit{T}}_{\mathit{i}}-{\mathit{T}}_{\mathit{i}}^{\ast }\right|$	0.09189	1.2261	0.9877	1.1316
Maximum relative error	$\underset{1\le i\le n}{max}\left|\frac{{\mathit{T}}_{\mathit{i}}^{\ast }-{\mathit{T}}_{\mathit{i}}}{{\mathit{T}}_{\mathit{i}}}\right|$	0.063%	2.364%	1.238%	1.273%
Average relative error	$\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|\frac{{\mathit{T}}_{\mathit{i}}^{\ast }-{\mathit{T}}_{\mathit{i}}}{{\mathit{T}}_{\mathit{i}}}\right|$	0.013%	0.327%	0.200%	0.182%
Standard Deviation	$\frac{1}{\sqrt{n}}\sqrt{{\displaystyle \sum }_{i=1}^n{\left|\frac{{\mathit{T}}_{\mathit{i}}^{\ast }-{\mathit{T}}_{\mathit{i}}}{{\mathit{T}}_{\mathit{i}}}\right|}^2}$	3.1925 × 10−6	8.0440 × 10−5	6.2091 × 10−7	4.57 × 10−5

gives a comparison of the errors in the reconstruction process. The conditions corresponded to $\tilde{n}=64$ and $\lambda =0.005$, and the “measurement data” $\mathit{C}$ were error free. In the table $\mathit{T}={({\mathit{T}}_{\mathbf{1}},{\mathit{T}}_{\mathbf{2}},\cdots ,{\mathit{T}}_{\mathit{n}})}^{\mathit{T}}$ containing the theoretical values and ${\mathit{T}}^{\ast }={({\mathit{T}}_{\mathbf{1}}^{\ast },{\mathit{T}}_{\mathbf{2}}^{\ast },\cdots ,{\mathit{T}}_{\mathit{n}}^{\ast })}^{\mathit{T}}$ were reconstructed by Equation (9).

In addition to the above error-free cases, noisy-data cases were also evaluated.

Table 4. Model Ⅳ with errors in TOF.

Parameter	Value
$\delta$	0.01	0.0075	0.005	0.0025	0.001
Maximum absolute error	62.7365	47.26638	32.43192	18.40133	11.22825
Average absolute error	13.4561	10.13784	6.88038	3.617338	1.802721
Maximum relative error	0.08926	0.067117	0.045886	0.025141	0.015198
Average relative error	0.02266	0.017059	0.011584	0.006055	0.002979
Standard deviation	0.02828	0.021248	0.014478	0.007602	0.003837

shows a case for model Ⅳ, where there were $\left[-\mathsf{\delta },\mathsf{\delta }\right]$ type errors added to the “measurement data”. In this case, the TOF with errors, $F_1$, was calculated by Equation (42).

$$F_1=F·\left[1+\mathit{rand}\left(\mathit{size}\left(F\right)-0.5\right)·\left(2\delta \right)\right]$$

(42)

Table 5. Model Ⅳ with Gaussian errors in TOF.

Parameter	Value
$\mathsf{\delta }$	0.0005	0.0003	0.0001	0.001	0.005
Maximum absolute error	11.02863	9.889493	9.347564	13.77893	52.1729
Average absolute error	1.667104	1.363348	1.160435	2.61925	11.44429
Maximum relative error	0.01464	0.013525	0.012802	0.018683	0.077785
Average relative error	0.002745	0.002222	0.001873	0.00437	0.019302
Standard deviation	3.56 × 10−3	2.98 × 10−3	2.64 × 10−3	5.51 × 10−3	2.42 × 10−2

is the same model but with Gaussian errors in TOF ($F_2$), as calculated by Equation (43).

$$F_2=F·\left[1+\mathit{normrnd}\left(0,\delta ,\mathit{size}\left(F\right)\right)\right]$$

(43)

It can be seen from Table 3, Table 4 and Table 5 that the algorithm developed in this study significantly improved the accuracy of the reconstruction. In addition, it was demonstrated through the four different cases.

To evaluate the model proposed in this study, the results produced by this new model $\mathit{min}\left\{||\mathit{A}\mathit{G}-\mathit{F}{||}_2^2,+,{\lambda }^2||\mathit{M}\mathit{G}{||}_2^2\right\}$ were compared with the results from the standard regularization method, i.e., $\mathit{min}\{||\mathit{A}\mathit{G}-\mathit{F}{||}_2^2+{\lambda }^2||\mathit{G}{||}_2^2\}$. Model Ⅳ, expressed by Equation (35), was chosen for the comparison. Suppose the true image was ${\mathit{G}}_{\mathbf{0}}$, the values obtained by this method were denoted by ${\mathit{G}}_{\mathbf{1}}$, and the values from the standard regularization method were ${\mathit{G}}_{\mathbf{2}}$, with the regularization factor $\lambda =0.001$. The L_2 norms of the images and the reconstructed images were $||{\mathit{G}}_{\mathbf{0}}||{}_2=0.0606654115$, $||{\mathit{G}}_{\mathbf{1}}||{}_2=0.0606654755$ and $||{\mathit{G}}_{\mathbf{2}}||{}_2=0.0540761482$, respectively.

As for the errors, the maximum absolute error between ${\mathit{G}}_{\mathbf{1}}$ and ${\mathit{G}}_{\mathbf{0}}$ was $||{\mathit{G}}_{\mathbf{1}}-{\mathit{G}}_{\mathbf{0}}||{}_{\infty }=1{.256 \times 10}^{-5}$, the average error between ${\mathit{G}}_{\mathbf{1}}$ and ${\mathit{G}}_{\mathbf{0}}$ over 812 points was $||{\mathit{G}}_{\mathbf{1}}-{\mathit{G}}_{\mathbf{0}}||{}_1/812=9{.95982\mathrm{e}}^{-7}$, while the maximum relative error was $\left(\left|1-\frac{{\mathit{G}}_{\mathbf{1}\mathit{i}}}{{\mathit{G}}_{\mathbf{0}\mathit{i}}}\right|\right)0{.005829}_{max}$. The new method produced very small errors between ${\mathit{G}}_{\mathbf{1}}$ and ${\mathit{G}}_{\mathbf{0}}$. Temperature profile $T_1$ calculated from ${\mathit{G}}_{\mathbf{1}}$ was very close to the original temperature profile $T_0$, as seen in Table 3, Table 4 and Table 5. The maximum absolute error between ${\mathit{G}}_{\mathbf{2}}$ and ${\mathit{G}}_{\mathbf{0}}$ was $||{\mathit{G}}_{\mathbf{2}}-{\mathit{G}}_{\mathbf{0}}||{}_{\infty }=0.0042$. The average error between ${\mathit{G}}_{\mathbf{2}}$ and ${\mathit{G}}_{\mathbf{0}}$ over 812 points was $||{\mathit{G}}_{\mathbf{2}}-{\mathit{G}}_{\mathbf{0}}||{}_1/812=0.00131$. The temperature profile $T_2$ calculated from ${\mathit{G}}_{\mathbf{2}}$ had larger errors with regard to the original temperature $T_0$.

In order to illustrate the advantage of the reconstruction algorithm proposed in this study, five references about the temperature field reconstruction algorithm are discussed for comparison on the single-peak temperature field reconstruction error, which is explored in all these references. The specific data are presented in

Table 6. Comparison of single-peak temperature field reconstruction error with other reconstruction algorithms in the other references.

The Reconstruction Algorithm	Error in This Paper	Error in the Reference
Tikhonov-LSSVM (Tikhonov and the least squares support vector machine) in Ref. [24]	Maximum relative error 0.063%	Maximum relative error 0.75%
EF-RBFI (radial basis function interpolation method optimized by the evaluation function) in Ref. [25]	Root mean square error 0.0003%	Root mean square error 3.69%
Improved Tikhonov Regularization in Ref. [26]	Average relative error 0.013%	Average relative error 1.710%
GWO–ABP method (Adaboost.RT based BP neural network algorithm based on Grey wolf optimizer algorithm) in Ref. [27]	Average relative error 0.013%	Average relative error 1.16%
LQ-SVD (logarithmic–quadratic radial basis function and singular value decomposition algorithm) in Ref. [28]	Root mean square error 0.0003%	Root mean square error 3.0617%

. As can be seen from the comparison of various errors, the explicable neighboring-pixel reconstruction algorithm proposed in this study showed obvious superiority.

5. Conclusions

Reconstruction methods play a crucial role in CT technologies. In acoustic tomography, the distinct scarcity of probing paths causes severe detrimental effect in the image reconstruction. In this study, the authors analyzed the dependence of a solution of the inverse problem upon the full column rank and proposed an explicable neighboring-pixel reconstruction algorithm to force a unique optimal solution by a new form of the regularization term, i.e., the neighboring correlation method.

Numerical simulations were carried out to verify the newly proposed algorithm. Through reconstruction of four representative cases, i.e., centrally symmetrical, stratified distribution, multipeak distribution, and mixed distribution, accurate temperature reconstruction results were obtained that clearly verified the effectiveness of the proposed algorithm. Comparison with the standard Tikhonov regularization formula also showed the superiority of the new method. Error analyses were performed for the above four cases, and the average relative errors were 0.013%, 0.327%, 0.200%, and 0.182%, respectively. Additionally, the results with various Gaussian noises did not significantly deteriorate the reconstruction performance, validating the robustness of the algorithm.

Other merits were also found of the proposed method. Our method was explicable because it gave the formula solution, for which it was easy to calculate the error. The fast speed was also remarkable due to a majority of the calculations being performed beforehand; thus, the calculation burden was much reduced for online reconstruction.