Comprehensive Parametric Study of Blockage Effect on the Performance of Horizontal Axis Hydrokinetic Turbines
Abstract
:1. Introduction
1.1. Hydrodynamic Parameters
1.2. Blockage Effects
1.3. Previous Work
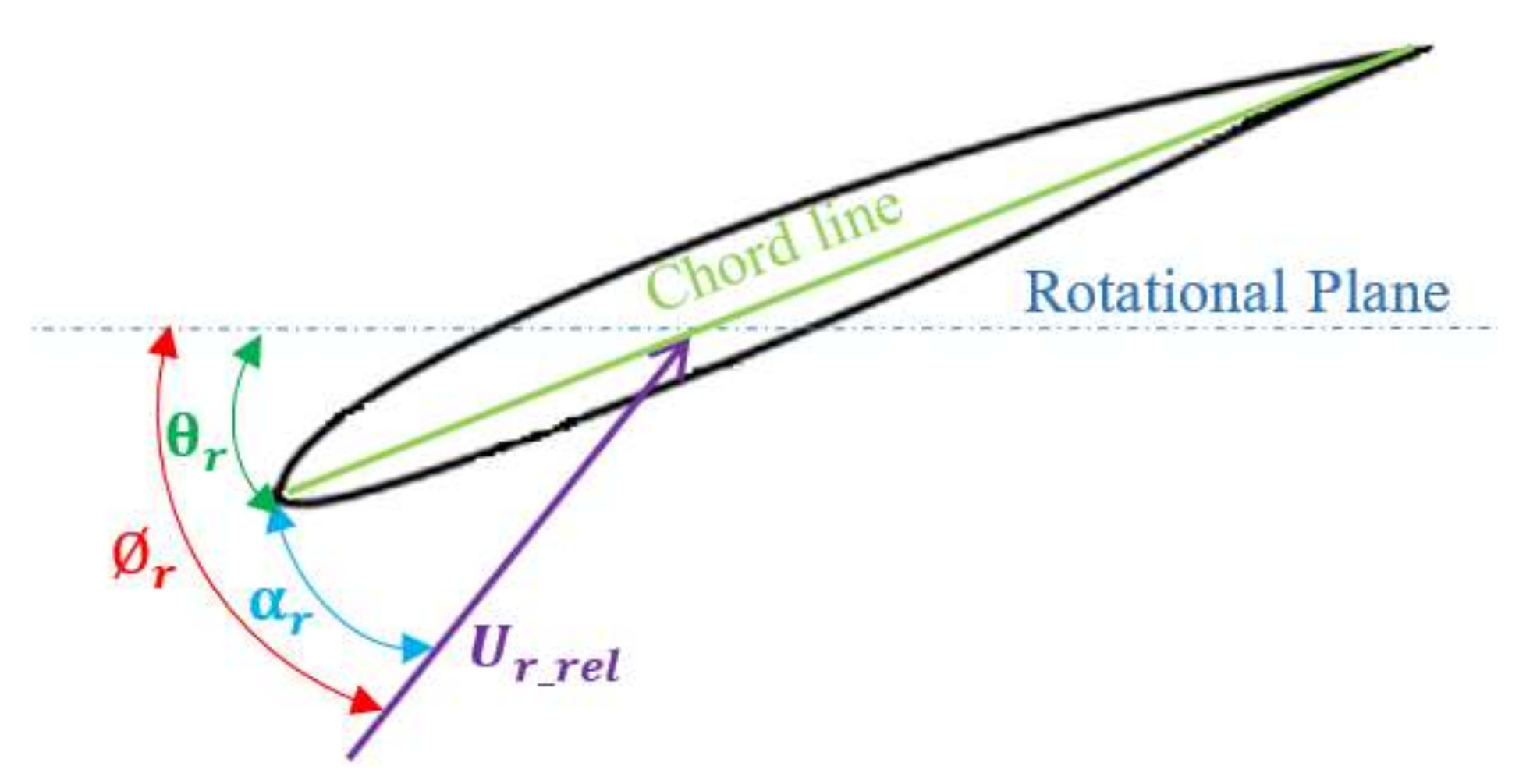
2. Hydrokinetic Turbine Principle Definitions
3. Computational Fluid Dynamics
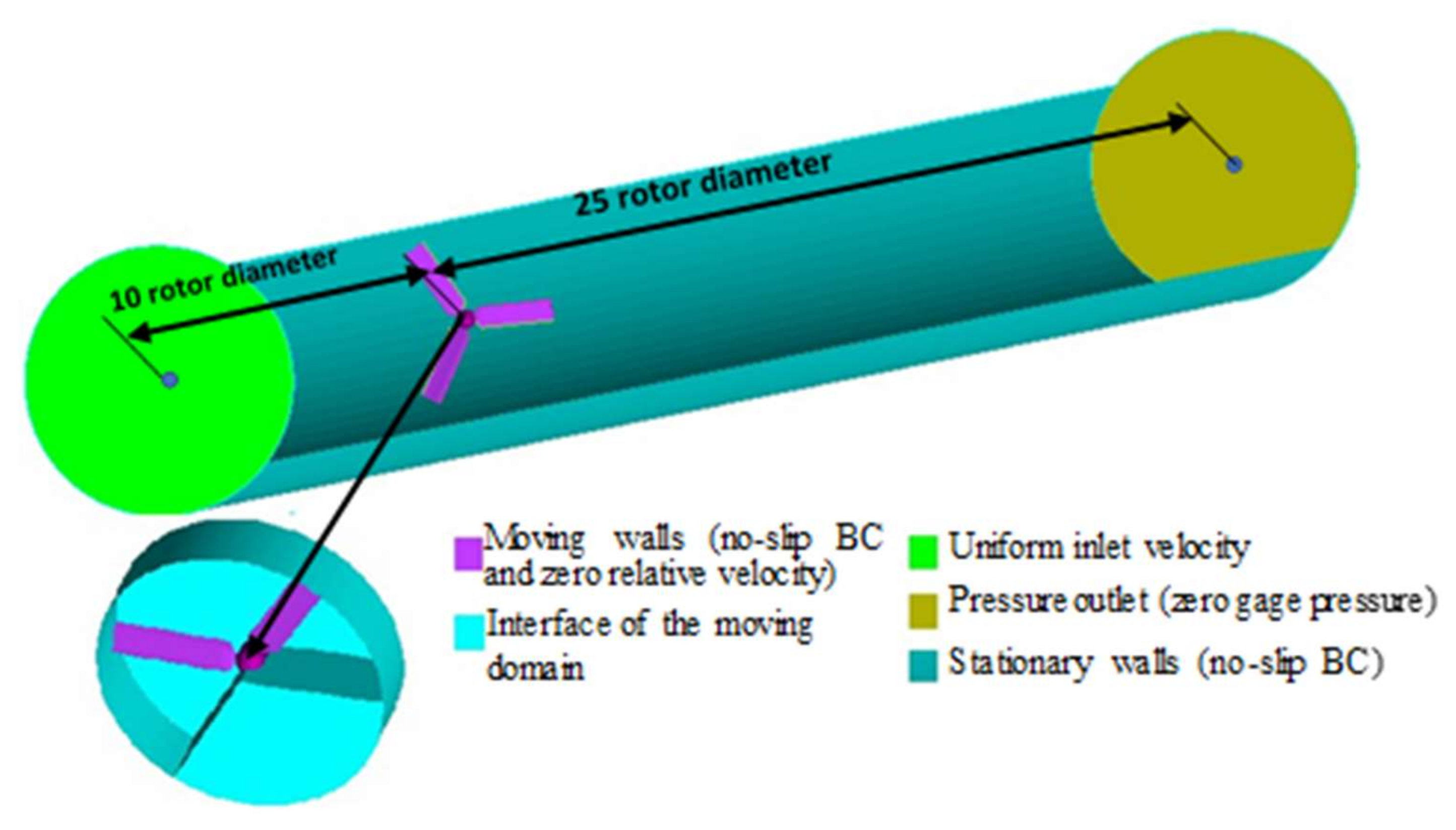
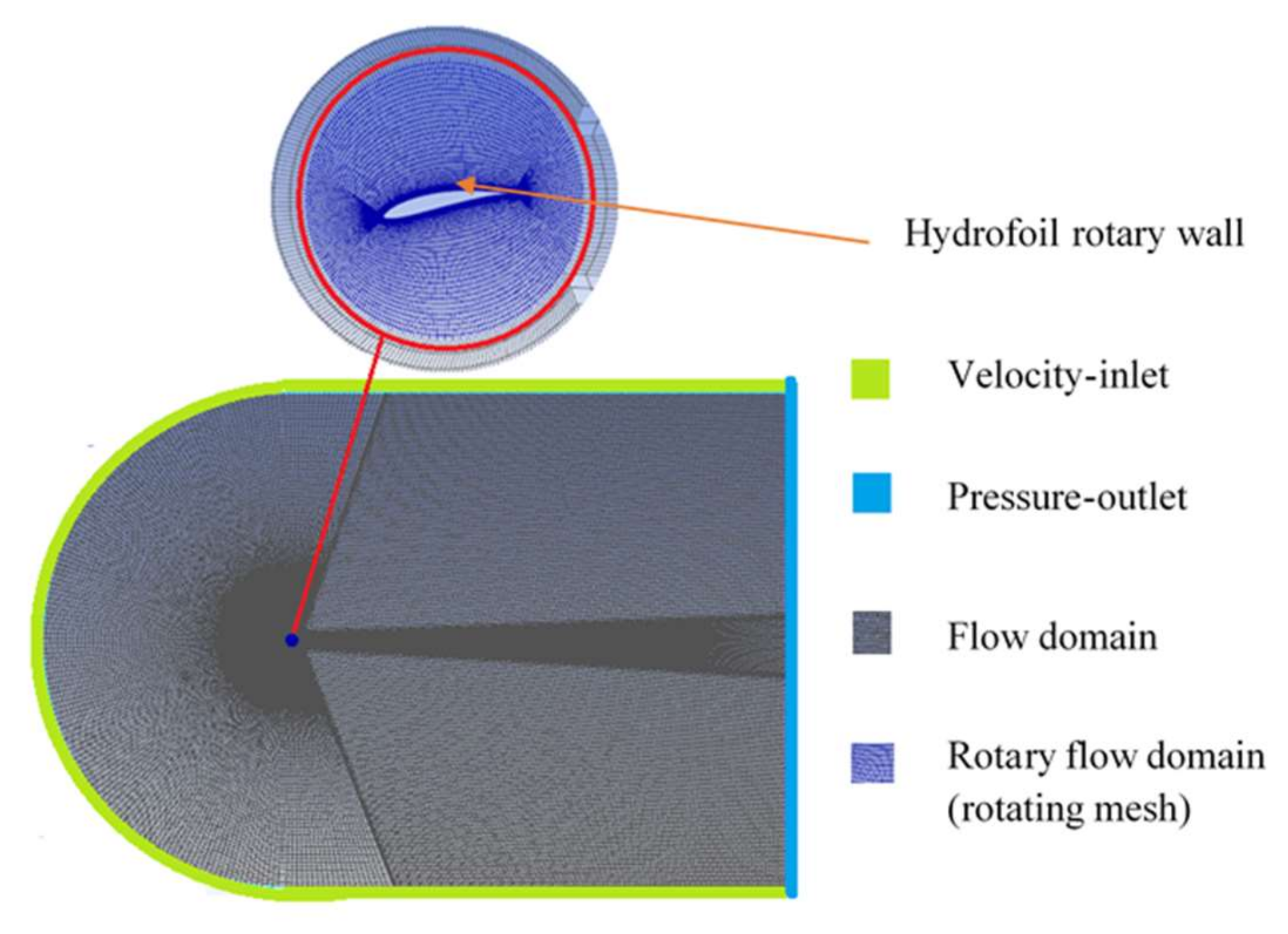
3.1. Geometry and Meshing
3.2. Turbulence Modeling
3.2.1. SST k-ω Model
3.2.2. Moving Reference Frame
3.2.3. Model Setup
3.3. Grid Independent Investigation
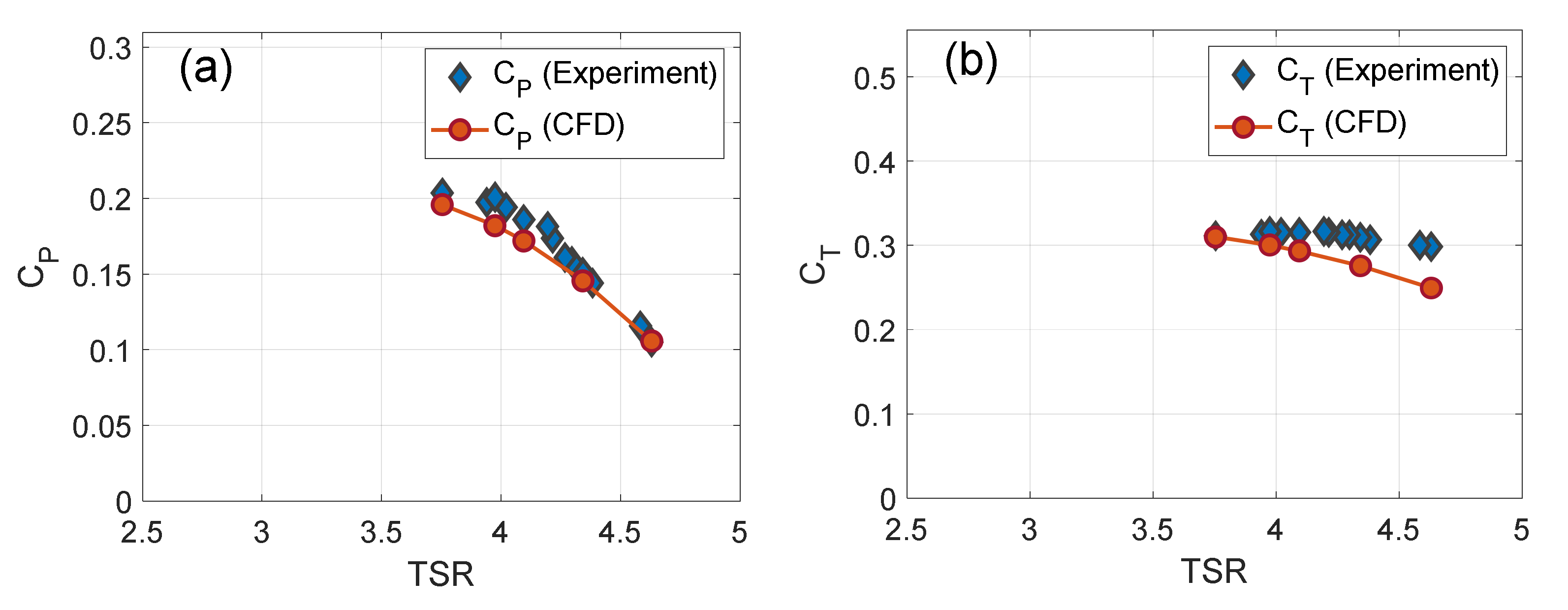
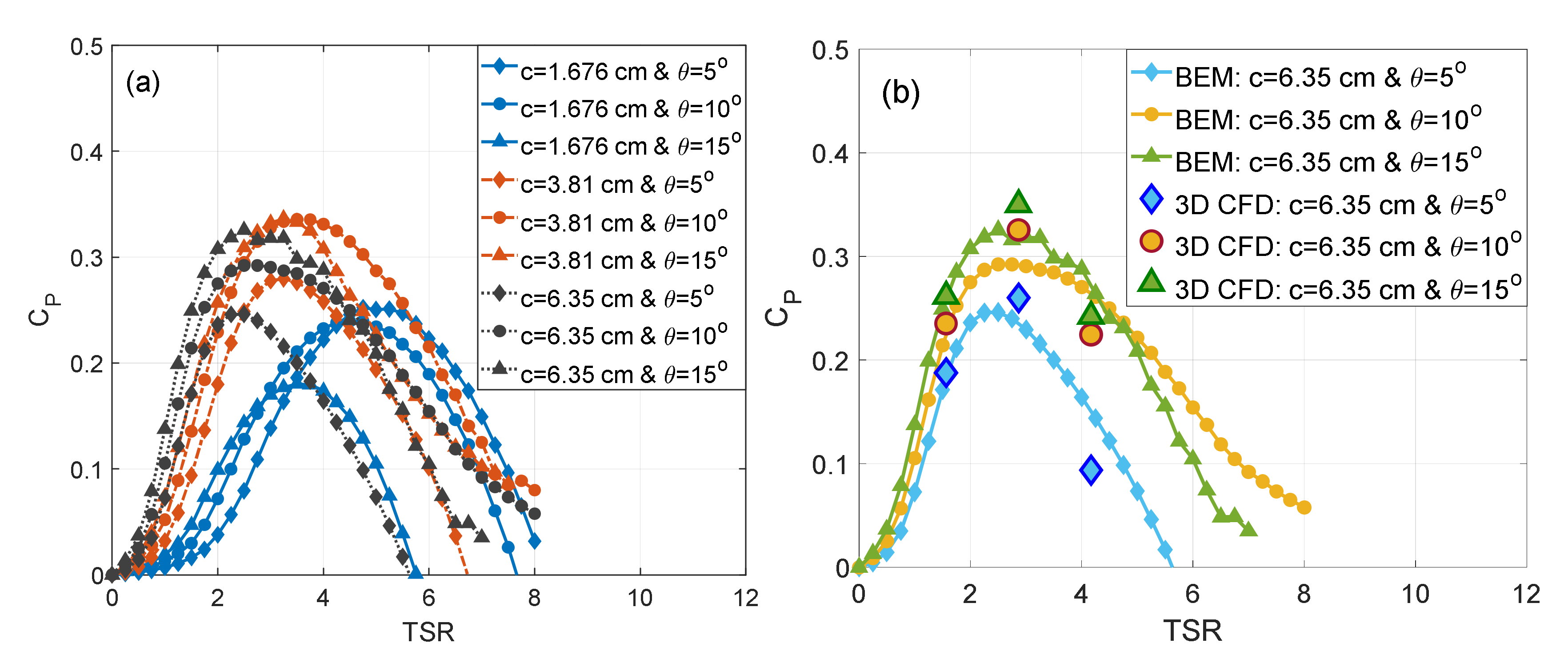
3.4. Experimental Validation
4. Evaluating the Operational Rotational Speed
5. Experimental Design
6. Results and Discussion
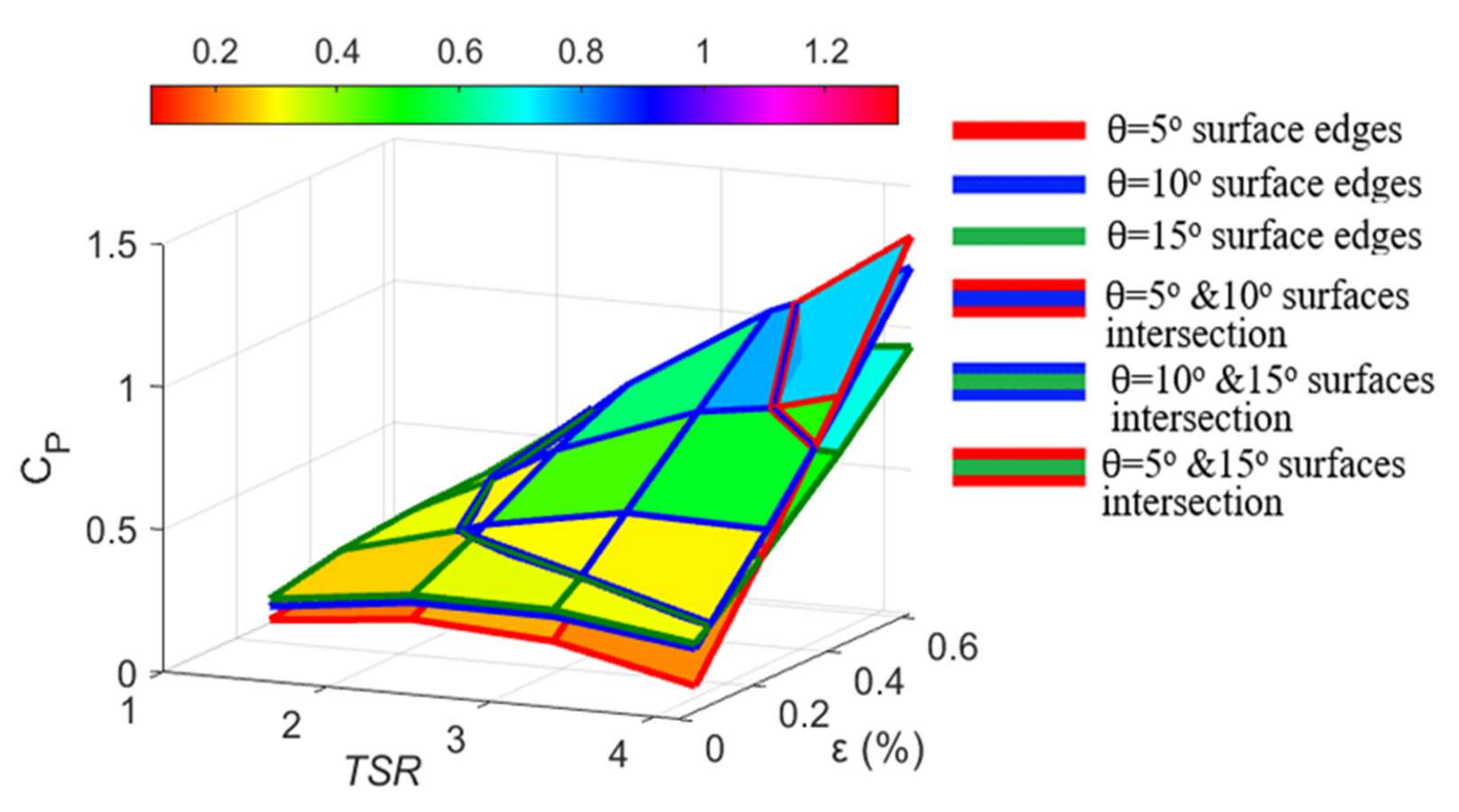
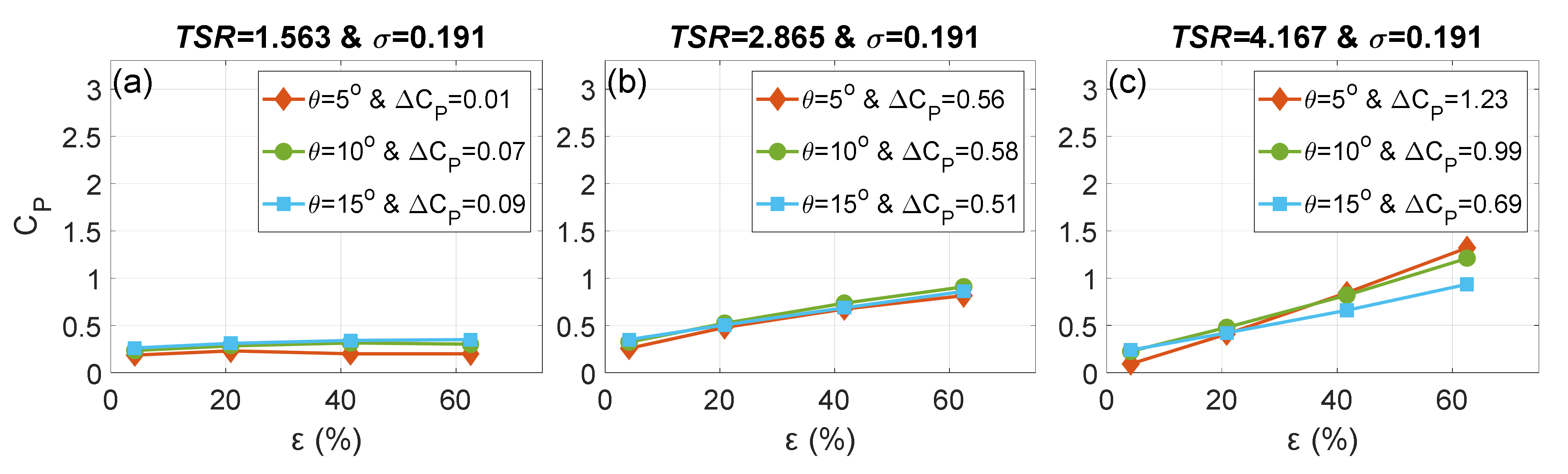
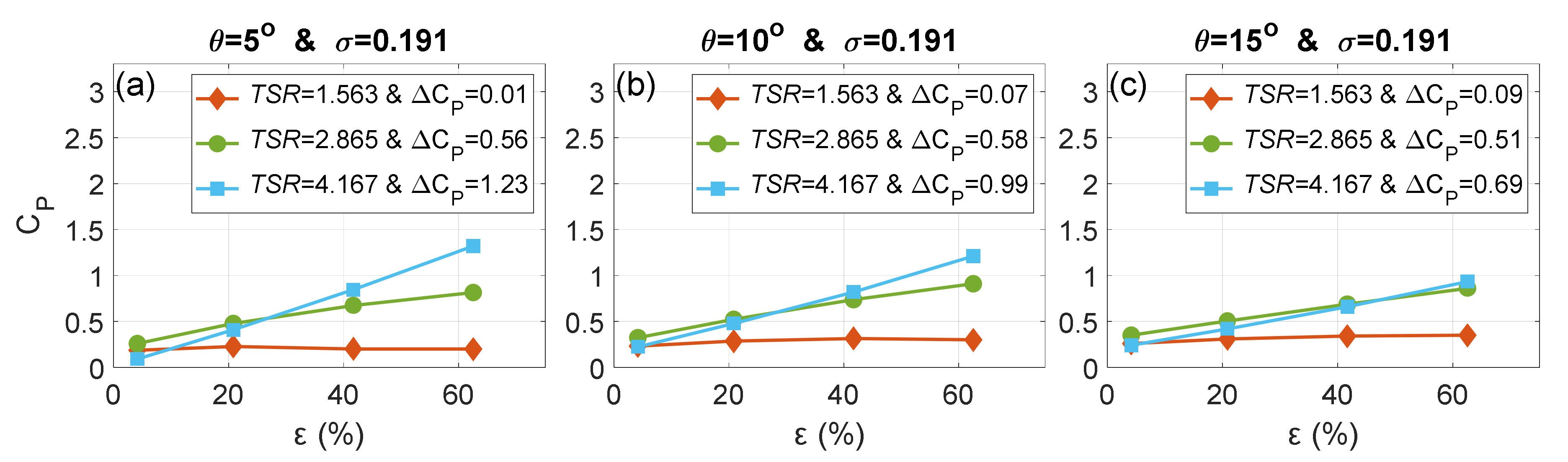
6.1. Influence of the DOE Parameters on the Blockage Behavior
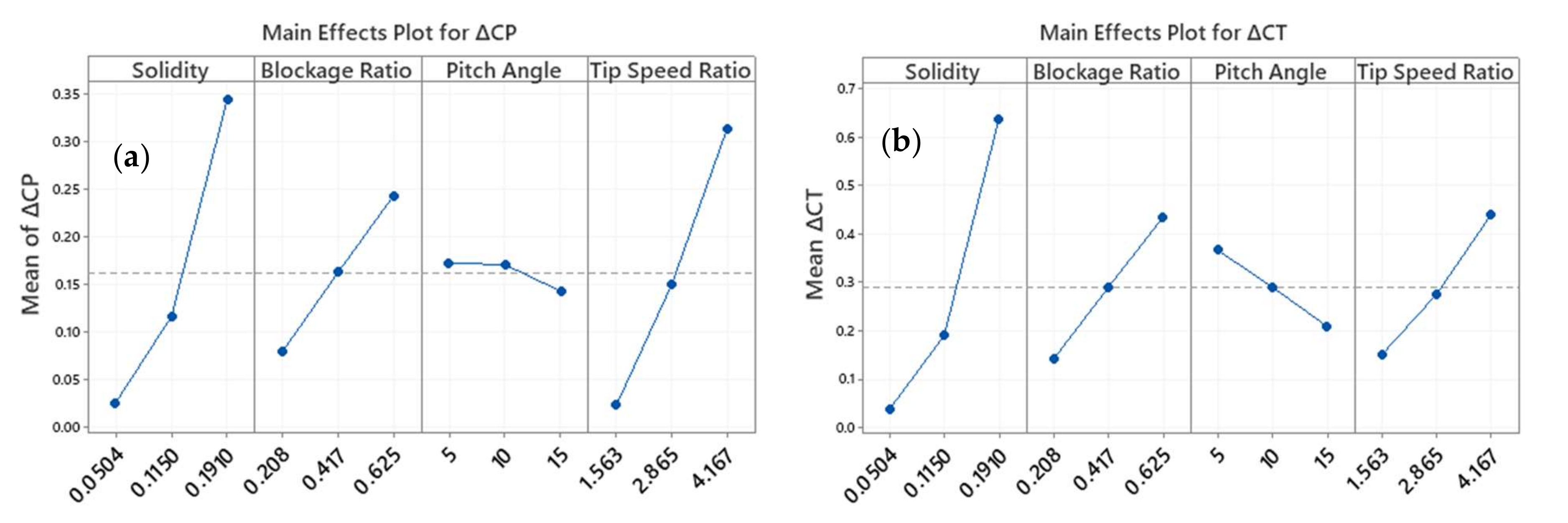
6.2. Analysis of Variance of the DOE Parameters
7. Practical Implications
- When designing a confined hydrokinetic turbine, designers should be aware of the sensitivity of the design variables to the confinement effects.
- After optimizing the turbine for an open environment, further considerations should be given toward design parameters. Priority should be given in the following order: the solidity, blockage ratio, rotational speed, and pitch angle.
- Interaction effects should also be considered; for example, the performance of the highest solidity rotor changed from the lowest in an open flow (due to the increased flow impedance) to the highest in a confined flow (due to the increased kinetic flux).
8. Conclusions
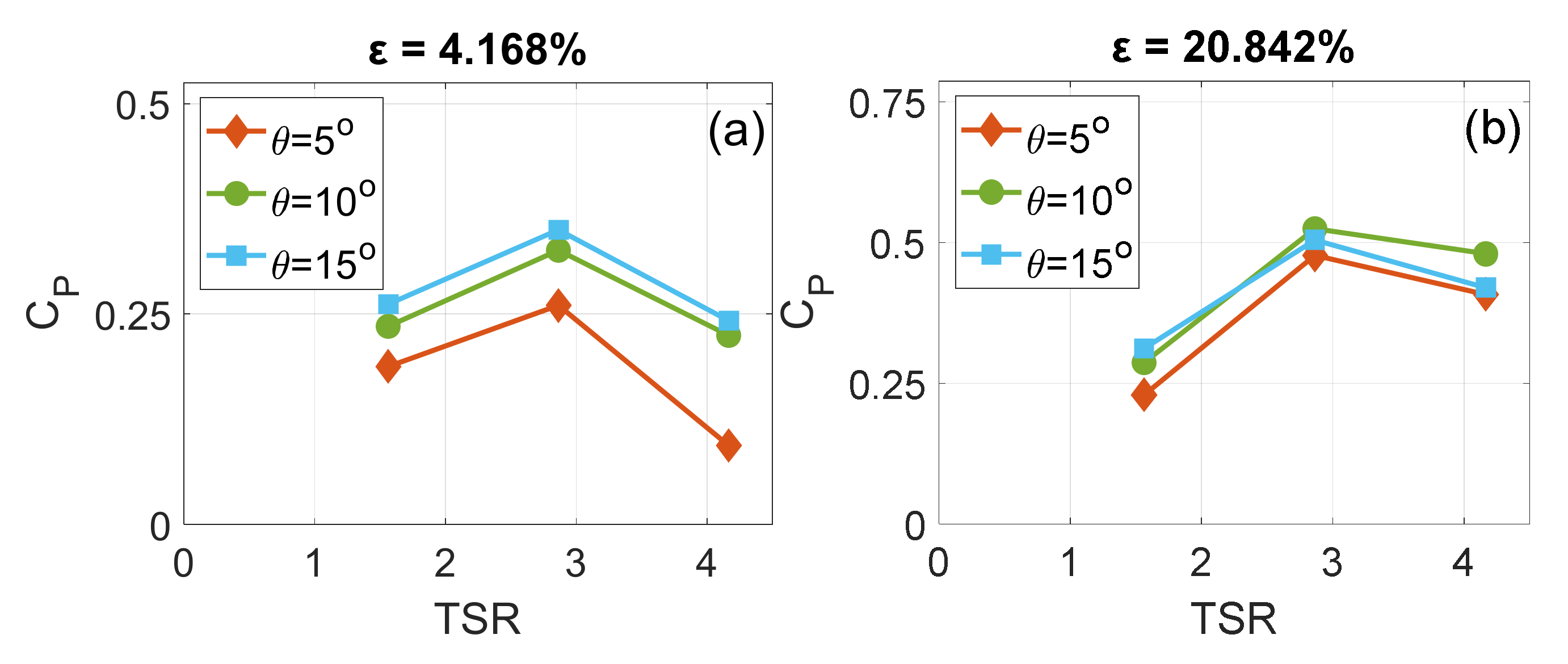
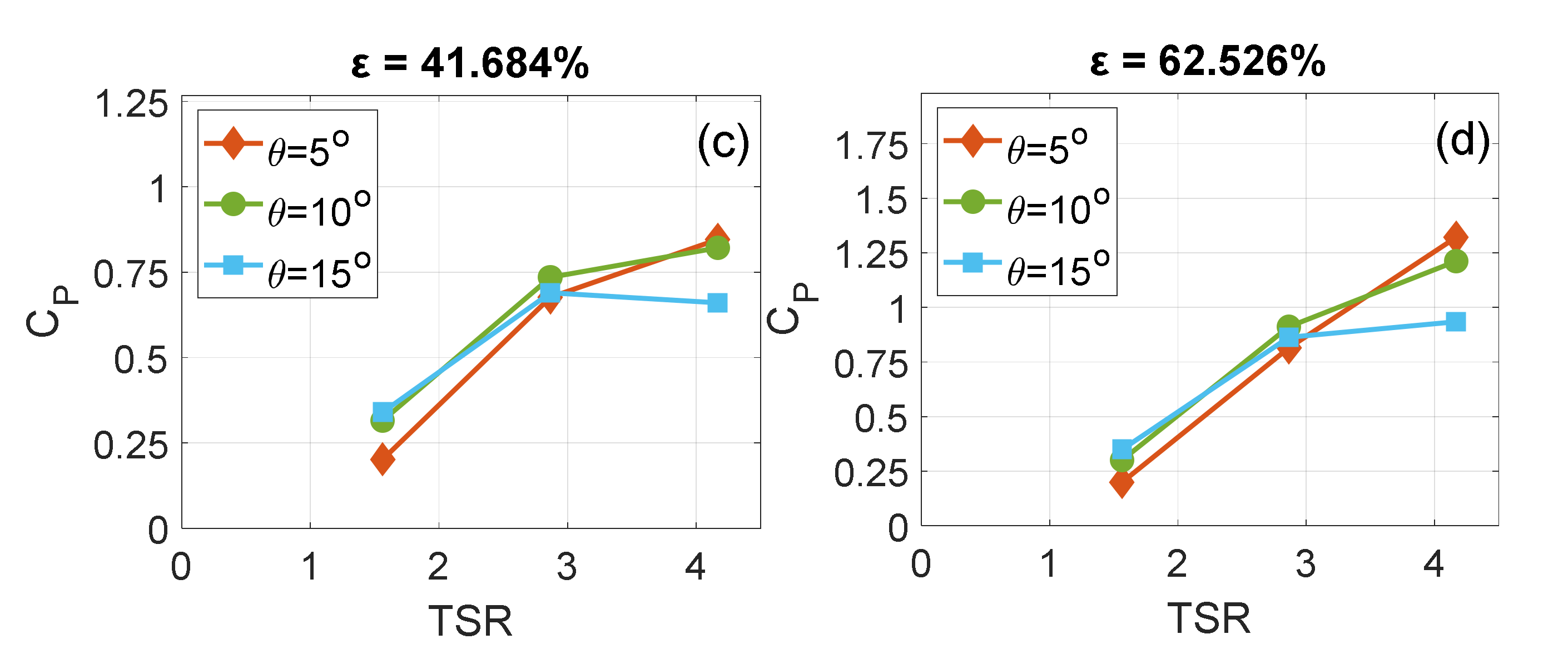
- CP was insensitive to θ alteration at relatively low TSRs as ε increased. The effect of varying θ was noticeable at the high TSR. The ∆CP was inversely proportional to θ at the TSR of 4.167. That was due to the decrease in the angle of attack to levels below the optimum values.
- For all pitch angles, the rate of increment of CP with respect to ε was proportional to the TSR. This proportionality was attributed to the augmented wake turbulence and the improvement in the angles of attack along the blade span due to the increase in rotational speed.
- The blockage effects were proportional to the solidity level, and this proportionality increased with increasing TSR. Additionally, the performance of the highest solidity rotor changed from the poorest to the highest as increased.
- The ε*θ,*ε*θ, and ε*θ*TSR interactions do not have significant effects on ∆CP. All other linear, 2-way, and 3-way interactions are statistically significant in affecting the ∆CP.
- All model, linear, 2-way, and 3-way (excluding ε*θ*TSR) interactions are statistically significant in affecting the ∆CT.
- All 4-way interactions do not have significant effects on both response variable
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Batten, W.M.J.; Bahaj, A.S.; Molland, A.F.; Chaplin, J.R. Hydrodynamics of marine current turbines. Renew. Energy 2006, 31, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Aghsaee, P.; Markfort, C.D. Effects of flow depth variations on the wake recovery behind a horizontal-axis hydrokinetic in-stream turbine. Renew. Energy 2018, 125, 620–629. [Google Scholar] [CrossRef]
- Bahaj, A.; Myers, L.; Rawlinson-Smith, R.; Thomson, M. The effect of boundary proximity upon the wake structure of horizontal axis marine current turbines. J. Offshore Mech. Arct. Eng. 2012, 134, 021104. [Google Scholar] [CrossRef]
- Kolekar, N.; Banerjee, A. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Ryi, J.; Rhee, W.; Hwang, U.C.; Choi, J.-S. Blockage effect correction for a scaled wind turbine rotor by using wind tunnel test data. Renew. Energy 2015, 79, 227–235. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Impact of channel blockage on the performance of axial and cross-flow hydrokinetic turbines. Renew. Energy 2017, 103, 239–254. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Molland, A.F.; Chaplin, J.R.; Batten, W.M.J. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Watanabe, S.; Yamaoka, W.; Furukawa, A. Unsteady Lift and Drag Characteristics of Cavitating Clark Y-11.7% Hydrofoil. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 052009. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Li, Z.; Fan, M.; Wang, M.; Zhang, L. Prediction and multi-objective optimization of tidal current turbines considering cavitation based on GA-ANN methods. Energy Sci. Eng. 2019, 7, 1896–1912. [Google Scholar] [CrossRef] [Green Version]
- Ashrafi, Z.N.; Ghaderi, M.; Sedaghat, A. Parametric study on off-design aerodynamic performance of a horizontal axis wind turbine blade and proposed pitch control. Energy Convers. Manag. 2015, 93, 349–356. [Google Scholar] [CrossRef]
- Rector, M.C.; Visser, K.D.; Humiston, C. Solidity, blade number, and pitch angle effects on a one kilowatt HAWT. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; pp. 1–10. [Google Scholar]
- Duquette, M.M.; Visser, K.D. Numerical Implications of Solidity and Blade Number on Rotor Performance of Horizontal-Axis Wind Turbines. J. Sol. Energy Eng. 2003, 125, 425–432. [Google Scholar] [CrossRef]
- Subhra Mukherji, S.; Kolekar, N.; Banerjee, A.; Mishra, R. Numerical investigation and evaluation of optimum hydrodynamic performance of a horizontal axis hydrokinetic turbine. J. Renew. Sustain. Energy 2011, 3, 063105. [Google Scholar] [CrossRef] [Green Version]
- Sarlak, H.; Nishino, T.; Martínez-Tossas, L.; Meneveau, C.; Sørensen, J.N. Assessment of blockage effects on the wake characteristics and power of wind turbines. Renew. Energy 2016, 93, 340–352. [Google Scholar] [CrossRef] [Green Version]
- Abutunis, A.; Fal, M.; Fashanu, O.; Chandrashekhara, K.; Duan, L. Coaxial horizontal axis hydrokinetic turbine system: Numerical modeling and performance optimization. J. Renew. Sustain. Energy 2021, 13, 024502. [Google Scholar] [CrossRef]
- Madrigal, T.H.; Mason-Jones, A.; O’Doherty, T.; O’Doherty, D.M. The effect of solidity on a tidal turbine in low speed flow. In Proceedings of the 2nd European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1 September 2017; pp. 1–9. [Google Scholar]
- Morris, C.; Mason-Jones, A.; O’Doherty, D.M.; O’Doherty, T. The influence of solidity on the performance characteristics of a tidal stream turbine. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–7. [Google Scholar]
- Abutunis, A.; Taylor, G.; Fal, M.; Chandrashekhara, K. Experimental evaluation of coaxial horizontal axis hydrokinetic composite turbine system. Renew. Energy 2020, 157, 232–245. [Google Scholar] [CrossRef]
- Chen, T.; Liou, L. Blockage corrections in wind tunnel tests of small horizontal-axis wind turbines. Exp. Therm. Fluid Sci. 2011, 35, 565–569. [Google Scholar] [CrossRef]
- Whelan, J.I.; Graham, J.M.R.; Peiró, J. A free-surface and blockage correction for tidal turbines. J. Fluid Mech. 2009, 624, 281–291. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. The efficiency of a turbine in a tidal channel. J. Fluid Mech. 2007, 588, 243–251. [Google Scholar] [CrossRef] [Green Version]
- Houlsby, G.; Draper, S.; Oldfield, M. Application of Linear Momentum Actuator Disc Theory to Open Channel Flow; University of Oxford: Oxford, UK, 2008. [Google Scholar]
- Barnsley, M.; Wellicome, J. Final Report on the 2nd Phase of Development and Testing of a Horizontal Axis Wind Turbine Test Rig for the Investigation of Stall Regulation Aerodynamics; Carried out under ETSU Agreement E.5A/CON5103/1746; 1990. [Google Scholar]
- De Arcos, F.Z.; Tampier, G.; Vogel, C.R. Numerical analysis of blockage correction methods for tidal turbines. J. Ocean Eng. Mar. Energy 2020, 6, 183–197. [Google Scholar] [CrossRef]
- Ross, H.; Polagye, B. An experimental assessment of analytical blockage corrections for turbines. Renew. Energy 2020, 152, 1328–1341. [Google Scholar] [CrossRef] [Green Version]
- Masters, I.; Chapman, J.C.; Willis, M.R.; Orme, J.A.C. A robust blade element momentum theory model for tidal stream turbines including tip and hub loss corrections. J. Mar. Eng. Technol. 2011, 10, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Ning, S.A. A simple solution method for the blade element momentum equations with guaranteed convergence. Wind Energy 2014, 17, 1327–1345. [Google Scholar] [CrossRef]
- Badshah, M.; VanZwieten, J.; Badshah, S.; Jan, S. CFD study of blockage ratio and boundary proximity effects on the performance of a tidal turbine. IET Renew. Power Gener. 2019, 13, 744–749. [Google Scholar] [CrossRef]
- Schluntz, J.; Willden, R. The effect of blockage on tidal turbine rotor design and performance. Renew. Energy 2015, 81, 432–441. [Google Scholar] [CrossRef]
- Dixon, S.L. Fluid Mechanics and Thermodynamics of Turbomachinery; Butterworth-Heinemann: Woburn, MA, USA, 2005. [Google Scholar]
- Fal, M.; Hussein, R.; Chandrashekhara, K.; Abutunis, A.; Menta, V. Experimental and numerical failure analysis of horizontal axis water turbine carbon fiber-reinforced composite blade. J. Renew. Sustain. Energy 2021, 13, 014501. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Gharali, K.; Johnson, D.A. Numerical modeling of an S809 airfoil under dynamic stall, erosion and high reduced frequencies. Appl. Energy 2012, 93, 45–52. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Rahimian, M.; Walker, J.; Penesis, I. Performance of a horizontal axis marine current turbine—A comprehensive evaluation using experimental, numerical, and theoretical approaches. Energy 2018, 148, 965–976. [Google Scholar] [CrossRef]
- Bai, C.-J.; Wang, W.-C.; Chen, P.-W. Experimental and numerical studies on the performance and surface streamlines on the blades of a horizontal-axis wind turbine. Clean Technol. Environ. Policy 2017, 19, 471–481. [Google Scholar] [CrossRef]
- Johnson, D.A.; King, L.S. A mathematically simple turbulence closure model for attached and separated turbulent boundary layers. AIAA J. 1985, 23, 1684–1692. [Google Scholar] [CrossRef]
- Breton, S.-P. Study of the Stall Delay Phenomenon and of Wind Turbine Blade Dynamics Using Numerical Approaches and NREL’s Wind Tunnel Tests. Ph.D. Thesis, Department of Civil and Transport Engineering, Norwegian University of Science and Technology, Trondheim, Norway, 2008. [Google Scholar]
- Herráez, I.; Stoevesandt, B.; Peinke, J. Insight into Rotational Effects on a Wind Turbine Blade Using Navier–Stokes Computations. Energies 2014, 7, 6798–6822. [Google Scholar] [CrossRef] [Green Version]
- Thumthae, C.; Chitsomboon, T. Optimal angle of attack for untwisted blade wind turbine. Renew. Energy 2009, 34, 1279–1284. [Google Scholar] [CrossRef]
- Sanderse, B. Aerodynamics of Wind Turbine Wakes—Literature Review; Energy Research Center of the Netherlands (ECN): Petten, The Netherlands, 2009; pp. 1–49. [Google Scholar]
- Kolekar, N.; Banerjee, A. A coupled hydro-structural design optimization for hydrokinetic turbines. J. Renew. Sustain. Energy 2013, 5, 053146. [Google Scholar] [CrossRef] [Green Version]
- Fluent, A. 18.2, Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Kirke, B. Hydrokinetic turbines for moderate sized rivers. Energy Sustain. Dev. 2020, 58, 182–195. [Google Scholar] [CrossRef]
- Lee, M.-H.; Shiah, Y.C.; Bai, C.-J. Experiments and numerical simulations of the rotor-blade performance for a small-scale horizontal axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2016, 149, 17–29. [Google Scholar] [CrossRef]
- Abutunis, A.; Hussein, R.; Chandrashekhara, K. A neural network approach to enhance blade element momentum theory performance for horizontal axis hydrokinetic turbine application. Renew. Energy 2019, 136, 1281–1293. [Google Scholar] [CrossRef]
- Glauert, H. Airplane propellers. In Aerodynamic Theory; Springer: Berlin/Heidelberg, Germany, 1935; pp. 169–360. [Google Scholar]
- Hansen, M.O. Aerodynamics of Wind Turbines; Routledge: London, UK, 2013. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Wilson, R.E.; Lissaman, P.B. Applied Aerodynamics of Wind Power Machines; Oregon State University: Corvallis, OR, USA, 1974. [Google Scholar]
- Buhl, M.L. A New Empirical Relationship between Thrust Coefficient and Induction Factor for the Turbulent Windmill State; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2005. [Google Scholar]
- Du, Z.; Selig, M.S. A 3-D stall-delay model for horizontal axis wind turbine performance prediction. In Proceedings of the 1998 ASME Wind Energy Symposium, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Eggers, A.; Chaney, K.; Digumarthi, R. An assessment of approximate modeling of aerodynamic loads on the UAE rotor. In Proceedings of the ASME 2003, Wind Energy Symposium, Reno, NV, USA, 6–9 January 2003; pp. 283–292. [Google Scholar]
- Viterna, L.A.; Corrigan, R.D. Fixed Pitch Rotor Performance of Large Horizontal Axis Wind Turbines; NASA Lewis Research Center: Cleveland, OH, USA, 1982. [Google Scholar]
- Maskell, E. A Theory of the Blockage Effects on Bluff Bodies and Stalled Wings in a Closed Wind Tunnel; Aeronautical Research Council: London, UK, 1963. [Google Scholar]
- Guntur, S.; Sørensen, N.N. A study on rotational augmentation using CFD analysis of flow in the inboard region of the MEXICO rotor blades. Wind Energy 2015, 18, 745–756. [Google Scholar] [CrossRef]


| Geometry/Operation Type | Specification |
|---|---|
| Hydrofoil | Eppler 395 |
| Number of blades (N) | 3 blades |
| Rotor radius (R) | 15.557 cm (6.125 in.) |
| Chord length (c) | 1.676, 3.81, 6.35 cm (0.66, 1.5, 2.5 in.) |
| Rotor solidity () | 0.0504, 0.115, 0.191 |
| Pitch angle (θ) | 5°, 10°, 15°, |
| Flow domain circular cross-section radius | 0.197, 0.241, 0.341, 0.762 m (7.746, 9.487, 13.416, 30 in.) |
| Flow velocity (U) | 1.5 m/s |
| Levels | Parameters | |||
|---|---|---|---|---|
| ε (%) | TSR | |||
| Low | 20.842 | 0.0504 | 5 | 1.563 |
| Medium | 41.684 | 0.115 | 10 | 2.865 |
| High | 62.533 | 0.191 | 15 | 4.167 |
| Source | Degrees of Freedom | Adjusted Sum of Squares | Adjusted Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 64 | 4.501 | 0.070 | 52.55 | 1.363 × 10−11 |
| Linear | 8 | 2.974 | 0.372 | 277.74 | 1.100 × 10−15 |
| 2 | 1.454 | 0.727 | 543.22 | 2.000 × 10−15 | |
| ε (%) | 2 | 0.360 | 0.180 | 134.43 | 9.905 × 10−11 |
| θ (°) | 2 | 0.015 | 0.007 | 5.58 | 0.015 |
| TSR | 2 | 1.145 | 0.572 | 427.73 | 1.290 × 10−14 |
| 2-Way Interactions | 24 | 1.253 | 0.052 | 39.02 | 4.059 × 10−10 |
| *ε (%) | 4 | 0.283 | 0.071 | 52.95 | 5.001 × 10−09 |
| *θ (°) | 4 | 0.050 | 0.013 | 9.40 | 4.163 × 10−04 |
| *TSR | 4 | 0.593 | 0.148 | 110.78 | 1.898 × 10−11 |
| ε (%)*θ (°) | 4 | 0.002 | 0.000 | 0.35 | 0.838 ** |
| ε (%)*TSR | 4 | 0.266 | 0.067 | 49.77 | 7.879 × 10−09 |
| θ (°)*TSR | 4 | 0.058 | 0.015 | 10.89 | 1.858 × 10−04 |
| 3-Way Interactions | 32 | 0.274 | 0.009 | 6.40 | 1.379 × 10−04 |
| *ε (%)*θ (°) | 8 | 0.008 | 0.001 | 0.79 | 0.623 ** |
| *ε (%)*TSR | 8 | 0.178 | 0.022 | 16.61 | 2.178 × 10−06 |
| *θ (°)*TSR | 8 | 0.074 | 0.009 | 6.88 | 5.595 × 10−04 |
| ε (%)*θ (°)*TSR | 8 | 0.014 | 0.002 | 1.34 | 0.295 ** |
| Error | 16 | 0.021 | 0.001 | ||
| Total | 80 | 4.523 |
| Source | Degrees of Freedom | Adjusted Sum of Squares | Adjusted Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 64 | 10.661 | 0.167 | 58.46 | 5.916 × 10−12 |
| Linear | 8 | 7.858 | 0.982 | 344.72 | 2.000 × 10−16 |
| 2 | 5.230 | 2.615 | 917.72 | 0.000 | |
| ε (%) | 2 | 1.158 | 0.579 | 203.11 | 4.253 × 10−12 |
| θ (°) | 2 | 0.333 | 0.167 | 58.44 | 4.420 × 10−08 |
| TSR | 2 | 1.138 | 0.569 | 199.60 | 4.863 × 10−12 |
| 2-Way Interactions | 24 | 2.325 | 0.097 | 34.00 | 1.169 × 10−09 |
| *ε (%) | 4 | 0.892 | 0.223 | 78.26 | 2.691 × 10−10 |
| *θ (°) | 4 | 0.384 | 0.096 | 33.72 | 1.303 × 10−07 |
| *TSR | 4 | 0.533 | 0.133 | 46.76 | 1.245 × 10−08 |
| ε (%)*θ (°) | 4 | 0.057 | 0.014 | 4.96 | 0.009 |
| ε (%)*TSR | 4 | 0.263 | 0.066 | 23.07 | 1.776 × 10−06 |
| θ (°)*TSR | 4 | 0.197 | 0.049 | 17.24 | 1.187 × 10−05 |
| 3-Way Interactions | 32 | 0.477 | 0.015 | 5.23 | 4.933 × 10−04 |
| *ε (%)*θ (°) | 8 | 0.066 | 0.008 | 2.87 | 0.034 |
| *ε (%)*TSR | 8 | 0.174 | 0.022 | 7.65 | 3.065 × 10−04 |
| *θ (°)*TSR | 8 | 0.196 | 0.024 | 8.58 | 1.553 × 10−04 |
| ε (%)*θ (°)*TSR | 8 | 0.042 | 0.005 | 1.84 | 0.143 ** |
| Error | 16 | 0.046 | 0.003 | ||
| Total | 80 | 10.707 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abutunis, A.; Menta, V.G. Comprehensive Parametric Study of Blockage Effect on the Performance of Horizontal Axis Hydrokinetic Turbines. Energies 2022, 15, 2585. https://doi.org/10.3390/en15072585
Abutunis A, Menta VG. Comprehensive Parametric Study of Blockage Effect on the Performance of Horizontal Axis Hydrokinetic Turbines. Energies. 2022; 15(7):2585. https://doi.org/10.3390/en15072585
Chicago/Turabian StyleAbutunis, Abdulaziz, and Venkata Gireesh Menta. 2022. "Comprehensive Parametric Study of Blockage Effect on the Performance of Horizontal Axis Hydrokinetic Turbines" Energies 15, no. 7: 2585. https://doi.org/10.3390/en15072585
APA StyleAbutunis, A., & Menta, V. G. (2022). Comprehensive Parametric Study of Blockage Effect on the Performance of Horizontal Axis Hydrokinetic Turbines. Energies, 15(7), 2585. https://doi.org/10.3390/en15072585






