The Young’s Modulus and Poisson’s Ratio of Hard Coals in Laboratory Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimens
| Chronostratigraphic Division | Lithostratigraphic Units/Beds | No. of Seams | ||
|---|---|---|---|---|
| Carboniferous | Westphalian | Krakow Sandstone Series | Libiąż | 110–119 |
| Łaziska | 201–215 | |||
| Mudstone Series | Orzesze | 301–326 | ||
| Załęże * | 327–406 | |||
| Namurian | Upper Silesian Sandstone Series | Ruda | 407–419 | |
| Saddle * | 501–510 | |||
| Jejkowice | - | |||
| Paralic Series | Poruba | 601–630 | ||
| Jaklovec | 701–723 | |||
| Hrušov | 801–848 | |||
| Petřkovice | 901–915 | |||
2.2. Experimental Program
| Parameter | Methodology |
|---|---|
| Applied stress condition: σ1 > 0, σ2 = σ3 Differential stress | Young’s modulus and stress parameters were determined in conventional triaxial compression tests, using a Karman pressure chamber and confining pressures of σ2 = σ3 = 10, 20, 30, and 50 MPa, strain rates of 5 × 10−5 to 10−4 s−1 and 10−1 s−1, and cylindrical specimens with a diameter of 30 mm and a slenderness of 3 [27]. |
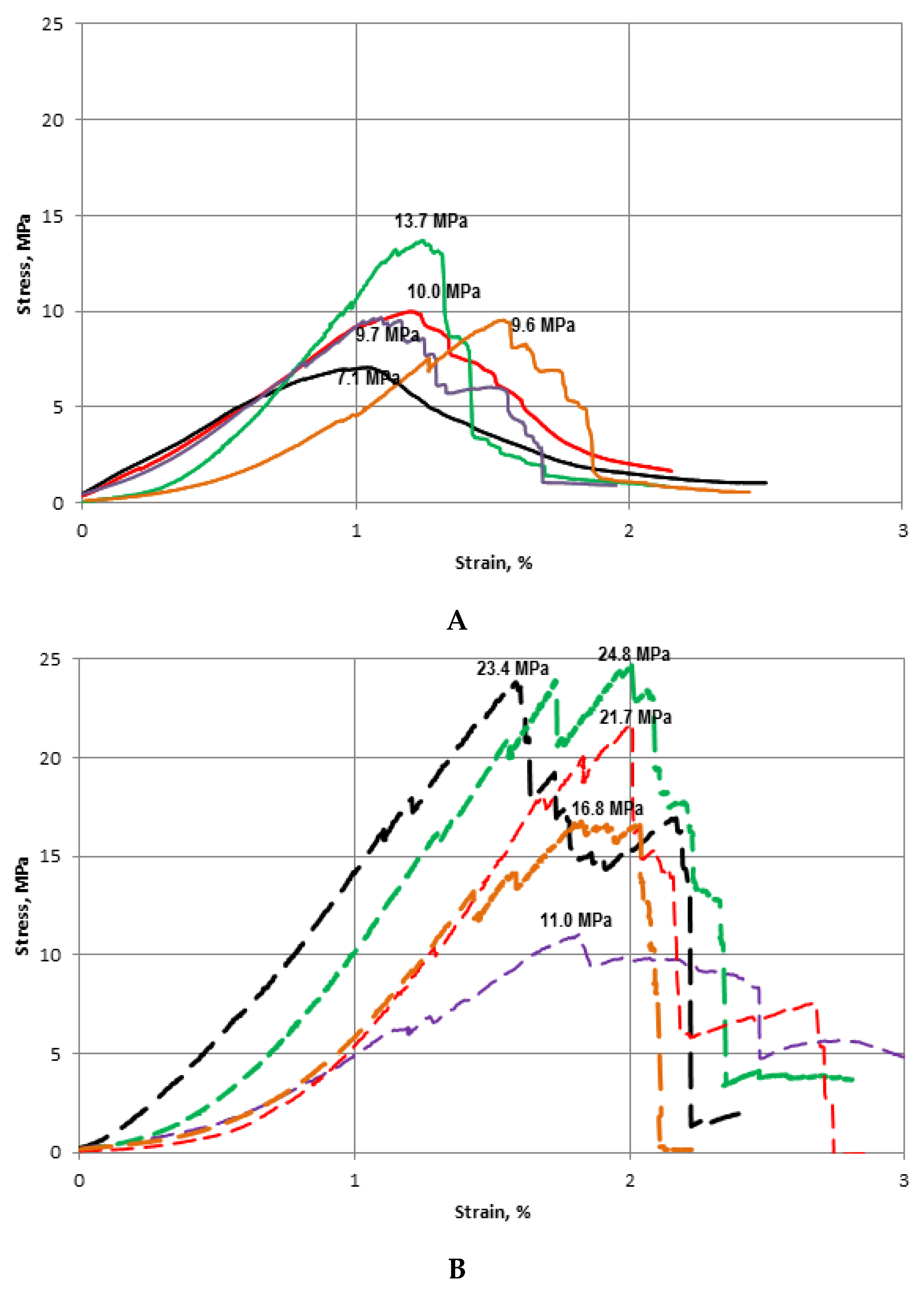
| Applied stress condition: σ1 > 0, σ2 = σ3 = 0 Uniaxial compressive strength Static Young’s modulus Static Poisson’s ratio | The specimens were tested in air-dry conditions. Specimen shape: cube with a base edge of 50 mm or cylinder with a diameter of 50 mm. Slenderness of the specimens: 1.0. An empirical factor of 0.89 was used to account for a specimen slenderness of over 2.0, as recommended by the ISRM. Load direction: perpendicular to the lamination. Piston rate: about 0.008 mm/s, i.e., the strain rate of rock in the area of mining excavations. Young’s modulus was determined over the entire height of the compressed rock specimen as a tangent of the inclination angle of the tangent to the x-axis, which is a linear approximation of the stress and strain characteristic. Poisson’s ratio was determined within the longitudinal elastic strains and using a roller chain with a sensor for recording and measuring circumferential strains [3,7,22,25,27]. |
| Dynamic elastic moduli and conditions of testing | Confining pressure, 21.1 MPa; pore pressure, 8.8 MPa; effective pressure, 12.3 MPa; temperature, 37 °C. Core specimens with a diameter of 1.5 inches; a length depending on the condition of individual specimens was cut out perpendicular to the lamination. Before testing, specimens were saturated with a 2% potassium chloride solution in a vacuum chamber, at a pressure of 1 bar, for at least 12 h, before being additionally saturated with the same solution at a backpressure of at least 500 psi, into the core holder of the ultrasonic device [26,28]. |
3. Results and Discussion
- Maximum vertical stress, σ1 (uniaxial compressive strength, UCS), and differential stress, σ1–σ3;
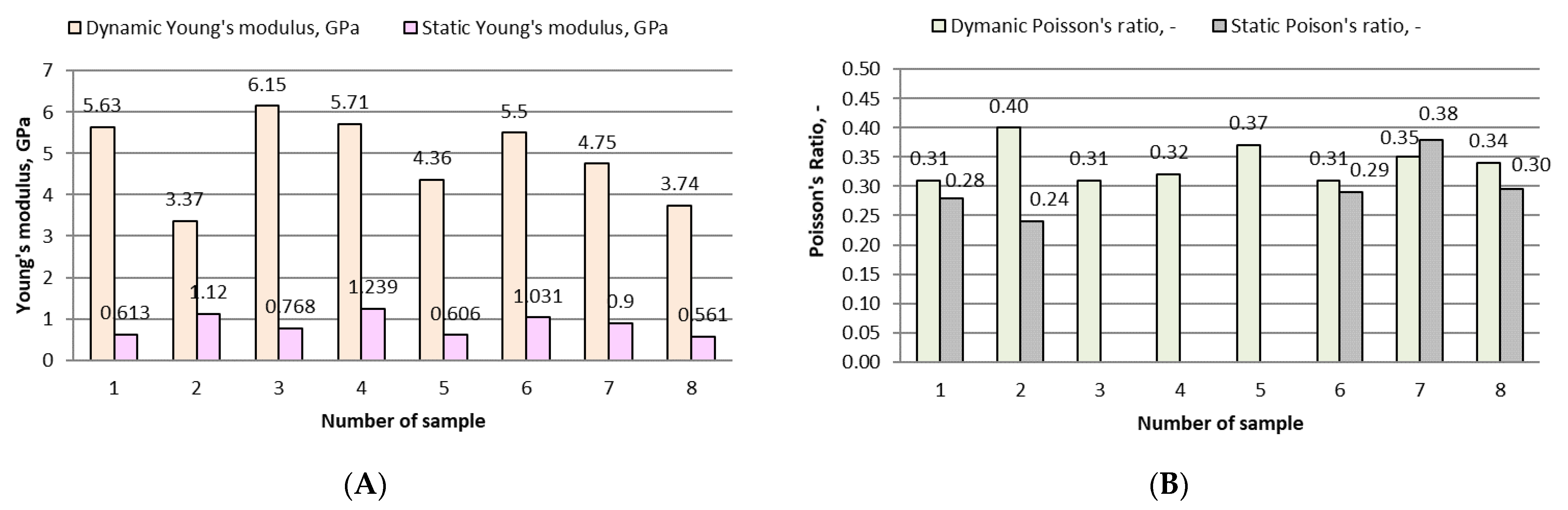
- Young’s modulus: static, Est, and dynamic, Edyn;
- Poisson’s ratio: static νst and dynamic νdyn;
- Bulk density, ρo;
- Total porosity, P.
4. Conclusions
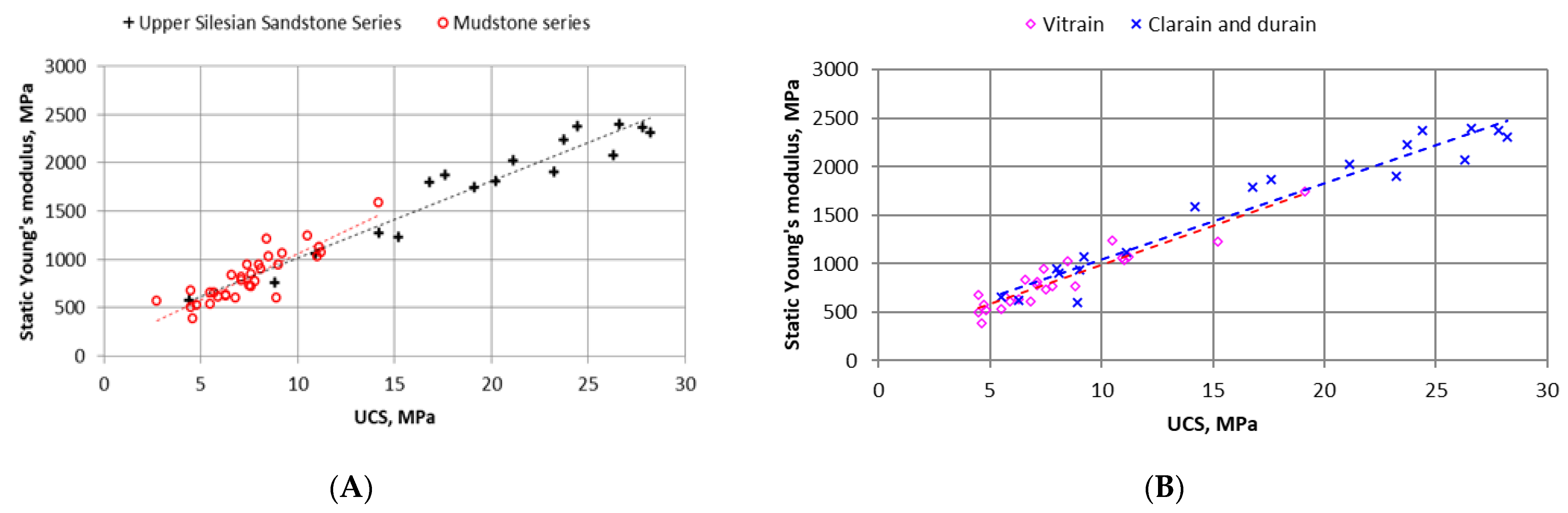
- The geologic age of coal, as well as its petrographic structure, had a significant influence on the dependence between uniaxial compressive strength and the static Young’s modulus determined on the basis of the stress and strain curve (R2 = 0.76–0.96).
- The functional dependences determined on the basis of tests conducted under a complex state of stress and at various confining pressures and high strain rates were characterized by a very high correlation between the differential stress and the static Young’s modulus.
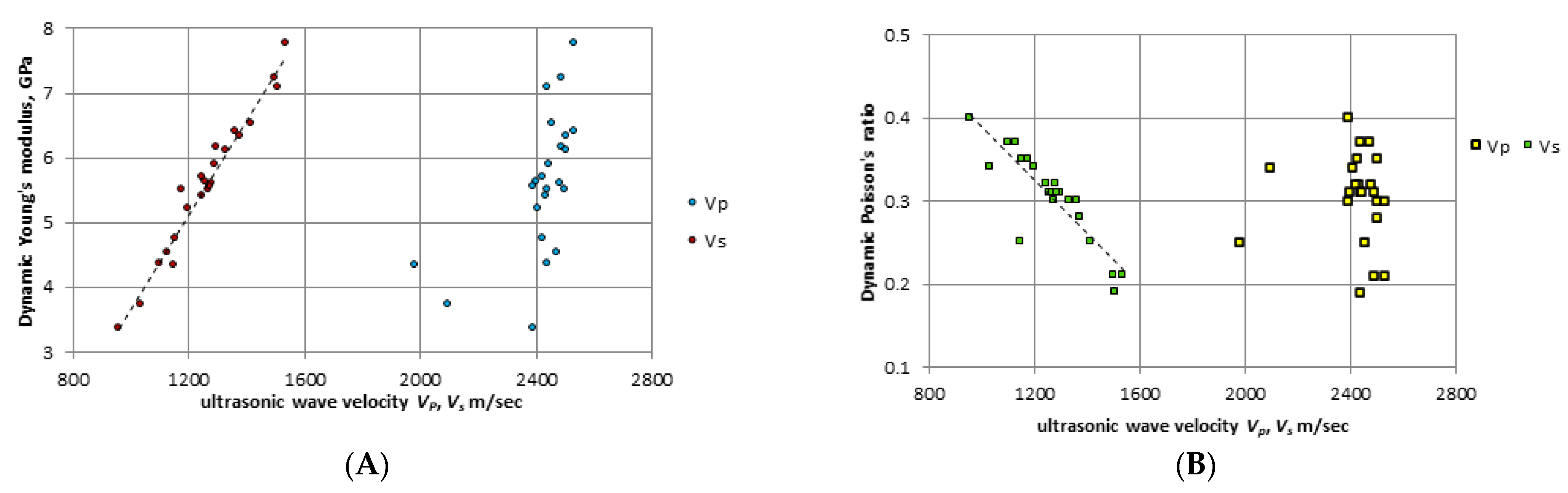
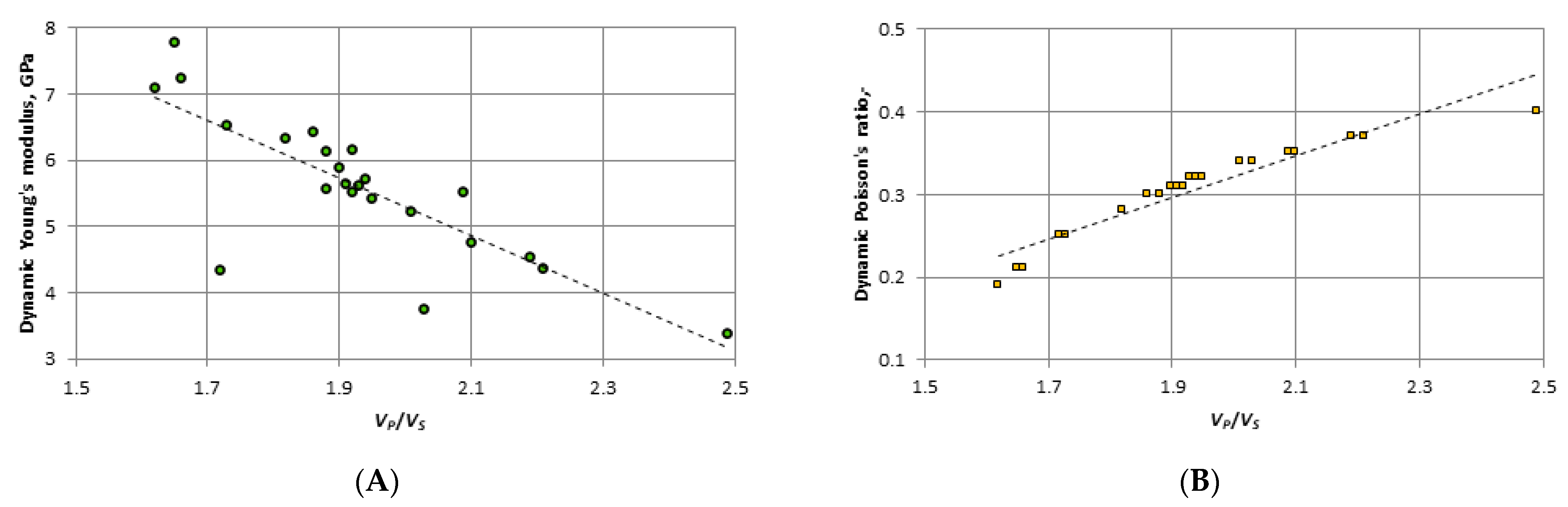
- A strong and very strong correlation between the S-wave velocity and the elastic parameters (R2 = 0.76–0.96) were obtained on the basis of the conducted laboratory ultrasonic tests. However, no correlation was observed between the P-wave velocity and the elastic parameters, which also confirms the results of experiments conducted by other researchers. The determined values of VP/VS for carboniferous coals revealed a strong correlation with the dynamic Young’s modulus (R2 = 0.65) and a very strong linear dependence with the dynamic Poisson’s ratio (R2 = 0.89).
- Testing of the studied carboniferous coals demonstrated a weak linear correlation between porosity and the Young’s modulus and Poisson’s ratio.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UCS | uniaxial compressive strength |
| USCB | Upper Silesian Coal Basin |
| ISRM | International Society for Rock Mechanics |
| Est | static Young’s modulus |
| νst | static Poisson’s ratio |
| σ1 | axial stress, vertical stress |
| σ2, σ3 | radial stress, horizontal stress |
| ρo | bulk density |
| P | total porosity |
| VP | P-wave velocity |
| VS | S-wave velocity |
| Edyn | dynamic Young’s modulus |
| νdyn | dynamic Poisson’s ratio |
| BI | brittleness index |
References
- Jizba, D.L. Mechanical and Acoustical Properties of Sandstones and Shales. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1991. [Google Scholar]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013, 78, D381–D392. [Google Scholar] [CrossRef]
- Bukowska, M. Skłonność Górotworu do Tąpań—Geologiczne i Geomechaniczne Metody Badań; Central Mining Institute: Katowice, Poland, 2012. (In Polish) [Google Scholar]
- Martinez-Martinez, J.; Benavente, D.; Garcia-del-Cura, M. A comparison of the static and dynamic elastic modulus in carbonate rocks. Bull. Eng. Geol. Environ. 2012, 71, 263–268. [Google Scholar] [CrossRef]
- Elkatatny, S.; Mahmoud, M.; Mohamed, I.; Abdulraheem, A. Development of a new correlation to determine the static Young’s modulus. J. Pet. Explor. Prod. Technol. 2018, 8, 17–30. [Google Scholar] [CrossRef]
- Massaq, A.; Rusinek, A.; Alosak, M. Method for determination of the dynamic elastic modulus for composite materials. Eng. Trans. 2016, 61, 301–315. [Google Scholar]
- Małkowski, P.; Ostrowski, Ł.; Brodny, J. Analysis of Young’s modulus for Carboniferous sedimentary rocks and its relationship with uniaxial compressive strength using different methods of modulus determination. J. Sustain. Min. 2018, 17, 145–157. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Moussa, T. Estimation of Static Young’s Modulus for Sandstone Formatting Using Artificial Neural Networks. Energies 2019, 12, 2125. [Google Scholar] [CrossRef]
- Walentek, A. Analysis of the applicability of the convergence control method for gateroad design based on conducted underground investigations. Arch. Min. Sci. 2019, 64, 765–783. [Google Scholar] [CrossRef]
- Walentek, A.; Janoszek, T.; Prusek, S.; Wrana, A. Influence of longwall gateroad convergence on the process of mine ventilation network-model tests. Int. J. Min. Sci. Technol. 2019, 29, 585–590. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Ning, J.; Qiu, P. Experimental Study on Mechanical Properties, Failure Behavior and Energy Evolution of Different Coal-Rock Combined Specimens. Appl. Sci. 2019, 9, 4427. [Google Scholar] [CrossRef]
- Bukowska, M.; Bukowski, P. Changes of Properties of Carboniferous Rock Mass and the Occurrence of Some Natural Hazards in the Conditions of Flooding of Roadways within Abandoned Coal Mines. J. Min. Sci. 2021, 57, 759–774. [Google Scholar] [CrossRef]
- Wojtecki, Ł.; Iwaszenko, S.; Apel, D.B.; Bukowska, M.; Makówka, J. Use of machine learning algorithms to assess the state of rockburst hazard in underground coal mine openings. J. Rock Mech. Geotech. Eng. 2022, in press. [Google Scholar] [CrossRef]
- Tao, Y.; Du, H.; Zhang, R.; Feng, J.; Deng, Z. Experiment Study on Mechanical Evolution Characteristics of Coal and Rock under Three-Dimensional Triaxial Stress. Appl. Sci. 2022, 12, 2445. [Google Scholar] [CrossRef]
- Kasza, P. Hydraulic fracturing in unconventional reservoirs and methods of their analysis. Prace Naukowe INiG—PIB 2019, 226, 1–147, (In Polish with English Abstract). [Google Scholar] [CrossRef]
- Economides, M.; Martin, T. Modern Fracturing Enhancing Natural Gas Production; ET Publishing: Houston, TX, USA, 2007. [Google Scholar]
- Rickman, R.; Mullen, M.; Petre, E.; Grieser, B.; Kundert, D. A practical use of shale petrophysics for stimulation designing optimalization: All shale plays are not clones of the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; SPE 115258. Society of Petroleum Engineers: Houston, TX, USA, 2008. [Google Scholar] [CrossRef]
- Grieser, W.; Bray, J. Identification of production potential in unconventional reservoirs. In Proceedings of the Production and Operations Symposium, Oklahoma City, OK, USA, 31 March 2007; SPE 106623. Society of Petroleum Engineers: Houston, TX, USA, 2007. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, P.; Dong, S.; Huang, Y.; Zhang, M. Brittleness index analysis of coal samples. Acta Geophys. 2019, 67, 789–797. [Google Scholar] [CrossRef]
- Moska, R. Brittleness index of coal from Upper Silesian Coal Basin. Acta Geodyn. Geomater. 2021, 18, 91–101. [Google Scholar] [CrossRef]
- Zheng, Z.; Khodaverdian, M.; McLennan, J.D. Static and Dynamic Testing of Coal Specimens. 1991 SCA Conference Paper 9120.
- Bukowska, M. Post-critical mechanical properties of sedimentary rocks in the Upper Silesian Coal Basin (Poland). Arch. Min. Sci. 2015, 60, 517–534. [Google Scholar] [CrossRef][Green Version]
- Jureczka, J. (Ed.) Litologia i litostratygrafia karbonu. In Profile Głębokich Otworów Wiertniczych; Państwowego Instytutu Geologicznego: Warsaw, Poland, 2018; Volume 152, pp. 89–93, (In Polish with English Summary). [Google Scholar]
- Kovari, K.; Tisa, A.; Einstein, H.H.; Franklin, J.A. Suggested methods for determining the strength of rock materials in triaxial compression: Revised version. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 283–290. [Google Scholar]
- Klepaczko, J.R. On the rate sensitivity of coal. Eng. Trans. 1983, 31, 341–359. [Google Scholar]
- Fjær, E.; Holt, R.M.; Horsrund, P.; Raanen, A.M.; Risnes, R. Petroleum Related Rock Mechanics; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Ulusay, R.; Hudson, J.A. (Eds.) The Complete ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 1974–2006; Commission on Testing Methods—ISRM: Ankara, Turkey, 2007. [Google Scholar]
- Bourbie, T.; Coussy, O.; Zinszner, B. (Eds.) Acoustic of Porous Media; Technip: Paris, Frace, 1987. [Google Scholar]
- Dziedzic, A.; Łukaszewski, P. Methodological conditions of geomechanical tests under triaxial stress state of rocks taken from large depths. Nafta-Gaz 2015, 1, 3–10, (In Polish with English Abstract). [Google Scholar]
- Puskarczyk, E.; Krakowska, P.; Wawrzyniak-Guz, K.; Jarzyna, J. Badania prędkości fal sprężystych i charakterystyka naprężeniowo-odkształceniowa w warunkach trójosiowego ściskania wybranych skał klastycznych i węglanowych. Zesz. Nauk. Inst. Gospod. Surowcami Energią PAN 2017, 101, 313–322, (In Polish with English Abstract). [Google Scholar]
- Brotons, V.; Tomas, R.; Ivorra, S.; Grediaga, A.; Martinez-Martinez, J.; Benavente, D.; Gomez-Heras, M. Improved correlation between the static and dynamic elastic modulus of different types of rocks. Miner. Struct. 2016, 49, 3021–3037. [Google Scholar] [CrossRef]
- Eissa, E.A.; Kazi, A. Relation between static and dynamic Young’s moduli for rocks. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1988, 25, 479–482. [Google Scholar] [CrossRef]
- Al-Shayea, N.A. Effect of testing methods and conditions on the elastic properties of limestone rock. Eng. Geol. 2004, 74, 139–156. [Google Scholar] [CrossRef]
- Fei, W.; Huiyuan, B.; Jun, Y.; Yonghao, Z. Correlation of dynamic and static elastic parameters of rock. Electron. J. Geotech. Eng. 2016, 21, 1551–1560. [Google Scholar]
- Davarpanah, S.M.; Van, P.; Vasarhelyi, B. Investigation of the relationship between dynamic and static deformation moduli of rocks. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 29. [Google Scholar] [CrossRef]
- Wu, H.; Dong, S.; Li, D.; Huang, Y.; Qi, X. Experimental study on dynamic elastic parameters of coal samples. Int. J. Min. Sci. Technol. 2015, 25, 447–452. [Google Scholar] [CrossRef]
- Morcote, A.; Mavko, G.; Prasad, M. Dynamic elastic properties of coal. Geophysics 2010, 75, E227–E234. [Google Scholar] [CrossRef]
- Azimian, A.; Ajaloeian, R. An empirical correlation of uniaxial Compressive strength with P-wave velocity and point load strength index on marly rocks using statistical method. Geotech. Geol. Eng. 2014, 32, 206–215. [Google Scholar] [CrossRef]





| Number of Samples | UCS | Est | νst | |||
|---|---|---|---|---|---|---|
| Mean Values MPa | SD MPa | Mean Values MPa | SD MPa | Mean Values - | SD - | |
| 4 | 11.2 | 2.2 | 1069 | 327 | 0.25 | 0.06 |
| 4 | 5.9 | 1.3 | 613 | 175 | 0.28 | 0.04 |
| 4 | 6.3 | 2.1 | 638 | 303 | * | - |
| 3 | 6.6 | 0.1 | 836 | 16 | * | - |
| 4 | 14.2 | 1.7 | 1585 | 151 | 0.27 | 0.05 |
| 3 | 11.1 | 2.9 | 1120 | 227 | 0.24 | 0.03 |
| 1 | 7.8 | - | 768 | - | * | - |
| 1 | 5.5 | - | 536 | - | * | - |
| 3 | 10.5 | 1.5 | 1239 | 246 | * | - |
| 4 | 6.8 | 2.4 | 606 | 331 | * | - |
| 3 | 7.1 | 5.8 | 814 | 766 | 0.22 | 0.06 |
| 3 | 8.9 | 0.7 | 601 | 159 | 0.26 | 0.06 |
| 3 | 9.0 | 2.1 | 942 | 309 | 0.32 | 0.08 |
| 2 | 4.7 | 1.4 | 573 | 276 | 0.34 | 0.08 |
| 2 | 4.6 | 0.6 | 389 | 75 | 0.29 | 0.09 |
| 4 | 8.0 | 2.9 | 945 | 372 | 0.22 | 0.10 |
| 4 | 7.1 | 2.6 | 784 | 421 | 0.32 | 0.05 |
| 4 | 8.5 | 1.2 | 1031 | 230 | 0.29 | 0.02 |
| 2 | 8.1 | 2.1 | 900 | 324 | 0.38 | 0.01 |
| 2 | 5.5 | 2.8 | 654 | 542 | 0.29 | 0.04 |
| 4 | 6.3 | 0.8 | 619 | 248 | 0.28 | 0.05 |
| 4 | 4.5 | 2.1 | 503 | 127 | 0.31 | 0.08 |
| 4 | 4.5 | 3.0 | 673 | 479 | 0.27 | 0.10 |
| 4 | 7.4 | 2.8 | 948 | 308 | 0.25 | 0.08 |
| 3 | 5.7 | 0.6 | 656 | 68 | 0.16 | 0.02 |
| 2 | 4.8 | 1.4 | 523 | 146 | 0.16 | 0.06 |
| 2 | 11.0 | 2.4 | 1033 | 394 | 0.28 | 0.06 |
| 2 | 9.2 | 0.2 | 1066 | 155 | 0.39 | 0.06 |
| 4 | 7.5 | 2.9 | 734 | 470 | 0.27 | 0.11 |
| 4 | 26.6 | 4.4 | 2399 | 382 | 0.30 | 0.05 |
| 3 | 19.1 | 1.9 | 1751 | 151 | 0.37 | 0.02 |
| 2 | 23.2 | 0.8 | 1903 | 96 | 0.24 | 0.12 |
| 3 | 15.2 | 1.1 | 1233 | 178 | 0.23 | 0.04 |
| 3 | 8.8 | 2.1 | 765 | 251 | 0.37 | 0.02 |
| 2 | 10.9 | 0.4 | 1061 | 404 | 0.24 | 0.12 |
| 3 | 26.3 | 5.7 | 2073 | 402 | 0.36 | 0.05 |
| 3 | 27.8 | 7.7 | 2371 | 340 | 0.31 | 0.05 |
| 4 | 28.2 | 3.0 | 2312 | 348 | 0.30 | 0.08 |
| 3 | 24.4 | 2.8 | 2372 | 149 | 0.33 | 0.02 |
| 3 | 21.1 | 3.5 | 2026 | 367 | 0.34 | 0.08 |
| 2 | 23.7 | 11.1 | 2234 | 612 | 0.30 | 0.08 |
| 4 | 16.8 | 2.7 | 1794 | 220 | 0.20 | 0.08 |
| 3 | 17.6 | 0.9 | 1872 | 125 | 0.24 | 0.12 |
| Number of Samples | VP m/s | VS m/s | VP/VS - | Edyn GPa | νdyn - |
|---|---|---|---|---|---|
| 1 | 2409 | 1200 | 2.01 | 5.21 | 0.34 |
| 1 | 2399 | 1259 | 1.91 | 5.63 | 0.31 |
| 1 | 2435 | 1250 | 1.95 | 5.41 | 0.32 |
| 1 | 2392 | 959 | 2.49 | 3.37 | 0.40 |
| 1 | 2488 | 1299 | 1.92 | 6.15 | 0.31 |
| 1 | 2421 | 1249 | 1.94 | 5.71 | 0.32 |
| 1 | 2441 | 1104 | 2.21 | 4.36 | 0.37 |
| 1 | 2441 | 1271 | 1.92 | 5.50 | 0.31 |
| 1 | 2481 | 1283 | 1.93 | 5.61 | 0.32 |
| 1 | 2425 | 1154 | 2.10 | 4.75 | 0.35 |
| 1 | 2098 | 1034 | 2.03 | 3.74 | 0.34 |
| 1 | 2389 | 1273 | 1.88 | 5.56 | 0.30 |
| 1 | 2441 | 1509 | 1.62 | 7.09 | 0.19 |
| 1 | 2504 | 1377 | 1.82 | 6.33 | 0.28 |
| 1 | 2530 | 1537 | 1.65 | 7.77 | 0.21 |
| 1 | 2491 | 1501 | 1.66 | 7.24 | 0.21 |
| 1 | 1982 | 1150 | 1.72 | 4.34 | 0.25 |
| 1 | 2500 | 1175 | 2.09 | 5.50 | 0.35 |
| 1 | 2446 | 1289 | 1.90 | 5.89 | 0.31 |
| 1 | 2457 | 1416 | 1.73 | 6.52 | 0.25 |
| 1 | 2503 | 1332 | 1.88 | 6.12 | 0.30 |
| 1 | 2533 | 1364 | 1.86 | 6.41 | 0.30 |
| 1 | 2472 | 1130 | 2.19 | 4.52 | 0.37 |
| Lithostratigraphic Series | Coal Lithotype | UCS stress Condition σ1 > 0, σ2 = σ3 = 0 MPa | Static Young’s Modulus MPa | Static Poisson’s Ratio - | Bulk Density kg/m3 |
|---|---|---|---|---|---|
| Mudstone Series | Vitrain | 4.5–11.2 | 389–1069 | 0.16–0.34 | 1112–1376 |
| Clarain | 5.5–11.1 | 601–1239 | 0.24–0.39 | 1220–1302 | |
| Durain/vitrain | 8.0–14.2 | 942–1585 | 0.22–0.32 | 1229–1366 | |
| Upper Silesian Sandstone Series | Vitrain | 8.8–19.1 | 765–1751 | 0.23–0.37 | 1268–1490 |
| Clarain | 21.1–28.2 | 1903–2399 | 0.24–0.36 | 1262–1384 |
| Coals | Mudstone Series | Upper Silesian Sandstone Series |
|---|---|---|
| Vitrain | Very low and low strength | Very low and low strength |
| Clarain | High strength | |
| Durain/vitrain | Not present in the rock mass in the sampling regions |
| Relationship | R2 Coefficient | Estimated SSE Standard Error |
|---|---|---|
| Mudstone Series Est = 94.824UCS + 107.18 | 0.7623 | 128.79 |
| Upper Silesian Sandstone Series Est = 79.592UCS + 216.47 | 0.9278 | 159.44 |
| Vitrain Est = 80.56UCS + 179.52 | 0.8842 | 106.55 |
| Clarain and durain Est = 78.905UCS + 255.48 | 0.9386 | 170.55 |
| Relationship | R2 Coefficient | Estimated SSE Standard Error |
|---|---|---|
| Est = 11,471(σ1–σ3) + 2417.9 strain rates = 10−5 to 10−4 s−1; confining pressures of 10, 20, 30, and 50 MPa | 0.9543 | 83.78 |
| Est = 5932(σ1–σ3) + 2878.1 strain rates = 10−1 s−1; confining pressures of 10, 20, 30, and 50 MPa | 0.8455 | 106.62 |
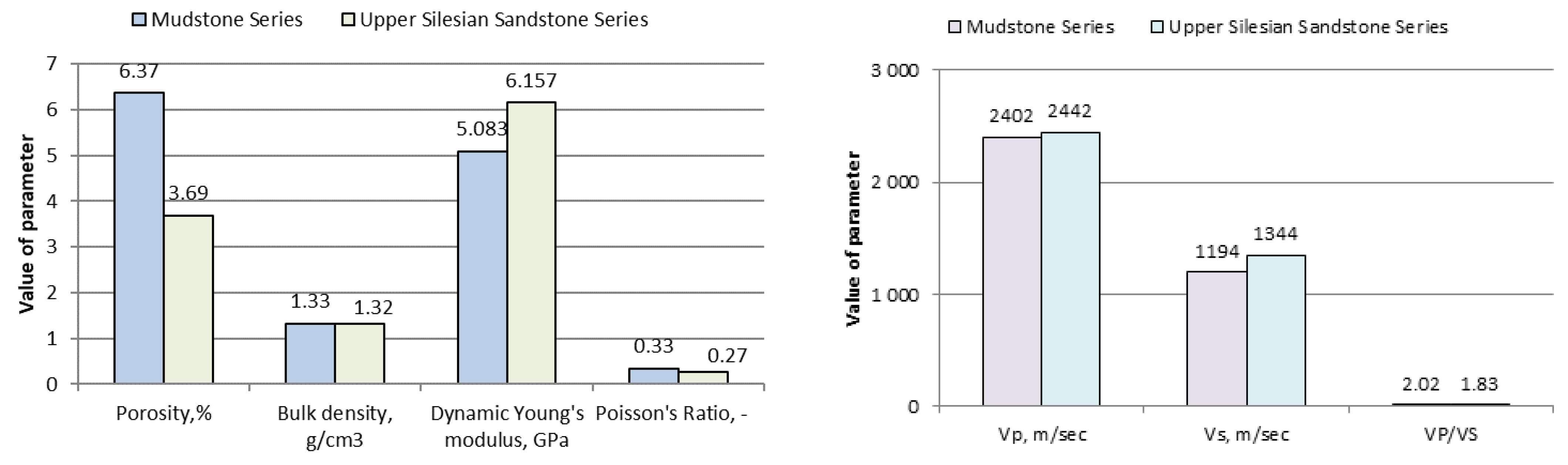
| Parameter | SI Unit | Min. Value | Max. Value |
|---|---|---|---|
| Compressional (P) wave velocity | m/s | 1982 | 2533 |
| Shear (S) wave velocity | m/s | 959 | 1537 |
| VP/VS | - | 1.62 | 2.49 |
| Dynamic Young’s modulus | GPa | 3.370 | 7.770 |
| Dynamic Poisson’s ratio | - | 0.19 | 0.40 |
| Porosity | % | 1.96 | 8.72 |
| Bulk density | kg/m3 | 1290 | 1390 |
| Relationship | R2 Coefficient | Estimated SSE Standard Error |
|---|---|---|
| Edyn = 0.0073VS − 3.637 | 0.9643 | 0.2100 |
| Edyn = −4.3609(VP/VS) + 14.017 | 0.6485 | 0.6590 |
| νdyn = 0.0003VS + 0.7072 | 0.7579 | 0.0270 |
| νdyn = 0.2524 (VP/VS) − 0.1825 | 0.8990 | 0.0170 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bukowska, M.; Kasza, P.; Moska, R.; Jureczka, J. The Young’s Modulus and Poisson’s Ratio of Hard Coals in Laboratory Tests. Energies 2022, 15, 2477. https://doi.org/10.3390/en15072477
Bukowska M, Kasza P, Moska R, Jureczka J. The Young’s Modulus and Poisson’s Ratio of Hard Coals in Laboratory Tests. Energies. 2022; 15(7):2477. https://doi.org/10.3390/en15072477
Chicago/Turabian StyleBukowska, Mirosława, Piotr Kasza, Rafał Moska, and Janusz Jureczka. 2022. "The Young’s Modulus and Poisson’s Ratio of Hard Coals in Laboratory Tests" Energies 15, no. 7: 2477. https://doi.org/10.3390/en15072477
APA StyleBukowska, M., Kasza, P., Moska, R., & Jureczka, J. (2022). The Young’s Modulus and Poisson’s Ratio of Hard Coals in Laboratory Tests. Energies, 15(7), 2477. https://doi.org/10.3390/en15072477






