Computational Model of Shell and Finned Tube Latent Thermal Energy Storage Developed as a New TRNSYS Type
Abstract
:1. Introduction
2. Physical Problem
3. Computational Model
4. Numerical Procedure and Experimental Validation
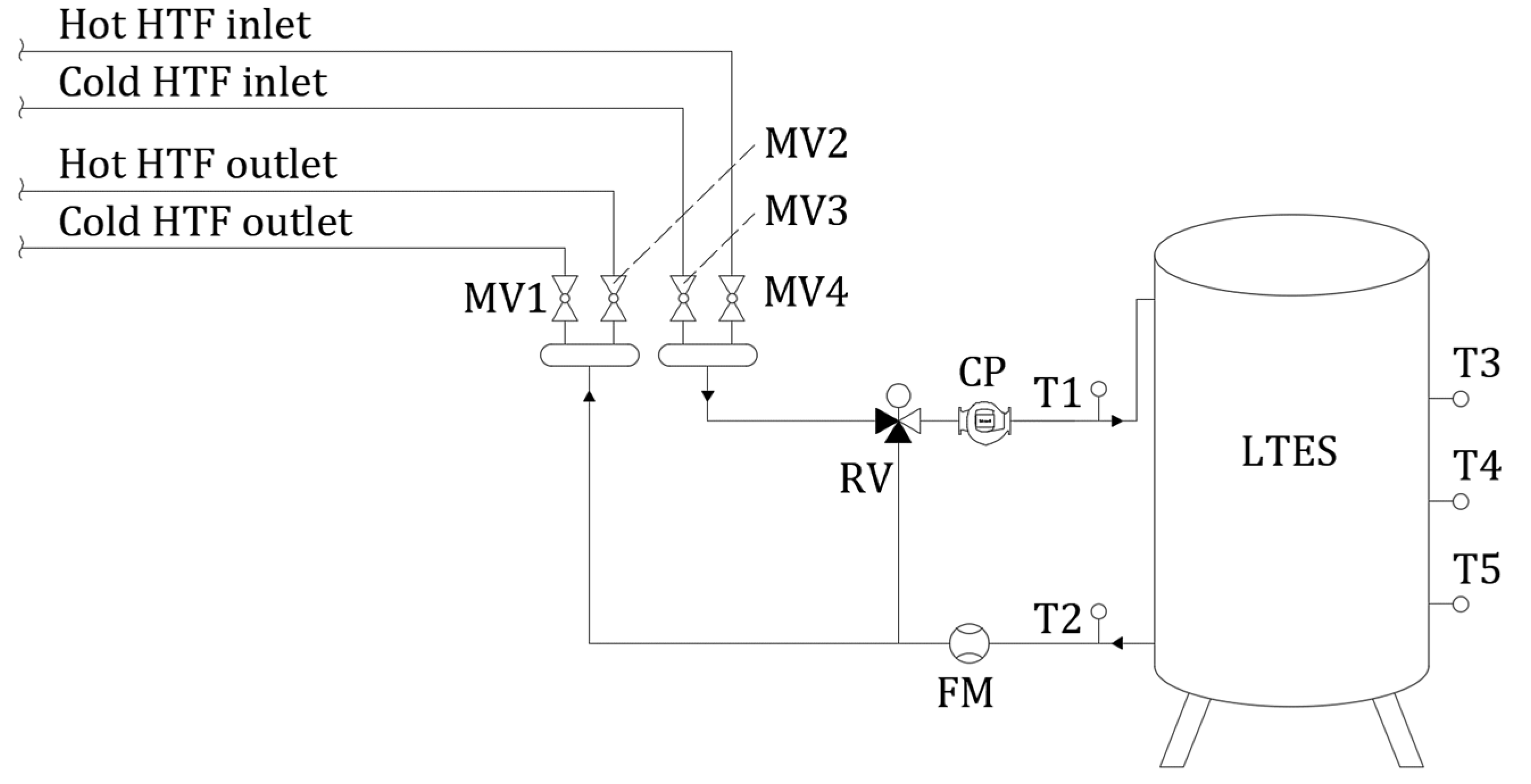
4.1. Numerical Setup
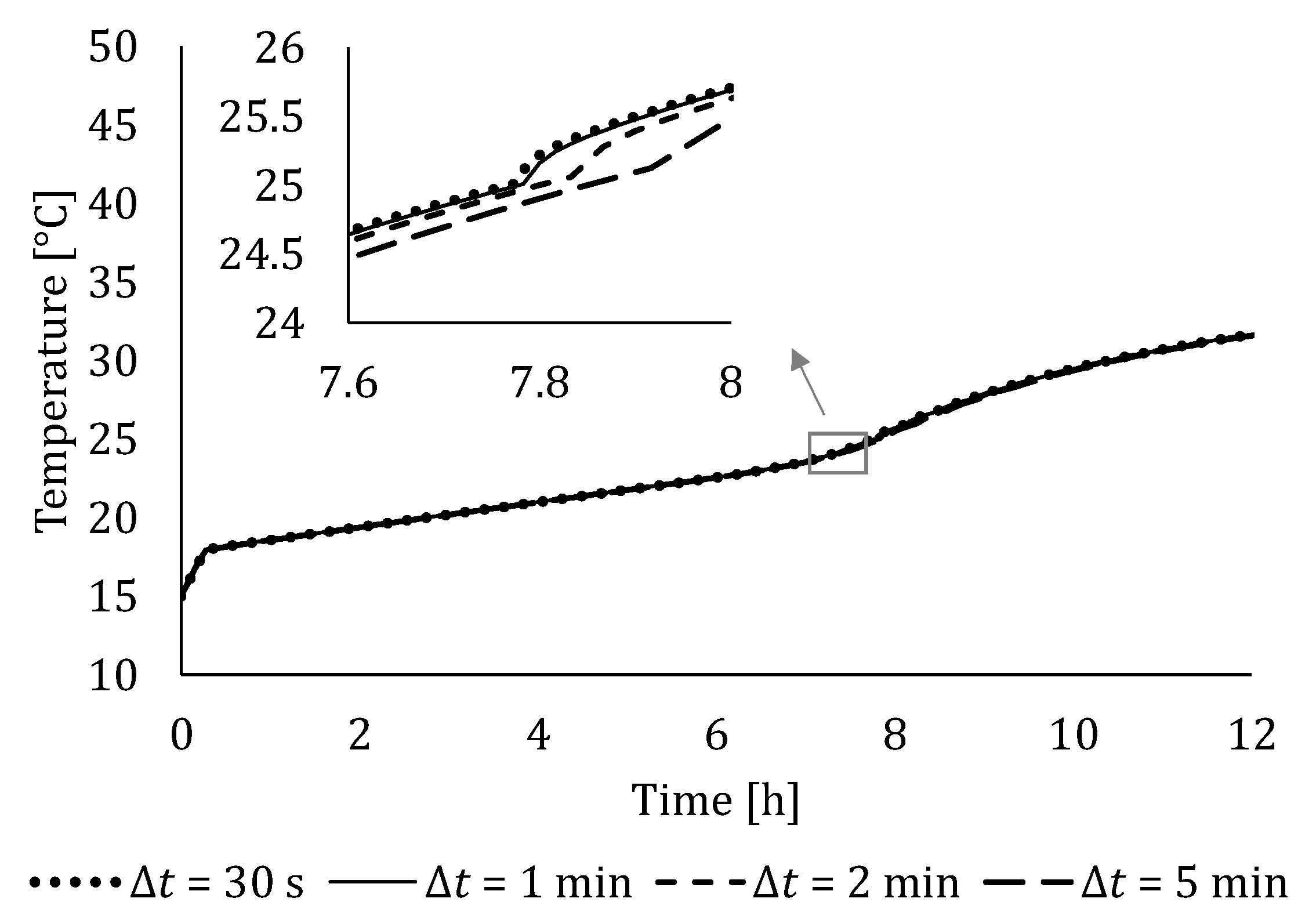
4.2. Independency Analysis of Number of Segments and Time Step Size
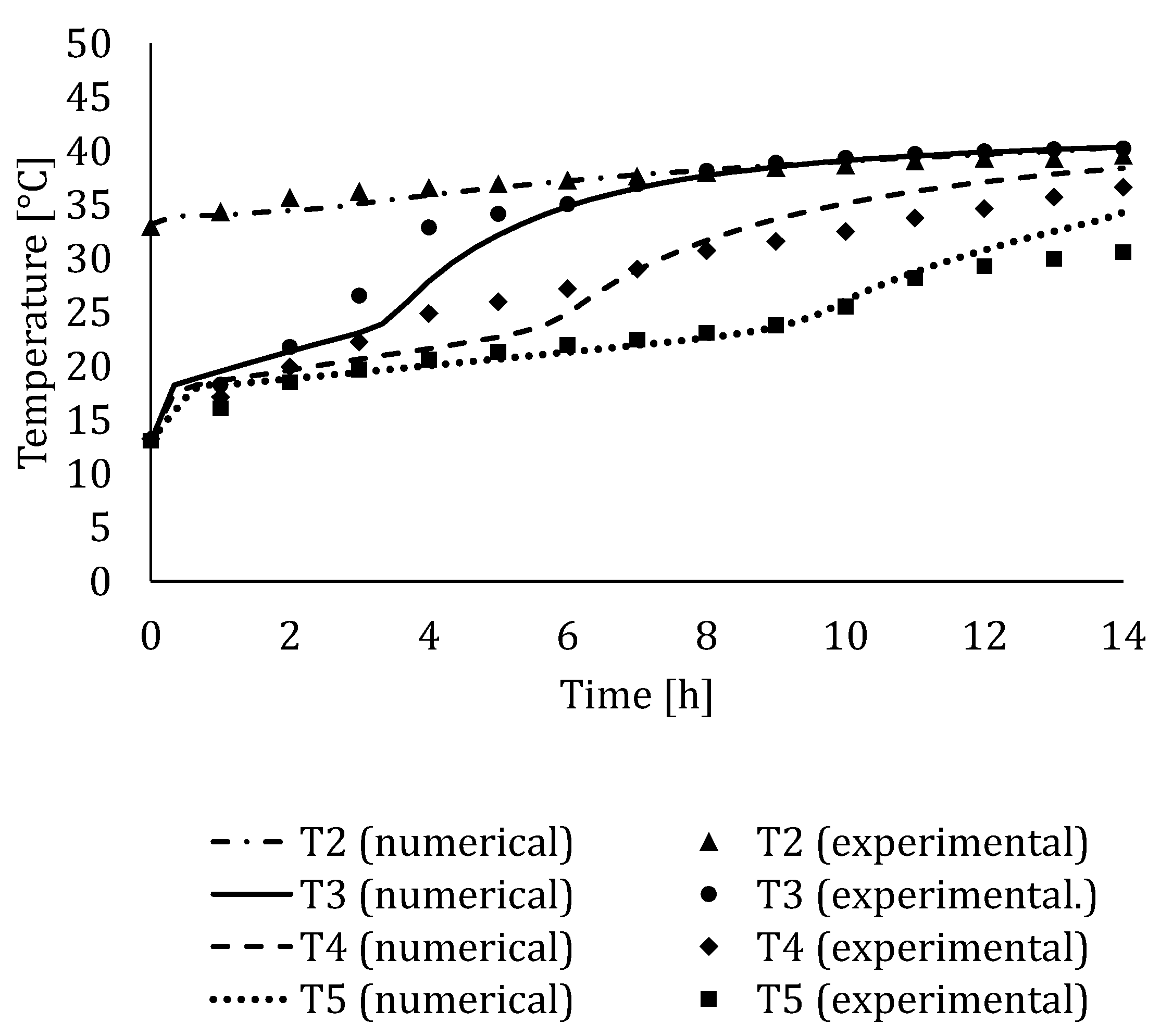
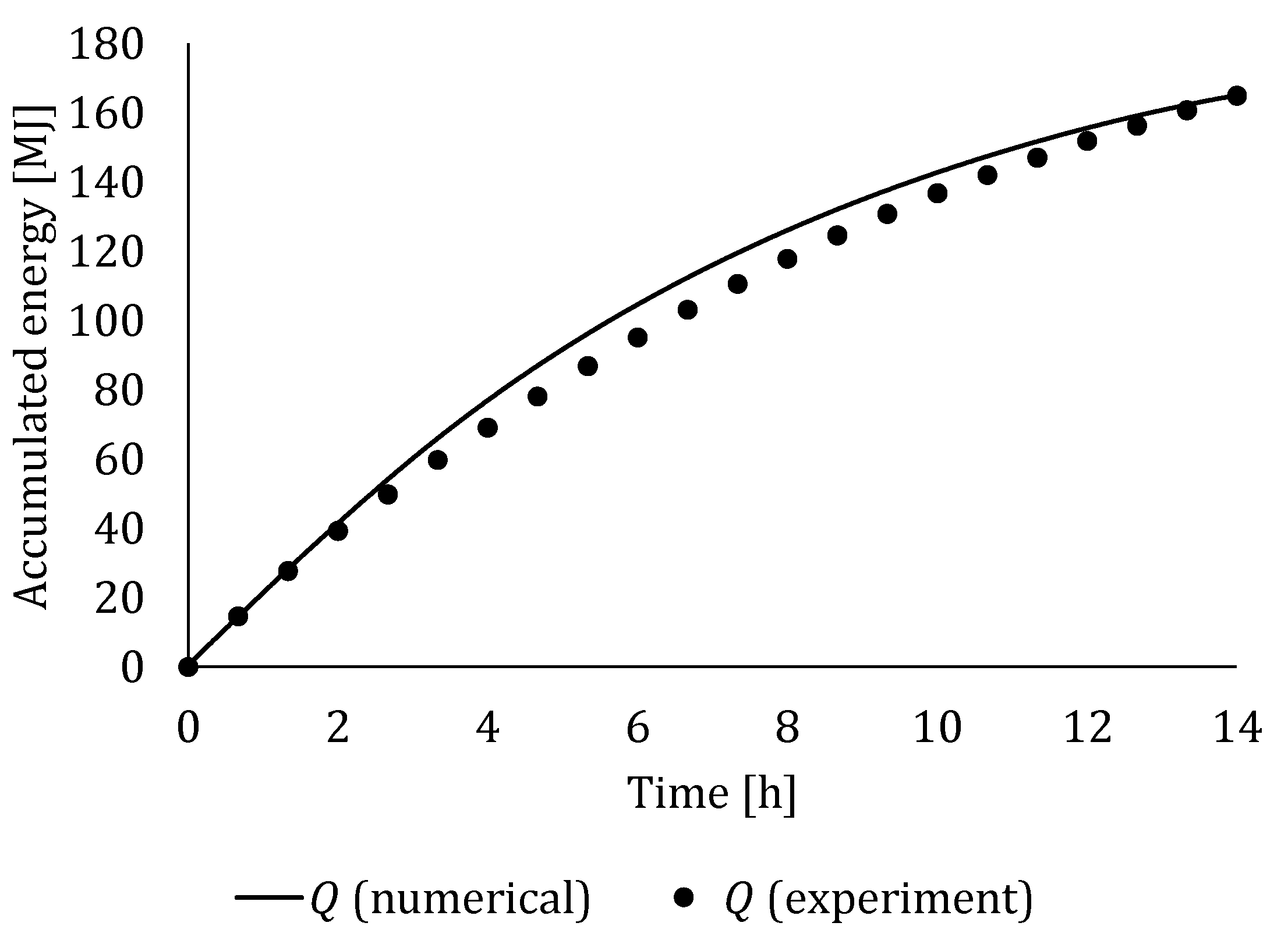
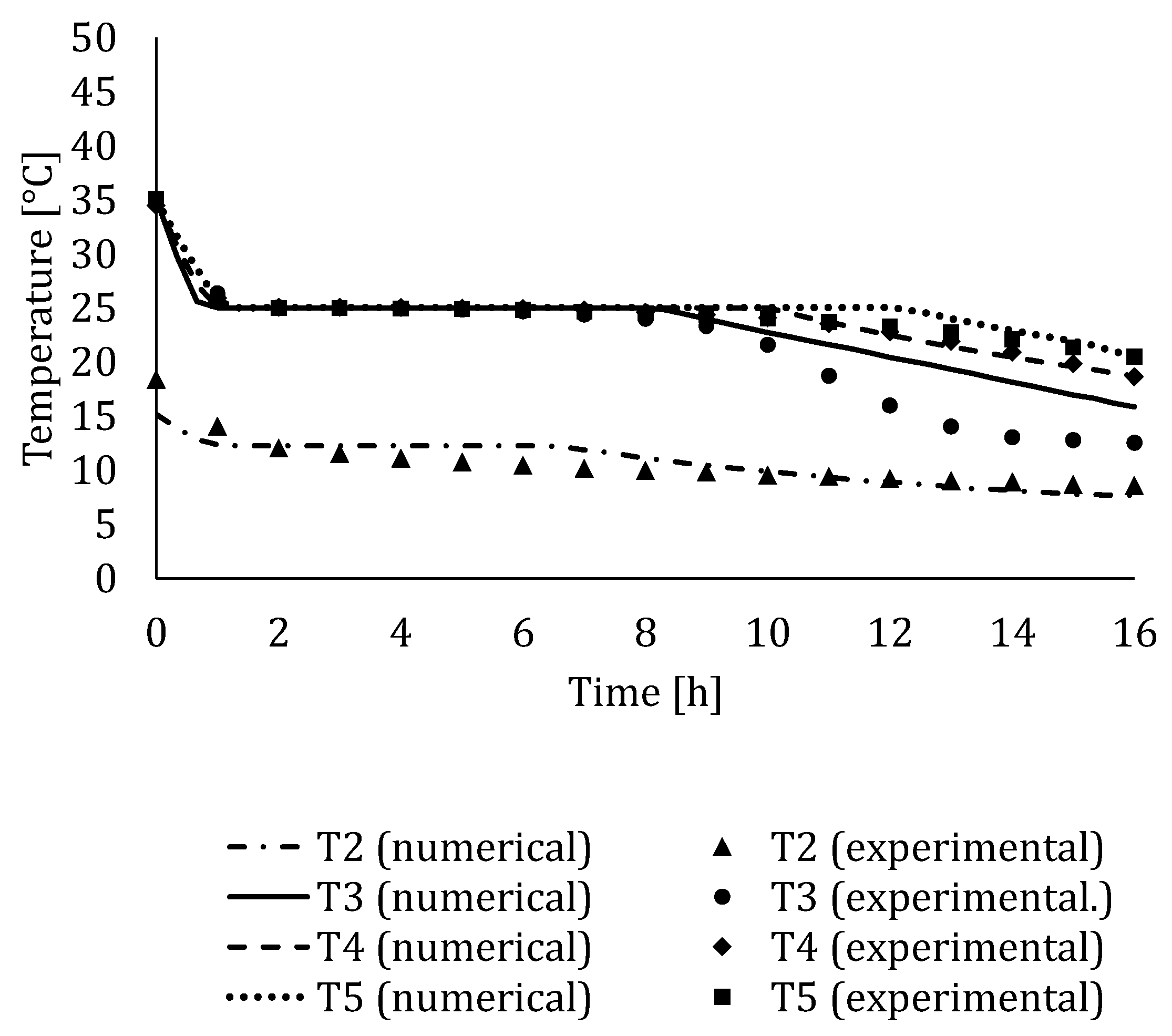
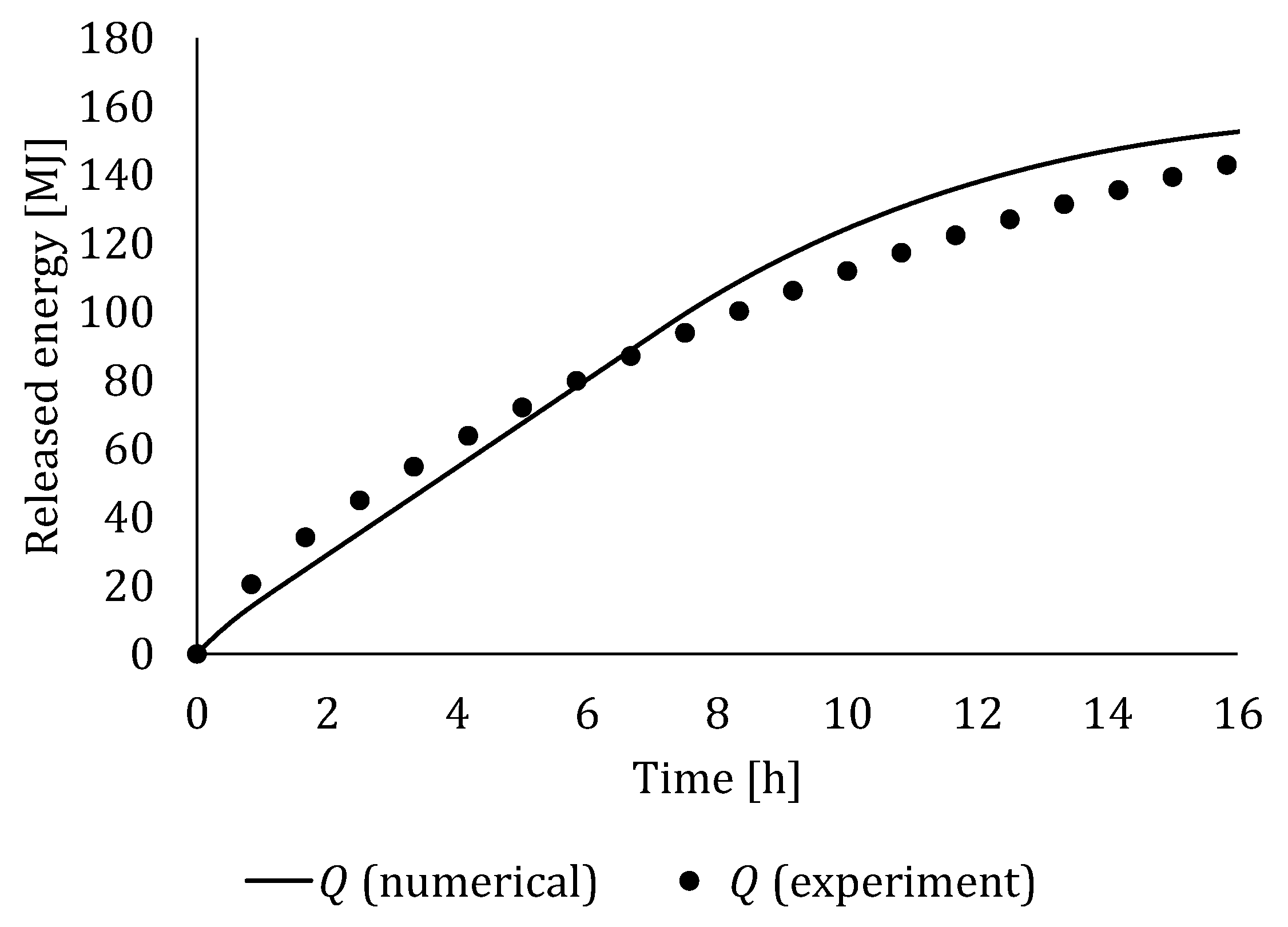
4.3. Experimental Validation
5. Application of the Developed Model
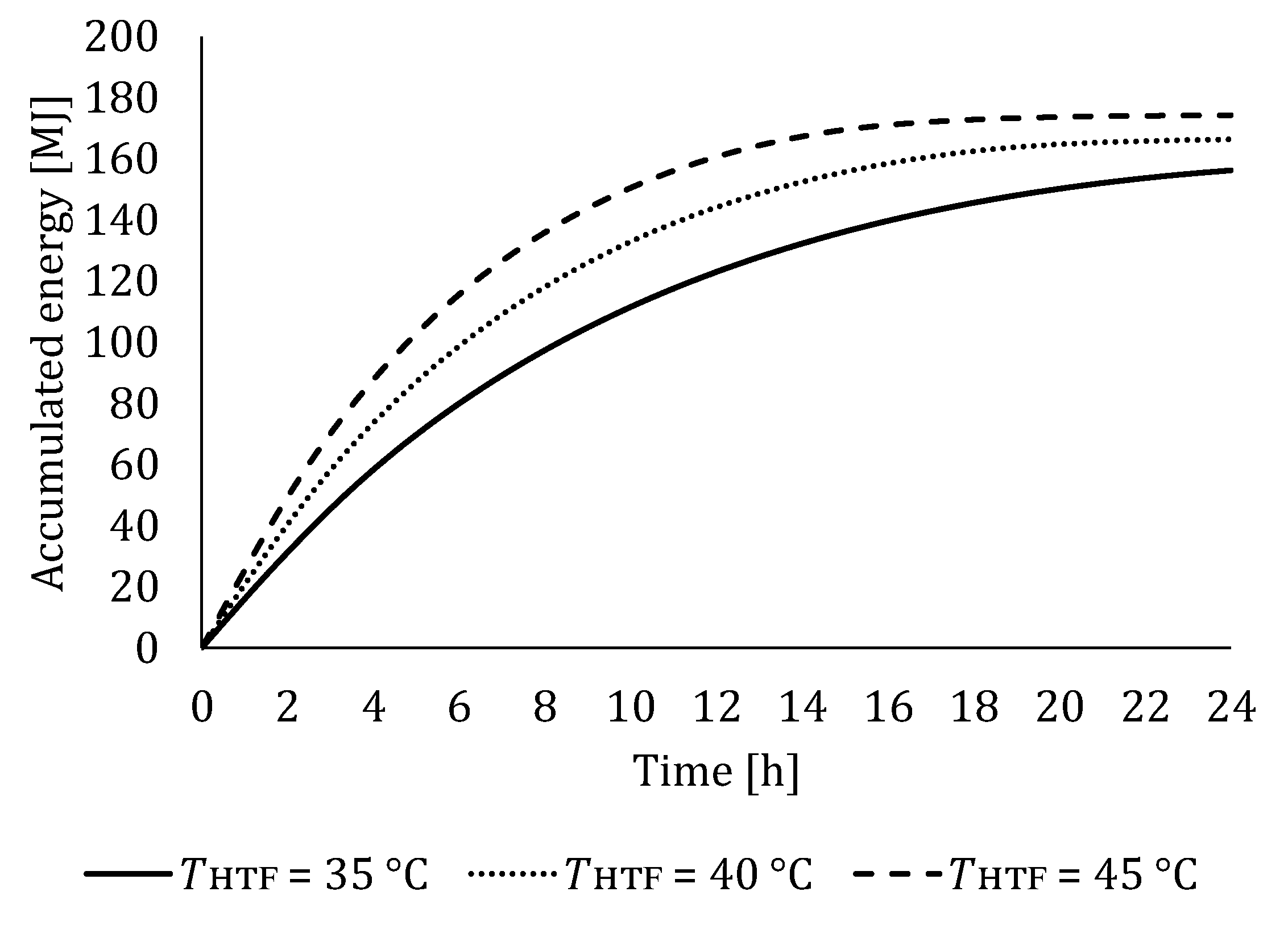
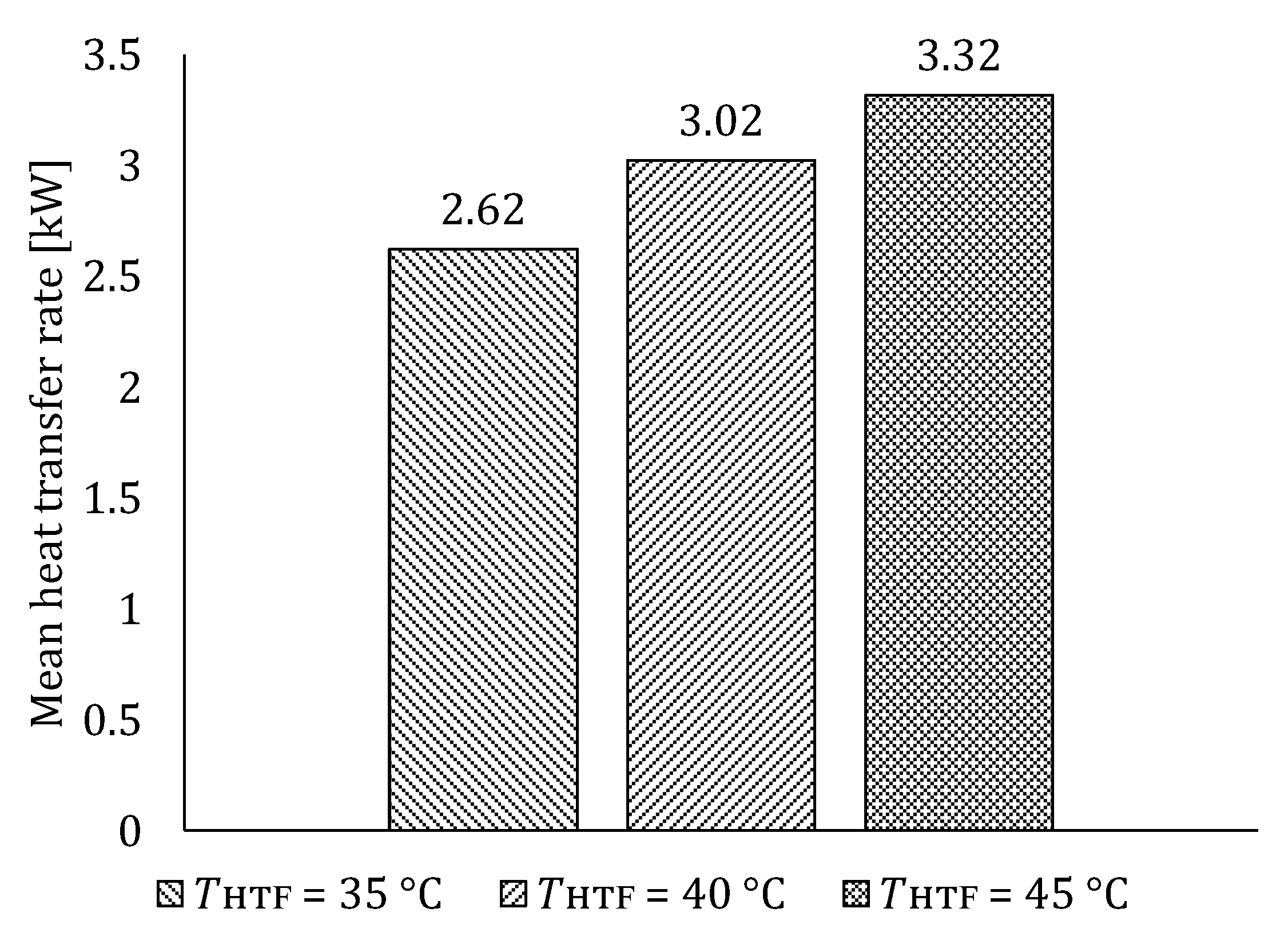
5.1. The Influence of HTF Inlet Temperature
5.1.1. Influence of HTF Inlet Temperature on LTES Thermal Performance during Charging
5.1.2. Influence of HTF Inlet Temperature on LTES Thermal Performance during Discharging
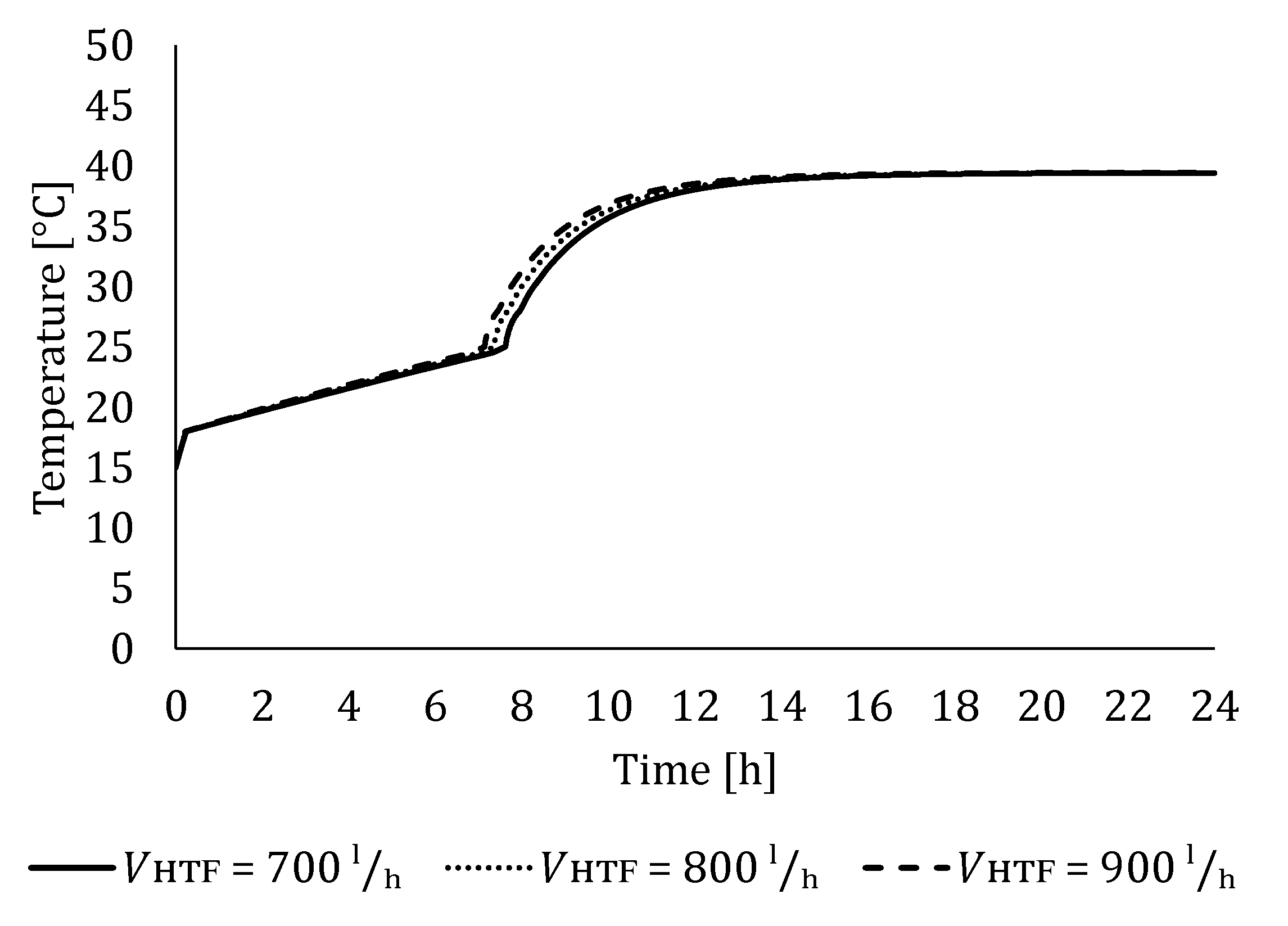
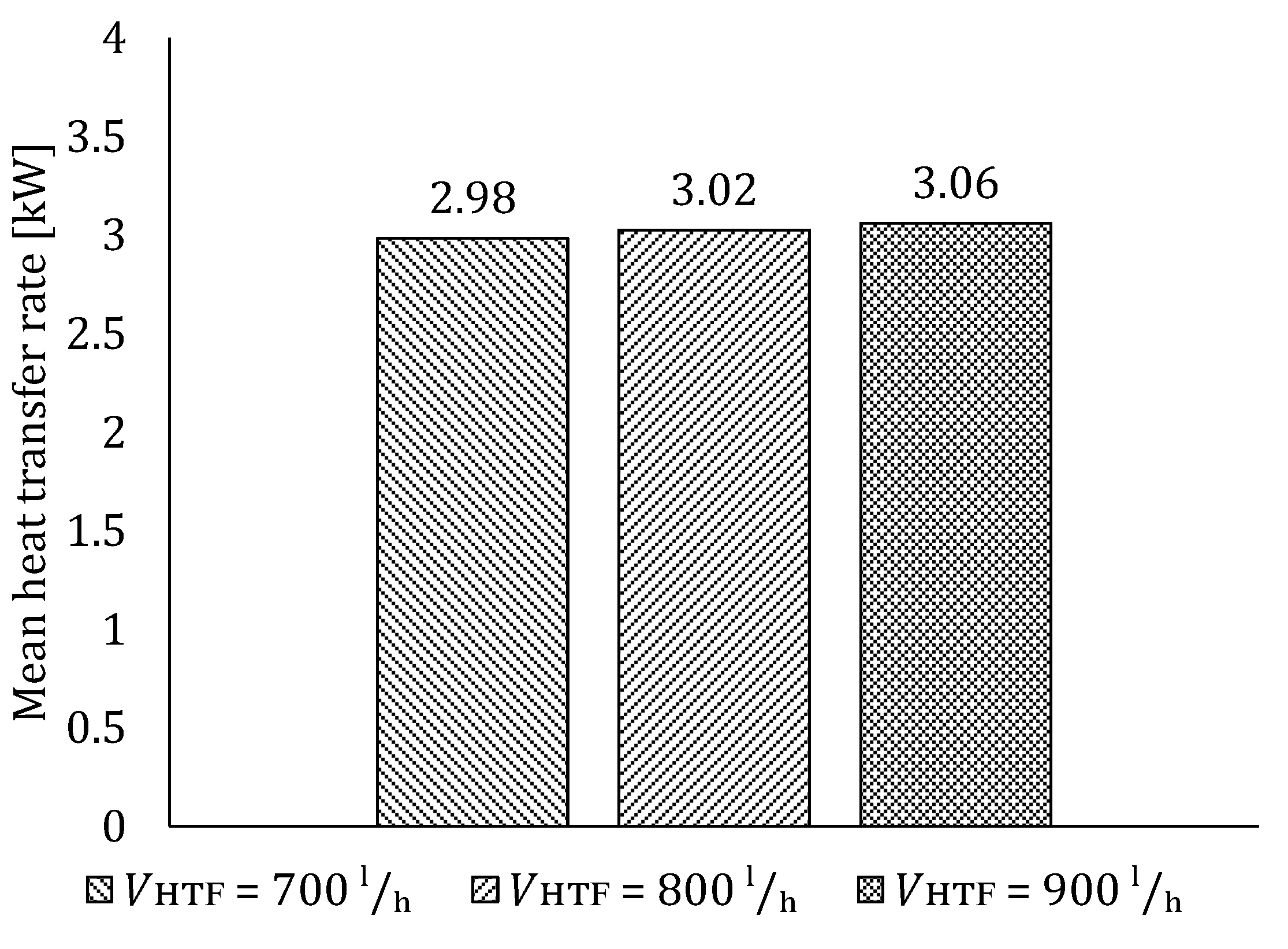
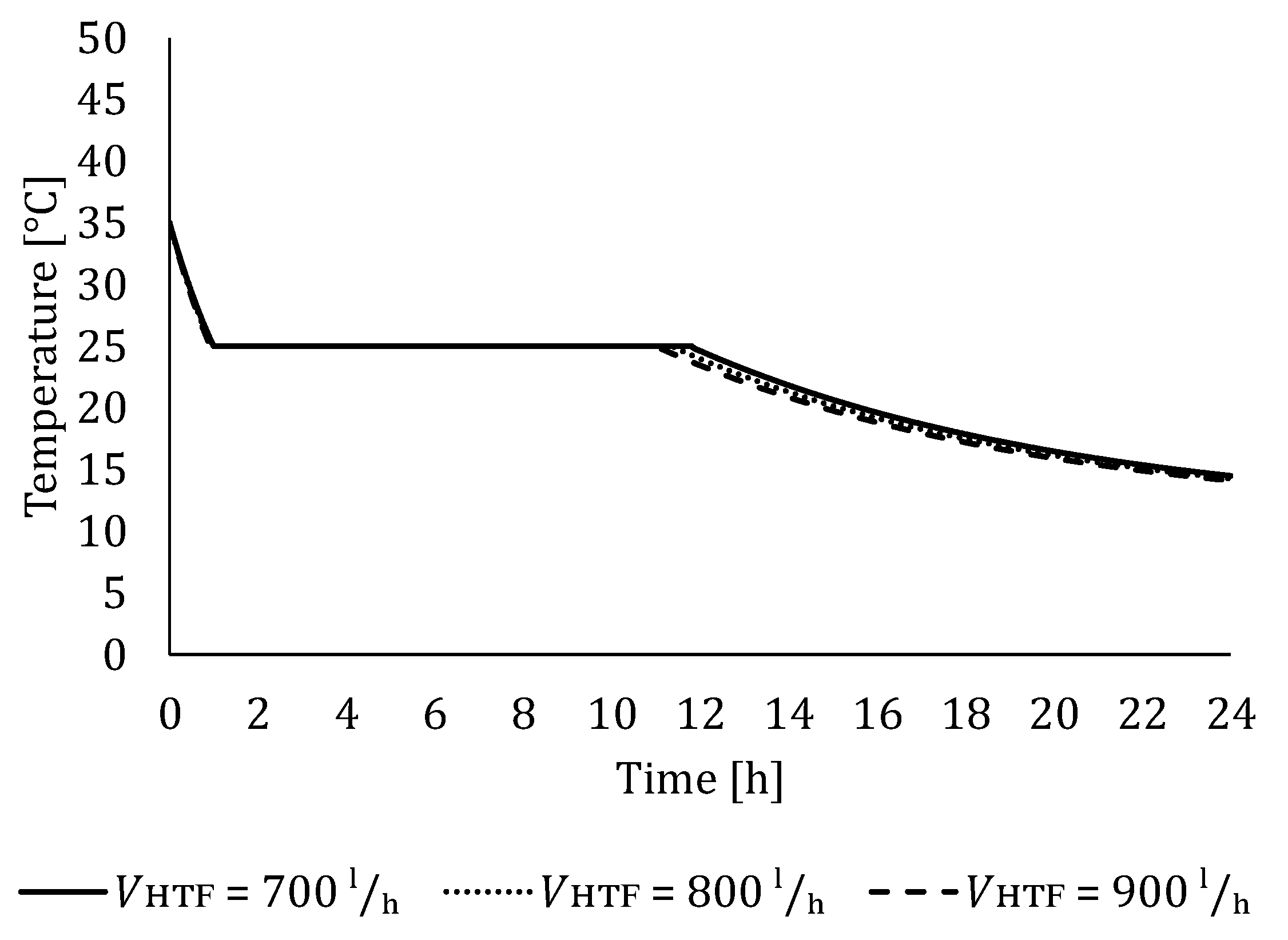
5.2. The Influence of HTF Flow Rate
5.2.1. Influence of HTF Flow Rate on LTES Thermal Performance during Charging
5.2.2. Influence of HTF Flow Rate on LTES Thermal Performance during Discharging
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Af | Fin area in the ith segment (m2) |
| Ahx,i | Heat transfer area between HTF and PCM in the ith segment (m2) |
| AIF | Interface area between neighboring segments (m2) |
| Ain | Inside tube heat transfer area (m2) |
| As,i | Area of the ith segment to environment (m2) |
| a | Thermal diffusivity (m2/s) |
| B | Fin width (m) |
| b | Coefficient (-) |
| C | Coefficient (-) |
| c | Specific heat capacity (J/kgK) |
| D | LTES tank inside diameter (m) |
| di | Tube inside diameter (m) |
| do | Tube outside diameter (m) |
| ft | Fin thickness (m) |
| g | Gravitational acceleration (m/s2) |
| H | Specific enthalpy (J/kg) |
| h | Convective heat transfer coefficient (W/m2K) |
| k | Thermal conductivity coefficient (W/mK) |
| keq | Equivalent thermal conductivity coefficient (W/mK) |
| L | Fin length & LTES tank height (m) |
| l | Latent heat (J/kg) |
| Mass flow of the HTF (kg/s) | |
| mPCM,i | Mass of the PCM in ith segment (kg) |
| n | Coefficient (-) |
| nf | Number of fins per tube (-) |
| nt | Number of tubes (-) |
| Pr | Prandtl number (-) |
| Exchanged heat flux (W) | |
| Thermal losses through the LTES outer wall (W) | |
| R1 | Thermal resistance on the inside of the tubes (K/W) |
| R2 | Thermal resistance through tube wall (K/W) |
| R3 | Thermal resistance on the outside of the tubes (K/W) |
| R4 | Thermal resistance on the fin surface (K/W) |
| Ra | Rayleigh number (-) |
| Re | Reynolds number (-) |
| T | Temperature (K) |
| Tm | Melting temperature (K) |
| t | Time (s) |
| tp | Tube pitch (m) |
| U | Total heat transfer coefficient (W/m2K) |
| uHTF | HTF inlet velocity (m/s) |
| Greek symbols | |
| β | Thermal expansion coefficient (1/K) |
| γ | Liquid fraction (-) |
| ΔTm | Mean logarithmic temperature difference (K) |
| δPCM | Average PCM thickness between two adjacent fins (m) |
| δx | Height of the ith segment (m) |
| ηf | Fin efficiency (-) |
| μ | Dynamic viscosity (Pa s) |
| ν | Kinematic viscosity (m2/s) |
| ρ | Density (kg/m3) |
| Subscripts | |
| env | Environment |
| HTF | Heat transfer fluid |
| i | ith segment |
| in | Inlet |
| liquidus | PCM liquidus temperature |
| loss | Thermal losses to the environment |
| n | Number of LTES segments |
| out | Outlet |
| PCM | Phase change material |
| solidus | PCM solidus temperature |
| t | Tube |
References
- European Commission. EU Energy in Figures—Statistical Pocketbook; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- Osterman, E.; Stritih, U. Review on compression heat pump systems with latent thermal energy storage for heating and cooling of buildings. J. Energy Storage 2021, 39, 102569. [Google Scholar] [CrossRef]
- Pardiñas, A.A.; Justo Alonso, M.; Diz, R.; Husevåg Kvalsvik, K.; Fernández-Seara, J. State-of-the-art for the use of phase-change materials in tanks coupled with heat pumps. Energy Build. 2017, 140, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Kapsalis, V.; Karamanis, D. Solar thermal energy storage and heat pumps with phase change materials. Appl. Therm. Eng. 2016, 99, 1212–1224. [Google Scholar] [CrossRef]
- Comakli, O.; Kaygusuz, K.; Ayhan, T. Solar-assisted heat pump and energy storage for residential heating. Sol. Energy 1993, 51, 357–366. [Google Scholar] [CrossRef]
- Minglu, Q.; Liang, X.; Deng, S.; Yiqiang, J. Improved indoor thermal comfort during defrost with a novel reverse-cycle defrosting method for air source heat pumps. Build. Environ. 2010, 45, 2354–2361. [Google Scholar] [CrossRef]
- Long, J.Y.; Zhu, D.S. Numerical and experimental study on heat pump water heater with PCM for thermal storage. Energy Build. 2008, 40, 666–672. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N. Experimental investigation and improvement in heat transfer of paraffin PCM RT58 storage system to take advantage of low peak tariff rates for heat pump applications. Int. J. Low-Carbon Technol. 2013, 8, 260–270. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Li, J.; Cai, B.; Zhang, F.; Tao, L.; Yang, L.; Zhang, Y.; Zhou, J. Experimental research on a solar air-source heat pump system with phase change energy storage. Energy Build. 2020, 228, 110451. [Google Scholar] [CrossRef]
- Qu, S.; Ma, F.; Ji, R.; Wand, D.; Yang, L. System design and energy performance of a solar heat pump heating system with dual-tank latent heat storage. Energy Build. 2015, 105, 294–301. [Google Scholar] [CrossRef]
- Kelly, N.J.; Tuohy, P.G.; Hawkes, A.D. Performance assessment of tariff-based air source heat pump load shifting in a UK detached dwelling featuring phase change-enhanced buffering. Appl. Therm. Eng. 2014, 71, 809–820. [Google Scholar] [CrossRef] [Green Version]
- da Cunha, J.P.; Eames, P. Compact latent heat storage decarbonization potential for domestic hot water and space heating applications in the UK. Appl. Therm. Eng. 2018, 134, 396–406. [Google Scholar] [CrossRef]
- Lu, J.; Tang, Y.; Li, Z.; He, G. Solar heat pump configuration for water heating system in China. Appl. Therm. Eng. 2021, 187, 116570. [Google Scholar] [CrossRef]
- Han, Z.; Zheng, M.; Kong, F.; Wang, F.; Li, Z.; Bai, T. Numerical simulation of solar assisted ground-source heat pump heating system with latent heat energy storage in severely cold area. Appl. Therm. Eng. 2008, 28, 1427–1436. [Google Scholar] [CrossRef]
- Pyltaria, M.T.; Tzivanidis, C.; Bellos, E.; Antonopoulos, A.A. Energetic investigation of solar assisted heat pump underfloor heating systems with and without phase change materials. Energy Convers. Manag. 2018, 173, 626–639. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Y.; Wang, F.; Song, M.; Ma, Z. Study on performance evaluation of CO2 heat pump system integrated with thermal energy storage for space heating. Energy Procedia 2019, 158, 1380–1389. [Google Scholar] [CrossRef]
- Delač, B.; Pavković, B.; Lenić, K. Design, monitoring and dynamic model development of a solar heating and cooling system. Appl. Therm. Eng. 2018, 142, 489–501. [Google Scholar] [CrossRef]
- Kirincic, M.; Trp, A.; Lenic, K. Influence of natural convection during melting and solidification of paraffin in a longitudinally finned shell-and-tube latent thermal energy storage on the applicability of developed numerical models. Renew. Energy 2021, 179, 1329–1344. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D.R.; Salah, N.B.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 12–130. [Google Scholar] [CrossRef]
- Leonhardt, C.; Müller, D. Modelling of Residential Heating Systems using a Phase Change Material Storage System. In Proceedings of the 7th Modelica Conference, Como, Italy, 20–22 September 2009. [Google Scholar] [CrossRef] [Green Version]
- Feng, G.; Liu, M.; Huang, K.; Qiang, X.; Chang, Q. Development of a math module of shell and tube phase-change energy storage system used in TRNSYS. Energy 2019, 183, 428–436. [Google Scholar] [CrossRef]
- Belmonte, J.F.; Eguia, P.; Molina, A.E.; Almendros-Ibanez, J.A.; Salgado, R. A simplified method for modeling the thermal performance of storage tanks containing PCMs. Appl. Therm. Eng. 2016, 95, 394–410. [Google Scholar] [CrossRef]
- Schranzhofer, H.; Heinz, A. Validation of TRNSYS simulation model for PCM energy storages and PCM wall construction elements. In Proceedings of the Ecostock Conference, Pomona, CA, USA, 31 May–2 June 2006. [Google Scholar]
- Helmns, D.; Blum, D.H.; Dutton, S.M.; Carey, V.P. Development and validation of a latent thermal energy storage model using Modelica. Energies 2021, 14, 194. [Google Scholar] [CrossRef]
- Gowreesunker, B.L.; Tassou, S.A.; Kolokotroni, M. Coupled TRNSYS-CFD simulations evaluating the performance of PCM plate heat exchangers in an airport terminal building displacement conditioning system. Build. Environ. 2013, 65, 132–145. [Google Scholar] [CrossRef] [Green Version]
- Kirincic, M.; Trp, A.; Lenic, K. Numerical evaluation of the latent heat thermal energy storage performance enhancement by installing longitudinal fins. J. Energy Storage 2021, 42, 103085. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.; Ghafoor, A. A review of performance enhancement of PCM based latent heat storage system within the context of materials, thermal stability and compatibility. Energy Convers. Manag. 2016, 115, 132–158. [Google Scholar] [CrossRef]
- Agyenim, F.; Eames, P.; Smyth, M. Heat transfer enhancement in medium temperature thermal energy storage system using a multitube heat transfer array. Renew. Energy 2010, 35, 198–207. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.B.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Experimental study of melting and solidification of PCM on a triplex tube heat exchanger with fins. Energy Build. 2014, 68, 33–41. [Google Scholar] [CrossRef]
- Longeon, M.; Soupart, A.; Fourmigue, J.F.; Bruch, A.; Marty, P. Experimental and numerical study of annular PCM storage in the presence of natural convection. Appl. Energy 2013, 112, 175–184. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P. Numerical and experimental study of heat transfer characteristics of a shell-tube latent heat storage system: Part I—Charging process. Energy 2015, 79, 337–350. [Google Scholar] [CrossRef]
- Zukowski, M. Mathematical modeling and numerical simulation of a short term thermal energy storage system using phase change material for heating applications. Energy Convers. Manag. 2007, 48, 155–165. [Google Scholar] [CrossRef]
- Adine, H.A.; Qarnia, H.E. Numerical analysis of the thermal behavior of a shell-and-tube heat storage unit using phase change materials. Appl. Math. Model. 2009, 33, 2132–2144. [Google Scholar] [CrossRef]
- Voller, V.R.; Cross, M.; Markatos, N.C. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Meth. Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. 1988, 13, 297–318. [Google Scholar] [CrossRef]
- Gil, A.; Peiro, G.; Oro, E.; Cabeza, L.F. Experimental analysis of the effective thermal conductivity enhancement of PCM using finned tubes in high temperature bulk tanks. Appl. Therm. Eng. 2018, 142, 736–744. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.A. An experimental investigation of discharge/solidification cycle of paraffin in novel shell and tube with longitudinal fins based latent heat storage system. Energy Convers. Manag. 2017, 154, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Trp, A. An experimental and numerical investigation of heat transfer during technical grade paraffin melting and solidification in a shell-and-tube latent thermal energy storage unit. Sol. Energy 2005, 79, 648–660. [Google Scholar] [CrossRef]
- Agarwal, A.; Sarviya, R.M. An experimental investigation of shell and tube latent heat storage for solar dryer using paraffin wax as heat storage material. Eng. Sci. Technol. Int. J. 2016, 19, 619–631. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.L.; Gong, Y.; Zhu, X. Air flow and heat transfer in louver-fin round-tube heat exchanger. J. Heat Transf. 2007, 129, 200–210. [Google Scholar] [CrossRef]
- Kroger, D.G. Air-Cooled Heat Exchangers and Cooling Towers; PennWell Corporation: Tulsa, OK, USA, 2004. [Google Scholar]
- Kakac, S.; Shah, R.K.; Aung, W. Handbook of Single-Phase Convective Heat Transfer; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Longman Scientific and Technical: Essex, UK, 1995. [Google Scholar]
- Narayanan, M.; de Lima, A.F.; de Azevedo Dantas, A.F.O.; Commerell, W. Development of a coupled TRNSYS-MATLAB simulation framework for model predictive control of integrated electrical and thermal residential renewable energy system. Energies 2020, 13, 5761. [Google Scholar] [CrossRef]
- Dolado, P.; Lazaro, A.; Marin, J.M.; Zalba, B. Characterization of melting and solidification in a real scale PCM-air heat exchanger: Numerical model and experimental validation. Energy Convers. Manag. 2011, 52, 1890–1907. [Google Scholar] [CrossRef]
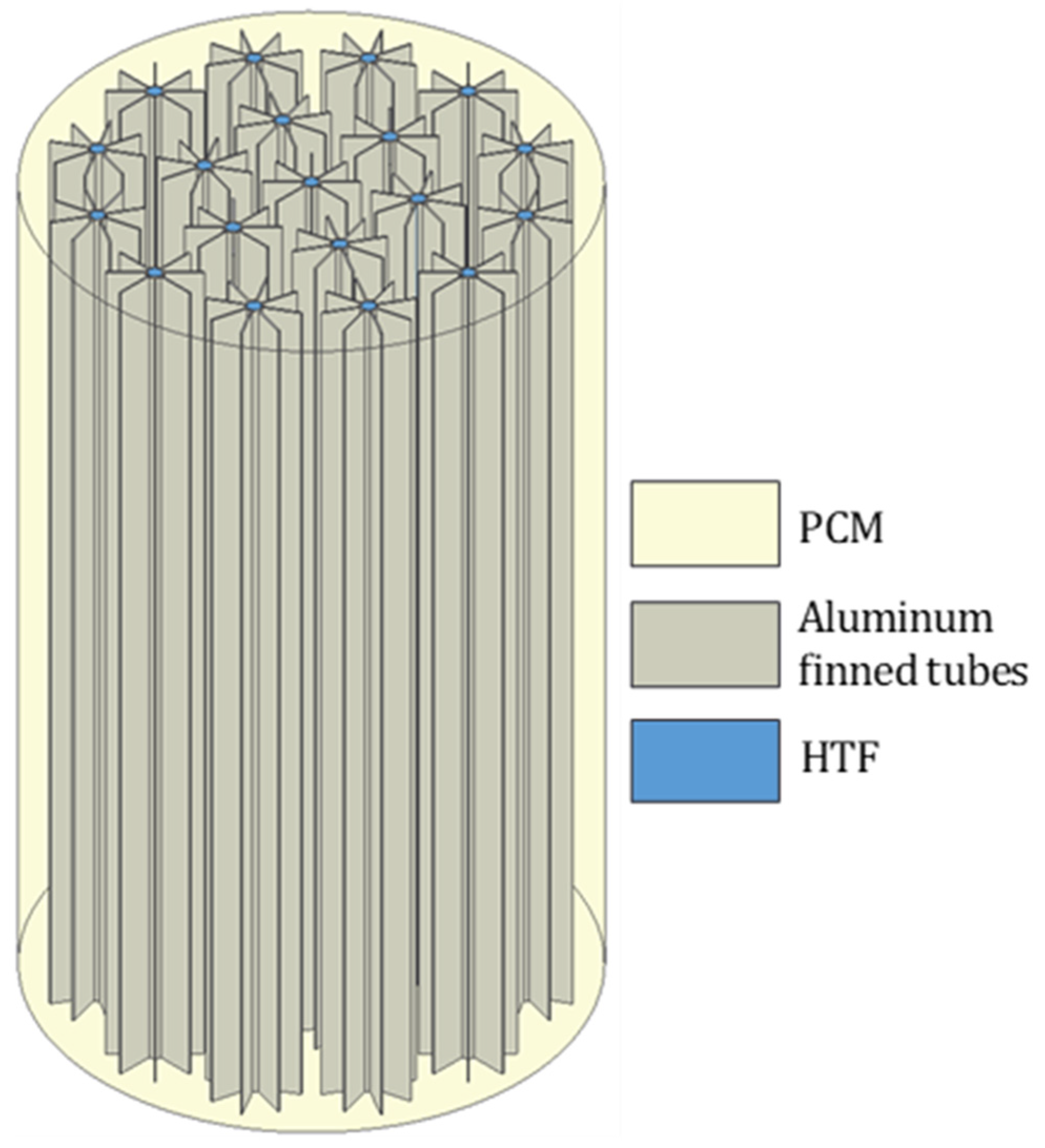
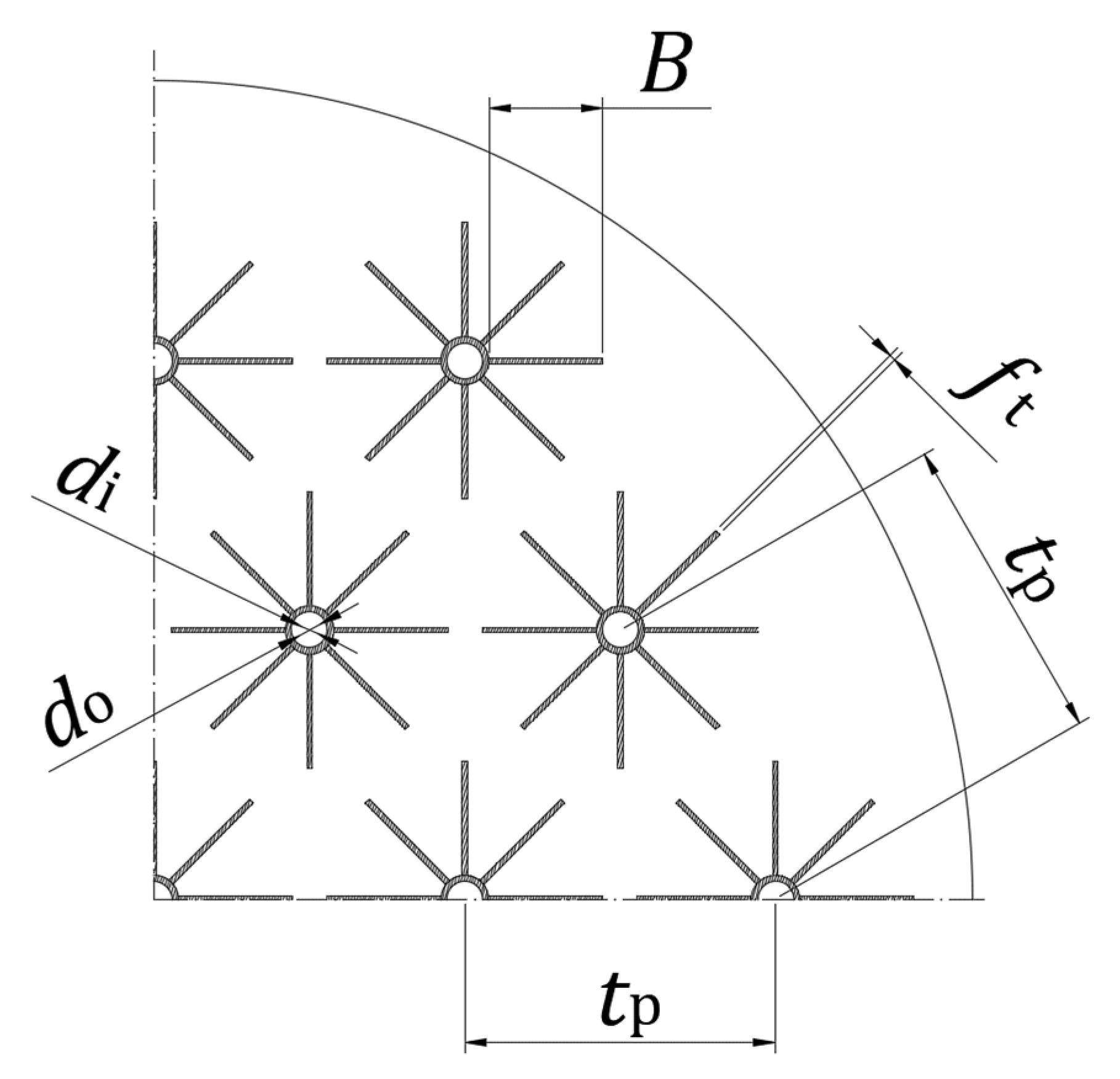
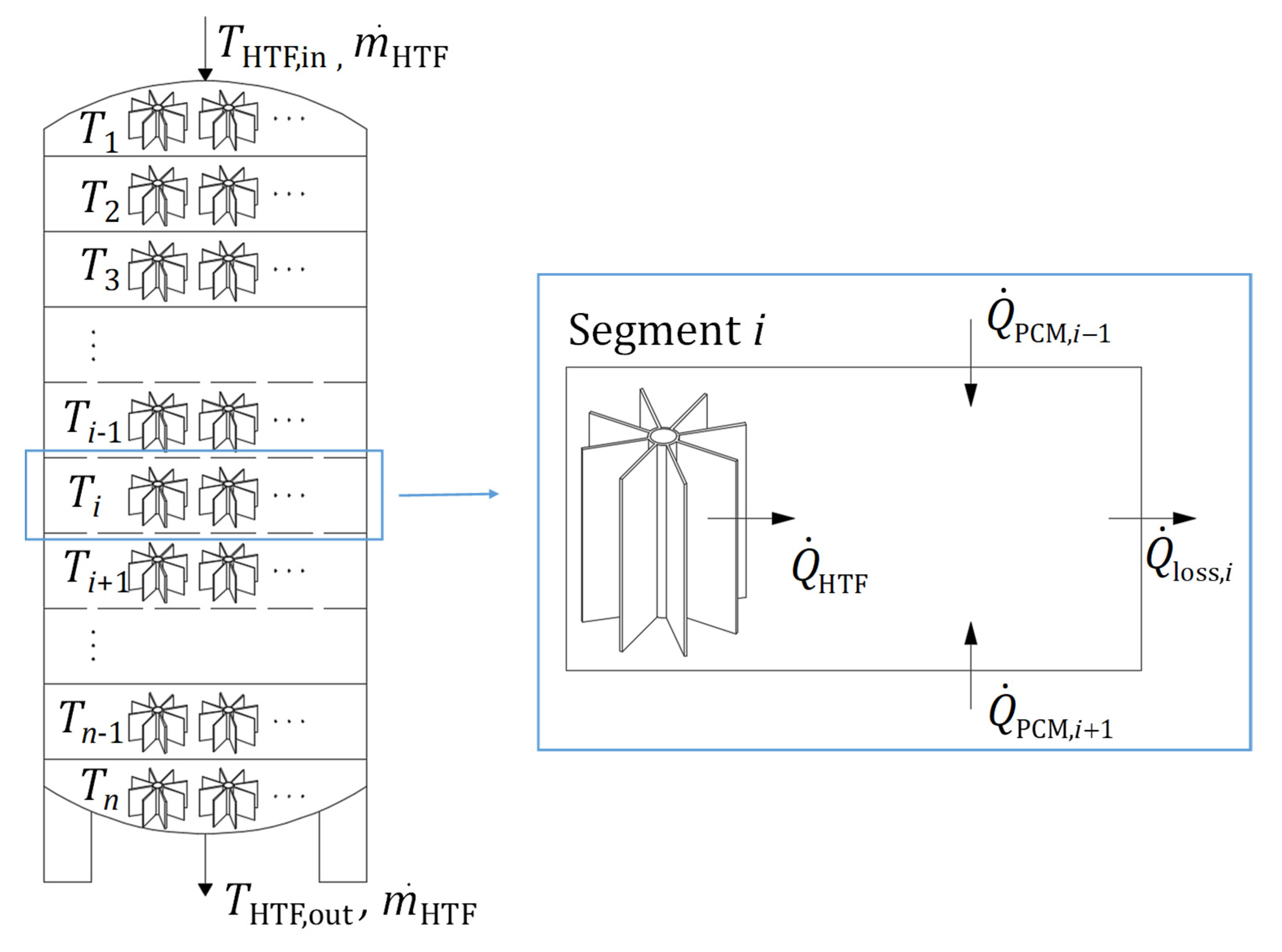
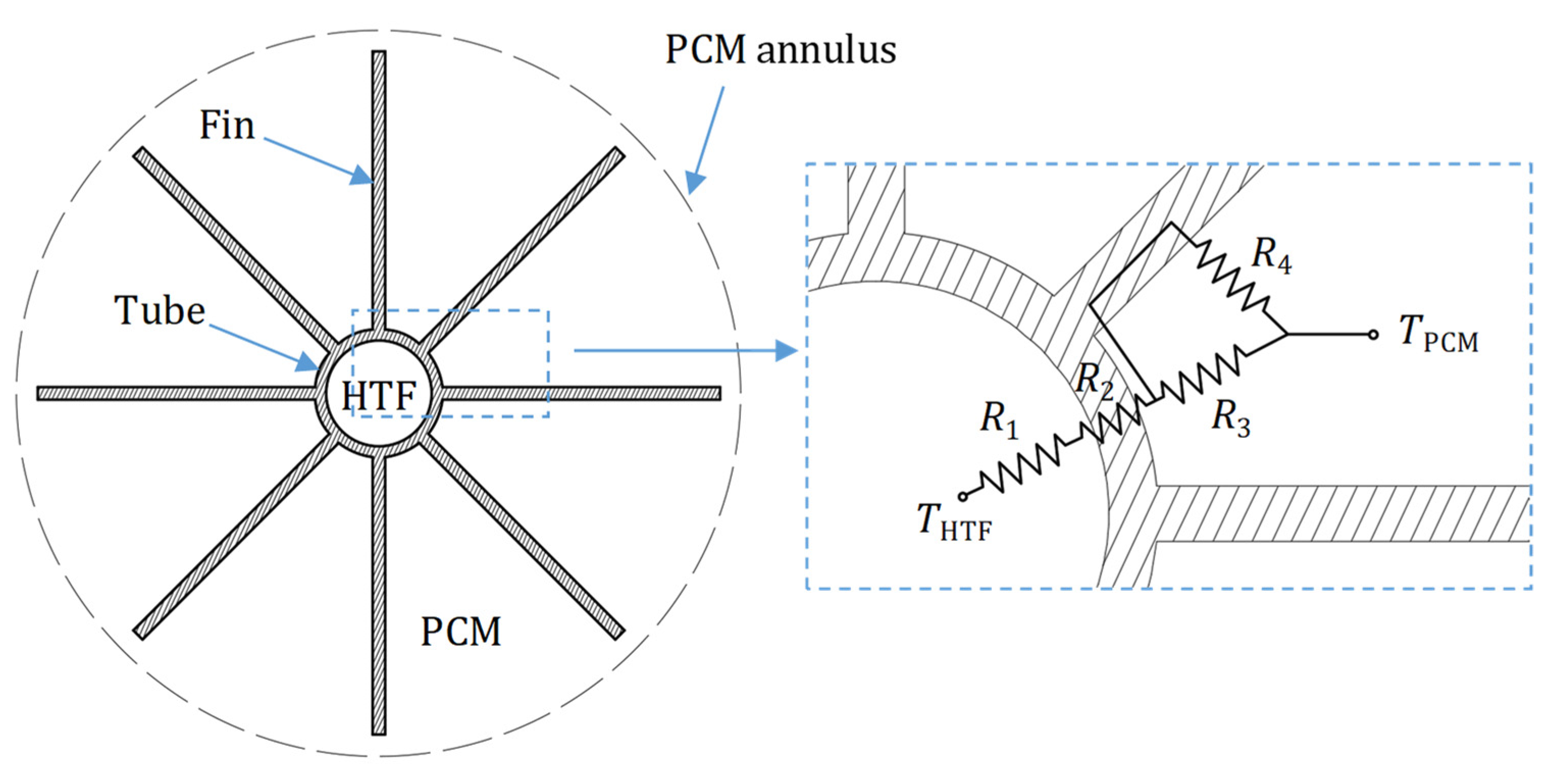









| LTES tank height, L [mm] | 1550 |
| LTES tank diameter, D [mm] | 950 |
| Tubes diameters, do/di [mm] | 30/25 |
| Number of tubes, nt [-] | 19 |
| Number of fins per tube, nf [-] | 8 |
| Fin thickness, ft [mm] | 1 |
| Fin width, B [mm] | 66 |
| Tube pitch, tp [mm] | 180 |
| Properties | PCM | Water | Aluminum | |
|---|---|---|---|---|
| Liquid | Solid | |||
| Density [kg/m3] | 760 | 880 | 998.2 | 2719 |
| Thermal conductivity [W/mK] | 0.2 | 0.6 | 202.4 | |
| Specific heat capacity [J/kgK] | 2000 | 4182 | 871 | |
| Kinematic viscosity of PCM [mm2/s] | 4.7 | 1.005 | - | |
| Latent heat [J/kg] | 170,000 | - | - | |
| Melting | Solidification | - | - | |
| Liquidus temperature [°C] | 25 | 25 | - | - |
| Solidus temperature [°C] | 18 | 25 | - | - |
| Thermal expansion coefficient [1/K] | 0.001 | - | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torbarina, F.; Lenic, K.; Trp, A. Computational Model of Shell and Finned Tube Latent Thermal Energy Storage Developed as a New TRNSYS Type. Energies 2022, 15, 2434. https://doi.org/10.3390/en15072434
Torbarina F, Lenic K, Trp A. Computational Model of Shell and Finned Tube Latent Thermal Energy Storage Developed as a New TRNSYS Type. Energies. 2022; 15(7):2434. https://doi.org/10.3390/en15072434
Chicago/Turabian StyleTorbarina, Fran, Kristian Lenic, and Anica Trp. 2022. "Computational Model of Shell and Finned Tube Latent Thermal Energy Storage Developed as a New TRNSYS Type" Energies 15, no. 7: 2434. https://doi.org/10.3390/en15072434
APA StyleTorbarina, F., Lenic, K., & Trp, A. (2022). Computational Model of Shell and Finned Tube Latent Thermal Energy Storage Developed as a New TRNSYS Type. Energies, 15(7), 2434. https://doi.org/10.3390/en15072434






