Optimal Allocation of Distributed Generators in Active Distribution Networks Using a New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm
Abstract
:1. Introduction
- An in-depth review of the optimal allocation of the distributed generator (OADG) methods in active distribution networks, picking out the need for a new hybrid metaheuristic method to solve the problem.
- A new Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm (O-SCMDEA) is proposed in this paper for solving the OADG problem.
- The OADG problem is formulized with three separate mono-objectives (real power loss minimization, voltage deviation minimization and maximization of the voltage stability index) and a multi-objective framework combining the above three for DGs in two different modes (unity power factor and constant lagging power factor) of the operation.
- One small (33 bus) and two bigger (118 bus and 136 bus) test systems are considered for results validation and for comparison with recent state-of-the-art metaheuristic approaches for solving the OADG problem.
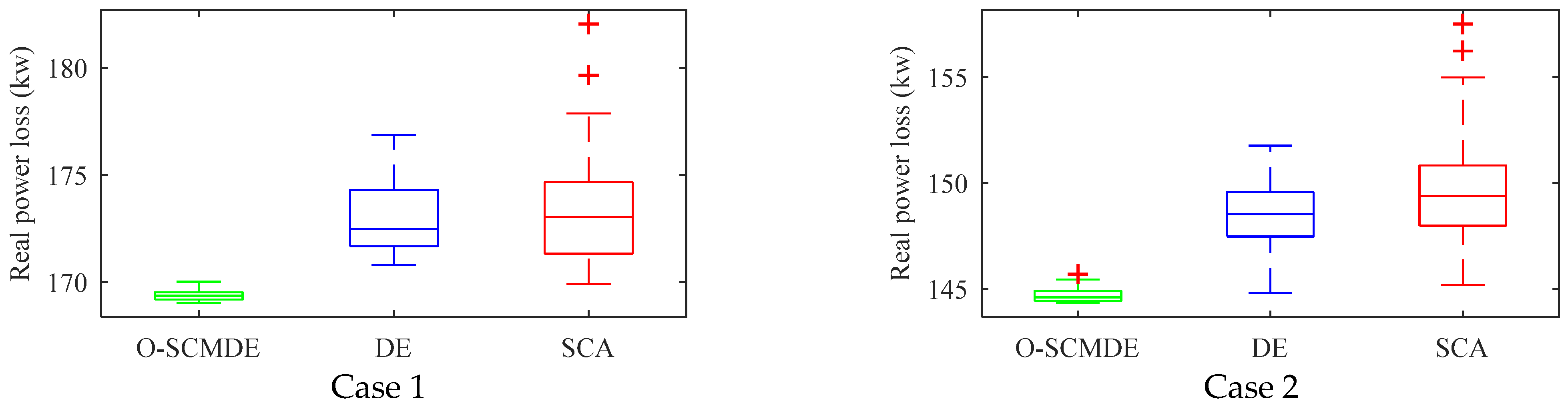
- A statistical analysis of the results is presented to establish the robustness of the proposed algorithm and genuineness of the obtained results, which includes box plots for all the test systems, Shapiro–Wilk tests and Kolmogorov–Smirnov tests for normality check of the results and Friedman–ANOVA and Wilcoxon signed-rank tests for the post hoc analysis.
2. Opposition Based Sine Cosine Muted Differential Evolution Algorithm
2.1. Initialization
2.2. SCA Based Mutation
2.3. Crossover
2.4. Selection
2.5. Oppositional Learning
| Algorithm 1 Pseudo-code for replacing weaker individuals with their opposite population | |
| % Xp: Population | |
| % OXp: Opposite population | |
| % fitness: fitness of the population (f(Xp)) | |
| % favg: Average fitness of the population | |
| 1. | |
| 2. | for i = 1: NP |
| 3. | if fitness(i) > favg |
| 4. | Generate OXp(i) using Equation (7) |
| 5. | Replace Xp(i) with OXp(i) |
| 6. | Replace f(Xp(i)) with f(OXp(i)) |
| 7. | end if |
| 8. | end for |
| Algorithm 2 Pseudo code of O-SCMDE Algorithm | |
| 1. | Initialize the parameters of the O-SCMDEA (NP, D, G and CR) |
| 2. | Generate the initial population Xp (randomly) using Equation (19) |
| 3. | Evaluate the fitness (fitness) of the initial population Xp |
| 4. | Replace the weaker individuals by their respective opposite population using Algorithm 1 |
| 5. | Shortlist the best individual of the population, Xbest |
| 6. | Initialize the iteration counter k = 0. |
| 7. | while k < G |
| 8. | for i = 1: NP |
| 9. | Perform mutation operation using Equation (3) |
| 10. | Perform crossover operation using Equation (5) |
| 11. | Reinitialize the individual using Equation (2) in case limit violation |
| 12. | Perform selection operation using Equation (6) |
| 13. | Compute the fitness of updated individual |
| 14. | Replace the weaker individuals by their respective opposite population using Algorithm 1 |
| 15. | Update the best individual, |
| 16. | end for |
| 17. | Increment iteration counter, k = k + 1 |
| 18. | end while |
| 19. | Output the best individual, Xbest |
3. Optimal DG Allocation Problem Formulation
3.1. Mono Objective Formulation
3.1.1. Real Power Loss
3.1.2. Voltage Deviation
3.1.3. Voltage Stability Index
3.2. Multi-Objective Formulation
3.2.1. Index for Real Power Loss Minimization (IRPL)
3.2.2. Index for Voltage Deviation Minimization (IVD)
3.2.3. Index for Inverse Voltage Stability Index Minimization (IIVSI)
3.2.4. Multi-Objective Function (MOF)
3.3. Constraints
- Bus Voltage Constraint:
- Branch Flow Constraint:
- DG Position Constraint:
- DG Capacity Constraints:
4. Implementation of O-SCMDEA for Optimal DG Allocation
- Scenario I: Real Power Loss Minimization as defined in Equation (8).
- Scenario II: Voltage Deviation Minimization as defined in Equation (10).
- Scenario III: Reciprocation of the Minimum Voltage Stability Index Minimization as defined in Equation (12).
- Scenario IV: Multi-objective function (MOF) as defined in Equation (17).
- Step 1:
- Read the distribution system data. Initialize the control parameters of O-SCMDEA (NP, G and CR).
- Step 2:
- Using Equation (22), randomly generate the initial target vectors, Xp, that contain the possible size and location of the DGs.
- Step 3:
- Evaluate the objective function (as per the respective scenarios) using the appropriate Equations (8), (10), (12) and (17). To calculate the objective function, a forward–backward sweep load flow, as used in Reference [50], was used.
- Step 4:
- Replace the weaker individuals of the population by their opposite population using Equation (7) and update the best individual. For the minimization problem, the individual whose fitness value is higher than the average fitness of the population is considered weak.
- Step 5:
- Set the generation counter as k = 1.
- Step 6:
- Perform the mutation and crossover operations using Equations (3) and (5), respectively.
- Step 7:
- Check the limits of the decision variables and, in the case of a violation of the limits, reinitialize the corresponding population using Equation (2).
- Step 8:
- Perform the selection operation using Equation (6).
- Step 9:
- Replace the weaker individuals of the population by their opposite population using Equation (7).
- Step 10:
- If the maximum generation is reached, then go to Step 11; otherwise, increment the iteration counter k = k + 1 and go to Step 6.
- Step 11:
- Display the optimal size and location of the DGs.
5. Results and Discussion
5.1. Test System 1 (33 Bus)
5.1.1. Scenario I
5.1.2. Scenario II
5.1.3. Scenario III
5.1.4. Scenario IV
5.2. Test System 2 (118 Bus)
5.2.1. Scenario I
5.2.2. Scenario II
5.2.3. Scenario III
5.2.4. Scenario IV
5.3. Test System 3 (136 Bus)
5.3.1. Scenario I
5.3.2. Scenario II
5.3.3. Scenario III
5.3.4. Scenario IV
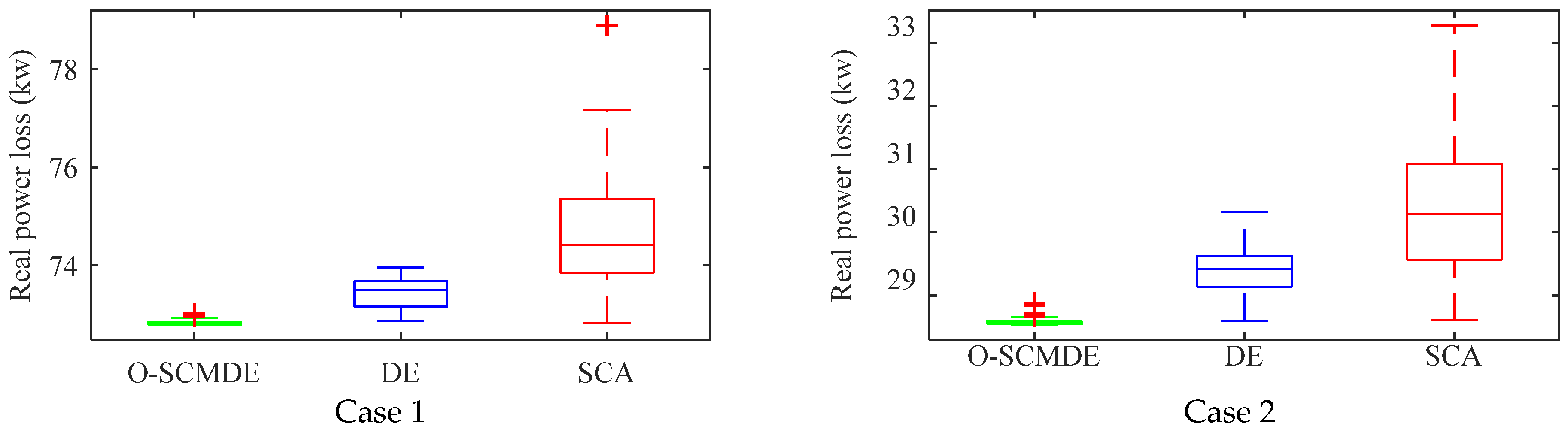
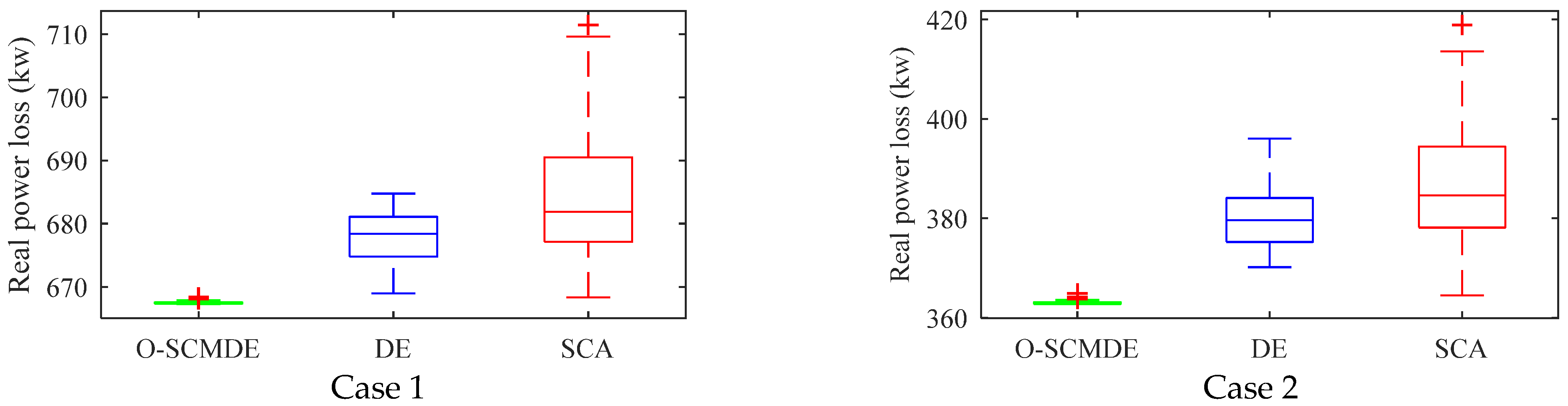
5.4. Statistical Analysis
5.5. Solution Quality
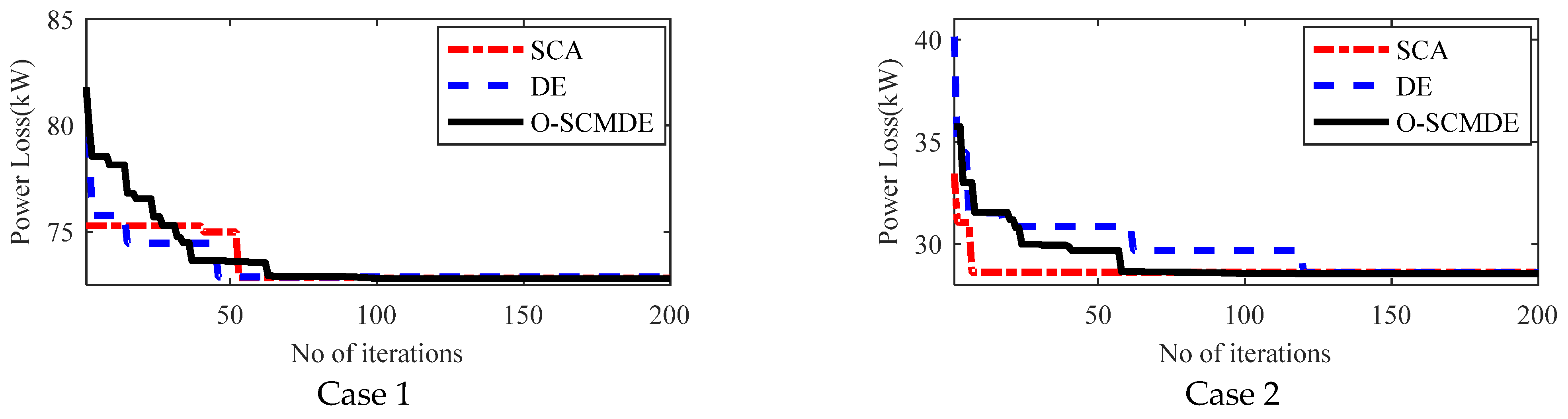
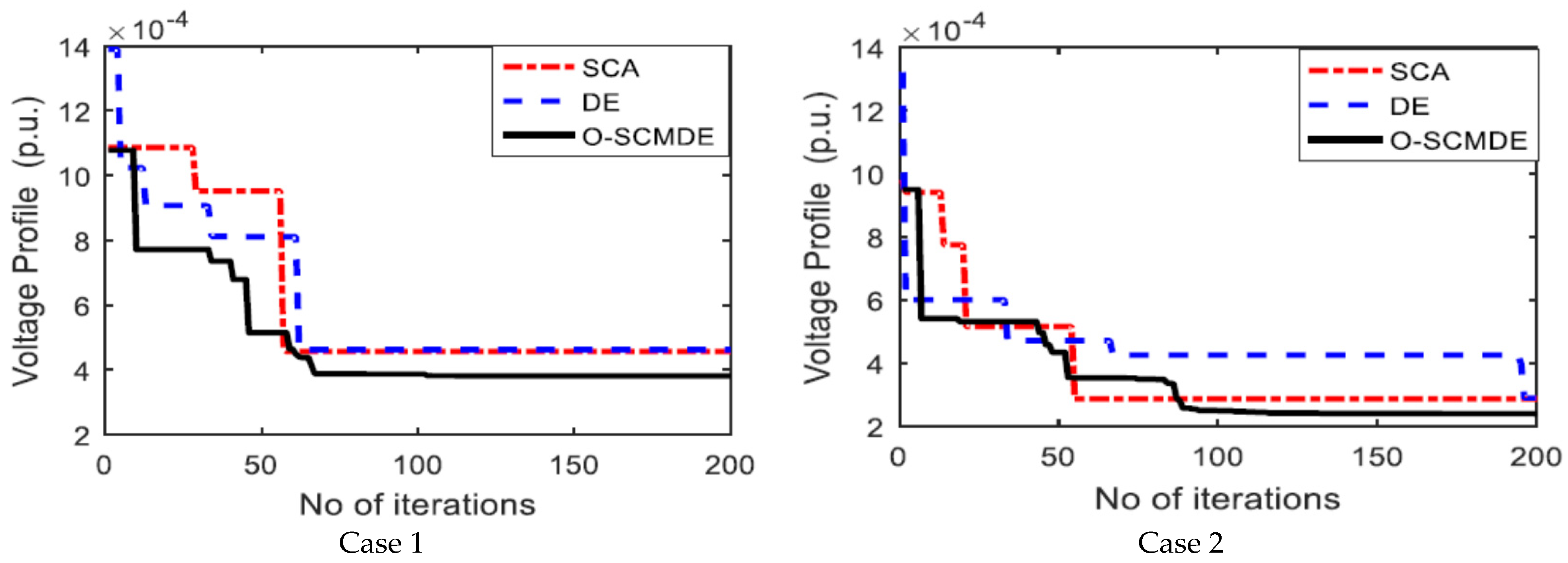
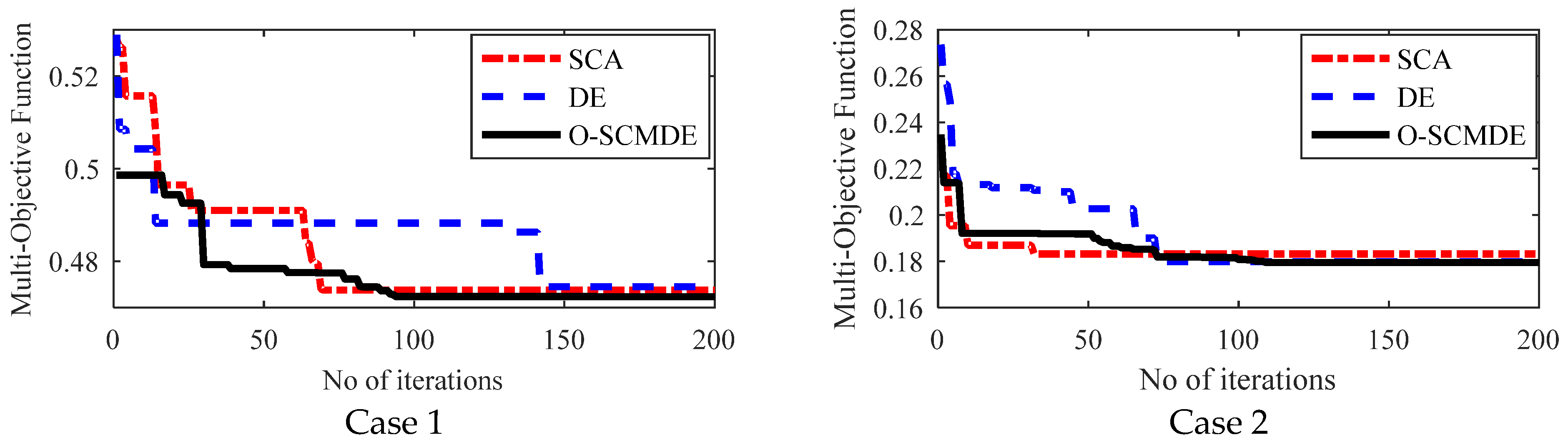
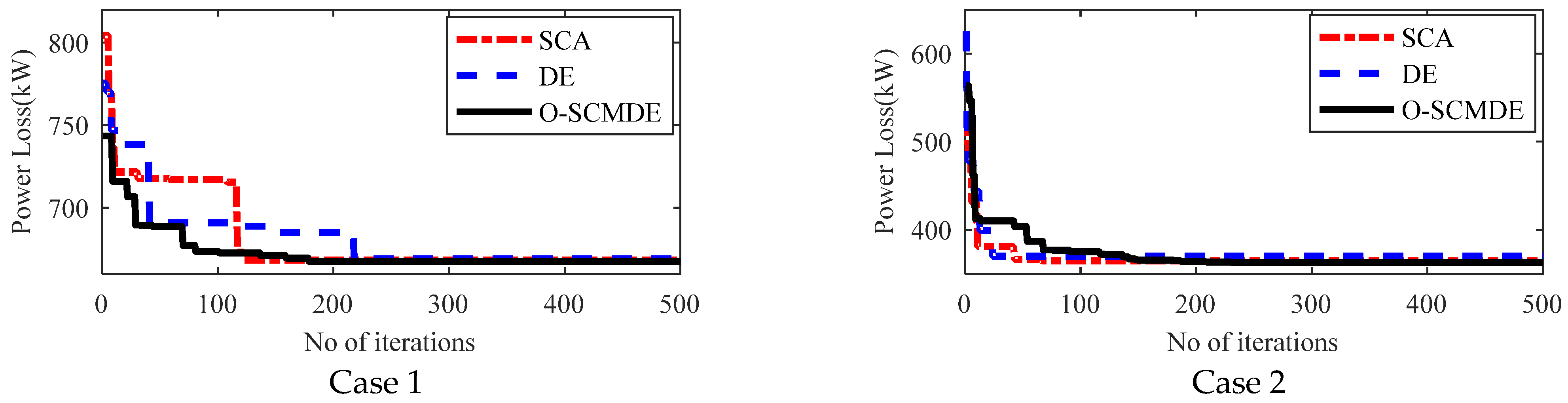
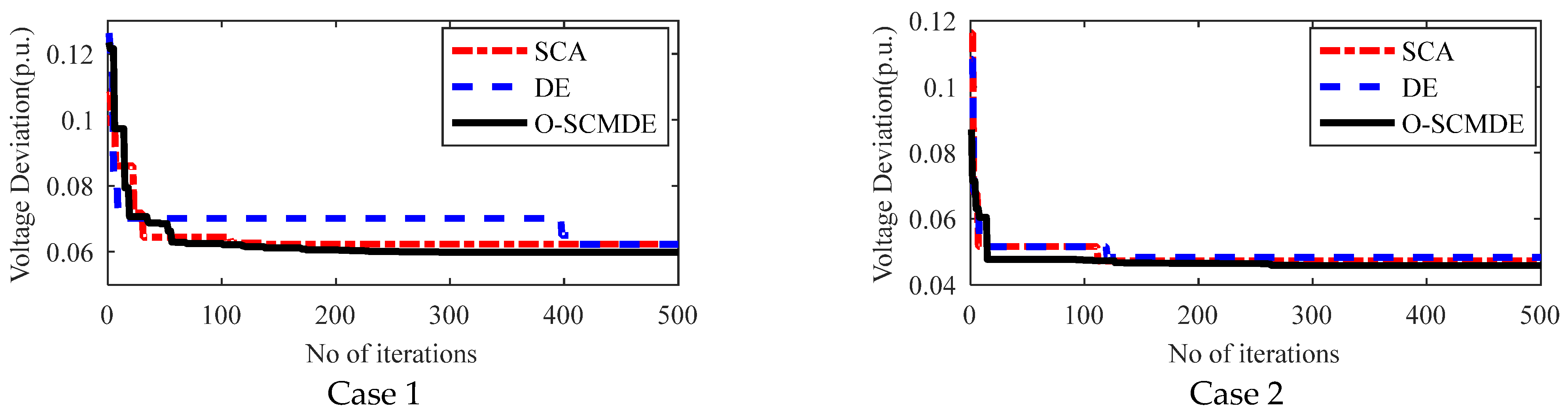
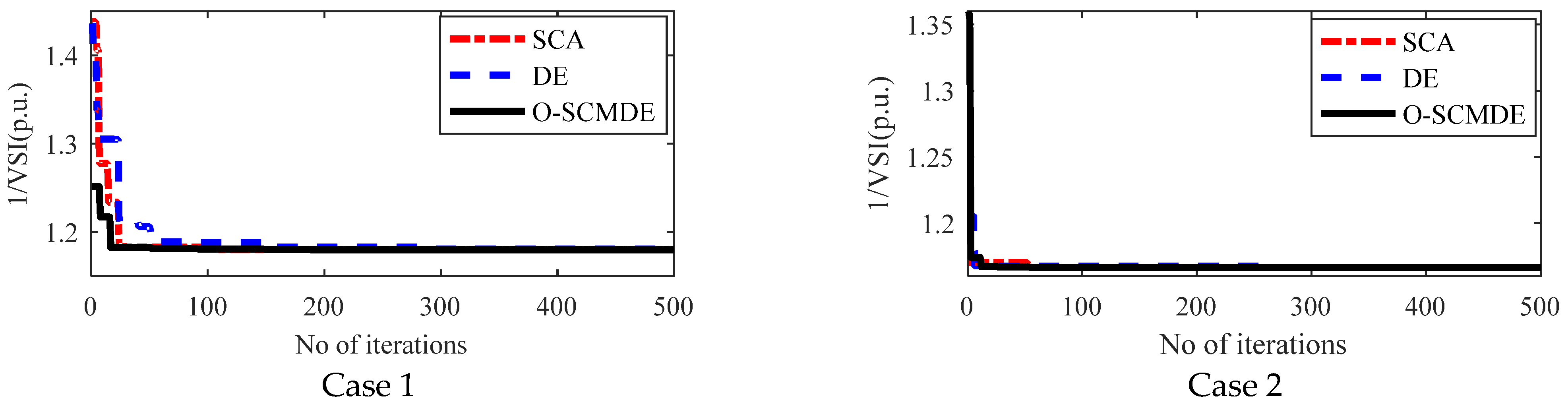
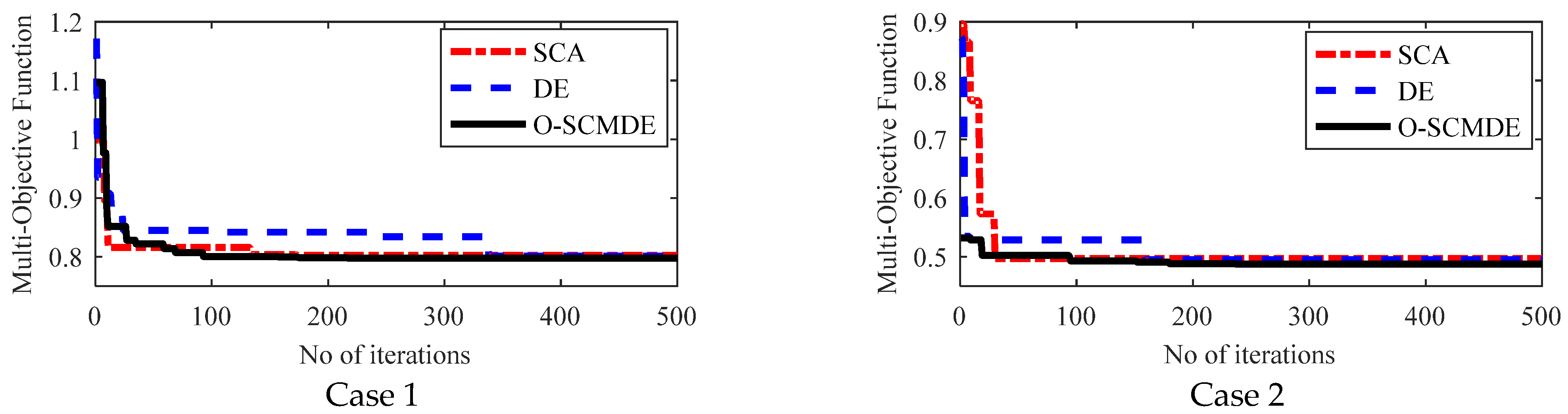
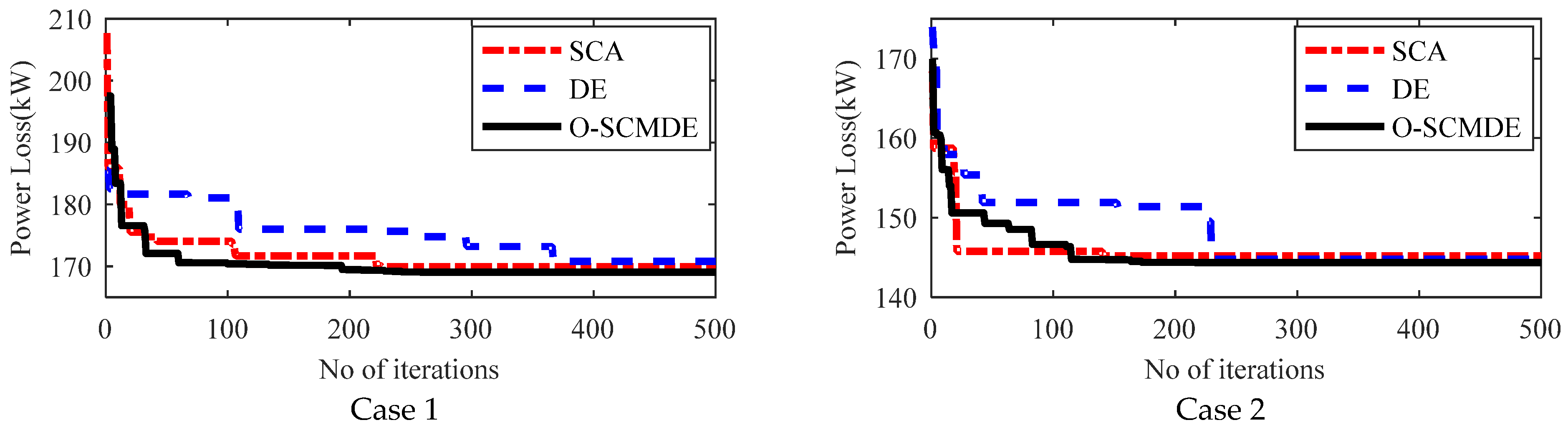
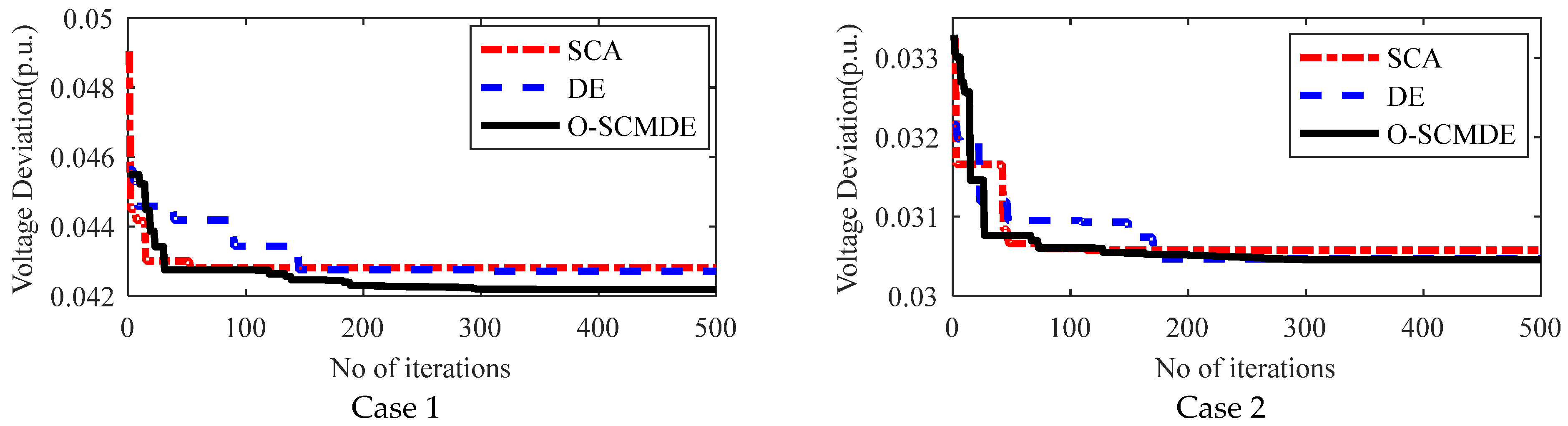
5.6. Convergence Charecteristics
5.7. Computational Time
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Willis, H.L. Analytical methods and rules of thumb for modeling DG-distribution interaction. In Proceedings of the IEEE PES Summer Meeting, Seattle, WA, USA, 16–20 July 2000; pp. 1643–1644. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M. Analytical approaches for optimal placement of distributed generation sources in power systems. IEEE Trans. Power Syst. 2004, 19, 2068–2076. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Analytical Expressions for DG Allocation in Primary Distribution Networks. IEEE Trans. Energy Convers. 2010, 25, 814–820. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Bakar, A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulanathan, N. Multiple Distributed Generator Placement in Primary Distribution Network for Loss Reduction. IEEE Trans. Ind. Electron. 2013, 60, 1700–1708. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, S.; Chanda, C.K. An analytical approach for allocation and sizing of distributed generations in radial distribution network. Int. Trans. Electr. Energy Syst. 2017, 27, e2322. [Google Scholar] [CrossRef]
- Mahmoud, K.; Yorino, N.; Ahmed, A. Optimal Distributed Generation Allocation in Distribution Systems for Loss Minimization. IEEE Trans. Power Syst. 2016, 31, 960–969. [Google Scholar] [CrossRef]
- Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. The Optimal Placement and Sizing of Distributed Generation in an Active Distribution Network with Several Soft Open Points. Energies 2021, 14, 1084. [Google Scholar] [CrossRef]
- Diaaeldin, I.; Aleem, S.A.; El-Rafei, A.; Abdelaziz, A.; Zobaa, A.F. Optimal Network Reconfiguration in Active Distribution Networks with Soft Open Points and Distributed Generation. Energies 2019, 12, 4172. [Google Scholar] [CrossRef] [Green Version]
- Sultana, S.; Roy, P. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Hegazy, Y.G.; El-Khattam, W.; Othman, M.M. Optimal Planning of Distributed Generators in Distribution Networks Using Modified Firefly Method. Electr. Power Compon. Syst. 2015, 43, 320–333. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Krill herd algorithm for optimal location of distributed generator in radial distribution system. Appl. Soft Comput. J. 2016, 40, 391–404. [Google Scholar] [CrossRef]
- Saha, S.; Mukherjee, V. Optimal placement and sizing of DGs in RDS using chaos embedded SOS algorithm. IET Gener. Transm. Distrib. 2016, 10, 3671–3680. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Quasi-Oppositional Swine Influenza Model Based Optimization with Quarantine for optimal allocation of DG in radial distribution network. Int. J. Electr. Power Energy Syst. 2016, 74, 348–373. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Vo, D.N. A novel stochastic fractal search algorithm for optimal allocation of distributed generators in radial distribution systems. Appl. Soft Comput. 2018, 70, 773–796. [Google Scholar] [CrossRef]
- Jayasree, M.S.; Sreejaya, P.; Bindu, G.R. Multi-Objective Metaheuristic Algorithm for Optimal Distributed Generator Placement and Profit Analysis. Technol. Econ. Smart Grids Sustain. Energy 2019, 4, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Nematshahi, S.; Rajabi Mashhadi, H. Application of Distribution Locational Marginal Price in optimal simultaneous distributed generation placement and sizing in electricity distribution networks. Int. Trans. Electr. Energy Syst. 2019, 29, e2837. [Google Scholar] [CrossRef]
- Kumar, S.; Mandal, K.; Chakraborty, N. A novel opposition-based tuned-chaotic differential evolution technique for techno-economic analysis by optimal placement of distributed generation. Eng. Optim. 2019, 52, 303–324. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Elamvazuthi, I.; Vo, D.N. An improved meta-heuristic method to maximize the penetration of distributed generation in radial distribution networks. Neural Comput. Appl. 2020, 32, 10159–10181. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Elamvazuthi, I.; Vo, D.N. A Quasi-Oppositional-Chaotic Symbiotic Organisms Search algorithm for optimal allocation of DG in radial distribution networks. Appl. Soft Comput. 2020, 88, 106067. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F. Efficient optimization technique for multiple DG allocation in distribution networks. Appl. Soft Comput. 2020, 86, 105938. [Google Scholar] [CrossRef]
- Hemeida, M.G.; Ibrahim, A.A.; Mohamed, A.A.A.; Alkhalaf, S.; El-Dine, A.M.B. Optimal allocation of distributed generators DG based manta ray based optimization algorithm. Ain Shams Eng. J. 2021, 12, 609–619. [Google Scholar] [CrossRef]
- Kawambwa, S.; Hamisi, N.; Mafole, P.; Kundaeli, H. A cloud model based symbiotic organism search algorithm for DG allocation in radial distribution network. Evol. Intell. 2021, 15, 545–562. [Google Scholar] [CrossRef]
- Dash, S.K.; Mishra, S.; Pati, L.R.; Satpathy, P.K. Optimal Allocation of Distributed Generators Using Metaheuristic Algorithms—An Up-to-Date Bibliographic Review. In Green Technology for Smart City and Society; Lecture Notes in Networks and Systems; Sharma, R., Mishra, M., Nayak, J., Naik, B., Pelusi, D., Eds.; Springer: Singapore, 2020; Volume 151, pp. 553–561. [Google Scholar]
- Prabha, D.R.; Jayabarathi, T. Optimal placement and sizing of multiple distributed generating units in distribution networks by invasive weed optimization algorithm. Ain Shams Eng. J. 2016, 7, 683–694. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.H.; Mehanna, M.; Othman, E. Optimal planning of RDGs in electrical distribution networks using hybrid SAPSO algorithm. Int. J. Electr. Comput. Eng. IJECE 2020, 10, 6153–6163. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F. Voltage stability analysis based on optimal placement of multiple DG types using hybrid optimization technique. Int. Trans. Electr. Energy Syst. 2020, 30, e12551. [Google Scholar] [CrossRef]
- Kansal, S.; Kumar, V.; Tyagi, B. Hybrid approach for optimal placement of multiple DGs of multiple types in distribution networks. Int. J. Electr. Power Energy Syst. 2016, 75, 226–235. [Google Scholar] [CrossRef]
- Moradi, M.; Abedini, M. A novel method for optimal DG units capacity and location in Microgrids. Int. J. Electr. Power Energy Syst. 2016, 75, 236–244. [Google Scholar] [CrossRef]
- Suresh, M.; Edward, J.B. A hybrid algorithm based optimal placement of DG units for loss reduction in the distribution system. Appl. Soft Comput. 2020, 91, 106191. [Google Scholar] [CrossRef]
- Tolba, M.A.; Rezk, H.; Tulsky, V.; Diab, A.A.Z.; Abdelaziz, A.Y.; Vanin, A. Impact of Optimum Allocation of Renewable Distributed Generations on Distribution Networks Based on Different Optimization Algorithms. Energies 2018, 11, 245. [Google Scholar] [CrossRef] [Green Version]
- Hassan, A.S.; Sun, Y.; Wang, Z. Multi-objective for optimal placement and sizing DG units in reducing loss of power and enhancing voltage profile using BPSO-SLFA. Energy Rep. 2020, 6, 1581–1589. [Google Scholar] [CrossRef]
- Radosavljevic, J.; Arsic, N.; Milovanovic, M.; Ktena, A. Optimal Placement and Sizing of Renewable Distributed Generation Using Hybrid Metaheuristic Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 499–510. [Google Scholar] [CrossRef]
- Pesaran, M.H.A.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Seyedi, H. A hybrid genetic particle swarm optimization for distributed generation allocation in power distribution networks. Energy 2020, 209, 118218. [Google Scholar] [CrossRef]
- Samala, R.K.; Kotapuri, M.R. Optimal allocation of distributed generations using hybrid technique with fuzzy logic controller radial distribution system. SN Appl. Sci. 2020, 2, 191. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Raut, U.; Mishra, S. A new Pareto multi-objective sine cosine algorithm for performance enhancement of radial distribution network by optimal allocation of distributed generators. Evol. Intell. 2020, 14, 1635–1656. [Google Scholar] [CrossRef]
- Qin, K.; Huang, V.L.; Suganthan, P. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Mirjalili, S.Z.; Saremi, S.; Mirjalili, S. Sine Cosine Algorithm: Theory, Literature Review, and Application in Designing Bend Photonic Crystal Waveguides. Nat. Inspired Optim. 2019, 811, 201–217. [Google Scholar]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Nenavath, H.; Jatoth, R.K. Hybridizing sine cosine algorithm with differential evolution for global optimization and object tracking. Appl. Soft Comput. 2018, 62, 1019–1043. [Google Scholar] [CrossRef]
- Li, Q.; Ning, H.; Gong, J.; Li, X.; Dai, B. A Hybrid Greedy Sine Cosine Algorithm with Differential Evolution for Global Optimization and Cylindricity Error Evaluation. Appl. Artif. Intell. 2020, 35, 171–191. [Google Scholar] [CrossRef]
- Kumar, S.; Mandal, K.; Chakraborty, N. Optimal DG placement by multi-objective opposition based chaotic differential evolution for techno-economic analysis. Appl. Soft Comput. 2019, 78, 70–83. [Google Scholar] [CrossRef]
- Nagaballi, S.; Kale, V.S. Pareto optimality and game theory approach for optimal deployment of DG in radial distribution system to improve techno-economic benefits. Appl. Soft Comput. 2020, 92, 106234. [Google Scholar] [CrossRef]
- Saha, S.; Mukherjee, V. A novel multi-objective chaotic symbiotic organisms search algorithm to solve optimal DG allocation problem in radial distribution system. Int. Trans. Electr. Energy Syst. 2019, 29, e2839. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A comprehensive review on power distribution network reconfiguration. Energy Syst. 2017, 8, 227–284. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.; Salama, M.M. Opposition versus randomness in soft computing techniques. Appl. Soft Comput. 2008, 8, 906–918. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A simple algorithm for distribution system load flow with distributed generation. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar]
- Latreche, Y.; Mokhlis, H. Optimal Multi-DG Units Incorporation in Distribution Systems using Single and Multi-Objective Approaches based on Water Cycle Algorithm. J. Electr. Syst. 2020, 16, 530–549. [Google Scholar]
- Tran, T.T.; Truong, K.H.; Vo, D.N. Stochastic fractal search algorithm for reconfiguration of distribution networks with distributed generations. Ain Shams Eng. J. 2020, 11, 389–407. [Google Scholar] [CrossRef]
- Othman, M.M.; Hegazy, Y.; Abdelaziz, A. Electrical energy management in unbalanced distribution networks using virtual power plant concept. Electr. Power Syst. Res. 2017, 145, 157–165. [Google Scholar] [CrossRef]
- Shaheen, A.; Elsayed, A.; El-Sehiemy, R.A.; Abdelaziz, A.Y. Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Appl. Soft Comput. 2021, 98, 106867. [Google Scholar] [CrossRef]





| Publication Year [Ref.] | OADG Solution Strategy | Objective Function | Test System | Review Remarks |
|---|---|---|---|---|
| 2014 [11] | QOTLBO | PL, VSI, VD | 33b, 69, 118 | Considers only UPF DGs, a suboptimal solution. Does not consider bigger test systems. |
| 2016 [13] | KHA | PL, VSI | 33b, 69, 118 | Complicated to adapt and has more (five) tuning parameters. |
| 2016 [14] | CSOS | PL, VSI, VD | 33b, 69, 118 | Considers only UPF DGs. |
| 2016 [15] | QOSIMO-Q | PL, VSI, VD | 33b, 69 | Tested on small- and medium-scale networks, and the algorithm requires more (eight) tuning parameters. |
| 2018 [16] | SFSA | PL, VSI, VD | 33b, 69, 118 | Gives suboptimal results. |
| 2019 [17] | FPA | PL, MLI | 33b, 69, 301 Kerala State Electricity Board | Considers two DGs for allocations and each having a maximum capacity of 5 MVA. |
| 2019 [18] | GA | DLMP | 33 | Applied to one small-scale test system only. |
| 2019 [19] | OTCDEA | CI, VDI, LFCI | 33b, 69, 118 | Proposed algorithm takes large iterations to converge. |
| 2020 [20] | QOCSOS | PL | 33b, 69, 118 | Only power loss is considered as the objective function for OADG. |
| 2020 [21] | QOCSOSA | PL, VSI, VD | 33b, 69, 118 | Employs five tuning parameters, and the computational time is comparatively higher. |
| 2020 [22] | CSCA | PL, VSI, VD | 33a, 69 | Larger test systems are not considered. |
| 2021 [23] | MRFO | PL | 33b, 69, 85 | Considers a mono-objective for OADG. |
| 2021 [24] | CMSOS | PL, VSI, VD | 33b, 69 | Gives suboptimal solutions. Larger test systems are not considered. |
| 2016 [26] | LSF (L), IWO (S) | PL, OC, VD | 33a, 69 | Bigger test systems are not considered. Gives suboptimal results. |
| 2020 [27] | LSF, SAPSO | PL | 33b | Considers a single objective and applied to a small-scale test system only. |
| 2020 [28] | ATGA | PL, VSI | 33b, 69, 94 Portuguese system | Gives suboptimal results. |
| 2016 [29] | PSO (L), IAM (S) | PL | 33b, 69 | Bigger test systems are not considered. Gives suboptimal results. OADG is solved for mono-objective functions. |
| 2016 [30] | GA-IWA | PL, VSI, VD | 33b, 69 | Bigger test systems are not considered. Gives suboptimal results. |
| 2020 [31] | GCSA | PL, VD, OC | 33b, 69 | Allocates single DG only. Bigger test systems are also not considered. |
| 2020 [34] | PPSOGSA | AEL, Profit | 69 | Bigger test systems are not considered. |
| 2020 [35] | HGAPSO | PL (real & reactive), VD | 33a, 69 | Bigger test systems are not considered. |
| 2020 [36] | AL-PSO | PL, OC, VSI | 33a | Bigger test systems are not considered. |
| 2020 [39] | Pareto based MOSCA | PL, VSI, YEL, PGE | 33b, 69 | Bigger test systems are not considered. |
| 2019 [45] | Pareto based MOCDEA | PL, YEL, VD | 33b, 69 | Bigger test systems are not considered. |
| 2020 [46] | Pareto based IRRO | TI, NS | 33b, 69 | Bigger test systems are not considered. |
| 2019 [47] | Pareto based MOCSOSA | PL (real & reactive), TVD, VSI | 33b, 69 | Bigger test systems are not considered. |
| Test Systems | Total Real Power Load, kW | Total Reactive Power Load, kVAr | Total Real Power Loss, kW (f1) | Total Reactive Power Loss, kVAr | Minimum Bus Voltage (p.u.) | Voltage Deviation (f2) | Critical VSI (p.u.) | RCVSI (f3) |
|---|---|---|---|---|---|---|---|---|
| 33 bus | 3715 | 2300 | 210.9824 | 143.0219 | 0.9038 @ 18 | 0.1338 | 0.6672 | 1.4988 |
| 118 bus | 22,710 | 170,410 | 1298.1 | 978.7196 | 0.8688 @ 77 | 0.3576 | 0.5697 | 1.7552 |
| 136 bus | 18,314.0 | 7932.5 | 320.3508 | 702.9169 | 0.9307 @ 117 | 0.1188 | 0.7502 | 1.3331 |
| Test Systems | SCA | DEA | O-SCMDEA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max_Iter | Pop_Size | Max_Iter | Pop_Size | F | CR | G | NP | CR | |
| 33 bus | 200 | 50 | 200 | 50 | 0.7 | 0.8 | 200 | 50 | 0.8 |
| 118 bus/ 136 bus | 500 | 100 | 500 | 100 | 500 | 100 | |||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 14 | 0.7802 | 72.8198 | 0.0150 | 1.1375 | 0.8791 | 78.8917 | 74.6769 | 1.1374 |
| 30 | 1.0446 | ||||||||
| 24 | 1.1454 | ||||||||
| DEA | 30 | 1.1008 | 72.8592 | 0.0155 | 1.1351 | 0.8810 | 73.9534 | 73.4328 | 0.3145 |
| 24 | 1.0528 | ||||||||
| 14 | 0.7435 | ||||||||
| O-SCMDEA | 30 | 1.0483 | 72.7777 | 0.0151 | 1.1362 | 0.8801 | 73.0041 | 72.8252 | 0.0571 |
| 13 | 0.8052 | ||||||||
| 24 | 1.0936 | ||||||||
| QOCSOS [21] | 13 | 0.8017 | 72.7869 | 0.0151 | 1.1357 | 0.8805 | 74.7540 | 72.9041 | 0.3811 |
| 24 | 1.0913 | ||||||||
| 30 | 1.0537 | ||||||||
| WCA [51] | 13 | 0.8017 | 72.786 | 0.0151 | - | 1 | - | - | - |
| 24 | 1.0913 | ||||||||
| 30 | 1.0536 | ||||||||
| SFSA [16] | 13 | 0.8020 | 72.785 | 0.015099 | 1.1357 | 0.8805 | - | - | - |
| 24 | 1.0920 | ||||||||
| 30 | 1.0537 | ||||||||
| OTCDE [19] | 13 | 801.80 | 72.785 | - | - | - | - | - | - |
| 24 | 1091.31 | ||||||||
| 30 | 1053.60 | ||||||||
| Case 2: Allocation of 0.95 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 30 | 1.2206 | 28.6078 | 0.0020 | 1.0558 | 0.9471 | 33.2674 | 30.3201 | 0.9705 |
| 14 | 0.8277 | ||||||||
| 24 | 1.1112 | ||||||||
| DEA | 30 | 1.2513 | 28.6044 | 0.0024 | 1.0569 | 0.9462 | 30.3226 | 29.4010 | 0.4340 |
| 14 | 0.7732 | ||||||||
| 24 | 1.1755 | ||||||||
| O-SCMDEA | 30 | 1.2411 | 28.533 | 0.0021 | 1.0541 | 0.9487 | 28.8763 | 28.5867 | 0.0700 |
| 13 | 0.8287 | ||||||||
| 24 | 1.1250 | ||||||||
| QOCSOS [21] | 24 | 1.1838 | 28.534 | 0.0021 | 1.0494 | 0.9530 | 28.5929 | 28.5361 | 0.0106 |
| 13 | 0.8738 | ||||||||
| 30 | 1.3048 | ||||||||
| WCA [51] | 13 | 0.8301 | 28.534 | 0.002078 | 1 | 1 | - | - | - |
| 24 | 1.1246 | ||||||||
| 30 | 1.2395 | ||||||||
| SFSA [16] | 13 | 0.8743 | 28.533 | 0.002073 | 1.0493 | 0.95298 | - | - | - |
| 24 | 1.1849 | ||||||||
| 30 | 1.3048 | ||||||||
| OTCDE [19] | 13 | 830.23 | 28.533 | - | - | - | - | - | - |
| 24 | 1124.65 | ||||||||
| 30 | 239.56 | ||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 25 | 1.3751 | 116.8960 | 0.5 × 10−3 | 1.0344 | 0.9667 | 0.0013 | 0.0008 | 0.0002 |
| 12 | 1.4687 | ||||||||
| 32 | 1.4828 | ||||||||
| DEA | 24 | 1.4291 | 107.2524 | 0.4619 × 10−3 | 1.0366 | 0.9647 | 0.8250 × 10−3 | 0.7111 × 10−3 | 0.0703 × 10−3 |
| 31 | 1.4269 | ||||||||
| 12 | 1.4613 | ||||||||
| O-SCMDEA | 31 | 1.5000 | 111.6069 | 0.3814 × 10−3 | 1.0326 | 0.9684 | 0.7146 × 10−3 | 0.4943 × 10−3 | 0.0879 × 10−3 |
| 24 | 1.4863 | ||||||||
| 12 | 1.4491 | ||||||||
| QOCSOS [21] | 31 | 1.2599 | 111.0718 | 0.6571 × 10−3 | 1.0685 | 0.9359 | |||
| 13 | 0.9551 | ||||||||
| 07 | 1.5000 | ||||||||
| WCA [51] | 13 | 1.196655 | 115.228 | 0.512 × 10−3 | - | 0.977675 | - | - | - |
| 25 | 0.524835 | ||||||||
| 30 | 1.993288 | ||||||||
| SFSA [16] | 7 | 1.4871 | 111.15 | 0.6597 × 10−3 | 1.0687 | 0.9358 | - | - | - |
| 13 | 0.9604 | ||||||||
| 31 | 1.2638 | ||||||||
| Case 2: Allocation of 0.95 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 24 | 1.2490 1.4013 0.9588 | 31.4342 | 0.2861 × 10−3 | 1.0307 | 0.9702 | 0.8116 × 10−3 | 0.5374 × 10−3 | 0.1279 × 10−3 |
| 30 | |||||||||
| 13 | |||||||||
| DEA | 13 | 0.9566 1.3744 1.3858 | 32.468 | 0.2890 × 10−3 | 1.0297 | 0.9712 | 0.5686 × 10−3 | 0.4293 × 10−3 | 0.0657 × 10−3 |
| 24 | |||||||||
| 30 | |||||||||
| O-SCMDEA | 30 | 1.4399 | 32.3676 | 0.2401 × 10−3 | 1.0284 | 0.9724 | 0.4381 × 10−3 | 0.3176 × 10−3 | 0.0401 × 10−3 |
| 13 | 0.9270 | ||||||||
| 24 | 1.3715 | ||||||||
| QOCSOS [21] | 24 | 1.3733 | 32.4008 | 0.2283 × 10−3 | 1.0235 | 0.9771 | - | - | - |
| 30 | 0.9577 | ||||||||
| 13 | 1.5637 | ||||||||
| WCA [51] | 13 | 0.876717 | 34.403 | 0.2240 × 10−3 | - | 0.9777 | - | - | |
| 24 | 1.237255 | ||||||||
| 29 | 1.613168 | ||||||||
| SFSA [16] | 13 | 0.9579 | 32.405 | 0.2285 × 10−3 | 1.0235 | 0.9770 | - | - | - |
| 24 | 1.3736 | ||||||||
| 30 | 1.4856 | ||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 24 | 1.4992 | 114.4541 | 0.0005 | 1.0313 | 0.9696 | 1.0590 | 1.0421 | 0.0070 |
| 11 | 1.4836 | ||||||||
| 32 | 1.4865 | ||||||||
| DEA | 31 | 1.4945 | 118.8705 | 0.0013 | 1.0337 | 0.9674 | 1.0470 | 1.0400 | 0.0030 |
| 24 | 1.3392 | ||||||||
| 13 | 1.4868 | ||||||||
| O-SCMDEA | 11 | 1.5000 | 112.5075 | 0.0006 | 1.0291 | 0.9717 | 1.0351 | 1.0314 | 0.0012 |
| 25 | 1.4923 | ||||||||
| 30 | 1.5000 | ||||||||
| QOCSOS [21] | 12 | 1.5000 | 108.0213 | 0.0006607 | 1.0293 | 0.9716 | - | - | - |
| 31 | 1.5000 | ||||||||
| 25 | 0.7151 | ||||||||
| WCA [51] | 10 | 2.100652 | 272.135 | 0.025093 | - | 0.822707 | - | - | - |
| 11 | 1.372366 | ||||||||
| 32 | 0 | ||||||||
| SFSA [16] | 12 | 1.4997 | 107.977 | 0.000664 | 1.0294 | 0.9714 | - | - | - |
| 25 | 0.7136 | ||||||||
| 31 | 1.4999 | ||||||||
| Case 2: Allocation of 0.95 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 25 | 1.4844 | 81.2643 | 0.0187 | 1.0215 | 0.9789 | 1.0234 | 1.0220 | 0.0004 |
| 16 | 1.4806 | ||||||||
| 30 | 1.4968 | ||||||||
| DEA | 24 | 1.4788 | 62.1462 | 0.0078 | 1.0215 | 0.9789 | 1.0223 | 1.0219 | 0.0002 |
| 32 | 1.4638 | ||||||||
| 12 | 1.4989 | ||||||||
| O-SCMDEA | 24 | 1.4973 | 53.7577 | 0.0055 | 1.0213 | 0.9791 | 1.0216 | 1.0215 | 0.0001 |
| 30 | 1.5000 | ||||||||
| 10 | 1.4989 | ||||||||
| QOCSOS [21] | 24 | 1.5789 | 39.8066 | 0.0009318 | 1.0223 | 0.9782 | - | - | - |
| 30 | 1.5742 | ||||||||
| 11 | 1.2162 | ||||||||
| WCA [51] | 6 | 0.888185 | 138.628 | 0.019185 | 0.822704 | - | - | - | |
| 30 | 2.423977 | ||||||||
| 32 | 0.488649 | ||||||||
| SFSA [16] | 10 | 1.3198 | 40.136 | 0.001061 | 1.0223 | 0.9782 | - | - | - |
| 24 | 1.5731 | ||||||||
| 30 | 1.4764 | ||||||||
| Case 1: Allocation of UPF-DGs | ||||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Best | Worst | Average | Standard Deviation |
| SCA | 30 | 1.4245 | 80.6305 | 0.0045 | 1.0728 | 0.9322 | 0.4738 | 0.5078 | 0.4921 | 0.0077 |
| 14 | 0.9425 | |||||||||
| 24 | 1.1843 | |||||||||
| DEA | 13 | 1.0004 | 80.6471 | 0.0044 | 1.0742 | 0.9309 | 0.4745 | 0.4953 | 0.4841 | 0.0049 |
| 24 | 1.1667 | |||||||||
| 30 | 1.3908 | |||||||||
| O-SCMDEA | 13 | 0.9894 | 81.7494 | 0.0040 | 1.0679 | 0.9364 | 0.4724 | 0.4777 | 0.4742 | 0.0014 |
| 30 | 1.4449 | |||||||||
| 24 | 1.1465 | |||||||||
| QOCSOS [21] | 24 | 1.1309 | 77.0414 | 0.006514 | 1.0908 | 0.9168 | - | - | - | - |
| 13 | 0.9564 | |||||||||
| 30 | 1.2935 | |||||||||
| SFSA [16] | 13 | 0.9647 | 77.410 | 0.006232 | 1.0891 | 0.9182 | - | - | - | - |
| 24 | 1.1337 | |||||||||
| 30 | 1.3018 | |||||||||
| Case 2: Allocation of 0.95 LPF-DGs | ||||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Best | Worst | Average | Standard Deviation |
| SCA | 11 | 1.1537 | 32.2575 | 0.0004 | 1.0276 | 0.9731 | 0.1831 | 0.2340 | 0.1974 | 0.0097 |
| 30 | 1.2885 | |||||||||
| 24 | 1.1456 | |||||||||
| DEA | 30 | 1.3258 | 31.7068 | 0.0004 | 1.0272 | 0.9735 | 0.1798 | 0.1975 | 0.1870 | 0.0044 |
| 24 | 1.1302 | |||||||||
| 12 | 1.0967 | |||||||||
| O-SCMDEA | 30 | 1.3600 | 32.0436 | 0.0003 | 1.0255 | 0.9751 | 0.1795 | 0.1824 | 0.1804 | 0.0007 |
| 24 | 1.1699 | |||||||||
| 12 | 1.0808 | |||||||||
| QOCSOS [21] | 24 | 1.2062 | 29.3450 | 0.0006917 | 1.0316 | 0.9694 | - | - | - | - |
| 13 | 0.9635 | |||||||||
| 30 | 1.3829 | |||||||||
| SFSA [16] | 13 | 0.9657 | 29.383 | 0.000673 | 1.0312 | 0.9697 | - | - | - | - |
| 24 | 1.2066 | |||||||||
| 30 | 1.3849 | |||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 71 | 2.9858 | 668.3339 | 0.1025 | 1.2045 | 0.8302 | 711.4617 | 684.4184 | 10.2363 |
| 50 | 3.0869 | ||||||||
| 109 | 2.9708 | ||||||||
| DEA | 50 | 2.7890 | 668.9599 | 0.1001 | 1.2137 | 0.8239 | 684.7815 | 678.0098 | 4.1155 |
| 71 | 3.2081 | ||||||||
| 110 | 2.8750 | ||||||||
| O-SCMDEA | 50 | 2.8836 | 667.2830 | 0.1038 | 1.2067 | 0.8287 | 668.3581 | 667.4956 | 0.2334 |
| 71 | 2.9785 | ||||||||
| 109 | 3.1198 | ||||||||
| SFSA [52] | 71 | 2.9786 | 667.29 | - | - | - | - | - | - |
| 109 | 3.1199 | ||||||||
| 50 | 2.8833 | ||||||||
| Case 2: Allocation of 0.866 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 71 | 2.8122 | 364.5265 | 0.0581 | 1.1820 | 0.8460 | 418.9182 | 385.9170 | 12.4081 |
| 110 | 3.2202 | ||||||||
| 50 | 3.2935 | ||||||||
| DEA | 110 | 2.8251 | 370.1841 | 0.0531 | 1.1731 | 0.8524 | 396.0838 | 379.8858 | 5.9381 |
| 50 | 3.5118 | ||||||||
| 72 | 3.1777 | ||||||||
| O-SCMDEA | 71 | 3.0191 | 362.7833 | 0.0552 | 1.1768 | 0.8497 | 364.9054 | 363.0446 | 0.4034 |
| 50 | 3.2795 | ||||||||
| 110 | 3.1123 | ||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 51 | 4.4391 | 872.6374 | 0.0623 | 1.1807 | 0.8470 | 0.0719 | 0.0657 | 0.0027 |
| 110 | 4.3284 | ||||||||
| 73 | 4.5226 | ||||||||
| DEA | 113 | 3.9466 | 919.0408 | 0.0623 | 1.1818 | 0.8462 | 0.0726 | 0.0670 | 0.0022 |
| 53 | 4.4626 | ||||||||
| 71 | 4.3906 | ||||||||
| O-SCMDEA | 109 | 4.5420 | 846.4178 | 0.0598 | 1.1799 | 0.8475 | 0.0610 | 0.0603 | 0.0003 |
| 52 | 4.5327 | ||||||||
| 71 | 4.5420 | ||||||||
| Case 2: Allocation of 0.866 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 108 | 3.5205 | 402.1593 | 0.0473 | 1.1682 | 0.8560 | 0.0545 | 0.0502 | 0.0021 |
| 48 | 4.2757 | ||||||||
| 70 | 3.6499 | ||||||||
| DEA | 49 | 4.2750 | 417.6226 | 0.0483 | 1.1682 | 0.8560 | 0.0523 | 0.0499 | 0.0013 |
| 109 | 4.2741 | ||||||||
| 70 | 3.7444 | ||||||||
| O-SCMDEA | 109 | 3.5587 | 480.7784 | 0.0458 | 1.1665 | 0.8572 | 0.0472 | 0.0465 | 0.0003 |
| 47 | 4.5419 | ||||||||
| 69 | 4.5420 | ||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 71 | 4.5127 | 791.5745 | 0.0743 | 1.1801 | 0.8474 | 1.1895 | 1.1837 | 0.0028 |
| 52 | 4.1823 | ||||||||
| 110 | 2.3826 | ||||||||
| DEA | 73 | 4.5297 | 887.3179 | 0.0691 | 1.1806 | 0.8470 | 1.1865 | 1.1827 | 0.0017 |
| 107 | 4.1548 | ||||||||
| 53 | 4.0613 | ||||||||
| O-SCMDEA | 70 | 4.5420 | 813.3903 | 0.0620 | 1.1799 | 0.8475 | 1.1799 | 1.1799 | 0.0000 |
| 111 | 4.1298 | ||||||||
| 50 | 4.4931 | ||||||||
| Case 2: Allocation of 0.866 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size/pf, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 69 | 4.2171 | 491.1881 | 0.0574 | 1.1667 | 0.8571 | 1.1713 | 1.1680 | 0.0013 |
| 50 | 4.5155 | ||||||||
| 109 | 2.5253 | ||||||||
| DEA | 75 | 4.0919 | 532.5343 | 0.0645 | 1.1666 | 0.8572 | 1.1687 | 1.1674 | 0.0006 |
| 35 | 4.5372 | ||||||||
| 113 | 2.9958 | ||||||||
| O-SCMDEA | 71 | 3.8966 | 418.3989 | 0.0483 | 1.1665 | 0.8572 | 1.1665 | 1.1665 | 0.0000 |
| 47 | 4.5420 | ||||||||
| 110 | 3.7129 | ||||||||
| Case 1: Allocation of UPF-DGs | ||||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Best | Worst | Average | Standard Deviation |
| SCA | 72 | 3.5674 | 688.6312 | 0.0829 | 1.1950 | 0.8369 | 0.8023 | 0.8596 | 0.8173 | 0.0129 |
| 50 | 3.4299 | |||||||||
| 109 | 3.2648 | |||||||||
| DEA | 50 | 3.2784 | 700.4404 | 0.0792 | 1.1878 | 0.8419 | 0.8010 | 0.8255 | 0.8115 | 0.0067 |
| 110 | 3.3129 | |||||||||
| 71 | 4.0025 | |||||||||
| O-SCMDEA | 50 | 3.6013 | 693.8726 | 0.0789 | 1.1914 | 0.8394 | 0.7976 | 0.7987 | 0.7979 | 0.0004 |
| 109 | 3.5000 | |||||||||
| 71 | 3.7778 | |||||||||
| Case 2: Allocation of 0.866 LPF-DGs | ||||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Best | Worst | Average | Standard Deviation |
| SCA | 49 | 3.6552 | 382.2600 | 0.0493 | 1.1722 | 0.8531 | 0.4968 | 0.5400 | 0.5146 | 0.0129 |
| 71 | 3.6823 | |||||||||
| 110 | 3.2913 | |||||||||
| DEA | 109 | 3.6156 | 377.8895 | 0.0502 | 1.1722 | 0.8531 | 0.4948 | 0.5201 | 0.5047 | 0.0060 |
| 50 | 3.6505 | |||||||||
| 72 | 3.3616 | |||||||||
| O-SCMDEA | 110 | 3.1823 | 367.2104 | 0.0508 | 1.1724 | 0.8530 | 0.4877 | 0.4896 | 0.4881 | 0.0005 |
| 71 | 3.2768 | |||||||||
| 50 | 3.6255 | |||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 106 | 2.6695 | 169.9215 | 0.0561 | 1.1683 | 0.8559 | 182.0513 | 173.3227 | 2.5778 |
| 52 | 2.2958 | ||||||||
| 14 | 2.1442 | ||||||||
| DEA | 106 | 2.4656 | 170.8067 | 0.0578 | 1.1788 | 0.8483 | 176.8662 | 172.9326 | 1.5905 |
| 32 | 2.0684 | ||||||||
| 11 | 2.1037 | ||||||||
| O-SCMDEA | 11 | 2.3138 | 169.0198 | 0.0543 | 1.1644 | 0.8588 | 170.0238 | 169.3736 | 0.2329 |
| 106 | 2.7471 | ||||||||
| 29 | 2.0813 | ||||||||
| SFSA [52] | 11 | 2.3284 | 169.22 | - | - | - | - | - | - |
| 29 | 2.0639 | ||||||||
| 106 | 2.8411 | ||||||||
| Case 2: Allocation of 0.866 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 28 | 1.9321 | 145.1953 | 0.0314 | 1.1247 | 0.8892 | 157.5103 | 149.7313 | 2.5098 |
| 14 | 1.9132 | ||||||||
| 106 | 2.5198 | ||||||||
| DEA | 11 | 1.9540 | 144.8097 | 0.0315 | 1.1247 | 0.8892 | 151.7665 | 148.6051 | 1.6503 |
| 106 | 2.7060 | ||||||||
| 28 | 1.9279 | ||||||||
| O-SCMDEA | 29 | 1.9853 | 144.3359 | 0.0314 | 1.1247 | 0.8892 | 145.7097 | 144.7496 | 0.3791 |
| 11 | 2.1430 | ||||||||
| 106 | 2.6509 | ||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 112 | 2.5454 | 313.3257 | 0.0428 | 1.1247 | 0.8892 | 0.0458 | 0.0436 | 0.0008 |
| 139 | 2.4247 | ||||||||
| 39 | 2.6735 | ||||||||
| DEA | 108 | 2.5399 | 292.4590 | 0.0427 | 1.1247 | 0.8892 | 0.0435 | 0.0431 | 0.0002 |
| 109 | 2.3667 | ||||||||
| 36 | 2.7387 | ||||||||
| O-SCMDEA | 107 | 2.7471 | 317.7009 | 0.0422 | 1.1247 | 0.8892 | 0.0426 | 0.0423 | 0.0001 |
| 35 | 2.7471 | ||||||||
| 111 | 2.7459 | ||||||||
| Case 2: Allocation of 0.866 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 32 | 2.1588 | 156.1567 | 0.0306 | 1.1247 | 0.8892 | 0.0310 | 0.0307 | 0.0001 |
| 53 | 1.9880 | ||||||||
| 107 | 2.3991 | ||||||||
| DEA | 33 | 1.9622 | 156.6345 | 0.0305 | 1.1247 | 0.8892 | 0.0307 | 0.0306 | 0.0001 |
| 107 | 2.4224 | ||||||||
| 49 | 2.1238 | ||||||||
| O-SCMDEA | 107 | 2.4250 | 155.5813 | 0.0305 | 1.1247 | 0.8892 | 0.0305 | 0.0305 | 0.0000 |
| 28 | 2.0162 | ||||||||
| 52 | 2.0359 | ||||||||
| Case 1: Allocation of UPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 83 | 2.5450 | 282.6227 | 0.0507 | 1.1244 | 0.8894 | 1.1244 | 1.1244 | 0.0000 |
| 116 | 1.3566 | ||||||||
| 107 | 2.6755 | ||||||||
| DEA | 105 | 2.0635 | 240.5822 | 0.0526 | 1.1244 | 0.8894 | 1.1244 | 1.1244 | 0.0000 |
| 80 | 2.6144 | ||||||||
| 107 | 2.4912 | ||||||||
| O-SCMDEA | 105 | 1.7622 | 241.6850 | 0.0582 | 1.1244 | 0.8894 | 1.1244 | 1.1244 | 0.0000 |
| 108 | 2.3341 | ||||||||
| 76 | 2.7160 | ||||||||
| Case 2: Allocation of 0.866 LPF-DGs | |||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Worst | Average | Standard Deviation |
| SCA | 107 | 2.0087 | 218.5893 | 0.0459 | 1.1163 | 0.8958 | 1.1163 | 1.1163 | 0.0000 |
| 07 | 1.4092 | ||||||||
| 84 | 2.6585 | ||||||||
| DEA | 78 | 2.1711 | 239.5010 | 0.0491 | 1.1163 | 0.8958 | 1.1163 | 1.1163 | 0.0000 |
| 02 | 0.9261 | ||||||||
| 114 | 1.6455 | ||||||||
| O-SCMDEA | 09 | 1.3358 | 212.7348 | 0.0445 | 1.1163 | 0.8958 | 1.1163 | 1.1163 | 0.0000 |
| 112 | 1.9140 | ||||||||
| 85 | 2.2992 | ||||||||
| Case 1: Allocation of UPF-DGs | ||||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Best | Worst | Average | Standard Deviation |
| SCA | 28 | 2.4913 | 177.2554 | 0.0500 | 1.1374 | 0.8792 | 0.9749 | 1.0299 | 1.0063 | 0.0135 |
| 111 | 2.7243 | |||||||||
| 14 | 1.8872 | |||||||||
| DEA | 16 | 2.0078 | 176.6420 | 0.0505 | 1.1361 | 0.8802 | 0.9741 | 0.9979 | 0.9837 | 0.0066 |
| 127 | 2.3062 | |||||||||
| 108 | 2.7415 | |||||||||
| O-SCMDEA | 108 | 2.7471 | 174.6281 | 0.0489 | 1.1358 | 0.8805 | 0.9594 | 0.9663 | 0.9630 | 0.0022 |
| 11 | 2.5168 | |||||||||
| 29 | 2.3742 | |||||||||
| Case 2: Allocation of 0.866 LPF-DGs | ||||||||||
| Methods | Optimal Bus | Optimal DG Size, MW | RPL, kW | VD (p.u.) | RCVSI (p.u.) | CVSI (p.u.) | Best | Worst | Average | Standard Deviation |
| SCA | 14 | 1.8750 | 145.0432 | 0.0314 | 1.1247 | 0.8892 | 0.7668 | 0.8213 | 0.7906 | 0.0145 |
| 106 | 2.5911 | |||||||||
| 29 | 1.9050 | |||||||||
| DEA | 29 | 1.9134 | 146.2388 | 0.0316 | 1.1247 | 0.8892 | 0.7715 | 0.7917 | 0.7777 | 0.0059 |
| 106 | 2.4123 | |||||||||
| 09 | 2.1102 | |||||||||
| O-SCMDEA | 106 | 2.6099 | 144.3639 | 0.0314 | 1.1247 | 0.8892 | 0.7645 | 0.7687 | 0.7664 | 0.0013 |
| 11 | 2.1151 | |||||||||
| 29 | 1.9888 | |||||||||
| Test Systems | p-Values at 5% Significance Level | |||
|---|---|---|---|---|
| Shapiro–Wilk Test | Kolmogorov–Smirnov Test | |||
| Case 1 | Case 2 | Case 1 | Case 2 | |
| 33 bus | 2.0326 × 10−6 | 3.0820 × 10−8 | 1.74 × 10−45 | 1.74 × 10−45 |
| 118 bus | 1.5110 × 10−6 | 2.5179 × 10−8 | 1.74 × 10−45 | 1.74 × 10−45 |
| 136 bus | 1.0532 × 10−4 | 3.7513 × 10−4 | 1.74 × 10−45 | 1.74 × 10−45 |
| Test Systems | Methods | |||||
|---|---|---|---|---|---|---|
| SCA | DEA | O-SCMDEA | ||||
| Case 1 | Case 2 | Case 1 | Case 2 | Case 1 | Case 2 | |
| 33 bus | 1.1374 | 0.9705 | 0.3145 | 0.4340 | 0.0571 | 0.0700 |
| 118 bus | 10.2363 | 12.4081 | 4.1155 | 5.9381 | 0.2334 | 0.4034 |
| 136 bus | 2.5778 | 2.5098 | 1.5905 | 1.6503 | 0.2329 | 0.3791 |
| Test Systems | Methods | |||
|---|---|---|---|---|
| OSCMDE Versus SCA | OSCMDE Versus DEA | |||
| Case 1 | Case 2 | Case 1 | Case 2 | |
| 33 bus | 5.3181 × 10−17 | 1.8392 × 10−17 | 3.7392 × 10−17 | 5.0155 × 10−17 |
| 118 bus | 7.5041 × 10−18 | 7.5041 × 10−18 | 7.0661 × 10−18 | 7.0661 × 10−18 |
| 136 bus | 7.5041 × 10−18 | 1.2120 × 10−17 | 7.0661 × 10−18 | 1.9517 × 10−17 |
| Test Systems | Methods | |||||
|---|---|---|---|---|---|---|
| SCA | DEA | O-SCMDEA | ||||
| Case 1 | Case 2 | Case 1 | Case 2 | Case 1 | Case 2 | |
| 33 bus | 4.1963 s | 4.0840 s | 7.6427 s | 7.4453 s | 11.2348 s | 10.9250 s |
| 118 bus | 14.0647 s | 13.7444 s | 27.4197 s | 27.2257 s | 39.7063 s | 38.3187 s |
| 136 bus | 21.4209 s | 21.3897 s | 42.0096 s | 39.1550 s | 63.6492 s | 56.9987 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dash, S.K.; Mishra, S.; Abdelaziz, A.Y.; Alghaythi, M.L.; Allehyani, A. Optimal Allocation of Distributed Generators in Active Distribution Networks Using a New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm. Energies 2022, 15, 2267. https://doi.org/10.3390/en15062267
Dash SK, Mishra S, Abdelaziz AY, Alghaythi ML, Allehyani A. Optimal Allocation of Distributed Generators in Active Distribution Networks Using a New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm. Energies. 2022; 15(6):2267. https://doi.org/10.3390/en15062267
Chicago/Turabian StyleDash, Subrat Kumar, Sivkumar Mishra, Almoataz Y. Abdelaziz, Mamdouh L. Alghaythi, and Ahmed Allehyani. 2022. "Optimal Allocation of Distributed Generators in Active Distribution Networks Using a New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm" Energies 15, no. 6: 2267. https://doi.org/10.3390/en15062267
APA StyleDash, S. K., Mishra, S., Abdelaziz, A. Y., Alghaythi, M. L., & Allehyani, A. (2022). Optimal Allocation of Distributed Generators in Active Distribution Networks Using a New Oppositional Hybrid Sine Cosine Muted Differential Evolution Algorithm. Energies, 15(6), 2267. https://doi.org/10.3390/en15062267







