Abstract
With increasing attention to climate change, the penetration level of renewable energy sources (RES) in the electricity network is increasing. Due to the intermittency of RES, gas-fired power plants could play a significant role in backing up the RES in order to maintain the supply–demand balance. As a result, the interaction between gas and power networks are significantly increasing. On the other hand, due to the increase in peak demand (e.g., electrification of heat), network operators are willing to execute demand response programs (DRPs) to improve congestion management and reduce costs. In this context, modeling and optimal implementation of DRPs in proportion to the demand is one of the main issues for gas and power network operators. In this paper, an emergency demand response program (EDRP) is implemented locally to reduce the congestion of transmission lines and gas pipelines more efficiently. Additionally, the effects of optimal implementation of local emergency demand response program (LEDRP) in gas and power networks using linear and non-linear economic models (power, exponential and logarithmic) for EDRP in terms of cost and line congestion and risk of unserved demand are investigated. The most reliable demand response model is the approach that has the least difference between the estimated demand and the actual demand. Furthermore, the role of the LEDRP in the case of hydrogen injection instead of natural gas in the gas infrastructure is investigated. The optimal incentives for each bus or node are determined based on the power transfer distribution factor, gas transfer distribution factor, available electricity or gas transmission capability, and combination of unit commitment with the LEDRP in the integrated operation of these networks. According to the results, implementing the LEDRP in gas and power networks reduces the total operation cost up to 11% and could facilitate hydrogen injection to the network. The proposed hybrid model is implemented on a 24-bus IEEE electricity network and a 15-bus gas network to quantify the role and value of different LEDRP models.
1. Introduction
Due to the unbalanced growth in power consumption in recent years, there are problems such as congestion, lack of generation, and rising energy prices during peak hours. The constant increase in demand during peak hours imposes a high cost on the network to increase production and transmission line capacities [1]. Demand response (DR) is a technical–economic solution that allows consumers to optimize their energy consumption according to the needs of energy suppliers. Therefore, it is necessary to use demand response programs (DRPs) to reduce consumption at peak times, which price elasticity matrix (PEM) method is one of the most common approaches for DRP [2]. Lack of sufficient information from the network is one of the problems for the implementation of DR. Various methods are proposed to improve the lack of information caused by non-ideal communication in a multi-energy system when implementing distributed DR. The combined method of Steiner tree distribution and modified randomized alternating direction method of multipliers algorithm is one of the best ways to improve the lack of information [3]. However, respecting the privacy and security of end-users in the distribution network when executing DR is one of the requirements of the operators that can be calculated through indirect processing of transformer data and the demand profile of end-users [4]. Another method of DR implementation has been employed to maximize the participants’ profits from active market participation using the improved weighting method [5]. Additionally, to solve the problem of real-time response, a predictive control model based on the roller optimization stage strategy can be used [6]. On the other hand, some models of price-based DRPs are not suitable for motivation-based DRPs because this modeling method adds network operating costs [7]. Congestion management (CM) methods include preventive and corrective strategies, in which, in the preventive CM, available transmission capability (ATC) is used optimally. In other words, preventive CM methods focus on customer involvement to reduce the congestion of lines by using the optimal consumption pattern. In [8], to increase the ATC of the lines, the DR approach is compared to the use of flexible AC transmission (FACT) devices. It was demonstrated that implementing the DR has been more beneficial than using FACT devices. The method of calculating ATC based on power transfer distribution factor (PTDF) is presented, and it is demonstrated that this method improves power-line congestion and reduces operating costs [9].
Due to the nature of unit commitment (UC) and DRPs that focus on demand and supply sectors, the combination of these two approaches prevents the creation of additional costs and new peaks and valleys, which is useful for determining the optimal price and incentive [10]. In addition to classical optimization methods, methods such as game theory can be used to solve the integration of DRP and UC [11]. In reference [11], incentives are paid to the consumers at all times, which is not a practical and economical method. Additionally, they have used the linear model for DR modeling and did not consider other modeling approaches. Furthermore, some researches only considered the cost reduction and improvement of load curve features when simultaneously optimizing UC and DR programs (incentive-based [12] and price-based [13]), and have not considered transmission line congestion. From environmental aspects, according to the international agreements on pollution reduction and development of RESs by 2030, the share of intermittent renewable energy sources such as solar and wind power plants will increase significantly [14]. Due to the uncontrollable and changeable performance of renewable resources, gas-fired power plants (GFPP) [15], energy storage systems [16] and DR have an essential role in compensating for RES variability. In the 2014 UK gas system, the gas demand for GFPP was nearly 50% (218 TWh out of 469 TWh), indicating the importance of the interaction of gas and power networks. The interaction of gas and power networks with dynamic security considerations can be studied through the mechanism of simultaneous and asynchronous operation of gas and power networks [17]. In the asynchronous operation method, the operation of gas and power networks are optimized through a repetitive loop. First, security-constrained unit commitment (SCUC) is checked in the power network, and then the required gas demand for GFPP is applied during the gas system operation. If the gas system is not able to deliver the gas to the plants, the production of the GFPP is reduced; hence, other types of power plants should supply the electricity until the gas system conditions are met [18]. However, in a simultaneous operation, the operation of gas and power networks are optimized at the same time. Increasing the reliability and reducing operating costs are the advantages of the simultaneous operation of gas and power networks compared to asynchronous operation [19]. The authors in reference [20] employed a probabilistic steady-state analysis and it was shown that the simultaneous operation of the integrated network (i.e., electricity, gas, heating) has a much more complex uncertainty than the separate operation of these systems. It was also demonstrated that the use of power-to-gas (P2G) and power-to-heating (P2H) systems, despite increasing the uncertainty and complexity during optimization, can be useful in controlling demand.
In the literature, to the best of our knowledge, the modeling and local implementation of DR in the simultaneous operation of gas and power networks is not investigated. Hence, this paper focuses on the emergency demand response program (EDRP), which is a type of incentive-based DR. In the voluntary EDRP, incentives are paid to consumers for reduced or interrupted consumption during peak hours, wherein there is no penalty for not executing the EDRP for the consumers. The contributions of this paper are as follows: (i) the employment of a preventive optimization problem based on emergency; (ii) in addition to the linear model, the implementation of non-linear models including, exponential, power, and logarithmic (i.e., due to the fact that the use of a linear model may lead to significant errors in estimating demand and impose high costs on the network); (iii) the effect of implementing the EDRP in both gas and power networks are compared to implementing the EDRP in the power network; (iv) local implementation of EDRP; and (v) the possibility of injecting hydrogen instead of natural gas to the gas network is investigated, and the role of DR in both networks is quantified. The proposed hybrid model is applied to a 24-bus IEEE power network and a 15-node gas network to determine the optimal and most reliable scenario. The rest of this paper is structured as follows: the problem is formulated in the Section 1 of the paper. Section 2 describes how to implement the local emergency demand response program (LEDRP). In Section 3, the numerical results of the simulation are presented. Finally, in Section 4, this research is concluded.
2. Problem Formulation
To solve this problem, first, the calculation methods of PTDF and ATC are discussed. Afterwards, different models of DRP are demonstrated, and finally, the optimal implementation of the LEDRP and UC in the gas and power networks is presented [7,20].
2.1. PTDFs and ATC Formulation
The transmission coefficient is determined in the power network by PTDF and in the gas network by the gas transfer distribution factor (GTDF). PTDF shows the sensitivity rate of each line to the variation of active power consumption of each bus. GTDF indicates the sensitivity rate of each pipe to the variation of gas consumption of each node. The PTDFs are defined in (1), which is equal to the ratio of active power variation in line l to the power changes at bus i (for calculating the GTDFs the power is substituted by the gas flow). The larger the coefficient (), the more effectively the bus i can change the power through line l. Therefore, the bus has to participate more with higher incentive payments. The same can be carried out for the gas system when implementing an LEDRP in the gas systems.
The power transmission limit of each line during operation is obtained in (2). The minimum transmission limit of line l is equal to which is obtained through (3).
2.2. Economic Models of DR
Price elasticity indicates the sensitivity of demand to price changes. In (4), new demand per hour is obtained through the new price, initial demand, initial cost per hour, and PEM. Energy costs are the result of prices, incentives, and penalties. Equation (4) is the cost of the opportunity to use energy in period t′ relative to period t [21].
PEM per hour includes internal and external values. The internal elasticity values show the change in a load of the hour t relative to the price change in the same hour. The values of external elasticity present the amount of change in demand at the hour t due to the change in cost at hour t′. The values of internal and external elasticity for a day (24 h) (PEM) are calculated as shown in (5) [22].
The consumer participation in DRP is based on profit. The overall benefit of the consumer is obtained through (6), where B(d(t)) is the benefit that customers earn by consuming d(t) at t time. and are the paid incentives and the received fines as a result of the change in consumption, respectively. To obtain the maximum profit, the derivative of (6) must be zero. The maximum consumer benefit is stated in (7). The most common benefit function (B) is the quadratic function shown in (8) [23,24]. By combining (7) and (8), a single-period model of DR (PEM diagonal elements only) is derived in (9). Additionally, the multi-period demand model (non-diagonal elements in PEM) is calculated according to (10). Finally, the hybrid linear DR model, which includes one-period and multi-period demand models, is calculated (11) [7,25].
The linear model of DR has a higher risk of uncertainty than non-linear models. Therefore, in this paper, in addition to the linear model, non-linear DR models are also implemented. Non-linear hybrid DR models (power, exponential and logarithmic) are given in (12)–(14), respectively [7,25]:
2.3. Modeling of the Economic Dispatch in the Power and Gas Networks
Economic dispatch is the essential approach applied in the gas and power networks to achieve optimal production of generation units throughout the dispatch period [26]. Because of the minimum on/off time condition and the cost of startup/shut down of the power plants, it is more appropriate to use the UC method for optimal production of generation units. The objective function of the gas and power networks simultaneous operation with the LEDRP is shown in (15):
The terms of and in (15) are the new demand for each bus and node, respectively, which are obtained through (11)–(14). The objective function (15) includes the cost of electricity production, the cost of point-valves of power plants, the costs of startup and shutdown, the cost of implementing the LEDRP in the electrical system, the cost of gas, and the cost of the LEDRP in the gas system, respectively. To implement the LEDRP in the gas network, the coefficient is set to 1 (0 for not implementing the LEDRP in the gas network). The cost of implementing EDRP in the power network is presented in (16).
The objective function (15) is minimized subject to the constraints of the integrated operation of gas and power networks. Operational constraints of the gas system, including the operation of compressors and linepack, are listed in (17)–(32). Additionally, the operating constraints related to the power network are given in (33)–(43). The minimum and maximum gas injection range of the gas terminal is shown in (17).
Equation (18) shows the allowable range of gas volume inside gas tanks (). Equation (19) calculates the amount of gas in the tanks based on the previous time state () and the inlet gas flow () and the outlet gas flow () to tank q for time t. Equations (20) and (21) determine the inlet gas flow range and the outlet gas flow range, respectively [15,26].
GFPP gas consumption is calculated through (22) in proportion to their production rate (), gas heating amount (), and gas generator heat efficiency (). The new GFPP gas consumption is added to the corresponding node gas consumption in (23). The balance of supply and consumption in the gas system is presented in (23). The “Panhandle A” formulation for gas flow [27], which shows the gas flow rate of gas passing through pipelines using the pressure difference between the two nodes, is indicated in (24) [15,26].
Electric compressors have also been used to increase the pressure of the gas system. The power consumption of the compressor that should be considered as the demand in the power network balance is shown in (25). The allowable range of the inlet-to-outlet pressure ratio of the compressor unit is indicated in (26). Equation (27) presents the maximum inlet gas volume to the compressor unit. Furthermore, the pressure constraints on the compressor gas flow are shown in (28) [15,26].
The pressure constraint on the nodes of gas is shown in (29). The range of gas flow within the gas pipeline is expressed in (30). Moreover, according to the conditions mentioned above, the gas inside the pipelines should be considered in the gas system. The linepacks correlation with the average pressure inside the pipelines is shown in (31). Under dynamic conditions, the inlet and outlet gas flow to the pipeline change in ratio to the change of supply and demand of nodes. According to the congestion law, a change in the total gas volume in a pipeline is equivalent to a change in the flow of inlet and outlet gas to the pipelines. Thus, (31) is replaced with (32) [15,26].
In the power system, the minimum up/down time for thermal generation units are shown in (33) and (34). The power supply–demand balance constraint is shown in (35). The generation capacity limit for the thermal generation units is specified in (36). Additionally, the increasing / decreasing limitation of ramp rate production of power plants is indicated in constraints (37) and (38), respectively. The power transmission within the lines is presented in (39). The capacity limit passing through each line is shown in (40). Additionally, the essential reserve per hour during the planning period is indicated in (41). The amount of spinning reserve of the electricity network is shown (42). The prohibited operation zones (POZs) constraint for generation unit g is presented in (43) [15,27]. It should be pointed out that that each network’s incentive range is considered from 0.1 to 10 multiplied by the initial price in the same network [28].
2.4. Solution Methodology
In this section, first, LEDRP implementation in the integrated gas and power networks is presented in detail. Then, the differences in LEDRP implementation in the integrated gas and power networks with the LEDRP implementation in the power network is expressed. The method of determining the optimal average incentive of each network for the implementation of the LEDRP in the integrated gas and power networks is based on: ATC of power lines, gas changes within pipes, PTDFs of each bus relative to critical lines, GTDFs of each node relative to the critical pipe, and optimization of the objective function (15). The algorithm for implementing the LEDRP in both networks is shown in Figure 1. Initial data are first provided as the input. Afterwards, with the implementation of UC and the non-local EDRP in integrated gas and power networks, the total cost (TC) (including the supply cost of energy and implementation cost of DR), critical lines, critical pipes, PTDFs related to critical lines, and GTDFs related to critical pipes are determined. At this stage of optimization, the same incentive of the buses (α) and the same incentive of the gas network nodes (γ) are specified. According to the ATC values of lines and pipes during peak hours, the critical lines and pipes are identified. Then, a coefficient is given to each bus and node, based on the PTDFs and the GTDFs related to the critical lines and pipes, respectively. In this context, each bus or terminal, which is more effective in improving the congestion of electricity transmission lines and gas pipelines, has a higher coefficient. The incentive of each bus or node is obtained by multiplying the coefficient of bus or node at the average incentive of the related network. The new demand for each bus or node is determined through its own incentive and EDRP model (linear or non-linear). Finally, the operation of gas and power networks (including UC approach) is performed with the new demand of each bus per hour to determine the total cost and the condition of the power lines and gas pipes during the optimization.
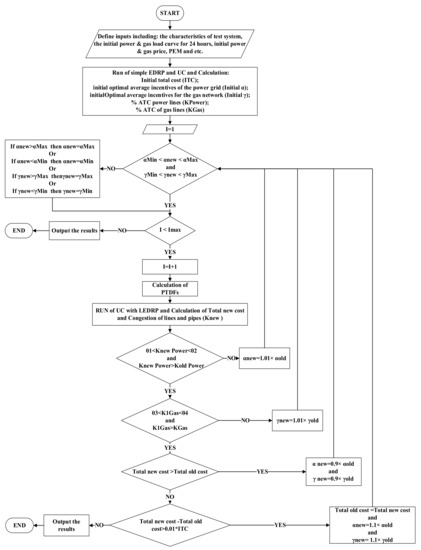
Figure 1.
Solution algorithm in the integrated gas and power networks.
At each step of optimizing the LEDRP, the following conditions are checked:
Condition 1: At each stage before the start of UC optimization along with the LEDRP in the gas and power networks, the incentives of each network are checked separately to be within acceptable limits. If the incentive passes the maximum or minimum allowable value, the incentive amount will be adjusted to the permissible limit.
Condition 2: In each step before the start of the optimization operation, the iteration numbers is checked. If the number of iterations exceeds the allowable limit, the optimization is terminated, and the obtained data from the last iteration are given as the output.
Condition 3: The congestion status of power lines is checked for placement within an acceptable operating range. If the ATC of lines is less than the acceptable operating range, the new power incentive becomes 1.01 multiplied by the power incentive of the same step. The new incentive is then re-checked through the first condition.
Condition 4: The variation status of the linepack is checked for placement within an acceptable operating range. If variation in the linepack is more than the acceptable operating range for the standard deviation, the new gas incentive becomes 1.01 times the gas incentive of the same step. The new incentive is then re-checked through the first condition.
Condition 5: The TCs of the new and the previous stage are compared. If the new TC of the integrated network compared to the previous stage is increased, the new incentive will be 0.9 incentives in the prior stage of each network. Afterwards, the UC will be running again with the LEDRP with new incentives. If the TC is not increased, the next condition is checked.
Condition 6: The difference between the new TC and the previous TC is examined. If the difference between the new TC and the previous TC is less than a percentage of the previous TC, the optimization operation ends. Additionally, if there is a greater difference between the costs, the new incentive for the gas and power networks will be updated by 1.1 multiplied by the incentive of the same step. Then, the electricity and gas system incentives are examined through the first condition, and the optimization operation continues again with the new incentive.
Determining the optimal average incentive to respond to local emergency demand is only in the power network when operating the integrated network simultaneously, as mentioned in the above method. The only difference with the above method is that the fourth condition, which examines the changes in the gas incentive, is no longer checked. The average power incentive is determined using the ATC of the power lines, PTDFs associated with the critical line for each bus, and the optimization operations between the integrated gas and power networks supply costs and LEDRP costs (Equation (15)).
3. Numerical Simulation and Results
3.1. Test System and Scenarios
To analyze the performance of the proposed model in different scenarios, the model is implemented on an IEEE 24-bus electricity network and a 15-node gas network (Figure 2) [29]. Due to the non-linear and binary conditions of the optimization problem, the CPLEX and DICOPT solvers of GAMS software [17] are used on a system with the following configurations: processor of Intel (R) Core (TM) i7-7500U @ 2.70 GHz 2.90 GHz and RAM of 12 GB.
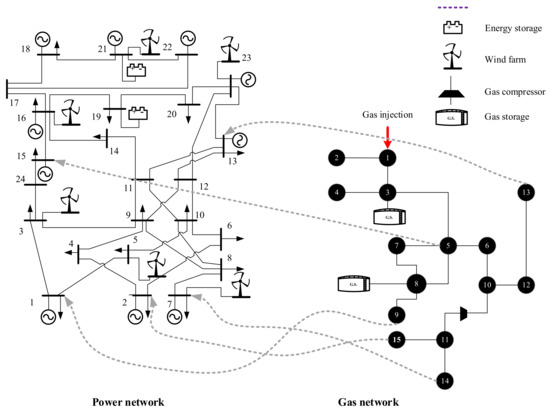
Figure 2.
Studied integrated gas and power networks [29].
Valley, off-peak, and peak demand hours in the gas and power networks are listed in Table 1. Additionally, the experimental PEM matrix values are shown in Figure 3 [10,26]. The maximum participation of each bus in the implementation of the EDRP is 20% of the load. The power price in the valley, off-peak, and peak is USD 15, 25, and 35 per MW, respectively. The price of gas is USD 350,000/(106 × m3) [29].

Table 1.
State of hours in gas and power networks.
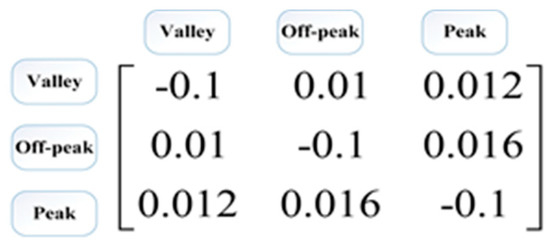
Figure 3.
PEM matrix values.
To compare different LEDRP models, Scenarios 1–5 are defined. Afterwards, to investigate the role of different LEDRP approaches in the integrated operation of gas and power networks, Scenarios 6–9 are defined. Sequentially, Scenarios 10–12 are defined to compare different LEDRP approaches with each other. Finally, the role of the linear LEDRP, in the operation of decarbonized gas and power networks, in case that hydrogen (H2), as a low/zero-carbon energy carrier, is injected instead of natural gas (NG) into the existing gas infrastructure, is investigated (Scenarios 13–14). Details of the scenarios are given in Table 2. First, the implementation effects of EDRP in the power network only and the integrated gas and power networks using DR models are compared. The difference between the objective function in scenarios (1 to 12) is the coefficient in (15). The coefficient equals 0 when the LEDRP is performed only in the power network, and the coefficient is 1 when the LEDRP is executed in both networks.

Table 2.
Details of different scenarios.
3.2. Results and Discussion
3.2.1. Computational Performance
The computational performance of optimizing the integrated operation of gas and power networks during the implementation of the DRP is another important factor in choosing the best DR model. In this context, one of the parameters affecting the computational performance is the number of non-linear variables, increasing the number of iterations and solving time. As shown in Table 3, due to the lower complexity of the linear LEDRP, a shorter optimization time is achieved (i.e., Scenario 2 compared to Scenarios 3–5, and Scenario 6 compared to Scenarios 7–9). Furthermore, the power model, which has the lowest risk from the point of view of energy probability, needs more time to solve the problem due to the more non-linear variables, and consequently, the optimization time is up to 28% more than the linear model. Therefore, the network management operator must determine the appropriate model according to a trade-off between the optimization time, the probability of unsupplied energy, and the operating cost.

Table 3.
Comparison of different models of LEDRP in terms of computer calculations.
3.2.2. Operational Analysis
The costs of the different scenarios are presented in Table 4. Compared to the base case (Scenario 1), the maximum reduction in the TC of the integrated gas and power networks occurs in Scenario 6 (LEDRP linear model in both networks) with a TC of USD 3.083 m (~11%) and the lowest TC reduction in Scenario 3 (LEDRP power model only in the power network) with a TC of USD 3.275 m (~5%). Additionally, according to the results presented in Table 4, the LEDRP in both networks, compared to the LEDRP in the power network, further reduces the cost of the integrated gas and power networks as well as the optimal incentive for the power network.

Table 4.
Effects of LEDRP.
The reduction in TC in the LEDRP in the integrated gas and power networks is not only due to the LEDRP in the gas network. As seen in Figure 4, the implementation of the LEDRP in the gas network has reduced the TC of the power network because of some of the limitations of the gas network peak have been removed by implementing the LEDRP in the gas network. By removing gas restrictions, the power network can make more use of GFPPs that have lower operating costs. On the other hand, according to the results, the highest cost reduction occurs in linear modeling compared to other models due to a reduction in the total demand and peak of demand, reducing the TC of the integrated gas and power networks.

Figure 4.
Total cost of power and gas networks.
As shown in Figure 5 and Figure 6, the linear load response model has the largest peak reduction and, the power model has the smallest peak reduction in response to the incentives. Due to the modeling impacts, despite higher incentives, less reduction in the peak demand is occurred in the power model compared to the linear model. Additionally, the status of the LEDRP in the power network only using linear, power, exponential, and logarithmic models with optimal incentives resulting from optimization operations has a trend similar to Figure 6. Due to the model structure and initial energy price, mainly interruptible loads participate in the EDRP, and the share of shiftable loads is small. Figure 5 and Figure 6 demonstrate that a small amount of peak demand has shifted to non-peak hours, indicating that the major loads participating in peak hours were interruptible types.
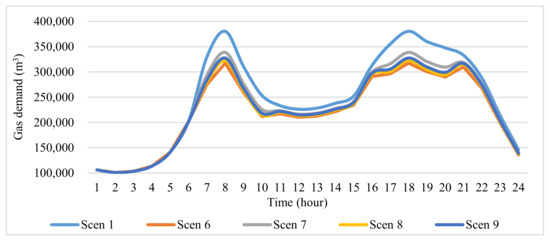
Figure 5.
Impact of LEDRP on gas network consumption curve.
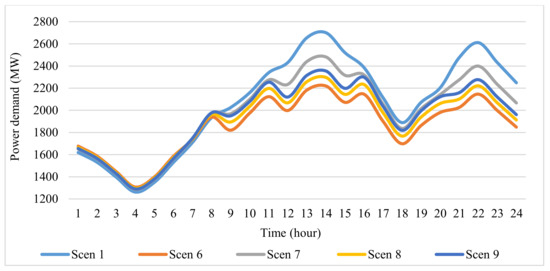
Figure 6.
The effect of LEDRP on the power consumption curve.
Important indicators for evaluating the electricity load curve include total load, peak reduction (PC), peak-to-valley (PTV), load factor (LF), and load reduction percentage, which are presented in Table 5 for different scenarios. According to Table 5, the LEDRP in all scenarios has improved the indices of the power load curve. The highest improvement in indices of load curve is achieved in Scenario 2 with USD 23.86/MW incentive.

Table 5.
Load characteristics of the curve in different scenarios.
The reduction in the peak in the LEDRP depends on the modeling method and incentive payment to the consumer. Since the optimal incentive of the power network in the LEDRP of the integrated gas and power networks is less than in the LEDRP of the power network, the LEDRP of the integrated gas and power networks has less impact on the power network consumption curve. In this context, based on Figure 7, the peak of the electricity consumption curve in the power network during implementation of the LEDRP in the power network is decreasing more than implementing the LEDRP in the integrated gas and power networks. However, due to the utilization of cheaper power plants during the LEDRP’s implementation in the integrated gas and power networks, the cost of power network operation is lower.
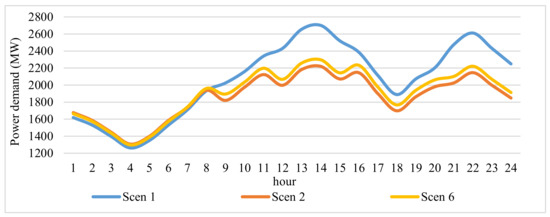
Figure 7.
The effect of linear LEDRP method on electricity consumption curve.
One of the purposes of the LEDRP is to reduce the congestion of power lines and standard deviation of gas changes inside pipes. The congestion of power lines may cause the grid to shut down due to the cascade effect or increase the operating costs of the network by forcing the use of expensive power plants instead of cheap ones. Prior to the LEDRP during peak hours, power lines between 7–8 and 17–22 buses were overloaded. However, after the implementation of the LEDRP, the additional load during peak hours, which may jeopardize the system security is reduced, and the average and standard deviation of ATC percentage of the critical lines, is increased throughout the day. Figure 8 indicates the standard deviation and average of the ATC percentage of all lines and the critical line. As demonstrated, with the implementation of the LEDRP, the average and standard deviation of critical lines and all power lines in all scenarios are improved.
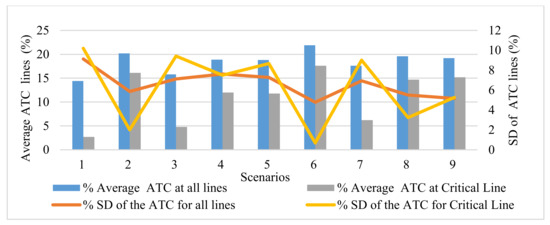
Figure 8.
Standard deviation and average of ATC lines during the implementation of LEDRP.
Furthermore, it is shown that Scenario 6 (implementation of the linear model of the LEDRP in both networks) is the best scenario due to a further increase in the mean and further decrease in the standard deviation. The lower standard deviation of gas changes in the gas pipe leads to the more efficient operation of the gas network and causes less stress on the operation of the gas network. According to Figure 9, Scenario 6 results in the smallest standard deviation (5.99%) in the linepack compared to other scenarios, making it a potential candidate for implementation of the LEDRP.
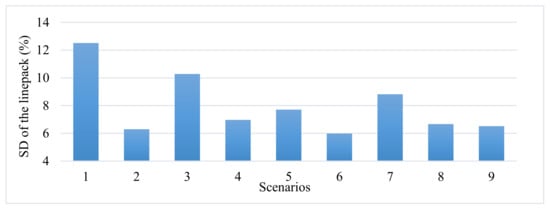
Figure 9.
Standard deviation of linepack changes in the gas network.
It is worth mentioning that the demand estimation error by different DR models should be taken into account. If a non-conservative and unreliable demand model is used to estimate the demand, the system may not be able to keep the supply–demand balance, which increases the cost of the system. Therefore, choosing an accurate demand model could have considerable effects on the results.
Figure 10 shows the load curve estimation error, which is the difference between linear and non-linear DR models (). In this figure, it is assumed that the estimated demand of the linear model is the real demand, and it is compared with the estimated demand of the non-linear models. The most considerable difference between estimated demand and actual demand occurs in Scenario 10. Negative values indicates that the demand estimated by the model is lower than the actual demand. The power model is a reliable model due to the lower estimate of the peak demand reduction for implementing the LEDRP than other models (with the same incentive). However, it is worth mentioning that according to Table 4 as well as Figure 8 and Figure 9, the LEDRP of the power model in both networks (despite the highest incentive compared to other models when implementing the LEDRP in both networks) reduces the TC by 2%, the average percentage of line congestion by 9%, and the standard deviation of linepack gas changes by 2% less than the linear model (as the best scenario in terms of cost reduction and congestion). Finally, the power model is more suitable for estimating the DR due to the low reduction in peak demand for the integrated gas and power networks, despite increasing costs, lower reduction in line congestion, and changes in linepack standard deviation. Since the cost of unsupplied demand is not considered, considering this cost is possible to offset the increased cost caused by the improving reliability. In other words, if the network operator wants to carry out a conservative estimate to predict the effect of the LEDRP, the power model should be implemented instead of the linear model to estimate the load.
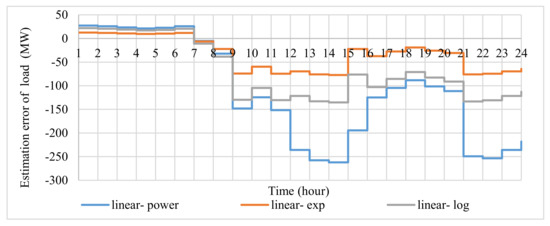
Figure 10.
Load curve estimation error.
Moreover, LEDRP implementation in the integrated gas and power networks in similar modeling improves the TC by 3%, the line congestion, and the standard deviation of gas changes inside gas pipes by 1% compared to the LEDRP implementation alone in the power network. The choice of a reliable and conservative demand estimator is such that a selected model predicts the maximum amount of demand. The power model (conservative option) has the highest predicted value of peak demand and the highest difference of peak demand compared to the linear model. Thus, despite the reduced lower cost, congestion, and peak of the load curve, the power model is more reliable for estimating demand because the cost of non-supply is neglected here, which may offset these costs. In other words, the system operator should choose the power model for demand estimation instead of the linear model.
3.2.3. Injection of Hydrogen through the Gas Infrastructure
In Scenarios 13 and 14, the injection of hydrogen through the infrastructure is investigated. Hydrogen is a carbon-free source of energy and could thus facilitate the transition to a decarbonized energy system. Low/zero-carbon hydrogen could be produced through fossil fuels along with carbon capture and storage (CCS), i.e., “blue” hydrogen, or in an electrolysis process, i.e., “green” hydrogen. In this context, Scenarios 13 and 14 are defined, in which, compared to Scenarios 1 and 6, hydrogen is injected into the gas network instead of natural gas. As presented in Table 6, it is demonstrated that in Scenario 13, due to the physics of hydrogen flow within the pipelines, hydrogen is not entirely delivered to the demand centers and the gas power plants; hence, load shedding of 50 MWh in the power network and 0.165 (106 × m3) in the gas network occurred. However, in Scenario 14, due to the flexibility provided by DRP (similar to Scenario 6), the supply–demand balance in both systems is maintained. It is worth mentioning that in the natural gas scenarios (Scenarios 1–12), the unserved demand is zero.

Table 6.
The amount of energy not provided in different scenarios.
4. Conclusions
In this paper is the effect of LEDRP models and their implementation environment during the simultaneous operation of gas and power networks is investigated. The incentive for each bus or node is determined in the LEDRP based on the PTDFs, GTDFs, ATC, and the combined optimization of the LEDRP and UC. The proposed hybrid model is applied to a 24-bus IEEE network and a 15-node gas network to quantify different LEDRP modeling approaches. According to the results, considering the LEDRP in gas and power networks (compared with applying the LEDRP in power network only) reduces the TC by 3%, the power-line congestion by 1%, and the standard deviation of the gas pipes linepacks by 1%. Furthermore, due to the implementation of the DRPs in the gas network, as well as the occurrence of different peak hours in gas and electricity demand, the GFPP are utilized cost-efficiently. As a result, the most considerable savings are achieved when the linear LEDRP is implemented in both networks. The total operation costs of gas and power networks compared to the base case (no LEDRP implementation) are reduced by nearly 11%. In regard to the modeling of consumers’ behavior in return for payment incentives in the LEDRP, the linear model is more appropriate than other models in terms of cost reduction, line congestion, and standard deviation of linepack changes. However, if the load reduction does not materialize as expected, the linear model is more challenging from an unserved demand point of view. The power model is the most reliable due to a lower peak reduction than other models with the same incentive. By applying this model, challenges related to the lack of generation and the cost of supply and demand imbalances are not imposed on the system. However, the power model increases the TC by about 2%, the average power line congestion by 9%, and the standard deviation of gas pipe linepack changes by 2% compared to other models. In this regard, if an incorrect and unreliable DR model is chosen to estimate demand, the network power plants may not be able to supply the demand and consequently, the operational cost of the network will be high. Therefore, according to the results, the system operator must select the power model to estimate the demand, despite the increase in cost. Furthermore, it was demonstrated that the DRP could facilitate hydrogen injection into the gas infrastructure by maintaining the supply–demand balance.
Author Contributions
Conceptualization, H.A., M.T.A. and G.S.; methodology, M.M.D. and H.A.; software, M.M.D.; validation, M.M.D. and H.A.; formal analysis, M.M.D. and H.A.; investigation, M.M.D. and H.A.; resources, H.A., M.T.A. and G.S.; data curation, M.M.D. and H.A.; writing—original draft preparation, M.M.D.; writing—review and editing, H.A., M.T.A. and G.S.; visualization, M.M.D. and H.A.; supervision, H.A., M.T.A. and G.S.; project administration, M.T.A.; funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EPSRC-funded programs grant numbers EP/K000446/1 and EP/T022949/1, And the APC was funded by EPSRC.
Informed Consent Statement
Not Applicable.
Acknowledgments
The authors gratefully acknowledge the EPSRC-funded programs “UK Carbon Capture and Storage (UKCCSRC)” under grant number EP/K000446/1 as well as the “Zero-Carbon Emission Integrated Cooling, Heating and Power (ICHP) Networks” under award number EP/T022949/1.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Abbreviations | l | Transmission lines index | |
| ATC | Available transmission capability | n | Node index |
| CCS | carbon capture and storage | p | Pipeline index |
| CM | Congestion management | s | Terminal nodes index |
| DR | Demand response | t | Time index |
| DRPs | demand response programs | q | Storage index |
| EDRP | Emergency demand response program | Parameters | |
| FACT | Flexible AC transmission | Cost coefficients for generation unit g | |
| GFPP | Gas-fired power plants | Susceptance of line l (℧) | |
| GTDF | Gas transfer distribution factor | Cost of gas supply (USD/m3) | |
| LEDRP | Local emergency demand response program | Startup/Shutdown cost of generating unit g (USD) | |
| LF | Load factor | Initial demand of node n at time t in the gas network (106 × m3) | |
| PC | Peak reduction | Diameter of pipe p (mm) | |
| PEM | Price elasticity matrix | Initial demand of i bus and t time at the power network (MW) | |
| P2H | Power to heating | Point-valve effect coefficients for generation unit g | |
| P2G | Power to gas | Maximum/Minimum gas storage level of facility q (m3) | |
| PTDF | Power transfer distribution factor | Gas heating value | |
| PTV | Peak to valley | Length of pipe p (m) | |
| SCUC | Security-constrained unit commitment | Initial gas stored in the pipe p and time t (106 × m3) | |
| TC | Total cost | Number of POZs for the generation unit g | |
| UC | Unit commitment | Thermal limitation for line l at time t (MW) | |
| Index | Maximum/Minimum output power for generation unit g (MW) | ||
| c | Compressor index | Wind power at bus i and time t (MW) | |
| g | generation unit index | Upper limits for the Rth POZ (MW) | |
| i,j | Bus index | Lower limits for the Rth POZ (MW) | |
| Maximum/Minimum pressure limits at node n (Pa) | Thermal efficiency of gas-fired power plants | ||
| Maximum power consumption of compressor c (Pa) | Gas density under standard condition (0.713 kg/m3) | ||
| Maximum/Minimum range for gas flow within pipeline p (m3/h) | Variables | ||
| Maximum/Minimum gas flow rate to compressor c (m3/h) | Available transfer capability of line l (MW) | ||
| Maximum output of the q gas storage (m3/h) | B(d(t)) | The benefit of consuming energy d(t) at time t (USD) | |
| Maximum/Minimum capacity of gas flow rate of terminal s (8.5 × 106 × m3/h) | Gas price at time t (USD/(106 × m3)) | ||
| Maximum input of the q gas storage (m3/h) | Cost of EDRP in the power network (USD) | ||
| Ramp-down of the generation unit g (MW/h) | Electricity demand at node i and time t (MW) | ||
| The maximum ratio of the inlet /outlet pressure in compressors (1.5) | Gas demand at node n, time t (106 × m3) | ||
| Gas constant for natural gas (518 J/(kg × K)) | d(t) | consumed energy at time t (MW) | |
| Ramp-up of the generation unit g (MW/h) | Gas storage level of storage facility q at time t (m3) | ||
| Startup ramp of the generation unit g (MW/h) | Incentives applied to bus i of the power network at time t (USD/MW) | ||
| Shutdown ramp of the generation unit g (MW/h) | Commitment status of generation unit g at time t (0 OR 1) | ||
| Gas temperature under standard condition (288 ‘degree’ K) | Incentives applied to node n of the gas network at time t (USD/(106 × m3)) | ||
| Minimum up/down time of thermal generation unit g (h) | Total received incentives at time t from the network (USD) | ||
| Natural gas compressibility factor (0.95) | Linepack in pipeline p and time t (m3/h) | ||
| Polytrophic exponent of a gas compressor | Pressure at node n and time t (Pa) | ||
| Pipeline efficiency (80%) | Non-execution penalty of DR at time t (USD) | ||
| Compressor efficiency (80%) | The average pressure inside the pipe p and time t (Pa) | ||
| Initial electricity price at hour t (USD) | The sensitivity coefficient of line l to the changing demand in the bus i | ||
| Consumption power of c compressor at time t (MW) | Gas flow of the pipeline p at time t (m3/h) | ||
| Inlet gas pressure to compressor c at time t (Pa) | Outlet gas flow related to the pipeline p at time t (m3/h) | ||
| Outlet gas pressure from compressor c at time t (Pa) | Essential spinning reserve at time t (MW) | ||
| Power flow of the line l at time t (MW) | Transfer limitation associated with line l and bus i (MW) | ||
| Total paid fines at time t to the network (USD) | Volume of gas related to pipeline p at time t (m3) | ||
| Produced power of the power plant g at the time t (MW) | Voltage angle for line l at time t (rad) | ||
| Outlet gas from the storage q at time t (m3/h) | Electricity price at hour t (USD) | ||
| Gas consumption of gas-fired power plant g at time t (m3/h) | Power change in bus i (MW) | ||
| Inlet gas from the storage q at time t (m3/h) | Power change in line l (MW) | ||
| Gas flow through c compressor at time t (m3/h) | α | Optimal average power incentive (USD/MW) | |
| Inlet gas flow to the pipeline p at time t (m3/h) | γ | Optimal average gas incentive (USD/(106 × m3)) | |
| Gas flow rate related to terminal at node s and time t (m3/h) |
References
- Hines, P.; Apt, J.; Talukdar, S. Large blackouts in North America: Historical trends and policy implications. Energy Policy 2009, 37, 5249–5259. [Google Scholar] [CrossRef]
- Zhao, S.; Ming, Z. Modeling demand response under time-of-use pricing. In Proceedings of the 2014 International Conference on Power System Technology (POWERCON), Chengdu, China, 20–22 October October 2014; pp. 1948–1955. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Yang, C.; Xie, S.; Zhang, Y. Distributed Demand Response for Multi-Energy Residential Communities with Incomplete Information. IEEE Trans. Ind. Inform. 2020, 17, 547–557. [Google Scholar] [CrossRef]
- El-Bayeh, C.Z.; Eicker, U.; Alzaareer, K.; Brahmi, B.; Zellagui, M. A Novel Data-Energy Management Algorithm for Smart Transformers to Optimize the Total Load Demand in Smart Homes. Energies 2020, 13, 4984. [Google Scholar] [CrossRef]
- Li, C.; Yao, Y.; Zhao, C.; Wang, X. Multi-Objective Day-Ahead Scheduling of Power Market Integrated with Wind Power Producers Considering Heat and Electricity Trading and Demand Response Programs. IEEE Access 2019, 7, 181213–181228. [Google Scholar] [CrossRef]
- Cui, H.; Xia, W.; Yang, S.; Wang, X. Real-time emergency demand response strategy for optimal load dispatch of heat and power micro-grids. Int. J. Electr. Power Energy Syst. 2020, 121, 106127. [Google Scholar] [CrossRef]
- Aalami, H.A.; Moghaddam, M.P.; Yousefi, G.R. Evaluation of non-linear models for time-based rates demand response programs. Int. J. Electr. Power Energy Syst. 2015, 65, 282–290. [Google Scholar] [CrossRef]
- Shayesteh, E.; Yousefi, A.; Moghaddam, M.P.; Yousefi, G.R. An economic comparison between incorporation of FACTS devices and demand response programs for ATC enhancement. In Proceedings of the 2008 IEEE Canada Electric Power Conference, Vancouver, BC, Canada, 6–7 October 2008; pp. 1–6. [Google Scholar]
- Kumar, A.; Kumar, M. Available transfer capability determination using power transfer distribution factors. Int. J. Inf. Comput. Technol. 2013, 3, 1035–1040. [Google Scholar]
- Arif, A.; Javed, F.; Arshad, N. Integrating renewables economic dispatch with demand-side management in micro-grids: A genetic algorithm-based approach. Energy Effic. 2014, 7, 271–284. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Multi-objective dynamic economic emission dispatch of electric power generation integrated with game theory-based demand response programs. Energy Convers. Manag. 2015, 89, 963–974. [Google Scholar] [CrossRef]
- Abdi, H.; Dehnavi, E.; Mohammadi, F. Dynamic economic dispatch problem integrated with demand response (DEDDR) considering non-linear responsive load models. IEEE Trans. Smart Grid 2015, 7, 2586–2595. [Google Scholar] [CrossRef]
- Dehnavi, E.; Abdi, H. Optimal pricing in time of use demand response by integrating with dynamic economic dispatch problem. Energy 2016, 109, 1086–1094. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Hourly electricity demand response in the stochastic day-ahead scheduling of coordinated electricity and natural gas networks. IEEE Trans. Power Syst. 2015, 31, 592–601. [Google Scholar] [CrossRef]
- Ameli, H.; Qadrdan, M.; Strbac, G. Coordinated operation of gas and electricity systems for flexibility study. Front. Energy Res. 2020, 8. [Google Scholar] [CrossRef]
- Tafarte, P.; Kanngießer, A.; Dotzauer, M.; Meyer, B.; Grevé, A.; Millinger, M. Interaction of electrical energy storage, flexible bioenergy plants and system-friendly renewables in wind-or solar PV-dominated regions. Energies 2020, 13, 1133. [Google Scholar] [CrossRef] [Green Version]
- Sardou, I.G.; Khodayar, M.E.; Ameli, M.T. Coordinated operation of natural gas and electricity networks with microgrid aggregators. IEEE Trans. Smart Grid 2016, 9, 199–210. [Google Scholar] [CrossRef]
- Liu, F.; Bie, Z.; Wang, X. Day-ahead dispatch of integrated electricity and natural gas system considering reserve scheduling and renewable uncertainties. IEEE Trans. Sustain. Energy 2018, 10, 646–658. [Google Scholar] [CrossRef]
- Rostami, A.M.; Ameli, H.; Ameli, M.T.; Strbac, G. Secure Operation of Integrated Natural Gas and Electricity Transmission Networks. Energies 2020, 13, 4954. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, X.; Li, X.; Yan, W. Probabilistic steady-state operation and interaction analysis of integrated electricity, gas and heating systems. Energies 2018, 11, 917. [Google Scholar] [CrossRef] [Green Version]
- Nikzad, M.; Mozafari, B. Reliability assessment of incentive-and priced-based demand response programs in restructured power systems. Int. J. Electr. Power Energy Syst. 2014, 56, 83–96. [Google Scholar] [CrossRef]
- Wang, F.; Ge, X.; Yang, P.; Li, K.; Mi, Z.; Siano, P.; Duić, N. Day-ahead optimal bidding and scheduling strategies for DER aggregator considering responsive uncertainty under real-time pricing. Energy 2020, 213, 118765. [Google Scholar] [CrossRef]
- Schweppe, F.C.; Caramanis, M.C.; Tabors, R.D.; Bohn, R.E. Spot Pricing of Electricity; Springer Science and Business Media: Berlin, Germany, 2013. [Google Scholar]
- Roos, G.; Lane, I.E. Industrial power demand response analysis for one port real-time pricing. IEEE Trans. Power Syst. 1998, 13, 159–164. [Google Scholar] [CrossRef]
- Aalami, H.A.; Moghaddam, M.P.; Yousefi, G.R. Modeling and prioritizing demand response programs in power markets. Electr. Power Syst. Res. 2010, 80, 426–435. [Google Scholar] [CrossRef]
- Dehnavi, E.; Abdi, H. Determining optimal buses for implementing demand response as an effective congestion management method. IEEE Trans. Power Syst. 2016, 32, 1537–1544. [Google Scholar] [CrossRef]
- Ameli, H.; Qadrdan, M.; Strbac, G.; Ameli, M.T. Investing in flexibility in an integrated planning of natural gas and power systems. IET Energy Syst. Integr. 2020, 2, 101–111. [Google Scholar] [CrossRef]
- He, C.; Zhang, X.; Liu, T.; Wu, L.; Shahidehpour, M. Coordination of interdependent electricity grid and natural gas network—a review. Curr. Sustain./Renew. Energy Rep. 2018, 5, 23–36. [Google Scholar] [CrossRef]
- Shabazbegian, V.; Ameli, H.; Ameli, M.T.; Strbac, G. Stochastic optimization model for coordinated operation of natural gas and electricity networks. Comput. Chem. Eng. 2020, 142, 107060. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).