A Horse Herd Optimization Algorithm (HOA)-Based MPPT Technique under Partial and Complex Partial Shading Conditions
Abstract
:1. Introduction
1.1. Prior Works
1.2. Contribution
- Its superiority is underlined by the experimental results and, since only one parameter is used for the exploration and exploitation phase it results, in terms of quick tracking, in almost zero oscillations.
- The HOA particles are able to remain stationary and the oscillation becomes equal to zero when a cycle of iteration ends, and the power converging efficiency is approximately 99.1%. The absence of this characteristic in PSO and ACS, etc. results in the loss of power and unwanted oscillations.
- The comparison between the HOA and the existing scheme is performed under four different scenarios of weather conditions. The HOA technique can harvest maximum energy under PS and CPS. Moreover, the results of tracking the MPP under different PS and CPS scenarios are represented in the experimental part of this paper, which clearly shows that the HOA technique performs better with respect to convergence rate and zero oscillation, as well as fast-tracking in comparison to P&O, InC, PSO, ACS, and DFO. The HOA technique does not oscillate on GM and will successfully reach a steady state, resulting in the increase in efficiency of the overall system.
1.3. Organization
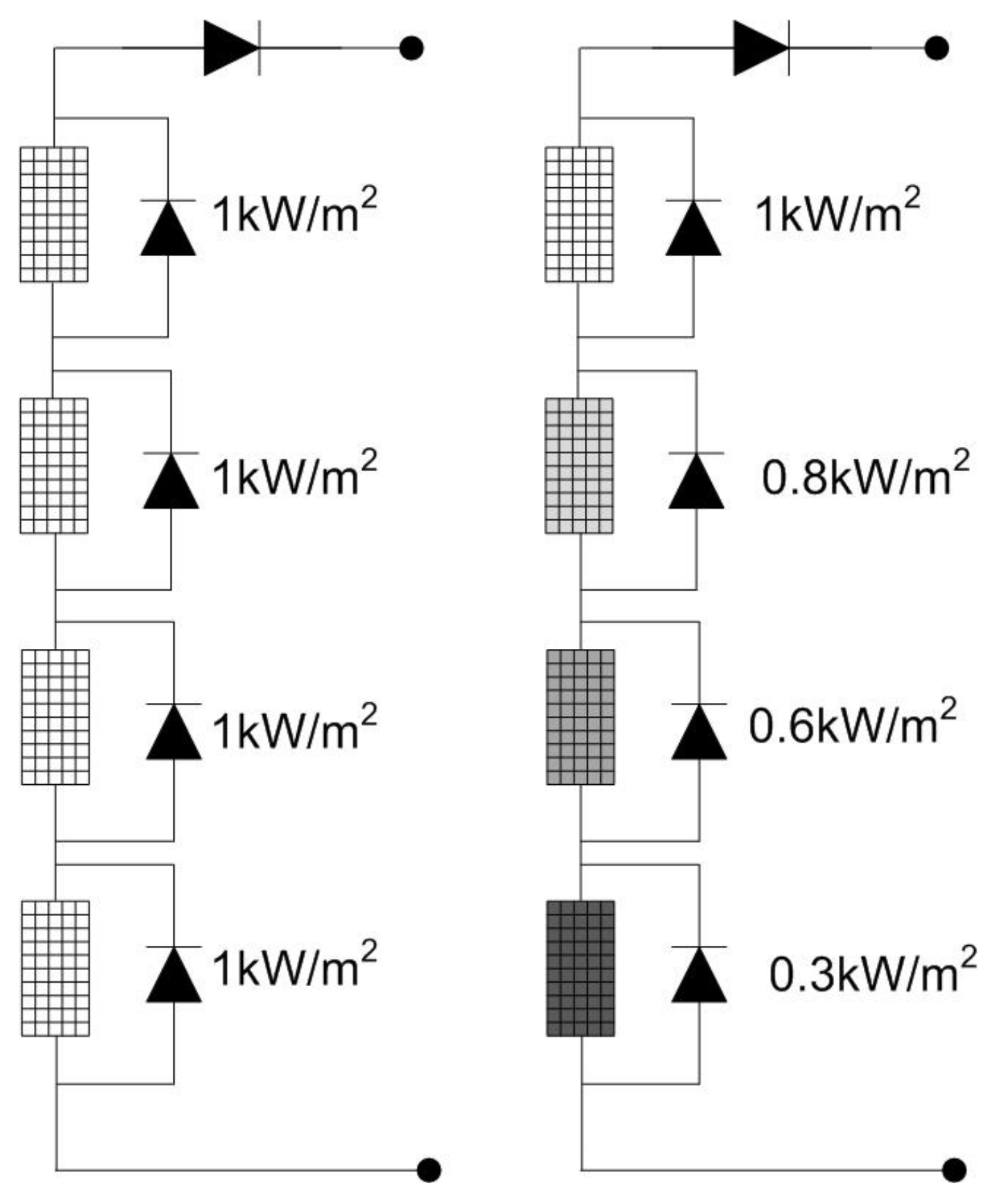
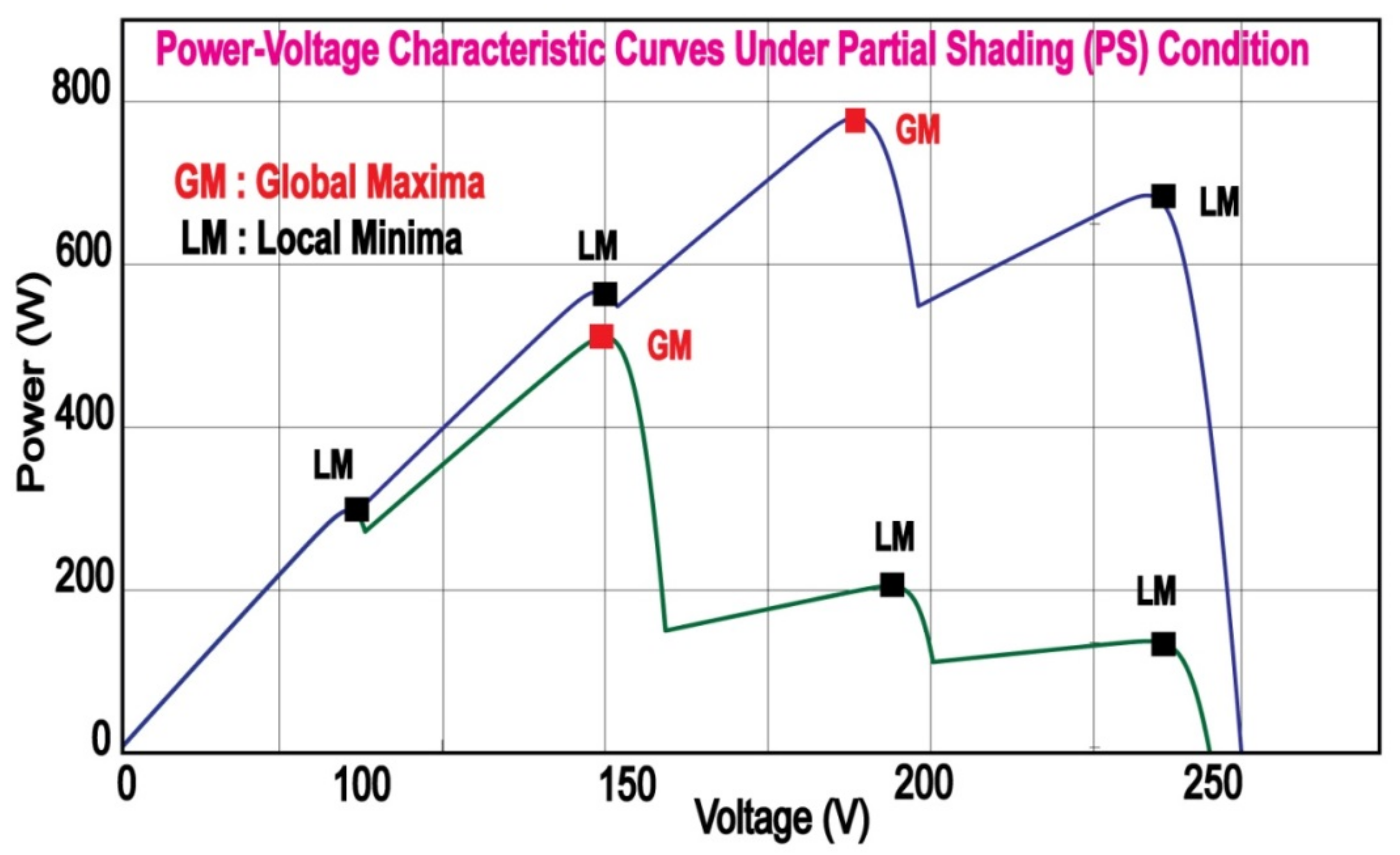
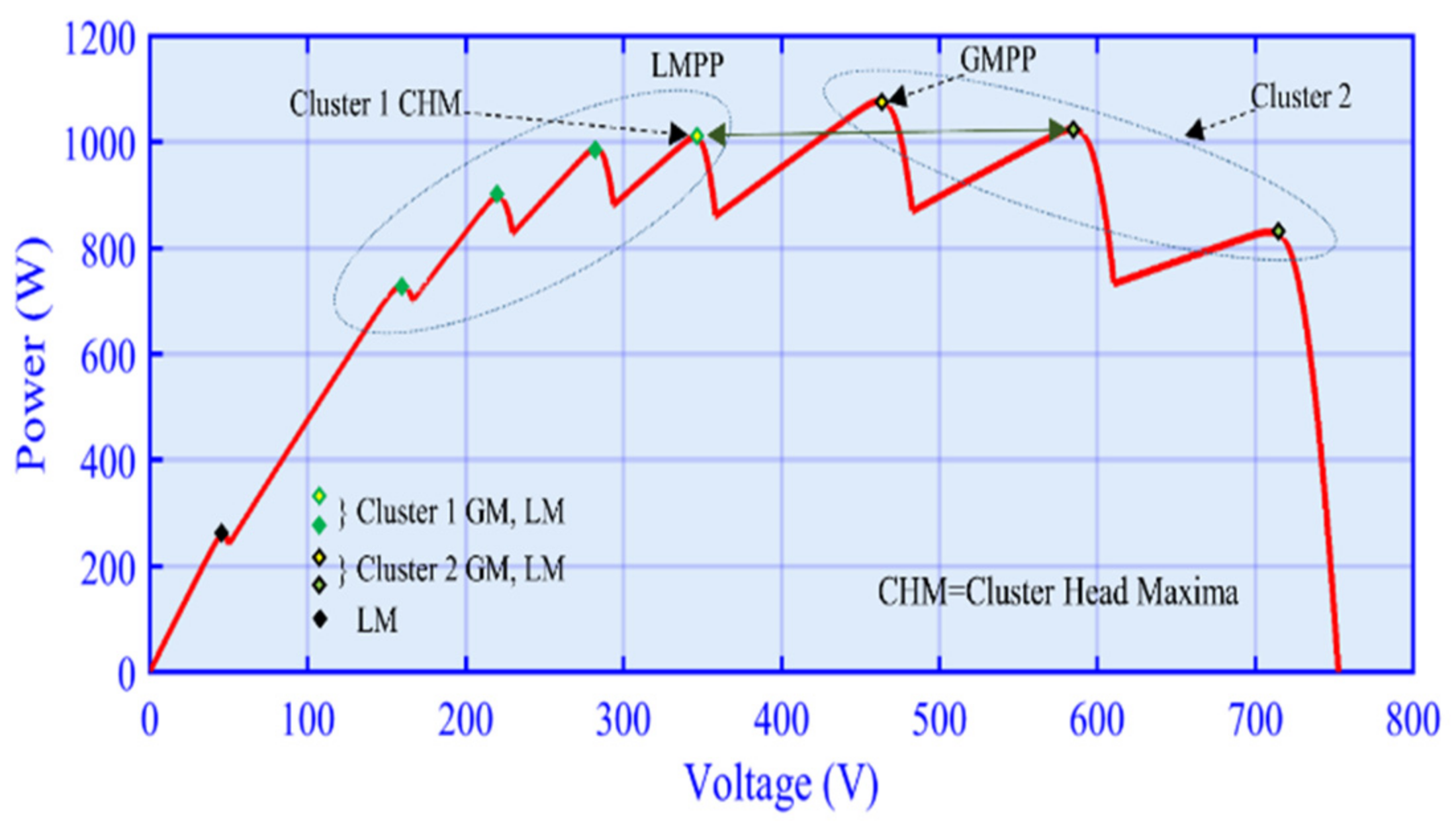
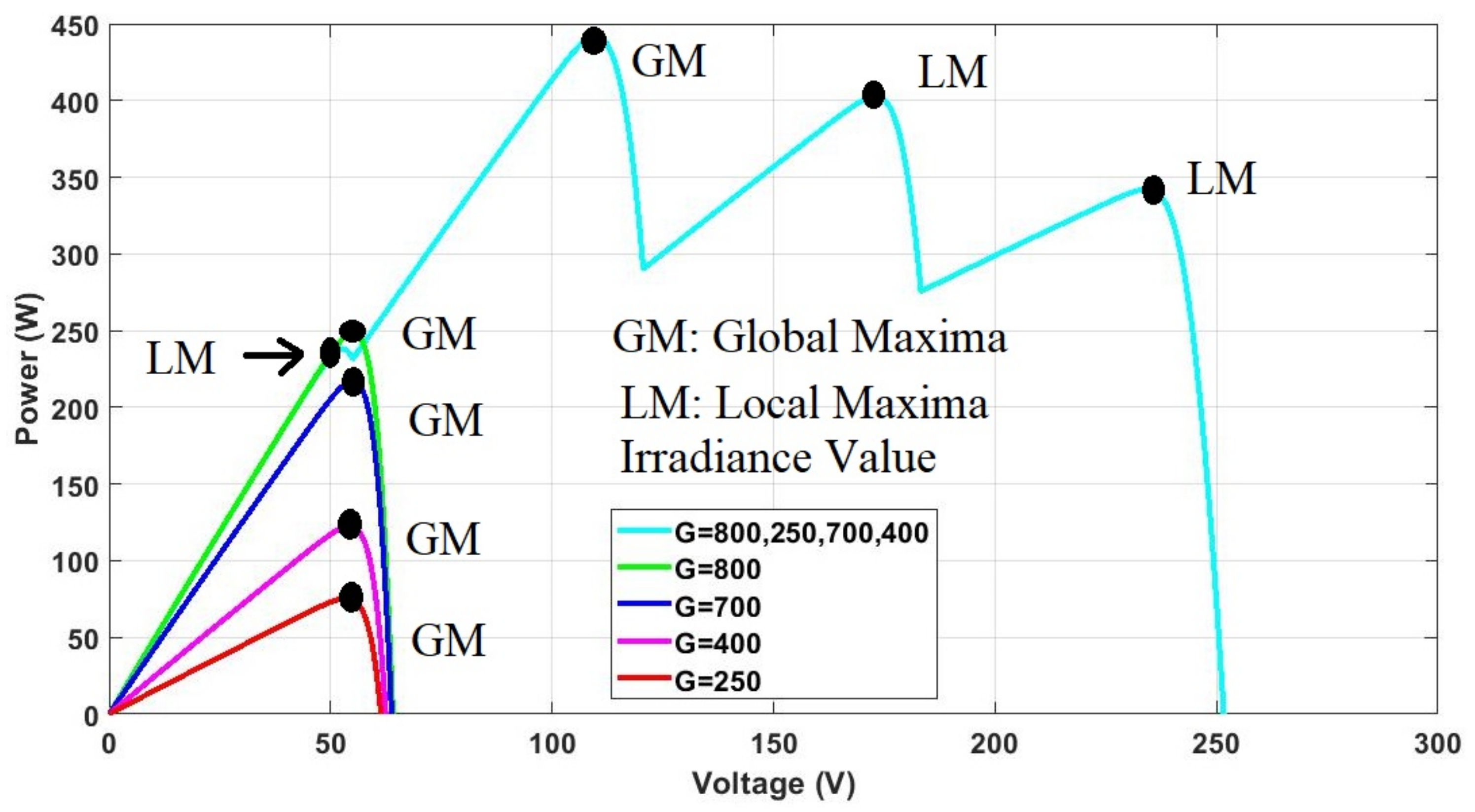
2. Partial and Complex Partial Shade
3. Mathematical Model of the HOA Algorithm
- denotes the horse position.
- shows the range of each horse.
- describes the current number of iterations.
- illustrates the velocity of the vector of that horse.
3.1. Grazing (Gra)
3.2. Hierarchy (H)
3.3. Sociability (Soc)
- describes the vector of social motion that is presented by the horse.
- shows the orientation of that horse in the direction of group .
- iter, the iteration is reduced in every cycle, has a parameter of .
- expresses the total number of horses.
- age represents the age range of each horse.

3.4. Imitation (Im)
- expresses the vector of motion that represents the horse around the average of the best horse at P position.
- shows the orientation of that horse in the direction of the group on the iteration. This is reduced in every cycle, with a parameter of .
- represents the number of horses in the best positions, where is 10% of the selected horses.
- is a reduction factor per cycle for .
3.5. Defense Mechanism (DefMec)
- describes the escape vector of the horse, based around the average position of a horse in the worst P position.
- shows the number of horses in the worst positions, where is 20% of the total horses.
- represents the reduction factor per cycle for iIter that was calculated earlier.
3.6. Roam (Ro)
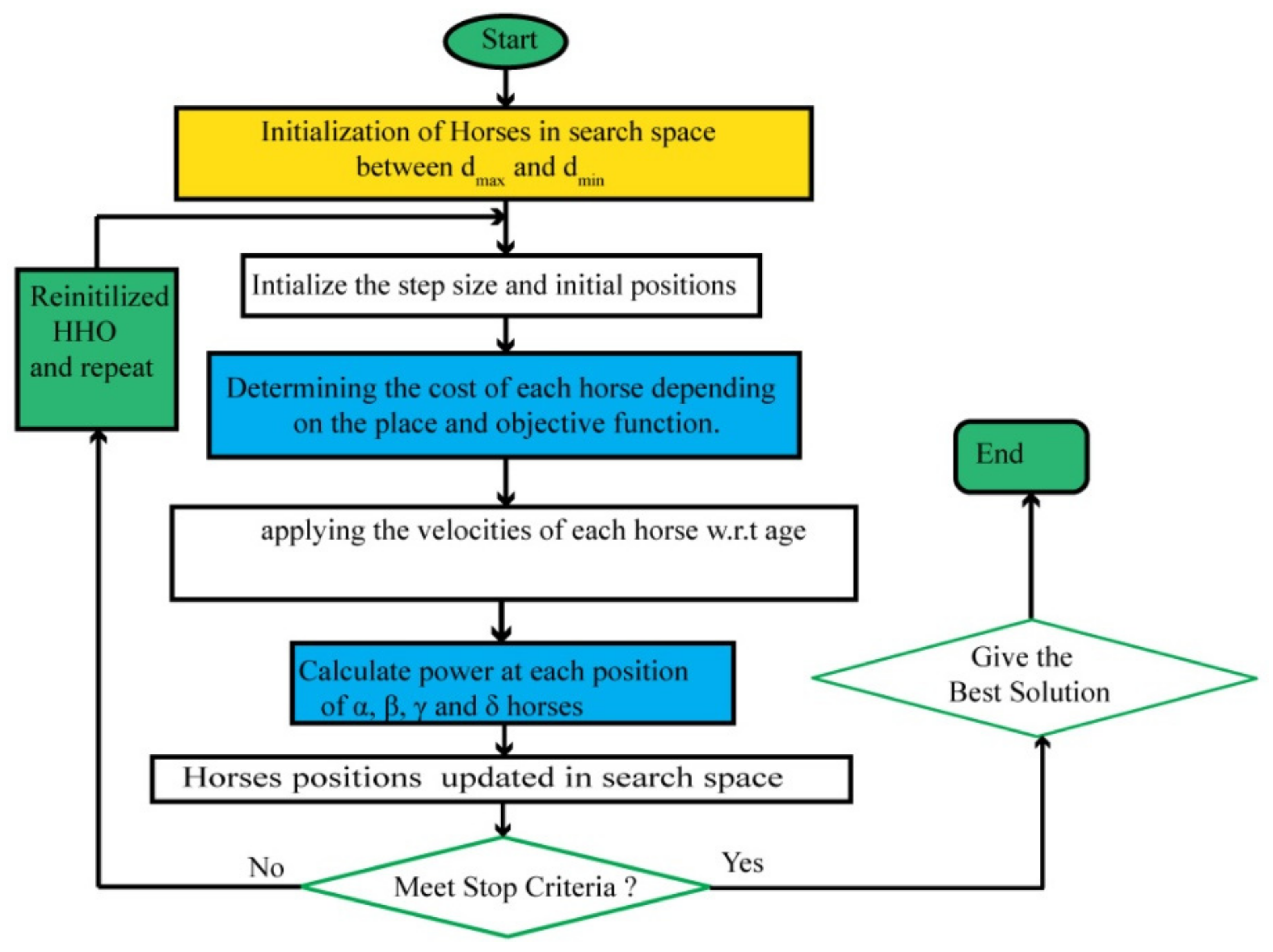
- The α horses will get the best reactions and also serve as role models for the rest. They take over the coaching role as they begin their hunt for the optimum reaction and develop an exploited strategy. When the characteristics of grazing and defensive mechanisms must be used, this behavior occurs.
- The β horses diligently look for the most likely ideal locations, paying great attention to α.
- The γ horses are created using all their inherent behaviors. They seem to be useful for both the explorative and exploitative phases, even though they exhibit both strong and arbitrary movements.
- Young horses seem to be more rambunctious and livelier, making them more suited to the exploring period.
- The horse herd optimization algorithm (HOA) is a novel MPPT approach that has been developed.
- To collect the GM, the proposed approach needed fewer iterations.
- In PS and CPS situations, the proposed approach shows almost no oscillation and can collect GM.
- Experiments and findings show that the proposed approach with interims of rapid searching and minimal oscillation is preferable.
- A statistical study is performed to determine the algorithm’s efficiency, detecting speed, and steady-state reaction.
- (a)
- Basic configuration: providing variables with a boundary limit and other factors.
- (b)
- Initializing: creating a suitable space with a uniform random selection of horses.
- (c)
- Checking fitness level: determining the cost of each horse, depending on the place and objective function.
- (d)
- Evaluating age: assessing the ages of (α, β, γ, and δ) horses.
- (e)
- Implement the velocity: with respect to every horse’s age, apply the velocity.
- (f)
- Revise the position: updating the position of all horses in the search space.
- (g)
- End: if the stop criteria are not met, go to step (c).
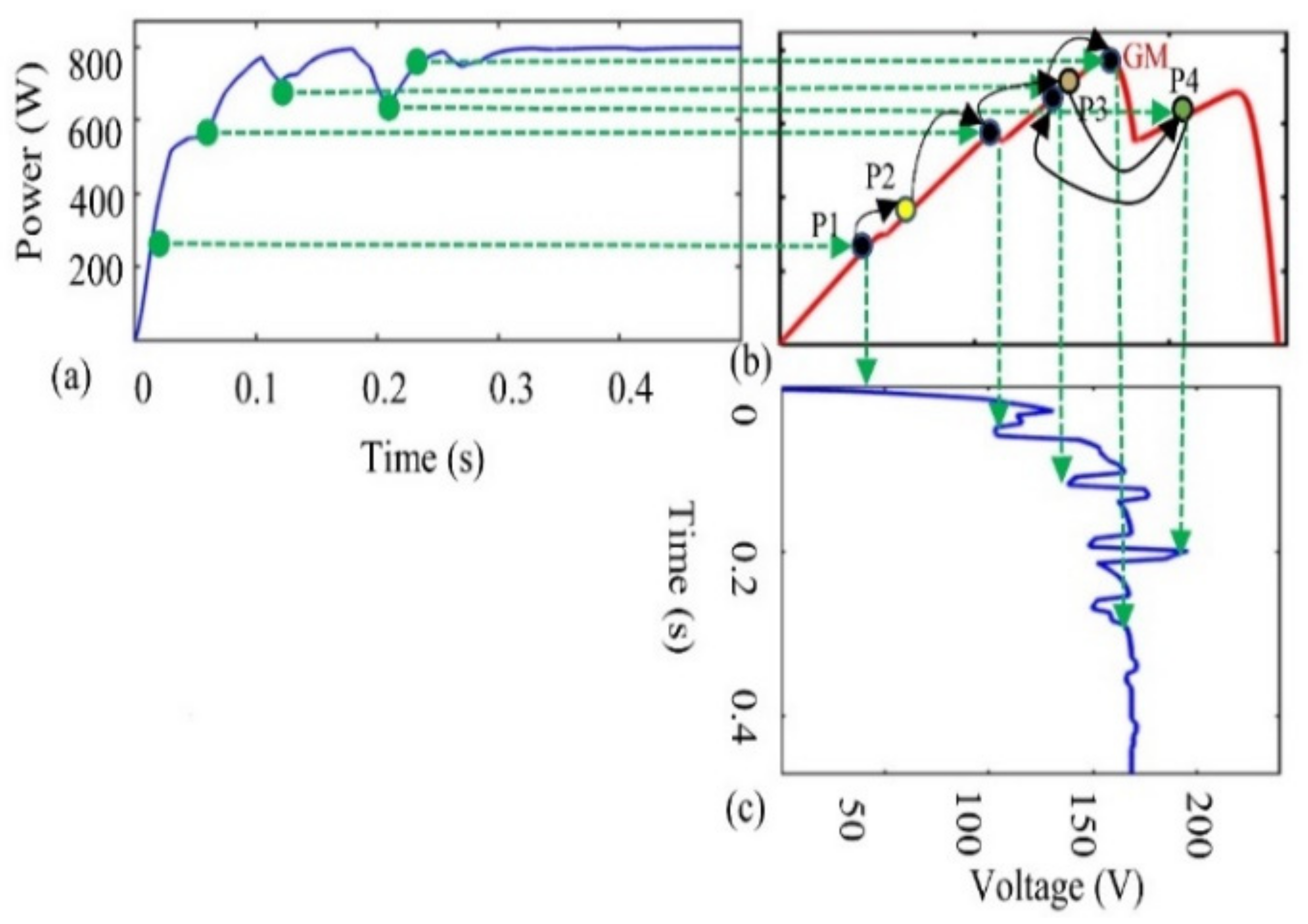
4. Tracking Mechanism of HOA
HOA under Complex Partial Shading (CPS) Conditions
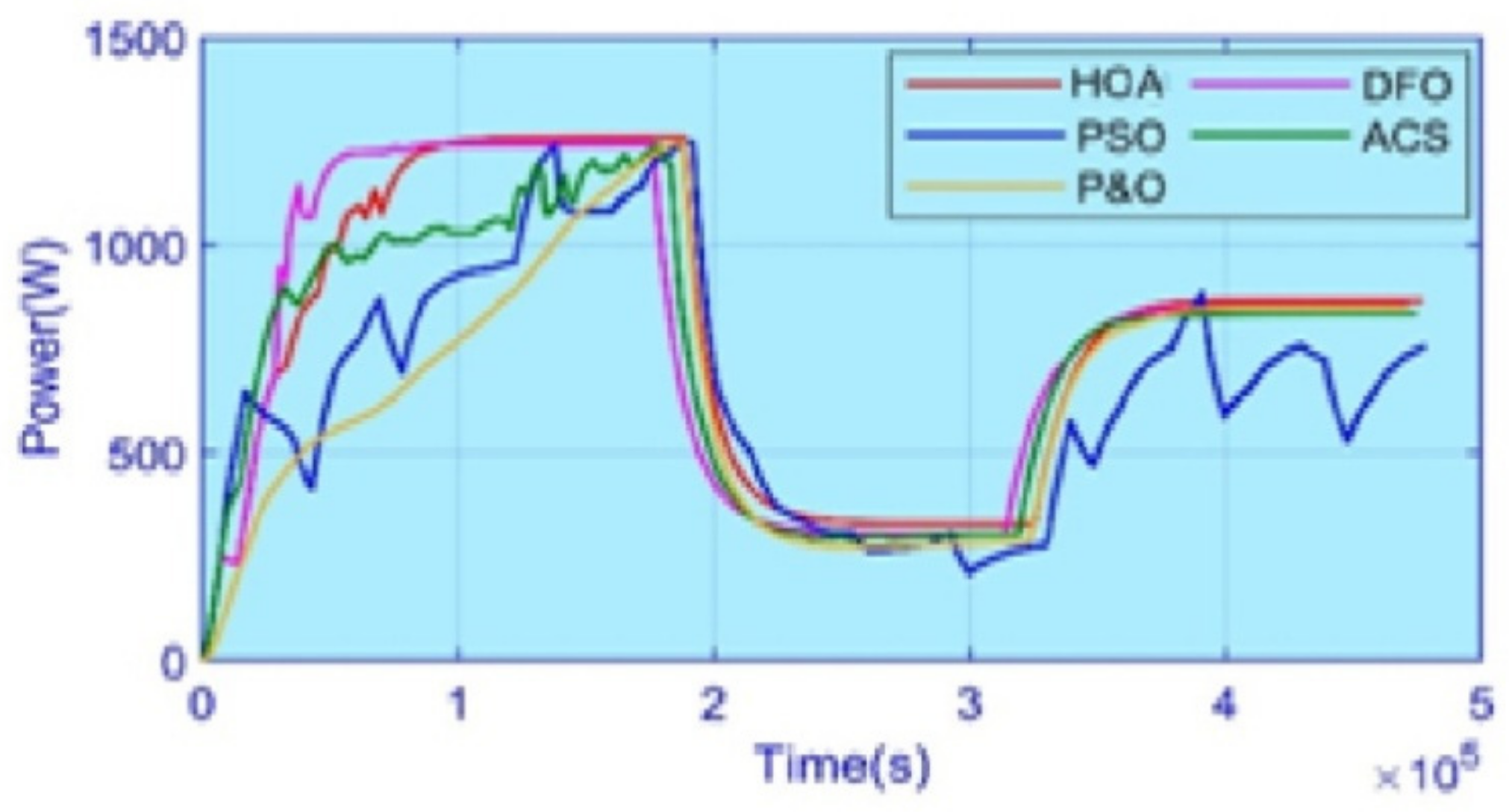
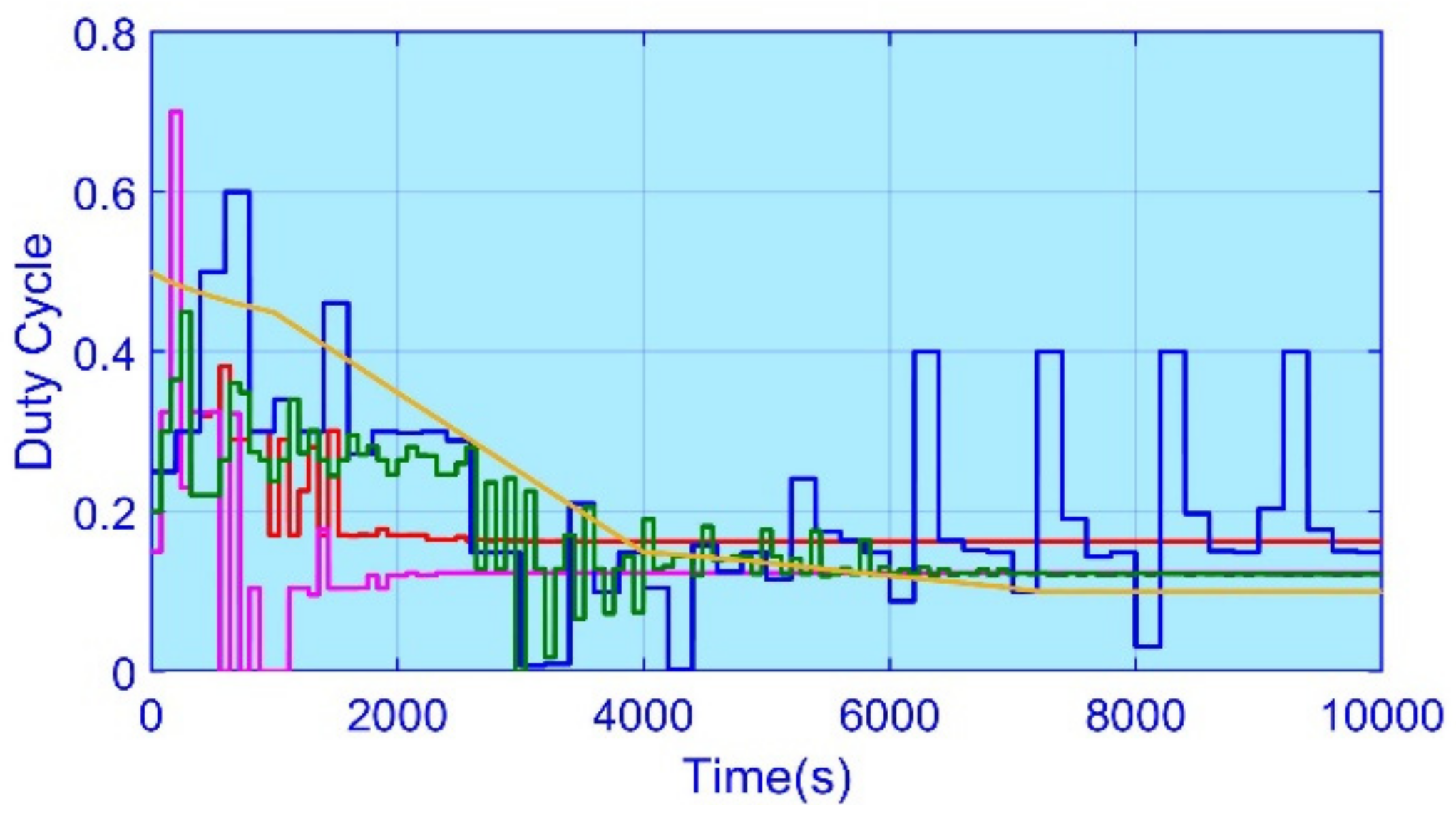
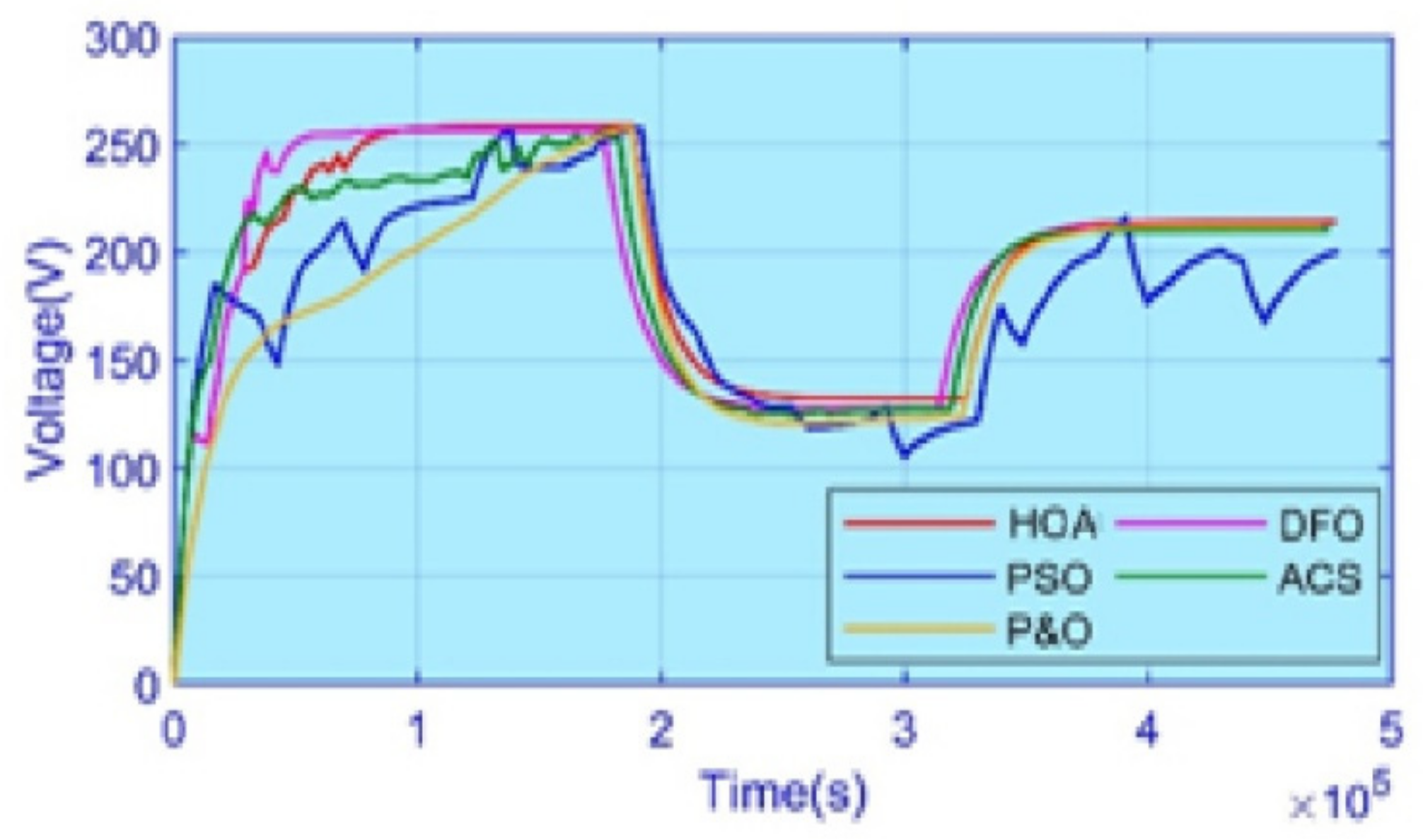
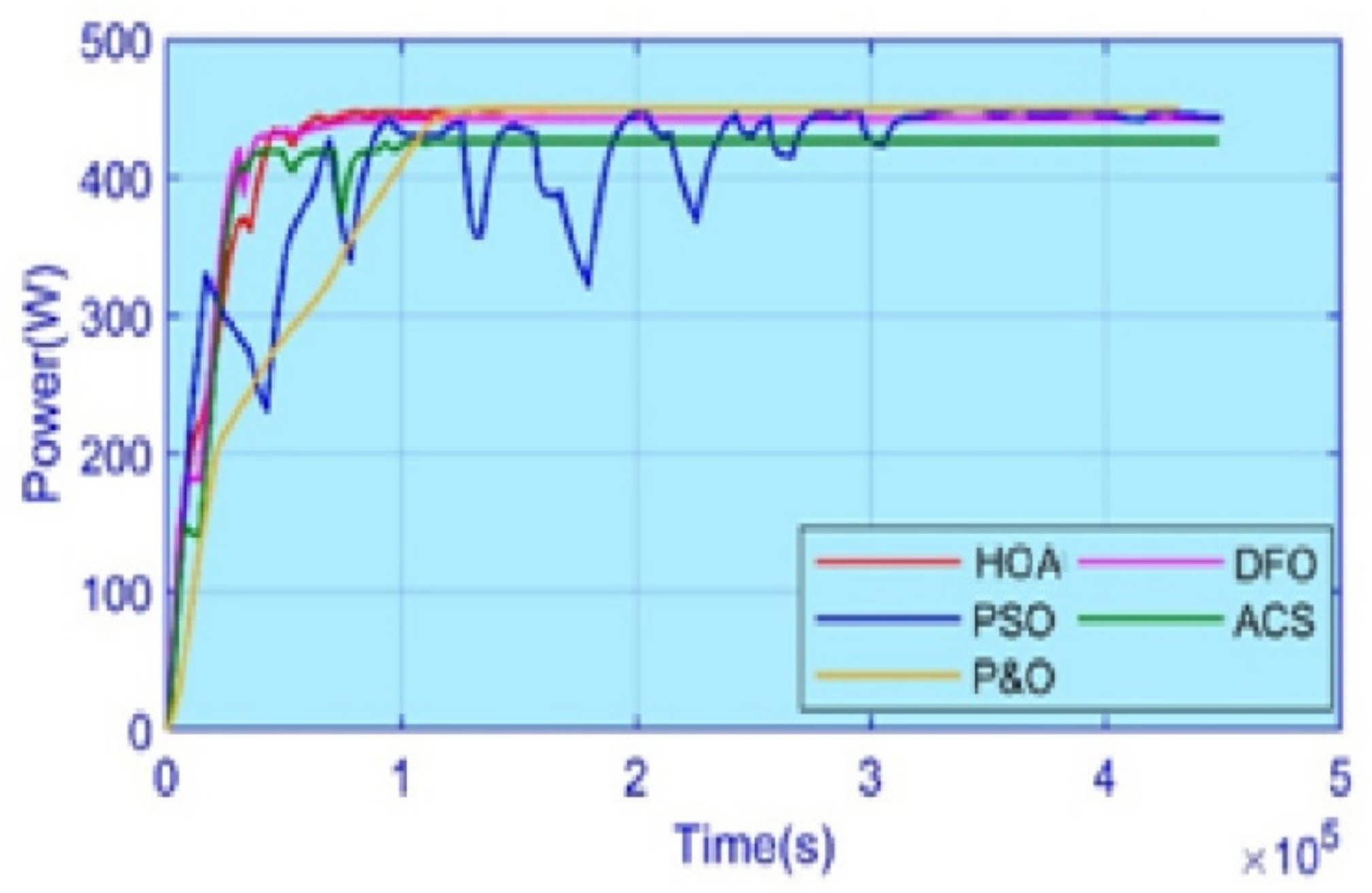
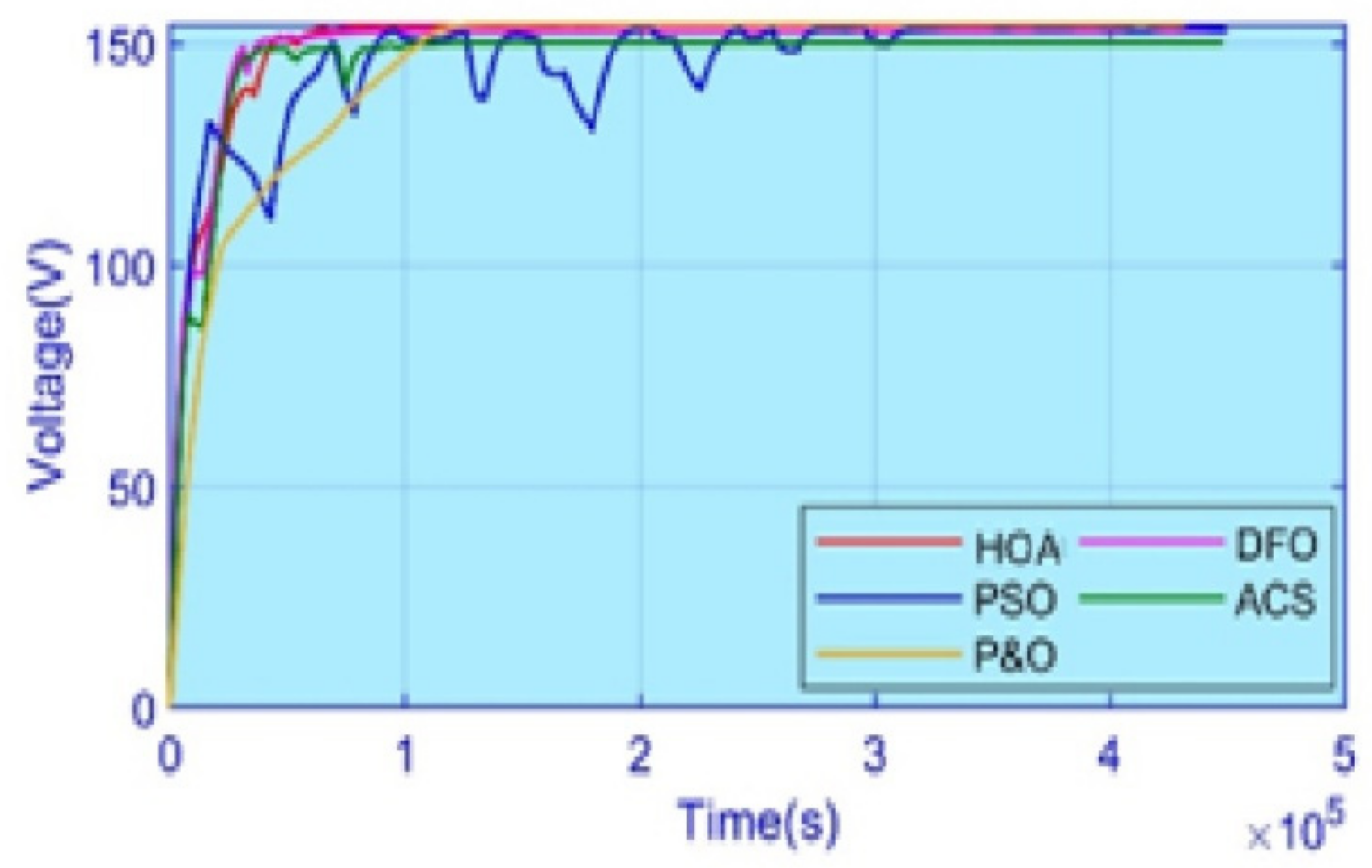
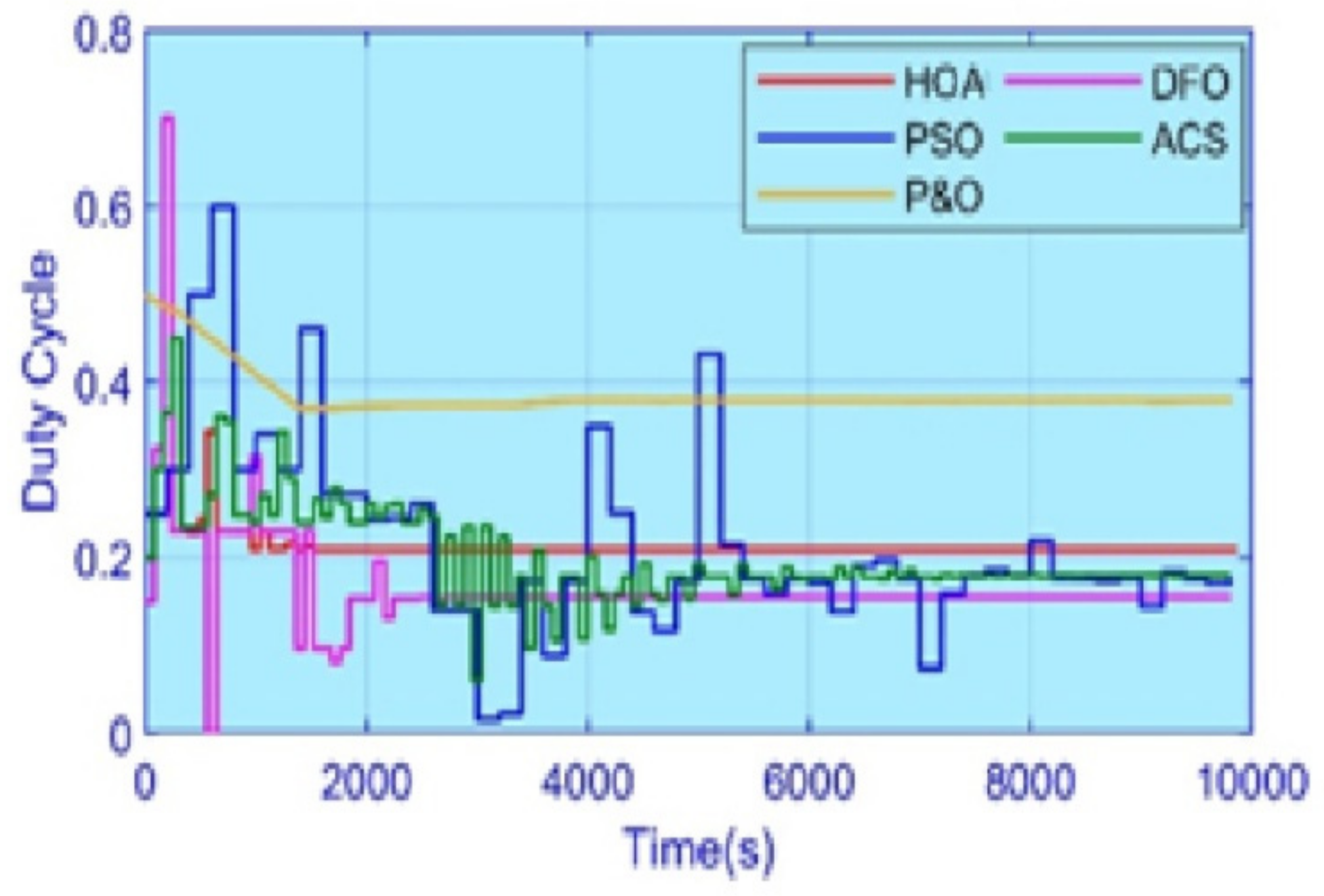
5. Experimental Results
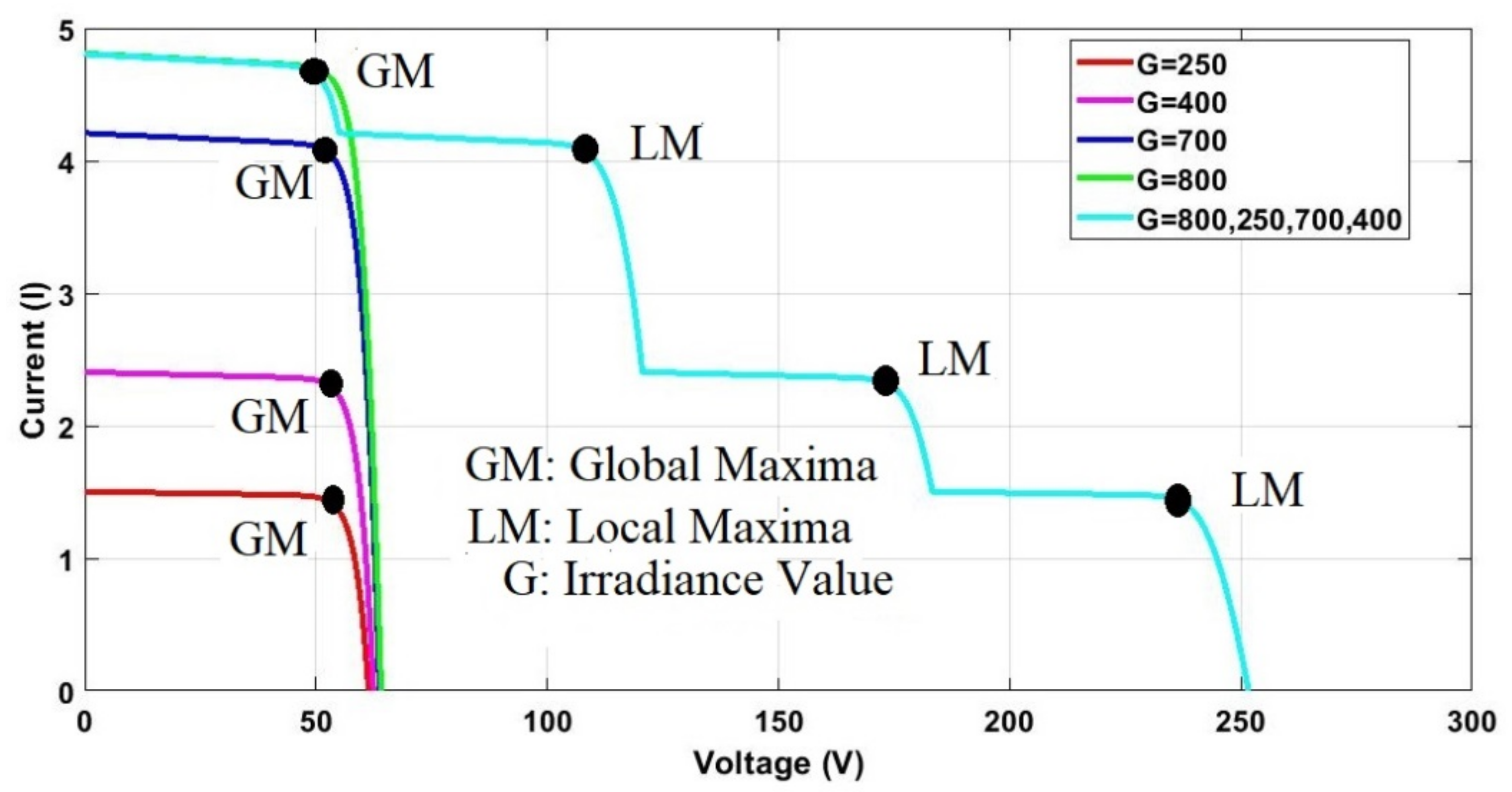
5.1. Case 1: Fast-Changing Irradiance
5.2. Case 2: PS Scenario 1
5.3. Case 3: PS Scenario 2
5.4. Case 4: Complex Partial Shading
| Cases | |||||
|---|---|---|---|---|---|
| Case4 | PV1 = 0.4 | PV2 = 0.2 | PV3 = 0.6 | PV4 = 0.3 | 1078 |
| PV5 = 0.5 | PV6 = 0.4 | PV7 = 0.2 | PV8 = 0.3 | ||
| PV9 = 1.00 | PV10 = 0.8 | PV11 = 0.7 | PV12 = 1.0 | ||

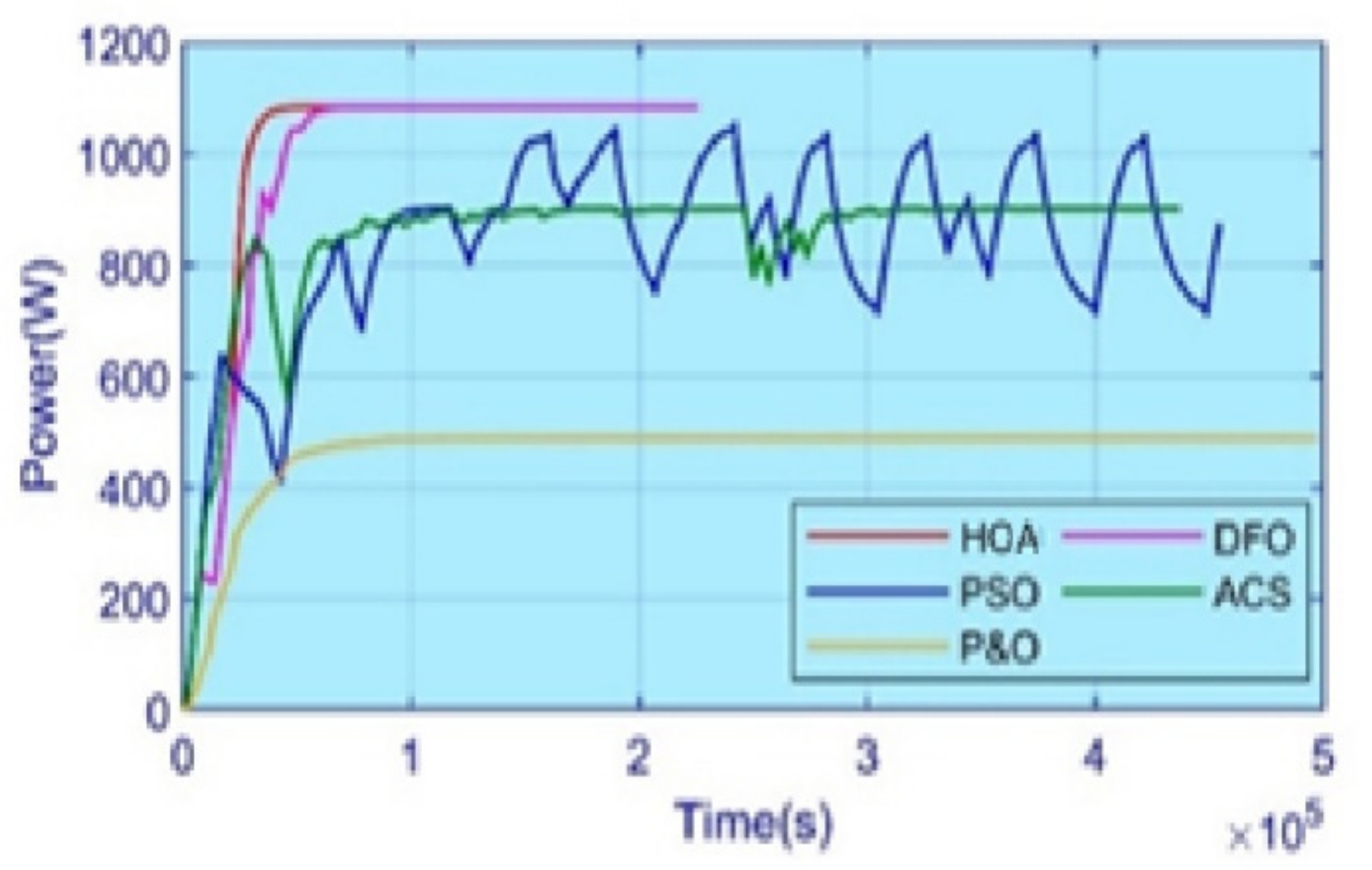

5.5. Efficiency and Performance Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Capuano, L. U.S. Energy Information Administration’s International Energy Outlook 2020; US Department of Energy: Washington, DC, USA, 2020; p. 7. Available online: https://www.Eia.Gov/Outlooks/Ieo/ (accessed on 20 September 2021).
- Eldin, A.H.; Refaey, M.; Farghly, A. A Review on Photovoltaic Solar Energy Technology and its Efficiency. In Proceedings of the 17th International Middle-East Power System Conference (MEPCON’15), Mansoura, Egypt, 15–17 December 2015; pp. 1–9. [Google Scholar]
- Sarwar, S.; Javed, M.Y.; Jaffery, M.H.; Arshad, J.; Rehman, A.U.; Shafiq, M.; Choi, J.-G. A Novel Hybrid MPPT Technique to Maximize Power Harvesting from PV System under Partial and Complex Partial Shading. Appl. Sci. 2022, 12, 587. [Google Scholar] [CrossRef]
- Javed, M.Y.; Hasan, A.; Rizvi, S.T.H.; Hafeez, A.; Sarwar, S.; Telmoudi, A.J. Water Cycle Algorithm (WCA): A New Technique to Harvest Maximum Power from PV. Cybern. Syst. 2021, 1–23. [Google Scholar] [CrossRef]
- Javed, M.Y.; Mirza, A.F.; Hasan, A.; Rizvi, S.T.H.; Ling, Q.; Gulzar, M.M.; Safder, M.U.; Mansoor, M. A Comprehensive Review on a PV Based System to Harvest Maximum Power. Electronics 2019, 8, 1480. [Google Scholar] [CrossRef] [Green Version]
- Radjai, T.; Rahmani, L.; Mekhilef, S.; Gaubert, J.P. Implementation of a modified incremental conductance MPPT algorithm with direct control based on a fuzzy duty cycle change estimator using dSPACE. Sol. Energy 2014, 110, 325–337. [Google Scholar] [CrossRef]
- Mohanty, P.; Bhuvaneswari, G.; Balasubramanian, R.; Dhaliwal, N.K. MATLAB based modeling to study the performance of different MPPT techniques used for solar PV system under various operating conditions. Renew. Sustain. Energy Rev. 2014, 38, 581–593. [Google Scholar] [CrossRef]
- Krishna, K.S.; Kumar, K.S. A review on hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2015, 52, 907–916. [Google Scholar] [CrossRef]
- Zafar, M.H.; Khan, N.M.; Mirza, A.F.; Mansoor, M.; Akhtar, N.; Qadir, M.U.; Khan, N.A.; Moosavi, S.K.R. A novel meta-heuristic optimization algorithm based MPPT control technique for PV systems under complex partial shading condition. Sustain. Energy Technol. Assess. 2021, 47, 101367. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Mirza, A.F.; Ling, Q.; Javed, M.Y.; Mansoor, M. Novel MPPT techniques for photovoltaic systems under uniform irradiance and Partial shading. Sol. Energy 2019, 184, 628–648. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.F.; Ling, Q. Harris Howk optomization-Based MPPT Control for PV Systems under Partial Shading Conditions. J. Clean. Prod. 2020, 274, 1–19. [Google Scholar] [CrossRef]
- Farh, H.M.H.; Eltamaly, A.M. Maximum Power Extraction from the Photovoltaic System under Partial Shading Conditions. Smart Energy Grid Des. Isl. Ctries 2020, 107–129. [Google Scholar] [CrossRef]
- Rezk, H.; Al-Oran, M.; Gomaa, M.R.; Tolba, M.A.; Fathy, A.; Abdelkareem, M.A.; Olabi, A.; El-Sayed, A.H.M. A novel statistical performance evaluation of most modern optimization-based global MPPT techniques for partially shaded PV system. Renew. Sustain. Energy Rev. 2019, 115, 109372. [Google Scholar] [CrossRef]
- Mills, D.S.; McDonnell, S.M.; McDonnell, S. (Eds.) The Domestic Horse: The Origins, Development and Management of Its Behaviour; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Krueger, K.; Heinze, J. Horse sense: Social status of horses (Equus caballus) affects their likelihood of copying other horses’ behavior. Anim. Cogn. 2008, 11, 431–439. [Google Scholar] [CrossRef] [PubMed]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Horse herd optimization algorithm: A nature-inspired algorithm for high-dimensional optimization problems Knowledge-Based. Systems 2021, 213, 106711. [Google Scholar] [CrossRef]
- Bogner, F. A Comprehensive Summary of The Scientific Literature on Horse Assisted Education in Germany. Ph.D. Thesis, Van Hall Larenstein, Leeuwarden, The Netherlands, 2011. [Google Scholar]
- Mansoor, M.; Mirza, A.F.; Ling, Q.; Javed, M.Y. Novel Grass Hopper optimization based MPPT of PV systems for complex partial shading conditions. Sol. Energy 2020, 198, 499–518. [Google Scholar] [CrossRef]
- Mirza, A.F.; Mansoor, M.; Ling, Q.; Yin, B.; Javed, M.Y. A Salp-Swarm Optimization based MPPT technique for harvesting maximum energy from PV systems under partial shading conditions. Energy Convers. Manag. 2020, 209, 112625. [Google Scholar] [CrossRef]
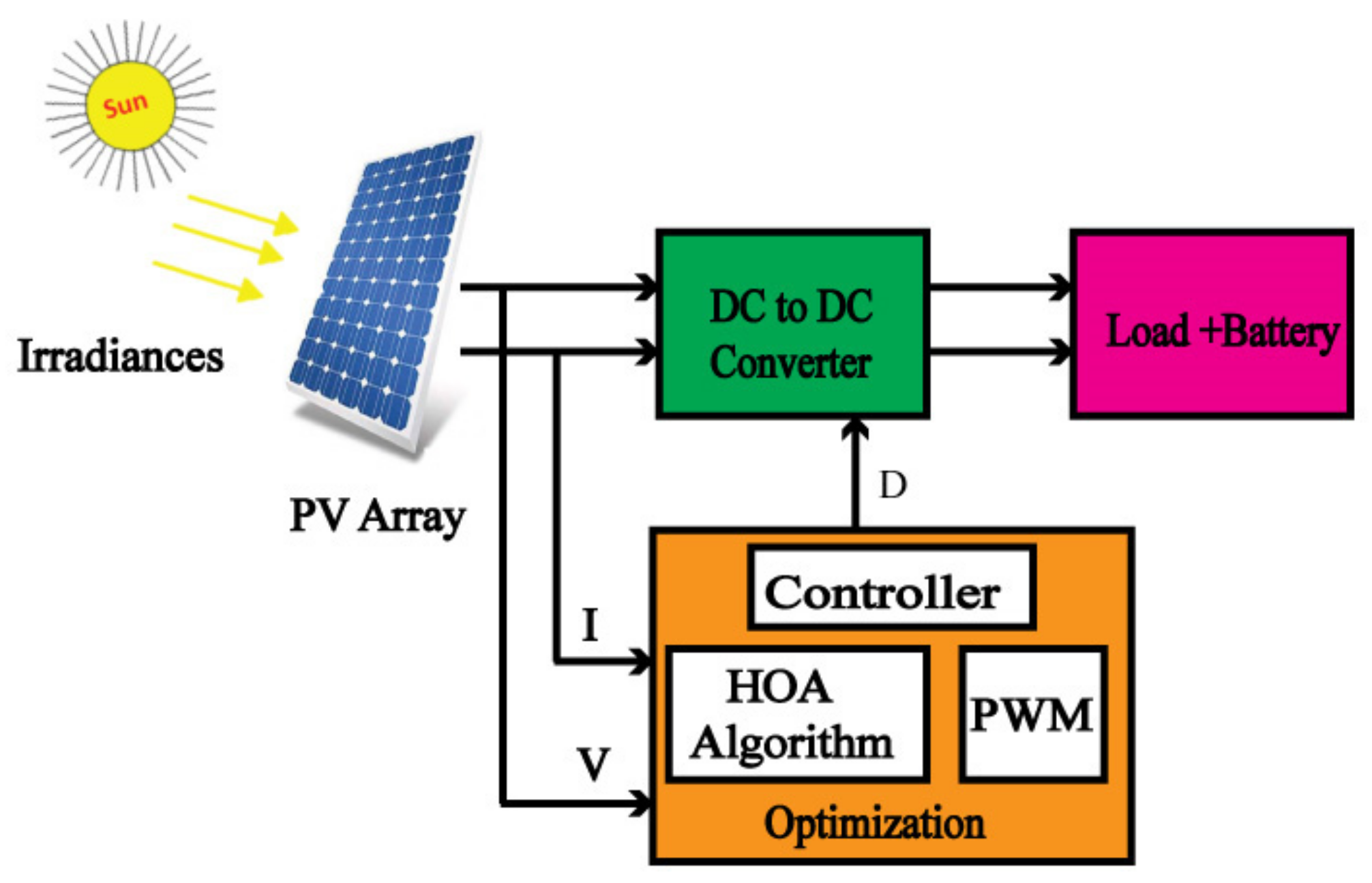
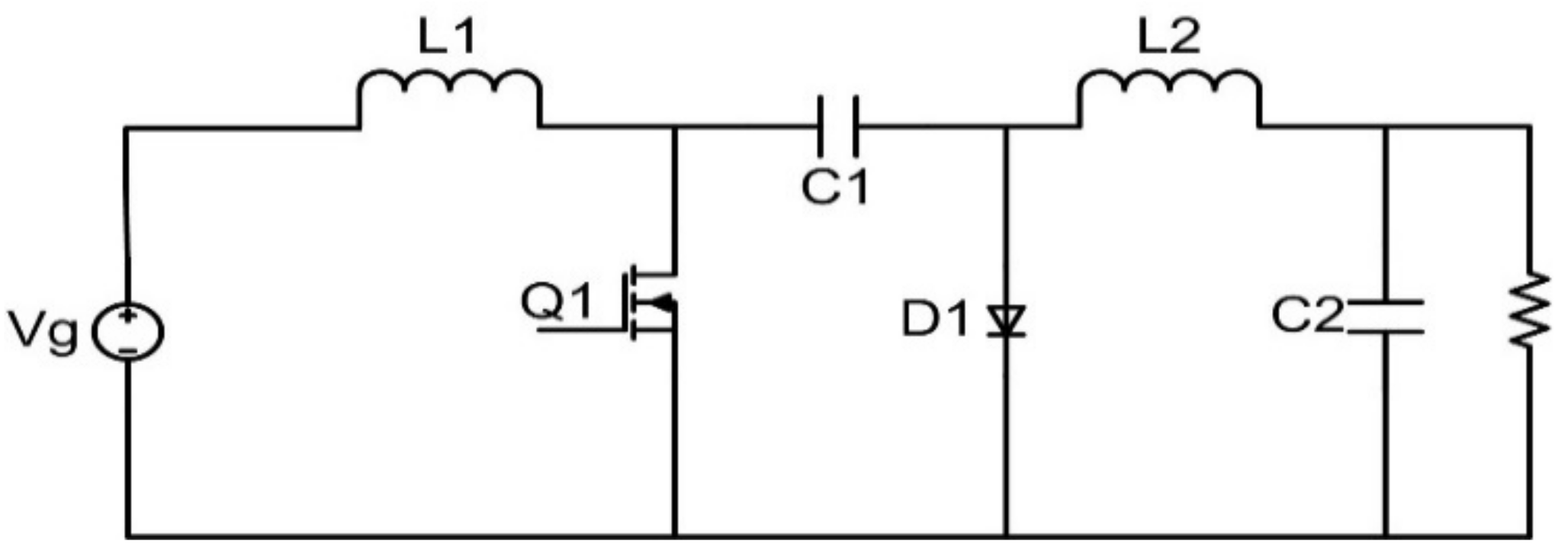


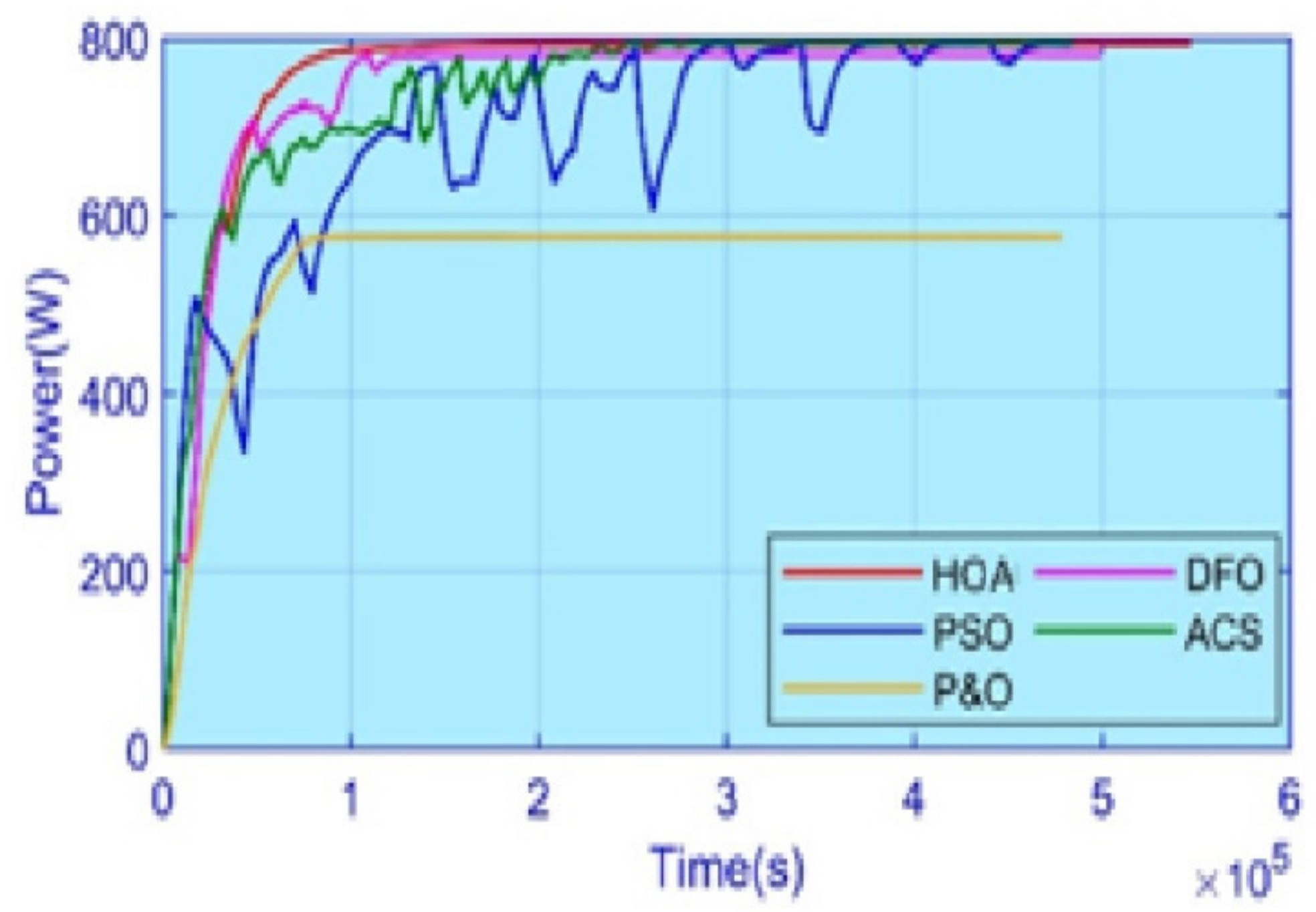
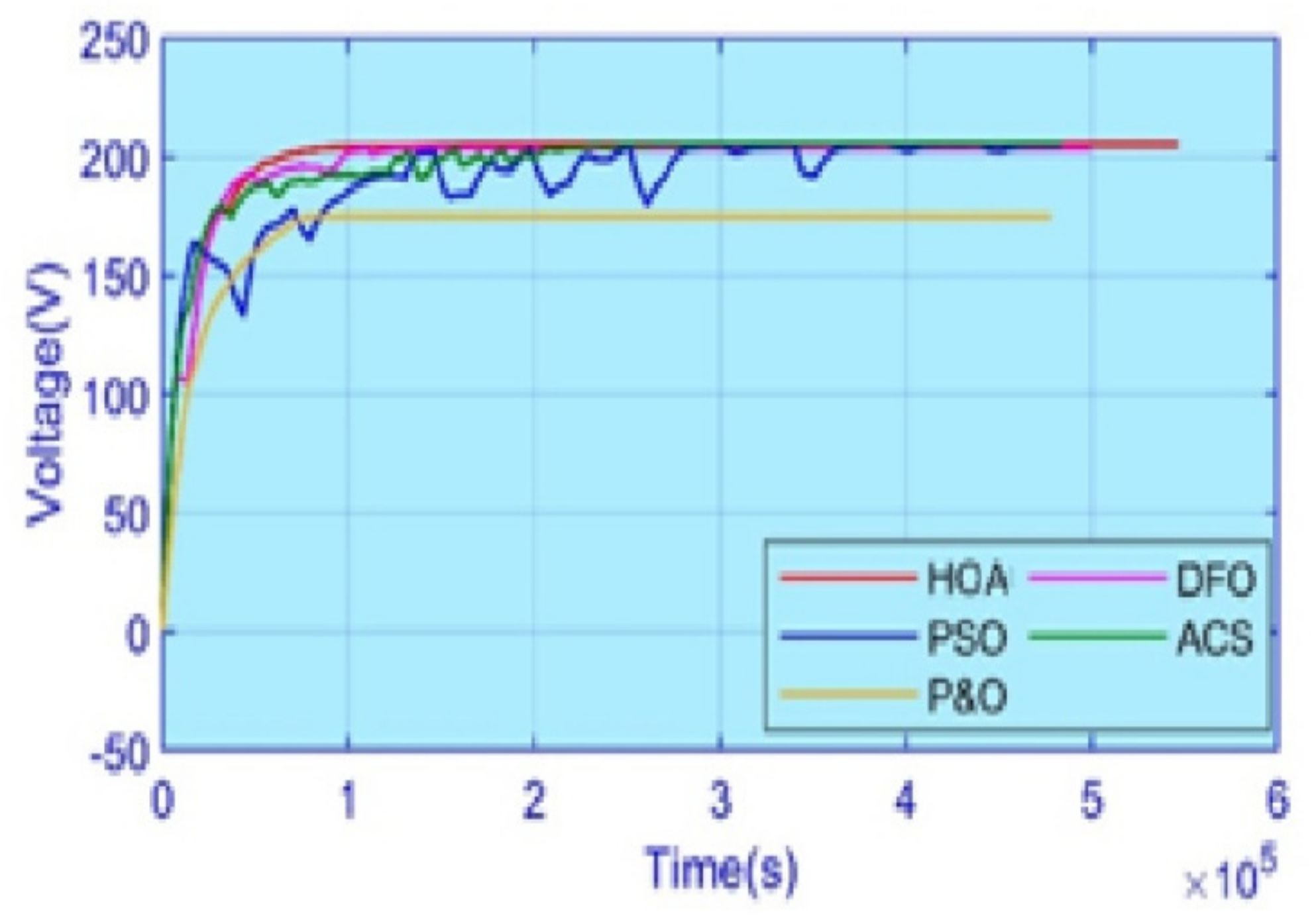
| Method | Irradiance Scheme | Convergence Time (s) | GM Settle Time (s) | GM Existed | Power at GM | Power Tracking (W) | Energy Value (kWh) | Efficiency (%) |
|---|---|---|---|---|---|---|---|---|
| DFO | Case 1 | 0.24 | 0.28 | Yes | 1260 | 1259 | 1.66 | 99.9 |
| Case 2 PS | 0.26 | 0.43 | Yes | 450 | 448.7 | 0.85 | 99.5 | |
| Case 3PS | 0.19 | 0.21 | Yes | 796 | 793.5 | 1.55 | 99.7 | |
| Case 4CPS | 0.19 | 0.22 | Yes | 1078 | 1075 | 2.12 | 99.8 | |
| HOA | Case 1 | 0.16 | 0.20 | Yes | 1260 | 1259.9 | 1.66 | 99.9 |
| Case 2 PS | 0.19 | 0.37 | Yes | 450 | 449.7 | 0.86 | 99.8 | |
| Case 3PS | 0.19 | 0.22 | Yes | 796 | 795.8 | 2.12 | 99.9 | |
| Case 4CPS | 0.17 | 0.25 | Yes | 1078 | 1077 | 1.65 | 99.8 | |
| P&O | Case 1 | 0.12 | 0.12 | Yes | 1260 | 1237 | 0.46 | 98.1 |
| Case 2 PS | LM | LM | No | 450 | 220 | 0.47 | 67.7 | |
| Case 3PS | LM | LM | No | 796 | 238 | 0.51 | 32.0 | |
| Case 4CPS | LM | LM | No | 1078 | 262 | 1.64 | 24.7 | |
| PSO | Case 1 | 0.47 | 0.70 | Yes | 1260 | 1257 | 0.83 | 94.6 |
| Case 2 PS | 0.41 | 0.81 | Yes | 450 | 439.2 | 1.48 | 97.6 | |
| Case 3PS | 0.68 | 0.70 | Yes | 796 | 791.5 | 2.10 | 99.4 | |
| Case 4CPS | 0.42 | 0.50 | Yes | 1078 | 1068 | 1.65 | 99.2 | |
| ACS | Case 1 | 0.46 | 0.69 | Yes | 1260 | 1258 | 0.83 | 99.8 |
| Case 2 PS | 0.30 | 0.84 | Yes | 450 | 420 | 1.49 | 95.5 | |
| Case 3PS | 0.35 | 0.45 | Yes | 796 | 778.6 | 2.10 | 97.8 | |
| Case 4CPS | 0.40 | 0.56 | Yes | 1078 | 1067 | 3.10 | 99.2 |
| Cases | |||||
|---|---|---|---|---|---|
| PV1 | PV2 | PV3 | PV4 | (W) | |
| Case1Fast Changing | 1, 0.7, 0.3 | 1, 0.7, 0.3 | 1, 0.7, 0.3 | 1, 0.7, 0.3 | 1260, 880, 380 |
| Case2 (Partial Shading) | 0.8 | 0.25 | 0.7 | 0.4 | 449.7 |
| Case3 (Partial Shading) | 0.5 | 0.8 | 1.0 | 0.9 | 796.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarwar, S.; Hafeez, M.A.; Javed, M.Y.; Asghar, A.B.; Ejsmont, K. A Horse Herd Optimization Algorithm (HOA)-Based MPPT Technique under Partial and Complex Partial Shading Conditions. Energies 2022, 15, 1880. https://doi.org/10.3390/en15051880
Sarwar S, Hafeez MA, Javed MY, Asghar AB, Ejsmont K. A Horse Herd Optimization Algorithm (HOA)-Based MPPT Technique under Partial and Complex Partial Shading Conditions. Energies. 2022; 15(5):1880. https://doi.org/10.3390/en15051880
Chicago/Turabian StyleSarwar, Sajid, Muhammad Annas Hafeez, Muhammad Yaqoob Javed, Aamer Bilal Asghar, and Krzysztof Ejsmont. 2022. "A Horse Herd Optimization Algorithm (HOA)-Based MPPT Technique under Partial and Complex Partial Shading Conditions" Energies 15, no. 5: 1880. https://doi.org/10.3390/en15051880
APA StyleSarwar, S., Hafeez, M. A., Javed, M. Y., Asghar, A. B., & Ejsmont, K. (2022). A Horse Herd Optimization Algorithm (HOA)-Based MPPT Technique under Partial and Complex Partial Shading Conditions. Energies, 15(5), 1880. https://doi.org/10.3390/en15051880








