Design and Optimization of a Novel Microchannel Battery Thermal Management System Based on Digital Twin
Abstract
:1. Introduction
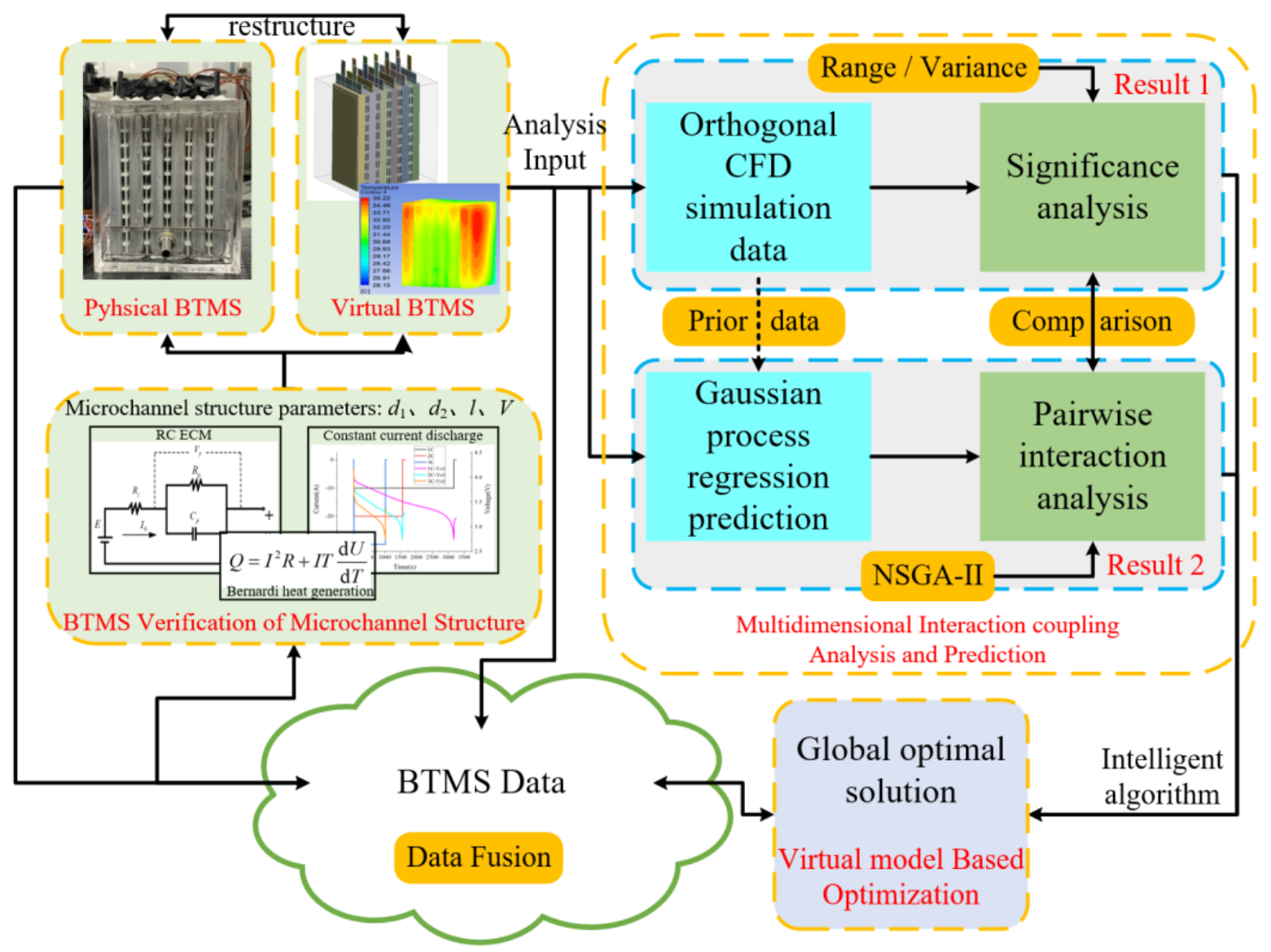
2. The Microchannel Battery Thermal Management System and Digital Twin-Based Design
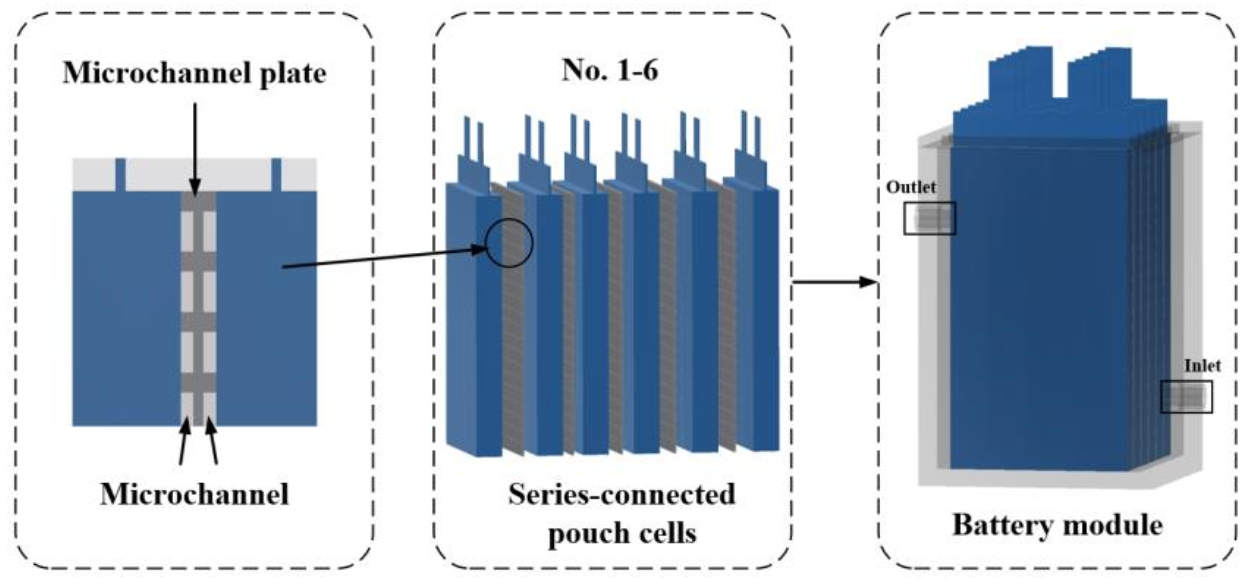
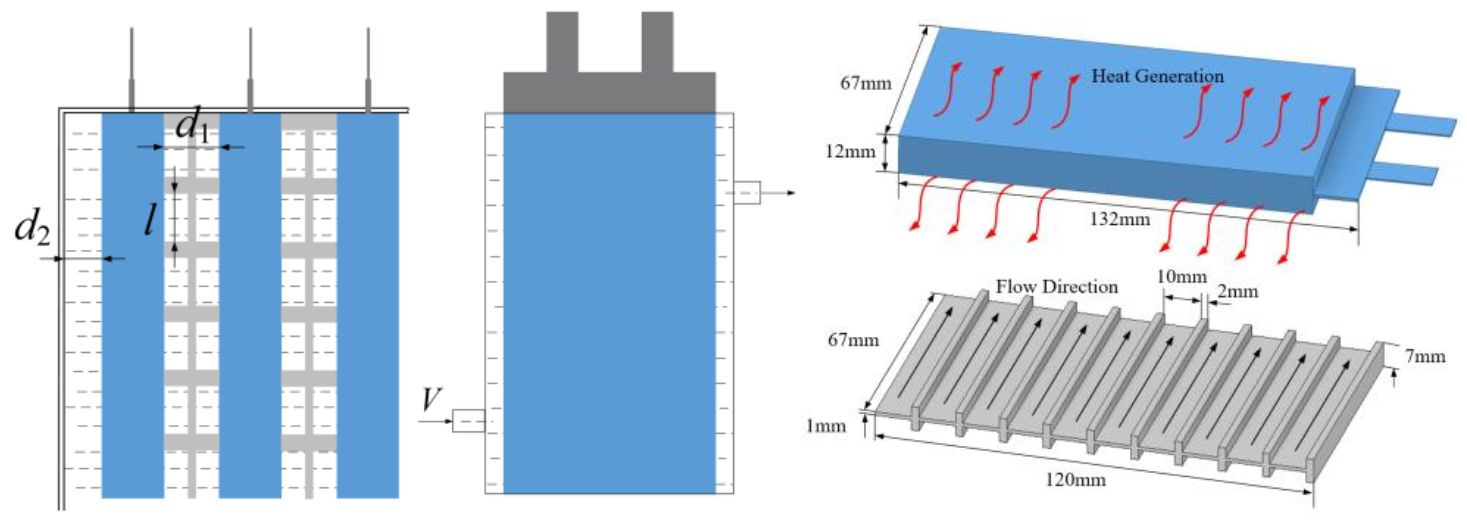
2.1. Introduction and Analysis of the Microchannel Battery Thermal Management System
2.2. Digital Twin-Based Design of the Microchannel Battery Thermal Management System
3. Virtual Calculation and Simulation Model
3.1. Governing Equations of the Digital Twin Virtual Model
3.2. Cell Heat Generation of the Digital Twin Virtual Model
- (a)
- The material of the cell is evenly distributed and isotropic.
- (b)
- The material property will not change with the temperature and SOC (state of charge).
- (c)
- The heat source is distributed uniformly in all of the areas of the cell.
3.3. Initial and Boundary Conditions of the Digital Twin Virtual Model
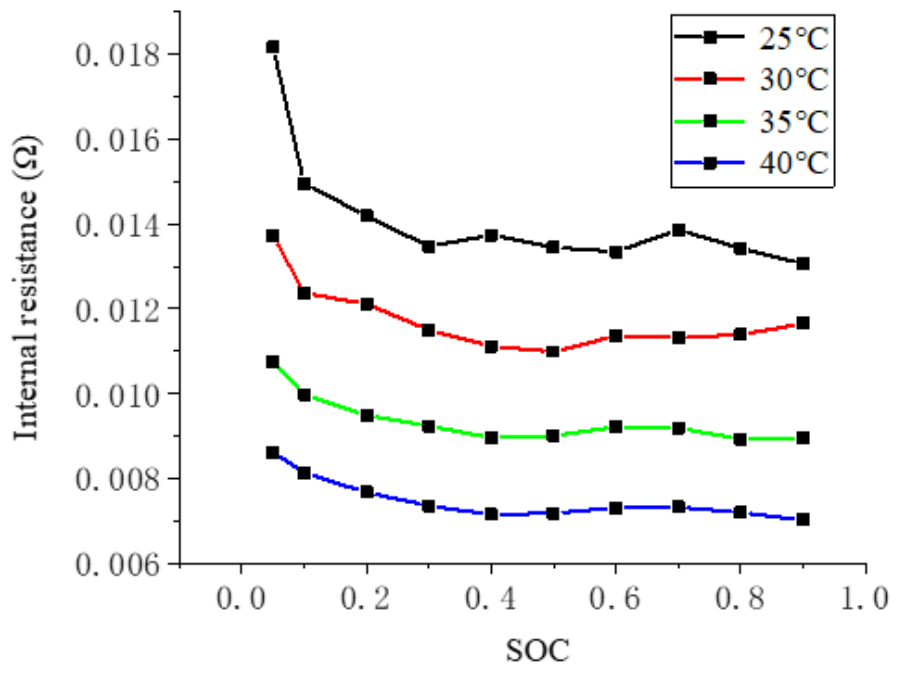
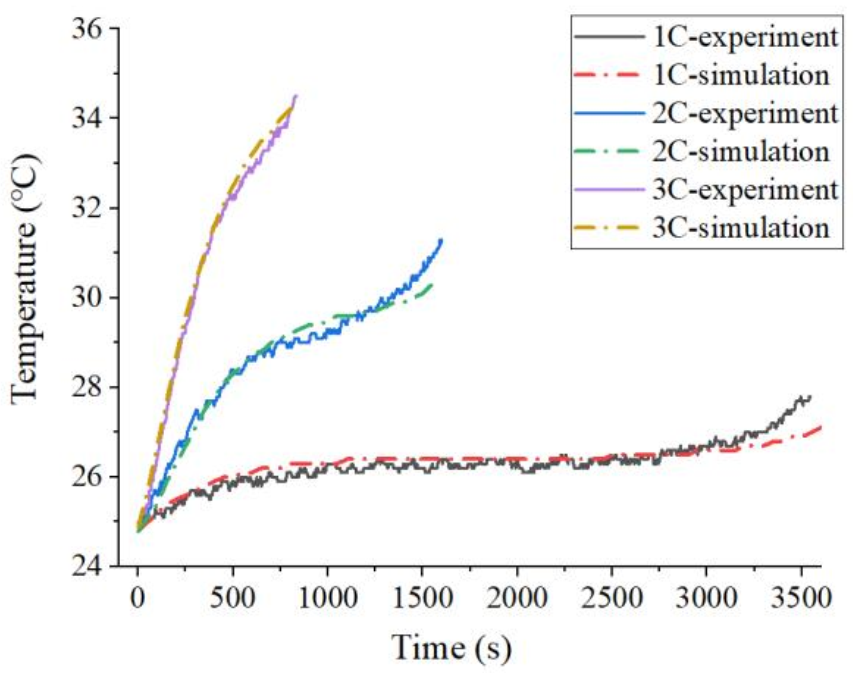
3.4. Experiment and Validation of the Digital Twin Virtual Model
4. Digital Twin Virtual Model Based Optimization of the BTMS
4.1. Gaussian Process Regression of the Digital Twin Virtual Model Based Optimization
4.2. Orthogonal Design of the Digital Twin Virtual Model Based Optimization
4.3. NSGA-II Method of the Digital Twin Virtual Model Based Optimization
5. Results and Discussions
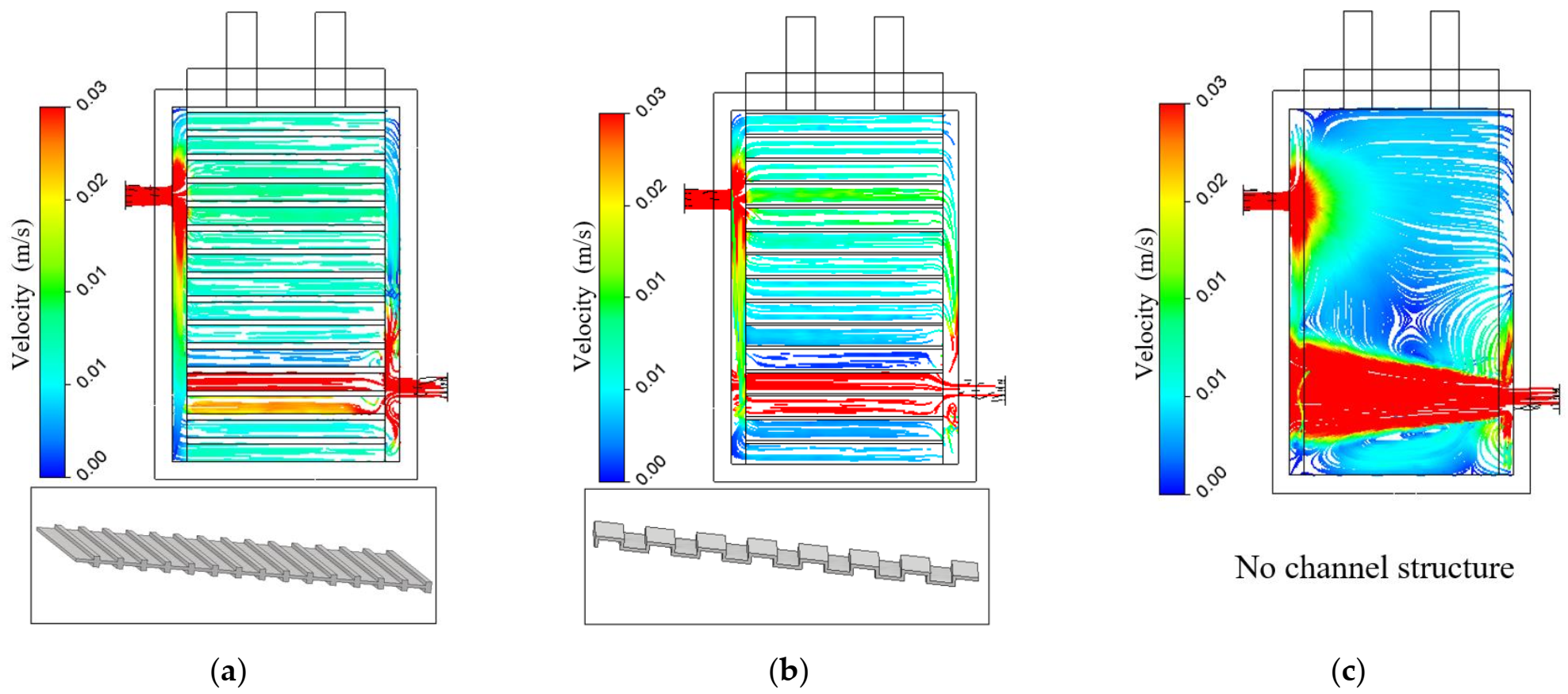
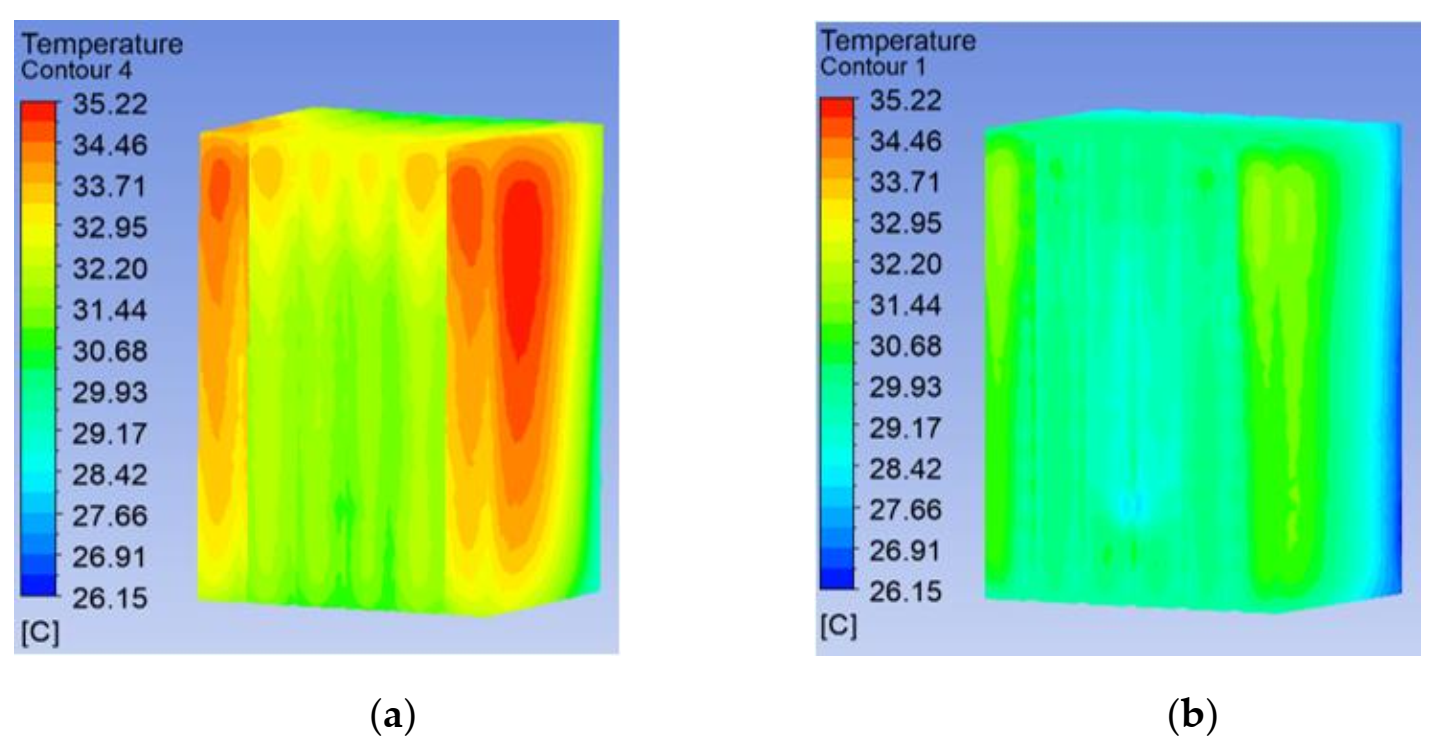
5.1. Streamline Analysis of Microchannel Structure
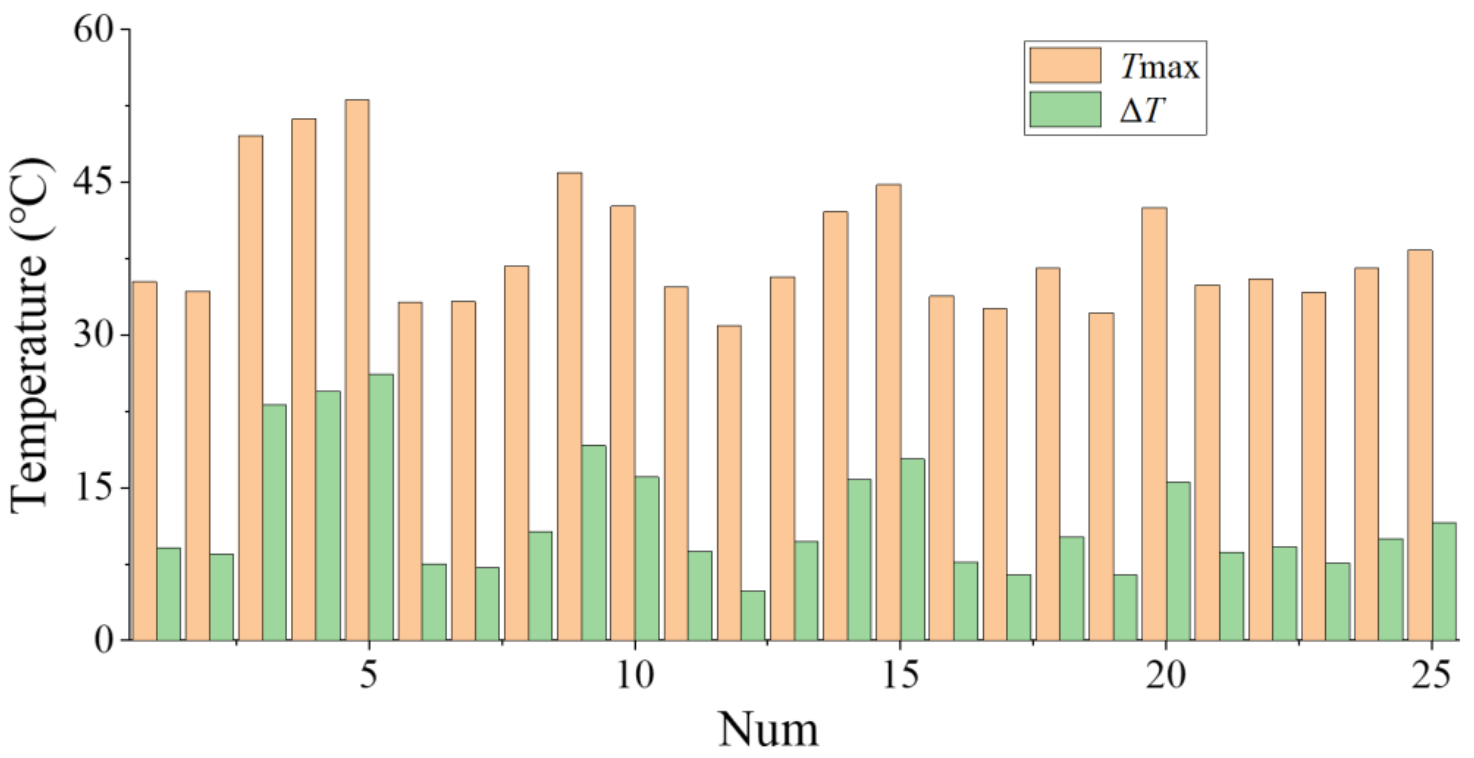
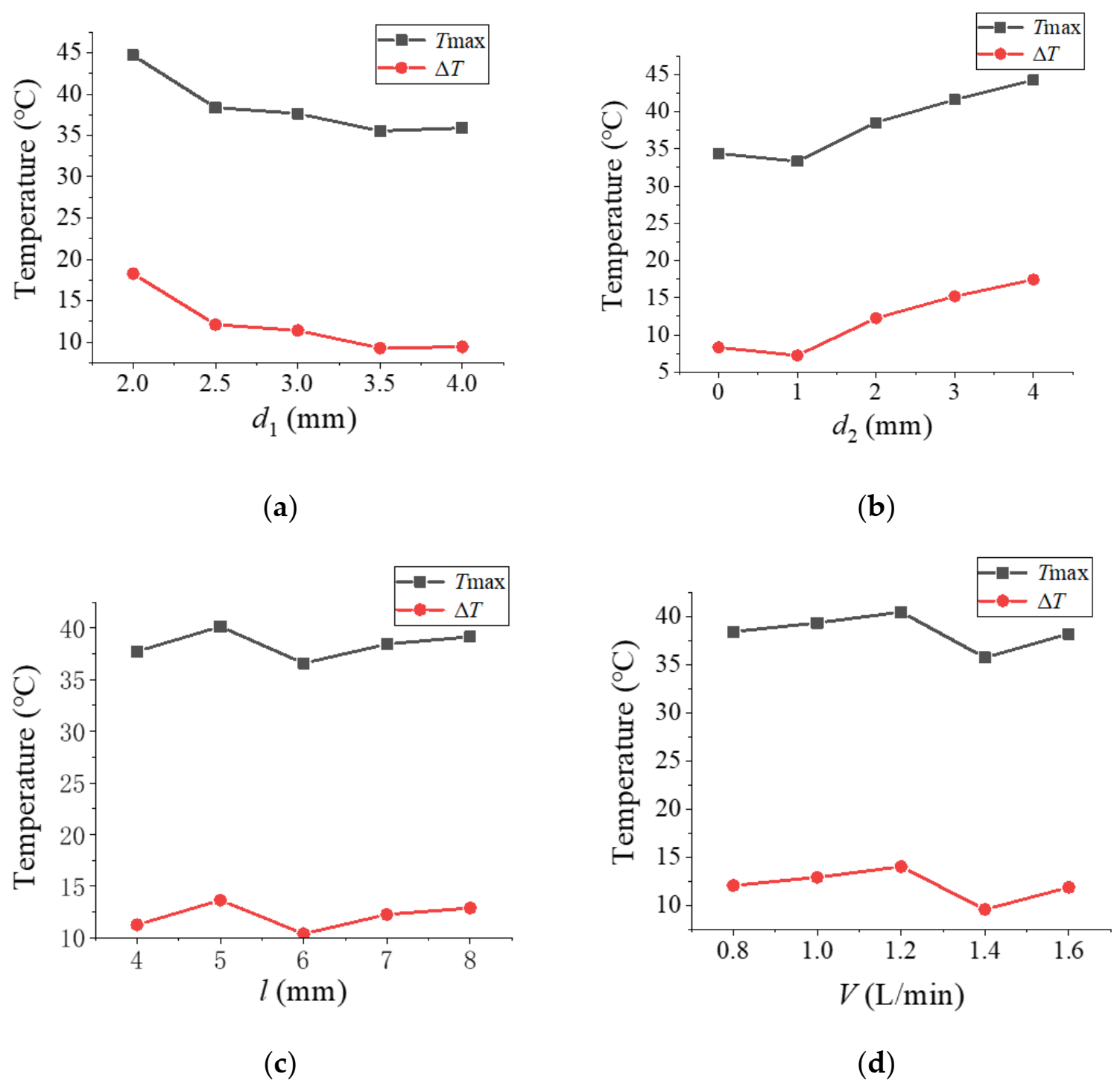
5.2. Orthogonal Analysis Based on Digital Twin Virtual Model
5.3. Gaussian Process Regression Analysis Based on Digital Twin Virtual Model
5.4. Multi-Objective Optimization and Comparison Based on Digital Twin Virtual Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Num | Factors | Test Index | Num | Factors | Test Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d1 | d2 | l | V | E1 | E2 | Tmax | ΔT | d1 | d2 | l | V | E1 | E2 | Tmax | ΔT | ||
| 1 | 2 | 0 | 4 | 0.8 | 1 | 1 | 35.22 | 9.07 | 14 | 3 | 3 | 8 | 0.8 | 2 | 2 | 42.1 | 15.84 |
| 2 | 2 | 1 | 6 | 1.4 | 5 | 2 | 34.27 | 8.5 | 15 | 3 | 4 | 5 | 1.4 | 1 | 3 | 44.75 | 17.8 |
| 3 | 2 | 2 | 8 | 1 | 4 | 3 | 49.57 | 23.1 | 16 | 3.5 | 0 | 6 | 1.6 | 2 | 3 | 33.79 | 7.7 |
| 4 | 2 | 3 | 5 | 1.6 | 3 | 4 | 51.23 | 24.48 | 17 | 3.5 | 1 | 8 | 1.2 | 1 | 4 | 32.62 | 6.43 |
| 5 | 2 | 4 | 7 | 1.2 | 2 | 5 | 53.11 | 16.18 | 18 | 3.5 | 2 | 5 | 0.8 | 5 | 5 | 36.58 | 10.15 |
| 6 | 2.5 | 0 | 8 | 1.4 | 3 | 5 | 33.25 | 7.47 | 19 | 3.5 | 3 | 7 | 1.4 | 4 | 1 | 32.15 | 6.47 |
| 7 | 2.5 | 1 | 5 | 1 | 2 | 1 | 33.26 | 7.15 | 20 | 3.5 | 4 | 4 | 1 | 3 | 2 | 42.47 | 15.56 |
| 8 | 2.5 | 2 | 7 | 1.6 | 1 | 2 | 36.75 | 10.69 | 21 | 4 | 0 | 5 | 1.2 | 4 | 2 | 34.93 | 8.65 |
| 9 | 2.5 | 3 | 4 | 1.2 | 5 | 3 | 45.95 | 19.15 | 22 | 4 | 1 | 7 | 0.8 | 3 | 3 | 35.5 | 9.2 |
| 10 | 2.5 | 4 | 6 | 0.8 | 4 | 4 | 42.63 | 16.06 | 23 | 4 | 2 | 4 | 1.4 | 2 | 4 | 34.15 | 7.61 |
| 11 | 3 | 0 | 7 | 1 | 5 | 4 | 34.75 | 8.73 | 24 | 4 | 3 | 6 | 1 | 1 | 5 | 36.61 | 9.98 |
| 12 | 3 | 1 | 4 | 1.6 | 4 | 5 | 30.95 | 4.88 | 25 | 4 | 4 | 8 | 1.6 | 5 | 1 | 38.3 | 11.6 |
| 13 | 3 | 2 | 6 | 1.2 | 3 | 1 | 35.71 | 9.69 | |||||||||
References
- Moussa, A.; Bekrar, A.; Trentesaux, D.; Aissani, N.; Bouamrane, K. Manufacturing 4.0 Operations Scheduling with Agv Battery Management Constraints. Energies 2020, 13, 4948. [Google Scholar]
- Jun, X.; Mei, X.; Wang, X.; Fu, Y.; Zhao, Y.; Wang, J. A Relative State of Health Estimation Method Based on Wavelet Analysis for Lithium-Ion Battery Cells. IEEE Trans. Ind. Electron. 2021, 68, 6973–6981. [Google Scholar]
- Jiang, Y.; Xu, J.; Hou, W.; Mei, X. A Stack Pressure Based Equivalent Mechanical Model of Lithium-Ion Pouch Batteries. Energy 2021, 221, 119804. [Google Scholar] [CrossRef]
- Vima, M.; Saxena, R.; Kumar, K.; Kalam, A.; Tripathi, B. Review on Battery Thermal Management Systems for Energy-Efficient Electric Vehicles. Renew. Sustain. Energy Rev. 2021, 151, 111611. [Google Scholar]
- Mahesh, P.; Panchal, S.; Kim, N.; Lee, M.Y. Cooling Performance Characteristics of 20 Ah Lithium-Ion Pouch Cell with Cold Plates Along Both Surfaces. Energies 2018, 11, 2550. [Google Scholar]
- Guo, Z.; Xu, J.; Xu, Z.; Mubashir, M.; Wang, H.; Mei, X. A Three-Heat-Source Electro-Thermal Coupled Model for Fast Estimation of the Temperature Distribution of a Lithium-Ion Battery Cell. IEEE Trans. Transp. Electrif. 2021, 1. [Google Scholar] [CrossRef]
- Xu, J.; Mei, X.; Wang, H.; Wang, J. A Hybrid Self-Heating Method for Batteries Used at Low Temperature. IEEE Trans. Ind. Inform. 2021, 17, 4714–4723. [Google Scholar] [CrossRef]
- Pranjali, R.T.; Gupta, M.M.; Joshi, S.S. Developments in Battery Thermal Management Systems for Electric Vehicles: A Technical Review. J. Energy Storage 2021, 35, 102255. [Google Scholar]
- Wang, H.; Tao, T.; Xu, J.; Shi, H.; Mei, X.; Gou, P. Thermal Performance of a Liquid-Immersed Battery Thermal Management System for Lithium-Ion Pouch Batteries. J. Energy Storage 2022, 46, 103835. [Google Scholar] [CrossRef]
- Tao, W.; Tseng, K.J.; Zhao, J.; Wei, Z. Thermal Investigation of Lithium-Ion Battery Module with Different Cell Arrangement Structures and Forced Air-Cooling Strategies. Appl. Energy 2014, 134, 229–238. [Google Scholar]
- Rajib, M.; Park, C. Reciprocating Air Flow for Li-Ion Battery Thermal Management to Improve Temperature Uniformity. J. Power Sources 2011, 196, 5685–5696. [Google Scholar]
- Ming, X.X.; Sun, X.D.; Hu, D.H.; Li, R.Z.; Tang, W. Research on Heat Dissipation Performance and Flow Characteristics of Air-Cooled Battery Pack. Int. J. Energy Res. 2018, 42, 3658–3671. [Google Scholar]
- Kai, C.; Wang, S.; Song, M.; Chen, L. Structure Optimization of Parallel Air-Cooled Battery Thermal Management System. Int. J. Heat Mass Transf. 2017, 111, 943–952. [Google Scholar]
- Kai, C.; Song, M.; Wei, W.; Wang, S. Structure Optimization of Parallel Air-Cooled Battery Thermal Management System with U-Type Flow for Cooling Efficiency Improvement. Energy 2018, 145, 603–613. [Google Scholar]
- Kai, C.; Chen, Y.; She, Y.; Song, M.; Wang, S.; Chen, L. Construction of Effective Symmetrical Air-Cooled System for Battery Thermal Management. Appl. Therm. Eng. 2020, 166, 114679. [Google Scholar]
- Hakeem, A.A.A.; Solyali, D. Configuration, Design, and Optimization of Air-Cooled Battery Thermal Management System for Electric Vehicles: A Review. Renew. Sustain. Energy Rev. 2020, 125, 109815. [Google Scholar]
- Jie, L.; Zou, D.; Wang, Y.; Wang, S.; Huang, L. Battery Thermal Management Systems (Btms) Based on Phase Change Material (Pcm): A Comprehensive Review. Chem. Eng. J. 2022, 430, 132741. [Google Scholar]
- Ravindra, J.; Afzal, A.; Panchal, S. A Novel Battery Thermal Management System Using Nano-Enhanced Phase Change Materials. Energy 2021, 219, 119564. [Google Scholar]
- Weixiong, W.; Yang, X.; Zhang, G.; Ke, X.; Wang, Z.; Situ, W.; Li, X.; Zhang, J. An Experimental Study of Thermal Management System Using Copper Mesh-Enhanced Composite Phase Change Materials for Power Battery Pack. Energy 2016, 113, 909–916. [Google Scholar]
- Rao, Z.; Huo, Y.; Liu, X.; Zhang, G. Experimental Investigation of Battery Thermal Management System for Electric Vehicle Based on Paraffin/Copper Foam. J. Energy Inst. 2015, 88, 241–246. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S.; Wu, M.; Lin, Z.; Li, F. Experimental Investigation on Thermal Management of Electric Vehicle Battery with Heat Pipe. Energy Convers. Manag. 2013, 65, 92–97. [Google Scholar] [CrossRef]
- Rao, Z.; Huo, Y.; Liu, X. Experimental Study of an Ohp-Cooled Thermal Management System for Electric Vehicle Power Battery. Exp. Therm. Fluid Sci. 2014, 57, 20–26. [Google Scholar] [CrossRef]
- Xin, Y.; Zhao, Y.; Quan, Z. Thermal Management System of Lithium-Ion Battery Module Based on Micro Heat Pipe Array. Int. J. Energy Res. 2018, 42, 648–655. [Google Scholar]
- Zhang, Z.; Wei, K. Experimental and Numerical Study of a Passive Thermal Management System Using Flat Heat Pipes for Lithium-Ion Batteries. Appl. Therm. Eng. 2020, 166, 114660. [Google Scholar] [CrossRef]
- Wang, J.; Gan, Y.; Liang, J.; Tan, M.; Li, Y. Sensitivity Analysis of Factors Influencing a Heat Pipe-Based Thermal Management System for a Battery Module with Cylindrical Cells. Appl. Therm. Eng. 2019, 151, 475–485. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of Different Coolants and Cooling Strategies on the Cooling Performance of the Power Lithium Ion Battery System: A Review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Anthony, J.; Kim, I.Y. Design Optimization of Electric Vehicle Battery Cooling Plates for Thermal Performance. J. Power Sources 2011, 196, 10359–10368. [Google Scholar]
- Jarrett, A.; Kim, I.Y. Influence of Operating Conditions on the Optimum Design of Electric Vehicle Battery Cooling Plates. J. Power Sources 2014, 245, 644–655. [Google Scholar] [CrossRef]
- Wang, H.; Tao, T.; Xu, J.; Mei, X.; Liu, X.; Gou, P. Cooling Capacity of a Novel Modular Liquid-Cooled Battery Thermal Management System for Cylindrical Lithium Ion Batteries. Appl. Therm. Eng. 2020, 178, 115591. [Google Scholar] [CrossRef]
- Liu, H.; Chika, E.; Zhao, J. Investigation into the Effectiveness of Nanofluids on the Mini-Channel Thermal Management for High Power Lithium Ion Battery. Appl. Therm. Eng. 2018, 142, 511–523. [Google Scholar] [CrossRef]
- Rao, Z.; Qian, Z.; Kuang, Y.; Li, Y. Thermal Performance of Liquid Cooling Based Thermal Management System for Cylindrical Lithium-Ion Battery Module with Variable Contact Surface. Appl. Therm. Eng. 2017, 123, 1514–1522. [Google Scholar] [CrossRef]
- Wei, L.; Xiao, M.; Peng, X.; Garg, A.; Gao, L. A Surrogate Thermal Modeling and Parametric Optimization of Battery Pack with Air Cooling for Evs. Appl. Therm. Eng. 2019, 147, 90–100. [Google Scholar]
- Jiaqiang, E.; Xu, S.; Deng, Y.; Zhu, H.; Zuo, W.; Wang, H.; Chen, J.; Peng, Q.; Zhang, Z. “Investigation on Thermal Performance and Pressure Loss of the Fluid Cold-Plate Used in Thermal Management System of the Battery Pack. Appl. Therm. Eng. 2018, 145, 552–568. [Google Scholar]
- Fei, T.; Zhang, M.; Liu, Y.; Nee, A.Y.C. Digital Twin Driven Prognostics and Health Management for Complex Equipment. CIRP Ann. 2018, 67, 169–172. [Google Scholar]
- Meng, Z.; Tao, F.; Nee, A.Y.C. Digital Twin Enhanced Dynamic Job-Shop Scheduling. J. Manuf. Syst. 2021, 58, 146–156. [Google Scholar]
- Zhang, C.; Zhou, Q.; Li, Y.; Hua, L.; Xu, H. The Digital Twin Modelling of the Electrified Vehicle Based on a Hybrid Terminating Control of Particle Swarm Optimization. IFAC-Pap. 2021, 54, 552–557. [Google Scholar] [CrossRef]
- Haber, G.R.; Quiza, R.; Villalonga, A.; Arenas, J.; Castano, F. Digital Twin-Based Optimization for Ultraprecision Motion Systems with Backlash and Friction. IEEE Access 2019, 7, 93462–93472. [Google Scholar]
- Guo, Z.; Xu, J.; Xu, Z.; Mubashir, M.; Wang, H.; Mei, X. A Lightweight Multi-Channel Direct Contact Liquid Cooling System and Its Optimization for Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2021, 1. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef] [Green Version]
- Cong, W.; Zhang, G.; Li, X.; Huang, J.; Wang, Z.; Lv, Y.; Meng, L.; Situ, W.; Rao, M. Experimental Examination of Large Capacity Lifepo4 Battery Pack at High Temperature and Rapid Discharge Using Novel Liquid Cooling Strategy. Int. J. Energy Res. 2018, 42, 1172–1182. [Google Scholar]





| Parameter | Rated Voltage (V) | Rated Capacity (mAh) | Cut-Off Voltage (V) | Mass (kg) | Dimension (mm) |
|---|---|---|---|---|---|
| Value | 3.7 | 10,000 | 3.0–4.2 | 0.23 | 132 × 67 × 12 |
| Materials | Thermal Conductivity (W/m·K) | Density (kg/m3) | Specific Heat (J/kg·K) |
|---|---|---|---|
| Cell body | 3.27 | 2543.92 | 1679 |
| Copper (negative pole) | 388 | 8978 | 381 |
| Aluminum (positive pole) | 202 | 2719 | 871 |
| Discharge Rate | 1 C | 2 C | 3 C |
|---|---|---|---|
| Maximum temperature (°C) | 27.8 | 31.3 | 34.5 |
| Temperature deviation (°C) | 0.7 | 0.9 | 0.1 |
| Index | Factors | |||
|---|---|---|---|---|
| d1 | d2 | l | V | |
| RTmax | 9.158 | 10.932 | 3.548 | 4.75 |
| RΔT | 9.004 | 10.208 | 3.26 | 4.45 |
| MSj(Tmax) | 68.17 | 108.07 | 9.14 | 15.47 |
| Fj(Tmax) | 4.47 | 7.09 | \ | \ |
| MSj(ΔT) | 67.28 | 95.00 | 8.36 | 13.48 |
| Fj(ΔT) | 4.92 | 6.95 | \ | \ |
| Significance 1 | *** | **** | * | ** |
| F(4,16) | α0.005 = 5.64 | α0.01 = 4.77 | ||
| α0.025 = 3.73 | α0.05 = 3.01 | |||
| Parameter | d1 | d2 | l | V | Tmax | ΔT |
|---|---|---|---|---|---|---|
| Initial structure | 2 | 0 | 4 | 0.8 | 35.2 | 9.07 |
| Orthogonal optimization | 3.5 | 1 | 6 | 1.4 | 31.8 | 5.76 |
| Gaussian regression optimization | 3.14 | 0.8 | 6.2 | 1.6 | 30.6 | 4.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Xu, J.; Guo, Z.; Wang, H.; Sun, Z.; Mei, X. Design and Optimization of a Novel Microchannel Battery Thermal Management System Based on Digital Twin. Energies 2022, 15, 1421. https://doi.org/10.3390/en15041421
Xu Z, Xu J, Guo Z, Wang H, Sun Z, Mei X. Design and Optimization of a Novel Microchannel Battery Thermal Management System Based on Digital Twin. Energies. 2022; 15(4):1421. https://doi.org/10.3390/en15041421
Chicago/Turabian StyleXu, Ziming, Jun Xu, Zhechen Guo, Haitao Wang, Zheng Sun, and Xuesong Mei. 2022. "Design and Optimization of a Novel Microchannel Battery Thermal Management System Based on Digital Twin" Energies 15, no. 4: 1421. https://doi.org/10.3390/en15041421
APA StyleXu, Z., Xu, J., Guo, Z., Wang, H., Sun, Z., & Mei, X. (2022). Design and Optimization of a Novel Microchannel Battery Thermal Management System Based on Digital Twin. Energies, 15(4), 1421. https://doi.org/10.3390/en15041421









