Energy-Based Approaches in Estimating Actual Evapotranspiration Focusing on Land Surface Temperature: A Review of Methods, Concepts, and Challenges

Abstract

The surface energy balance (SEB) model is a physically based approach in which aerodynamic principles and bulk transfer theory are used to estimate actual evapotranspiration. A wide range of different methods have been developed to parameterize the SEB equation; however, few studies addressed solutions to the SEB considering the land surface temperature (LST). Therefore, in the current review, a clear and comprehensive classification is provided for energy-based approaches considering the key role of LST in solving the energy budget. In this regard, three general approaches are presented using LSTs derived by climate and land surface models (LSMs), satellite-based data, and energy balance closure. In addition, this review surveys the concepts, required inputs, and assumptions of energy-based LSMs and SEB algorithms in detail. The limitations and challenges of aforementioned approaches including land surface temperature, surface energy imbalance, and calculation of surface and aerodynamic resistance network are also assessed. According to the results, since the accuracy of resulting LSTs are affected by weather conditions, surface energy closure, and use of vegetation/meteorological information, all approaches are faced with uncertainties in determining ET. In addition, for further study, an interactive evaluation of water and energy conservation laws is recommended to improve the ET estimation accuracy.

1. Introduction

Evapotranspiration (ET), which consists of evaporation (physical component) and transpiration (biological component) simultaneously, is defined as the process of water loss from the earth’s surface to the atmosphere. ET is the largest outgoing water flux, consuming more than half of the absorbed solar radiation and converting 60% of precipitation into water vapor [1]. Therefore, an accurate estimate of temporal and spatial changes in ET is considered an essential prerequisite for a broad range of applications such as agricultural management, drought monitoring, water use efficiency, atmospheric circulation and weather forecasting, energy and food security, carbon balance and plant growth, and hydrological modeling.

A common classification for the determination of ET includes direct and indirect methods. Techniques such as the lysimeter, sap flow (SF), eddy covariance (EC), Bowen ratio (BR), and scintillometer measure ET directly while indirect methods employ specified equations to estimate the latent heat flux [2]. Direct methods cannot be suitable spatial representatives for large-scale ET mapping due to costly setup and maintenance, flow distortion around the sensors, and point measurements [3,4,5]. In contrast, indirect methods, those that benefit from physical concepts for estimating ET, are capable of providing the spatial distributions of ET with an acceptable accuracy over large areas.

Indirect methods of ET estimation include mass transfer (MT) models, aerodynamic models, resistance-based models, radiation or temperature-based models, and energy balance models [6,7]. Mass transfer models, which estimate ET based on the difference in vapor pressure between the surface and reference height, are unsuitable for canopies with long-term water stress. Aerodynamic methods parameterize ET using the vertical gradient of the vapor pressure and eddy diffusivity. These methods are able to provide accurate estimates of ET using conventional data sources; however, considerable errors occurring in heterogeneous conditions restrict their wide employment. By relating the water vapor transport to the vapor pressure gradient and resistance network, resistance models were formed to estimate ET for both leaf and canopy. At the canopy scale, the method may be inappropriate due to assuming an identical location for sources and sinks of heat and vapor transfer. The models based on radiation or temperature data are popular empirical methods that are mainly used to estimate potential ET. Finally, Surface Energy Balance (SEB) models, which are the most popular physically based concept for simulating land surface processes including evapotranspiration, estimate ET based on the energy conservation law. Many complex algorithms have been developed for forecasting different parts of the energy balance [8]. SEB models rest on the assumption that the available surface energy is partitioned between heating the air and soil, transferring water vapor from the evaporating surface to the atmosphere, as well as heat storage for non-advective conditions. SEB algorithms and LSMs are governed by the land surface temperature (LST) as a significant boundary condition and driving force, and different solutions of the SEB equation can be presented using different retrieval methods of LST for estimating latent heat flux. Therefore, the current review was designed to provide a comprehensive assessment of energy-based models with a view to highlighting the key role of LST in the classification of these models.

In general, three types of approaches have been classified to estimate actual ET using LST and SEB. As the first approach, Penman–Monteith (PM) is a single-layer model combining energy balance and mass transfer concepts [9,10]. The PM equation follows the big leaf assumption, where the plant canopy is modeled as a big leaf to parameterize the transpiration through canopy stomatal conductance [11,12,13,14]. Given the changes in leaf distribution due to the variations in leaf size and density, plant height, and leaf angle, this assumption leads to unrealistic modeling of the canopy structure [11]. On the other hand, the variable of land surface temperature in the PM model is eliminated, and instead, ET is estimated using the slope of the saturation vapor pressure curve at air temperature. Despite the aforementioned assumptions, the PM model is widely used because of its simple nature and physically sound basis, and it was proven that the model is sufficient for simulating the ET of densely vegetated canopies [15]. TOPUP [16] and PROMET [17] are examples of one-layer PM-based models. For sparse canopies, the PM model tends to neglect the evaporation from the soil due to the big leaf theory [13], especially in models of the mosaic type. Therefore, two-layer models were introduced by Shuttleworth and Wallace [18], in which mass and heat interactions between soil and vegetation are used to estimate evaporation from bare soil and transpiration from plants and moist living surfaces. Being more complicated, multi-layer models, which have more than one canopy layer, compute the resistance network separately for discrete layers within the canopy [14,15]. These models are more flexible and capable of providing accurate ET than the two previous models under different weather and crop growing conditions. Although the first approach enjoys noticeable popularity, its accuracy can decrease because of the LST elimination. To address this issue, continuous LSMs can be used to solve the mass and energy balances simultaneously [19]. In these models, the energy balance equation in which all energy fluxes depend on LST is solved by a numerical method such as the Newton–Raphson method to find the LST that closes the equation [20]. ET can be subsequently estimated by the computed LST and MT equation, which uses the mean values of surface layer variables and turbulent transfer principles [21]. There are some examples for the application of LSMs in the literature, including the calibration of the Variable Infiltration Capacity (VIC) model for improving the accuracy of ET estimates [22], the solving of energy and water balances using the TOPLATS model [22,23,24,25], determination of the hydraulic properties of soil with the Noah land surface model [26], and validation of the Flash-Flood Event-Based Spatially Distributed Rainfall-Runoff Transformation Energy Water Balance (FEST-EWB) model using satellite LST [27,28].

The last approach calculates ET as a residual of the SEB equation (after the acquisition of all other energy fluxes) or a fraction of potential/reference ET. In this approach, LST information is derived from satellite thermal infrared (TIR) data, which makes it the most widely applied method to provide ET estimates with a relatively high degree of accuracy for an extended range of purposes (such as irrigation management [29], drought analysis [30], agricultural irrigation water requirement [31], water accounting [32,33,34], and water productivity [35]). However, the application of the approach is limited by cloud contamination, and TIR remote sensing-based LST retrievals under cloudy conditions cause discontinuities in ET calculations. Models using the TIR LST-based approach are divided into (1) one-source models, which assess vegetation and soil as a single component of the energy budget, and (2) two-source models, which assess the energy budget of vegetation and soil separately. One-source models include the Surface Energy Balance System (SEBS) [5], Mapping Evapotranspiration at High Resolution with Internalized Calibration (METRIC) [29], Surface Energy Balance Algorithm for Land (SEBAL) [36], Simplified Surface Energy Balance Index (S-SEBI) [37], and Operational Simplified Surface Energy Balance (SSEBop) [38,39]. Two-source models include the Two Source Energy Balance (TSEB) [40], Atmosphere–Land Exchange Inverse model (ALEXI) [41], Dual Temperature Difference (DTD) [42], and Enhanced Two-Source Evapotranspiration Model for Land (ETEML) [43].

ET simulation is faced with numerous challenges, both conceptually and practically. Firstly, the SEB closure and its effect on quantifying ET are discussed. During the past decades, it became evident that the SEB equation could not be closed completely [44,45]. In most cases, especially across EC sites, the available energy was found to be larger than the sum of turbulent fluxes (i.e., sensible and latent heat) [44,46]. The difference between available energy and turbulent fluxes is called the surface energy imbalance or the SEB closure problem, which can be 10% to 30% of the available energy (e.g., [47,48,49,50,51,52,53]). The underlying reasons for the surface energy imbalance can be classified into four groups: instrumental and measurement/computation errors such as systematic errors of soil heat and net radiation fluxes, errors related to data processing and analysis such as correction algorithms, sub-mesoscale transport processes, and neglected additional sources of energy (canopy heat storage, air heat storage, etc.) [54].

The second challenge is that of parameterization of the resistance network including the surface and aerodynamic resistances for vegetation and bare soil, and the evaluation of their impacts on the ET process. Canopy resistance (or surface resistance) is influenced by agronomical and climatological variables such as soil water content, canopy structure, etc. [55,56,57]. Since surface resistance is difficult to model mathematically and physically, empirical equations have received significant attention [55]. Although empirical methods need to be calibrated, many researchers have recommended them for practical use [55,57,58,59,60]; however, it was pointed out that empirical formulas lead to noticeable uncertainties in estimating resistance parameters [61]. The most common way of determining the canopy resistance has been presented in the Jarvis-type models, which consider environmental factors such as the air temperature, soil water condition, and vapor pressure of the atmosphere [62,63,64]. In addition to surface resistance, aerodynamic resistance to water and heat transfer also plays a crucial role in determining the latent heat flux [65]. Therefore, it must be computed considering different atmospheric and surface characteristics such as surface roughness, wind speed profile, atmospheric stability condition, air temperature, etc. Various methods ranging from the simplest (just the function of wind speed) to more sophisticated and accurate methods have been developed to calculate the aerodynamic resistance [66,67,68,69,70]. In this respect, the formulations by Thom [71], Brutsaert [72], and Monteith and Unsworth [73], which use a logarithmic form of the wind speed profile, are the most common methods.

This paper reviews the energy-based approaches used in the estimation of ET with a particular emphasis on the quantification of the land surface temperature. In this regard, the SEB algorithms, energy-based LSMs, and Penman–Monteith approach, along with related concepts and assumptions, are discussed in the following sections. In addition, this review highlights the main limitations and challenges by which the application of energy-based models is restricted. At the end, an initiative perspective on estimating ET is presented using water–energy systems. It should be noted that lists of acronyms and symbols are represented in Appendix A, and solutions of ET estimation approaches are provided in Appendix B. Figure 1 represents the flow diagram of the current review.

2. Materials and Methods

As mentioned, this paper reviews three energy-based approaches in terms of the estimation of ET with a particular emphasis on quantifying the land surface temperature. In this section, the Penman–Monteith approach, energy-based LSMs, and SEB algorithms are discussed.

2.1. Approach 1: Penman–Monteith (PM)-Based MODELS

The Penman equation, which is a semi-empirical formula developed by Penman [9], estimates the evaporation from open-water surfaces based on the mass transfer and energy balance concepts using monthly weather data, including solar radiation, air temperature, wind speed, and vapor content. The original Penman equation is defined as:

$$E=\frac{\Delta \times L{E}_n+\gamma \times L{E}_a}{\Delta +\gamma }$$

(1)

where E is the evaporation rate (kg/m²s), $L{E}_n$ is the evaporation rate due to net radiation (kg/m² s), $\Delta$ is the slope of the saturation vapor pressure curve at air temperature T (kPa/°C), $\gamma$ is the psychrometric constant (kPa/°C), and $L{E}_a$ is the evaporation rate due to mass transfer (kg/m²s), which is obtained from an empirical mass transfer formula. The Bucket model [74] is the earliest attempt to model surface processes, employing the single-source Penman approach based on Budyko’s concept [75]. This model overestimates evaporation from vegetated and bare soil surfaces; however, some modifications can be applied to reduce the biases of the model [76,77]. By considering physical principles for estimating LE_a over soil and vegetated surfaces, Monteith [10] improved the Penman model by introducing canopy and aerodynamic resistances, and the popular Penman–Monteith equation was formed. The combination of aerodynamic-based ET (representing the mass transfer concept) and SEB-based sensible heat flux (representing the energy budget concept) through the Bowen ratio ($\beta$) is the basis of the PM model, as shown below:

$$\beta =\frac{H}{LE}=\frac{(R_n-G-LE)}{\frac{{\rho }_a{C}_p\left(e_o-e_a\right)}{\gamma \left(r_a+r_s\right)}}$$

(2)

where H is the sensible heat flux (W·m⁻²), LE is the latent heat flux (W·m⁻²), $R_n$ is the net radiation flux (W·m⁻²), G is the soil heat flux (W·m⁻²), ${\rho }_a$ is the air density (Kg·m⁻³), $C_p$ is the specific heat capacity of air at constant pressure (J·kg⁻¹·K⁻¹), $r_s$ is the surface resistance (s·m⁻¹), $r_a$ is the aerodynamic resistance to heat and/or vapor transport (s·m⁻¹), $e_a$ is the actual vapor pressure of air (kPa), and $e_o$ represents the vapor pressure within the leaf (kPa), which is assumed to be equivalent to the saturation vapor pressure corresponding to the LST [6]. H is obtained from Equation (3), and by replacing it and arranging Equation (2), LE can be calculated using Equation (4):

$$H=\frac{{\rho }_a{C}_p\left(LST-T_a\right)}{r_a}$$

(3)

$$LE=\frac{R_n-G}{1+\beta }=\frac{R_n-G}{1+\gamma \frac{\left(r_a+r_s\right)\left(LST-T_a\right)}{\left(e_o-e_a\right)r_a}}$$

(4)

where $T_a$ is the air temperature (K).

The main challenge for solving Equation (4) is related to land surface temperature information. Since the accurate measurement of the land surface temperature was not possible in the 1960s, the air surface temperature gradient could not be used to compute the sensible heat flux. Hence, a psychrometric approximation, which is represented by Equation (5), was implemented to eliminate LST from the PM equation, as shown in Equation (6) [78]:

$$\Delta =\frac{e_o-e_a}{LST-T_a}=\frac{(e_o-e_a)-(e_s-e_a)}{LST-T_a}$$

(5)

$$LE=\frac{R_n-G}{1+\beta }=\frac{R_n-G}{1+\frac{\gamma }{\Delta }\left[1-\frac{\left(e_s-e_a\right)}{\left(e_o-e_a\right)}\right]\frac{\left(r_a+r_s\right)}{r_a}}$$

(6)

According to the aerodynamic expression for LE, the relationship given by Equation (7) can be replaced in Equation (6), and the final PM equation is written as Equation (8):

$$\frac{e_o-e_a}{e_s-e_a}=\frac{LE}{L{E}_a}\frac{r_a+r_s}{r_a}$$

(7)

$$LE=\frac{R_n-G}{1+\beta }=\frac{R_n-G}{1+\frac{\gamma }{\Delta }\left[1-\frac{\left(e_s-e_a\right)}{\left(e_o-e_a\right)}\right]\frac{\left(r_a+r_s\right)}{r_a}}$$

(8)

where $T_a$ is the air temperature (K), and $e_s$ is the saturation vapor pressure at T_a (kPa).

The PM model is known as a robust approach in providing ET estimates due to a number of reasons: (1) it defines an energy limit on the ET rate; (2) it theoretically uses a combination of main factors affecting the ET process; (3) it provides both the simulation and prediction of ET successfully; and (4) the obtained ET is not sensitive to input data. Despite the theoretical appeal of the PM model, its application is restricted by the need for ground-based measurements such as humidity, wind speed, air temperature, surface roughness parameters, and vapor pressure deficit [79]. In addition, temporal upscaling from an instantaneous scale to a longer time scale presents PM-based models with some challenges under cloudy weather conditions [80]. The PM model follows a one-layer or big leaf concept in which the canopy is modeled as a big leaf and the parameterization of heat and vapor transport is implemented using single-surface/aerodynamic resistances. FAO-56 from the Food and Agricultural Organization is an important application of the big leaf approach [81]. In addition, the TOPUP model [82,83] benefits from a simplified big leaf approach with limited parameters in which ET can occur from three main pathways: the interception store, the root zone store, and the groundwater table. Although the TOPUP model is widely used, the accuracy of its results decrease due to the simplified structure, big leaf approximation, and ignoring of the impact of land surface temperature on the ET process [83]. Another model employing the big leaf approach is Process Oriented Models for Evapotranspiration (PROMET), developed by [17]. PROMET includes a kernel model for treating the ET process and a spatial data modeler for adjusting the spatial scale of data to that of the model. The spatial data modeler is the reason that the PROMET model is capable of estimating ET on different scales, from a field to a landscape scale. The Moderate Resolution Imaging Spectroradiometer (MODIS) ET algorithm (or MOD16 algorithm) improved the performance of the PM model by including the environmental stress factors into the canopy resistance [79]. In addition, Mu et al. [84] revised the MODIS ET model by accounting for nighttime ET and dividing the canopy into dry and wet surfaces (i.e., E = E_wet (canopy interception) + E_s (soil evaporation) + E_c (plant transpiration)). Further, a Jarvis–Stewart-type canopy resistance was introduced by Zhang et al. [85] based on LAI and environmental factors. One of the significant revisions for the PM model is the Penman–Monteith–Leuning (PML) method that considers the impacts of the air humidity deficit and radiation through biophysical modeling [86]. PML estimates plant transpiration via the PM equation, soil evaporation via the Priestley–Taylor equation, and canopy conductance via the Leuning model [87,88]:

$$LE=\frac{\Delta \times R_{n,c}+\left(\rho C_p/\gamma \right)VPD{g}_a}{\Delta +1+g_a/g_c}+\frac{f\Delta \left(R_{n,s}-G\right)}{\Delta +1}$$

(9)

where $R_{n,c}$ is the net radiation for canopy (W/m²), $R_{n,s}$ is the net radiation for soil (W/m²), $g_a$ is the aerodynamic conductance (m/s), $g_c$ is the canopy conductance (m/s), VPD is the vapor pressure deficit (kPa), and f is a factor related to the potential evaporation of the soil surface (dimensionless).

The big leaf method was reported to be suitable only for describing ET from fully vegetated surfaces [73]. For sparse canopies, where the surface can be separated into vegetated and bare soil parts, the one-source PM model tends to fail due to neglecting the soil evaporation. Therefore, a patch (or tile) approach, which was first presented by Avissar and Pielke [89], was used to distinguish fluxes of soil evaporation and plant transpiration with no interaction. One example of a patch model is the Interaction Soil–Biosphere–Atmosphere (ISBA) model, which uses a patch approach to partition the soil and canopy components, and estimates ET as a sum of the soil evaporation, plant transpiration, and interception [90]. Another example is the Surface Energy and Water Balance (SEWAB) model, in which the total latent heat flux is divided into bare soil evaporation and plant transpiration via a vegetation fraction and the component ET is estimated by coupling the water balance and surface energy budget [91]. For more heterogeneous surfaces, a multi-patch approach can be applied to divide the grid into multiple uncoupled patches [92]. However, some studies discovered the interaction between canopy and soil fluxes [93,94], which led to the formation of two-source models.

Two-source models include a canopy layer in addition to the soil layer, and the heat and vapor fluxes can interact between the components. Unlike the patch approach that considers the heterogeneity along the surface, two-layer models account for the vertical heterogeneity of components. Three types of resistance, besides the aerodynamic and surface resistances of single-layer models, are included in two-layer models, which regulate the heat and vapor transfers between the mean canopy airflow and canopy surface, the mean canopy airflow and soil surface, and the mean canopy airflow and a standard height. Determining the resistance network of two-layer models is complex due to the over-parameterization and the need for their calibration [83,95]. Therefore, multi-objective approaches were suggested to implement the models when prior information is limited [96]. The model introduced by Shuttleworth and Wallace [18] and the ETLook algorithm [97] are examples of the two-layer approach, which solve the PM equation for soil and canopy separately:

$$E=\frac{\Delta (R_{n,s}-G)+\rho c_p\left(e_s-e_a\right)r_{a,s}^{-1}}{\Delta +\mathsf{\gamma }\left(1+\frac{r_{s,s}}{r_{a,s}}\right)}$$

(10)

$$Tr=\frac{\Delta (R_{n,c})+\rho c_p\left(e_s-e_a\right)r_{a,c}^{-1}}{\Delta +\mathsf{\gamma }\left(1+\frac{r_{s,c}}{r_{a,c}}\right)}$$

(11)

where E is evaporation (W·m⁻²), Tr is transpiration (W·m⁻²), and the s and c indices indicate the soil and canopy, respectively.

To consider the vertical canopy structure in detail, especially for a tall-vegetated ecosystem, multi-layer models were developed by extending the canopy structure to more than two layers (e.g., [98,99]). These models estimate the heat and water fluxes for each layer separately, and canopy-related fluxes are integrated over the canopy height. An example of a multi-layer structure is the Stanghellini model [100], which estimates the ET of greenhouse crops by including the LAI impacts within multiple layers of the canopy (Equation (12)).

$$LE=\frac{\Delta R_{net}+\left(2LAI\rho c_{p}VPD\right)/r_e}{\gamma (1+\left(\frac{\Delta }{\gamma }\right)+\left(\frac{r_i}{r_e}\right)}$$

(12)

where $r_i$ is the canopy’s internal resistance (s/m), and $r_e$ is the canopy’s external resistance (s/m).

The remote-sensing-based Ecosystem–Atmosphere Simulation Scheme (EASS) model is another multi-layer land surface model that adopts the PM equation for the estimation of components of ET by using a two-leaf strategy, which improves the accuracy of energy fluxes by almost 10% compared to the one-leaf strategy [101]. A modified version of EASS, the Dynamic Land Model (DLM), uses the PM equation to estimate ET for three components:$E_c$ (evaporation from water intercepted by canopy), $E_s$ (evaporation and sublimation from the soil), and $T{r}_c$ (canopy transpiration) [101,102]:

To obtain $E_c$ and $T{r}_c$, the DLM model adopts a leaf stratification strategy similar to EASS in which LAI is calculated for shaded and sunlit leaves separately [101]. It is worth noting that the turbulence within the canopy and also time-consuming computational processes with detailed data requirements (such as crop physiology and crop architecture information) limit the application of the multi-layer models at regional scales [15,98]. Figure 2 shows the schematic diagrams of the models discussed in the current section, i.e., the Penman model, the PM model (one-layer model), the patch model, the two-layer model, and the multi-layer model.

2.2. Approach 2: Land Surface Models (LSMs)

Since the late 1980s, advanced energy-based LSMs have been introduced to estimate water content, vegetation and soil temperature, and biogeochemical fluxes using sophisticated equations. Input data for LSMs include meteorological data (air temperature, air humidity, air pressure, shortwave and longwave radiation, wind speed and direction, and precipitation) and soil/vegetation information [103]. LSMs can calculate soil evaporation, plant transpiration, and evaporation from the water intercepted by the canopy using the PM and MT equations [104]. MT-based models relate ET to the vertical gradient of the vapor pressure and eddy diffusivity [105], and they are typically used under neutral atmospheric conditions. However, these models can be applied under unsteady conditions using atmospheric stability functions mainly quantified by Monin–Obukhov Similarity Theory (MOST) [106]. To solve the MT equation, the land surface temperature must be known, which is directly obtained from the energy balance equation at the surface. In other words, radiative and turbulent heat fluxes are written as functions of LST, and surface temperature values (known as the Equilibrium Energy Balance Temperature, EEBT) are calculated by closing the energy balance at the surface (Equation (13)):

$$R_n\left(EEBT\right)-G\left(EEBT\right)-H\left(EEBT\right)-\lambda ET\left(EEBT\right)=\frac{C_H\delta T_c}{\Delta t}$$

(13)

where $C_s$ is the surface heat capacity, and $\delta T_c$ is the change in the land surface temperature of the system over time $\Delta t$. Some of the main LSMs based on the direct solution of the energy balance at the land surface are discussed below:

Biosphere–Atmosphere Transfer Scheme (BATS)

In 1981, a Soil–Vegetation–Atmosphere Transfer (SVAT) scheme was developed using the approaches of [107] in formulating the soil temperature and vegetation interception [108]. Further, Dickinson [109] improved the 1981 version by considering the conceptual resistance network and physical soil hydrology scheme, which made it appropriate for use in large-scale atmospheric models. In 1986, a notable improvement concerning the assignment of soil type and land cover was applied using a popular available global land cover dataset [110]. This modified version was called the Biosphere–Atmosphere Transfer Scheme (BATS), which could be implemented in both on-line and off-line ways [111].

The BATS scheme includes three soil layers and one vegetation layer, accounting for three surface temperatures of the canopy, surface soil, and subsurface soil layer. In the BATS model, a demand–supply approach is utilized to calculate evaporation from the soil surface ($E_a$) as the minimum of the $E_p$($\mathrm{potential} \mathrm{evaporation}$) and $E_0$ (diffusion-limited maximum evaporation) [109].

On the other hand, the canopy evapotranspiration includes two parts of transpiration from dry foliage and evaporation from wet foliage. It should be noted that the BATS model considers vegetation as a uniform and porous surface with zero heat capacity, and neglects photosynthetic/respiratory energy transfer. The wet and dry canopy evaporation values are obtained from Equations (14) and (15), respectively:

$$E_{dew}=\frac{{\rho }_a{f}_{cw}\left[q_s\left(T_c\right)-q_s\right]}{r_a}$$

(14)

$$E_{tr}=\min (E_{tr,dem},E_{tr,sup})$$

(15)

where ${\rho }_a$ is the air density, $q_s$ is the saturation specific humidity, $T_c$ is the canopy temperature, $f_{cw}$ is the fractional area of the canopy occupied by water, $E_{tr,dem}$ is the transpiration by atmospheric demand, and $E_{tr,sup}$ is the water supply by roots.

Simple Biosphere Model (SiB)

The Simple Biosphere Model (SiB) was developed by Sellers et al. [112] based on a land surface parameterization design originally used to compute exchanges of heat, water, and momentum. The land surface parameterization scheme utilizes two distinct vegetation layers so that the upper layer includes the perennial canopy of shrubs or trees and the lower layer includes the ground cover of grasses and other herbaceous plants. In addition, the physical and physiological characteristics of the vegetation layers, which determine the aerodynamic transfer of sensible heat, water vapor, and momentum from the vegetation and soil components to a reference level, govern the interception of radiation and the transfer of moisture through the atmosphere–soil–plant system [112]. SiB calculates the variables of evapotranspiration and surface temperature for layers as follows:

• Two temperatures (i.e., the temperature of the canopy vegetation, $T_c ,$and the temperature of both the ground cover and the soil surface, $T_{gs}$):

  $$C_c\frac{\partial T_c }{\partial t}=R_{n,c}-H_c-\lambda E_c$$

  (16)

  $$C_{gs}\frac{\partial T_{gs} }{\partial t}=R_{n,gs}-H_{gs}-\lambda E_{gs}$$

  (17)
• The evapotranspiration from the canopy, $E_c$, has two parts: (1) $E_{wc}$, evaporation from the wetted fraction of the canopy, and (2) $E_{dc}$, transpiration of the soil water extracted by the root zone and water lost from the dry fraction of the canopy.

  $$\lambda E_{wc}=\frac{\left[e\ast (T_c\right)-e_a] }{{\overline{r}}_b}\frac{\rho c_p }{\gamma }{W}_c$$

  (18)

  $$\lambda E_{dc}=\frac{\left[e\ast (T_c\right)-e_a] }{{\overline{r}}_c+{\overline{r}}_b}\frac{\rho c_p }{\gamma }\left(1-W_c\right)$$

  (19)
• The evapotranspiration from the ground cover and soil surface, $E_{gs}$, has three parts: (1) $E_{wg}$ and (2) $E_{dg}$, which correspond to $E_{wc}$ and $E_{dc}$ for the ground cover, and (3) $E_s$, direct evaporation from the soil surface.

  $$\lambda E_{wg}=\frac{\left[e_s\left(T_{gs}\right)-e_a\right] }{r_d}\frac{\rho c_p }{\gamma }{W}_g{V}_g$$

  (20)

  $$\lambda E_{dg}=\frac{\left[e_s\left(T_{gs}\right)-e_a\right] }{r_g+r_d}\frac{\rho c_p }{\gamma }\left(1-W_g\right)V_g$$

  (21)

  $$\lambda E_s=\frac{\left[f_h{e}_s\left( T_{gs}\right)-e_a\right] }{r_{surf}+r_d}\frac{\rho c_p }{\gamma }\left(1-V_g\right)$$

  (22)

  where the c and gs indices indicate the canopy and ground cover/soil surface, $T$ is the surface temperature (K), $C$ is the heat capacity (J/K·m²), λ is the latent heat of vaporization (J/kg), ${\overline{r}}_b$ is the bulk boundary layer resistance (s/m), $r_d$ is the aerodynamic resistance between the ground and canopy airflow (s/m), ${\overline{r}}_c$ is the bulk stomatal resistance of the upper story vegetation (s/m), $r_g$is the bulk stomatal resistance of the ground vegetation (s/m), $r_{surf}$ is the bare soil surface resistance (s/m), $f_h$ is the relative humidity within the pore space of the surface soil layer, $V_g$is the fractional cover of the ground cover, and $W_c$ and $W_g$ are the wetness fractions of the canopy and the ground cover.

Mosaic Land Surface Model

The Mosaic LSM uses the “mosaic” strategy in which a grid square can be separated into homogeneous sub-areas, i.e., tiles of the mosaic, which contain a single bare soil or vegetation type [113]. This characteristic allows the model to consider the sub-grid heterogeneity and coexisting of different vegetation types in a grid square area. The various types of surfaces that can be included in each tile include the following: (1) broadleaf deciduous trees; (2) broadleaf evergreen trees; (3) broadleaf shrubs; (4) grassland (groundcover); (5) dwarf trees (tundra); (6) needle-leaf trees; (7) desert soil; and (8) bare soil. If two tiles represent the same surface properties, they can be aggregated together into a single tile. Parameterizing the energy balance of each tile is analogous to that of a single vegetation version of the SiB model; however, it can be simplified to be written in PM form. The interaction between the tiles is only established through the atmosphere, and also each tile can be coupled to the atmosphere independently. It is worth noting that the concept of the coupling strategy for the Mosaic model is different from that for models that assume a homogeneous mixture of vegetation types within a grid square (such as SiB). Mosaic LSM eschews the simultaneous computation of ground cover transpiration and other fluxes via the removal of the interactive ground cover vegetation pathway for evaporation. Finally, the total evaporation rate, E, can be written as [113]:

$$E=\frac{\rho ϵ }{p_s}\frac{\left[e\ast (T_s\right)-e_a] }{r_{eff}+r_a}$$

(23)

where $e_s\left(T_s\right)$ is the saturation vapor pressure at the surface temperature of the canopy and soil, which is derived by averaging the variables over the tiles for a grid cell, $ϵ$ is the ratio of the molecular weight of the water vapor to that of dry air, $p_s$ is the surface pressure, $r_{eff}$ is the single effective resistance composed of the $r_c$, $r_d$, and $r_{surf}$ resistances, and $r_a$ is the aerodynamic resistance between the canopy airflow and the reference height.

Variable Infiltration Capacity (VIC) Model

The Variable Infiltration Capacity (VIC) model is a macroscale land surface model that uses a mosaic scheme to represent the land cover classes within a grid cell. By solving the full energy and water balances, this model simulates land–atmospheric fluxes for each grid independently. Key features of the VIC model are its applicability for continental scale and its open-source availability. Early VIC models included two soil layers with a resolution of one or more degrees per grid cell. Later, Liang et al. [114] found that adding a thin top layer (5–15 cm) significantly improved the results of evapotranspiration in arid climates. Even though most applications use three layers, this version of the model is able to use an arbitrary number of soil layers [115].

In addition to plant transpiration and soil evaporation, which are parameterized by PM formulation, VIC simulates evaporation from the water intercepted by the vegetation. The evaporation from the canopy layer of the nth class, $E_c\left[n\right]$, is [116]:

$$E_c\left[n\right]=f\left[n\right]\times E_c^{\ast }\left[n\right]$$

(24)

where n is surface cover class index, $E_c^{\ast }\left[n\right]$ is maximum canopy evaporation, and $f\left[n\right]$is the fraction of the time step required for the evaporation from the water intercepted by the canopy. The transpiration during the time step is then:

$$\begin{array}{c}{E}_t\left[n\right]=\left(1-f\left[n\right]\right)\times E_p\left[n\right]\frac{r_a\left[n\right]}{r_a\left[n\right]+r_0\left[n\right]+r_c\left[n\right]}+\\ f\left[n\right]\times \left[1-{\left(\frac{W_i\left[n\right]}{W_{im}\left[n\right]}\right)}^{2/3}\right]\times E_p\left[n\right]\frac{r_a\left[n\right]}{r_a\left[n\right]+r_0\left[n\right]+r_c\left[n\right]}\end{array}$$

(25)

where $E_p$ is the potential evaporation (which is calculated by the PM equation with zero canopy resistance [117]), $r_0\left[n\right]$is the architectural resistance, $W_i\left[n\right]$ is the intercepted water amount, and $W_{im}\left[n\right]$ is the maximum amount of intercepted water. The first term indicates the fraction of the time step for which no evaporation occurs from the intercepted water, and the second term indicates the fraction of the time step for which both plant transpiration and evaporation from the interception occur.

Bare soil evaporation only occurs from the first layer ($E_1)$, meaning that the evaporation from the second layer is assumed to be zero (i.e., $E_2$ = 0). When the first soil layer is saturated, the evaporation occurs at the potential rate $E_p\left[N+1\right]$.

In addition, when the first layer is unsaturated, it evaporates at a rate $E_1$ which varies corresponding to the topography, infiltration, and soil characteristics. $E_1$ is also calculated via the formulation provided by Franchini and Pacciani [118], which follows the structure of the Xinanjian model [119]. It is noteworthy that for finding the land surface temperature at each time step, similar to other MT-based LSMs, the surface energy balance equation is iteratively solved using a trial-and-error strategy.

Noah Land Surface Model

The original OSU LSM included two soil layers and it used the thermal conduction equation and Richardson’s equation for soil temperature and soil moisture, respectively [120]. Later, it was enhanced to include more soil layers (from two to four layers), and the formulation of the canopy resistance was also improved [121]. As an outcome, Noah LSM was developed by the National Centers for Environmental Prediction (NCEP) and several agencies [122]. According to this model, the surface temperature is obtained from a single linearized SEB equation representing the combined vegetation/soil surface [120]. In addition, the soil heat flux is determined via the diffusion equation for the ith soil layer temperature, $T_i$ [121]:

$$\Delta z_i{C}_i\frac{\partial T_i }{\partial t}={\left(K_t\frac{\partial T }{\partial z}\right)}_{z_{i+1}}-{\left(K_t\frac{\partial T }{\partial z}\right)}_{z_i}$$

(26)

where z is the depth of the soil layer, C is the volumetric heat capacity, and $K_t$ is the thermal conductivity (C and $K_t$ are calculated by volumetric soil water content). The prediction of $T_i$ is performed using the fully implicit Crank–Nicholson scheme.

The total evaporation, E, is considered to be the sum of the direct evaporation from the top shallow soil layer, $E_{\mathrm{dit}}$, the evaporation from the interception storage of the canopy, $E_{\mathrm{c}}$, and the transpiration from the roots and the canopy, $E_{\mathrm{t}}$ [121].$E_{\mathrm{dit}}$ is calculated by Equation (27):

$$E_{\mathrm{dit}}=(1-{\sigma }_f) MIN\left(\left[-D {\left(\frac{\partial \mathsf{\Theta }}{\partial z}\right)}_{z_1}-K_{z_1}\right],E_p\right)$$

(27)

where $\Theta$ is the volumetric soil water content, D is the soil water diffusivity, $E_p$ is the potential evaporation, and ${\sigma }_f$ is the fraction of green vegetation. $E_{\mathrm{dit}}$ can proceed at the potential rate $E_p$ when the soil surface is rather moist. Otherwise, direct evaporation occurs at the rate by which the top soil layer can transfer water upward from below.

Canopy evaporation from intercepted water and plant transpiration values are obtained from Equations (28) and (29), respectively:

$$E_c={\sigma }_f{E}_p{\left(\frac{W_c}{S}\right)}^n$$

(28)

$$E_t={\sigma }_f{E}_p{B}_c \left[1-{\left(\frac{W_c}{S}\right)}^n\right]$$

(29)

where $W_c$ is the maximum wetness fraction of canopy S, and $B_c$ embodies the canopy resistance, including the soil moisture stress. The factor ${\left(W_c/\mathrm{S}\right)}^n$is considered to be a weighting coefficient to suppress $E_t$ in favor of $E_c$ due to the canopy surface becoming increasingly wet.

Table 1. A summary of the MT-based LSMs that follow approach 2.

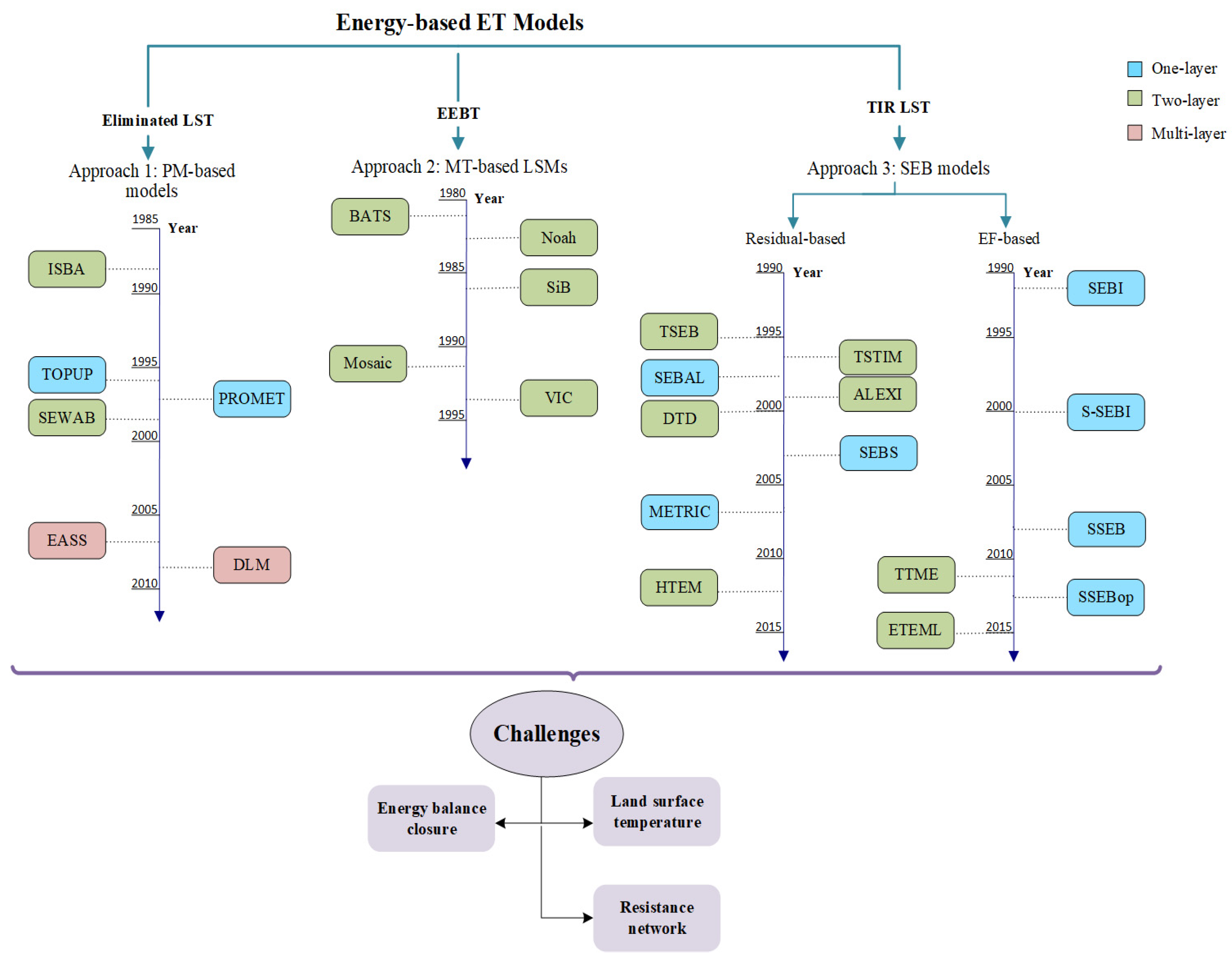
Model	Type	Main Assumptions	Advantages	Disadvantages	Mosaic Scheme
BATS	Two-layer	Using the demand–supply approach for calculating evaporation Heat capacity of foliage is assumed to be zero; therefore, the energy of the photosynthesis/respiration process is neglected	Offline and Online version High vertical resolution	When the soil is dry, it will underestimate the latent heat flux Low horizontal resolution	✕
SiB	Two-layer	The soil heat flux is modeled by using a Slab model Using an explicit backward-differencing scheme to calculate the $T_c$ and $T_{gs}$ The variations of leaf area density are assumed to be constant over height	High vertical resolution Providing better estimates for the time-varying exchanges of water, energy, and carbon for croplands Containing a crop phenology module to specifically simulate corn, soybeans, and wheat (SiBcrop)	Complicated calculation Difficulty capturing spatial heterogeneity Low horizontal resolution	✕
Mosaic	Two-layer	Using the ‘‘mosaic” strategy to consider sub-grid heterogeneity The energy balance equation for each sub-grid is simplified enough to be written in Penman–Monteith form	Computationally efficient Flexibility (various vegetation types)	Low horizontal resolution Modeling a Savanna as a mosaic can lead to significant errors	✓
VIC	Two-layer	Hydrologically based Using the mosaic scheme Evaporation and transpiration are parameterized by the Penman–Monteith formulation	Fine resolution (vertical and horizontal) Suitable performance over larger regions Open-source availability	Inefficiency in snowpack-related parameterizations Due to the non-closure of the energy budget, some conflicting results may arise	✓
Noah	Two-layer	Linearization of the surface energy balance for the Tskin calculation The prediction of the ith soil layer temperature is performed using the fully implicit Crank–Nicholson scheme	Advanced snowpack-related physics Offline and Online version	Insufficient consideration of vertical soil profile heterogeneity Under the conditions of high radiative forcing, it will underestimate the LST	✕

includes a summary of the characteristics of MT-based LSMs that follow approach 2.

2.3. Approach 3: Surface Energy Balance (SEB) Models

Approach 3 includes the residual methods and evaporative fraction (EF)-based models, which estimate ET using surface–air temperature difference or absolute LST. In residual methods, ET is obtained as a remainder term of the SEB equation, i.e., by subtracting sensible and soil heat fluxes from net radiation, a residual energy flux is achieved that is called ET. The surface energy balance for estimating ET is of the form:

$$\lambda ET=R_n-G-H$$

(30)

where λET (or LE) is the latent heat flux (W·m⁻²), and λ indicates the latent heat of vaporization (J·kg⁻¹ °C⁻¹). The SEBAL, METRIC, SEBS, TSEB, TSTIM, ALEXI, DTD, and HTEM models are indexed under this classification. On the other hand, EF-based models use an evaporative fraction to estimate the latent heat flux, including the SEBI, S-SEBI, SSEB, SSEBop, TTME, and ETEML models.

Similar to approach 2, this approach also requires LST data as a key prerequisite to quantify the energy fluxes. Satellite TIR sensors, such as AVHRR (Advanced Very High Resolution Radiometer), MODIS (Moderate Resolution Imaging Spectroradiometer), ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer), and Landsat, provide temporal and spatial distributions of surface temperature data with an acceptable accuracy. Different methods have been proposed to derive LST from TIR data, which are explained in subsequent sections, as well as SEB models that employ these TIR-derived LSTs for estimating ET and other energy fluxes.

2.3.1. Retrieval of LST from Satellite TIR Observations

LST information for this approach is obtained from satellite TIR observations. Since the LST estimation from the radiation of the TIR spectral region depends on atmospheric effects and emissivity [123,124], the extraction of LST requires corrections for emissivity, as well as radiometric and atmospheric effects [124]. Various algorithms have been developed to extract the LST information from the sensors using the radiative transfer equation (RTE), including single-channel methods, multichannel methods, multitemporal methods, and multiangle methods.

The Single-channel (or mono-channel) method, which was proposed by Hook et al. [125], estimates LST using a corrected radiance measured in a single channel through the inverted RTE [125,126,127,128,129,130]. The accuracy of the method is primarily limited by the atmospheric profile, surface emissivity, and corrections for the topographic and atmospheric effects [131,132,133]. However, the accuracy of these methods is acceptable in retrieving LST if the emissivity and atmospheric profile are known.

The Multichannel method, unlike the single-channel method in which the land surface emissivity and atmospheric profiles must be known at the satellite overpass, estimates LST without the need for additional information. For the first time, McMillin [134] proposed a split-window algorithm to calculate the surface temperature of sea by the differential atmospheric absorption in the two channels. Since then, many studies attempted to use different split-window algorithms for retrieving LST (e.g., [135,136,137,138,139,140,141,142,143,144,145]), which include linear and nonlinear split-window algorithms, linear or nonlinear multichannel algorithms, and the temperature emissivity separation method. A linear algorithm utilizes a simple relationship between the land surface temperature and the two brightness temperatures corresponding to the two TIR channels [134]. Given the error of linear methods due to the linearization of RTE, nonlinear approaches were developed based on a nonlinear relationship between LST and the top-of-atmosphere brightness temperatures [141,144,146,147,148]. By considering more than two TIR channels, LST can be also obtained from a linear or nonlinear combination of brightness temperatures similar to split-window algorithms [149,150]. In comparison with two-channel algorithms, multichannel algorithms are more accurate in retrieving LST [151]; however, adding more channels is associated with an increase in measurement errors.

The Multiangle Method, which is based on differential atmospheric absorption, employs various viewing angles to reduce the effect of atmospheric water vapor on LST [142,152,153]. Sobrino and Jiménez-Muñoz [154] compared a dual-angle algorithm with a nonlinear split-window algorithm in terms of the accuracy of retrieved LSTs, and the results indicated that the dual-angle algorithm was more appropriate than the split-window algorithm. However, it should be pointed out that multiangle methods have angular dependence on the LST and emissivity [155]. In addition, different viewing angles may provide different specifications for an object, and therefore, this method is not a suitable approach for unstable atmospheric conditions and heterogonous areas.

The Multitemporal Method [156] employs different times to estimate LST and includes the two-temperature and the physics-based day/night operational methods. The two-temperature method utilizes multiple observations to reduce the unknowns so that the number of measurements is equal to that of the unknowns. The main assumption of this method is that changes in the land surface emissivity are considered constant over time. Although the method is straightforward with a simple formulation, solutions may be unstable due to high-correlated equations [156,157]. Similar to multiangle methods, this method can only be employed in homogenous areas [158]. The physics-based day/night operational (D/N) method was developed to retrieve LST from day and night TIR data [159]. In fact, this method is a modified version of the two-temperature method, which utilizes two time observations to retrieve LST and land surface emissivity simultaneously. To improve the accuracy of the LST estimation, two variables, air temperature and atmospheric water vapor, are considered to adjust initial atmospheric profiles. Even though the D/N method is more accurate than other methods in retrieving the LST quantities, it suffers from misregistration problems and variations of the viewing zenith angle. To overcome the misregistration issues, the pixels can be aggregated into coarser spatial scales [158]. In addition, the combined use of night and daytime observations with a larger weight on the daytime information and the combination of the viewing angle-based method, split-window, and the D/N algorithm can be implemented to modify the LST retrievals.

2.3.2. SEB Algorithms

The SEB models consist of two categories, one-source (or single-source) and two-source (or dual-source) models, which solve the SEB equation using TIR LST to estimate ET as the residual of the difference between the available energy (R_n-G) and the loss due to the sensible heat flux or as a fraction of potential/reference ET. One-source SEB models analyze the soil and canopy by using a combined energy budget while two-source models are capable of partitioning the radiometric surface temperature into soil and canopy components to estimate soil evaporation and plant transpiration. Accordingly, a large number of SEB models have been developed, which are discussed in detail in the following sub-sections.

One-Source (or One-Layer) Models

Surface Energy Balance Index (SEBI)

Choudhury and Menenti [160] developed the Surface Energy Balance Index (SEBI) based on an evaporative fraction to compute the relative ET using the crop water stress index [161,162] redefined by theoretical pixel-wise ranges for LST and LE. In this method, upper and lower limits are defined based on the difference between the air and surface temperature. Evaporation is assumed to be zero in dry conditions, and total available energy (with a maximum value of surface temperature) is then assigned to the sensible heat flux. On the other hand, the minimum LST under wet conditions is obtained from the potential ET (PET) using the Penman–Monteith equation with the assumption of zero internal resistance. Finally, the relative latent heat flux is calculated from the equation given below [163]:

$$LE=L{E}_p \left(1-\frac{\left(LST-T_{pbl}\right)\times r_a^{-1}-(LS{T}_{min}-T_{pbl})\times r_{a,min}^{-1}}{(LS{T}_{max}-T_{pbl})\times r_{a,max}^{-1}-(LS{T}_{min}-T_{pbl})\times r_{a,min}^{-1}}\right)$$

(31)

where $LE$ is the latent heat flux (W/m²), $L{E}_p$ is the potential latent heat flux (W/m²), $LST$ is the land surface temperature (K), $T_{pbl}$ is the average temperature of the planetary boundary layer (K), $LS{T}_{min}$ and $LS{T}_{max}$ are the minimum and maximum land surface temperatures, respectively, r_a represents the aerodynamic resistance (s/m), and r_a,min and r_a,max are the minimum and maximum aerodynamic resistances (s/m), respectively. It should be kept in mind that the pixel-wise conception of SEBI is employed in other models, i.e., SEBAL, SEBS, and S-SEBI, with different definitions of dry and wet limits.

Surface Energy Balance Algorithm for Land (SEBAL)

The SEBAL algorithm utilizes satellite imagery and meteorological measurements for estimating ET within a single-source surface energy budget [36]. This algorithm addresses the problems of early one-source SEB models concerning the local application and the failure in spatiotemporal scalability. In addition, SEBAL is capable of handling TIR images with different resolutions and provides a strong tool for estimating spatiotemporal changes in ET with minimal data requirements.

The complexity of the SEBAL model is a result of the computation process of sensible heat flux and aerodynamic resistance due to changes in the weather and surface characteristics. As a result, SEBAL considers an internal calibration using two reference pixels chosen by the user’s judgment for estimating the sensible heat flux and stability-corrected aerodynamic resistance during an iterative procedure [36]. It should be noted that the iterative calibration process can reduce the effect of errors associated with LST observations on the algorithm [164].

The reference points include cold pixels, where ET = PET (or reference ET) and H = 0, and hot pixels, where ET = 0 and H = R_n − G. The successful application of SEBAL depends on the accurate selection of these pixels in the scene, which is implemented through a subjective procedure. According to [36], the cold and hot pixels are defined as a water body and a bare agricultural field, respectively. However, the aforementioned definitions can be unrealistic in some situations such as areas with extreme weather conditions, semi-arid areas without any water bodies, mountainous basins, and generally, heterogeneous landscapes due to the invalid linear relationship between LST and dT (which is the near-surface temperature difference) [165,166]. In addition, SEBAL is restricted by different atmospheric stability regimes and bumpy land surfaces, and errors in the TIR land surface temperature or dT can affect the H estimates. Because of these drawbacks in SEBAL, the physically based model of SEBS was developed, which is described as follows.

Surface Energy Balance System (SEBS)

The Surface Energy Balance System (SEBS) is a well-known model first proposed by Su [5]. The SEBS, a derivative of SEBI, is implemented using spectral radiance and reflectance observations in combination with ground-based data for estimating the surface energy balance and the atmospheric turbulent fluxes. In this model, a new SEB-based formulation is presented for calculating the evaporative fraction at limiting cases (i.e., completely dry and wet areas) using a non-subjective procedure. At the dry boundary, ET is assumed to be zero, and the sensible heat flux reaches its maximum value (i.e., $H_{dry}=Rn – G$). In contrast, ET occurs at a potential rate limited by energy availability at the wet boundary, and sensible heat flux takes its minimum value (i.e., $H_{wet}=Rn – G-L{E}_{wet}$). The evaporative fraction (EF) is finally expressed as:

$$EF=\frac{LE}{R_n-G}=\left(1-\frac{H-H_{wet}}{H_{dry}-H_{wet}}\right)\frac{L{E}_{wet}}{R_n-G}$$

(32)

where H is the sensible heat flux (W/m²), $H_{dry}$ and $H_{wet}$ are the sensible heat fluxes for the dry and wet boundaries (W/m²), respectively, and $L{E}_{wet}$ is the latent heat flux for the wet condition (W/m²). This method is capable of estimating ET in various spatial scales from local to regional under all atmospheric stability conditions using the Bulk Atmospheric Similarity theory [167] for atmospheric boundary layer scaling [5] and the Monin–Obukhov Atmospheric Surface Layer theory [106] for surface layer scaling. In addition, the roughness length for heat transfer is computed using an extended model as well as surface parameters such as albedo, emissivity, canopy cover, etc. It is worth noting that the SEBS algorithm does not require any prior knowledge of turbulent heat fluxes, and the consideration of SEB at the calibration limits can mitigate the uncertainties originating from LST and atmospheric variables. However, enormous amounts of required data and the relatively complex structure of the model can cause inconveniences in data-sparse regions. In addition, SEBS is the most sensitive single-source model to the aerodynamic parameters and surface–air temperature gradient [168,169].

Simplified Surface Energy Balance Index (S-SEBI)

Similar to the SEBI model, the Simplified Surface Energy Balance Index (S-SEBI) calculates the latent heat flux by an evaporative fraction, which is dependent on wet and dry conditions [37]:

$$LE=\frac{T_H-LST}{T_H-T_{LE}}\left(R_n-G\right)$$

(33)

where $T_H$represents the temperature for dry conditions controlled by radiation (K), and $T_{LE}$ shows the temperature for wet conditions controlled by evaporation (K). $T_H$ corresponds to the minimum LE (i.e., LE_dry = 0) and maximum H (i.e., H_dry = R_n − G), and $T_{LE}$ corresponds to the maximum LE (i.e., LE_wet = R_n − G) and minimum H (i.e., H_wet = 0). In the S-SEBI model, $T_H$ and $T_{LE}$ are determined by the image itself, which has constant atmospheric conditions with dry and wet pixels, while SEBI estimates extreme temperatures through an external data source [170].

In addition, $T_H$ and $T_{LE}$ can be regressed to the surface albedo, and LE is calculated as shown below:

$$LE=\frac{(a_{max}+b_{max}\alpha )-LST}{(a_{max}+b_{max}\alpha )-(a_{min}+b_{min}\alpha )}\left(R_n-G\right)$$

(34)

where $\alpha$ is the surface albedo (dimensionless), and $a_{max}$, $b_{max}$, $a_{min}$, and $b_{min}$ are regression coefficients.

Since the main concept of the model is derived from the contrast between the minimum and maximum land surface temperature for dry and wet limits, this method can only be applied to homogenous areas with both dry and wet parts and constant atmospheric conditions across the image [37,171]. S-SEBI does not calculate sensible heat flux, which makes the method different from other SEB models. Furthermore, there is no need for additional data except the surface temperature and surface albedo derived from remotely sensed imagery to estimate ET. Unlike other models, such as SEBAL, which consider a fixed temperature for extreme conditions, the S-SEBI model regulates the variations of LST in proportion to albedo values over dry and wet conditions. It should be noted that the determination of LST for extreme areas is location-specific under unstable atmospheric conditions over large areas. According to Rocha et al. [172], dependency on LST for the S-SEBI model is less than other models of ET estimation.

Mapping Evapotranspiration with high Resolution and Internalized Calibration (METRIC)

To reduce computational errors of remote sensing-based SEB models in mapping ET over heterogeneous surfaces, METRIC, developed by Allen et al. [29], focuses on an automatic internalized calibration of the SEB equation. The calibration process primarily depends on the air surface temperature difference retrieved radiometrically to simplify the calculation of H. In this way, two anchor pixels, similar to the SEBAL algorithm, are defined to describe the evaporative boundary conditions of the SEB. Cold (or wet) and hot (or dry) reference pixels are chosen in a well-irrigated field with full crop cover and a bare, dry field, respectively. Unlike the SEBAL algorithm, which has an assumption of zero evapotranspiration at the hot pixel, METRIC uses a daily soil water balance model to verify whether ET of the hot pixel is equal to zero. This modified assumption of non-zero evapotranspiration makes the estimates of H more reliable [173], and the selection process of candidate pixels is employed more accurately [174]. At the cold pixel, ET is equated to 1.05 times the reference evapotranspiration, which is not applicable during non-growing seasons as well as early growing seasons [175]. To reduce the uncertainties of selecting the anchor pixels, some studies have employed different search algorithms to automate the selection process (e.g., [176,177]).

METRIC uses the reference ET to scale instantaneous evapotranspiration instead of the evaporative fraction employed by SEBAL, which can better take into account the effects of wind speed and humidity variations. Both METRIC and SEBAL use the near-surface temperature gradient instead of the TIR land surface temperature, which eliminates the systemic bias of LST [178]. The SEBAL and METRIC models underestimate ET in non-agricultural and arid areas with extreme weather conditions [4]. In such situations, SEBS can be a suitable alternative because of its non-subjective approach in selecting the limiting cases [174].

Simplified Surface Energy Balance (SSEB)

To rapidly estimate ET over large areas, a simplified and cost-effective method called Simplified Surface Energy Balance (SSEB) was developed by Senay et al. [38]. A joint use of LST and reference ET is the basis of the SSEB model so that reference ET is adjusted by ET fraction calculated from the LST data. Finally, actual ET is acquired by the following Equations (35) and (36):

$$E{T}_a=EF\times \beta \times E{T}_r$$

(35)

$$EF=\frac{T_h-LST}{T_h-T_c}$$

(36)

where $E{T}_a$ (m) is the actual ET, $EF$ (dimensionless) is the evaporative fraction, $\beta$ (dimensionless) is a coefficient for considering the specifications of the reference crop (such as corn, alfalfa, and wheat), $E{T}_r$ (m) is the reference ET calculated by the standardized Penman–Monteith equation [81],$T_h$ (K) is the average LST for a set of three hot pixels, $T_c$ (K) is the average LST for a set of three cold pixels, and LST represents the value of the land surface temperature for any given pixel in the scene.

Similar to the SEBAL and METRIC models, SSEB scales ET between the minimum and maximum ET (corresponding to hot and cold pixels, respectively) in proportion to changes in LST. However, SSEB employs the LST scalar to directly derive ET without the estimation of sensible heat flux. On the other hand, SSEB ignores the soil heat flux and albedo, thus underestimating ET for surfaces with low albedo and overestimating ET for surfaces with high ground heat flux and high albedo. Therefore, some corrections such as the Normalized Difference Vegetation Index (NDVI) and Digital Elevation Model (DEM) corrections can be applied to improve SSEB for heterogeneous landscapes [179].

Operational Simplified Surface Energy Balance (SSEBop)

Another remote sensing one-source model is the Operational Simplified Surface Energy Balance (SSEBop) [39], which was established based on SSEB’s theory [38]. The SSEBop model, unlike SEBAL, METRIC, and SSEB, utilizes a non-subjective procedure in order to select the hot and cold reference pixels. Since the required data for this model are LST, $E{T}_r$, and air temperature, SSEBop benefits from a much easier concept than other one-source models. In addition, SSEBop is more applicable in comparison with METRIC and SEBAL over large regions because SSEBop simulates the SEB model using fewer parameters. The actual ET is calculated using a procedure that is similar to that of SSEB, as shown below:

$$E{T}_a=E{T}_f\times \beta \times E{T}_r$$

(37)

The land surface temperature for the cold pixel ($T_c$) is calculated using the corrected air temperature with the assumption of clear-sky conditions. By adding the dT to $T_c$, the land surface temperature for the hot pixel ($T_h$) is computed. It is worth noting that dT is obtained by employing the partial solution of the SEB for the cold pixel (where ET = 0 and H is maximal) and the hot pixel (where ET is maximal and H is minimal). SSEBop may misestimate the ET values on surfaces with low vegetation cover and high albedo due to the underestimation of TIR LST. In this regard, a mask or correction factor is applied to these areas in order to increase LST.

Two-Source (or Two-Layer) Models

Two-source models employ the surface temperature of the soil and canopy to estimate the evaporation and transpiration. Given that the LST derived by TIR sensors is a single temperature, various approaches are adopted to decompose the surface temperature into the soil and vegetation temperatures, as explained below.

Two Source Energy Balance (TSEB)

The Two-Source Energy Balance (TSEB) model estimates evaporation from soil and transpiration from the canopy separately [40]. Accordingly, the SEB equation is solved for the soil and vegetation components by partitioning the energy fluxes based on the radiometric surface temperature (T_rad) derived from remote sensing platforms. To calculate the ensemble radiometric surface temperature, the brightness temperatures at multiple angles are employed as follows:

$$T_{br}\left(\theta \right)=[\epsilon \left(\theta \right){\left(T_{rad}\left(\theta \right){)}^N+\left(1-\epsilon \left(\theta \right)\right)T_{sky}^N\right]}^{1/N}$$

(38)

where $T_{br}\left(\theta \right)$ represents the brightness temperature at a viewing angle $\theta$ (K), $\epsilon \left(\theta \right)$ is the thermal emissivity at $\theta$ (dimensionless), and T_sky is the hemispherical brightness temperature of the sky. T_rad is divided into the thermodynamic temperatures of vegetation and soil by a radiometer view fraction ($f\left(\theta \right)$) via Equation (39):

$$T_{rad}\left(\theta \right)={\left[f\left(\theta \right)T_c{}^N+\left(1-f\left(\theta \right)\right)T_s^N\right]}^{1/N}$$

(39)

where $T_c$ and $T_s$ express the surface temperatures for the canopy and soil, respectively. $T_c$ and $T_s$ are used to compute the sensible heat flux, and LE for the canopy and soil are calculated using the residual approach of the energy budget, expressed as:

$$L{E}_s=R_{net,s}-H_s-G$$

(40)

$$L{E}_c=R_{net,c}-H_c$$

(41)

where $L{E}_s$ and $L{E}_c$ are the latent heat fluxes for the soil and canopy (W/m²), $R_{net,s}$ and $R_{net,c}$ show the net radiation fluxes for the soil and canopy surfaces (W/m²), which are mainly estimated by Beer’s Law, G is the soil heat flux (W/m²), and $H_s$ and $H_c$ are the sensible heat fluxes for the soil and canopy components, calculated by decomposed T_rad:

$$H_s={\rho }_a{c}_p\left(\frac{T_s-T_a}{r_s+r_a}\right)$$

(42)

$$H_c={\rho }_a{c}_p\left(\frac{T_c-T_a}{r_a}\right)$$

(43)

where ${\rho }_a$ is the air density at constant pressure (Kg·m⁻³), $C_p$ is the specific heat capacity of the air at constant pressure (J·kg⁻¹·K⁻¹), $T_a$ is the air temperature (K), $r_s$ is the resistance of the boundary layer to heat flux just above the soil surface (s/m), and $r_a$ is the aerodynamic resistance (s/m).

If the brightness temperature is observed at a single view zenith angle, the relationships of Priestly–Taylor and Penman–Monteith are used to estimate $T_c$ and plant transpiration, called TSEB-PT [40] and TSEB-PM [180], respectively, and $T_s$ is then computed using Equation (39). One of the main difficulties in such methods is that the coefficients of Priestly–Taylor and Penman–Monteith vary over the heterogeneous areas [40,181,182].

Two-Source Time-Integrated Model (TSTIM)

The Two-Source Time-Integrated Model (TSTIM) is a modification of the TSEB model, which combines TSEB with a planetary boundary layer integrated by time for the measurement of turbulent fluxes at the regional to continental scales [183]. To estimate the sensible heat flux, TSTIM utilizes two instantaneous satellite-based surface temperatures during the morning with a 4-h interval. Accordingly, an instantaneous estimate for H is related to a radiometric surface temperature using the surface layer component of the model, and thus, a time-integrated value for sensible heat flux is obtained from these instantaneous estimates [184]. Another flux is estimated by the planetary boundary layer component of the model, and during an iterative procedure, TSTIM converges on estimates for H by means of a comparison between time-integrated fluxes. Due to the combination of the sensible heat flux with the temporal variations of the surface temperature and temperature of the boundary layer, the requirement for measuring air temperature is eliminated. Furthermore, the temporal variations of radiometric temperature can reduce the effects of biases of T_rad on the computed fluxes. Therefore, the TSTIM model is less sensitive to systematic biases of remotely sensed surface temperature in comparison with TSEB. It is worth noting that the calculations required to estimate LE for this model are similar to the TSEB model when two surface temperatures are observed (see the previous section), except Equation (44) that is simplified by linearizing, as in:

$$T_{rad}\left(\theta \right)\approx f\left(\theta \right)T_c+\left(1-f\left(\theta \right)\right)T_s$$

(44)

Atmosphere–Land Exchange Inverse Model (ALEXI)

The TSEB scheme can be employed to generate maps of daily energy fluxes at a continental scale using brightness temperature variations derived by the Meteosat Second Generation (MSG) and Geostationary Operational Environmental Satellites (GOES), the land cover map derived by AVHRR, and weather data within a time-integrated framework called the Atmosphere–Land Exchange Inverse Model (ALEXI) [41]. The real-time daily energy fluxes of LE, H, G, R_n, and soil moisture are obtained from this model with a spatial resolution of 5 to 10 km [174]. In order to improve the spatial resolution of the resulting fluxes, DisALEXI [185], which follows a spatially disaggregated technique, was developed using LST retrieved from polar orbiting satellites.

Dual Temperature Difference (DTD)

Another two-source time-integrated model is Dual Temperature Difference (DTD), which utilizes two LST observations similar to the TSTIM and ALEXI models [42]. However, DTD benefits from a simpler structure and fewer input data, thereby making it more applicable than the two previous models. As with TSEB, the partitioning of LST for the soil and canopy components in the DTD model is based on a fraction of the radiometer view. The flux H can be computed by Equation (45):

$$H=\frac{\rho c_p\left(T_{rad}-T_a \right)– f\left(\theta \right)\times H_c\times r_a}{\left(1-f\left(\theta \right)\right)\left(r_s+r_a\right)}$$

(45)

By applying Equation (45) two times and subtracting the flux H at t₁ from that at t₂, the main equation of the DTD model is obtained [42].

Finally, the total latent heat flux at time t₂ (LE_t2 in W/m²) is estimated as a remainder term of the SEB equation:

$$L{E}_{t2}=R_{n,t2}-H_{t2}-G_{t2}$$

(46)

and the latent heat flux for soil (LE_s in W/m²) is also calculated as a residual term:

$$L{E}_s=LE-L{E}_C$$

(47)

where $L{E}_C$ is the latent heat flux for the canopy (W/m²), which is obtained from the relationship of the Priestly–Taylor coefficient.

Two-source Trapezoid Model for Evapotranspiration (TTME)

Two-source models can estimate the LST for soil and canopy components using either surface temperature observations at a single viewing angle or radiometric temperature observations at two-view zenith angles. To retrieve the LST data from a single observation, vegetation index (VI)/LST space-based models were developed using a VI/LST space, which is defined as a triangular or trapezoidal space formed by the scatter plot of VI versus LST [186]. In addition, VI/LST spaces include isolines of soil moisture, which are used to represent the soil surface temperature [186,187,188]. Trapezoidal spaces are more adequate in determining water scarcity and moisture stress, plant transpiration, and aerodynamic behavior of the surface in comparison with triangular spaces. Space-based models, unlike non-space-based models, do not require the parametrization of resistance network, and therefore, the ET modeling is implemented without the need for excessive data such as plant physiology and micrometeorology information [189,190,191,192,193,194]. The two-source Trapezoid Model for Evapotranspiration (TTME) is one of the space-based models that utilizes a trapezoidal f_c-T_rad framework and soil wetness isopleths for estimating SEB components [188]. Flux LE is estimated using a patch approach by which the latent heat flux for vegetation and soil is weighted through a canopy fraction ($f_c$):

$$LE=f_{c}L{E}_c+\left(1-f_c\right)L{E}_s$$

(48)

where $L{E}_c$ denotes the latent heat flux for the canopy $\left(L{E}_c=R_{net,c}\times E{F}_c\right)$ and $L{E}_s$ denotes the latent heat flux for the soil $\left(L{E}_s=(R_{net,s}-G\right)\times E{F}_s)$. To estimate evaporative fractions, the radiometric temperature is divided into surface temperatures for the canopy and soil by the upper and lower boundary conditions, i.e., (T_rad = T_s,max, f_c = 0) for a bare surface with the highest humidity, (T_rad = T_s,min, f_c = 0) for a bare soil with the lowest humidity, (T_rad = T_c,min, f_c = 1) for a fully vegetated area with the lowest temperature, and (T_rad = T_c,max, f_c = 1) for a fully vegetated area with the highest temperature.

Hybrid dual-source scheme and Trapezoid framework-based Evapotranspiration Model (HTEM)

HTEM is a modified version of the TTME model in which a hybrid dual-source framework of the patch and layer methods is employed for estimating surface energy fluxes [195]. The layer approach is used to assign R_n values for the canopy and soil components established based on Beer’s law, and the patch approach is used to decompose the net radiation flux into the sensible heat, ground heat, and latent heat fluxes weighted by a canopy fraction. In addition, a sub-model is defined to partition the bulk LST into soil and vegetation surface temperatures, which is the same as that of TTME. As with TSEB, HTEM determines the sensible heat fluxes of the soil and canopy based on Ohm’s law, and the latent heat fluxes for the soil and canopy are computed as residual terms of the SEB equation:

$$L{E}_s=\left(\frac{R_{net,s}-G}{1-f_c}\right)-H_s$$

(49)

$$L{E}_c=\left(\frac{R_{net,c}}{f_c}\right)-H_c$$

(50)

Enhanced Two-Source Evapotranspiration Model for Land (ETEML)

A key point of VI/LST space-based models is their relatively independent structure in terms of site-specific calibration of parameter sets [186,196]. However, the application of these models is restricted by several issues, including (1) the requirement for a large space to contain a wide range of canopy fractions and soil moisture levels, limiting the application of models over heterogeneous regions [80], (2) the correct selection of wet and dry edges [197,198], (3) satisfying the assumption of the isoline control by soil moisture availability [197], and (4) the difficulty of coupling the VI/LST space-based models with other models due to different selections of wet/dry edges [199].

To overcome some of the issues, the Enhanced Two-Source Evapotranspiration Model for Land (ETEML) was developed by describing a theoretical VI/LST space [43]. Similar to other models, the flux decomposition into soil and canopy is employed using a patch approach, and the component latent heat fluxes can be estimated as follows:

$$L{E}_s=\left(1-SWDI\right)\times PE{T}_s$$

(51)

$$L{E}_c=\left(1-CWSI\right)\times PE{T}_c$$

(52)

where $SWDI$ denotes the soil water deficit index (dimensionless), $CWSI$ is the crop water stress index (dimensionless), $PE{T}_s$ is the potential ET for the soil (W/m²), and $PE{T}_c$ is the potential ET for the canopy (W/m²).

To derive $PE{T}_s$ and $PE{T}_c$, a theoretical VI/LST space is determined for each pixel in which the surface–air temperature difference is used instead of the absolute LST. Accordingly, four boundary points, i.e., dry bare soil, saturated bare soil, fully vegetated and well-watered surface, and fully vegetated surface with well-watered conditions, are defined for each pixel based on the R_n, T_a, G, and vapor pressure deficit quantities. In addition, the radiometric surface temperature for each pixel is divided into soil and canopy temperatures based on the described theoretical VI/LST trapezoid space, as follows:

$$T_c-T_a=K_s\times \left(1-f_c\right)+\left(LST-T_a\right)$$

(53)

$$T_s-T_a=\left(LST-T_a\right)-K_s\times f_c$$

(54)

where $K_s$ is the isoline slope.

Table 2. A summary of the remote sensing ET models that follow approach 3.

Type	Model	Data Requirements	LST Configuration	Main Assumption	Strength	Weakness	Temporal Resolution	Spatial Scale
One-Source	SEBI	LST, W, Tpbl, hpbl,	Absolute LST	Based on the CWSI and pixel-wise concept	Practical even for surfaces without wet and dry pixels	Characteristics of the planetary boundary layer are needed Relatively poor accuracy	Day	Regional
	SEBAL	LST, NDVI, $\mathsf{\alpha }$, W, Ta, RH	Surface–air temperature gradient	Internal calibration by anchor pixels through a subjective procedure Uses the air surface temperature gradient instead of absolute LST Defining a linear relationship between LST and dT	Minimum ground data requirement Able to use slope and aspect in heterogeneous lands Physical concept Internal calibration Solves all the energy fluxes	Time-consuming Cost-intensive Limited by different stability atmospheric conditions and heterogeneous surfaces Uncertainties due to user’s judgment in selecting anchor pixels	Day, Month, Season, Year	Field to regional
	SEBS	$\mathrm{LST}, \mathrm{NDVI}, \mathsf{\alpha }$, hpbl, ea, es, W, Ta, RH,	Absolute LST	EF is used by calibrating the limit points through a non-subjective procedure	Applicable for all atmospheric stability conditions Physical concept No need for prior knowledge on turbulent heat fluxes Calculates roughness length by a developed submodule Selects the reference pixels automatically	Complex structure High data requirements High sensitivity to the air surface temperature gradient and aerodynamic parameters	Day, Month	Local to regional
	S-SEBI	LST, NDVI, α,${\mathrm{T}}_{\mathrm{a}}$	Absolute LST	The process of determining the wet and dry conditions is albedo dependent	No need for additional data Dependency on LST is less than other models Capable of regulating variations of LST in proportion to albedo Temperatures for dry and wet conditions can be determined by the image itself	Does not solve H Applicable for homogenous areas with constant atmospheric conditions Dependency of extreme LSTs on location	Day, Month	Basin
	METRIC	LST, NDVI, LAI, W, RH, Ta, Sh	Surface–air temperature gradient	Internal calibration by anchor pixels through a subjective procedure Using the air surface temperature gradient instead of absolute LST Defining a linear relationship between LST and dT	Minimum ground data requirement Able to use slope and aspect in heterogeneous lands Solves all the energy fluxes Physical concept Internal calibration Uses a soil water balance to determine the hot pixel	Time-consuming Cost-intensive Uncertainties due to user’s judgment in selecting anchor pixels ET underestimation in arid and non-agricultural areas	Day, Month, Season, Year	Field to regional
	SSEB	LST, NDVI, DEM, W, RH, Ta, Sh	Surface–air temperature gradient	Joint use of LST and reference ET	Simple Cost-effective Operational model Provides the rapid ET estimates over large regions	Does not solve H and G ET underestimation in surfaces with low albedo and ET overestimation in surfaces with high G and high albedo High sensitivity to LST	Day, Month, Season	Basin to regional
	SSEBop	LST, Ta, Albedo, NDVI	Surface–air temperature gradient	Selecting the reference pixels by a non-subjective procedure ET is linearly scaled between evapotranspiration of hot and cold pixels (in proportion to LSTs of hot and cold pixels), dT is obtained from a linear relationship with LST	Simple, cost-effective, and operational model Low computational effort Selects the reference pixels automatically	Does not solve H and G Does not use surface and aspect in heterogeneous lands	Day, Month, Season, Year	Basin to regional
Two-Source	TSEB	LST, W, Ta, LAI	LST observations at one or two viewing angles	Energy fluxes can be determined by one or two LST observations	Usable at conditions with high VPD and low meteorological data	Determination of Priestly–Taylor and Penman–Monteith coefficients	Day, Month, Season	Local to regional
	TSTIM	LST, LAI, W	Temporal changes in LST	Time-integrated structure Uses LST data at two times (t1 and t2)	No need for measuring ${\mathrm{T}}_{\mathrm{a}}$ Less sensitive to systematic biases of LST	Requires LST data with a high temporal resolution	Day, Month, Season, Year	Regional to continental
	ALEXI	LST, W, LAI, LULC	Temporal changes in LST	Time-integrated structure Considering temporal variations of LST Satellite-based	Generates maps of daily energy fluxes as well as soil moisture over large scales	Requires LST data with a high temporal resolution	Day	Continental
	DTD	LST, LAI, Ta, W	Two LST observations at two times	Time-integrated structure	Simple structure with a few input data Operational model Less sensitive to errors of absolute LST and meteorological data, No need for modeling boundary layer development	Determines the Priestley–Taylor coefficient Requires LST data with a high temporal resolution	Day	Regional
	TTME	NDVI, LST, $\mathsf{\alpha }$, Ta, W	LST observation at a single viewing angle	VI/LST space-based Uses a trapezoidal framework with specified boundary conditions Patch approach for estimating ET	Simple structure with few input data requirements No need for computing the resistance network	Misestimates energy fluxes due to the temperature-dependent cold edge Different selections of wet/dry edgesNeeds a flat surface with a large number of pixels	Day	Regional
	HTEM	LAI, Albedo, Ta, LST, ea, NDVI, W	LST observation at one viewing angle	Uses a trapezoidal framework for estimating energy fluxes	Hybrid dual-source scheme of the patch and layer methods No need for computing the resistance network	Inappropriate in complex surfaces Different selections of wet/dry edges Needs a flat surface with a large number of pixels	Day	Regional
	ETEML	LST, Albedo, LULC, LAI, NDVI, Crop height, W, ${\mathrm{T}}_{\mathrm{a}}$, VPD	Surface–air temperature difference	Based on a theoretical VI/LST space for each pixel	Appropriate for complex and heterogeneous conditions No need for computing the resistance network	Too many inputs	Day	Local to regional

NDVI = Normalized Difference Vegetation Index; LAI = Leaf Area Index; $\mathsf{\alpha }$ = surface albedo; ${\mathrm{T}}_{\mathrm{a}}$ = air temperature; W = wind speed; e_a = actual vapor pressure; e_s = saturated vapor pressure; RH = relative humidity; T_pbl = average temperature of planetary boundary layer; h_pbl = height of planetary boundary layer; LULC = Land Use Land Cover; Sh = sunshine hours.

shows a summary of SEB algorithms, one-source and two-source models, and LST configurations.

It is worth noting that a wide range of remotely sensed ET products, such as MODIS (MOD16), AVHRR, GLEAM, and SSEBop, were developed based on the SEB algorithms to provide spatiotemporal changes in evapotranspiration at different scales. In addition to internal uncertainties caused by the estimation method (stated before in detail in Section 2), ET estimates include some external inaccuracies related to the input data. Satellite data with high spatial resolution (such as ASTER and Landsat) suffer from low return rates, and the platforms with coarse spatial resolution (such as SMAP and MODIS) have low temporal resolution. In addition, delays in data collection by sensors, which vary from an hour to several days, make practical applications challenging. Another major uncertainty is the spatial scale mismatch that occurs between coarse meteorological data and fine vegetation information [195]. In addition, biome-specific physiological parameters and the leaf area index, which are assumed to be constant over space and time, can lead to the errors in ET retrieval, as is the case for the MOD16 product.

3. Limitations and Challenges

3.1. Land Surface Temperature

As stated above, PM-based models use remotely sensed vegetation indices and meteorological data instead of LST information, and practically, the resistance terms r_a and r_s are determinative for implementing these models. This assumption, i.e., the big leaf basis and elimination of LST information, leads to a decrease in the accuracy of ET results [83]. On the other hand, the models following approach 3 require cloud-free LST images and atmospheric corrections for mapping ET values, although it is not straightforward to retrieve cloud-free LST from TIR data in large scales with monsoon climates due to large spatio-temporal gaps [97]. In other words, TIR radiation is sensitive to atmospheric effects such as water vapor, surface emissivity, and cloud cover, and this leads to discontinuous information for ET estimation [97,183,200]. In this regard, LST observations with high temporal and spatial resolutions are useful to provide cloud-free surface temperature information [174]. In addition, microwave remote sensing can be a suitable surrogate for providing LST in all-sky conditions because it is not limited by cloud cover; however, its coarse spatial resolution causes ET estimation to only be possible for large scales [201].

Another important challenge of TIR remote sensing in estimating energy fluxes is that the radiometric surface temperature (T_rad) derived by satellite is assumed to be equivalent to the aerodynamic temperature of the surface (T_aero), which is defined as a bulk effective, unmeasurable temperature for estimating heat fluxes in the atmospheric surface layer [202,203,204,205]. While the relationship between T_rad and T_aero is not clear, they cannot be considered equal because of the difference between the thermodynamic temperatures of vegetation and soil components. Therefore, one of the error factors in estimating ET, unlike the atmospheric correction of T_rad, is related to the assumption that the difference between these two temperatures can be ignored [79].

Component temperatures contribute to the aerodynamic and brightness temperatures in proportion to the roughness length and view geometry of the sensor [40,203,204,205,206,207]. This issue is intensified for one-source models employing a single LST observation for estimating the sensible heat flux so that depending on the viewing angle of the sensor, differences between T_aero and T_rad for the canopy and soil can be more than 10 degrees [203,204,205,208]. A common solution for reducing the errors due to this assumption is that an excessive resistance, associated with heat transfer, is introduced to reflect the difference between the heat and momentum transfer [209,210]. However, this method is limited due to the need for calibrating the parameters concerning resistance changes in space and time [210,211]; that is why many models were developed without using the excessive resistance term [212,213,214].

Absolute measurements of LST lead to considerable errors when applied to partially vegetated surfaces [215], and the effects of the canopy architecture and viewing geometry on the LST retrievals are troublesome in semi-arid areas with partial canopy cover [40]. To overcome the issues of sensitivity of SEB algorithms to errors of absolute LST, models that employ a temperature gradient instead of an absolute surface temperature have been developed to reduce the errors associated with the air temperature [29,36]; however, this issue still causes uncertainties over heterogeneous areas. To address this challenge, two-source models, which decompose LST and energy balance regimes into soil and vegetation components, and include the resistances in boundary layers of components by accounting for the difference between T_aero and T_rad, have been proposed to estimate ET over complex surfaces [40,216].

In addition to TIR LST data, land surface temperature values can be obtained from the energy closing at the land surface (i.e., approach 2, which uses the MT equation). Unlike TIR-based LST, which is restricted under overcast weather conditions, EEBT derived by approach 2 is usable in all-sky condition; however, in such situations, the relationships used to calculate energy fluxes and as well as the proper energy closure have a significant effect on the quality of the achieved LST responses. If the energy balance equation is dictated to close, the quantities of LST can be less or more than its real values.

3.2. Energy Balance Closure

In addition to fluxes H, LE, G, and R_n, the SEB equation includes some neglected effects that make it unclosed, i.e., the Imb term:

$$R_n=\lambda ET+G+H+Imb$$

(55)

Many studies have reported an underestimation of turbulent fluxes compared to available energy, showing a non-closed energy balance (e.g., [217,218,219,220,221,222]. A large number of underlying reasons can cause the non-closure of SEB, which can be classified into four categories: instrumental and measurement/computation errors, errors related to data processing and analysis, sub-mesoscale transport processes, and neglected sources of energy [54].

Sensors are responsible for instrumental errors when measuring wind speed [223,224], soil humidity [54], net radiation [225], and ground heat flux [226,227]. Several methods were proposed to satisfy the assumption of zero vertical wind over the averaging time; however, some of them failed to achieve this condition and led to errors in the processing chain [228,229,230]. In addition, some corrections need to be applied to the measured flux of the EC system to avoid the lack of SEB closure [231]. Over heterogeneous surfaces, EC systems are not capable of measuring the non-turbulently transported energy, and as a result, energy fluxes are underestimated due to sub- mesoscale transport processes [232,233]. On the other hand, ignoring the additional thermal terms, i.e., the soil heat storage, potential energy of air and water, and biomass and photosynthesis/respiration heat storage, can cause considerable errors, especially in areas with tall vegetation [234,235,236].

With these considerations in mind, SEB closure seems to occur for a horizontally uniform, non-vegetated surface with vertical fluxes [54]. However, such an assumption cannot be realistic in practical applications, and effort is required to achieve an acceptable SEB closure. If the SEB equation is not appropriately closed, ET estimation models that follow approach 1 overestimate the evapotranspiration quantities due to adding the Imb term to the ET [200]. Similarly, approach 2 misestimates ET values because LSTs are obtained from an energy balance dictated to be closed. However, utilizing the land surface temperature for calculating all the energy terms leads to an increase in the accuracy of estimated fluxes [237]. Accordingly, ET estimation models employing the MT equation and obtained LST from the SEB closing (i.e., approach 2) are more accurate than the other models. In contrast, PM-based models are less accurate in estimating energy fluxes due to the elimination of land surface temperature.

3.3. Resistance Network

Depending on the parameterization of the resistance network, resistance-based ET models, including PM-based models (approach 1), MT-based LSMs (approach 2), and residual- and EF-based models (approach 3), are grouped into one, two, and multi-layer structures; therefore, accurate quantification of the resistance network is important to better estimate turbulent fluxes [238,239,240,241]. The resistance network can include aerodynamic and surface resistances in the on-layer structure as well as boundary layer and canopy bulk stomatal resistances in the multi-layer scheme [40,92,241,242,243].

Measuring the aerodynamic resistance is difficult because of its unmeasurable parameters such as the roughness length and atmospheric stability coefficient [244]. Various methods have been proposed to estimate aerodynamic resistance, which can be classified into three groups: empirical, semi-empirical, and methods following MOST [65]. The degree of validity and simplification in solution are the most important characteristics of the aerodynamic resistance estimation models. Unlike MOST-based methods that differentiate eddy diffusivities for heat and momentum transfer (e.g., [71,245]), most empirical approaches assume that the roughness length for momentum and heat transfer are identical (e.g., [120,246,247,248]), which makes it a simple method but invalid for sparsely vegetated surfaces. Similar to MOST-based models, semi-empirical methods also consider a distinction between the eddy diffusivities of heat and the momentum transfer (e.g., [69,249]). In addition to the surface property of roughness length [65], the atmospheric stability condition is considered as a crucial parameter to account for the micrometeorological changes in estimating aerodynamic resistance, which can be assumed to be neutral when a stable wind speed profile and a homogeneous LST are dominant at the near-surface [250]. Under stable conditions, the profiles of air temperature and wind speed follow the linear equations, and there is an exact solution for estimating aerodynamic resistance. While the aforementioned profiles follow non-linear equations under unstable conditions, an iterative process is needed to obtain an exact solution for aerodynamic resistance. In this regard, two indicators, the Richardson number [251] and the Monin–Obukhov stability length [106], have been proposed to characterize non-neutral conditions, which are mainly adopted for non-iterative and iterative procedures, respectively [36,209,252,253,254].

In addition to the aerodynamic resistance, the application of ET estimation models is also limited by the accurate parameterization of canopy resistance [55], which can be considered as the diffusive resistance to water vapor transfer from stomatal cavities of leaves [255]. Estimating the surface resistance is challenging because of the combined physiological and climatological effects included in the concept of resistance [10]. Considering the big leaf approach, Szeicz and Long [256] proposed a widely used method based on the effective LAI for estimating canopy surface resistance. Afterwards, Jarvis [257] presented a novel method based on the summation of resistance values of individual leaves within a canopy. To progress this method toward a more complicated one, Lhomme [258] introduced a multilayer approach, which estimates canopy resistance as a physiological parameter in zero-evaporation conditions. The sap flux method, by considering a moderator between canopy- and leaf-level measurements, provides estimates of the canopy resistance that agree well with the canopy conductance measured using a photometer [259,260]. Even though this method avoids disturbance of the leaf boundary layer, its application is more widespread for woody canopies than agronomic vegetation [255]. Some methods were also proposed to estimate canopy resistance based on a linear [261] and nonlinear [262] relationship between aerodynamic and climatic resistance. The empirical basis of these methods leads to the need for the calibration of parameters [55,57,58,59,60], and in most cases, they are faced with great uncertainties in estimating ET [61]. To eliminate the need for calibration, Todorovic [263] introduced a mechanistic model, in which canopy resistance is estimated based on a relationship between aerodynamic resistance and climatic variables. However, this method failed to estimate the resistance in some study cases [264]. Without including the effect of aerodynamic resistance on the canopy resistance, Jarvis [62] proposed a method in which the canopy resistance depends on environmental factors such as the vapor pressure deficit and solar radiation. This method was completed by considering more environmental factors, and was named the Jarvis–Stewart equation [62,63]. Even though the Jarvis–Stewart equation is a widely used method for estimating canopy resistance, it is, especially in LSMs, mostly used in a specific growth stage of the crop [238].

4. Conclusions and Perspective

LST is the most important factor in determining the biophysical processes in land–atmosphere boundary areas including ET. Due to the absence of a sufficiently dense network of stations measuring LST, the surface temperature values are obtained from indirect methods, which leads to the development of various models of ET estimation. The current review provided a clear classification for ET models based on available retrieval methods of LST information. The first approach includes PM-based models, which follow a psychrometric assumption based on eliminating LST; instead, they use remotely sensed vegetation indices and meteorological data for estimating ET. Despite the wide popularity of this approach, the assumption of ignoring LST leads to decreased accuracy in the resulting ET. With the development of LSMs, which simulate the Soil–Vegetation–Atmosphere system by using sophisticated parameterizations, the land surface temperature data (known as the Equilibrium Energy Balance Temperature, EEBT) result from closing the energy balance equation at the land surface, which forms approach 2. The EEBT values are valid for the all-sky condition; however, a precise formulation for the SEB equation and an acceptable SEB closure are needed to ensure the accuracy of the ET results. By providing spatiotemporal distribution of LST via TIR-based earth observation data, approach 3 was made to map ET over large and heterogeneous regions. Different methods were proposed to derive LST from TIR data, which are grouped into four classes of single-channel methods, multichannel methods, multitemporal methods, and multiangle methods. In addition, a wide range of models, residual- and EF-based, were developed to employ these TIR-derived LSTs to estimate ET through energy conservation principles. Despite the strength of these models in determining energy fluxes, all of the above approaches face a number of limitations in estimating ET. One of the most important challenges is related to the accuracy of LST information. As stated above, approach 1 suffers from the assumption of ignoring LST and approach 2 may estimate unrealistic LST values if the surface energy balance is not properly closed. In addition, the models following approach 3 require cloud-free LST images, but it is not straightforward to retrieve cloud-free LST from TIR data, and it can lead to a decrease in the accuracy of the ET results. It should be noted that models using approach 3 assume that the radiometric surface temperature derived by satellite is equivalent to the aerodynamic temperature of the surface, which can be one source of error. Therefore, models such as SEBAL and METRIC have been developed to reduce the uncertainty due to the aforementioned assumption using the air surface temperature gradient instead of absolute LST. On the other hand, it was proven that the SEB equation cannot be closed completely. Neglected effects, including instrumental and measurement/computation errors, errors related to data processing and analyzing, sub-mesoscale transport processes, and ignored sources of energy, can affect the LST and ET results. As the last important challenge, the complicated parametrization of resistance network can limit the application of ET estimation models. Different configurations of the resistance network (surface and aerodynamic resistances) lead to the development of different resistance-based models, including one-layer, two-layer, and multi-layer models. Given the unmeasurable parameters of the resistance network, empirical, semi-empirical, and MOST-based methods were introduced to estimate the aerodynamic and surface resistances. Empirical and semi-empirical methods mainly require the calibration of parameters while the MOST-based approach can provide a stronger tool in estimating the resistance network.

ET evaluation involves energy and mass conservation laws [265]. However, available methods of ET estimation that belong to either approach 1 or 3 are determined largely by energy availability, without explicit water resource constraints. Similarly, Ets estimated using LSMs (approach 2), despite their use of the energy–water equation system, are mainly limited by energy resources due to the one-way solution of the system. In such situations, ET values are overestimated or underestimated under extremely dry and wet conditions, which lead to larger time periods for drought recovery and larger potential for floods, respectively. Therefore, for the future work, a simultaneous and interactive evaluation of water and surface energy balances is recommended to reciprocally connect the atmospheric demand, available surface radiation, and water availability. Accordingly, the SEB closure is conducted to derive LST values using a forward derivation, and ET can then be estimated based on the computed LST and MT equation. By applying ET to the water balance model, the surface soil moisture is updated and then used to compute the LST and ET values at the next time step. In this regard, a two-way interaction is formed between the surface and hydrological properties, i.e., LST, ET, and soil moisture, which is capable of implementing the accurate and correct conceptual relationships between components.