A Comparative Analysis of Maximum Power Point Techniques for Solar Photovoltaic Systems
Abstract
1. Introduction
2. Modelling of a Photovoltaic Cell
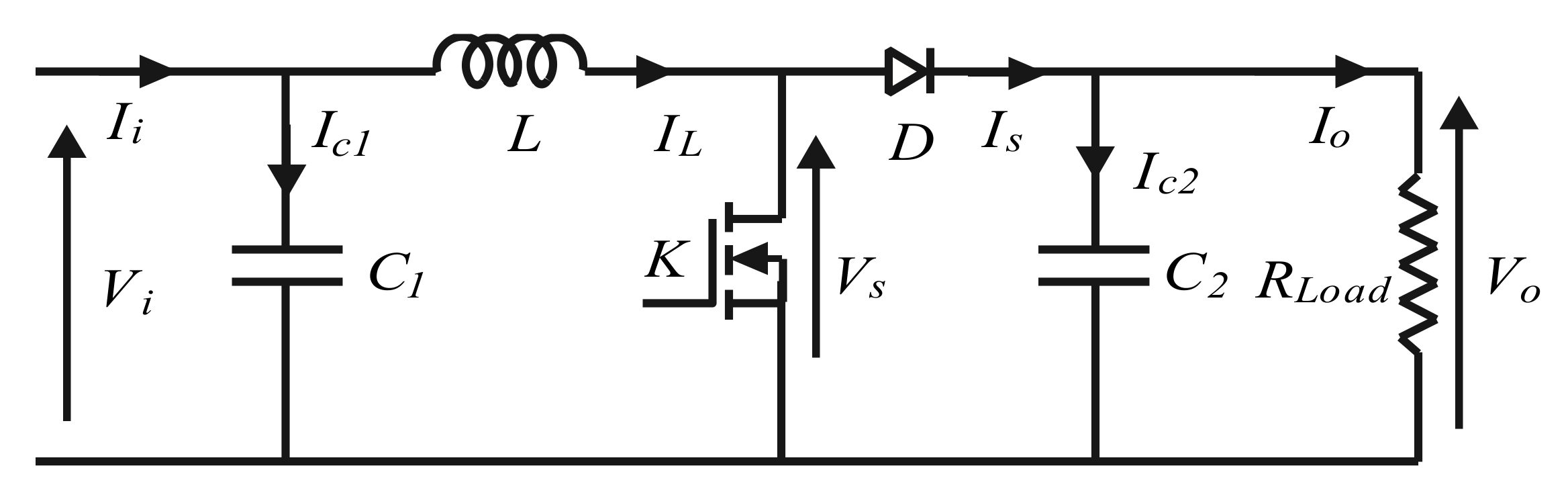
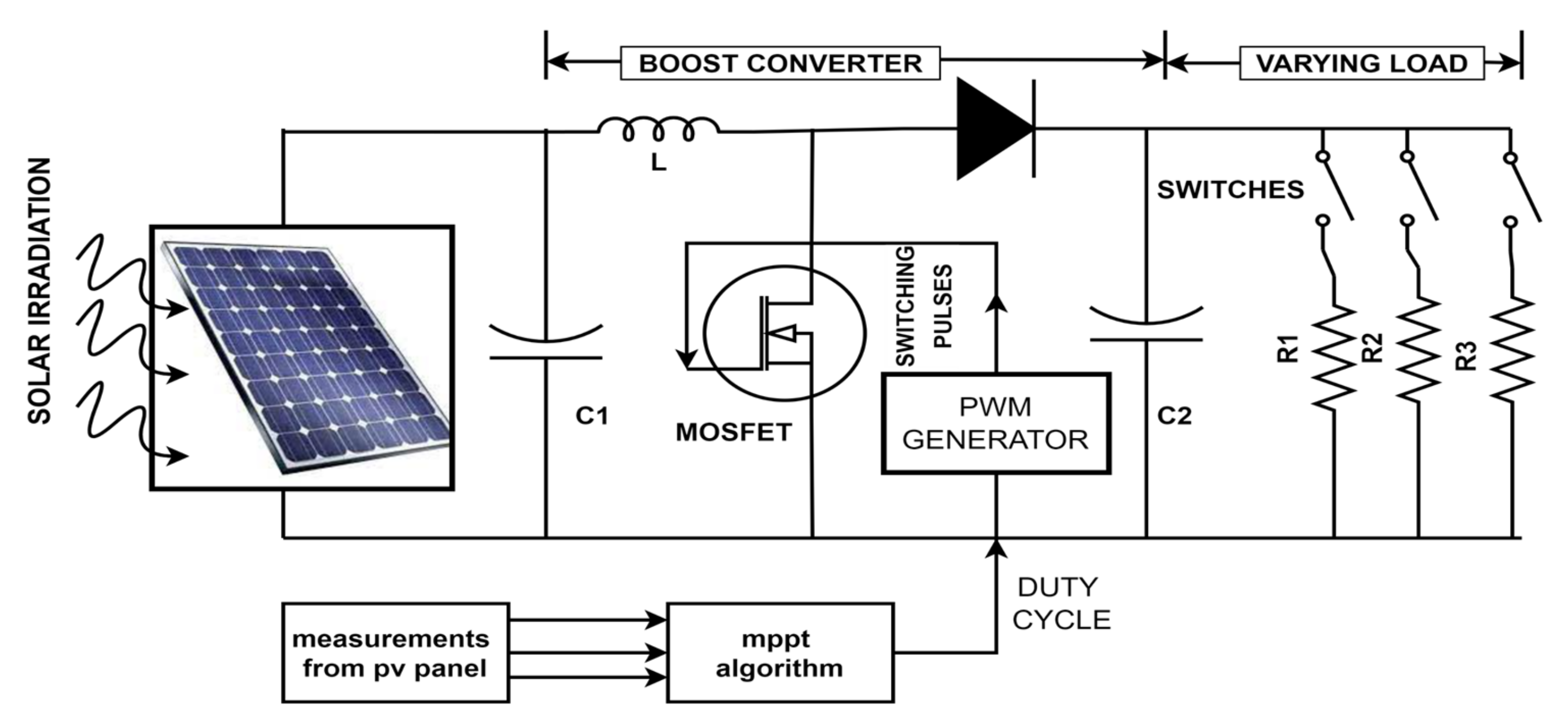
3. DC-DC Boost Converter
4. MPPT Control
4.1. MPPT Algorithms
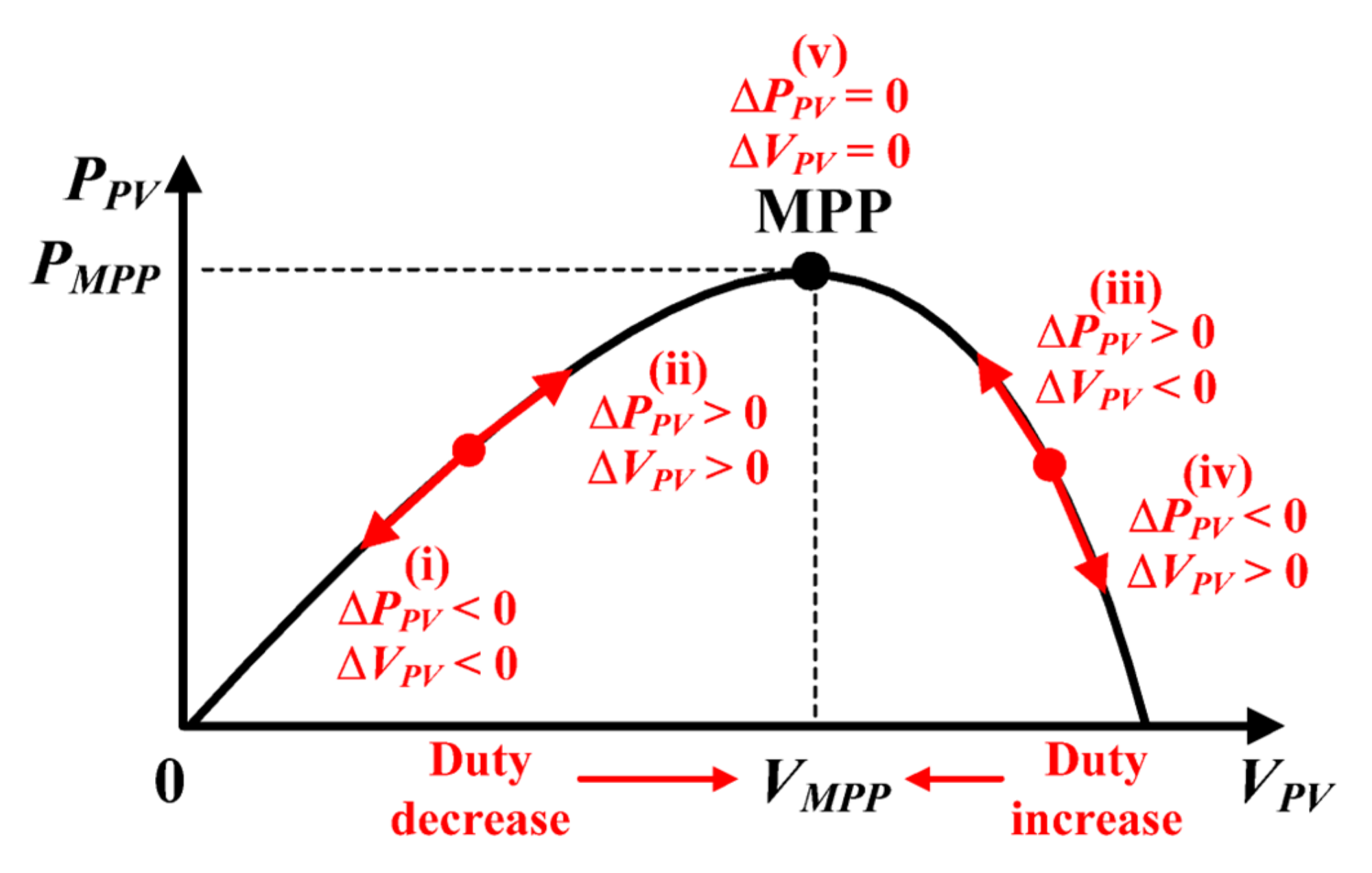
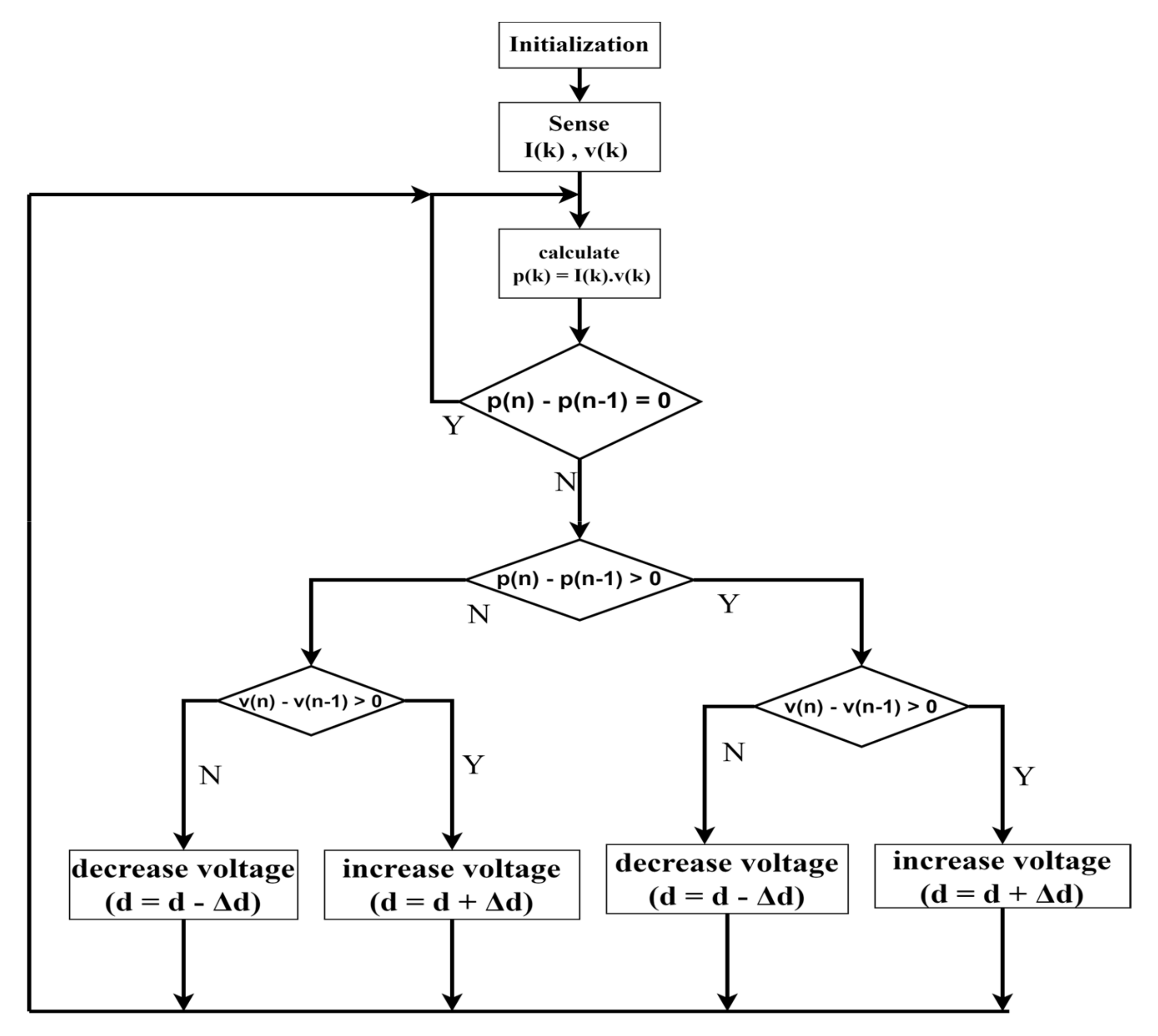
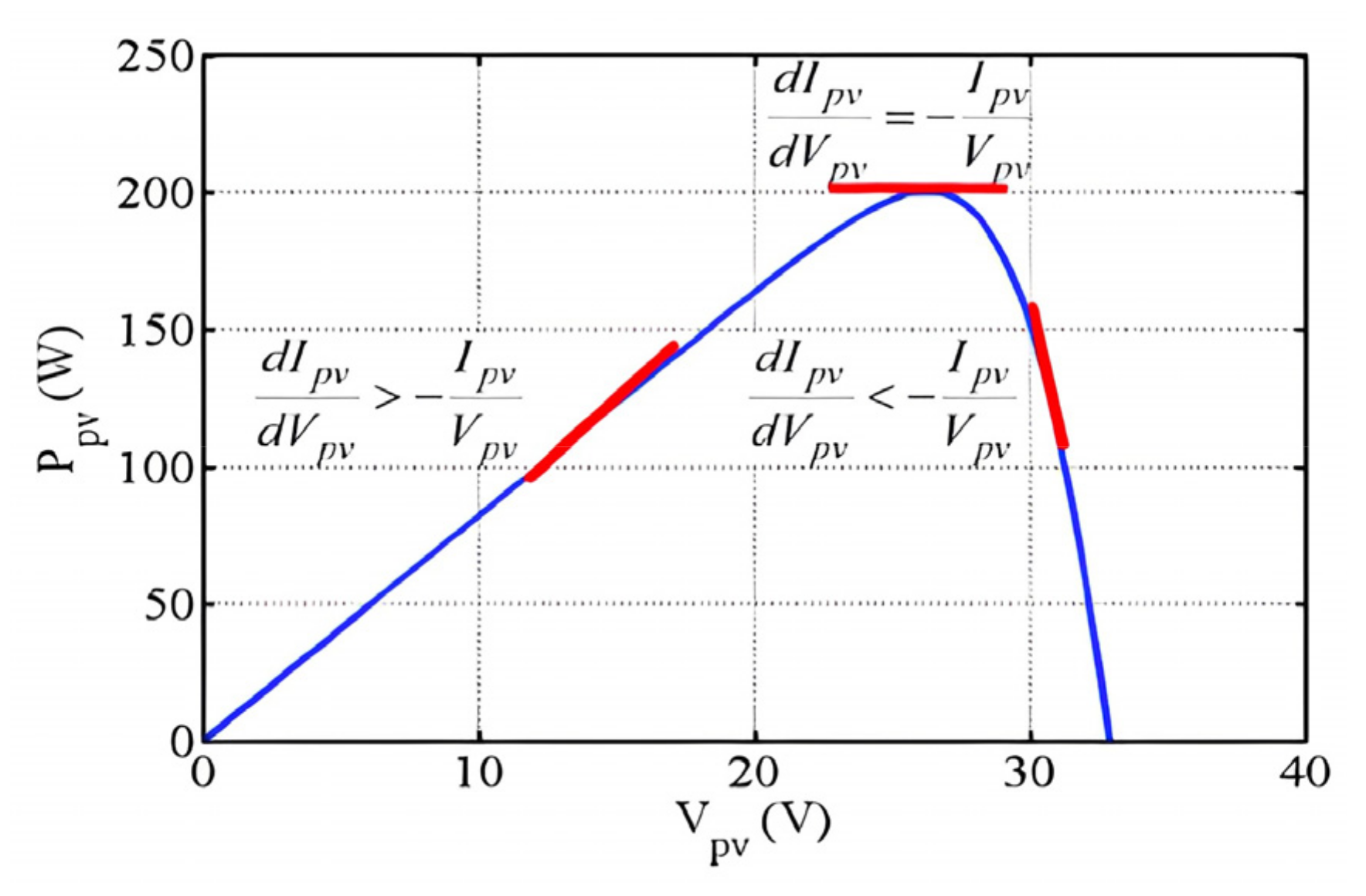
4.2. Perturb and Observe Method
4.3. Incremental Conductance Method
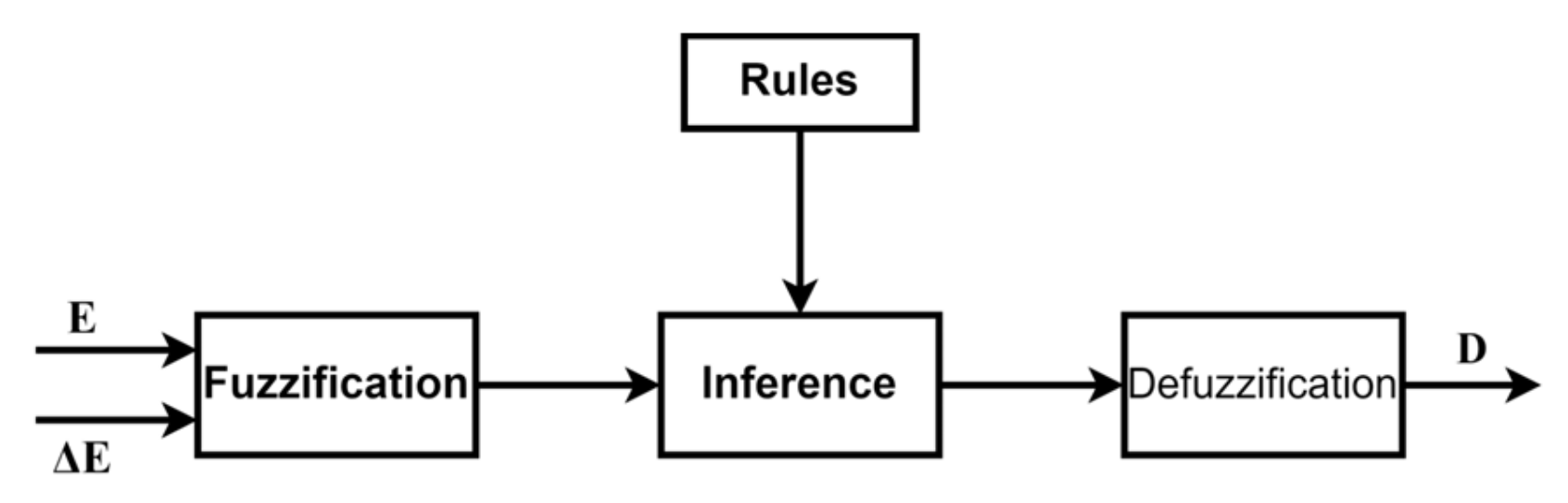
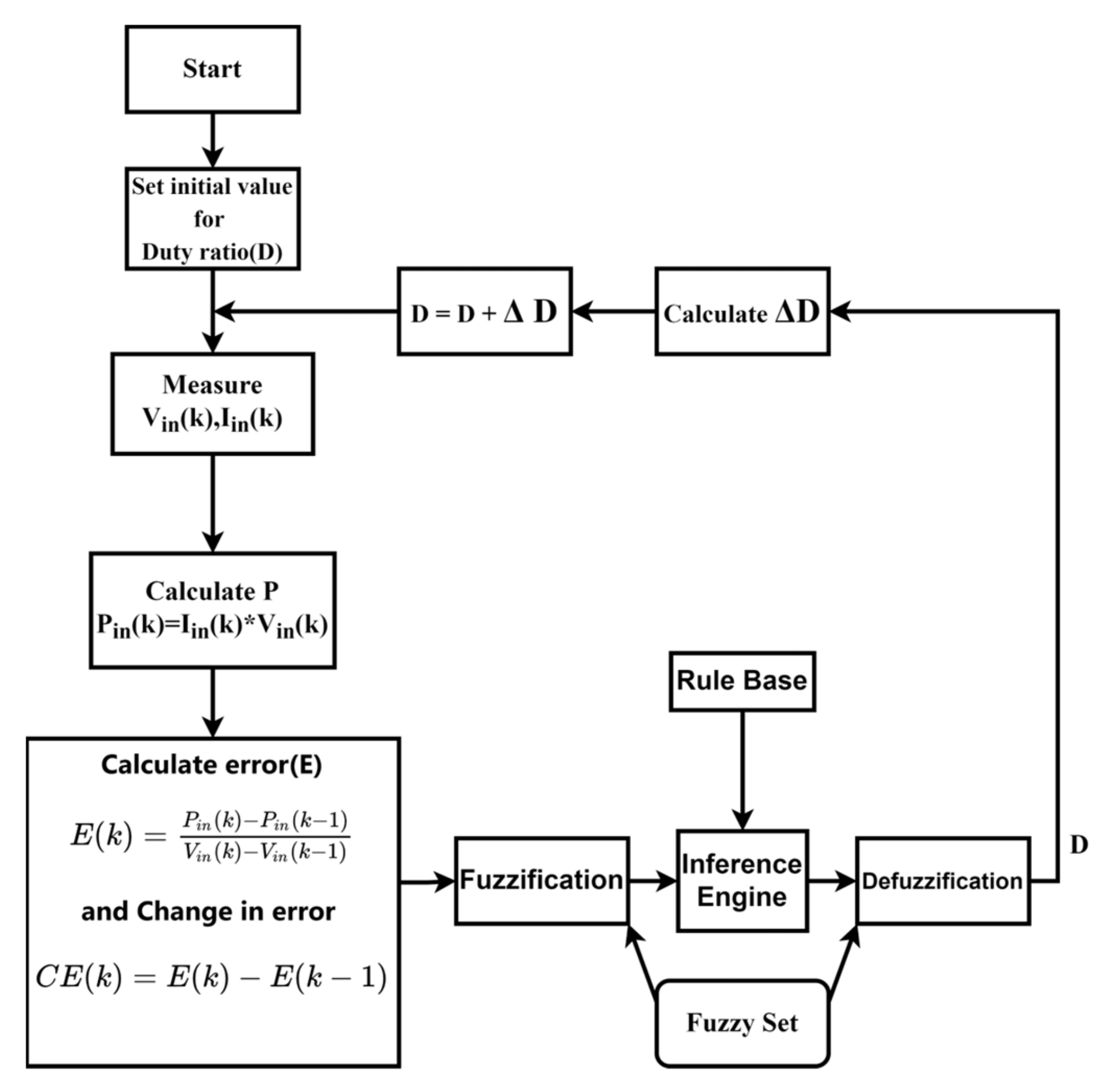
4.4. Fuzzy Logic Controller Method
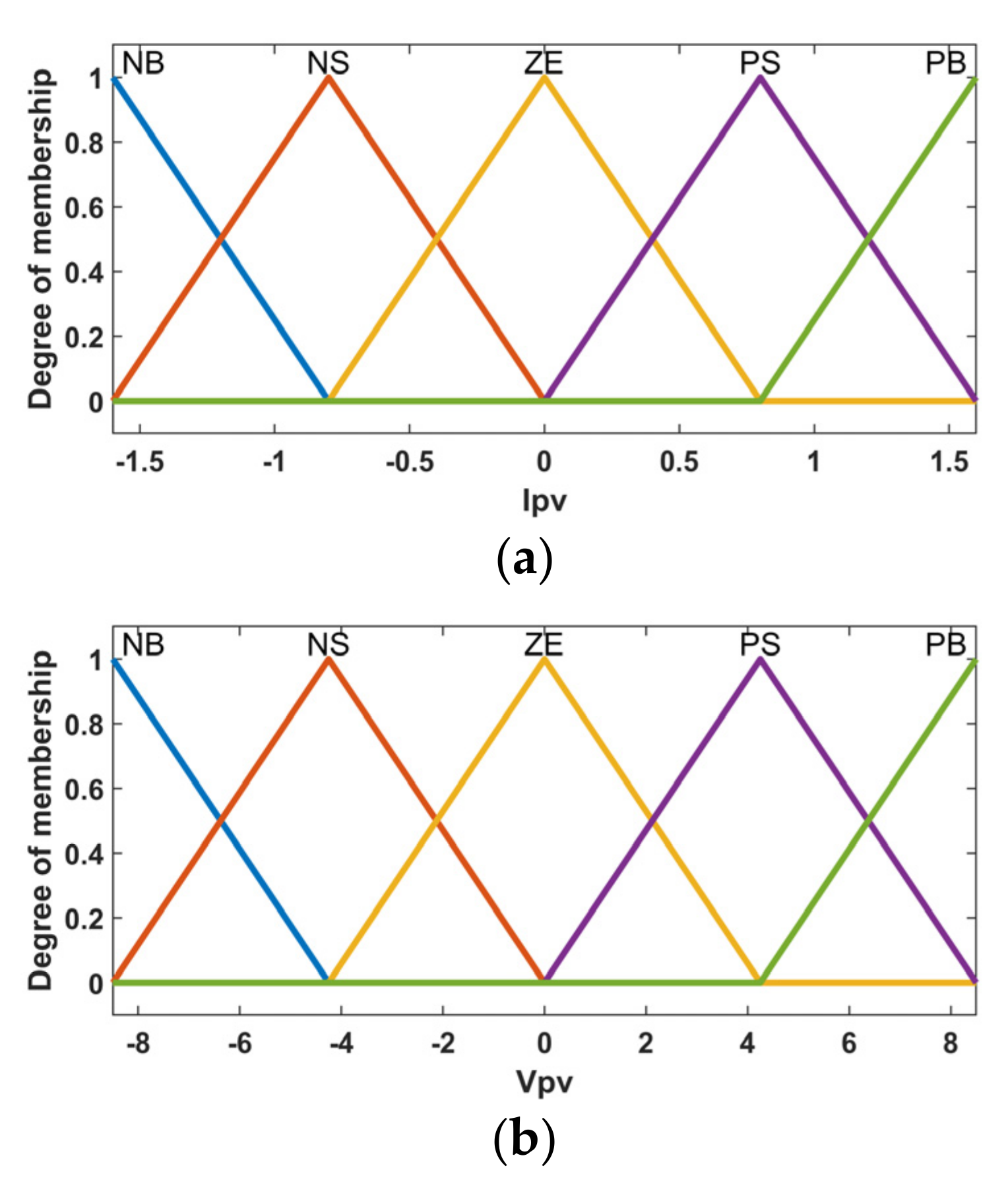
4.4.1. Fuzzification
4.4.2. Fuzzy Inference System (FIS)
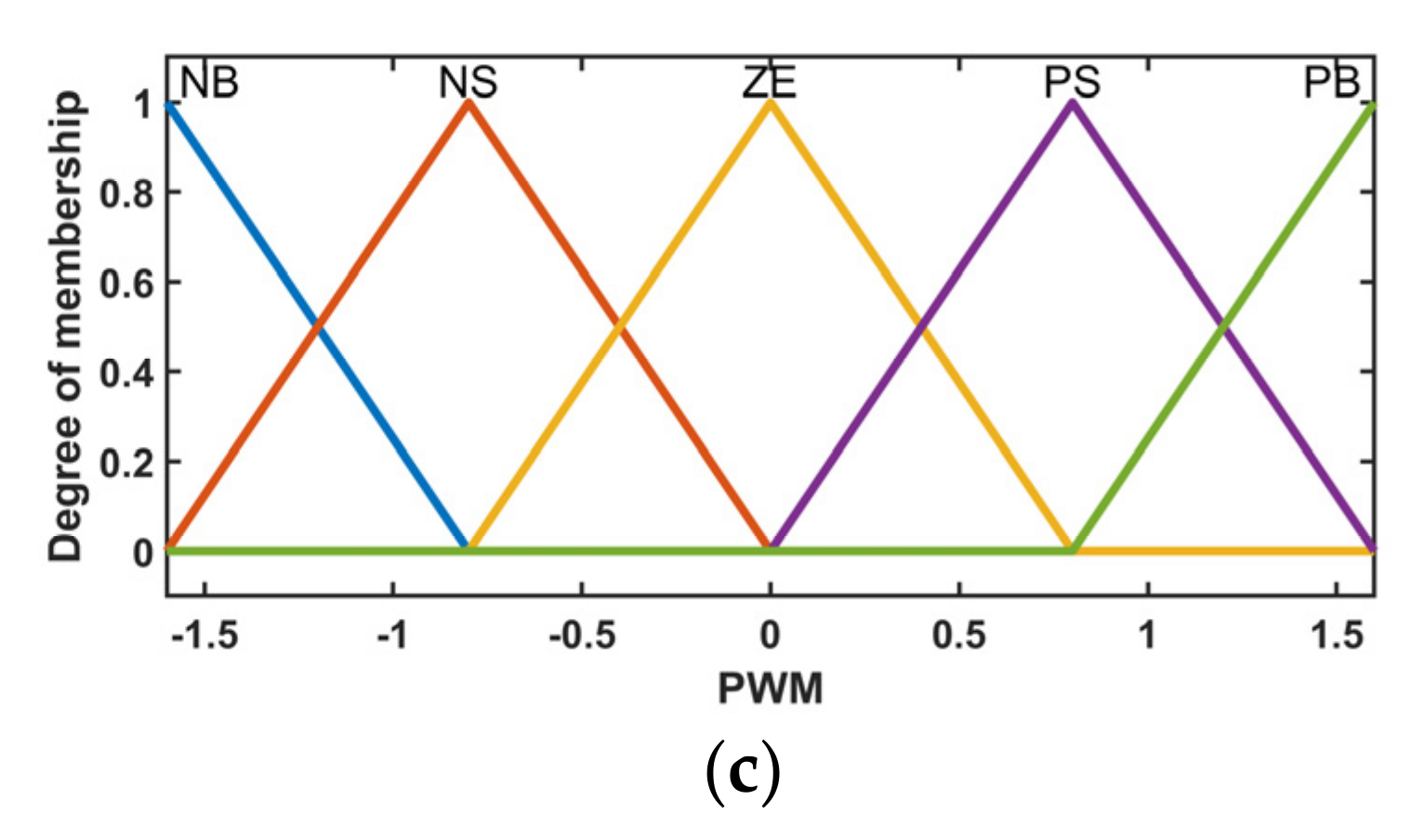
4.4.3. Defuzzification
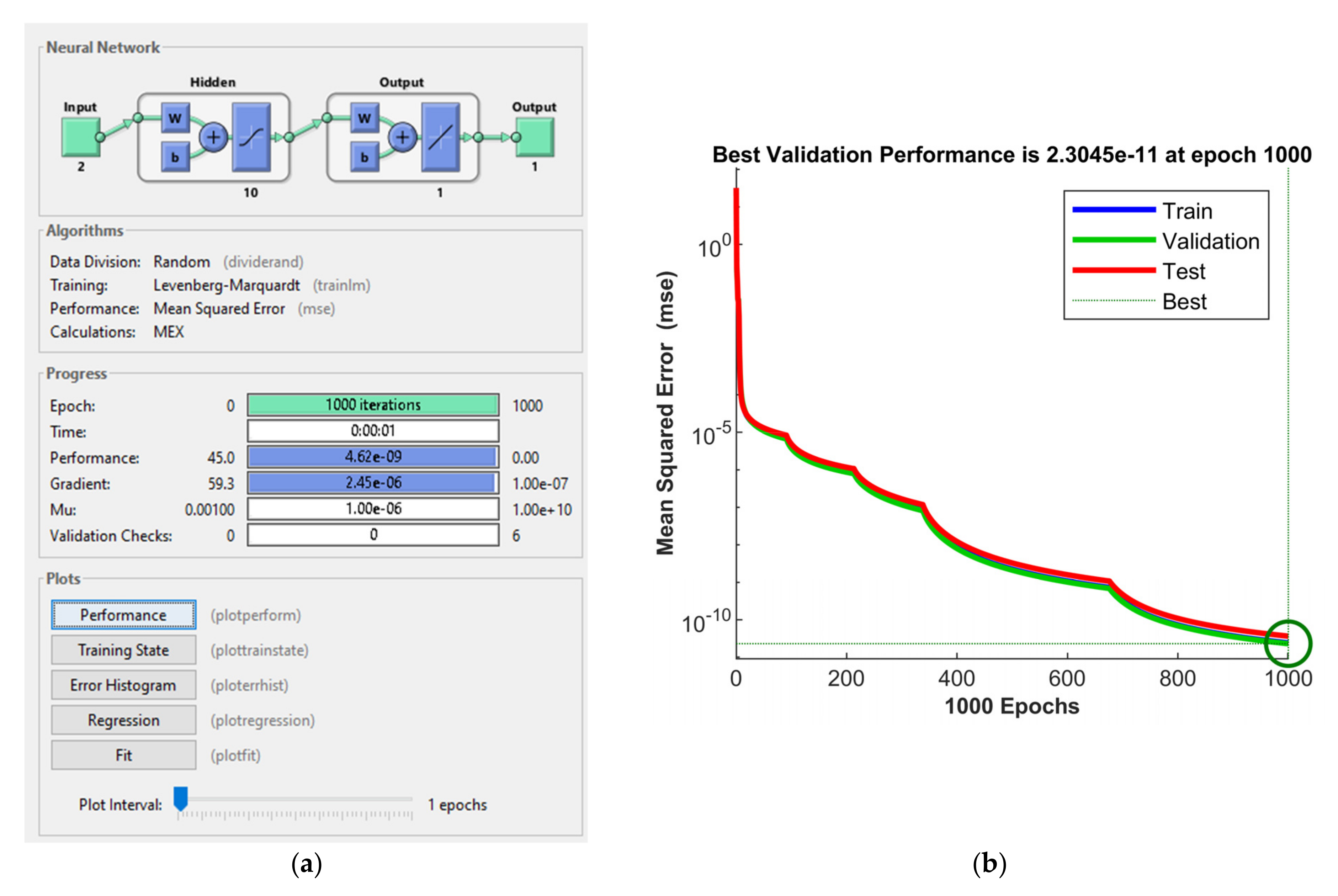
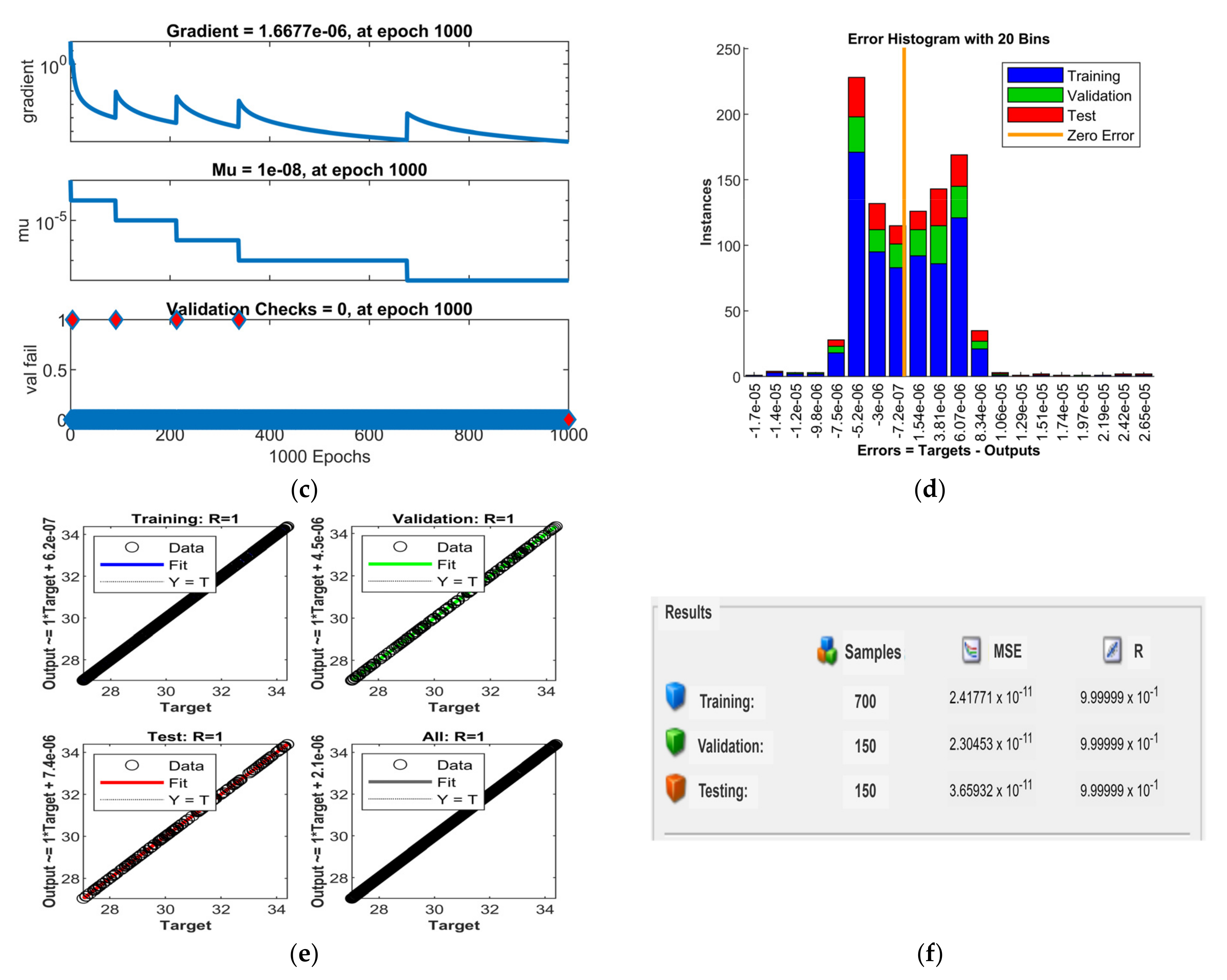
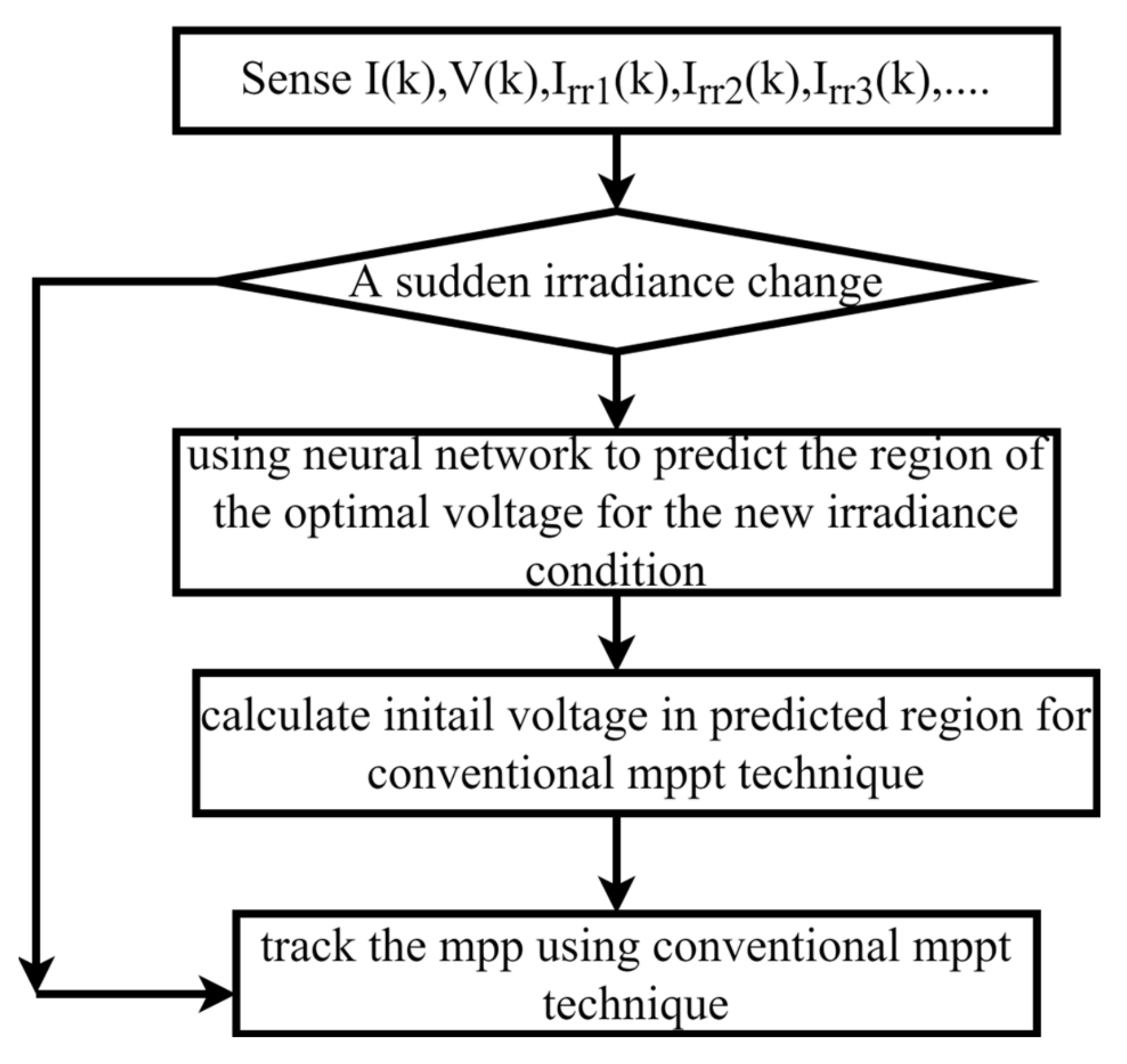
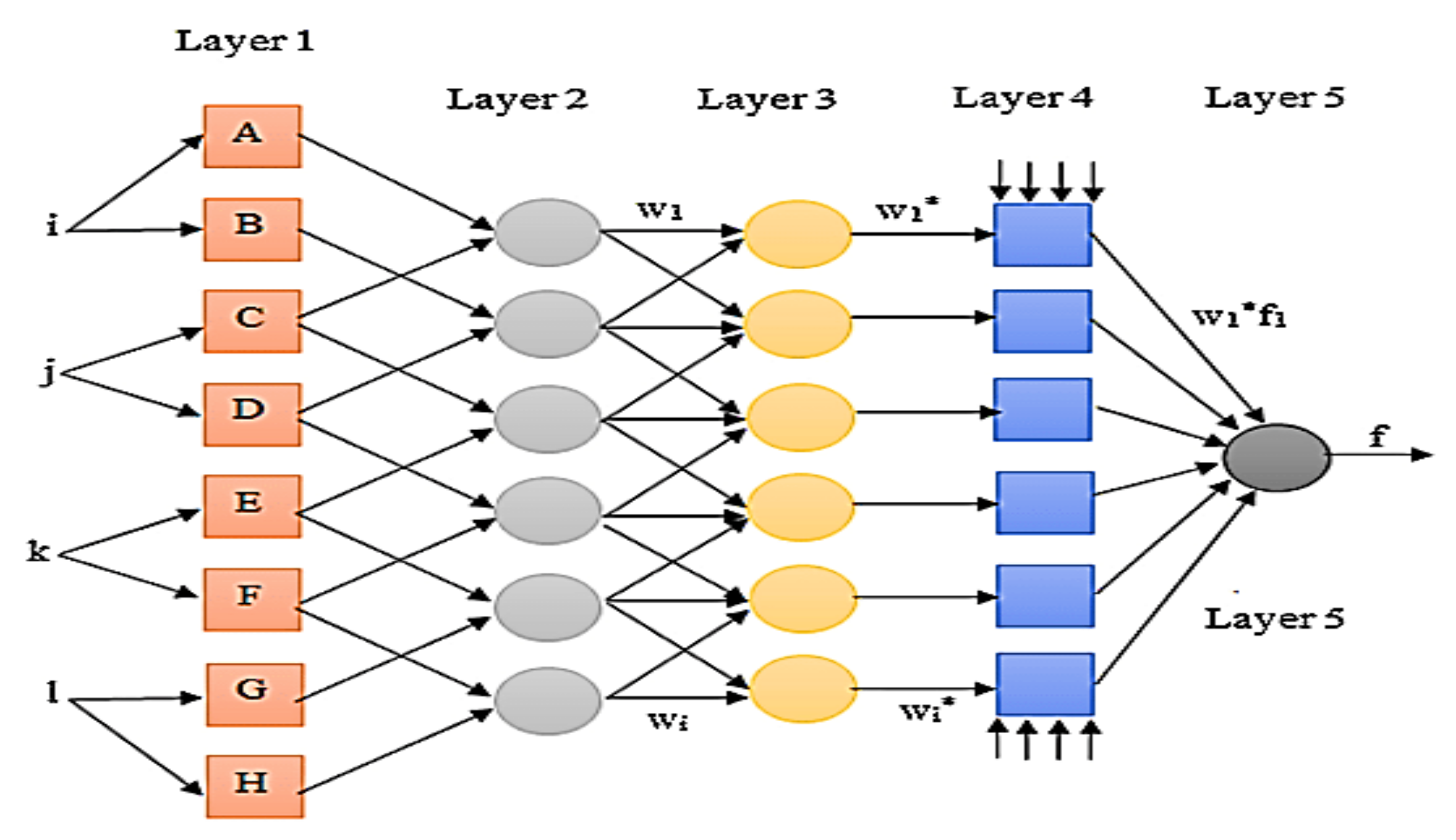
4.5. Neural Network Method
- Solar panel data used for training the neural network and ANFIS
- Short circuit current = 8.66 A;
- Maximum power point current = 8.15 A;
- Open-source voltage = 37.3 V;
- Maximum power point voltage = 30.7;
- Alpha = 0.086998;
- Beta = −0.36901;
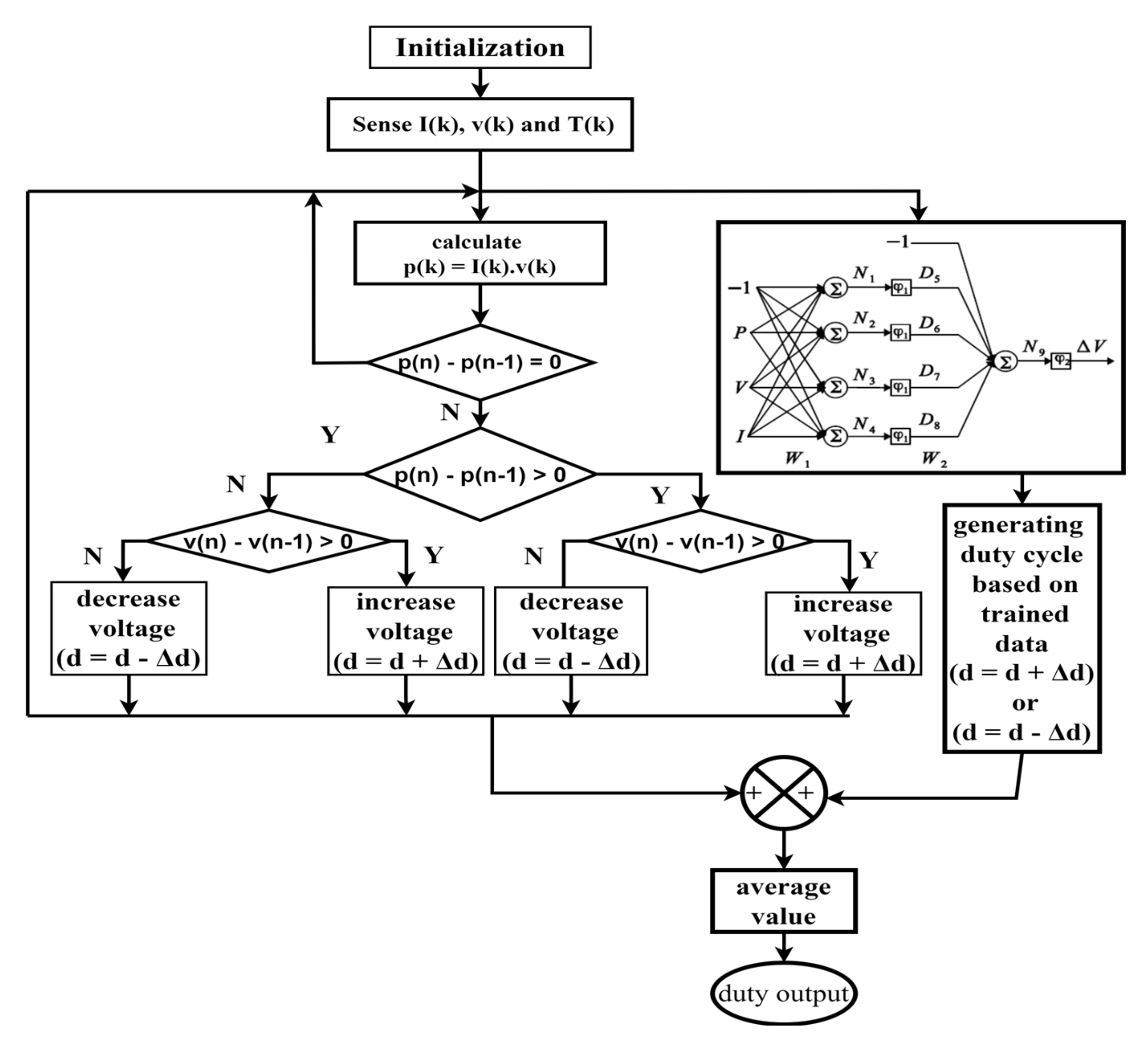
4.6. ANFIS Method (Adaptive Neuro-Fuzzy Inference System)
Adaptive Neuro-Fuzzy Controller
- Rule i: if E(k) is Xi1 and CE(k) is Xi2, then
- (Duty)i is the changing duty cycle and
- Xij is the membership function.
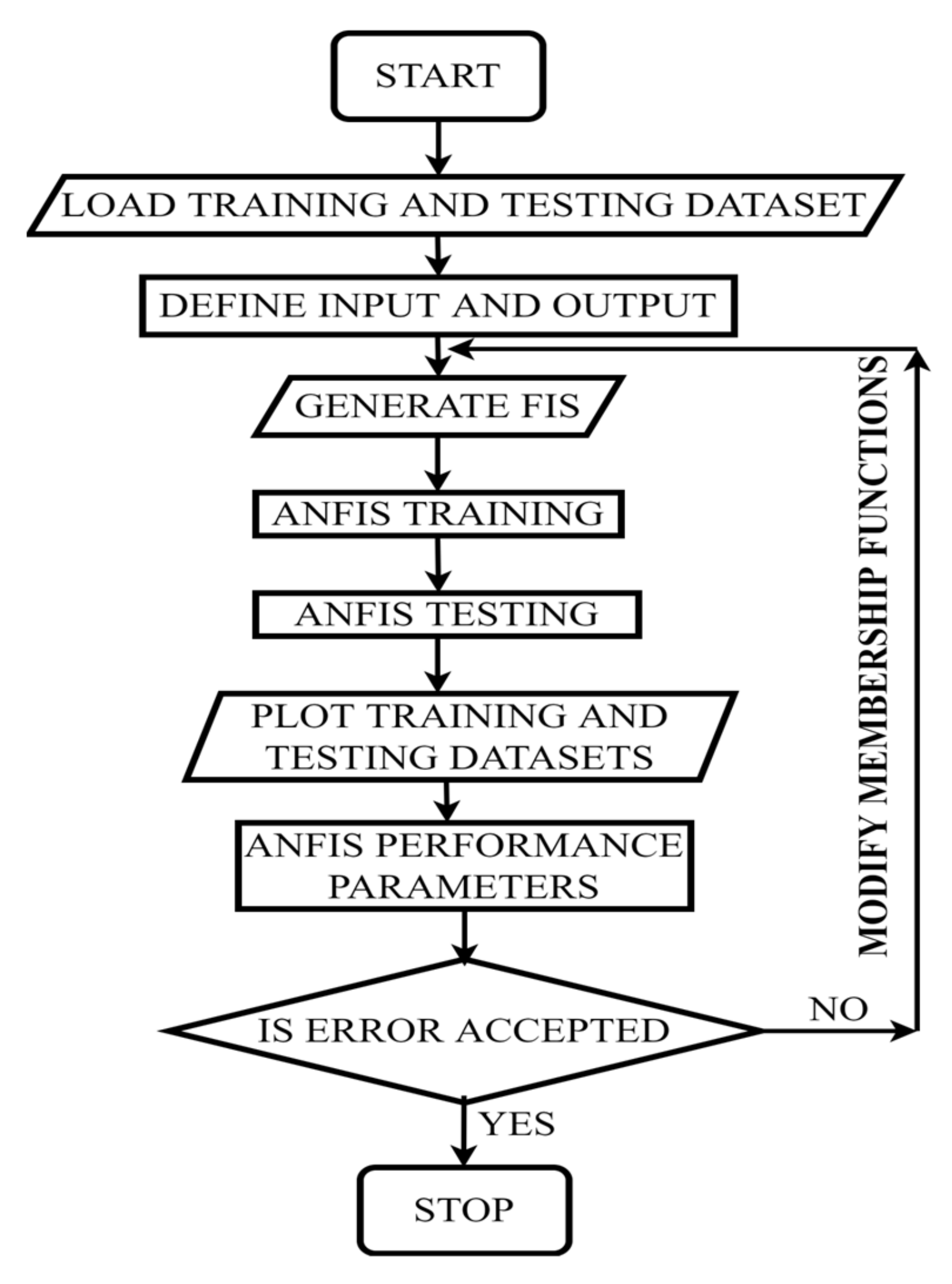
4.7. Hybrid Method (Neural Network and P&O)
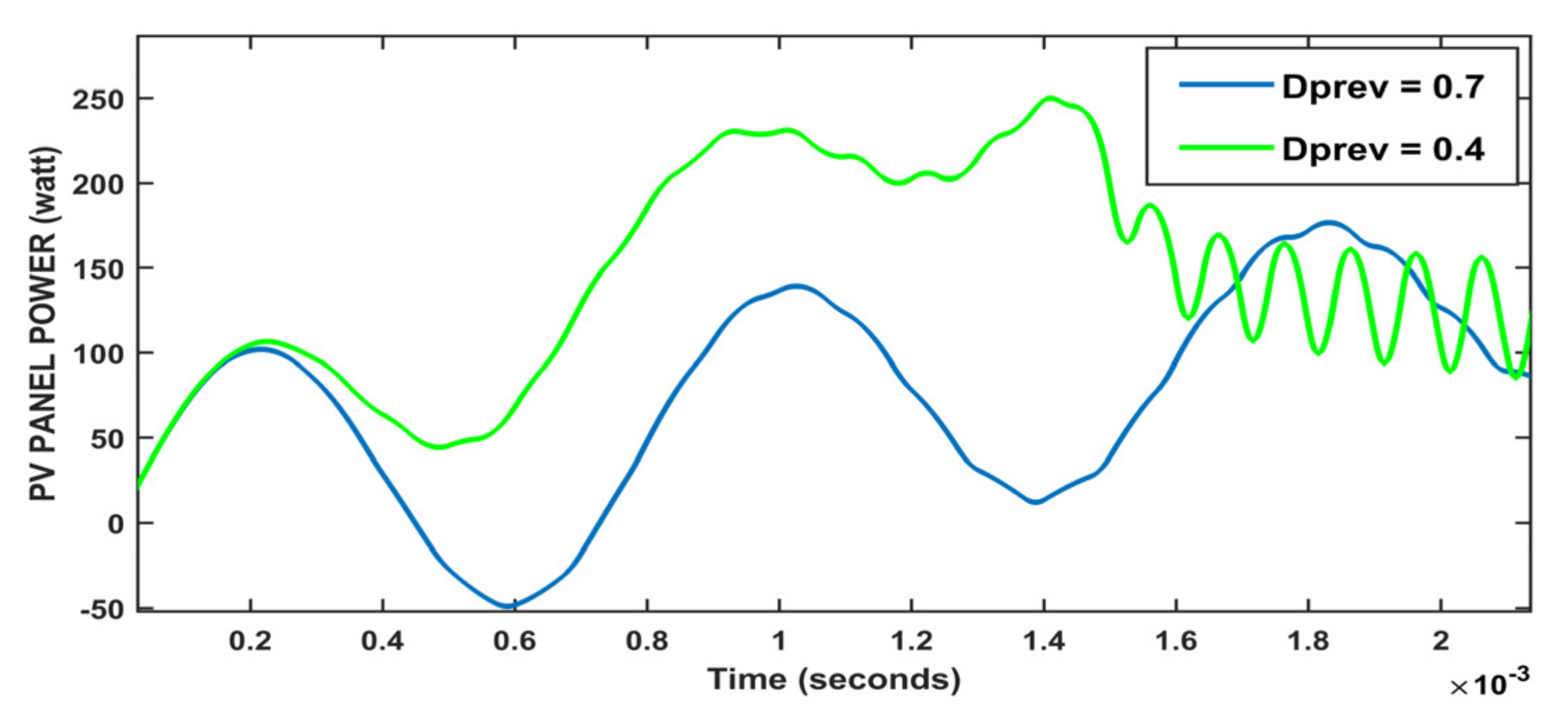
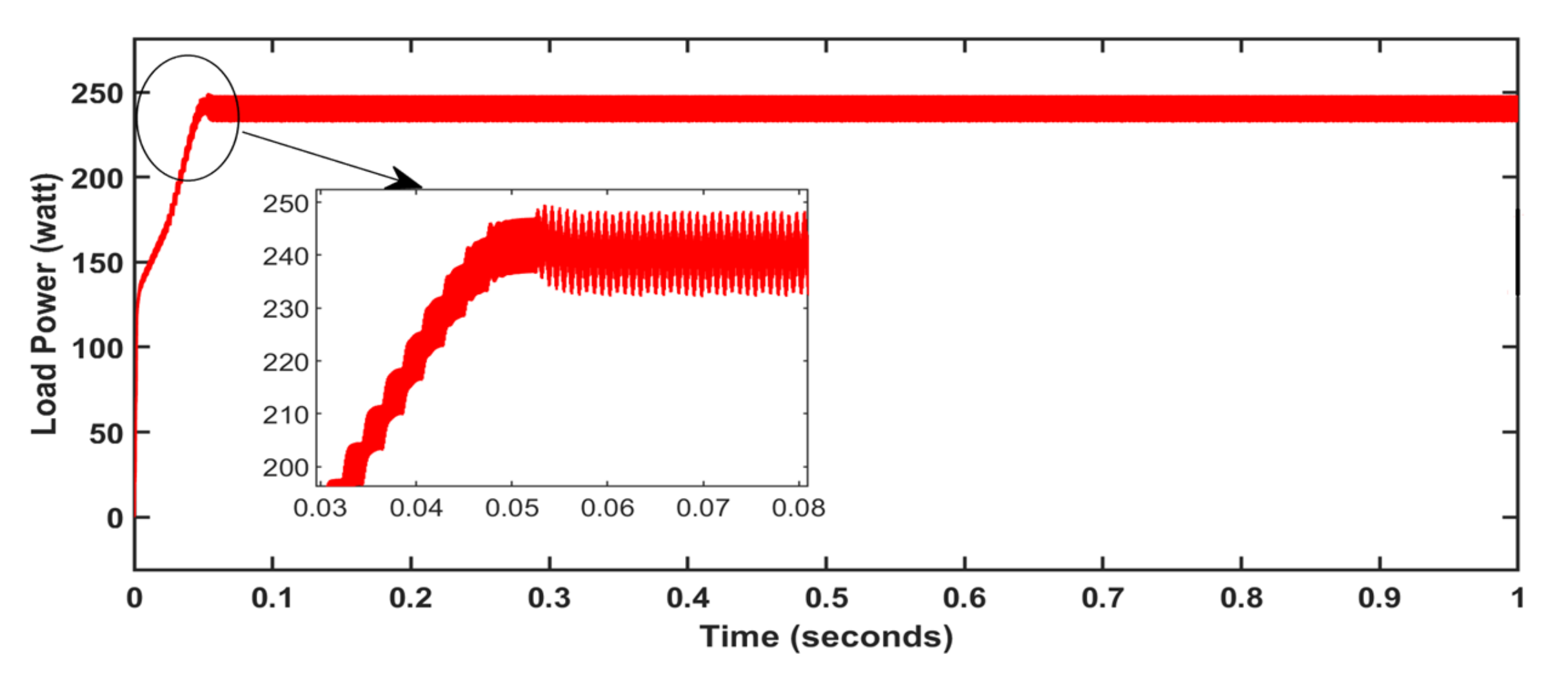
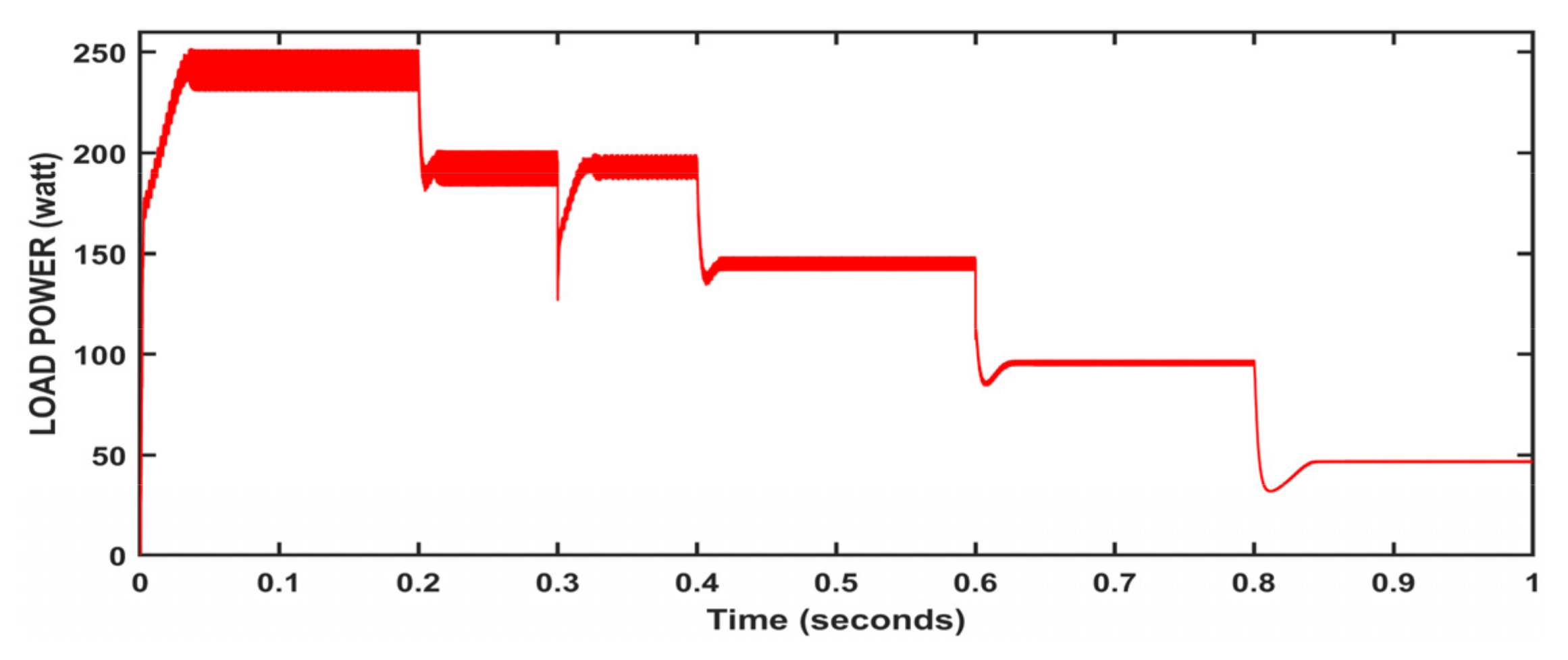
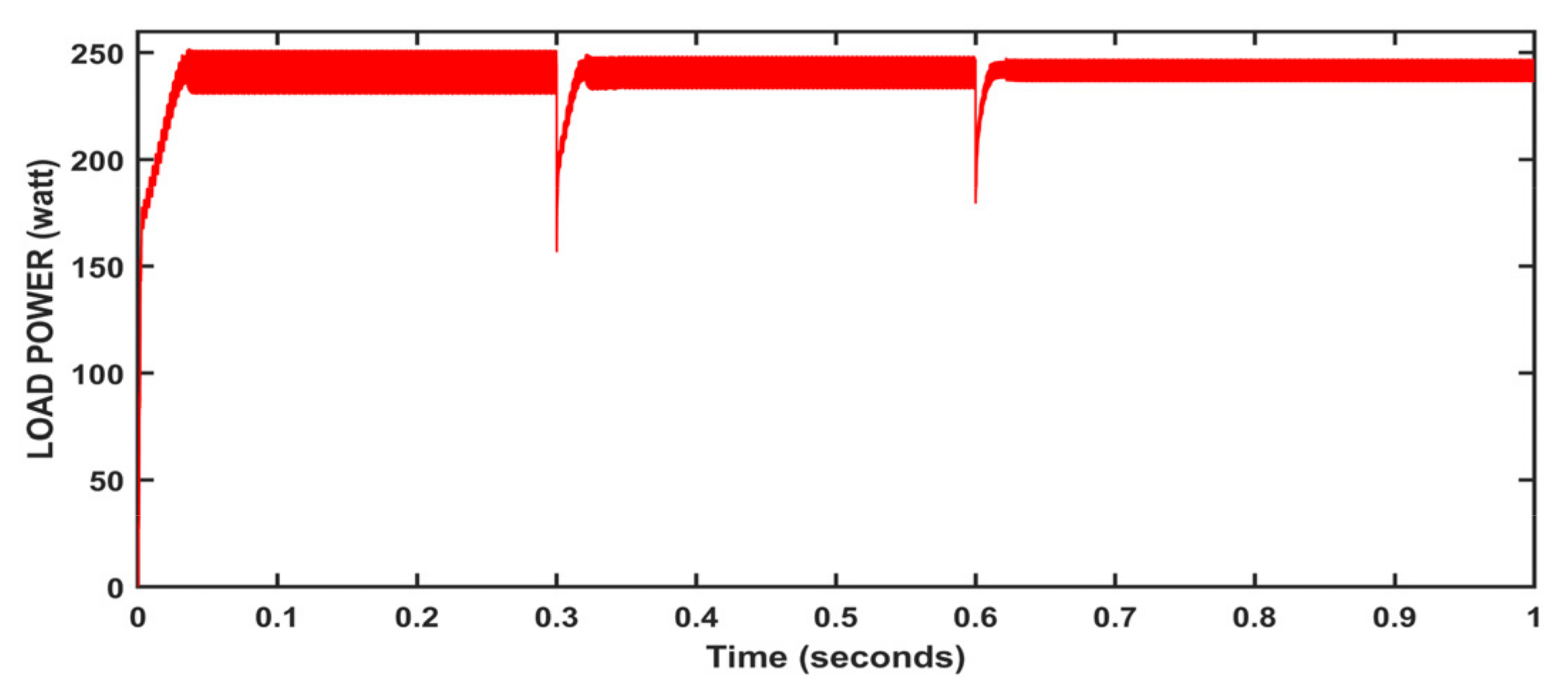
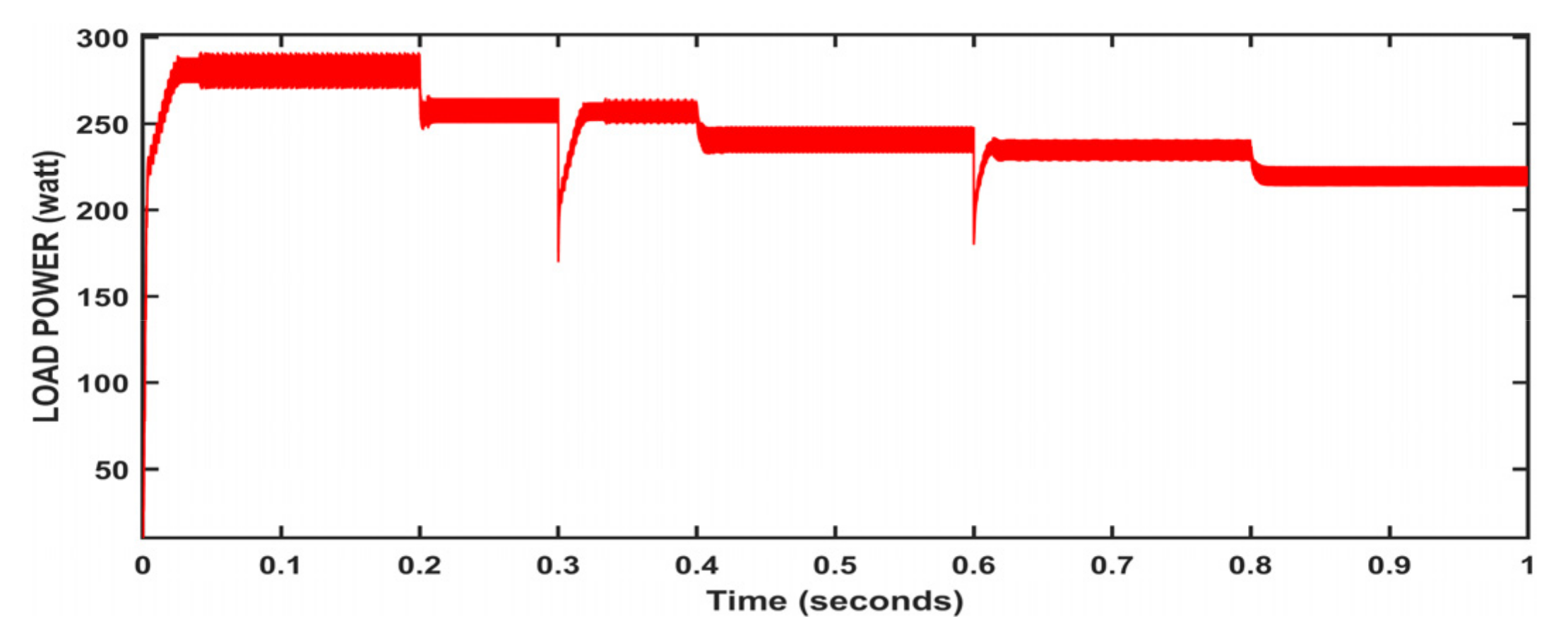
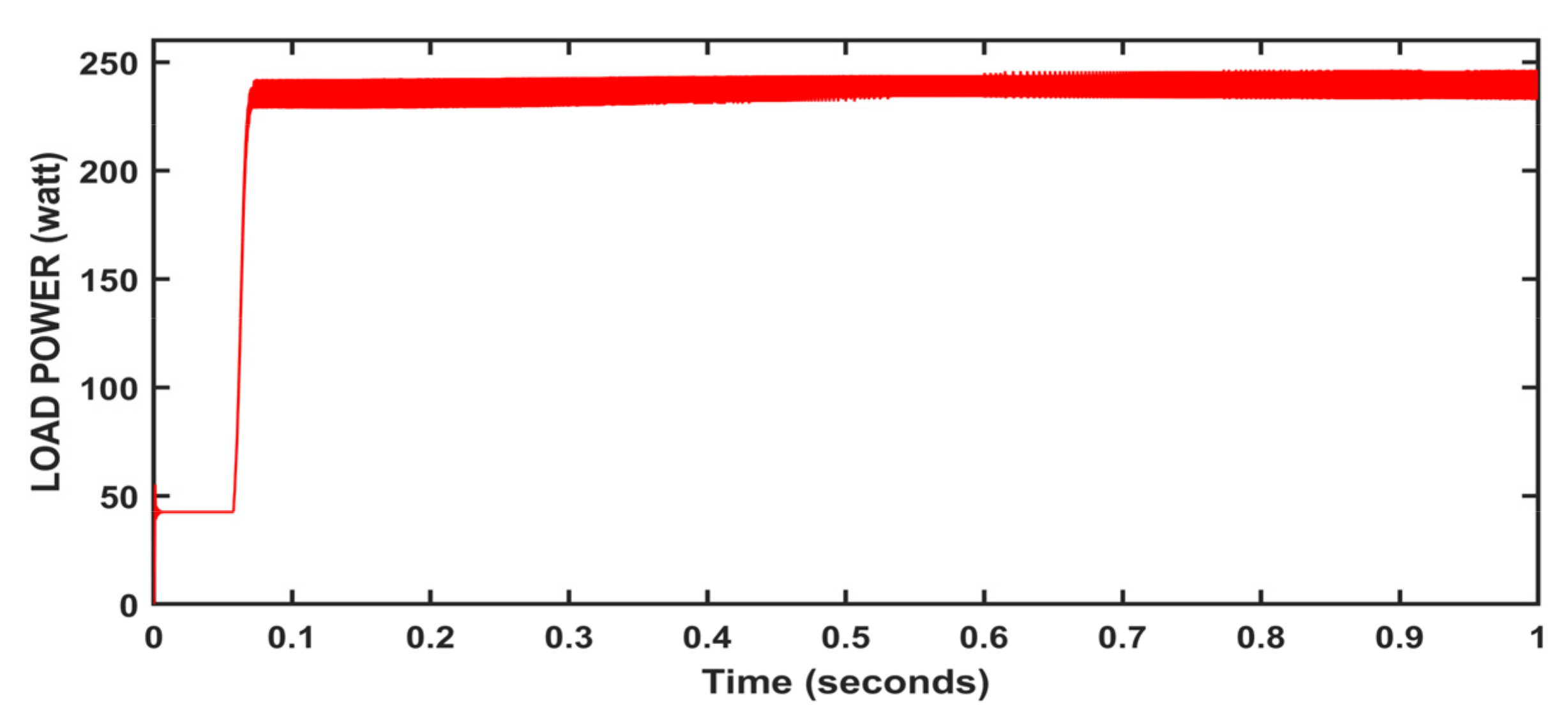
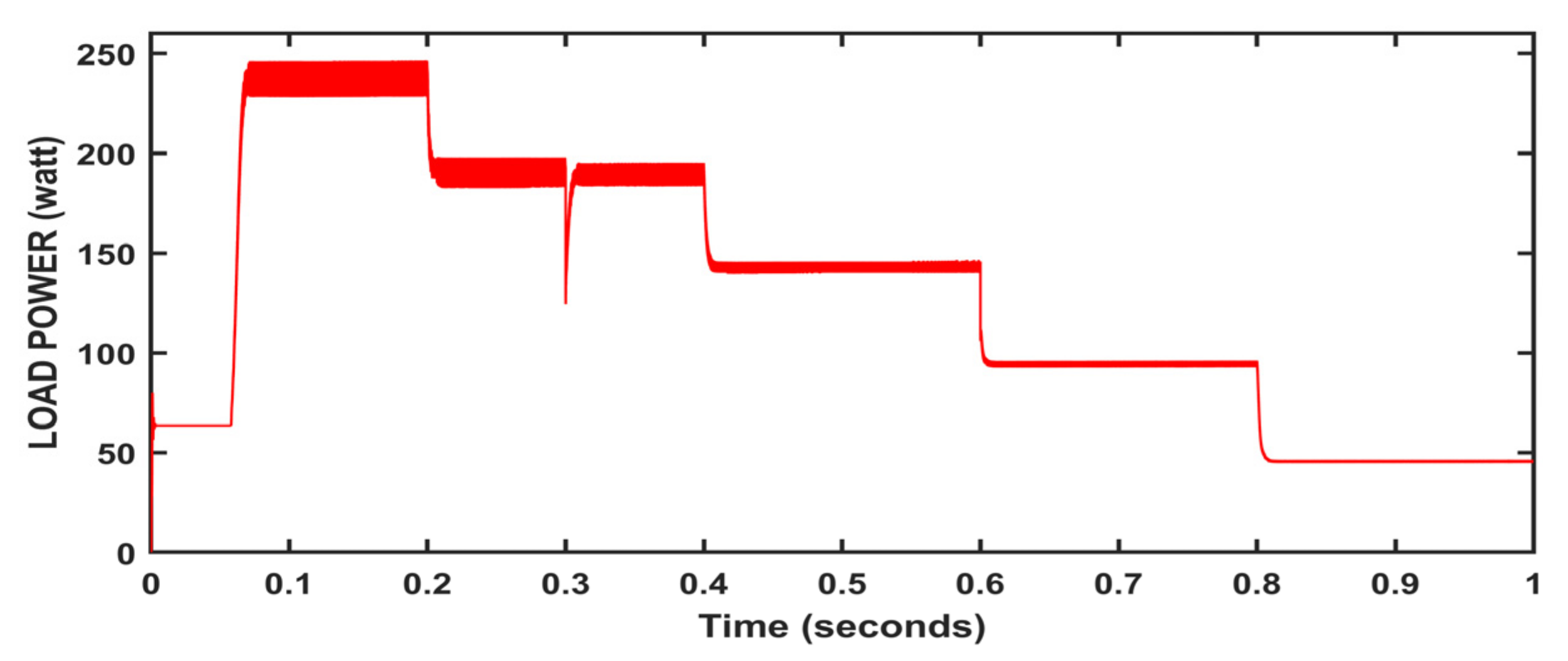
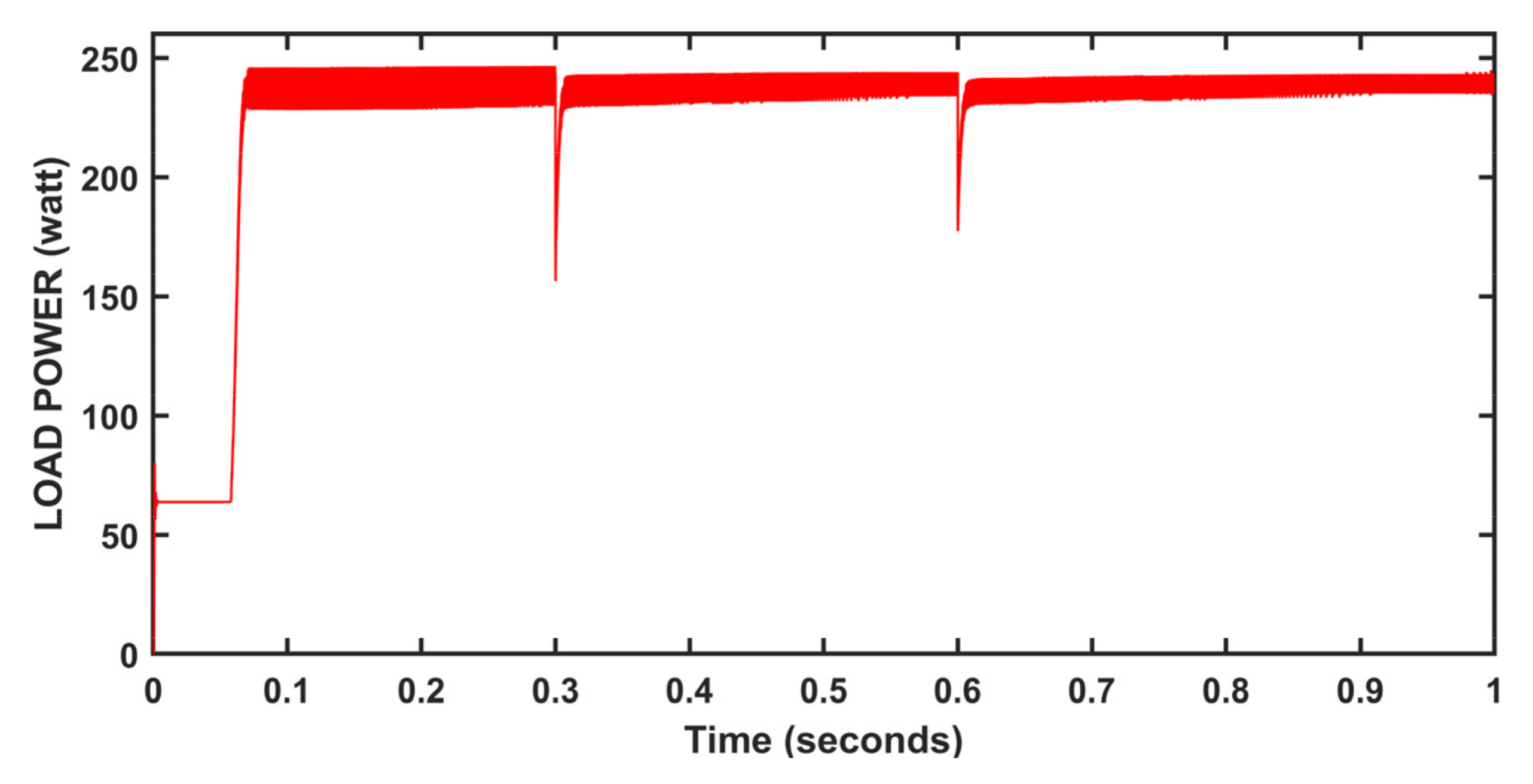
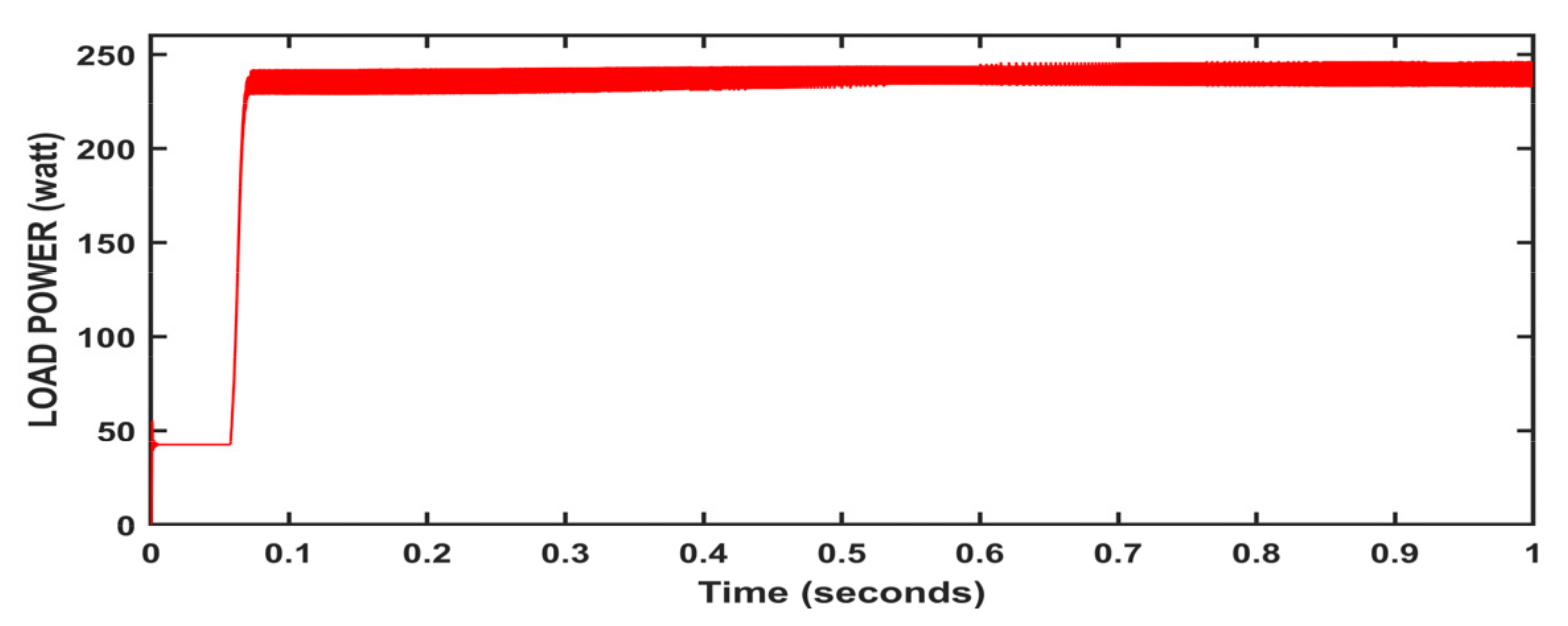
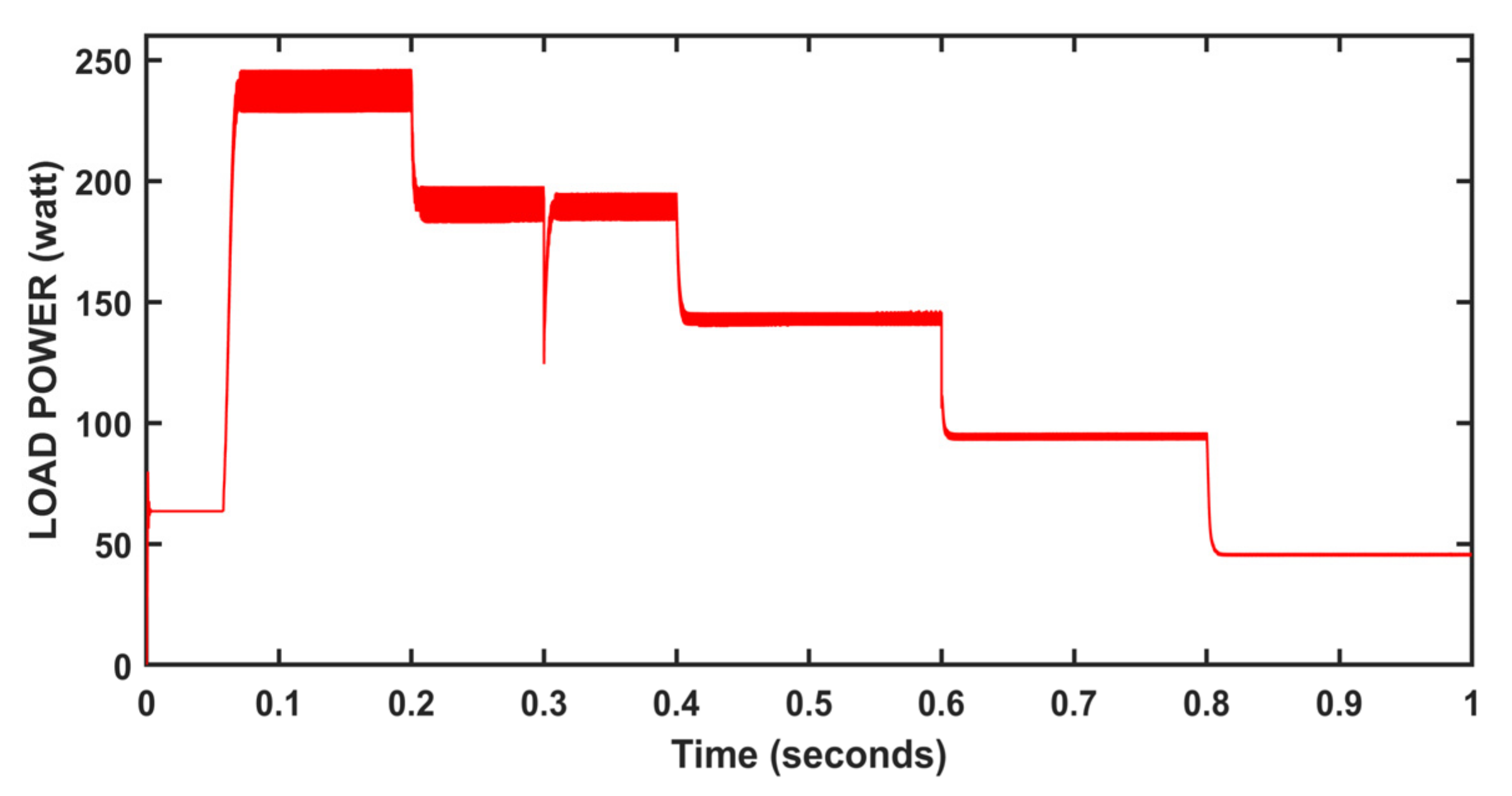
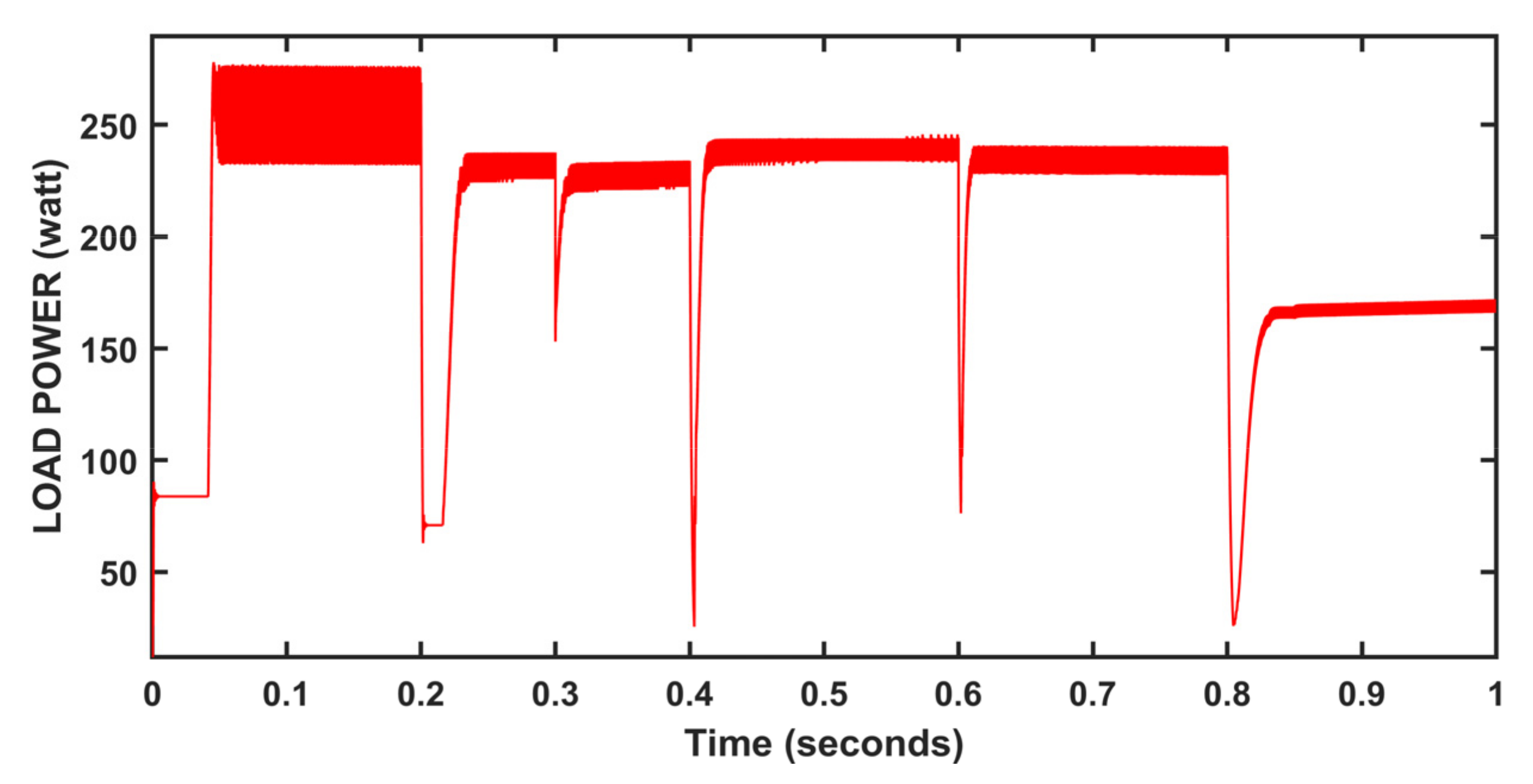
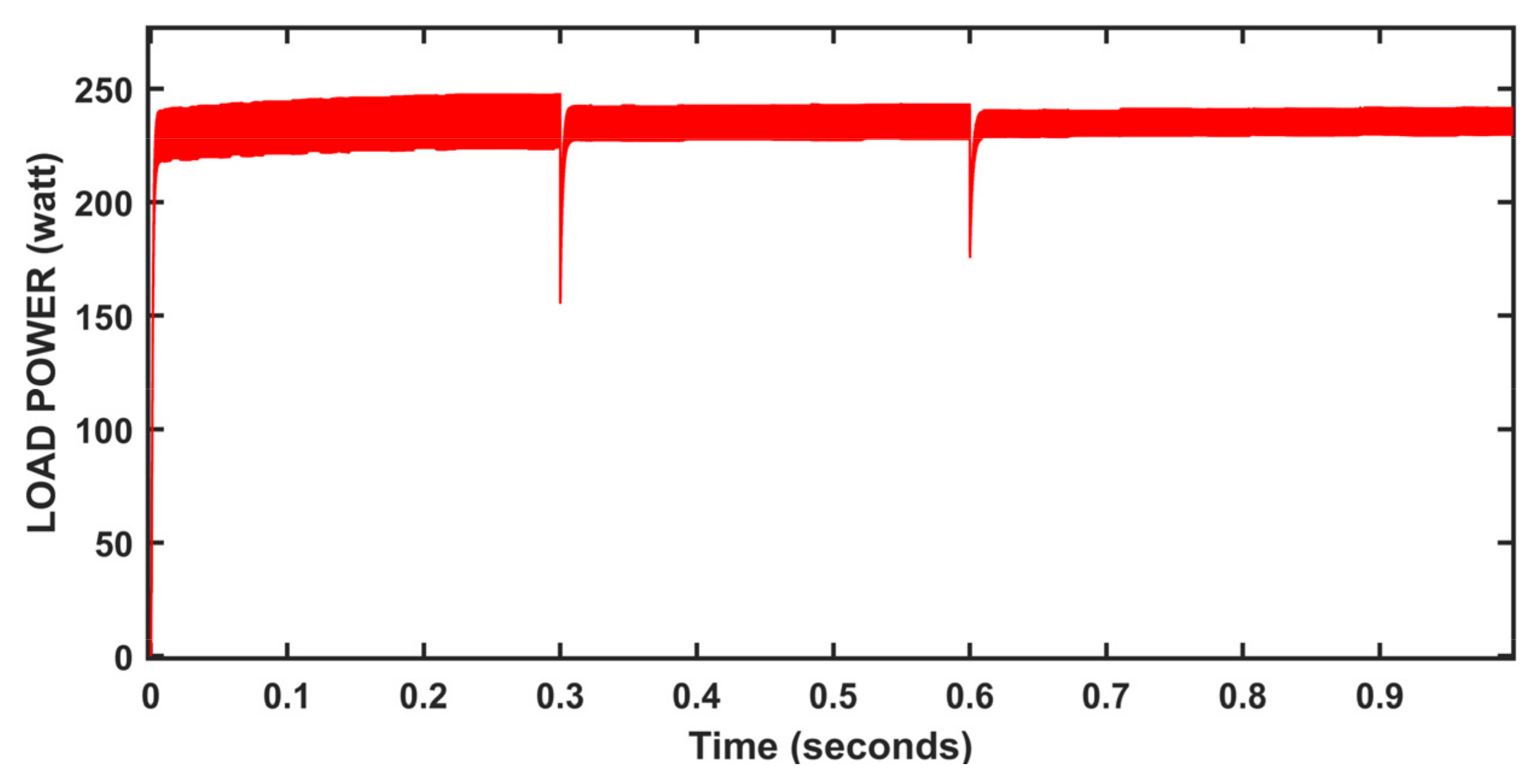
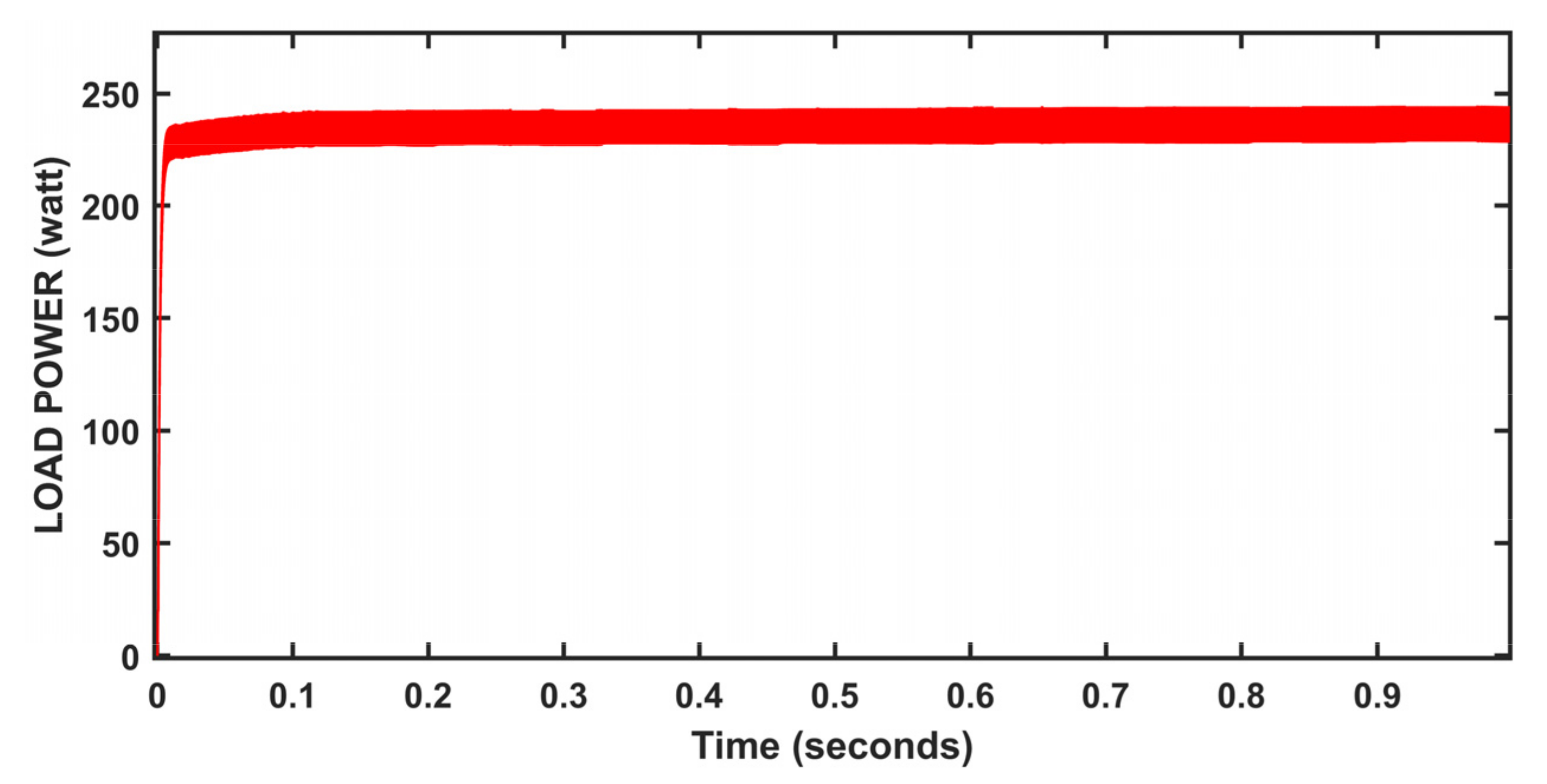
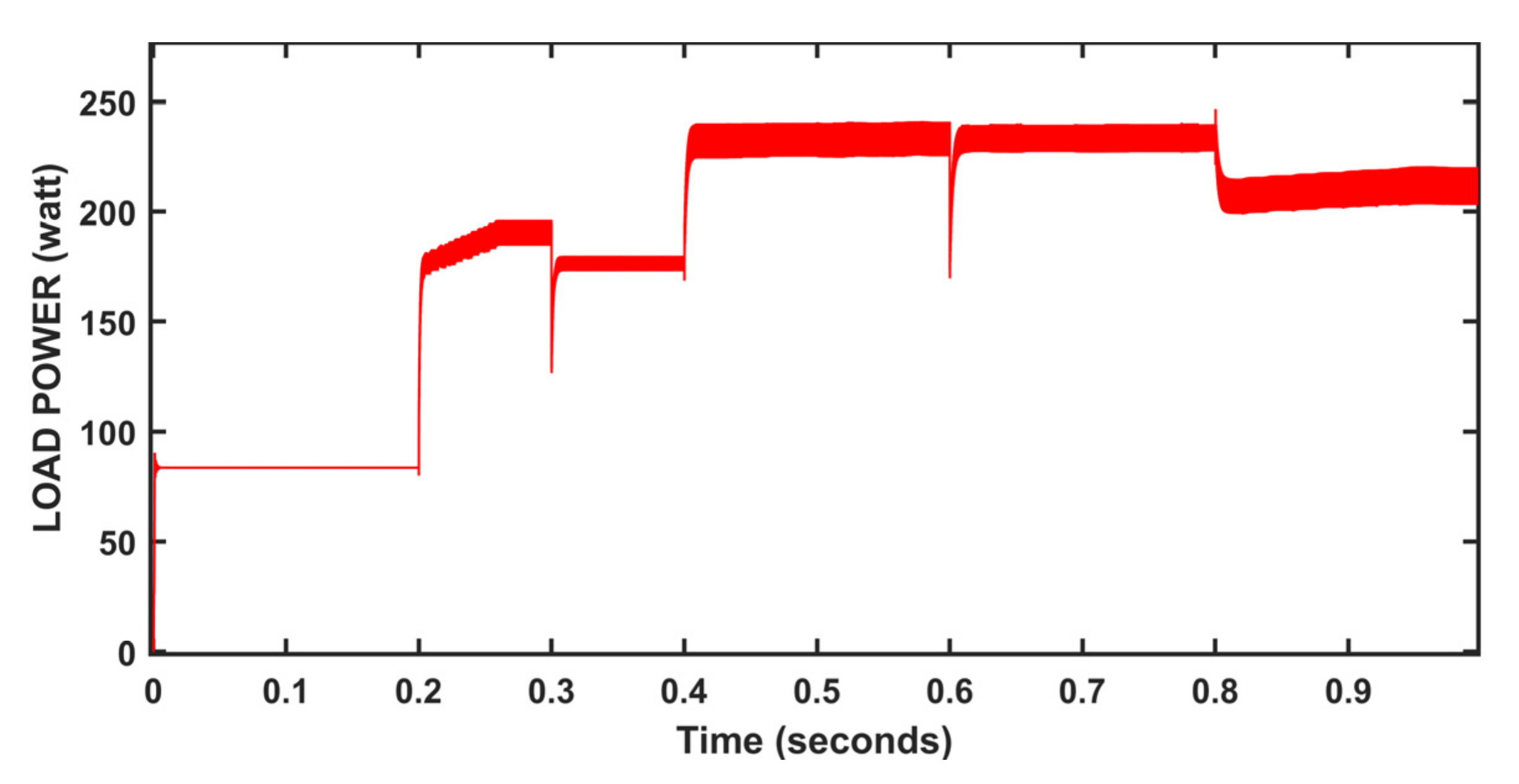
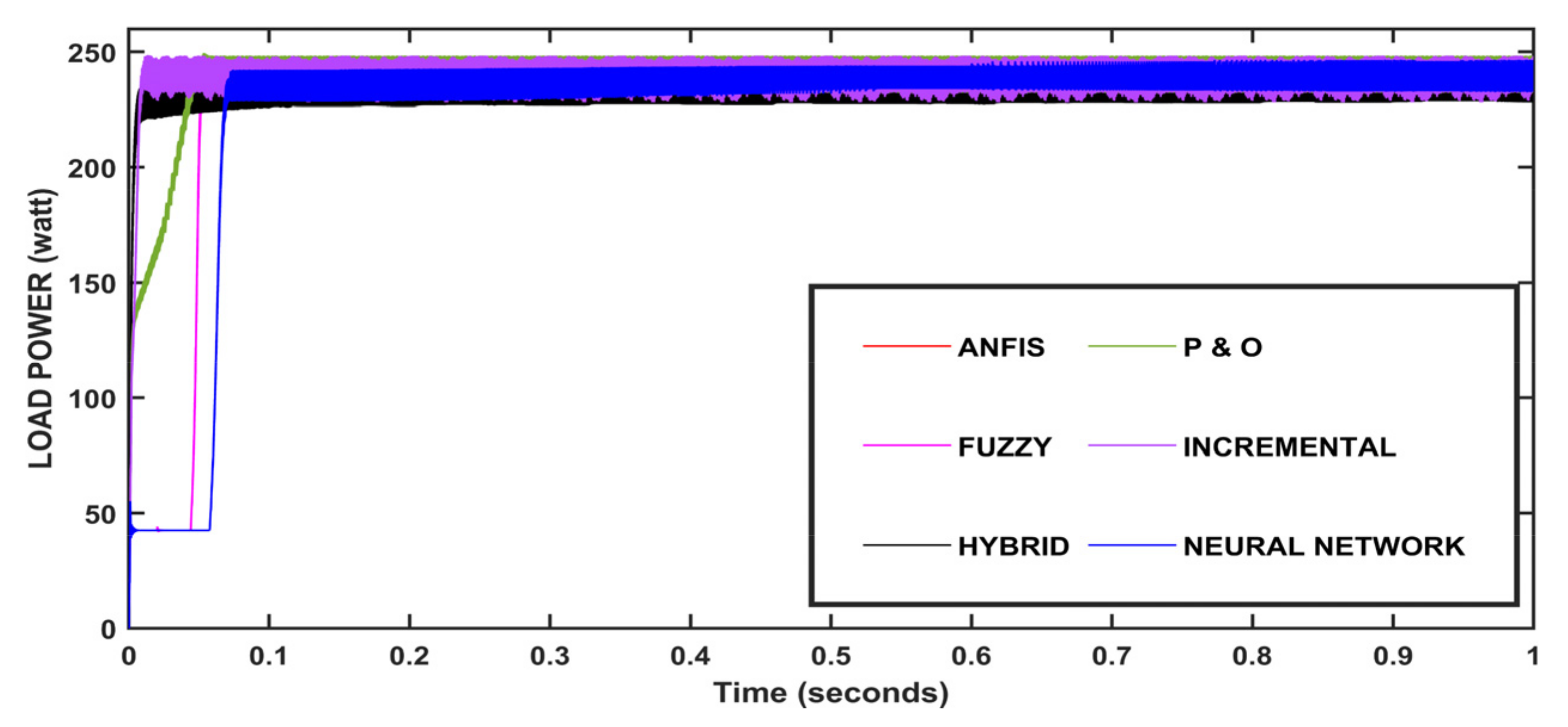
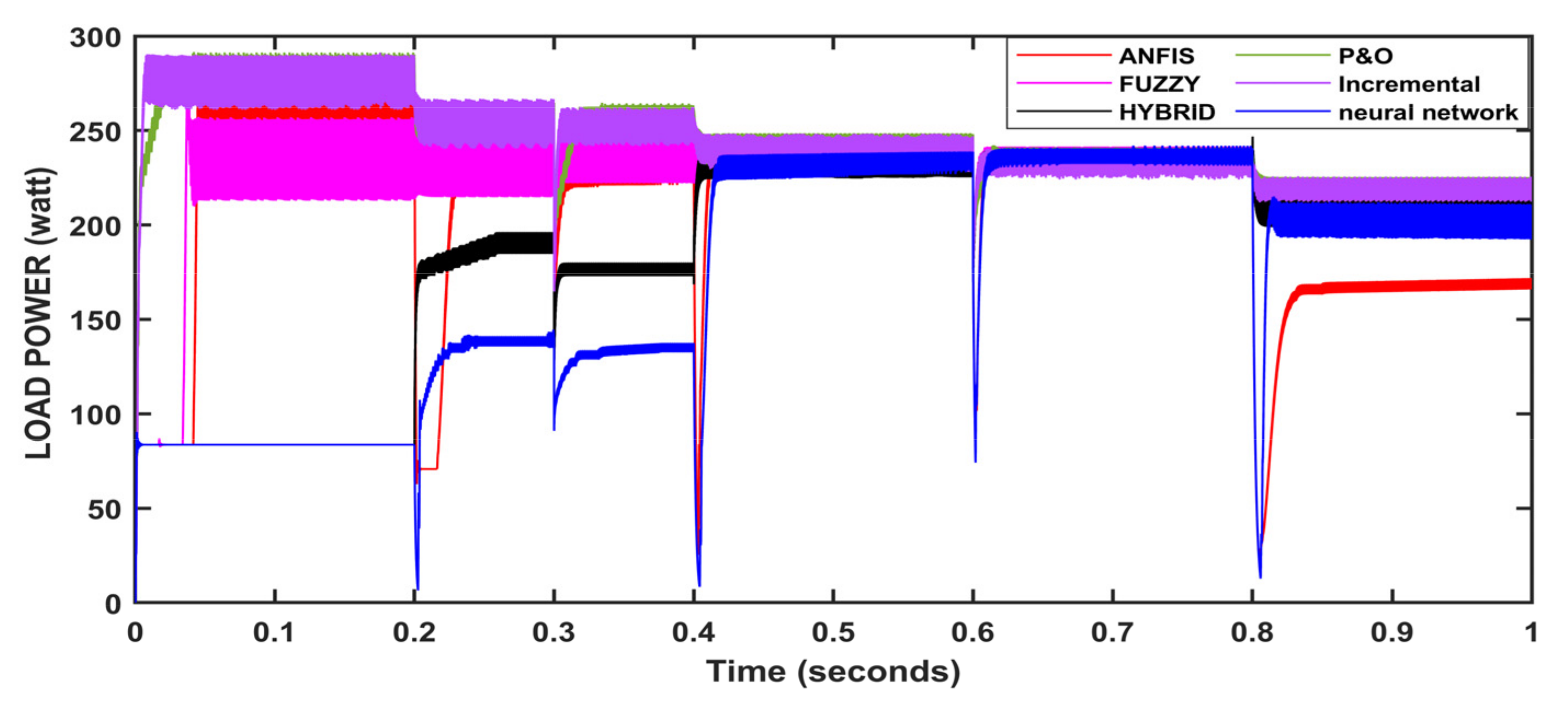
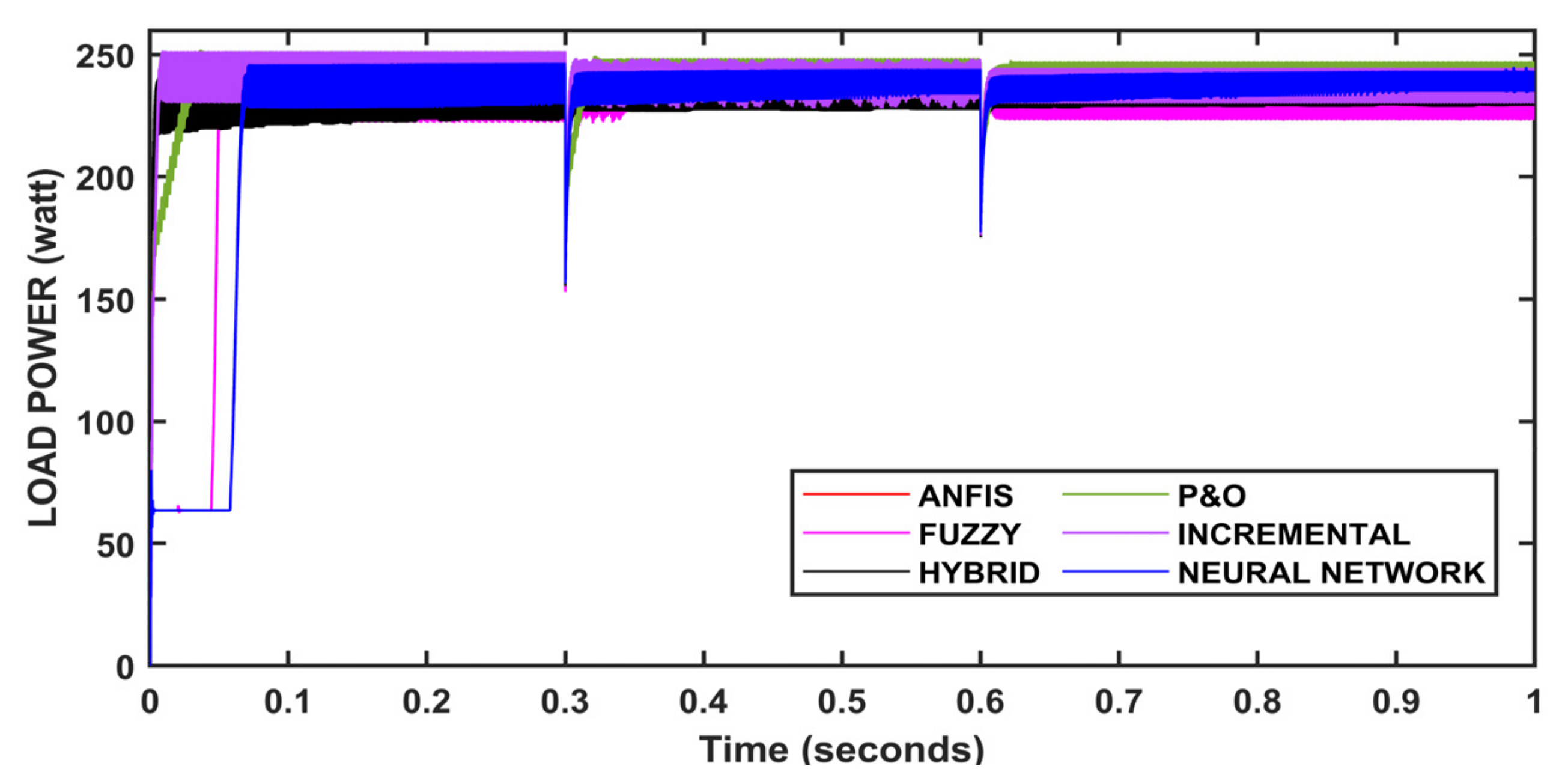
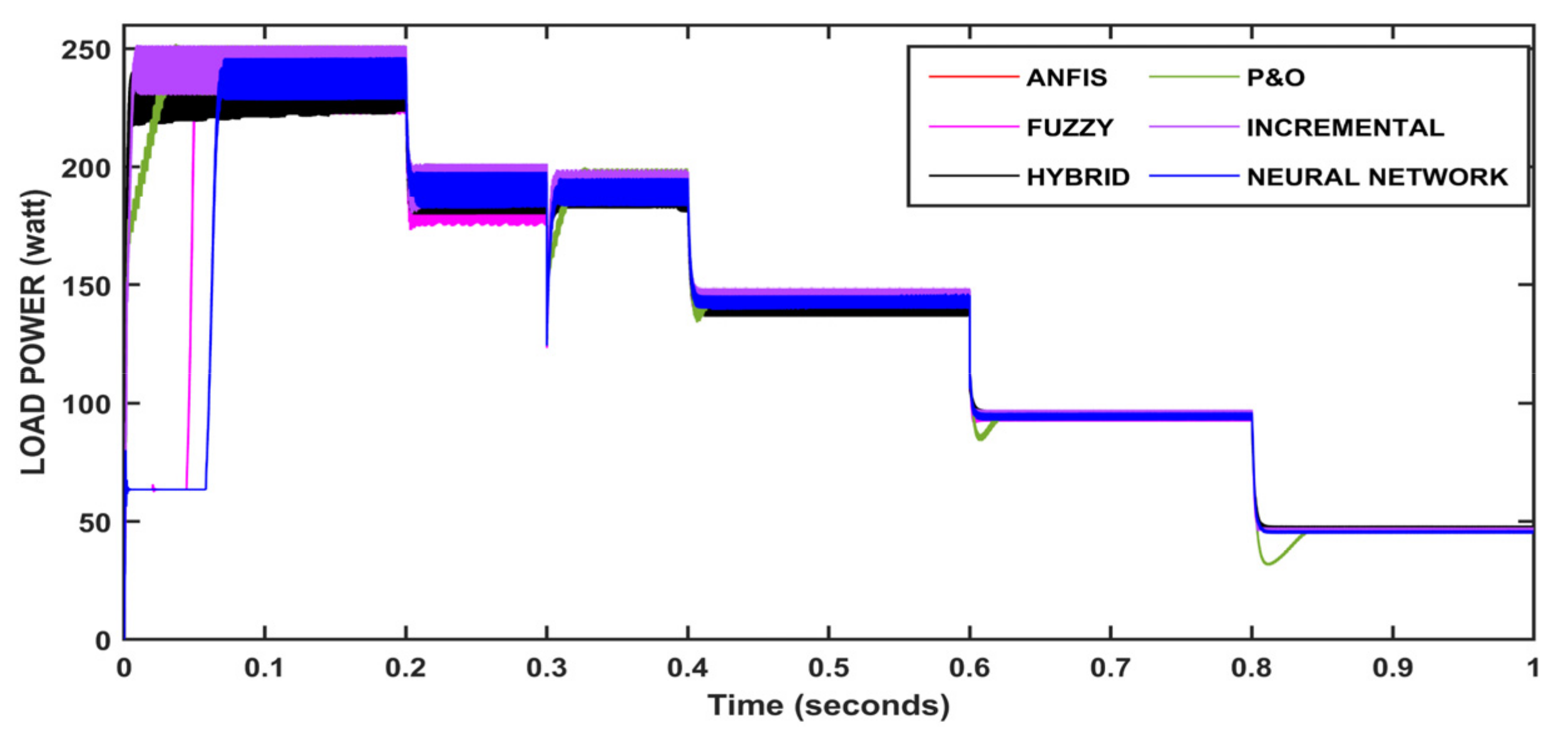
5. Results and Discussion
6. Conclusions
7. Future Scope
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beriber, D.; Talha, A. MPPT techniques for PV systems. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istambul, Turkey, 13–17 May 2013; pp. 1437–1442. [Google Scholar] [CrossRef]
- Saleh, A.; Azmi, K.F.; Hardianto, T.; Hadi, W. Comparison of MPPT Fuzzy Logic Controller Based on Perturb and Observe (P&O) and Incremental Conductance (InC) Algorithm on Buck-Boost Converter. In Proceedings of the 2018 2nd International Conference on Electrical Engineering and Informatics (ICon EEI), Batam, Indonesia, 16–17 October 2018; pp. 154–158. [Google Scholar] [CrossRef]
- Selman, N.H. Comparison Between Perturb & Observe, Incremental Conductance and Fuzzy Logic MPPT Techniques at Different Weather Conditions. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 12556–12569. [Google Scholar] [CrossRef]
- Sridhar, R.; Jeevananathan, D.; Selvan, N.; Banerjee, S. Modeling of PV Array and Performance Enhancement by MPPT Algorithm. Int. J. Comput. Appl. 2010, 7, 35–39. [Google Scholar] [CrossRef]
- Zainudin, H.N.; Mekhilef, S. Comparison Study of Maximum Power Point Tracker Techniques for PV Systems. In Proceedings of the 14th International Middle East Power Systems Conference (MEPCON’10), Cairo, Egypt, 19–21 December 2010; pp. 750–755. [Google Scholar]
- Kalashani, M.B.; Farsadi, M. New Structure for Photovoltaic Systems with Maximum Power Point Tracking Ability. Int. J. Power Electron. Drive Syst. 2014, 4, 489. [Google Scholar] [CrossRef]
- Berrera, M.; Dolara, A.; Faranda, R.; Leva, S. Experimental Test of Seven Widely-Adopted MPPT Algorithms. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Jyothy, L.P.; Sindhu, M.R. An Artificial Neural Network based MPPT Algorithm for Solar PV System. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 375–380. [Google Scholar] [CrossRef]
- Reisi, A.R.; Moradi, M.H.; Jamasb, S. Classification and comparison of maximum power point tracking techniques for photovoltaic system: A review. Renew. Sustain. Energy Rev. 2013, 19, 433–443. [Google Scholar] [CrossRef]
- Subudhi, B.; Pradhan, R. A Comparative Study on Maximum Power Point Tracking Techniques for Photovoltaic Power Systems. IEEE Trans. Sustain. Energy 2013, 4, 89–98. [Google Scholar] [CrossRef]
- Lee, H.-S.; Yun, J.-J. Advanced MPPT Algorithm for Distributed Photovoltaic Systems. Energies 2019, 12, 3576. [Google Scholar] [CrossRef]
- Khosrojerdi, F.; Taheri, S.; Cretu, A.-M. An adaptive neuro-fuzzy inference system-based MPPT controller for photovoltaic arrays. In Proceedings of the 2016 IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Hijazi, R.; Karami, N. Neural Network Assisted Variable-Step-Size P&O for Fast Maximum Power Point Tracking. In Proceedings of the 2020 32nd International Conference on Microelectronics (ICM), Aqaba, Jordan, 14–17 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Narendiran, S.; Sahoo, S.K.; Das, R.; Sahoo, A.K. Sahoo, Fuzzy logic controller based maximum power point tracking for PV system. In Proceedings of the 2016 3rd International Conference on Electrical Energy Systems (ICEES), Chennai, India, 17–19 March 2016; pp. 29–34. [Google Scholar] [CrossRef]
- Abdullah, G.; Aziz, M.S.; Hamad, B.A. Comparison between neural network and P&O method in optimizing MPPT control for photovoltaic cell. Int. J. Electr. Comput. Eng. 2020, 10, 5083–5092. [Google Scholar] [CrossRef]
- Sarvi, M.; Azadian, A. A comprehensive review and classified comparison of MPPT algorithms in PV systems. Energy Syst. 2021, 13, 281–320. [Google Scholar] [CrossRef]
- Atri, P.K.; Modi, P.S.; Gujar, N.S. Comparison of Different MPPT Control Strategies for Solar Charge Controller. In Proceedings of the 2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), Mathura, India, 28–29 February 2020; pp. 65–69. [Google Scholar] [CrossRef]
- Chtouki, I.; Wira, P.; Zazi, M. Comparison of Several Neural Network Perturb and Observe MPPT Methods for Photovoltaic Applications. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 909–914. [Google Scholar] [CrossRef]
- Khosravi, M.; Heshmatian, S.; Khaburi, D.A.; García, C.; Rodríguez, J. A Novel Hybrid Model-Based MPPT Algorithm Based on Artificial Neural Networks for Photovoltaic Applications. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Dahiya, A.K. Implementation and Comparison of Perturb & Observe, ANN and ANFIS Based MPPT Techniques. In Proceedings of the 2018 International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Kacimi, N.; Grouni, S.; Idir, A.; Boucherit, M.S. New improved hybrid MPPT based on neural network-model predictive control-kalman filter for photovoltaic system. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1230–1241. [Google Scholar] [CrossRef]
- Kanimozhi, K.; Rabi, B.R.M. Development of Hybrid MPPT Algorithm for Maximum Power Harvesting under Partial Shading Conditions. Circuits Syst. 2016, 7, 1611–1622. [Google Scholar] [CrossRef]
- Bataineh, K. Improved hybrid algorithms-based MPPT algorithm for PV system operating under severe weather conditions. IET Power Electron. 2019, 12, 703–711. [Google Scholar] [CrossRef]
- Aurilio, G.; Balato, M.; Graditi, G.; Landi, C.; Luiso, M.; Vitelli, M. Fast Hybrid MPPT Technique for Photovoltaic Applications: Numerical and Experimental Validation. Adv. Power Electron. 2014, 2014, 125918. [Google Scholar] [CrossRef]
- Sarwar, S.; Javed, M.Y.; Jaffery, M.H.; Arshad, J.; Rehman, A.U.; Shafiq, M.; Choi, J.-G. A Novel Hybrid MPPT Technique to Maximize Power Harvesting from PV System under Partial and Complex Partial Shading. Appl. Sci. 2022, 12, 587. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, optimization, intelligent and classical PV MPPT techniques: A Review. CSEE J. Power Energy Syst. 2021, 7, 9–33. [Google Scholar] [CrossRef]
- Azzouz, S.; Messalti, S.; Harrag, A. A Novel Hybrid MPPT Controller Using (P&O)-neural Networks for Variable Speed Wind Turbine Based on DFIG. Model. Meas. Control A 2019, 92, 23–29. [Google Scholar] [CrossRef]
- Arjun, M.; Zubin, J.B. Artificial Neural Network Based Hybrid MPPT for Photovoltaic Modules. In Proceedings of the 2018 International CET Conference on Control, Communication, and Computing (IC4), Thiruvananthapuram, India, 5–7 July 2018; pp. 140–145. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A New Sensorless Hybrid MPPT Algorithm Based on Fractional Short-Circuit Current Measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar] [CrossRef]
- Pakkiraiah, G.B.; Durga, S. Research Survey on Various MPPT Performance Issues to Improve the Solar PV System Efficiency. J. Sol. Energy 2016, 2016, 8012432. [Google Scholar] [CrossRef]
- Bhukya, L.; Kedika, N.R.; Salkuti, S.R. Enhanced Maximum Power Point Techniques for Solar Photovoltaic System under Uniform Insolation and Partial Shading Conditions: A Review. Algorithms 2022, 15, 365. [Google Scholar] [CrossRef]
- Javed, M.R.; Waleed, A.; Virk, U.S.; Hassan, S.Z.U. Comparison of the Adaptive Neural-Fuzzy Interface System (ANFIS) based Solar Maximum Power Point Tracking (MPPT) with other Solar MPPT Methods. In Proceedings of the 2020 IEEE 23rd International Multitopic Conference (INMIC), Bahawalpur, Pakistan, 5–7 November 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Singh, M.D.; Shine, V.J.; Janamala, V. Application of Artificial Neural Networks in Optimizing MPPT Control for Standalone Solar PV System. In Proceedings of the 2014 International Conference on Contemporary Computing and Informatics (IC3I), Mysore, India, 27–29 November 2014; pp. 162–166. [Google Scholar] [CrossRef]
- Khanam, J.; Foo, S.Y. Neural Networks Technique for Maximum Power Point Tracking of Photovoltaic Array. In Proceedings of the SoutheastCon, St. Petersburg, FL, USA, 19–22 April 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hayder, W.; Sera, D.; Ogliari, E.; Lashab, A. On Improved PSO and Neural Network P&O Methods for PV System under Shading and Various Atmospheric Conditions. Energies 2022, 15, 7668. [Google Scholar] [CrossRef]
- Dagal, I.; Akın, B.; Akboy, E. MPPT mechanism based on novel hybrid particle swarm optimization and salp swarm optimization algorithm for battery charging through simulink. Sci. Rep. 2022, 12, 2664. [Google Scholar] [CrossRef] [PubMed]
- Ali, Z.M.; Alquthami, T.; Alkhalaf, S.; Norouzi, H.; Dadfar, S.; Suzuki, K. Novel hybrid improved bat algorithm and fuzzy system based MPPT for photovoltaic under variable atmospheric conditions. Sustain. Energy Technol. Assess. 2022, 52, 102156. [Google Scholar] [CrossRef]
- Gong, L.; Hou, G.; Huang, C. A two-stage MPPT controller for PV system based on the improved artificial bee colony and simultaneous heat transfer search algorithm. ISA Transactions 2022. [Google Scholar] [CrossRef]
- Manna, S.; Akella, A.K.; Singh, D.K. A Novel MRAC-MPPT Scheme to Enhance Speed and Accuracy in PV Systems. Iran. J. Sci. Technol. Trans. Electr. Eng. 2022. [Google Scholar] [CrossRef]
- Manna, S.; Singh, D.K.; Akella, A.K.; Abdelaziz, A.Y.; Prasad, M. A novel robust model reference adaptive MPPT controller for Photovoltaic systems. Sci. Iran. 2022. [Google Scholar] [CrossRef]
- Badoud, A.E.; Mekhilef, S.; Bouamama, B.O. A Novel Hybrid MPPT Controller Based on Bond Graph and Fuzzy Logic in Proton Exchange Membrane Fuel Cell System: Experimental Validation. Arab. J. Sci. Eng. 2021, 47, 3201–3220. [Google Scholar] [CrossRef]

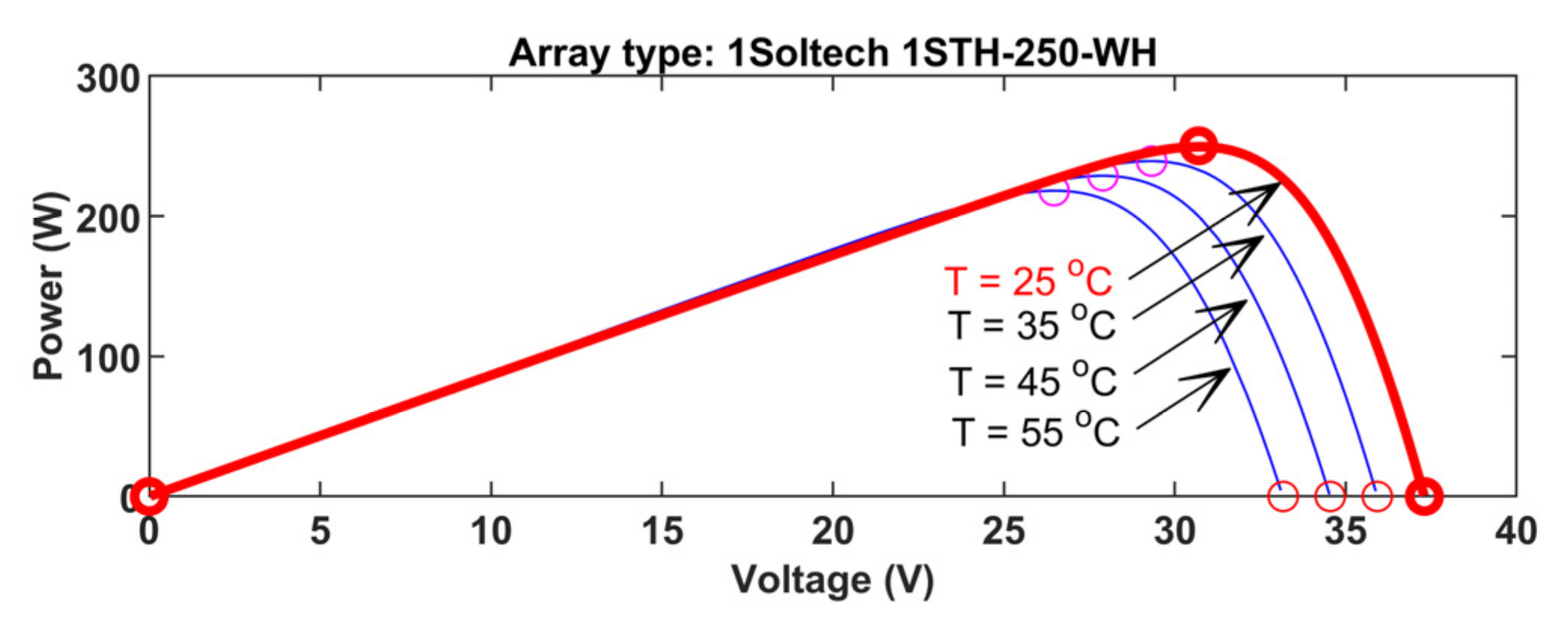
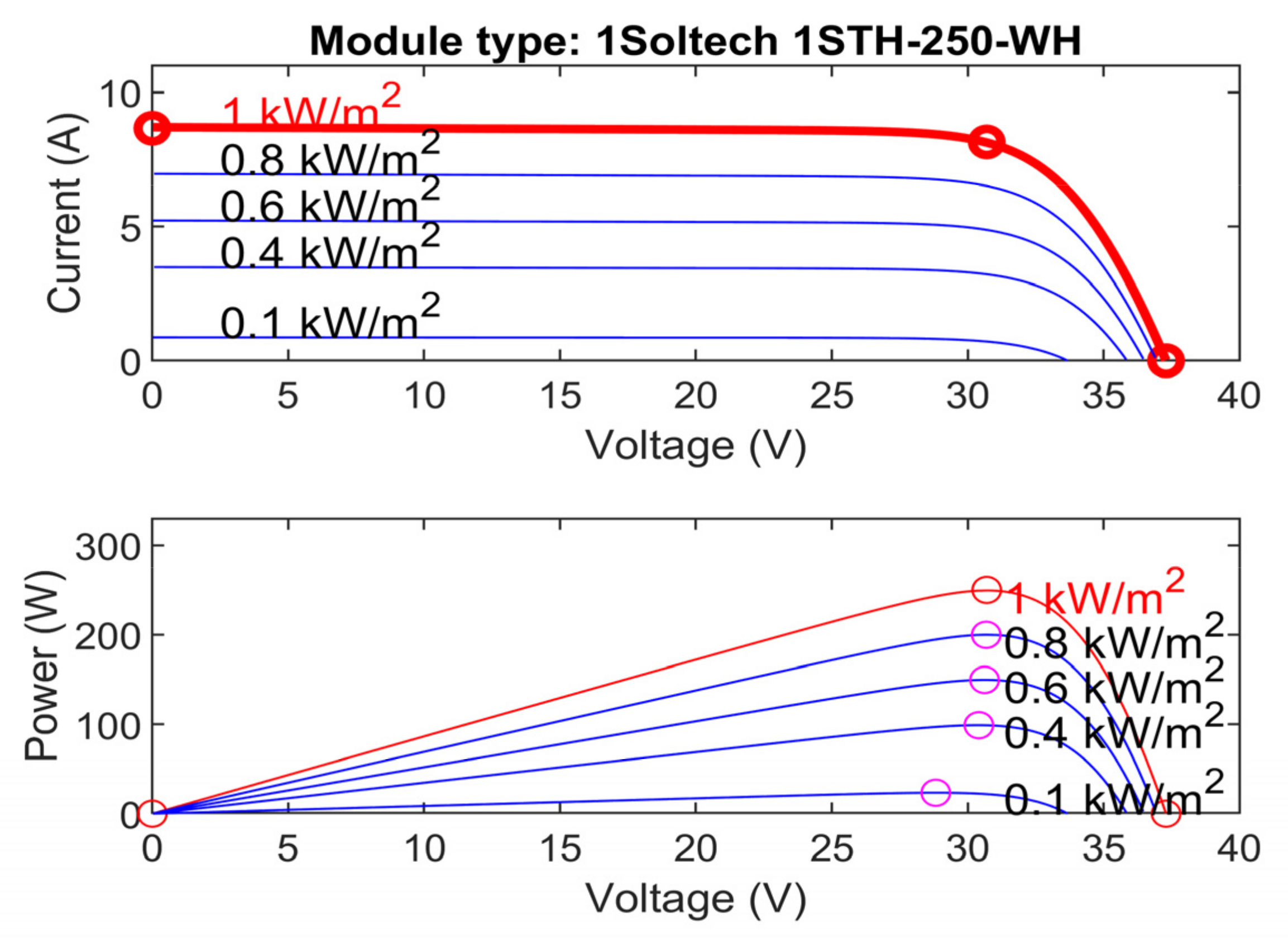





| Parameter | Specifications |
|---|---|
| Maximum power | 250.20 W |
| Open circuit voltage | 37.3 V |
| Voltage at maximum power point | 30.7 V |
| Short circuit current | 8.66 A |
| Current at maximum power point | 8.15 A |
| Parameter | Time (sec) | Value |
|---|---|---|
| Irradiance | (0, 0.2, 0.4, 0.6, 0.8) | (1000, 800, 600, 400, 200) w/m2 |
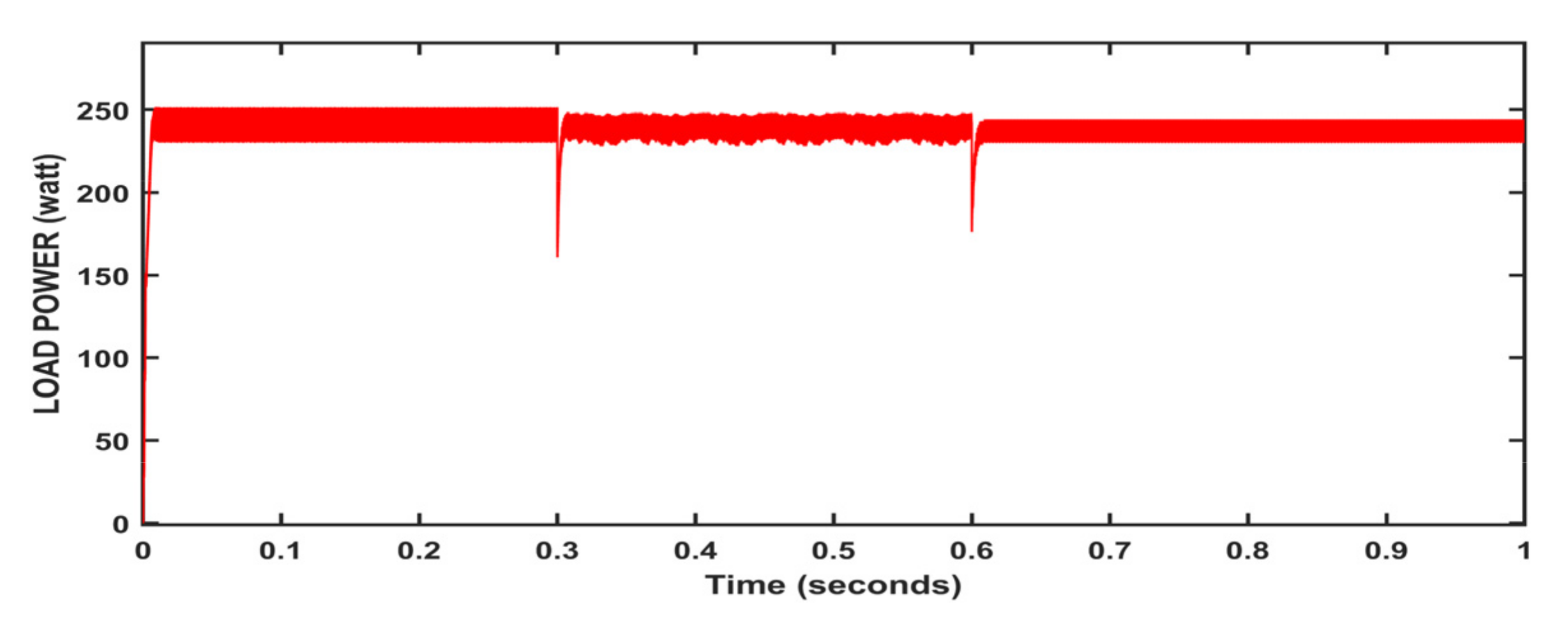
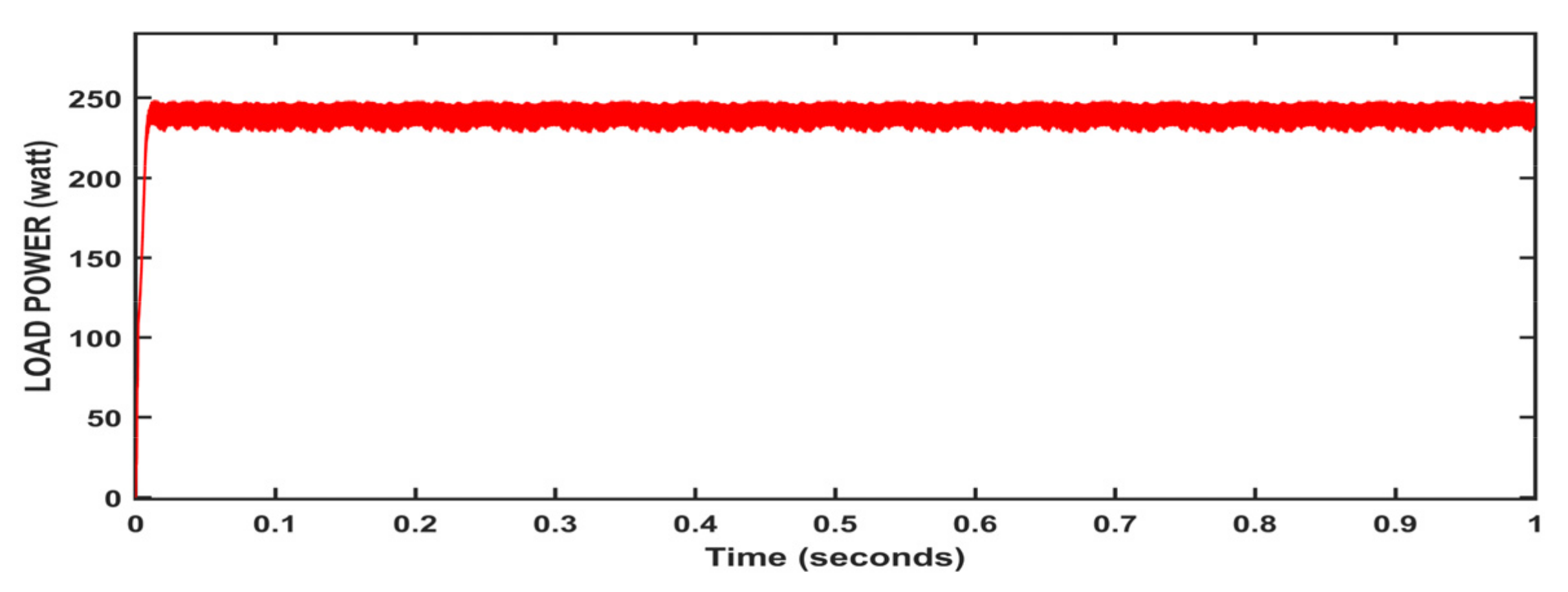
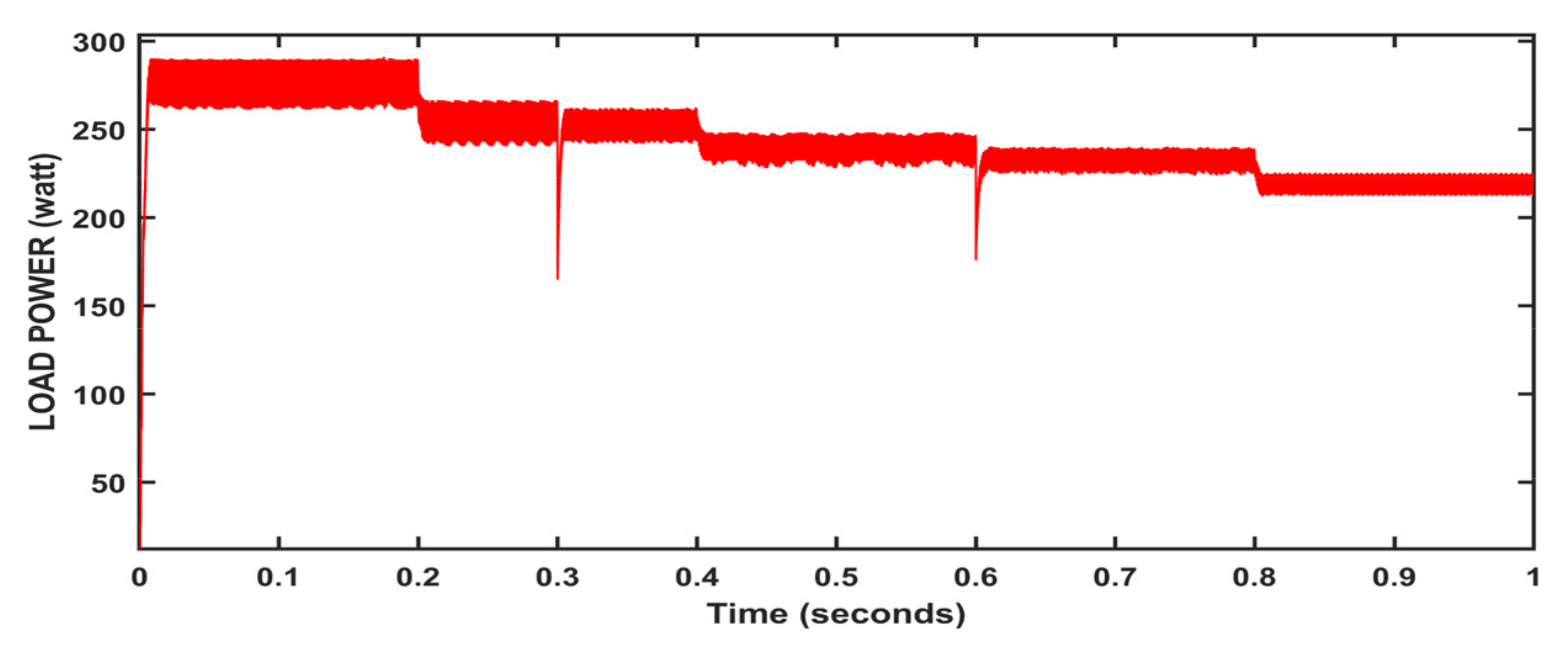
| Temperature Load | (0, 0.2, 0.4, 0.6, 0.8) (0, 0.3, 0.6) | (−15, 10, 25, 30, 45) Celsius (20, 30, 40) Ω |
| NB | NS | ZE | PS | PB | |
|---|---|---|---|---|---|
| NB | PB | PS | NB | NS | NS |
| NS | PS | PS | NB | NS | NS |
| ZE | NS | NS | NS | PB | PB |
| PS | NS | PB | PS | NB | PB |
| PB | NB | NB | PB | PS | PB |
| Specifications | Data | Validation and Test Data of 1000 Samples | ||
|---|---|---|---|---|
| Toolbox | NNTOOL box | Type of Sample | Samples (%) | Total Samples |
| Wizard: Input-output and curve fitting | Fitting app | Training | 70% | 700 samples |
| Input data to network | 1000 points input data of irradiation, temperature | Validation | 15% | 150 samples |
| Target data/desired network output | 1000 points data of voltage | Testing | 15% | 150 samples |
| Samples | Matrix—rows | |||
| Number of hidden neurons | 10 | |||
| Training Algorithm | Levenberg–Marquardt | |||
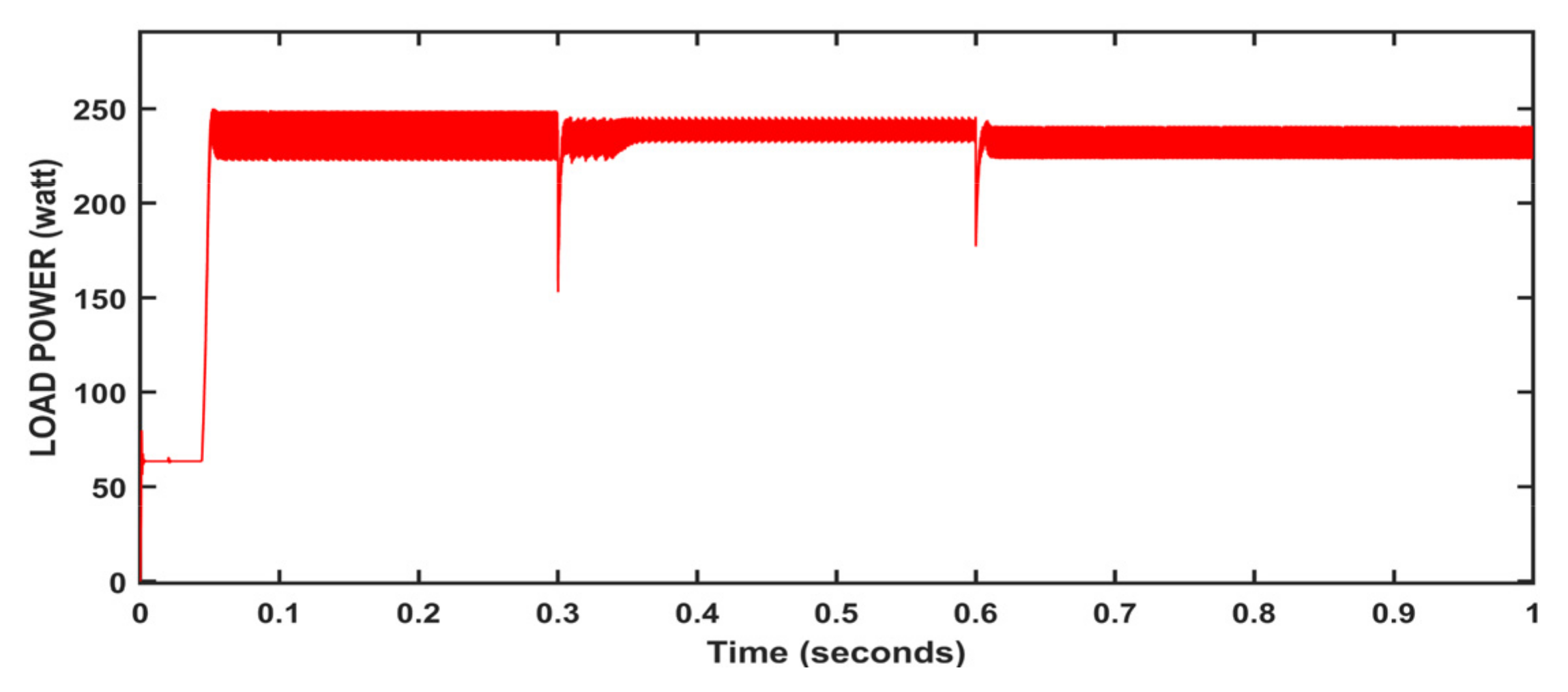
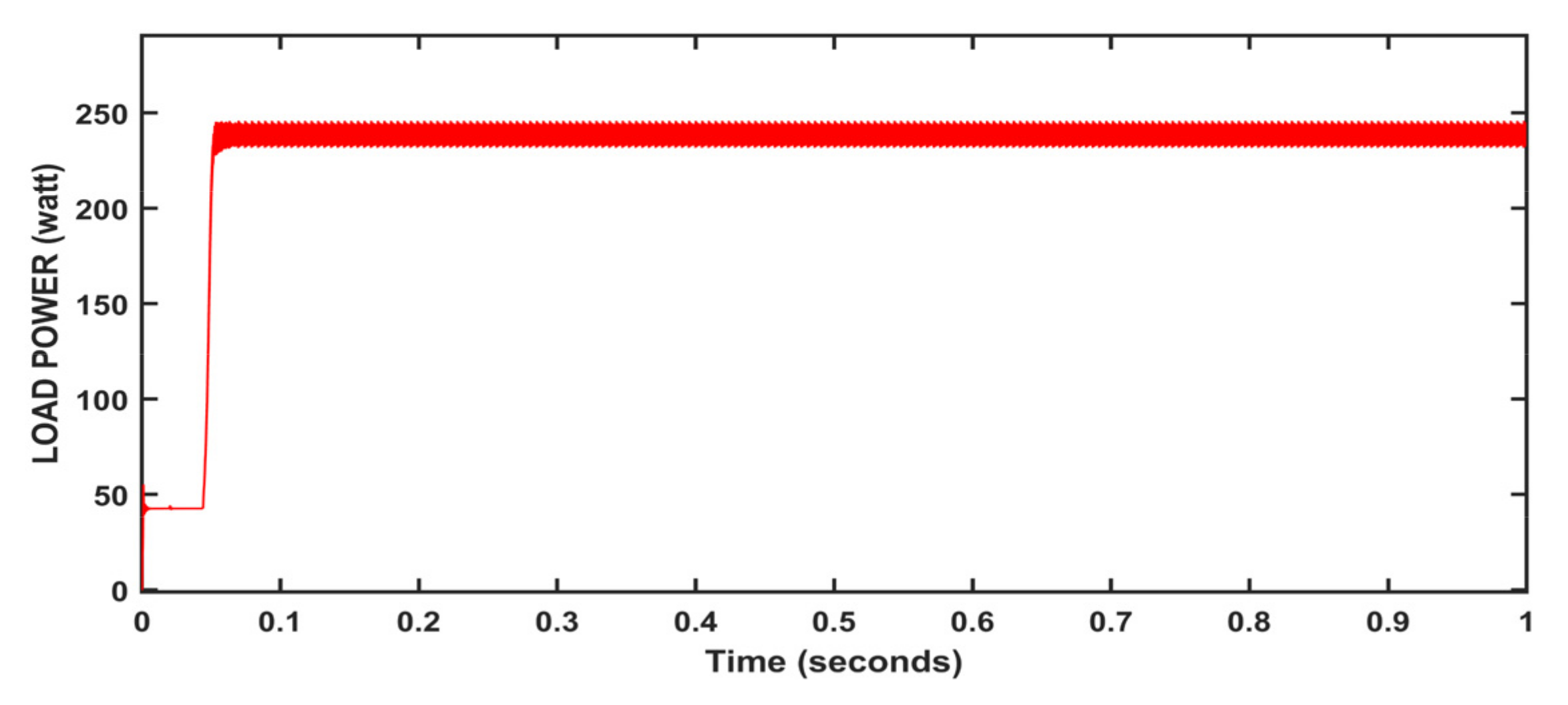
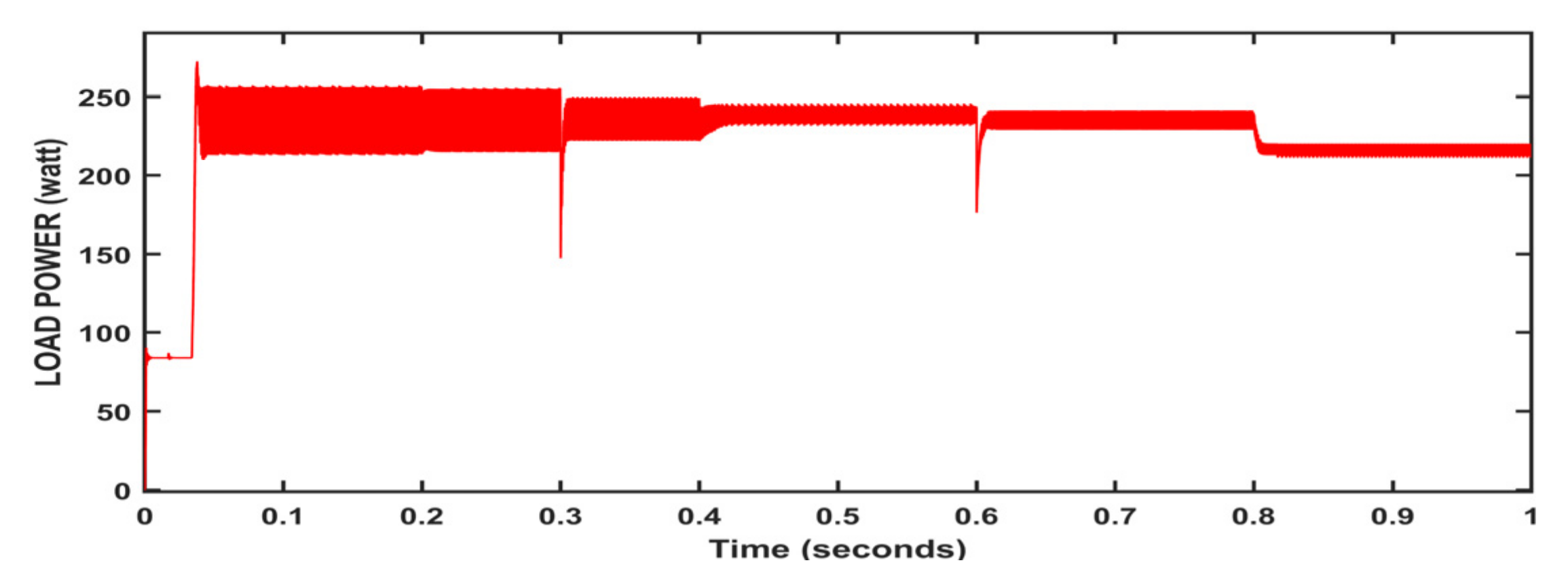
| Items | P&O Method | Incremental Conductance Method | Fuzzy Logic Control Method | ANFIS Method | Neural Network Method | Hybrid Controller Model |
|---|---|---|---|---|---|---|
| Dynamic behaviour | Poor | Medium | Medium | Good | Good | Fast |
| Transient behaviour | Bad | Bad | Good | Good | Good | Fast |
| (oscillations) Steady-state | Large | Moderate | Small | Small | Small | Very small |
| requirements | P&O algorithm | Incremental conductance algorithm | Fuzzy logic membership functions | ANFIS training data | Neural network training data | Neural network and P&O combined |
| Static error | High | High | Low | Low | Low | low |
| Controller accuracy | Low | Medium | Accurate | Accurate | Accurate | Accurate |
| Tracking speed | Slow | Slow | Fast | Fast | Fast | Faster |
| System complexity | Simple power calculations | Simple | Medium | Medium | Medium | Medium |
| Temperature characteristics | Poor | Poor | Good | Good | Good | Better |
| Parameters tuning | No | No | Yes | Yes | Yes | Yes |
| MPPT Method | Convergence Time(s) | Irradiation: 1000 w/m2 | Values | Comment |
|---|---|---|---|---|
| P_max: 250 w/m2 | ||||
| P&O method | 0.004 | P_avg | 237.4 | Oscillations occur |
| %ɳPV | 94.96 | |||
| Incremental Conductance method | 0.006 | P_avg | 239.1 | Oscillations occur |
| %ɳPV | 95.60 | |||
| Fuzzy logic control method | 0.04 | P_avg | 242.2 | Long convergence time |
| %ɳPV | 96.88 | |||
| Neural network method | 0.205 | P_avg | 244.6 | Better dynamic performance |
| %ɳPV | 97.84 | |||
| ANFIS control method | 0.046 | P_avg | 244.4 | Under dynamic response |
| %ɳPV | 97.76 | |||
| Hybrid Method | 0.2005 | P_avg | 247 | Fast response |
| %ɳPV | 98.80 |
| Method Name | Real-Time (s) (Varying Conditions) | Real-Time (s) (Constant Conditions) |
|---|---|---|
| P&O | 4.633 | 3.875 |
| Incremental conductance | 9.2635 | 5.771 |
| Fuzzy logic control | 423.88 | 372.41 |
| Neural network | 7.701 | 4.6345 |
| ANFIS | 50.5595 | 41.07 |
| Hybrid | 6.154 | 5.667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devarakonda, A.K.; Karuppiah, N.; Selvaraj, T.; Balachandran, P.K.; Shanmugasundaram, R.; Senjyu, T. A Comparative Analysis of Maximum Power Point Techniques for Solar Photovoltaic Systems. Energies 2022, 15, 8776. https://doi.org/10.3390/en15228776
Devarakonda AK, Karuppiah N, Selvaraj T, Balachandran PK, Shanmugasundaram R, Senjyu T. A Comparative Analysis of Maximum Power Point Techniques for Solar Photovoltaic Systems. Energies. 2022; 15(22):8776. https://doi.org/10.3390/en15228776
Chicago/Turabian StyleDevarakonda, Ashwin Kumar, Natarajan Karuppiah, Tamilselvi Selvaraj, Praveen Kumar Balachandran, Ravivarman Shanmugasundaram, and Tomonobu Senjyu. 2022. "A Comparative Analysis of Maximum Power Point Techniques for Solar Photovoltaic Systems" Energies 15, no. 22: 8776. https://doi.org/10.3390/en15228776
APA StyleDevarakonda, A. K., Karuppiah, N., Selvaraj, T., Balachandran, P. K., Shanmugasundaram, R., & Senjyu, T. (2022). A Comparative Analysis of Maximum Power Point Techniques for Solar Photovoltaic Systems. Energies, 15(22), 8776. https://doi.org/10.3390/en15228776









