A Study of Neural Network Framework for Power Generation Prediction of a Solar Power Plant

Abstract

In the process of creating a prediction model using artificial intelligence by utilizing a deep neural network, it is of utmost significance to know the amount of insolation that has an absolute effect on the quantity of power generation of a solar cell. To predict the power generation quantity of a solar power plant, a deep neural network requires previously accumulated power generation data of a power plant. However, if there is no equipment to measure solar radiation in the internal facilities of the power plant and if there is no record of the existence of solar radiation in the past data, it is inevitable to obtain the solar radiation information of the nearest point in an effort to accurately predict the quantity of power generation. The site conditions of the power plant are affected by the geographical topography which acts as a stumbling block while anticipating favorable weather conditions. In this paper, we introduce a method to solve these problems and predict the quantity of power generation by modeling the power generation characteristics of a power plant using a neural network. he average of the error between the actual quantity and the predicted quantity for the same period was 1.99, that represents the predictive model is efficient to be used in real-time.

1. Introduction

The Solar Photovoltaic Power Generation System (SPV PG System) is mainly composed of a PN junction semiconductor device with a photoelectric effect mechanism that converts light into electricity. This device, that is, the Solar Cell, consists of a junction of N-type and P-type semiconductors implemented according to the number of outermost electrons, which is an atomic characteristic of a material doping silicon that is used as a fundamental material. The principle of power generation is to supply direct current electrical energy to the circuit by obtaining energy to transfer electric charges with light energy using the electric field effect that occurs when two semiconductors with different properties are fused together and by utilizing the method of excitation by photon’s impact energy.

The ability to generate electricity from light does not necessarily mean that the intensity and amount of light are related to the quantity of power generation. We already know that the photoelectric effect does not depend on the brightness of the light, that is, the amount of light, but on the wavelength $\lambda$ of the light according to the equation which describes the relationship between the wavelength and energy of light according to Planck’s law as given in Equation (1).

$$E\left(\lambda ,T\right)=\frac{2h{c}^2}{{\lambda }^5}\frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}\frac{W}{m^2\mu m}$$

(1)

This fact is consequential for predicting the amount of electricity generated by the solar power plant based on the particular time during the day. The brightness of sunlight before 10 a.m. and after 3 p.m. is radiant and very bright compared to the brightness of about 4 h centered on noon. However, the wavelength of light passing through the atmosphere varies according to the thickness of the atmosphere (AM; Air Mass). When the distance that penetrates the atmosphere is long, visible light and infrared light which have long wavelengths are predominant even when the sun is bright.

Seasonally, the declination angle ranges from 23.5${}^{\circ }$ to −23.5${}^{\circ }$ due to the influence of the angle between the earth’s orbital trajectory and the sun’s trajectory, and the altitude of the sun changes, which greatly affects the brightness and wavelength of light. In addition, the temperature characteristics of silicon semiconductors are based on a temperature of 25 °C. In other words, non-linear characteristics changes depending on the temperature conditions which ultimately affects power generation.

These factors, i.e., wavelength and brightness of light, season, temperature, humidity, and the insolation are not independent of each other. Although it is possible to numerically calculate the dependency relationship between individual variables and the amount of power generation, the way each element operates is not independent, so the climatic, environmental, and temporal changes such as temperature and insolation are interlinked with each other, and it is not easy to reflect the climatic characteristics of the geographical location of power plants.

By utilizing the characteristics of the diode, analysis and interpretations are put together in [1]. The characteristics of the solar cell are similar to the diode as a consequence of the highest structural similarities. The complexity, however, is indescribable when considering the electrical relevance and influence shown in the configuration of the module, which is a set of these cells, the string, which is the set of modules, and the array, which is the set of strings. Moreover, it is not easy to model the characteristics of a solar power plant when considering the effect of the inverter that converts DC power into AC power and the effect through grid connection.

Nevertheless, the expansion of renewable energy increases the instability of the power system, and in particular, solar power generation has output fluctuations and intermittent power generation characteristics which are liable to vary and change as a consequence of the variable weather conditions and environment of renewable energy generation. Due to the nature of the power plant equipment failure occurs over time. To solve this problem, solar power generation requires a technology to predict power generation output and a power plant diagnosis technology, and various studies [2,3], etc. are in progress.

Furthermore, there is often a difference in the amount of power generated by power plants of the same capacity located at the same latitude. Therefore, we tried to create a predictive model that includes non-linearly related variables, rather than a difficult way to calculate the synthetic conditions.

2. Materials and Methods

2.1. Difference between Mathematical Model and Neural Network Prediction Model

Using interrelated inputs and outputs to find a transfer function that determines the output by the input is a conventional system analysis method. There are various methods to interpret the relationship between the input and the output from a temporal point of view and find the most approximate functional relationship, a kinematic relationship or an electrical engineering relationship can also be implemented as a model through physical analysis.

As mentioned above, there are many implemented cases of solar power generation facilities modeling with a similar diode due to a similar configuration to that of a diode and introducing methods to analyze the DC link of an SPV power plant in relation to temperature and solar radiation [4,5,6,7,8,9,10,11,12,13]. However, the power plant includes AC power generation facilities converted through inverters, thus it is paramount to include these components in the modeling phase. This is because the power generation capacity of a power plant is finally evaluated by calculating the total quantity of the AC power being generated.

To create a power plant model by reviewing research, it is necessary to analyze the influence of various factors affecting solar power generation, especially climate which includes temperature and humidity, and environmental conditions such as geography and topography, for predicting and diagnosing the amount of solar power generation. In addition, these factors have a very non-linear complex relationship and influence that also affects each other. For this reason, it is very difficult to predict and diagnose the amount of power generation by analyzing and understanding the functionality of all the involved factors, furthermore, it is complex to connect them comprehensively by analyzing individual correlations experimentally and mathematically. Therefore, we would apply a comprehensive analysis given these complications. As a result, it is intended to make a comprehensive judgment without subdividing the comprehensive correlations of various factors that affect AC power production. Of course, for the result of “AC power production”, considering the relationship of each related and interacting factor is a way to increase the understanding of the facility, but the main objective is to make it possible to predict the efficiency of the power plant facilities, the form of depreciation which is a reduction in the value of the asset with the passage of time and abnormal symptoms by tracking the change in the amount of power generation through a power generation model with the minimum error between the predicted amount and the actual measurement. Above all, to diagnose and improve efficiency, the difference between the actual change and the predicted change in power production must be reliable.

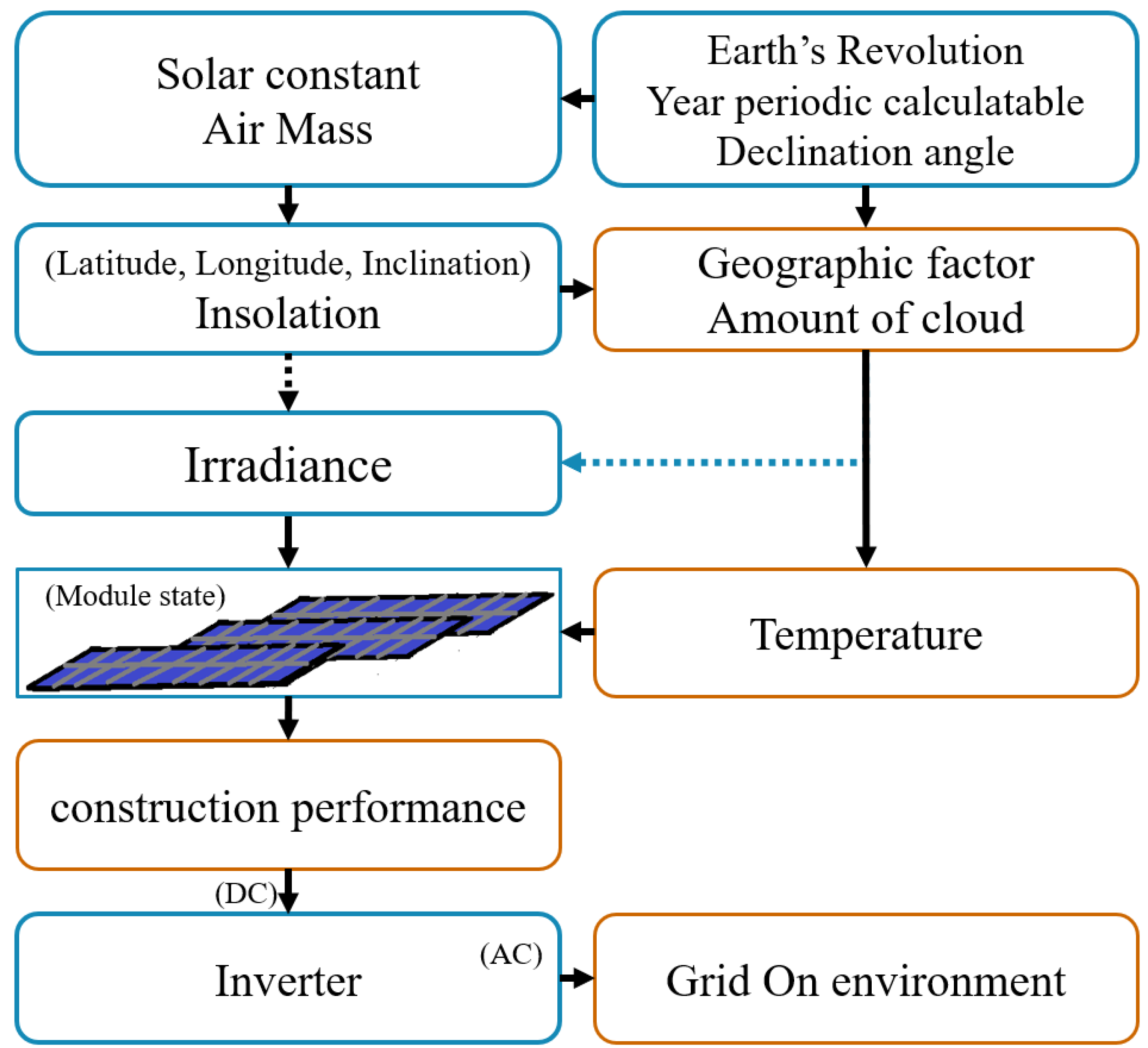
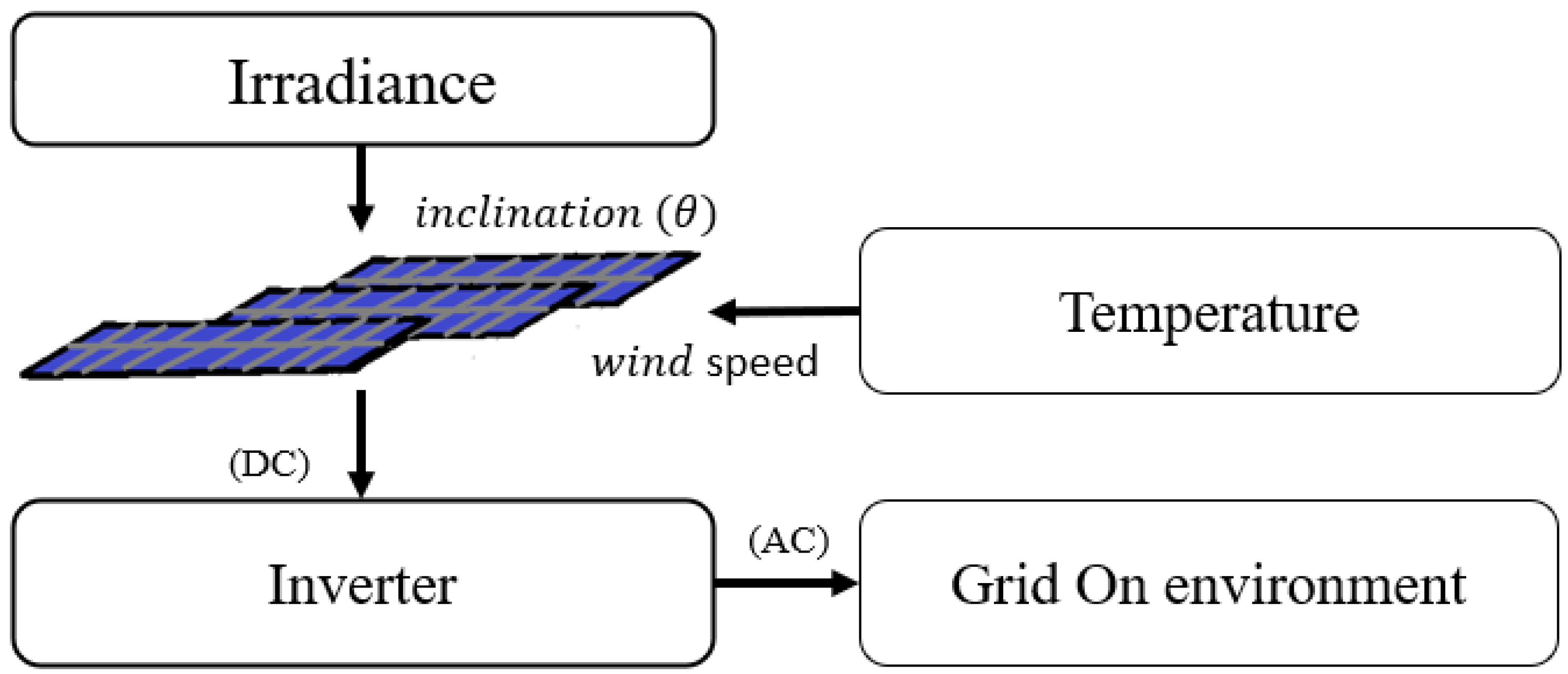
For such a precise prediction model, it is necessary to find out which inputs determine the size of the output through the relationship of factors related to power production. Figure 1 schematically illustrates these decisive factors.

Blocks with blue lines in Figure 1 are linear elements that are relatively easy to model numerically. On the other hand, the brown lines are the factors that are difficult to quantify and are non-linear, and have statistical characteristics.The angled block is the most vital factor in determining the amount of power generation, and an important characteristic of the SPV power plant lies in this part. Naturally by considering the efficiency loss of the devices which changes organically and this loss further adds up the complexity level. It is not easy to find a transfer function using a mathematical model for a system with high complexity, non-linearity, and interdependence between variables. In particular, it is more difficult to formulate an equation and make a model considering the location and topographical characteristics of the power plant because the climatic effect of the topography is taken into account. As electricity trading through planned transmission for power generation of new and renewable power generation facilities is being discussed, the errors which result in these numerical models have repercussions which leads to the difficulty in predicting the amount of power generation and perform planned transmission. Therefore, rather than inducing an input/output relationship in the form of a transfer function through a functional model based on a calculation formula, it is more appropriate to secure a non-linear element as much as possible and build a statistical or empirical model according to the overall pattern. For this reason, we would like to present a method for obtaining a nonlinear PV power plant model that models the power plant characteristics according to the statistical pattern characteristics using a neural network. We will use deep learning (DL) to simulate a model. In recent times Artificial Intelligence (AI) has given solutions to many research problems like medical imaging [14] and bio-informatics [15,16,17,18,19]. Neural networks form the backbone for the DL model and by utilizing neural networks we will simulate an irradiance prediction model which will predict the amount of power generation. In this way, the SPV power plant model will be simulated using neural network.

In this paper, the amount of solar energy that can be calculated from the elevation angle of the sun at a specific point using declination angle, latitude, and time is called “Insolation”, Energy was set to “Irradiance”. We distinguish these two words in this paper.

First of all, in order to predict and diagnose the amount of power generation, we predict the amount of generation among numerous input variables in order to understand the maximum temporal correlation of the trends of non-linear factors and predict the amount of generation through a model which is simulated by using a neural network. It is important to select the variables that have the greatest influence on the calculations to minimize the computation time of the computer and make it suitable for accurate and fast predictions. For this purpose, we analyze the data from the Korea Meteorological Administration over the years and we consider the time period during a day which is relative to the actual operational data of the solar power plant which was obtained over the years. In this way, we can find the factors that have a high influence on photovoltaic power generation. We want to quickly predict and generate SPV power generation at 2-hour intervals for 24 h.

2.2. Construction of Power Generation and Weather Variable Data

The first important thing in predicting the generation amount of an SPV power plant would be to model the characteristics of the quantity of power being generated by the power plant. The characteristic of a power plant should be to define the amount of power generation as an output with respect to the insolation used as an input in a relational expression. Of course, a functional relationship can be considered as a method of using a numerical model, but since we are implementing a model using a neural network, we prepared a dataset with the relationship between the input variable and the correct answer. The important thing here is that insolation is not measured, but estimated by calculation. Tomorrow’s insolation is predictable by the sun’s declination angle $\delta$ and the elevation angle $\theta$ calculated from the latitude $\varphi$ and longitude or azimuth $\omega$ at the location of the power plant [20], as shown in Equations (2) and (3).

$$\delta =23.5sin\left[\frac{360\left(n-79\right)}{365}\right]$$

(2)

$$sin\mathrm{\Theta }=cos\delta cos\varphi cos\omega +sin\delta sin\varphi$$

(3)

Here, the corrected solar constant G_on can be calculated by reflecting the solar perihelion and aphelion to the solar constant G_s. It can be calculated mathematically as in Equation 4. In addition, the solar constant G_s can be slightly reflected in solar energy fluctuations through observations on solar activity.

$$G_{on}=G_s\left[1+0.034cos\frac{360n}{365}\right]$$

(4)

Insolation, which can be calculated according to season and time, does not forecast the weather. That is, insolation is a very important input variable for power generation, but irradiance reaching the atmosphere and the surface is not calculated as insolation. Naturally, irradiance varies with time due to changes in the atmosphere and geographic requirements. It is not easy to predict the irradiance in the terrain that reflects the factors with such complex changes from the calculated insolation. For this reason, predicting the irradiance irradiated to the SPV power plant using weather information predicted from the calculated insolation is difficult to identify the independent causal relationship of individual variables, so the method of predicting the comprehensive relationship as a statistical pattern is more suitable. However, it is difficult to predict within the desired time because it is limited by time and computer performance to predict including all relevant variables for terrain, environment, climate, and meteorology. Therefore, it is necessary to select variables that have a large influence on irradiance in consideration of the correlation that can be obtained through various conditions data which is collected previously based on the amount of power generation in the past. Through the relationship between the irradiance irradiated to the power plant and the amount of power obtained in this way, it is possible to check the performance of the power plant included in the output value of the amount of power generation without modeling the characteristics of the power plant. In other words, it is possible to compare and evaluate the performance of a power plant through the difference between the actual power generation and the predicted power generation compared to the design capacity of the power plant due to irradiance and various factors.

Radovan et al. [21] developed a method of predicting insolation based on shadow prediction by clouds and said that it can be used as a prediction standard for solar energy production. Durrani et al. [22] proposed a PV yield prediction system based on multiple feed-forward neural network irradiance forecast models. They said for an accurate prediction of the PV power the neural network model is the preferred choice. Solano et al. [23] said accurate solar radiation forecasting is essential to operate power systems safely under high shares of photovoltaic generation. Furthermore, a solar forecasting methodology is proposed using machine learning. Sudharshan et al. [24] explains the impact of different irradiance forecasting techniques for solar energy prediction models by their characteristics and metric performance with additionally adding merits and drawbacks of each. They said solar energy forecasting models improve the reliability of the solar plant in microgrid operations.

In Figure 2, the irradiance that can be predicted at 2-hour intervals is rearranged according to the acquired time based on the past big data such as weather forecasts and power generation. At this time, the polluted parts such as data missing at the time intervals which are similar or unclear records are removed from the weather forecast or power generation data. Through this preprocessing of data in order which is based on time, the input data is matched with the output data of the amount of power generation to form a training dataset. First, a dataset was prepared using the period from August 2018 to January 2021 in unit hours.

In

Table 1. Seosan county’s ASOS dataset and calculate insolation to learn for building a model of irradiance [36.7766${}^{\circ }$126.4939${}^{\circ }$25.25m].

Time	Temp. °C	Wind Speed m/s	Wind Direction	Humidity	Amount of Cloud	Hour	Real Irradiance	Calc. Insolation
1 August 2018 5:00	26.2	0.6	50	88	0	5	0	0
1 August 2018 6:00	26.4	1.3	50	89	0	6	0.01	0
1 August 2018 7:00	27.6	0.7	50	84	1	7	0.31	0.1692
1 August 2018 8:00	30.4	0.8	360	74	0	8	0.96	0.7992
1 August 2018 9:00	32.2	1.1	360	64	0	9	1.66	1.5408
1 August 2018 10:00	33.8	2.1	340	58	2	10	2.31	2.2212
1 August 2018 11:00	34.9	2.2	20	50	1	11	2.82	2.7612
1 August 2018 12:00	35.6	1.8	360	52	2	12	3.02	3.1032
1 August 2018 13:00	35.8	2.7	340	50	2	13	2.85	3.222
1 August 2018 14:00	36.5	3.7	340	44	2	14	3.18	3.1032
					⋮
					⋮
					⋮
31 January 2021 16:00	9.8	3.7	200	61	9	16	0.73	0.7344
31 January 2021 17:00	9.4	3.6	200	63	8	17	0.24	0.2052
31 January 2021 18:00	7.8	2	200	70	8	18	0.04	0
31 January 2021 19:00	6.7	1.5	200	75	8	19	0	0
31 January 2021 20:00	6.2	0.8	200	77	8	20	0	0

, climate data such as temperature is a summary of observation data from meteorological stations by time. The measured irradiance and calculated irradiance in the last two columns show the actual measured and calculated data based on the weather station. It is natural that the calculated insolation differs from the measured irradiance due to the influence of climate, that is, the influence of humidity such as clouds and fog, and temperature. This is the reason why we model the irradiance irradiated to the SPV power plant in a non-linear way. 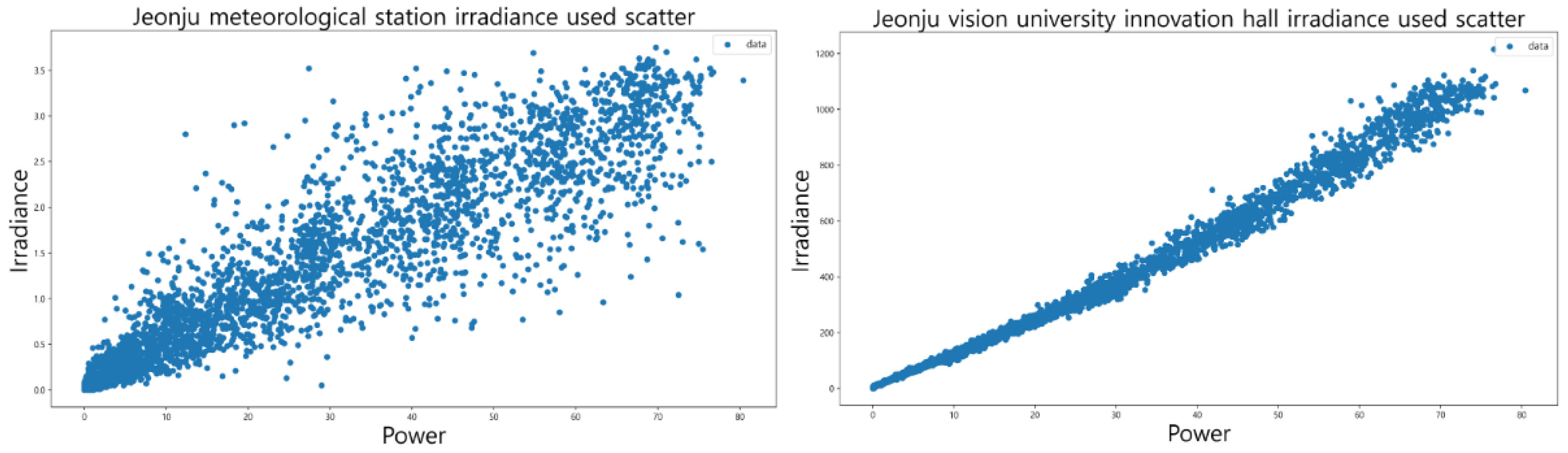Based on the data from Seosan, the generation amount of the SPV power plant [37.05550${}^{\circ }$, 126.5144${}^{\circ }$] located in Dangjin, close to Seosan was compared. Comparing the generation amount of the Dangjin power plant with the observed irradiance of Seosan, it can be seen that the observed irradiance and the generation amount do not have a constant relationship. Here, if the power generation including temperature is plotted as a power generation-irradiance scatter plot, it will look like as in Figure 3.

The graph demonstrates the distinctive upward sloping of the data. In other words, the increase in irradiance seems to have a linear relationship with the increase in power generation. In addition, the temperature in colors shows the characteristics of the weather with high irradiance, and it seems that there is a relationship between high irradiance in summer and rising temperature. The higher the irradiance, the higher the temperature even with the same amount of power. This is related to the bandgap of silicon, which is the main component of a solar cell, and occurs because electrons in the valence band are excited to the conduction band by the photoelectric effect and the remaining energy is converted into thermal energy [20]. In other words, classifying power generation by temperature is not as distinguishable as using irradiance. In this way, the degree of influence on the amount of power generation can be confirmed as a relationship of correlation. For correlation, the Pearson correlation coefficient method was used, and the correlations for May, August, October, and January were individually checked in consideration of seasonal factors as shown in

Table 2. Pearson correlation coefficients of monthly irradiance and SPV power amount.

Month	1	2	3	4	5	6	7	8	9	10	11	12
Coefficient	0.94	0.96	0.97	0.95	0.93	0.94	0.89	0.91	0.95	0.96	0.96	0.95

.

It can be seen that the correlation between the summer and winter seasons is not relatively close at all. Since the correlation coefficient between spring and autumn is relatively large, it can be inferred that it is affected by temperature. However, the correlation between December and January, which is winter, is not high, so it cannot be said that it has a proportional relationship with temperature. In Figure 3, the data tends to be dispersed in areas with high temperatures on the basis of 10 ${}^{\circ }C$, but in January in Table 2, it is confirmed that the correlation coefficient is 0.94, which is the same as in June. It is judged that the dispersibility in the power generation and irradiance scatterplots is affected by other meteorological variables besides temperature.

2.3. Configuration of SPV Generation Amount and Weather Variable Data for the Jeonju Region

In order to understand the correlation of weather variables according to the difference in the location of the weather observation point, irradiance and temperature of the power plant at the Jeonju Vision University Innovation Hall, which are the power plant meteorological variable data, and the power generation amount of the power plant at the Jeonju Vision University Innovation Hall, from July 2014 to 2020, a dataset was prepared using data in units of one hour for August.

In

Table 3. Jeonju meteorological station & Vision college irradiance data [35.84092${}^{\circ }$ 127.11718${}^{\circ }$ 60m].

1l	Jeonju Meteorological Station			Vision College Irradiance Data
Time	Temp °C	Total Amount of Cloud	Real Irradiance	Temp °C	Real Irradiance
11 July 2014 05:00	19.8	3	NaN	22.83	0.82
11 July 2014 06:00	19.7	0	0.03	22.93	15.94
11 July 2014 07:00	21.4	0	0.33	24.09	75.97
11 July 2014 08:00	24	2	0.96	25.62	157.49
11 July 2014 09:00	25.9	5	1.65	26.09	217.8
11 July 2014 10:00	27	3	2.27	27.32	320.11
11 July 2014 11:00	29.3	2	2.64	28.92	511.92
11 July 2014 12:00	31	3	2.93	30.78	688.26
11 July 2014 13:00	31.1	3	3.1	31.45	841.26
11 July 2014 14:00	31.8	4	2.38	32.97	1014.54
			⋮
			⋮
			⋮
31 August 2020 16:00	26.6	9	0.74	29.05	147.67
31 August 2020 17:00	26.8	9	0.18	28.22	26.59
31 August 2020 18:00	26.6	9	0.11	27.71	32.35
31 August 2020 19:00	26.8	8	0.06	27.47	7.37
31 August 2020 20:00	26.5	8	0	27.29	1

, climate data such as temperature are organized by time-based on observation data, from meteorological stations. We try to find the reason why the irradiance and the amount of power generation do not have a constant relationship shown in Figure 3. The two irradiances with a difference in the location of the weather observation point have different units, the Jeonju Weather Station irradiance (MJ/m2) and the Jeonju Vision University Innovation Hall SPV Power Plant irradiance (W/m2), respectively. If this is drawn as two generation-irradiance scatter plots based on the generation amount of the non-generation SPV power plant, it can be seen as Figure 4.

It can be seen that the Pearson correlation coefficient of the Jeonju Meteorological Observatory, which has a location different from the power plant, shows a similar value to the accumulation of the Pearson correlation coefficient of the Dangjin SPV generation-Seosan irradiance derived in Table 3, and the SPV insolation of the Jeonju Vision University Innovation Center-Pearson correlation of the power plant. The coefficient is 0.99, which is close to 1, and it is confirmed that it has strong linearity. That is, the factor that has the greatest influence on the correlation between power generation-irradiance data is determined by the difference in distance between the SPV power plant and the weather station.

In addition, the difference in dispersibility was visually compared in Figure 4. First of all, since the unit of irradiance in Jeonju Vision University is $W/m^2$, the unit of insolation of the Korea Meteorological Administration is unified as MJ/m${}^2$ and visualized as a single scatter plot, a clear difference can be seen. When

Table 4. Pearson correlation coefficients of location difference irradiance and SPV power amount.

Irradiance	Jeonju Meteorological Station	Vision College Irradiance Data
Coefficient	0.92	0.99

and Figure 4 are confirmed, the difference in the generation-irradiance Pearson correlation coefficient affects the predicted value on the generation amount when data from a weather station with a difference in distance from the power plant is used when predicting the amount of solar power generation. When the deep learning model is trained, the distribution on the left of Figure 4 is the range of the predicted value of generation when insolation with a difference in distance from the power plant is used, and the distribution on the right of Figure 4 is the range of the predicted value of the generation when the insolation of the power plant is utilized.

2.4. A Study through the Scatter Plot of Total Cloudiness and Solar Insolation

The difference between comparing the data of the Jeonju power plant with the generation amount obtained by obtaining its own irradiance data within the SPV power plant and comparing it with the data from an observatory located at a distance of 4.25 km shows how much irradiance affects the prediction of the generation amount. It is clear that the distribution of solar radiation is scattered with respect to the amount of power generation. It can be seen that the reason why insolation that affects power generation is not precise is that it creates regional differences in irradiance due to the influence of climate and topography even though it is a relatively short distance of 4 km. However, there is no significant difference in insolation because there is a spatial similarity in which the difference between latitude and longitude is not large. Therefore, what is the factor that makes similar insolation into different irradiance due to the characteristics of climate and topography? Clouds block the sunlight in the air. That is, in places with similar latitude and longitude, the difference in total cloudiness according to climate and topography makes the difference in irradiance.

The Total Amount of Cloud provided by the weather station is divided into “TAC 10 steps” for forecasting. A low level indicates sunny and a high level indicates cloudy due to lots of clouds. In the data set including the observation data provided in this way, insolation, which calculated the number of similar clouds step by step, and the measured irradiance were compared and divided into 5 groups. Total cloudiness levels 0–2 are group 1, total cloudiness levels 3–4 are group 2, total cloudiness levels 5–6 are group 3, total cloudiness levels 7–8 are group 4, total cloudiness levels 9–10 are group 5 to visualize the relationship between irradiance and power generation according to the irradiance measurement location.

The upper part in Figure 5 shows the distribution of irradiance at the weather station for the non-generation SPV plant according to five groups of total cloudiness. In TAC group 1, the degree of dispersion is not severe, but it can be seen that TAC groups 3 and 4 show very severe dispersion. Furthermore, regardless of the TAC group, when the irradiance is small, the degree of dispersion is not severe, but when the irradiance is high, it tends to be very severe. The reason for the low irradiance is that the amount of power generation is small in the early morning and late afternoon hours, so there is little volatility. TAC groups 4 and 5 have a very low distribution of irradiance due to the number of heavy clouds, and when looking at the location of the data points in the scatter plot, errors that are illogical data such as data in the lower right direction are also seen, indicating that the error of the data is the most severe.

On the other hand, the lower part shows the self-irradiance distribution for the non-generation SPV plant. Although the degree of data dispersion is low and the irradiance is high, the dispersion of power generation is not large and shows a relatively linear distribution. In particular, compared to the graph above, TAC groups 4 and 5 also show a very linear relationship, and there is no illogical data distribution throughout. In particular, the data from TAC group 1 has several values of irradiance with respect to the amount of power generation, because the 1-hour interval data clearly shows the relationship of 15${}^{\circ }$/h in the altitude of the sun proving that the irradiance in the weather is almost, only variable that determines the amount of power generation.

The points where the irradiance of the weather station was lower than the irradiance of the non-band are confirmed in the scatterplots of total cloudiness groups 1, 3, and 5. In particular, when the power generation is about 30 kW, the irradiance of the meteorological station is confirmed to be about 0 MJ/m${}^2$. This difference seems to have occurred because the insolation value of the power plant and the meteorological observatory with a difference in the distance caused a large difference in the insolation value due to an instantaneous change in the total amount of cloud cover. Therefore, when predicting the amount of solar power generation, when data from a weather station with a difference in distance from the power plant is used, the above difference acts as a factor lowering the accuracy of the generation forecast.

In the end, predicting the difference in the total amount of clouds at the SPV power plant far from the observatory based on the station’s starting point weather forecast is a way to accurately predict the irradiance affecting the SPV power plant. Moreover, it can be seen that when the irradiance is large, the effect of temperature also increases, having a complex effect on the amount of power generation. Through this correlation, it can be seen that the prediction of irradiance is an important variable that can determine the amount of power generation. Usually, meteorological stations do not predict irradiance but forecast total cloudiness and temperature. Therefore, it is urgently necessary to predict irradiance based on the weather forecast.

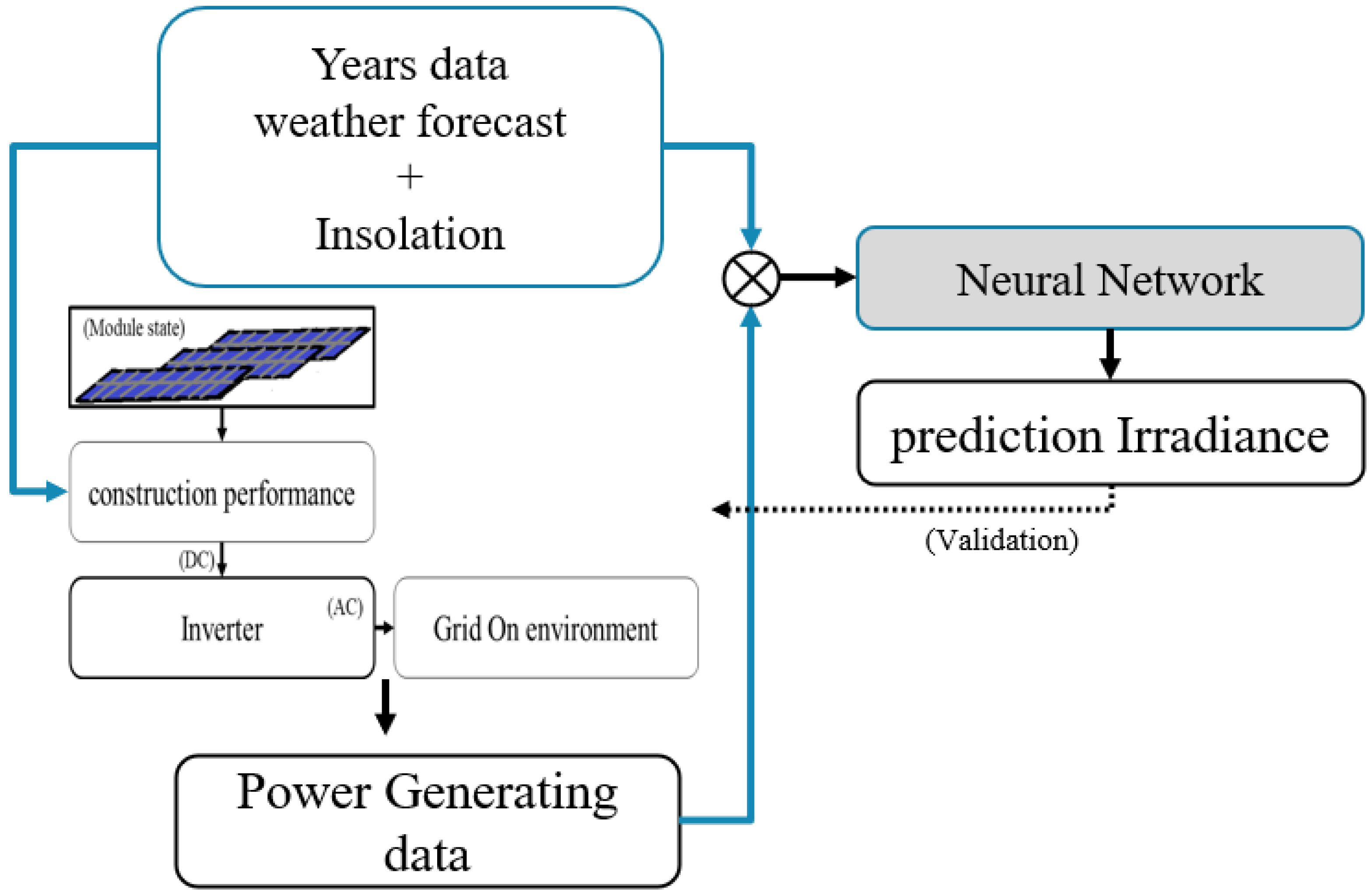
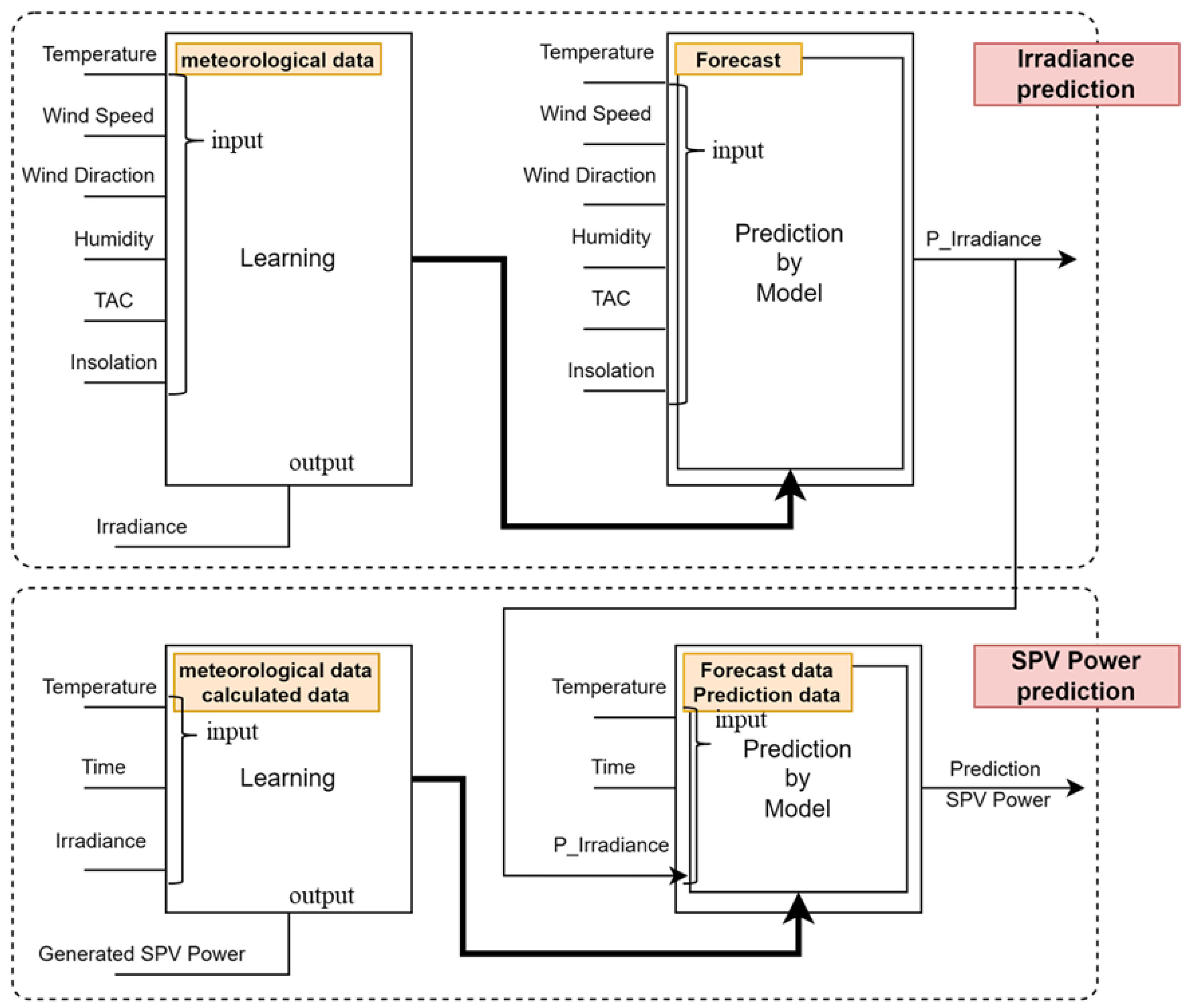
3. Irradiance Prediction Model to Get Directly above at an SPV Power Plant

The station’s starting point weather forecast is released 8 h before 00:00 on 24 sets of 5 indicators from 00:00 to 23:00 the next day in 1-hour increments. It is necessary to predict the irradiance of the day by inputting the insolation of the day that can be calculated through this data and the location information of the SPV power plant. Since the Korea Meteorological Administration does not predict irradiance, it does not directly predict the amount of SPV generation using the weather forecast, but first predicts the irradiance near the SPV power plant and uses it as the input irradiance for predicting the amount of power generation in the SPV power plant prediction model as shown in Figure 6.

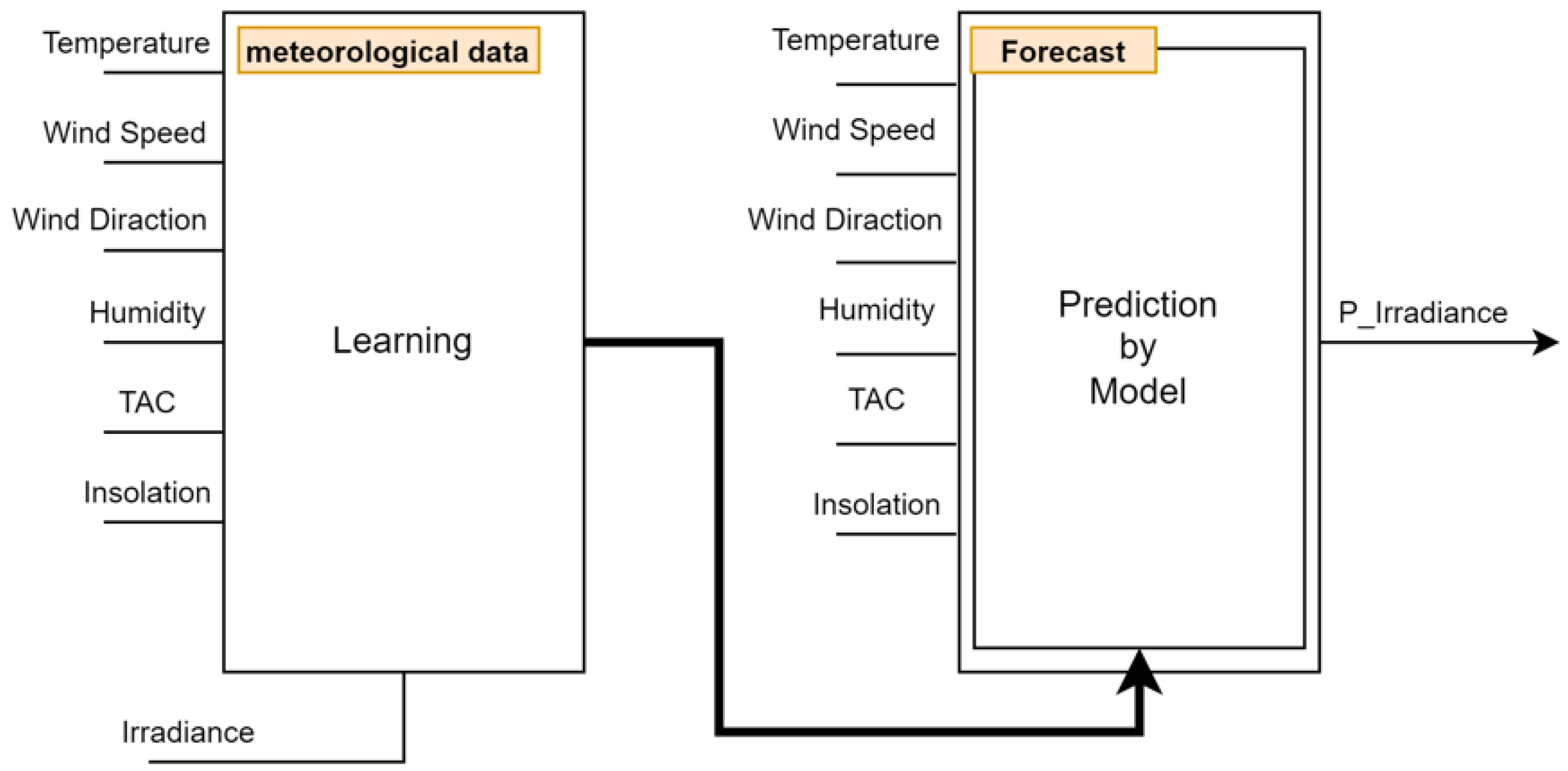
In order to make a model for predicting irradiance, the training data was obtained from multi-year past data provided by the weather station. In this paper, data from Seosan Meteorological Observatory and Jeonju Meteorological Observatory were obtained and utilized. Past weather observation data contains irradiance data observed by date and time. A data set using this observed irradiance as the correct answer output was trained through deep learning.

The neural network structure consists of 6 dense layers having 256 nodes in each layer, with 448, 8320, 33024, 32896, 8256, 1040, and 17 variables for each layer. The structure used for calculation was used. The ReLU function was used as the activation function.

Table 5. Deep layer neural network structure to make an irradiance prediction model.

Layer (Type)	Output Shape	Param #	Activation_Function
dense (Dense)	(None, 64)	448	’relu’
dense_1 (Dense)	(None, 128)	8320	’relu’
dense_2 (Dense)	(None, 256)	33024	’relu’
dense_3 (Dense)	(None, 128)	32896	’relu’
dense_4 (Dense)	(None, 64)	8256	’relu’
dense_5 (Dense)	(None, 16)	1040	’relu’
dense_6 (Dense)	(None, 1)	17	-

shows a summarized view of the network architecture used for predicting irradiance.

MSE (Mean Squared Error) has been used as the loss function. For optimization, Adam has been used as the optimizer setting the batch size as 16, with 110 epochs. The parameter selection method was rather experiential. If epoch 250 exceeded that saw an overfitting. Thus, we determined the end of epoch number to epoch 250. Furthermore, batch size 30 reason got good effect two-days interval setting than one-day or three-days. Moreover, early stopping and hyper-parameter tuning was performed in order to validate our findings.

It has been explained above that the weather data of the meteorological station cannot be the same as that of the SPV power plant. However, it should be recalled that the station data is the only one that most closely resembles the weather of the SPV power plant. Therefore, it is to predict the weather of the SPV power plant through the weather information of the observatory. However, the meteorological information of the power plant can be attached here. If the irradiance observed from the power plant is input instead of the weather station data and learned, the irradiance of the power plant will be predicted more precisely.

In addition, in the process of modeling the characteristics of the SPV power plant, which will be described next, the relationship between the SPV power plant and the observed irradiance is modeled through a learning structure that uses the past irradiance data as input.

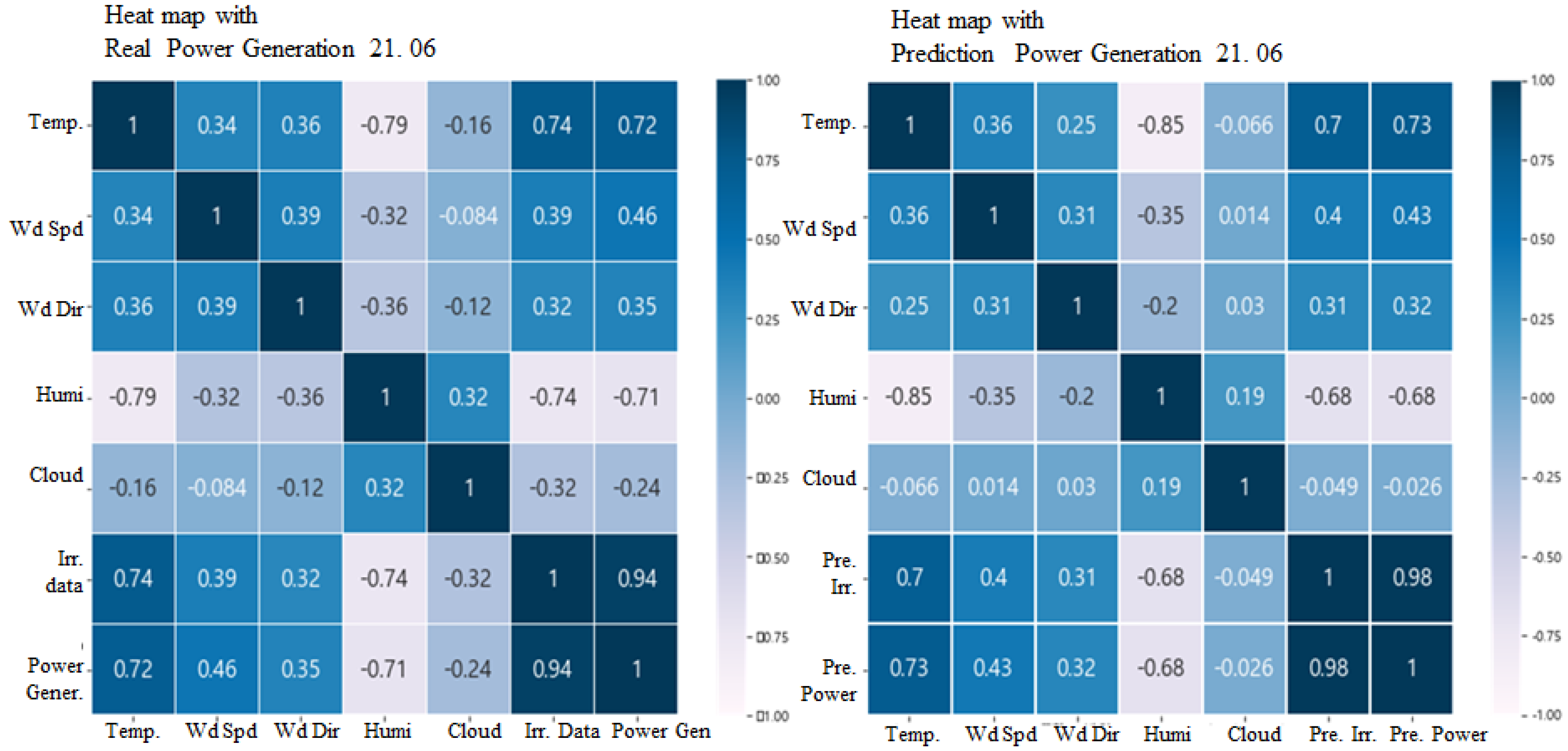
If the past irradiance data used at this time is the standard of the meteorological station, the insolation amount of the station is consistently related to the generation amount of the SPV power plant. Then, when predicting the amount of power generation, the wind direction, wind speed, temperature and humidity affect the power generation prediction model, not the irradiance and total cloud volume. To confirm this correlation, the Pearson correlation coefficient between the predicted power generation and the input data was confirmed using the test evaluation data. The correlation between the actual power generation and the total amount of clouds observed was −0.24 as shown in the first heatmap of Figure 7, but the correlation coefficient between the amount of power generated and the total amount of clouds predicted by the meteorological observation data of the same period was −0.026 as shown in the second heatmap of Figure 7. Overall, the correlation coefficients of temperature, wind speed, wind direction, and humidity with respect to total cloudiness decreased at very large ratios of −0.066, 0.014, 0.03, and 0.19. Above all, the correlation coefficient between total cloudiness and predicted irradiance was very small at −0.049.

The correlation coefficient of irradiance, which affects the amount of power generation, is relatively high. These results are reflected in the predicted irradiance because the factors of total cloudiness are already deeply involved. When only meteorological observation data were analyzed, total cloudiness and irradiance had a greater negative correlation than other factors. As previously analyzed, since the effect on irradiance is different for each stage of total cloudiness, it can be seen that there is a great correlation considering that all stages of total cloudiness are correlated with a comprehensive judgment. On the other hand, in the correlation analysis using predictive data, the correlation is very low, showing that the predictive model has already reflected the effect or the influence of the total amount of cloudiness when generating the forecast data.

In other words, the irradiance prediction method proposed by us proves that it is a power generation forecasting method that overcomes the difference in the total amount of cloud due to geographical and topographical influences. As a result of learning through the model constructed in this way, the following graph was obtained by comparing the irradiance of Seosan with the data observed at the Seosan Meteorological Observatory. The weather information used to predict the irradiance was based on the forecast data of the Seosan Meteorological Observatory and was predicted based on the actual forecast data.

In Figure 8, the horizontal axis represents the number of data. 24 data per day were displayed for 60 days. The vertical axis is the irradiance magnitude. Predicted data are indicated by dotted lines. As shown in the graph, it can be confirmed that the predicted data and the observed data have similar values. However, the reason that the prediction between data 648 and data 696 differs greatly from the observation is that there was an error in the forecasted weather information.

4. Power Generation Forecasting Model

The size of the power generation is linked to the change in temperature and the size of irradiance determined by insolation and total cloud as shown in Figure 9. The previously predicted irradiance reflects this correlation and reflects the location information of the SPV power plant and changes in the weather due to topography and geographic factors. Now, we want to make a model that can predict the amount of power generation for the characteristics of the power plant.

The method proposed in this paper points out that the size of irradiance is not sophisticated when the location of the SPV power plant and the location of the meteorological station do not match.

Likewise, it is difficult to reflect the various characteristics of the power plant in detail, but the structure of the array, which is the core of the DC power generation part of the SPV system, the change of the inclination angle, the composition of the string composing the array, and the characteristics of the module implementing the string are all understood and connected. There are many things to consider, such as the proficiency of wires and the condition of connectors. The characteristics of SPV power plants are also sensitive to changes in electrical characteristics such as ground resistance and insolation resistance. Moreover, there are many non-linearities in how to gradually reflect the aging of SPV facilities over time. The characteristics of not only the DC part but also the AC part are very complex, and larger changes should be taken into account when considering the grid connection.

For this reason, it is difficult to implement a numerical model that functions as an input/output relational expression for an SPV power plant. Therefore, we constructed a data set with power generation data, irradiance, temperature, and time as variables, and implemented a power generation model by implementing and learning a deep neural network based on the configured data. The used neural network consists of a total of 7 network layers, and each layer is designed to have a maximum of 256 nodes and a minimum of 16 nodes. If each layer was configured in the form of a fully connected configuration, the relu function was used as the activation function.

Table 6. Deep layer neural network structure to make an SPV Power Plant model.

Layer (Type)	Output Shape	Param #	Activation_Function
dense (Dense)	(None, 64)	256	’relu’
dense_1 (Dense)	(None, 128)	8320	’relu’
dense_2 (Dense)	(None, 256)	33024	’relu’
dense_3 (Dense)	(None, 128)	32896	’relu’
dense_4 (Dense)	(None, 64)	8256	’relu’
dense_5 (Dense)	(None, 16)	1040	’relu’
dense_6 (Dense)	(None, 1)	17	-

summarizes the neural network architecture.

The difference from irradiance prediction is that there are 8 models from sequential 0 to sequential 7 because each model for the time group is created. In the deep learning architecture, the loss function used is the MSE (Mean Squared Error), and for optimizing the network, the Adam optimizer algorithm was applied, setting the input batch size to 30 and 250 epochs.

The SPV power generation prediction model, that is, the SPV Plant model, obtained by learning the deep neural network structure constructed in this way, predicts the power generation amount based on the input data composed of the previously predicted irradiance prediction amount and temperature and time information.

The data set for learning in Figure 10 was prepared so that the input and output can be compared and the error can be updated by the backpropagation method based on the labeled weather observation data and the generation data having the structure of the input data and the output data. Prediction of power generation was made at two-hour intervals, and for the efficiency and speed of calculation, it was configured to learn and predict data from 5 to 20:00 in 24 h.

5. Predictive Test Results through the Generated Model

5.1. If There Is no Irradiance Data in the SPV Power Plant

The SPV power plant in Seosan does not have its own irradiance measurement equipment. Therefore, when constructing an irradiance prediction model for power generation prediction, meteorological data from the nearest Seosan Meteorological Observatory was used. The distance between the observatory and the power plant is about 31 km in a straight line.

The irradiance was first predicted by the process suggested in Figure 10. The calculated Insolation was derived based on the location of the power plant. The data of the Dangjin SPV power plant in Seosan used for modeling is the data having 24 data sets at one-hour intervals during the period from August 2018 to November 2020. A total of 14.274 data sets were used, excluding data from 20:00 pm to 5 am the next day, when the insolation was 0. Of these, 11.883 sets were used for training and 1424 sets were used for validation. After that, 967 data sets with valid irradiance among 62 days of data from 20 December to 21 January, were used for the test. The data tested after creating a model through deep learning is shown as a graph in Figure 11.

Comparing the predicted generation and the actual generation in this period, the maximum value of the actual generation within the period is 787. The average of the errors between the actual and predicted quantities in the same period was 21.48, but since the comparison of the two values had errors in the negative as well as in the positive direction, the RMS was 74.96 and the standard deviation was about 71.82. The maximum value of the actual power generation during the period was 787, and it was confirmed that the size of the deviation was about 10% when the maximum power generation of the power plant was viewed as the power plant capacity.

5.2. If There Is Irradiance Data in the SPV Power Plant

Jeonju Bidae SPV power plant is equipped with its own irradiance measurement equipment, so you can check the size of irradiance along with power generation data.

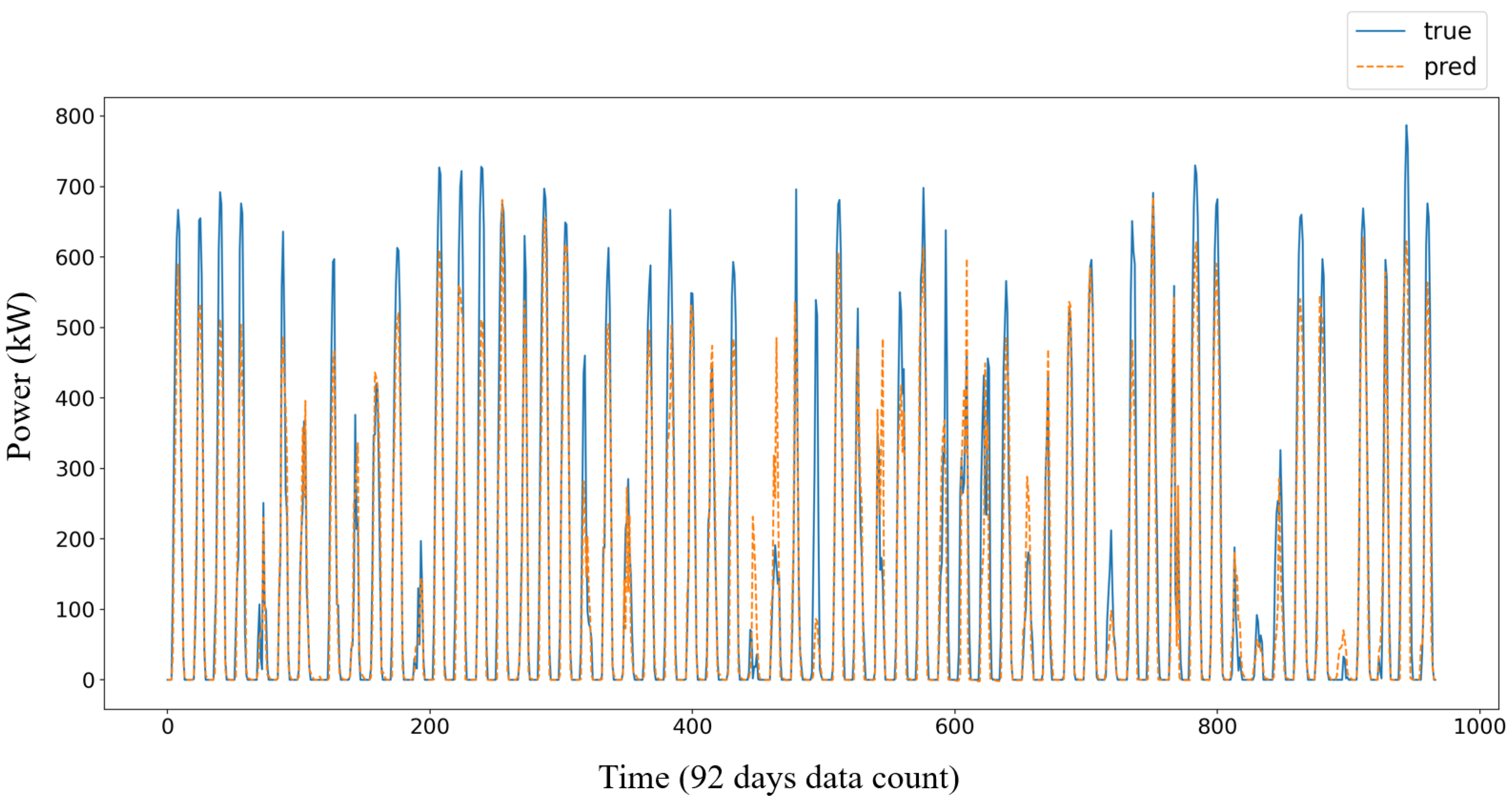
Therefore, these data were used when constructing an irradiance prediction model for power generation prediction. The irradiance was first predicted by the process suggested in Figure 10. The calculated Insolation was derived based on the location of the power plant. The data of the Jeonju non-unit SPV power plant used for modeling is having 24 data sets with one-hour intervals for one day, from January 2018 to June 2020. A total of 7829 data sets were used, excluding the data from 20:00 p.m. to 5 a.m. the next day when the insolation is 0 among these data sets. Of these, 6329 sets were used for training and 553 sets were used for validation. After that, 947 data sets with valid irradiance among 92-day data from October, 20, to December, 20 were used for the test. The data tested after creating a model through deep learning is shown as a graph in Figure 12.

Comparing the predicted generation and the actual generation in this period, the maximum value of the actual generation within the period is 787. The average of the error between the actual quantity and the predicted quantity for the same period was 1.99, but since the comparison of the two values had errors in the negative as well as in the positive direction, the RMS was 7.17 and the standard deviation was about 6.88. The maximum value of the actual power generation during the period was 78.59, and it was confirmed that the size of the deviation was about 9% when the maximum power generation of the power plant was viewed as the power plant capacity. The deviation of the error from the prediction of Seosan was similar.

Therefore, these data were used when constructing an irradiance prediction model for power generation prediction. The irradiance was first predicted by the process suggested in Figure 10. The calculated Insolation was derived based on the location of the power plant. The data of the Jeonju non-unit SPV power plant used for modeling is data having 24 data sets with one-hour intervals for one day from January 2018 to June 2020. A total of 7829 data sets were used, excluding the data from 20:00 p.m. to 5 a.m. the next day when the insolation is 0 among these data sets. Of these, 6329 sets were used for training and 553 sets were used for validation. After that, 947 data sets with valid irradiance among 92-day data from October, 20, to December, 20 were used for the test. The data tested after creating a model through deep learning are shown as a graph in Figure 12.

Comparing the predicted generation and the actual generation in this period, the maximum value of the actual generation within the period is 787. The average of the error between the actual quantity and the predicted quantity for the same period was 1.99, but since the comparison of the two values had errors in the negative as well as the positive direction, the RMS was 7.17 and the standard deviation was about 6.88. The maximum value of the actual power generation during the period was 78.59, and it was confirmed that the size of the deviation was about 9% when the maximum power generation of the power plant was viewed as the power plant capacity. The deviation of the error from the prediction of Seosan was similar. This can be summarized in

Table 7. Evaluation index value which is prediction model performance with test data.

Error: Real Value—Error Value	Seosan: No Own Irradiance Data	Jeonju: Own Irradiance Data Available
The maximum real value within the times	787	78.59
Error mean within the times	21.48	1.99
Error RMS within the times	74.96	7.17
Standard deviation of error within the times	71.82	6.88
Ratio to Maximum of Deviation	9.12 %	8.75 %

. We also have compared the relationship between various weather variables and power generation through heatmap in Figure 7.

Comparing the above two cases, the prediction method predicts irradiance, and the method of predicting the amount of generation using the predicted irradiance has a device that can measure irradiance in the power plant and has data and the generation amount prediction for the power plant that does not. It was confirmed that there was no significant difference. Although the difference was not large, there is a device that can measure irradiance relatively, so the SPV power plant with the data is advantageous for predicting power generation. It has also been shown that it is possible to create a model that predicts the magnitude of irradiance.

The Neural network predicted result total mean MAPE(%) checked 12.94% in Table 3 of the paper [22]. This result is more than high in our ratio to maximum of deviation in Table 7. As a result, We improve to get the result using proposed network.

6. Conclusions

In this paper, the correlation between the amount of electricity generated and the weather variables for the selection of model variables for the generation of solar power plants, the relationship between various weather variables and the amount of generation was confirmed with heatmaps and scatter plots, and the characteristics between each data were identified. In addition, when there is a difference in the distance between the solar power plant and the weather station, the difference between the amount of power generation and the amount of insolation is confirmed, and the effect of the amount of total cloud on the prediction of irradiance is confirmed, showing that information on total amount of cloud is essential for irradiance prediction.

Through this correlation study, the main input variables necessary to establish the model required for power generation prediction are derived, and the amount of input and calculation of the neural network model is reduced to streamline the hidden layer stage and the basis for establishing a power generation prediction model capable of fast and accurate prediction has been prepared. In addition, it was shown that the effect on estimation accuracy was very large when meteorological data with different distances were used for estimating the amount of electricity generated by solar power plants. Through these results, when data from a weather station near a power plant is used for power generation prediction or diagnosis in a place that does not have a device that can measure irradiance in the power plant, additional security for the distance between the power plant and the observatory can be achieved using a deep neural network method. It was also shown that it is possible through the double prediction model to which the learning method is applied. In the future, it is expected that it can serve as a basis for expanding the irradiance prediction method to predict the amount of power generation for new power plants that do not have or lack data other than the method that utilizes the data of the power plant.