A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications
Abstract
1. Introduction
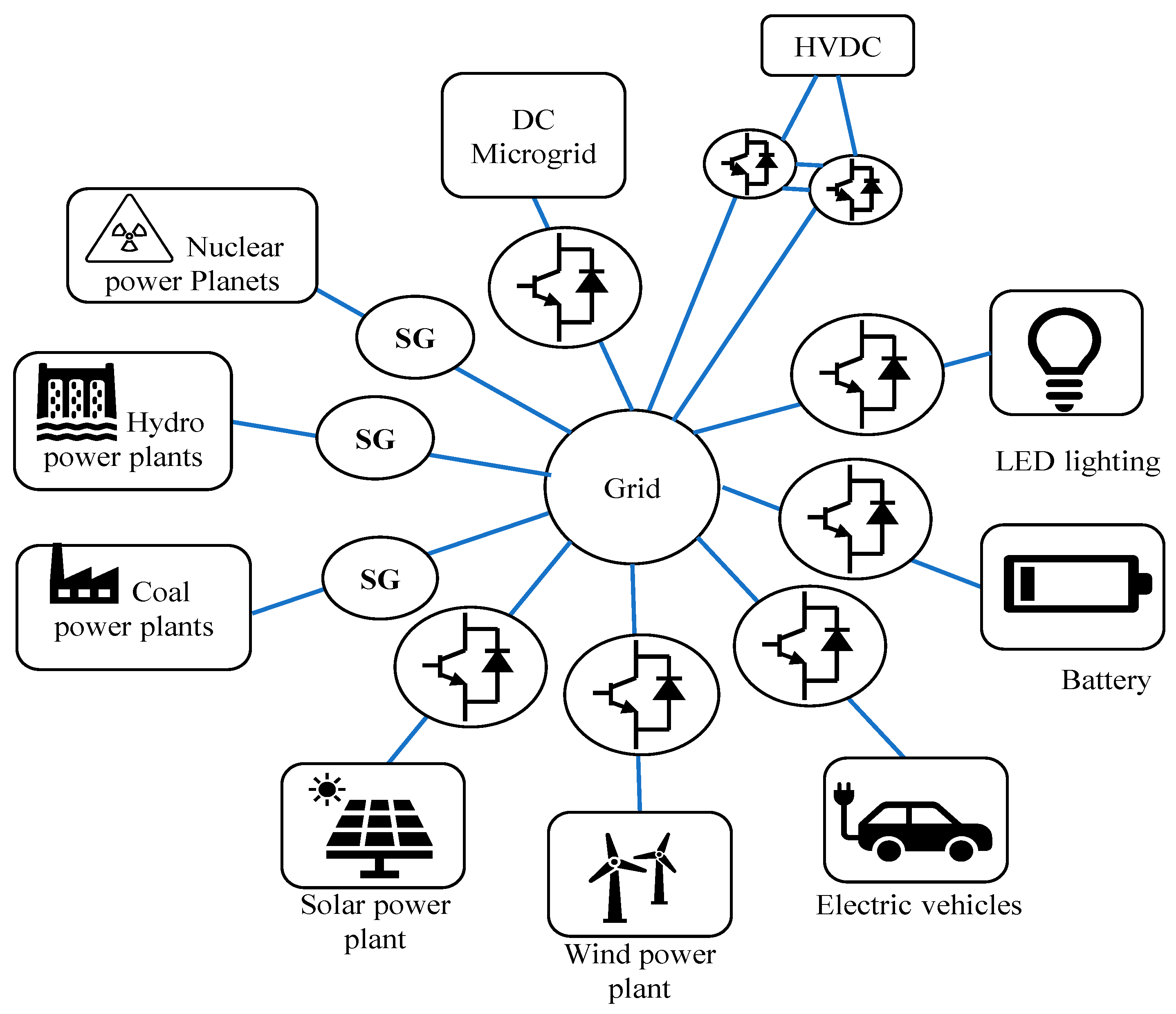
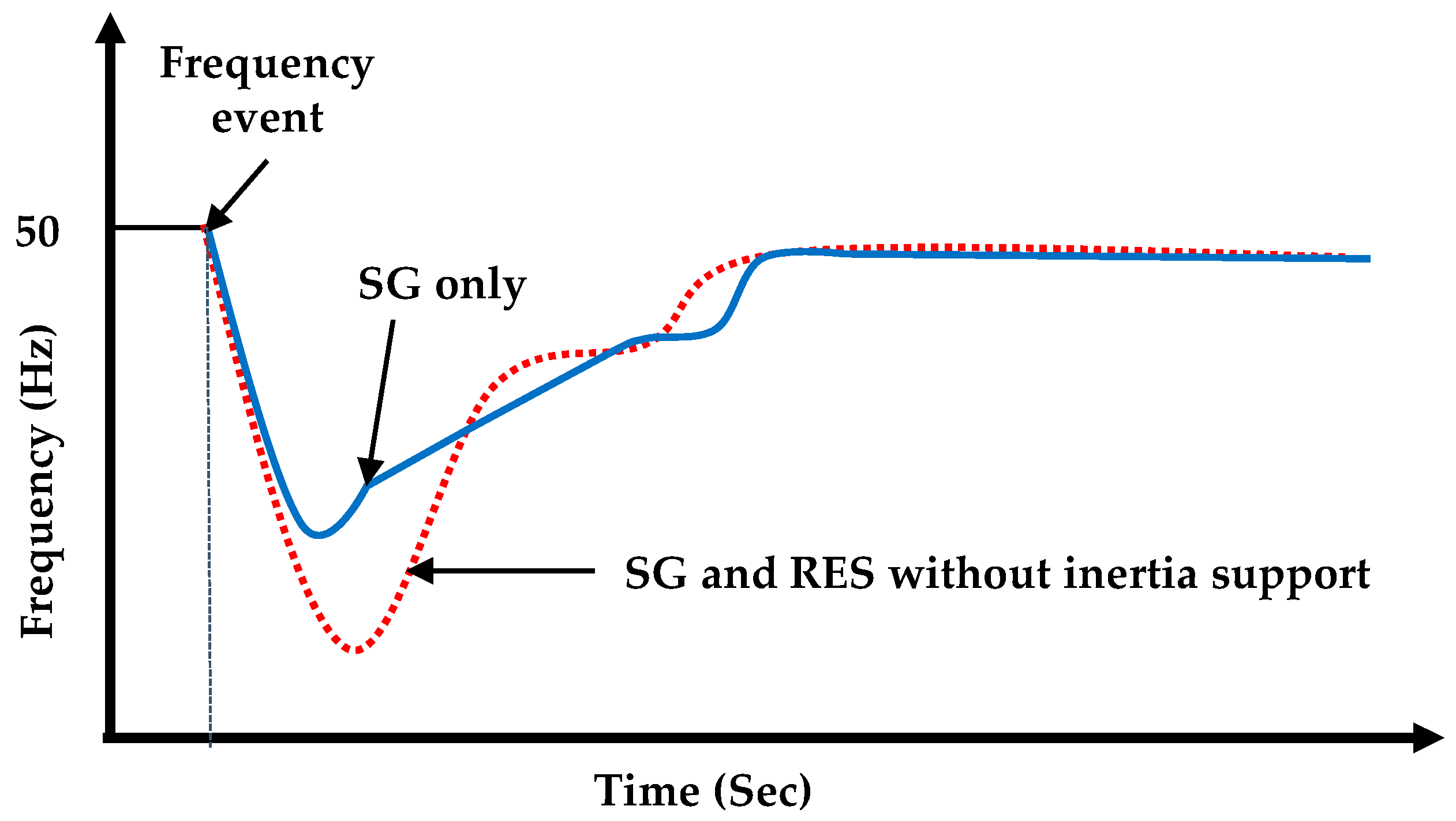
- Traditional power electronics control approaches of dc–ac converters have quick dynamics. However, the synchronous machine (SM) has slow dynamics and significant inertia. At a substantial distributed energy resources (DER) penetration, the grid’s equivalent rotational inertia will greatly decrease. The frequency stability will suffer as a result of this [5].
- The intermittent power supplied by DERs will be quickly provided to the grid using the fast-response feature of dc–ac converters. Instability in frequency, angle, and voltage will result from these interactions [16]. Similarly, large-size dc microgrids and parallel inverters are challenging to explore, particularly when the DERs and DC-ACconverters have comparable dynamics. DERs, on the other hand, are normally controlled by maximum power point tracking (MPPT) and hence are not dispatchable. As a result, these DC-ACconverters are unable to offer sufficient up-reserve to sustain grid frequency [16,17].
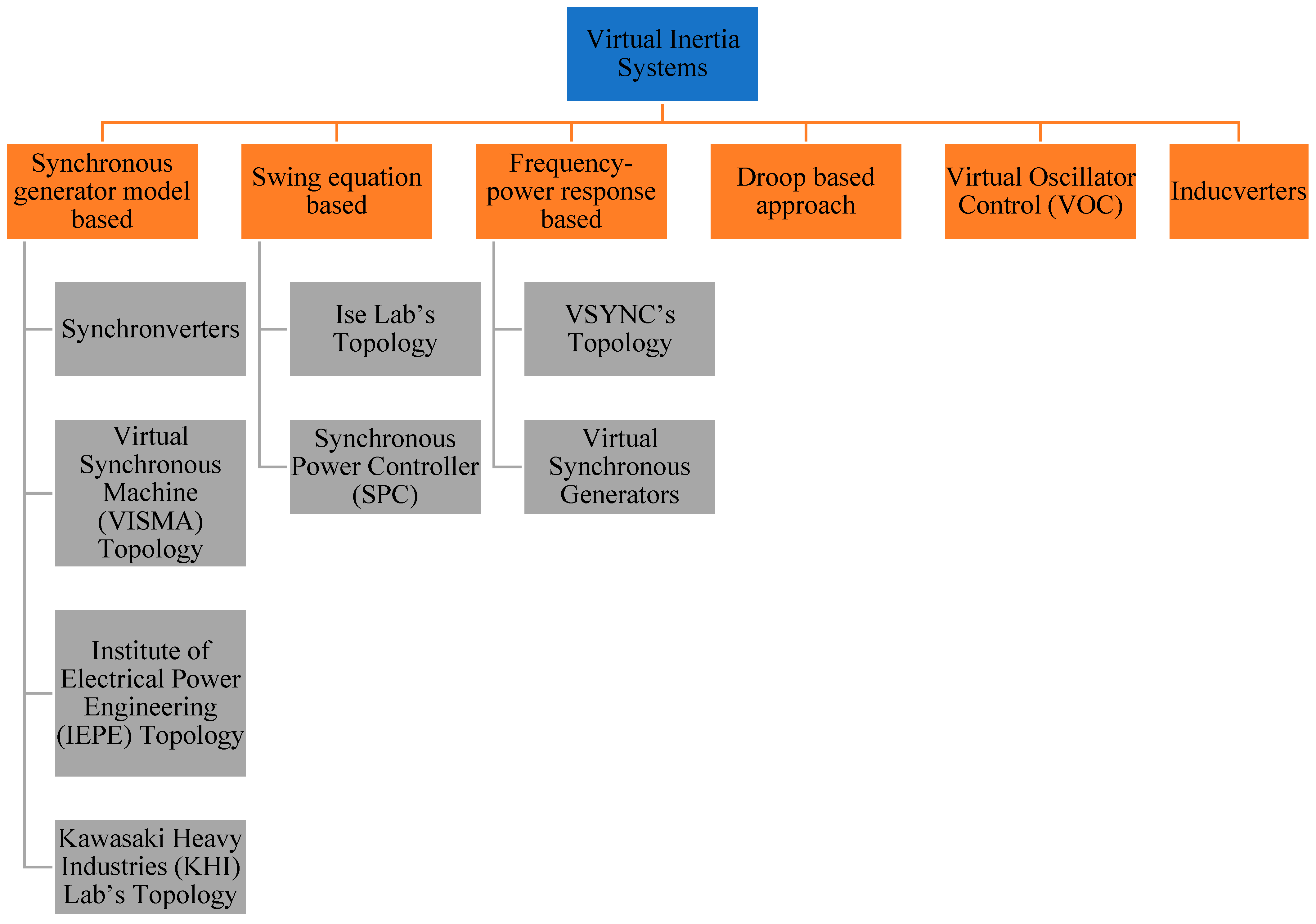
2. Current Virtual Inertia Topologies
2.1. Topology Based on Synchronous Generator Model
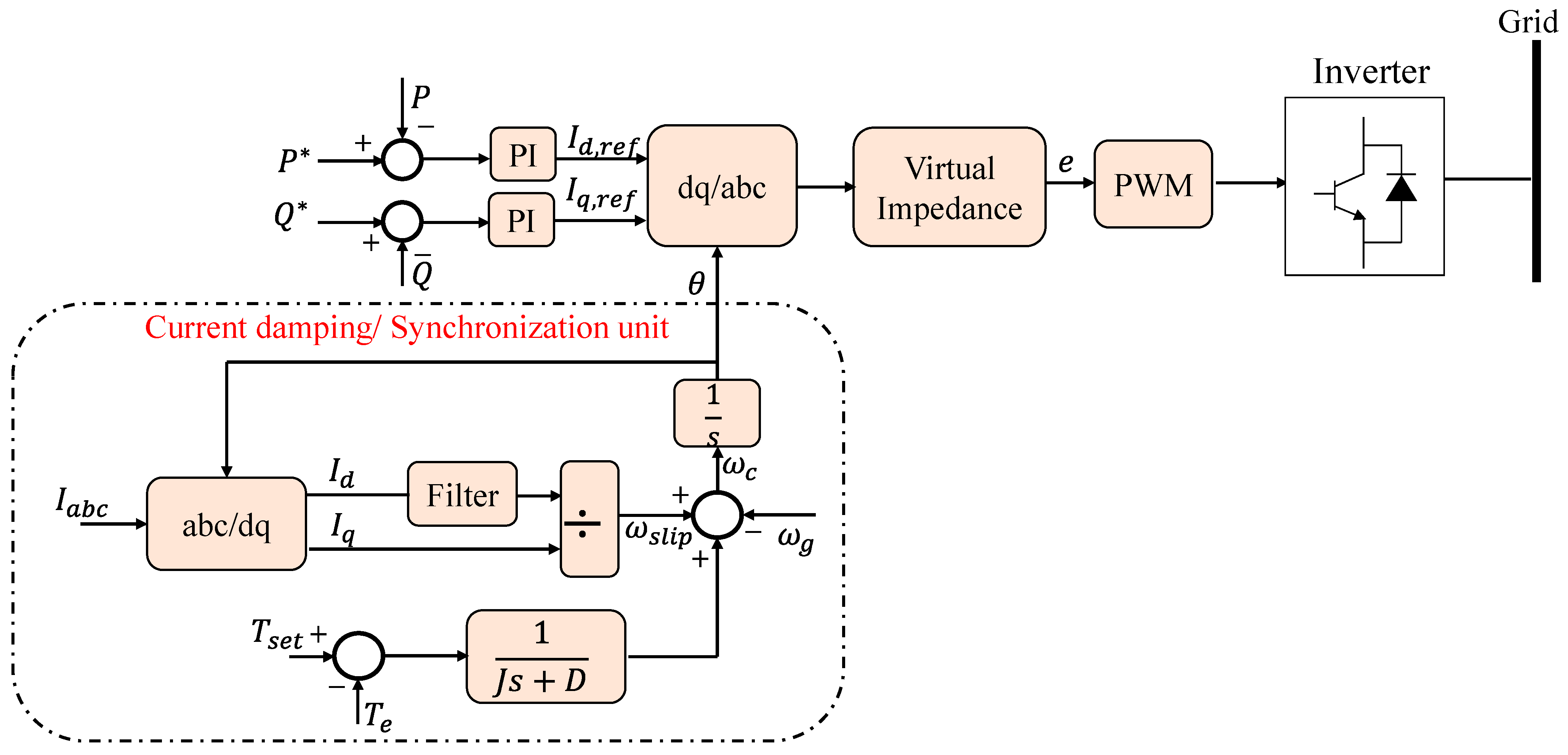
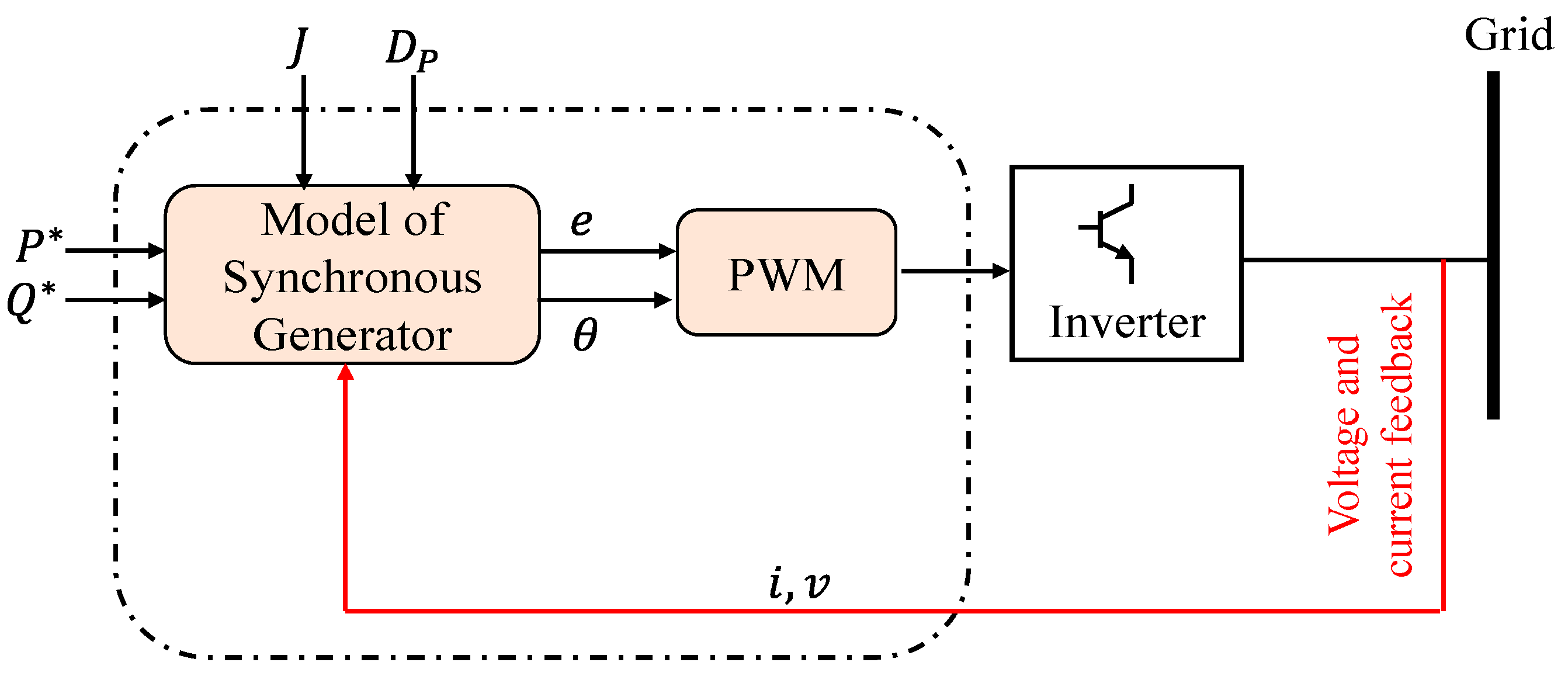
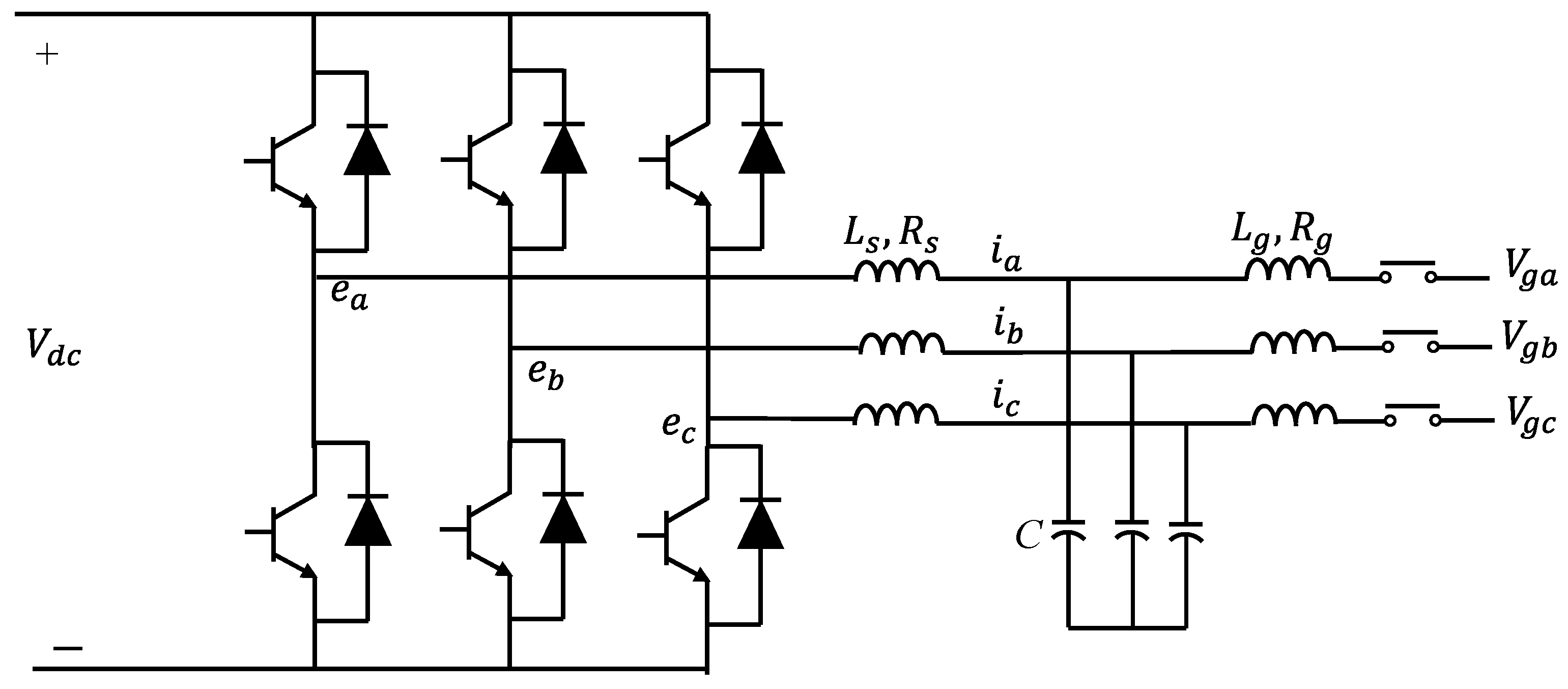
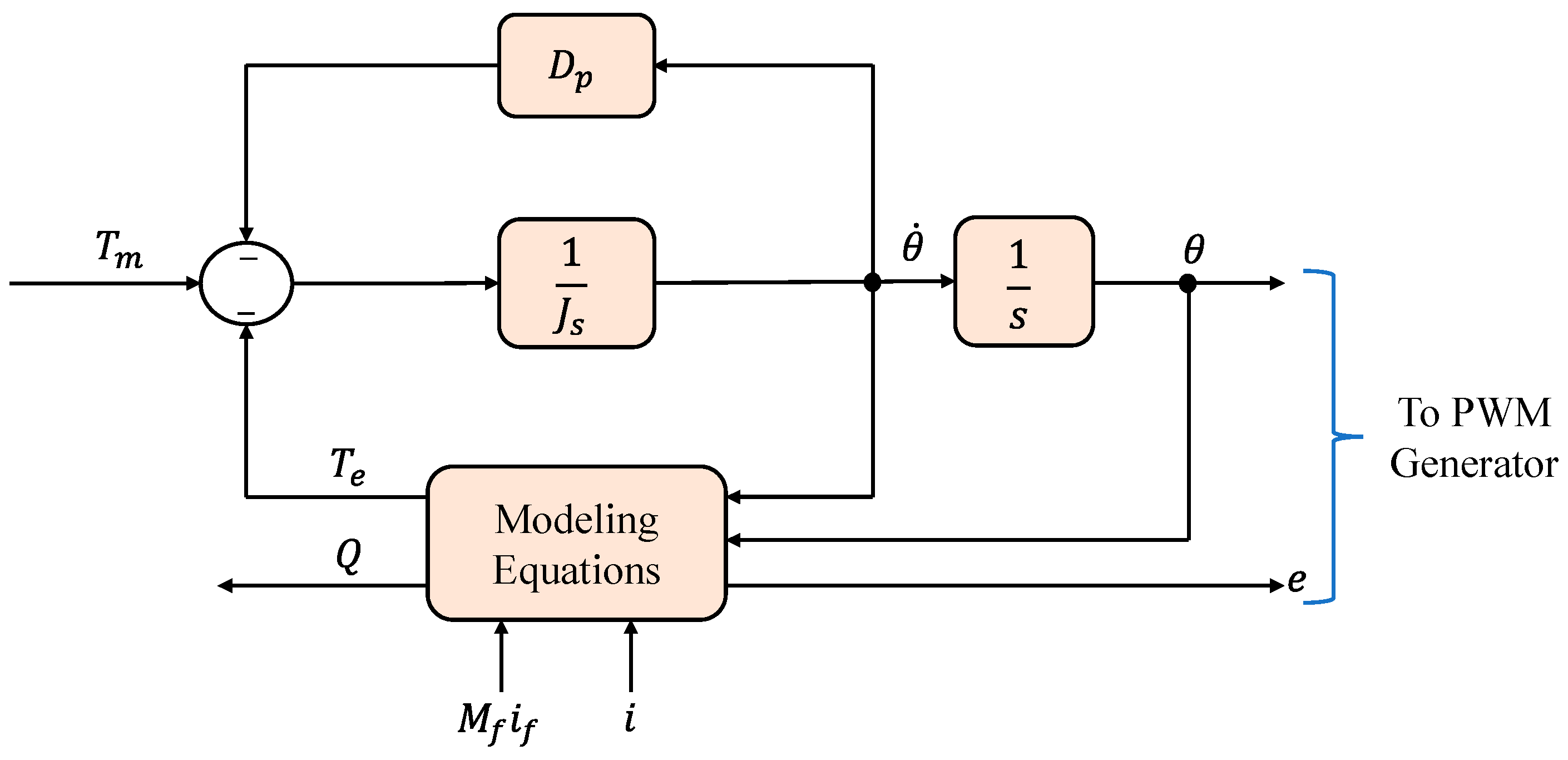
2.1.1. Synchronverters
2.1.2. Kawasaki Heavy Industries (KHI)
2.1.3. VISMA and IEPE Topologies
2.2. A Swing Equation-Based Topology
2.2.1. Ise Lab’s Topology
2.2.2. Synchronous Power Controller (SPC)
2.3. Inducverters
2.4. Virtual Oscillator Control (VOC)
2.5. Frequency–Power Response-Based Topologies
Virtual-Synchronous Generators (VSG)
2.6. Droop-Based Approaches
3. Virtual-Synchronous Generator (VSG) Principles and Control Orders
3.1. VSM Model with High Order
3.2. Model of Low-Order VSM
4. VSG Operation Control
4.1. Active and Reactive Power Controls
4.2. Voltage and Frequency Control
5. Virtual Inertia (VI) Control Strategies
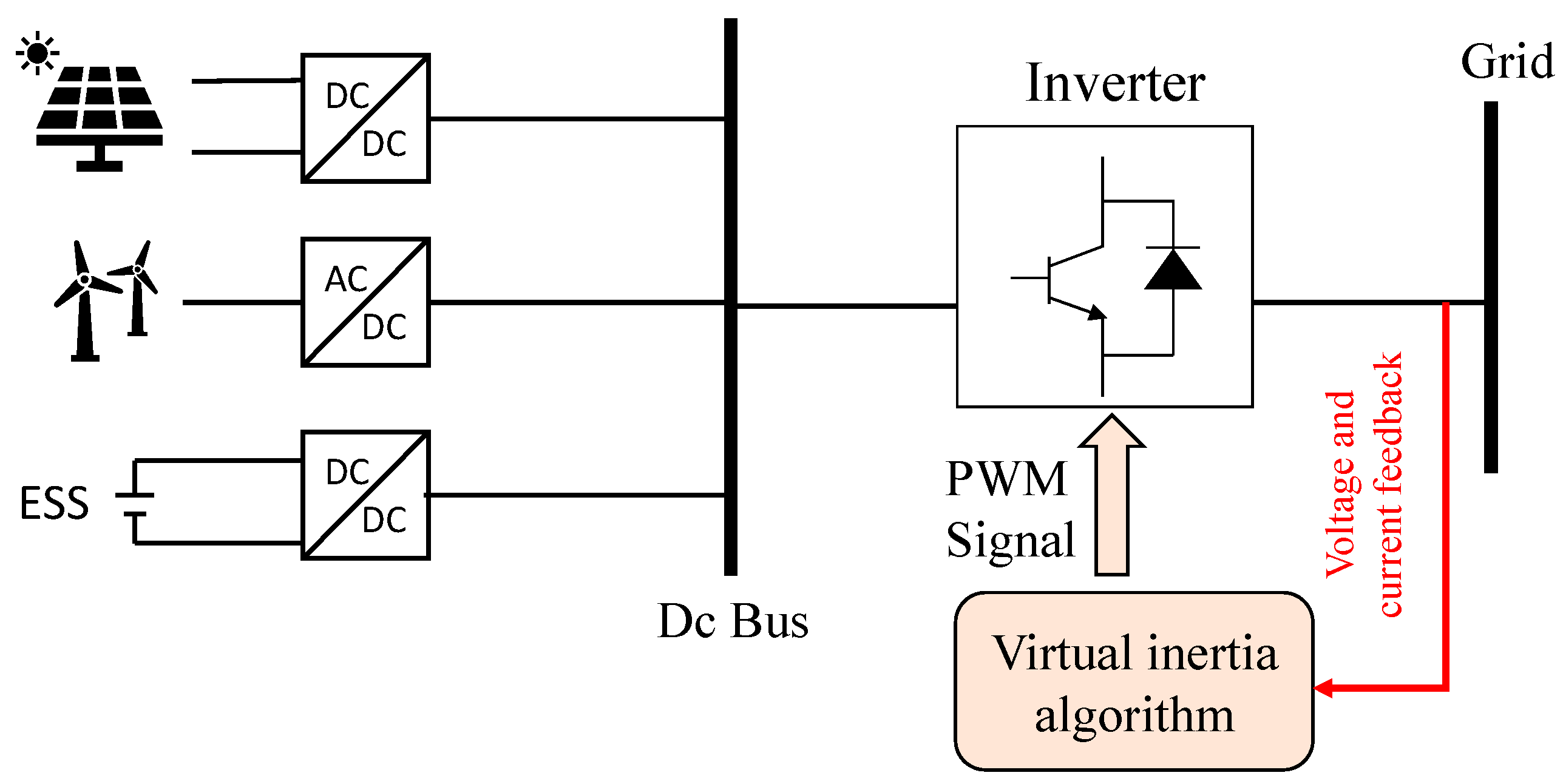
6. Energy Storage
7. Future Research Scope
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| AVR | Automatic voltage regulator |
| BESSs | Battery energy storage systems |
| DER | Distributed energy resources |
| DG | Distributed generation |
| ESS | Energy storage system |
| FM | Frequency modulation |
| GDC | Generalized droop control |
| HESS | Hybrid energy storage system |
| IEPE | Institute of Electrical Power Engineering |
| KHI | Kawasaki Heavy Industries |
| MPC | Model predictive control |
| MPPT | Maximum power point tracking |
| PCC | Point of common coupling |
| PLL | Phase-locked loop |
| PV | Photovoltaics |
| PWM | Pulse width modulation |
| RES | Renewable energy sources |
| ROCOF | Rate of change of frequency |
| SG | Synchronous generator |
| SM | Synchronous machine (SM) |
| SOC | State of charge |
| SPC | Synchronous power controller |
| TSO | Transmission system operators |
| VI | Virtual inertia |
| VSG | Virtual-synchronous generator |
| VSM | Virtual synchronous machine |
| VSMG | VSM-based microgrid |
| VOC | Virtual oscillator controller |
References
- REN22, R. Global Status Report, 2022. 2022. Available online: https://www.ren21.net/ (accessed on 21 October 2022).
- Edrah, M.; Lo, K.L.; Anaya-Lara, O. Impacts of high penetration of DFIG wind turbines on rotor angle stability of power systems. IEEE Trans. Sustain. Energy 2015, 6, 759–766. [Google Scholar] [CrossRef]
- Kahani, R.; Jamil, M.; Iqbal, M.T. Direct Model Reference Adaptive Control of a Boost Converter for Voltage Regulation in Microgrids. Energies 2022, 15, 5080. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Huang, A.Q. Integration of DC microgrids as virtual synchronous machines into the AC grid. IEEE Trans. Ind. Electron. 2017, 64, 7455–7466. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions-A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Hossain, M.J.; Blaabjerg, F. Evolution of microgrids with converter-interfaced generations: Challenges and opportunities. Int. J. Electr. Power Energy Syst. 2019, 109, 160–186. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R.; Ramachandaramurthy, V. A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 2015, 41, 1423–1436. [Google Scholar] [CrossRef]
- Bajaj, M.; Singh, A.K. Grid integrated renewable DG systems: A review of power quality challenges and state-of-the-art mitigation techniques. Int. J. Energy Res. 2020, 44, 26–69. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.-Y. Virtual inertia-based inverters for mitigating frequency instability in grid-connected renewable energy system: A review. Appl. Sci. 2019, 9, 5300. [Google Scholar] [CrossRef]
- Hartmann, B.; Vokony, I.; Táczi, I. Effects of decreasing synchronous inertia on power system dynamics—Overview of recent experiences and marketisation of services. Int. Trans. Electr. Energy Syst. 2019, 29, e12128. [Google Scholar] [CrossRef]
- Chown, G.; Wright, J.G.; Van Heerden, R.P.; Coker, M. System inertia and Rate of Change of Frequency (RoCoF) with increasing non-synchronous renewable energy penetration. In Proceedings of the 8th CIGRE Southern Africa Regional Conferenc, Cape Town, South Africa, 14-17 November 2017. [Google Scholar]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar]
- Mandal, R.; Chatterjee, K. Virtual inertia emulation and RoCoF control of a microgrid with high renewable power penetration. Electr. Power Syst. Res. 2021, 194, 107093. [Google Scholar] [CrossRef]
- Modi, N.; Yan, R. Low inertia power systems: Frequency response challenges and a possible solution. In Proceedings of the 2016 Australasian Universities Power Engineering Conference (AUPEC), Brisbane, Australia, 25–28 September 2016; pp. 1–6. [Google Scholar]
- Rahman, M.S.; Oo, A. Distributed multi-agent based coordinated power management and control strategy for microgrids with distributed energy resources. Energy Convers. Manag. 2017, 139, 20–32. [Google Scholar] [CrossRef]
- Rangu, S.K.; Lolla, P.R.; Dhenuvakonda, K.R.; Singh, A.R. Recent trends in power management strategies for optimal operation of distributed energy resources in microgrids: A comprehensive review. Int. J. Energy Res. 2020, 44, 9889–9911. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual inertia: Current trends and future directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Beck, H.-P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Rehman, H.U.; Yan, X.; Abdelbaky, M.A.; Jan, M.U.; Iqbal, S. An advanced virtual synchronous generator control technique for frequency regulation of grid-connected PV system. Int. J. Electr. Power Energy Syst. 2021, 125, 106440. [Google Scholar] [CrossRef]
- Tamrakar, U.; Galipeau, D.; Tonkoski, R.; Tamrakar, I. Improving transient stability of photovoltaic-hydro microgrids using virtual synchronous machines. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Serban, I.; Ion, C.P. Microgrid control based on a grid-forming inverter operating as virtual synchronous generator with enhanced dynamic response capability. Int. J. Electr. Power Energy Syst. 2017, 89, 94–105. [Google Scholar] [CrossRef]
- Cheema, K.M. A comprehensive review of virtual synchronous generator. Int. J. Electr. Power Energy Syst. 2020, 120, 106006. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Modelling, implementation, and assessment of virtual synchronous generator in power systems. J. Mod. Power Syst. Clean Energy 2020, 8, 399–411. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, L.; Chen, Q.; Zhou, K.; Hua, T. Multi-VSG-based frequency regulation for uninterruptible power AC micro-grid with distributed electric vehicles. Int. J. Electr. Power Energy Syst. 2022, 137, 107785. [Google Scholar] [CrossRef]
- Zhong, Q.-C. Virtual Synchronous Machines: A unified interface for grid integration. IEEE Power Electron. Mag. 2016, 3, 18–27. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2010, 58, 1259–1267. [Google Scholar] [CrossRef]
- Hirase, Y.; Abe, K.; Sugimoto, K.; Shindo, Y. A grid-connected inverter with virtual synchronous generator model of algebraic type. Electr. Eng. Jpn. 2013, 184, 10–21. [Google Scholar] [CrossRef]
- Ise, T.; Bevrani, H. Virtual synchronous generators and their applications in microgrids. In Integration of Distributed Energy Resources in Power Systems; Elsevier: Amsterdam, The Netherlands, 2016; pp. 282–294. [Google Scholar]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous power controller with flexible droop characteristics for renewable power generation systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- Tamrakar, U. Optimization-Based Fast-Frequency Support in Low Inertia Power Systems; South Dakota State University: Brookings, SD, USA, 2020. [Google Scholar]
- Sakimoto, K.; Miura, Y.; Ise, T. Stabilization of a power system with a distributed generator by a virtual synchronous generator function. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 1498–1505. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 451–458. [Google Scholar] [CrossRef]
- Tarrasó, A.; Verdugo, C.; Lai, N.B.; Candela, J.I.; Rodriguez, P. Synchronous power controller for distributed generation units. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 4660–4664. [Google Scholar]
- Rakhshani, E.; Remon, D.; Cantarellas, A.; Garcia, J.M.; Rodriguez, P. Modeling and sensitivity analyses of VSP based virtual inertia controller in HVDC links of interconnected power systems. Electr. Power Syst. Res. 2016, 141, 246–263. [Google Scholar] [CrossRef]
- Zhang, W.; Remon, D.; Rodriguez, P. Frequency support characteristics of grid-interactive power converters based on the synchronous power controller. IET Renew. Power Gener. 2017, 11, 470–479. [Google Scholar] [CrossRef]
- Zhang, W.; Remon, D.; Mir, A.; Luna, A.; Rocabert, J.; Candela, I.; Rodriguez, P. Comparison of different power loop controllers for synchronous power controlled grid-interactive converters. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3780–3787. [Google Scholar]
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-less converters with auto-synchronization and emulated inertia capability. IEEE Trans. Smart Grid 2015, 7, 1660–1674. [Google Scholar] [CrossRef]
- Hu, J.; Ma, H. Synchronization of the carrier wave of parallel three-phase inverters with virtual oscillator control. IEEE Trans. Power Electron. 2016, 32, 7998–8007. [Google Scholar] [CrossRef]
- Padmawansa, N.U.; Arachchige, L.N.W. Improving Transient Stability of an Islanded Microgrid Using PV Based Virtual Synchronous Machines. In Proceedings of the 2020 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 28–30 July 2020; pp. 543–548. [Google Scholar]
- Wang, R.; Chen, L.; Zheng, T.; Mei, S. VSG-based adaptive droop control for frequency and active power regulation in the MTDC system. CSEE J. Power Energy Syst. 2017, 3, 260–268. [Google Scholar] [CrossRef]
- Alsiraji, H.A.; El-Shatshat, R. Comprehensive assessment of virtual synchronous machine based voltage source converter controllers. IET Gener. Transm. Distrib. 2017, 11, 1762–1769. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, L.; Guo, Y.; Mei, S. Comprehensive control strategy of virtual synchronous generator under unbalanced voltage conditions. IET Gener. Transm. Distrib. 2018, 12, 1621–1630. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.-P. Comparison of methods for implementing virtual synchronous machine on inverters. In Proceedings of the International Conference on Renewable Energies and Power Quality, Vigo, Spain, 27–29 July 2022; pp. 414–424. [Google Scholar]
- Cheema, K.M.; Mehmood, K. Improved virtual synchronous generator control to analyse and enhance the transient stability of microgrid. IET Renew. Power Gener. 2020, 14, 495–505. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive virtual inertia control strategy of VSG for micro-grid based on improved bang-bang control strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Li, P.; Hu, W.; Xu, X.; Huang, Q.; Liu, Z.; Chen, Z. A frequency control strategy of electric vehicles in microgrid using virtual synchronous generator control. Energy 2019, 189, 116389. [Google Scholar] [CrossRef]
- Karimi, A.; Khayat, Y.; Naderi, M.; Dragičević, T.; Mirzaei, R.; Blaabjerg, F.; Bevrani, H. Inertia response improvement in AC microgrids: A fuzzy-based virtual synchronous generator control. IEEE Trans. Power Electron. 2019, 35, 4321–4331. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A generalized droop control for grid-supporting inverter based on comparison between traditional droop control and virtual synchronous generator control. IEEE Trans. Power Electron. 2018, 34, 5416–5438. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Bi, D.; Wen, Y.; Dai, Y.; Yin, X.; Shen, Z.J. Droop control strategy incorporating coupling compensation and virtual impedance for microgrid application. IEEE Trans. Energy Convers. 2019, 34, 277–291. [Google Scholar] [CrossRef]
- Yu, Y.-j.; Cao, L.-k.; Zhao, X. A novel control strategy of virtual synchronous generator in island micro-grids. Syst. Sci. Control Eng. 2018, 6, 136–145. [Google Scholar] [CrossRef]
- Kerdphol, T.; Watanabe, M.; Hongesombut, K.; Mitani, Y. Self-adaptive virtual inertia control-based fuzzy logic to improve frequency stability of microgrid with high renewable penetration. IEEE Access 2019, 7, 76071–76083. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Xu, D. A new optimal robust controller for frequency stability of interconnected hybrid microgrids considering non-inertia sources and uncertainties. Int. J. Electr. Power Energy Syst. 2021, 128, 106651. [Google Scholar] [CrossRef]
- Skiparev, V.; Machlev, R.; Chowdhury, N.R.; Levron, Y.; Petlenkov, E.; Belikov, J. Virtual inertia control methods in islanded microgrids. Energies 2021, 14, 1562. [Google Scholar] [CrossRef]
- Belila, A.; Amirat, Y.; Benbouzid, M.; Berkouk, E.M.; Yao, G. Virtual synchronous generators for voltage synchronization of a hybrid PV-diesel power system. Int. J. Electr. Power Energy Syst. 2020, 117, 105677. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. MPC-controlled virtual synchronous generator to enhance frequency and voltage dynamic performance in islanded microgrids. IEEE Trans. Smart Grid 2020, 12, 953–964. [Google Scholar] [CrossRef]
- Shi, K.; Ye, H.; Song, W.; Zhou, G. Virtual inertia control strategy in microgrid based on virtual synchronous generator technology. IEEE Access 2018, 6, 27949–27957. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, Q.; Zeng, H. Multi-loop virtual synchronous generator control of inverter-based DGs under microgrid dynamics. IET Gener. Transm. Distrib. 2017, 11, 795–803. [Google Scholar] [CrossRef]
- Bose, U.; Chattopadhyay, S.K.; Chakraborty, C.; Pal, B. A novel method of frequency regulation in microgrid. IEEE Trans. Ind. Appl. 2018, 55, 111–121. [Google Scholar] [CrossRef]
- Xu, T.; Jang, W.; Overbye, T. Commitment of fast-responding storage devices to mimic inertia for the enhancement of primary frequency response. IEEE Trans. Power Syst. 2017, 33, 1219–1230. [Google Scholar] [CrossRef]
- Renjit, A.A.; Guo, F.; Sharma, R. An analytical framework to design a dynamic frequency control scheme for microgrids using energy storage. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 1682–1689. [Google Scholar]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Hongesombut, K.; Küfeoğlu, S. Virtual inertia control-based model predictive control for microgrid frequency stabilization considering high renewable energy integration. Sustainability 2017, 9, 773. [Google Scholar] [CrossRef]
- Hu, W.; Wu, Z.; Dinavahi, V. Dynamic analysis and model order reduction of virtual synchronous machine based microgrid. IEEE Access 2020, 8, 106585–106600. [Google Scholar] [CrossRef]
- Yan, W.; Cheng, L.; Yan, S.; Gao, W.; Gao, D.W. Enabling and evaluation of inertial control for PMSG-WTG using synchronverter with multiple virtual rotating masses in microgrid. IEEE Trans. Sustain. Energy 2019, 11, 1078–1088. [Google Scholar] [CrossRef]
- Qu, S.; Wang, Z. Cooperative control strategy of virtual synchronous generator based on optimal damping ratio. IEEE Access 2020, 9, 709–719. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, L.; Feng, X.; Guo, H. An adaptive control strategy for virtual synchronous generator. IEEE Trans. Ind. Appl. 2018, 54, 5124–5133. [Google Scholar] [CrossRef]
- Rasool, A.; Yan, X.; Rasool, U.; Abbas, F.; Numan, M.; Rasool, H.; Jamil, M. Enhanced control strategies of VSG for EV charging station under a low inertia microgrid. IET Power Electron. 2020, 13, 2895–2904. [Google Scholar] [CrossRef]
- Rasool, A.; Fahad, S.; Yan, X.; Rasool, H.; Jamil, M.; Padmanaban, S. Reactive Power Matching Through Virtual Variable Impedance for Parallel Virtual Synchronous Generator Control Scheme. IEEE Syst. J. 2022. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y.; Turschner, D.; Beck, H.-P. Enhanced virtual inertia control based on derivative technique to emulate simultaneous inertia and damping properties for microgrid frequency regulation. IEEE Access 2019, 7, 14422–14433. [Google Scholar] [CrossRef]
- Abuagreb, M.; Allehyani, M.F.; Johnson, B.K. Overview of Virtual Synchronous Generators: Existing Projects, Challenges, and Future Trends. Electronics 2022, 11, 2843. [Google Scholar] [CrossRef]
- Obaid, Z.A.; Cipcigan, L.; Muhssin, M.T.; Sami, S.S. Control of a population of battery energy storage systems for frequency response. Int. J. Electr. Power Energy Syst. 2020, 115, 105463. [Google Scholar] [CrossRef]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An improved virtual inertia control for three-phase voltage source converters connected to a weak grid. IEEE Trans. Power Electron. 2018, 34, 8660–8670. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Behi, B.; Baniasadi, A.; Arefi, A.; Gorjy, A.; Jennings, P.; Pivrikas, A. Cost–benefit analysis of a virtual power plant including solar PV, flow battery, heat pump, and demand management: A western australian case study. Energies 2020, 13, 2614. [Google Scholar] [CrossRef]
- Mallemaci, V.; Mandrile, F.; Rubino, S.; Mazza, A.; Carpaneto, E.; Bojoi, R. A comprehensive comparison of Virtual Synchronous Generators with focus on virtual inertia and frequency regulation. Electr. Power Syst. Res. 2021, 201, 107516. [Google Scholar] [CrossRef]
- Sang, W.; Guo, W.; Dai, S.; Tian, C.; Yu, S.; Teng, Y. Virtual Synchronous Generator, a Comprehensive Overview. Energies 2022, 15, 6148. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A battery/ultracapacitor hybrid energy storage system for implementing the power management of virtual synchronous generators. IEEE Trans. Power Electron. 2017, 33, 2820–2824. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Q.; Hu, Y.; Zhang, H.; Guo, Z. Active power reserve photovoltaic virtual synchronization control technology. Chin. J. Electr. Eng. 2020, 6, 1–6. [Google Scholar] [CrossRef]
- Mercier, P.; Cherkaoui, R.; Oudalov, A. Optimizing a battery energy storage system for frequency control application in an isolated power system. IEEE Trans. Power Syst. 2009, 24, 1469–1477. [Google Scholar] [CrossRef]
- Saleh, S.; Ahshan, R.; Al-Durra, A. Developing and Testing Model Predictive Control to Minimize Ground Potentials in Transformerless Interconnected Five-Level Power Electronic Converters. IEEE Trans. Ind. Appl. 2021, 57, 3500–3510. [Google Scholar] [CrossRef]
- Saleh, S.; Ahshan, R. Resolution-level-controlled WM inverter for PMG-based wind energy conversion system. IEEE Trans. Ind. Appl. 2012, 48, 750–763. [Google Scholar] [CrossRef]
- Ahshan, R. Pumped hydro storage for microgrid applications. In Recent Advances in Renewable Energy Technologies; Elsevier: Amsterdam, The Netherlands, 2022; pp. 323–354. [Google Scholar]
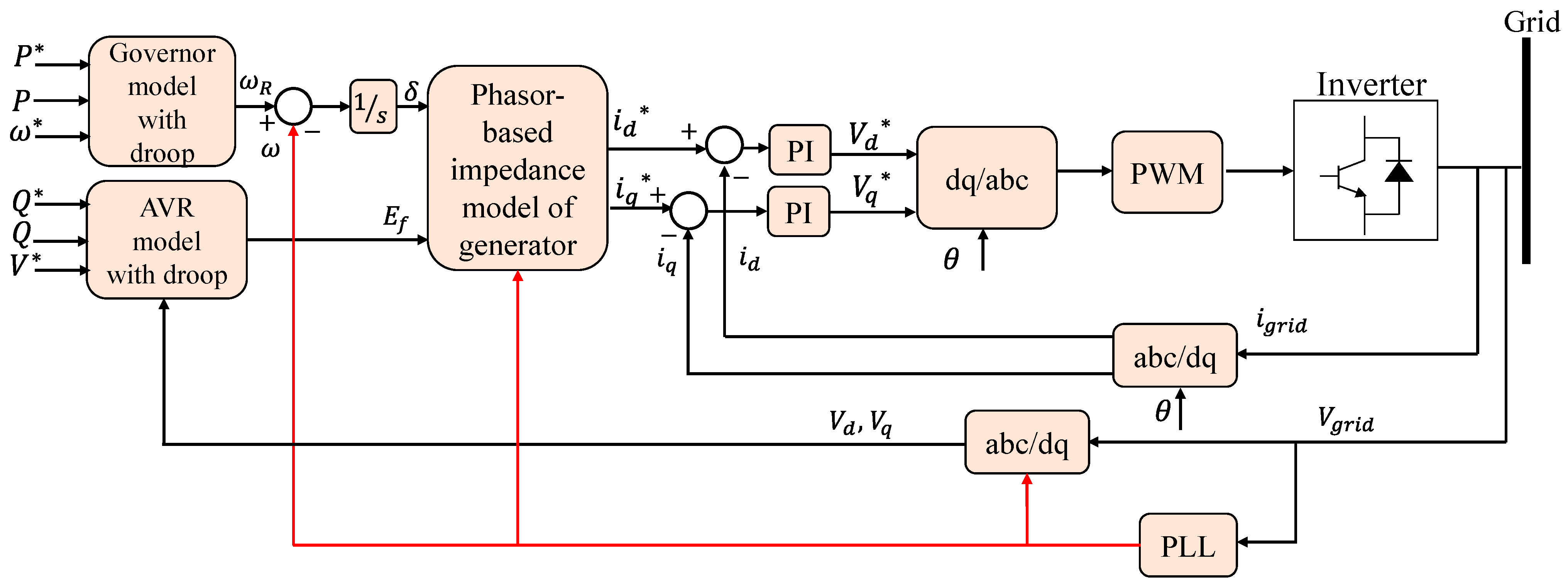
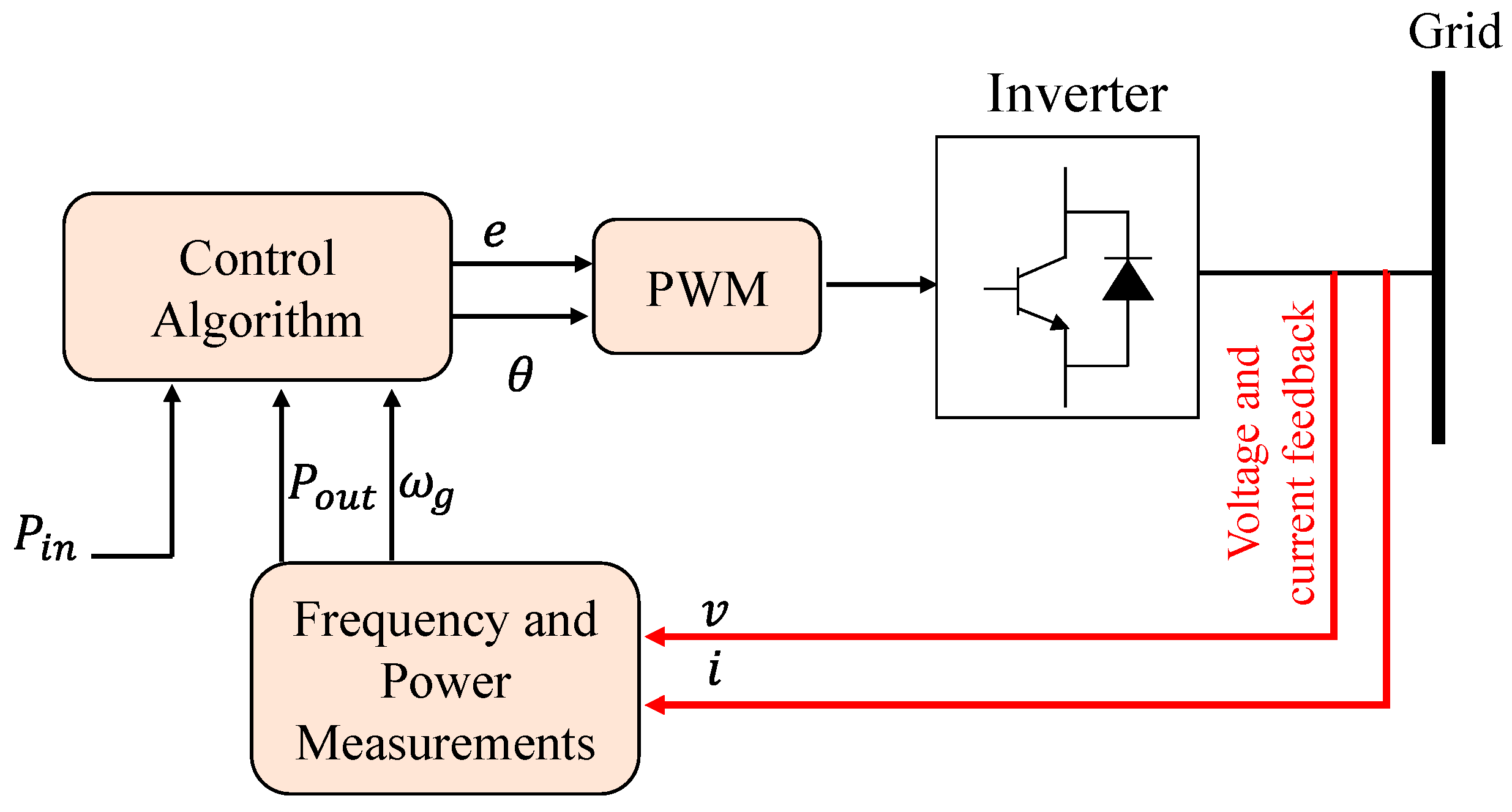
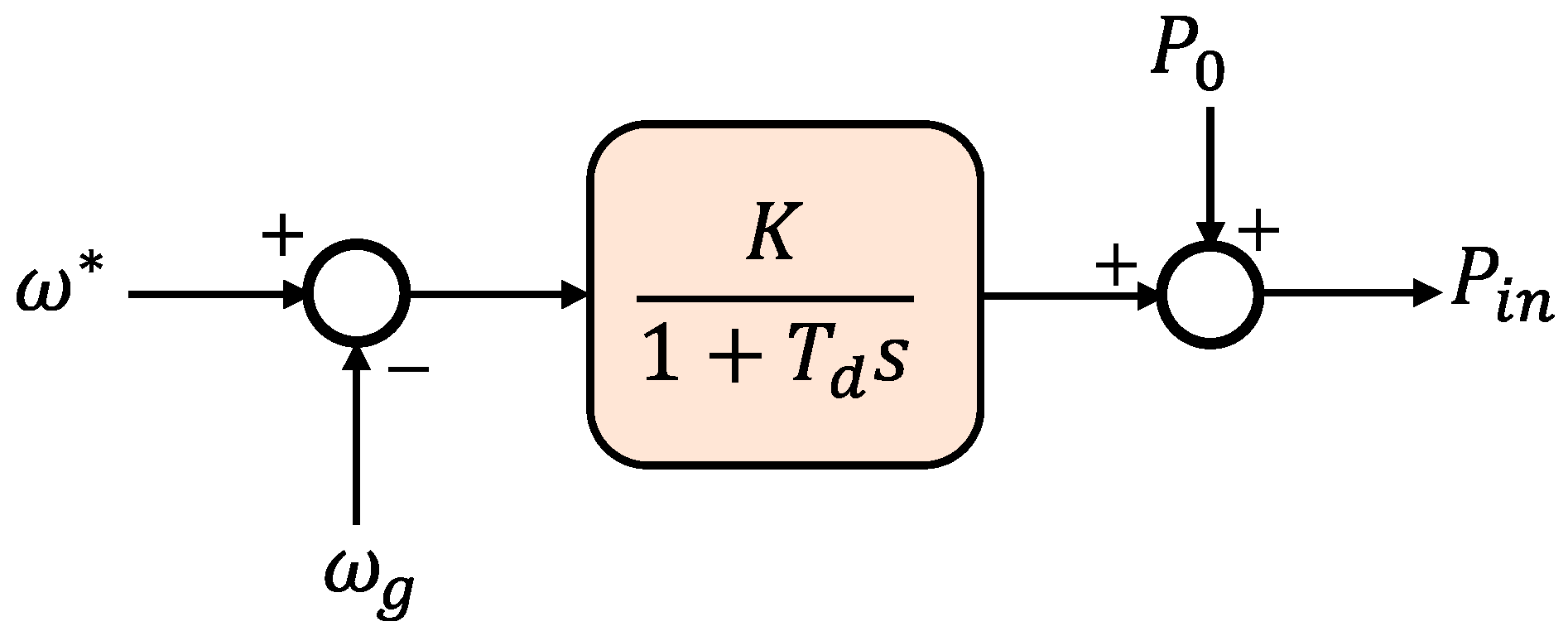
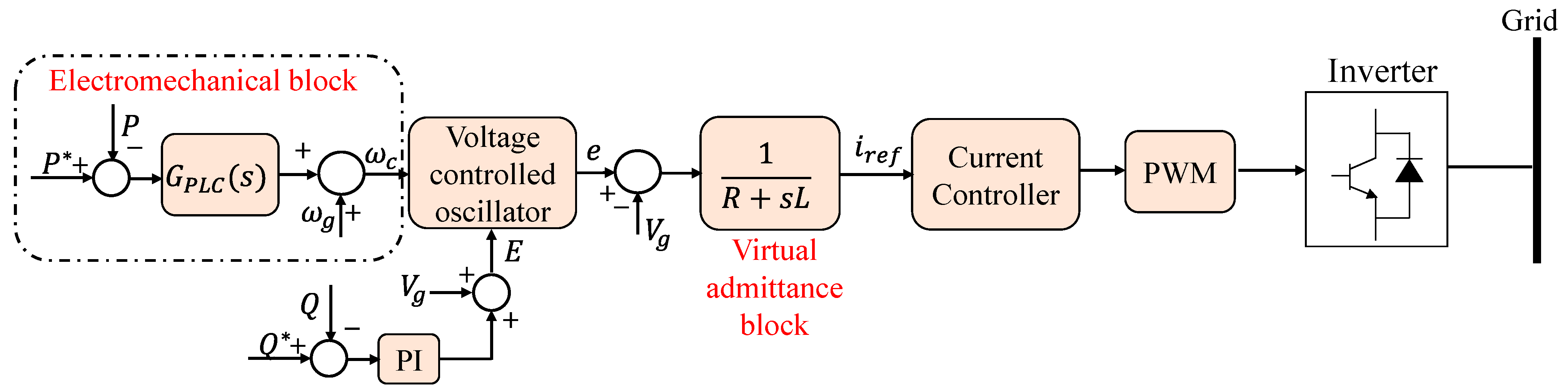
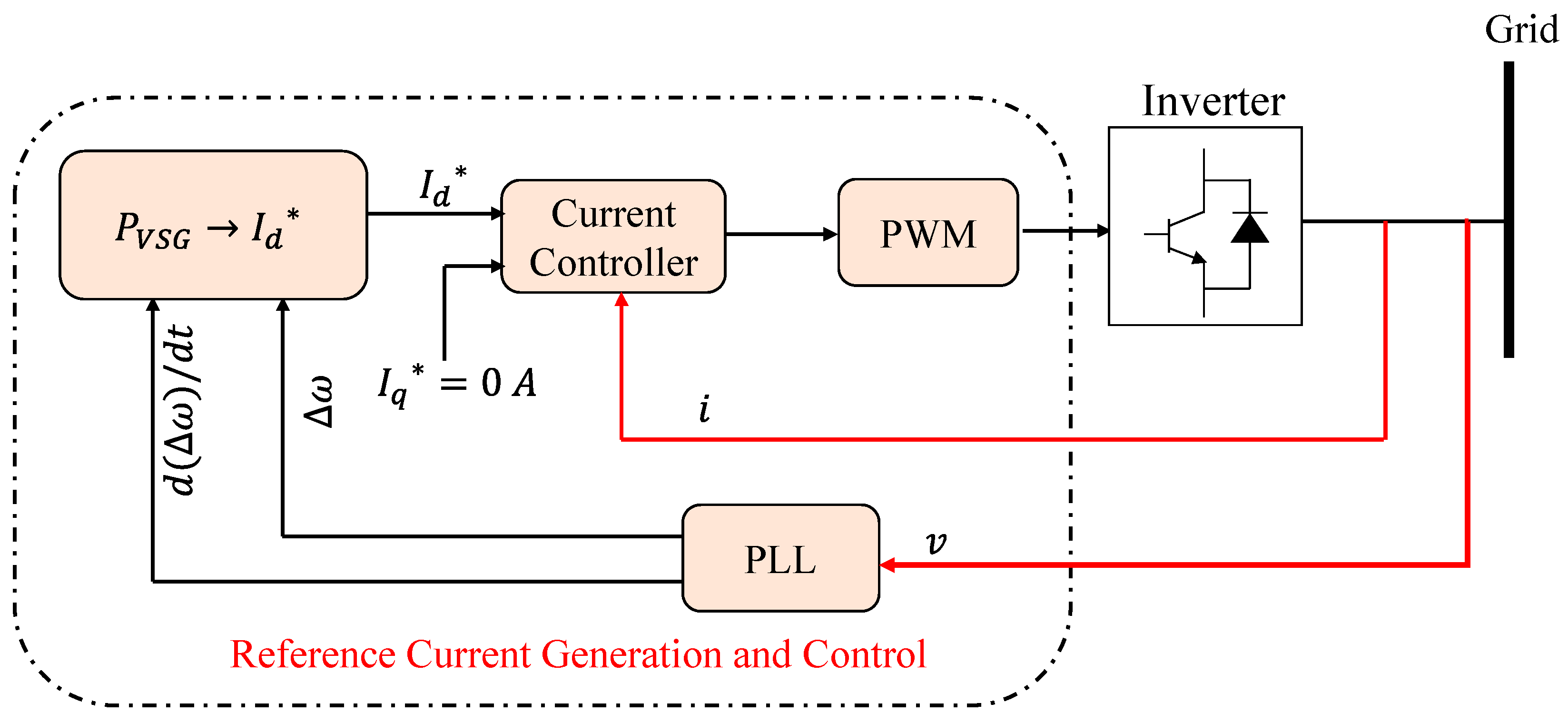
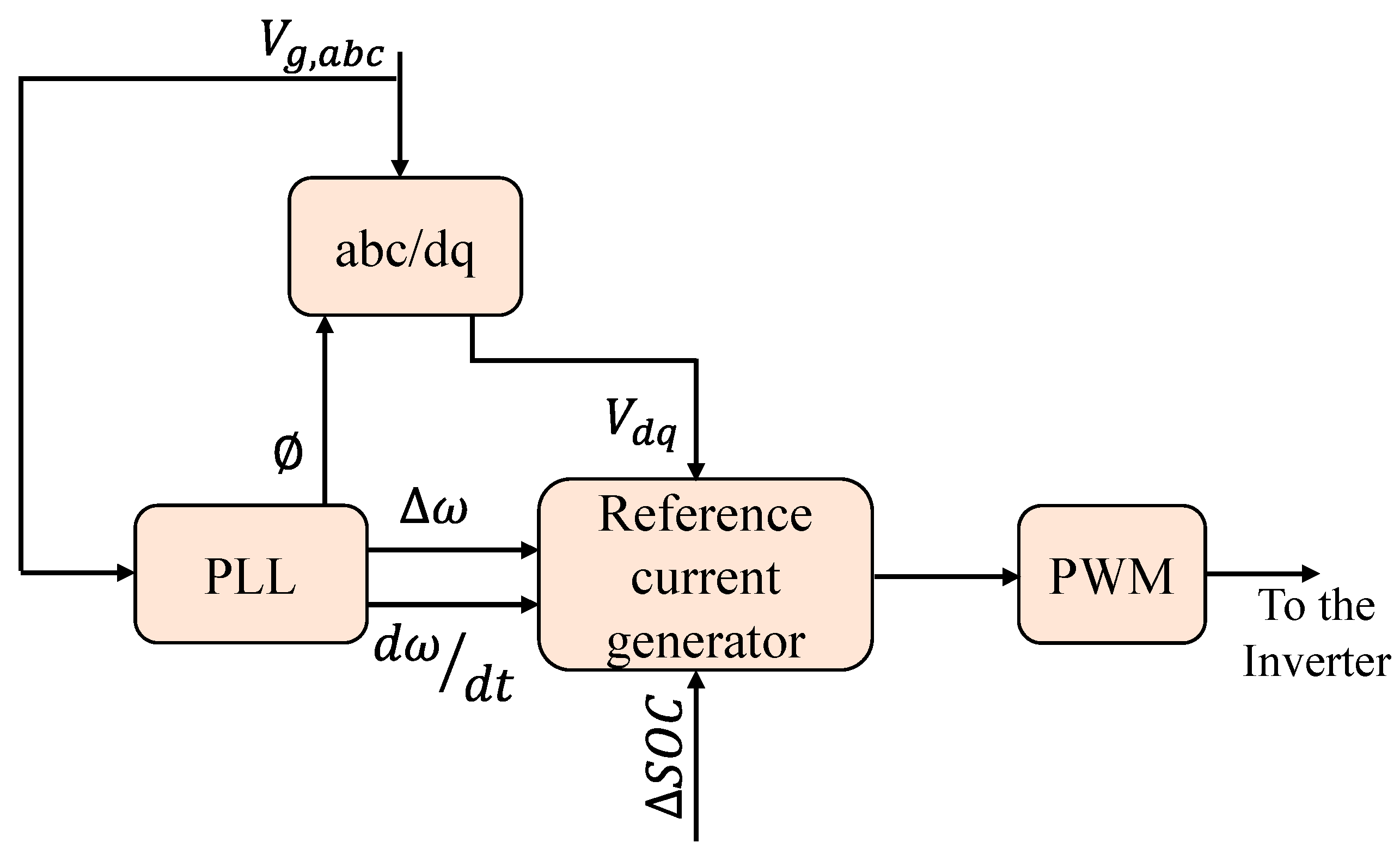
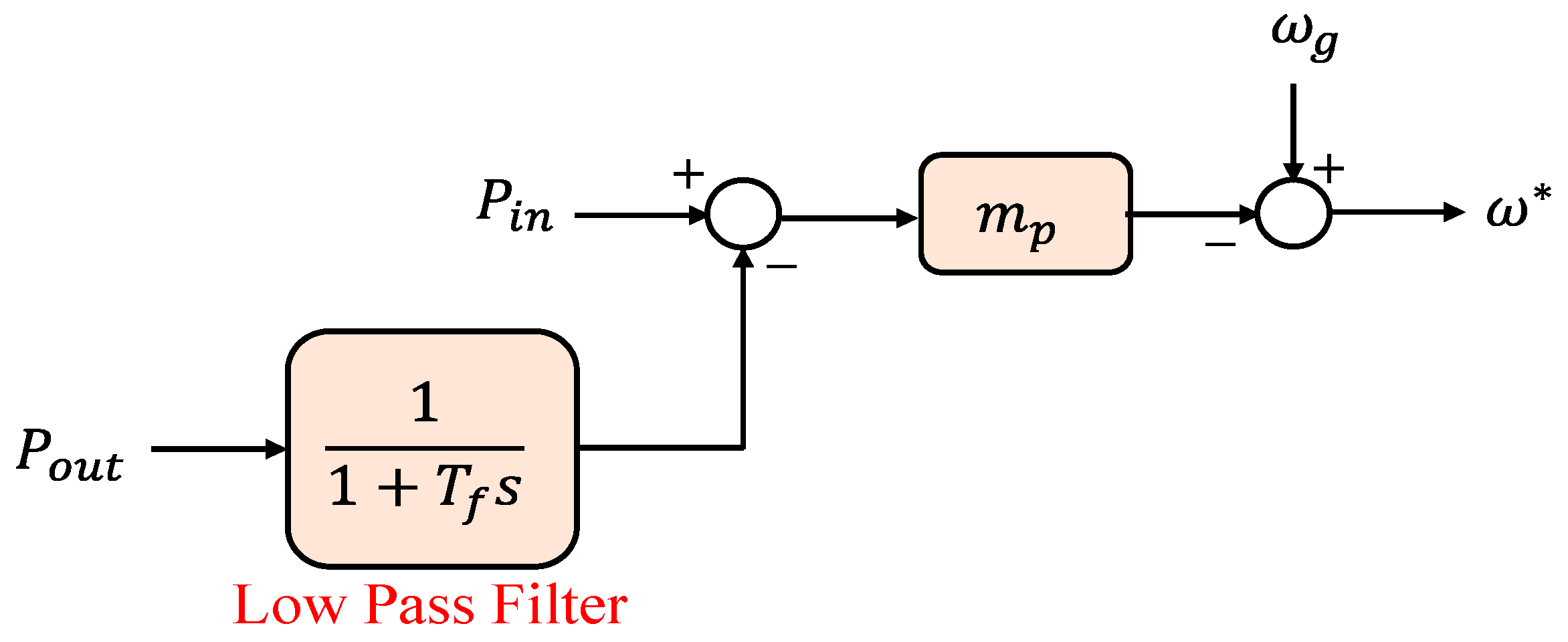
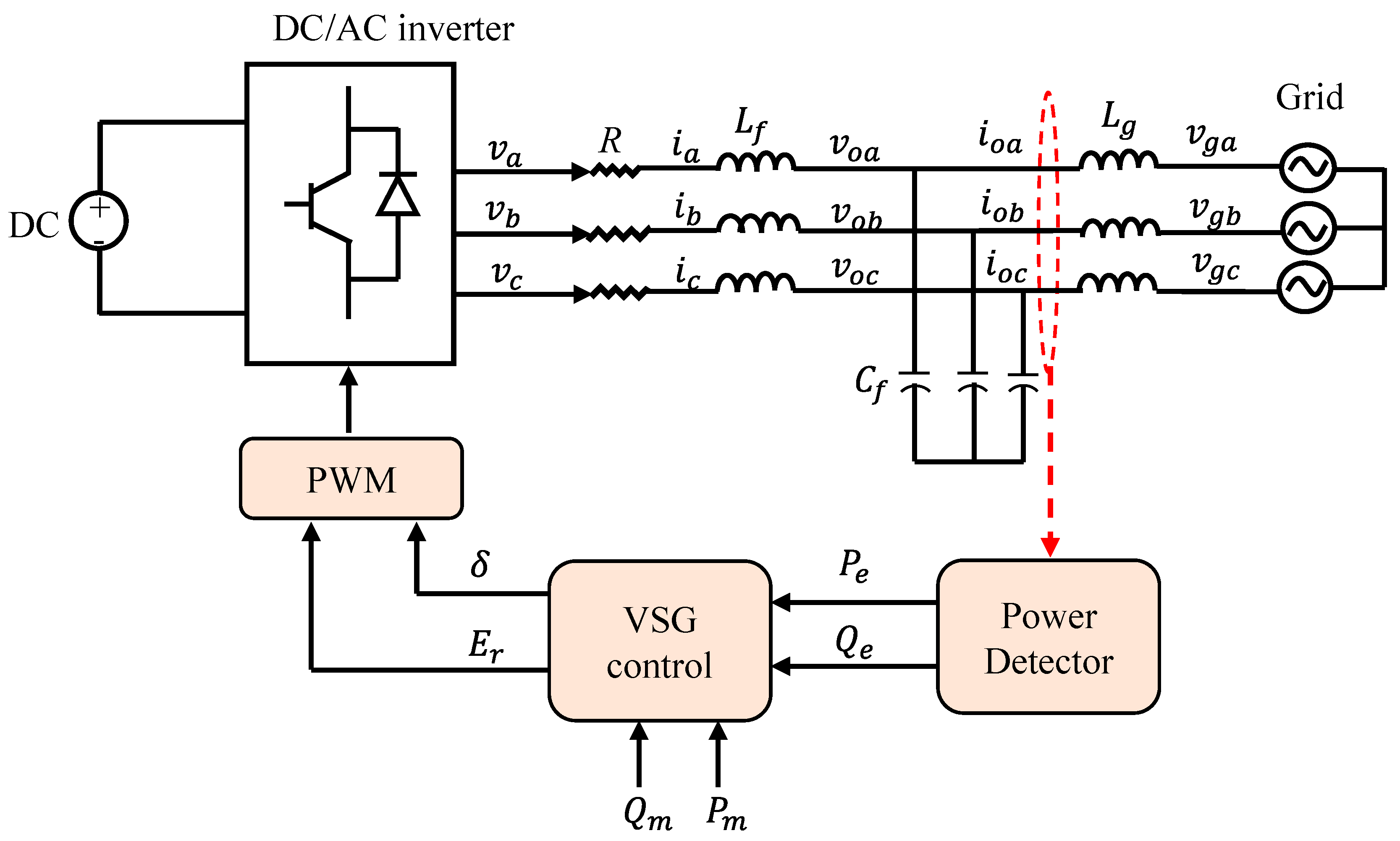

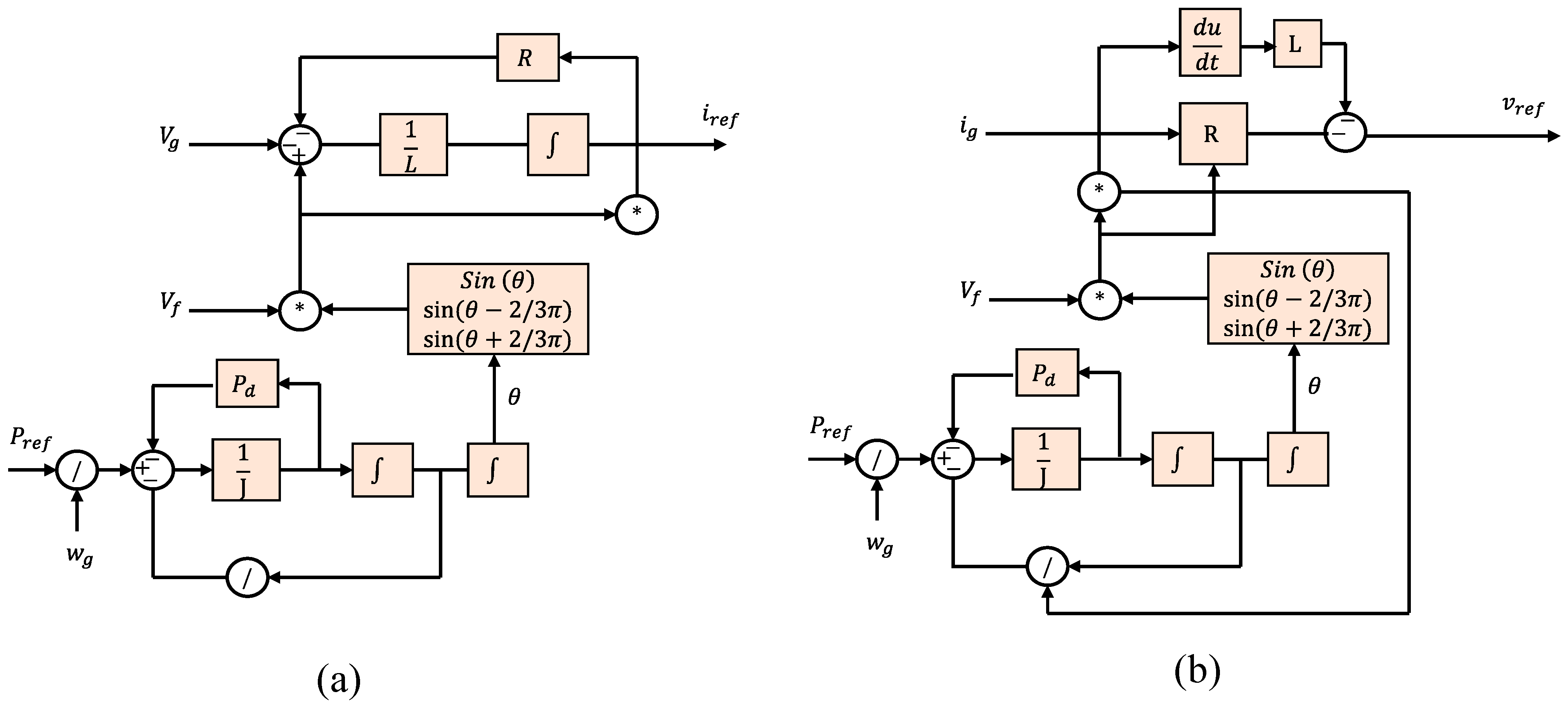
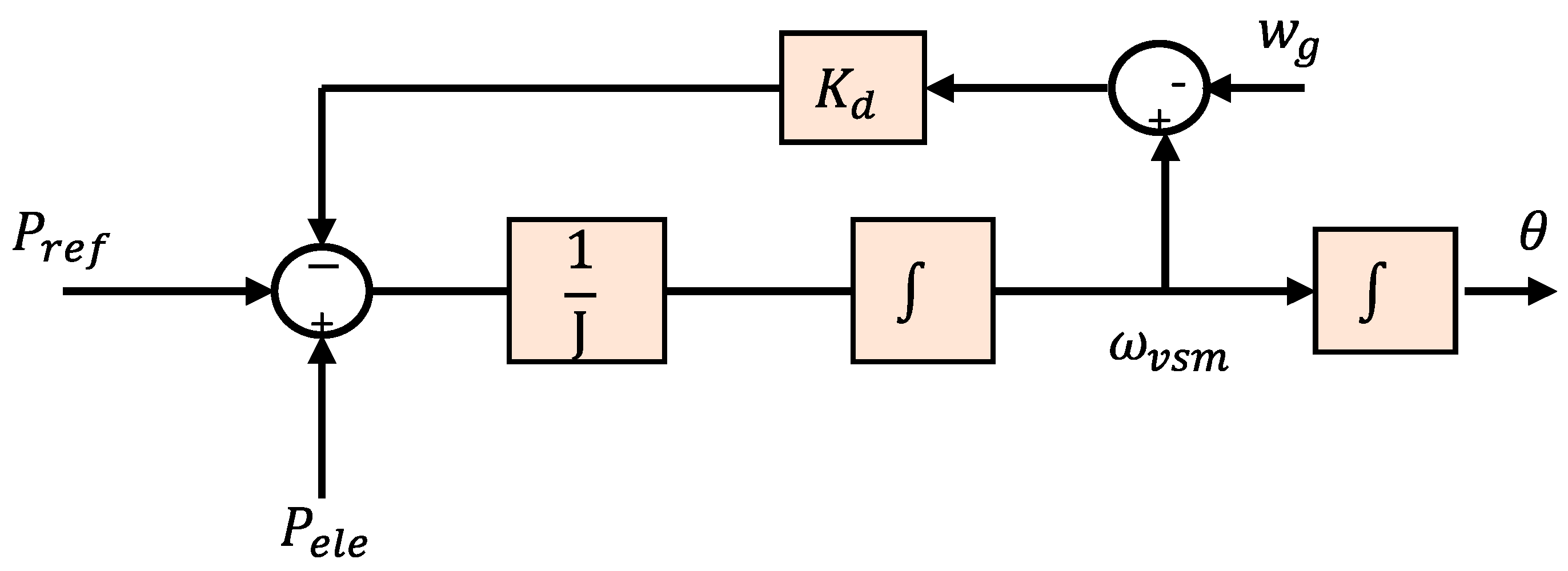
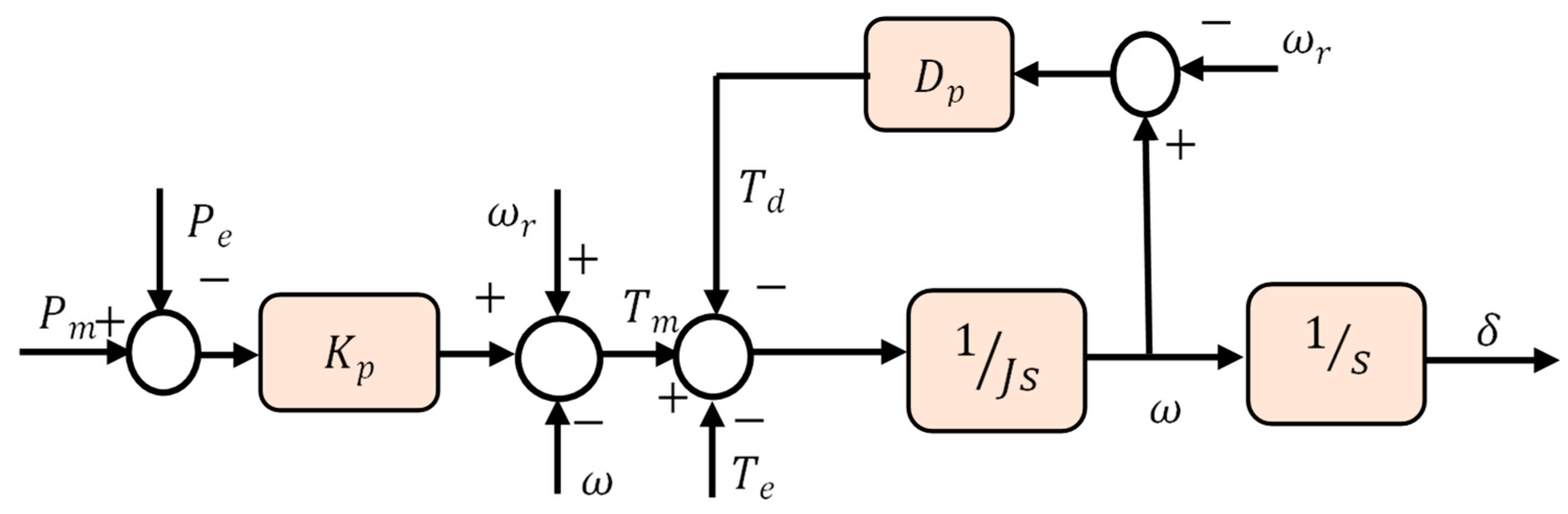
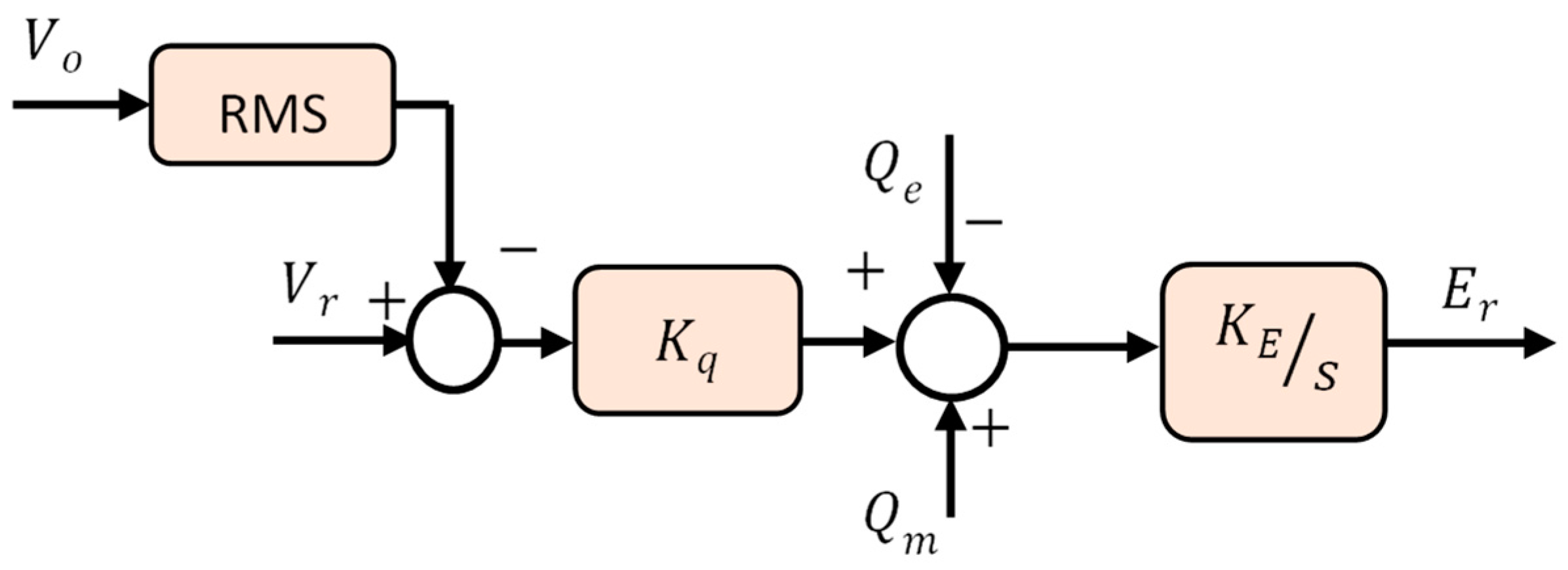
| Topologies | Type | Ref. | Features | Strength | Weaknesses | PLL |
|---|---|---|---|---|---|---|
| Synchronverters | Synchronous Generator Model-Based Topology | [6,23,26,27] |
|
|
| Required for initial synchronization |
| Kawasaki Heavy Industries (KHI) | Synchronous Generator Model-Based Topology | [18,28,29] |
|
| ||
| VISMA and IEPE topologies | Synchronous Generator Model-Based Topology | [23,30,31] |
| VISMA:
| VISMA:
| Required for initial synchronization |
| Ise Labs Topology | A Swing Equation-Based Topology | [18,32,33] |
|
|
| Required for initial synchronization |
| Synchronous Power Controller (SPC) | A Swing Equation-Based Topology | [6,34,35,36,37] |
|
|
| |
| Inducverters | [6,38] |
|
| |||
| Virtual Oscillator Control (VOC) | [18,39] |
|
| |||
| VSYNC VSG Topology | Frequency–Power Response-Based | [6,18,40] |
|
|
| Needed |
| Droop-Based Approaches | [18] |
|
| Needed |
| Control Type | Control Method | Advantage | Drawbacks | Complexity | Robustness |
|---|---|---|---|---|---|
| Classical | Robust H-infinity |
|
| Medium | High |
| Coefficient diagram method |
|
| Medium | High | |
| Advanced algorithms | Fuzzy-logic-based controller |
|
| High | High |
| Reinforcement learning-based controller |
|
| Very High | High | |
| Hybrid algorithm | PI/PID and particle-swarm optimization |
|
| Low | Low |
| Model-predictive control |
|
| High | High |
| Energy Storage Type | Efficiency (%) | Power Capability (MW) | Lifetime | Response Time | Charge Time |
|---|---|---|---|---|---|
| Lithium Batteries | 90–95 | 0.015–50 | 3–15 k times | <100 milliseconds | Hours |
| Flywheels | 85–96 | 0.1–20 | >15 years | <2 milliseconds | Minutes |
| Supercapacitors | 65–80 | 0.05–0.1 | 500 k times | <1 milliseconds | Seconds |
| Superconducting magnetic | >95 | 1–10 | >30 years | <2 milliseconds | Seconds |
| Issues/Functionalities | Pumped Hydro-Storage—Alone | Pumped Hydro-Storage—Flywheel Energy Stoarge | Pumped Hydro-Stoarge—Battery | Pumped Hydro-Storage—Fuel Cell | Pumped Hydro-Storage—Superconducting Magnetic Energy Storage | Pumped Hydro-Storage—Supercapacitor |
|---|---|---|---|---|---|---|
| Power quality | X | √ | √ | * | √ | √ |
| Energy management | √ | √ | √ | √ | √ | √ |
| Intermittency mitigation | X | √ | √ | * | * | √ |
| Back-up for renewable power integration | √ | √ | √ | √ | * | √ |
| Back-up for emergency | X | √ | * | * | * | * |
| Load following and ramping | X | * | √ | * | √ | * |
| Time shifting | √ | √ | √ | √ | √ | √ |
| Peak shaving | √ | √ | √ | √ | √ | √ |
| Load leveling | √ | √ | √ | √ | √ | √ |
| Seasonal energy storage | * | * | * | √ | * | * |
| Low-voltage ride through | X | √ | √ | * | * | √ |
| Black start | * | * | √ | √ | * | * |
| Voltage control and regulation | X | * | √ | * | * | √ |
| Grid fluctuation mitigation | X | √ | √ | * | √ | √ |
| Spinning reserve | X | * | √ | * | * | X |
| Uninterruptible power supply | X | √ | √ | * | * | √ |
| Transmission system upgrade deferral | √ | √ | √ | √ | * | √ |
| Standing reserve | * | * | √ | √ | * | * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shadoul, M.; Ahshan, R.; AlAbri, R.S.; Al-Badi, A.; Albadi, M.; Jamil, M. A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies 2022, 15, 8406. https://doi.org/10.3390/en15228406
Shadoul M, Ahshan R, AlAbri RS, Al-Badi A, Albadi M, Jamil M. A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies. 2022; 15(22):8406. https://doi.org/10.3390/en15228406
Chicago/Turabian StyleShadoul, Myada, Razzaqul Ahshan, Rashid S. AlAbri, Abdullah Al-Badi, Mohammed Albadi, and Mohsin Jamil. 2022. "A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications" Energies 15, no. 22: 8406. https://doi.org/10.3390/en15228406
APA StyleShadoul, M., Ahshan, R., AlAbri, R. S., Al-Badi, A., Albadi, M., & Jamil, M. (2022). A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies, 15(22), 8406. https://doi.org/10.3390/en15228406