Model Predictive Control for Solid State Transformers: Advances and Trends
Abstract
1. Introduction
2. MPC Strategies in Complete SST Configurations
2.1. MPC in Non-Modular SST Configurations
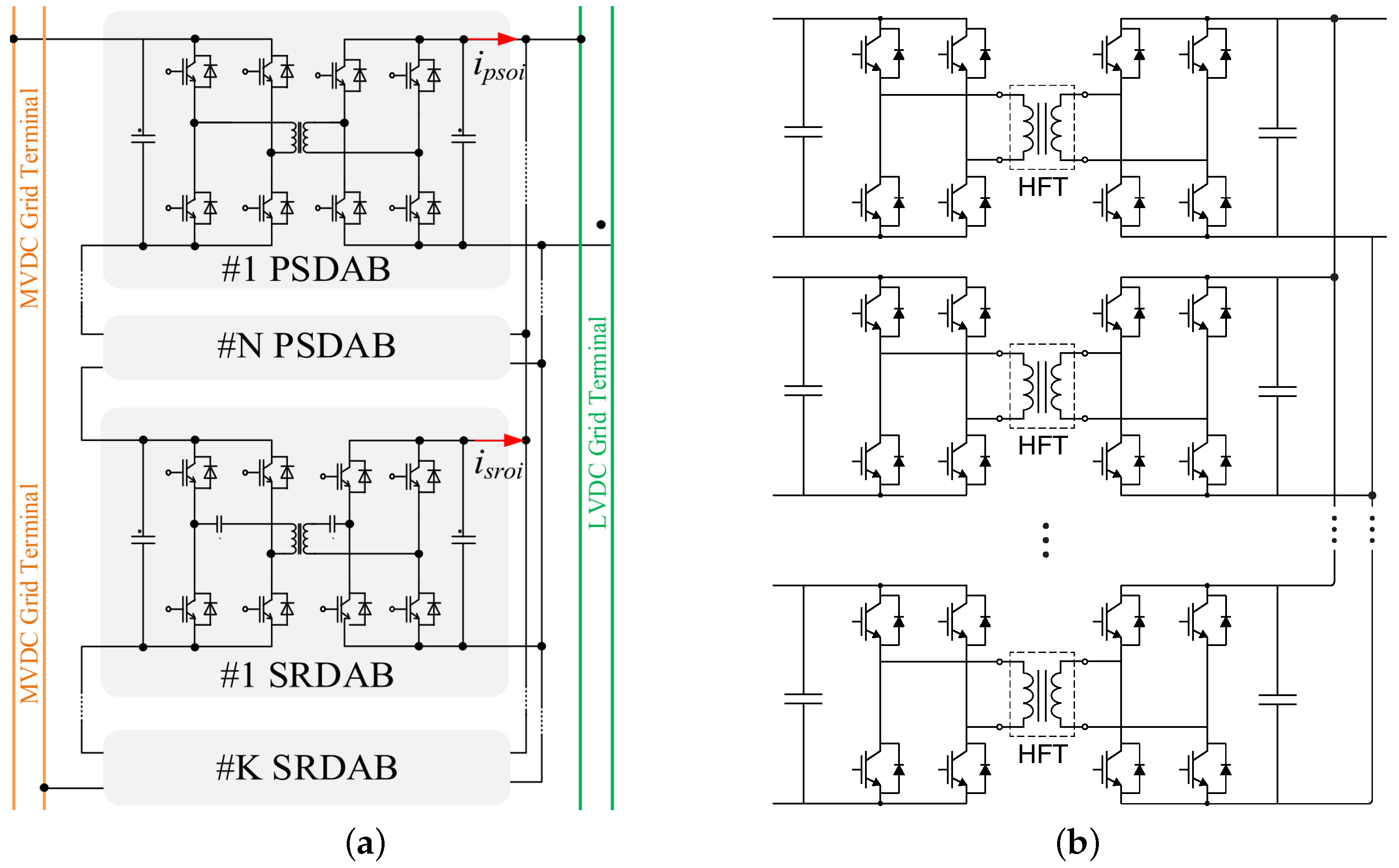
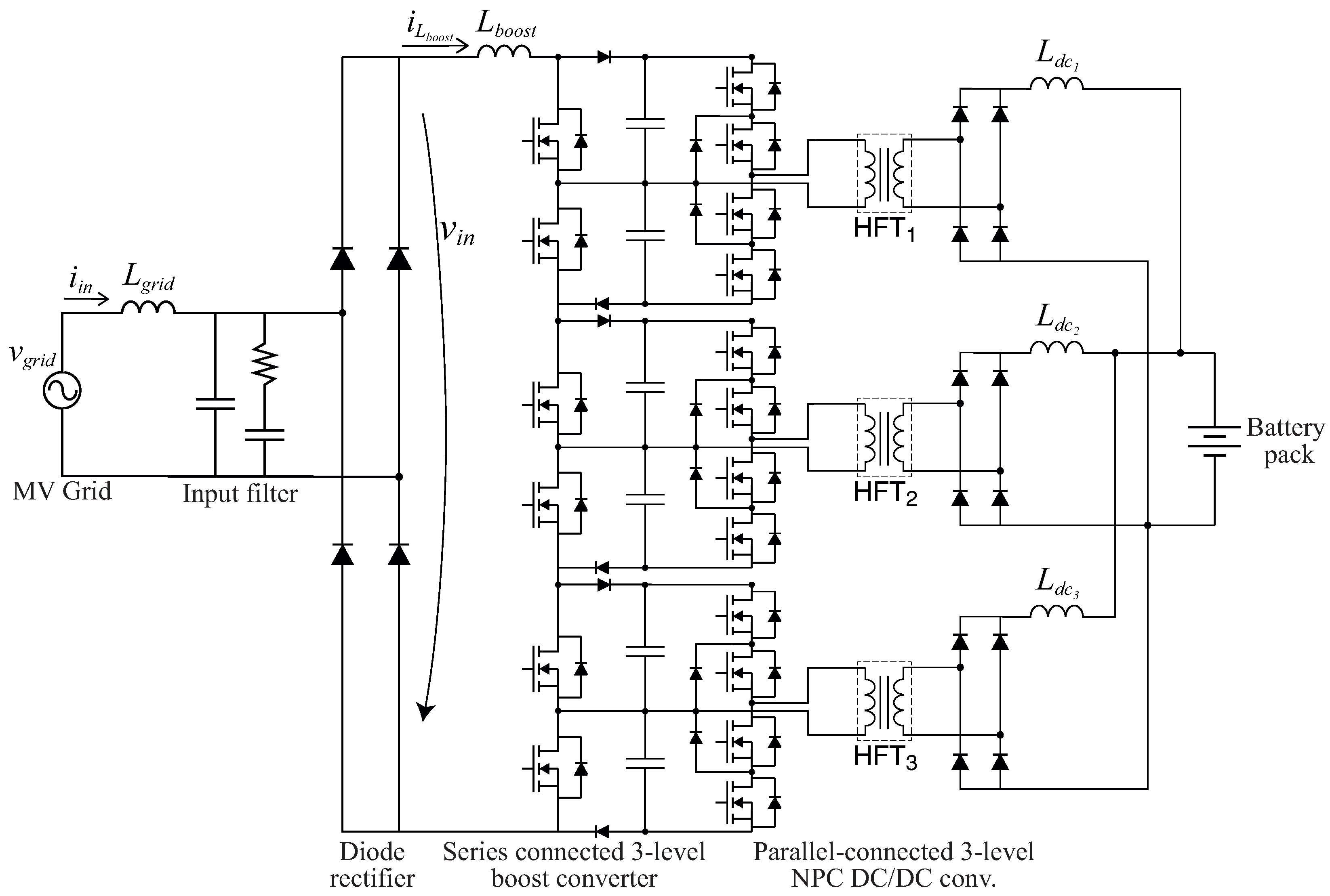
2.2. MPC in Modular SST Configurations
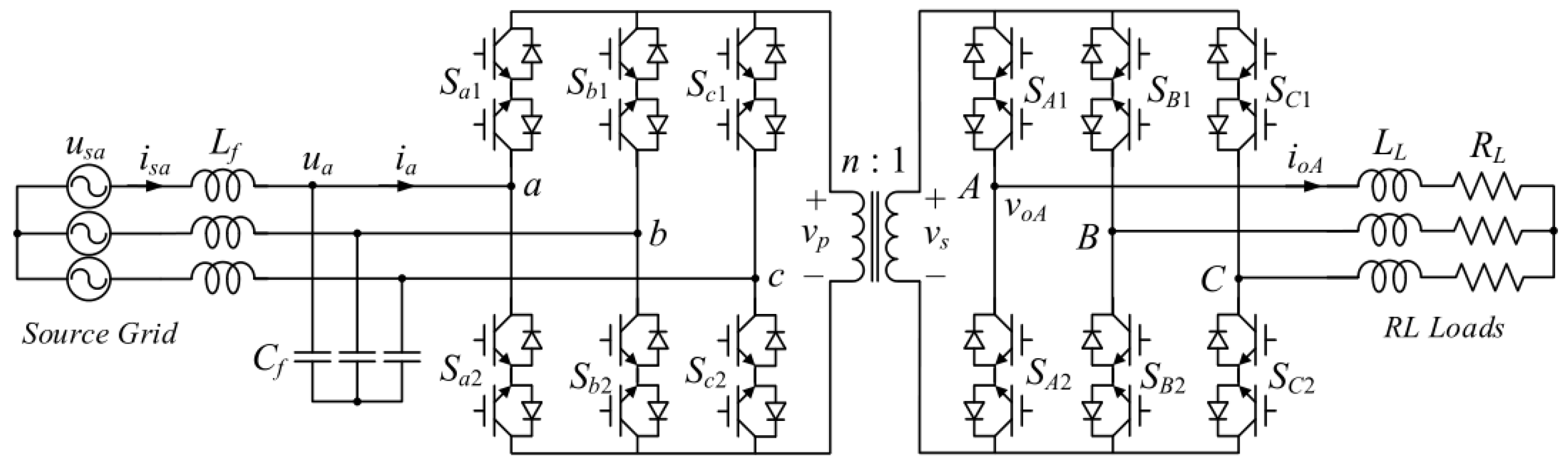
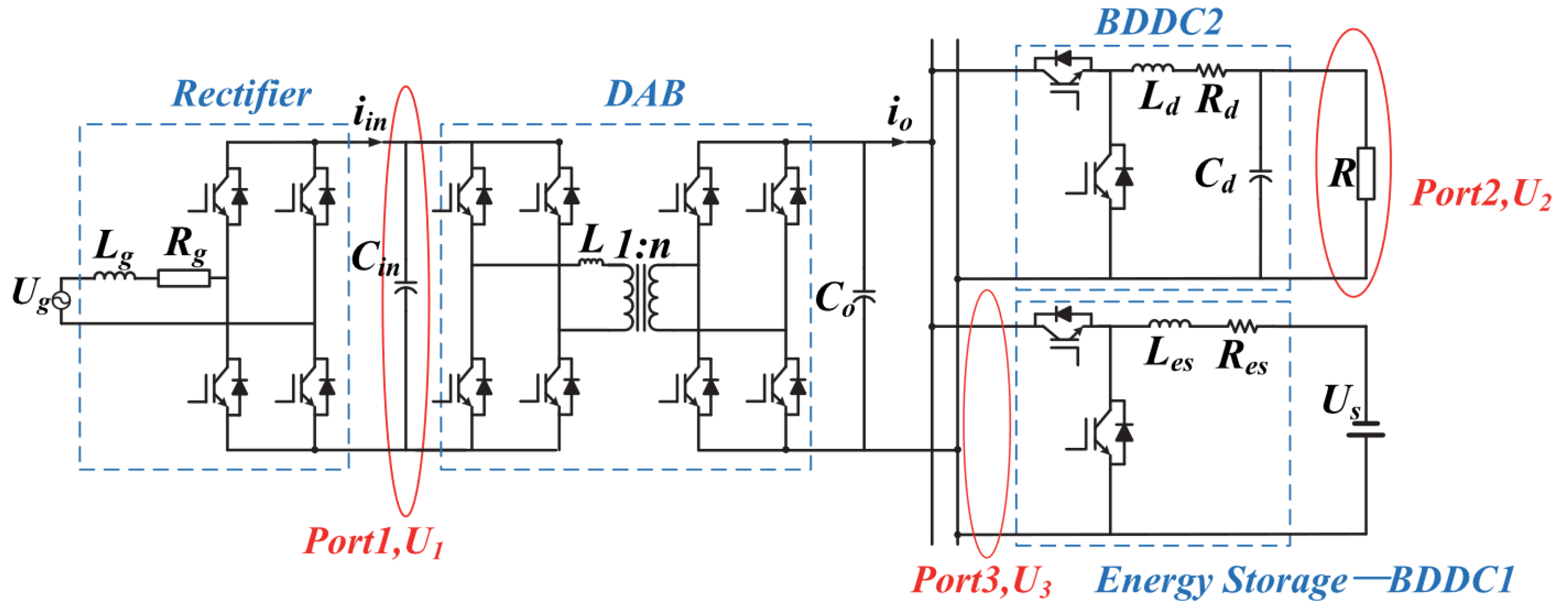
3. MPC in Converter Topologies Typically Used in SSTs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| 2LC | 2-level converter |
| 3LNPC | 3-level neutral point clamped |
| BDDC | bidirectional DC/DC converter |
| CCS-MPC | continuous control set model predictive control |
| CHBC | cascaded h-bridge converter |
| DAB | dual active bridge |
| DPS | dual phase-shift |
| DSP | digital signal processor |
| FCS-MPC | finite control set model predictive control |
| FCC | flying-capacitor converter |
| FFC | feed-forward compensation |
| FPGA | field-programmable gate array |
| HFT | high-frequency transformer |
| HVAC | high-voltage AC |
| HVDC | high-voltage DC |
| I-MMC | isolated modular multilevel converter |
| MDCS-MPC | moving discretized control set model predictive control |
| MMC | modular multilevel converter |
| MPC | model predictive control |
| MPPS | model predictive priority switching |
| LVAC | low-voltage AC |
| LVDC | low-voltage DC |
| PEC | power electronics converter |
| PET | power electronics transformer |
| PI | proportional-integral |
| PWM | pulse width modulation |
| SST | solid state transformer |
| S4T | soft-switching solid state transformer |
| TLB | three-level boost |
| ZVS | zero voltage switching |
References
- Feng, J.; Chu, W.Q.; Zhang, Z.; Zhu, Z.Q. Power Electronic Transformer-Based Railway Traction Systems: Challenges and Opportunities. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1237–1253. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ker, P.J.; Lipu, M.S.H.; Choi, Z.H.; Rahman, M.S.A.; Muttaqi, K.M.; Blaabjerg, F. State of the Art of Solid-State Transformers: Advanced Topologies, Implementation Issues, Recent Progress and Improvements. IEEE Access 2020, 8, 19113–19132. [Google Scholar] [CrossRef]
- Huber, J.E.; Kolar, J.W. Applicability of Solid-State Transformers in Today’s and Future Distribution Grids. IEEE Trans. Smart Grid 2019, 10, 317–326. [Google Scholar] [CrossRef]
- Shamshuddin, M.A.; Rojas, F.; Cardenas, R.; Pereda, J.; Diaz, M.; Kennel, R. Solid State Transformers: Concepts, Classification, and Control. Energies 2020, 13, 2319. [Google Scholar] [CrossRef]
- Syed, I.; Khadkikar, V. Replacing the Grid Interface Transformer in Wind Energy Conversion System With Solid-State Transformer. IEEE Trans. Power Syst. 2017, 32, 2152–2160. [Google Scholar] [CrossRef]
- Vadakkedath Madhavan, H.; Kumar, C.; Liserre, M. An MVDC-Based Meshed Hybrid Microgrid Enabled Using Smart Transformers. IEEE Trans. Ind. Electron. 2022, 69, 3722–3731. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, J.; Ai, Y.; Yang, J.; Zhang, J.; You, X. Power-Linked Predictive Control Strategy for Power Electronic Traction Transformer. IEEE Trans. Power Electron. 2020, 35, 6559–6571. [Google Scholar] [CrossRef]
- Sarker, P.C.; Islam, M.R.; Guo, Y.; Zhu, J.; Lu, H.Y. State-of-the-Art Technologies for Development of High Frequency Transformers with Advanced Magnetic Materials. IEEE Trans. Appl. Supercond. 2019, 29, 7000111. [Google Scholar] [CrossRef]
- Xu, J.; Wang, K.; Wu, P.; Li, Z.; Liu, Y.; Li, G.; Zheng, W. FPGA-Based Submicrosecond-Level Real-Time Simulation of Solid-State Transformer With a Switching Frequency of 50 kHz. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4212–4224. [Google Scholar] [CrossRef]
- Huber, J.E.; Kolar, J.W. Volume/weight/cost comparison of a 1MVA 10 kV/400 V solid-state against a conventional low-frequency distribution transformer. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Volume/Weight/Cost Comparison of a 1MVA 10 kV/400 V Solid-State against a Conventional Low-Frequency Distribution Transformer, Pittsburgh, PA, USA, 14–18 September 2014; pp. 4545–4552. [Google Scholar] [CrossRef]
- Chen, H.; Divan, D. Soft-Switching Solid-State Transformer (S4T). IEEE Trans. Power Electron. 2018, 33, 2933–2947. [Google Scholar] [CrossRef]
- Nair, A.C.; Fernandes, B.G. Solid-State Transformer Based Fast Charging Station for Various Categories of Electric Vehicles With Batteries of Vastly Different Ratings. IEEE Trans. Ind. Electron. 2021, 68, 10400–10411. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part I: Basic Concepts and Advanced Strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model Predictive Control of Power Electronic Systems: Methods, Results, and Challenges. IEEE Open J. Ind. Appl. 2020, 1, 95–114. [Google Scholar] [CrossRef]
- Pérez-Guzmán, R.E.; Rivera, M.; Wheeler, P.W. Recent Advances of Predictive Control in Power Converters. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 1100–1105. [Google Scholar] [CrossRef]
- Lim, C.S.; Lee, S.S.; Cassandra Wong, Y.C.; Nutkani, I.U.; Goh, H.H. Comparison of Current Control Strategies Based on FCS-MPC and D-PI-PWM Control for Actively Damped VSCs With LCL-Filters. IEEE Access 2019, 7, 112410–112423. [Google Scholar] [CrossRef]
- Caseiro, L.M.A.; Mendes, A.M.S.; Cruz, S.M.A. Cooperative and Dynamically Weighted Model Predictive Control of a 3-Level Uninterruptible Power Supply With Improved Performance and Dynamic Response. IEEE Trans. Ind. Electron. 2020, 67, 4934–4945. [Google Scholar] [CrossRef]
- Oliveira, T.; Caseiro, L.; Mendes, A.; Cruz, S.; Perdigão, M. Model Predictive Control for Paralleled Uninterruptible Power Supplies with an Additional Inverter Leg for Load-Side Neutral Connection. Energies 2021, 14, 2270. [Google Scholar] [CrossRef]
- Abu-Siada, A.; Budiri, J.; Abdou, A.F. Solid State Transformers Topologies, Controllers, and Applications: State-of-the-Art Literature Review. Electronics 2018, 7, 298. [Google Scholar] [CrossRef]
- Saleh, S.A.M.; Richard, C.; Onge, X.F.S.; McDonald, K.M.; Ozkop, E.; Chang, L.; Alsayid, B. Solid-State Transformers for Distribution Systems–Part I: Technology and Construction. IEEE Trans. Ind. Appl. 2019, 55, 4524–4535. [Google Scholar] [CrossRef]
- Mishra, D.K.; Ghadi, M.J.; Li, L.; Hossain, M.J.; Zhang, J.; Ray, P.K.; Mohanty, A. A review on solid-state transformer: A breakthrough technology for future smart distribution grids. Int. J. Electr. Power Energy Syst. 2021, 133, 107255. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Abu-Rub, H.; Ge, B. Model predictive control of matrix converter based solid state transformer. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 1248–1253. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Abu-Rub, H.; Ge, B.; Balog, R.S.; Xue, Y. Model predictive control of a matrix-converter based solid state transformer for utility grid interaction. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Liu, Y.; Bayhan, S. Real-time implementation of finite control set model predictive control for matrix converter based solid state transformer. Int. J. Hydrogen Energy 2017, 42, 17976–17983. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Ge, B.; Abu-Rub, H. Interactive Grid Interfacing System by Matrix-Converter-Based Solid State Transformer With Model Predictive Control. IEEE Trans. Ind. Inform. 2020, 16, 2533–2541. [Google Scholar] [CrossRef]
- Raaed Faleh Hassan, D. Design and software implementation of solid state transformer. Int. J. Eng. Technol. 2018, 7, 1776. [Google Scholar] [CrossRef][Green Version]
- Buticchi, G.; Tarisciotti, L.; Wheeler, P.; Shao, S.; Chen, L. Current and Voltage Model Predictive Control for a Three-Stage Smart Transformer. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Buticchi, G.; De Carne, G.; Yang, J.; Gu, C.; Wheeler, P. Unified Cost Function Model Predictive Control for a three-stage Smart Transformer. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 3468–3475. [Google Scholar] [CrossRef]
- Sun, Q.; Li, Y.; Ma, D.; Zhang, Y.; Qin, D. Model Predictive Direct Power Control of Three-Port Solid-State Transformer for Hybrid AC/DC Zonal Microgrid Applications. IEEE Trans. Power Deliv. 2022, 37, 528–538. [Google Scholar] [CrossRef]
- du Toit, D.; Mouton, H.d.T.; Kennel, R.; Stolze, P. Predictive Control of Series Stacked Flying-Capacitor Active Rectifiers. IEEE Trans. Ind. Inform. 2013, 9, 697–707. [Google Scholar] [CrossRef]
- Zheng, L.; Han, X.; Prasad Kandula, R.; Divan, D. Dynamic DC-Link Current Minimization Control to Improve Current-Source Solid-State Transformer Efficiency. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 1636–1641. [Google Scholar] [CrossRef]
- Zheng, L.; Prasad Kandula, R.; Divan, D. Predictive Direct DC-Link Control for Active Power Decoupling of A Single-Phase Reduced DC-Link MV Solid-State Transformer. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4124–4129. [Google Scholar] [CrossRef]
- An, Z.; Kandula, R.P.; Divan, D. Feed-Forward Compensation for Model Predictive Control in Tri-port Current-Source Medium-Voltage String Inverters for PV-Plus-Storage Farms. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 3430–3435. [Google Scholar] [CrossRef]
- Xiao, Q.; Chen, L.; Jia, H.; Wheeler, P.W.; Dragičević, T. Model Predictive Control for Dual Active Bridge in Naval DC Microgrids Supplying Pulsed Power Loads Featuring Fast Transition and Online Transformer Current Minimization. IEEE Trans. Ind. Electron. 2020, 67, 5197–5203. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Chen, L.; Shao, S.; Dragičević, T.; Wheeler, P.; Zanchetta, P. Finite Control Set Model Predictive Control for Dual Active Bridge Converter. IEEE Trans. Ind. Appl. 2022, 58, 2155–2165. [Google Scholar] [CrossRef]
- du Toit, D.; Mouton, T.; Kennel, R.; Stolze, P. Predictive control for a series stacked flying-capacitor active rectifier. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 1809–1814. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Kandasamy, K.; Divan, D. Fast Dynamic Control of Stacked Low Inertia Converters. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3126–3133. [Google Scholar] [CrossRef]
- Yan, D.; Marellapudi, A.; Kandula, R.P.; Divan, D. Oversampling Multi-Variable Control for Soft-Switching Solid-State Transformer. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 3476–3483. [Google Scholar] [CrossRef]
- Zheng, L.; Han, X.; Kandula, R.P.; Kandasamy, K.; Saeedifard, M.; Divan, D. 7.2 kV Three-Port Single-Phase Single-Stage Modular Soft-Switching Solid-State Transformer with Active Power Decoupling and Reduced DC-Link. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 1575–1581. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Divan, D. Soft-Switching Solid-State Transformer With Reduced Conduction Loss. IEEE Trans. Power Electron. 2021, 36, 5236–5249. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Divan, D. New Single-Stage Soft-Switching Solid-State Transformer with Reduced Conduction Loss and Minimal Auxiliary Switch. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 560–567. [Google Scholar] [CrossRef]
- Zheng, L.; Han, X.; An, Z.; Kandula, R.P.; Kandasamy, K.; Saeedifard, M.; Divan, D. SiC-Based 5-kV Universal Modular Soft-Switching Solid-State Transformer (M-S4T) for Medium-Voltage DC Microgrids and Distribution Grids. IEEE Trans. Power Electron. 2021, 36, 11326–11343. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Kandasamy, K.; Divan, D. Stacked Low-Inertia Converter or Solid-State Transformer: Modeling and Model Predictive Priority-Shifting Control for Voltage Balance. IEEE Trans. Power Electron. 2021, 36, 8934–8952. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Divan, D. Robust Predictive Control for Modular Solid-State Transformer With Reduced DC Link and Parameter Mismatch. IEEE Trans. Power Electron. 2021, 36, 14295–14311. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, C.; Srdic, S.; Lukic, S.M. Predictive Control of a Series-Interleaved Multicell Three-Level Boost Power-Factor-Correction Converter. IEEE Trans. Power Electron. 2018, 33, 8948–8960. [Google Scholar] [CrossRef]
- Kong, D.; Zhang, Z.; Liu, C.; Tian, W.; Gao, X.; Kennel, R. Modulated Model Predictive Control of Power Electronics Transformer Based on Isolated Modular Multilevel Converter. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 831–835. [Google Scholar] [CrossRef]
- Haghgooyi, P.; Khaburi, D.A.; Khosravi, M.; Heshmatian, S.; Rodriguez, J.; Peñailillo, C.G. A Hybrid Control Method Based on Model Predictive Control for Controlling the Rectifier Stage of Power Electronic Transformers. In Proceedings of the 2019 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Quanzhou, China, 31 May–2 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Bifaretti, S.; Clare, J.C. Modulated Model Predictive Control for a Seven-Level Cascaded H-Bridge Back-to-Back Converter. IEEE Trans. Ind. Electron. 2014, 61, 5375–5383. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Wheeler, P.; Clare, J.C.; Bifaretti, S. Multiobjective Modulated Model Predictive Control for a Multilevel Solid-State Transformer. IEEE Trans. Ind. Appl. 2015, 51, 4051–4060. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Divan, D. Predictive Direct DC-Link Control for 7.2 kV Three-Port Low-Inertia Solid-State Transformer With Active Power Decoupling. IEEE Trans. Power Electron. 2022, 37, 11673–11685. [Google Scholar] [CrossRef]
- Srdic, S.; Liang, X.; Zhang, C.; Yu, W.; Lukic, S. A SiC-based high-performance medium-voltage fast charger for plug-in electric vehicles. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar] [CrossRef]
- Liu, C.; Liu, C.; Cai, G.; Ying, H.; Zhang, Z.; Shan, R.; Pei, Z.; Song, X. An Isolated Modular Multilevel Converter (I-M2C) Topology Based on High-Frequency Link (HFL) Concept. IEEE Trans. Power Electron. 2020, 35, 1576–1588. [Google Scholar] [CrossRef]
- Watson, A.J.; Wheeler, P.W.; Clare, J.C. Field programmable gate array based control of Dual Active Bridge DC/DC Converter for the UNIFLEX-PM project. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Zan, W.; Chai, M.; Bhandari, S.; Panda, S.K. Advanced Model Predictive Control Methods for Bidirectional Three-Phase Two-Level Converter for Solid State Transformers. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 244–249. [Google Scholar] [CrossRef]
- Liu, B.; Zha, Y.; Zhang, T.; Chen, S. Predictive direct power control for rectifier stage of solid state transformer. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 201–204. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, R.Y.; Kim, S.I. Generalized Model Predictive Control Method for Single-Phase N-Level Flying Capacitor Multilevel Rectifiers for Solid State Transformer. IEEE Trans. Ind. Appl. 2019, 55, 7505–7514. [Google Scholar] [CrossRef]
- Park, D.H.; Kim, R.y. Model Predictive Control with Reduced Computation for N-cell Cascaded Flying Capacitor H-Bridge Converter in Solid-State Transformer. In Proceedings of the 2022 International Power Electronics Conference (IPEC—Himeji 2022—ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 720–724. [Google Scholar] [CrossRef]
- Lezana, P.; Norambuena, M.; Aguilera, R.P. Dual-Stage Control Strategy for a Flying Capacitor Converter Based on Model Predictive and Linear Controllers. IEEE Trans. Ind. Inform. 2022, 18, 2203–2212. [Google Scholar] [CrossRef]
- Park, D.H.; Tahir, H.; Lee, J.D.; Kim, R.Y. Hierarchical Single-Objective Model Predictive Control With Reduced Computational Burden in Cascaded H-Bridge Converter Based on 3-Level Flying Capacitor Unit Cell. IEEE Access 2022, 10, 54730–54741. [Google Scholar] [CrossRef]
- Garcia, C.; Mohammadinodoushan, M.; Yaramasu, V.; Norambuena, M.; Davari, S.A.; Zhang, Z.; Khaburi, D.A.; Rodriguez, J. FCS-MPC Based Pre-Filtering Stage for Computational Efficiency in a Flying Capacitor Converter. IEEE Access 2021, 9, 111039–111049. [Google Scholar] [CrossRef]
- Kim, S.H.; Jang, Y.H.; Kim, R.Y. Modeling and Hierarchical Structure Based Model Predictive Control of Cascaded Flying Capacitor Bridge Multilevel Converter for Active Front-End Rectifier in Solid-State Transformer. IEEE Trans. Ind. Electron. 2019, 66, 6560–6569. [Google Scholar] [CrossRef]
- Jang, Y.H.; Kim, S.H.; Kim, R.Y. Model Predictive Control for Cascaded Flying Capacitor Cell Multilevel Converter. In Proceedings of the 2018 Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 30 October–2 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- He, T.; Wu, M.; Lu, D.D.C.; Song, K.; Zhu, J. Model Predictive Sliding Control for Cascaded H-Bridge Multilevel Converters With Dynamic Current Reference Tracking. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1409–1421. [Google Scholar] [CrossRef]
- Baier, C.R.; Ramirez, R.O.; Marciel, E.I.; Hernandez, J.C.; Melin, P.E.; Espinosa, E.E. FCS-MPC Without Steady-State Error Applied to a Grid-Connected Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Power Electron. 2021, 36, 11785–11799. [Google Scholar] [CrossRef]
- Ramírez, R.O.; Baier, C.R.; Villarroel, F.; Espinoza, J.R.; Pou, J.; Rodríguez, J. A Hybrid FCS-MPC With Low and Fixed Switching Frequency Without Steady-State Error Applied to a Grid-Connected CHB Inverter. IEEE Access 2020, 8, 223637–223651. [Google Scholar] [CrossRef]
- Ramírez, R.O.; Baier, C.R.; Espinoza, J.; Villarroel, F. Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter. Energies 2020, 13, 5475. [Google Scholar] [CrossRef]
- Chai, M.; Gorla, N.B.Y.; Panda, S.K. Improved Performance With Dual-Model Predictive Control for Cascaded H-Bridge Multilevel Converter. IEEE Trans. Ind. Appl. 2019, 55, 4886–4899. [Google Scholar] [CrossRef]
- Nasiri, M.R.; Farhangi, S.; Rodriguez, J. Model Predictive Control of a Multilevel CHB STATCOM in Wind Farm Application Using Diophantine Equations. IEEE Trans. Ind. Electron. 2019, 66, 1213–1223. [Google Scholar] [CrossRef]
- Xiao, Q.; Jin, Y.; Jia, H.; Mu, Y.; Ji, Y.; Teodorescu, R.; Blaabjerg, F. Modulated Model Predictive Control for Multilevel Cascaded H-Bridge Converter-Based Static Synchronous Compensator. IEEE Trans. Ind. Electron. 2022, 69, 1091–1102. [Google Scholar] [CrossRef]
- He, T.; Wu, M.; Aguilera, R.P.; Lu, D.D.C.; Liu, Q.; Vazquez, S. Low Computational Burden Model Predictive Control for Single-Phase Cascaded H-Bridge Converters Without Weighting Factor, (early access). IEEE Trans. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Cuzmar, R.H.; Pereda, J.; Aguilera, R.P. Phase-Shifted Model Predictive Control to Achieve Power Balance of CHB Converters for Large-Scale Photovoltaic Integration. IEEE Trans. Ind. Electron. 2021, 68, 9619–9629. [Google Scholar] [CrossRef]
- Gómez, P.J.; Galván, L.; Galván, E.; Carrasco, J.M.; Vázquez, S. Optimal Switching Sequence Model Predictive Control for Single-Phase Cascaded H-Bridge. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, G.; Wang, L.; Yuan, Y.; Zhou, J. A Novel Clustered Voltage Balance for Cascaded H-Bridge STATCOM with CCS-MPC. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, X.; Liu, H.; Mi, Y.; Ji, L.; Wang, Y.; Fu, Y. Improved two-stage model predictive control method for modular multi-level converter. IET Electr. Power Appl. 2021, 15, 1205–1216. [Google Scholar] [CrossRef]
- Wu, W.; Wang, D.; Peng, Z.; Liu, X. Model predictive direct power control for modular multilevel converter under unbalanced conditions with power compensation and circulating current reduction. ISA Trans. 2020, 106, 318–329. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; He, Z.; Yue, Y.; Xu, Q.; Huang, X.; Chen, Y.; Luo, A. A Novel Two-Stage Model Predictive Control for Modular Multilevel Converter With Reduced Computation. IEEE Trans. Ind. Electron. 2019, 66, 2410–2422. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Wu, W.; Ma, J.; Fang, Y.; Peng, Z.; Wang, D. Predictor-Based Neural Network Finite-Set Predictive Control for Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2021, 68, 11621–11627. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Song, S.; Ouyang, S.; Wu, H.; Yang, Y. Modified Increased-Level Model Predictive Control Methods With Reduced Computation Load for Modular Multilevel Converter. IEEE Trans. Power Electron. 2019, 34, 7310–7325. [Google Scholar] [CrossRef]
- Li, M.; Chang, X.; Dong, N.; Liu, S.; Yang, H.; Zhao, R. Arm-Current-Based Model Predictive Control for Modular Multilevel Converter Under Unbalanced Grid Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3195–3206. [Google Scholar] [CrossRef]
- Poblete, P.; Neira, S.; Aguilera, R.P.; Pereda, J.; Pou, J. Sequential Phase-Shifted Model Predictive Control for Modular Multilevel Converters. IEEE Trans. Energy Convers. 2021, 36, 2691–2702. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, X.; Chen, Y. Model Predictive Arm Current Control for Modular Multilevel Converter. IEEE Access 2021, 9, 54700–54709. [Google Scholar] [CrossRef]
- Jin, Y.; Xiao, Q.; Jia, H.; Mu, Y.; Ji, Y.; Dragieevic, T.; Teodorescu, R.; Blaabjerg, F. A Novel Sliding-Discrete-Control-Set Modulated Model Predictive Control for Modular Multilevel Converter. IEEE Access 2021, 9, 10316–10327. [Google Scholar] [CrossRef]
- Zhang, W.; Tan, G.; Wang, Q.; Zhang, X. A model predictive control method based on space vector modulation for MMC. In Proceedings of the 2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 1–4 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Fuchs, S.; Jeong, M.; Biela, J. Long Horizon, Quadratic Programming Based Model Predictive Control (MPC) for Grid Connected Modular Multilevel Converters (MMC). In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 1805–1812. [Google Scholar] [CrossRef]
- Gajare, P.M.; Chakraborty, R.; Dey, A. A Simplified Modulated Model Predictive Control for Modular Multilevel Converter. In Proceedings of the 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25–26 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, W.; Sun, P.; Zhou, G.; Sailijiang, G.; Zhang, Z.; Liu, Y. A Low-Computation Indirect Model Predictive Control for Modular Multilevel Converters. J. Power Electron. 2019, 19, 529–539. [Google Scholar] [CrossRef]
- Mora, A.; Urrutia, M.; Cardenas, R.; Angulo, A.; Espinoza, M.; Diaz, M.; Lezana, P. Model-Predictive-Control-Based Capacitor Voltage Balancing Strategies for Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2019, 66, 2432–2443. [Google Scholar] [CrossRef]
- Gao, X.; Pang, Y.; Xia, J.; Chai, N.; Tian, W.; Rodriguez, J.; Kennel, R. Modulated Model Predictive Control of Modular Multilevel Converters Operating in a Wide Frequency Range. IEEE Trans. Ind. Electron. 2022, 1–12. [Google Scholar] [CrossRef]
- Gao, G.; Lei, W.; Cui, Y.; Li, K.; Hu, X.; Xu, J.; Lv, G. Model Predictive Control of Dual Active Bridge Converter Based on the Lookup Table Method. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 183–186. [Google Scholar] [CrossRef]
- Guennouni, N.; Chebak, A.; Machkour, N. Optimal Dual Active Bridge DC-DC Converter Operation with Minimal Reactive Power for Battery Electric Vehicles Using Model Predictive Control. Electronics 2022, 11, 1621. [Google Scholar] [CrossRef]
- Hosseinzadehtaher, M.; Khan, A.; Baker, M.W.; Shadmand, M.B. Model Predictive Self-healing Control Scheme for Dual Active Bridge Converter. In Proceedings of the 2019 2nd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 19–21 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Han, M.; He, H.; Wang, X.; Dong, Z.; Zhang, Z. Current-Sensorless Model Predictive Control of Dual Active Bridge Converters with Kalman Filter. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 663–667. [Google Scholar] [CrossRef]
- Akter, P.; Uddin, M.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. Model predictive control of bidirectional isolated DC-DC converter for energy conversion system. Int. J. Electron. 2015, 102, 1407–1427. [Google Scholar] [CrossRef]
- López, M.; Mijatovic, N.; Rodriguez, J.; Dragičević, T. Voltage Control Strategy for DAB power converter based on MDCS-MPC. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 584–588. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, X.; Nong, R.; Li, Z.; Zheng, T.Q.; Kobrle, P. Multi-objective Optimization Control for Input-Series Output-Parallel Dual-Active-Bridge DC-DC Converter in EER Application. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 2408–2413. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Li, Z.; Zhao, C.; Gao, F.; Xu, F.; Wang, P. Extended-State-Observer Based Model Predictive Control of a Hybrid Modular DC Transformer. IEEE Trans. Ind. Electron. 2022, 69, 1561–1572. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Li, Z.; Zhao, C.; Gao, F.; Hu, Y.; Luo, L.; Luan, K.; Wang, P. Model predictive control of input-series output-parallel dual active bridge converters based DC transformer. IET Power Electron. 2020, 13, 1144–1152. [Google Scholar] [CrossRef]
- An, F.; Song, W.; Yu, B.; Yang, K. Model Predictive Control With Power Self-Balancing of the Output Parallel DAB DC–DC Converters in Power Electronic Traction Transformer. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1806–1818. [Google Scholar] [CrossRef]
- Martin, S.; Li, H. Model Predictive Control of an Arm Inductor-less MMC-based DC SST. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 2113–2119. [Google Scholar] [CrossRef]
- Martin, S.P.; Dong, X.; Li, H. Model Development and Predictive Control of a Low-Inertia DC Solid State Transformer (SST), (early access). IEEE J. Emerg. Sel. Top. Power Electron. 2022. [Google Scholar] [CrossRef]
- Martin, S.; Li, H.; Anubi, O. Modulated MPC for Arm Inductor-Less MVDC MMC With Reduced Computational Burden. IEEE Trans. Energy Convers. 2021, 36, 1776–1786. [Google Scholar] [CrossRef]
- Akbar, S.M.; Hasan, A.; Watson, A.; Wheeler, P.; Odhano, S. Finite Control Set Model Predictive Control of Isolated DC/DC Modular Multilevel Converter. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 5282–5289. [Google Scholar] [CrossRef]

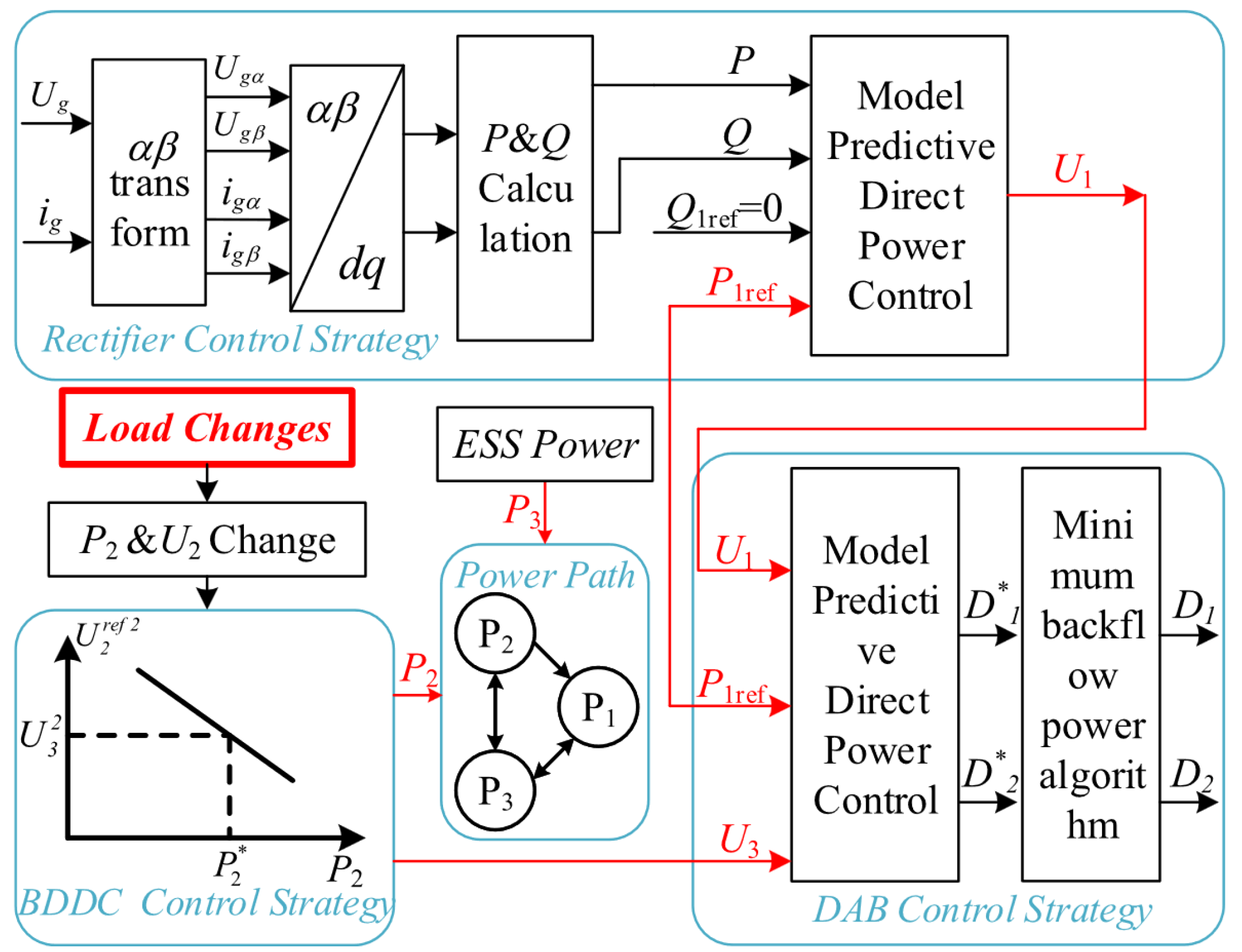
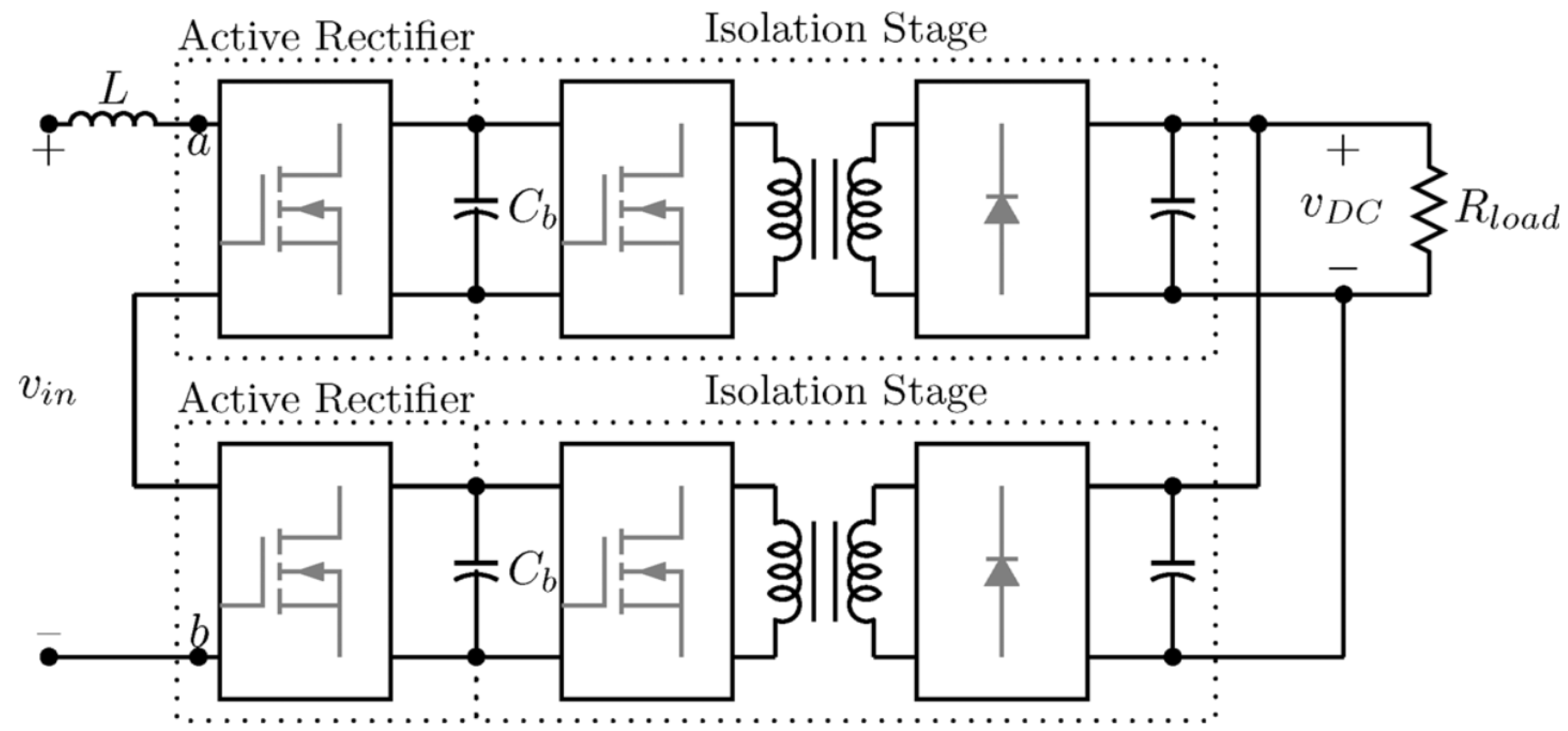
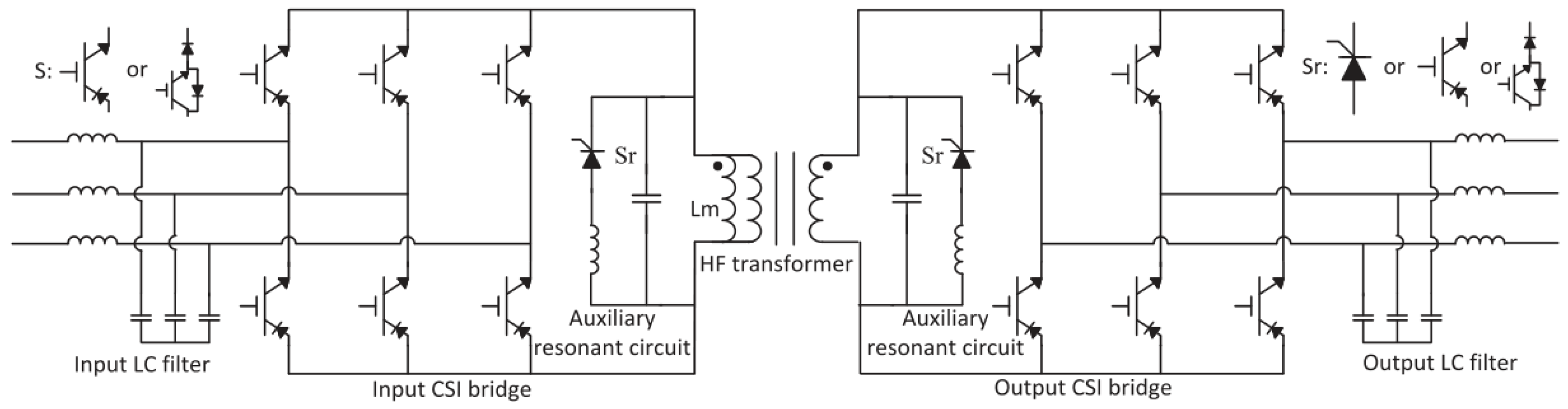
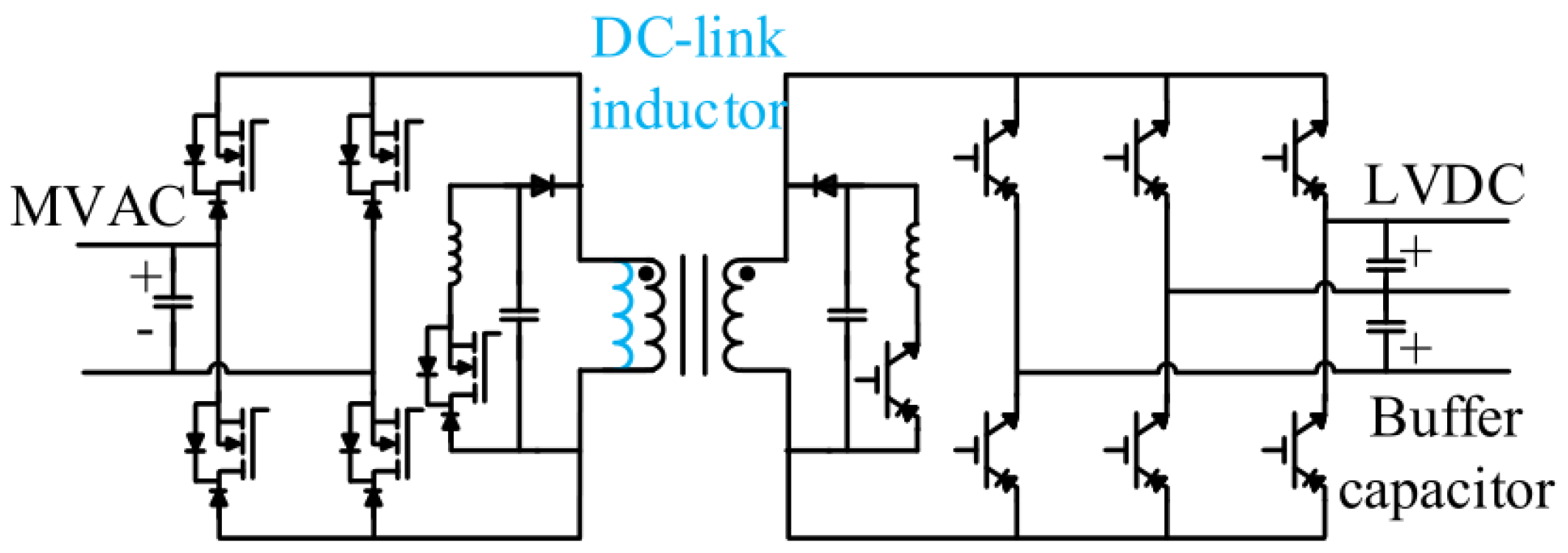
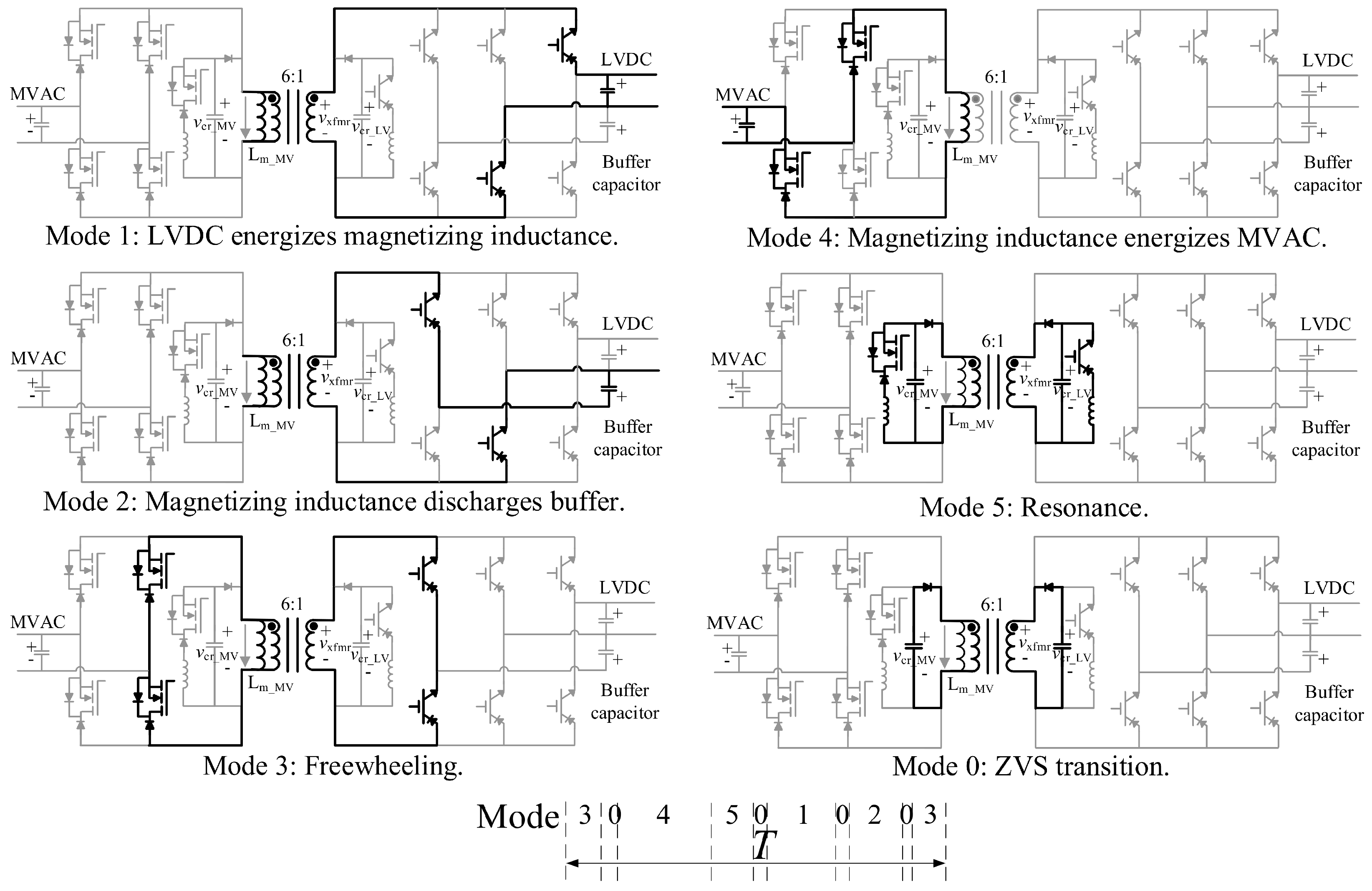

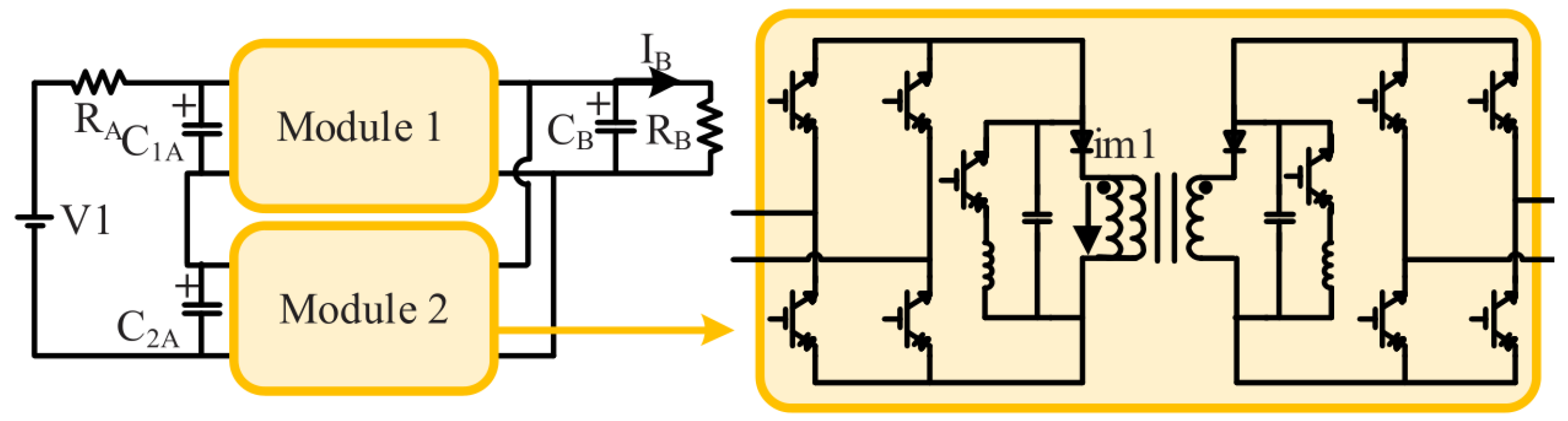
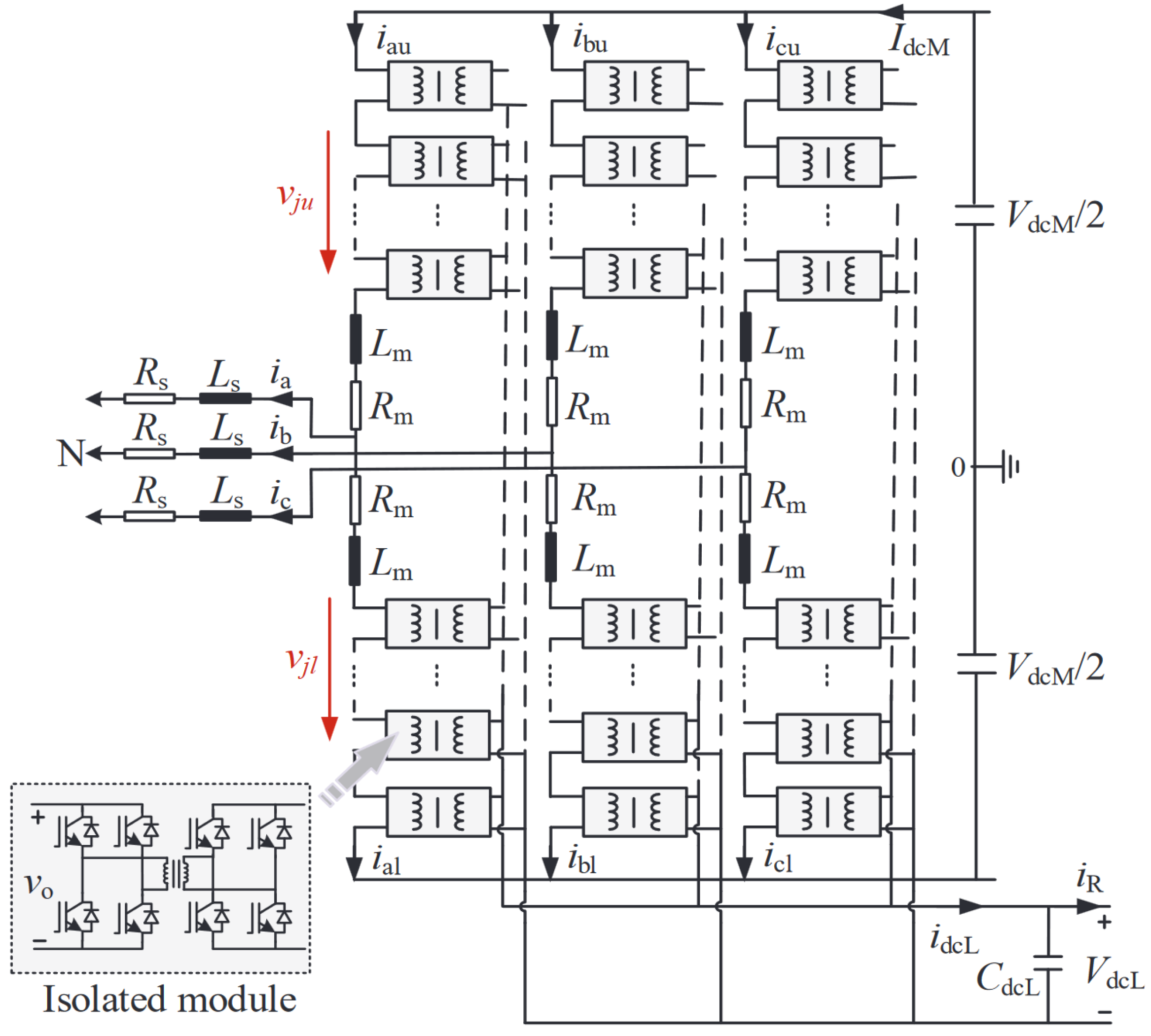
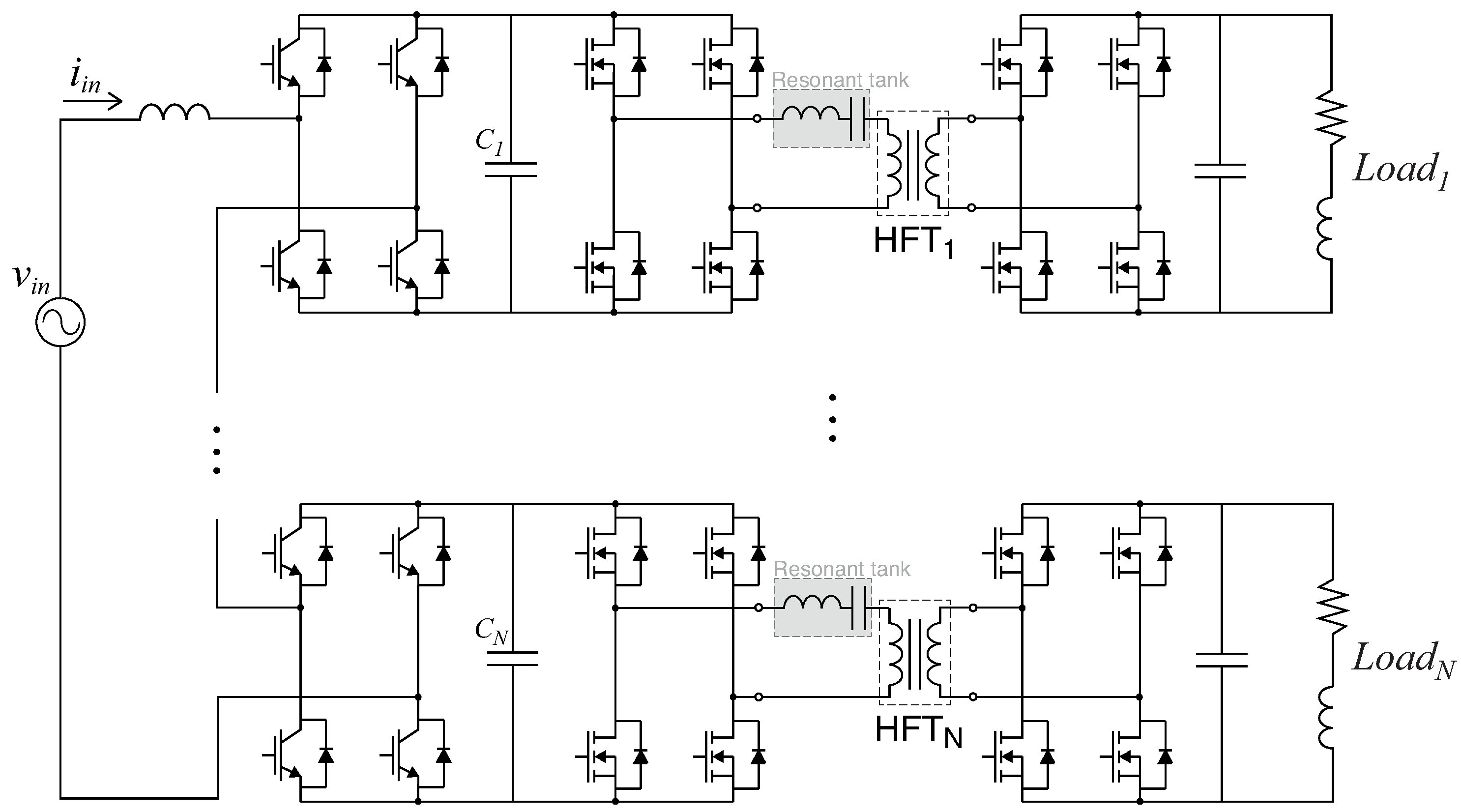



| Work | Application (According to the Authors) | Conversion Stages | Converters/Topology | MPC in All Stages | Type of MPC | Physical Controllers |
|---|---|---|---|---|---|---|
| [24] | Smart grids | AC/AC | Matrix converters | Yes | FCS-MPC | - (w/out exp. validation) |
| [25,26] | Smart grids | AC/AC | Matrix converters | Yes | FCS-MPC | Not mentioned |
| [27] | Smart grids | AC/AC | Matrix converters | Yes | FCS-MPC | dSpace platforms |
| [28] | Smart grids | AC/DC, DC/DC and DC/AC | Vienna rectifier, multilevel DC/DC conv., 3LNPC | Yes | FCS-MPC | - (w/out exp. validation) |
| [29] | Smart grids | AC/DC, DC/DC (and DC/AC) | 2LC, DAB (and 2LC) | Yes | FCS-MPC | - (w/out exp. validation) |
| [30] | Smart grids | AC/DC, DC/DC and DC/AC | 2LC, DAB, 2LC | Yes | FCS-MPC | - (w/out exp. validation) |
| [31] | Smart grids | AC/DC, DC/DC and DC/DC | 2LC, DAB, DC/DC conv. | No | FCS-MPC (2LC) and CCS-MPC (DAB) | DSP + FPGA |
| [32] | Not mentioned | AC/DC and DC/DC | 3LBTB FCC, Diode Rectifier | No | FCS-MPC (AC/DC stage) | FPGA |
| [33] | Various | Flexible (AC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [34] | Various | Flexible (AC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [35] | Not mentioned | Flexible (DC/AC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| Work | Application (According to the Authors) | Conversion Stages | Converters/Topology | MPC in All Stages | Type of MPC | Physical Controllers |
|---|---|---|---|---|---|---|
| [41] | Various | Flexible (AC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [52] | Various | Flexible (AC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [39] | Various | Flexible (DC/DC) | Improved soft-switching SST | Yes | CCS-MPC | - |
| [45] | Various | Flexible (DC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [46] | Various | Flexible (DC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [44] | MVDC microgrids, distrib. grids | Flexible (DC/DC; AC/DC) | Improved soft-switching SST | Yes | CCS-MPC | DSP + FPGA |
| [47] | EV charg., datacenters, DC distrib. | AC/DC, DC/DC | Diode rectifier, SI-3LBC, 3LNPC-based DC/DC converter | No | CCS-MPC (SI-3LBC) | DSP |
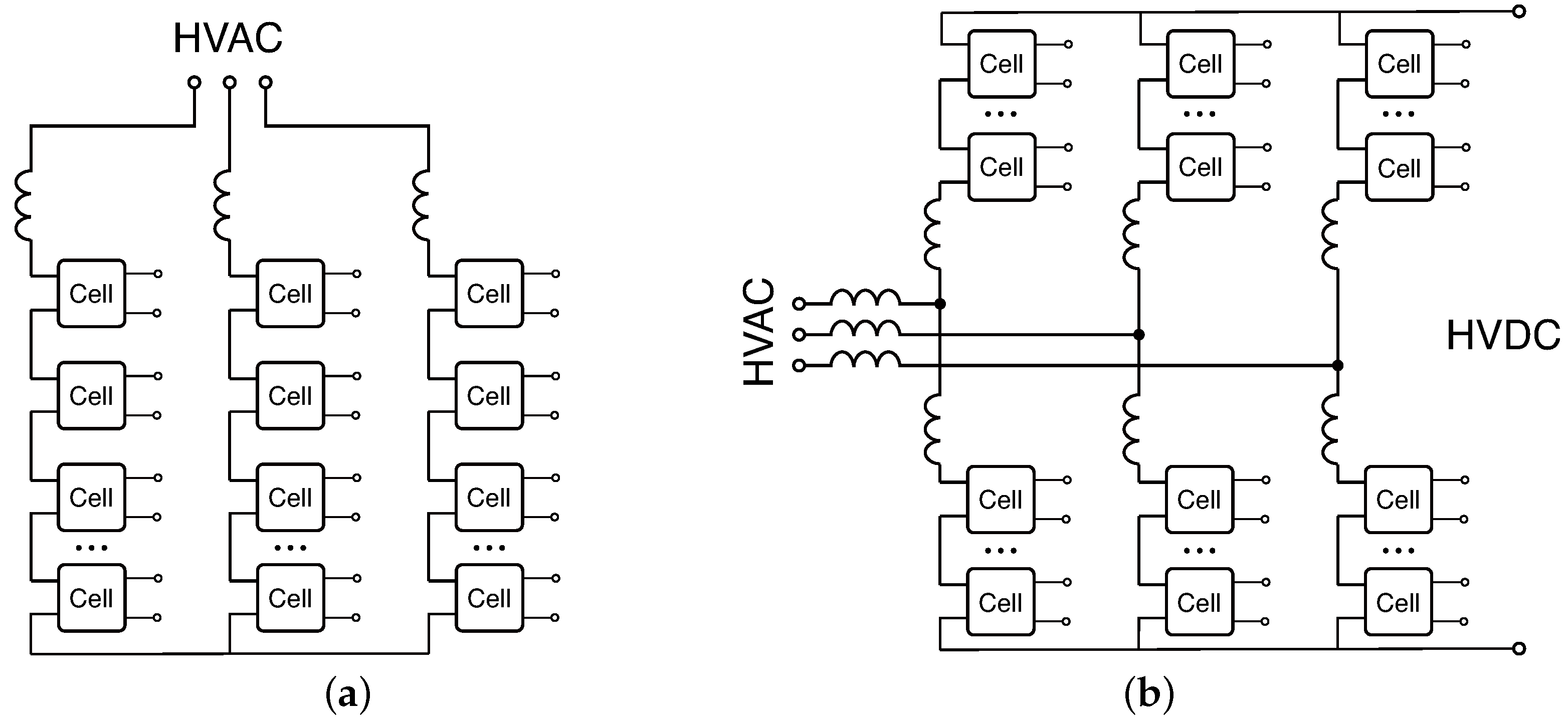
| [48] | Smart grids | AC/DC | MMC with DAB-based cells | Yes | CCS-MPC | - |
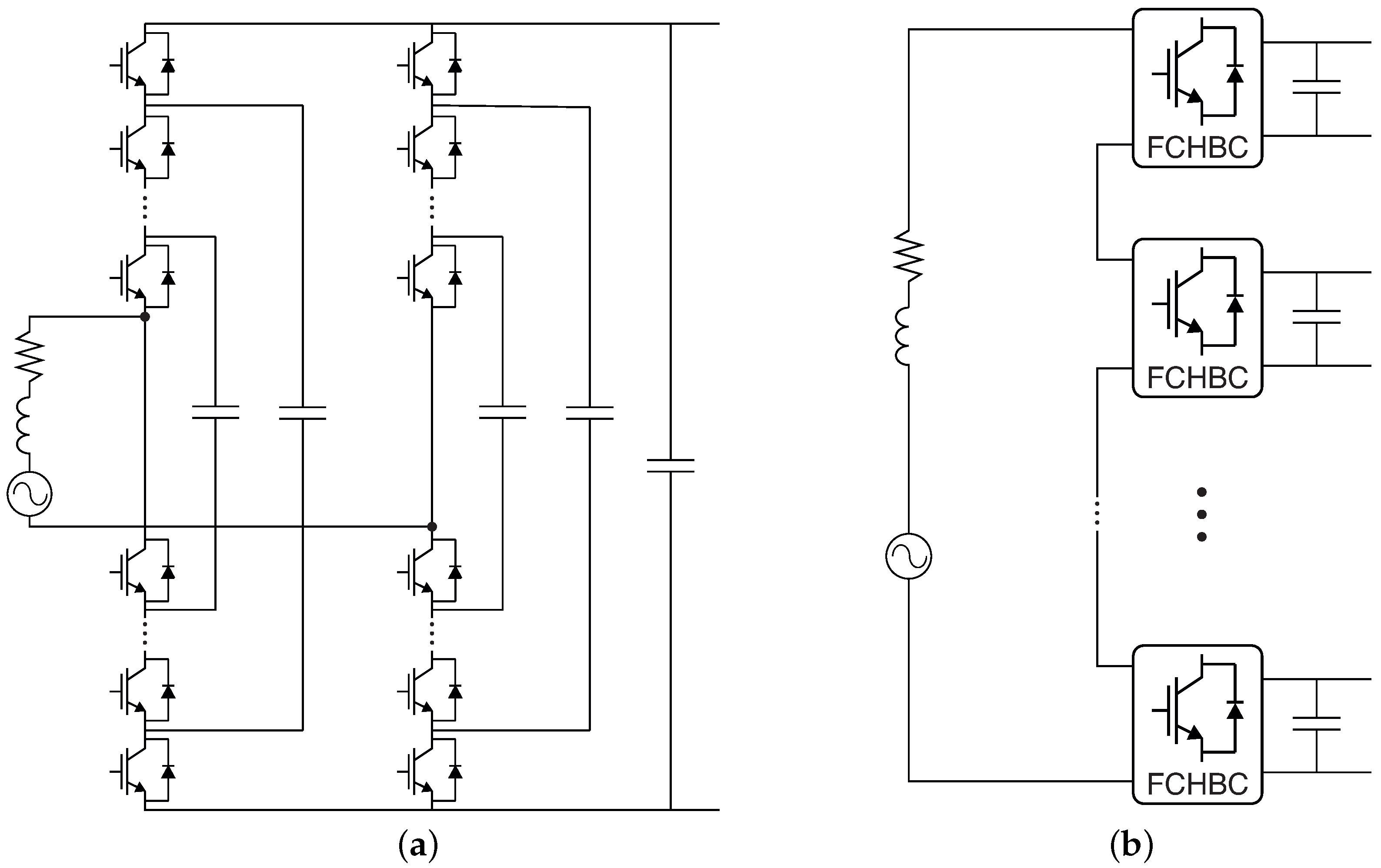
| [49] | Railway traction | AC/DC, DC/DC | CHBC, resonant DABs | No | FCS-MPC (CHBC) | - |
| [8] | Railway traction | AC/DC, DC/DC | CHBC, DABs | Yes | CCS-MPC | DSP + FPGA |
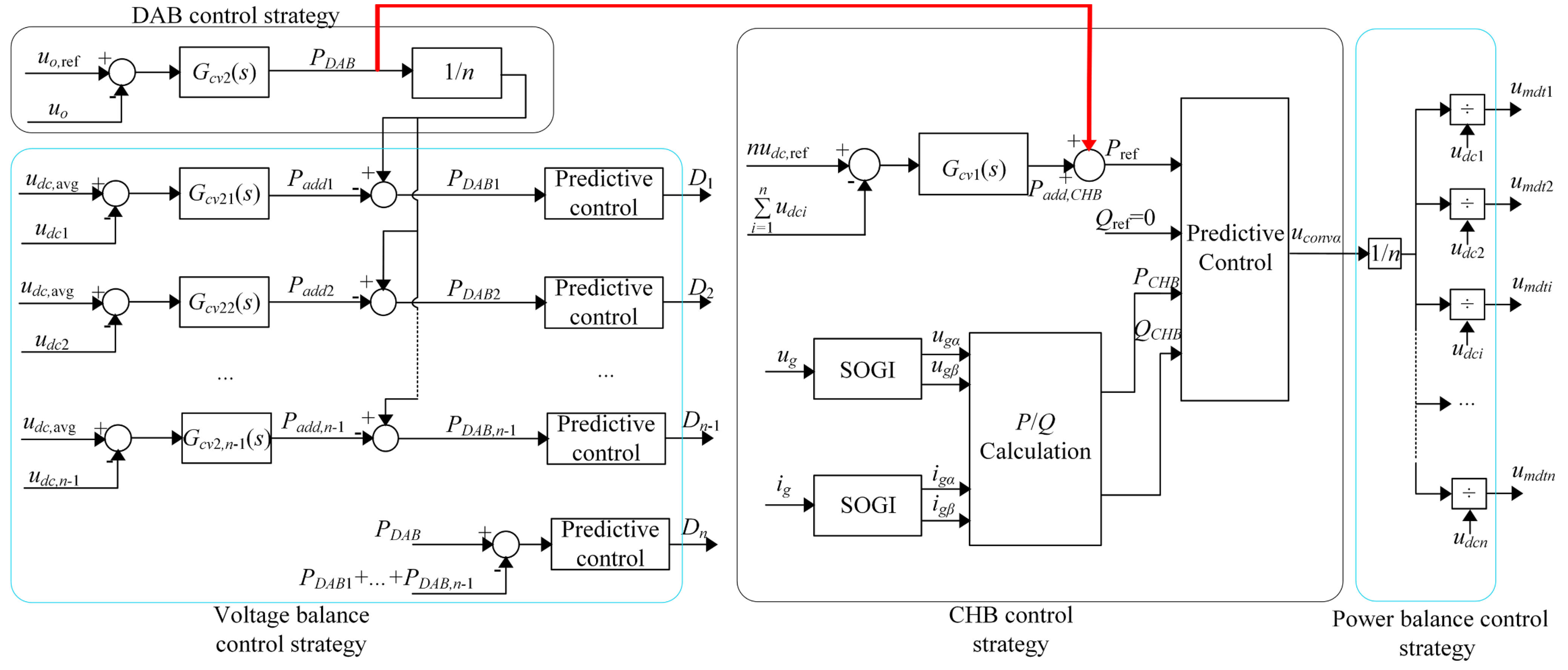
| [50] | AC/AC interconnection | AC/DC, DC/DC and DC/AC | CHBC, DABs, CHBC | No | CCS-MPC (CHBCs) | DSP + FPGA |
| [51] | AC grids interfacing | AC/DC, DC/DC and DC/AC | CHBC, DABs, CHBC | No | CCS-MPC (CHBCs) | DSP + FPGA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, T.; Mendes, A.; Caseiro, L. Model Predictive Control for Solid State Transformers: Advances and Trends. Energies 2022, 15, 8349. https://doi.org/10.3390/en15228349
Oliveira T, Mendes A, Caseiro L. Model Predictive Control for Solid State Transformers: Advances and Trends. Energies. 2022; 15(22):8349. https://doi.org/10.3390/en15228349
Chicago/Turabian StyleOliveira, Tiago, André Mendes, and Luís Caseiro. 2022. "Model Predictive Control for Solid State Transformers: Advances and Trends" Energies 15, no. 22: 8349. https://doi.org/10.3390/en15228349
APA StyleOliveira, T., Mendes, A., & Caseiro, L. (2022). Model Predictive Control for Solid State Transformers: Advances and Trends. Energies, 15(22), 8349. https://doi.org/10.3390/en15228349