A New Optimal Thermal-Based Adaptive Frequency Control for Bidirectional DC–DC Converter with Full-Range ZVS
Abstract
1. Introduction
- The full-range ZVS can be achieved by the use of the proposed OTC, and there is no need for any expensive current sensors or complex ZCD circuits. Only the low-cost NTC resistors are required to detect the temperature which is much cheaper than the traditional methods are.
- The proposed OTC to achieve full-range ZVS does not depend on accurate circuit parameters and voltage or current sampling values. Hence, the susceptibility of the parameters is reduced, and the control method is simple without the need for complicated calculations.
- The temperature of the semiconductor device is directly monitored, which can effectively protect the device.
2. Theory of Operation
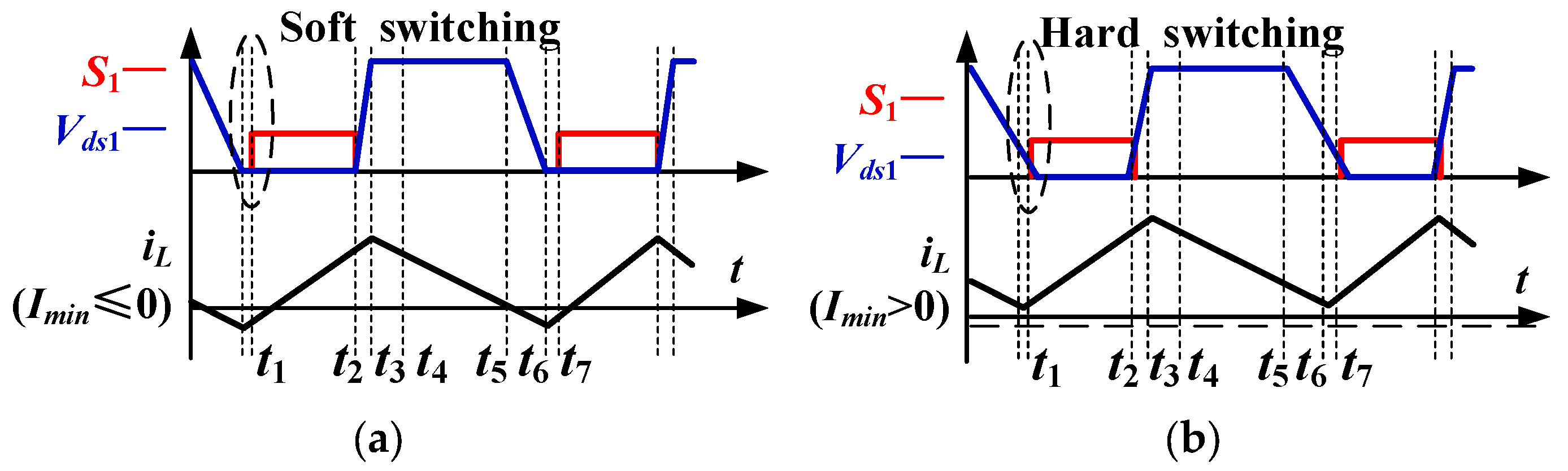
2.1. Operation of Bidirectional Converter with BCM
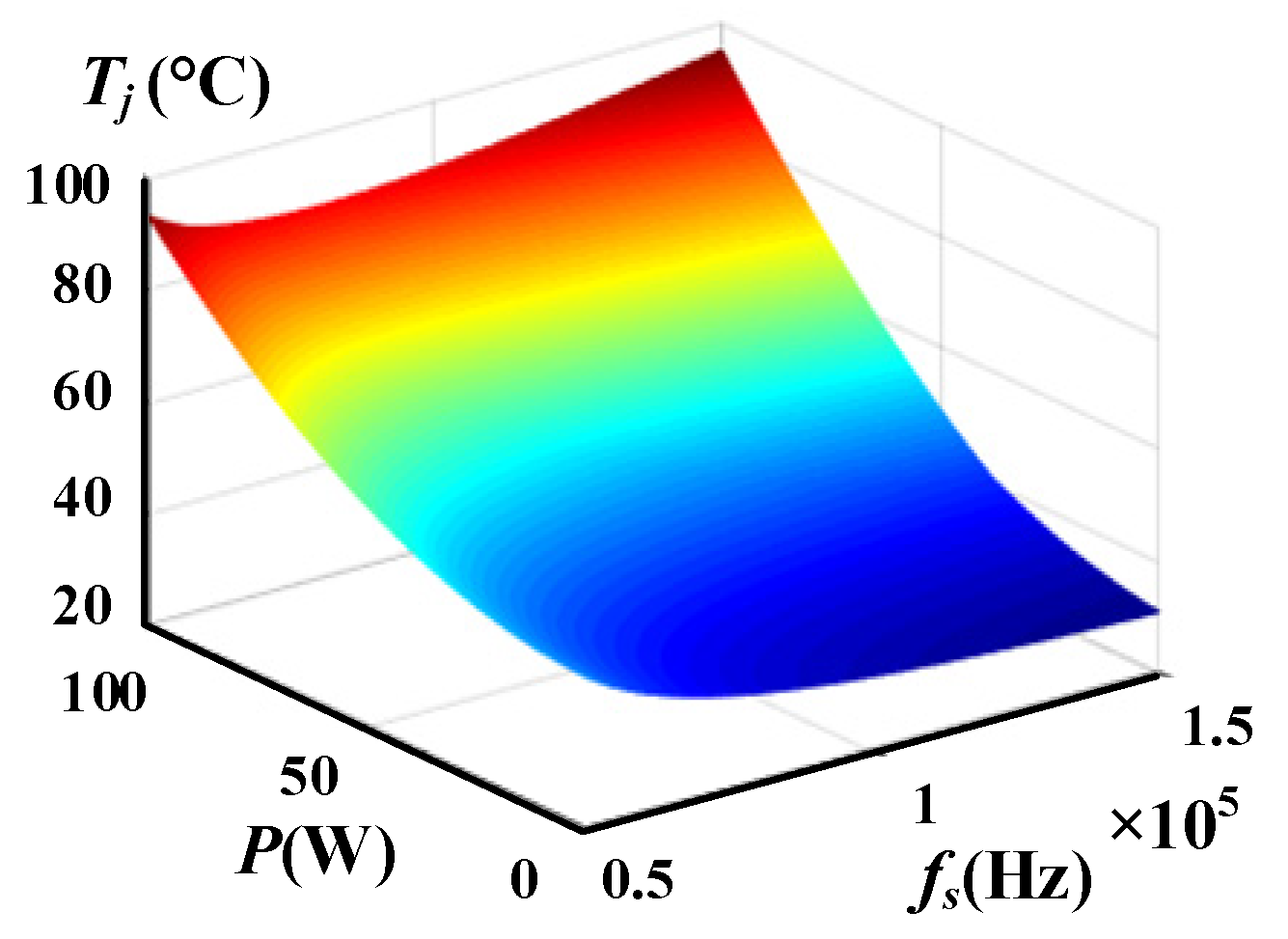
2.2. The Relationship between Switching Frequency and Switch Temperature
3. Optimal Thermal-Based Adaptive Frequency Control
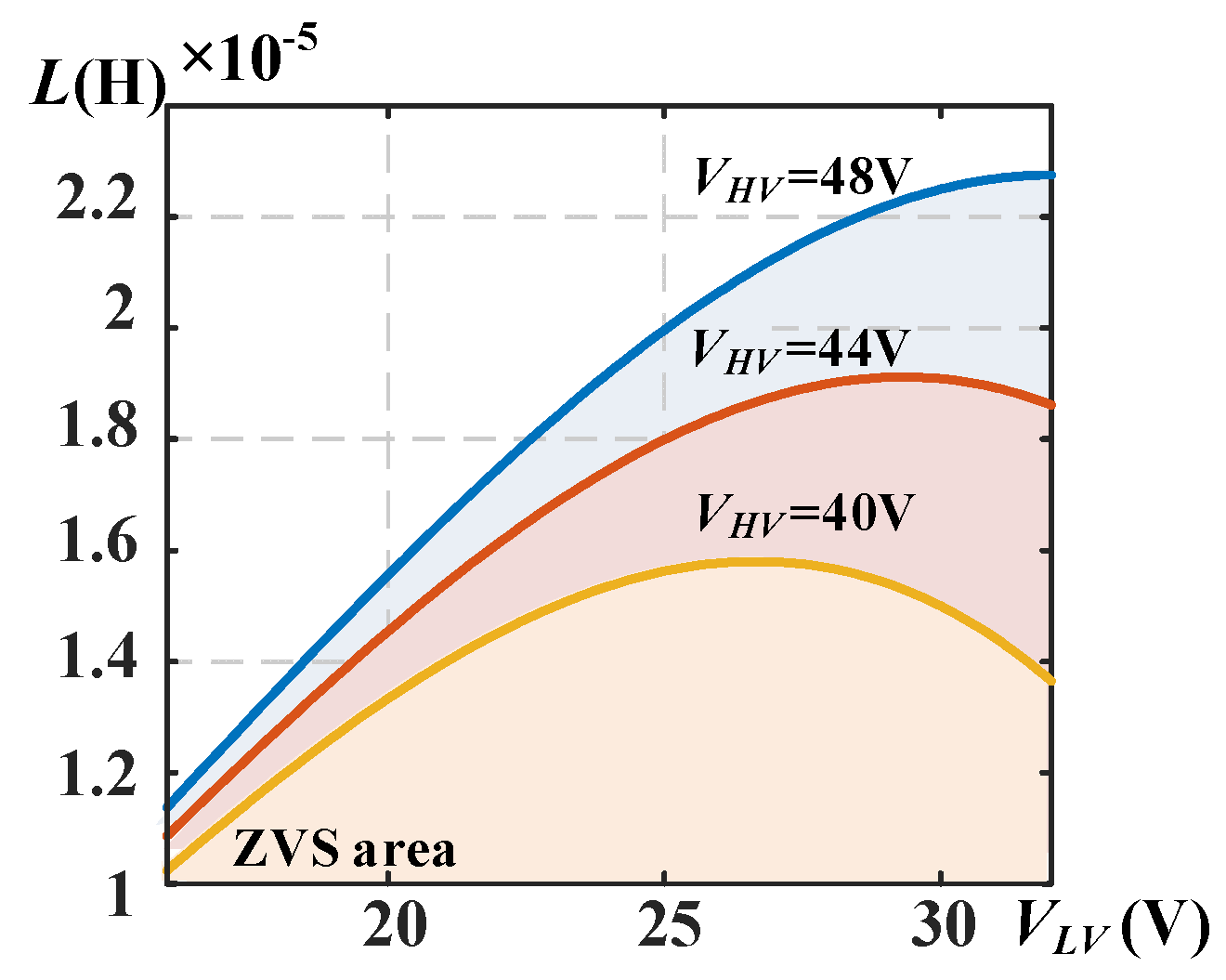
3.1. Optimal Temperature Control (OTC) Algorithm
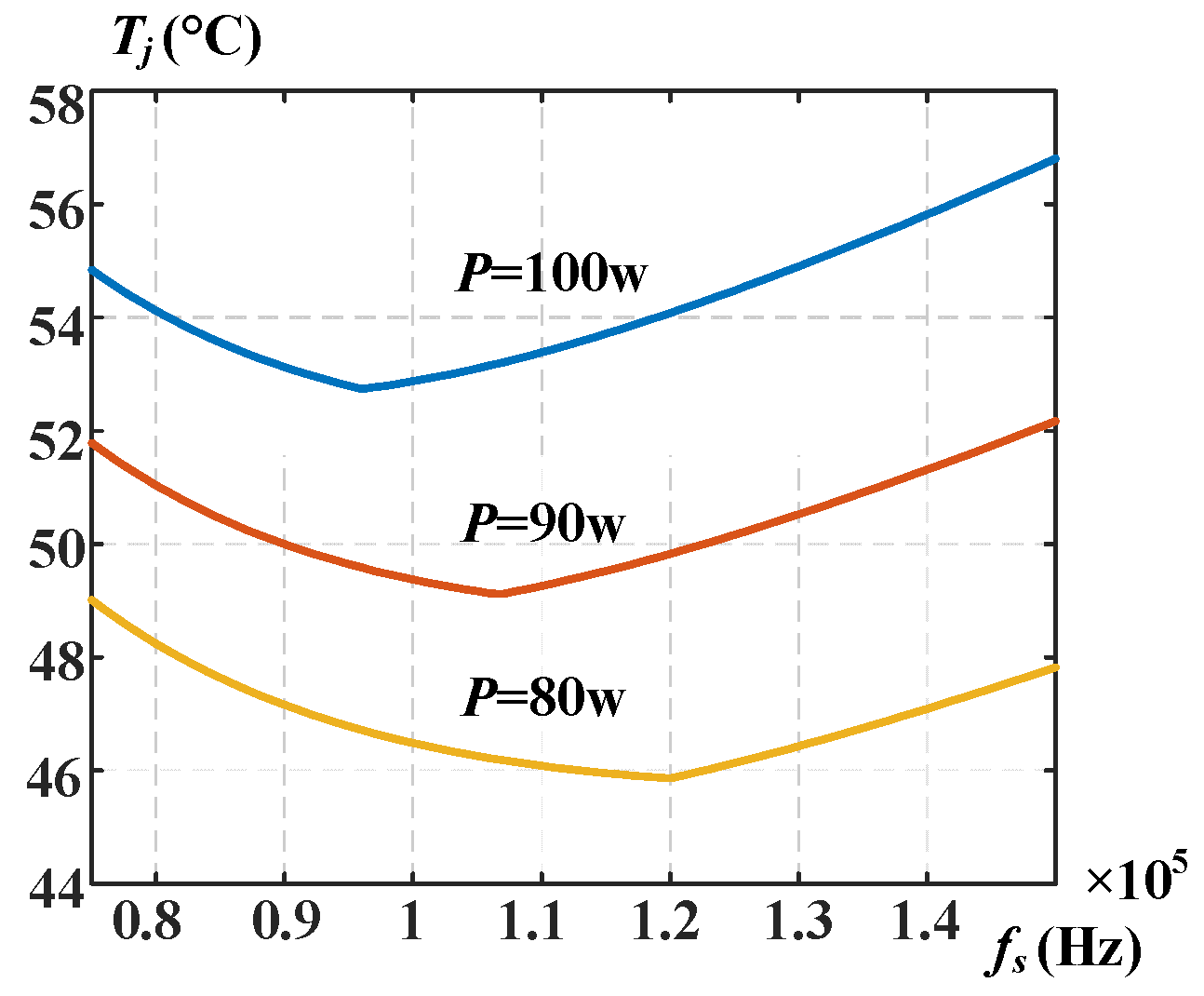
3.2. Simulation of Proposed Method
3.3. Conparison of ZVS Methods
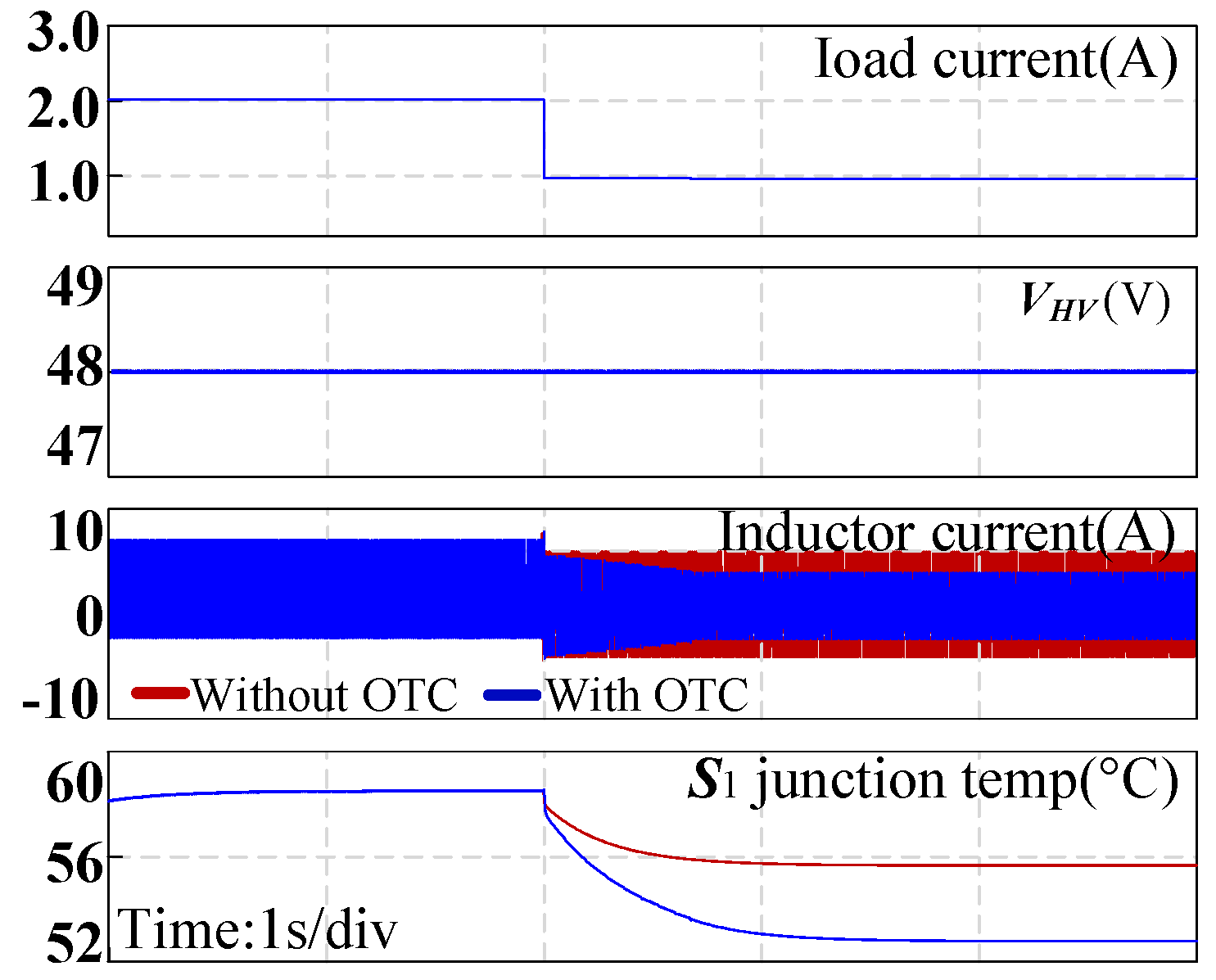
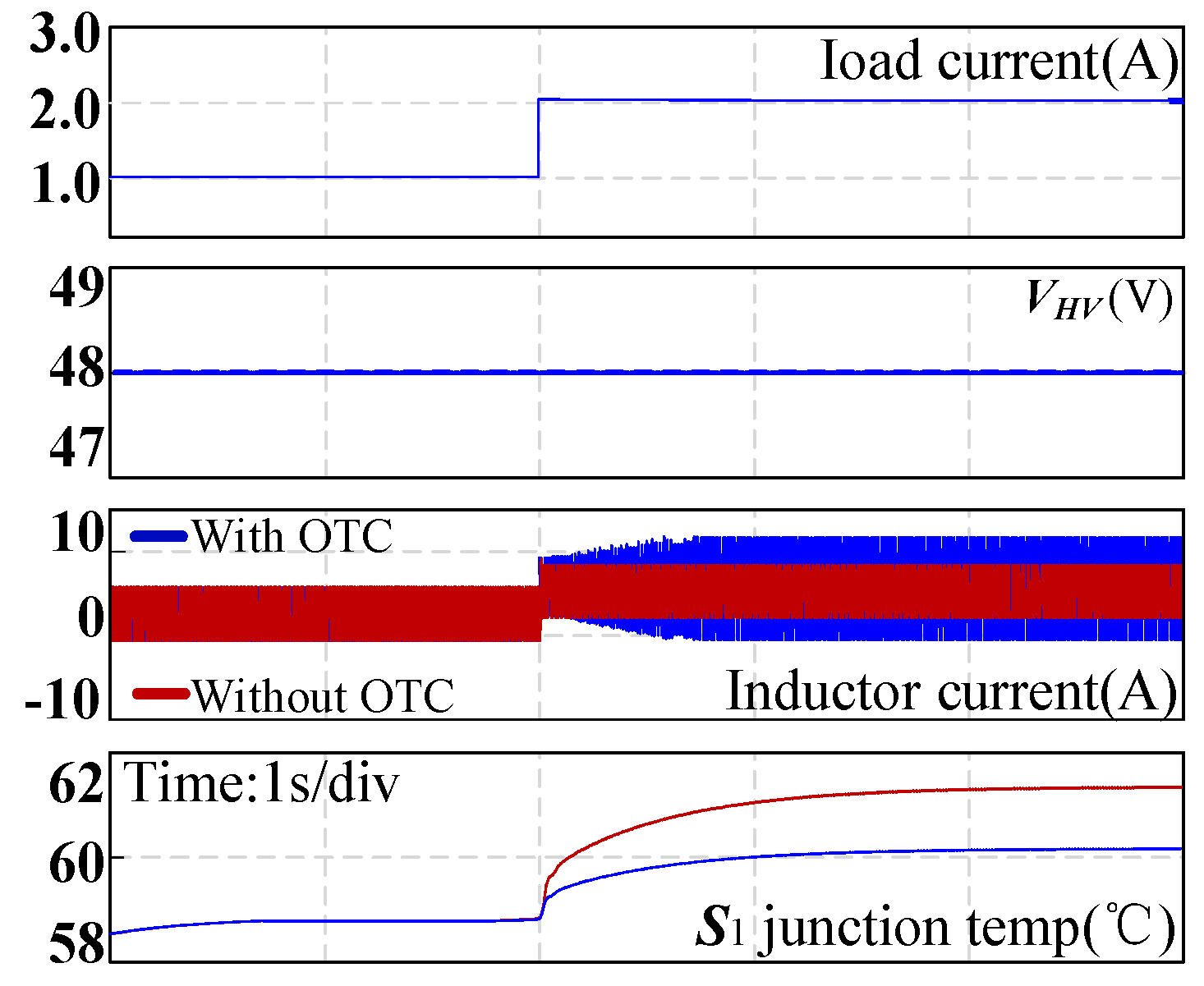
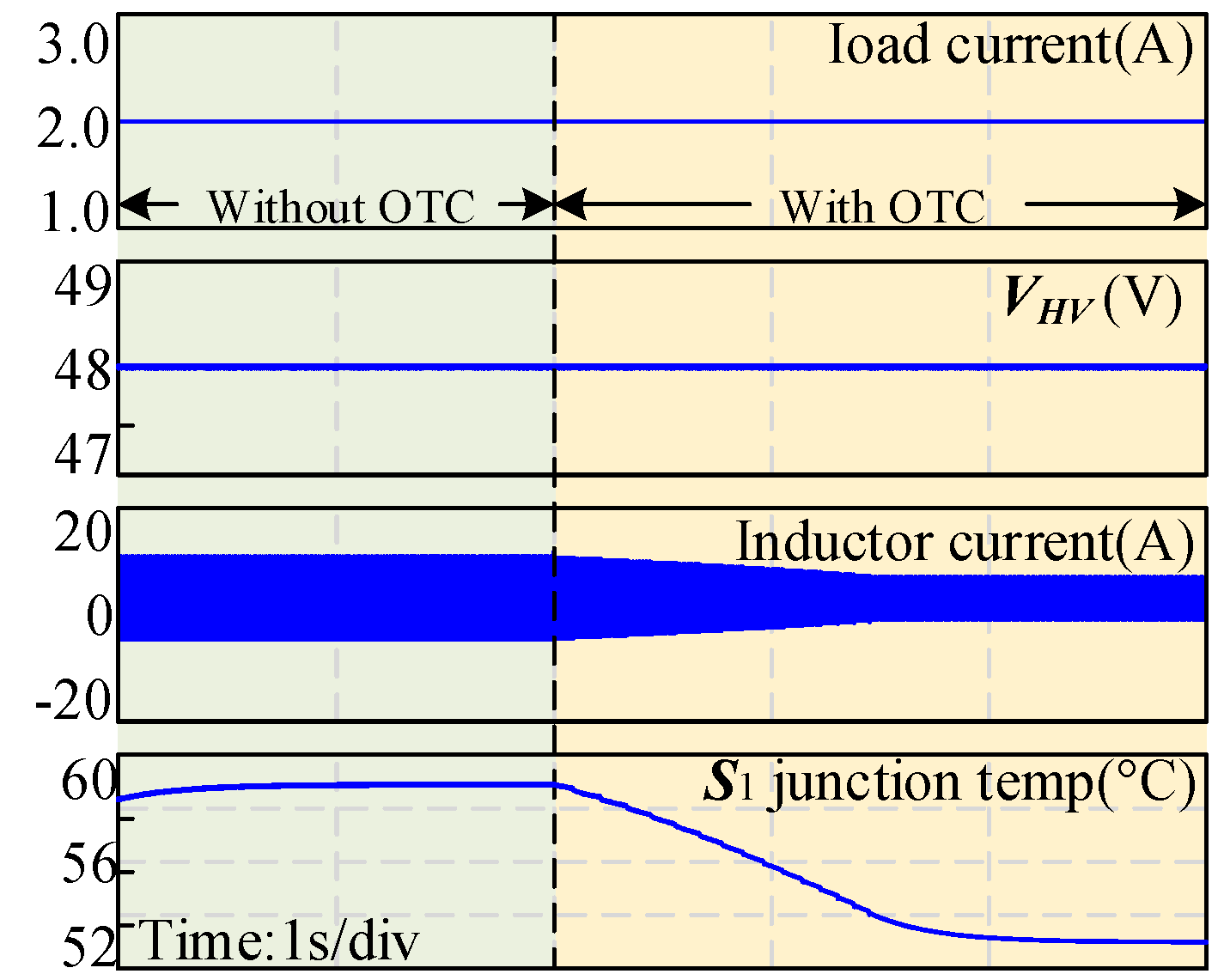
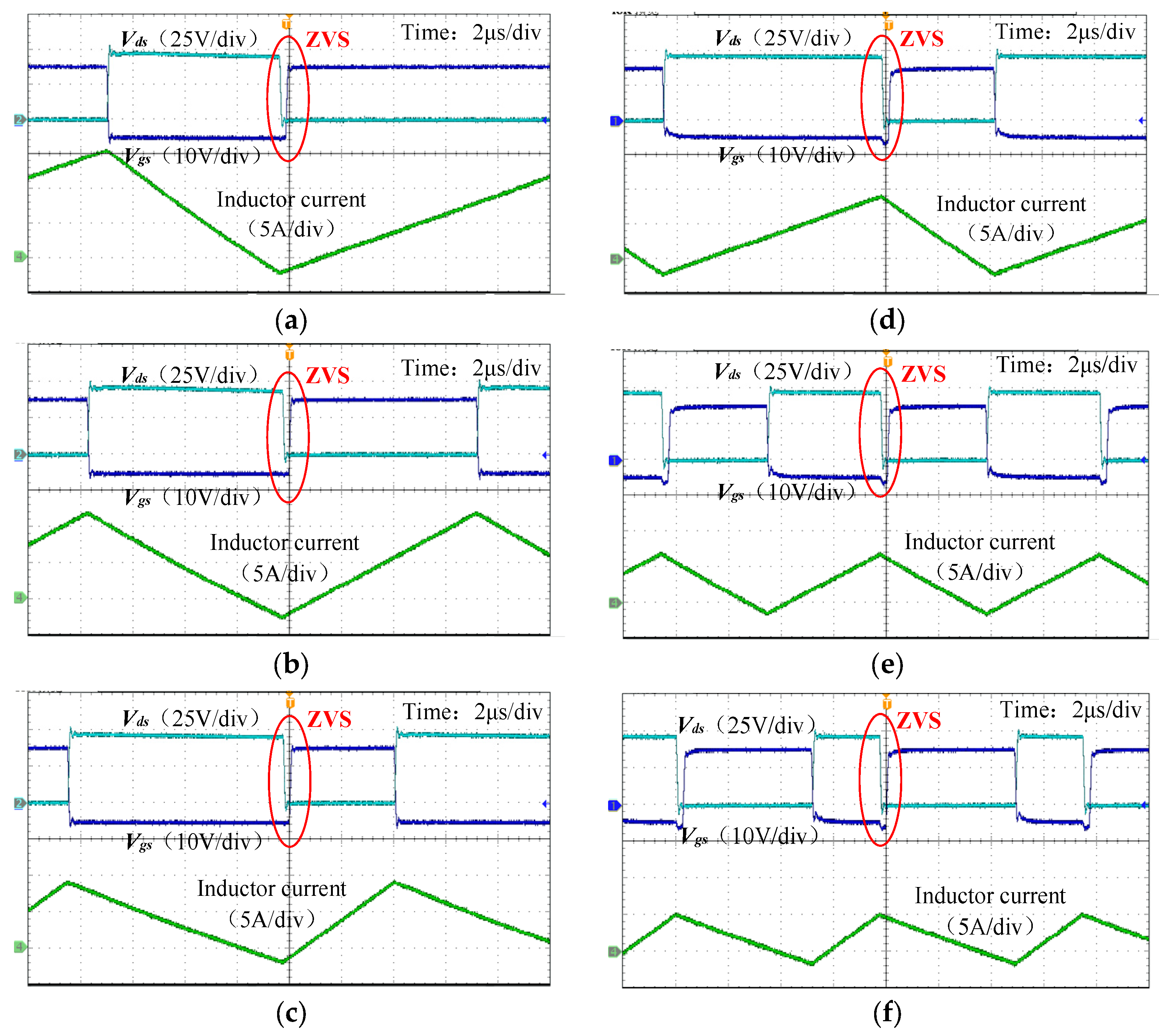
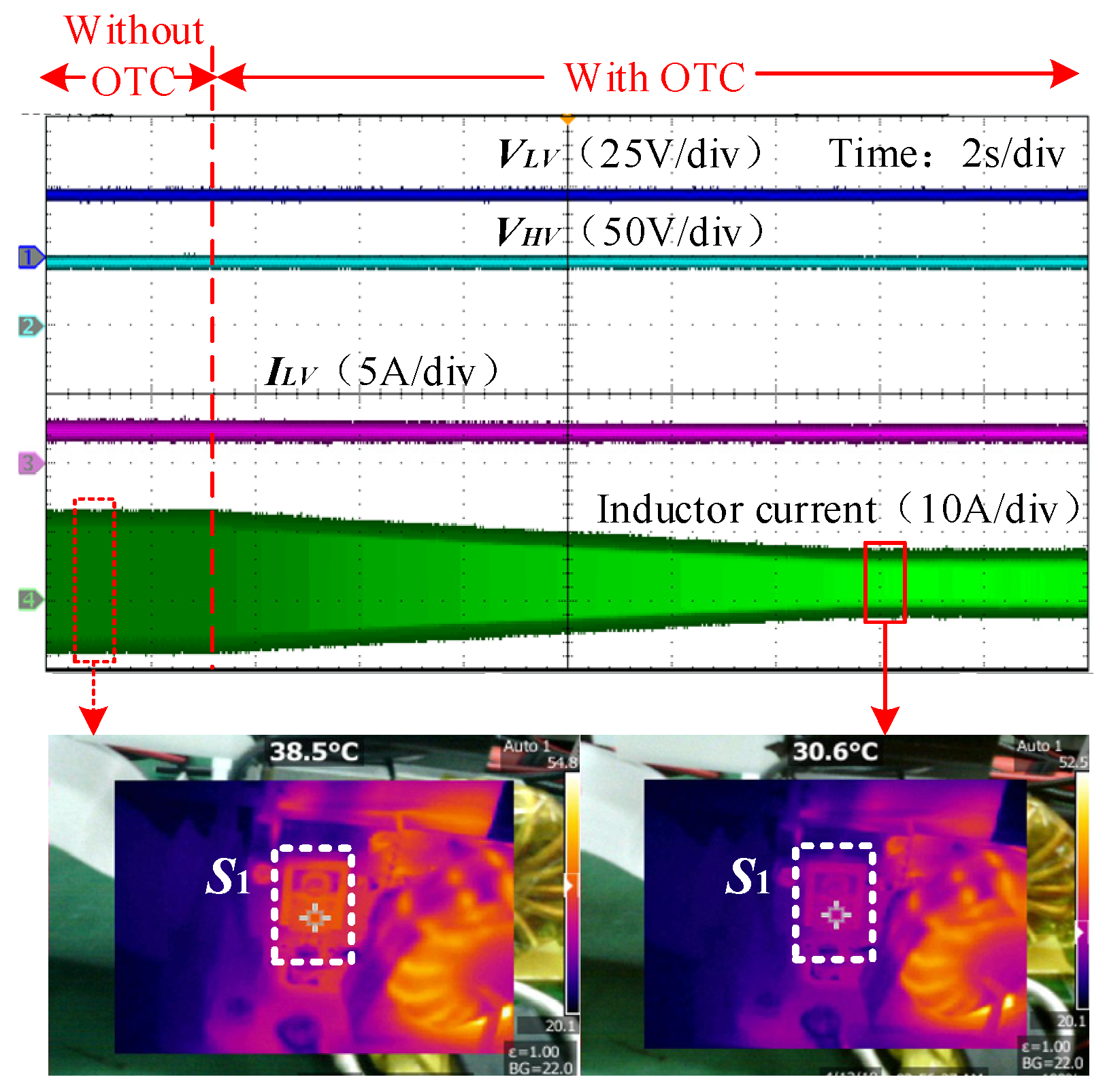
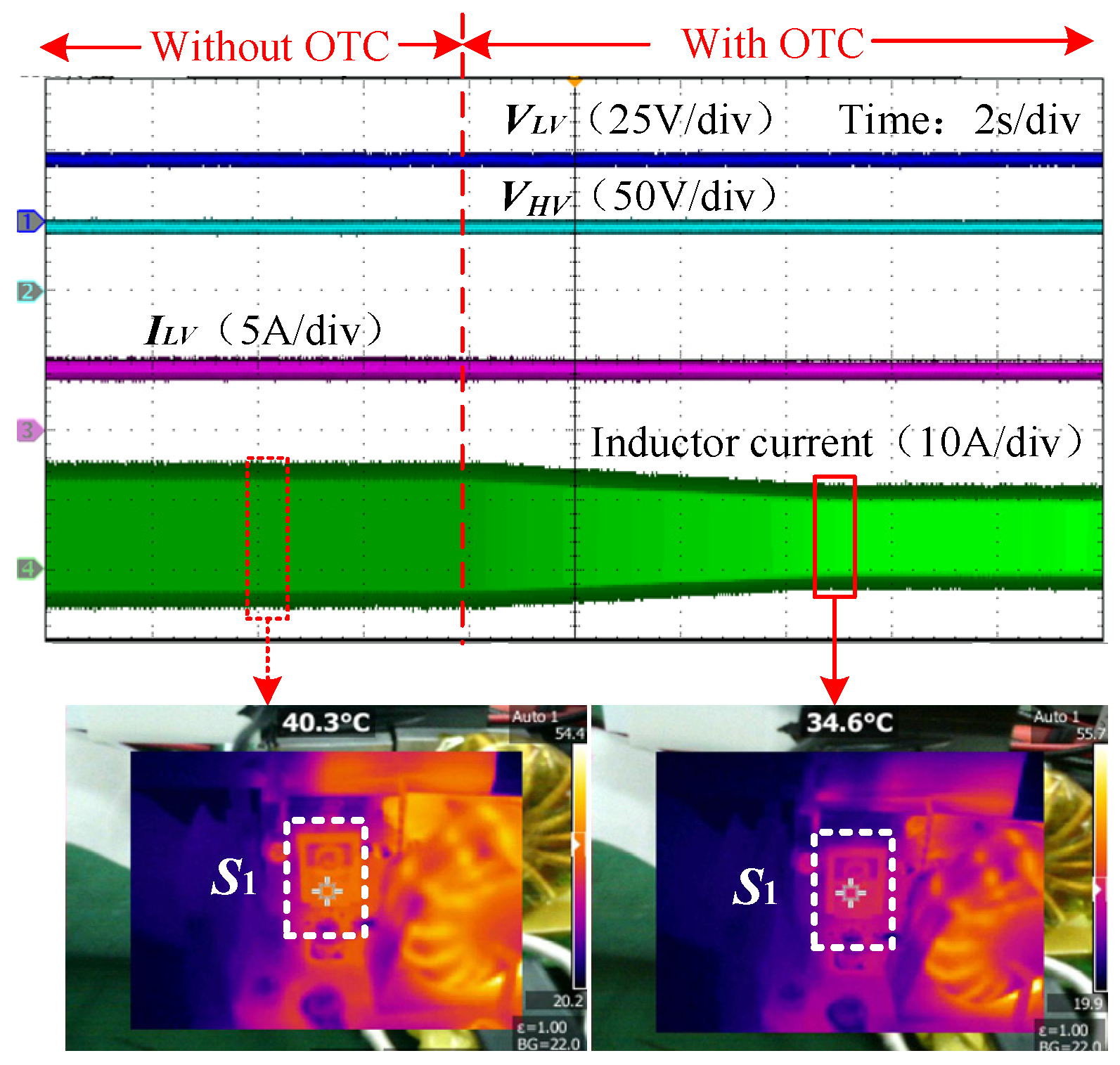
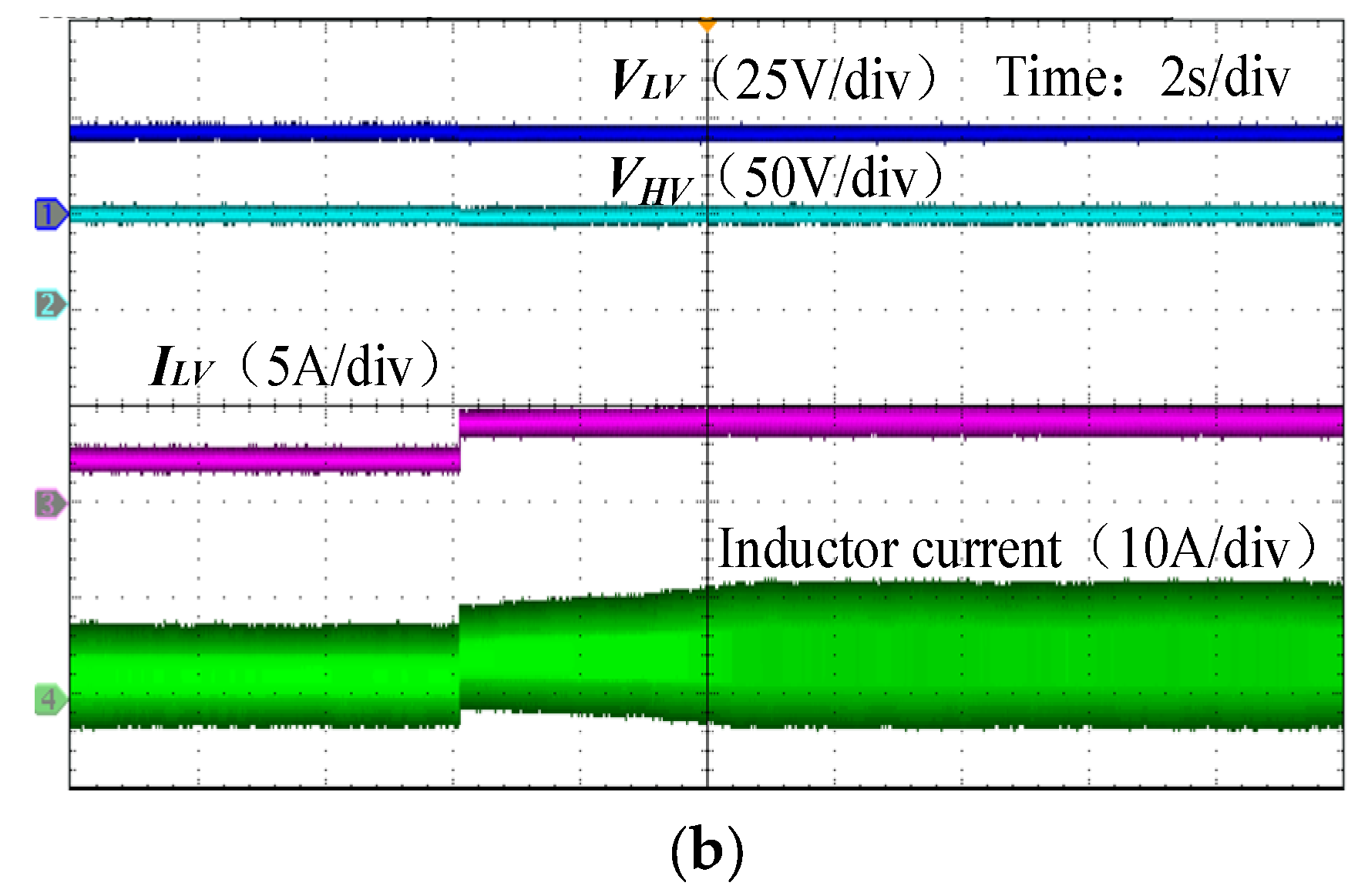
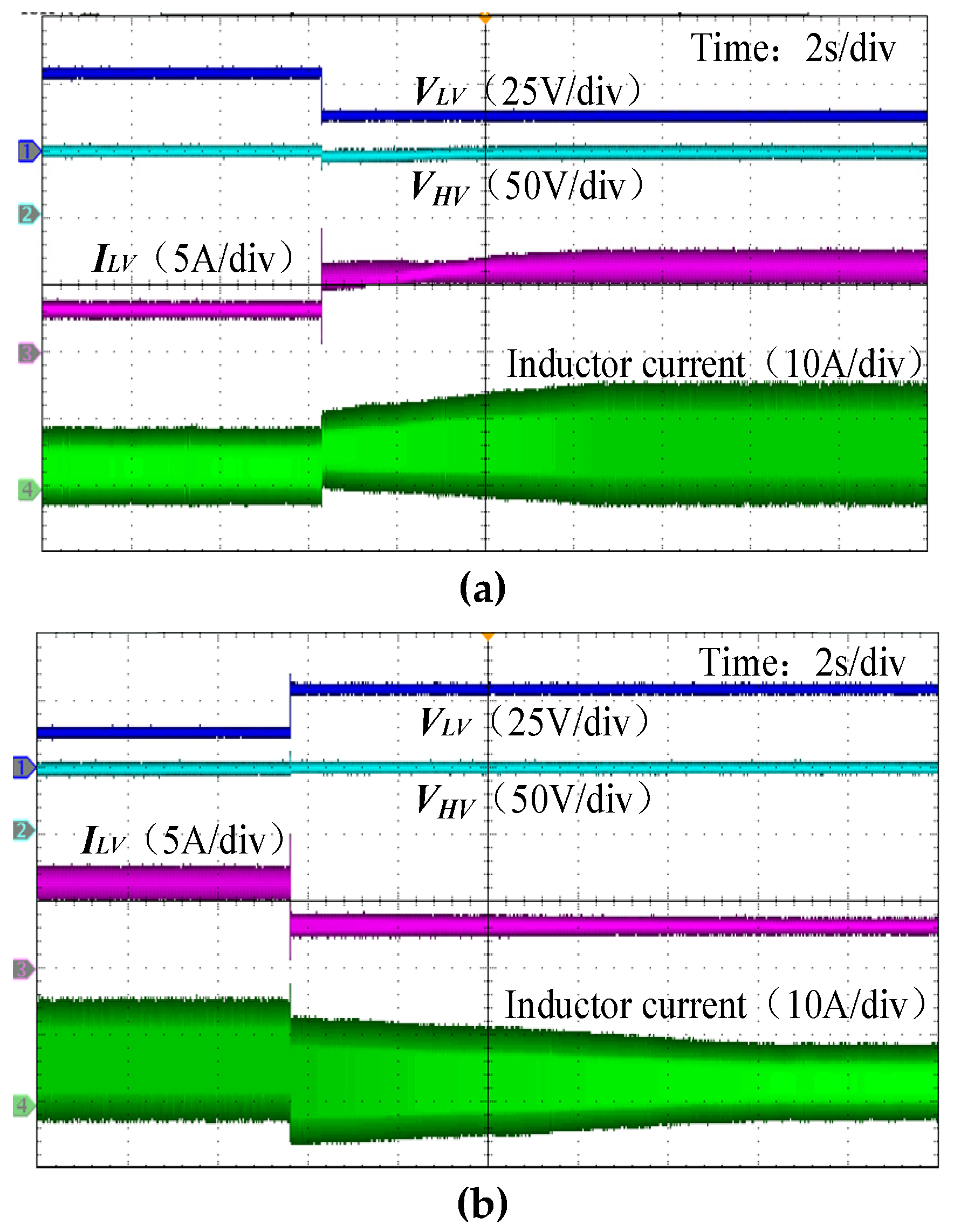
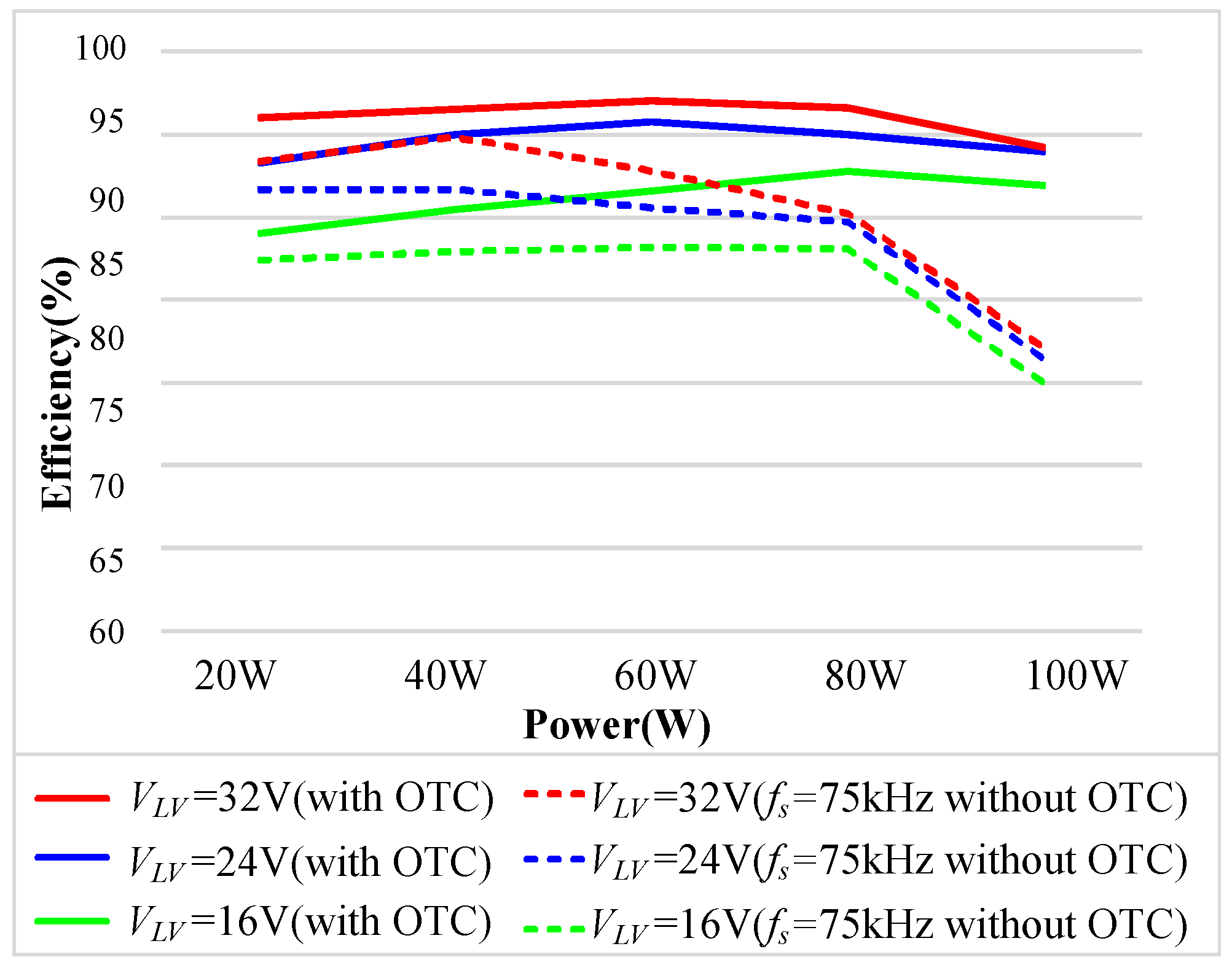
4. Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Loss analysis of Imin > 0 (without ZVS)
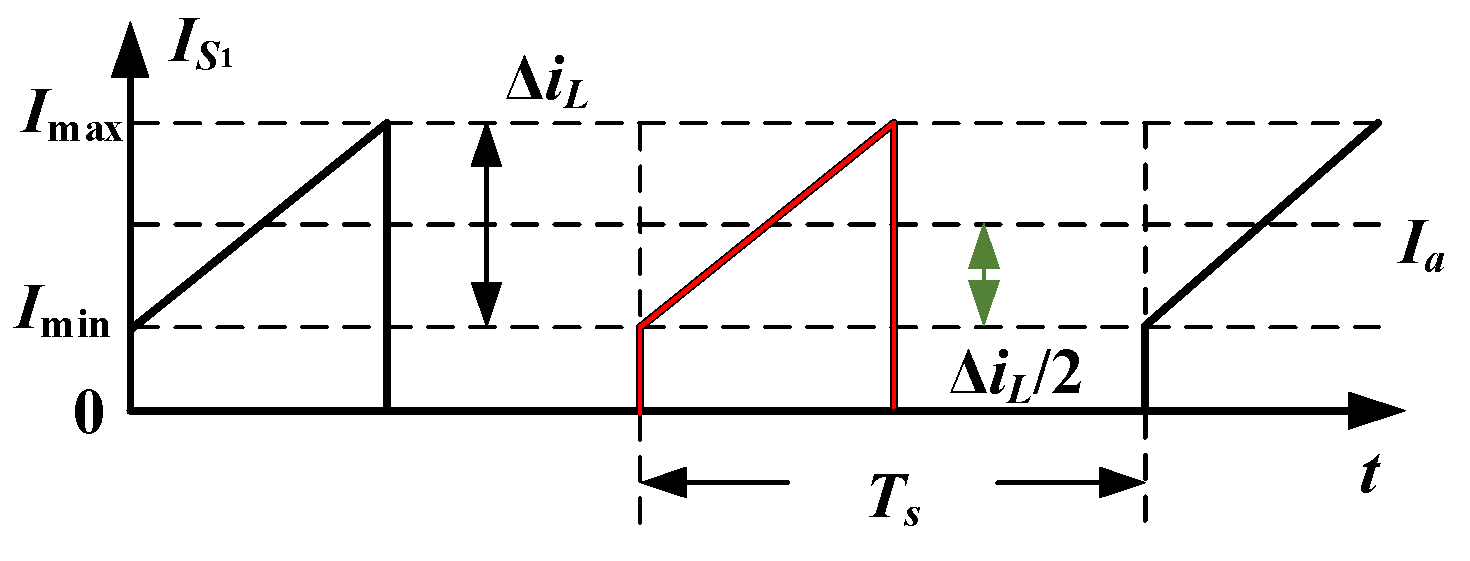
- 2.
- Loss analysis of Imin ≤ 0 (with ZVS)

References
- Xu, Q.; Vafamand, N.; Chen, L.; Dragičević, T.; Xie, L.; Blaabjerg, F. Review on Advanced Control Technologies for Bidirectional DC/DC Converters in DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1205–1221. [Google Scholar] [CrossRef]
- Jiang, W.; Fahimi, B. Active Current Sharing and Source Management in Fuel Cell–Battery Hybrid Power System. IEEE Trans. Ind. Electron. 2010, 57, 752–761. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, B.; Jasni, J.; Radzi, M.A.M.; Azis, N.; Zhang, Q. Model Control and Digital Implementation of the Three Phase Interleaved Parallel Bidirectional Buck–Boost Converter for New Energy Electric Vehicles. Energies 2022, 15, 7178. [Google Scholar] [CrossRef]
- Wu, H.; Sun, K.; Chen, L.; Zhu, L.; Xing, Y. High Step-Up/Step-Down Soft-Switching Bidirectional DC–DC Converter with Coupled-Inductor and Voltage Matching Control for Energy Storage Systems. IEEE Trans. Ind. Electron. 2016, 63, 2892–2903. [Google Scholar] [CrossRef]
- Shen, J.; Khaligh, A. A Supervisory Energy Management Control Strategy in a Battery/Ultracapacitor Hybrid Energy Storage System. IEEE Trans. Transp. Electrif. 2015, 1, 223–231. [Google Scholar] [CrossRef]
- Kim, N.-G.; Han, B.; Jo, S.-W.; Kim, M. High-Voltage-Gain Soft-Switching Converter Employing Bidirectional Switch for Fuel-Cell Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 8731–8743. [Google Scholar] [CrossRef]
- Khan, M.A.; Ahmed, A.; Husain, I.; Sozer, Y.; Badawy, M. Performance Analysis of Bidirectional DC–DC Converters for Electric Vehicles. IEEE Trans. Ind. Appl. 2015, 51, 3442–3452. [Google Scholar] [CrossRef]
- Das, P.; Laan, B.; Mousavi, S.A.; Moschopoulos, G. A Nonisolated Bidirectional ZVS-PWM Active Clamped DC–DC Converter. IEEE Trans. Power Electron. 2009, 24, 553–558. [Google Scholar] [CrossRef]
- Hwang, T.; Park, S. Seamless Boost Converter Control Under the Critical Boundary Condition for a Fuel Cell Power Conditioning System. IEEE Trans. Power Electron. 2012, 27, 3616–3626. [Google Scholar] [CrossRef]
- Wu, H.; Lu, J.; Shi, W.; Xing, Y. Nonisolated Bidirectional DC–DC Converters with Negative-Coupled Inductor. IEEE Trans. Power Electron. 2012, 27, 2231–2235. [Google Scholar] [CrossRef]
- Chiang, C.; Chen, C. Zero-Voltage-Switching Control for a PWM Buck Converter Under DCM/CCM Boundary. IEEE Trans. Power Electron. 2009, 24, 2120–2126. [Google Scholar] [CrossRef]
- Qahouq, J.A.A.; Abdel-Rahman, O.; Huang, L.; Batarseh, I. On Load Adaptive Control of Voltage Regulators for Power Managed Loads: Control Schemes to Improve Converter Efficiency and Performance. IEEE Trans. Power Electron. 2007, 22, 1806–1819. [Google Scholar] [CrossRef]
- Lee, C.-S.; Oh, Y.-J.; Na, K.-Y.; Kim, Y.-S.; Kim, N.-S. Integrated BiCMOS Control Circuits for High-Performance DC–DC Boost Converter. IEEE Trans. Power Electron. 2013, 28, 2596–2603. [Google Scholar] [CrossRef]
- Yan, W.; Li, W.; Liu, R. A Noise-Shaped Buck DC–DC Converter with Improved Light-Load Efficiency and Fast Transient Response. IEEE Trans. Power Electron. 2011, 26, 3908–3924. [Google Scholar] [CrossRef]
- Panov, Y.; Jovanovic, M.M. Adaptive off-time control for variable frequency, soft-switched flyback converter at light loads. IEEE Trans. Power Electron. 2002, 17, 596–603. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, A.Q. Variable Frequency Average Current Mode Control for ZVS Symmetrical Dual-Buck H-Bridge All-GaN Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 4416–4427. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, H.; Wu, J.; Yang, X.; Wang, L. Adaptive Driving Scheme for ZVS and Minimizing Circulating Current in MHz CRM Converters. IEEE Trans. Power Electron. 2021, 36, 3633–3637. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, Y.; Guo, Z.; Wu, Y.; Zhang, Z.; Chen, Q. Simple Analog-Based Accurate Variable On-Time Control for Critical Conduction Mode Boost Power Factor Correction Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 4025–4036. [Google Scholar] [CrossRef]
- Liu, C.; Lee, H.; Liao, P.; Chen, Y.; Chung, M.; Chen, P. Dual-Source Energy-Harvesting Interface with Cycle-by-Cycle Source Tracking and Adaptive Peak-Inductor-Current Control. IEEE J. Solid-State Circuits 2018, 53, 2741–2750. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, P.-H.; Okuma, Y.; Ishida, K.; Ryu, Y.; Watanabe, K.; Sakurai, T.; Takamiya, M. A 0.6 V Input CCM/DCM Operating Digital Buck Converter in 40 nm CMOS. IEEE J. Solid-State Circuits 2014, 49, 2377–2386. [Google Scholar] [CrossRef]
- Radić, A.; Straka, A.; Prodić, A. Synchronized Zero-Crossing-Based Self-Tuning Capacitor Time-Constant Estimator for Low-Power Digitally Controlled DC–DC Converters. IEEE Trans. Power Electron. 2014, 29, 5106–5110. [Google Scholar] [CrossRef]
- Michal, V. Inductor Current Zero-Crossing Detector and CCM/DCM Boundary Detector for Integrated High-Current Switched-Mode DC–DC Converters. IEEE Trans. Power Electron. 2014, 29, 5384–5391. [Google Scholar] [CrossRef]
- Kim, J.; Shim, M.; Jung, J.; Kim, H.; Kim, C. A DC–DC Boost Converter with Variation Tolerant MPPT Technique and Efficient ZCS Circuit for Thermoelectric Energy Harvesting Applications. In Proceedings of the 2014 19th Asia and South Pacific Design Automation Conference (ASP-DAC), Singapore, 20–23 January 2014; pp. 35–36. [Google Scholar]
- Liu, Y.-C.; Syu, Y.-L.; Dung, N.A.; Chen, C.; Chen, K.-D.; Kim, K.A. High-Switching-Frequency TCM Digital Control for Bidirectional-Interleaved Buck Converters Without Phase Error for Battery Charging. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2111–2123. [Google Scholar] [CrossRef]
- Baek, J.; Choi, W.; Cho, B. Digital Adaptive Frequency Modulation for Bidirectional DC–DC Converter. IEEE Trans. Ind. Electron. 2013, 60, 5167–5176. [Google Scholar] [CrossRef]
- Reverter, F.; Gasulla, M. Optimal inductor current in boost DC/DC converters regulating the input voltage applied to low-power photovoltaic modules. IEEE Trans. Power Electron. 2017, 32, 8. [Google Scholar] [CrossRef]
- Wang, J.-M.; Wu, S.-T. A Synchronous Buck DC–DC Converter Using a Novel Dual-Mode Control Scheme to Improve Efficiency. IEEE Trans. Power Electron. 2017, 32, 9. [Google Scholar] [CrossRef]
- Reverter, F.; Gasulla, M. Optimal inductor current in boost DC/DC converters operating in burst mode under light-load conditions. IEEE Trans. Power Electron. 2016, 31, 15–20. [Google Scholar] [CrossRef]
- Konjedic, T.; Korošec, L.; Truntič, M.; Restrepo, C.; Rodič, M.; Milanovič, M. DCM-Based Zero-Voltage Switching Control of a Bidirectional DC–DC Converter with Variable Switching Frequency. IEEE Trans. Power Electron. 2016, 31, 3273–3288. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.; Gao, Y.; Erickson, R.W.; Maksimovic, D. Online Efficiency Optimization of a Closed-Loop Controlled SiC-Based Bidirectional Boost Converter. IEEE Trans. Power Electron. 2022, 37, 4008–4021. [Google Scholar] [CrossRef]
- Vazquez, A.; Martin, K.; Arias, M.; Sebastian, J. Variable-Width Hysteretic Analog Control for QSW-ZVS and TCM Source/Sink Converters. IEEE Trans. Power Electron. 2020, 35, 3. [Google Scholar] [CrossRef]
- Lazar, M.C.; Shreelakshmi, M.P. Efficient Bidirectional DC-DC Converter Using Digital Adaptive Frequency Modulation. In Proceedings of the 2021 IEEE International Power and Renewable Energy Conference (IPRECON), Kerala, India, 24–26 September 2021; pp. 1–6. [Google Scholar]
- Wang, J.-M.; Wu, S.-T. Sensorless control scheme for synchronous buck converter. IET Circuits Devices Syst. 2016, 10, 181–191. [Google Scholar] [CrossRef]
- Abu Qahouq, J.A. Control Scheme for Sensorless Operation and Detection of CCM and DCM Operation Modes in Synchronous Switching Power Converters. IEEE Trans. Power Electron. 2010, 25, 2489–2495. [Google Scholar] [CrossRef]
- Waffler, S.; Kolar, J.W. A Novel Low-Loss Modulation Strategy for High-Power Bidirectional Buck Boost Converters. IEEE Trans. Power Electron. 2009, 24, 6. [Google Scholar] [CrossRef]
- Park, C.; Choi, S. Quasi-Resonant Boost-Half-Bridge Converter with Reduced Turn-Off Switching Losses for 16 V Fuel Cell Application. IEEE Trans. Power Electron. 2013, 28, 11. [Google Scholar] [CrossRef]
- Wu, T.-F.; Lai, Y.-S.; Hung, J.-C.; Chen, Y.-M. Boost Converter with Coupled Inductors and Buck–Boost Type of Active Clamp. IEEE Trans. Ind. Electron. 2008, 55, 1. [Google Scholar] [CrossRef]






| Designed Parameters | Value |
|---|---|
| Input voltage (VLV) | 16–32 V |
| Output voltage (VHV) | 48 V |
| Rated power (P) | 100 W |
| Inductance (L1) | 10 μH |
| Core type | Kool Mµ |
| Capacitance (C) | 100 μF |
| PI controller | Kp = 0.28, Ki = 2 |
| MOSFET | IPP200N15N3G |
| Switching frequency | 75–150 kHz |
| Topologies | Traditional Boost Converter [35] | Active Clamping Boost Converter [36] | Quasi Resonant Boost Converter [37] | Bidirectional Converter in This Paper |
|---|---|---|---|---|
| Number of switches | 1 MOSFET 1 Diode | 2 MOSFET 1 Diode | 1 MOSFET 1 Diode | 2 MOSFET 0 Diode |
| Passive component | 3 | 3 | 4 | 2 |
| Soft switching | CCM/DCM | CCM/DCM | CCM/DCM | BCM |
| Switching frequency | Fixed frequency | Fixed frequency | Fixed frequency | Variable frequency |
| Efficiency | Low | High | High | High |
| Output range | Wide | Medium | Medium | Wide |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Cheng, S.; Xu, J.; Xiang, C.; Yu, T. A New Optimal Thermal-Based Adaptive Frequency Control for Bidirectional DC–DC Converter with Full-Range ZVS. Energies 2022, 15, 8250. https://doi.org/10.3390/en15218250
Zhang L, Cheng S, Xu J, Xiang C, Yu T. A New Optimal Thermal-Based Adaptive Frequency Control for Bidirectional DC–DC Converter with Full-Range ZVS. Energies. 2022; 15(21):8250. https://doi.org/10.3390/en15218250
Chicago/Turabian StyleZhang, Lulin, Shu Cheng, Jingtao Xu, Chaoqun Xiang, and Tianjian Yu. 2022. "A New Optimal Thermal-Based Adaptive Frequency Control for Bidirectional DC–DC Converter with Full-Range ZVS" Energies 15, no. 21: 8250. https://doi.org/10.3390/en15218250
APA StyleZhang, L., Cheng, S., Xu, J., Xiang, C., & Yu, T. (2022). A New Optimal Thermal-Based Adaptive Frequency Control for Bidirectional DC–DC Converter with Full-Range ZVS. Energies, 15(21), 8250. https://doi.org/10.3390/en15218250






