Performance Prediction and Working Fluid Active Design of Organic Rankine Cycle Based on Molecular Structure
Abstract
1. Introduction
1.1. Working Fluid Selection
1.2. Thermophysical Property Prediction and Molecular Design
1.3. Contribution of This Work
- The accurate prediction of thermophysical properties was realized based on the QSPR model.
- The evaporation enthalpy, evaporation entropy, and thermal efficiency of the working fluid were calculated, and the errors between the results of “QSPR+WFPM” and those of REFPROP were analyzed.
- The thermodynamic performance limits the ORC system, and the thermophysical properties of the ideal working fluid were investigated at typical geothermal source conditions. Working fluids were actively designed at the molecular scale on the basis of these properties.
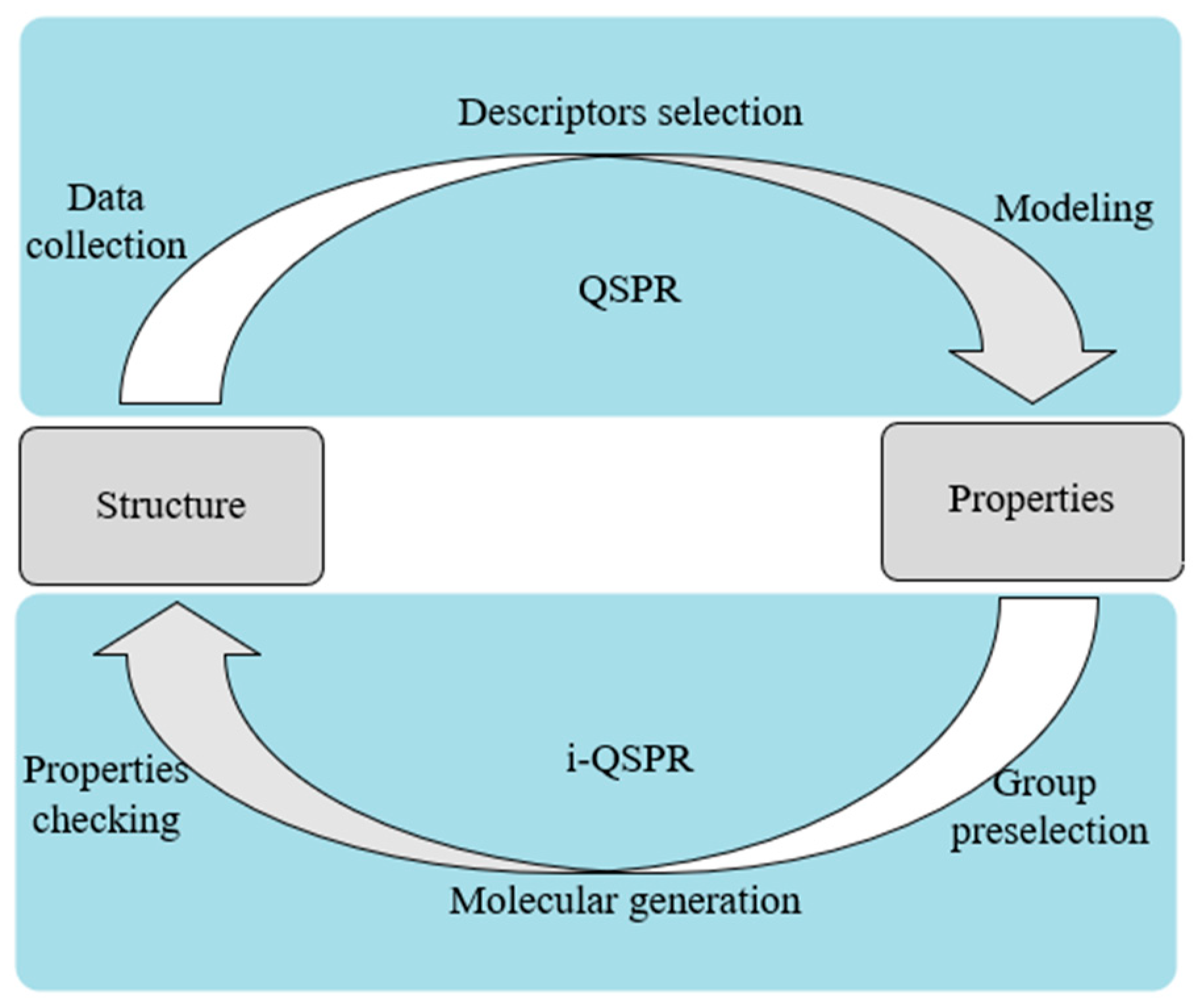
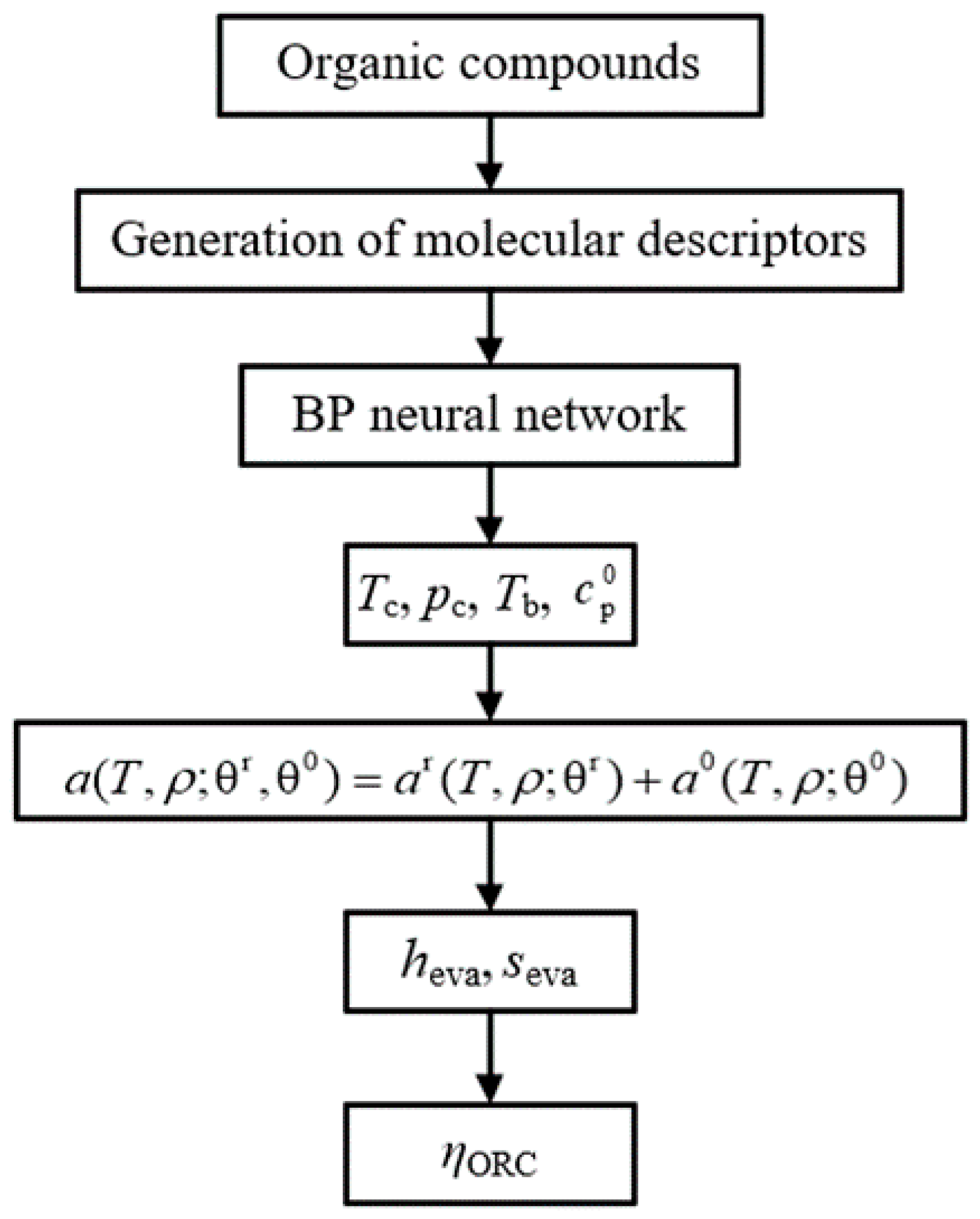
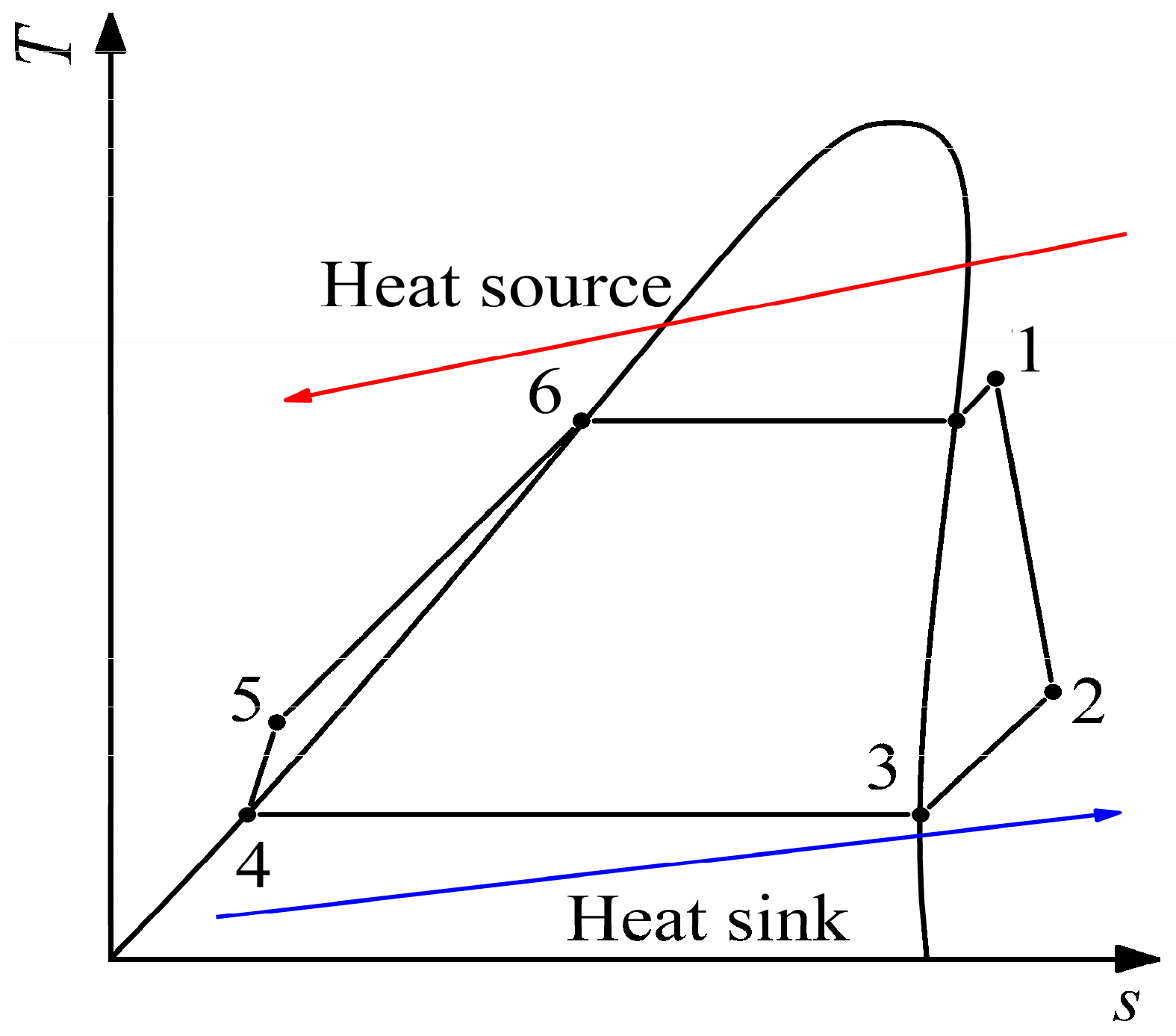
2. Theoretical Model
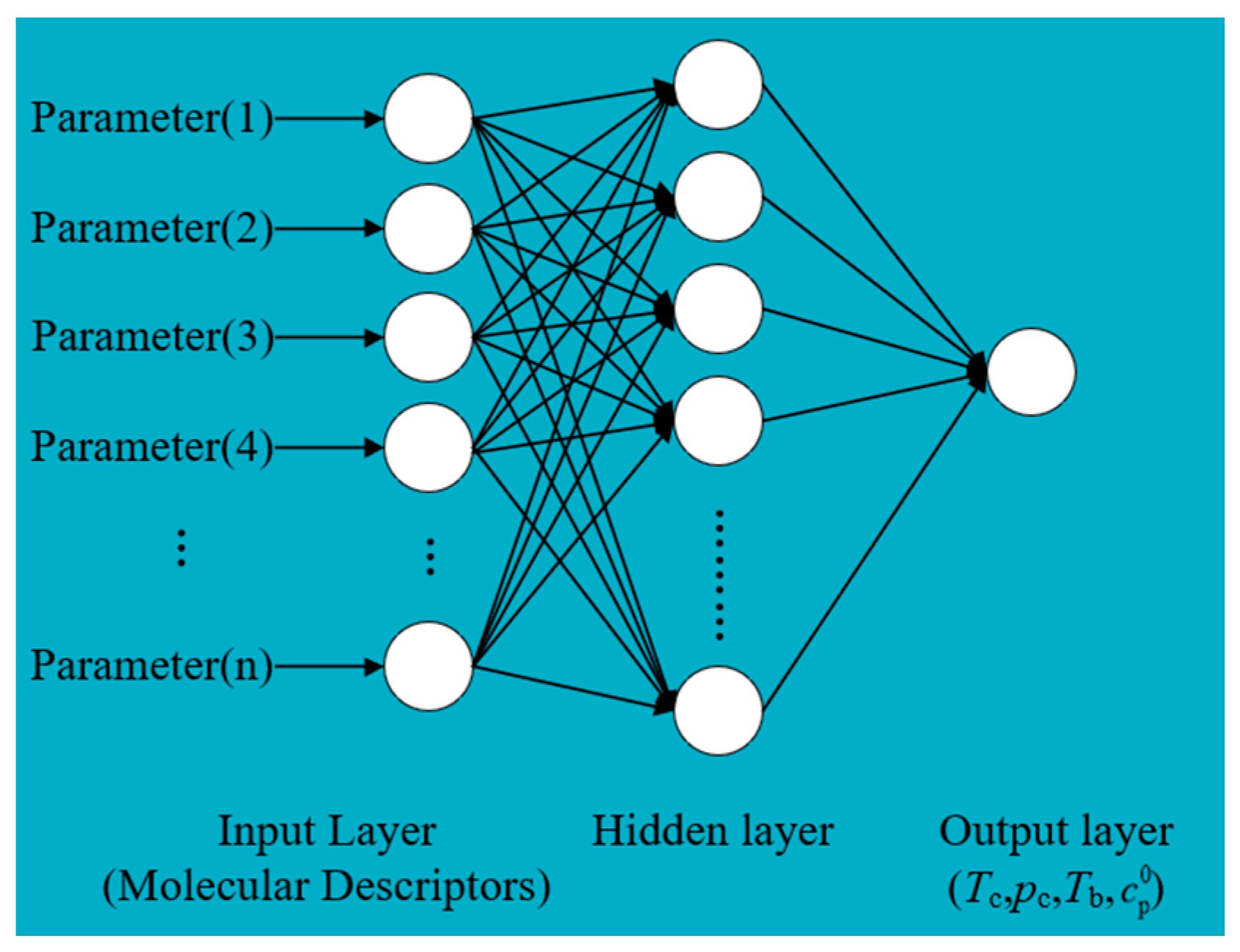
3. QSPR Modeling
3.1. Data Collection
3.2. Molecular Descriptor Calculation and Selection
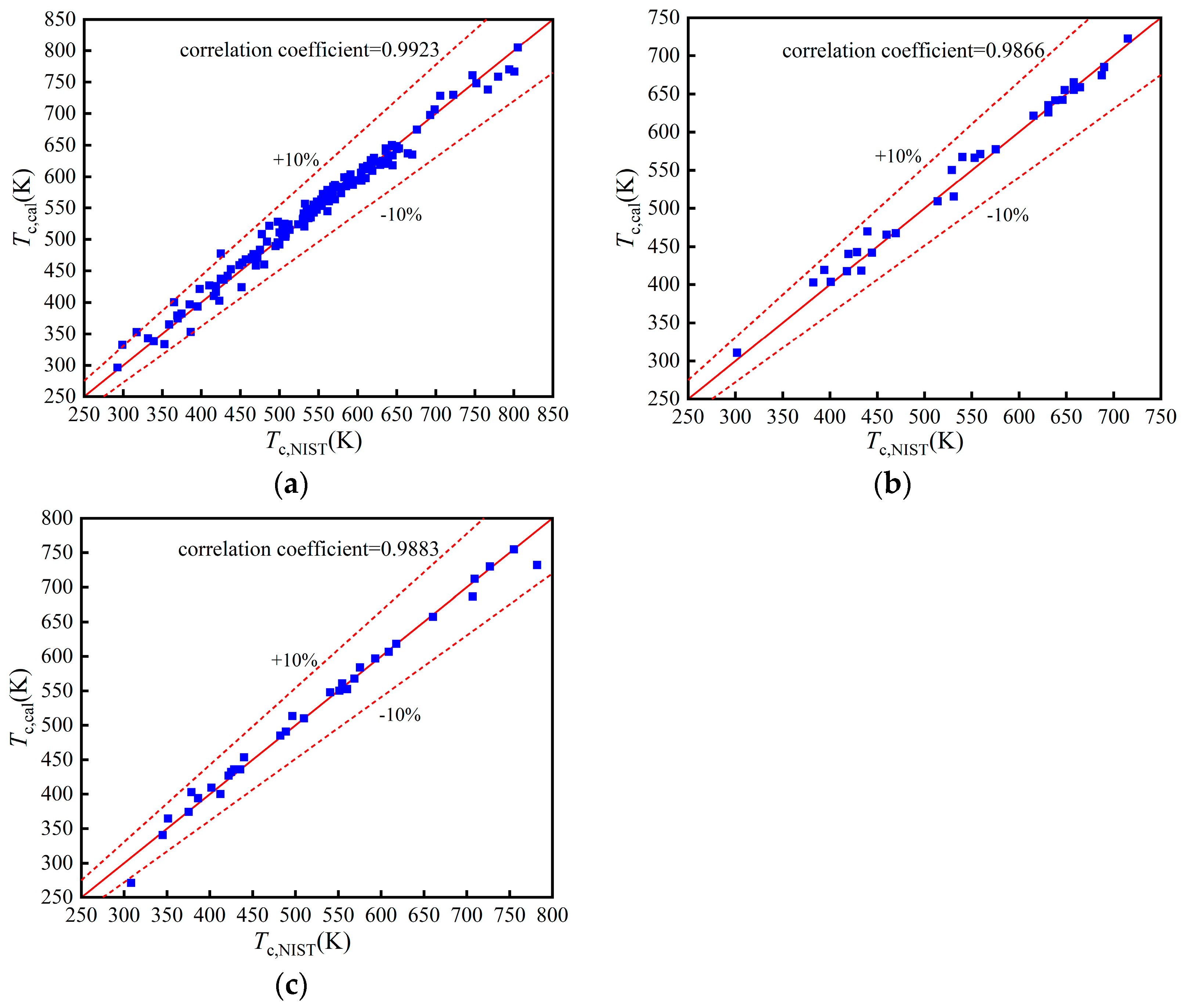
3.3. Model Establishment and Evaluation
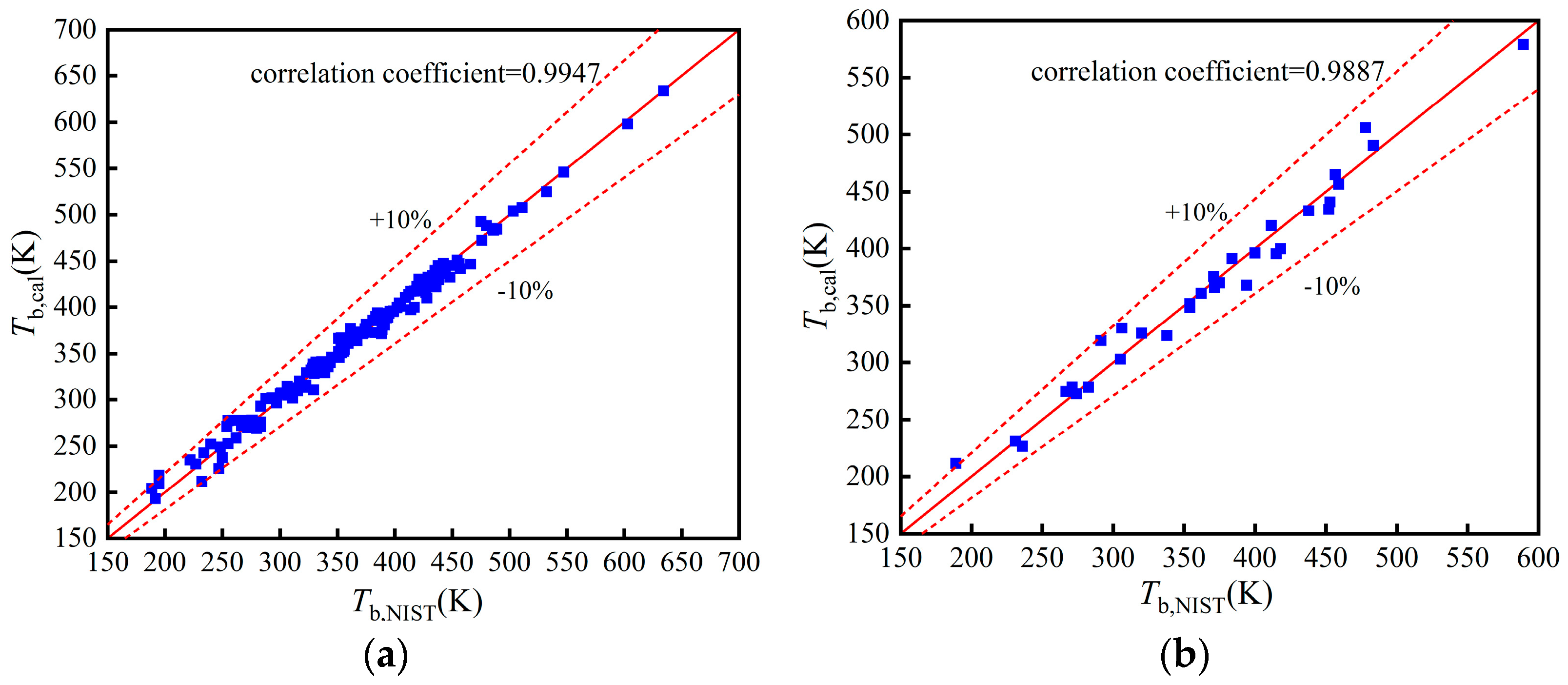
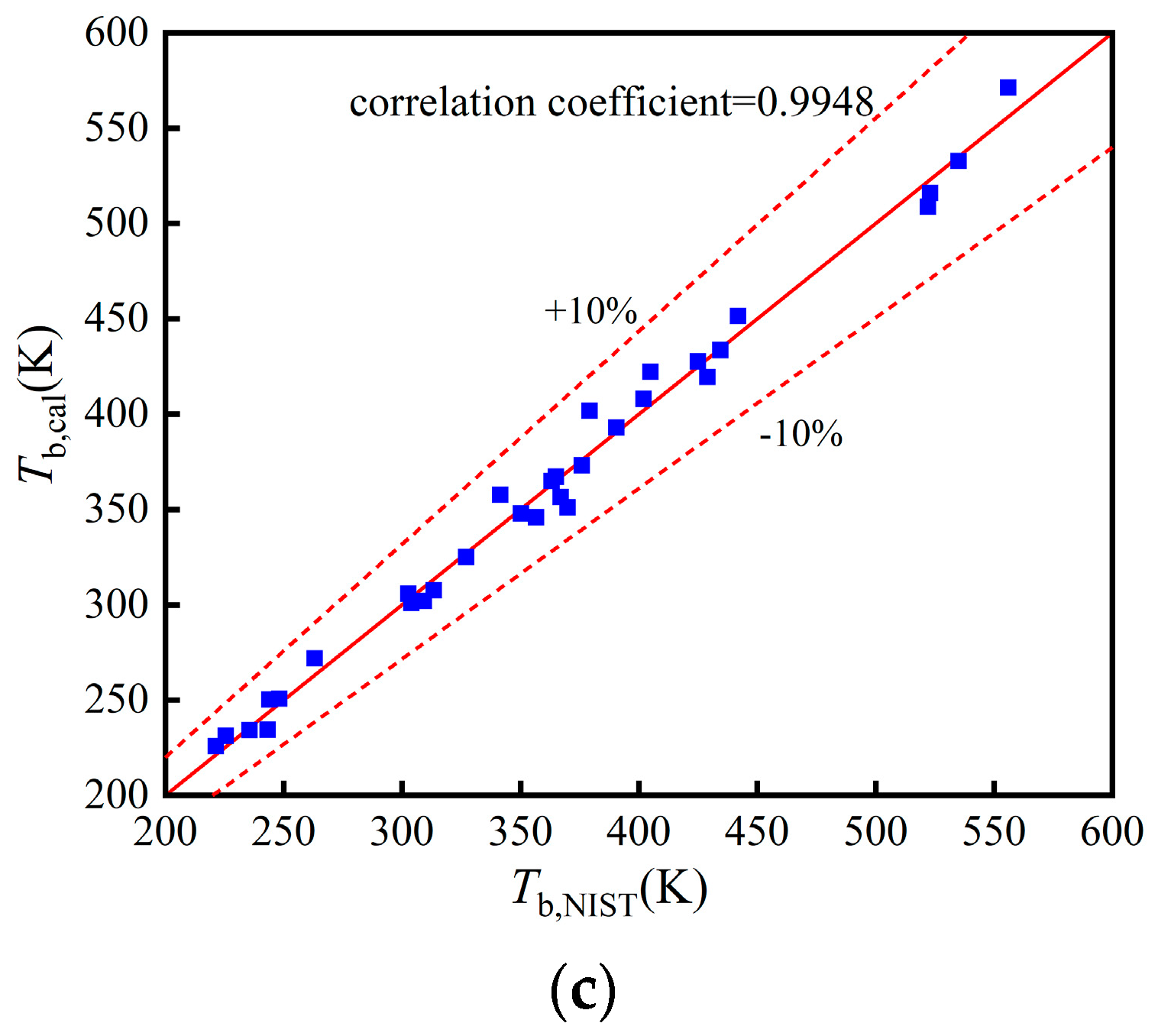
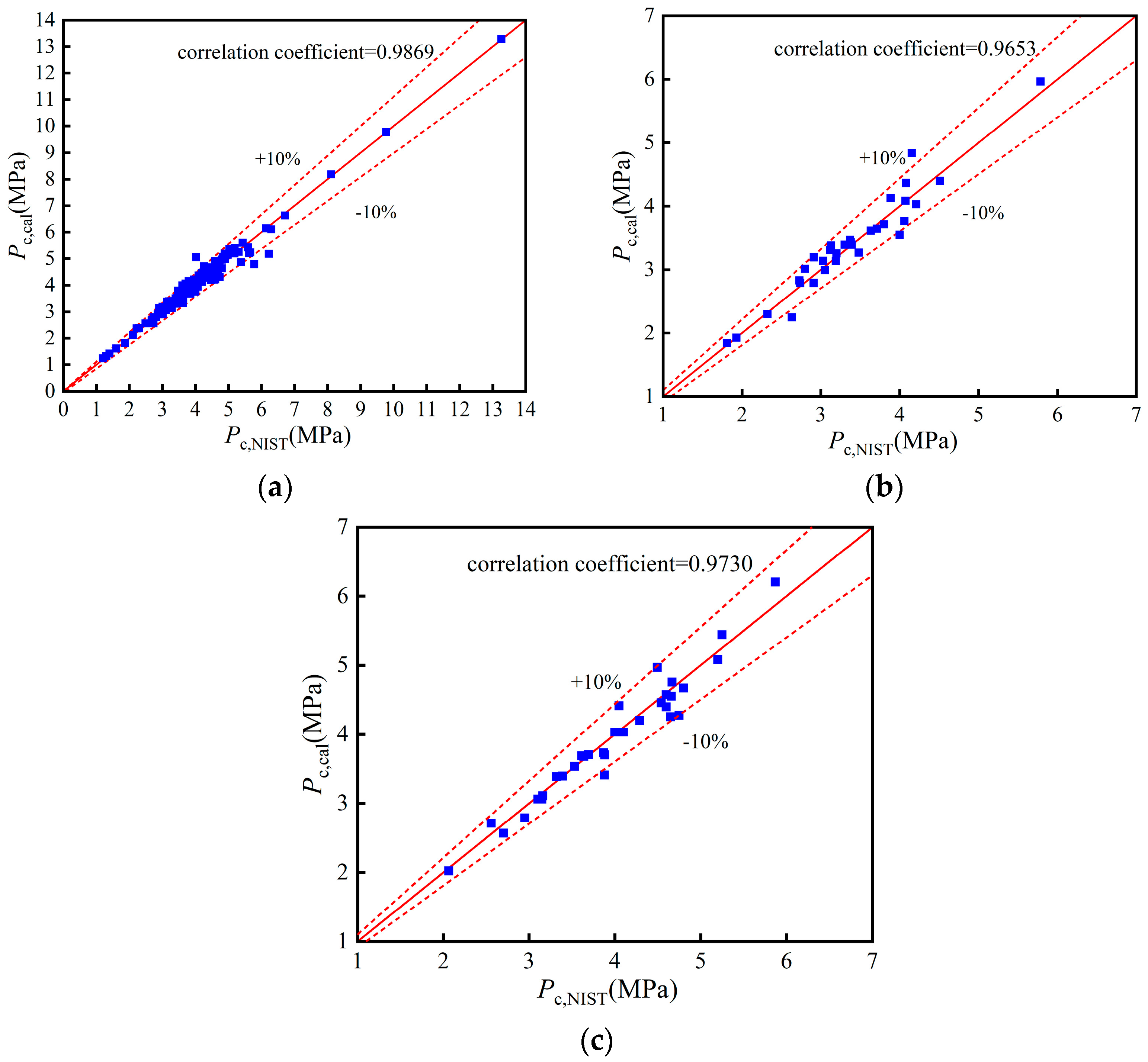
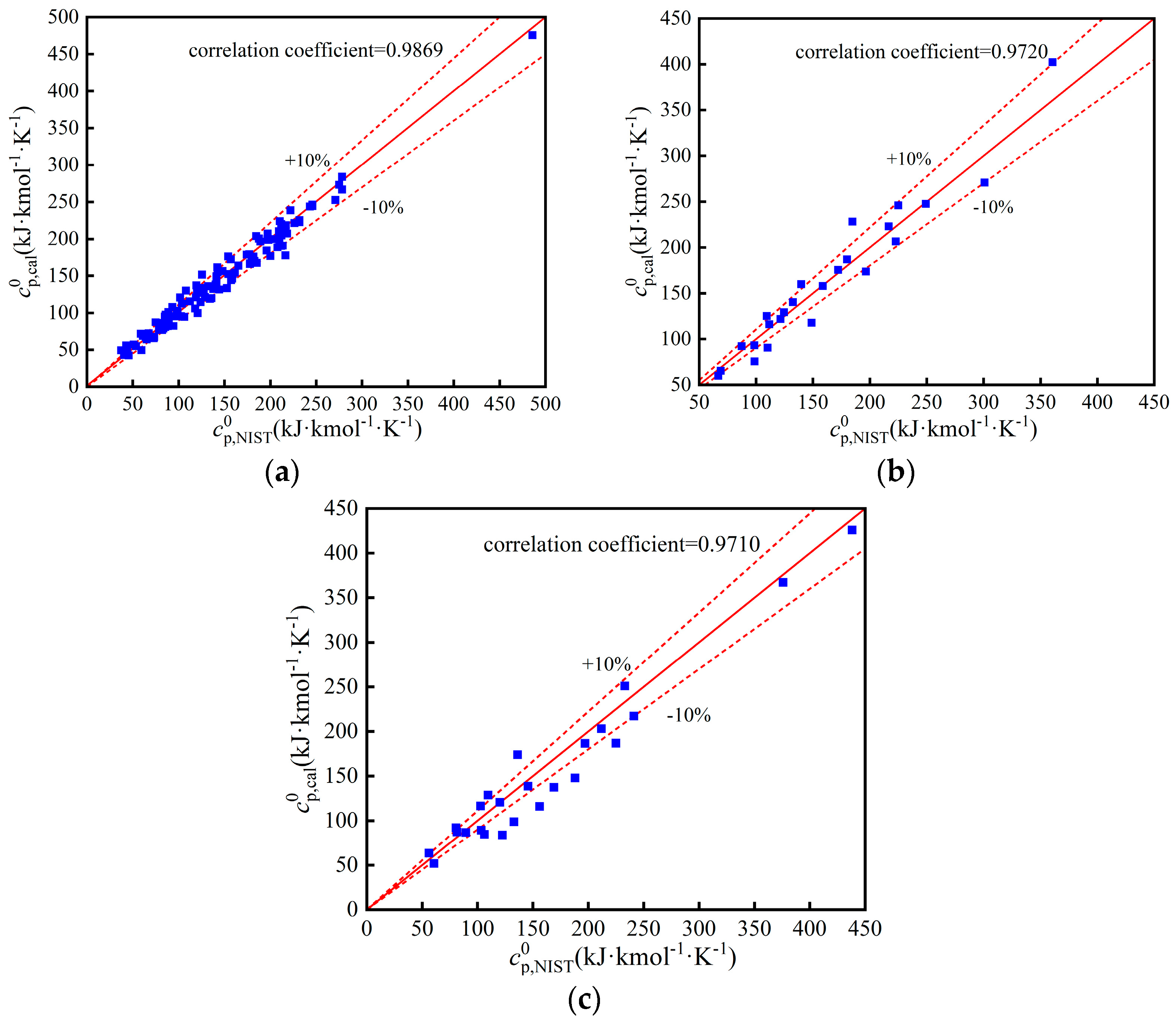
4. Model Validation
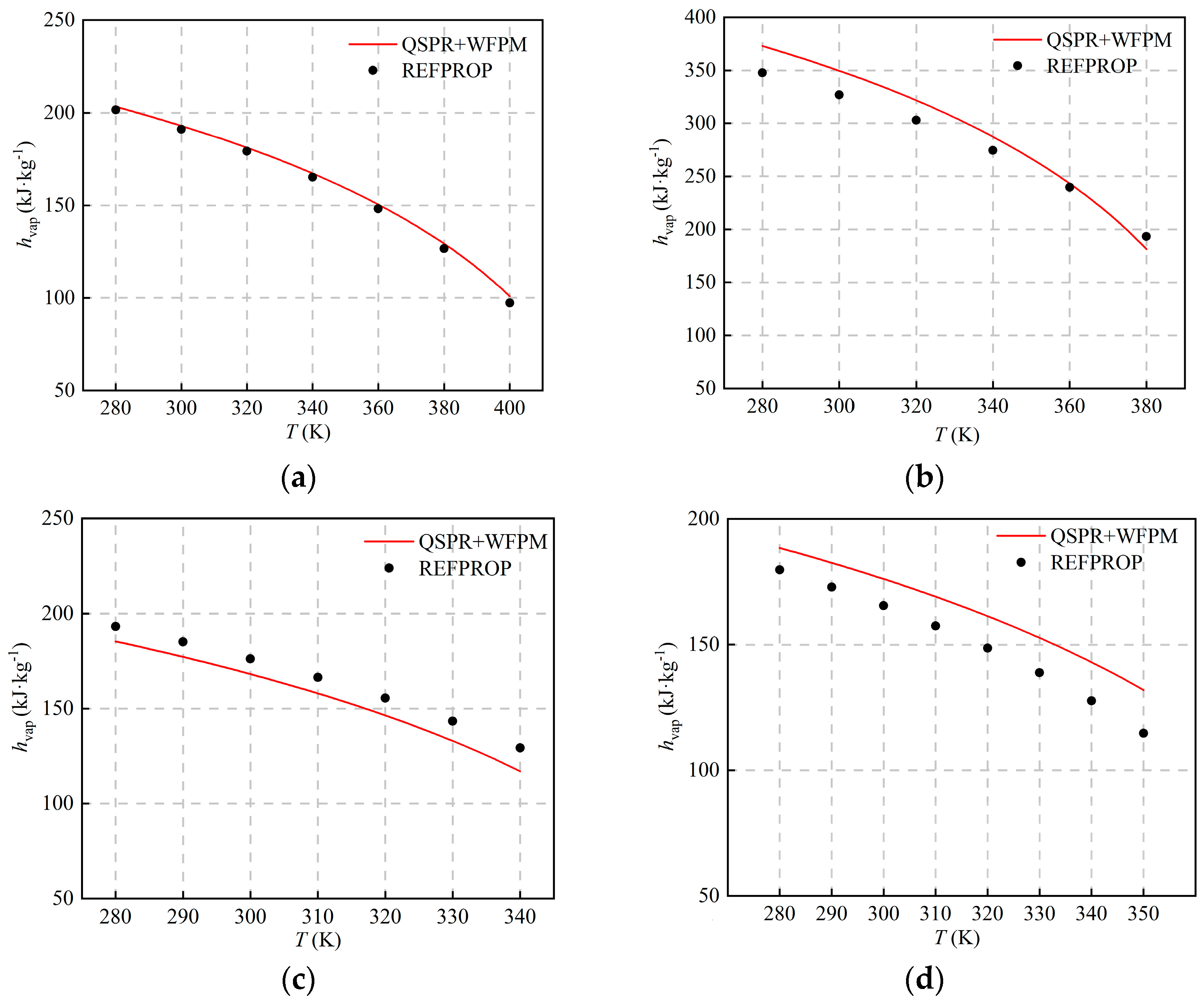
4.1. Validation of Working Fluid Thermophysical Properties
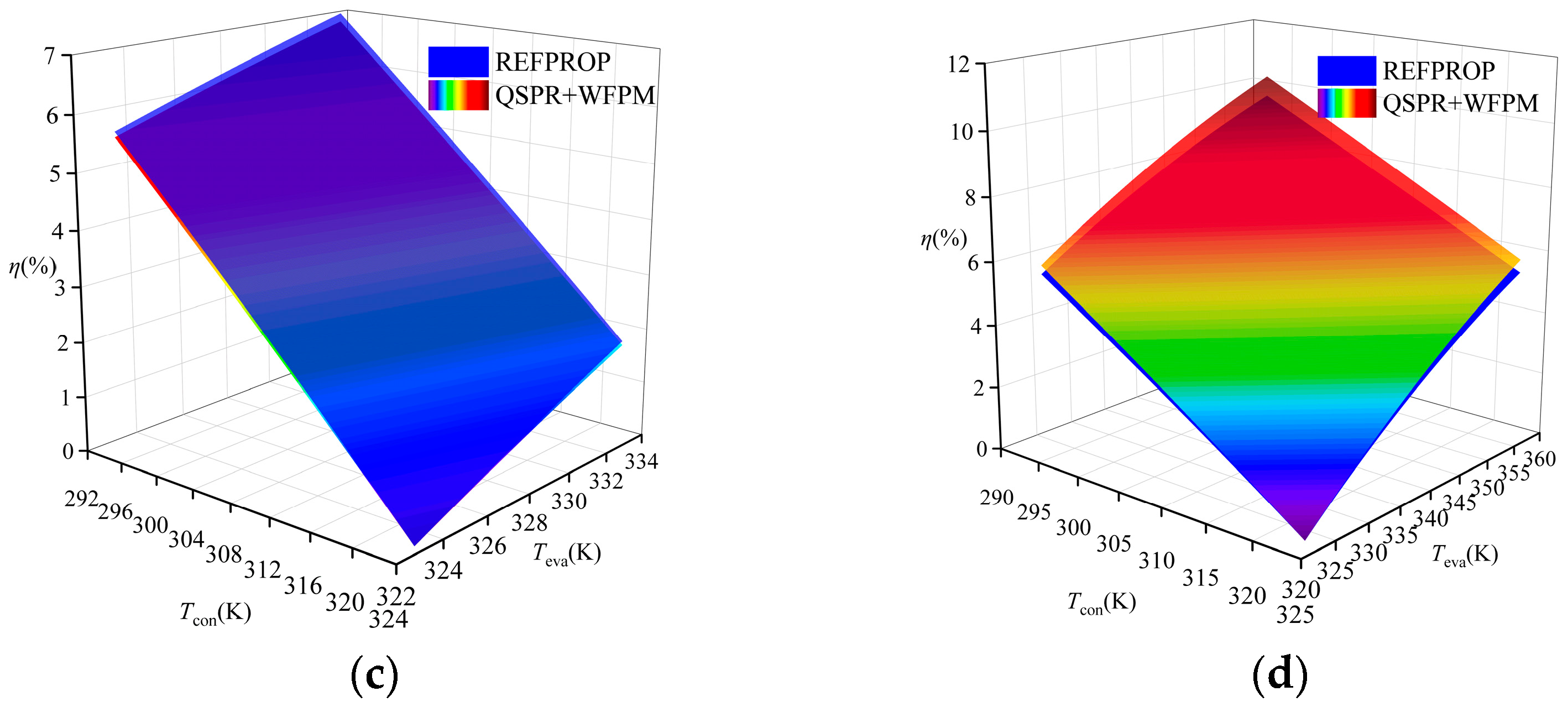
4.2. Verification of ORC System Performance
- The pressure and heat dissipation losses in the system components and pipelines are ignored.
- The whole system is in stable operation or operates at steady-state conditions.
- The heat exchange capacity in the evaporator is 126 kW regardless of the limitation of the pinch point temperature difference between the actual heat source and the circulating working fluid.
- The evaporation temperature range is 323.15–0.9 Tc. The condensing temperature is 293.15–323.15 K. The superheat degree is 10 K.
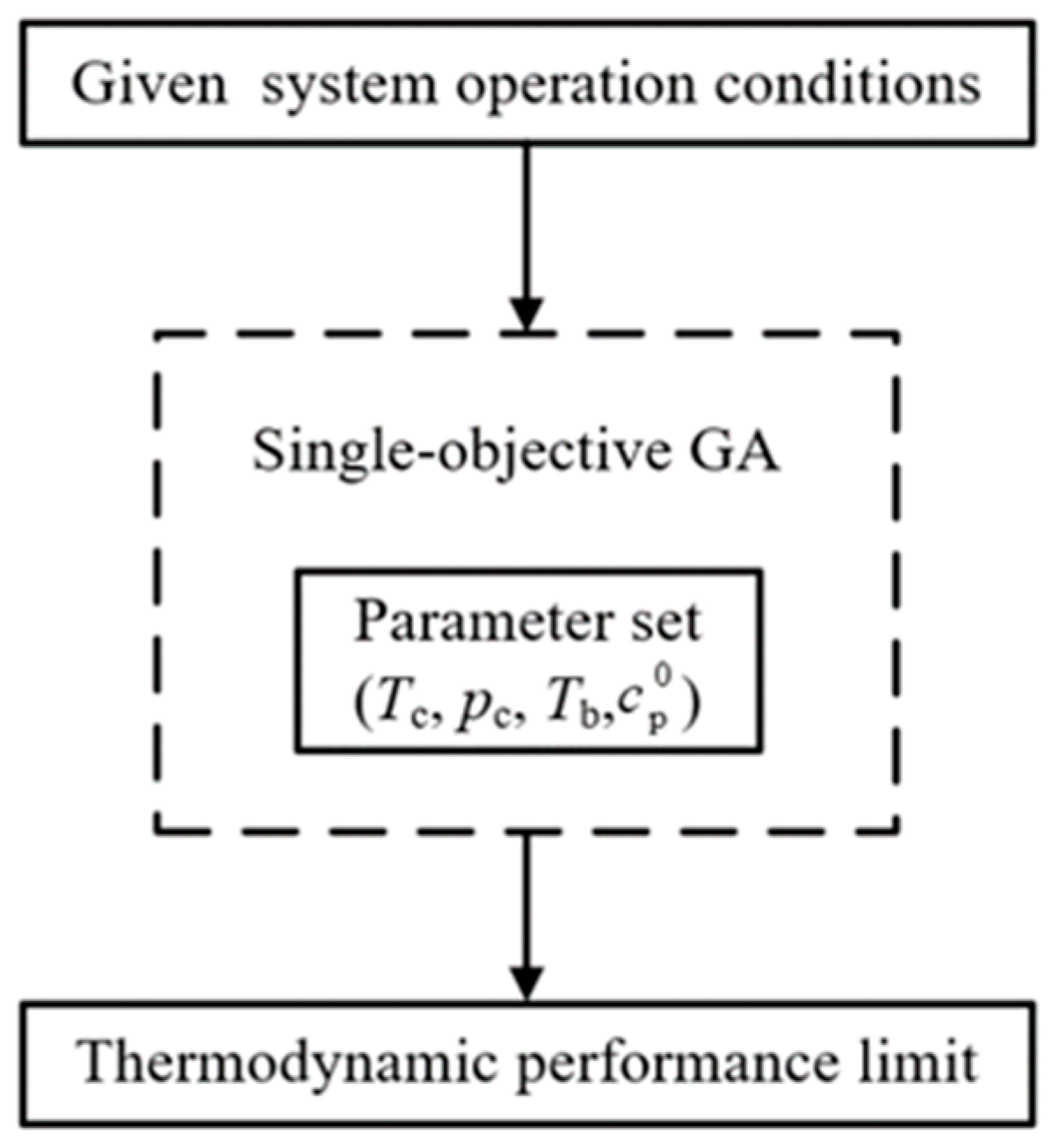
5. Method of Working Fluid Design
5.1. Optimization Problem
5.2. Working Fluid Active Design
- The generation of candidate working fluids. The elements in the periodic table that can be used as working fluids of ORC are limited [45]. In this study, six molecular groups were selected according to the working fluids commonly used in ORC, namely, –CH2–, >C<, >C=, –F, –CH<, and –H. The maximum number of C atoms was set to four in order to simplify the calculation. Moreover, all working fluids including alkanes, alkenes, and cycloalkanes were generated under the constraints of chemical structure. A total of 244 candidate working fluids were obtained. The molecular descriptors of the candidate working fluids calculated by AlvaDesc, Tc,ca, and pc,ca, were calculated by QSPR.
- The analysis of the thermophysical property error. In the process of the working fluid design, constructing a working fluid that exactly matches the two properties of the ideal working fluid is difficult. The RE between Tc,ca and Tc,id is α, and the RE between pc,ca and pc,id is β. The values of α and β can be adjusted to obtain the candidate working fluid.
6. Conclusions
- 1.
- BP neural network QSPR models have a high accuracy. The AARDs of Tc, pc, Tb, and are 2.01%, 2.1%, 3.68%, and 8.45%, respectively. The models can predict the thermophysical properties of novel working fluids.
- 2.
- The “QSPR+WFPM” coupling model can estimate ORC performance based on molecular structure. The AARDs of hvap and svap are below 8.44%, and the ARDs of thermal efficiency are less than 6%.
- 3.
- A method of working fluid active design using i-QSPR is presented. By taking the typical geothermal heat source as an example, the thermophysical properties of the ideal working fluid can be calculated, and the alternatives to ideal working fluids were found in 244 potential ORC working fluids.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| a | Molar Helmholtz free energy, J/mol |
| AARD | Average absolute relative deviation, % |
| ARD | Average relative deviation, % |
| b | Constant |
| BP | Back propagation |
| c | Specific heat, J/mol.K |
| CAMD | Computer aided molecular design |
| EoS | Equation of state |
| GA | Genetic algorithm |
| h | Enthalpy, kJ/kg |
| i-QSPR | Inverse quantitative structure-property relationship |
| k | Coefficient of ideal gas isobaric heat capacity fitted function, J/mol.K |
| m | Generalized parameter |
| Working fluid molar flow rate, mol/s | |
| MLR | Multiple linear regression |
| ORC | Organic Rankine cycle |
| p | Pressure, MPa |
| PC-SAFT | perturbed-chain statistical associating fluid theory |
| Heat, kJ | |
| QSPR | Quantitative structure-property relationship |
| R | Universal gas constant, J/mol.K |
| RE | Relative error, % |
| RMSE | Root mean square error |
| s | Entropy, kJ/kmol.K |
| SRK | Soave-Redlich-Kwong |
| T | Temperature, K |
| v | Molar volume, m3/mol |
| Greeks | |
| α | α function |
| β | Relative error of Tc, % |
| γ | Relative error of pc, % |
| ρ | Density, mol/m3 |
| θ | Parameter set |
| ω | Acentric factor |
| η | Thermal efficiency, % |
| Subscripts | |
| b | Boiling point |
| r | Corresponding state properties |
| c | Critical properties |
| ca | Candidate working fluid |
| cal | Calculated value |
| con | Condenser |
| eva | Evaporator |
| exp | Expander |
| id | Ideal working fluid |
| vap | Evaporation property |
| 1,2,3,4,5,6,7 | State points |
| 0 | Reference state |
| Superscripts | |
| res | Residual properties |
| 0 | Ideal gas properties |
Appendix A
References
- Bai, J.W.; Ding, T.; Wang, Z.; Chen, J.H. Day-Ahead Robust Economic Dispatch Considering Renewable Energy and Concentrated Solar Power Plants. Energies 2019, 12, 3832. [Google Scholar] [CrossRef]
- Shin, J.S.; Park, J.W.; Kim, S.H. Measurement and Verification of Integrated Ground Source Heat Pumps on a Shared Ground Loop. Energies 2020, 13, 1752. [Google Scholar] [CrossRef]
- Xu, Y.H.; Zhang, H.G.; Yang, F.B.; Tong, L.; Yang, Y.F.; Yan, D.; Wang, C.Y.; Ren, J.; Wu, Y.T. Experimental study on small power generation energy storage device based on pneumatic motor and compressed air. Energy Conv. Manag. 2021, 234, 113949. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Linke, P.; Papadopoulos, A.I.; Grujic, A.S. On the role of working fluid properties in Organic Rankine Cycle performance. Appl. Therm. Eng. 2012, 36, 406–413. [Google Scholar] [CrossRef]
- Hu, B.; Guo, J.J.; Yang, Y.; Shao, Y.Y. Selection of working fluid for organic Rankine cycle used in low temperature geothermal power plant. Energy Rep. 2022, 8, 179–186. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-economic optimization of waste heat recovery organic Rankine cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.B.; Zhang, H.G.; Xing, C.D.; Wang, C.Y.; Zhang, W.J.; Wang, Y. Energy, economic and environmental dynamic response characteristics of organic Rankine cycle (ORC) system under different driving cycles. Energy 2022, 246, 123438. [Google Scholar] [CrossRef]
- Abbas, W.K.A.; Vrabec, J. Cascaded dual-loop organic Rankine cycle with alkanes and low global warming potential refrigerants as working fluids. Energy Conv. Manag. 2021, 249, 114843. [Google Scholar] [CrossRef]
- Xu, J.H.; Yu, C. Critical temperature criterion for selection of working fluids for subcritical pressure Organic Rankine cycles. Energy 2014, 74, 719–733. [Google Scholar] [CrossRef]
- Aghahosseini, S.; Dincer, I. Comparative performance analysis of low-temperature Organic Rankine Cycle (ORC) using pure and zeotropic working fluids. Appl. Therm. Eng. 2013, 54, 35–42. [Google Scholar] [CrossRef]
- Meng, F.X.; Wang, E.H.; Zhang, B. Possibility of optimal efficiency prediction of an organic Rankine cycle based on molecular property method for high-temperature exhaust gases. Energy 2021, 222, 119974. [Google Scholar]
- Aparoy, P.; Reddy, K.K.; Reddanna, P. Structure and ligand based drug design strategies in the development of novel 5–LOX inhibitors. Curr. Med. Chem. 2012, 19, 3763–3778. [Google Scholar] [CrossRef] [PubMed]
- Khetib, Y.; Meniai, A.H.; Gari, A.; Sedraoui, K. Refrigerants design for an absorption refrigeration machine using group contribution methods. Chem. Eng. Commun. 2021, 1948409. [Google Scholar] [CrossRef]
- Su, W.; Zhao, L.; Deng, S. Developing a performance evaluation model of Organic Rankine Cycle for working fluids based on the group contribution method. Energy Conv. Manag. 2017, 132, 307–315. [Google Scholar] [CrossRef]
- Su, W.; Zhao, L.; Deng, S. Simultaneous working fluids design and cycle optimization for Organic Rankine cycle using group contribution model. Appl. Energy 2017, 202, 618–627. [Google Scholar] [CrossRef]
- Chen, C.H.; Su, W.; Yu, A.F.; Lin, X.X.; Zhou, N.J. Combining cubic equations with group contribution methods to predict cycle performances and design working fluids for four different Organic Rankine cycles. Energy Conv. Manag. X 2022, 15, 100245. [Google Scholar] [CrossRef]
- Brown, J.S.; Brignoli, R.; Daubman, S. Methodology for estimating thermodynamic parameters and performance of working fluids for organic Rankine cycles. Energy 2014, 73, 818–828. [Google Scholar] [CrossRef]
- Lampe, M.; Stavrou, M.; Bucker, H.M.; Gross, J.; Bardow, A. Simultaneous optimization of working fluid and process for organic Rankine cycles using PC-SAFT. Ind. Eng. Chem. Res. 2014, 53, 8821–8830. [Google Scholar] [CrossRef]
- Yan, D.; Yang, F.B.; Zhang, H.G.; Xu, Y.H.; Wang, Y.; Li, J.; Ge, Z. How to Quickly Evaluate the Thermodynamic Performance and Identify the Optimal Heat Source Temperature for Organic Rankine Cycles? Energy Resour. Technol. 2022, 144, 112106. [Google Scholar] [CrossRef]
- Yang, F.F.; Yang, F.B.; Chu, Q.F.; Liu, Q.; Yang, Z.; Duan, Y.Y. Thermodynamic performance limits of the organic Rankine cycle: Working fluid parameterization based on corresponding states modeling. Energy Conv. Manag. 2020, 217, 113011. [Google Scholar] [CrossRef]
- Yang, F.F.; Yang, F.B.; Liu, Q.; Chu, Q.F.; Yang, Z.; Duan, Y.Y. Thermodynamic analysis of working fluids: What is the highest performance of the sub- and trans-critical organic Rankine cycles? Energy 2022, 241, 122512. [Google Scholar] [CrossRef]
- Abudour, A.M.; Mohammad, S.A.; Robinson, R.L.; Gasem, K.A.M. Predicting PR EOS binary interaction parameter using readily available molecular properties. Fluid Phase Equilib. 2017, 434, 130–140. [Google Scholar] [CrossRef]
- Abooali, D.; Sobati, M.A. Novel method for prediction of normal boiling point and enthalpy of vaporization at normal boiling point of pure refrigerants: A QSPR approach. Int. J. Refrig. 2014, 40, 282–293. [Google Scholar] [CrossRef]
- Banchero, M.; Manna, L. Comparison between multi-linear- and radial-basis-function-neural-network-based QSPR Models for the prediction of the critical temperature, critical pressure and acentric factor of organic compounds. Molecules 2018, 23, 1379. [Google Scholar] [CrossRef] [PubMed]
- Joback, K.G.; Reid, R.C. Estimation of pure-component properties from group-contributions. Chem. Eng. Commun. 1987, 57, 233–243. [Google Scholar] [CrossRef]
- Lan, T.; Wang, Y.R.; Ali, R.; Liu, H.; Liu, X.Y.; He, M.G. Prediction and measurement of critical properties of gasoline surrogate fuels and biofuels. Fuel Process. Technol. 2022, 228, 107156. [Google Scholar] [CrossRef]
- Weis, D.C.; Faulon, J.L.; LeBorne, R.C.; Visco, D.P. The signature molecular descriptor. 5. The design of hydrofluoroether foam blowing agents using inverse-QSAR. Ind. Eng. Chem. Res. 2005, 44, 8883–8891. [Google Scholar] [CrossRef]
- Faulon, J.L.; Visco, D.P.; Pophale, R.S. The signature molecular descriptor. 1. Using extended valence sequences in QSPR and QSPR studies. J. Chem. Inf. Comput. Sci. 2003, 43, 707–720. [Google Scholar] [CrossRef]
- Faulon, J.L.; Churchwell, C.J.; Visco, D.P. The signature molecular descriptor. 2. Enumerating molecules from their extended valence sequences. J. Chem. Inf. Comput. 2003, 43, 721–734. [Google Scholar] [CrossRef]
- Lim, J.; Ryu, S.; Kim, J.W.; Kim, W.Y. Molecular generative model based on conditional variational autoencoder for de novo molecular design. J. Cheminformatics 2018, 10, 31. [Google Scholar] [CrossRef]
- Danishuddin; Khan, A.U. Descriptors and their selection methods in QSAR analysis: Paradigm for drug design. Drug Discov. Today 2016, 21, 1291–1302. [Google Scholar] [CrossRef] [PubMed]
- Miyao, T.; Kaneko, H.; Funatsu, K. Inverse QSPR/QSAR Analysis for Chemical Structure Generation (from y to x). J. Chem. Inf. Model. 2016, 56, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.H.; Dinivahi, M.V.; Jeng, C.Y. New acentric factor correlation based on the Antoine equation. Ind. Eng. Chem. Res. 1993, 32, 241–244. [Google Scholar] [CrossRef]
- Consonni, V.; Ballabio, D.; Todeschini, R. Comments on the definition of the Q(2) parameter for QSAR validation. J. Chem. Inf. Model. 2009, 49, 1669–1678. [Google Scholar] [CrossRef] [PubMed]
- Dearden, J.C.; Cronin, M.T.D.; Kaiser, K.L.E. How not to develop a quantitative structure–activity or structure–property relationship (QSAR/QSPR). SAR QSAR Environ. Res. 2009, 20, 241–266. [Google Scholar] [CrossRef] [PubMed]
- NIST. Available online: http://webbook.nist.gov/chemistry/cas-ser.html. (accessed on 9 March 2022).
- AlvaDesc-Alvascience. Available online: https://www.alvascience.com/alvadesc/ (accessed on 10 May 2022).
- Moosavi, M.; Sedghamiz, E.; Abareshi, M. Liquid density prediction of five different classes of refrigerant systems (HCFCs, HFCs, HFEs, PFAs and PFAAs) using the artificial neural network-group contribution method. Int. J. Refrig. 2014, 48, 188–200. [Google Scholar] [CrossRef]
- Espinosa, G.; Yaffe, D.; Arenas, A.; Cohen, Y.; Giralt, F. A fuzzy ARTMAP-based quantitative structure−property relationship (QSPR) for predicting physical properties of organic compounds. Ind. Eng. Chem. Res. 2001, 40, 2757–2766. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Mehrpooya, M. Prediction of some important physical properties of sulfur compounds using quantitative structure–properties relationships. Mol. Divers. 2008, 12, 143–155. [Google Scholar] [CrossRef]
- Imran, M.; Park, B.S.; Kim, G.J.; Lee, D.H.; Usman, M.; Heo, M. Thermo-economic optimization of regenerative organic Rankine cycle for waste heat recovery applications. Energy Conv. Manag. 2014, 87, 107–118. [Google Scholar] [CrossRef]
- Wang, T.Y.; Zhang, Y.J.; Zhang, J.; Peng, Z.J.; Shu, G.Q. Comparisons of system benefits and thermo-economics for exhaust energy recovery applied on a heavy-duty diesel engine and a light-duty vehicle gasoline engine. Energy Conv. Manag. 2014, 84, 97–107. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.B.; Zhang, H.G.; Xing, C.D.; Yu, M.Z.; Wang, Y. Investigation and multi-objective optimization of vehicle engine-organic Rankine cycle (ORC) combined system in different driving conditions. Energy 2022, 263, 125672. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.B.; Zhang, H.G.; Xing, C.D.; Zhang, W.J.; Wang, Y.; Yao, B.F. Dynamic response assessment and multi-objective optimization of organic Rankine cycle (ORC) under vehicle driving cycle conditions. Energy 2022, 263, 125551. [Google Scholar] [CrossRef]
- McLinden, M.; Brown, J.; Brignoli, R.; Kazakov, A.; Domanski, P. Limited options for low-global-warming-potential refrigerants. Nat. Commun. 2017, 8, 14476. [Google Scholar] [CrossRef] [PubMed]
- Fontalvo, A.; Solano, J.; Pedraza, C.; Bula, A.; Quiroga, A.G.; Padilla, R.V. Energy, Exergy and Economic Evaluation Comparison of Small-Scale Single and Dual Pressure Organic Rankine Cycles Integrated with Low-Grade Heat Sources. Entropy 2017, 19, 476. [Google Scholar] [CrossRef]





| Property | Descriptor | Group |
|---|---|---|
| Tc | X3sol | Connectivity indices |
| CATS2D_00_DD | Pharmacophore descriptors | |
| F06[C-O] | 2D Atom Pairs | |
| SHED_AL | Pharmacophore descriptors | |
| Eta_D_AlphaB | eta delta alpha b index | |
| GATS1e | 2D autocorrelations | |
| SpMaxA_AEA(bo) | Edge adjacency indices | |
| X2sol | Connectivity indices | |
| Eta_betaP_A | ETA indices | |
| NssCH2 | Atom-type E-state indices | |
| pc | SM5_D/Dt | 2D matrix-based descriptors |
| CATS2D_07_AL | Pharmacophore descriptors | |
| Hy | Molecular properties | |
| F06[C-N] | 2D Atom Pairs | |
| CMC-80 | Drug-like indices | |
| piPC10 | Walk and path counts | |
| SpMin7_Bh(s) | Burden eigenvalues | |
| GATS1e | 2D autocorrelations | |
| P_VSA_charge_8 | P_VSA-like descriptors | |
| B06[C-N] | 2D Atom Pairs | |
| Tb | X3sol | Connectivity indices |
| CATS2D_00_DD | Pharmacophore descriptors | |
| HVcpx | Information indices | |
| F06[C-N] | 2D Atom Pairs | |
| GATS1e | 2D autocorrelations | |
| X2sol | Connectivity indices | |
| nRCN | Functional group counts | |
| SpMAD_Dz(v) | 2D matrix-based descriptors | |
| F06[C-O] | 2D Atom Pairs | |
| Chi1_EA(dm) | Edge adjacency indices | |
| TIC3 | Information indices | |
| SpMAD_Dz(v) | 2D matrix-based descriptors | |
| ATSC4m | 2D autocorrelations | |
| RNCG | Charge descriptors | |
| J_Dz(p) | 2D matrix-based descriptors | |
| GATS2m | 2D autocorrelations | |
| JGI5 | 2D autocorrelations | |
| Chi1_EA(dm) | Edge adjacency indices | |
| phLevel1 | Chirality descriptors | |
| Eig11_AEA(bo) | Edge adjacency indices |
| Properties | Training Set | Validation Set | Test Set | Total Set | |
|---|---|---|---|---|---|
| Tb | Data point | 152 | 32 | 32 | 216 |
| AARD/(%) | 1.9381 | 2.0381 | 2.9517 | 2.1031 | |
| RMSE | 8.3961 | 9.2421 | 13.0771 | 9.3593 | |
| Tc | Data point | 152 | 32 | 32 | 216 |
| AARD/(%) | 2.0331 | 2.0293 | 1.8869 | 2.0109 | |
| RMSE | 13.8645 | 12.7925 | 14.0122 | 13.7332 | |
| pc | Data point | 152 | 32 | 32 | 216 |
| AARD/(%) | 3.5374 | 3.6892 | 4.4833 | 3.6837 | |
| RMSE | 0.2204 | 0.2066 | 0.2138 | 0.2169 | |
| Data point | 114 | 24 | 24 | 162 | |
| AARD/(%) | 7.2998 | 8.9453 | 13.4422 | 8.4536 | |
| RMSE | 11.3718 | 18.9047 | 23.0043 | 14.9113 |
| RMSE | ||||
|---|---|---|---|---|
| Tc (K) | pc (MPa) | Tb (K) | ||
| This work | 13.7 | 0.22 | 9.36 | 8.45 |
| Mauro Banchero et al. [24] | 8.8 | 0.13 | - | - |
| Gabriela Espinosa et al. [39] | 30.2 | 0.3 | 27.7 | - |
| Farhad Gharagheizi et al. [40] | 17.7 | 0.17 | - | - |
| Working Fluid | Tc (K) | pc (MPa) | Tb (K) | ω | ||
|---|---|---|---|---|---|---|
| R600a | NIST | 407.70 | 3.65 | 96.64 | 262.00 | 0.1840 |
| Calculated | 402.20 | 3.80 | 84.83 | 264.14 | 0.2565 | |
| RE(%) | −1.35 | 4.10 | −12.22 | 0.82 | 39.40 | |
| R245fa | NIST | 427.01 | 3.65 | 115.28 | 288.20 | 0.3783 |
| Calculated | 425.44 | 3.40 | 112.91 | 288.48 | 0.3756 | |
| RE(%) | −0.37 | −6.85 | −2.06 | 0.10 | −0.71 | |
| R134a | NIST | 374.10 | 4.06 | 85.03 | 246.60 | 0.3268 |
| Calculated | 370.30 | 4.04 | 89.66 | 241.43 | 0.2807 | |
| RE(%) | −1.02 | −0.49 | 5.45 | −2.10 | −14.11 | |
| R1234ze(E) | NIST | 382.51 | 3.64 | 99.65 | 254.18 | 0.3130 |
| Calculated | 398.29 | 3.62 | 95.50 | 261.29 | 0.2652 | |
| RE(%) | 4.13 | −0.55 | −4.16 | 2.80 | −15.27 |
| R245fa | R600a | R134a | R1234ze(E) | ||
|---|---|---|---|---|---|
| hvap | AARD (%) | 1.51% | 4.95% | 5.61% | 8.44% |
| MAE (kJ·kg−1) | 2.24 | 14.81 | 8.92 | 12.39 | |
| svap | AARD (%) | 1.51% | 4.95% | 5.61% | 8.44% |
| MAE (kJ·kg−1·k−1) | 0.0065 | 0.047 | 0.029 | 0.039 |
| Item | Thermodynamic Formula |
|---|---|
| Expansion process | |
| Condensation process | |
| Compression process | |
| Evaporation process | |
| Thermal efficiency |
| Parameter | Lower Limit | Upper Limit |
|---|---|---|
| Teva (K) | 323.15 | 0.9Tc |
| Tsup (K) | 0 | 20 |
| Tcon (K) | 293.15 | 323.15 |
| Tc (K) | 350 | 550 |
| pc (MPa) | 2 | 5 |
| Tb (K) | 110 | 310 |
| (J·mol−1·K−1) | 60 | 250 |
| Parameter | Value |
|---|---|
| Population size | 1000 |
| Selection function | Tournament |
| Tournament size | 10 |
| Elite count | 50 |
| Crossover fraction | 0.75 |
| Mutation function | Adaptive mutation |
| Mutation rate | 0.3 |
| Maximum iteration number | 500 |
| Heat Sourse (K) | η (%) | Teva (K) | Tcon (K) | Tsup (K) | Tc,id (K) | pc,id (MPa) | Tb,id (K) | |
|---|---|---|---|---|---|---|---|---|
| 473.15 | 13.10 | 383.19 | 293.26 | 19.85 | 431.41 | 4.95 | 160.32 | 60.00 |
| 523.15 | 17.59 | 433.36 | 293.37 | 19.97 | 481.52 | 4.96 | 177.24 | 60.05 |
| Molecular Structure | Chemical Formula | Tc (K) | pc (MPa) | Tb (K) | η (%) | |
|---|---|---|---|---|---|---|
 | C3H4F2 | 432.52 | 4.80 | 294.80 | 30.63 | 12.98 |
 | C3H3F3 | 429.03 | 4.36 | 283.36 | 60.97 | 12.83 |
 | C3H4F2 | 436.83 | 4.31 | 303.06 | 35.30 | 12.22 |
| Molecular Structure | Chemical Formula | Tc (K) | pc (MPa) | Tb (K) | η (%) | |
|---|---|---|---|---|---|---|
 | C4H3F5 | 481.50 | 3.32 | 318.83 | 71.34 | 14.63 |
 | C4H6F4 | 481.59 | 2.90 | 317.87 | 133.60 | 14.61 |
 | C4H7F3 | 483.07 | 3.13 | 327.02 | 126.80 | 13.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Yang, F.; Zhang, H.; Yan, Y.; Yang, A.; Liang, J.; Yu, M. Performance Prediction and Working Fluid Active Design of Organic Rankine Cycle Based on Molecular Structure. Energies 2022, 15, 8160. https://doi.org/10.3390/en15218160
Pan Y, Yang F, Zhang H, Yan Y, Yang A, Liang J, Yu M. Performance Prediction and Working Fluid Active Design of Organic Rankine Cycle Based on Molecular Structure. Energies. 2022; 15(21):8160. https://doi.org/10.3390/en15218160
Chicago/Turabian StylePan, Yachao, Fubin Yang, Hongguang Zhang, Yinlian Yan, Anren Yang, Jia Liang, and Mingzhe Yu. 2022. "Performance Prediction and Working Fluid Active Design of Organic Rankine Cycle Based on Molecular Structure" Energies 15, no. 21: 8160. https://doi.org/10.3390/en15218160
APA StylePan, Y., Yang, F., Zhang, H., Yan, Y., Yang, A., Liang, J., & Yu, M. (2022). Performance Prediction and Working Fluid Active Design of Organic Rankine Cycle Based on Molecular Structure. Energies, 15(21), 8160. https://doi.org/10.3390/en15218160







