Aerodynamic Shape Optimization with Grassmannian Shape Parameterization Method
Abstract
1. Introduction
2. Shape Deformation on Discrete Section of Airfoil
3. Airfoil Shape Optimization
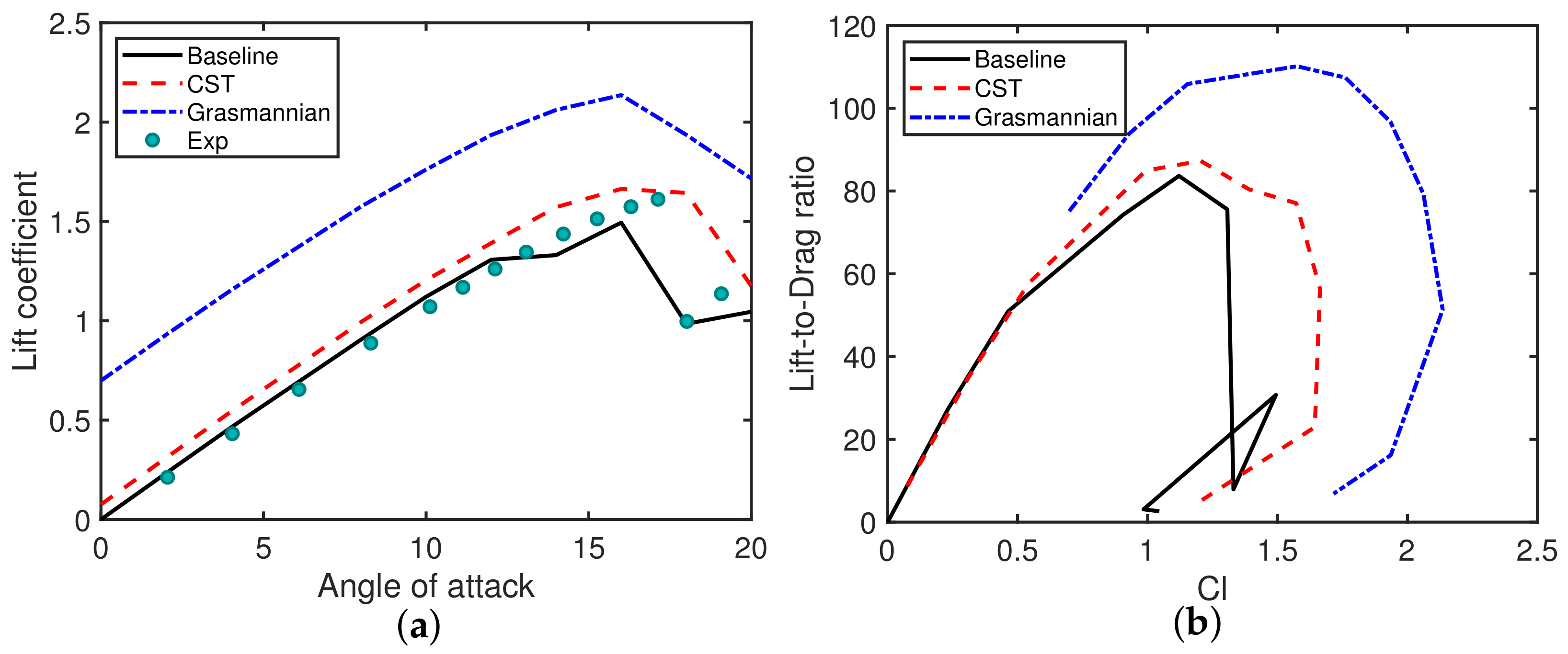
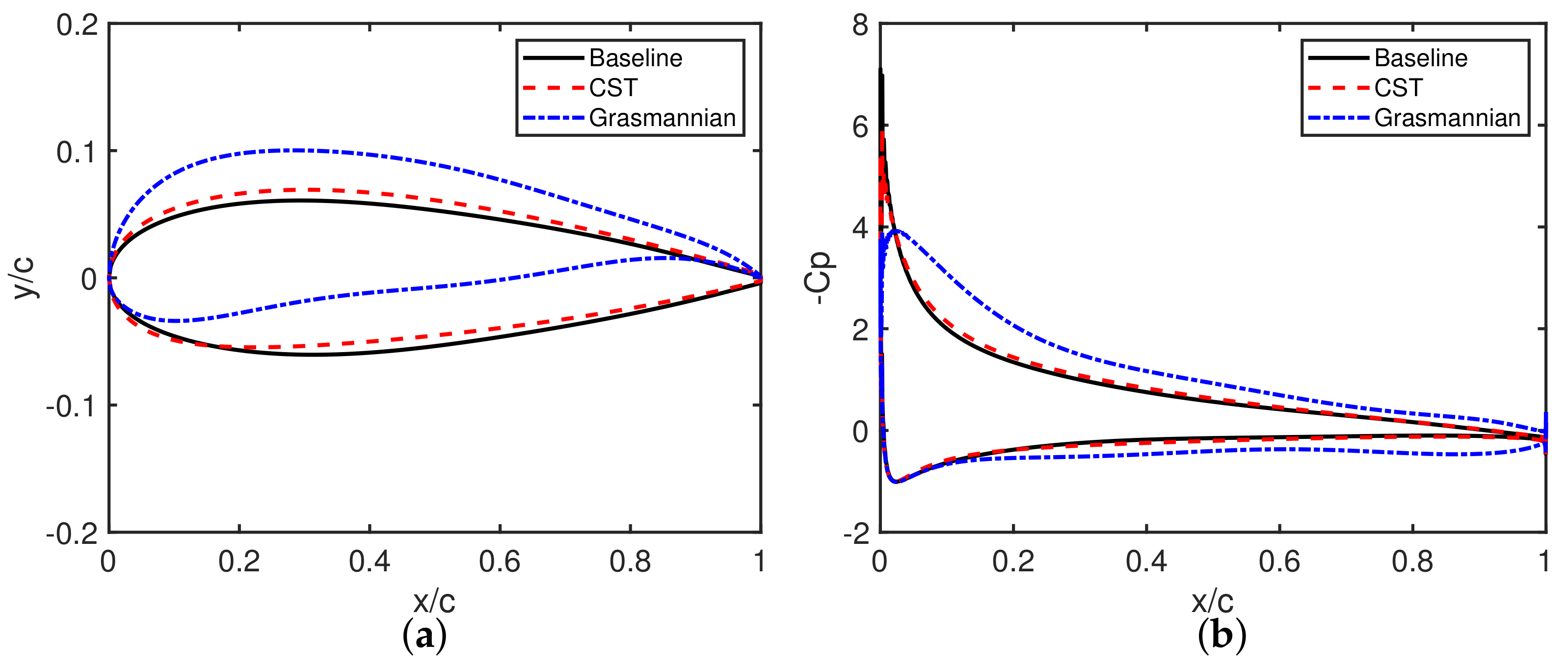
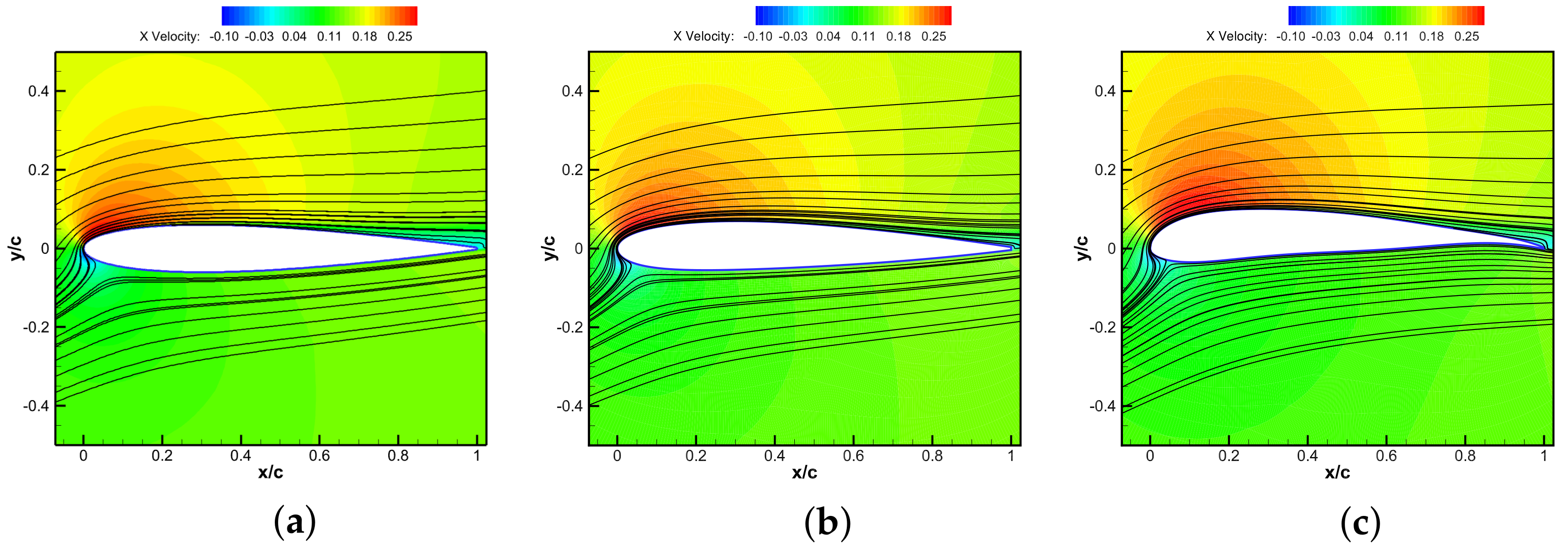
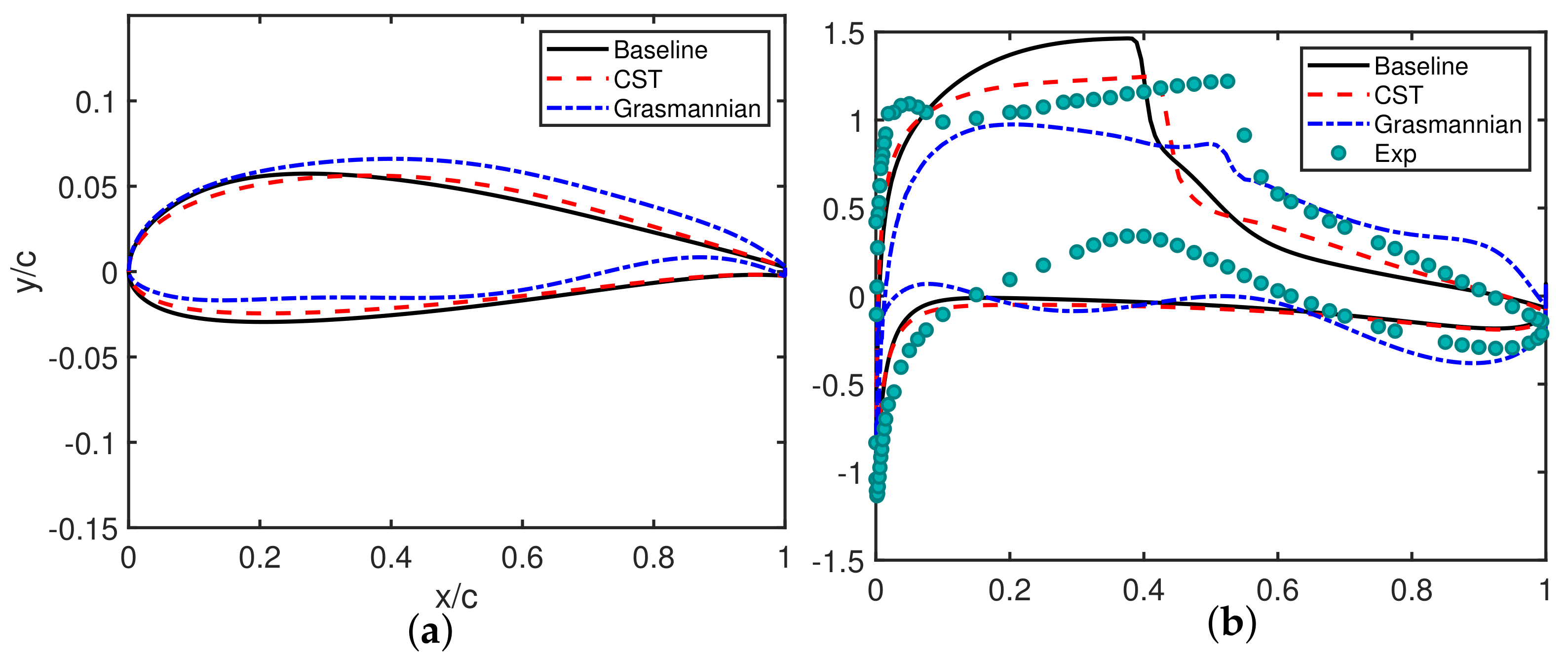
3.1. Subsonic Airfoil Optimization
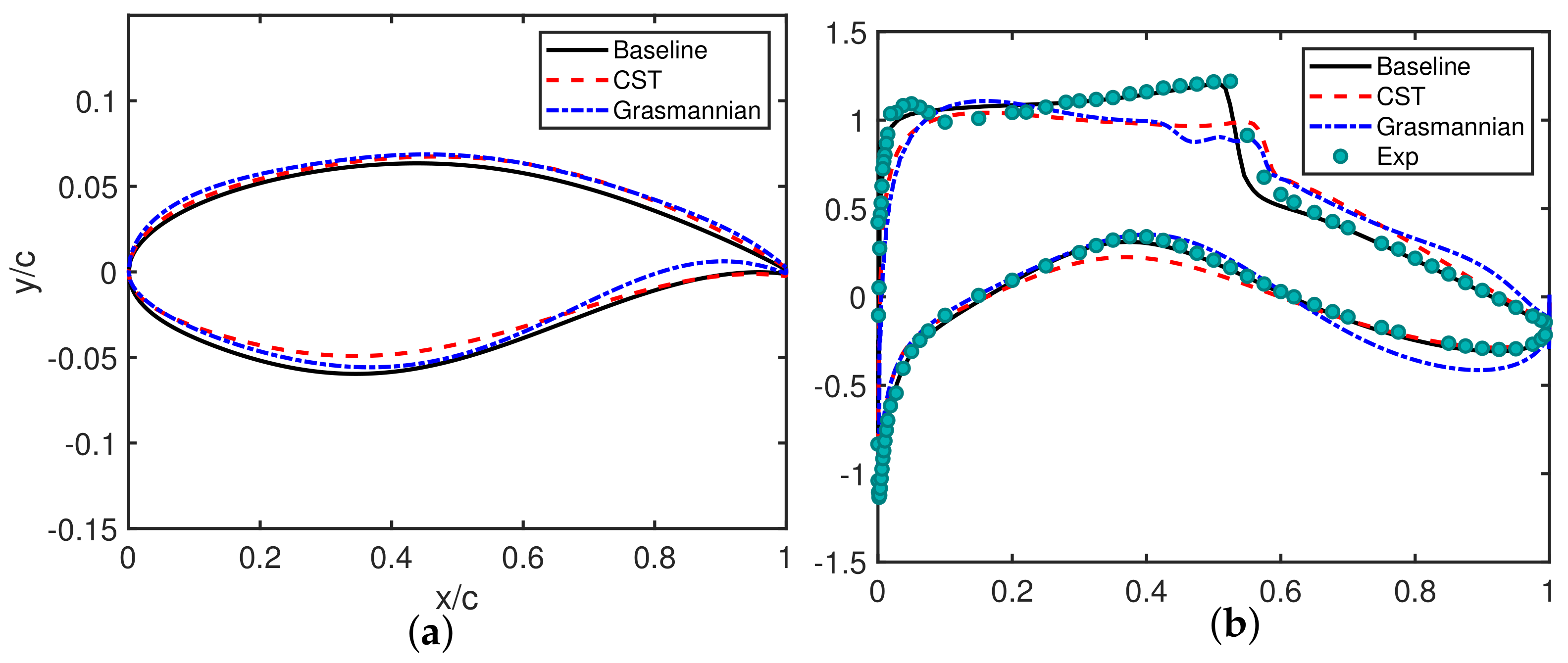
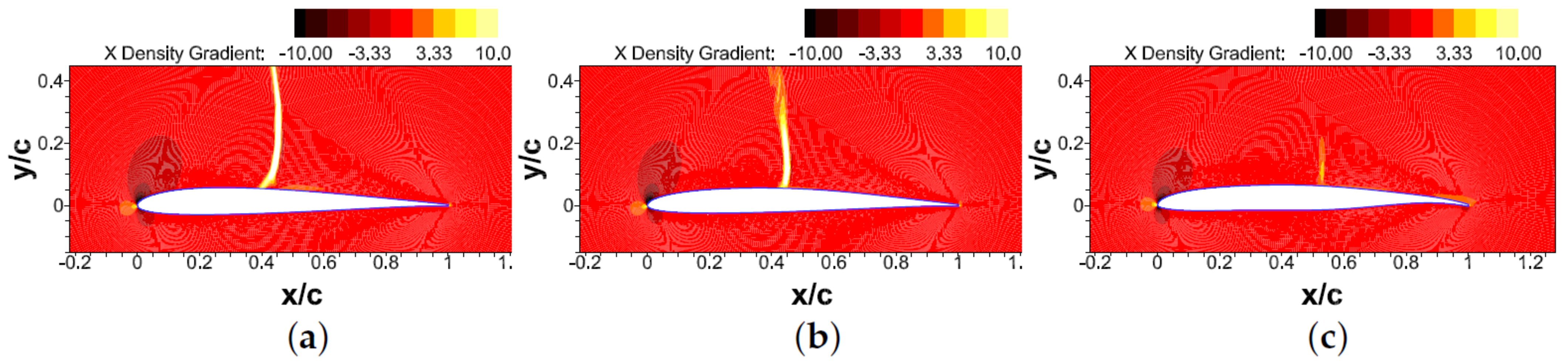
3.2. Transonic Airfoil Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PARSEC | Parametric section |
| CST | Class-shape function transformation |
| DR | Dimension reduction |
| POD | Proper orthogonal decomposition |
| SVD | Singular value decomposition |
| ASM | Active subspace method |
| QOI | Quality of interest |
| LAS | Landmark-affine standardization |
| PCA | Principal component analysis |
| PGA | Principal geodesic analysis |
| GSP | Grassmannian shape parameterization |
References
- Lighthill, M. A New Method of Two-Dimensional Aerodynamics Design. Aeronautical Research Council. 1945. Available online: https://reports.aerade.cranfield.ac.uk/handle/1826.2/3876 (accessed on 21 October 2014).
- Volpe, G.; Melnik, R. Role of constraints in inverse design for transonic airfoils. AIAA J. 1984, 22, 1770–1778. [Google Scholar] [CrossRef]
- Drela, M.; Giles, M.B. Viscous-inviscid analysis of transonic and low Reynolds number airfoils. AIAA J. 1987, 25, 1347–1355. [Google Scholar] [CrossRef]
- Krist, S.L. CFL3D User’s Manual, Version 5.0; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 1998. [Google Scholar]
- Jameson, A.; Reuther, J. Control theory based airfoil design using the Euler equations. In Proceedings of the 5th Symposium on Multidisciplinary Analysis and Optimization, Panama City, FL, USA, 7–9 September 1994; p. 4272. [Google Scholar]
- Jameson, A.; Kim, S. Reduction of the adjoint gradient formula for aerodynamic shape optimization problems. AIAA J. 2003, 41, 2114–2129. [Google Scholar] [CrossRef][Green Version]
- Zingg, D.W.; Nemec, M.; Pulliam, T.H. A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization. Eur. J. Comput. Mech./Revue Européenne de Mécanique Numérique 2008, 17, 103–126. [Google Scholar] [CrossRef]
- Nemec, M.; Zingg, D.W.; Pulliam, T.H. Multipoint and multi-objective aerodynamic shape optimization. AIAA J. 2004, 42, 1057–1065. [Google Scholar] [CrossRef]
- He, X.; Li, J.; Mader, C.A.; Yildirim, A.; Martins, J.R. Robust aerodynamic shape optimization—From a circle to an airfoil. Aerosp. Sci. Technol. 2019, 87, 48–61. [Google Scholar] [CrossRef]
- Zhang, Z.; De Gaspari, A.; Ricci, S.; Song, C.; Yang, C. Gradient-Based Aerodynamic Optimization of an Airfoil with Morphing Leading and Trailing Edges. Appl. Sci. 2021, 11, 1929. [Google Scholar] [CrossRef]
- Venter, G.; Sobieszczanski-Sobieski, J. Particle swarm optimization. AIAA J. 2003, 41, 1583–1589. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Yagiz, B.; Kandil, O.; Baysal, O. Particle swarm optimization of suction and blowing on airfoils at transonic speeds. J. Aircr. 2010, 47, 1955–1965. [Google Scholar] [CrossRef]
- Wang, Y.y.; Zhang, B.q.; Chen, Y.c. Robust airfoil optimization based on improved particle swarm optimization method. Appl. Math. Mech. 2011, 32, 1245–1254. [Google Scholar] [CrossRef]
- Li, J.; Gao, Z.; Huang, J.; Zhao, K. Robust design of NLF airfoils. Chin. J. Aeronaut. 2013, 26, 309–318. [Google Scholar] [CrossRef][Green Version]
- Yang, B.; Xu, Q.; He, L.; Zhao, L.; Gu, C.G.; Ren, P. A novel global optimization algorithm and its application to airfoil optimization. J. Turbomach. 2015, 137, 041011. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Aerodynamic Design Optimization of a Morphing Leading Edge and Trailing Edge Airfoil–Application on the UAS-S45. Appl. Sci. 2021, 11, 1664. [Google Scholar] [CrossRef]
- Sobieczky, H. Parametric airfoils and wings. In Recent Development of Aerodynamic Design Methodologies; Springer: Berlin/Heidelberg, Germany, 1999; pp. 71–87. [Google Scholar]
- Masters, D.A.; Taylor, N.J.; Rendall, T.; Allen, C.B.; Poole, D.J. Geometric comparison of aerofoil shape parameterization methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- Hicks, R.M.; Henne, P.A. Wing design by numerical optimization. J. Aircr. 1978, 15, 407–412. [Google Scholar] [CrossRef]
- Ahn, J.; Kim, H.J.; Lee, D.H.; Rho, O.H. Response surface method for airfoil design in transonic flow. J. Aircr. 2001, 38, 231–238. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Z.; Zhi, J.; Kretov, A. Aerothermodynamic Optimization of Aerospace Plane Airfoil Leading Edge. J. Aerosp. Technol. Manag. 2017, 9, 503–509. [Google Scholar] [CrossRef]
- Xu, S.; Chen, H.; Zhang, J. A study of Nash-EGO algorithm for aerodynamic shape design optimizations. Struct. Multidiscip. Optim. 2019, 59, 1241–1254. [Google Scholar] [CrossRef]
- Yirtici, O.; Tuncer, I.H. Aerodynamic shape optimization of wind turbine blades for minimizing power production losses due to icing. Cold Reg. Sci. Technol. 2021, 185, 103250. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, H.; Yang, K.; Dong, H.; Gao, Z. Research on blade design method of multi-blade centrifugal fan for building efficient ventilation based on Hicks-Henne function. Sustain. Energy Technol. Assessments 2021, 43, 100971. [Google Scholar] [CrossRef]
- Kulfan, B.M. Universal parametric geometry representation method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Zhu, F.; Qin, N. Intuitive class/shape function parameterization for airfoils. AIAA J. 2014, 52, 17–25. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, L.; Moschetta, J.M.; Zhao, J.; Yan, G. Optimization of nano-rotor blade airfoil using controlled elitist NSGA-II. Int. J. Micro Air Veh. 2014, 6, 29–42. [Google Scholar] [CrossRef]
- Liu, X.; He, W. Airfoil optimization design based on the pivot element weighting iterative method. Algorithms 2018, 11, 163. [Google Scholar] [CrossRef]
- Akram, M.T.; Kim, M.H. Aerodynamic shape optimization of NREL S809 airfoil for wind turbine blades using reynolds-averaged navier stokes model—Part II. Appl. Sci. 2021, 11, 2211. [Google Scholar] [CrossRef]
- Cinquegrana, D.; Iuliano, E. Investigation of adaptive design variables bounds in dimensionality reduction for aerodynamic shape optimization. Comput. Fluids 2018, 174, 89–109. [Google Scholar] [CrossRef]
- Sripawadkul, V.; Padulo, M.; Guenov, M. A comparison of airfoil shape parameterization techniques for early design optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010; p. 9050. [Google Scholar]
- Poole, D.J.; Allen, C.B.; Rendall, T. Aerofoil design variable extraction for aerodynamic optimization. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2705. [Google Scholar]
- Poole, D.J.; Allen, C.B.; Rendall, T.C. Metric-based mathematical derivation of efficient airfoil design variables. AIAA J. 2015, 53, 1349–1361. [Google Scholar] [CrossRef]
- Grey, Z.J.; Constantine, P.G. Active subspaces of airfoil shape parameterizations. AIAA J. 2018, 56, 2003–2017. [Google Scholar] [CrossRef]
- Li, J.; Cai, J.; Qu, K. Surrogate-based aerodynamic shape optimization with the active subspace method. Struct. Multidiscip. Optim. 2019, 59, 403–419. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Adjoint-free aerodynamic shape optimization of the common research model wing. AIAA J. 2021, 59, 1990–2000. [Google Scholar]
- Li, J.; Zhang, M.; Tay, C.M.J.; Liu, N.; Cui, Y.; Chew, S.C.; Khoo, B.C. Low-Reynolds-number airfoil design optimization using deep-learning-based tailored airfoil modes. Aerosp. Sci. Technol. 2022, 121, 107309. [Google Scholar] [CrossRef]
- Doronina, O.A.; Grey, Z.J.; Glaws, A. Grassmannian Shape Representations for Aerodynamic Applications. arXiv 2022, arXiv:2201.04649. [Google Scholar]
- Edelman, A.; Arias, T.A.; Smith, S.T. The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl. 1998, 20, 303–353. [Google Scholar] [CrossRef]
- Bryner, D.; Klassen, E.; Le, H.; Srivastava, A. 2D affine and projective shape analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 998–1011. [Google Scholar] [CrossRef]
- Fletcher, P.T.; Lu, C.; Pizer, S.M.; Joshi, S. Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Trans. Med. Imaging 2004, 23, 995–1005. [Google Scholar] [CrossRef]
- Karcher, H. Riemannian center of mass and so called karcher mean. arXiv 2014, arXiv:1407.2087. [Google Scholar]
- Menter, F.R. Improved Two-Equation k-Omega Turbulence Models for Aerodynamic Flows; Technical Report; NASA Ames Research Center Moffett Field: Santa Clara, CA, USA, 1992. [Google Scholar]
- Ladson, C.L. Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section; National Aeronautics and Space Administration, Scientific and Technical Information (STI) Program: Hampton, VA, USA, 1988; Volume 4074. [Google Scholar]
- Cook, P.; McDonald, M.; Firmin, M. Aerofoil Rae 2822-Pressure Distributions, and Boundary Layer and Wake Measurements. Experimental Data Base For Computer Program Assessment; AGARD Report AR; AGARD: Neuilly-sur-Seine, France, 1979; Volume 138. [Google Scholar]
- Whitcomb, R.T. Review of NASA supercritical airfoils. In Proceedings of the International Council of the Aeronautical Sciences Congress, Haifa, Israel, 25–30 August 1974. Number ICAS PAPER 74-10. [Google Scholar]
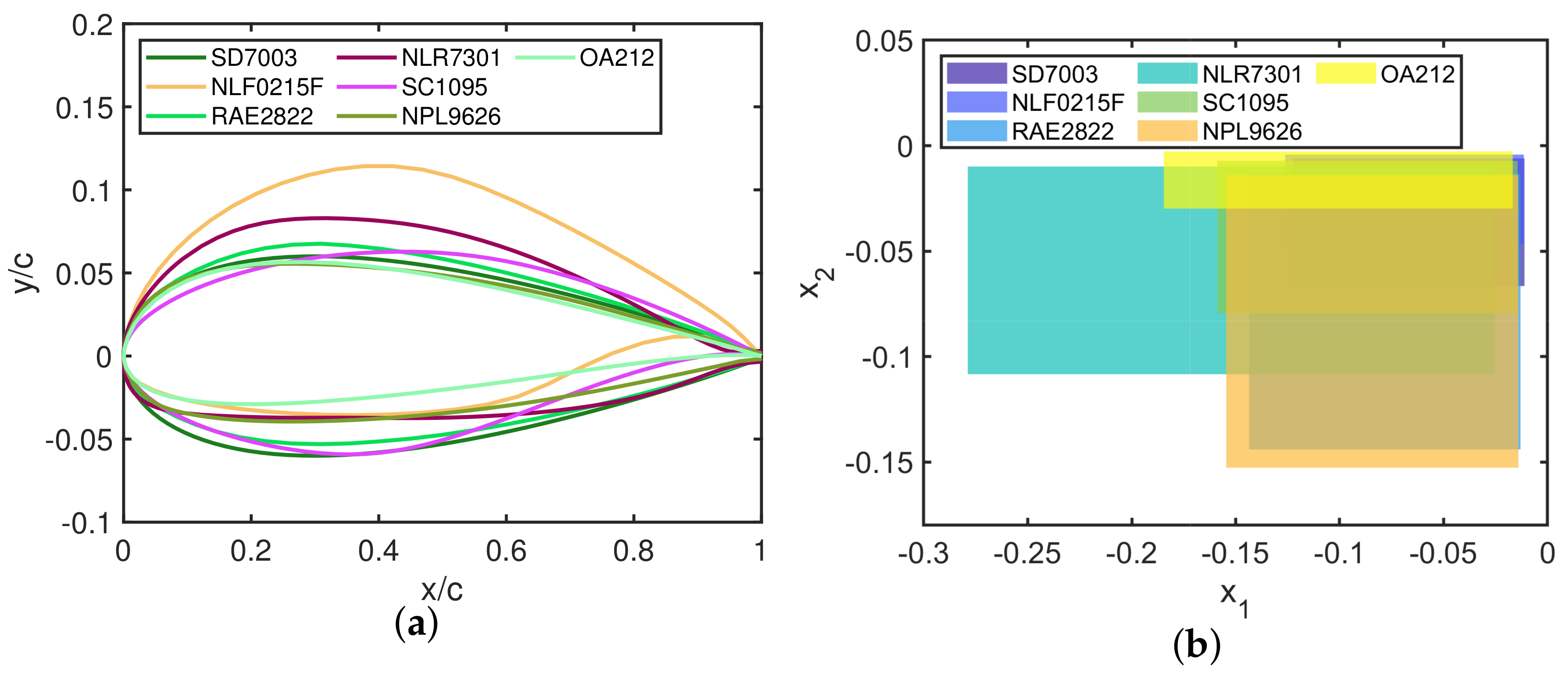
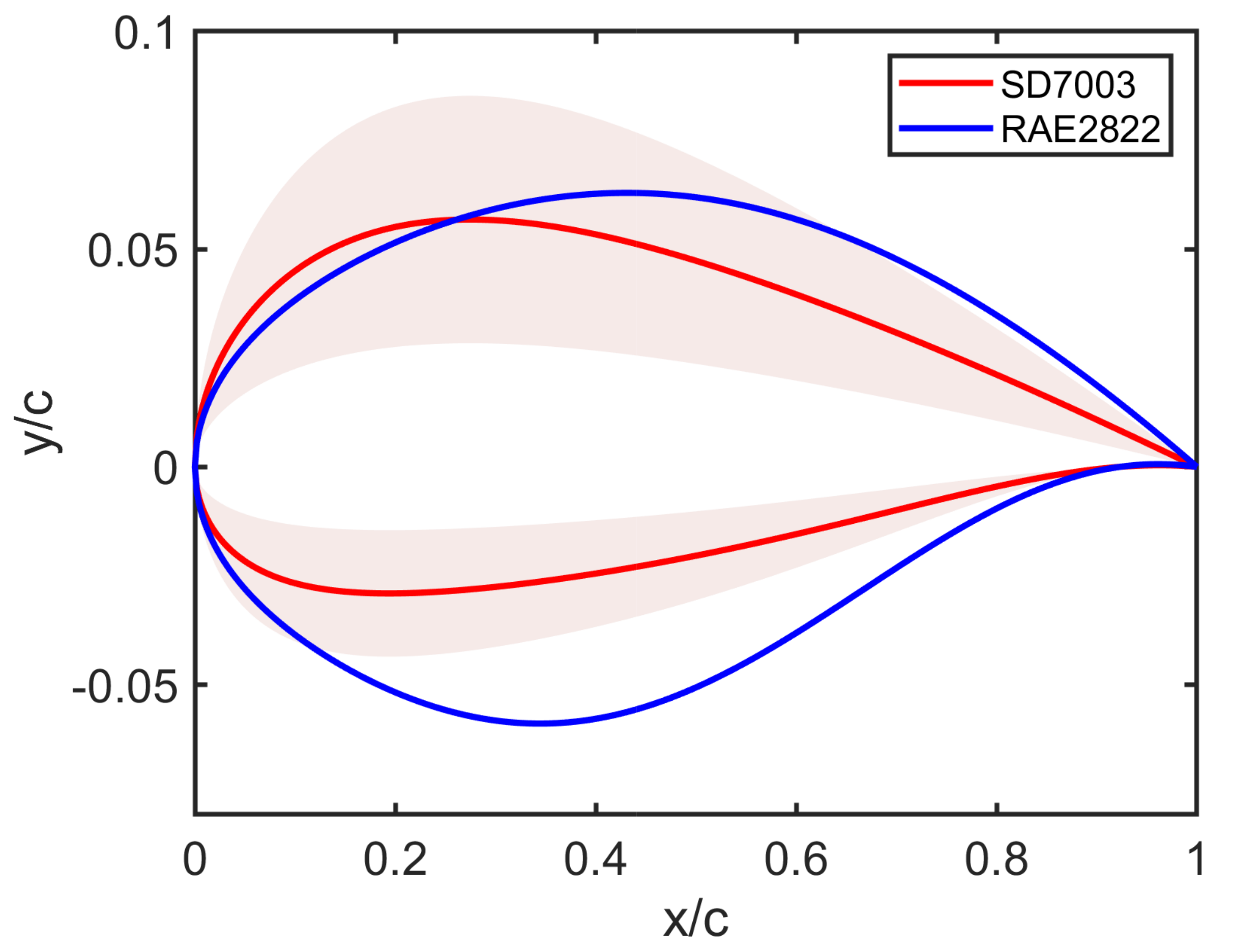
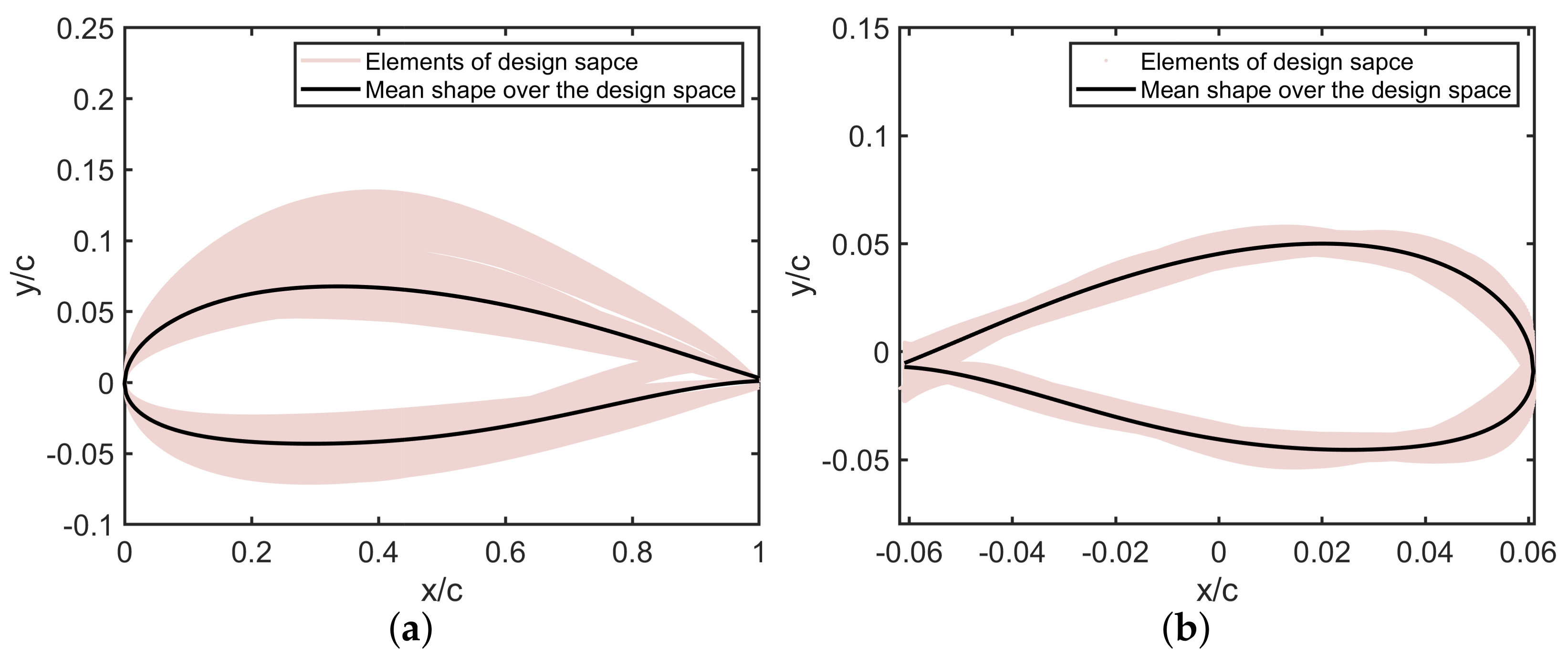
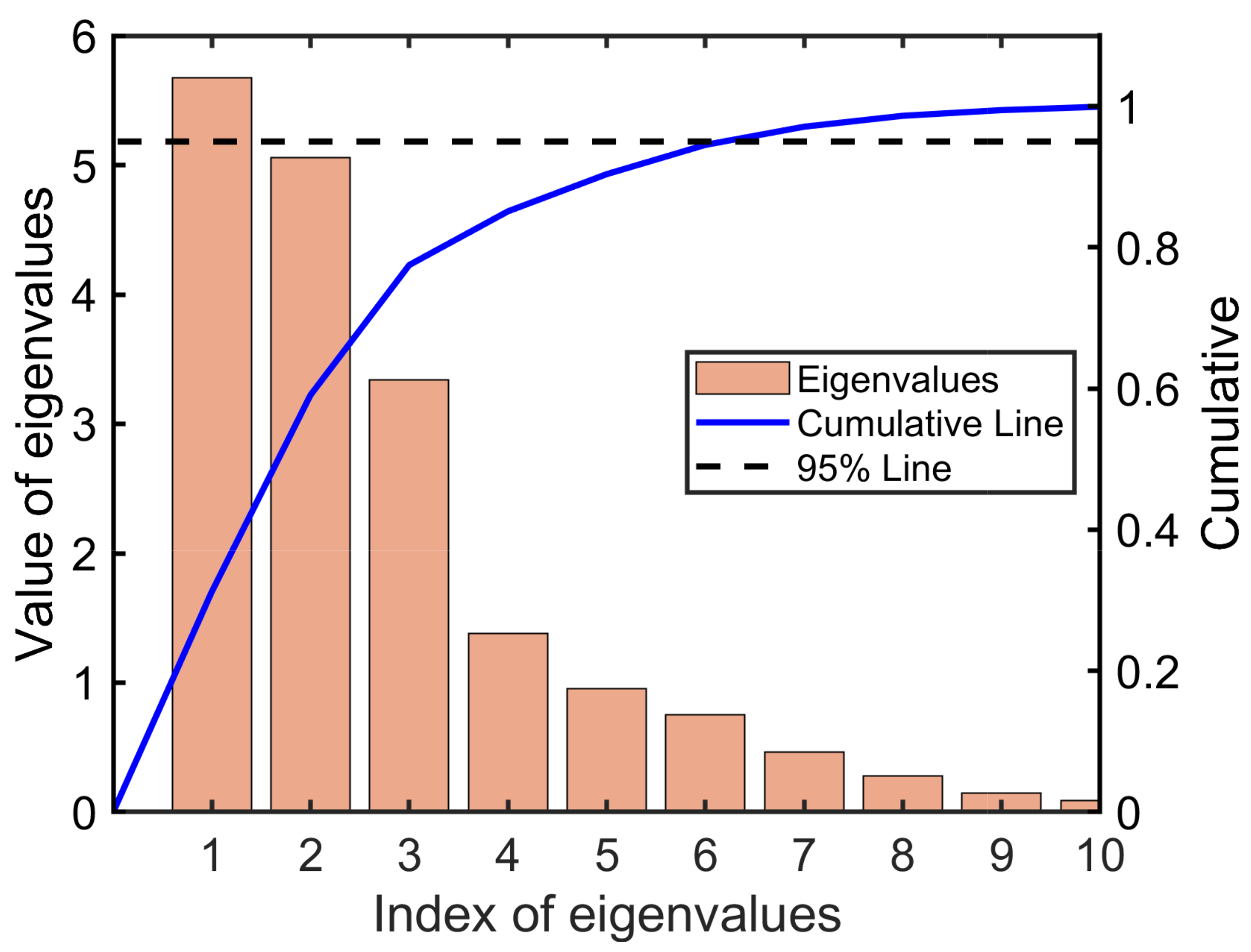
| Airfoil | |||||
| Lower Surface | |||||
| SD7003 | −0.1113 | −0.0605 | −0.0611 | −0.0561 | 0.0217 |
| NLF0215F | −0.1147 | −0.0424 | −0.1336 | −0.1815 | 0.3003 |
| RAE2822 | −0.1305 | −0.1309 | −0.2340 | −0.0665 | 0.0325 |
| NLR7301 | −0.2535 | −0.0985 | −0.3397 | −0.1388 | 0.1041 |
| SC1095 | −0.1444 | −0.0722 | −0.1158 | −0.0858 | −0.0929 |
| NPL9626 | −0.1405 | −0.1388 | −0.1419 | −0.1111 | −0.1558 |
| OA212 | −0.1678 | −0.0271 | −0.1266 | −0.1237 | −0.1613 |
| Airfoil | |||||
| Upper Surface | |||||
| SD7003 | 0.1585 | 0.1642 | 0.1203 | 0.1240 | 0.1092 |
| NLF0215F | 0.2278 | 0.2581 | 0.4142 | 0.1965 | 0.3958 |
| RAE2822 | 0.1277 | 0.1404 | 0.1877 | 0.1968 | 0.1990 |
| NLR7301 | 0.3120 | 0.1051 | 0.3163 | 0.2542 | 0.2345 |
| SC1095 | 0.1797 | 0.1334 | 0.1318 | 0.1417 | 0.1245 |
| NPL9626 | 0.1708 | 0.1849 | 0.1763 | 0.1268 | 0.1840 |
| OA212 | 0.1890 | 0.2806 | 0.1116 | 0.3548 | 0.0038 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Pang, B.; Li, X.; Chen, G. Aerodynamic Shape Optimization with Grassmannian Shape Parameterization Method. Energies 2022, 15, 7722. https://doi.org/10.3390/en15207722
Zhang Y, Pang B, Li X, Chen G. Aerodynamic Shape Optimization with Grassmannian Shape Parameterization Method. Energies. 2022; 15(20):7722. https://doi.org/10.3390/en15207722
Chicago/Turabian StyleZhang, Yang, Bo Pang, Xiankai Li, and Gang Chen. 2022. "Aerodynamic Shape Optimization with Grassmannian Shape Parameterization Method" Energies 15, no. 20: 7722. https://doi.org/10.3390/en15207722
APA StyleZhang, Y., Pang, B., Li, X., & Chen, G. (2022). Aerodynamic Shape Optimization with Grassmannian Shape Parameterization Method. Energies, 15(20), 7722. https://doi.org/10.3390/en15207722







