A Capacity Optimization Method for a Hybrid Energy Storage Microgrid System Based on an Augmented ε- Constraint Method

Abstract

In general, microgrids have a high renewable energy abandonment rate and high grid construction and operation costs. To improve the microgrid renewable energy utilization rate, the economic advantages, and environmental safety of power grid operation, we propose a hybrid energy storage capacity optimization method for a wind–solar–diesel grid-connected microgrid system, based on an augmented ε- constraint method. First, the battery is coupled with a seasonal hydrogen energy storage system to establish a hybrid energy storage model that avoids the shortcomings of traditional microgrid systems, such as a single energy storage mode and a small capacity. Second, by considering the comprehensive cost and carbon emissions of the power grid within the planning period as the objective function, the abandonment rate of renewable energy as the evaluation index, and the electric energy storage and seasonal hydrogen energy storage system operating conditions as the main constraints, the capacity allocation model of the microgrid can be constructed. Finally, an augmented ε- constraint method is implemented to optimize the model above; the entropy–TOPSIS method is used to select the configuration scheme. By comparative analysis, the results show that the optimization method can effectively improve the local absorption rate of wind and solar radiation, and significantly reduce the carbon emissions of microgrids.

1. Introduction

Microgrids are important carriers of distributed energy resources, but their energy resource acceptance capabilities are limited. Therefore, reasonable equipment capacity allocation in the microgrid is of great significance in improving the operation and economic benefits of microgrid systems.

The optimal microgrid system capacity configuration is based on the selection of a distributed energy resource system and the construction of an energy storage system [1]. In a microgrid, constructing an effective and reliable energy storage model for a distributed energy resource system can mitigate the effects of the randomness and intermittency of distributed energy generation on the power grid, and improve microgrid operation [2]. However, traditional microgrid energy storage methods involve mostly single energy storage systems, which face various problems, such as a small energy storage capacity, a short adjustment period, and long-term supply and demand imbalances [3]. 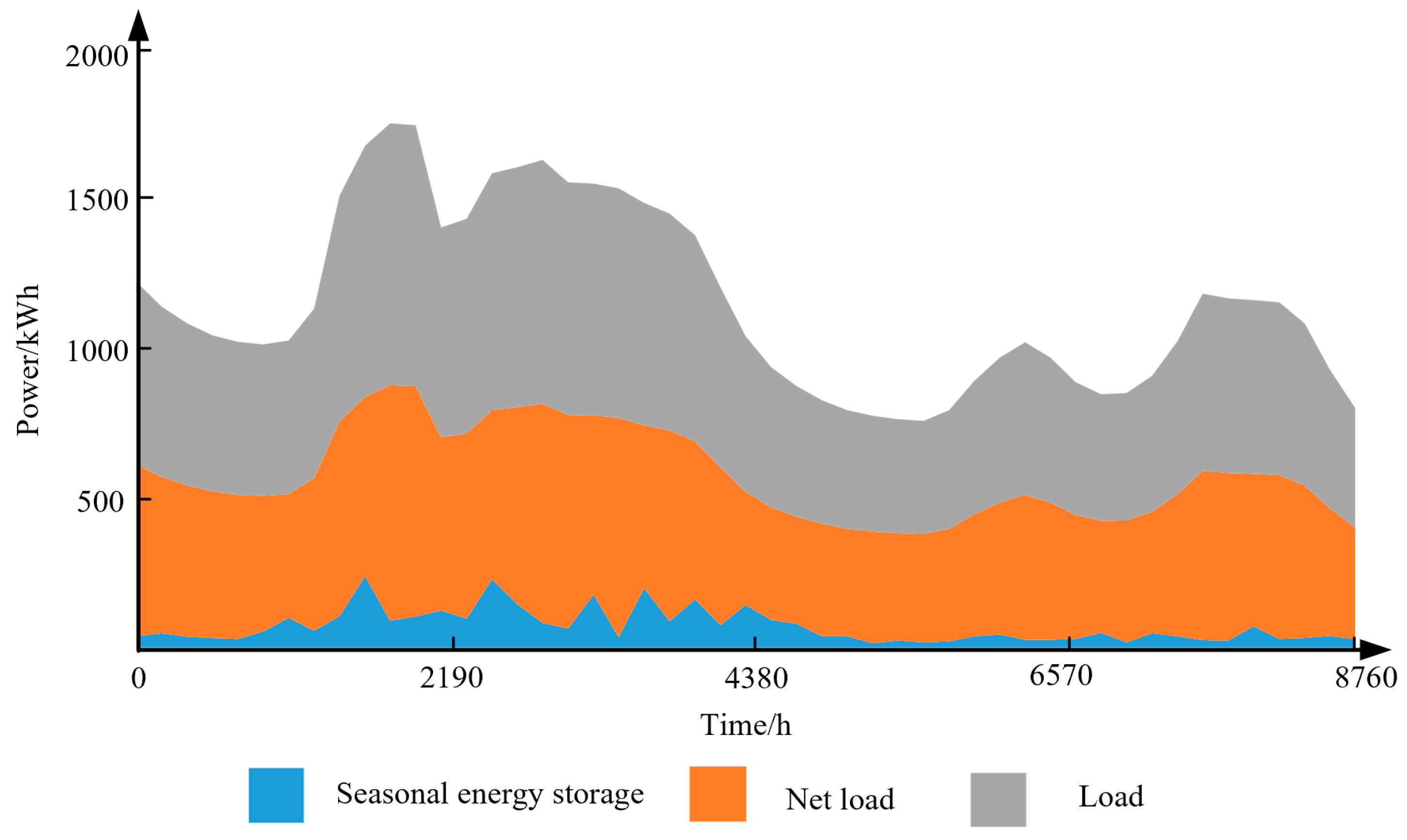Long-term hydrogen energy storage has the advantages of low loss, large energy storage capacity, high energy conversion efficiency, and strong economic benefits [4]. Additionally, hydrogen energy storage can be combined with electric energy storage to compensate for its short-term issues, obtain complementary advantages, and enable stepped energy system applications, providing a theoretical basis for supporting high-permeability energy generation. Therefore, we propose a hybrid energy storage system, formed by coupling batteries and seasonal hydrogen energy storage systems, the function of Seasonal Energy Storage can be seen at Appendix A Figure A1. Furthermore, in a power system configuration with a high proportion of renewable energy, seasonal hydrogen energy storage has significant advantages of energy conservation and emission reduction. Additionally, it can balance the overall electric load throughout the year, improve power quality, and optimize the interactions between renewable energy and load [5].

In recent years, energy storage methods have developed from single energy storage systems in a traditional power grid, to multiple energy storage systems combined in a grid [6]. Some examples of hybrid energy storage systems include batteries with supercapacitors, and batteries with pumped storage systems. However, due to various limitations, such as service life and energy density, there are restrictions on the large-scale application of hybrid energy power grids [7], classification and characteristics of relevant energy storage devices can be seen at Appendix A 

Table A1. Classification of Energy Storage System.

Types of Energy Storage	Type of Stored Energy	Typical Representatives
Mechanical energy storage	The potential energy of water	Pumped storage
	Kinetic energy of gas pressure	Compressed air storage
	Kinetic energy of the rotating mass	Flywheel Energy Storage
Electric energy storage	Electricity in magnetic fields	Superconducting magnetic energy storage
	Electricity in an electric field	Supercapacitor
Electrochemical Energy Storage	Electrochemical energy in the electrode	Classic Battery Energy Storage
	Electrochemical energy in electrolyte	Redox battery energy storagehybrid flow battery energy storage
Thermal Energy Storage	Heat energy in particle motion	Sensitive thermal storage device
	Heat storage by heat absorption reaction	Thermochemical Energy Storage
Chemical Energy Storage	Conversion to gas	Electricity and gas power plants
	Conversion to fuel	Power fluid system
	Converted to chemical products	Electric Power Chemical Plant

and

Table A2. Characteristics of Different Energy Storage Devices.

Energy Storage Type	Supercapacitor	Lead-Acid Batteries	Lithium Battery	Hydrogen Energy Storage
Energy density Wh/kg	5–10	30–50	120–180	500
Power density W/kg	1000–18,000	200–500	1000	1 kW–1 GW
Circulation efficiency (%)	>95	75–90	85–98	40–70
Response time (s)	0.001–0.02	>0.02	0.01–0.02	1 s-h
Energy release time	1 ms–1 s	1 s–10 h	1 s–10 h	1 s–24 h
Cycle life (times)	>50,000	2000–4000	2000–10,000	20 years

. Therefore, hydrogen energy storage has attracted wide attention, as it is a new energy storage method with the advantages of cleanliness, high energy density, and large capacity [8].

Regarding the applications of hydrogen energy storage in microgrids, wind–solar stations, and integrated energy systems, scholars have published relevant studies that explore the economic and environmental benefits of hydrogen energy storage [9,10,11]. Wen et al. proposed an electric–hydrogen hybrid energy storage system topology that took full advantage of the large capacity of hydrogen energy storage to reduce power fluctuations and energy loss in the power grid. This system also supports the flexible grid connection capabilities of wind farms. However, this model considered a day as the dispatch cycle and did not take full advantage of hydrogen energy storage for long-term energy transfer; therefore, the economy and cycle efficiency of hydrogen energy storage in this system were low [12]. Xu et al. considered the investment cost, system cumulative error, and system carbon emissions as the objective functions-solving model of the hydrogen energy storage optimal configuration. The study proposed that the hydrogen energy storage system could flexibly participate in system scheduling, and greatly improve the renewable energy consumption rate. However, this model-configured hydrogen energy storage was only a single energy storage system, which was not strong enough to cope with sudden changes in the power grid and had poor system stability, making it difficult to use in practical engineering applications [13]. Bakhtiari et al. designed a new hybrid energy system that included wind and photovoltaic power, and hydrogen energy storage systems. A target fitness function was used to establish a system model that considered the power supply probability loss, power difference between power generation and storage capacity, and net present value to achieve a better capacity optimization effect. However, this model did not consider energy exchange with the grid, resulting in a waste of part of the generated distributed exchange energy source power [14]. A hydrogen energy storage system configuration in the microgrid can help stabilize energy generation fluctuations, improve power quality, and achieve effective utilization of wind and solar resources [15].

Depending on the scale of construction of the microgrid, the cost components considered are also different when building the objective function with the goal of economy.

For the microgrid containing hydrogen energy storage with a large planning area, because of the large scale of grid and the long distance between devices, it is often necessary to calculate the connection costs and transmission costs between the devices separately, which has become an important part of the cost function [16,17]. For some small microgrids, the construction site area and the equipment spacing are already constrained at the early stages of planning and design. This means that the transmission distance of hydrogen energy is short, and the proportion of transmission cost in the total cost will be much smaller than the investment cost of equipment and aging cost, etc. Therefore, this part has been included in the initial investment cost of the equipment and does not need to be listed separately in the economic objective function [18,19].

For the solution algorithm, to determine the optimal microgrid capacity configuration, researchers mainly use intelligent and deterministic algorithms. Common intelligent algorithms, such as the particle swarm optimizer (PSO), genetic algorithm (GA), and gray wolf optimizer (GWO) [20,21]. Common deterministic algorithms include the linear weighted method (LWM), linear programming method (LPM), and multi-weight method (MWM) [22,23,24].

When solving a multi-objective microgrid configuration model, intelligent algorithms are implemented by many researchers because of their good adaptability in dealing with multi-objective optimization problems (MOP). Jia et al. comprehensively analyzed the power grid operation stability and costs. Moreover, the researchers fully considered the charge state of the hybrid energy storage system, and used the PSO to optimize the model parameters. The optimized configuration results were robust. However, this algorithm has various problems, such as insufficient convergence ability and difficulty in jumping out of local optimization [25]. Chen et al. constructed a hybrid energy storage allocation model with maximum whole-life net revenue accounting for carbon trading, and solved it using the adaptive chaotic particle swarm optimization algorithm (ACPSO). This algorithm exploits the characteristics of chaotic perturbation complexity and stochasticity, and has better convergence speed and optimal finding capability. However, it still suffers from the unstable output of the global optimal solution [26]. Li et al. successively considered the reliability and economics of the power supply system, and used the beetle antennae search (BAS) algorithm to configure the optimal capacity. The solution algorithm introduced BAS, which can easily find the global optimal solution, and has a high optimization speed compared with that of the genetic algorithm (GA) with better nonlinear programming. This improvement eliminated the local optimal solution, and yielded stable and reliable capacity matching results. However, the algorithm has many control variables and can accept a deteriorating solution with a certain probability [27].

While intelligent algorithms have good optimization effects, they also have issues, such as easily falling into localized optimization solutions and being unable to efficiently find the optimal solution of a multi-objective function. A deterministic algorithm can avoid these shortcomings by finding the multi-objective optimal configuration and scheduling of microgrids, due to its fast global search capability.

Ding et al. built a bilinear programming model by considering the uncertainty of grid access to wind power that could accurately solve the upper and lower boundaries of the interval. The spatial branch-and-bound (B&B) algorithm was used to avoid the issue that the traditional genetic algorithm easily falls into: local optimization. Therefore, the universal optimal solution of the model was found [28]. Liang et al. constructed a dual-objective problem of cogeneration with the goal of minimizing total costs and pollutant emissions. Through simulation analyses, it was found that the use of the improved ε- constraint method to solve multi-objective problem models could greatly shorten the computation time compared to those of classic intelligent algorithms, such as the fast nondominated sorting genetic algorithm II (NSGA-II) and the enhanced Pareto evolutionary algorithm (SPEA-II). Additionally, solving the model with the ε- constraint method improved the effectiveness of the Pareto solution set, and the economic and environmental benefits of the configuration results significantly improved [29]. Marcos et al. proposed a stochastic multi-objective solution framework for home energy management systems [30]. The operation speed of the ε- constraint method was found to greatly decrease as the number of objective functions increased to more than three, while the operation time of the method also significantly increased when the number of scenarios increased to more than six. Thus, the traditional ε- constraint method has difficulty solving optimization problems containing three or more objective functions, but it is more capable and less computationally expensive in bi-objective and bi-scenario optimization. Therefore, this paper chose the ε- constraint method and improved it to the augmented ε- constraint (AUGMECON) method, to solve the double objective function and double scenarios problem, greatly improving the accuracy and speed of operation.

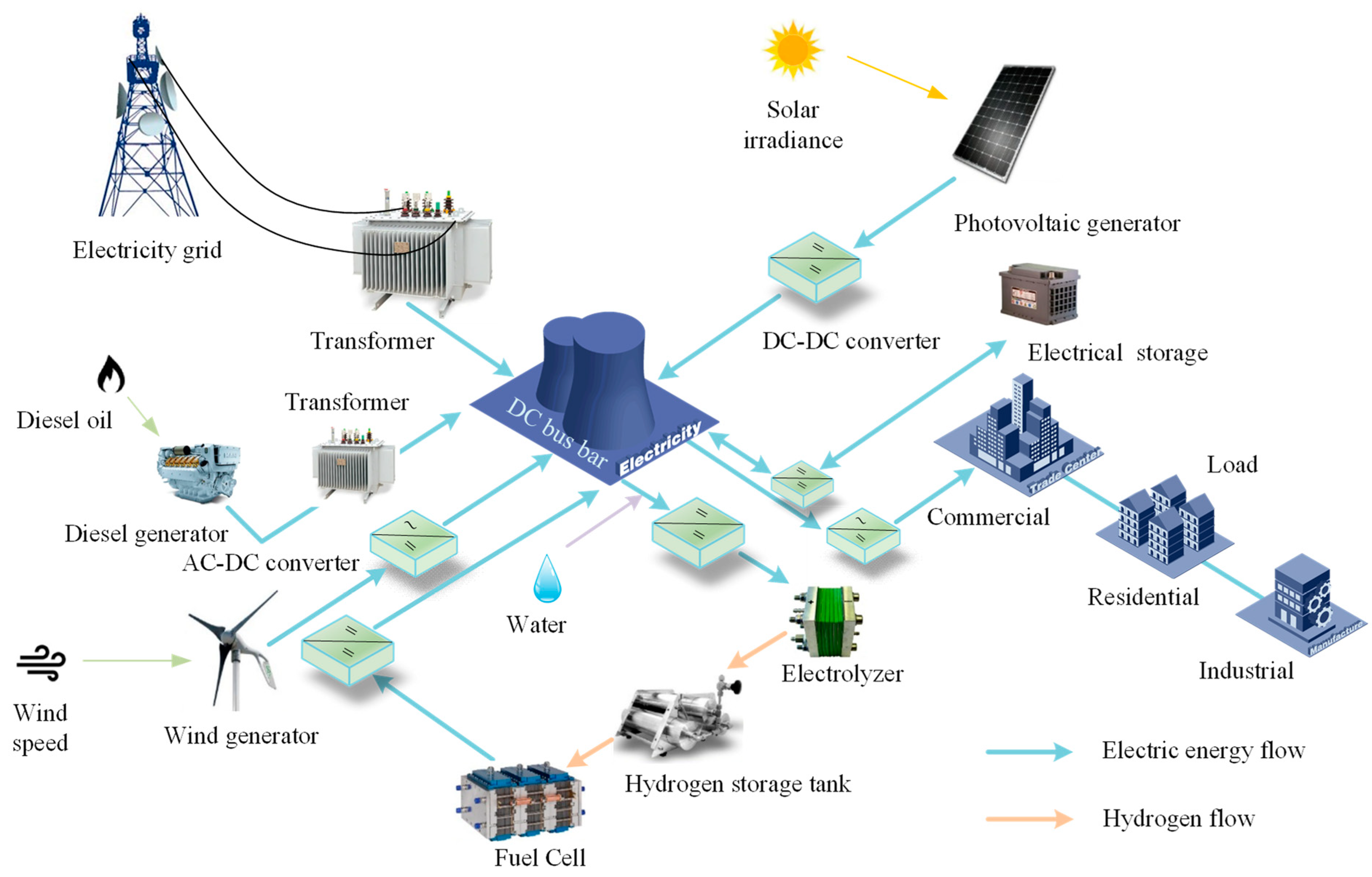
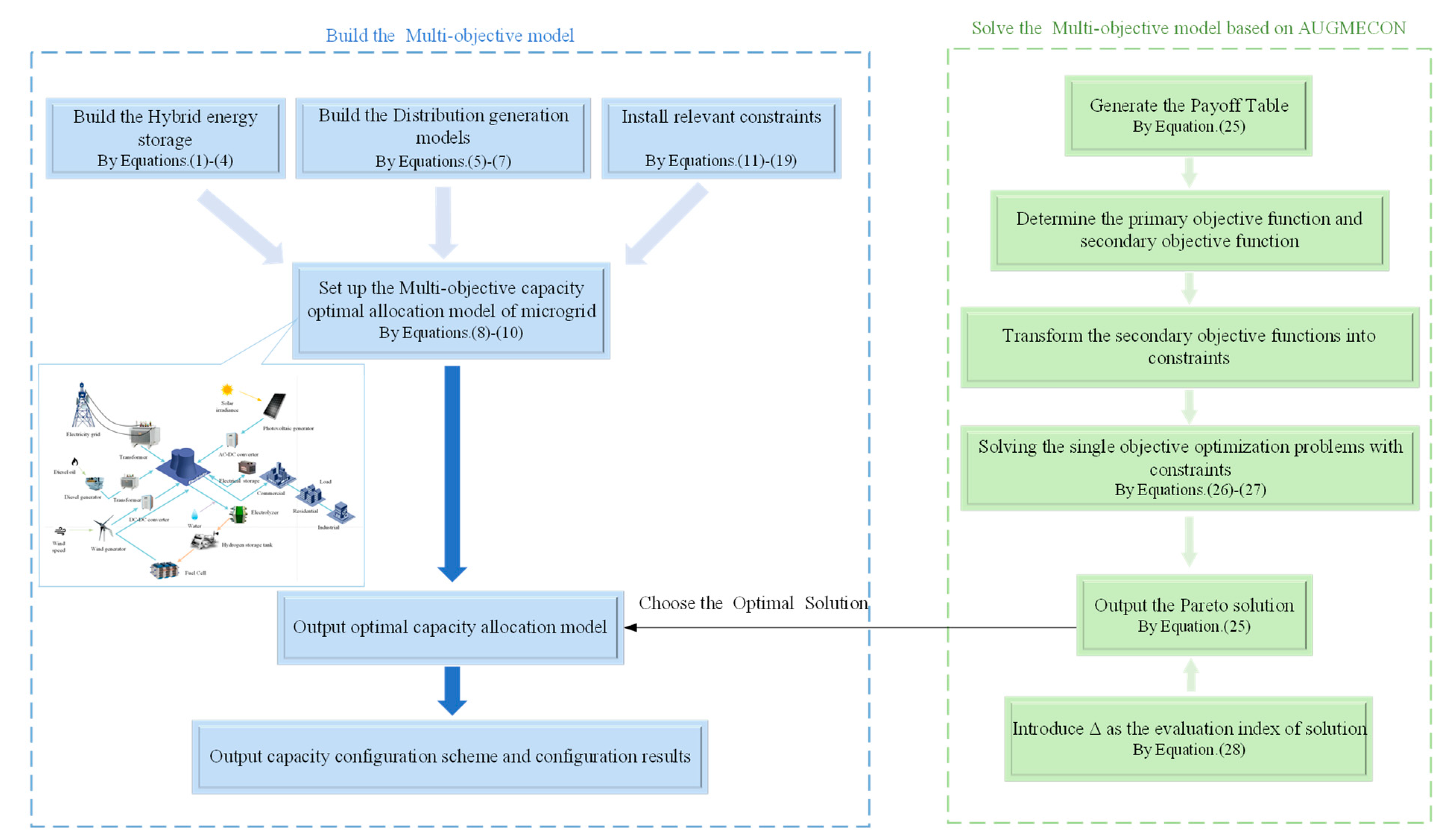
In this paper, a capacity-optimized configuration method for a wind-solar-diesel-hydrogen grid-connected microgrid system is proposed, based on the augmented ε- constraint (AUGMECON) method. First, mathematical models of distributed energy resources, electric energy storage, and seasonal hydrogen energy storage systems in the microgrid are established. Then, the economic and environmental benefits of the microgrid system are taken as the objective functions. The distributed energy characteristics, the energy storage system operating conditions, and the renewable energy abandonment rate are considered in the multi-objective mixed-integer linear programming (MILP) function. Thus, an optimal configuration model for microgrid capacity is constructed. Afterwards, AUGMECON is compared to other algorithms to verify its superiority, and is then used to solve the model. The entropy weight and technique for order preference by similarity to an ideal solution (entropy–TOPSIS) method is used to select the configuration scheme to build the optimal model, and the optimal configuration scheme is exported. Finally, to verify the practicability of the method proposed in this paper, the data concerning the wind and solar resources and the load in an integrated wind power plant are input into the model for a simulation analysis; the results are compared to those of different energy storage models. In addition, typical days in different seasons are selected to further analyze the configuration and operation of the proposed system.

2. Structure and Model of Microgrid

To establish a wind–solar–diesel grid-connected microgrid system with seasonal hydrogen energy storage, a distributed energy system is selected in this paper. The system includes photovoltaic arrays, wind turbines, and diesel units. Based on the above, the microgrid is equipped with diesel engines and has grid connection characteristics. With increasing load demand, it can flexibly purchase power from the main power grid and use diesel generators to generate electricity. Therefore, the model can flexibly deal with deviations caused by changes in the amortization period. The specific structure is shown in Figure 1. The relevant parameters of the microgrid model and their meanings are shown in

Table 1. Relevant Parameters of Microgrid and Their Meanings.

Parameter	Meaning	Parameter	Meaning
CPV	Rated output power of photovoltaic array	ZES,0	Initial energy of electrical energy storage
CPV	Rated output power of photovoltaic array	ZES,y,24	Electric energy stored in the 24th hour of day y
CDG	Rated output power of diesel engine	Zi,max	The upper limit of the capacity configuration of device i
CI	Equipment investment costs for microgrid	ZES,Tn	The amount of hydrogen in the hydrogen storage tank at the Tn hour
CR	Equipment replacement costs for microgrid	αDG	Fuel consumption curve coefficient of diesel engine
CM	Equipment operation and maintenance costs for microgrid	βDG	Fuel consumption curve coefficient of diesel engine
CB	Costs incurred by the microgrid to purchase electricity from the main grid	ηES,self	Self-discharge efficiency of electrical energy storage
d1	Euclidean distance from the other endpoint to the limit point	ηES,c	Charging efficiency of electric energy storage
di	Euclidean distance between two adjacent points	ηES,d	Discharge efficiency of electric energy storage
d	Average of Euclidean distances for all adjacent points	ηEL	Efficiency of electrolyzer
df	Euclidean distance between an endpoint and a limit	ηHT	Efficiency of hydrogen storage tank
EES(t)	Electric energy storage at time t	HHV	High calorific value of hydrogen
EHT(t)	Capacity of hydrogen energy storage tank at time t	ηFC	Efficiency of fuel cell
Elost	Cumulative Renewable Energy Disposal	δ	Power temperature coefficient of PV
EQ	The actual cumulative amount of renewable energy generation	T	current surface temperature of PV
GSTC	Light intensity in standard environment	Tr	reference temperature
GAC	current light intensity	v	real-time wind speed
mHT(t)	Hydrogen quality of hydrogen storage tank at time t	vr	Rated speed of wind turbine
PPV(t)	Output power of the photovoltaic array at time t	vci	Rated cut-in speed of wind turbine
PWT(t)	Output power of the wind turbine at time t	R	number of value points
PDG(t)	Output power of diesel engine at time t	vco	Rated cut-out speed of wind turbine
PL(t)	Power of load at time t	fuel	Diesel fuel consumption
PES,c(t)	Charging power of the electric energy storage at time t	kCRF	Fund recovery factor
PES,d(t)	Discharge power of electric energy storage at time t	N	The planned life of the microgrid
PEL	Power of electrolyzer	λi	Capacity configuration unit price of device i
PEL-HT(t)	Output power from the electrolyzer to the hydrogen storage tank at time t	ni	The number of replacements of device i within the planning period of the microgrid
PHT-FC(t)	Output power from the hydrogen storage tank to the fuel cell at time t	rM	Operation and maintenance costs of microgrids as a percentage of investment costs
PFC(t)	Output power of fuel cell at time t	TN	Operation cycle of microgrid
Pe(t)	Power purchased of the microgrid from the main grid at time t	λe	The purchase price of electricity for the microgrid from the main grid
Pe,max	Maximum power purchased by the microgrid from the main grid	λoil	Unit price of diesel
ZHT,0	The initial hydrogen storage capacity of the hydrogen storage tank	re	Average carbon intensity of grid electricity purchases
zi	Configure capacity of device i	roil	Diesel carbon emission intensity

.

2.1. Hybrid Energy Storage System Model

In a hybrid energy storage system based on a combination of electric energy storage and seasonal hydrogen energy storage, electric energy storage is used for suppressing fluctuations caused by sudden changes in the microgrid load demand. In contrast, seasonal hydrogen energy storage is used for establishing large-scale, long-term electric energy storage and transfer technology. The hybrid energy storage system proposed in this paper can flexibly respond to sudden microgrid changes and long-term electricity consumption behavior.

2.1.1. Electric Energy Storage Model

In this paper, a lithium-iron-phosphate battery is selected with a short response time and high cycle efficiency for electric energy storage.

On a daily-time scale, the electric energy storage system is charged to store surplus power during periods when wind and solar power generation are high, and the stored power is released when there is little to no PV or wind power generation, to ensure normal power supply to the load.

The relationship between the electric energy storage capacity and the charging and discharging power is as follows:

$$E_{\mathrm{ES}}(t)=\left(1-{\eta }_{\mathrm{ES},\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{f}}\right)E_{\mathrm{ES}}(t-1)+\Delta t\left[{\eta }_{\mathrm{ES},c}\times P_{\mathrm{ES},c}(t)-\frac{P_{\mathrm{ES},d}(t)}{{\eta }_{\mathrm{ES},d}}{\eta }_{\mathrm{ES},d}\right]$$

(1)

2.1.2. Seasonal Hydrogen Energy Storage Model

The hydrogen energy storage system consists of the electrolyzer, hydrogen storage tank, and fuel cell. To improve the flexibility of the model, the proton exchange membrane electrolyzer and proton exchange membrane fuel cell, with excellent dynamic performance and high specific power, are selected [26]. The mathematical models for each component of the system are as follows:

(1) The electrolyzer is energized to electrolyze water for hydrogen gas production, completing the electricity-to-hydrogen conversion process. The output power is denoted as follows:

$$P_{\mathrm{E}\mathrm{L}-\mathrm{H}\mathrm{T}}(t)={\eta }_{\mathrm{E}\mathrm{L}}{P}_{\mathrm{E}\mathrm{L}}(t)$$

(2)

(2) The hydrogen in the storage tank comes from the electrolytic water reaction in the electrolyzer, and is output to the fuel cell as a power supply. Ignoring hydrogen self-loss, the storage capacity and quality of the storage tank are denoted as follows:

$$\left\{\begin{array}{l}{E}_{\mathrm{HT}}(t)=E_{\mathrm{HT}}(t-1)+\Delta t\left[P_{\mathrm{E}\mathrm{L}-\mathrm{H}\mathrm{T}}(t)-\frac{P_{\mathrm{HT}-\mathrm{F}\mathrm{C}}(t)}{{\eta }_{\mathrm{HT}}}\right]\\ m_{\mathrm{HT}}(t)=\frac{P_{\mathrm{HT}-\mathrm{F}\mathrm{C}}(t)}{HHV}\end{array}\right.$$

(3)

(3) The fuel cell converts hydrogen chemical energy into electrical energy, completing the hydrogen to electricity conversion process. The output power is expressed as follows:

$$P_{\mathrm{F}\mathrm{C}}(t)={\eta }_{\mathrm{FC}}{P}_{\mathrm{HT}-\mathrm{F}\mathrm{C}}(t)$$

(4)

2.2. Wind-Solar Station Model

The wind–solar station consists of the photovoltaic array, the wind turbine, and the diesel engine. The specific model is as follows.

2.2.1. Photovoltaic Array Model

The actual output power of the photovoltaic array is mainly influenced by the solar light intensity and ambient temperature, which can be expressed as follows:

$$P_{\mathrm{PV}}(t)=C_{\mathrm{PV}}{G}_{\mathrm{AC}}\frac{1+\delta \left(T-T_{\mathrm{r}}\right)}{G_{\mathrm{S}\mathrm{T}\mathrm{C}}}$$

(5)

2.2.2. Wind Turbine Model

The output power of the wind turbine is related to the wind speed, and it can be expressed as follows:

$$P_{\mathrm{WT}}(t)=\left\{\begin{array}{c}\hfill 0\hfill \\ \hfill \begin{array}{ccc}& C_{\mathrm{WT}}\left(v-v_{\mathrm{ci}}\right)/v_r-v_{\mathrm{ci}}& ,\end{array}\hfill \\ \hfill C_{\mathrm{WT}}\hfill \\ \hfill 0\hfill \end{array}\begin{array}{c}0\le v\le v_{c\mathrm{i}}\\ v_{\mathrm{ci}}\le v\le v_r\\ v_r\le v\le v_{co}\\ v_{co}\le v\end{array}\right.$$

(6)

2.2.3. Diesel Engine Model

The efficiency of a diesel engine is closely related to its operation mode, and the relationship between fuel consumption and power can be expressed as follows:

$$fuel={\alpha }_{\mathrm{D}\mathrm{G}}{C}_{\mathrm{D}\mathrm{G}}+{\beta }_{\mathrm{D}\mathrm{G}}{P}_{\mathrm{DG}}(t)$$

(7)

3. Multi-Objective Capacity Optimization Configuration of Microgrids with Seasonal Hydrogen Storage

The optimal allocation decision variables in this paper are C_PV, C_WT, C_DG, E_ES, P_ES, P_EL, E_HT, and P_FC, which describe the capacity allocation related to microgrid economics and environmental friendliness. Two objective functions of the microgrid are considered: the lowest integrated cost and the lowest carbon emissions.

3.1. Comprehensive Cost of the Microgrid

The comprehensive cost of the microgrid includes the initial equipment investment cost, the replacement costs, the operation and maintenance costs, and the purchase costs of the main grid power. The cost can be expressed as in Equation (8).

$$F_1=\left(C_{\mathrm{I}}+C_{\mathrm{R}}+C_{\mathrm{M}}+C_{\mathrm{B}}\right)$$

(8)

The specific expressions in Equation (8) are as follows:

$$\left\{\begin{array}{l}{C}_{\mathrm{I}}=k_{\mathrm{C}\mathrm{R}\mathrm{F}}{\displaystyle \sum _i{\lambda }_i{z}_i}\\ C_{\mathrm{R}}=k_{\mathrm{CRF}}{\displaystyle \sum _i{n}_i{\lambda }_i{z}_i}\\ C_{\mathrm{M}}=r_{\mathrm{M}}{C}_{\mathrm{I}}\\ C_{\mathrm{B}}={\displaystyle \sum _{t=1}^{TN}\left\{{\lambda }_{\mathrm{e}}{P}_{\mathrm{e}}(t)+{\lambda }_{\mathrm{oil}}[{\alpha }_{\mathrm{DG}}{P}_{\mathrm{n}-\mathrm{D}\mathrm{G}}+{\beta }_{\mathrm{DG}}{P}_{\mathrm{DG}}(t)]\right\}}\Delta t\end{array}\right.$$

(9)

where k_CRF represents the fund recovery factor. The expression is k_CRF = r(1 + r)^N/(1 + r)^N − 1, where r is the discount rate. The i-related parameters are shown in

Table 2. Decision Variable Parameter Cross Reference.

Parameter	Meaning	Parameter	Meaning
PV	Photovoltaic array	P	Electric energy storage power
WT	Wind Turbine	EL	Electrolyzer
DG	Diesel Engine	HT	Hydrogen storage tank
ES	Electric energy storage capacity	FC	Fuel Cell

.

3.2. Carbon Emissions of the Microgrid

There are two main sources of carbon emissions from the microgrid: the carbon emissions from purchasing electricity from the main grid E_e, and the carbon emissions from diesel generator operation E_DG. Thus, the carbon emissions can be expressed as follows:

$$F_2={\displaystyle \sum _{t=1}^{T_N}\left\{r_{\mathrm{e}}{P}_{\mathrm{e}}\left(t\right)+r_{\mathrm{oil}}\left[{\alpha }_{\mathrm{DG}}{P}_{\mathrm{n}-DG}+{\beta }_{\mathrm{DG}}{P}_{\mathrm{DG}}(t)\right]\right\}}\Delta t$$

(10)

3.3. Restraint Conditions

3.3.1. Power Balance Constraint

To ensure the system power balance during grid operation, the following constraints are imposed:

$$P_{\mathrm{PV}}(t)+P_{\mathrm{WT}}(t)+P_{\mathrm{DG}}(t)+P_{\mathrm{ES},\mathrm{d}}(t)+P_{\mathrm{FC}}(t)+P_{\mathrm{e}}(t)=P_{\mathrm{L}}(t)+P_{\mathrm{ES},\mathrm{c}}(t)+P_{\mathrm{E}\mathrm{L}}(t)$$

(11)

3.3.2. Electrical Energy Storage Constraints

Electrical energy storage is used to solve the daily supply-demand imbalance with the following relevant constraints:

(1) The electrical energy storage charge state constraint.

$$0.1Z_{\mathrm{E}\mathrm{S}}\le Z_{\mathrm{ES}}\left(t\right)\le 0.9Z_{\mathrm{E}\mathrm{S}}$$

(12)

(2) The constraints of charging and discharging power from the electrical storage system. The system cannot charge and discharge at the same time to prolong the service life.

$$\begin{array}{l}0\le P_{\mathrm{ES},\mathrm{c}}\left(t\right)\le N_1\\ 0\le P_{\mathrm{E}\mathrm{S},\mathrm{d}}\left(t\right)\le N_2\end{array}$$

(13)

where N₁ = min {Z_p, Mμ₁}, and N₂ = min {Z_p, M(1-μ₁)}. M is a large positive number. μ₁ is a 0–1 variable. The electrical energy storage is charging when μ₁ = 1, and discharging when μ₁ = 0.

(3) The electrical energy storage operating cycle constraint; the electrical energy remaining in the last period of the day is equal to the initial electrical energy.

$$Z_{\mathrm{ES},0}=Z_{\mathrm{ES},y,24}$$

(14)

where y∈{1,2,…365}.

3.3.3. Seasonal Hydrogen Energy Storage Constraints

Unlike electrical energy storage systems, seasonal hydrogen storage systems are responsible for the long-term coordination of power supply and demand with the following relevant constraints:

$$Z_{\mathrm{HT},0}=Z_{\mathrm{HT},T_{\mathrm{n}}}$$

(15)

(1) Hydrogen storage tank status constraints.

$$0.05Z_{\mathrm{HT}}\le Z_{\mathrm{HT}}\left(t\right)\le Z_{\mathrm{HT}}$$

(16)

(2) Electrolyzer and fuel cell operating power and behavioral constraints. The system cannot operate the electrolyzer and fuel cell at the same time.

$$\begin{array}{l}0\le P_{\mathrm{EL}}\left(t\right)\le O_1\\ 0\le P_{\mathrm{FC}}\left(t\right)\le O_2\end{array}$$

(17)

where O₁ = min {Z_EL,Mμ₂}, and O₂ = min {Z_FC,M(1 − μ₂)}. μ₂ is a 0–1 variable. The electrolyzer is operating when μ₂ = 1, and the fuel cell is operating when μ₂ = 0.

(3) Hydrogen storage operating cycle constraint. The amount of hydrogen remaining in the storage tank in the last period of the year is equal to the initial hydrogen storage capacity.

Where T_n∈{0,1,…, T_N}.

3.3.4. Investment Constraints

Due to the limitations of the construction site scope, the capacity of each microgrid equipment configuration must be within a reasonable range. The relevant constraint can be expressed as follows:

$$\begin{array}{l}0\le Z_i\le Z_{i,\mathrm{m}\mathrm{a}\mathrm{x}}\\ k_{\min }\le \frac{Z_{\mathrm{E}\mathrm{S}}}{Z_{\mathrm{p}}}\le k_{\max }\end{array}$$

(18)

3.3.5. The Operational Constraints

When the system is running, each device output can not exceed its maximum power. Therefore, the relevant constraint can be expressed as follows:

$$\left\{\begin{array}{l}0\le P_{\mathrm{e}}\left(t\right)\le P_{\mathrm{e},\mathrm{m}\mathrm{a}\mathrm{x}}\\ 0\le P_{\mathrm{P}\mathrm{V}}\left(t\right)\le C_{\mathrm{PV}}\\ 0\le P_{\mathrm{W}\mathrm{T}}\left(t\right)\le C_{\mathrm{W}\mathrm{T}}\\ 0\le P_{\mathrm{D}\mathrm{G}}\left(t\right)\le C_{\mathrm{DG}}\end{array}\right.$$

(19)

The values of the important parameters used for the construction of the microgrid system are shown in

Table 3. Values of Important Parameters.

Related Parameters	Specific Values	Related Parameters	Specific Values
rM	1%	N	20 years
Pe,max	500 kWh	TN	8760 h
aDG	0.08415 L/kWh	re	0.65 kg/kWh
bDG	0.2461 L/kWh	roil	2.5 kg/L
r	0.05	kmin	2
kmax	5

.

3.4. Evaluation Index of the Microgrid System

The renewable energy abandonment rate is an important measure of the degree to which grid-connected microgrids utilize their generated power and their self-balancing capabilities. The rate can be described as follows:

$$Rate=\frac{E_{\mathrm{lost}}}{E_{\mathrm{Q}}+E_{\mathrm{lost}}}$$

(20)

where the smaller the rate is, the higher the renewable energy utilization.

The objective scalar function solved in this paper is expressed as follows:

$$F\left(x\right)=\min F_1\left(x\right)+\min F_2\left(x\right)$$

(21)

where x∈X, x is the vector of the decision variables, and X is the feasible domain of x. The augmented ε- constraint method is used to solve the model.

3.5. Operation Control Strategy of Microgrid

The operation control strategy of the microgrid determines the power output sequence of each resource in the microgrid, which directly affects the operation of the electric energy storage and hydrogen storage system, and thus, the merits of the configuration scheme. The operation strategy flow of the proposed microgrid system is shown in Figure 2.

A: After the load demand power is satisfied, all the remaining power of the distributed power generation system is used to charge the electric energy storage.

B: After the load demand power is satisfied, part of the remaining power of the distributed power generation system is used to charge the electric energy storage, and the other part is converted to hydrogen and stored through the electrolyzer.

C: After the distributed power generation system meets the load demand power, it charges the battery until saturation, and then provides sufficient energy for the electrolyzer. The remaining renewable energy abandonment; energy abandonment rate is calculated as Rate_WT; Rate_PV.

D: The system shortage power is all provided by the electric energy storage.

E: The electric energy storage is fully discharged to provide part of the shortage power for the system, and the remaining part is provided by the fuel cell power generation.

F: Full discharge of the electric energy storage and full power generation of the fuel cell provide part of the power for the system, and the subsequent shortage of power is provided by the diesel generator.

G: The battery is fully discharged and the fuel cell is fully generated to supplement part of the system power, and the subsequent power shortage is provided by the main grid.

4. Capacity Optimization Allocation Model of Microgrid System Based on the Augmented ε- Constraint Method

Based on the model in this paper, which contains 0–1 integer variables that characterize the charging and discharging states of electrical and hydrogen energy storage, the operating characteristics of the equipment are determined. It is proposed to use the ε- constraint method and to employ AUGMECON in order to solve the MILP [31,32].

4.1. The Augmented ε- Constraint Method

The ε- constraint method is a solution method that retains only a single objective function, and transforms the other objective functions into constraints. However, the solution process requires approximating the extreme value points by sorting, expanding, and compressing, which is a tedious step that makes it difficult to find the maximum possible value of the minimizing objective function.

This issue can be resolved by proposing the augmentation-constraint method to transform the inequality constraint corresponding to the nonprincipal objective, into an equation constraint by introducing relaxation variables. Other objective functions are transformed into equation constraints to participate in the optimization. A relaxation variable penalty function is also introduced to overcome the influence of the objective function nonconvexity on the solution quality, and to ensure solution nondominance. Thus, the expression of the objective function is as follows:

$$F\left(x\right)=\min F_1\left(x\right)+\min F_2\left(x\right)$$

(22)

Equation (22) is bounded by Equation (23):

$$\begin{array}{l}{F}_2\left(x\right)+s_2=e_2\\ \begin{array}{ccc}& \dots & \end{array}\\ F_n\left(x\right)+s_n=e_n\\ \begin{array}{cc}x\in X& s_n\ge 0\end{array}\end{array}$$

(23)

where ε is a sufficiently small constant between 10⁻³ and 10⁻⁶, s_n is the slack variable, and r_i is the width of the range of values of the i-th objective function. The formula is the difference between the maximum and minimum values of the column, expressed as r_i = F_i^max − F_i^min. e_i is the step adjustment value, and the formula is calculated as follows:

$$e_i=F_i^{\mathrm{m}\mathrm{i}\mathrm{n}}+\frac{k\times r_i}{g}$$

(24)

where i∈{2,…,n}, k∈{1,…,g}. By iterating k from 0 to g repeatedly, the value of e_i is adjusted continuously, and the model is iteratively calculated after each adjustment. Then, a set of Pareto-optimal solutions required for the objective function can be obtained.

4.2. Multi-Objective Function Solution Based on the Augmented ε- Constraint Method

This section specifies the multi-objective function that is solved based on the AUGMECON method, and the specific process of the capacity optimization allocation model of the microgrid system, as shown in Figure 3. The augmented ε- constraint method can accurately find the range of values of the objective function. Thus, the effectiveness of the Pareto front is significantly improved. The solution process is as follows:

(1) Generating the payoff table

The payoff table is used to confirm the upper and lower bounds of each objective Pareto front function. The specific payment table is shown in

Table 4. Bi-Objective Function Payment Table.

	F1	F2
minF1	Z11	Z12
minF2	Z21	Z22

.

Where:

$$\left\{\begin{array}{c}{z}_{11}=\underset{x\in {\rm X}}{\min }{F}_1\\ z_{12}=\underset{x\in {\rm X}}{\min }\{F_2:F_1=z_{11}\}\\ z_{22}=\underset{x\in {\rm X}}{\min }{F}_2\\ z_{21}=\underset{x\in {\rm X}}{\min }\{F_1:F_2=z_{22}\}\end{array}\right.$$

(25)

In the table, F₁(x) is used as the unique objective function for calculation. Then, the obtained decision variables are brought into F₁(x) and F₂(x) to obtain the corresponding objective function values Z₁₁ and Z₁₂. Z₁₁ and Z₁₂ correspond to the minimum and maximum values of the objective F₁ in the first column of the payoff table, respectively.

Similarly, the above operations are performed on the second objective function F₂(x) to obtain Z₂₁ and Z₂₂, which correspond to the minimum and maximum values of objective F₂ in the second column of the payment table, respectively.

(2) Solving the new optimization problem constraints

F₁(x) is taken as the primary objective function, and the secondary objective function F₂(x) is treated as the constraint. The range of values of F₂(x) are divided into g segments. The new single-objective optimization problem is solved as follows:

$$F=\min F_1+\epsilon \times \frac{s_2}{r_2}$$

(26)

where the constraint of Equation (26) is F₂ + s₂ = e₂. In the formula, r₂ = Z₂₁ − Z₂₂. e₂ is calculated by Equation (27).

$$e_2=z_{22}+\frac{k\times r_2}{g}$$

(27)

In this paper, g = 40. By continuously adjusting the value of e₂ and iterating the above equation, the desired Pareto front solutions are calculated.

(3) Evaluation indicators

In this paper, Δ is introduced as the evaluation index of the Pareto distribution characteristics.

$$\Delta =\frac{d_{\mathrm{f}}+d_1+{\displaystyle \sum _{i=1}^{R-1}\left|d_i-\overline{d}\right|}}{d_{\mathrm{f}}+d_1+(R-1)\overline{d}}$$

(28)

A smaller Δ represents a more uniform Pareto front solution distribution with better characteristics.

(4) Filtering the optimal compromise solution

After finding the Pareto front through the above steps, the optimal compromise solution is derived by evaluating all noninferior solutions with the entropy–TOPSIS method [33]. Specifically, the entropy weighting method is used to determine the weights of the two objective functions. The TOPSIS method sorts and selects the solution that is closest to the positive ideal solution in terms of Euclidean distance [Z₁₁, Z₂₂], and farthest from the negative ideal solution in terms of Euclidean distance [Z₂₁, Z₁₂], as the optimal compromise solution under the given weights.

4.3. Specific Process of the Capacity Optimization Allocation Model of Microgrid System Based on the AUGMECON Method

Step 1: Select each microgrid-distributed energy source and build a distributed energy system model.

Step 2: Establish a composite energy storage system model that involves a coupling between electric energy storage and seasonal hydrogen storage systems.

Step 3: Construct a microgrid capacity optimization allocation model that prioritizes the economic and environmental benefits of the microgrid system.

Step 4: By considering the operating conditions and characteristics of each device, set the relevant constraints and evaluation indexes of the microgrid system.

Step 5: Solve the multi-objective optimization model with constraints by using the AUGMECON method, and output the Pareto front solution set.

Step 6: Select the optimal compromise solution in the solution set with the entropy–TOPSIS method.

Step 7: Output the optimal compromise solution to construct the optimal capacity allocation model.

Step 8: Output the system capacity configuration scheme and the configuration results.

5. Example Analysis

In Section 5, experimental validation and analysis are performed for the models and algorithms proposed in this paper. In Section 5.1, first, the environment of the simulation experiment and the data and sources related to the model input are explained, and second, four different microgrid scenarios are built. In Section 5.2, the effectiveness of the algorithm proposed in this paper is verified. In Section 5.3, the algorithm of this paper is applied to the above four microgrid scenarios to verify the effectiveness of the model. Finally, in Section 5.4, the operation of scenario 3 and scenario 4, on typical days of the seasons in a year, is focused on in three examples, and the sensitivity analysis of the key parameters affecting the objective function is carried out to further prove the rationality and practicality of the proposed method in this paper.

5.1. Example Scenarios and Related Parameter Settings

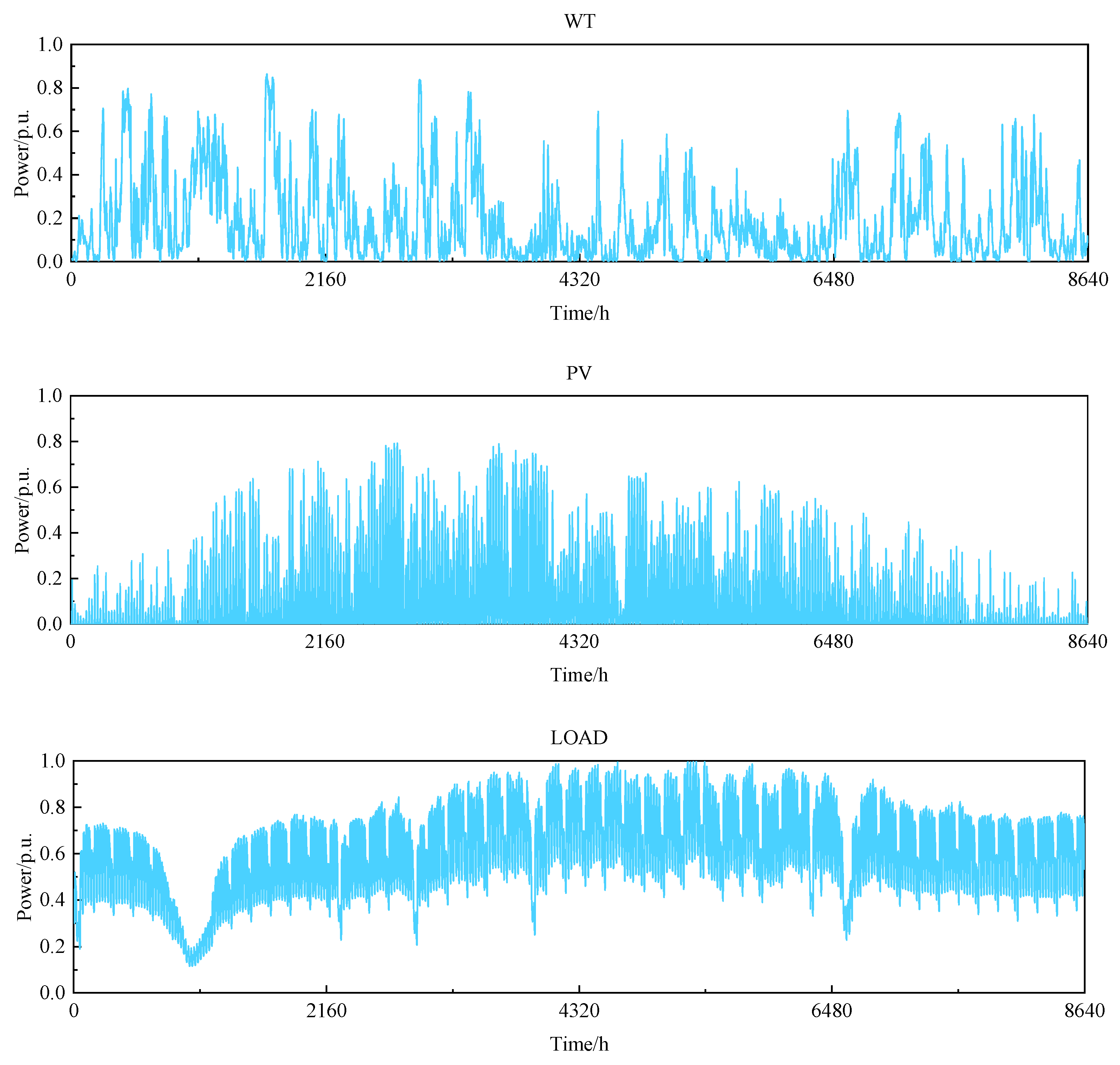
The solver used in this paper is Gurobi, and the example uses the modeling language Yalmip to quickly solve the problem in MATLAB. The real-world data of a grid-connected microgrid in an integrated wind power plant in Belgium are used as the input data. The actual annual load data for the microgrid at an hourly resolution, and the standardized values for wind and light power generation, are shown in Figure 4 [34].

Table 5. TOU Power Price.

Time Division	Electricity Price (€/kW·h)
1:00–7:00	0.04144
23:00–24:00
7:00–11:00	0.0916
15:00–19:00
21:00–23:00
11:00–15:00	0.1439
19:00–21:00

and

Table 6. Investment Parameters of Microgrid Equipment.

Equipment	Investment Unit Price (€)	Efficiency	Life (years)
Wind Turbine	1006.6€/kW	-	20
Photovoltaic Array	1294.2 EUR/kW	-	20
Diesel Engine	83.404 EUR/kW	40%	20
Electric Energy Storage	Capacity unit price: 301.9 EUR/kWh Power unit price: 115.04 EUR/kW	Charge and discharge rate:90% Self-discharge rate:1%	10
Electrolyzer	1150.4 EUR/kW	71%	20
Hydrogen Storage Tanks	3000 EUR/kg	95%	20
Fuel Cell	4000 EUR/kW	55%	10

give the unit price of the power purchased from the main grid and the investment parameters of each piece of microgrid equipment, respectively [35,36].

To analyze the effectiveness of configuring seasonal hydrogen energy storage, four scenarios are chosen as follows:

Scenario 1: Multi-objective capacity optimization configuration of a microgrid with electrical energy storage and without seasonal hydrogen storage systems.

Scenario 2: Multi-objective capacity optimization configuration of a microgrid with seasonal hydrogen storage and without electrical storage systems.

Scenario 3: Multi-objective capacity optimization configuration of a microgrid with both electrical energy storage and hydrogen energy storage systems for short-cycle energy storage.

Scenario 4: Multi-objective capacity optimization configuration of short-cycle electrical energy storage and seasonal hydrogen energy storage for seasonal energy storage.

5.2. Comparative Analysis of the AUGMECON Method and Other Algorithms

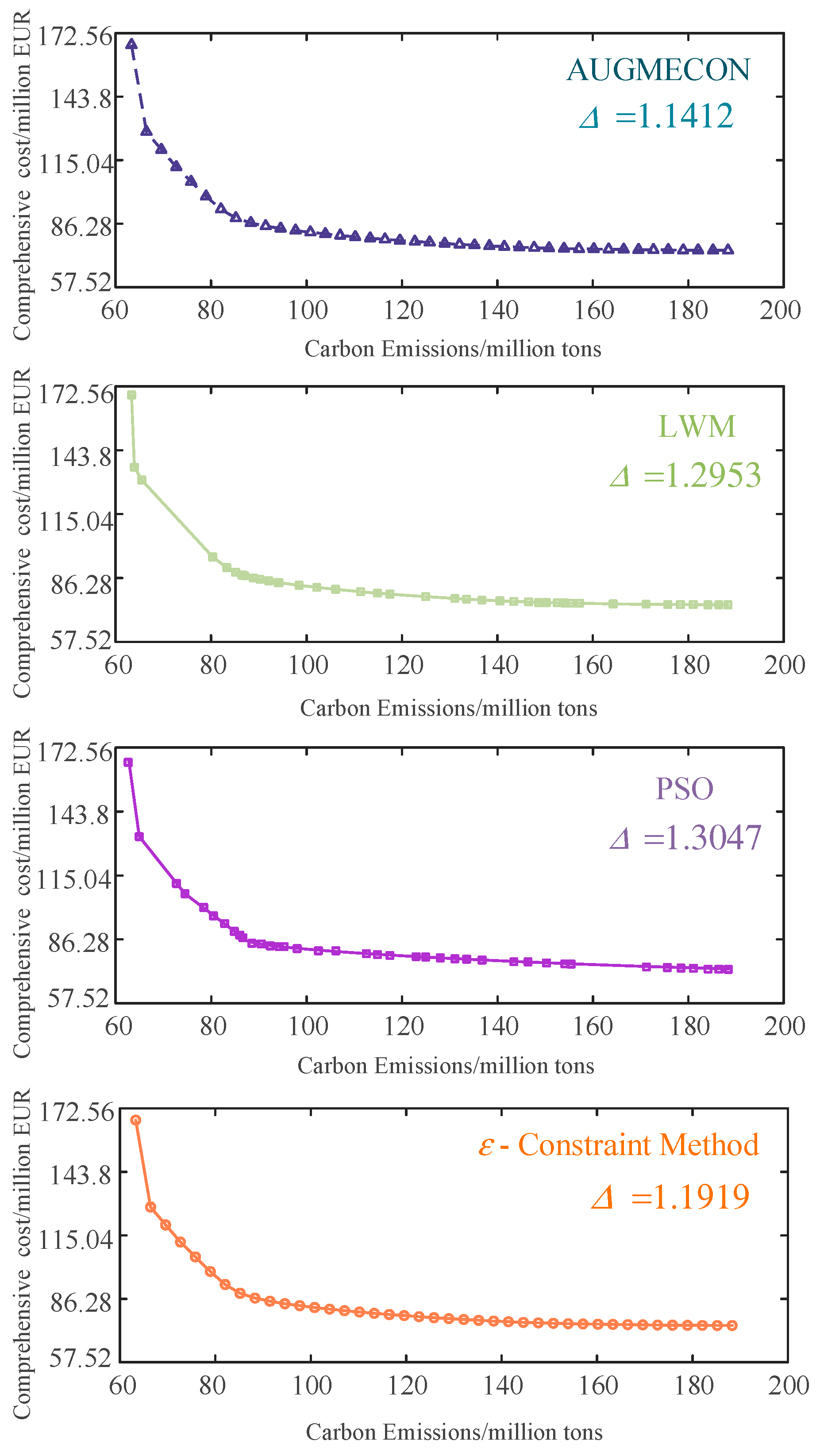
To verify the effectiveness of the AUGMECON method, it and the ε- constraint method, linear weighting method (LWM), and PSO are used to solve the multi-objective microgrid capacity optimization allocation problem to obtain the Pareto front graph.

The degree of concavity of the Pareto curve reflects the superiority of the frontier solution in the curve. Δ is the indicator of the distributivity of the frontier solution; the smaller it is, the more uniform the distribution of the frontier solution and the better the distribution characteristics.

As shown in Figure 5 and

Table 7. Comparison of Multi-objective Algorithms.

Algorithms	Computational Time Overall/s
ε- constraint	28.84
LWM	26.01
PSO	25.93
AUGMECON	20.69

, the frontier solutions of the LWM and the PSO are not uniformly distributed and have poor distributional properties. The above two algorithms are 8.1% and 8.6% worse than the ε- constraint method in terms of distributivity index, respectively. However, these two algorithms are 9.8% and 10.1% faster than the ε- constraint method in terms of operation speed, respectively. Through data analysis, the ε- constraint method, linear weighting method, and particle swarm algorithm each have advantages in terms of frontier solutions and computational power.

The frontiers of the AUGMECON method and ε- constraint method are close, the degree of concavity of these two algorithms is more pronounced and better, overall, than the LWM and the PSO. Additionally, as shown alongside the algorithm computing time analysis in Table 7, the AUGMECON method is 28.3%, 20.1%, and 20.2% faster than the ε- constraint method, LWM, and PSO, respectively, in terms of solution speed. The AUGMECON method has a lower Δ value, a more uniform distribution of solution sets, and a better diversity of solution sets. Therefore, a better Pareto solution sets can be obtained by the AUGMECON method.

5.3. Analysis and Comparison of Different Energy Storage Solutions

After the superiority of AUGMECON has been demonstrated in Section 5.3, this section will experimentally verify and analyze the effectiveness of the model proposed in this paper. Based on the four different microgrid models built in Section 5, AUGMECON is applied to each of the four scenarios in this section. The Pareto front for the multi-objective problems of Scenarios 1–4 is obtained by the AUGMECON method, as follows.

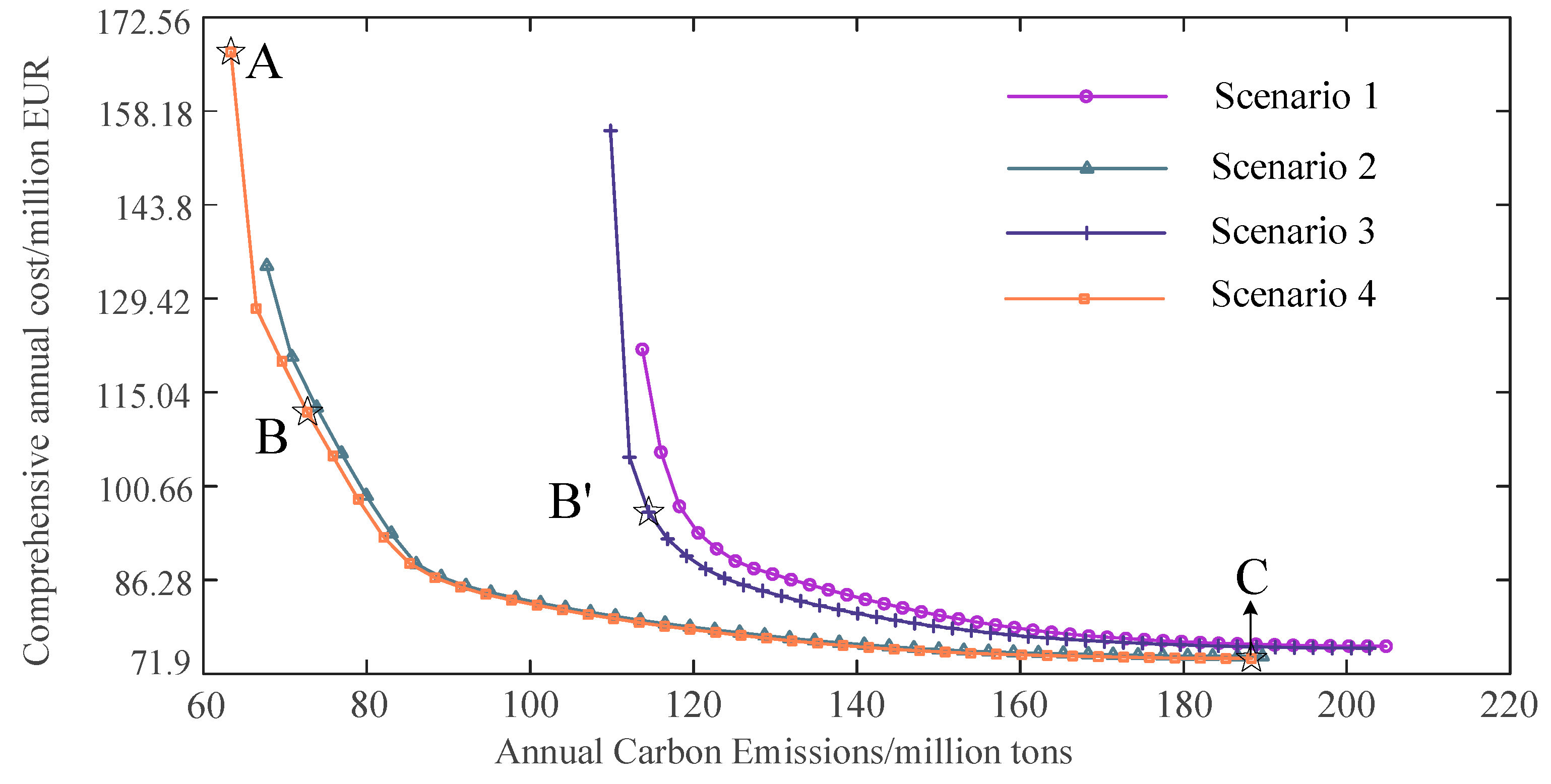
In the Pareto diagram, the closer the curve, as a whole, is to the origin, then the Pareto solution set on this curve is better. As shown in Figure 6, Scenarios 1–3 are all further away from the origin than Scenario 4; thus, Scenarios 1–3 are all dominated by the Pareto front of Scenario 4.

First, Scenario 1 and 2 are compared. The analysis showed that the microgrid configured according to Scenario 2 had less carbon emissions while spending the same combined annual cost. This proves that seasonal hydrogen storage has a significant energy saving and emission reduction effect. Then, Scenario 3 and 4 are compared, and the results indicate that Scenario 4 requires a lower comprehensive annual cost charge for the same carbon emission conditions. This proves that it is more economical and practical to use hydrogen storage as seasonal energy storage for long-time cycle dispatch operation compared to the short-time.

5.4. Capacity Optimization Allocation Results and Analysis

In this section, three examples are used to analyze the capacity configuration scenarios and the configuration results with the incremental-bound method under Scenario 4. In addition, this section features a comparison and analysis of the capacity change and typical daily operation of the energy storage system for Scenarios B and B’, to further validate the model proposed in this paper.

5.4.1. Example 1

The work in Example 1 consists of selecting the optimal compromise solution among the frontier solutions calculated using AUGMECON under Scenario 4. Configuration schemes A, B, and C, shown in Figure 6, correspond to the optimal solution, with F₂ as a single objective; the optimal double objective, the solution derived from the entropy–TOPSIS method; and the optimal solution, with F₁ as a single objective, respectively.

Table 8. Capacity Configuration Scheme for Each Equipment of Microgrid.

Configuration Options	A	B	C
CPV/kWp	3000	3000	1433.6
CWT/kWp	3000	3000	2539
CDG/kW	0	0	267.6
ZES/kW	3270.9	1191.5	172.8
Zp/kWh	1457.4	352.1	77
ZEL/kW	2500	1057.8	198.8
ZHT/kg	12,594.5	7595.3	315.9
ZFC/kW	1954.3	586.6	274.2

and

Table 9. Capacity Configuration Results of Microgrid Equipment.

Configuration Results	A	B	C
F1/million EUR	167.25	112.01	74.24
F2/million tons	63.3	72.7	188.3
RateWT	1.86%	11.57%	21.53%
RatePV	2.3%	0.79%	10.43%

give the capacity configuration options and results for each device in the microgrid at points A, B, and C, under Scenario 4. B’ corresponds to the bi-objective optimal compromise solution of Scenario 3, derived from the entropy–TOPSIS method.

First, Option C employs low-capacity PV, WT, electric storage, and hydrogen storage with high-capacity diesel to minimize the combined annual cost of the microgrid. Although the cost is reduced, the configuration yields high carbon emissions and poor environmental friendliness. Second, to reduce carbon emissions, Option A uses large-capacity electrical and hydrogen energy storage to consume as much renewable power as possible. However, the total configuration cost is too high to be of practical use. Finally, Option B appropriately increases the capacities of both types of energy storage, significantly reduces carbon emissions without sacrificing excessive economic benefits, and achieves an optimal compromise between the annual combined cost and annual carbon emissions. Therefore, compared with Option A and Option C, Option B is able to achieve a higher level of satisfaction with both economic and environmental objectives, and has good engineering practicality.

5.4.2. Example 2

To further verify the validity of the proposed model, and to also analyze the configuration scheme and operation strategy of electrical and hydrogen energy storage, a comparative analysis is conducted using Options B’ and B.

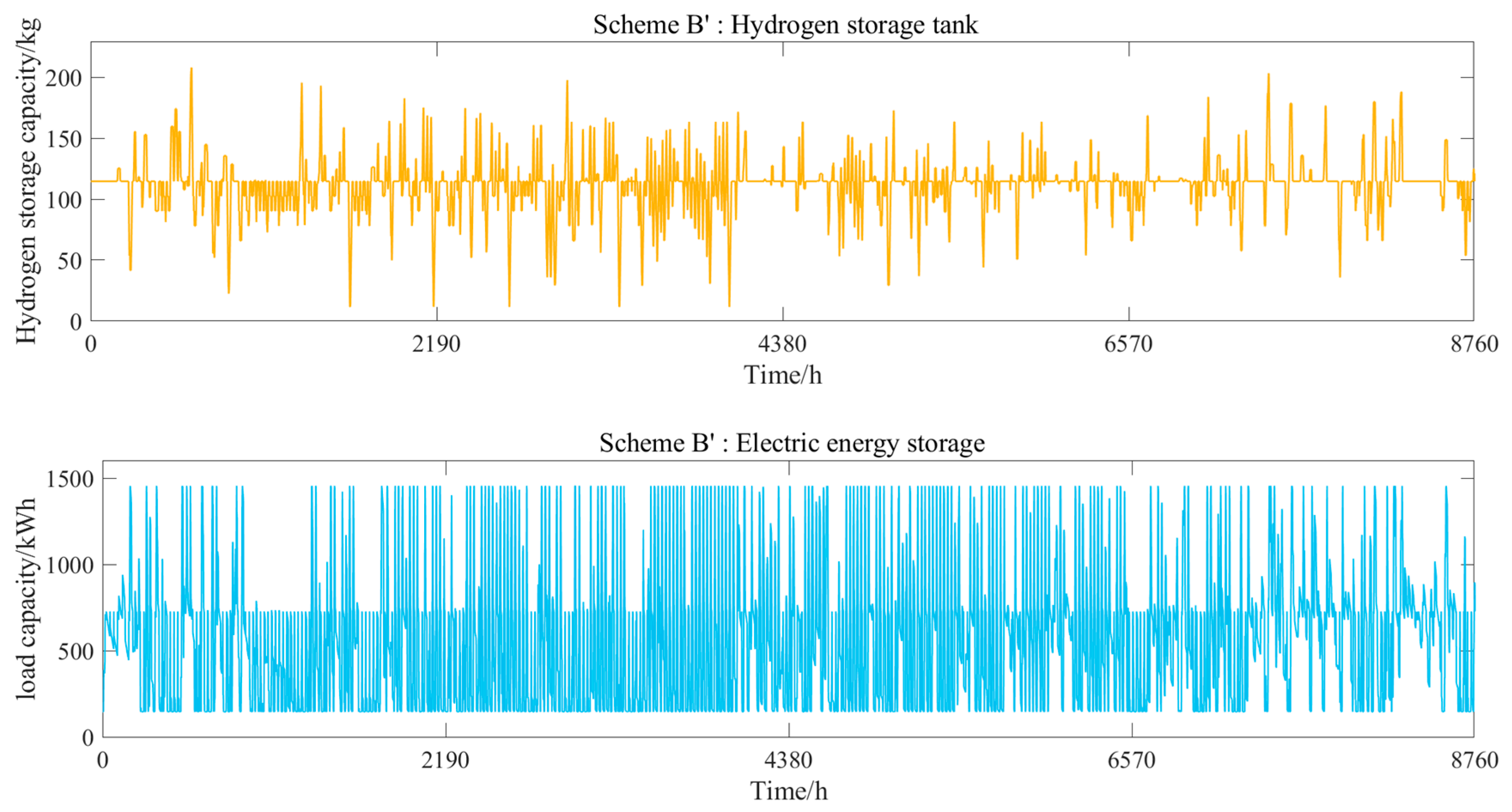
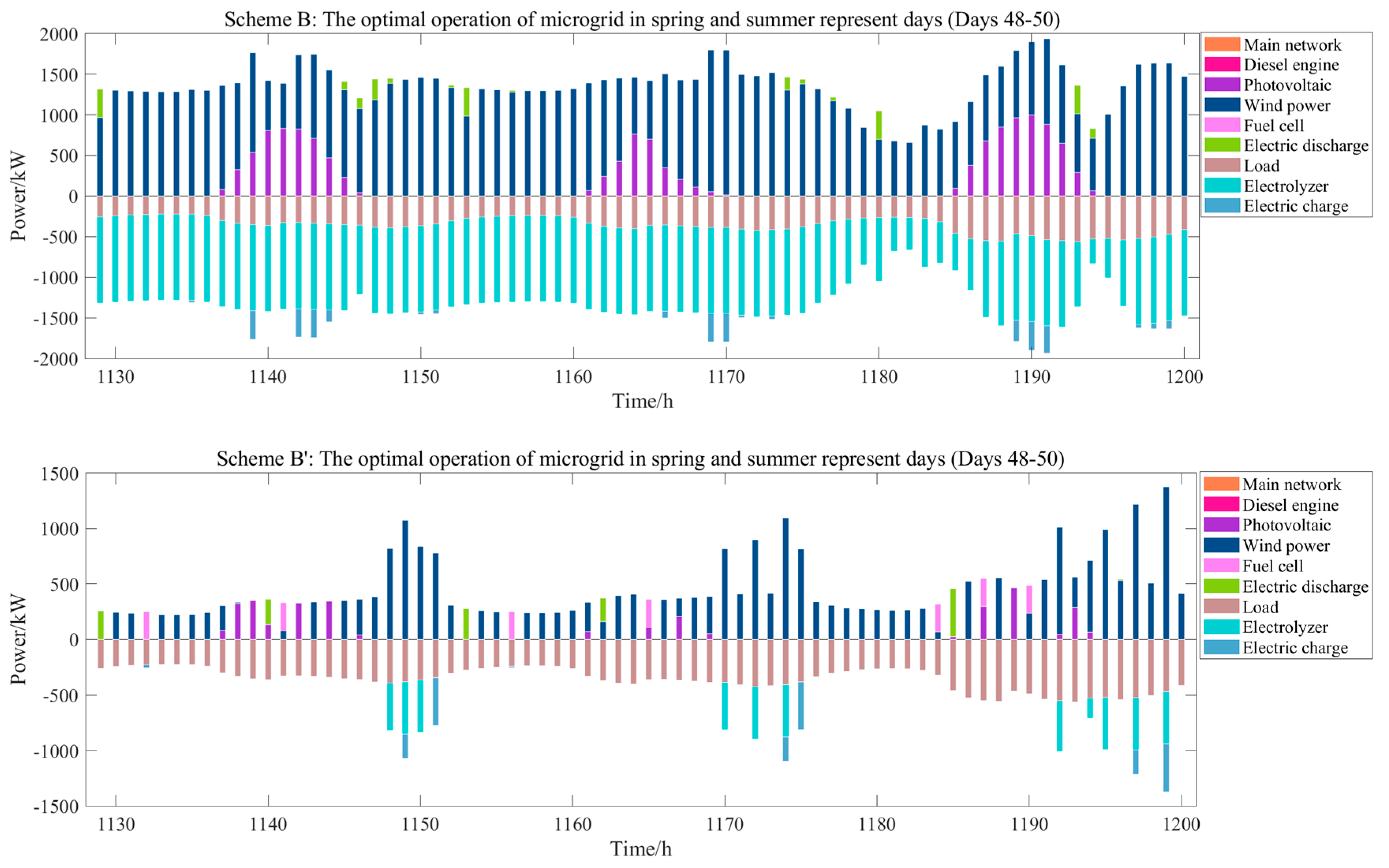
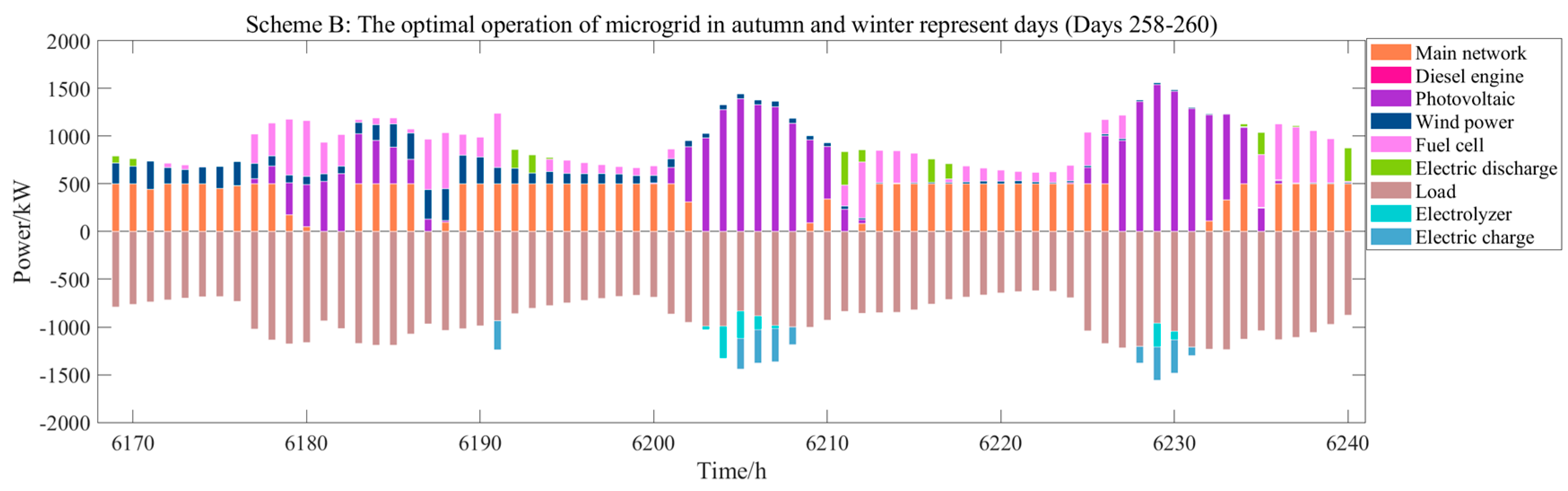
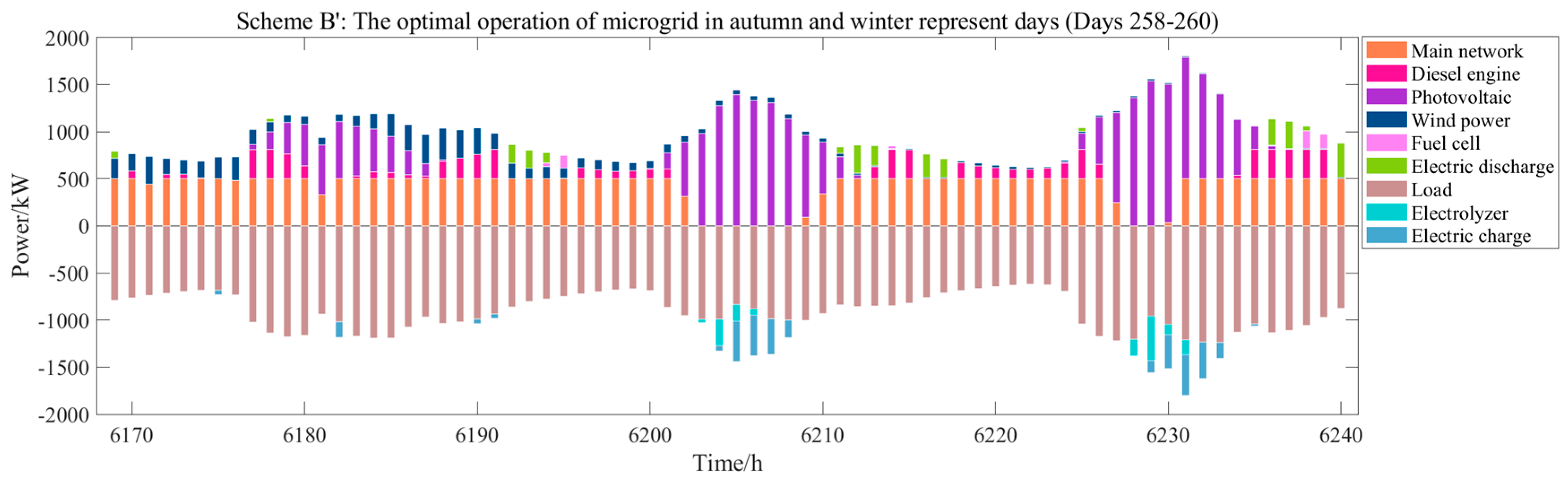
Figure 7 shows the variation in the storage capacity of the two scenarios, corresponding to the electrical energy storage and hydrogen storage tanks. Figure 8 shows the operation of the two scenarios on a typical day in spring and summer. Figure 9 shows the operation of both scenarios for a typical day in autumn and winter.

By analyzing Figure 7, Figure 8 and Figure 9, when configuration scheme B’ is employed, and because the hydrogen storage system operates daily, the microgrid system struggles to consume the renewable energy generation in the spring and summer, when the scenery resources are abundant. This will lead to the large-scale abandonment of the scenery resources; therefore, it needs to be equipped with a higher capacity distributed generation system, which greatly increases the construction investment cost. Meanwhile, in the autumn and winter, when natural resources are scarce, in order to respond to load demand, the power purchase of microgrids is greatly increased, which increases the system operation cost and carbon emissions. However, the role played by energy storage here is very small and does not correspond to the expected function of energy storage to regulate peaks and fill valleys from a long cycle. Therefore, this configuration scheme does not bring out the maximum advantages of energy storage.

When configuration scheme B is employed, the hydrogen storage system operates on an annual basis, and the microgrid system relies on scenery generation for autonomous operation when scenery resources are abundant. The capacity of the distributed generation system required is greatly reduced compared to configuration scheme B’, and the corresponding investment cost is significantly reduced. The excess scenic power generation is used for electrolysis to produce hydrogen, which can be transferred to be released in autumn and winter, and thus, reducing the microgrid power purchase and achieving economical and environmentally friendly operation of the system.

The analysis of the operation of configuration scheme B’ and configuration scheme B further strongly proves the effectiveness of the model proposed in this paper.

5.4.3. Example 3

Studies around the world have used the method of varying the key system parameters and then calculating the corresponding optimal solution to analyze the effect of input parameter changes on the output results [37]. In this section, a sensitivity analysis is carried out to evaluate the impacts of key parameters on the objective function.

With the development of production capacity, the system power load demand increases, and the corresponding distributed power, output power, energy storage power, and capacity will change, affecting the system acquisition cost, the operation and maintenance cost, and the total cycle cost of the system. With the iterative improvement of the hydrogen energy industry chain and technological progress, the cost of hydrogen production and storage will show a decreasing trend in the immediate and long-term development process, and the high investment cost of the hydrogen storage system has a direct impact on the optimal configuration of the microgrid. Therefore, a sensitivity analysis of hydrogen production, storage costs, and load demand will be carried out with the arithmetic examples below.

(1) Example 1: The climatic input conditions and the cost of each part of the system remain unchanged, and the residential electric load increases by 10%.

(2) Example 2: The climatic input conditions and residential load demand of the system remain unchanged, and the acquisition cost of fuel cells, electrolytic cells, and hydrogen storage tanks in the system decreases by 10%.

The configuration results in

Table 10. Results of Configuration.

Configuration Options	Initial Situation B	Electric Load Increases by 10%	Hydrogen System Cost Reduces 10%
CPV/kWp	3000	2886.2	2699.6
CWT/kWp	3000	3501.8	3112.5
CDG/kW	0	247.6	0
ZES/kW	1191.5	1392.3	1075.9
Zp/kWh	352.1	384.4	329.6
ZEL/kW	1057.8	1255.9	1124.5
ZHT/kg	7595.3	6748.9	7744.3
ZFC/kW	586.6	630	600.5
F1/million EUR	112.01	121.7	108.28
F2/million tons	72.7	72.5	68.4

show that: as the demand for electricity load expands, the total capacity of the power supply required by the system will increase. Under the power curves of the PV, wind turbine, and load in this study, it is shown that the capacity of PV slightly decreases and the capacity of the wind turbine greatly increases, while the capacities of the electrolyzer and fuel cell increase. Therefore, it is necessary to prepare for expansion in the early stages of construction. As the cost of the hydrogen energy system decreases, the PV capacity greatly decreases and the hydrogen energy equipment capacity increases. The low-carbon emission reduction effect is significant, and the development prospects of the hydrogen energy system are highly optimistic as the technology evolves.

6. Conclusions

To increase the economic benefits and environmental friendliness of microgrids, this paper proposes a capacity optimization allocation method for a wind–solar–diesel grid-connected microgrid system with hybrid energy storage, based on the AUGMECON method. By comparing different energy storage configuration models and optimization algorithms, the effectiveness and superiority of the proposed models and algorithms in this paper are proven. The specific conclusions are as follows:

(1) The augmented ε- constraint method can effectively solve the double objective optimization model in this paper. The AUGMECON method is found to obtain a Pareto front solution set with greater validity, better distribution characteristics, and higher computational speed than the solution sets found with the ε- constraint method and the other three algorithms.

(2) The constructed hybrid energy storage model that couples battery and seasonal hydrogen storage systems greatly enhances local consumption of renewable energy. The proposed model greatly improves the economic benefits and environmental friendliness of system operation, compared to those in existing studies on short-cycle energy storage.

In summary, the microgrid capacity optimization allocation method proposed in this paper has good effectiveness and can quickly obtain the economic and low-carbon target configuration of a microgrid with good results. In future research, we will continue to combine device refinement models to determine the optimal configuration of microgrid capacity.