Experimental Study and CFD Modeling of Fluid Flow and Heat Transfer Characteristics in a Mini-Channel Heat Sink Using Simcenter STAR-CCM+ Software

Abstract

The present work describes an experimental study and CFD modeling of fluid flow and heat transfer characteristics in a heat sink with several asymmetrical heated mini-channels. The data from the experimental research were the basis for numerical calculations. During experiments, the temperature measurement of the outer heater surface was performed by infrared thermography to verify the results of numerical calculations performed in Simcenter STAR-CCM+ software. The main objective was to determine the values of the parameters tested to evaluate the intensity of the heat transfer processes. In the numerical simulations, important variables, mainly the working fluid, heater material, the spatial orientation of the test section, and the number of mini-channels, were assumed. The results of the numerical computations were discussed. Due to simulations, it was possible to indicate which parameters tested in terms of heat transfer turned out to be the most effective. Furthermore, a mesh dependency analysis based on the grid convergence index (GCI) was performed. The residuals, as good indicators of convergence, achieved low values. Generally, the data presented showed satisfactory convergence of the results achieved as a result of the computational procedure.

1. Introduction

Over the past two decades, the flow of fluid in small gaps has been extensively studied to obtain high efficiency for the cooling of electronic devices. The undoubted advantage of such technical solutions is the high heat transfer intensity and the possibility of significantly reducing the dimensions of heat exchangers. A reduction of energy consumption in the implementation of various technological processes and supplies is urgently needed. Additional benefits of using compact heat exchangers in systems of micro-or minigaps include the low weight of devices and low consumption of materials for their production as a result of miniaturization. Mini-gap heat exchangers have a wide range of practical applications in the automotive and nuclear industry, chemical engineering, bioengineering, and renewable heat sources. Recently, microchannels have been widely used in automotive air conditioning systems, fuel cells, and microelectronics.

The miniaturization of electronic systems is progressing rapidly. The reliability of these systems depends mainly on the temperature of the electronic elements. Therefore, proper temperature management becomes a key issue when the heat flux increases whereas the electronic component size decreases. In systems operating with large heat fluxes, such as in the electronics industry, heat transfer due to forced convection is highly efficient.

In the early 1980s, the problem of achieving compact and high-performance forced liquid cooling of planar integrated circuits was posed [1]. A new, very compact, water-cooled integral heat sink for silicon integrated circuits was proposed and tested. It was stated that, by allowing high power densities, the heat sink may greatly enhance the feasibility of ultra-high-speed VLSI circuits.

Lazarek and Black [2] focused on flow boiling heat transfer in circular mini-channels. The local heat transfer coefficient, pressure drop, and critical heat flux were measured for saturated boiling of R-113 in a mini-channel of 0.31 cm diameter and heated lengths of 12.3 and 24.6 cm. The research was performed for vertical, co-current upflow, and downflow configurations of the test section. The heat transfer correlation for the local heat transfer coefficient, which expresses the Nusselt number as a function of the liquid Reynolds number and boiling number proposed by the authors, has been widely used up to now.

Bowers and Mudawar [3] tested a mini-channel heat sink (diameter 2.54 mm) and a micro-channel heat sink (diameter 510 μm) with a heated surface for their high heat flux performance with flow boiling of R-113. A pressure drop model was also developed. The authors focused on analyzing thermal conduction within the heat sink to determine the optimum channel geometry based on the dimensionless cell width and heat sink thickness. The authors stated that mini- and micro-channel heat sinks are capable of achieving heat fluxes in excess of 200 W/cm² with both low flow rates and low pressure drops. Key findings included an indication of dimensionless heat sink thickness (thickness of heat sink per channel diameter) with values of approximately 1.2 as a good compromise between maintaining low thermal resistance and providing adequate structural strength.

Investigations on the transfer of boiling heat transfer during flow in mini-channels of a rectangular cross-section and various dimensions, oriented horizontally and heated uniformly, were described by Peng et al., for example, in [4]. In this work, the forced flow convection of water through rectangular micro-channels (hydraulic diameters of 0.133–0.367 mm) was experimentally investigated. The authors indicated that a laminar heat transfer regime occurred at a Reynolds number of 200–700, and fully turbulent connective heat transfer was reached at Reynolds numbers in the range of 400–1500. It was noticed that the transition Reynolds number diminished with the diminishing of the micro-channel diameter. The geometric parameters of the micro-channels were found to be important variables that could significantly affect the flow characteristics and heat transfer. The authors specified that the laminar connective heat transfer reached a maximum value when the aspect ratio (channel height per its width) was approximately 0.75, and turbulent heat transfer was optimal when the aspect ratio was in the range of 0.5–0.75.

Bao et al. [5] presented the results of research on boiling heat transfer during the R-11 and HCFC123 flow along the uniformly heated circular mini-channel, which was horizontally oriented. It was found that the heat transfer coefficients are independent of the mass flux and vapor quality, but they are strong functions of the heat flux and system pressure in the saturated boiling region. The authors stated that the heat transfer is mainly dependent on nucleate boiling as the dominant mechanism over a wide range of flow conditions, whereas convective effects are less important (because of the relatively low Reynolds numbers and liquid conductivity). The experimental data were compared with some existing correlations. Furthermore, none of the correlations examined predicted the experimental data over the whole range examined, but most of them identified the dominance of nucleate boiling.

Kandlikar in [6] presented fundamental questions related to the presence of nucleate boiling and the characteristics of flow boiling in micro- and mini-channels compared to conventional channels. Classification of channels due to their hydraulic diameter was performed. Moreover, the mechanisms of heat transfer, the flow patterns, and other phenomena accompanying the flow of fluids in confined spaces including the effect of configuration of heat exchanger on the heat transfer and pressure drop performance were discussed. According to the author, heat transfer studies in micro-channels indicate that, as a first-order estimate, heat transfer and pressure drop prediction schemes may be predicted using the correlations developed for large diameter tubes. Furthermore, it was underlined that the heat transfer rate in multichannel evaporators is different from that in single-channel evaporators under the same set of operating conditions. In the design of evaporators with small diameter channels, the length-to-diameter ratio depends on the characteristics of the heat transfer and pressure drop. Larger pressure drops are generally accepted in evaporators with small diameter channels.

Over the next years, researchers became interested in convective heat transfer during flow in mini-gaps, including the liquid change of the phase to the intensity of heat transfer as in [7,8]. The previous results of the authors and selected state-of-the-art covered works focused on heat transfer during flow in mini-channels of rectangular cross-sections were presented in numerous publications. The results of flow boiling heat transfer time-dependent research were described in [9]. Steady-state experiments were the basis of heat transfer analyses discussed in [10,11]. The results of numerical calculations performed with the use of ADINA software were shown in [12,13]. Flow boiling heat transfer experiments with the use of an annular mini-gap was described in [14]

For the analysis of experimental data, analytical methods were often used, the solutions of which had to be simplified in the solution of mathematical heat and flow models. At present, commercial computational programs are used to perform mathematically advanced numerical procedures in order to perform either simulations or computations using experimental data. Today, the Finite Element Method (FEM) and the Finite Volume Method (FVM) are commonly used for the study of heat transfer processes in compact heat exchangers of various constructions. Numerical investigations cover computational fluid dynamics needed for fluid flow.

Numerical analyses of specific design solutions of devices with mini- or micro-channels and compact heat exchangers were the subject of an increasing number of works in the literature.

Zhou et al. in [15] proposed modeling of boiling flow in microchannels for nucleation characteristics and performance optimization. The interface separating the two-fluid phases was tracked by the LSM, which was used to calculate multiphase flow problems. The Level Set Two-Phase Flow Model was used to simulate the nucleate boiling of water in microchannels as a model for computing multiphase flow problems with the help of the COMSOL solver. Comparisons of the performance of the enhanced and plain-wall microchannels were also performed and discussed. The objective of [16] was to numerically study the dynamical behavior of the bubble with a smaller growth rate and its influence on the fluid flow and heat transfer in the microchannel. An improved hybrid-lattice Boltzmann model was used in the computations as a tool to simulate the flow behavior and heat transfer performance in microchannels. The authors performed case studies using the developed LB model. A two-dimensional microchannel (0.2 mm x 5.3 mm) was considered. The numerical results obtained concern bubble dynamics, such as the influence of bubble growth and departure on flow disturbance.

The objective of the investigation described in [17] was to develop a numerical model to analyze the boiling of subcooled flow in segmented finned microchannels. Simulations were performed for a single row of segmented finned microchannels with boundary conditions similar to experimental conditions. The predicted numerical results were compared with our own experimental results. Temperature and pressure fluctuations during the subcooled flow boiling condition were investigated. The predicted flow patterns were similar to the experimental results. Simulations were performed using the ANSYS Fluent code and the volume of fluid (VOF) method was used to model the two phases in nucleate flow boiling.

Ameur in [18] investigated the impact of corrugated baffles inserted in a rectangular channel heat exchanger on the flow and thermal distribution of fluid. The shear thinning behavior of the working fluid was assumed. With the aim of the computer tool ICEM CFD, the geometry of the problem was studied and the computer code CFX was used in computations. The SIMPLE algorithm was used to perform pressure–velocity coupling. Several cases of the corrugated baffle configuration were studied. One of them was indicated as the best.

Lee et al. in [19] provided the results of numerical simulations of bubble growth and heat transfer associated with flow boiling in a finned microchannel. Phase interfaces were determined by a sharp-interface level set method that was modified to include the effect of phase change at the liquid–vapor interface and to treat the non-slip and contact angle conditions on the immersed solid surface of fins. The effects of the fin height, spacing, and length on the flow boiling in a microchannel were investigated. The computational results showed that the flow boiling in a microchannel was significantly enhanced when the liquid–vapor–solid interface contact region increased with the addition of fins.

Zhuan and Wang in [20] performed simulations of boiling flows of R-134a and R-22 in a circular micro-channel. The vapor–liquid interface was captured using the VOF method. Based on bubble lifting, growth, and coalescence behavior, the flow pattern transition related to bubble evolution in the microchannel was determined. The flow patterns at the micro-channel outlet predicted by simulation were in agreement with the flow structures observed in experiments. The peak bubble frequency at the outlet and the general shape of the bubble frequency distribution at the outlet from the simulation were found to be consistent with the experimental results.

Anandan and Ramalingam in [21] presented a literature review focused on high heat flux cooling of electronic equipment and devices. Cooling methods were categorized as: air cooling, liquid cooling, heat pipes, refrigeration cooling, thermoelectric cooling, and phase change material-based cooling. Furthermore, each of the methods was characterized. The main issue pointed out was thermal management of electronics and development of new effective cooling schemes using advanced materials and manufacturing methods, with a special focus on (micro) electronic equipment.

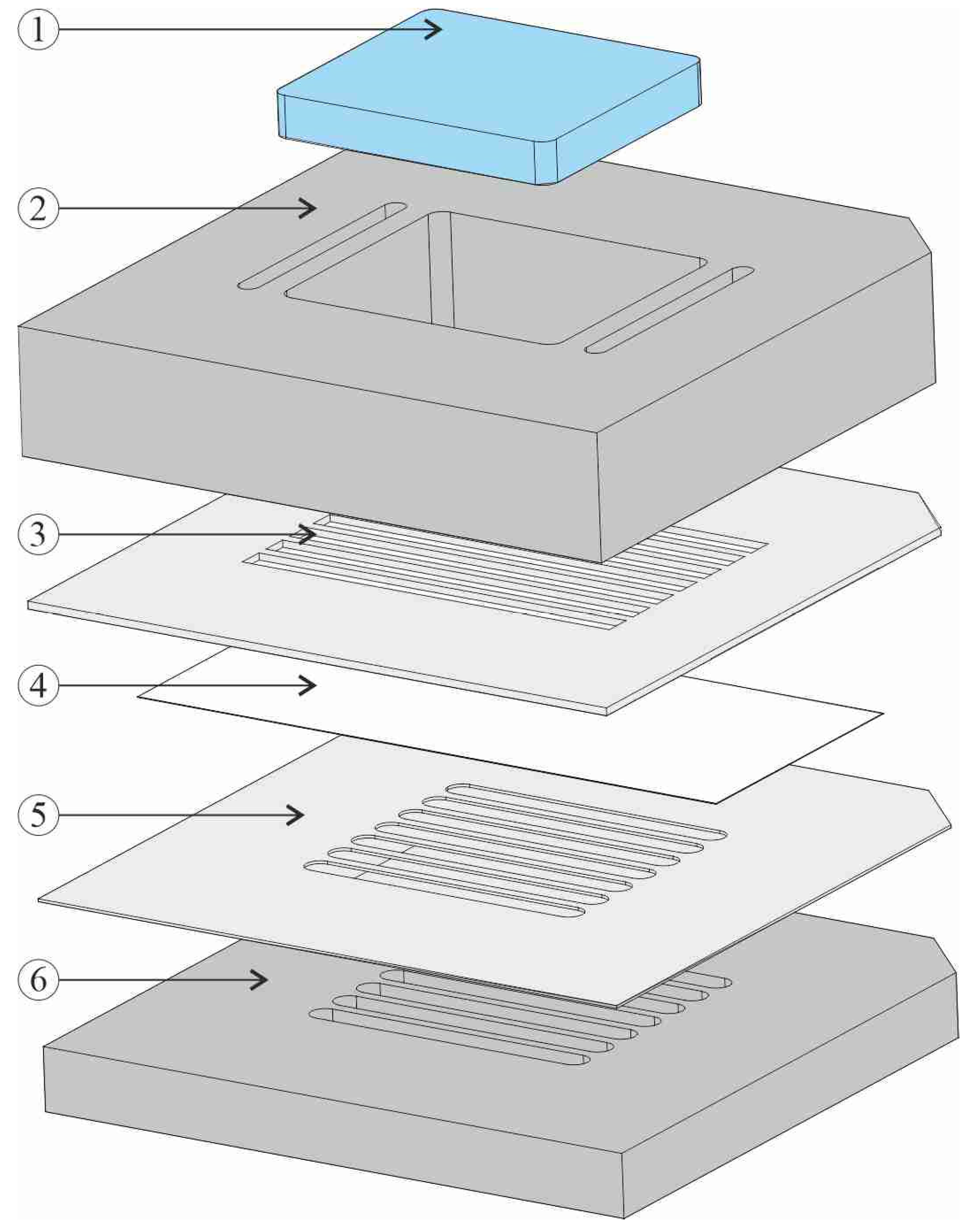
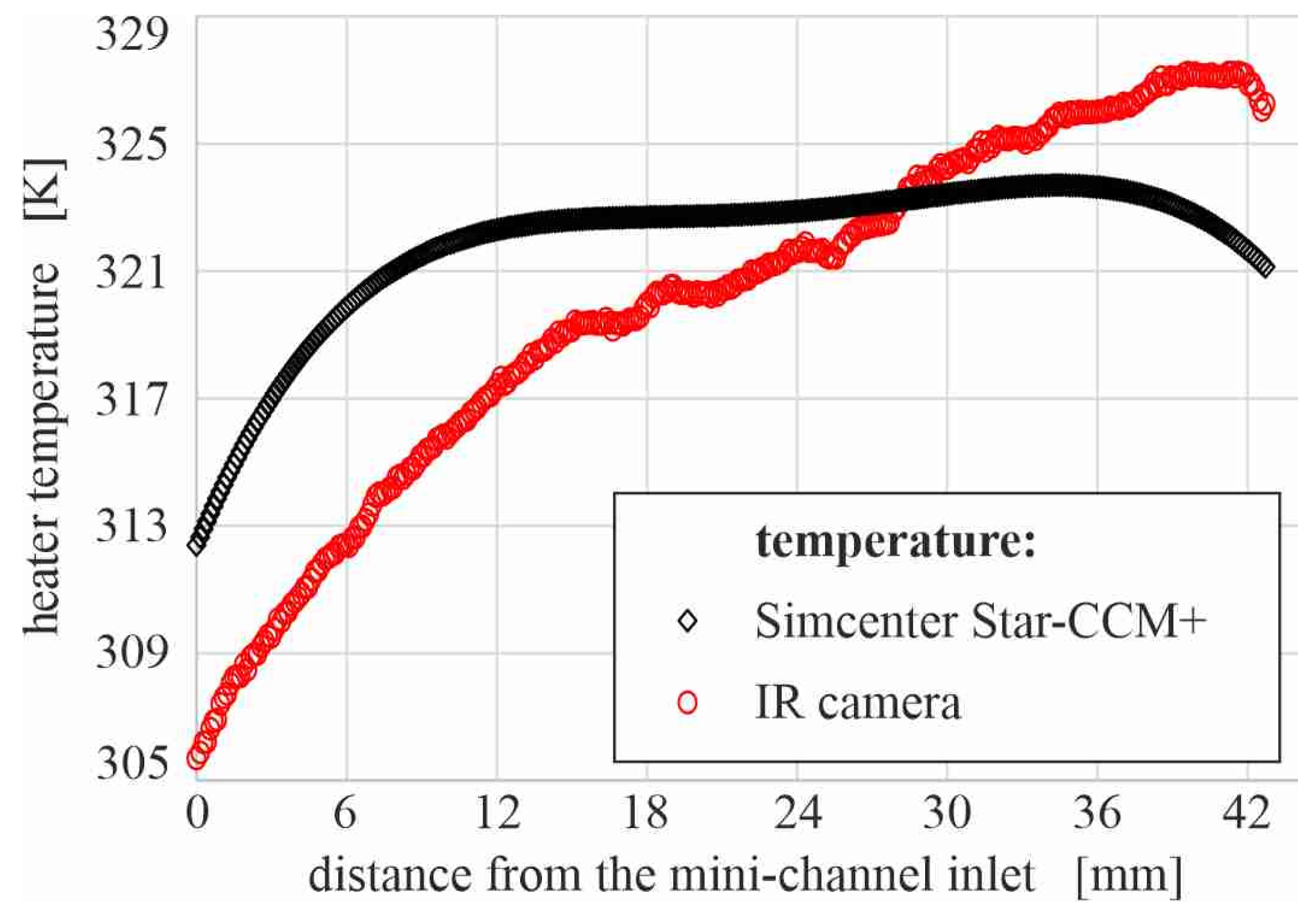
This study aimed to perform a numerical analysis of fluid flow and heat transfer in a mini-channel heat exchanger. A novelty of this work was the development of a numerical model for analyzing subcooled flow boiling in parallel mini-channels and performing numerical calculations using commercial software by Simens-Simcenter STAR-CCM+ software. Experimental data describing the heat transfer during flow boiling in mini-channels of various spatial orientation of the flow under different operating conditions are needed to validate the results from numerical calculations. Simulations can give us information on how to construct mini heat exchangers and select thermal and flow parameters for their work to obtain high thermal efficiency.

2. Experimental Investigations

2.1. Experimental Stand

The experimental stand is illustrated in Figure 1 as a block diagram (Figure 1a) and a pictorial diagram (Figure 1b). In the flow loop, a cooler (Fluorinert FC-72) circulates. The flow loop consists of a test section with several parallel mini-channels, a compensating tank, a heat exchanger, a circulating pump with a filter, and a mass flow meter. The data and image acquisition system comprises digital cameras (an infrared camera and a high-speed camera), data acquisition stations, and a PC computer. The set up is equipped with a heat source (power supply unit), an ammeter, and a voltmeter.

2.2. Test Section

A test section comprises several or a dozen mini-channels. In the investigations presented, seven parallel mini-channels were tested. Each mini-channel was 1 mm deep and 4 mm wide. The length of the mini-channels corresponding to the measurement of the wall temperature due to infrared thermography was 43 mm.

In Figure 2a,b, the views of the test section from two opposite sides of the test section, that is, from the side on which infrared thermography temperature measurements are performed (Figure 2a) and from the side where two-phase flow patterns are observed (Figure 2b). Figure 2c shows a thermographic view of the test section corresponding to the view shown in Figure 2a. Figure 3 illustrates details of the test section presenting a top view (Figure 3a) and both cross-sections (Figure 3b,c).

In Figure 4, a schematic diagram is presented that illustrates the individual components of the test section. Materials of the base parts of the test section are as follows:

• A channel body (2) and a front cover (6)-made of aluminum alloy;
• A 0.1 mm thick heated foil (4)-made of Haynes-230 alloy;
• Insulation spacers (3,5)-cut from a Teflon plate of 1 mm thickness (3) and 0.2 mm thickness (5); in one of the spacers (3) the side walls of the mini-channels are formed;
• The viewing plate (1)-made of glass.

Figure 4. A schematic diagram showing the individual components of the test section, 1—glass plate, 2—channel body, 3, 5—spacers, 4—heated foil, 6—front cover.

Figure 4. A schematic diagram showing the individual components of the test section, 1—glass plate, 2—channel body, 3, 5—spacers, 4—heated foil, 6—front cover.

The test section, at the inlet and the outlet of the mini-channel, was equipped with the thermocouples K-type and pressure meters. One of the mini-channels’ walls was a thin foil resistive heated (the Joule effect) by the heat source.

During the experiments, the test section was vertically positioned with upward flow in the channels. The following experimental parameters were recorded: thermograms from the infrared camera (measurements of the temperature of the outer surface of the mini-channel wall), the current supplied to the heated foil and the voltage drop (values of the imposed heat flux), and the mass flow rate. Thermocouples and pressure meters monitored the fluid temperature and pressure values at the inlet and outlet collectors. Fluid flow images from the high-speed digital camera helped to control the boiling process during fluid flow in mini-channels.

2.3. Research Procedure and Measurement Errors

During each experimental set, a working fluid at the temperature below its boiling point flows into the inlet collector and is then supplied to the mini-channels. Measurements are recorded during increasing electrical power supplied to the heater. The temperature of the heated mini-channel wall was measured using an infrared camera on the outer side. Signals from thermocouples and pressure meters concerning measurements at the inlet and outlet to/from the test section, atmospheric pressure, current supplied to the heater, the voltage drop across the heater, and mass flow rate are recorded by two data acquisition stations.

Three series of experiments were selected for analysis, with Fluorinert FC-72 being the working fluid. The main characteristics of these experimental series, Nos. #1, #2, and #3, are presented in

Table 1. The base characteristics of the selected experimental series.

No. of Experimental Series	#1	#2	#3	#4
Temperature of FC-72 at the Inlet (K)	287.55	287.55	286.15	287.55
Temperature of Ambient Air (K)	295.35	295.55	295.35	293.15
Atmospheric Pressure (kPa)	95.76	96.97	96.93	101.32
Inlet Overpressure (kPa)	95.83	97.09	97.25	101.38
Outlet Overpressure (kPa)	95.72	97.08	97.15	101.28
Mass Flow Rate (kg/h)	20.79	22.25	40.40	20.76
Heat Flux Supplied to the Heater (W)	80.72	70.48	88.66	64.00

. The data from series No. #4 shown in Table 1 are the basis for the numerical calculations provided in Section 6. The errors of the main experimental parameters are listed in

Table 2. Errors of the main experimental parameters.

Parameter	Error
Temperature of the Heater (K or %) (FLIR A655SC infrared camera)	± 2 K or ± 2% in measured temperature range
Temperature of the Working Fluid at the Inlet, K-type Thermocouple (K)	1.5 K—nominal error 0.34 K—the absolute error, including additionally calibration [10,22]
Mass Flow Rate (%)	± 0.15% of the full scale
Overpressure at the Inlet (%)	± 0.05% of the full scale
Heat Flux (%) (Based on Electrical Measurement Data and the Heater Dimensions)	3.4% [23]

.

3. Numerical Calculations

Numerical calculations were performed using Simcenter STAR-CCM+ software version 2020.2.1 Build 15.04.010 installed on a PC computer (main PC characteristics: Intel Core i9 CPU processor (24 cores), 3.50 GHz of clock speed, and 256 GB of RAM). Details on the calculation methodology within this numerical environment can be found in [24]. It is assumed that heat and flow transfer problems should be solved due to suitable equations with the assumption of proper boundary conditions. The governing equations for the fluid cover continuity equation, momentum equation, and energy equation as follows:

• Continuity equation:

$$\frac{\partial }{\partial t}{\int }_V\rho dV+{\oint }_A\rho v·d\mathit{a}={\int }_V{S}_u dV$$

(1)

where: t—time, V—volume, a—the area vector, ρ—the density, v—the velocity, S_u—a user-specified source term;

• Momentum equation:

$$\frac{\partial }{\partial t}{\int }_V\rho v dV+{\oint }_A\rho v\otimes v·d\mathit{a}=-{\oint }_{A}pI·d\mathit{a}+{\oint }_{A}T·d\mathit{a}+{\int }_V{f}_b dV+{\int }_V{s}_u dV$$

(2)

where: p—pressure, T—the viscous stress tensor, $f_b$—the resultant of body forces, $s_u$—a user-specified source term, I—identity tensor;

• Energy equation:

$$\frac{\partial }{\partial t}{\int }_V\rho E dV+{\oint }_A\rho Hv·d\mathit{a}=-{\oint }_{A}q·d\mathit{a}+{\oint }_{A}T·vd\mathit{a}+{\int }_V{f}_b ·vdV+{\int }_V{S}_u dV$$

(3)

where: E—the total energy, H—the total enthalpy, q—the heat flux.

The following assumptions were made:

• The fluid temperature at the inlet of the mini-channel and the overpressure pressure at the outlet were taken into account under the boundary conditions;
• The fluid flow in the mini-channel was incompressible with a constant mass flow rate;
• The independence of the properties of the materials in temperature was assumed despite the Haynes-230 alloy;
• Heat losses from the test section to the ambient air were assumed.

The convergence took about 26,000 iterations and 40–48 h of CPU time.

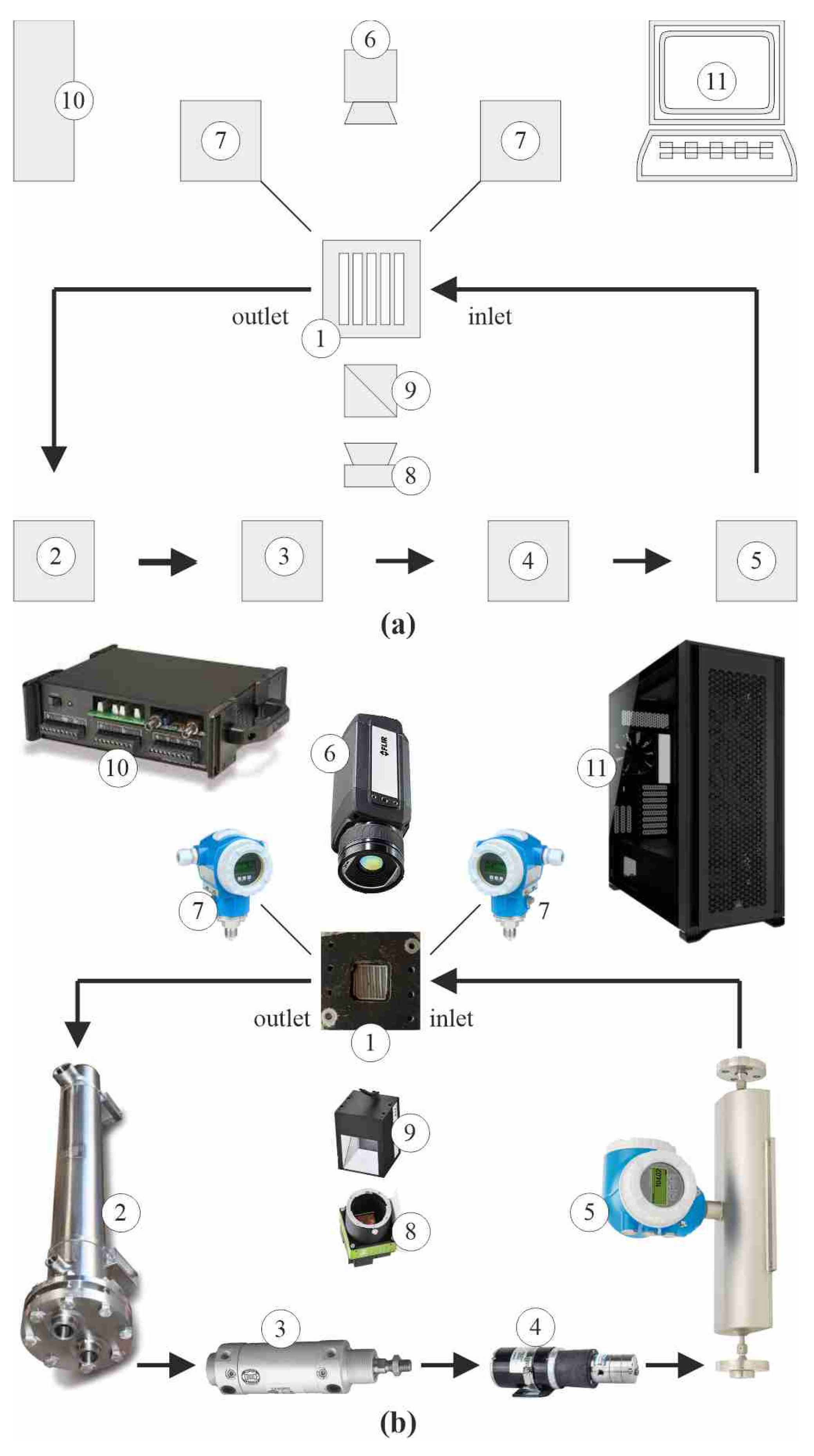
The main experimental parameters taken into account in the numerical computation are listed in Table 1 as series No. #4.

In

Table 3. The main physical properties of the materials used in the numerical calculations.

Material	Density (kg·m−3)	Dynamic Viscosity (Pa·s)	Specific Heat (J·kg−1·K−1)	Thermal Conductivity (W·m−1·K−1)
Fluid
FC-72	1680	6.4·10−4	1100	0.057
HFE-7100	1510	5.8·10−4	1183	0.069
Solid
Aluminum	2702	-	903	237
Teflon	2160	-	702	0.21
Glass	2500	-	840	1.4
Haynes-230	8970	-	400	8.9÷14.4 in the temperature range from 293.1 (K) to 673.1 (K)
Copper	8940		386	398

, the main physical properties of the materials used in the calculations are specified: for the fluid region and each element of the solid region, respectively. In addition, the physical properties of HFE-7100 (as the working fluid) and copper (as the heater material) were used only for numerical simulations.

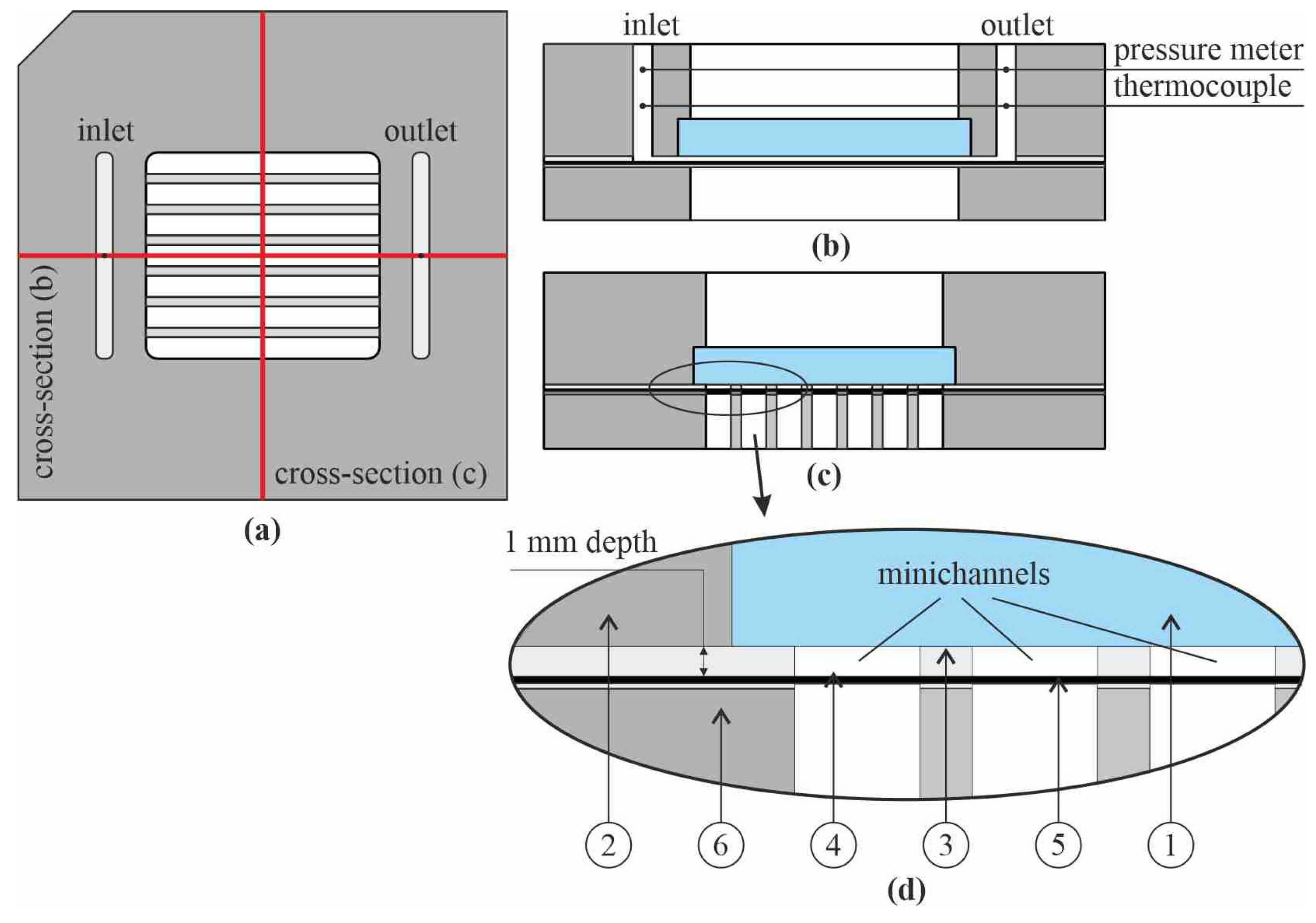
Figure 5 illustrates 2D views of the channel body and the working fluid in the test section (as the solid and fluid regions assumed in the simulations). The typical meshes that were assumed in the numerical calculations are shown, while some details are enlarged.

The fundamental strategy for computer simulations and verification of numerical analysis is the identification and quantification of errors in the computational solution. The most important activity in verification testing is systematically refining the grid size and time step [25]. Therefore, the mesh refinement study was performed as part of the verification procedure.

To ensure the convergence stability of the numerical computations, a mesh dependency analysis based on the grid convergence index (GCI) was performed. This method is recommended by the Fluids Engineering Division of the American Society of Mechanical Engineers (ASME) [26,27]. The GCI was originally proposed by Roache in 1994 and is based on the Richardson extrapolation idea. Mesh dependency studies based on GCI were carried out to estimate the numerical accuracy resulting from mesh resolution. To define the accuracy discretization error, the model was meshed with three grids with different sizes to obtain a range of 3–15 million cells. The GCI was calculated according to the procedure described in [26].

Firstly, in the CFD model, three base grid sizes of different resolutions (1, 2, and 3 mm) were selected. To define the representative cell size (h), the following dependence was used:

$$h={\left[\frac{1}{N}\sum _{i=o}^N\left(\Delta V_i\right)\right]}^{\frac{1}{3}}$$

(4)

where: ΔV_i—volume of the i-th cell, N—total number of cells in the CFD model.

The smallest mean representative cell size from the calculation was h₁ = 1.49 × 10⁻⁴ (for 15,110,063 cells in the grid) and the largest cell size was equal to h₃ = 2.46 × 10⁻⁴ (for 3,338,533 cells in the grid).

The grid refinement factor r defines that the selected meshes are sufficiently different. This factor was determined as follows:

$$r=\frac{h_{coarse}}{h_{fine}}$$

(5)

where h_fine represents the finer mesh. If h₁ < h₂ < h₃, the following dependences were proposed to define grid refinement factors:

$$r_{21}=\frac{h_2}{h_1}; r_{32}=\frac{h_3}{h_2}$$

(6)

The order of convergence p was determined from the following dependence:

$$p=\frac{\left|\ln \left|\frac{e_{32}}{e_{21}}\right|+\ln \left(\frac{r_{21}^p-1·sgn\left(\frac{e_{32}}{e_{21}}\right)}{r_{32}^p-1·sgn\left(\frac{e_{32}}{e_{21}}\right)}\right) \right|}{\ln \left(r_{21}\right)}$$

(7)

where:

$$e_{32}={\varnothing }_3-{\varnothing }_2; e_{21}={\varnothing }_2-{\varnothing }_1$$

(8)

while ∅ denotes the value of the crucial variable for the specific numerical simulation of the solution obtained for each base grid size.

In further calculations, the highest temperature of the outer heated foil surface (∅₁, ∅₂ and ∅₃) was chosen as the crucial variable.

The approximate relative error was estimated as follows:

$$e_a^{21}=\left|\frac{{\varnothing }_1-{\varnothing }_2}{{\varnothing }_1}\right|$$

(9)

Calculations of $e_a^{32}$ were performed in analogy.

The GCI is defined by the following equation:

$$GC{I}_{21}=\frac{F_s ·e_a^{21}}{\left(r_{21}^p-1\right)}$$

(10)

where F_s is a safety factor. For three or more meshes in CFD simulations, the recommended value is equal to 1.25 and represents 95% confidence in the calculated error bound [26,27,28]. Finally, the determined values of the GCIs are listed in

Table 4. Calculation of the grid convergence index.

h (-)	N (-)	$\mathit{\varphi }$	r (-)	$\mathit{e}$	p (-)	ea (%)	GCI (%)
1.49 × 10−4 (h1)	15,110,063 (N1)	323.22 (${\varphi }_1$)	1.3063 $(r_{21})$	0.37 $(e_{21})$	1.808	0.1 $(e_a^{21})$	0.23 $(GC{I}_{21})$
1.94 × 10−4 (h2)	6,777,328 (N2)	323.59 (${\varphi }_2$)	1.2661 $(r_{32})$	1.29 $(e_{32})$		0.4 $\left(e_a^{32}\right)$	0.94 $\left(GC{I}_{32}\right)$
2.46 × 10−4 (h3)	3,338,533 (N3)	324.89 (${\varphi }_3$)	-	-		-	-

.

Following the GCI calculation procedure, after selection of three base grid sizes of different resolutions to verify the results from numerical computations, it was found that the fine and coarse GCI were 0.23% and 0.94%, respectively. The reduction between coarse and fine GCI values showed the most reliable results. The base grid size of 1 mm is indicated as the preferred size for simulations.

4. Results and Discussion

4.1. Overall Results of the Numerical Computations

The 2D results of the computations using Simcenter STAR-CCM+ software are illustrated in Figure 6.

The distributions of temperature, velocity, and absolute pressure in mini-channels are presented in Figure 6a, Figure 6b, and Figure 6c, respectively. The calculations were performed with the assumptions regarding meshes and boundary conditions, and with the use of differential equations—Equations (1)–(3). The data are presented as screenshots from Simcenter STAR-CCM+ software, which were obtained from the calculations according to the longitudinal symmetry axis of the test section. In Figure 7, the results of the numerical calculations are shown as the 2D temperature distributions on the outer surface (Figure 7a) and on the fluid-heated plate contact surface (Figure 7b). Additionally, the cross-sectional temperature distributions in the test section are shown in Figure 8.

The absolute pressure distribution along the mini channel shown in Figure 6a is evidence of a pressure drop from the inlet to the outlet part of the mini-channel, related to the appearance of friction losses along the length of the channel (major energy losses). Local pressure changes related to minor energy losses at the channel inlet and outlet, on the scale and pressure range presented, are not observable.

The fluid velocity distribution in the mini-channel illustrated in Figure 6c indicates that the highest flow turbulence occurs in the outlet part of the channel (in the outlet chamber). These issues require a thorough analysis for different flow velocities and are planned in further analyses.

After studying the temperature results shown in Figure 6b, Figure 7 and Figure 8, it can be stated that the observed temperature distribution is typical of the case for an asymmetrically heated mini-channel. The temperature distributions on the outer surface of the heated foil indicate an increasing temperature from the inlet to the outlet of the test section. The subcooled liquid flows laminarly into the channel, whereas its wall is uniformly heated (see Figure 7). With a gradual increase in the electric power supplied to the foil, resulting in imposed heat flux, the heat transfer between the foil and the working fluid in the mini-channel proceeds by single-phase forced convection. A further increase in heat flux leads to the boiling incipience, and the appearance of the first bubbles. Then, the subcooled boiling region starts. In the area close to the foil, the liquid became superheated, while in the core of the flow, it remained subcooled. Rapid cooling of the fluid is observed in the direction perpendicular to the thickness of the heated foil and the depth of the mini-channel in the cross-sectional temperature distribution shown in Figure 8.

It should be emphasized that this work focuses on the results concerning the calculation of the temperature distribution in the test section because they are the basis for the determination of the values of the heat transfer coefficient on the fluid–heater contact surface. The values obtained allow us to evaluate the intensity of heat transfer processes. Comparisons of previous results obtained for flow boiling in mini-channels in the subcooled and saturated boiling regions show that the values of the heat transfer coefficient are several times higher for saturated boiling compared to subcooled boiling [10,11].

4.2. Comparison of the Results from Numerical Computations with Those Obtained from the Experiments

As a verification of the results from numerical computations, a comparison with the experimental data was provided. The temperature field obtained as a result of numerical computations was compared with the data collected during the experiment carried out in the research setup. Figure 9a shows the 2D temperature distribution in the test section from the side of the outer surface of the heater. A stabilized temperature distribution can be seen on the aluminum elements of the test section and an increasing temperature of the heater surface from the inlet to the outlet of the mini-channels. For comparison, the temperature distribution on the heater surface corresponding to that previously discussed, recorded by an infrared camera during the laboratory experiment, is presented in Figure 9b. When analyzing the temperature results shown in Figure 9, it can be stated that the distribution and the surface temperature values are similar.

Two dependencies of the heated plate temperature on the distance from the minichannel inlet are presented in Figure 10. Both were based on the input data from the Series No. #1 (see Table 1). The thermography measurements (due to infrared thermography) and the results from numerical calculations are shown from the comparison on one graph. This comparison helps to validate the results of the numerical calculations.

When analyzing the results shown in Figure 10, it was noticed that the local values of the heated plate surface temperature, obtained as a result of the numerical simulations, are similar to those obtained from the experimental measurement, and both relationships show a similar course.

The average relative difference ε between the heated foil temperature obtained from the experimental measurement and from numerical computations was calculated from the following formula:

$$\epsilon =\frac{1}{P}\sum _{i=1}^P\frac{\left|T_{f,exp}\left(x_i\right)-T_{f,calc}\left(x_i\right)\right|}{T_{f,exp}\left(x_i\right)}$$

(11)

where: T_f,exp—the heated foil temperature recorded during the experimental measurement due to infrared thermography, T_f,calc—the heated foil temperature obtained from numerical computations according to Simcenter STAR-CCM+ software, i—i-th point, and P—number of points.

The average relative difference ε equals 8.5%. The greatest differences between the values of the foil temperature obtained from experimental measurement and those calculated using Simcenter STAR-CCM+ software are observed near the mini-channel inlet. It was assessed that such a comparison allowed for the validation of the own results obtained from the calculations carried out with the use of the commercial program.

The residuals are good indicators of convergence. When analyzing the residual versus time at the end of the calculation, it should be clear that most of the residuals flatten out. Generally, in the numerical procedure using Simcenter STAR-CCM+ when film casting is in a steady state, it is recommended to run film casting until the relative change in residuals is less than 10⁻⁸ [24].

According to the dependence of the residuals gained after calculation using Simcenter STAR-CCM+ software, it was observed that after about 5000 iterations, each crucial residual (Energy, Continuity, X-momentum, Y-momentum, and Z-momentum) flattens out. Two of them reached an averaged value of 10⁻⁷ (‘Energy’ and ‘Continuity’). The residual of ‘X momentum’ obtained a value close to 10⁻⁸ while the residuals of ‘Y momentum’ and ‘Z momentum’ achieved values below 10⁻⁹. Furthermore, the turbulent dissipation rate (T-dr) and turbulent kinetic energy Tke, were the lowest (values below 10⁻¹³).

In conclusion, the presented data prove that satisfactory convergence of the results was achieved as a result of the computational procedure, the numerical model was correctly defined, and the effect of implementing the computation procedure is assessed as satisfactory.

5. Numerical Simulations

Numerical simulations included calculations with the following variable parameters of the experiment: working fluid (FC-72 or HFE-7100), heater material (Haynes-230, copper and aluminum), changeable spatial orientation of the test section (horizontal, with the fluid flowing above the heater, named ‘0°’, and vertical with the fluid upflow, named ‘90°’), and various numbers of mini-channels in the test section (7, 9, 11, and 15).

Input data used in the numerical simulations in Simcenter STAR-CCM+ software, concerning the working fluid, heater material, spatial orientation of the test section, and number of mini-channels, are listed in

Table 5. Overall characteristics of the data used in the numerical simulations.

No. of Simulation Series	Working Fluid	Heater Material	Spatial Orientation	Number of Mini-Channels
1	FC-72 HFE-7100	Haynes-230	90°	7
2	FC-72	Haynes-230 Copper Aluminum	90°	7
3	FC-72	Haynes-230	90° 0°	7
4	FC-72	Haynes-230	90°	7, 9, 11, 15

. The main experimental parameters taken into account in the simulations are presented in Table 1 as for Series No. #4.

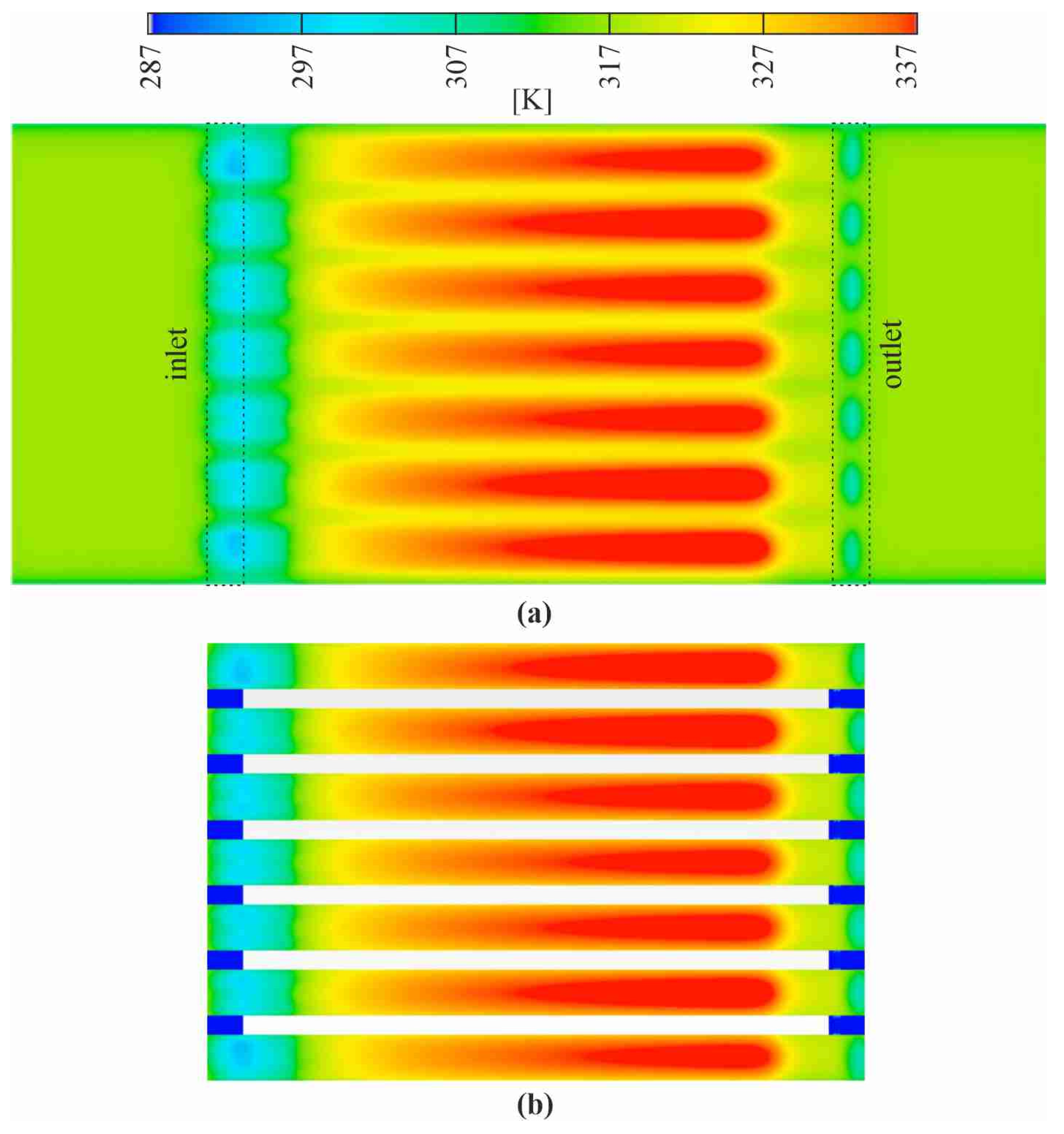
Figure 11, Figure 12, Figure 13 and Figure 14 illustrate the dependence of the heat transfer coefficient at the heater–fluid interface as a function of the distance from the mini-channel. The inlet and outlet parts of the tested length of the mini-channel were omitted due to the large spread of data. The key physical properties of the fluids and material of the heater taken into account in the numerical calculations are specified in Table 3.

Figure 11 shows local heat transfer coefficients for two selected working fluids: Fluorinert FC-72 and fluid HFE-7100 (Novec^TM 7100 Engineered Fluid), both manufactured by 3M. The fluids differ in their physical properties (see Table 3).

Analyzing the results presented in Figure 11, it is obvious that the use of the FC-72 allows even 70% higher values of the heat transfer coefficient compared to the HFE-7100. Generally, the heat transfer process is known to depend on the thickness of the thermal boundary layer and the density of active nucleation sites. The thin liquid film evaporation has proven to be the heat transfer mechanism governing flow boiling in typical multi-micro or mini-channel heat sinks. The main physical properties of two tested working fluids, i.e., density, viscosity, and surface tension, differ. All these conditions strongly affect the convective heat transfer during the flow in narrow spaces, even more intense if subcooled boiling occurs, and single vapor bubbles appear.

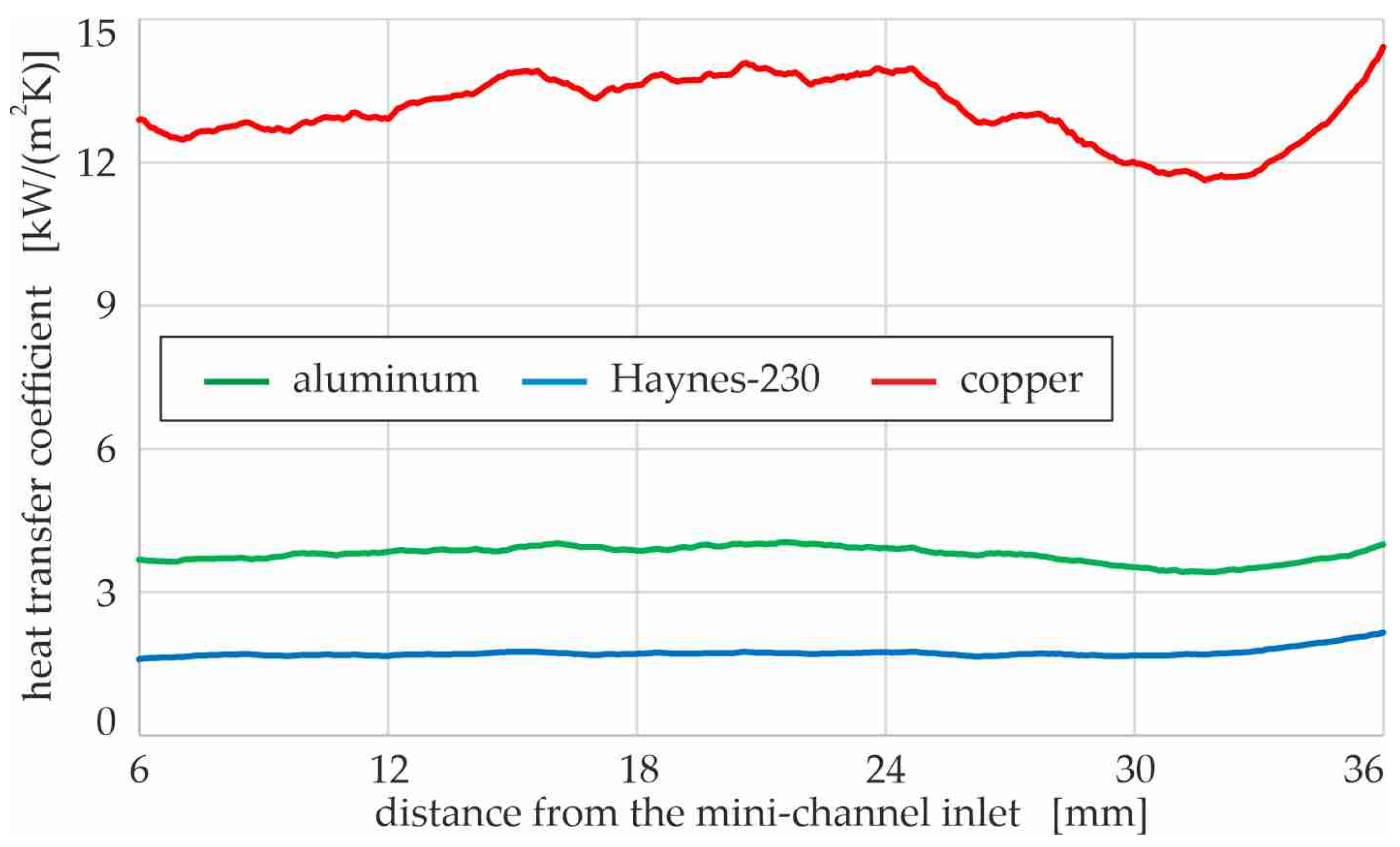
The dependence of the heat transfer coefficient as a function of the distance from the mini-channel inlet, assuming that the heater was made of: Haynes-230 alloy, copper, and aluminum, is presented in Figure 12. The most important physical property due to the analysis performed is that the listed materials differ in the value of the thermal conductivity coefficient (see Table 3).

The highest values of the heat transfer coefficient were recorded when a heater made of cooper was used in the simulations, and moderate values of coefficient were achieved for the aluminum heater. The lowest values of the heat transfer coefficient were observed for the application of Haynes-230 alloy as the heated foil. Both the physical properties of the heating surface in contact with the fluid, including the thermal conductivity and surface wettability, as well as the properties of the fluid, especially its surface tension, and cohesion forces, all affect the heat transfer processes. When analyzing subcooled boiling, it should be taken into account that bubble growth is accredited to intensive evaporation of a thin liquid layer trapped between a vapor bubble and a channel wall, and the physical properties of both are crucial to heat transfer development.

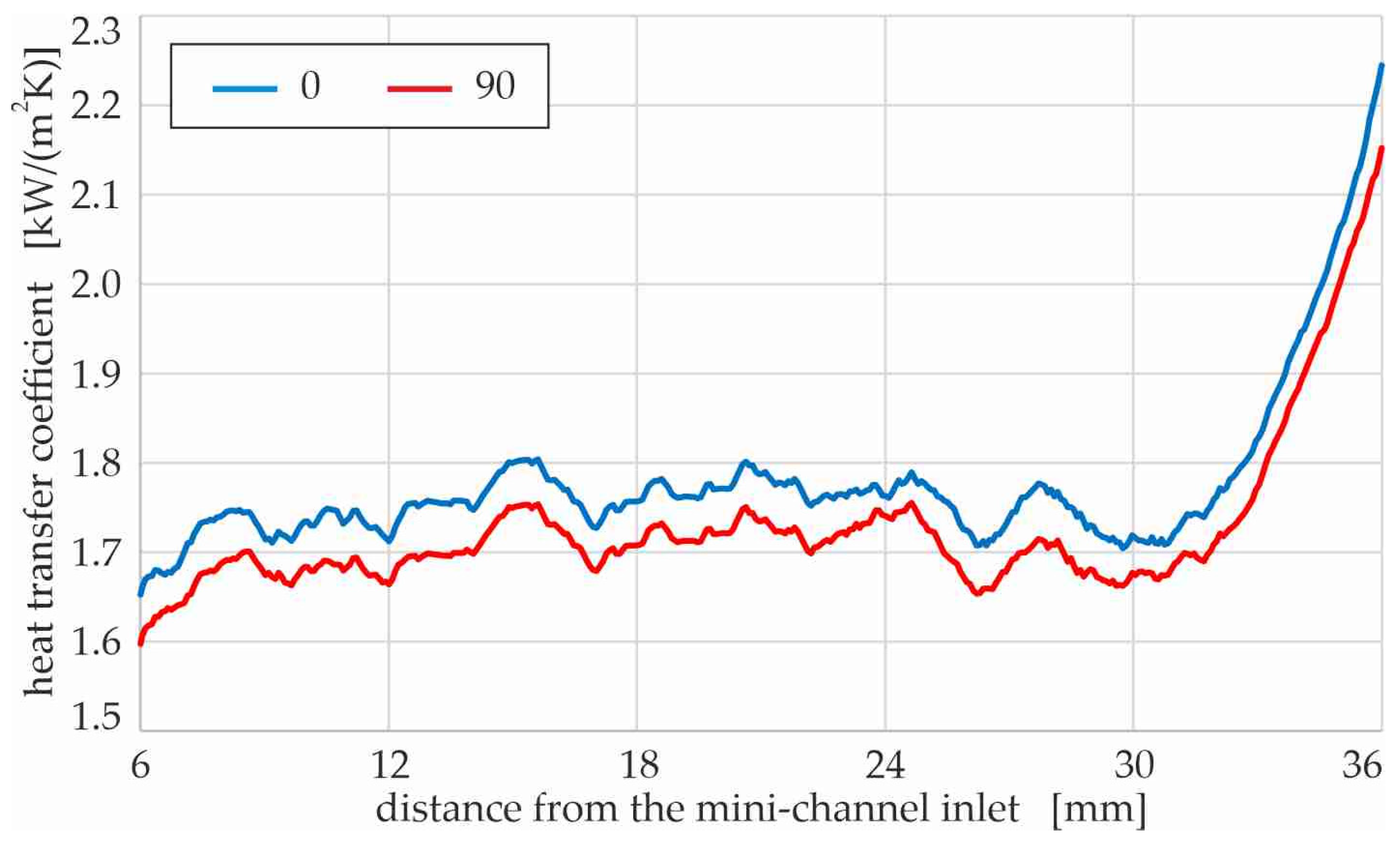
The heat transfer coefficient versus the distance from the mini-channel inlet, assuming two spatial orientations of the test section: vertical with fluid upflow (‘90’) and horizontal with fluid flow above a heater, are presented in Figure 13.

Similar local values of the heat transfer coefficient were obtained, although the horizontal position of the test section seems to be slightly more favorable than the two tested positions. However, it should be noted that these two orientations were previously verified as the most effective for the operation of the test section with mini-channels in previous articles by Piasecka et al. [10,11]. 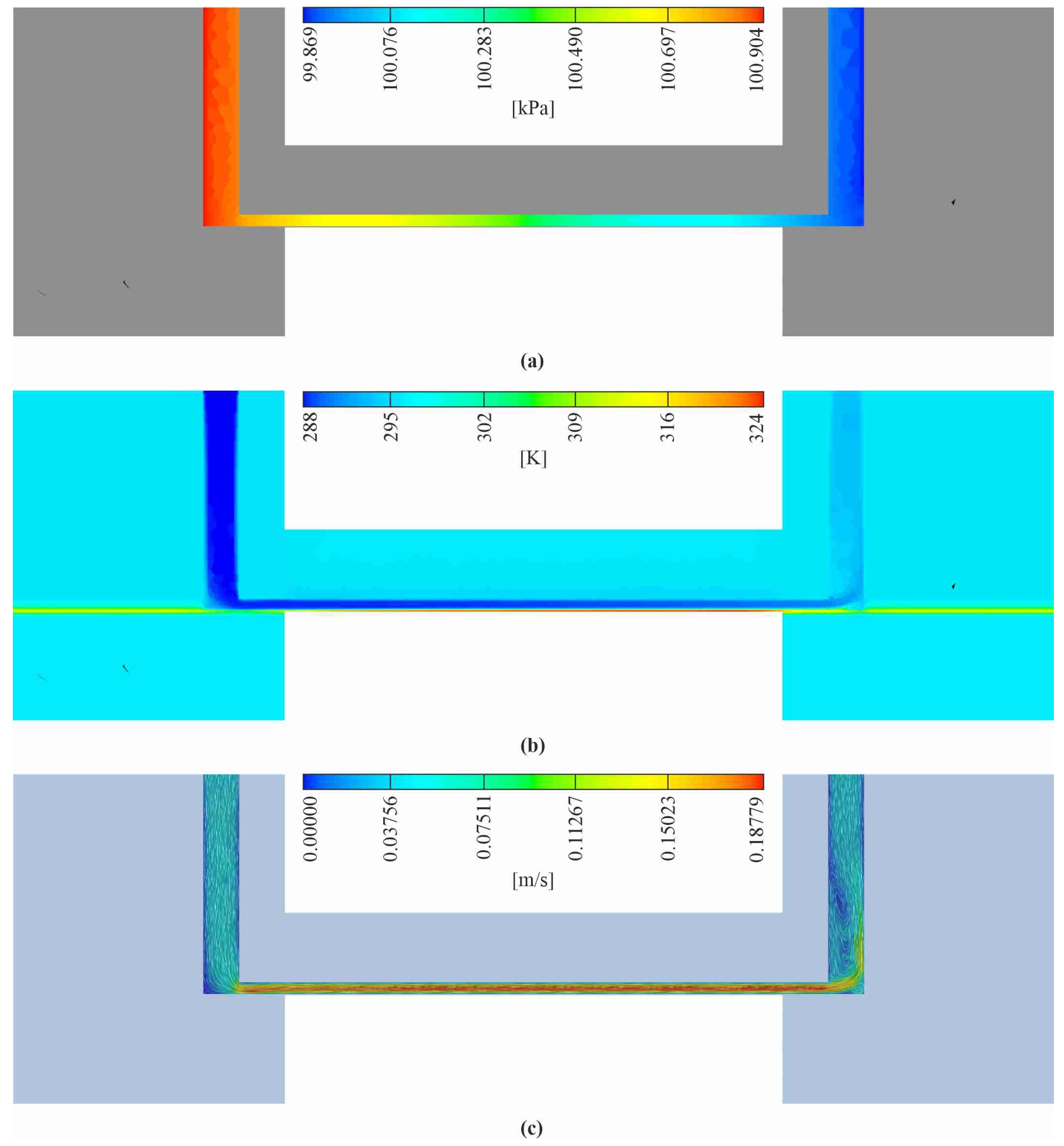An example distribution of velocity is shown in Figure 6c. It could be taken into account that some differences should occur when various orientations of the test section are tested. The velocity field is non-uniform, and it changes with the flow orientation. In the case of subcooled boiling, the forces of gravity and buoyancy affecting the vapor bubbles have a very strong effect on the heat transfer during the flow in mini-channels.

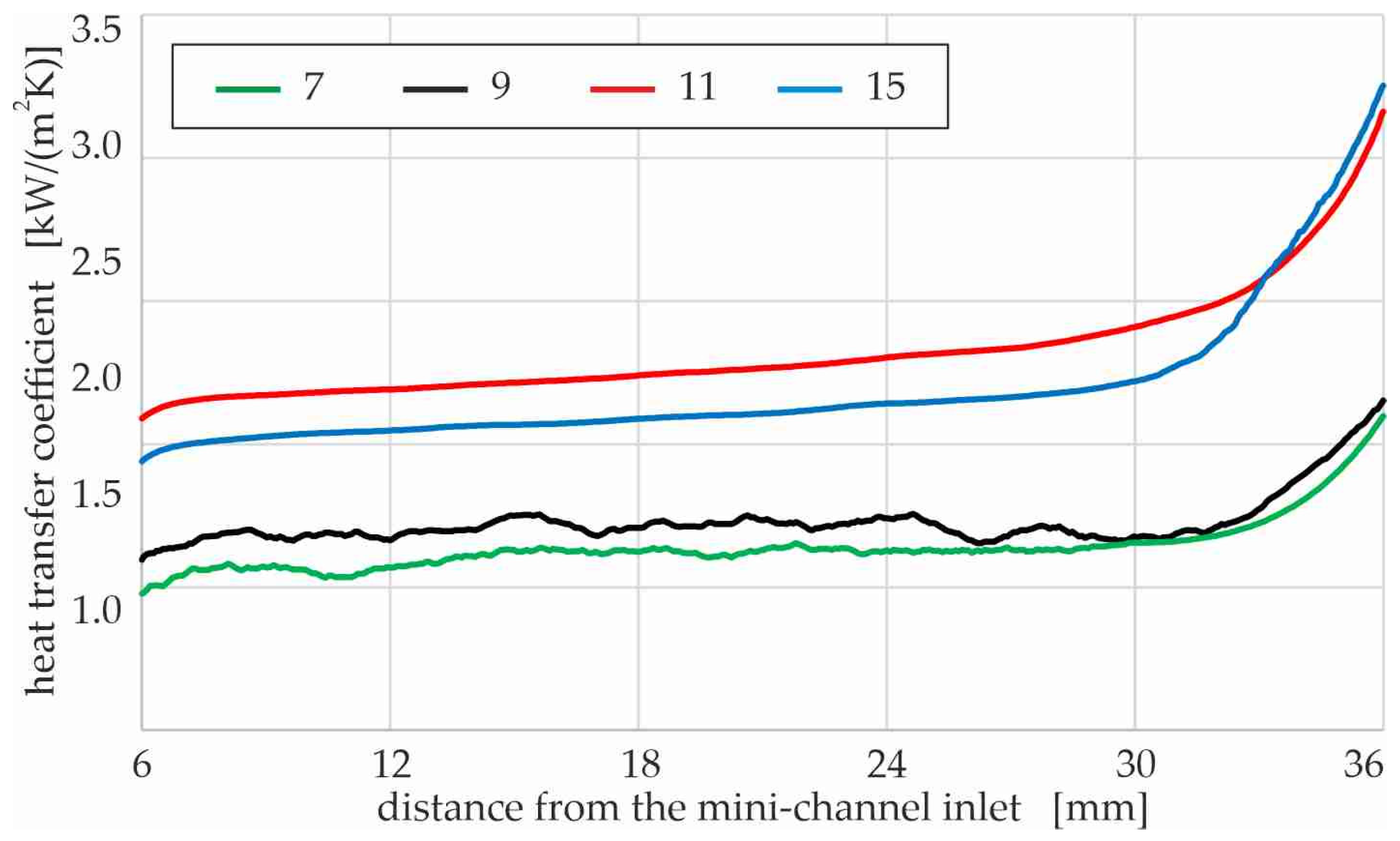
The heat transfer coefficient versus the distance from the mini-channel inlet, assuming four different numbers of mini-channels produced in the test section, i.e., 7, 9, 11, and 15, is illustrated in Figure 14.

As can be seen from the simulation results presented in Figure 14, among the tested numbers of mini-channels, it is more advantageous in terms of the intensity of heat exchange in the test section to design a higher number of mini-channels, that is, 11 or 15. The test section with 6 and 9 mini-channels caused the heat transfer coefficient values to be lower by up to 50% compared to 11 or 15 mini-channels. It should be underlined that when considering the influence of the number of channels on heat transfer, the influence of decreasing the mass flow rate in a singular mini-channel is assumed in the numerical computation. In each simulation, the constant value of the mass flow rate was considered for all cases in this study, for the entire test section. Therefore, increasing the number of channels directly corresponds to a decrease in the flow rate in a single mini-channel. The experimental results from research reported in the literature often differs, and are even sometimes contradictory. For laminar flow, when single-phase flow or subcooled boiling occurs, higher values of the heat transfer coefficient values are often obtained in the literature and were observed on the basis of the previous studies of the authors.

In [29,30], it was observed that for a constant Reynolds number, the heat transfer coefficient increases with an increasing mini-channel length / hydraulic diameter ratio. The authors of [31] underlined that the mass flux plays different roles on the heat transfer coefficient. In the subcooled flow boiling region, increasing the mass flux slightly reduces the local heat transfer coefficients. In our case of the study, it is not possible to verify the relationship mass flux–channel length/hydraulic diameter ratio, because both mentioned parameters changed in each test. However, when analyzing the results obtained for previous experiment, such a relationship is predicted.

6. Conclusions

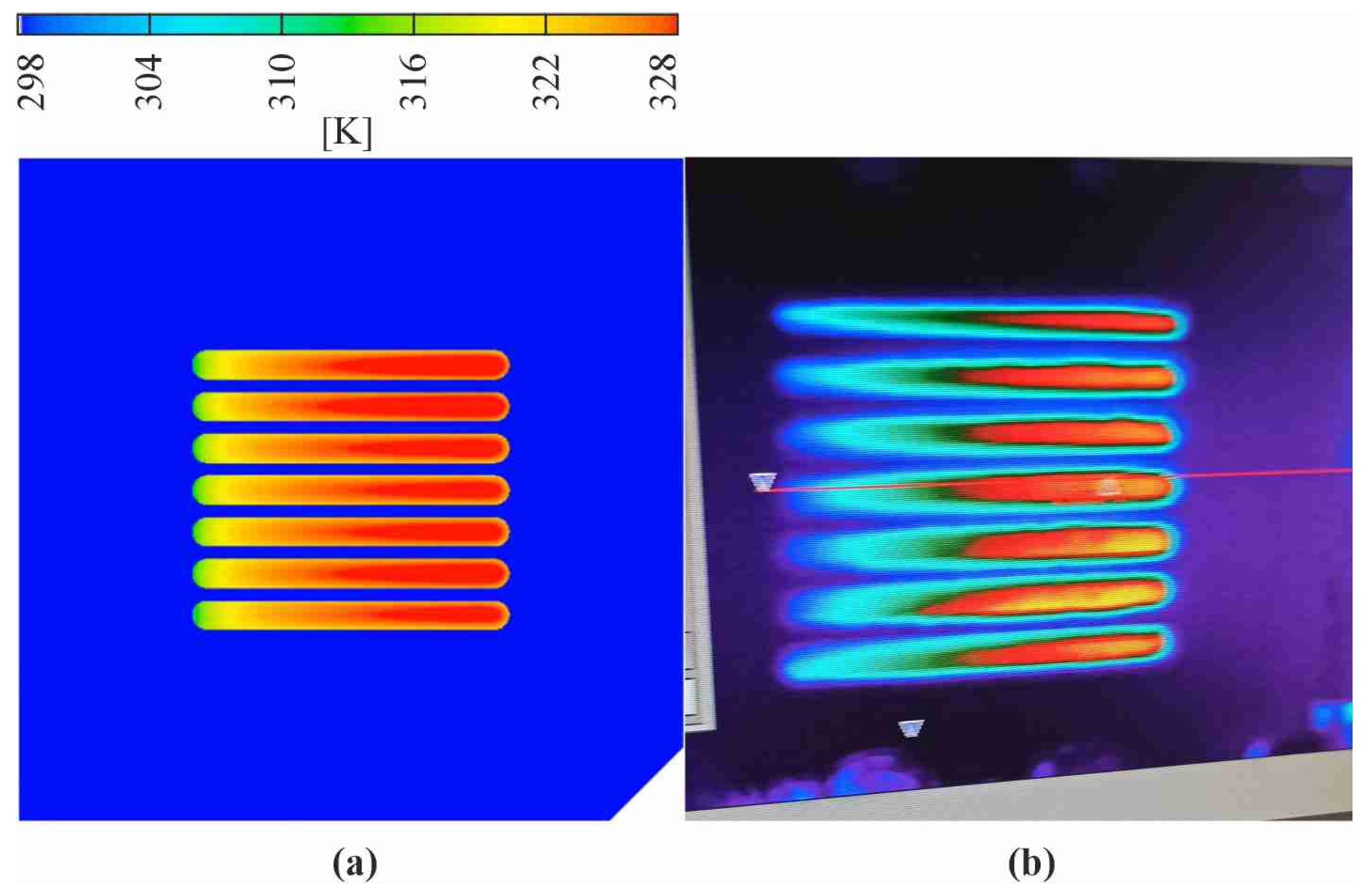
This work presents the results of CFD modeling of fluid flow and heat transfer performed in Simcenter STAR-CCM+ software. The results of the numerical simulations were confronted with the calculations using the data from the experiments. In the experimental rig, an essential element was a test section with mini-channels. The main parameters were measured during experiments, including measurement of the temperature distribution on the heater realized due to infrared thermography.

It is known that the heat transfer coefficient is primarily influenced by the fluid properties, mass flux, effective heat flux, channel geometry (cross-section area and aspect ratio), and spatial orientation of the flow. Finding the values of the parameters tested to evaluate the intensity of the heat transfer processes was the main goal of the numerical simulations. As the tested variables, the following were taken into consideration: the working fluid—two refrigerants (FC-72 and HFE-7100), heater material (Haynes-230 alloy, aluminum, and copper), the spatial orientation of the test section (vertical with fluid upflow and horizontal with fluid flow above the heater), and the number of mini-channels produced in the test section (7, 9, 11, and 15). The computations help indicate which parameters tested in terms of heat transfer turned out to be the most effective.

The results of the numerical computations were discussed. To ensure the convergence stability of the numerical computations of the selected problem, i.e., heat transfer during flow in mini-channels, a mesh dependency analysis based on the grid convergence index (GCI) was performed. Generally, the data presented showed satisfactory convergence of the results achieved as a result of the computational procedure.

The next investigation focuses on improving the proposed calculations with commercial software, i.e., to Simcenter STAR-CCM+ and also ANSYS CFX/Fluent and ADINA. The results of experimental research combined with the use of numerical computations including simulations are expected to expand the knowledge of heat transfer during the boiling of flows into mini-channel and micro-channel heat sinks within a wide range of parameters for various geometries and spatial orientations of the channels. Confronting the numerical simulations with the data from the experiments helps to verify the correctness of the numerical computations. The results of numerical simulations are useful for designing mini-channel heat exchangers. Their main advantage is that they do not require a large number of experiments, which makes them much cheaper and less time-consuming. If the validation of the numerical results by comparison with the experimental results is adequately ensured, it can be assumed that they are also reliable.