Sorption and Spatial Distribution of 137Cs, 90Sr and 241Am on Mineral Phases of Fractured Rocks of Nizhnekansky Granitoid Massif
Abstract
1. Introduction
2. Materials and Methods
2.1. Characterization of the Whole Fractured Sample and Samples of Mineral Phases
2.2. Characterization of the Model Water Solution
2.3. Conditions for Sorption Experiments on the Discs of Sample R-11
2.4. Conditions for Sorption Experiments on Crushed Mineral Phases
2.5. Determination of Mineral Phases in Sample R-11 (SEM-EDX, Micro XRF)
2.6. Determination of the Proportion of the Area Occupied by a Single Mineral Phase in the Sample R-11
2.7. Digital Radiography Method
2.8. Determination of Sorption Parameters (the Degree of Sorption, Distribution Coefficients, Relative Sorption Efficiency)
2.9. Modeling of Radionuclides Sorption
3. Results
3.1. Characterization of Rock Fractured Sample R-11
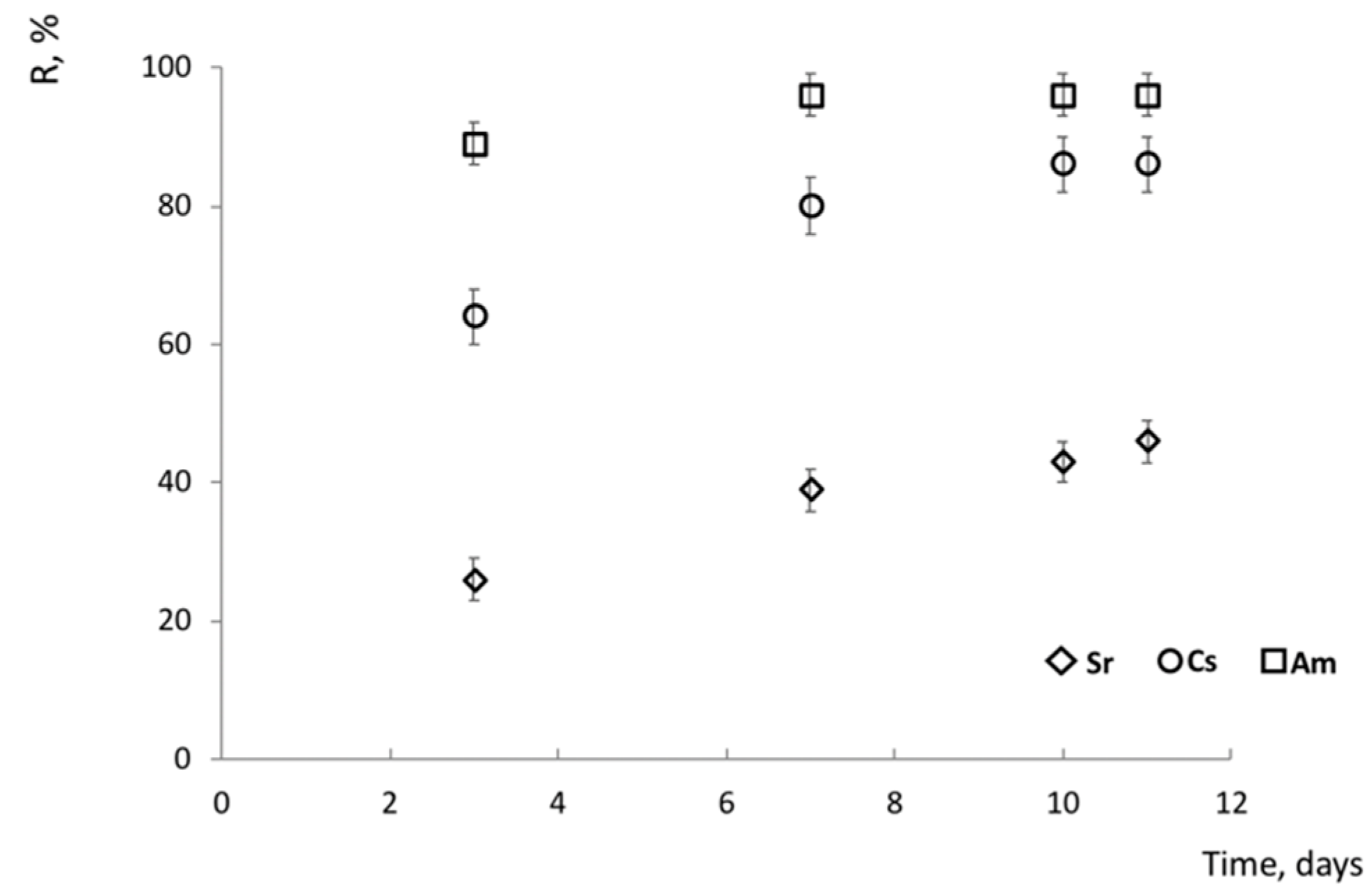
3.2. Sorption Experiments on Polished Discs of Sample R-11
3.3. Spatial Microdistribution of Radionuclides on the Surface of Discs of Sample R-11
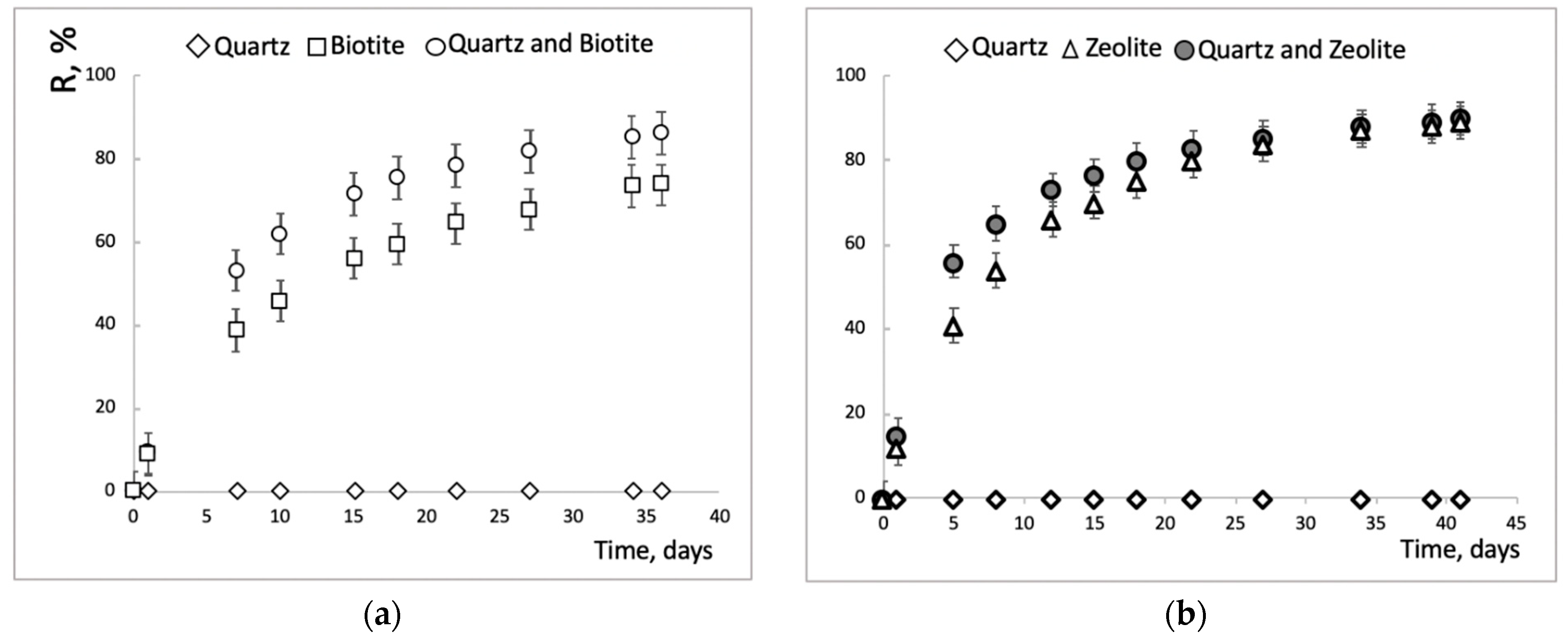
3.4. Sorption Experiments on Crushed Minerals, Imitating the Mineral Phases of Fractured sample R-11
3.5. Modeling of Cesium, Strontium and Americium Sorption on the Fractured Rock Sample
3.5.1. Modeling of Cesium Sorption
3.5.2. Modeling of Strontium Sorption
3.5.3. Modeling of Americium Sorption
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- McKinley, I.G.; Russell Alexander, W.; Blaser, P.C. Development of Geological Disposal Concepts. Radioact. Environ. 2007, 9, 41–76. [Google Scholar] [CrossRef]
- IAEA. Geological Disposal Facilities for Radioactive Waste. Specific Safety Guide; IAEA: Vienna, Austria, 2011; p. 124. [Google Scholar]
- NDA. Geological Disposal, Generic Environmental Safety Case—Main Report; NDA: Didcot, UK, 2016; p. 185. [Google Scholar]
- Pusch, R. Geological Storage of Radioactive Waste; Springer International Publishing: Berlin/Heidelberg, Germany, 2008; Volume 53, ISBN 9783540773320. [Google Scholar]
- Alexander, W.R.; Kickmaier, W.; Vomvoris, S.; Kaku, K.; McKinley, I.G. Nagra’s grimsel URL: From underground testing to the demonstration of disposal systems. In Proceedings of the 10th International Conference on Environmental Remediation and Radioactive Waste Management ICEM’05 2005, Glasgow, Scotland, 4–8 September 2005; pp. 1678–1683. [Google Scholar]
- Hölttä, P. Radionuclide Migration in Crystalline Rock Fractures. Academic Dissertation; University of Helsinki: Helsinki, Finland, 2002; p. 55. [Google Scholar]
- Michael, B. Stephens Forsmark Site Investigation. Bedrock Geology—Overview and Excursion Guide; SKB Report; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2010; p. 52. [Google Scholar]
- Ota, K.; Abe, H.; Kunimaru, T. Horonobe Underground Research Laboratory Project Synthesis of Phase I Investigations 2001–2005, Volume “Geoscientific Research”; JAEA: Ibaraki-Ken, Japan, 2011. [Google Scholar]
- Laverov, N.P.; Yudintsev, S.V.; Kochkin, B.T.; Malkovsky, V.I. The Russian Strategy of Using Crystalline Rock as a Repository for Nuclear Waste. Elements 2016, 12, 253–256. [Google Scholar] [CrossRef]
- Jardin, L.J.; Gupalo, T.A. Development of a Comprehensive Plan for Scientific Research, Exploration, and Design: Creation of an Underground Radioactive Waste Isolation Facility at the Nizhnekansky Rock Massif; ISTC: Moscow, Russia, 2005; p. 474. [Google Scholar]
- Igin, V.; Krasilnikov, V. Creation of System of Final Isolation (Disposal) of Radioactive Waste in the Russian Federation. Mrs Adv. 2020, 5, 275–282. [Google Scholar] [CrossRef]
- Gupalo, V.S. Spatial Characterization of the Physical Process Parameters in Rock Mass during Construction of the Underground Facility for the RW Disposal. Russ. J. Earth Sci. 2019, 19, 670. [Google Scholar] [CrossRef]
- Mahmoudzadeh, B.; Liu, L.; Moreno, L.; Neretnieks, I. Solute Transport in Fractured Rocks with Stagnant Water Zone and Rock Matrix Composed of Different Geological Layers-Model Development and Simulations. Water Resour. Res. 2013, 49, 1709–1727. [Google Scholar] [CrossRef]
- Cvetkovic, V.; Cheng, H.; Widestrand, H.; Byegård, J.; Winberg, A.; Andersson, P. Sorbing Tracer Experiments in a Crystalline Rock Fracture at Äspö (Sweden): 2. Transport Model and Effective Parameter Estimation. Water Resour. Res. 2007, 43, 1–16. [Google Scholar] [CrossRef]
- Neretnieks, I. Channeling with Diffusion into Stagnant Water and into a Matrix in Series. Water Resour. Res. 2006, 42, 1–15. [Google Scholar] [CrossRef]
- Vandergraaf, T.T.; Drew, D.J.; Archambault, D.; Ticknor, K.V. Transport of Radionuclides in Natural Fractures: Some Aspects of Laboratory Migration Experiments. J. Contam. Hydrol. 1997, 26, 83–95. [Google Scholar] [CrossRef]
- Hu, Q.H.; Möri, A. Radionuclide Transport in Fractured Granite Interface Zones. Phys. Chem. Earth 2008, 33, 1042–1049. [Google Scholar] [CrossRef]
- Rozov, K.B.; Rumynin, V.G.; Nikulenkov, A.M.; Leskova, P.G. Sorption of 137Cs, 90Sr, Se, 99Tc, 152(154)Eu, 239(240)Pu on Fractured Rocks of the Yeniseysky Site (Nizhne-Kansky Massif, Krasnoyarsk Region, Russia). J. Environ. Radioact. 2018, 192, 513–523. [Google Scholar] [CrossRef]
- Metcalfe, R.; Milodowski, A.E.; Field, L.P.; Wogelius, R.A.; Carpenter, G.; Yardley, B.W.D.; Norris, S. Natural Analogue Evidence for Controls on Radionuclide Uptake by Fractured Crystalline Rock. Appl. Geochem. 2021, 124, 104812. [Google Scholar] [CrossRef]
- Ticknor, K.V.; Vandergraaf, T.T.; Kamineni, D.C. Radionuclide Sorption on Primary and Fracture-Filling Minerals from the East Bull Lake Pluton, Massey, Ontario, Canada. Appl. Geochem. 1989, 4, 163–176. [Google Scholar] [CrossRef]
- Petrov, V.G.; Vlasova, I.E.; Rodionova, A.A.; Yapaskurt, V.O.; Korolev, V.V.; Petrov, V.A.; Poluektov, V.V.; Hammer, J.; Kalmykov, S.N. Preferential Sorption of Radionuclides on Different Mineral Phases Typical for Host Rocks at the Site of the Future Russian High Level Waste Repository. Appl. Geochem. 2019, 100, 90–95. [Google Scholar] [CrossRef]
- ENVI. ENVI User’s Guide Restricted Rights Notice; ENVI: Broomfield, CO, USA, 2009. [Google Scholar]
- Zhang, M.; Chen, Q.; Li, X.-F.; O’Donoghue, J.; Ruan, S.; Zanzonico, P.; Ling, C.C.; Humm, J.L. Image Deconvolution in Digital Autoradiography: A Preliminary Study. Med. Phys. 2008, 35, 522–530. [Google Scholar] [CrossRef]
- Rodionova, A.A.; Petrov, V.G.; Vlasova, I.E.; Yapaskurt, V.O.; Petrov, V.A.; Poluektov, V.V.; Hammer, J.; Kalmykov, S.N. Digital Radiography for Evaluating the Relative Efficiency of Radionuclide Sorption onto Various Rock Minerals. Radiochemistry 2019, 61, 37–43. [Google Scholar] [CrossRef]
- ImageJ User Guide. Available online: http://imagej.nih.gov/ij/docs/guide/user-guide.pdf (accessed on 25 August 2022).
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Book 6, Chap. A43; US Geological Survey: Lakewood, CO, USA, 2013; p. 497.
- Allard, B.; Beall, G.W. Sorption of Americium on Geologic Media. J. Environ. Sci. Health Part A Environ. Sci. Eng. 1979, 14, 507–518. [Google Scholar] [CrossRef]
- Moulin, V.; Stammose, D. Effect of Humic Substances on Americium (III) Retention onto Silica. MRS Proc. 1988, 127, 723. [Google Scholar] [CrossRef]
- Fröhlich, D.R.; Kaplan, U. Sorption of Am(III) on Clays and Clay Minerals: A Review. J. Radioanal. Nucl. Chem. 2018, 318, 1785–1795. [Google Scholar] [CrossRef]
- Wang, P.; Anderko, A.; Turner, D.R. Thermodynamic Modeling of the Adsorption of Radionuclides on Selected Minerals. I: Cations. Ind. Eng. Chem. Res. 2001, 40, 4428–4443. [Google Scholar] [CrossRef]
- Cornell, R.M. Adsorption of Cesium on Minerals: A Review. J. Radioanal. Nucl. Chem. Artic. 1993, 171, 483–500. [Google Scholar] [CrossRef]
- McKinley, J.P.; Zachara, J.M.; Heald, S.M.; Dohnalkova, A.; Newville, M.G.; Sutton, S.R. Microscale Distribution of Cesium Sorbed to Biotite and Muscovite. Environ. Sci. Technol. 2004, 38, 1017–1023. [Google Scholar] [CrossRef] [PubMed]
- Muuri, E.; Ikonen, J.; Matara-aho, M.; Lindberg, A.; Holgersson, S.; Voutilainen, M.; Siitari-Kauppi, M.; Martin, A. Behavior of Cs in Grimsel Granodiorite: Sorption on Main Minerals and Crushed Rock. Radiochim. Acta 2016, 104, 575–582. [Google Scholar] [CrossRef]
- Baek, W.; Ha, S.; Hong, S.; Kim, S.; Kim, Y. Cation Exchange of Cesium and Cation Selectivity of Natural Zeolites: Chabazite, Stilbite, and Heulandite. Microporous Mesoporous Mater. 2018, 264, 159–166. [Google Scholar] [CrossRef]
- Rajec, P.; Mátel, L.; Orechovská, J.; Šúcha, J.; Novák, I. Sorption of Radionuclides on Inorganic Sorbents. J. Radioanal. Nucl. Chem. 1996, 208, 477–486. [Google Scholar] [CrossRef]
- Elizondo, N.V.; Ballesteros, E.; Kharisov, B.I. Cleaning of Liquid Radioactive Wastes Using Natural Zeolites. Appl. Radiat. Isot. 2000, 52, 27–30. [Google Scholar] [CrossRef]
- Smičiklas, I.; Dimović, S.; Plećaš, I. Removal of Cs1+, Sr2+ and Co2+ from Aqueous Solutions by Adsorption on Natural Clinoptilolite. Appl. Clay Sci. 2007, 35, 139–144. [Google Scholar] [CrossRef]
- Hu, B.; Hu, Q.; Xu, D.; Chen, C. Macroscopic and Microscopic Investigation on Adsorption of Sr(II) on Sericite. J. Mol. Liq. 2017, 225, 563–568. [Google Scholar] [CrossRef]
- Lee, S.S.; Fenter, P.; Park, C.; Sturchio, N.C.; Nagy, K.L. Hydrated Cation Speciation at the Muscovite (001)-Water Interface. Langmuir 2010, 26, 16647–16651. [Google Scholar] [CrossRef]
- Söderlund, M.; Ervanne, H.; Muuri, E.; Lehto, J. The Sorption of Alkaline Earth Metals on Biotite. Geochem. J. 2019, 53, 223–234. [Google Scholar] [CrossRef]
- Marinin, D.V.; Brown, G.N. Studies of Sorbent/Ion-Exchange Materials for the Removal of Radioactive Strontium from Liquid Radioactive Waste and High Hardness Groundwaters. Waste Manag. 2000, 20, 545–553. [Google Scholar] [CrossRef]
- Bellenger, J.P.; Staunton, S. Adsorption and Desorption of 85Sr and 137Cs on Reference Minerals, with and without Inorganic and Organic Surface Coatings. J. Environ. Radioact. 2008, 99, 831–840. [Google Scholar] [CrossRef] [PubMed]
- Zachara, J.M.; Cowan, C.E.; Resch, C.T. Sorption of Divalent Metals on Calcite. Geochim. Cosmochim. Acta 1991, 55, 1549–1562. [Google Scholar] [CrossRef]
- Lehto, J.; Puukko, E.; Lindberg, A.; Voutilainen, M. Batch Sorption Experiments of Cesium and Strontium on Crushed Rock and Biotite for the Estimation of Distribution Coefficients on Intact Crystalline Rock. Heliyon 2019, 5, e02296. [Google Scholar] [CrossRef] [PubMed]
- Godovikov, A.A. Mineralogy, 2nd ed.; Revised and Enlarged; Nedra: Moscow, Russia, 1983. [Google Scholar]
- Bradbury, M.H.; Baeyens, B. A Generalised Sorption Model for the Concentration Dependent Uptake of Caesium by Argillaceous Rocks. J. Contam. Hydrol. 2000, 42, 141–163. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B. Experimental and Modelling Investigations on Na-Illite: Acid-Base Behavior and the Sorption of Strontium, Nickel, Europium and Uranyl; Paul Scherrer Institute: Villigen, Switzerland, 2005. [Google Scholar]
- Bradbury, M.; Baeyens, B. Sorption of Eu on Na- and Ca-Montmorillonites: Experimental Investigations and Modelling with Cation Exchange and Surface Complexation. Geochim. Cosmochim. Acta 2002, 66, 2325–2334. [Google Scholar] [CrossRef]






| Component | Concentration, mg L−1 |
|---|---|
| Cl− | 36 |
| SO42− | 15 |
| CO32− | 18 |
| HCO3− | 79 |
| Na+ | 32.6 |
| K+ | 3.9 |
| Mg2+ | 10.2 |
| Ca2+ | 18.5 |
| Minerals | Quartz | Quartz, K(Na)-Feldspars | Quartz, K-Feldspars | Zeolite | Calcite | Chlorite |
|---|---|---|---|---|---|---|
| Disc (1) | ||||||
| Part of area, % | 15.2 | 31.9 | 19.8 | 12.8 | 10.0 | 10.3 |
| Occupied area, cm2 | 4.9 | 10.2 | 6.4 | 4.1 | 3.2 | 3.3 |
| Disk (2) | ||||||
| Part of area, % | 13.7 | 13.8 | 25.0 | 20.3 | 16.9 | 10.4 |
| Occupied area, cm2 | 4.4 | 4.5 | 8.0 | 6.5 | 5.4 | 3.3 |
| Disk (3) | ||||||
| Part of area, % | 10.9 | 14.6 | 24.0 | 29.0 | 15.0 | 6.5 |
| Occupied area, cm2 | 3.5 | 4.7 | 7.7 | 9.4 | 4.8 | 2.1 |
| System | Kd, mL g−1 | RSE | ||
|---|---|---|---|---|
| Minerals | Monomineral Sorption | Competitive Sorption | ||
| a | quartz | 3.2 | 2.5 | 0.2 |
| biotite | 1.2·103 | 2.7 × 103 | 1.1 | |
| b | quartz | 3.2 | 1.5 | 0.1 |
| zeolite | 4.4·103 | 4.6 × 103 | 1.0 | |
| Ion Exchange Reaction | lgKc | Cation Exchange Capacity, meq kg−1 |
|---|---|---|
| Planar Sites (PS) | 160 | |
| Cs+ + KX = CsX + K+ | 0.5 | |
| Cs+ + NaXb = CsX + Na+ | 1.6 | |
| K+ + NaX = KX + Na+ | 1.1 | |
| Type II sites | 40 | |
| Cs+ + KX = CsX + K+ | 1.5 | |
| Cs+ + NaX = CsX + Na+ | 3.6 | |
| K+ + NaX = KX + Na+ | 2.1 | |
| Frayed Edge Sites | 0.5 | |
| Cs+ + KX = CsX + K+ | 4.6 | |
| Cs+ + NaX = CsX + Na+ | 7.0 | |
| K+ + NaX = KX + Na+ | 2.4 |
| Surface Complexation Sites | Site Densities |
|---|---|
| ≡SsOH | 2 × 10−3 mol kg−1 |
| ≡Sw1OH | 4.5 × 10−2 mol kg−1 |
| ≡Sw2OH | 4.5 × 10−2 mol kg−1 |
| Ion Exchange Sites | Cation Exchange Capacity |
| X− | 200 meq kg−1 |
| Protonation/Deprotonation Reactions | log10K |
| ≡SsOH + H+ = ≡SsOH2+ | 5.5 |
| ≡SsOH = ≡SsO− + H+ | −6.2 |
| ≡Sw1OH + H+ = ≡Sw1OH2+ | 5.5 |
| ≡Sw1OH = ≡Sw1O− + H+ | −6.2 |
| ≡Sw2OH + H+ = ≡Sw2OH2+ | 9.0 |
| ≡Sw2OH = ≡Sw2O− + H+ | −10.5 |
| Ion Exchange Reactions | log10K |
| 2NaX + Sr2+ = SrX2 + 2Na+ | 1.04 |
| 3NaX + Al3+ = AlX3 + 3Na+ | 1.00 |
| Surface Complexation Reactions | log10K |
| ≡Sw2OH + Sr2+ = ≡Sw2OSr+ + H+ | −5.00 |
| Site Surface | Site Density, mol kg−1 |
|---|---|
| ≡SSOH | 2.0 × 10−3 |
| ≡SW1OH | 4.0 × 10−2 |
| ≡SW2OH | 4.0 × 10−2 |
| Cation Exchange Capacity, meq kg−1 | 8.7 × 10−1 |
| Protonation/Deprotonation Reactions | log10K |
| ≡SSOH + H+ = ≡SsOH2+ | 4.5 |
| ≡SSOH = ≡SsOH2+ + H+ | −7.9 |
| ≡SW1OH + H+ = ≡SW1OH2+ | 4.5 |
| ≡SW1OH = ≡SW1O− + H+ | −7.9 |
| ≡SW2OH + H+ = ≡SW2OH2+ | 6.0 |
| ≡SW2OH = ≡SW2O− + H+ | −10.5 |
| Surface Complexation Reactions | log10K |
| ≡SSOH + Am3+ = ≡SSOAm2+ + H+ | 1.8 |
| ≡SSOH + Am3+ + H2O = ≡SSOAmOH+ + 2H+ | −5.4 |
| ≡SSOH + Am3+ + 3H2O = ≡SSOAm(OH)3− + 4H+ | −22.1 |
| ≡SW1OH + Am3+ = ≡SW1OAm2+ + H+ | −0.5 |
| Ion exchange reactions | log10K |
| Am3+ + 3NaX = AmX3 + 3Na+ | 1.477 |
| Am3+ + 1.5CaX2 = AmX3 + 1.5Ca2+ | 1.283 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodionova, A.A.; Petrov, V.G.; Vlasova, I.E.; Rozov, K.B.; Nevolin, I.M.; Yapaskurt, V.O.; Rumynin, V.G.; Kalmykov, S.N. Sorption and Spatial Distribution of 137Cs, 90Sr and 241Am on Mineral Phases of Fractured Rocks of Nizhnekansky Granitoid Massif. Energies 2022, 15, 7440. https://doi.org/10.3390/en15197440
Rodionova AA, Petrov VG, Vlasova IE, Rozov KB, Nevolin IM, Yapaskurt VO, Rumynin VG, Kalmykov SN. Sorption and Spatial Distribution of 137Cs, 90Sr and 241Am on Mineral Phases of Fractured Rocks of Nizhnekansky Granitoid Massif. Energies. 2022; 15(19):7440. https://doi.org/10.3390/en15197440
Chicago/Turabian StyleRodionova, Anastasiya A., Vladimir G. Petrov, Irina E. Vlasova, Konstantin B. Rozov, Iurii M. Nevolin, Vasiliy O. Yapaskurt, Vyacheslav G. Rumynin, and Stepan N. Kalmykov. 2022. "Sorption and Spatial Distribution of 137Cs, 90Sr and 241Am on Mineral Phases of Fractured Rocks of Nizhnekansky Granitoid Massif" Energies 15, no. 19: 7440. https://doi.org/10.3390/en15197440
APA StyleRodionova, A. A., Petrov, V. G., Vlasova, I. E., Rozov, K. B., Nevolin, I. M., Yapaskurt, V. O., Rumynin, V. G., & Kalmykov, S. N. (2022). Sorption and Spatial Distribution of 137Cs, 90Sr and 241Am on Mineral Phases of Fractured Rocks of Nizhnekansky Granitoid Massif. Energies, 15(19), 7440. https://doi.org/10.3390/en15197440






