Islanded Microgrid Restoration Studies with Graph-Based Analysis
Abstract
1. Introduction
1.1. Research Gap and Motivation
1.2. Contribution and Organization
- Propose a systematic formulation for the black start of islanded droop-controlled multi-master microgrids considering incentive-based demand response and non-dispatchable DGs. Apart from our earlier work in [20], no other paper has developed a systematic model for the black start restoration of islanded droop-controlled multi-master microgrids to the best of our knowledge.
- Propose a graphical pre-processing approach that estimates the number of restoration steps needed to optimally restores the system. This helps to ensure that the solution model is as compact as possible.
2. Droop Reference Operation
3. Black Start Restoration Formulation for Islanded Multi-Master Microgrids
3.1. Objective Function
3.2. Initial Sequencing Constraints
3.3. Connectivity Constraints
3.4. Power Flow Constraints
3.5. DG Output Constraints
3.6. Demand Response Loads Constraints
3.7. Other Constraints
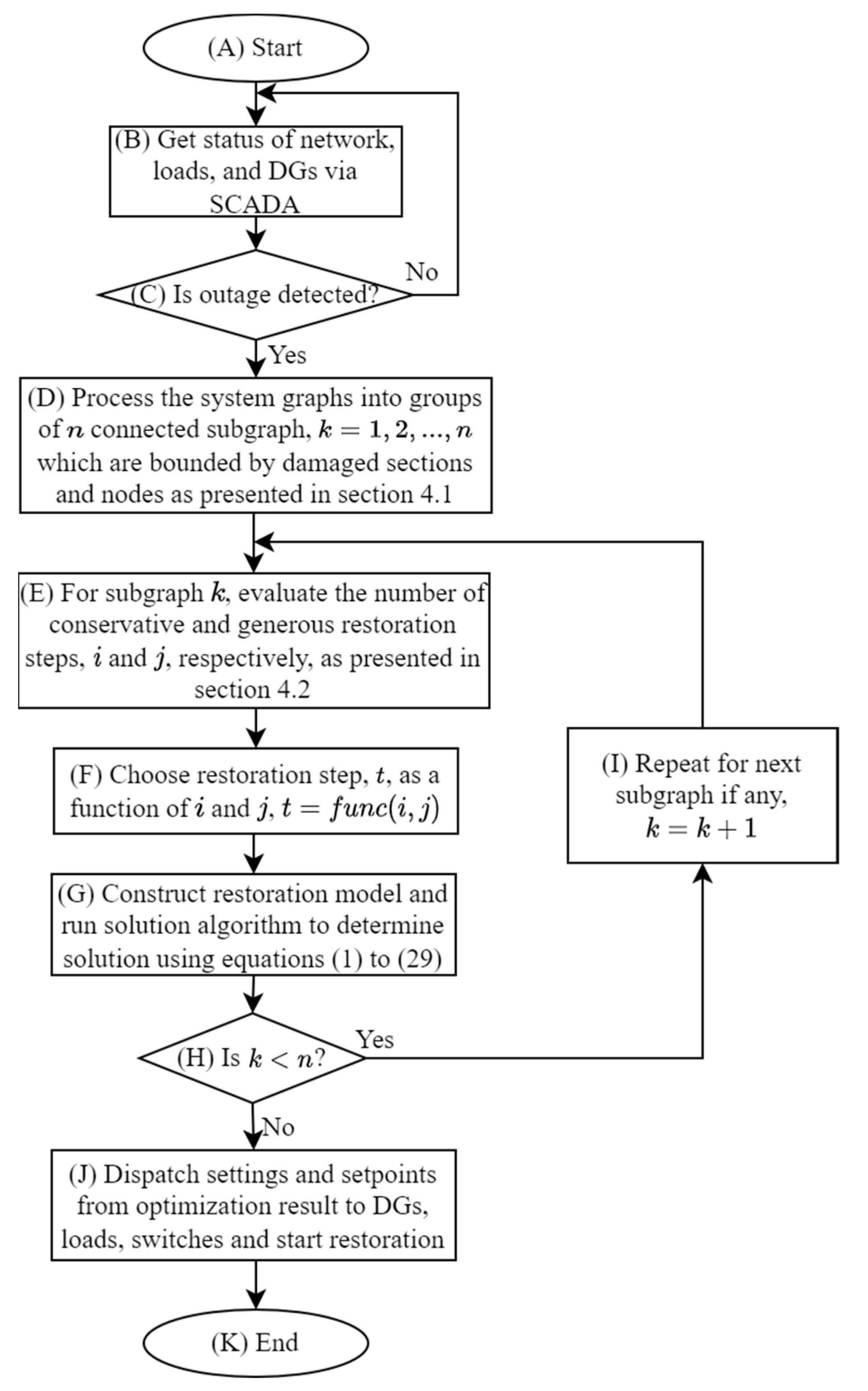
4. Improving Computation by Graphical Evaluation
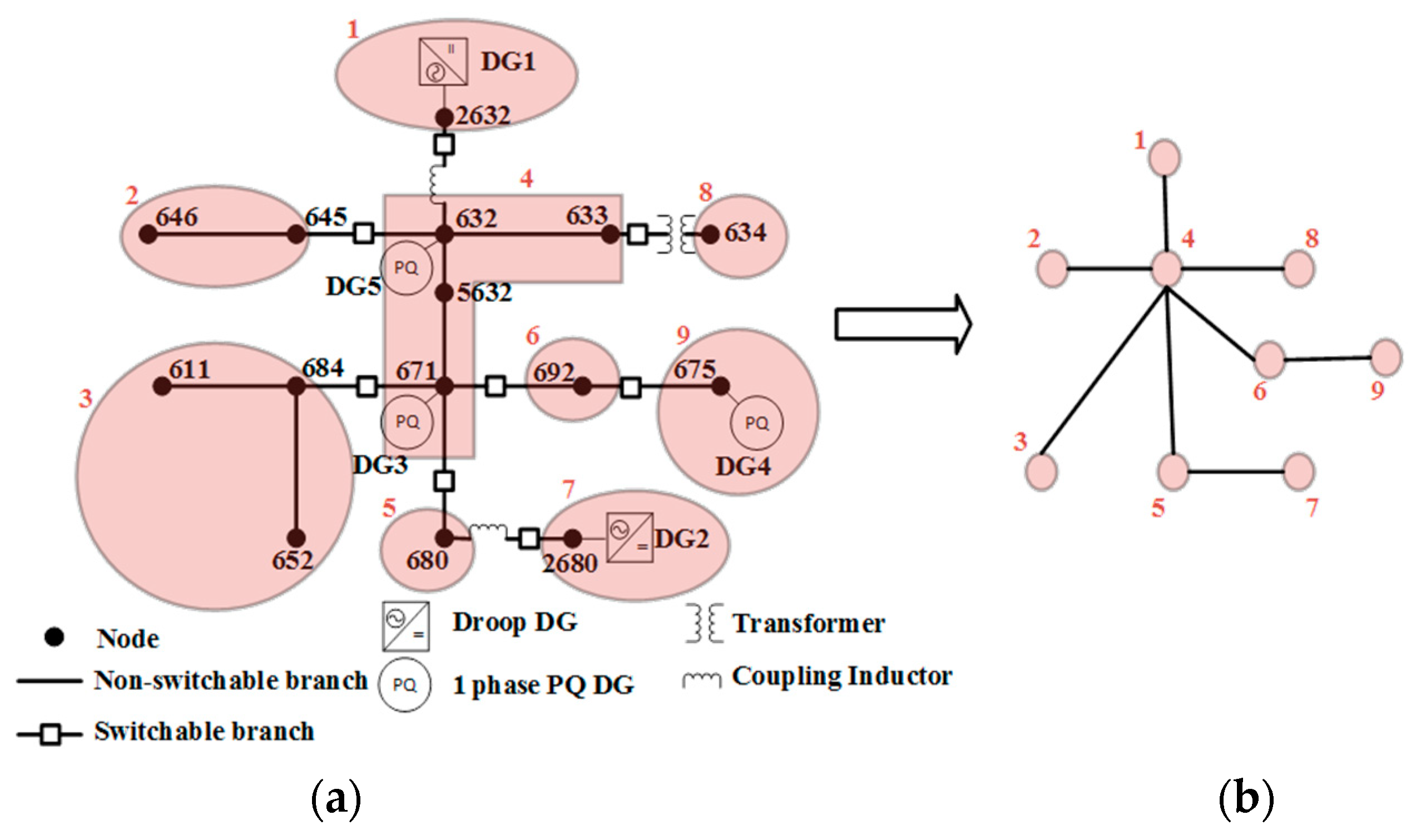
4.1. Network Graph Evaluation
4.2. Estimating the Number of Restoration Steps
4.2.1. Restoration Step Diameter and Radius
4.2.2. Generous and Conservative Restoration Steps Estimates
5. Case Studies and Discussion
5.1. Description of the Base Test System
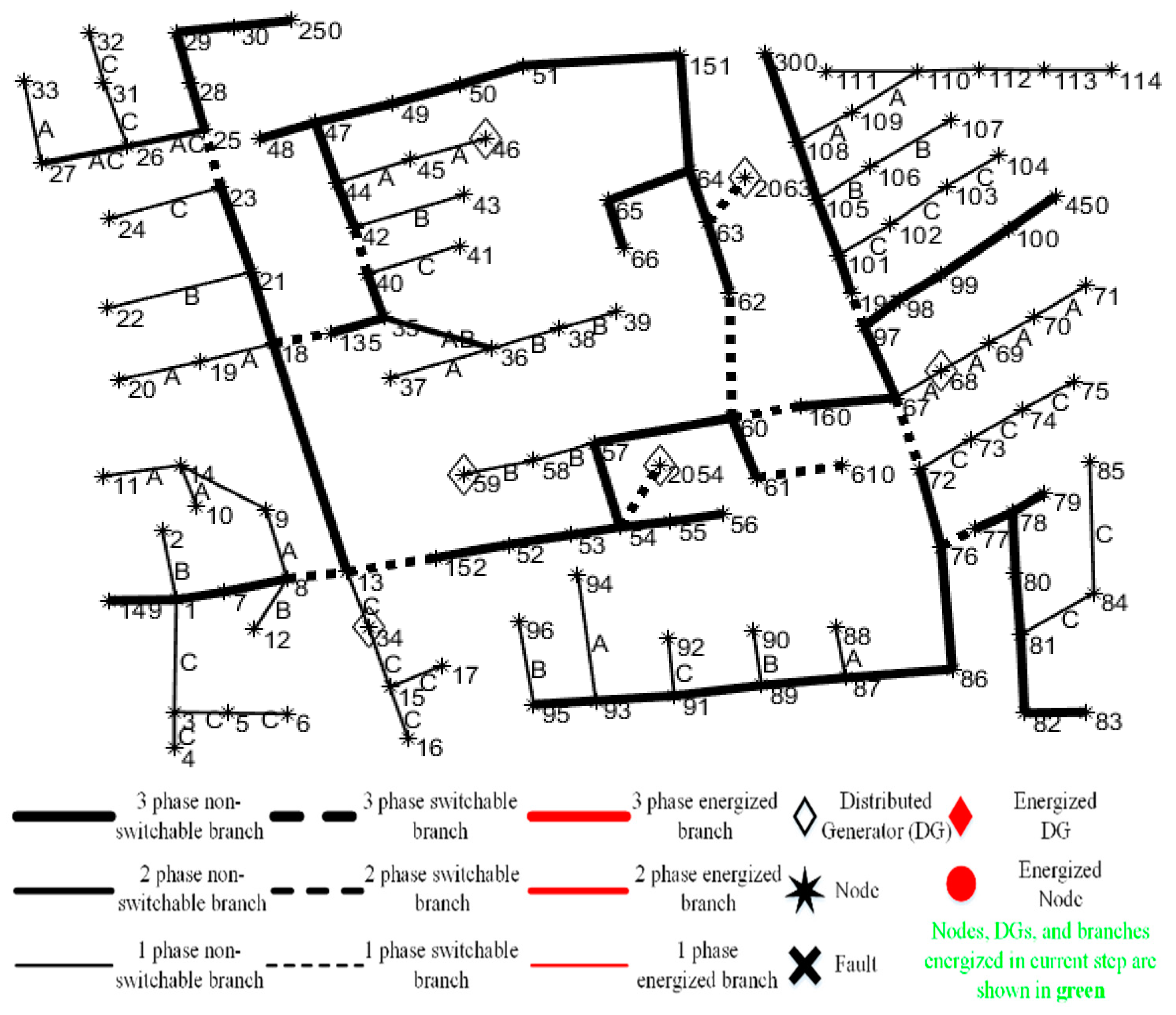
5.2. Restoration Solution
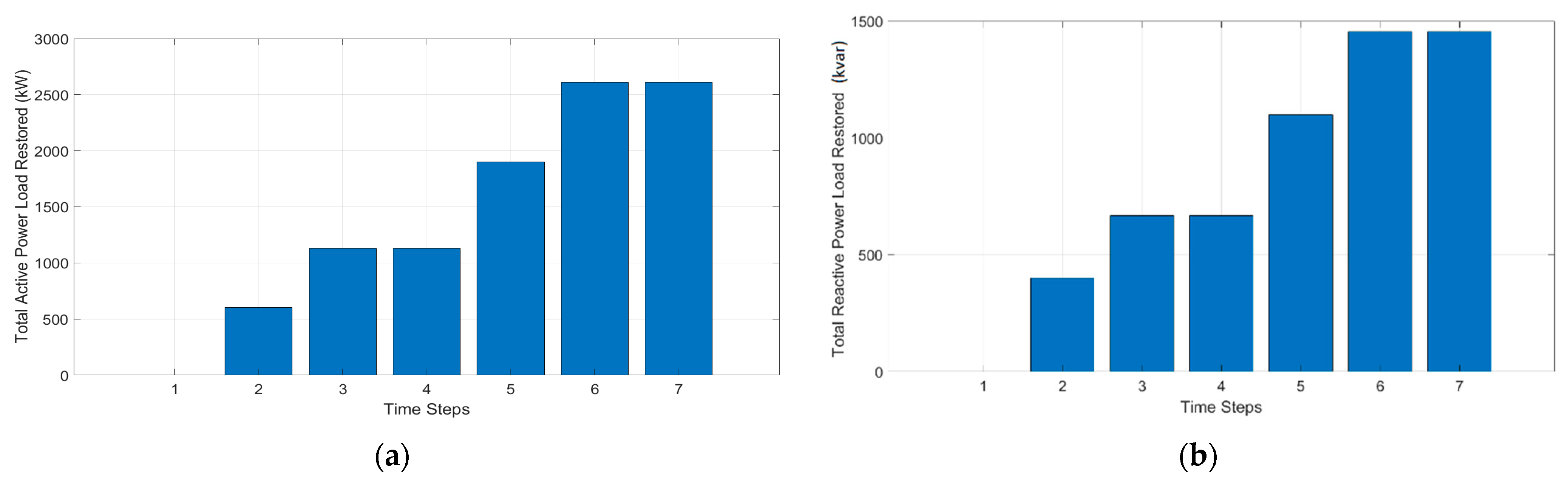
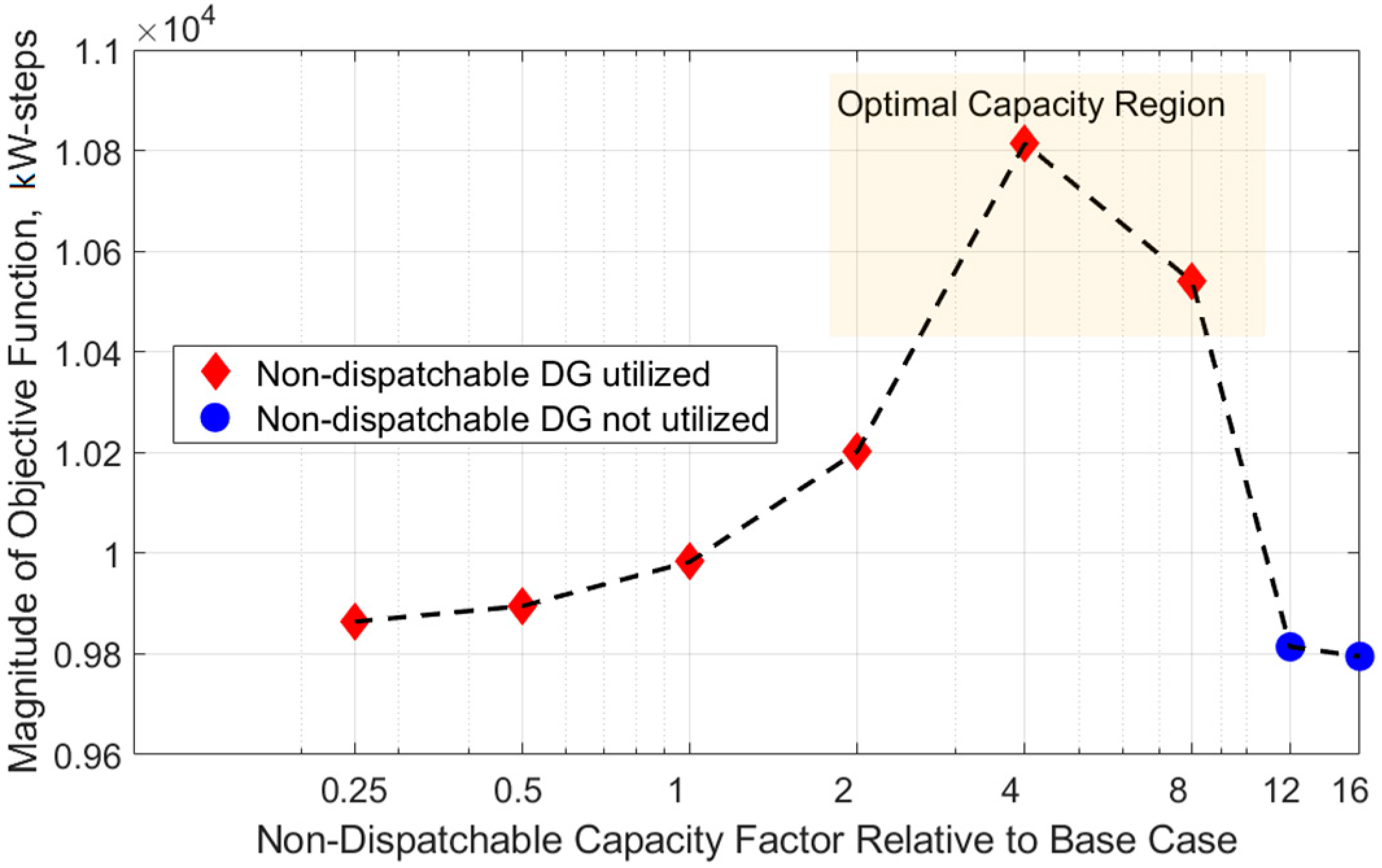
5.3. Non-Dispatchable DG Performance Studies
5.4. Demand Response Loads Performance Studies
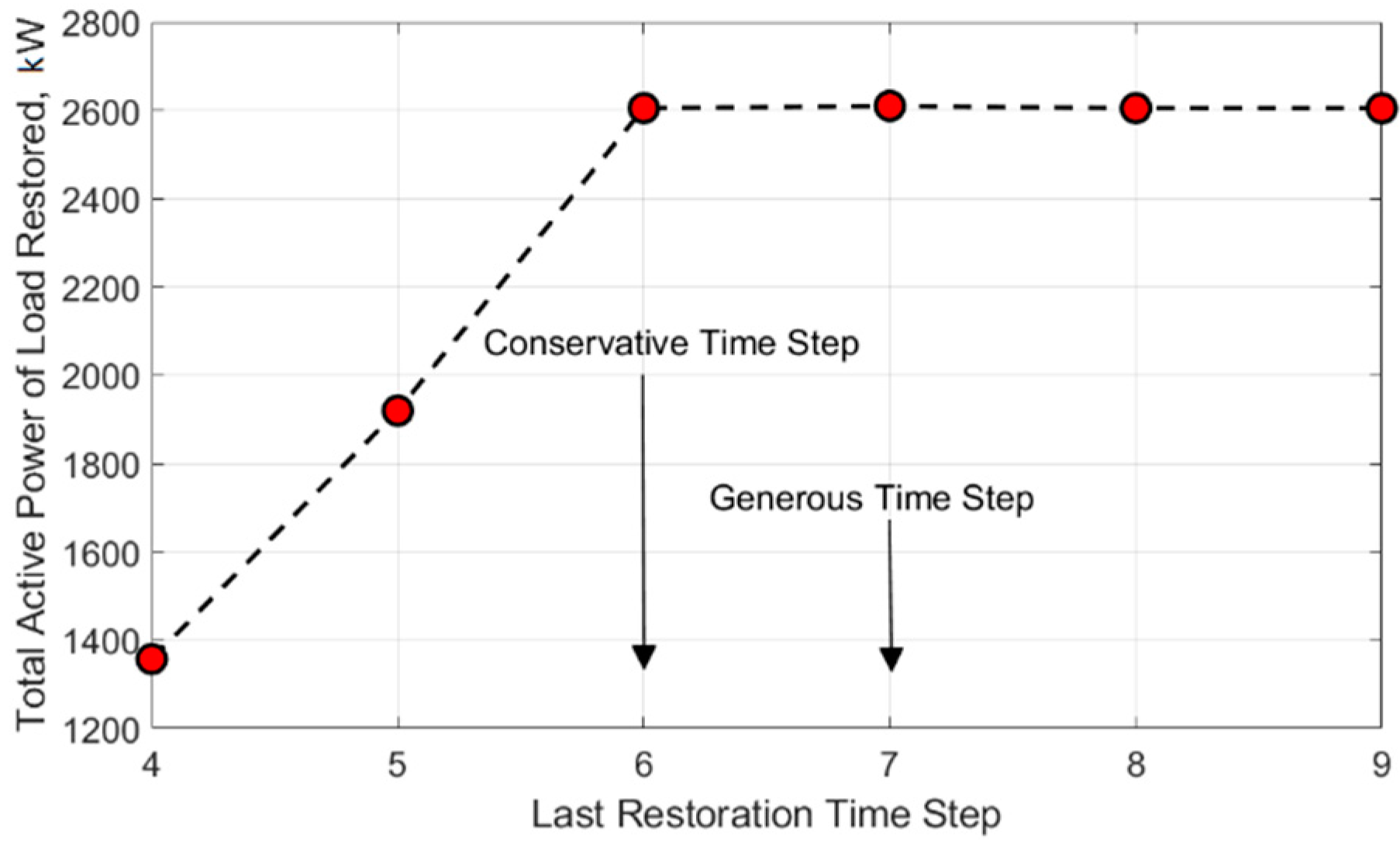
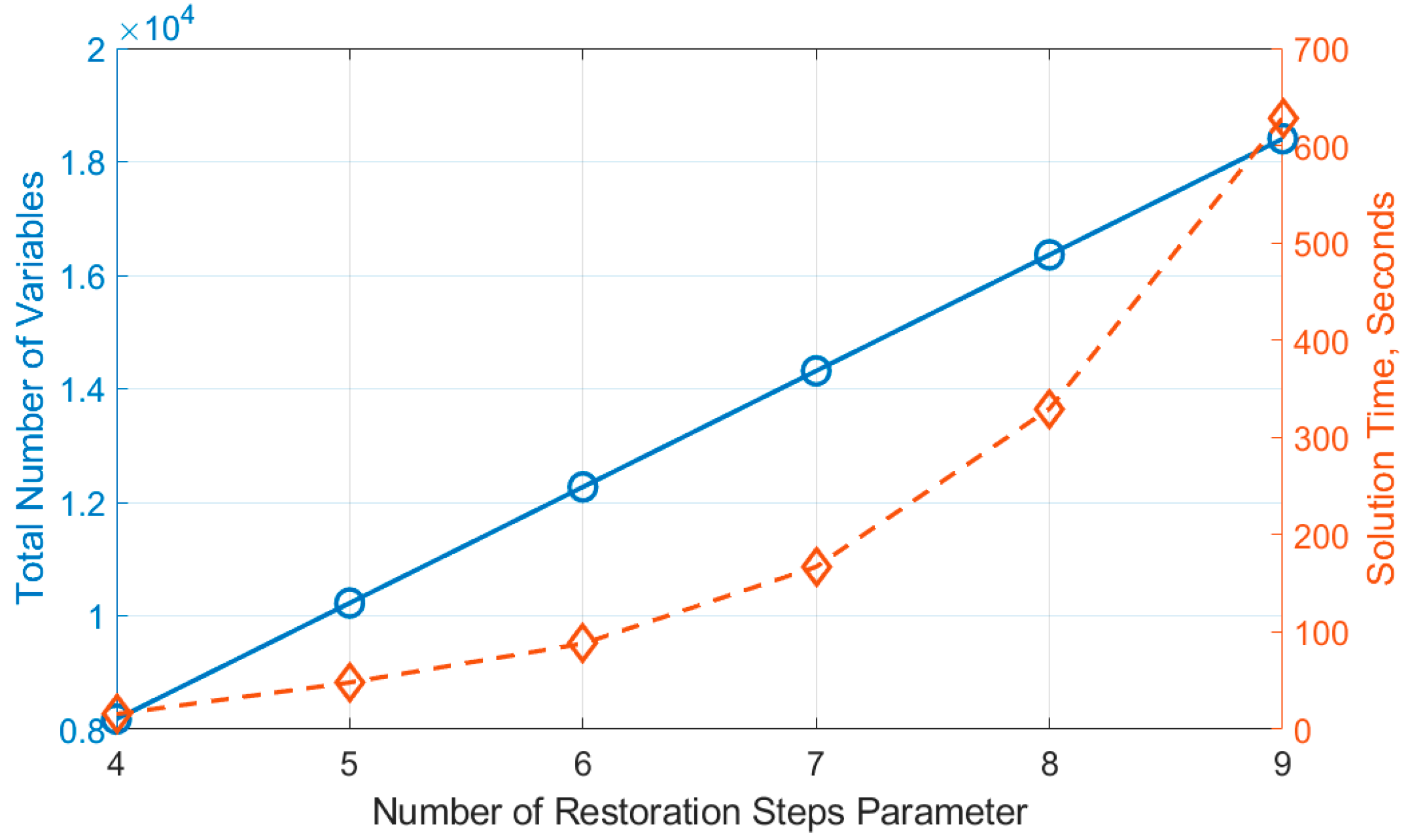
5.5. Effects of Restoration Steps
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Farrokhabadi, M.; Cañizares, C.A.; Simpson-Porco, J.W.; Nasr, E.; Fan, L.; Mendoza-Araya, P.A.; Tonkoski, R.; Tamrakar, U.; Hatziargyriou, N.; Lagos, D.; et al. Microgrid Stability Definitions, Analysis, and Examples. IEEE Trans. Power Syst. 2020, 35, 13–29. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Qiu, F. Resilient Distribution System by Microgrids Formation After Natural Disasters. IEEE Trans. Smart Grid 2016, 7, 958–966. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Wang, J.; Butler-Purry, K.L. Sequential Service Restoration for Unbalanced Distribution Systems and Microgrids. IEEE Trans. Power Syst. 2018, 33, 1507–1520. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Wang, J.; Butler-Purry, K.L. Multi-Time Step Service Restoration for Advanced Distribution Systems and Microgrids. IEEE Trans. Smart Grid 2018, 9, 6793–6805. [Google Scholar] [CrossRef]
- Fu, L.; Liu, B.; Meng, K.; Dong, Z.Y. Optimal Restoration of An Unbalanced Distribution System into Multiple Microgrids Considering Three-Phase Demand-Side Management. IEEE Trans. Power Syst. 2020, 36, 1350–1361. [Google Scholar] [CrossRef]
- Cai, S.; Xie, Y.; Wu, Q.; Xiang, Z.; Jin, X.; Zhang, M. Robust coordination of multiple power sources for sequential service restoration of distribution systems. Int. J. Electr. Power Energy Syst. 2021, 131, 107068. [Google Scholar] [CrossRef]
- Zhang, Q.; Bai, Y.; Wang, X. Optimal Recovery Scheme of Power System Considering Available Resources in Micro-Grids. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22 October 2021; pp. 1297–1302. [Google Scholar]
- Zhu, J.; Yuan, Y.; Wang, W. An exact microgrid formation model for load restoration in resilient distribution system. Int. J. Electr. Power Energy Syst. 2020, 116, 105568. [Google Scholar] [CrossRef]
- Ding, T.; Wang, Z.; Jia, W.; Chen, B.; Chen, C.; Shahidehpour, M. Multiperiod Distribution System Restoration With Routing Repair Crews, Mobile Electric Vehicles, and Soft-Open-Point Networked Microgrids. IEEE Trans. Smart Grid 2020, 11, 4795–4808. [Google Scholar] [CrossRef]
- Abessi, A.; Jadid, S.; Salama, M.M.A. A New Model for a Resilient Distribution System After Natural Disasters Using Microgrid Formation and Considering ICE Cars. IEEE Access 2021, 9, 4616–4629. [Google Scholar] [CrossRef]
- Kim, T.; Santoso, S.; Cunha, V.C.; Wang, W.; Dugan, R.; Ramasubramanian, D.; Maitra, A. Blackstart of Unbalanced Microgrids Using Grid-Forming Inverter with Voltage Balancing Capability. In Proceedings of the 2022 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), New Orleans, LA, USA, 25–28 April 2022; pp. 1–5. [Google Scholar]
- Du, Y.; Wu, D. Deep Reinforcement Learning From Demonstrations to Assist Service Restoration in Islanded Microgrids. IEEE Trans. Sustain. Energy 2022, 13, 1062–1072. [Google Scholar] [CrossRef]
- Du, Y.; Tu, H.; Lu, X.; Wang, J.; Lukic, S. Black-Start and Service Restoration in Resilient Distribution Systems With Dynamic Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3975–3986. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Lopes, J.P.; Moreira, C.L.; Madureira, A.G. Defining control strategies for MicroGrids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 2005, 20, 248–257. [Google Scholar] [CrossRef]
- Che, L.; Khodayar, M.; Shahidehpour, M. Only Connect: Microgrids for Distribution System Restoration. IEEE Power Energy Mag. 2014, 12, 70–81. [Google Scholar]
- Nuschke, M. Development of a microgrid controller for black start procedure and islanding operation. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 439–444. [Google Scholar]
- Bassey, O.; Butler-Purry, K.L. Black Start Restoration of Islanded Droop-Controlled Microgrids. Energies 2020, 13, 5996. [Google Scholar] [CrossRef]
- Chandorkar, M.C.; Divan, D.M.; Adapa, R. Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Ind. Appl. 1993, 29, 136–143. [Google Scholar] [CrossRef]
- Bassey, O. Control and Black Start Restoration of Islanded Microgrids. Ph.D. Thesis, Department of Electrical and Computer Engineering, Texas A&M University, College Station, TX, USA, 2020. [Google Scholar]
- Bassey, O.; Chen, C.; Butler-Purry, K.L. Linear power flow formulations and optimal operation of three-phase autonomous droop-controlled Microgrids. Electr. Power Syst. Res. 2021, 196, 107231. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Gan, L.; Low, S.H. Convex relaxations and linear approximation for optimal power flow in multiphase radial networks. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–9. [Google Scholar]
- Ahmadi, H.; Martı, J.R. Linear Current Flow Equations With Application to Distribution Systems Reconfiguration. IEEE Trans. Power Syst. 2015, 30, 2073–2080. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. IEEE Commun. Surv. Tutor. 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Marcus, D.A. Graph Theory: A Problem Oriented Approach; American Mathematical Society: Washington, DC, USA, 2008. [Google Scholar]
- Herke, S. Graph Theory: 51. Eccentricity, Radius & Diameter. Available online: https://www.youtube.com/watch?v=YbCn8d4Enos (accessed on 20 February 2021).
- PES Test Feeder. 2019. Available online: http://sites.ieee.org/pes-testfeeders/resources/ (accessed on 20 February 2021).



| Sets | |
|---|---|
| The number of elements in set A | |
| Set of branches, switchable and damaged branches, set of switchable branches between bus blocks | |
| Set of all DERs, subset of black start DGs, subset of droop-controlled DGs, subset of damaged DGs, subset of PQ DGs | |
| Set of loads, subset of switchable loads, subset of controllable loads (with demand response), and subset of damaged loads | |
| Set of time steps and | |
| Set of phase nodes, nodes, bus blocks, | |
| Binary Decision Variables (1—Energized, 0—Not Energized) | |
| Energization status of node at time step , , | |
| Energization status of DG at time step , , | |
| Energization status of line at time step , , | |
| Energization status of load at time step , , | |
| Continuous Decision Variables | |
| Used as subscript or superscript to denote variable or parameter in phase a, b, or c, respectively | |
| Active and reactive power output of PQ DG at step and phase , , | |
| Real and imaginary part of three-phase nodal voltage vector of node at step , , | |
| Real and imaginary part of three-phase current vector flowing from node to at step , , | |
| Real and imaginary part of three-phase current vector injected into node at step , , | |
| Voltage droop co-efficient of DG at step , , | |
| Frequency droop co-efficient of DG at step , , | |
| Droop reference active and reactive power output of DG at step , phase , , | |
| Nominal active and reactive power demand of load , phase , at time step , , , | |
| Parameters | |
| A large number chosen deliberately to manipulate the constraint equations | |
| Time interval between restoration steps and is assumed to be a constant value for all intervals | |
| Maximum absolute value of differential active and reactive power output of DG for each time step (DG ramp rate), | |
| Minimum and maximum active power output of DG , | |
| Minimum and maximum reactive power output of DG , | |
| Nominal active and reactive power value of load , phase , at time step (fixed to the same value for all time steps and is independent of whether the load has been restored or not), , , | |
| Impedance of line between nodes and , and | |
| Shunt admittance between nodes and , | |
| Active and reactive power output from the forecast of non-dispatchable PQ DG at step and phase , , , | |
| Label | Node | Type | Per Phase BaseMVA | Per Phase BaseKV | PU Coupling Inductor | Pmax (kW) | Pmin (kW) | Qmax (kvar) | Qmin (kvar) | Phase | Working? | Blackstart? | Ramp Rate % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DG1 | 2054 | Droop | 1 | 2.4018 | 0.3 | 1200 | 0 | 700 | −160 | ABC | Yes | Yes | 60 |
| DG2 | 2063 | Droop | 1 | 2.4018 | 0.3 | 1000 | 0 | 500 | −120 | ABC | Yes | Yes | 60 |
| DG3 | 34 | PQ | NA | NA | NA | 150 | 0 | 100 | −20 | C | Yes | No | 60 |
| DG4 | 46 | PQ | NA | NA | NA | 130 | 0 | 70 | −15 | A | Yes | No | 60 |
| DG5 | 59 | PQ | NA | NA | NA | 120 | 0 | 70 | −10 | B | Yes | No | 60 |
| DG6 | 68 | PQ (Renewable) | NA | NA | NA | 80 | 80 | 40 | 40 | A | Yes | No | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassey, O.; Butler-Purry, K.L. Islanded Microgrid Restoration Studies with Graph-Based Analysis. Energies 2022, 15, 6979. https://doi.org/10.3390/en15196979
Bassey O, Butler-Purry KL. Islanded Microgrid Restoration Studies with Graph-Based Analysis. Energies. 2022; 15(19):6979. https://doi.org/10.3390/en15196979
Chicago/Turabian StyleBassey, Ogbonnaya, and Karen L. Butler-Purry. 2022. "Islanded Microgrid Restoration Studies with Graph-Based Analysis" Energies 15, no. 19: 6979. https://doi.org/10.3390/en15196979
APA StyleBassey, O., & Butler-Purry, K. L. (2022). Islanded Microgrid Restoration Studies with Graph-Based Analysis. Energies, 15(19), 6979. https://doi.org/10.3390/en15196979






