Design of a Load Frequency Controller Based on an Optimal Neural Network

Abstract

A load frequency controller (LFC) is a crucial part in the distribution of a power system network (PSN) to restore its frequency response when the load demand is changed rapidly. In this paper, an artificial neural network (ANN) technique is utilised to design the optimal LFC. However, the training of the optimal ANN model for a multi-area PSN is a major challenge due to its variations in the load demand. To address this challenge, a particle swarm optimization is used to distribute the nodes of a hidden layer and to optimise the initial neurons of the ANN model, resulting in obtaining the lower mean square error of the ANN model. Hence, the mean square error and the number of epochs of the ANN model are minimised to about 9.3886 × 10⁻⁸ and 25, respectively. To assess this proposal, a MATLAB/Simulink model of the PSN is developed for the single-area PSN and multi-area PSN. The results show that the LFC based on the optimal ANN is more effective for adjusting the frequency level and improves the power delivery of the multi-area PSN comparison with the single-area PSN. Moreover, it is the most reliable for avoiding the fault condition whilst achieving the lowest time multiplied absolute error about 3.45 s when compared with the conventional ANN and PID methods.

1. Introduction

With the rapid economic development of human societies, the demand for electrical energy has increased noticeably because it has become a profitable auxiliary service in everyday lifestyles. Typically, the modern power system network (PSN) consists of many areas connected through tie lines and each area has its own generator to meet its own load with load neighbours [1,2,3]. On other side, the fluctional load demand causes an unstable frequency level in the PSN which is considered the major challenge to producing reliable electric energy for consumers [4,5,6,7,8]. The complexity of a multi-area PSN has a high effect on the power transmission line due to the non-linearities of various components of its power system. Therefore, it is quite important to design a decentred control action for individual areas [9,10,11]. A load frequency controller (LFC) is a substantial method to enhance the reliability of the PSN. This is because it maintains the frequency response level and enhances the output power delivery of the PSN when the load demand is changed rapidly by adjusting the speed governor of the generator-area PSN based on its own load demand [12,13,14]. In the early stages, the designers utilised the flywheel governor of a synchronous machine to restore the frequency level of the PSN. Unfortunately, it demonstrated an imperfect method due to the complex function of the LFC [12,15]. Next, an extra part was proposed to adjust the speed governor of the generator PSN based on several techniques. Those techniques can be classified into two branches: classical and advanced branches.

Recently, LFCs based on classical techniques such as a proportional-integral-derivative (PID), root locus, Bode plot and Nyquist diagram were widely used due to their sample implementation. However, they were not able to address the high fluctuation in frequency response under a competitive environment of the load demand specifically for the multi-area PSN owing to their poor dynamic performance [14,16,17,18]. This is because the classical controller is not able to address the high fluctuations of load disturbances due to its nonlinearity. In addition, an extra device is added with the primary part of the LFC controller. Hence, LFCs based on advanced techniques have been used recently. The major advantage of these techniques is that they do not require a high-level of a mathematical modelling to design their applications [19,20,21]. LFCs based on a fuzzy logic control (FLC), which is considered a prefatory type of the advanced techniques, have been applied widely in the past [22]. This is because they have the ability to propose a non-linear mathematical model based on the experimental knowledge of LFC. Therefore, several LFC controllers based on the FLC technique have been proposed, such as in ref. [23,24]. Those types of proposal have been focused on the tuning of membership functions of FLC based on several optimised algorithms. On the other side, the challenge of the experimental knowledge of a multi-area PSN has not been discussed, which is the major issue in designing an accurate LFC. A more advanced method is an artificial neural network (ANN) which predicts a heuristic output signal based on numerical data instead of experimental knowledge. In contrast, it requires training data and a processing strategy to design the optimal LFC model [25,26].

In this paper, an LFC is designed based on an ANN technique for a single-PSN and multi-PSNs. The training data of the proposed ANN model are collected and analysed from a Simulink LFC test, as shown in Figure 1. To address the major challenges of ANN technique, particle swarm optimization (PSO) is utilised. This optimization is divided into two sections: calculating the right structure of ANN technique and optimizing the initial neurons of the ANN model, resulting in the regression of ANN nodes; and the global training error of the ANN model is minimised. Consequently, the frequency response of the LFC system using the optimal ANN technique becomes the most reliable when compared with the conventional methods for the ANN and PID controllers due to its fast-processing time. In addition, it is valid to enhance the performance of the multi-area PSN under a fault condition. The rest of the paper is organised as follows: Section 2 presents the state of art on the optimal use of ANNs in an LFC system. Section 3 introduces the modelling of the LFC application. The principal work of the ANN approach and the PSO algorithm as well as the optimal ANN model are described in Section 4. Section 5 discusses the outcome results. Finally, Section 6 reports the conclusion.

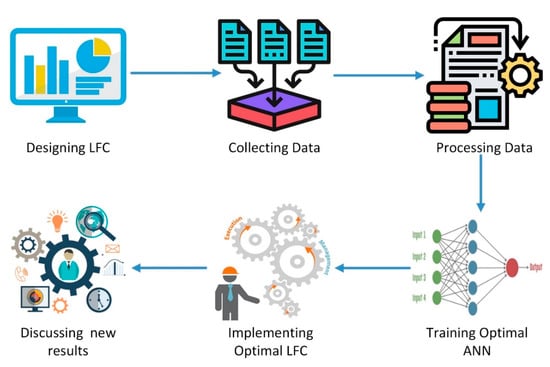
Figure 1. Work strategy procedure.

2. Related Works

Recently, ANN technique has received considerable attention for its use in the design of an optimal LFC system for power system applications. However, the designers have faced several issues when proposing a reliable controller based on this technique due to the diverse training strategy of ANN and the various load operation of PSN. Therefore, researchers have utilised many suggestions to address these issues. Among these, the authors in [27] designed a decentralised LFC based on a standard ANN and FLC technique individually. The proposed controllers are applied on two-area PSNs which are supplied by hydrothermal power generation units. The results demonstrate that these controllers reduce the transit time and minimise the oscillation when compared with conventional integral and PID controller under different step changes of a connected load demand.

In contrast, the authors in [28] designed a central load frequency control for two-area networks based on a back-propagation ANN technique. The input source generation of this power network is a steam turbine. The purpose of this work is to reduce the number of frequency controllers in large area power systems by selecting various different powers for a single ANN model. The results show that the operation work of the proposed ANN controller is better than a conventional controller under different states in terms of oscillation and deviation issues. The authors in [29] presented an active LFC based on a PID controller applied on a micro-grid power network.

This PID controller is tuned using hybrid particle swarm optimization and an artificial neural network. The micro-grid power network is powered by two sources; diesel generation and wind turbines, which provide two electrical stations and two local loads. The results indicate that this proposal minimises the frequency and power variations of the power system under different step-load changes. In addition, they refer to the side-effects of power stability caused by electrical stations and wind turbines. Similarity, the authors in [30] used ANN technique to tune the conventional PI for LFC. Then, it is applied on a multi-area PSN with a thermal power plant. The simulation results prove that the proposed PI-LFC enhances the dynamic frequency response under various load changes compared with the different tunings of conventional PI-LFC methods.

With the same idea, the authors in [31] proposed a decentred load frequency control based on ANN-PID technique for two-area networks. The parameters of the PID controller in this proposed model are adjusted by ANN technique; then it is applied to a steam turbine. The results show that this proposed controller tracks the desired frequency level of the power network, minimises the settling time and reduces overshoot when the connected load is changed at different states.

Due to the wide range of operating conditions of the power network, the standard training ANN technique is not able to predict the large deviation in frequency level when the load demand is changed suddenly. To solve this issue, the authors in [32] used the µ-synthesis technique to train the ANN based on the LFC to achieve a good performance with a simple ANN structure. The controller is simulated for a two-area PSN which is provided by two power generation steam turbines. The results prove that this proposed method has a fast response for the required frequency level of a power system under different operating conditions and various load demand. Similarity, the authors in [33] utilised a generalised neural network technique to optimise ANN-LFC based on a single PSN and a two-area PSN. This method is applied to a steam turbine governor to achieve a desired level frequency under various state conditions. This proposed controller shows that it has ability to work under various step-load changes when compared with a conventional PID controller. This is because it reduces the overshoot of the frequency.

With the same idea, the authors in [34] invested the dynamic neural network based on sigmoid functions, standard fuzzy and wavelet functions for adapting the LFC. They simulated a turbine governing system applied to a two-area power network to test this controller. The results based on this comparative study prove that the proposed ANN controller based on a dynamic wavelet network is a more robust response for adjusting the deviations in the load frequency system when the disturbance happens. In contrast, the authors in [35] proposed an optimal ANN to design the robust LFC using a sliding mode technique. The sliding mode technique is used to update the initial weights of the ANN. Then, it is applied on a two-area power system supplied by two different source generators: a steam turbine and a wind turbine. The results illustrate the adequate effect of the wind turbine when connected with power networks based on load demand test and the validity of this proposed method under several test conditions.

Similarity, the authors in [36] presented decentralised load frequency control based on ANN and GA to enhance the stability of the system. The novelty of this work is to find the optimal data for ANN using GA. The source of the power network is a thermal generator which provides two-area power systems. The results prove that this proposed control is able to hold the terminal voltage magnitude of thermal generator at a specified level under various condition states. Similarity, the authors in [37] adapted the parameters of a PID controller based on ANFIS, ANN and GA techniques to design the LFC for a multi-area PSN. The results prove that this PID-LFC controller enhances the performance of the multi-area PSN under different load conditions. In the same idea, the authors in [38] designed an LFC based on an optimal feedforward ANN using a sliding mode control strategy for a multi-area PSN with thermal plant sources. The structure of the ANN model and its weights are adjusted using a new modified adaptive training rule to enhance the prediction of the ANN technique under various states of operating conditions. The simulation results demonstrate that the proposed method is able to improve the stability of the multi-area PSN under the unmatched disturbance and unknown power integration. Similarity, the authors in [39] used the ANN technique to design the supplementary frequency controller for a single-area PSN. It is trained using reliable training data, and then it is applied to the wind turbine and steam turbine in the PSN of Taiwan. The results show that the proposed ANN can perform the frequency diversion of the experimental test when the fixed-gain controller is adjusted.

In contrast, the authors in [40] proposed a new FLC approach to address the issue of LFC in a multi-area PSN. To train the membership functions of the FLC model, a multilayer perceptron neural network based on the Levenberg–Marquardt algorithm is utilised. Then, Matignon’s stability method is used to test the proposed method under various time disturbances. The results show that the proposed LFC design is able to enhance the stability of the multi-area PSN compared with the conventional FLC.

As noticed from the state of art, several modifications have utilised the hybrid ANN technique to address the variations of load demand in multi-area PSNs, or else it has been used to adjust the parameters of the PID controller. However, they have not used a hybrid ANN based on two-step modifications based on the PSO algorithm to enhance the prediction of an ANN model accurately. Those steps are as follows: the correct structure of the ANN technique is addressed and then the initial neurons of the ANN model are calculated, resulting in the regression of ANN nodes and the global training error of the ANN model is minimised. Hence, the performance of this proposed LFC controller well be enhanced under various operating states. Literature reviews for using ANN technique in LFC design are summarised in Table 1.

Table 1. Summary literature reviews for using ANN technique in LFC design.

Authors	Year	Connected Area	Supplied Unit	Optimised Technique
Chaturvedi et al. [33]	1999	Single and two-area	Steam turbine	Generalised neural network
Oysal et al. [34]	2005	Two-area	Steam turbine	Wavelet function
Shayeghi et al. [32]	2006	Two-area	Steam turbine	µ-synthesis
Demiroren et al. [28]	2010	Two-area	Steam turbine	Back-propagation ANN
Verma et al. [27]	2013	Two-area	Hydrothermal turbine	Standard ANN
Lathwal et al. [36]	2013	Two-area	Steam turbine	Genetic algorithm
Mosaad et al. [37]	2014	Multi-area	Steam turbine	ANFIS, ANN and GA
Qian et al. [35]	2016	Two-area	Steam turbine and wind turbine	Slide-mode
Kumari et al. [31]	2017	Two-area	Steam turbine	PID-ANN
Safari et al. [29]	2019	Two-area	diesel generation and wind turbine	Hybrid PSO-ANN
Prasad et al. [38]	2020	Two-area	Thermal turbine	Sliding mode
Chien et al. [39]	2020	Single-area	Steam and wind turbine	ANN
Ramireddy et al. [30]	2021	Multi-area	Thermal turbine	PI-ANN
Shakibjoo et al. [40]	2022	Multi-area	Thermal turbine	Multilayer ANN based on Levenberg–Marquardt algorithm

3. Modelling of Load Frequency System

Typically, the power system network consists of a turbine, generator, and load demand. The generator produces electrical power for the load demand based on the mechanical power of the turbine. Although several types of connected turbines have been designed, such as hydrothermal and wind turbines, steam turbines are popularly used owing to their higher efficiency and lower cost [21]. The main structure of the typical steam turbine consists of the governor and reheater stage, as explained in Figure 2.

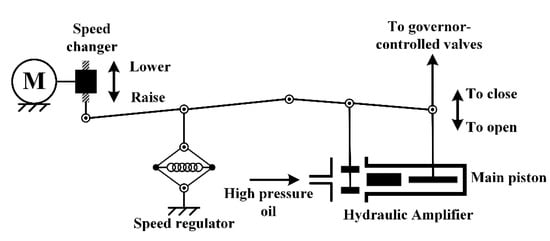
Figure 2. The schematic diagram of a typical steam turbine [30].

The normal operating state of the PSN is that it matches the total power generator with the total load demand. To address this challenge, the speed of connected turbine changes with regard to the load demand of the PSN. This happens when the size value of the input steam is regulated by the governor of the turbine to correspond with the updating load demand. Consequently, the frequency system will reset to a different value which may be offset from the standard frequency value of the PSN. To address this, the proposed control is designed to adjust the speed error of turbine with regard to the load demand. The proposed LFC will enhance the reliability of the PSN by regulating the frequency response level of the system into a desired operation point. The main objective of the LFC is that it resets the speed governor of the turbine based on the load demand. This happens when the LFC senses the power demand of the generator compared with the standard power of the PSN to adjust the turbine speed based on the required steam, as illustrated in Figure 3.

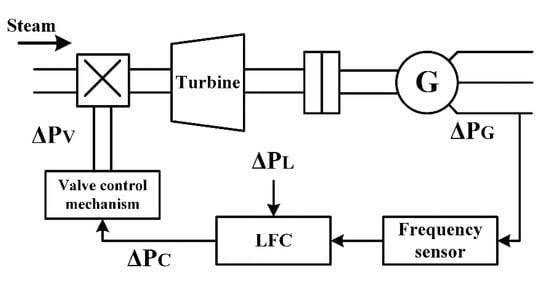
Figure 3. The schematic diagram of LFC [30].

3.1. Modelling of a Single-Area PSN

A model of a single PSN based on LFC is designed based on a transfer function, as proposed in Figure 4. It consists of a steam turbine, governor, synchronous generator and load demand. The speed of the synchronous generator is represented mathematically based on a swing equation, as explained in Equation (1) [22]:

$$\mathsf{\Omega }\left(s\right)=\frac{1}{2Hs}\left(\Delta P_m-\Delta P_e\right)$$

(1)

where Ω(s) is the speed of the synchronous generator, H is the inertia of the synchronous generator, ΔP_m is the historical change of the mechanical power, and ΔP_e is the historical change of the electrical power. Moreover, the modelling of the load demand is represented based on Equation (2):

$$\Delta P_e=\Delta P_L+\Delta \omega$$

(2)

where Δω is the load of a motor and ΔP_L is the load demand of a resistor. The modelling of the steam turbine is proposed based on the mechanical power which refers to the historical change of the steam value, as shown in Equation (3) [23]:

$$\frac{\Delta P_m\left(s\right)}{\Delta P_v\left(s\right)}=\frac{1}{1+{\tau }_g\left(s\right)}$$

(3)

where ΔP_v is the steam value of the turbine and τ_g is the time constant of the governor. Lastly, the speed governor of the steam turbine is modelled based on Equation (4) which is dependent on the historical change in the output power regarding the standard power value of the system.

$$\Delta P_g=\Delta P_{ref.}-\frac{\Delta \mathsf{\Omega }\left(s\right)}{R}$$

(4)

where P_g is the output power of the generator, P_ref. is the standard power of the PSN and R is the speed regulator of the governor. Based on Figure 5, it can be noticed that the relationship between the turbine speed and load demand is an inverse relationship. This happens when the output power changes with regard to the size of the steam turbine, as presented in Equation (5):

$$\Delta P_v\left(s\right)=\frac{1}{1+{\tau }_T}\Delta P_g\left(s\right)$$

(5)

where ${\tau }_T$is the time constant of the steam turbine speed and ΔP_v is the steam valve position of the turbine.

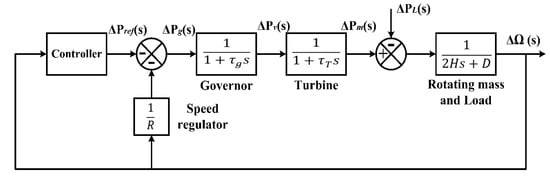
Figure 4. The block-diagram of a PSN based on LFC [30].

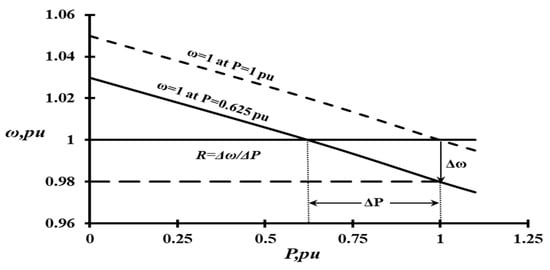
Figure 5. The state space characteristics of a governor.

3.2. Modelling of Two-Area PSN

The block diagram of the two-area PSN based on the transfer function is shown in Figure 6. Then, it is utilised to derive the state space equations of the system to obtain an accurate and valid simulation test. The nomenclature of the multi-area PSN is listed in Table 2. Each area PSN consists of three blocks; governor, turbine, and load demand with its own LFC connected by a tie line. Regarding this transfer function, nine state equations are derived for a two-area interconnected power system. Equations of control input can be expressed in Equations (6) and (7):

$${\dot{u}}_1=G_1\left(e_1\right)=G_1\left(B_1{x}_4+x_9\right)$$

(6)

$${\dot{u}}_2=G_2\left(e_2\right)=G_2\left(B_2{x}_8-x_9\right)$$

(7)

where u₁ and u₂ are the control input variables, e₁ and e₂ are Area 1 and Area 2 of AC frequency errors and B₁ and B₂ are the controller Gain. A state space model has been built with all nine states being fed back to a two-area interconnected power system, as illustrated in the Figure 7.

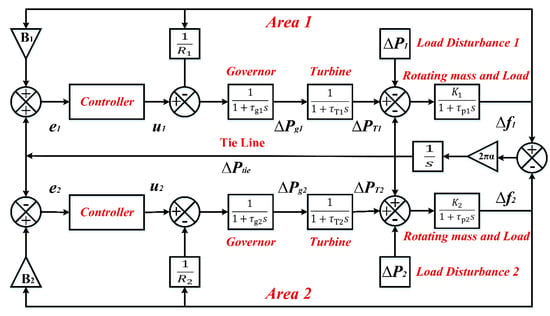
Figure 6. The block diagram of a two-area PSN based on a transfer function.

Table 2. Nomenclatures of the PSN.

Parameters	Definition
Δf	The Frequency Deviation
ΔPtie	Tie Line Power Deviation
R	The Regulations of Governor
G	Controller Gain
u1and u2	Control Inputs in Areas 1 and 2.
ΔPg1 and ΔPg2	Output power Deviations at Governor
ΔPt1 and ΔPt2	Output Deviations at Turbine
ΔP1 = D1	Load Disturbances in Area 1
ΔP2 = D2	Load Disturbances in Area 2.
K1  and K2	Constants of the PSN in Areas 1 and 2.
${\tau }_{P1}$ and ${\tau }_{P2}$	Time Constants of the PSN in Areas 1 and 2.
B1  and B2	Tie Line Frequency Bias at Areas 1 and 2.
A	Synchronizing Coefficient for Tie Line
${\tau }_{g1}$ and ${\tau }_{g2}$	Time Constants of Governor for Areas 1 and 2.
${\tau }_{T1}$ and ${\tau }_{T2}$	Turbine Time Constants for Areas 1 and 2

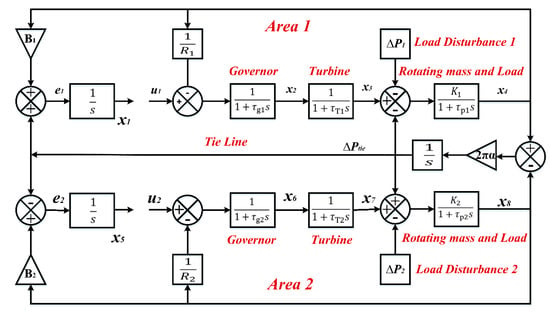
Figure 7. The block diagram of a two-area PSN based on a state space model.

The disturbance input variables are presented as: D₁ = ∆P₁ and D₂ = ∆P₂. The state variables for Area 1 of the PSN are illustrated as Equations (8)–(11):

$$x_1=\int e_1 dt$$

(8)

$$x_2=\Delta P_{g1}$$

(9)

$$x_3=\Delta P_{T1}$$

(10)

$$x_4=\Delta f_1$$

(11)

While the state variables for Area 2 are explained in Equations (12)–(15):

$$x_5=\int e_2 dt$$

(12)

$$x_6=\Delta P_{g2}$$

(13)

$$x_7=\Delta P_{T2}$$

(14)

$$x_8=\Delta f_2$$

(15)

Finally, the tie line is presented in Equation (16):

$$x_9=\Delta P_{tie}$$

(16)

Then, the rotating mass of the turbine and load demand of the PSN are represented in Equations (17)–(20):

$$x_4+{\tau }_{p1}{\dot{x}}_4=K_1\left(x_3-x_9-D_1\right)$$

(17)

$${\dot{x}}_4=\frac{K_1}{{\tau }_{p1}}{x}_3-\frac{K_1}{{\tau }_{p1}}{x}_4-\frac{K_1}{{\tau }_{p1}}{x}_9-\frac{K_1}{{\tau }_{p1}}{D}_1$$

(18)

$$x_8+{\tau }_{p2}{\dot{x}}_8=K_2\left(x_7-x_9-D_9\right)$$

(19)

$${\dot{x}}_8=\frac{K_2}{{\tau }_{p2}}{x}_7-\frac{K_2}{{\tau }_{p2}}{x}_8+\frac{K_2}{{\tau }_{p2}}{x}_9-\frac{K_2}{{\tau }_{p2}}{D}_1$$

(20)

For the steam turbine blocks, state space equations are utilised and presented in Equations (21)–(24):

$$x_3+{\tau }_{T1}{\dot{x}}_3=x_2$$

(21)

$${\dot{x}}_3=\frac{1}{{\tau }_{T1}}{x}_2-\frac{1}{{\tau }_{T1}}{x}_3$$

(22)

$$x_7+{\tau }_{T2}{\dot{x}}_7=x_6$$

(23)

$${\dot{x}}_7=\frac{1}{{\tau }_{T2}}{x}_6-\frac{1}{{\tau }_{T2}}{x}_7$$

(24)

While the governor blocks’ state space equations are illustrated in Equations (26)–(28):

$$x_2+{\tau }_{g1}{\dot{x}}_2=-\frac{1}{R_1}{x}_4+u_1$$

(25)

$${\dot{x}}_2=-\frac{1}{{\tau }_{g1}}{x}_2-\frac{1}{{\tau }_{g1}{R}_1}{x}_4+\frac{1}{{\tau }_{g1}}{u}_1$$

(26)

$$x_6+{\tau }_{g2}{\dot{x}}_6=-\frac{1}{R_2}{x}_8+u_2$$

(27)

$${\dot{x}}_6=-\frac{1}{{\tau }_{g2}}{x}_6-\frac{1}{{\tau }_{g2}{R}_2}{x}_8+\frac{1}{{\tau }_{g2}}{u}_2$$

(28)

Finally, the tie line block of the PSN is presented in Equation (29):

$${\dot{x}}_9=2\pi \alpha x_8-2\pi \alpha x_8$$

(29)

The aforementioned state equations can be expressed as a single vector matrix, as explained in Equation (30).

$$\dot{x}=Ax+Bu+\alpha D$$

(30)

where A is a 9 × 9 dimension square matrix called the state matrix, B and α are 9 × 2 dimension matrices called control and disturbance, respectively, ‘x’ is a 9 × 1 matrix which is the vector of input state space, ‘u’ is a 2 × 1 vector of the LFC and ‘d’ is the 2 × 1 vector of disturbance. The total vectors ‘x’, ’u’, ‘d’ can be combined in the state space formula as in Equations (32) and (33)

$$x={\left[\begin{array}{ccccccccc}{x}_1& x_2& x_3& x_4& x_5& x_6& x_7& x_8& x_9\end{array}\right]}^T$$

(31)

$$u=\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right] D=\left[\begin{array}{c}{D}_1\\ D_2\end{array}\right]$$

(32)

Lastly, the nine state space equations are represented in matrices (33)–(35):

$$A=\left[\begin{array}{ccccccccc}0& 0& 0& B_1& 0& 0& 0& 0& 1\\ 0& \frac{-1}{{\tau }_{g1}}& 0& \frac{-1}{{\tau }_{g1}{R}_1}& 0& 0& 0& 0& 0\\ 0& \frac{K_1}{{\tau }_{p1}}& \frac{-K_1}{{\tau }_{p1}}& 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{1}{{\tau }_{T1}}& \frac{-1}{{\tau }_{T1}}& 0& 0& 0& 0& \frac{1}{{\tau }_{T1}}\\ 0& 0& 0& 0& 0& 0& 0& B_2& 1\\ 0& 0& 0& 0& 0& \frac{-1}{{\tau }_{g2}}& 0& \frac{-1}{{\tau }_{g2}{R}_2}& 0\\ 0& 0& 0& 0& 0& \frac{1}{T_{t2}}& \frac{-1}{T_{t2}}& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{K_1}{{\tau }_{p2}}& \frac{-K_1}{{\tau }_{p2}}& 0\\ 0& 0& 0& 2\pi \sigma & 0& 0& 0& 2\pi \sigma & 0\end{array}\right]$$

(33)

$$B=\left[\begin{array}{cc}0& 0\\ \frac{1}{{\tau }_{g1}}& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& \frac{1}{{\tau }_{g2}}\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]$$

(34)

$$\mathsf{\alpha }=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ \frac{-K_1}{{\tau }_{p1}}& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& \frac{-K_2}{{\tau }_{p2}}\\ 0& 0\end{array}\right]$$

(35)

4. Materials and Method

4.1. Artificial Neural Network

An ANN technique is used as a prediction model to convert the extended handling mechanization into practical knowledge of an operation system [41,42]. The main objective of this model is that it is able to predict the actual output signal of the operation system based on random training data by converting the random collected data into a nonlinear mapping between input nodes and output nodes. It can be divided into two major kinds: feedforward network and feedback network, based on a structure mapping topology. However, the first type is thought to be the most-often utilised since it can be implemented with an extremely strong prediction without requiring a large amount of memory [43]. Based on the number of ANN layers, The feedforward model is also divided into three main types: single-layer, multi-layer, and radial-layer. However, due to its strong capacity for identifying the ideal weighting layer, the multi-layer feedforward ANN is regarded as the most popular variety [44].

The input layer, hidden layer, and output layer make up the three primary layers of the multi-layer feedforward ANN, as depicted in Figure 8. Those layers are connected through neurons based on weights and biases. The values of the summation weights and biases are distributed and calculated mathematically using Equation (36):

$$s_j={\displaystyle \sum }_{i=1}^n{w}_{ij}{x}_j+bj$$

(36)

where, x_j is the value of input signal, $w_{ij}$is the connection weights between the layers, $b_j$ is the weight value of nodes and n is the number of input signals. A back propagation (BP) algorithm is frequently used to learn and update the initial weights of the connected layers while a sigmoid activation function is also frequently employed to identify the output signal. The sigmoid activation function is presented in Equation (37):

$$f\left(s\right)=\frac{1}{1+e^{-sj}}$$

(37)

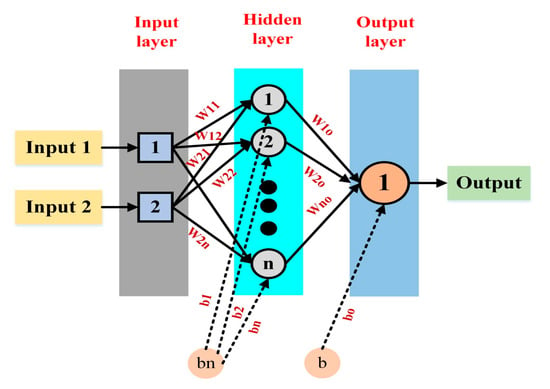
Figure 8. The schematic diagram for an ANN model.

The fundamental idea behind this technique is to enhance ANN performance by adjusting connected weights until an actual output signal results from this processing prediction. The concepts of this technique are dependent on the changing of a declining tendency regarding the step change value in the weighting $\left(\Delta w\right)$ as presented in Equation (38):

$$w_{ji}^l\left(t\right)=\eta w_{ji}^l\left(t-1\right)+\mu \Delta w_{ji}^l\left(t\right)$$

(38)

where $w_{ji}^l\left(t\right)$ is the current training weight and $w_{ji}^l\left(t-1\right)$ is the previous training weight, while $\eta$ is the learning rate and $\mu$ is the momentum coefficient. The BP algorithm’s processing is broken down into two steps: a forward step and a backward step, and throughout each step, the weightings of the ANN model are updated. In each update, the predicting value and actual value are calculated based on the equation of a mean squared error (MSE), as shown in Equation (39):

$$\mathrm{MSE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^m{\left[Y_j\left(i\right)-T_j\left(i\right)\right]}^2$$

(39)

where n is the number of input data and m is the number of output signals, while Y_j(i) and $T_j\left(i\right)$ are the actual output and the predicting output, respectively. The optimum structural topology for the ANN nodes is the first thing that needs to be addressed in order to improve this technique’s prediction. This is due to the fact that the ANN layers with a large number of nodes require lengthy computations, which causes an overfitting regression in the ANN process. In contrast, a small number of nodes in the ANN layers will cause a low computational time with a linear fitting regression [45,46,47,48,49]. Finding the ideal initial weights for the training nodes is the second stage in enhancing the performance of the ANN model. This results in an ANN model training that is quick and has a low MSE value. As mentioned, BP is used to train the ANN model. However, it will fail to find the optimised initial weights due to the size of $\Delta W$. If $\Delta W$ is large, this can lead to rapid training of the ANN model with large step research, thus resulting in a non-converged optimising solution. In contrast, if $\Delta W$ is small, this can lead to slower training with low step research, which mean that the training process is stopped before the minimum error is addressed.

4.2. PSO Algorithm

One of the highest modality-seeking instruments in industrial applications is the PSO algorithm, because it finds an accurate solution in several cases, where each case has the degree of a nominee settlement [50,51]. It is inspired by bird flocking behaviours, when they try to find food based on the experiences and movements of individuals and neighbours. The PSO algorithm finds the optimal solution after four major steps:

Step 1:

It starts to search the random actual value which is chosen based on the stage of a possible case.

Step 2:

The former and following best values for (P_bi) and (P_li) are compared in the same state.

Step 3:

The best and global best solution (G_bi) are adapted and recorded to address the global value by mathematical Equations (40) and (41):

$$V_i^{k+1}=w\times V_i^k+r_1\times c_1\times \left(P_{bi}-X_i^k\right)+r_2\times c_2\times \left(G_{bi}-X_i^k\right)$$

(40)

$$X_i^{k+1}=X_i^k+V_i^k$$

(41)

where, X_i is the current position of each step, V_i is the speed search, i is the optimal value, k is the iterations, w is the inertia weighting, c₁ is the cognitive coefficient, c₂ is the social coefficient and r₁ and r₂ are the random velocity values.

Step 4:

The best fitness value is determined and saved.

This procedure is continued to the iteration end until the PSO optimiser finds the best solution. In this work, the PSO algorithm is used to find the best topology of ANN structure and then the optimal primary weightings of ANN structure are addressed consequently.

4.3. Optimal Neural Network

As noted, a key factor in predicting a reliable output signal from this technique is the ANN model’s training strategy. In this work, two main strategies of training the ANN are used: selecting the right topology and optimizing the initial weight values of the ANN model. Therefore, the PSO algorithm with ANN model is utilised to address these challenges. The schematic diagram of the training ANN model based on the PSO algorithm is shown in Figure 9, while the main parameters of the optimal ANN algorithm are explained in Table 3. Firstly, the PSO optimiser is utilised to find the best topology of the ANN network based on a hybrid algorithm. This hybrid algorithm tests the number of neurons in the hidden layer progressively. This algorithm is explained in Figure 10. The outcome of the algorithm demonstrates that the neural network’s one hidden layer with 23 nodes, which has two inputs and one output, has the lowest training error while also having the optimal number of 93 neurons.

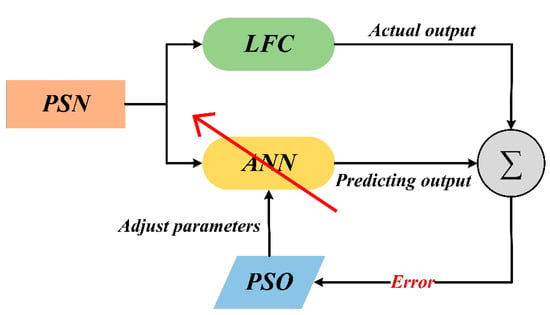
Figure 9. Schematic diagram of training ANN based on PSO.

Table 3. The parameters of an optimal ANN.

Types	Parameters
Input layer nodes of ANN	2
Output layer nodes of ANN	1
Hidden layer nodes of ANN	23
Neurons number of ANN	93
Swarm size of PSO	50
Inertia weighting of PSO	0.75
Cognitive coefficient of PSO	1.15

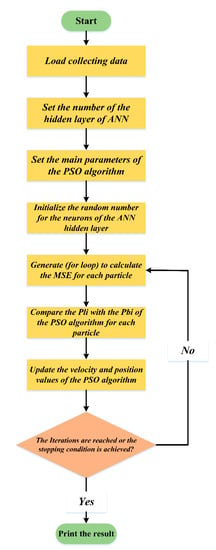
Figure 10. The first proposed algorithm to determine the optimised topology of the ANN.

A hybrid approach based on the PSO and ANN method is then developed in the second modification to discover the optimal starting weights of the ANN model once the topology of the ANN network has been addressed. When the original weight assumptions are corrected, these are proven to enhance the model’s output prediction. To do this, the PSO algorithm and the ANN approach are used. Figure 11 provides a description of the hybrid algorithm’s essential steps. This hybrid algorithm prints the optimal initial weights which are used to train the ANN model using the “nn-tool” command of MATLAB. Consequently, the MSE and number of epochs reduce to 9.3886 × 10⁻⁸ and 25, respectively, when compared with the value of the non-optimal ANN which was about 1.518 × 10⁻⁴ and 34, respectively, as shown in Figure 12. To sum up, Table 4 presents a training strategy for on optimised ANN inverse conventional ANN, while Table 5 explains the rudimentary statistical analysis of the optimal ANN method which confirms that the optimal ANN is the best choice to apply to the LFC system.

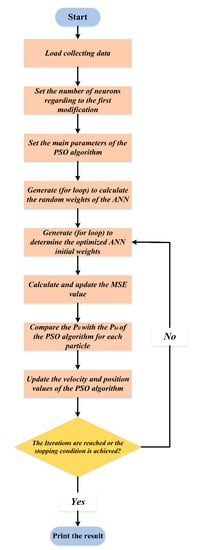
Figure 11. The second proposed algorithm to find the initial neurons of the ANN model.

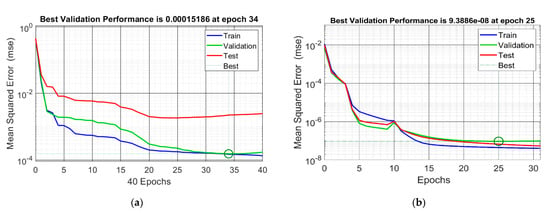
Figure 12. Best validation test of (a) conventional ANN and (b) optimised ANN.

Table 4. A training strategy for on optimised ANN VS conventional ANN.

Model	Number of Epochs	MSE
Optimised training	25	9.3886 × 10−8
Standard training	34	1.518 × 10−4

Table 5. Rudimentary statistical analysis of the optimal ANN.

Training No.	ANN Topology	Number of Neurons	MSE (Average ± STD)
1	2 × 10 × 1	41	0.0001518 ± 1.5 × 10−2
2	2 × 20 × 1	81	0.000881 ± 1.6 × 10−2
3	2 × 30 × 1	121	0.000618 ± 1.2 × 10−2
4	2 × 25 × 1	101	0.000169 ± 2.5 × 10−2
5	2 × 23 × 1	93	9.3886 × 10−8 ± 1.03 × 10−4

5. Results and Discussion

Using MATLAB Simulink, a single-area and two-area based on the optimal ANN, conventional ANN, and conventional PID approaches are constructed to assess and analyse the performance of the proposed LFC system. Section 3 explains the modelling of the single-area PSN and two-area PSN, while Table 6 lists the primary Simulink system parameters for the single-area PSN and two-area PSN based on an unsymmetrical system. Three scenarios of operating conditions are considered: step changing load from 0% to 50% for a single-area, step changing load from 10% to 20% for two areas, and step changing load at unbalanced conditions for two areas.

Table 6. Main parameters of the PSN for single-area and two-area.

Parameters	Values
	Single-Area	Area 1	Area 2
Base power (MVA)	250	1000	1000
The output power of the generation unit (MW)	250	250	400
The standard frequency of the system (Hz)	60	60	60
The speed regulation of the governor (pu)	0.066	0.05	0.0625
The time constant of the governor (s)	0.2	0.2 s	0.3 s
The time constant of the turbine (s)	0.5	0.5 s	0.6 s
The inertia constant of generator (s)	5	5	4
The frequency of sensitive load coefficient D	0.6	0.6	0.9
Frequency base factor B	1	20	16.92

In the first scenario, the step load disturbance, which has been applied on the single-area power network, is rapidly changed from 0% to 50% at 0 s, while the load demand is changed from 0 MW to 125 MW. As seen in Figure 13a, the frequency response of the LFC system utilizing the optimal ANN methodology is the most reliable when compared to the traditional methods for the ANN and PID controllers due to its quick processing time. In addition, compared to the traditional ANN and PID approaches, the transient state’s convergence time for the frequency response is the shortest. While the output delivering power of the system has the least overshoot. Whereas the power of the conventional ANN and conventional PID controllers have a higher overshoot, as presented in Figure 13b. In addition, it proves that the proposed method is able to adjust the power delivery when the mismatched power between the supplied value and demanded value is regulated precisely as shown in Figure 14. However, the effect of the proposed controller is not shown clearly when it is applied on the single-area PSN due to its lower non-linearities of various components of the power system compared with the multi-area PSN.

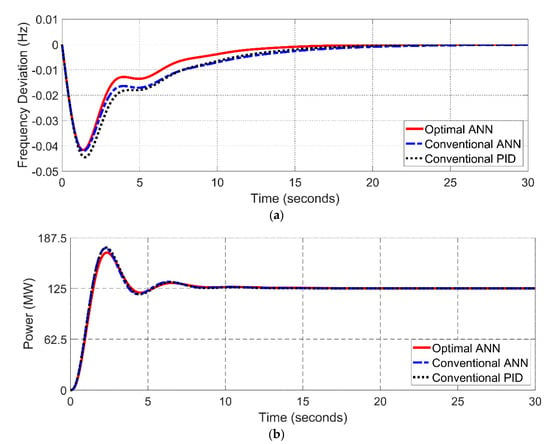
Figure 13. Step change load from 0% to 50% for a single-area PSN; (a) frequency, (b) power.

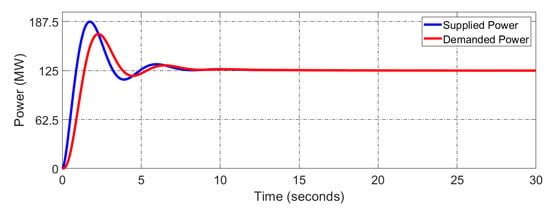
Figure 14. The active power mismatches between the supplied power and demanded power in the single-area.

In the second scenario, the optimal ANN controller is applied on two-area power networks instead of a single-area power network. The step-load disturbance is changed from 10% to 20% at 60 s which is accrued in the second area power system, while the load demand is changed from 100 MW to 200 MW. As shown in Figure 15a,b, the results of this scenario confirm that the optimal ANN controller enhances the performance of the frequency response and the power delivery when it mimics the overshoot, avoids the oscillation and reduces the transient time compared with the conventional ANN and PID controllers under various state conditions. In addition, it achieves the regulated state between the supplied power and demanded power of Area-1, as shown in Figure 16. However, the proposed method does not quickly avoid the damping oscillation for the second power system because it happens directly in this section of the power network, as presented in Figure 17. Whatever, it also achieves the regulated state between the supplied power and demanded power of Area-2, as shown in Figure 18. To show the validation of the optimal ANN (OANN) clearly, several operating conditions are collected and analysed based on Table 7 and Figure 19. Regarding this, the proposed method addresses the variations of the frequency system under different state conditions.

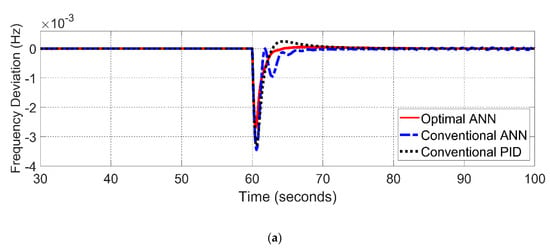
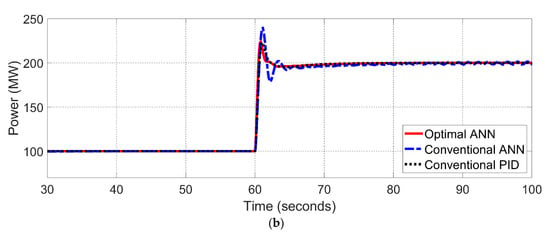
Figure 15. Step change load from 10% to 20% for a two-area PSN (Area 1): (a) frequency, (b) power.

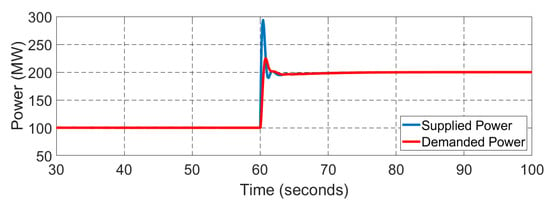
Figure 16. The active power mismatches between the supplied power and demanded power in Area 1.

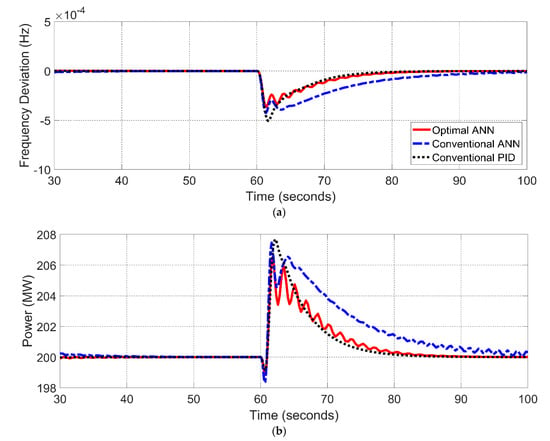
Figure 17. Step change load from 10% to 20% for a two-area PSN (Area 2): (a) frequency, (b) power.

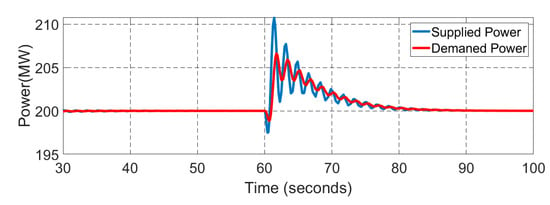
Figure 18. The active power mismatches between the supplied power and demanded power in Area 2.

Table 7. Frequency deviation of LFC for a two-area PSN based on numerical results.

Area 2			Area 1			Time
PID	ANN	OANN	PID	ANN	OANN
0.001061	0.001024	0.000132	0.00145	0.000521	0.000127	50
−0.00212	−0.00077	−0.00056	−0.00388	−0.00035	−0.00015	51
0.000966	0.001487	0.000486	9.27 × 10−5	0.000103	7.90E−05	52
0.000141	0.000826	−8.57 × 10−5	0.000856	0.000333	0.000298	53
−0.00199	−0.00167	−0.00154	4.85 × 10−5	0.000108	2.71 × 10−5	54
0.000754	0.000679	0.000532	0.000347	0.000139	4.75 × 10−5	55
5.45E−05	−0.00044	3.66 × 10−5	−0.00012	−8.58 × 10−5	−1.00 × 10−5	56
−0.00128	−0.00033	−0.00042	0.000112	0.000101	9.28 × 10−5	57
−0.00068	−0.00134	−0.00129	−2.57 × 10−5	6.92 × 10−5	1.01 × 10−5	58
−0.00819	−0.00174	−0.00149	−9.38 × 10−4	−0.00015	−0.00013	59
0.001967	0.001988	0.001617	−0.00019	−0.0002	−0.00015	60
−0.00066	−0.00051	−0.00038	−3.61 × 10−5	−9.54 × 10−5	−2.94 × 10−6	61
0.002452	0.002664	0.002146	5.09 × 10−5	5.00 × 10−5	8.87 × 10−6	62
−0.00908	−0.00491	−0.00415	1.21 × 10−5	5.95 × 10−5	9.07 × 10−6	63
0.009239	0.001811	0.000152	−0.00022	−9.25 × 10−5	−1.43 × 10−5	64
−0.00114	−0.00089	−0.00014	−0.00013	2.85 × 10−5	−1.73 × 10−5	65
−0.0092	−0.00124	−0.00085	−0.00018	−0.00019	−9.52 × 10−5	66
−0.00068	0.000161	−0.00014	5.84 × 10−5	4.98 × 10−5	4.84 × 10−5	67
0.000527	−0.00068	−0.00036	−0.0001	−0.00013	−6.32 × 10−5	68
0.003385	0.002645	0.002278	0.000158	0.000143	8.62 × 10−5	69
−0.00667	−0.00252	−0.00214	0.000322	0.000226	0.000219	70

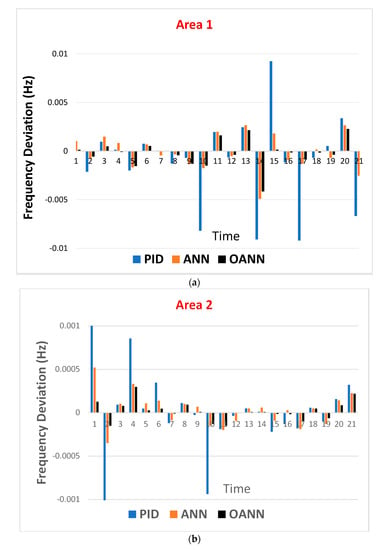
Figure 19. The frequency deviation of a LFC for a two-area PSN based on numerical results for optimal ANN compared with conventional ANN and conventional PID for; (a) Area-1, (b) Area-2.

To test the validity of the optimal ANN controller under a fault condition, a third scenario is designed. This scenario is proposed based on the unbalanced conditions when the step load disturbance is changed randomly with a power amplitude signal of 0.05 pu and a frequency scale variation of 50 (rad/s), while the load demand is changed randomly between 10 MW and 100 MW. As noticed from the zoomed-in section in Figure 20, the proposed method is the most accurate to address the optimal steady state value of frequency respace and power delivery compared with the conventional ANN and PID methods under various state conditions, being close to zero frequency deviation. Moreover, it demonstrates that the proposed method is able to adjust the power delivery under the fault condition due to the regulation of the mismatched power of the supplied value and demanded value as shown in Figure 21. However, it drifts away from zero point at the negative side. This is because the system was in an unbalanced state when we simulated the step load disturbance, and changed randomly for the fault condition. Finally, the optimal ANN controller is tested under an unmatched load demand to assess it at a randomly slight time change. The simulation started with 0.4 pu for Area 1 and Area 2, then the first area disturbance is changed to 0.8 pu, 0.2 pu, 0.6 pu, 0.2 pu, at 20 s, 40 s, 60 s, 80 s, respectively, while the second area disturbance is changed to 0.2 pu, 0.7 pu, 0.3 pu, 0.5 pu, at 20 s, 40 s, 60 s, 80 s, respectively. As shown in Figure 22, the frequency responses of Area 1 and Area 2 were reliable to avoid these random load disturbances when it was changed nonlinearly at various times. In addition, the tile line power of the PSN was stable at different states. To access the proposed method numerically, an integral of time multiplied absolute error (ITAE) formula is used (42) [14];

$$\mathrm{ITAE}={{\displaystyle \int }}_0^{t_{sim}}(\left|\Delta f_1\right|+\left|\Delta f_2\right|+\left|\Delta P_{tie}\right|.t.dt$$

(42)

where $\Delta f_1$ and $\Delta f_2$ are the frequency deviation for Area 1 and Area 2, respectively, $\Delta P_{tie}$ is the tie line power deviation, while tsim is the simulation time. Regarding the calculation of this formula, the ITAE of the optimal ANN method is achieved at about 3.45 s, whilst the conventional ANN and conventional PID controllers are reached to 7.89 s and 10.12 s respectively, as depicted in Table 8. This is because that the proposed ANN method has a low MSE with a smaller number of epochs to predict the accurate signal in a short processing time. As a result, it achieves low power losses as depicted in various scenario tests, resulting in obtaining a higher efficiency.

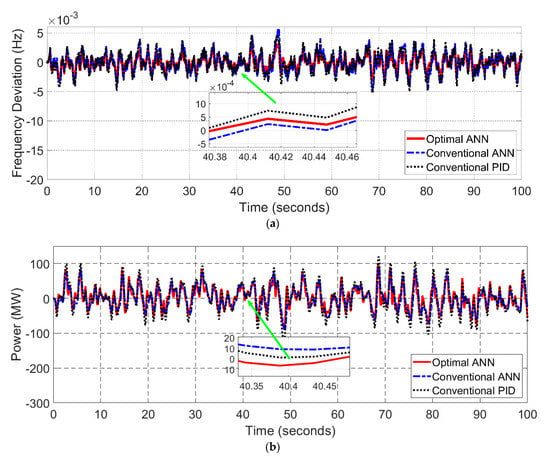
Figure 20. Step change load at an unbalance condition for a two-area PSN; (a) frequency, (b) power.

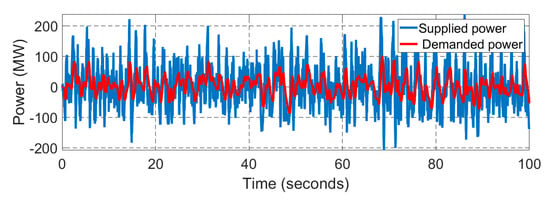
Figure 21. The active power mismatches between the supplied power and demanded power in Area 2 under fault condition.

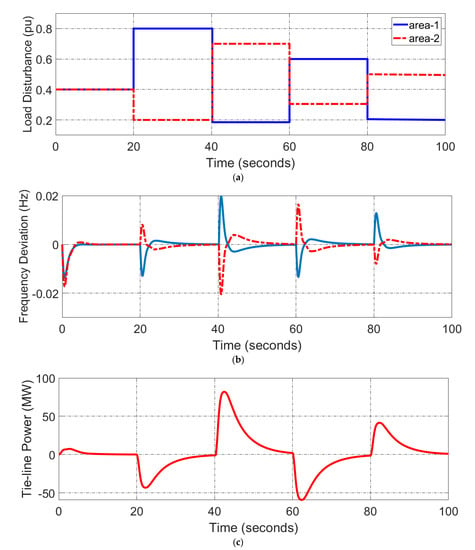
Figure 22. The response of optimal ANN for: (a) load disturbance, (b) frequency deviation, (c) tie line power.

Table 8. ITAE for optimal ANN, conventional and PID methods.

Method	ITAE
Optimal ANN	3.45 s
Conventional ANN	7.89 s
Conventional PID	10.12 s

6. Conclusions

An optimal neural network technique based on particle swarm optimization has been utilised to design the load frequency controller for a power system network. To sum up, the PSO algorithm has been used to adjust the main parameters of the ANN model which are the number of hidden layer nodes and the initial weightings of layers. Hence, the mean square error and the number of epochs of the ANN model are minimised to about 9.3886 × 10⁻⁸ and 25, respectively. As a result, it restores the frequency level and improves the power delivery of a multi-area PSN when compared with a single-area PSN. In addition, it avoids the fault condition compared with the conventional ANN and PID methods. Moreover, it achieved the lowest time multiplied absolute error of about 3.45 s, whilst the conventional ANN and conventional PID controllers reached 7.89 s and 10.12 s, respectively. In future research, it is highly recommended to apply the optimal ANN technique to an experiential multi-area PSN with a micro-grid such as a New England real test system (IEEE 39 bus system).