Study of Centrifugal Stiffening on the Free Vibrations and Dynamic Response of Offshore Wind Turbine Blades
Abstract
:1. Introduction
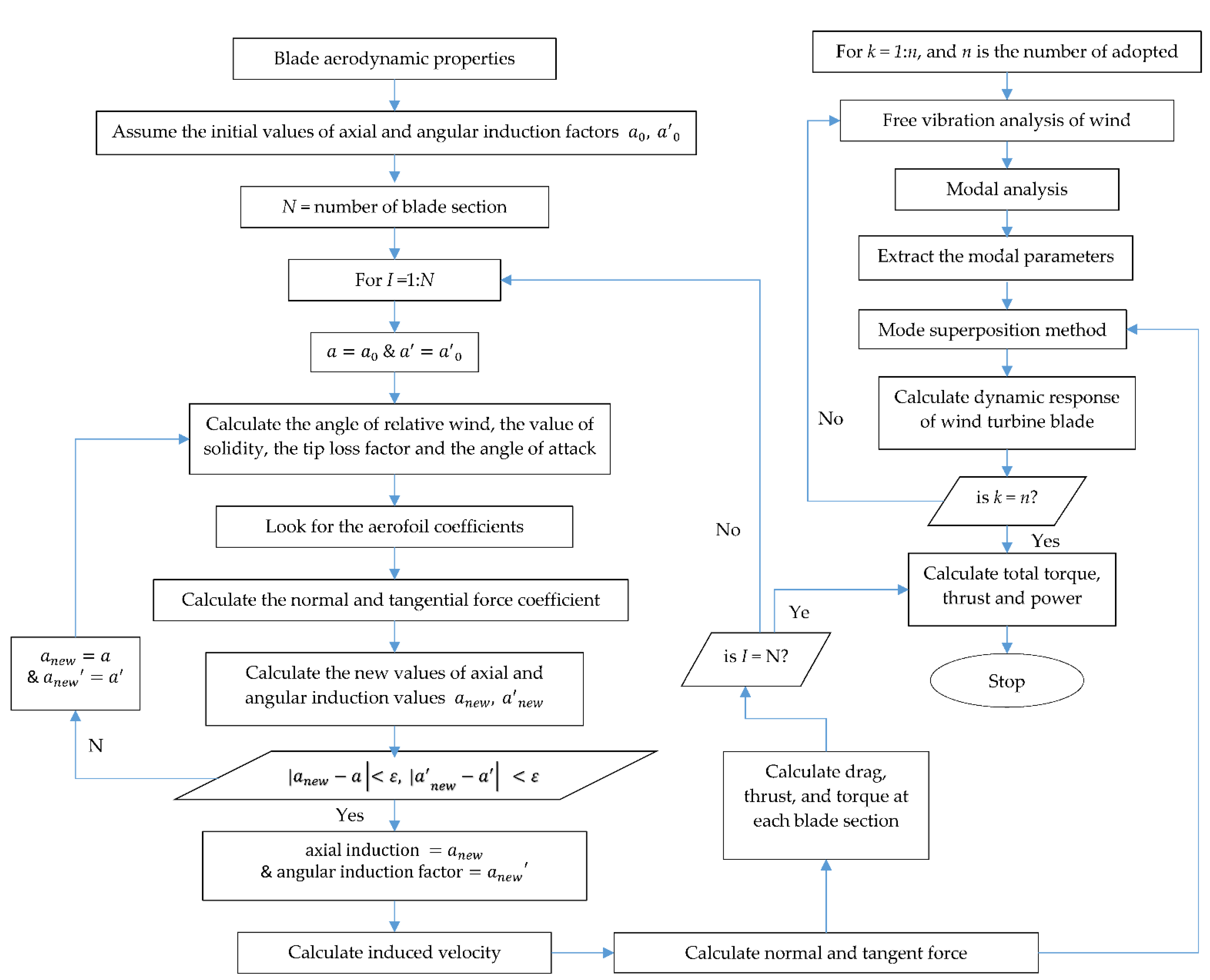
2. Methods in Modelling
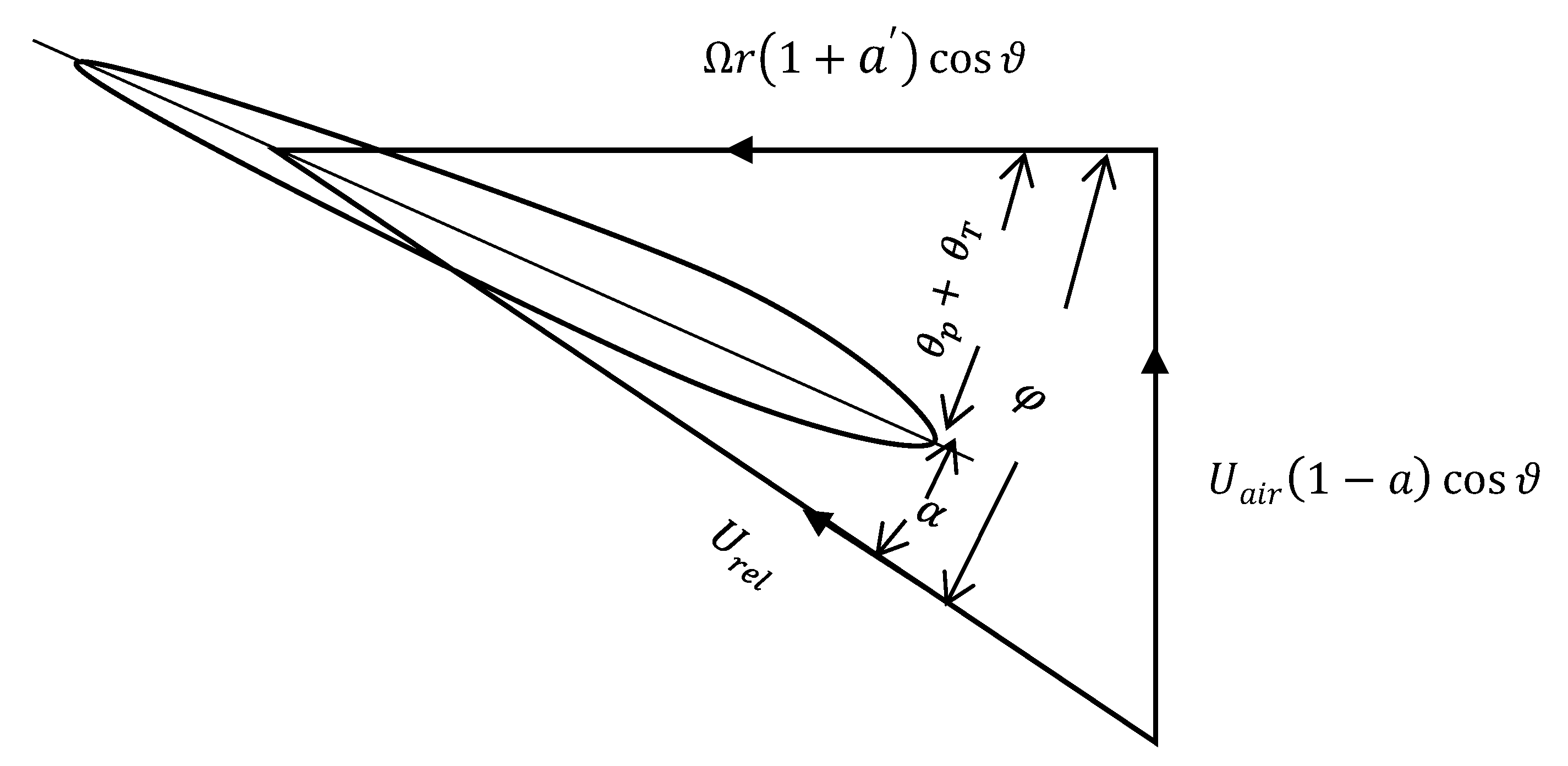
2.1. Aerodynamic Modelling
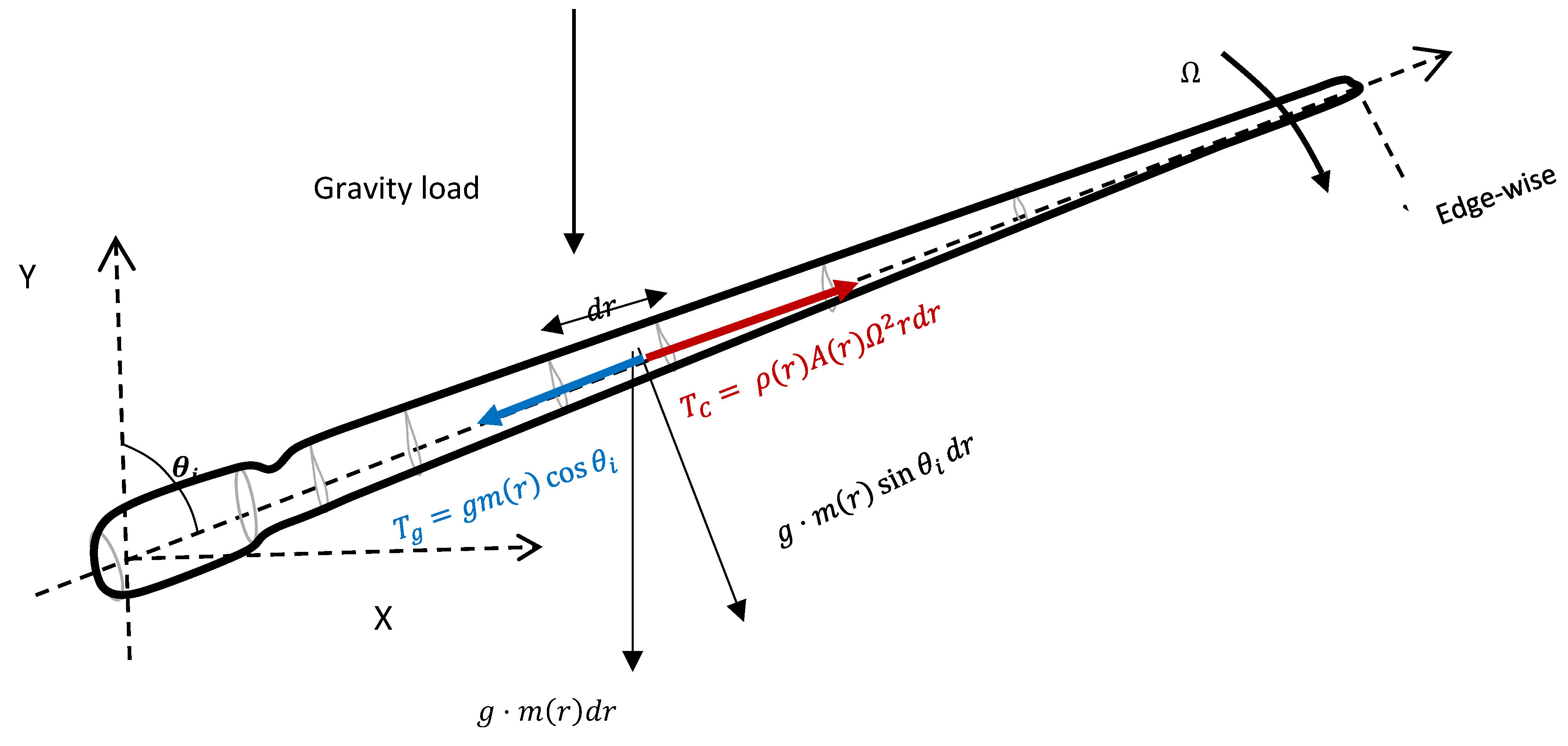
2.2. Gravitational Load
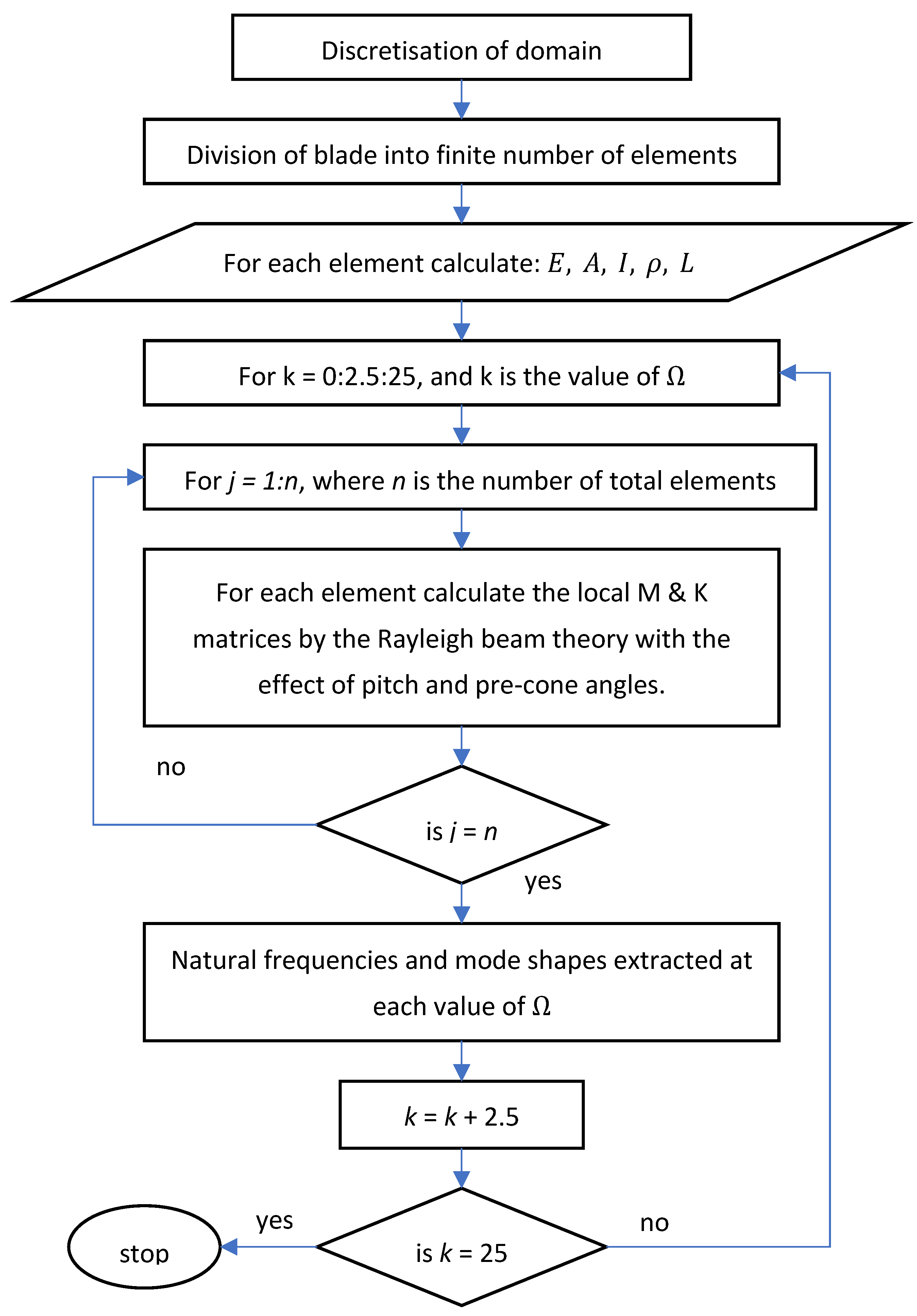
2.3. Blade Structural Model
3. Blade Dynamic Response
4. Effect of Rotation Speed on the Blade Modal Characteristics
5. Effect of Rotation Speed on the Blade Dynamic Responses
6. Conclusions
- The results obtained quantify how increasing the angular velocity of the blade impacts the natural frequencies and corresponding mode shapes. It was found that the centrifugal force effects for a speed of rotation of 12.1 RPM had a significant effect on the flap-wise deflection, where the dynamic deflection decreased by 21.5%. However, there was less impact in the edge-wise direction, where the dynamic deflection decreased by 8.2%. These results can be included in the analysis of turbine blades’ behaviour to increase offshore HAWTs’ reliability.
- The results from the study demonstrate that the angular speed directly affects the modal features, which directly leads to a decrease in the dynamic response. Additionally, the results show that the angular velocity affects behaviour in the flap-wise direction more than in the edge-wise direction.
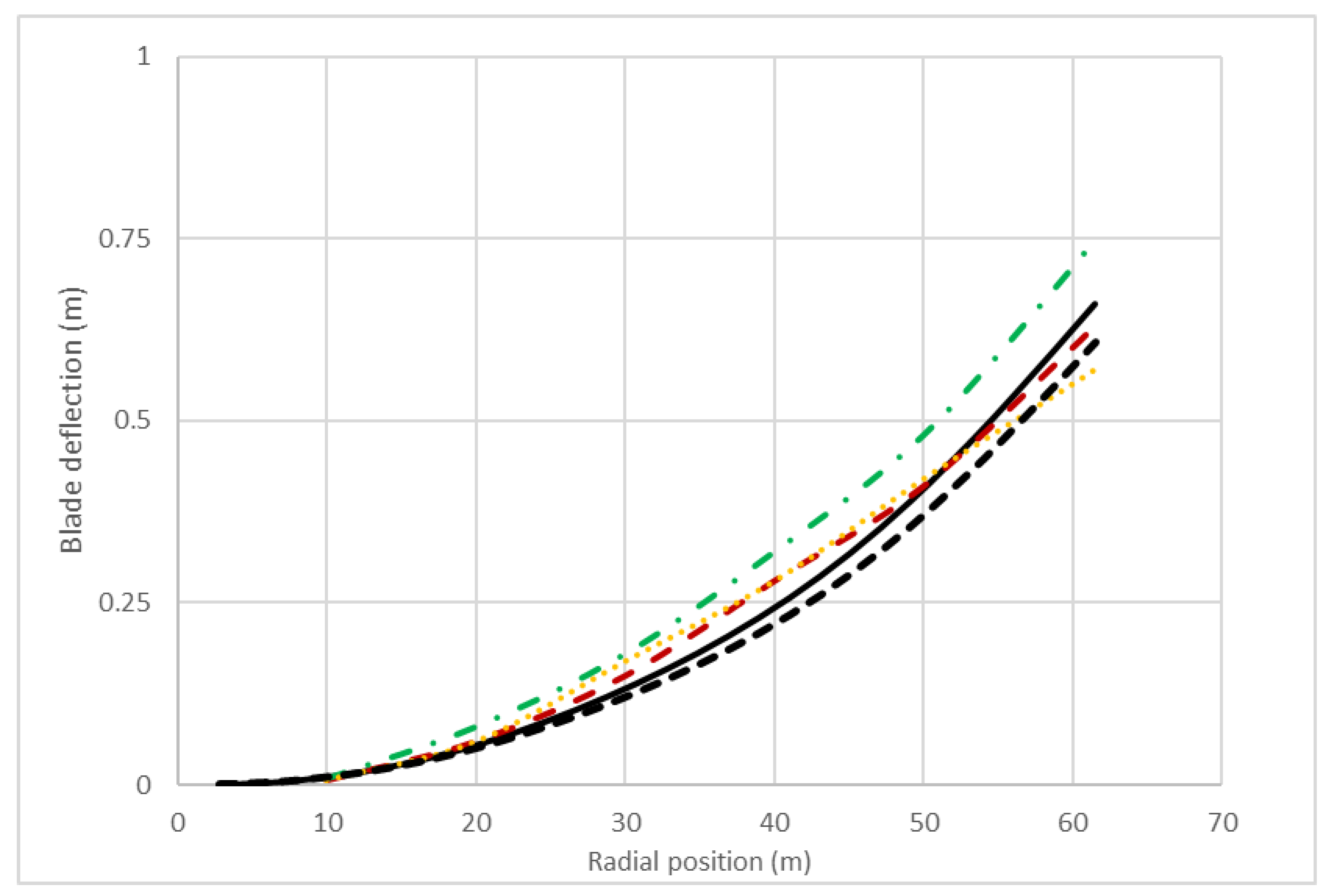
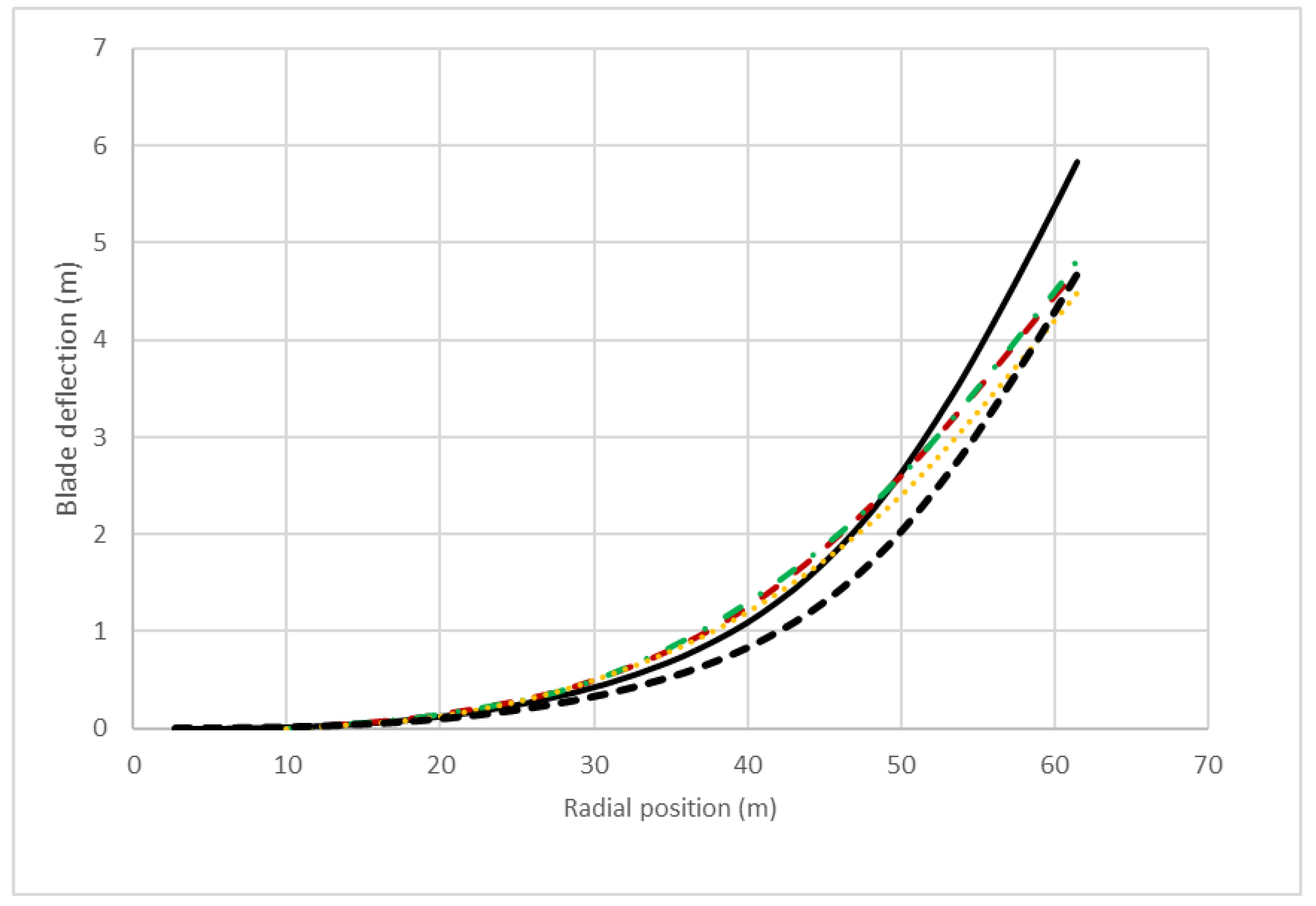
- There are differences between the present deflection values and their reference counterparts. The differences can be seen in the flap-wise and edge-wise directions at a rotational speed of 0 RPM. In the edge-wise curve, as shown in Figure 9, the results of this study come with the linear distribution in the difference between the response at 0 RPM and 12.1 RPM. On the other hand, the distribution of the curve at 0 RPM of the mentioned references goes more significant than the present result at 0 RPM in the middle blade length. At the same time, some of them go to be even less than the present result at 12.1 RPM at the blade’s tip.
- For the flap-wise results, the distribution of the curve at 0 RPM of the mentioned references is less than the present result at 0 RPM in the last blade quarter. Moreover, they are even less than the present result at 12.1 at the blade’s tip.
- The dynamic response results of this study obtained the Rayleigh theory for structure and BEM for aerodynamic forces. Adding the influence of rotational speed at 12.1 RPM leads to decreasing the dynamic response. In conclusion, this may improve the accuracy of prediction for free vibration analysis and the deflection values as well.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| L | Blade length (m) |
| D | Rotor diameter (m) |
| E | Modulus of elasticity (N/m2) |
| A | Blade cross-sectional area (m2) |
| I | Blade moment of inertia (m4) |
| Kinetic energy (J) | |
| Potential energy (J) | |
| Work due to external distributed force (J) | |
| Flap-wise displacement (m) | |
| External force (N) | |
| t | Time (s) |
| R | Hub radius (m) |
| g | Gravitational acceleration (m/s2) |
| Axial force due to centrifugal tension (N) | |
| Flap-wise deflection (m) | |
| Edge-wise deflection (m) | |
| Distance relative to the blade span ( | |
| The blade density ( | |
| Angular velocity of the blade ( | |
| Southwell coefficient | |
| Pitch angle (deg) | |
| Twist angle (deg) | |
| Pre-cone angle (deg) | |
| Angle of attack (deg) | |
| Total pitch angle (deg) | |
| Azimuth position of the blade | |
| Natural frequency(rad/s) | |
| Xh | Hub X-axis |
| Yh | Hub Y-axis |
| G | Local gyroscopic matrix |
| m | Local mass matrix |
| k | Local stiffness matrix |
| Normal aerodynamic force (N) | |
| Tangential aerodynamic force (N) | |
| Total pitch angle (rad) | |
| Induction velocity factors | |
| Lift force | |
| Drag force | |
| Airflow density | |
| Lift coefficient | |
| Drag coefficient | |
| Coefficient of sectional blade normal force | |
| Coefficient of sectional blade parallel force | |
| Airflow velocity (m/s) | |
| Column matrix of the excitation forces and/or moments | |
| Chord length (m) | |
| NREL | National Renewable Energy Laboratory |
| BEM | Blade element momentum |
References
- Gielen, D.; Gorini, R.; Wagner, N.; Leme, R.; Gutierrez, L.; Prakash, G.; Asmelash, E.; Janeiro, L.; Gallina, G.; Vale, G.; et al. Global Energy Transformation: A Roadmap to 2050; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Office for National Statistics. Wind Energy in the UK; Office for National Statistics: London, UK, 2021. [Google Scholar]
- Pimenta, F.; Pacheco, J.; Branco, C.M.; Teixeira, C.M.; Magalhães, F. Development of a digital twin of an onshore wind turbine using monitoring data. J. Phys. Conf. 2020, 1618, 022065. [Google Scholar] [CrossRef]
- Wang, M.; Wang, C.; Hnydiuk-Stefan, A.; Feng, S.; Atilla, I.; Li, Z. Recent progress on reliability analysis of offshore wind turbine support structures considering digital twin solutions. Ocean Eng. 2021, 232, 109168. [Google Scholar] [CrossRef]
- Sahu, K.; Alzahrani, F.A.; Srivastava, R.K.; Kumar, R. Evaluating the impact of prediction techniques: Software reliability perspective. Comput. Mater. Contin. 2021, 67, 1471–1488. [Google Scholar] [CrossRef]
- Attaallah, A.; Alsuhabi, H.; Shukla, S.; Kumar, R.; Gupta, B.K.; Khan, R.A. Analysing the Big Data Security Through a Unified Decision-Making Approach. Intell. Autom. Soft Comput. 2022, 32, 1071–1088. [Google Scholar] [CrossRef]
- Sivalingam, K.; Sepulveda, M.; Spring, M.; Davies, P. A review and methodology development for remaining useful life prediction of offshore fixed and floating wind turbine power converter with digital twin technology perspective. In Proceedings of the 2018 2nd International Conference on Green Energy and Applications (ICGEA), Singapore, 24–28 March 2018; pp. 197–204. [Google Scholar]
- Chou, J.S.; Chiu, C.K.; Huang, I.K.; Chi, K.N. Failure analysis of wind turbine blade under critical wind loads. Eng. Fail. Anal. 2013, 27, 99–118. [Google Scholar] [CrossRef]
- Hansen, M.O.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Jafari, M.; Hou, F.; Abdelkefi, A. Wind-induced vibration of structural cables. Nonlinear Dyn. 2020, 100, 351–421. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Vorpahl, F.; Popko, W.; Qvist, J.; Frøyd, L.; Chen, X.; Azcona, J.; Uzunoglu, E.; Guedes Soares, C.; et al. Offshore code comparison collaboration continuation within IEA wind task 30: Phase II results regarding a floating semisubmersible wind system. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 45547, p. V09BT09A012. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Rosen, J.; Tietze-Stöckinger, I.; Rentz, O. Model-based analysis of effects from large-scale wind power production. Energy 2007, 32, 575–583. [Google Scholar] [CrossRef]
- Ponta, F.L.; Otero, A.D.; Lago, L.I.; Rajan, A. Effects of rotor deformation in wind-turbine performance: The dynamic rotor deformation blade element momentum model (DRD–BEM). Renew. Energy 2016, 92, 157–170. [Google Scholar] [CrossRef]
- Jokar, H.; Mahzoon, M.; Vatankhah, R. Dynamic modeling and free vibration analysis of horizontal axis wind turbine blades in the flap-wise direction. Renew. Energy 2020, 146, 1818–1832. [Google Scholar] [CrossRef]
- Algolfat, A.; Wang, W.; Albarbar, A. Comparison of beam theories for characterisation of a NREL wind turbine blade flap-wise vibration. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022. [Google Scholar] [CrossRef]
- Rezaei, M.M.; Behzad, M.; Moradi, H.; Haddadpour, H. Modal-based damage identification for the nonlinear model of modern wind turbine blade. Renew. Energy 2016, 94, 391–409. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C. Aeroelastic analysis of a floating offshore wind turbine in platform-induced surge motion using a fully coupled CFD-MBD method. Wind Energy 2019, 22, 1–20. [Google Scholar] [CrossRef]
- Li, Z.; Wen, B.; Dong, X.; Peng, Z.; Qu, Y.; Zhang, W. Aerodynamic and aeroelastic characteristics of flexible wind turbine blades under periodic unsteady inflows. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104057. [Google Scholar] [CrossRef]
- Meng, H.; Jin, D.; Li, L.; Liu, Y. Analytical and numerical study on centrifugal stiffening effect for large rotating wind turbine blade based on NREL 5 MW and WindPACT 1.5 MW models. Renew. Energy 2022, 183, 321–329. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Li, S.; Xu, J. The influence of rotation on natural frequencies of wind turbine blades with pre-bend. J. Renew. Sustain. Energy 2020, 12, 023303. [Google Scholar] [CrossRef]
- Putter, S.; Manor, H. Natural frequencies of radial rotating beams. J. Sound Vib. 1978, 56, 2–175. [Google Scholar] [CrossRef]
- Sabale, A.; Gopal, K.N. Nonlinear aeroelastic response of wind turbines using Simo-Vu-Quoc rods. Appl. Math. Model. 2019, 65, 696–716. [Google Scholar] [CrossRef]
- Sabale, A.K.; Gopal, N.K. Nonlinear aeroelastic analysis of large wind turbines under turbulent wind conditions. AIAA J. 2019, 57, 10–4416. [Google Scholar] [CrossRef]
- Li, Y.; Castro, A.M.; Sinokrot, T.; Prescott, W.; Carrica, P.M. Coupled multi-body dynamics and CFD for wind turbine simulation including explicit wind turbulence. Renew. Energy 2015, 76, 338–361. [Google Scholar] [CrossRef]
- Sayed, M.; Klein, L.; Lutz, T.; Krämer, E. The impact of the aerodynamic model fidelity on the aeroelastic response of a multi-megawatt wind turbine. Renew. Energy 2019, 140, 304–318. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yu, D.O.; Kwon, O.J. Predicting wind turbine blade loads and aeroelastic response using a coupled CFD–CSD method. Renew. Energy 2014, 70, 184–196. [Google Scholar] [CrossRef]
- Algolfat, A.; Wang, W.; Albarbar, A. Comparison of Beam Theories for Simulating the Dynamic Response of a 5MW NREL Wind Turbine Blade Flap-wise and Edgewise Vibrations. J. Dyn. Monit. Diagn. 2022. [Google Scholar]
- Rao, S.S. The Finite Element Method in Engineering; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Jeong, M.S.; Cha, M.C.; Kim, S.W.; Lee, I.; Kim, T. Effects of torsional degree of freedom, geometric nonlinearity, and gravity on aeroelastic behavior of large-scale horizontal axis wind turbine blades under varying wind speed conditions. J. Renew. Sustain. Energy 2014, 6, 023126. [Google Scholar] [CrossRef]



| Rotational Speed (RPM) | 0 | 2.5 | 5 | 10 | 12.1 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|---|
| Mode No. | |||||||||
| 1 | 0.6808 | 0.6847 | 0.6961 | 0.7399 | 0.7643 | 0.8070 | 0.8914 | 0.9881 | |
| 2 | 1.9851 | 1.9891 | 2.0008 | 2.0471 | 2.0737 | 2.1219 | 2.2223 | 2.3448 | |
| 3 | 4.5433 | 4.5471 | 4.5585 | 4.6039 | 4.6303 | 4.6785 | 4.7807 | 4.9087 | |
| 4 | 8.1328 | 8.1366 | 8.1479 | 8.1932 | 8.2196 | 8.2680 | 8.3714 | 8.5022 | |
| 5 | 12.6749 | 12.6785 | 12.6893 | 12.7326 | 12.7579 | 12.8043 | 12.9039 | 13.0305 | |
| 6 | 18.0312 | 18.0351 | 18.0457 | 18.0878 | 18.1125 | 18.1577 | 18.2551 | 18.3793 | |
| 7 | 24.2141 | 24.2175 | 24.2278 | 24.2689 | 24.2930 | 24.3372 | 24.4325 | 24.5542 | |
| 8 | 31.3239 | 31.3273 | 31.3375 | 31.3783 | 31.4023 | 31.4463 | 31.5410 | 31.6624 | |
| 9 | 39.5653 | 39.5686 | 39.5785 | 39.6181 | 39.6413 | 39.6839 | 39.7758 | 39.8934 | |
| 10 | 48.1945 | 48.1982 | 48.2095 | 48.2544 | 48.2807 | 48.3292 | 48.4340 | 48.5686 | |
| Rotational Speed (RPM) | 0 | 2.5 | 5 | 10 | 12.1 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|---|
| Mode No. | |||||||||
| 1 | 1.1129 | 1.1149 | 1.1210 | 1.1449 | 1.15952 | 1.1837 | 1.2358 | 1.2997 | |
| 2 | 4.1808 | 4.1825 | 4.1876 | 4.2081 | 4.2208 | 4.2421 | 4.2892 | 4.3489 | |
| 3 | 9.7148 | 9.7165 | 9.7217 | 9.7426 | 9.7555 | 9.7773 | 9.8256 | 9.8874 | |
| 4 | 17.4666 | 17.4683 | 17.4735 | 17.4942 | 17.5069 | 17.5286 | 17.5766 | 17.6381 | |
| 5 | 27.6064 | 27.6081 | 27.6131 | 27.6333 | 27.6457 | 27.6668 | 27.7137 | 27.7737 | |
| 6 | 39.1638 | 39.1654 | 39.1704 | 39.1900 | 39.2022 | 39.2227 | 39.2685 | 39.3272 | |
| 7 | 52.4177 | 52.4193 | 52.4242 | 52.4438 | 52.4560 | 52.4765 | 52.5222 | 52.5809 | |
| 8 | 67.5379 | 67.5395 | 67.5444 | 67.5639 | 67.5759 | 67.5964 | 67.6419 | 67.7003 | |
| 9 | 84.2736 | 84.2752 | 84.2800 | 84.2994 | 84.3114 | 84.3317 | 84.3769 | 84.4350 | |
| 10 | 102.6051 | 102.6067 | 102.6114 | 102.6302 | 102.6418 | 102.6615 | 102.7053 | 102.7617 | |
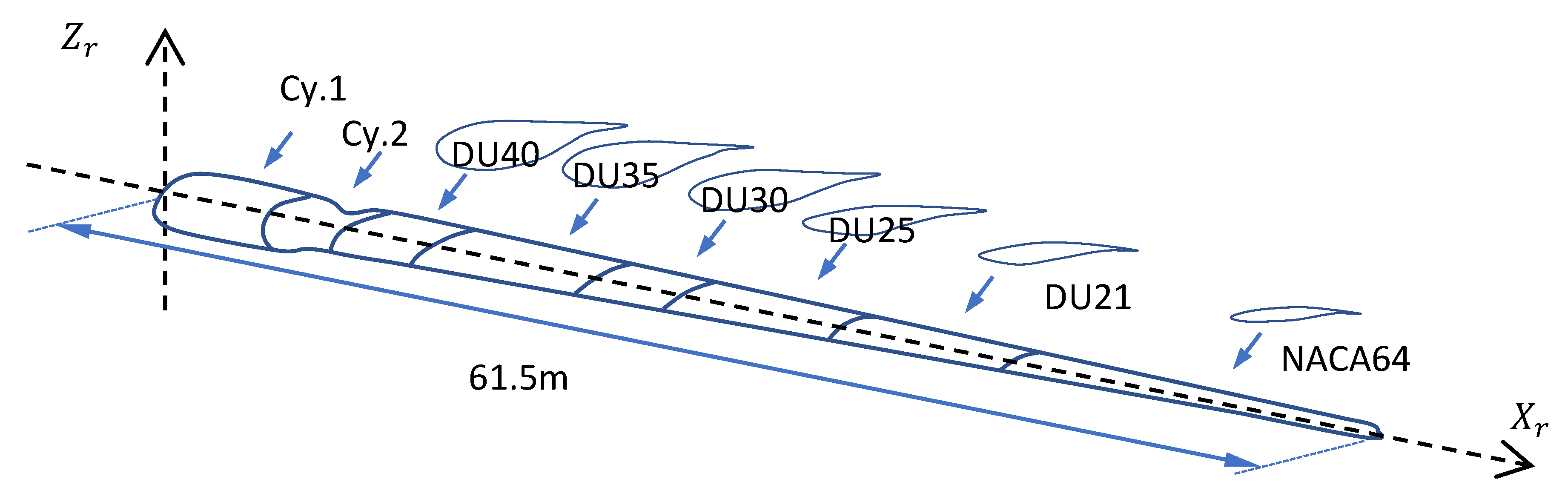
| Section | Position (m) | Chord (m) | Aerofoil | |
|---|---|---|---|---|
| 1 | 2.87 | 3.542 | 13.308 | Cylinder 1 |
| 2 | 5.60 | 3.854 | 13.308 | Cylinder 1 |
| 3 | 8.33 | 4.167 | 13.308 | Cylinder 2 |
| 4 | 11.75 | 4.557 | 13.308 | DU40_A17 |
| 5 | 15.85 | 4.652 | 11.480 | DU35_A17 |
| 6 | 19.95 | 4.458 | 10.162 | DU35_A17 |
| 7 | 24.05 | 4.249 | 9.011 | DU30_A17 |
| 8 | 28.15 | 4.007 | 7.795 | DU25_A17 |
| 9 | 32.25 | 3.748 | 6.544 | DU21_A17 |
| 10 | 36.35 | 3.502 | 5.361 | DU21_A17 |
| 11 | 40.45 | 3.256 | 4.188 | NACA_64_618 |
| 12 | 44.55 | 3.01 | 3.125 | NACA_64_618 |
| 13 | 48.65 | 2.764 | 2.319 | NACA_64_618 |
| 14 | 52.75 | 2.518 | 1.526 | NACA_64_618 |
| 15 | 56.17 | 2.313 | 0.863 | NACA_64_618 |
| 16 | 58.90 | 2.086 | 0.370 | NACA_64_618 |
| 17 | 61.63 | 1.419 | 0.106 | NACA_64_618 |
| Mode No. | Rayleigh (Hz) at Ω = 0 RPM Present Work | Rayleigh (Hz) at Ω = 12.1 RPM Present Work | B-Modes Hz at Ω = 0 RPM [NREL] | FAST Hz at Ω = 0 RPM [NREL] | [20] (Hz) at Ω = 0 RPM | [32] (Hz) at Ω = 0 RPM |
|---|---|---|---|---|---|---|
| 1 | 0.68 F | 0.764 F | 0.69 F | 0.68 F | 0.67 F | 0.68 F |
| 2 | 1.11 E | 1.16 E | 1.12 E | 1.10 E | 1.11 E | 1.10 E |
| 3 | 1.98 F | 2.07 F | 2.00 F | 1.94 F | 1.92 F | 1.98 F |
| 4 | 4.10 E | 4.22 E | 4.12 E | 4.00 E | 3.96 E | 3.99 E |
| 5 | 4.54 F | 4.63 F | 4.69 F | 4.43 F | 4.43 F | 4.66 F |
| No. | Reference | Flap-Wise Deflection (m) | Edge-Wise Deflection (m) |
|---|---|---|---|
| 1 | Li, et al., 2020 [20] | 4.49 | −0.57 |
| 2 | Sabal & Gopal, 2019a [24] | 4.41 | −0.57 |
| 3 | Jonkman et al., 2009 [13] | 5.47 | −0.61 |
| 4 | Yu & Kwon, 2014 [29] | 4.72 | −0.63 |
| 5 | Ponta et al., 2016 [15] | 3.85 | −0.56 |
| 6 | Sabale & Gopal, 2019b [25] | 4.55 | −0.62 |
| 7 | Jeong et al., 2014 [32] | 4.83 | −0.75 |
| 8 | Rezaei et al., 2016 [18] | 8.35 | −1.85 |
| 9 | present work: angular speed 0 RPM | 5.83 | −0.66 |
| 10 | present work: angular speed 12.1 RPM | 4.70 | −0.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algolfat, A.; Wang, W.; Albarbar, A. Study of Centrifugal Stiffening on the Free Vibrations and Dynamic Response of Offshore Wind Turbine Blades. Energies 2022, 15, 6120. https://doi.org/10.3390/en15176120
Algolfat A, Wang W, Albarbar A. Study of Centrifugal Stiffening on the Free Vibrations and Dynamic Response of Offshore Wind Turbine Blades. Energies. 2022; 15(17):6120. https://doi.org/10.3390/en15176120
Chicago/Turabian StyleAlgolfat, Amna, Weizhuo Wang, and Alhussein Albarbar. 2022. "Study of Centrifugal Stiffening on the Free Vibrations and Dynamic Response of Offshore Wind Turbine Blades" Energies 15, no. 17: 6120. https://doi.org/10.3390/en15176120
APA StyleAlgolfat, A., Wang, W., & Albarbar, A. (2022). Study of Centrifugal Stiffening on the Free Vibrations and Dynamic Response of Offshore Wind Turbine Blades. Energies, 15(17), 6120. https://doi.org/10.3390/en15176120







