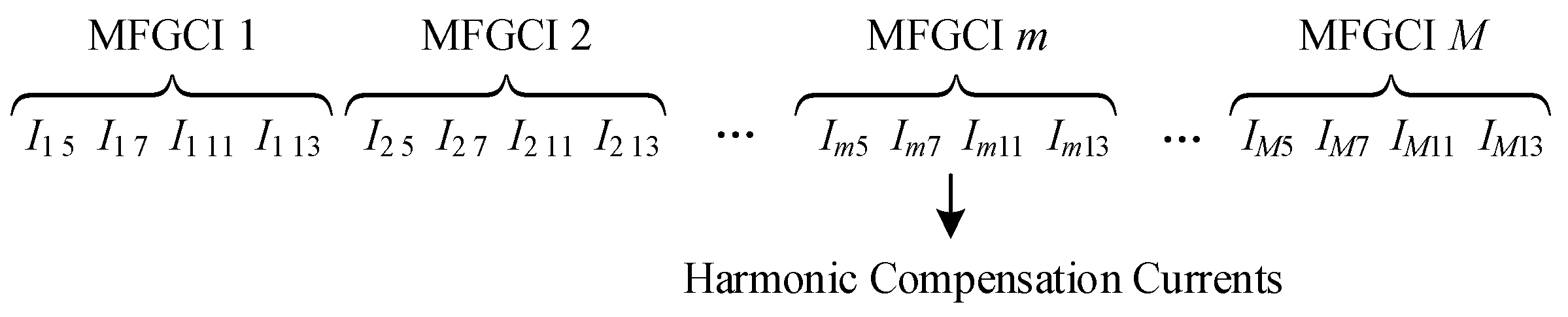1. Introduction
With the development and use of a large number of new energy devices, the random and massive access of non-linear loads, and the normalization of network power electronics, the harmonic pollution of microgrids is becoming a pressing issue [
1,
2]. On the one hand, with continuous expansion in the size of the microgrid, the distribution range of and level of pollution from harmonic sources are gradually increasing. The ability of microgrids to absorb power quality pollution is weak, and the powerful electronic equipment in the network is susceptible to power quality and has high requirements for waveforms, amplitude and frequency. This makes the power quality problem of microgrids even more pressing [
3,
4]. In [
5], a medium-sized industrial microgrid is calculated shows that the levels of total harmonic distortion have exceeded the limit value imposed in the standard. On the other hand, due to the decentralized and wide-area characteristics of microgrid harmonic sources [
6], the traditional method of centralized mitigation has the problems of a high installation cost of equipment, single function, and low utilization of equipment capacity, making it more difficult to meet the increasingly complex mitigation needs of network distribution and unsuitable for new energy microgrids with a decentralized distribution of multiple harmonic sources. Therefore, there is an urgent need to seek a power-quality mitigation method for local mitigation of harmonic pollution sources.
It is demonstrated that a multi-functional grid-connected inverter (MFGCI) can mitigate power-quality pollution on a local scale. The MFGCI has the same topology as the active power filter (APF) and only requires appropriate software upgrades to enable the integration of renewable energy, while considering the improvement of microgrid power quality [
7]. With its multitasking function, MFGCI not only improves the cost performance of grid-connected inverters, but also reduces investment costs by avoiding the installation of additional power-quality improvement devices in the microgrid.
In previous research on MFGCI structures, a sliding mode controller and a positive fundamental component estimator were used to calculate current and voltage to realize the simultaneous outputs of the active power and reactive power of MFGCI [
8]. In [
9], the design, development and implementation process of the MFGCI laboratory prototype with APF function is described. In [
10], a new type of MFGCI was studied. The MFGCI is composed of a three-phase DC/AC converter with three ports and a DC/DC converter at the front stage, and a 5kVA laboratory prototype was designed, which cannot only output active power but also compensate for harmonic current and reactive power. In [
11], MFGCI is proposed with the function of compensating harmonic current, reactive power and the three-phase imbalance on the basis of considering the power quality of microgrids and the effectiveness of grid-connected inverters.
To more effectively control reactive power and voltage, a type of shutdown series-switched MFGCI (SSS-MFGCI) was proposed in [
12], which achieved the four-quadrant operation of SSS-MFGCI through a bidirectional switch commutation method. In [
13], a MFGCI control scheme was designed that can suppress both steady and dynamic disturbances; the control scheme includes an inner-loop controller and an improved reference for the current generation algorithm. From the references [
8,
9,
10,
11,
12,
13], we can draw a clear conclusion that MFGCI achieves harmonic compensation or harmonic mitigation.
In research on operation control strategy, the authors of [
14] used SSS-MFGCI, which was first proposed in [
12], and set different operation modes according to various grid disturbances to realize the control of voltage swell, voltage sag and voltage imbalance. In [
15], SSS-MFGCI was applied to V2G based on [
14]. In [
16], an improved MFGCI power governance compensation algorithm based on the conservative power theory was proposed, and the small signal stability of MFGCI was analyzed using the impedance modeling method. In [
17], MFGCI is modelled based on impedance reconstruction model, realizes the purpose of MFGCI providing virtual inertia and eliminating harmonic resonance. In [
18], a multi-objective control strategy was designed, which enables the MFGCI to simultaneously output harmonic compensation current and reactive power through closed-loop active power control technology, compensating the harmonic and reactive power of the system. In [
19], a virtual impedance droop control and secondary power balance control were combined, and a comprehensive control strategy for MFGCIs was proposed, which can achieve harmonic mitigation and a three-phase unbalance suppression of the grid. In [
20], MFGCI can operate in shunt-connected and cascade-connected modes; therefore, the required compensation can be provided for current- or voltage-related power-quality issues with the assistance of bidirectional switches. In [
21], a power management algorithm was developed to determine the optimal operating mode of the MFGCI and realize selective power injection and power regulation. From the references [
14,
15,
16,
17,
18,
19,
20,
21], it is observed that active output, reactive output and harmonic compensation can be simultaneously realized through the control algorithm of MFGCI.
However, power quality management is only an auxiliary function of MFGCI. The compensation capacity that can be used in a single MFGCI is always limited. Microgrids often contain multiple grid-connected inverters, which can play a greater role if the compensation capacity of these grid-connected inverters is aggregated. In [
22], the study proposed a control method to coordinate multiple MFGCIs to participate in microgrid power quality management based on the Fryze–Buchholz–Dpenbrock (FBD) power theory. In [
23], a comprehensive power-quality evaluation (CPQE) index was proposed based on the mutation theory, and a multi-objective optimal compensation model with multiple MFGCIs was established with the objectives of optimizing the CPQE index and minimizing the occupied capacity of MFGCIs used for power-quality compensation.
Similar to [
23], a new comprehensive power-quality evaluation method was proposed in [
24], which used the G1 method and hybrid variable weight principle to establish a multi-objective optimal compensation model containing multiple MFGCIs with the objectives of optimizing the CPQE index and minimizing the occupied capacity of MFGCIs for power-quality compensation. In addition to local management, MFGCI can also be used for targeted power-quality management of specific nodes at remote ends. In [
25], a distribution control strategy of the MFGCI output current was proposed based on the remaining capacity of MFGCIs, the harmonic currents of the shunt nodes, and reactive currents of the shunt nodes. In [
26], an optimization model to realize the best operation state of the MFGCI and OLTC was proposed, which offers the best results in terms of voltage quality, minimum power losses and the longest OLTC life as the optimization objectives. In [
27], a new strategy for the cooperative and optimal allocation of VDAPF and SVG considering the contribution of MFGCI is proposed, focusing mainly on the capacity allocation of VDAPF and SVG. References [
22,
23,
24,
25,
26,
27] introduce corresponding control strategies for different application requirements, which can realize local and decentralized harmonics mitigation in microgrids. However, it cannot be ignored that the part of capacity of MFGCI needs to be occupied when compensating harmonics. Therefore, the relationship between the remaining capacity of MFGCI and the capacity required for harmonic compensation needs to be considered, and when the remaining capacity is small, some of the active power capacity can be appropriately reduced to improve the harmonic compensation capacity. A photovoltaic (PV) is connected to the grid through MFGCI.
In research on PV active power control, a new type of photovoltaic power generation module and its control strategy are proposed in [
28], which can ensure the continuous output of active power when the solar radiation intensity changes unexpectedly. In [
29], according to the solar irradiance and cloud cover at different stages of the day, the reference value of power per hour is optimized based on random dynamic programming to realize the PV active power control. However, the reduction in active power grid-connected capacity affects the economy of microgrid operation. The allocation of the MFGCI harmonic compensation capacity and active power grid-connected capacity to ensure the economy of microgrid operations with optimal power-quality improvement has not been thoroughly studied in the references [
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29].
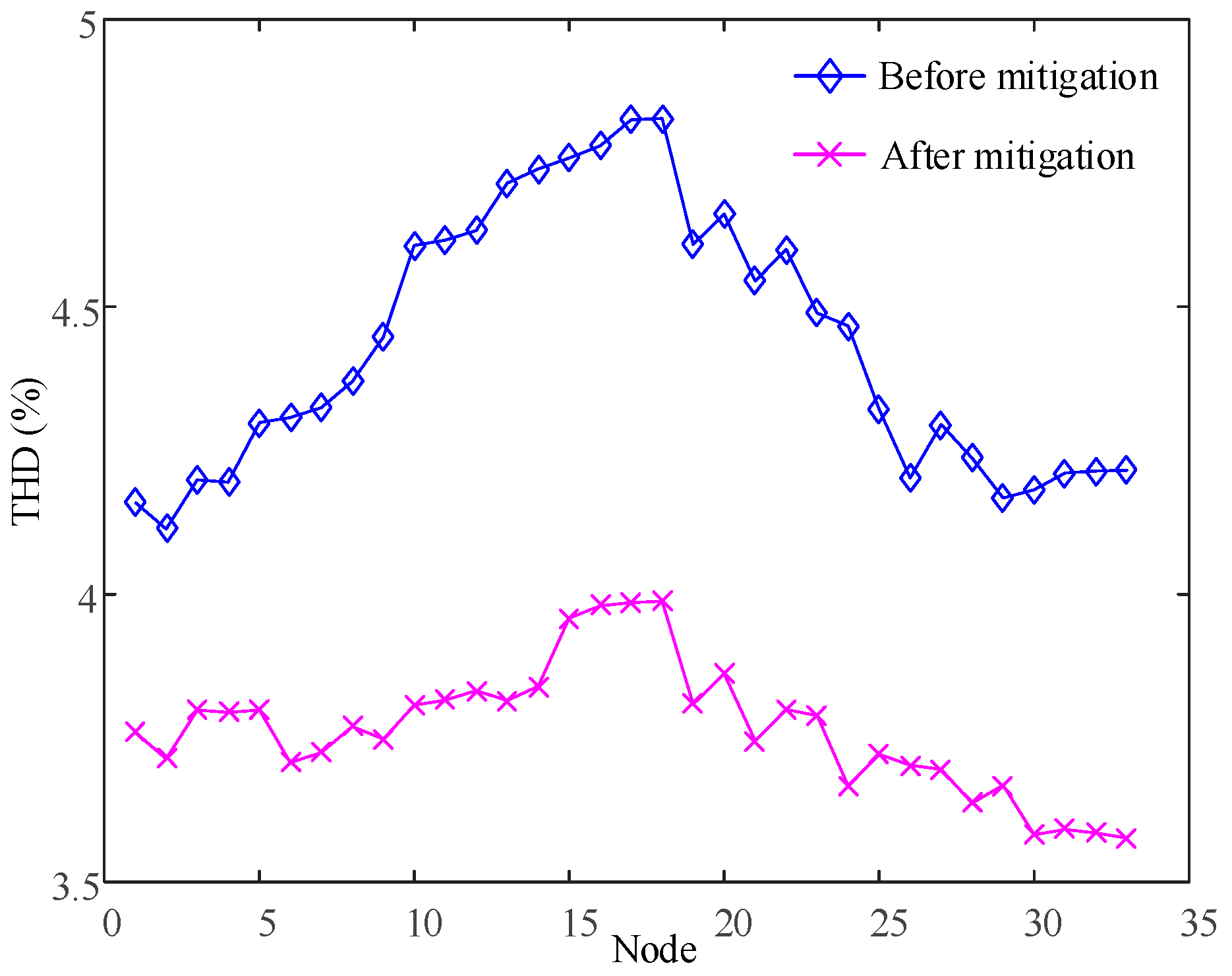
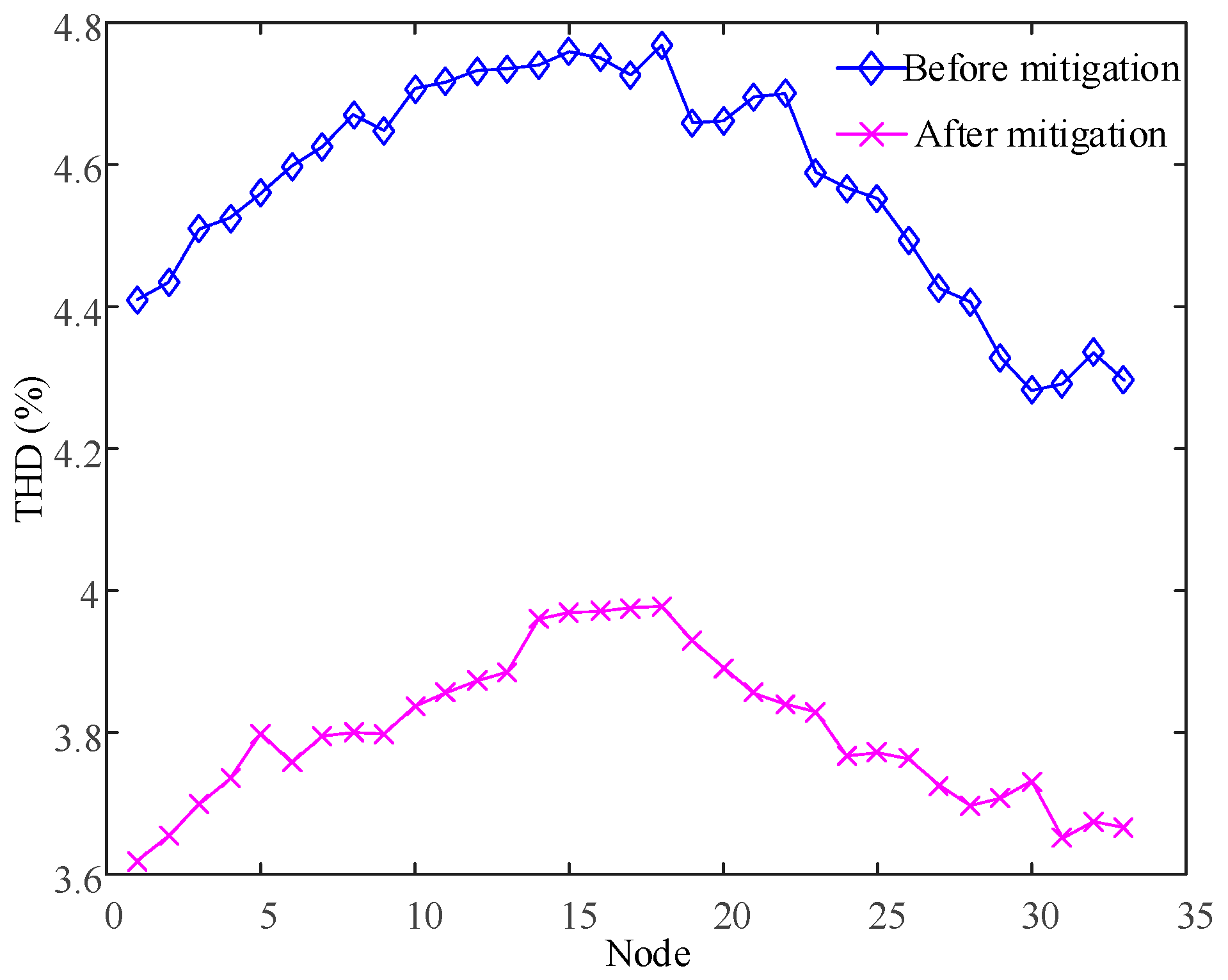
In order to integrate the active power grid-connected and harmonic mitigation functions of MFGCI and achieve the integrated optimization of system operation and harmonic mitigation, this paper solves the problem of allocating the active power grid-connected capacity and harmonic mitigation capacity of MFGCI through the use of microgrid active optimization and nodal harmonic mitigation. A two-layer optimization model was established for the integrated active power-harmonic mitigation capacity allocation of MFGCI, with the upper layer of active power optimization used to determine the optimal amount of MFGCIs to be connected to the grid. The lower layer for harmonic mitigation optimization determines the corresponding objective function according to the relationship between the total remaining capacity of the system and the size of the capacity required for harmonic mitigation, optimizing the harmonic mitigation scheme and the harmonic mitigation capacity of each MFGCI. A discrete binary-coded two-layer simulated annealing particle swarm algorithm (SAPSO) with a nested harmonic power flow calculation is used to solve the problem. The validation results show that the two-layer optimization model established in this paper not only ensures the optimal PV active grid-connected inverters, but also enables the harmonic mitigation of the system to achieve the best results.
4. Model Solving
The upper and lower models are interrelated; therefore, a fast optimization algorithm is needed. The discrete binary coded two-layer simulated annealing particle swarm optimization (SAPSO) with nested harmonic power flow calculation has the advantages of a simple and easy implementation, fast search speed and few parameter settings. It can find the global optimum in a short time. Therefore, the upper and lower objective functions are solved by SAPSO algorithm.
The upper-layer optimization solution parameters are set as follows: the particle population size is 200, the learning factor is 1.5, the inertia weight linearly decreases with a maximum value of 0.95 and minimum value of 0.7, and the maximum number of iterations is 300. The lower-layer optimization solution parameters are set as follows: the particle population size is 300, the learning factor is 1.5, the inertia weight linearly decreases with a maximum value of 0.95 and minimum value of 0.7, and the maximum number of iterations is 300.
4.1. Upper-Layer Particle Coding
In the upper-layer optimization, the optimization variable is the active power reduction; therefore, the upper-layer particle is the MFGCI active power reduction. It should be noted that a single particle can be a value or a group of values. If a microgrid contains
M-th MFGCIs, each particle is composed of
M-th MFGCI active power reductions. The upper-layer optimized particle structure is shown in
Figure 3. In the figure,
is the active power reduction in the
m-th MFGCI.
4.2. Lower-Layer Particle Coding
In the lower-layer optimization, the optimization variable is the harmonic compensation current; therefore, the lower-layer particle is the harmonic compensation current of MFGCI. In the lower-layer harmonic mitigation optimization, each particle contains an
M-th harmonic compensation current of MFGCIs, and each harmonic compensation current of MFGCI is divided into 5th, 7th, 11th and 13th harmonic compensation currents. The initial state of each particle in the lower-layer optimization is randomly generated within the range determined by the upper-layer optimization results and the constraint conditions. The lower-layer particle structure is shown in
Figure 4. In the figure,
,
,
,
are the 5th, 7th, 11th and 13th harmonic compensation currents output by the
m-th MFGCI, respectively:
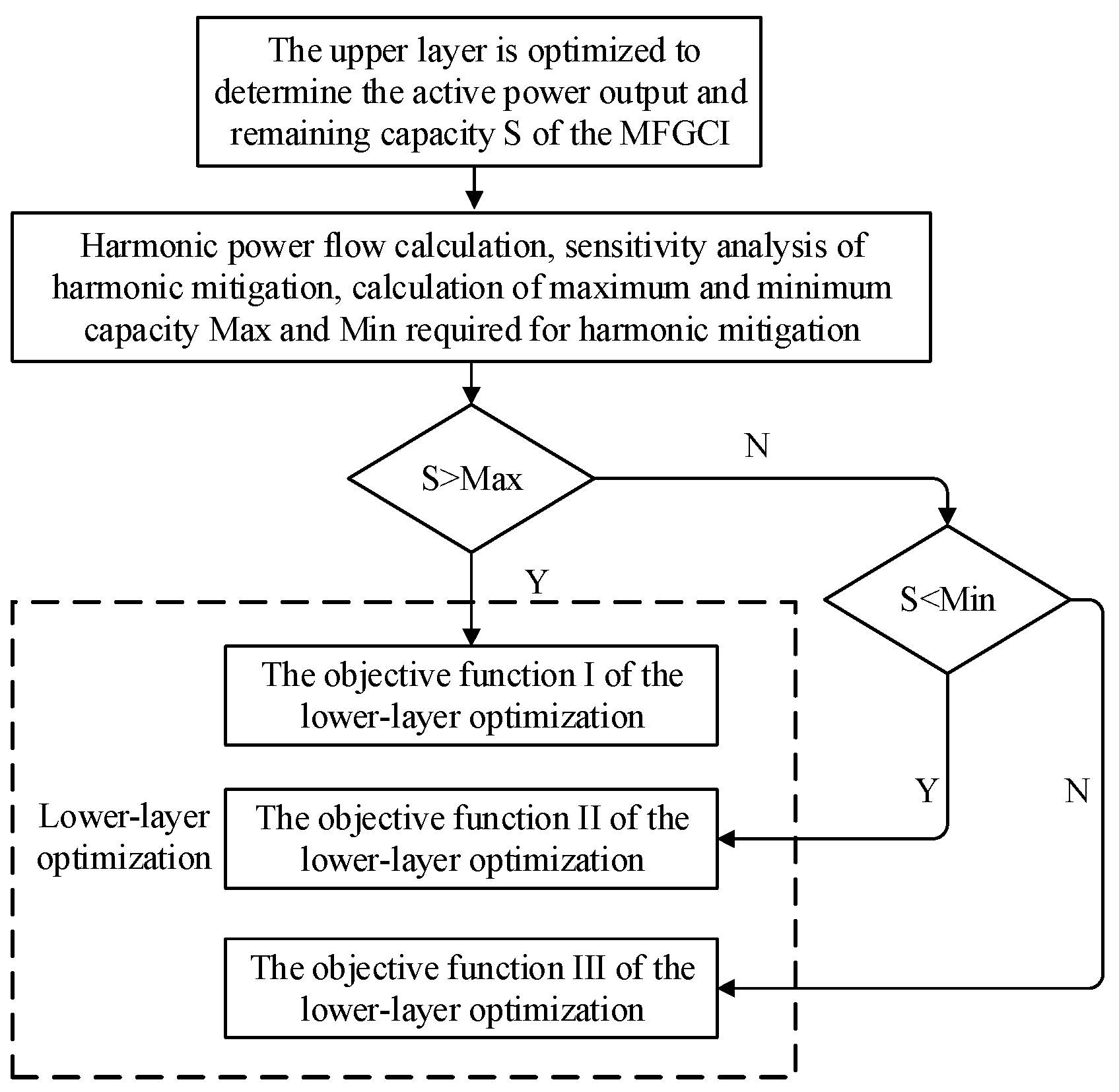
4.3. Model Solving Steps
Step 1: Collect real-time power information of photovoltaics and loads, and set the initial value of active power reduction to 0;
Step 2: Calculate the remaining capacity of the inverter that can be used for harmonic mitigation;
Step 3: Carry out harmonic power flow calculation to obtain the voltage harmonic distortion rate of each node;
Step 4: Determine whether there is a node with THD exceeding the standard in the system. If it does not exist, the optimization is over. If it exists, go to step 5;
Step 5: Perform harmonic mitigation sensitivity analysis on nodes whose THD exceeds the standard, and calculate the maximum and minimum capacity required for harmonic mitigation;
Step 6: The lower-layer optimizes particle coding and selects the corresponding objective function for harmonic mitigation optimization according to the relationship between the remaining capacity and the capacity required for harmonic mitigation;
Step 7: Determine whether the active work needs to be reduced. If not, output the optimization result, the optimization is over; if necessary, go to step 8;
Step 8: The upper layer optimizes the particle coding, performs the upper-layer active power optimization, and obtains the active power reduction in each MFGCI;
Step 9: Go to step 2 and continue to optimize until the optimal solution is obtained.
The flow chart of the model solution is shown in
Figure 5.