A Novel Overlap-Time Effect Suppression for Current Source Converter

Ding, Hao; Li, Quanjie; Yuan, Jing; Wang, Wei; Li, Mingming; Guerrero, Josep M.

doi:10.3390/en15166035

Open AccessArticle

A Novel Overlap-Time Effect Suppression for Current Source Converter

by

Hao Ding

¹

,

Quanjie Li

¹,

Jing Yuan

^1,*,

Wei Wang

¹,

Mingming Li

¹ and

Josep M. Guerrero

²

¹

Electrical Engineering Department, Yanshan University, Qinhuangdao 066004, China

²

Department of Energy Technology, Aalborg University, 9220 Aalborg, Denmark

^*

Author to whom correspondence should be addressed.

Energies 2022, 15(16), 6035; https://doi.org/10.3390/en15166035

Submission received: 14 July 2022 / Revised: 12 August 2022 / Accepted: 18 August 2022 / Published: 20 August 2022

Download

Browse Figures

Versions Notes

Abstract

:

In order to ensure the continuity of the DC-side inductor current, current source converter (CSC) needs to add overlap time between the drive signals, but the overlap time will introduce low order (mainly fifth and seventh) harmonics to the grid current, which seriously degrade the harmonic performance of grid current. At present, some research has been conducted to theoretically analyze and mitigate the overlap-time effect in CSC, including the use of positive-slope sawtooth wave or negative-slope sawtooth wave as the carrier wave, turning on the switch early or delaying turning it off, and eliminating the deviation effect by compensation algorithms, etc. However, existing overlap-time suppression schemes takes the nearest three vector synthesis reference vector scheme as the object of study, in other words, the effect of overlap time on the non-nearest three-vector synthesis reference vector scheme has not been considered. To address these issues, this paper takes the non-nearest three-vector synthesis reference vector scheme as the object of study to analyze the effect of overlap time on the driving signal and establishes the quantitative relationship between the current harmonics introduced in the grid current and overlap time through Fourier decomposition. Then, the design process of the proposed improved space vector modulation by constructing freewheeling channels to replace the overlap time is presented in detail. Finally, simulation and experimental results verify that the overlap-time suppression effect of the proposed scheme is about 100%.

Keywords:

current source converter; overlap time; space vector modulation

1. Introduction

PWM converters are divided into voltage-source converters (VSC) and current-source converters (CSC) according to the DC side energy storage element. The VSC has the advantages of simple structure, low loss, and many nonlinear controllers [1,2], so the VSC is widely used in industrial applications. However, the VSC is derived from the Boost circuit, and its output voltage is higher than the instantaneous value of the line voltage, so it cannot be adjusted from zero. Therefore, a DC/DC circuit needs to be added at the DC-side of the voltage-source converter to realize flexible voltage control [3], which undoubtedly increases the system size, cost and complexity of system control, and the reliability of the system is affected by the DC/DC circuits. The CSC is essentially similar to Buck circuits in that the DC output voltage is lower than the input AC voltage, so the DC output voltage can be flexibly adjusted from 0 V without additional DC/DC circuits, reducing the size and cost of the system.

A current-source converter also has the advantages of inherent current limiting and short-circuit protection capability, low switching dv/dt and high reliability [4]. Therefore, it is widely used in high-voltage direct-current transmission systems [5] and electric vehicles [6], wind/solar power generation systems [7,8], and so on. Moreover, with the wide application of reverse conducting insulated gate bipolar transistors (RC-IGBT), high temperature superconducting materials and wide band-gap semiconductors, the efficiency of the current source converter will be further improved [9,10,11], which will improve the problem of low efficiency of a current-source converter and further promote the development of current-source converters.

For voltage-source converters, dead time must be added between the switch drive signals to prevent direct conduction of the upper and lower bridge arm switches [12]. By contrast, current-source converters allow direct conduction of the upper and lower bridge arm switches, but they require a delayed turn-off or early turn-on of the drive signal to ensure the continuity of the DC side inductive current and to avoid the damage of power devices caused by the instantaneous drop of the DC side energy storage inductor current, and the delayed turn-off or early turn-on time is called the overlap time [13]. However, the overlap time brings additional low-order (mainly fifth and seventh) harmonics to the grid current, which aggravates the degree of grid current distortion.

So far, some research has been conducted to theoretically analyze and mitigate the overlap-time effect. A study on system stability revealed that the overlap time affects the system stability, but it is not explained in detail [14]. A study compared losses due to overlap time in different power devices and analyzed the degree of loss reduction in different power device combinations [15]. A natural soft-commutation PWM scheme reduces the overlap duration by achieving natural soft commutation during the switching process, but it only considers the unity power factor [16]. A comparative study of the grid current distortion caused by the overlap time under different space vector modulation segmentation has been investigated [17], but it did not consider the effect of overlap time on different vector synthesis methods. An overlap-time effect suppression is proposed by using positive-slope sawtooth wave or negative-slope sawtooth wave as the carrier wave, according to the polarity relationship of current and voltage [18], and this modulation strategy does reduce the number of overlap time in one switching cycle compared with the traditional modulation strategy, but there is still an overlap time effect, which does not completely suppress the nonlinear error caused by the overlap time. In [19], the switches are reasonably early turned on or delayed turned off according to the relationship between grid voltages in each sector, so as to achieve the effect of overlap-time effect suppression, but the algorithm is more complicated and difficult to implement. In [20], the vector deviation error of the output current waveform was analyzed, and a compensation algorithm was designed to eliminate the deviation effect. However, the compensation algorithm increased the complexity and processing time of the system, and the application of overlap time led to the loss of half-cycle symmetry of the modulated current, which could not be solved by the compensation method. In addition, the existing overlap-time effect suppression schemes are mainly designed for the nearest three-vector synthesis reference vector scheme, in other words, the effect of overlap time on the non-nearest three-vector synthesis reference vector scheme is not considered.

Aiming to solve these problems, this paper presents a method to ensure the continuity of DC-side inductor current by constructing a freewheeling channel without setting the overlap time. The main contributions of this paper are as follows:

(1): The effect of overlap time on grid current under the non-nearest three-vector synthesis reference vector scheme is analyzed, and the relationship is derived between the overlap time and the introduced harmonics in grid current.
(2): A novel overlap-time suppression method is proposed, that is, constructing a freewheeling channel by controlling specific switch (Freewheeling switch) to maintain conduction, thus ensuring the continuity of the DC-side inductor current, so that the proposed scheme does not need to incorporate overlap time.
(3): The experimental results obtained when the laboratory demonstrator uses a power of 200 W and the simulation results verify the correctness of the theoretical analysis and the effectiveness of the proposed overlap-time effect mitigation scheme.

The rest of this article is structured as follows. Section 2 analyzes the operation mechanism and the effect of overlap time on the non-nearest three-vector synthesis reference vector scheme. Then in Section 3, the improved modulation strategy by diode-clamp according to the relationship between the different grid voltage in each sector is described in detail. In Section 4, simulation results and experimental results are given to verify the correctness of the theoretical analysis and the effectiveness of the proposed scheme. In Section 5, the experimental and simulation results are discussed, and the limitations of the proposed scheme are presented. Finally, the conclusion is reached.

2. Related Work

The schematic diagram of the current-source converter is shown in Figure 1. S1~S6 represent six insulated gate bipolar transistors (IGBT), which are connected in series with six diodes VD₁–VD₆ to improve the reverse blocking capability of the device. The DC-side inductor L and capacitor C form a low-pass filter, which mainly plays the role of filtering the high harmonics and assisting the device to change the current.

At each moment, the CSC has an upper bridge arm switch and a lower bridge arm switch conducting. Therefore, the CSC has nine switching modes corresponding to nine current space vectors, consisting of six active vectors i₁–i₆ and three zero vectors i₀ (i₇–i₉) as shown in Table 1.

2.1. Operation Mechanism for Non-Nearest Three Vectors Scheme

Figure 2 shows the space current vector diagram and Figure 3 shows the terminal voltage for each phase. As shown in Figure 2 and Figure 3, the non-nearest three-vector scheme divides the space current vector diagram into 6 sectors (Sector x₁–x₆), and each sector includes two grid voltage relationships, so even if the same switching sequence is used in the same sector, the corresponding overlap time effects are not the same, while the non-nearest three-vector scheme divides the space current vector diagram into 12 sectors (Sectors 1–12), and the grid voltage relationships in each sector is determined.

To reduce the DC-side current ripple for a CSC, Guo et al. [21] proposed the non-nearest three-vector (i_n, i_n₊₁ and i_n₊₂, n = 1, 2, ..., 5) synthesis reference vector scheme. Taking the sector 1 as an example, the reference vector I_ref is synthesized through the non-nearest three vectors i₁, i₂ and i₃, and the dwell times of the three vectors can be calculated according to the principle of the ampere-second balance.

In the odd (1, 3, 5, 7, 9, 11) sectors, the dwell times for the three vectors are:

\begin{array}{l} T_{n} = T_{s} - m T_{s} \sin (\frac{π}{6} + θ) \\ T_{n + 1} = \sqrt{3} m T_{s} \sin (\frac{π}{3} + θ) - T_{s} \\ T_{n + 2} = T_{s} - T_{n} - T_{n + 1} \\ m = I_{ref} / i_{d c} \end{array}

(1)

where

θ

denotes the reference vector angle and

θ \in (0, π / 6)

, T_s denotes the switching period, m denotes the modulation index and i_dc denotes the DC-side inductor current.

In the even (2, 4, 6, 8, 10, 12) sectors, the dwell times for three vectors are:

\begin{array}{l} T_{n} = \sqrt{3} m T_{s} \sin (\frac{π}{3} - θ) - T_{s} \\ T_{n + 1} = m T_{s} \sin (θ - \frac{π}{6}) + T_{s} \\ T_{n - 1} = T_{s} - T_{n} - T_{n + 1} \end{array}

(2)

where

θ

denotes the reference vector angle and

θ \in (- π / 6, 0)

, T_s denotes the switching period, m denotes the modulation index.

The mechanism of the non-nearest three-vectors modulation scheme in sector 1 as shown in Figure 4.

2.2. Effect of Overlap Time with Non-Nearest Three Vectors Modulation Scheme

Taking sector 1 as an example to analyze the influence of overlap time, and the switching sequence is i₁ (S1, S6) i₂ (S1, S2) i₃ (S2, S3). When S6 switches to S2, S2 receives the turn-on signal but the S6 is not yet turned off due to the existence of overlap time, however, VD₂ bears the forward voltage u_bc (u_bc > 0), so the commutation from S6 to S2 can be changed in time, and there is no overlap-time effect. When S1 switches to S3, S3 receives the turn-on signal but S1 is not yet turned off due to the existence of overlap time. However, VD₃ bears the reverse voltage u_ba (u_ba < 0), so the commutation from S1 to S3 cannot be changed in time, and there is an overlap-time effect. The distribution of the overlap-time effect in sector 1 is shown in Figure 5, compared with the ideal drive situation. The current flows in phase A are extended by one overlap time t_ov, and in phase B is reduced by one overlap time. Affected by the overlap time, the ampere-second balance equation becomes:

\begin{array}{l} T_{1} i_{1} + (T_{2} + t_{o v}) i_{2} + (T_{3} - t_{o v}) i_{3} = I_{ref} T_{s} \\ \Rightarrow T_{1} i_{1} + T_{2} i_{2} + T_{3} i_{3} + t_{o v} i_{1} = I_{ref} T_{s} \end{array}

(3)

The deviation of dwell time of active vectors i₂, i₃ results in a current deviation from the expected reference current vector and introduces additional low-order harmonics in the modulated rectifier current waveforms.

Figure 6 shows the current deviation i_dev (i_dev = (t_ov/T_s) × i₁), which is mapped onto the three-phase coordinate axes to investigate the effect of current deviation on the grid current of the converter, where

Δ i_{s a}

,

Δ i_{s b}

and

Δ i_{s c}

are the deviation components of i_dev on the a-axis, B-axis and C-axis, respectively.

{\begin{cases} | Δ i_{s a} | = i_{d e v} \cos (\frac{π}{6}) = \frac{\sqrt{3}}{2} \frac{t_{o v}}{T_{s}} | i_{1} | = i_{d c} t_{o v} f_{s} \\ | Δ i_{s b} | = - i_{d e v} \cos (\frac{π}{6}) = - \frac{\sqrt{3}}{2} \frac{t_{o v}}{T_{s}} | i_{1} | = - i_{d c} t_{o v} f_{s} \\ | Δ i_{s c} | = i_{d e v} \cos (\frac{π}{2}) = 0 \end{cases}

(4)

By the above method, the relationship between the current error of each phase due to the overlap-time effect and the sector in one switching cycle can be obtained, as shown in Table 2.

To theoretically analyze influence introduced by overlap time, Fourier decomposition is applied to obtain the harmonic distribution of

Δ i_{s a}

,

Δ i_{s b}

and

Δ i_{s c}

. Since the deviation of current vectors is symmetric in three phases, only the decomposition result of

Δ i_{s a}

is given in the following:

Δ i_{s a} = \frac{i_{d c} t_{o v} f_{s}}{π} (6 - 2 \sqrt{3}) [\cos (ω t) + \sum_{k = 1}^{\infty} {(- 1)}^{k} \frac{1}{6 k \pm 1} \cdot \cos (6 k \pm 1) ω t \dots]

(5)

According to Equation (5), the overlap time not only affects the fundamental modulation waveform, but also introduces 6k ± 1 (k = 1, 2, ...) harmonics to the rectifier current. These harmonics are only related to the overlap time and the switching frequency f_s. To ensure correct switching commutation, a sufficiently long overlap time should be chosen. However, higher switching frequencies and larger overlap time lead to a worse harmonic distribution of the grid current, so it is very necessary to address the effects caused by the overlap time.

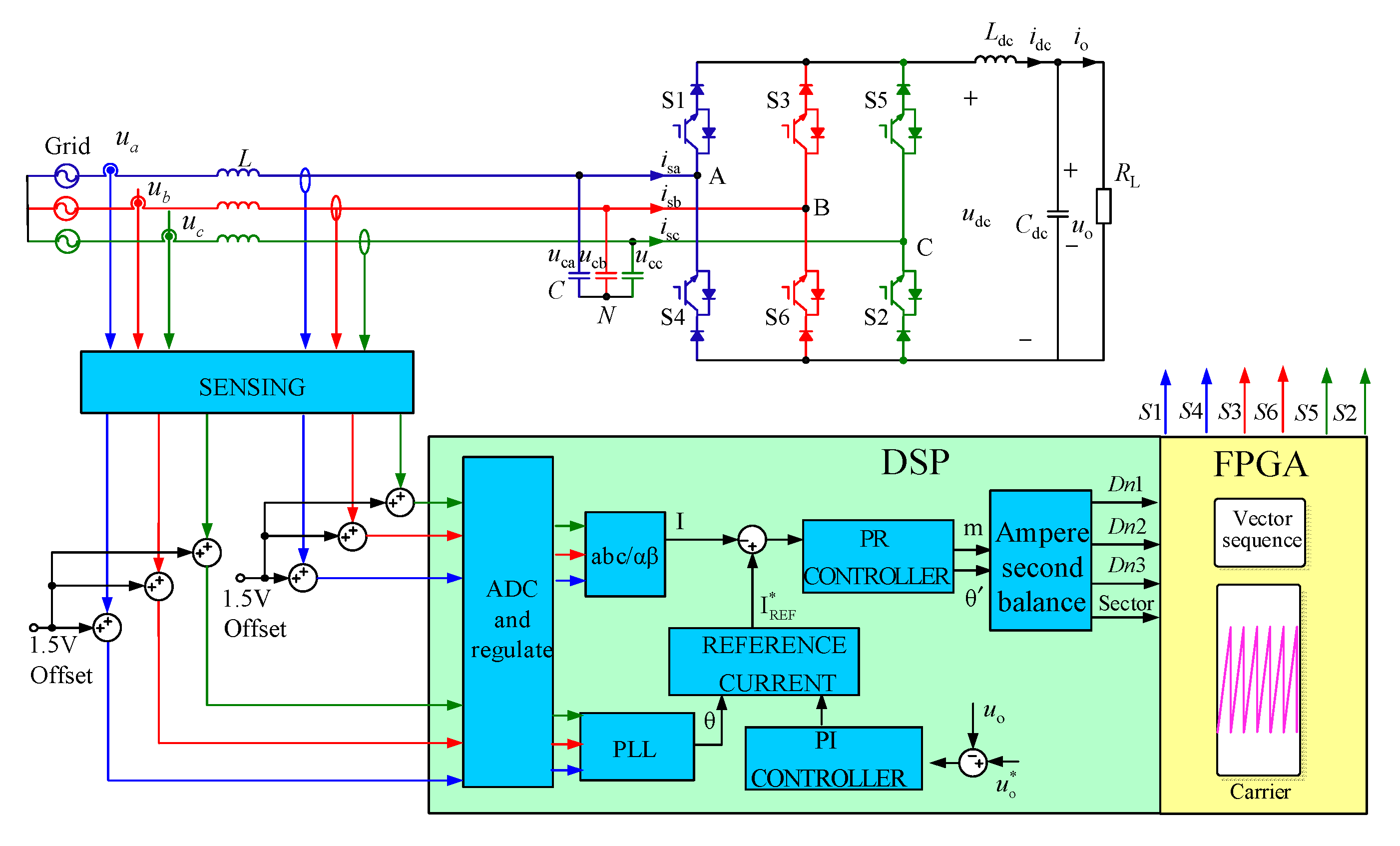
3. Materials and Methods

In order to increase the reverse blocking capability of the switch, a diode is usually connected in series with the switch. However, the conduction of the diode is determined by the voltage at the terminals of the diode, so even if the switch receives a turn-on signal, the current cannot flow through the switch if the diode cannot conduct due to the reverse voltage.

Based on the above discussion of the diode-clamp, a novel overlap-time suppression method is proposed, that is, by analyzing the relationship between the different grid voltage in each sector to control a specific switch (Freewheeling switch) to maintain conduction to build a freewheeling channel. Specifically, leave the switch of the upper bridge arm corresponding to the lowest voltage of u_a, u_b, u_c and the switch of the lower bridge arm corresponding to the highest voltage of u_a, u_b, u_c on as a freewheeling switch to prevent inductor current discontinuity.

When the switching characteristics cause the switch waiting to be turned off to be turned off, and the switch waiting to be turned on has not been turned on, the current can flow to the freewheeling channel, thus ensuring the continuity of DC side inductive current. In addition, since the freewheeling switch is selected by analyzing the grid voltage in each sector, the diode in series with the freewheeling switch is subjected to reverse voltage when the system is operating normally, and the current does not flow through the freewheeling channel, thus not affecting the normal operation of the current source converter. Take sector 1 as an example, u_a is the maximum and u_c is the minimum, so let S5 of the upper bridge arm and S4 of the lower bridge arm turn on. The freewheeling switch for each sector is shown in Table 3.

Taking sector 1 as an example, the grid voltage relationship is u_a > u_b > u_c, and the corresponding switching sequence is i₁ (S1, S6) i₂ (S1, S2) i₃ (S2, S3). By looking up Table 3, it can be seen that the switch S4 and S5 are always left on as the freewheeling switch, and the overlap time is not set. Figure 7 shows the switching process. The block diagram for implementation is shown in Figure 8. The specific operation process is as follows:

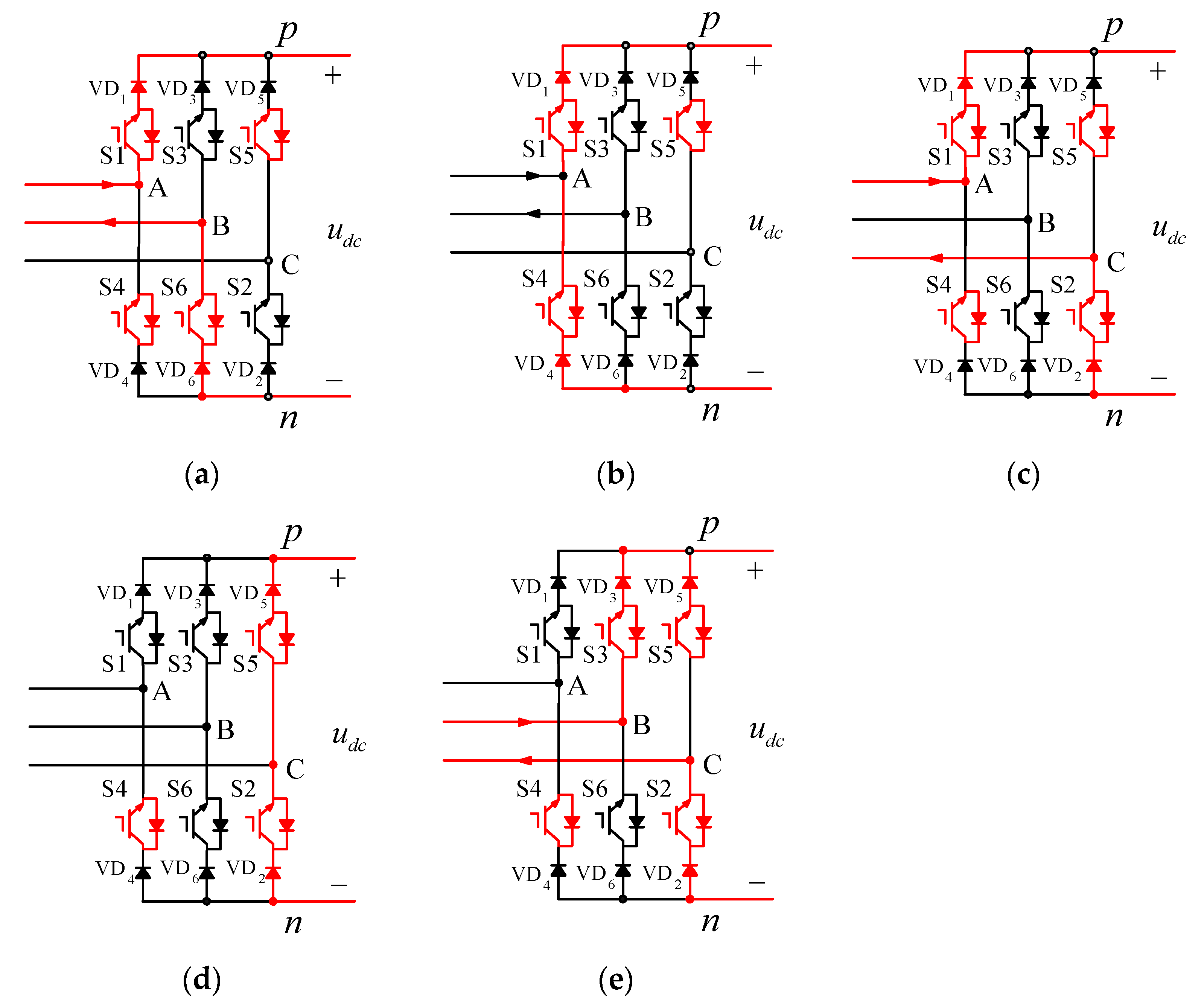
(1): As shown in Figure 7a, the switches S1, S6, S4, S5 receive the turn-on signal and are turned on, but the current can only flow from high voltage to low voltage. In other words, the diodes VD4 and VD5 are subject to reverse voltage because u_a > u_b > u_c, there the inductor current only flows through S1 and S6 at this time.
(2): As shown in Figure 7b, when S6 switches to S2, if the switch S6 to be turned off has been turned off and the switch S2 to be turned on has not been turned on due to the switching characteristics, the current will flow through the freewheeling switch S4, which will avoid discontinuity in the inductor current, and the inductor current flows through S1 and S4 at this time.
(3): As shown in Figure 7c, when the switch S2 is turned on, VD4 is subjected to a reverse voltage at this time, so the inductor current cannot flow through S4, and the inductor current flows through S1 and S2 at this time.
(4): As shown in Figure 7d, when the S1 switches to S3, if the S1 to be turned off has been turned off and the S3 to be turned on has not yet been turned on due to the switching characteristics, the current will flow through the freewheeling switch S5, thus avoiding discontinuity in the inductor current, and the inductor current flows through S2 and S5 at this time.
(5): As shown in Figure 7e, when the switch S3 is turned on, VD5 is subjected to a reverse voltage at this time, so the inductor current cannot flow through S5, and the inductor current flows through S3 and S2 at this time.

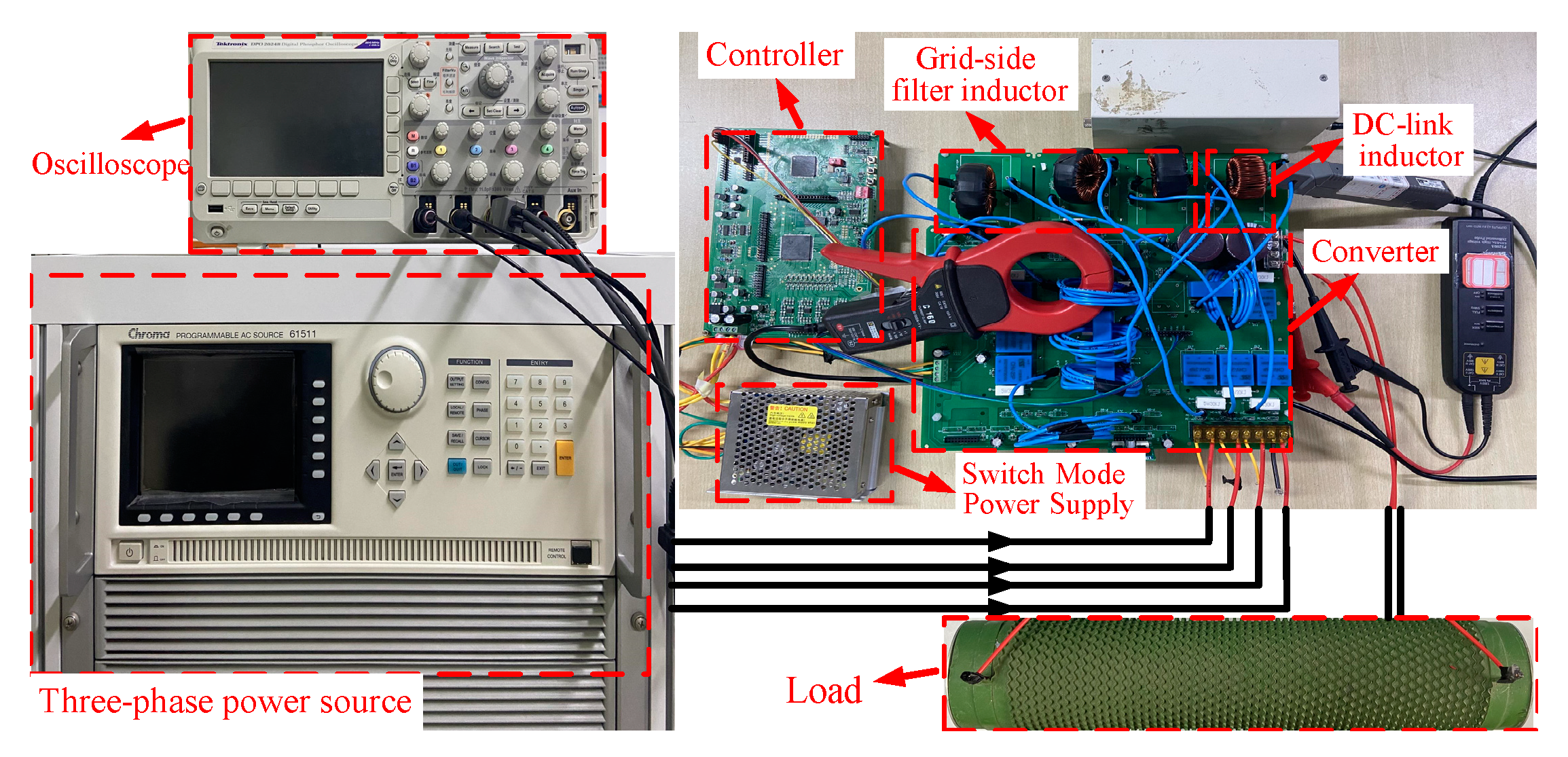
4. Main Results

In order to verify the effectiveness of the proposed control strategy, a simulation model was built using MATLAB/Simulink. In addition, the effectiveness and feasibility of the proposed control strategy were verified by experiments on a three-phase CSC prototype in Figure 9. The control algorithm was implemented on a TMS320F28335 DSP + XC3S400 FPGA digital platform. A Chroma Programmable ac Source 61511 was used as the three-phase power source to provide three-phase voltages to the CSC, and the switching device IGBT on the CSC platform was selected from Infineon’s 1KW40T120. Each power IGBT was connected in series with a diode, which was selected as a fast recovery diode of model DSEI30-10. The system and control parameters are shown in Table 4.

The driving waveform of switches are shown in Figure 10, and the proposed method controls switch differently to maintain conduction in different sectors. In sectors 1, 2, 3, 4, u_c is minimum, so S5 of the upper bridge arm is always turned on; In sectors 5, 6, 7, 8, u_a is minimum, so S1 of the upper bridge arm is always turned on; In sectors 9, 10, 11, 12, u_b is minimum, so S3 of the upper bridge arm is always turned on; In sectors 1, 2, 11, 12, u_a is maximum, so S4 of the lower bridge arm is always turned on; In sectors 3, 4, 5, 6, u_b is maximum, so S6 of the lower bridge arm is always turned on; In sectors 3, 4, 5, 6, u_b is maximum, so S6 of the lower bridge arm is always turned on. In sectors 3, 4, 5 and 6, u_b is the largest, so S6 of the lower bridge arm is always turned on; In sectors 7, 8, 9 and 10, u_c is the largest, so S2 of the lower bridge arm is always turned on.

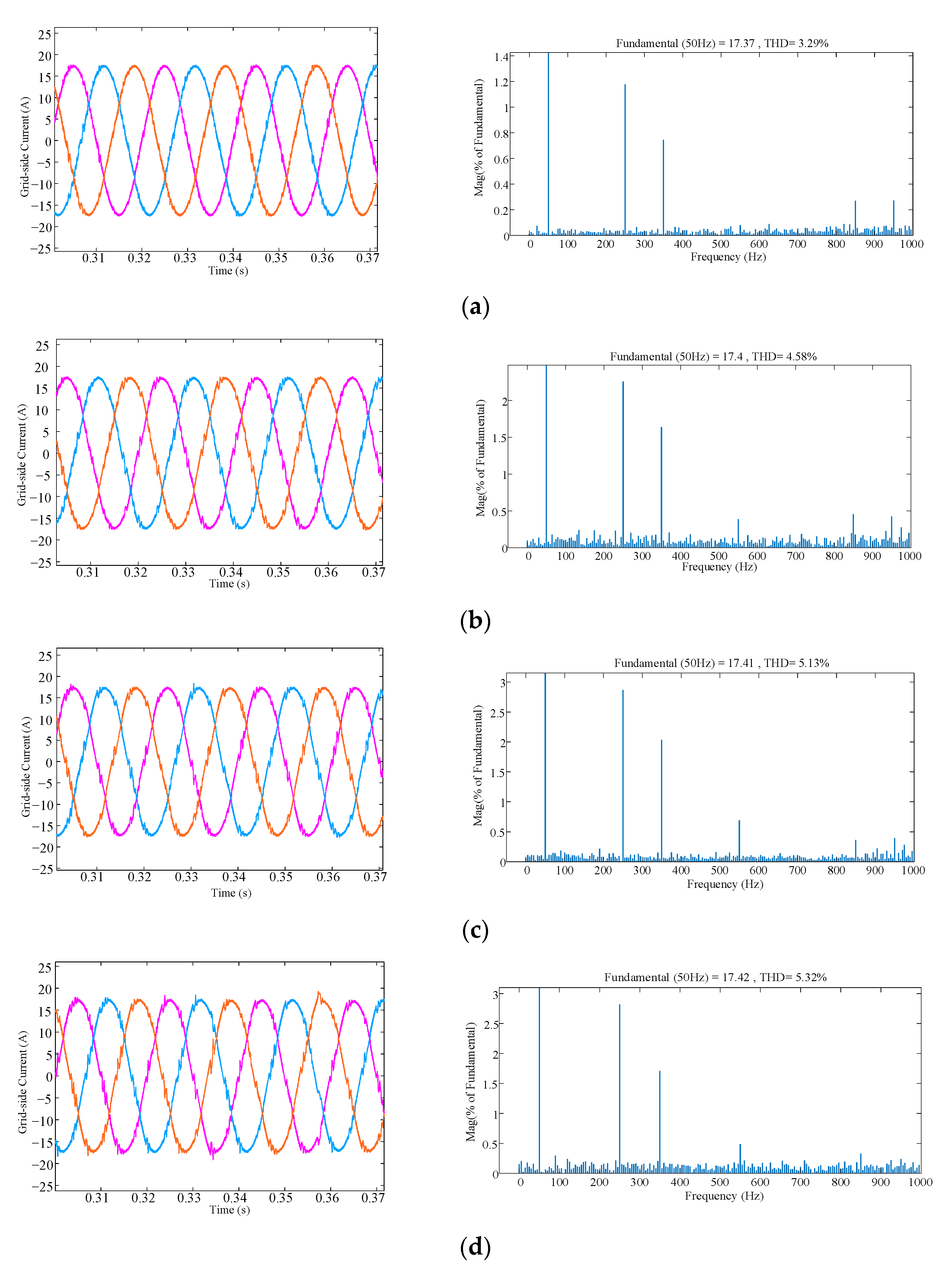
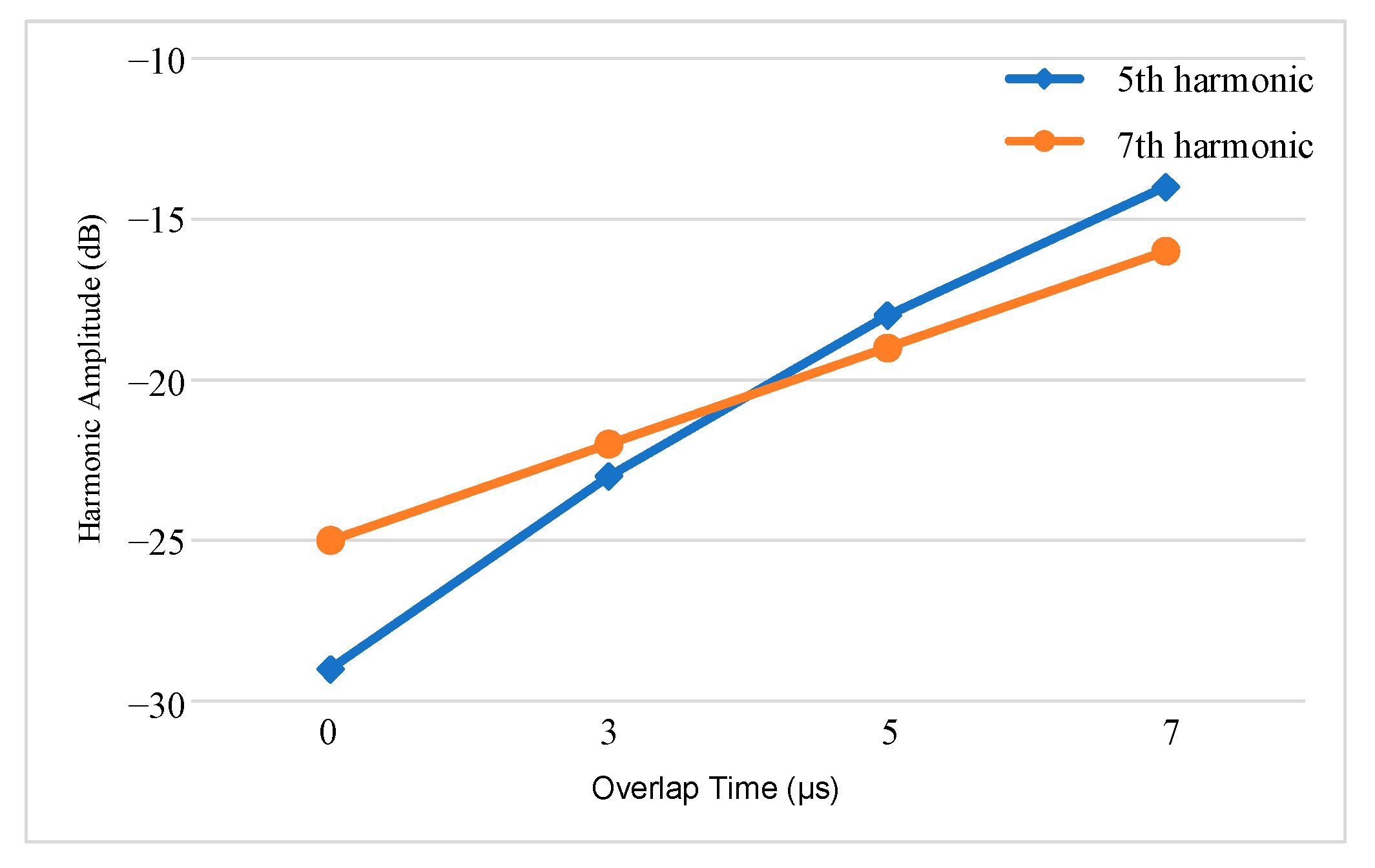
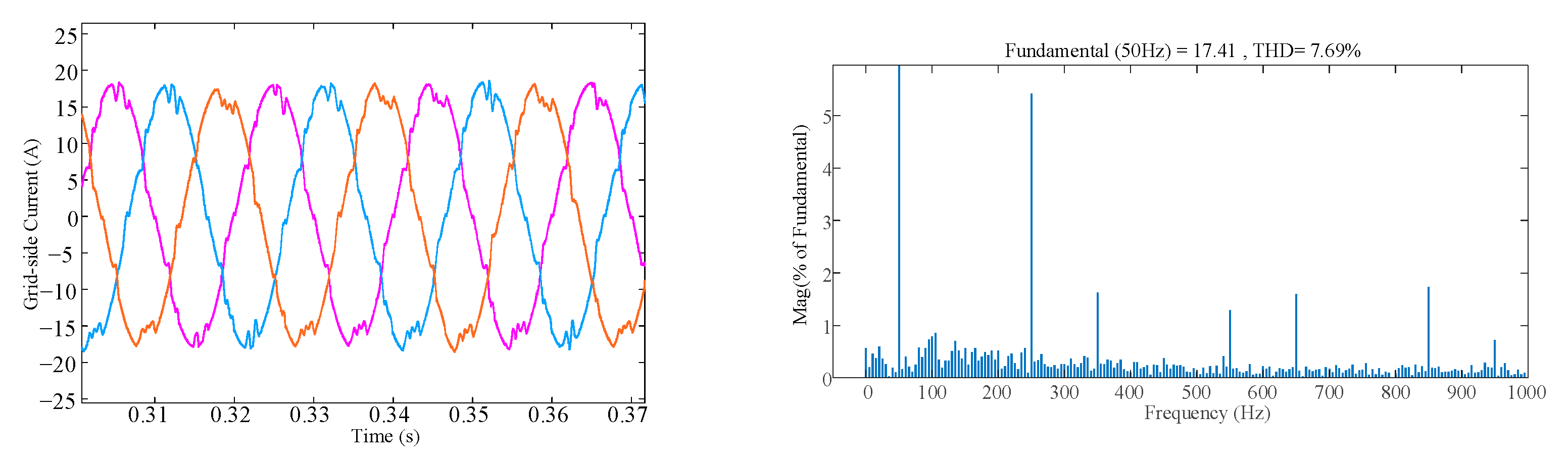
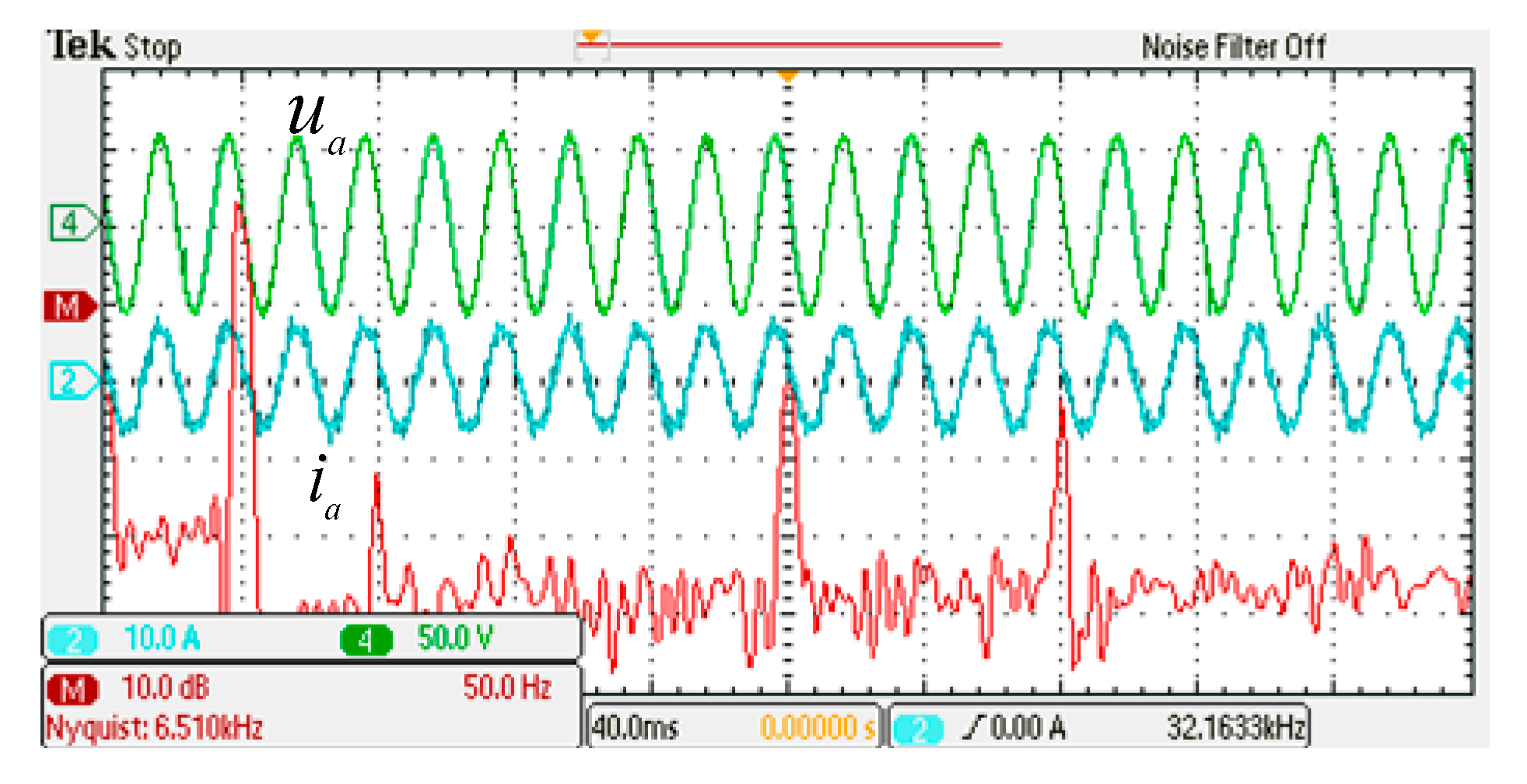
4.1. Results Analysis of Overlap-Time Variation

Figure 11 shows the grid current simulation waveforms and spectrum analysis for different overlap times at a switching frequency of 10 kHz. As shown in Figure 11, the total harmonic distortion (THD) of grid currents without adding the overlap time is 3.29%, and the 5th and 7th harmonic components are small. When the 3 μs overlap time is added, although the grid current distortion is 4.58%, which satisfies the requirements of IEEE Std 519-2014, the 5th and 7th harmonics increase significantly, and with the continued increase of overlap time, the 5th and 7th harmonic components increase more obviously, and the grid current distortion does not even satisfy the requirements of IEEE Std 519-2014.

Figure 12 shows the grid current experimental waveforms and the corresponding fast Fourier transform (FFT) analysis for different overlap times at a switching frequency of 10 kHz. It can be seen that the lower harmonics, especially the 5th and 7th harmonic components, increase significantly with the increase in overlap time. As shown in Figure 12a, the 5th and 7th harmonic components are −29 dB (5th) and −25 dB (7th) when the overlap time is not added, while when the overlap time of 7 μs is added, the 5th and 7th harmonic components are −14 dB (5th) and −16 dB (7th), respectively. Figure 13 shows the 5th and 7th harmonic amplitudes with different overlap times at 10 kHz switching frequency. As show in Figure 13, compared with the harmonic component amplitude without the overlap time, the 5th and 7th harmonic component amplitude corresponding to the overlap time of 7 μs is about double, and the grid current distortion increases due to the increase in the 5th and 7th harmonic components.

In general, the simulation results are consistent with the experimental results, showing that the 5th and 7th harmonic components introduced in the grid current increase with the overlap time, which proves the correctness of the theoretical analysis of Equation (5).

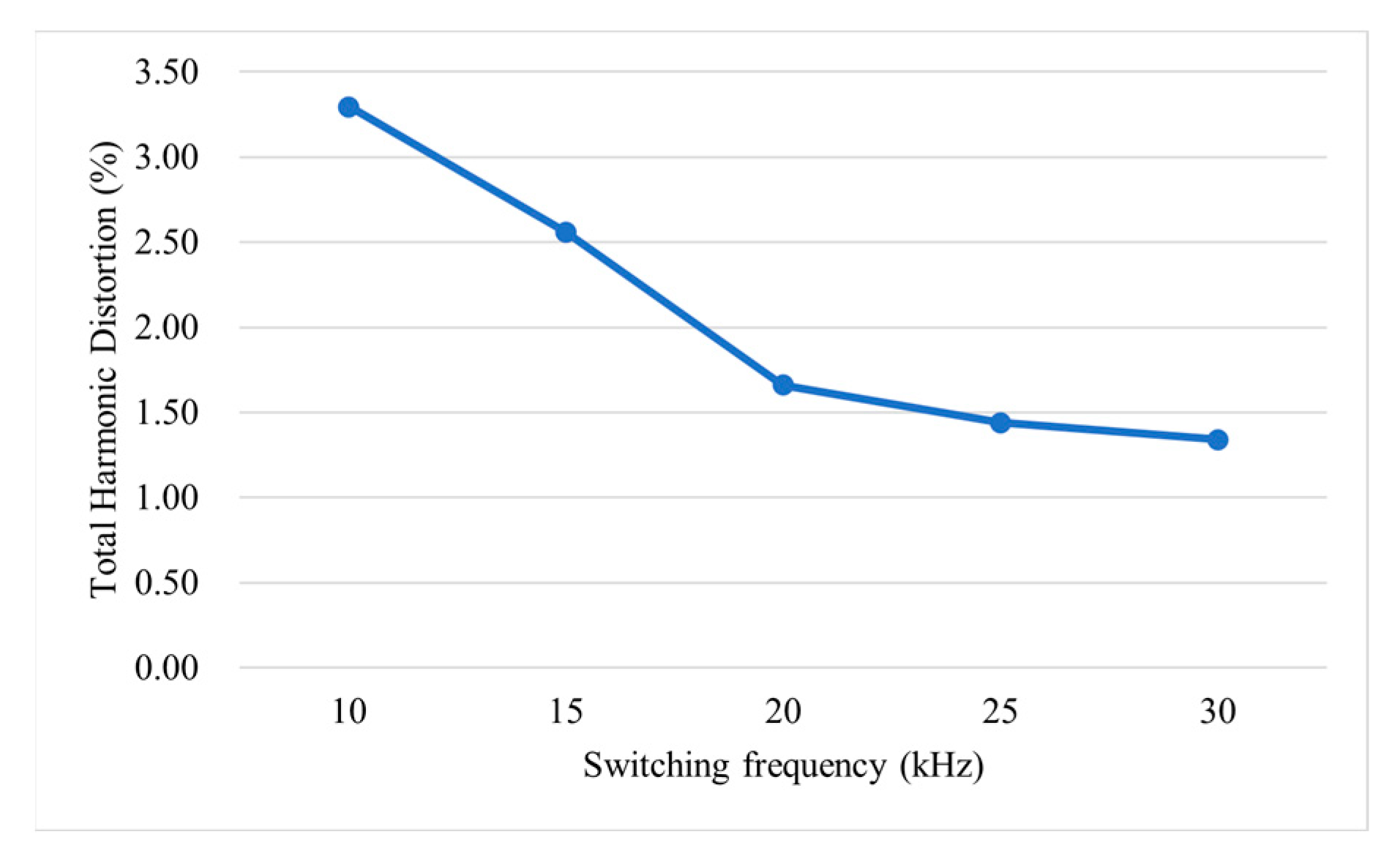
4.2. Results Analysis of Switching Frequency Variation

Figure 14 shows the grid current simulation waveform and spectrum analysis when the switching frequency is 40 kHz and the overlap time is set to 5 μs, which shows that the grid current distortion is 7.69%. Compared with Figure 11c, the 5th and 7th harmonic components and the THD of the grid current at the switching frequency of 40 kHz are significantly larger than those at the switching frequency of 10 kHz.

Figure 15 shows the grid current experimental waveform and the corresponding FFT analysis when the overlap time is 3 μs and the switching frequency is 40 kHz, whose 5th and 7th harmonic component amplitudes are −10 dB (5th) and −12 dB (7th), respectively, while the 5th and 7th harmonic component amplitudes are −23 dB (5th) and −22 dB (7th) at the switching frequency of 10 kHz as shown in Figure 12b. Compared with the 5th and 7th harmonic component amplitude at 10 kHz, the 5th and 7th harmonic component amplitude at 40 kHz switching frequency is about double, and the grid current waveform distortion is obvious.

In general, the simulation results are consistent with the experimental results, showing that the 5th and 7th harmonic components introduced in the grid current increase with the switching frequency, which proves the correctness of the theoretical analysis of Equation (5).

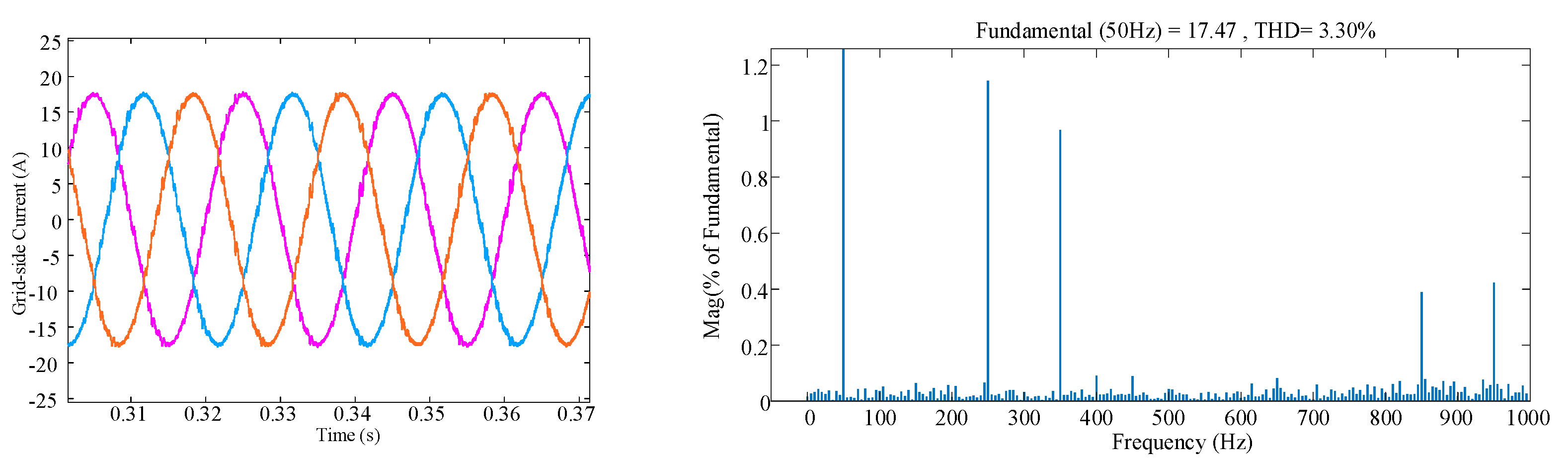
4.3. Result Analysis of The Proposed Scheme

Figure 16 shows the grid current simulation waveform and spectrum analysis of the proposed method. It can be seen that the grid current THD of the proposed scheme is 3.30% and the 5th and 7th order harmonic components are low, which is almost the same with the ideal situation of the grid current without overlap time in Figure 11a.

Figure 17 shows the experimental results of the grid current and the corresponding FFT analysis for the proposed method. It can be observed that the 5th and 7th harmonic components of the proposed scheme are −29 dB (5th) and −25 dB (7th), which are the same as the 5th and 7th harmonic components of Figure 12a when no overlap time is added.

Figure 18 shows the grid current THD of the proposed scheme at different switching frequencies. As shown in Figure 18, the proposed scheme can operate properly at different switching frequencies, and the THD decreases as the switching frequency increases.

Overall, the simulation results are consistent with the experimental results, which show that the proposed method improves the harmonic performance of the grid current and suppresses the low-order harmonics introduced by the overlap time through controlling the freewheeling switch to maintain conduction, and the proposed scheme can be used in different frequency situations.

5. Discussion

In this paper, the experimental and simulation results in Part 4.1 show that the 5th and 7th harmonic components introduced in the grid current increase with the overlap time. The experimental and simulation results in part 4.2 show that the 5th and 7th harmonic components introduced in the grid current increase with the switching frequency. Overall, the experimental and simulation results in Parts 4.1 and 4.2 verify that the theoretical analysis on Equation (5) is correct, i.e., the harmonic amplitude introduced in the grid current is proportional to the overlap time and switching frequency. In addition, the experimental and simulation results in Part 4.3 show that the proposed scheme can effectively suppress the overlap-time effect. Although the proposed overlap-time suppression scheme can effectively suppress the overlap-time effect, there are also limitations. First, the overlap-time suppression strategies in this paper are proposed on the basis of space vector modulation, so whether the proposed scheme can be applied to other modulation strategies needs to be further studied. Second, the diode connected in series with the switch will penalize the system’s efficiency. At present, the literature [22] proposed that two thyristors can be used instead of diodes to reduce system losses, and the literature [10] indicated that the use of new semiconductor power devices such as RC-IGBT, a SiC metal oxide semiconductor field effect transistor (MOSFET) and diodes can further improve the efficiency of current-source converters, in other words, follow-up study can try to use other active components to limit the losses.

6. Conclusions

In this paper, the non-nearest three-vector synthesis reference vector method is taken as the object of study to analyze the effect of overlap time on the current-source converter in detail, and the current deviation introduced due to the overlap time is analyzed by Fourier decomposition. The relationship between introduced harmonic and overlap time is derived numerically. An overlap suppression scheme method is proposed and verified by simulation and experimental results. The conclusions obtained are relisted as follows:

(1): The overlap time introduces the 6k + 1(k = 1, 2, 3, …) harmonics in the grid current, and these harmonic components increase with the switching frequency and the overlap time.
(2): The proposed method of constructing a freewheeling channel by controlling a specific switch (Freewheeling switch) to maintain conduction can eliminate the low-order harmonics introduced in the grid current by overlap time.
(3): Simulation and experimental results verify the correctness of the theoretical analysis and the validity of the proposed scheme. Moreover, it is worth noting that the overlap-time suppression effect of the proposed scheme is about 100%.

Author Contributions

Conceptualization, H.D., Q.L. and J.Y.; methodology, H.D., Q.L. and J.Y.; software, H.D., Q.L. and J.Y.; investigation, H.D., Q.L., J.Y., W.W., M.L. and J.M.G.; writing—original draft preparation, H.D. and Q.L.; writing—review and editing, H.D., Q.L., J.Y., W.W., M.L. and J.M.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (No.61903321), the Youth Foundation of Hebei Province Education Department (No.QN2019016) and Qinhuangdao Science and Technology Planning Project (No. 201805A013).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this paper:

CSC	Current-source converter
VSC	Voltage-source converter
DC	Direct current
AC	Alternating current
THD	Total harmonic distortion
IGBT	Insulated gate bipolar transistors
RC-IGBT	Reverse conducting insulated gate bipolar transistors
MOSFET	Metal oxide semiconductor field effect transistor
t_ov	Overlap time
FFT	Fast Fourier transform

References

Li, P.; Xiong, L.; Wu, F.; Ma, M.; Wang, J. Sliding mode controller based on feedback linearization for damping of sub-synchronous control interaction in DFIG-based wind power plants. Int. J. Electr. Power Energy Syst. 2019, 107, 239–250. [Google Scholar] [CrossRef]
Li, P.; Wang, J.; Xiong, L.; Wang, Z. Energy-Shaping Controller for DFIG-Based Wind Farm to Mitigate Subsynchronous Control Interaction. IEEE Trans. Power Syst. 2020, 36, 2975–2991. [Google Scholar] [CrossRef]
Aouichak, I.; Jacques, S.; Bissey, S.; Reymond, C.; Besson, T.; Le Bunetel, J.-C. A Bidirectional Grid-Connected DC–AC Converter for Autonomous and Intelligent Electricity Storage in the Residential Sector. Energies 2022, 15, 1194. [Google Scholar] [CrossRef]
Wang, H.; Wang, S.; Ding, H.; Shi, C.; Jia, D.; Chen, C.; Guerrero, J.M. An Novel Six-Segment Modulation Strategy for Three-Phase Isolated PFC Converter. Energies 2022, 15, 2598. [Google Scholar] [CrossRef]
Fu, X.; Wang, H.; Guo, X.; Shi, C.; Jia, D.; Chen, C.; Guerrero, J.M. A Novel Circulating Current Suppression for Paralleled Current Source Converter Based on Virtual Impedance Concept. Energies 2022, 15, 1952. [Google Scholar] [CrossRef]
Sun, Y.; Liu, Y.; Su, M.; Han, H.; Li, X.; Li, X. Topology and control of a split-capacitor four-wire current source inverter with leakage current suppression capability. IEEE Trans. Power Electron. 2018, 12, 10803–10814. [Google Scholar] [CrossRef]
Wei, Q.; Wu, B.; Xu, D.; Zargari, N.R. Further study on a PWM current-source-converter-based wind energy conversion system considering the DC-link voltage. IEEE Trans. Power Electron. 2019, 6, 5378–5387. [Google Scholar] [CrossRef]
Wei, Q.; Wu, B.; Xu, D.; Zargari, N.R. An Optimized Strategy for PWM Current Source Converter Based Wind Conversion Systems with Reduced Cost and Improved Efficiency. IEEE Trans. Power Electron. 2018, 2, 1202–1210. [Google Scholar] [CrossRef]
Dai, H.; Jahns, T.M.; Torres, R.A. Comparative Evaluation of Conducted Common-Mode EMI in Voltage-Source and Current-Source Inverters using Wide-Bandgap Switches. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 788–794. [Google Scholar]
Dai, H.; Jahns, T.M. Comparative investigation of PWM current source inverters for future machine drives using high-frequency wide band gap power switches. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 2601–2608. [Google Scholar]
Dai, H.; Jahns, T.M.; Torres, R.A. Development of High-Frequency WBG Power Modules with Reverse-Voltage-Blocking Capability for an Integrated Motor Drive using a Current-Source Inverter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1808–1815. [Google Scholar]
Chen, W.; Li, B.; Xu, D.; Cai, L. A Dead-Time Compensation Method for Voltage Source Inverters. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
Gaber, M.; Abdel-Rahim, O.; Orabi, M. Novel Overlap Method to Eliminate Vector Deviation Error in SVM of Current Source Inverters. IEEE Trans. Power Electron. 2021, 2, 2320–2333. [Google Scholar] [CrossRef]
Jiang, S.; Arraño-Vargas, F.; Shen, Z.; Konstantinou, G. The Impact of Overlap Period on the Stability of Current-Controlled Alternate Arm Converter Based on dq Frame Impedance Analysis. Electronics 2022, 11, 301. [Google Scholar] [CrossRef]
Rodríguez-Benítez, O.M.; Ponce-Silva, M.; Aquí-Tapia, J.A.; Claudio-Sánchez, A.; Vela-Váldes, L.G.; Lozoya-Ponce, R.E.; Cortés-García, C. Comparative Performance and Assessment Study of a Current-Fed DC-DC Resonant Converter Combining Si, SiC, and GaN-Based Power Semiconductor Devices. Electronics 2020, 9, 1982. [Google Scholar] [CrossRef]
Bai, Z.; Zhang, Z.; Ruan, X. A natural soft-commutation PWM scheme for current source converter and its logic implementation. IEEE Trans. Ind. Electron. 2011, 7, 2772–2779. [Google Scholar] [CrossRef]
Sayed, M.G.; Abdel-Rahim, O.; Orabi, M. Comparative Study to Investigate the Effect of Five VS Seven Segment Modulation Sequence on the Waveform Distortion Resulted by the Overlap Time in Current Source Inverter. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 576–580. [Google Scholar]
Qin, H.; Zhang, X.; Zhu, Z.; Ma, C.; Xu, H. Influence of overlap time on the AC grid current of current source PWM rectifier and restraining method. Trans. China Electrotech. Society. 2016, 12, 142–152. [Google Scholar]
Liu, P.; Wang, Z.; Xu, Y.; Xiao, H.; Li, Y.W. Optimal Overlap-Time Distribution of Space Vector Modulation for Current-Source Rectifier. IEEE Trans. Ind. Electron. 2021, 6, 4586–4597. [Google Scholar] [CrossRef]
Geng, Y.; Deng, R.; Dong, W.; Wang, K.; Liu, H.; Wu, X. An Overlap-Time Compensation Method for Current-Source Space-Vector PWM Inverters. IEEE Trans. Power Electron. 2018, 4, 3192–3203. [Google Scholar] [CrossRef]
Guo, X.; Yang, Y.; Wang, X. Optimal space vector modulation of current-source converter for DC-link current ripple reduction. IEEE Trans. Ind. Electron. 2019, 3, 1671–1680. [Google Scholar] [CrossRef]
Jacques, S.; Reymond, C.; Le Bunetel, J.-C.; Benabdelaziz, G. Comparison of the power balance in a Totem-Pole Bridgeless PFC Topology with several inrush current strategies. J. Electr. Eng. 2021, 72, 12–19. [Google Scholar] [CrossRef]

Figure 1. Schematic diagram of current-source converter.

Figure 2. Space current vector diagram.

Figure 3. Terminal voltage for each phase.

Figure 4. Mechanism for CSC With Non-Nearest Three Vectors modulation scheme in sector 1.

Figure 5. Overlap time effect in sector 1.

Figure 6. Mapping of the current deviation i_dev of i₁.

Figure 7. Switching process diagram. (a) S1, S6 are effectively turned on. (b) S6 switches to S2. (c) S1, S2 are effectively turned on. (d) S1 switches to S3. (e) S2, S3 are effectively turned on.

Figure 8. Block diagram for implementation.

Figure 9. Experimental system of a three-phase current source converter.

Figure 10. Switch drive waveform (a) Switch S1, S4. (b) Switch S3, S6. (c) Switch S2, S5. (Left: without overlap-time suppression scheme; right: proposed scheme).

Figure 11. Simulation results of the grid current with different overlap times at 10 kHz switching frequency. (a) t_ov = 0 μs. (b) t_ov = 3 μs. (c) t_ov = 5 μs. (d) t_ov = 7 μs.

Figure 12. The experimental waveforms of the grid currents and the corresponding FFT analysis for different overlap times at 10 kHz switching frequency. (a) t_ov = 0 μs. (b) t_ov = 3 μs. (c) t_ov = 5 μs. (d) t_ov = 7 μs.

Figure 13. Experimental waveforms of the 5th and 7th harmonic amplitudes with different overlap times at 10 kHz switching frequency.

Figure 14. Simulation results of grid currents with switching frequency of 40 kHz.

Figure 15. The experimental waveforms of the grid current and the corresponding FFT analysis for the 3 μs overlap time at 40 kHz switching frequency.

Figure 16. Simulation results of grid current with proposed method.

Figure 17. The experimental waveforms of the grid current and the corresponding FFT analysis for the proposed scheme at 10 kHz switching frequency.

Figure 18. The grid current THD with different switching frequencies.

Table 1. Switching states and space vectors of CSC.

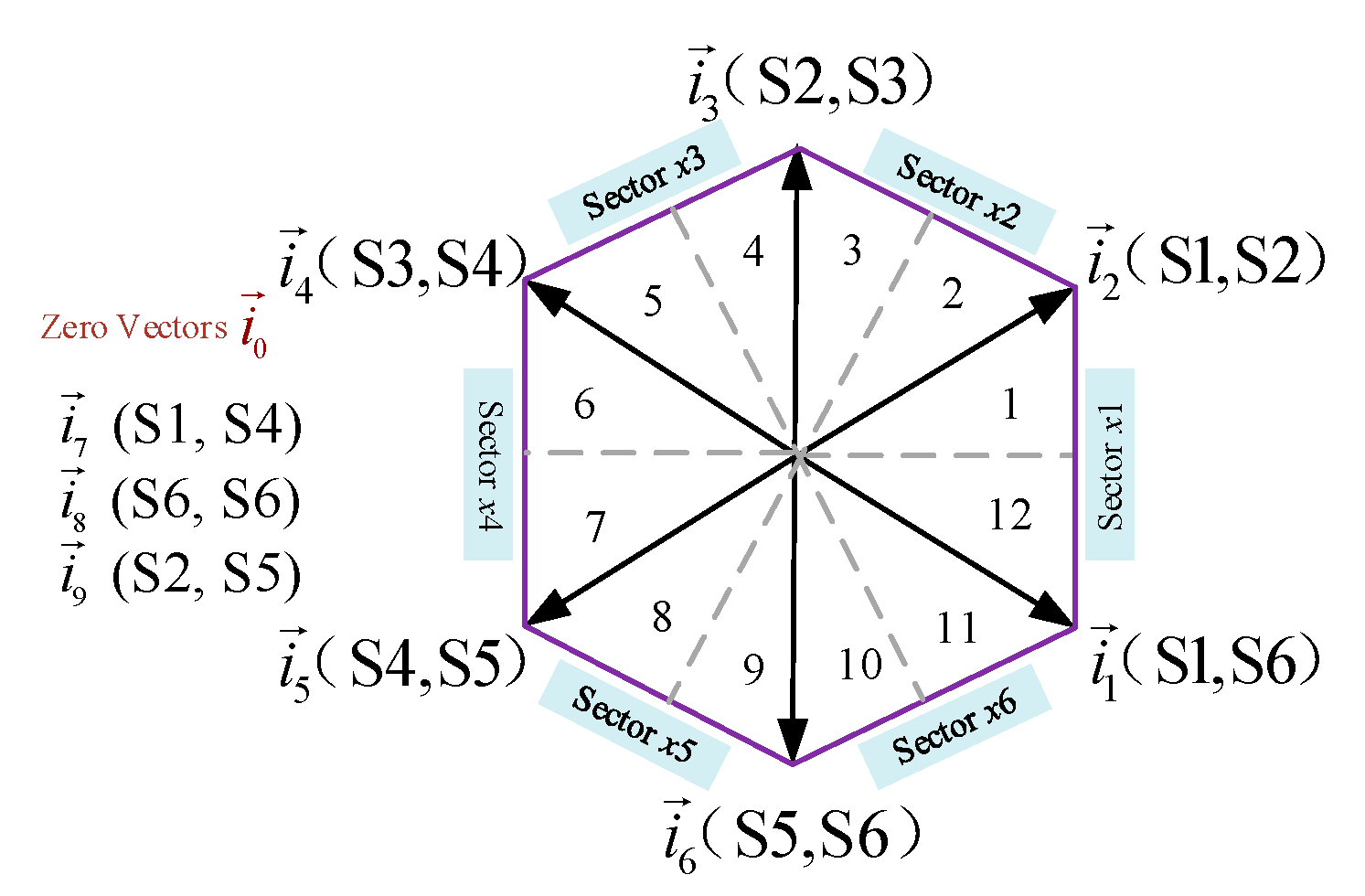
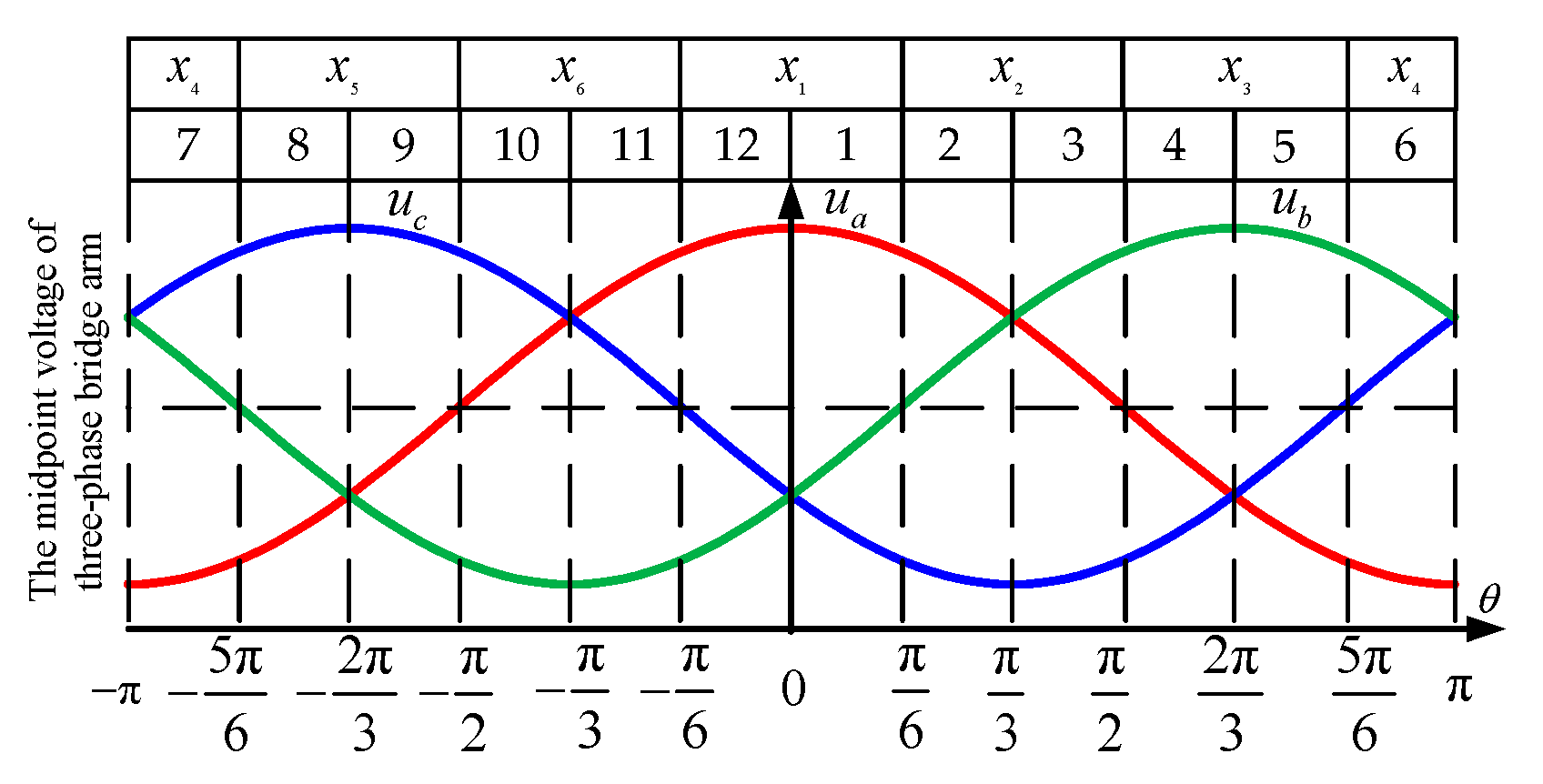
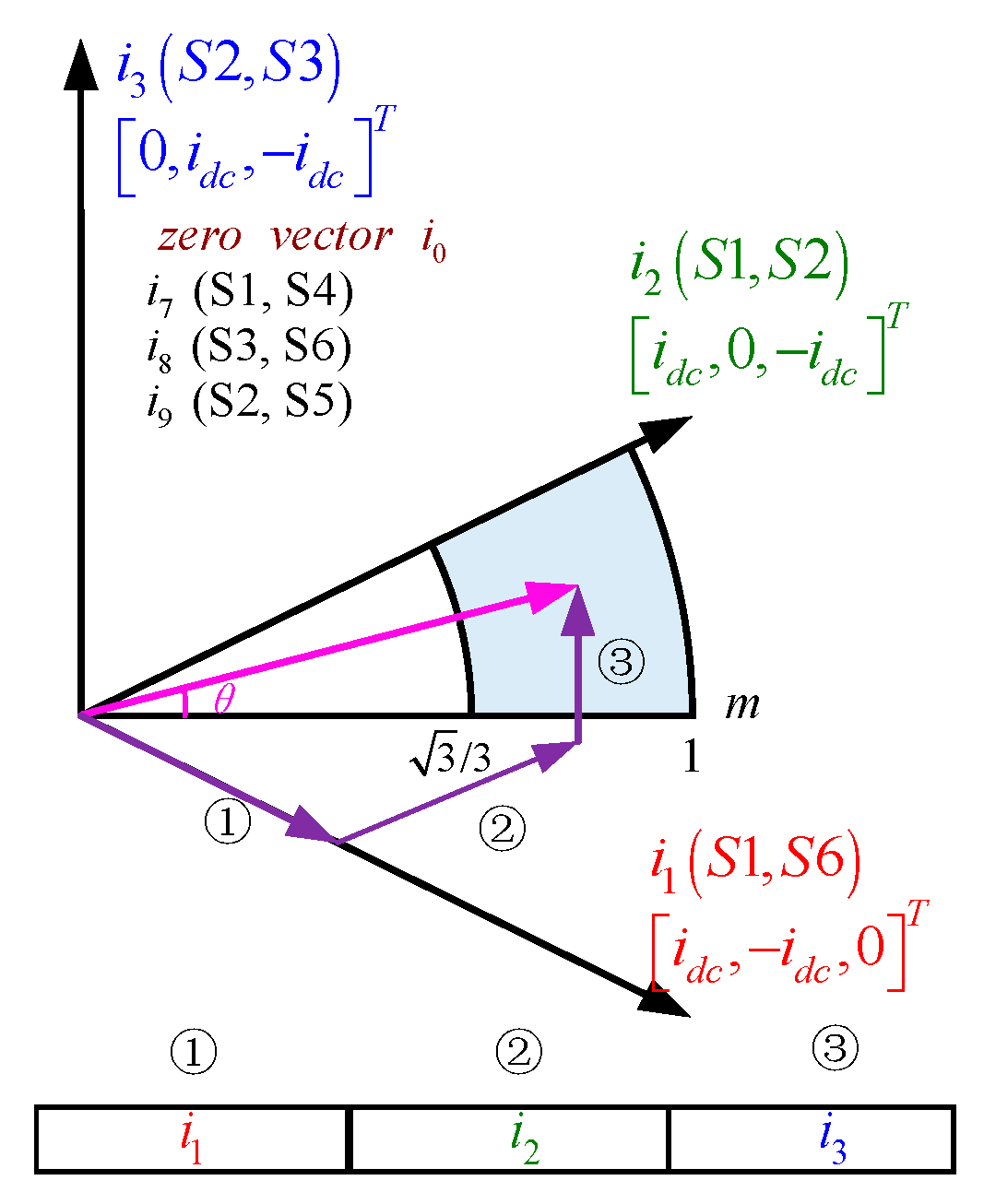
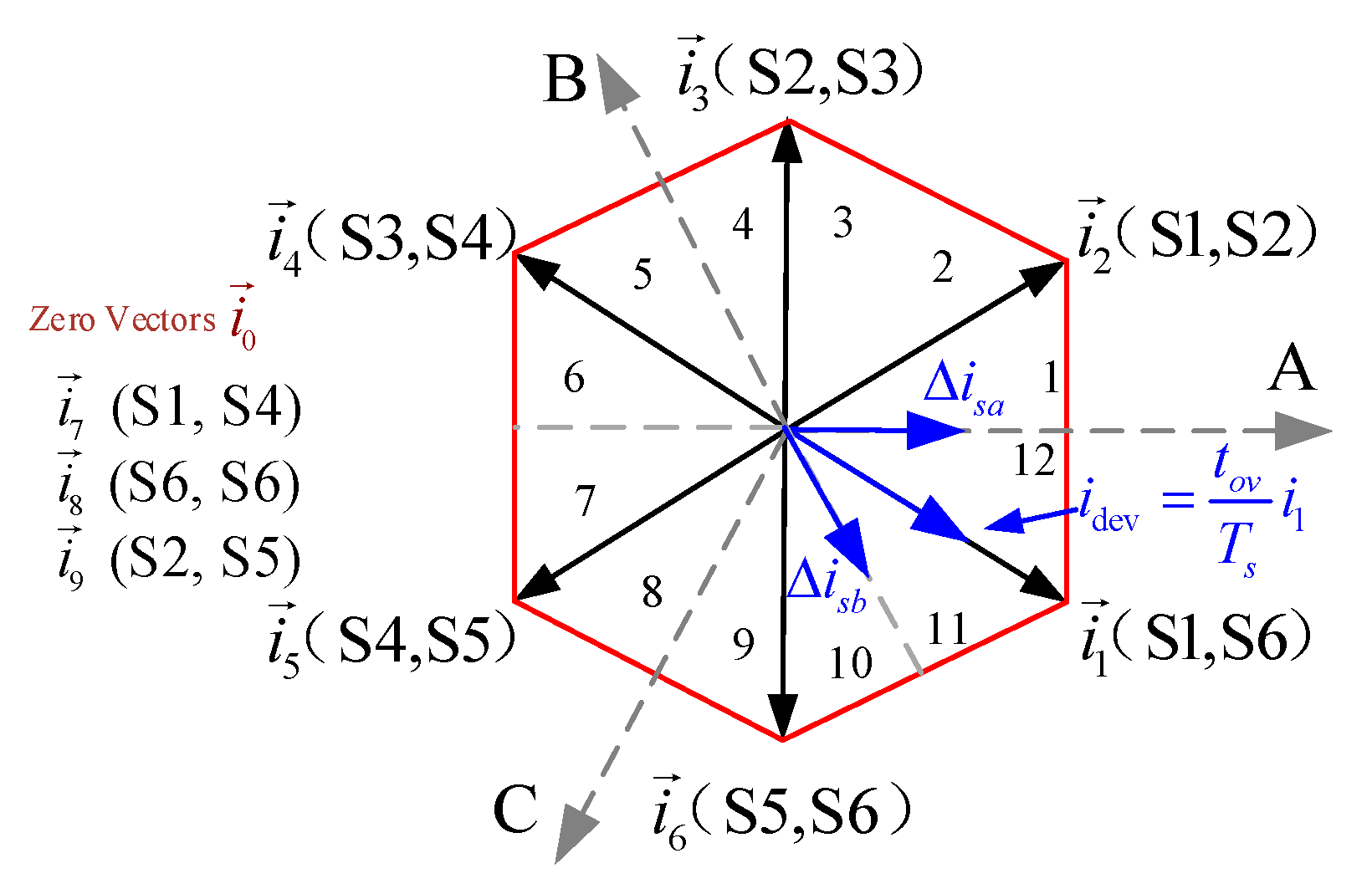
Type	Space Vector	Switching States
Active Vectors	i₁	S₁, S₆
	i₂	S₁, S₂
	i₃	S₂, S₃
	i₄	S₃, S₄
	i₅	S₄, S₅
	i₆	S₅, S₆
Zero Vectors	i₇	S₁, S₄
	i₈	S₃, S₆
	i₉	S₂, S₅

Table 2. Effect of overlap time with the non-nearest three vector.

Sector	Terminal Voltage	$Δ i_{s a}$	$Δ i_{s b}$	$Δ i_{s c}$
1	u_a > u_b > u_c	$i_{d c} t_{o v} f_{s}$	$- i_{d c} t_{o v} f_{s}$	0
2	u_a > u_b > u_c	0	$i_{d c} t_{o v} f_{s}$	$- i_{d c} t_{o v} f_{s}$
3	u_b > u_a > u_c	$i_{d c} t_{o v} f_{s}$	0	$- i_{d c} t_{o v} f_{s}$
4	u_b > u_a > u_c	$- i_{d c} t_{o v} f_{s}$	$i_{d c} t_{o v} f_{s}$	0
5	u_b > u_c > u_a	0	$i_{d c} t_{o v} f_{s}$	$- i_{d c} t_{o v} f_{s}$
6	u_b > u_c > u_a	$- i_{d c} t_{o v} f_{s}$	0	$i_{d c} t_{o v} f_{s}$
7	u_c > u_b > u_a	$- i_{d c} t_{o v} f_{s}$	$i_{d c} t_{o v} f_{s}$	0
8	u_c > u_b > u_a	0	$- i_{d c} t_{o v} f_{s}$	$i_{d c} t_{o v} f_{s}$
9	u_c > u_a > u_b	$- i_{d c} t_{o v} f_{s}$	0	$i_{d c} t_{o v} f_{s}$
10	u_c > u_a > u_b	$i_{d c} t_{o v} f_{s}$	$- i_{d c} t_{o v} f_{s}$	0
11	u_a > u_c > u_b	0	$- i_{d c} t_{o v} f_{s}$	$i_{d c} t_{o v} f_{s}$
12	u_a > u_c > u_b	$i_{d c} t_{o v} f_{s}$	0	$- i_{d c} t_{o v} f_{s}$

Table 3. Freewheeling switch in each sector.

Sector	Terminal Voltages	Freewheeling Switch
1	u_a > u_b > u_c	S4, S5
2	u_a > u_b > u_c	S4, S5
3	u_b > u_a > u_c	S5, S6
4	u_b > u_a > u_c	S5, S6
5	u_b > u_c > u_a	S1, S6
6	u_b > u_c > u_a	S1, S6
7	u_c > u_b > u_a	S1, S2
8	u_c > u_b > u_a	S1, S2
9	u_c > u_a > u_b	S2, S3
10	u_c > u_a > u_b	S2, S3
11	u_a > u_c > u_b	S3, S4
12	u_a > u_c > u_b	S3, S4

Table 4. System and control parameters.

Parameter	Symbol	Simulation	Experiment
Phase Voltage	V_i	220 V	40 V
DC Inductance	L_p	5 mH	5 mH
DC Capacitor	C_dc	940 μF	940 μF
Filter Inductance	L	2.5 mH	4 mH
Filter Capacitor	C	20 μF	9.4 μF
Load	R	20 Ω	30 Ω

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Ding, H.; Li, Q.; Yuan, J.; Wang, W.; Li, M.; Guerrero, J.M. A Novel Overlap-Time Effect Suppression for Current Source Converter. Energies 2022, 15, 6035. https://doi.org/10.3390/en15166035

AMA Style

Ding H, Li Q, Yuan J, Wang W, Li M, Guerrero JM. A Novel Overlap-Time Effect Suppression for Current Source Converter. Energies. 2022; 15(16):6035. https://doi.org/10.3390/en15166035

Chicago/Turabian Style

Ding, Hao, Quanjie Li, Jing Yuan, Wei Wang, Mingming Li, and Josep M. Guerrero. 2022. "A Novel Overlap-Time Effect Suppression for Current Source Converter" Energies 15, no. 16: 6035. https://doi.org/10.3390/en15166035

APA Style

Ding, H., Li, Q., Yuan, J., Wang, W., Li, M., & Guerrero, J. M. (2022). A Novel Overlap-Time Effect Suppression for Current Source Converter. Energies, 15(16), 6035. https://doi.org/10.3390/en15166035

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

A Novel Overlap-Time Effect Suppression for Current Source Converter

Abstract

1. Introduction

2. Related Work

2.1. Operation Mechanism for Non-Nearest Three Vectors Scheme

2.2. Effect of Overlap Time with Non-Nearest Three Vectors Modulation Scheme

3. Materials and Methods

4. Main Results

4.1. Results Analysis of Overlap-Time Variation

4.2. Results Analysis of Switching Frequency Variation

4.3. Result Analysis of The Proposed Scheme

5. Discussion

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI