Abstract
An incoming canonical spatially developing turbulent boundary layer (SDTBL) over a 2-D curved hill is numerically investigated via the Reynolds-averaged Navier–Stokes (RANS) equations plus two eddy-viscosity models: the SST (henceforth SST) and the Spalart–Allmaras (henceforth SA) turbulence models. A spatially evolving thermal boundary layer has also been included, assuming temperature as a passive scalar ( = 0.71) and a turbulent Prandtl number, , of 0.90 for wall-normal turbulent heat flux modeling. The complex flow with a combined strong adverse/favorable streamline curvature-driven pressure gradient caused by concave/convex surface curvatures has been replicated from wind-tunnel experiments from the literature, and the measured velocity and pressure fields have been used for validation purposes (the thermal field was not experimentally measured). Furthermore, direct numerical simulation (DNS) databases from the literature were also employed for the incoming turbulent flow assessment. Concerning first-order statistics, the SA model demonstrated a better agreement with experiments where the turbulent boundary layer remained attached, for instance, in , , and predictions. Conversely, the SST model has shown a slightly better match with experiments over the flow separation zone (in terms of and ) and in profiles just upstream of the bubble. The Reynolds analogy, based on the ratio, holds in zero-pressure gradient (ZPG) zones; however, it is significantly deteriorated by the presence of streamline curvature-driven pressure gradient, particularly due to concave wall curvature or adverse-pressure gradient (APG). In terms of second-order statistics, the SST model has better captured the positively correlated characteristics of and or positive Reynolds shear stresses ( > 0) inside the recirculating zone. Very strong APG induced outer secondary peaks in and turbulence production as well as an evident negative slope on the constant shear layer.
1. Introduction
1.1. Scope of the Present Work
There is still much to understand in the science of computational fluid dynamics (CFD) for turbulent flows, particularly, in the aspects of wall curvature effects with passive scalar transport. Describing this type of flow as “unpredictable” carries much weight as a mystery, so it is more appreciable in the present day to use the word “chaotic” instead. Still, chaos requires to be explained in a more emphatic way to strangers of this science. However, solving this issue will not occur in this work.
In the case of turbulent flow over a curved hill, separation zones will occur due to the strong adverse-pressure gradient (APG) or flow deceleration caused by the presence of convex wall curvature. An incoming horizontal airstream at 20 m/s passing over a simple curved protuberance of 1.284 m long with a radius of 1.08 m from the experiments of Baskaran et al. [1] is considered as a validation tool. In this scenario, a 2D numerical assessment will be performed with scope to the flow’s separation zone velocity and with the presence of temperature in the simulation as a passive scalar. First, a fundamental literature review will be carried out for flow separation by wall curvature and standard turbulent models. The numerical approach will be using a RANS (Reynolds-averaged Navier–Stokes) model. Using open-source CFD software OpenFOAM®, the velocity field will be solved in the scenario of considering a molecular Prandtl of 0.71 and 0.90 turbulent Prandtl number (i.e., air as the working fluid) and two turbulent models shear stress transport (SST) [2] and Spalart–Allmaras (SA) [3]. The inclusion of temperature is done based on the theory of passive scalar transport as in [4]. The turbulent transport of passive scalars is crucial in many industrial applications of technological importance, such as in turbine-blade film cooling, heat transfer in electronic/mechanical devices, chemicals dissolved in gases, and contaminant/humidity dispersed in atmospheric flow, to name a few examples. Furthermore, a passive scalar is defined as a diffusive contaminant that exists in such a low concentration in a flow that it does not affect the dynamics of the fluid motion (Warhaft [5]). However, that low concentration of passive scalar is sufficient to cause a significant impact on energy expenditures, air pollution, and the design of chemical processes. Results obtained will be discussed to finally present recommendations for future work improvement in this study. This article represents an improved extension of our conference paper (Paeres et al. [6]).
1.2. Background
Numerically solving the governing equations for turbulent flows requires much computational power, and often these resources are not readily available. Therefore, formulating models that significantly reduce the computational power requirement and maintain high precision between results and proper solution is a simply appreciable benefit. Among the existing CFD categories, the most commonly known are RANS (Reynolds-averaged Navier–Stokes), LES (large eddy simulation) and DNS (direct numerical simulation) [7]. As stated in the name, DNS directly solves the governing formulation of all fluid flows called the Navier–Stokes equations; it does not use turbulent models and requires significant computational resources. As a consequence, if one desires to perform DNS, it is mandatory to employ a highly scalable and efficient flow solver, not to mention if the idea is to predict spatially developing turbulent boundary layers (SDTBL) implying accurate turbulent time-dependent inflow conditions. Therefore, DNS requires researchers’ skills, expertise, and abilities in HPC and parallel programming not only during the running but also in the postprocessing stage [8]. With the advent of powerful supercomputers, it has become easier to push the boundaries of turbulent boundary layer simulations at higher Reynolds numbers via DNS [9,10]. On the other hand, LES models the dynamics and influence of Kolmogorov scales but is reasoned in using a borderline as a spatial filter; large-scale motions (called large eddies) are computed directly, and only the small-scale motions (considered eddies of thermal energy dissipation) are modeled, resulting in a significant reduction in computational resources compared to the DNS approach. However, this effort reduction depends on the analyzed geometry: it is well known that in wall-bounded flows even the “inertial subrange scales” located in the near wall region could be very small. Thus, the computing and running effort reduction by considering LES with respect to DNS could be limited to one order of magnitude, at most, according to the present author’s experience. Among these three categories, RANS is the approach where the simulation framework is highly simplified since the whole power spectra of flow fluctuations are modeled. Despite its simplicity and limitations on complex geometries, RANS may supply important insight into the flow. Within RANS literature for turbulent flows, there are four most popularly used turbulent models, namely: , standard , shear stress transport, and Spalart–Allmaras.
The term flow separation does not precisely imply that the actual fluid ceases contact with the body where the flowing occurs [11]. This detachment usually describes when the flow’s boundary layer abruptly modifies interactions with the body. For example, when a decelerated fluid around bodies flows in reverse or different directions from the streamwise. This event most often gives rise to turbulent fluctuations, causing their enhancement. It is essential to highlight that flow separation can be induced either by geometrical singularities, for example, in the presence of sharp corners, or by smooth geometry variations, such as those occurring over a curved wall [12]. The mere presence of a very strong adverse-pressure gradient (APG), depending on the magnitude, might be sufficient to cause flow detachment. From a computational point of view, flow separation or recirculation is one of the most challenging problems to tackle due to its high level of intermittency, huge turbulent scale separation, obvious three-dimensionality, and unsteadiness. Several LES and RANS studies (in isolated or in combined “hybrid” form) have been carried out in the past few decades with the purpose of shedding some light on the boundary layer detachment problem caused by strong adverse streamline curvature-driven pressure gradient [13,14,15,16]. Major conclusions in previously cited works can be summarized as follows: overall, LES and RANS approaches may predict quite well first-order statistics in turbulent boundary layers subject to strong APG, which significantly degrades for higher-order statistics.
The inspiration for the assessment presented here is from the experimental work of Baskaran et al. [1]. In their work, a horizontal air stream at 20 m/s passed over a simple curved convex hill of 1.284 m long with a radius of 1.08 m. The protuberance’s entrance and exit had a concave surface of −0.40 m and −0.48 m, respectively. Figure 1 shows an example of the geometries. In [1], the momentum boundary layer parameters (first and second-order statistics) were measured. Boundary layer thickness, displacement thickness, momentum thickness, and other integral parameters calculated were used to describe the flow’s characteristics and behavior. Other relevant information, such as streamwise pressure and skin friction at the wall, velocities profiles at specific streamwise locations, and Reynolds stresses, was also measured. Their main objective was “to study the response of turbulent boundary layers to sudden changes in surface curvature and pressure gradient” [1]. Although, the experimental data of the velocity field are used as a point of validation of our numerical approach, it is worth highlighting that the present study also considers temperature as a passive scalar which was not explicitly accounted for in the original experiment.
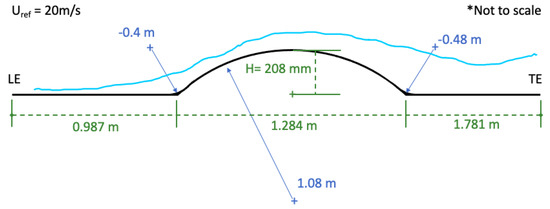
Figure 1.
Curved hill diagram. From [6]; reprinted by permission of the American Institute of Aeronautics and Astronautics, Inc.
In summary, and to the best of our knowledge, the combined effect of flow separation by strong streamline curvature-driven pressure gradients and passive scalar transport has not been fully addressed in the past, and knowledge on this matter is relatively scarce. Furthermore, the performance of widely used RANS models on very strong surface curvatures and separated flow is of great interest to the broader computational fluid dynamics community. To this end, we will resolve the Reynolds-averaged Navier–Stokes equations over a curved hill with experimental data points to assess the performance of two widely used CFD models. Furthermore, we will assess where each model excels and where they fail to capture the physics of the flow using the experimental data as ground truth. Some of the research questions to be addressed in this manuscript are as follows: (i) are the evaluated eddy viscosity models able to capture the outer peaks in Reynolds shear stresses (i.e., <> where the angle brackets mean time-averaged) as well as the inclination of the constant shear layer caused by strong APG?, (ii) is the flow separation bubble dominated by positively correlated and ?, (iii) what is the temperature profile trend inside the flow separation bubble?, (iv) is the Reynolds analogy preserved in strong streamline curvature-driven pressure gradients?, and (v) is the flow showing quasi-laminar features in zones where is highly decelerated?
2. Formulations
2.1. Reynolds Averaged Navier–Stokes Equation
Many RANS models are based on the Boussinesq hypothesis [7] and the Reynolds decomposition, i.e., the mathematical notion that each instant property can be written as the sum of mean and fluctuations fields; for example, , U being an instantaneous flow property, the average of U in time and the fluctuations of U. In RANS, the mean flow field is resolved whereas the fluctuations are modeled. For general compressible fluid flows [17], the governing equations (expressed following Einstein notation) are:
Conservation of mass:
Conservation of momentum:
Conservation of passive scalar, T being a scalar and assumed to follow a similar Navier–Stokes equation form
where S are the source terms. If the incompressibility assumption and the Reynolds decomposition are applied, the RANS models for Newtonian fluids have the following equations:
Continuity equation
Conservation of momentum
Note in Equation (5) how, by definition, the derivatives of mean variables with respect to time disappear but still is the emergence of a new term for the fluctuations variables. In RANS, the mean parameters are computationally solved, but the fluctuations terms remain unknown. It is precisely here where the Boussinesq hypothesis acts, enabling the models’ proposal for estimating the unknown terms and balancing the equations. Additionally, the density parameter at each partial derivative is pulled out due to the constant assumption of the incompressible condition.
2.2. Turbulent Flow Models
As said in the introduction, there are four most popular RANS models used. To understand these models is essential to describe four important parameters briefly. The first and principal is called turbulent kinematic viscosity, generally written as . Also known as eddy viscosity per density (), it is responsible for identifying the correct energy dissipation due to flow turbulence based on Boussinesq postulated [17]. is an apparent property for viscosity but accounts for the turbulent phenomenon. The second parameter is the turbulent kinetic energy (K), which is the kinetic energy per unit mass of turbulent fluctuations and is mathematically defined by:
Third is the turbulent dissipation ratio (), defining the ratio at which turbulent kinetic energy is converted to internal thermal energy. The mathematical description of is:
The last parameter is the specific dissipation rate of turbulent energy (). The variable is the ratio of the turbulent kinetic energy converted into internal thermal energy per unit of time and volume. For precisely having Hertz units, it is also known as frequency turbulence average. The relationship between to K and is generally written as Equation (8) where is a model constant that, for example, can be around 1.0 or even 0.09.
The turbulent model initially proposed by Launder and Spalding [18] is considered a high Reynolds number model and this indicates that its specialty is in good results away from near-wall [19]. This model is uses the scalar conservation Equation (3) to estimate K and . In essence, it says that the rate of change of K (or ) plus the transport of K (or ) by convection is equal to the transport of K (or ) by diffusion plus the production rate of K (or ) minus the destruction ratio of K (or ). The estimations are performed following Equation (10) for K and for Equation (11). Then, the eddy viscosity () is calculated with Equation (9) where the constants’ common values use are contained in Table 1.

Table 1.
Term representations and constant-coefficient values for the model.
The standard turbulence model was initially proposed by Wilcox [20]. This model is known as a low-Reynolds model, which means being good at predicting results in the near-wall [19]. Similar to the model, the standard turbulence model uses two scalar conservation equations to predict K and . The turbulent kinetic energy and specific dissipation rate are solved with Equations (14) and (15), respectively. The model’s coefficients values are shown in Table 2 while turbulent kinematic viscosity is calculated with Equation (13). Considering incompressible flow:

Table 2.
Recommended values for the coefficients in the standard model.
Menter proposed his shear stress transport model [2], also known as SST, where it unifies the advantages of the standard and models without inheriting their weaknesses [19]. Proposing a hybrid model, he reuses Reynolds stress computation and K-equation from Wilcox’s original model and transforms the -equation into a -equation. A decade later, Menter, along with Kuntz and Langtry, published a revised version of the turbulent model [21]. The updated version, commonly known as SST-2003 [22], is shown in Equations (16), (17), and (21) and the revised model constants are shown in Table 3. In the additional functions, Equations (18)–(20), y is the distance to the nearest wall. The SST also uses the scalar conservation formulation twice, for that reason, the three previous turbulent models are classified as two-equation models.

Table 3.
Revised values for the constants coefficients in the SST model.
Very different is the SA turbulent model, proposed by Spalart and Allmaras [3] and classified as a one-equation model since it only solves for a working variable of the turbulence model, . The principal parameter is computed by the scalar conservation Equation (22). The eddy viscosity is calculated with Equation (23), where is a wall-dumping function that causes zero value at the wall and reaches unity at high Reynolds number cases [17]. Additionally, is the production rate of related to the local mean vorticity as shown in Equation (24). The Spalart–Allmaras model has earned high popularity and is often used in the aerospace and aerodynamics industry for its high reduction in computational effort [23,24]. In addition, empirical adjustments to the eddy-viscosity turbulence model were performed in [25] to account for system rotation and streamline curvature effects based on the idea of Knight and Saffman [26]. In [27], the rotation-curvature correction of Spalart and Shur [25] was extended to the SST model. The new proposed version (SST-CC) was successfully tested on both wall-bounded and free shear turbulent flows with rotation and/or surface curvature. Of current interest, in a 2D channel flow with a U-turn, the SST-CC model performed well; however, it was stated that the model still predicted a slow flow recovery downstream of the separation bubble. Whereas the present study only considers standard SA and SST models without curvature correction, a future investigation may imply an assessment of model adjustments as in [25,27] in the curved hill configuration. The SA turbulent model’s recommended constant values are in Table 4.

Table 4.
SA turbulent model’s recommended constant values.
In summary, both turbulence models were not selected arbitrarily. We have chosen the best representatives from one and two-equation turbulence models. The Spalart–Allmaras (SA) model (or one-equation model) has been described to be incomplete by Wilcox [28] since any turbulence model would require at least two scales: a velocity scale and a length scale. However, the SA model has shown simplicity, robustness, and versatility in attached turbulent boundary layer simulations [3,29,30,31] including high-speed turbulent boundary layers [32,33]. Previously mentioned studies have emphasized a degradation in the SA model’s accuracy for more complex geometries with flow separation. In particular, the SA model under-predicted the size of the separation bubble. On the other hand, the hybrid SST model by Menter involves blending two well-known two-equation turbulence models: the standard model in the near wall region and the model in the outer region and freestream of the boundary layer to overcome the strong freestream sensitivity of the turbulence model. It is worth highlighting that the SST eddy viscosity model involves a further improvement based on the idea of the Johnson–King model, which assumes that the transport of the main turbulent shear stresses is critical in the simulations of strong adverse-pressure gradient (APG) flows prone to boundary layer detachment.
2.3. Flow Solver and Numerical Schemes
The software used to run all the CFD cases presented in this work was OpenFOAM®. The strategy implemented was to use the algorithm called semi-implicit method for pressure-linked equations consistent (SIMPLE-C) with a residual control value of 1 × 10 for all the variables or fields. For the specific-pressure field (P), the solver selected is called the geometric agglomerated algebraic multigrid solver along with a Gauss–Seidel smoother (GAMG), a relative tolerance of 0.1, and a tolerance of 1 × 10. For the passive scalar field, it was used the preconditioned bi-conjugate gradient (PBiCGStab) solver with a simplified diagonal-based incomplete LU preconditioner (DILU); relative tolerance was set to 0, and the tolerance 1 × 10. Lastly, for all the other variables (i.e., U, , K, ), the solver adopted was a smooth solver accompanied by a symmetric Gauss–Seidel smoother, and tolerances values equal to the P field. The relaxation factor for P was 0.3 meanwhile 0.7 for U, , K, and .
As for numerical schemes, the following were designated for the time, gradient, Laplacian, interpolation, surface-normal gradient, and wall distance calculation, respectively: steady state, Gauss linear, Gauss linear corrected, linear, corrected, and mesh wave method. The divergence schemes chosen were Gauss linear for the non-linear stress and the effective viscous stress; Gauss linear upwind for the divergence of the surface scalar field () with the passive scalar; bounded Gauss linear upwind for with U and with ; while for the divergence of with K and it was used bounded Gauss limited linear 1.
All the solvers and numerical schemes determined for the work presented were already available in the open-source software OpenFOAM version 7 as a standard option without any modification in the algorithms or implementation. For details on the approach of any method mentioned in this section, readers are referred to [7,17].
2.4. Boundary Layer Detection Based on Potential Flow
A potential flow is characterized as an inviscid and irrotational velocity field, described as the gradient of a scalar function. On the other hand, a boundary layer develops from strong viscous interactions within a small region, usually caused by the presence of a surface or vorticity source. The potential flow satisfies the Laplace equation as,
where is the scalar function, the potential velocity field is defined as , with the flow being irrotational, i.e., . However, since for any arbitrary velocity flow field expressed using finite, floating-point arithmetic, the divergence is not strictly zero, OpenFOAM implements a numerical scheme following Poisson’s equation to enforce a solenoidal field and conditions required for the irrotationality of the flow. This issue is not exclusive to OpenFOAM as it is an inherent limitation of finite-precision arithmetic using floating points. The scheme can be expressed as follows, where is the face flux of a finite volume as,
As done in Baskaran et al. [1], the edge of the boundary layer is determined based on the potential flow theory in curved geometries. It is the standard procedure used in the fluid dynamics theory since surface curvature locally induces a streamwise pressure gradient, making it challenging to identify the beginning of the inviscid zone above the turbulent boundary layer. Given that viscous interactions are not present in potential flows, the boundary layer can be described as the region where these viscous interactions can not be neglected (a somewhat simplistic description, but it suffices for the proposed methodology). We hypothesize that the edge of the boundary layer can be detected by searching for the region where the potential flow and the real viscous flow cross paths and exhibits similar behavior. According to Baskaran et al. [1], the edge of the boundary layer thickness, , is defined as “that wall distance at which the dynamic pressure is 99% of the free-stream value”. In the present work, we apply the following criteria for identifying the edge of the boundary layer:
Here, represents the wall-parallel component of the fluid flow, and n is the wall-normal coordinate. It is important to mention that the fulfillment of both criteria according to Equation (27) ensures an acceptable identification of the viscous–inviscid interface or boundary layer edge, particularly in the recirculation flow zone. The second derivative of in the wall-normal direction describes the local curvature of the velocity profile, which must be zero in the inviscid region. Figure 2 provides a pictorial representation of the intuition behind the approach employed in the present work. Note, in Figure 2a, that the viscous RANS solution starting from the wall highly disagrees with the potential solution. However, as the distance from the wall grows, viscous RANS tends asymptotically to the potential solution until further, in the free-stream, the viscous RANS solution is consistently very similar to the potential solution. Moreover, with the cyan color curve of station s = 2500 mm (at the separation bubble), note how the velocities first matched in a wall level without actually both solutions having the asymptotical behavior, confirming that the second criterion in Equation (27) is necessary. With the possibility of multiple wall levels with the solution’s paths crossed, the issue is solved by looking at the slopes. Figure 2b shows the wall-normal derivative of the streamwise velocities; note the asymptotical and overlapping behavior of the viscous solution towards the zero value and potential solution again. It can be intuitive that after some n distance, the absolute value of the wall-normal second derivative of viscous solution is going to be equal to the corresponding derivative of the potential solution; or at least, a smaller second derivative for the viscous solution compared to the potential solution due to the tendency to zero showed in both solutions.
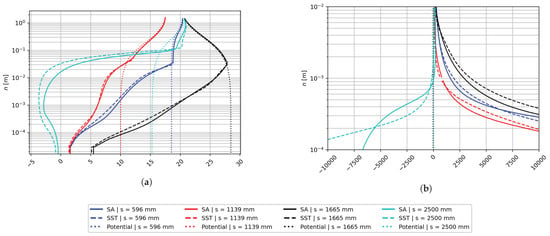
Figure 2.
(a) Potential flow and RANS wall normal profiles, in m/s; (b) wall-normal derivative of the streamwise velocity, in 1/s.
2.5. Turbulent Inflow Generation
Before beginning with the curved hill cases, a scenario of the turbulent flow over a flat plate was considered using SST and SA models. For all cases presented in this work, the classical no-slip condition was prescribed at the wall surfaces for the velocity fields; meanwhile, an isothermal condition of 293.15 K was prescribed for the thermal field. The top-surface boundary condition was set via a zero-gradient of all flow parameters (shear-less wall) and a zero-pressure gauge value at the outlet boundary. For the SA’s conditions, and were specified as zero at the walls, while = 1.5 × 10 m/s and = 1.1 × 10 m/s for both constant inlet and domain’s initial state. For the SST’s conditions, the turbulent intensity was assumed as 1%, giving K = 0.06 m/s and = 4000 1/s to be applied as Dirichlet conditions at the inlet plane and walls, while = 1.5 × 10 m/s was employed to initialize numerical predictions.
In the flat plate or turbulence inflow generator scenario, the total domain’s length was set to 3.85 m with an initial 0.15 m length as a slip-condition. Three meshes were designed, namely coarse, medium, and fine mesh, as described in Table 5. Furthermore, vertically end-to-start cell expansion ratios () were 4140, 3000, and 1900, respectively. The vertical cell expansion ratio, , is defined as the dimensionless relationship between the end cell near the top surface to the start cell in the near-wall region, i.e., . In the inlet plane, freestream conditions were set, i.e., 20 m/s for the horizontal velocity and 323.15 K for the static temperature (passive scalar).

Table 5.
Flat plate mesh cells’ horizontal distribution; from left to right.
In the curved hill scenario, mean flow solutions from the flat plate were extracted and injected as velocity and temperature inlet profiles to overcome the unrealistic freestream inlet profiles and avoid a lengthy inlet developing section. In addition, this recycling strategy allows better control of the inlet boundary layer parameters as a solid requirement for validating numerical predictions against wind-tunnel experiments. As shown later in this section, these “recycled” profiles are validated. Like in the flat plate scenario, the curved hill had three meshes: coarse, medium, and fine mesh; all three meshes with height divided into two blocks for an efficient cell distribution control. The coarse mesh had 200 cells in the first 25% of vertical distance with = 1000 and the other 75% of height with 100 cells in uniform distribution to comply with an acceptable mesh aspect ratio. In the medium mesh, the nearest block to the wall was only 3.5% of total height with 200 cells and = 386, while the outer region was composed of 200 cells with = 12. Similarly, the fine mesh possessed the vertical 3.5% and 96.5% split with the same end-to-start cell-expansion ratio as the medium mesh, but both regions were populated with 400 cells. Horizontally, all three meshes were divided into five blocks; Table 6 shows the resolution and the horizontal cell distribution.

Table 6.
Curved hill mesh cells’ horizontal distribution; from left to right.
Figure 3 and Figure 4 show schematics of the computational domains for the flat plate as well as for the curved hill. Figure 5a and Figure 6a display a full view of the fine meshes for the flat plate and curved hill domains, while the corresponding figures (b) are the near wall region close-ups, respectively. Figure 7a,b show the ZPG regions’ near-wall resolution for the flat plate and curved hill, also respectively.
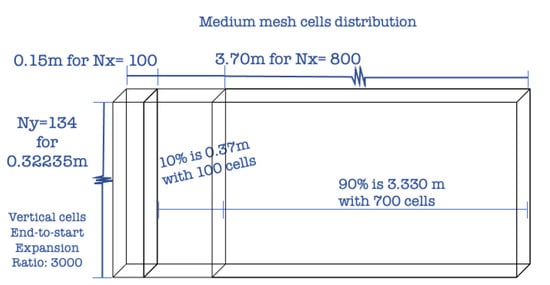
Figure 3.
Example of dimensions and cell distribution for flat plate medium mesh. From [6]; reprinted by permission of the American Institute of Aeronautics and Astronautics, Inc.
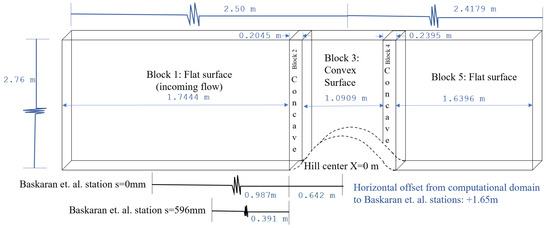
Figure 4.
Example of dimensions of curved hill computational domain (not at scale) [1].
Figure 5.
Schematic of the fine mesh configuration in the flat plate (turbulence precursor): (a) full view, (b) near wall region close-up.
Figure 6.
Schematic of the fine mesh configuration in the curved hill: (a) full view, and (b) near wall region close-up at the second concave surface.
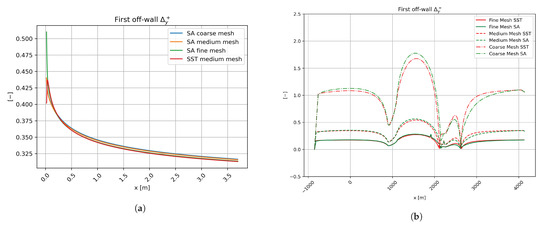
Figure 7.
Comparison of the dimensionless near-wall mesh resolution in: (a) the flat plate domain, and (b) the curved hill domain.
The flat plate simulations have shown excellent agreement with empirical correlations. The obtained information (i.e., velocity and thermal profiles) was used to inject a more realistic (and developed) boundary layer flow into the curved-hill domain inlet. Because Spalart–Allmaras cases were executed first, it was found that the results of coarse to fine mesh were sufficiently resolution independent; therefore, SST was only performed with coarse and medium resolutions. Figure 8a displays the boundary layer thickness and comparison with the -power law given in [34]. Figure 8b presents the skin friction coefficient and the theoretical formulation proposed by Kays and Crawford [35]. Regarding the passive scalar solution, the temperature boundary layer thickness is shown in Figure 9a; as it can be seen, the results are just differentiated by the turbulent model used. Furthermore, to validate the temperature fields, the Stanton number was used in Figure 9b by comparison with the theoretical formulation given by Kays and Crawford [35].
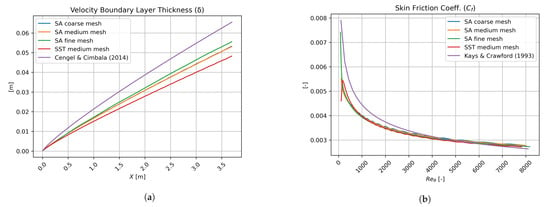
Figure 8.
Flat plate solutions of: (a) boundary layer thickness, and (b) skin friction coefficient. From [6]; reprinted by permission of the American Institute of Aeronautics and Astronautics, Inc.
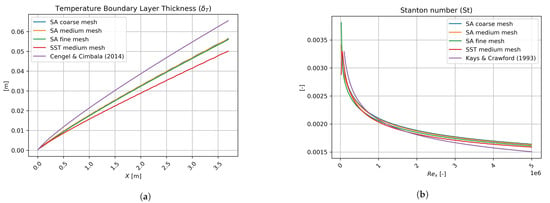
Figure 9.
Flat plate passive scalar solutions of: (a) temperature boundary layer thickness, and (b) stanton number.
Figure 10 shows the extracted streamwise velocity and thermal profiles from the flat plate simulations for the three meshes and based on the SA turbulence model at a location ( 2.458 m) where the local momentum-thickness Reynolds number, , is approximately 5659.7. Furthermore, in Figure 10a, the mean streamwise velocity is depicted in wall units (i.e., and ), where a consistent trend can be observed in all meshes. Here, where is the wall shear stress and is the fluid density. It is worth highlighting that we will use interchangeably and to denote wall-normal coordinates in this manuscript. In addition, a very good agreement is seen with DNS data from [9,10] at = 2354.7 and 4060, respectively. Some discrepancies can be detected around 10 and in the wake region (i.e., beyond the log region). The latter could be attributed to some Reynolds number dependency. Figure 10b exhibits the mean temperature profile (or passive scalar) normalized in wall units, as well. Here, , where T being the dimensional static temperature, is the wall temperature, and is the freestream temperature. The friction temperature is defined as , where is the wall heat flux and is the fluid specific heat. Moreover, an excellent collapse of the RANS results via the SA turbulence model is visualized in the linear viscous layer and buffer region (i.e., for ) as well as with DNS data from [4,9] at = 2354.7 and 800, respectively. In the log and wake region, significant differences can be observed between the RANS and DNS approaches. One can infer that the turbulent Prandtl number model employed in RANS simulations has performed quite well in the near wall region, whereas it has been able to reproduce moderately well the thermal field in the outer part of the turbulent boundary layer. Despite the fact that all meshes have generated similar outcomes, the solutions of SA medium mesh were selected for inflow in the curved hill cases (i.e., streamwise and wall-normal components of the mean velocity and temperature). Readers are referred to Appendix A for a comprehensive grid sensitivity study.
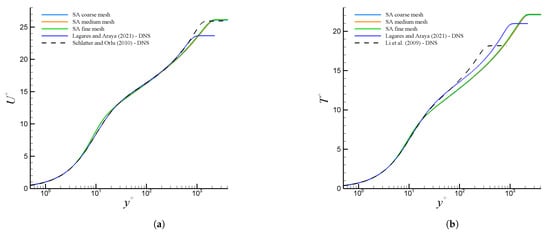
Figure 10.
Quality assessment of turbulent inflow profiles of: (a) mean streamwise velocity, , and (b) mean temperature, , in wall units.
3. Numerical Results and Discussion for the Curved Hill
Turning into the curved hill scenario, let us begin by setting our bases by contrasting our numerical predictions with experimental data from the paper “A turbulent flow over a curved hill Part 1”, [1]. Figure 11, Figure 12 and Figure 13 show contour results of kinematic pressure gauge (), streamwise velocity () and static temperature (T), respectively; via the SA turbulence model and fine mesh. Zero values of the kinematic pressure gauge were assigned to the outflow plane (reference or atmospheric pressure). It is very important to note that in this work the surface streamline distance (s) was matched to the presented in [1], also the wall-normal distance is represented with n. In the path of the shear-layer region (i.e., turbulent boundary layer), the following aspects can be mentioned. As the flow approaches the hill or obstacle, the pressure increases, the flow decelerates and the pressure gradient becomes strongly adverse. Zones with intense red color can be seen along the first concave region (987 mm < s < 1191.5 mm). The fluid velocity in the viscous and buffer layer decelerates, inducing a decrease in the skin friction coefficient, as will be shown later in the manuscript. However, no strong backflow or reverse flow is seen due to the moderate APG infringed. Whereas, the temperature generally shows a small gradient with just a small temperature drop in a very limited location at the peak of this pressure strong adverse gradient. In the geometry change from concave to convex, the pressure gradient switches to favorable (FPG), this is translated to streamwise velocity acceleration. This flow acceleration or FPG continues until the flow reaches the hill’s top. Clearly, the flow decelerates downhill, with a significant recovery of the pressure coefficient (as seen in Figure 14a). The presence of this strong APG (the pressure increase equals the dynamic pressure, since the change in −1) ends up in flow separation, with a posterior flow reattachment due to the presence of zero-pressure gradient (ZPG) zone, again. Temperature shows no change during this section with the exception of the very near wall. At the start of this separation zone, the temperature begins to drop. At the end of the hill, the separation “bubble” is noticeable due to the presence of a quasi-isothermal zone (in blue). The high level of mixing inside the separation bubble balances the static temperature. This is consistent with observations in the thermal boundary layer downstream of crossflow jet problems via DNS [36].
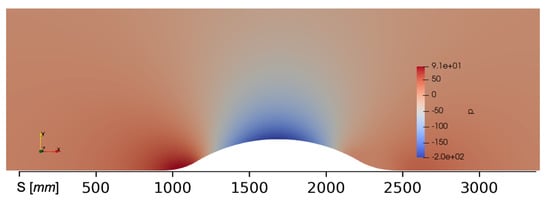
Figure 11.
Contours of kinematic pressure gauge in m/s. The image has been zoomed in to highlight the curved hill and immediate surroundings.
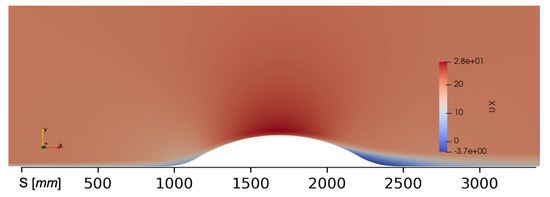
Figure 12.
Contours of streamwisevelocity in m/s. The image has been zoomed in to highlight the curved hill and immediate surroundings.
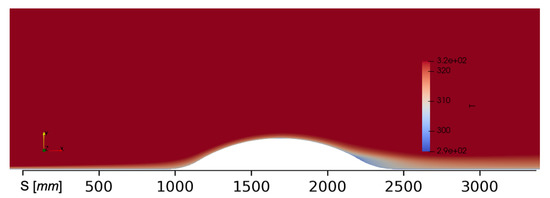
Figure 13.
Contours of the static temperature in K. The image has been zoomed in to highlight the curved hill and immediate surroundings.
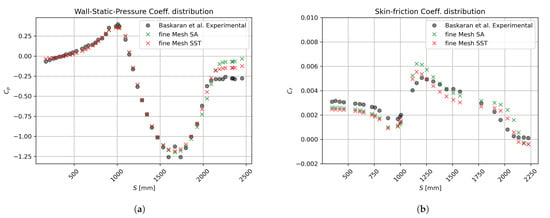
Figure 14.
Coefficients on wall compared to experimental data from [1]: (a) pressure coefficient, and (b) skin friction coefficient.
Figure 14a depicts the pressure coefficient along the computational domain. The pressure coefficient is defined as . Here, is the wall static pressure, is the freestream static or reference pressure, and is the freestream dynamic pressure. In general, a fair agreement is observed with experimental data by [1]. As the flow approaches the obstacle or hill, it decelerates due to the presence of an increasing pressure or APG. The maximum (≈0.375) is located at the hill feet. Interestingly, good performance of both turbulence models in reproducing the wall pressure coefficient was observed in the vicinity of the hilltop, where the streamwise pressure gradient abruptly switches from FPG to APG, passing through a very short ZPG-zone. It is expected that boundary layer flow experiences a severe distortion in that zone with combined pressure gradients. Major discrepancies occur by the end of the strong APG zone (second half of the hill) where back or recirculating flow can be found. This is consistent with the deficient performance of RANS-eddy viscosity models in capturing boundary layer detachment. While both turbulence models have predicted constant wall static pressures in the separation bubble (ZPG zone), which is physically sound; however, smaller pressure gauges were obtained by SA and SST, e.g., −0.0625 and −0.125, respectively, as compared to the measured valued of −0.25. In Figure 14b, the skin friction coefficient, , is depicted. The skin friction coefficient is defined as follows, , where is the wall shear stress. One can observe an opposite trend of as compared with the pressure coefficient . As the flow decelerates due to the presence of moderate APG nearby the hill feet (concave surface), it is seen a decreasing behavior of just downstream of the ZPG region where almost constant skin friction coefficient values are seen, as expected. However, it never reaches negative values, indicating that the mean flow does not separate. The wall shear stress then recovers as the flow starts to accelerate in the FPG region (convex surface). At roughly one-quarter of the curved hill (where the surface changes geometry from concave to convex) a meaningful increase of the wall shear stress and is observed since the flow strongly accelerates (FPG), and approximately a 100% increase can be seen with respect to the incoming under ZPG-flow conditions. Downhill, the pressure coefficient recovers (presence of APG), inducing a reduction in , to finally reach slightly negative values in the separation bubble ( 2100 mm). Obviously, the boundary layer flow should “pass-through” the laminar skin friction coefficient value before separating (i.e., < 0). This may indicate the presence of quasi-laminarized flow within 2000 mm < s < 2100 mm and in the near wall region [37] (extension of the viscous sub-layer). This supposition would be better addressed when discussing mean streamwise velocity and Reynolds shear stress profiles in the next pages. In summary, the SA and SST turbulence models have estimated similar and consistent values for regarding the experimental data from [1], perhaps the SA model has shown moderate supremacy, overall. The skin friction coefficient in the incoming ZPG zone is slightly under-predicted by both turbulence models (∼15% lower than in [1]). As previously mentioned, the most “challenging” situation for turbulence models has undoubtedly been the hilltop and vicinity since the flow goes through acceleration and deceleration in a very short distance. Major differences were computed as roughly 35% in that zone. According to [1], the location of the boundary layer detachment point was found to be situated at s = 2095 mm by extrapolation. The SA and SST models have predicted a separation point around 2100 mm, in very close agreement with experiments.
The streamwise variation of the Stanton number and the Reynolds analogy ratio (i.e., ) are shown in Figure 15. The Stanton number is defined as follows,
where is the wall heat flux defined as:
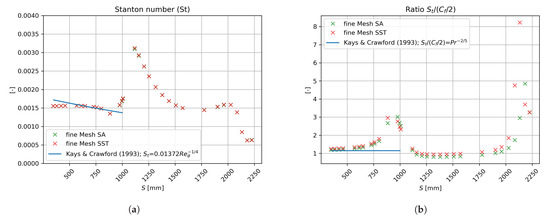
Figure 15.
Streamwise variation of: (a) Stanton number, and (b) ratio .
Here, k is the fluid thermal conductivity, is the fluid’s specific heat at constant pressure, and is the thermal gradient at the wall in the wall-normal direction. The Stanton number is a dimensionless number that relates the heat interchanged between the surface and the fluid to the thermal capacity of the fluid. From Figure 15a, one can observe nearly constant in the incoming flow (ZPG), which is typical in canonical or flat-plate boundary layers. A very good agreement was obtained with the empirical correlation by Kays and Crawford [35], who proposed a variation of as a function of the local momentum thickness Reynolds number, , for ZPG turbulent flows (adapted to = 0.71). The Stanton number (and heat transferred) peaks by 1125 mm, where () is located, demonstrating a high similarity between maximum viscous shear force and total heat transferred at the wall. This peak in the heat transfer (representing about an 80% increase regarding the incoming baseline ) is situated approximately by the end of the first concave bend. Downstream, the Stanton number decreases much faster than does, suggesting a non-similarity between these two boundary layer parameters. The strong changes of streamwise pressure gradients in this zone, which are sources of dissimilarity between the momentum and thermal boundary layer transport [38], are the reasons for that behavior. Beyond s = 1500 mm, a “plateau” is observed in values, and an abrupt reduction of the heat transfer is achieved by 2100 mm, caused by the presence of the flow recirculation zone. This separation bubble is characterized by a quasi-adiabatic process, since no heat transfer occurs between the surface and the fluid ( 0). Furthermore, the Stanton number can also be related to the skin friction coefficient via the Reynolds analogy (similarity between the viscous drag to the heat interchanged). We introduce the ratio in Figure 15b. An excellent agreement with the empirical correlation by [35] is seen in the ZPG zone. This ratio significantly departs from the unitary value by the hill feet (beginning of the concave bend, 987 mm). It is worth highlighting that remains very close to one in most of the curved hill for s > 1100 mm, getting large negative values in the vicinity of the separation bubble due to the very small (and negative) values of . In essence, both turbulence models have generated very similar Stanton numbers.
To the best of our knowledge, the implemented approach, based on a potential flow-based scheme, has shown robustness and accuracy in the detection of boundary layer edge parameters as well as its integral values in comparison to the classical criterion. This made the overall calculation of the parameters shown in Figure 16 and Figure 17 consistent in the presence of strong pressure gradients, and subsequently, severe boundary layer distortion. The boundary layer thickness is slightly underestimated, although it follows the experimental results’ behavior. Baskaran et al. have limited data in the separation bubble, and we focus on the sections highlighted by them [1]. The overestimated shape factor is likely due to an overestimation in the boundary layer’s edge velocity incurred when comparing the potential and RANS flow fields. Nonetheless, the comparisons along the hill are extremely favorable to our approach compared to the experimental baseline. Overall, the SA model has superior performance when compared to the SST [2]. This is particularly noticeable within the portion 800 mm < s < 1200 mm seen in the integral parameters prediction. Both turbulence models significantly over-predict the maximum shape factor, H, located at 1000. At this point, the meaningful thickening of the turbulent boundary layer is consistent with the presence of strong APG and flow deceleration (note the peak in Figure 14a). Consequently, the shape factor increases (up to ∼15% increases with respect to the incoming flow), and discrepancies in numerical results are within 25% regarding experimental values. Since the shape factor, H, is the ratio of the displacement thickness to the momentum thickness, the previously mentioned discrepancies on are caused by over-predictions on the displacement thickness, , as confirmed from Figure 17. In addition, the momentum thickness, , has been almost faithfully replicated by RANS as compared to experiments. This is consistent with the good agreement on the variation (see Figure 14b), since the momentum thickness is proportional to the drag force over the surface.
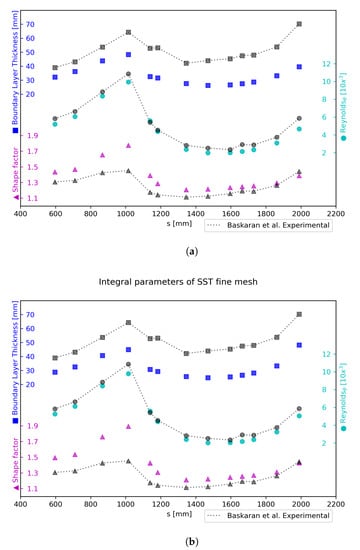
Figure 16.
Boundary layer thickness, shape factor, and momentum thickness Reynolds number compared to experimental data from [1]: (a) Spalart–Allmaras model, and (b) SST model.
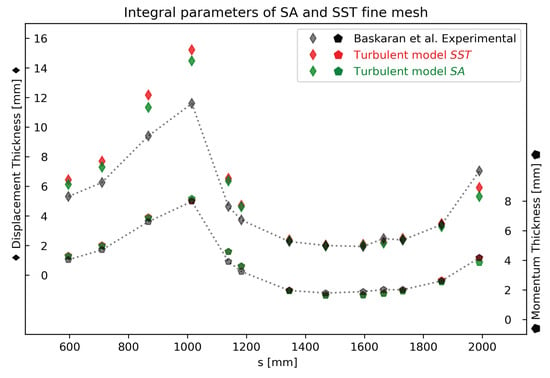
Figure 17.
Displacement thickness and momentum thickness compared to experimental data from [1].
For the creation of Figure 17, our potential flow-based scheme used Equations (30) and (31) to calculate displacement and momentum thickness parameters. Meanwhile, for Figure 16, the parameter used a reference velocity, , where after following the results of [1], it was found to be s = 596 mm, i.e., the reference station.
To assess the distortion of the momentum boundary layer due to the hill, we present wall normal, inner scaled profiles at several streamwise stations in Figure 18. Comparison is performed with experiments by [1] as well as against two DNS baselines by Schlatter and Orlu () [10] and Lagares and Araya () [9]. For the ZPG zone in Figure 18a, the inner scaled velocity profiles of both closure models collapse near perfectly with a very slight variation observed in the wake region where the SST variant predicts a slightly higher streamwise velocity, . Both DNS databases exhibit a high level of consistency (almost overlap), and a long log region can be seen due to the high Reynolds numbers considered. The flow starts to decelerate by the first concave bend beginning ( 710 mm), which causes a decrease in the skin friction coefficient and in the friction velocity as well. This is the reason for the slight upward movement of the wake in Figure 18b, which is over-predicted by the turbulence models. The effects of flow acceleration and FPG can be observed in Figure 18c,d, inducing a “hump” in velocity profiles over the log region, also reported by [39] in sink flows. The boundary layer suffers a significant distortion around the hilltop where a “plateau” in can be observed between and 1000 from experimental data. In this FPG zone, the SA model predictions are in better agreement with experiments by [1]. As discussed in Figure 14a, the pressure coefficient recovers from mm and the streamwise pressure gradient becomes more adverse. Therefore, one can describe the APG influence as steeper slopes of the velocity profiles within the log-wake region. Finally, the sudden deceleration (strong APG) of the boundary layer produces a recirculation bubble above the wall, i.e., between 2 to 1000 wall units, as can be seen in Figure 19, where streamwise velocity profiles can be seen at three different stations. While the SA model predicts a slightly stronger reversal flow, the SST model predicts a larger (in terms of wall-normal distance) bubble. This recirculation zone is characterized by a low level of velocity fluctuations (this will be confirmed later in the Reynolds shear stress profiles) and back (negative) flow, where almost constant values of can be observed (within 5 to 10 in wall units, according to the streamwise station). Beyond the separation zone in the wall-normal direction, the streamwise velocity exhibits very sharp increases towards the boundary layer edge, resembling Blasius velocity profiles. The substantial discrepancies observed in both turbulence models confirm our previous statement regarding the limitations of eddy viscosity models to accurately predict boundary layer detachment.
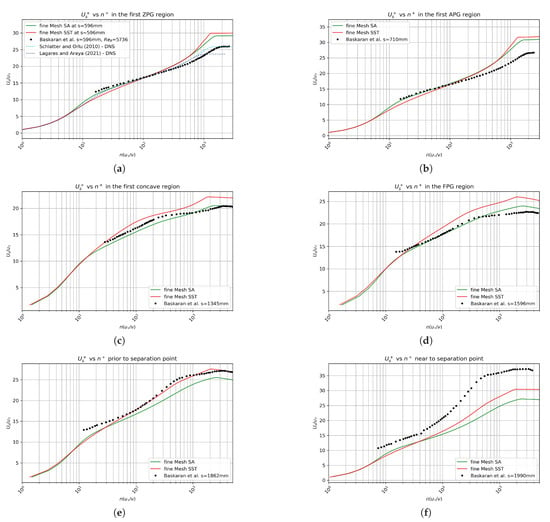
Figure 18.
Streamwise velocity profiles in wall units at locations of: (a) s = 596 mm; (b) s = 710 mm; (c) s = 1345mm; (d) s = 1596 mm; (e) s = 1862 mm; (f) s = 1990 mm.
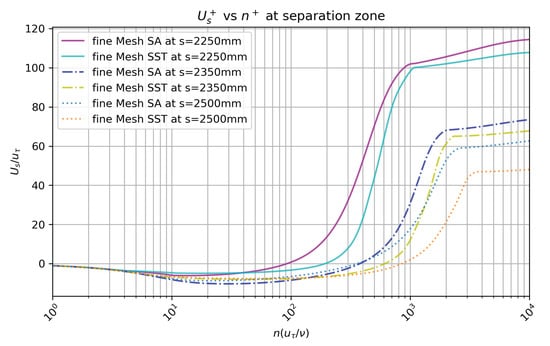
Figure 19.
Velocity profiles in the flow separation bubble at s = 2250 mm, 2350 mm, and 2500 mm.
We apply the Boussinesq hypothesis to estimate Reynolds shear stresses from the RANS output as per the equation:
In Figure 20, profiles of Reynolds shear stresses are plotted in inner units and several streamwise stations by considering the friction velocity at the reference station ( 596 mm or ZPG zone). This choice is based on the isolated assessment of the baseline (incoming) Reynolds shear stresses under combined streamwise pressure gradients caused by the curved hill. Moreover, we remove any scaling effect according to the local values of the friction velocity. At the ZPG station ( 596 mm), it can be seen that both turbulence models tend to capture the inner portion of the boundary layer with very good agreement with DNS from [9,10]. The comparison breaks down in the outer region where both models predict larger values, perhaps, caused by the higher Reynolds numbers considered in RANS predictions. The APG effect at s = 1139 mm is manifested as a clear secondary peak on around 800. We can infer that the flow is subject to a very strong deceleration or APG since the outer peak is larger (almost twice as large) than the inner peak, around 15. The SST model predicts a more intense outer peak, addressing one of the original research questions of this study. These outer secondary peaks of have also been reported by [38] in DNS of turbulent spatially developing boundary layers subject to strong streamwise APG. Moreover, outer streaks are enhanced by APG, which in turn cause local increases of streamwise velocity fluctuations and Reynolds shear stresses, according to DNS studies by Skote et al. [40]. Interestingly, a much stronger APG effect can be seen at s = 1990 mm, just upstream of the separation bubble, given by the inclined shear layer or “plateau” in the zone 10 < < 200. The larger the APG, the more inclined the shear layer [38]. At the flow recirculation zone, i.e., at s = 2500 mm, there is an appreciable attenuation of the Reynolds shear stresses in the near wall and buffer region ( < 100).
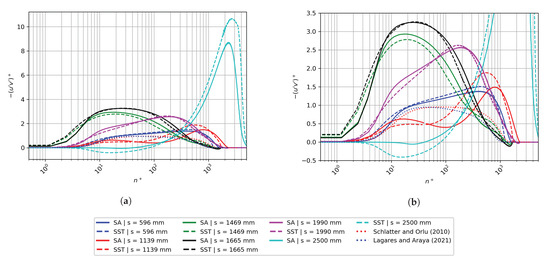
Figure 20.
(a) Inner-scaled Reynolds shear stresses; (b) zoomed view of the inner-scaled Reynolds shear stresses.
Furthermore, the SST model predicts large positive values of the cross-correlation inside the bubble (not seen in the SA model), which is consistent with previous DNS studies in flow separation [36,40]. Clearly, the very low values of the Reynolds shear stresses suggest that the flow is quasi-laminarized or on the verge of relaminarization [41] (viscous sublayer extended). On the other hand, the very large values of in the outer region (1000 < < 3000) plus the non-negligible wall normal gradients of the streamwise velocity indicate the presence of significant turbulence production (i.e., /) well above the separation bubble, and thus, the flow is highly turbulent in that zone, as will be shown in the next figure. The published data by Baskaran et al. [1] do not contain much information beyond the early portions of the separation bubble.
The turbulent kinetic energy (K) production, , inside the boundary layer can be evaluated by computing the term with the highest contribution to K and mean-flow kinetic energy equations. The time-averaged velocity gradients act against the Reynolds stresses, removing kinetic energy from the mean flow and transferring it to the fluctuating velocity field, Pope [42]. The turbulent kinetic energy is defined as in Equation (6); whereas the Boussinesq hypothesis leads to the following definition of in Equation (33), where the Reynolds shear stress definition in Equation (32) is employed. Figure 21 shows the principal term of K production in wall units at different streamwise stations, as done with the RANS-modeled Reynolds shear stresses. It was observed that the term in the mean flow gradient was negligible, even in zones with large wall curvatures. For the incoming flow (ZPG zone) at 596 mm, the SA turbulence model reproduces properly the turbulence production in the turbulent boundary layer, as contrasted to DNS from [9,10] at lower Reynolds numbers. Peak values are approximately 0.25 to 0.29 in the buffer layer at 10. While an increase in the term would suggest a mean flow deceleration; whereas, an enhancement of the fluctuating component of the velocity field and Reynolds shear stresses. Previous flow physics descriptions can be clearly seen at stations 1469 mm and 1665 mm. Down the hilltop, turbulence production begins to recover the inflow features (attenuation process) as the Reynolds shear stresses decrease in the viscous sub-layer and buffer region. In addition, flow deceleration by APG tends to destabilize the boundary layer, inducing turbulence intensification in the outer portion. Based on DNS studies by Skote et al. [40], the outer streaks are intensified by strong APG and can be related to local increases in turbulence production and <> (outer peaks). As seen in Figure 21, SA and SST models predict outer peaks of turbulence production around 1500–2500 at 2500 mm, where the separation bubble is thicker. Furthermore, the production of K inside the bubble is almost negligible, suggesting that the flow is locally quasi-laminar.
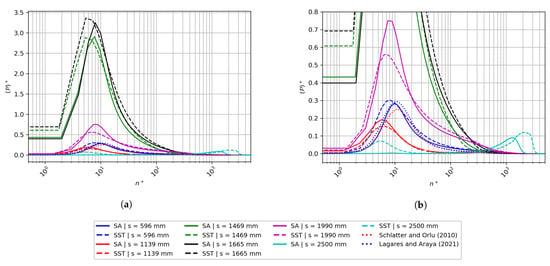
Figure 21.
(a) Inner-scaled K Production; (b) zoomed view of the inner-scaled K Production.
In general, the thermal boundary layer profiles presented in Figure 22 follow similar tendencies (i.e., Reynolds analogy) to those presented for the momentum boundary layer. This is expected since the temperature is modeled as a passive scalar. Particularly, a high level of similarity has been observed in ZPG zones since streamwise pressure gradient is a source of dissimilarity between momentum and thermal fields. For instance, nearby the hilltop, strong FPG effects were described by the presence of “humps” in velocity profiles over the log region. However, thermal profiles look very different at 1345 mm and 1596 mm, indicating Reynolds analogy breakdown. Actually, a significant portion of the thermal boundary could be represented by a logarithmic curve fitting, given by the observed “linear” behavior when plotted on a semi-log scale. From Figure 23, the separation bubble seems to elongate the thermal “plateau”, although the distortion effects are less “violent" than those seen in the momentum boundary layer. As expected, the predictions at the separation bubble seem to disagree more than on any other station between turbulence models. Interestingly, we can now visualize two distinctive logarithmic regions of the thermal profile: one log slope inside the bubble and the other (steeper) outside the separation zone up to the thermal boundary layer edge. This log behavior may open up the opportunity for future better turbulence modeling of passive scalar transport in flow separation. Furthermore, a deeper analysis must be performed in this sense, which falls outside the scope of the present manuscript and may be published elsewhere.
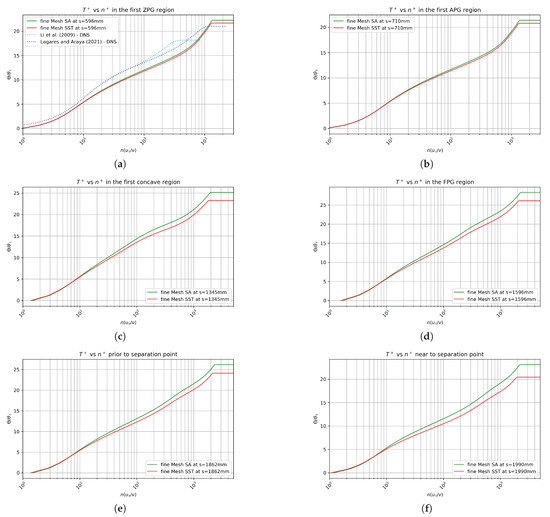
Figure 22.
Thermal profiles in wall units at locations of: (a) s = 596 mm; (b) s = 710 mm; (c) s = 1345mm; (d) s = 1596 mm; (e) s = 1862 mm; (f) s = 1990 mm.
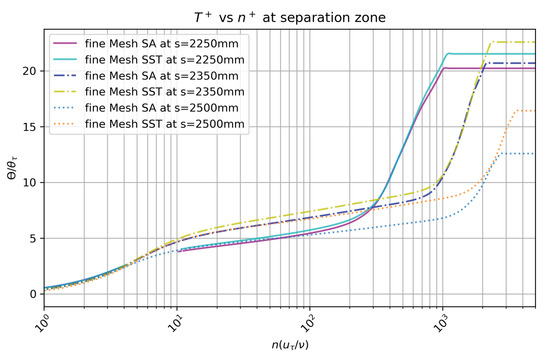
Figure 23.
Thermal profiles in the flow separation bubble at s = 2250 mm, 2350 mm, and 2500 mm.
It is worth highlighting that the 2D results presented in this work assume spanwise homogeneity. The main expected deviations when considering a full 3D domain and unsteady simulations can be summarized as follows: (i) the appearance of Grtler-like vortices due to the strong concave curvatures (−0.13 to −0.15, where is the local boundary layer thickness and R is the local radius of curvature) present in the complex geometry and (ii) flow separation bubble. Our previous experience on supersonic turbulent boundary layers subject to strong concave surfaces via DNS [43] dictated the existence of Grtler-like vortices caused by centrifugal forces, which in turn, enhanced spanwise flow fluctuations. However, no spanwise inhomogeneity has been observed in time-averaged flow statistics of turbulent flows. On the other hand, flow separation at the second concave surface should be ruled by unsteadiness and three-dimensionality effects. Even when the assumption of spanwise homogeneity may not be perfect, our results have shown reasonable agreement with wind-tunnel experiments.
4. Conclusions
We have presented a numerical study of a turbulent boundary layer subject to a curved hill. The study was limited to a Reynolds-averaged Navier Stokes simulation (RANS) plus two eddy-viscosity turbulence models (i.e., SST and SA). The domain geometry was reproduced following work by Baskaran et al. [1]. The inlet velocity components and temperature were recycled and injected from a precursor ZPG simulation to avoid a longer developing section and better control (and match with experiments) the incoming reference boundary layer parameters. By leveraging a boundary layer identification scheme based on a potential flow field, we showed very good agreement with the experimental data by Baskaran et al. [1]. This approach led to better identification of the turbulent boundary edge to compute the integral parameters and boundary layer thickness. Furthermore, the proposed methodology has been resilient and robust in the presence of strong pressure gradients and significant boundary layer distortion. Overall, the SA model had a better agreement with the experimental data in those zones where the turbulent boundary layer remained attached, for instance, in , , and predictions. On the contrary, the SST model has depicted slightly superior agreement with experiments in the separation bubble (in terms of and ) as well as in profiles just upstream of the bubble, capturing more evidently the positively correlated characteristics of and or positive . Both models have detected outer peaks of , turbulence production, and the inclined shear layer caused by strong APG. We also highlighted the more notable effect of the detachment on the velocity profile (with significant differences between turbulent model predictions) than on the thermal profile. Strong streamline curvature-driven pressure gradients cause a noticeable Reynolds analogy breakdown. However, more data are needed to judge their overall accuracy in the separation bubble objectively.
Additional sources of validation will be included to better characterize the considered model’s performance in strong pressure gradients. Further, we will extend this study to a 3D geometry and conduct a large eddy simulation (LES) to understand better the unsteadiness of the detached boundary layer and the laminarescent state we have hypothesized inside the separation bubble. Additionally, we will further investigate the proposed approach for boundary layer detection and its resiliency in more complex geometries and stronger pressure gradients; as well as extend the study to other turbulence closure models. One important variable not considered in this study in its current form is the effect of the curvature-driven pressure gradients on the thermal boundary layer as a function of .
Author Contributions
Conceptualization, G.A.; methodology, D.P.; software, D.P.; validation, D.P., C.L. and G.A.; formal analysis, D.P., C.L. and G.A.; investigation, D.P., C.L. and G.A.; resources, G.A; data curation, D.P. and G.A.; writing—original draft preparation, D.P., C.L. and G.A.; writing—review and editing, D.P., C.L. and G.A.; visualization, D.P.; supervision, G.A.; project administration, G.A.; funding acquisition, G.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Center for the Advancement of Wearable Technologies and the National Science Foundation under grant OIA-1849243. This material is based upon work supported by the National Science Foundation under Grant No. HRD-1906130 and Grant No. 1847241.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank German Saltar Rivera for his input at the start of this work. The reviewers are greatly acknowledged for their comments, which made us improve the quality of the present article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Grid Sensitivity Study
Figure A1 depicts the results of the grid independence test performed over the curved hill domain. Some clarifications: (i) we have picked up a highly distorted flow, namely, the flow separation zone, (ii) additionally, we have explored the performance of grid point distribution in zones where the boundary layer is attached. Turning to Figure A1a of the profiles, it can be seen a clear convergence of the three types of meshes (coarse, medium, and fine) in the SA and SST models; in particular, there is a high level of similarity between the medium and fine mesh. This confirms that the refinement strategy has been adequate. By contrasting both models, the SST model predicts a much thicker separation bubble, and significant discrepancies are visualized inside the momentum boundary layer. It is important to mention that the SST model by Menter [2] considers a further improvement to the eddy viscosity model and is based on the idea of the Johnson–King model. It determines that the transport of the main turbulent shear stresses is critical in the simulations of strong APG flows. Specifically, the Menter SST turbulence model has been developed to outperform in turbulent boundary layer flows subject to APG, with eventual separation. Unfortunately, in [1], the streamwise velocity profiles were not measured at the separation bubble in order to validate our RANS results, and thus, further studies should be performed in the future to assess the SST model under flow detachment. The thermal distribution inside the temperature boundary layer is displayed in Figure A1b. Similarly, the SST model underpredicts temperature (passive scalar) with respect to the SA model. Significant differences are observed in thermal results at each refinement level. However, the number of vertical points was increased from the coarse to the fine mesh by an x2.66 factor, and additionally, special care was taken in the near wall region of the fine mesh ( 0.15 in the separation bubble, or lower). At this point, we can only ensure that numerical predictions are error-free of grid resolution. Therefore, the numerical predictions’ accuracy of the thermal field is warranted and the fine mesh is deemed appropriate for the goals of this study. The errors presented in Figure A1 and Figure A2 are regarding the fine-grid convergence index (GCI), where the latter figure is for an additional station 596 mm corresponding to the ZPG region before the curved hill. The errors shown are much lower in the ZPG station compared to the complicated station at the separation zone of Figure A1, supporting our conclusion on the mesh convergence. The estimation of discretization errors follows the procedure as described by Celik et al. [44], which is obtained from coarse mesh quality relative to medium mesh quality and medium mesh relative to fine mesh, respectively.
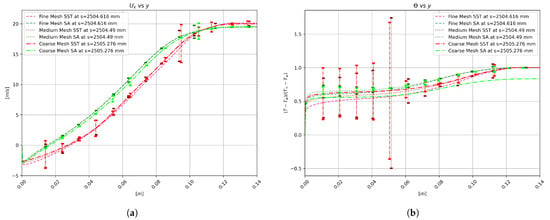
Figure A1.
Grid resolution independence assessment of: (a) streamwise velocity, (m/s), and (b) normalized temperature, ), at the separation bubble.
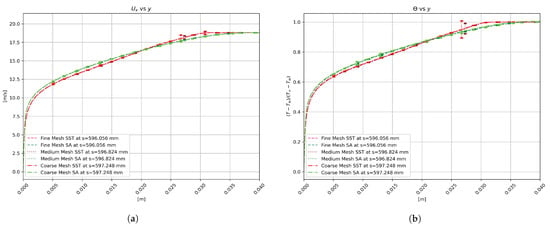
Figure A2.
Grid resolution independence assessment of: (a) streamwise velocity, (m/s), and (b) normalized temperature, ), at different streamwise locations.
Table A1 and Table A2 unveil the momentum and displacement thickness results and relative errors between meshes’ qualities, corresponding to the same stations of Figure 17 where the solutions of fine mesh were only displayed. In general, integral values of the turbulent boundary layers, i.e., and , exhibit a tendency to converge as the mesh is refined. Looking at Table A1, both SST and SA models had the highest discrepancy among grids at 1139 mm, with and , respectively. Table A2 shows how outstanding and low the relative errors for the momentum thickness are, where the most elevated error for the SST cases is in the FPG region ( 1596 mm). Meanwhile, for the SA cases is at 1139 mm. SA cases had more consistency and lower errors, even some reaching zero differences. Altogether, the relative errors are more than suitable for the presented assessment, favoring the momentum thickness compared to displacement thickness and SA slightly over SST for consistency. It is also observed that maximum discrepancies are concentrated at 1139 mm in both models and are within 30%. This zone, located around the first concave–convex surface intersection, seems to be one of the “hardest" to be simulated (aside from the flow separation bubble) since peaks on the were found there. Table A3 supplies a summary of the relative errors between different types of meshes at all streamwise stations. The low obtained values on the average relative errors (∼2%) confirm the numerical convergence in the refinement process.

Table A1.
Relative error of the displacement thickness.
Table A1.
Relative error of the displacement thickness.
| Stations (mm) | 596 | 710 | 867 | 1015 | 1139 | 1183 | 1345 | 1469 | 1596 | 1665 | 1730 | 1862 | 1990 |
| Experimental (mm) | 5.3108 | 6.2568 | 9.3987 | 11.5946 | 4.6352 | 3.7230 | 2.2703 | 2.0000 | 1.9325 | 2.4730 | 2.3716 | 3.4189 | 7.0338 |
| SST fine mesh (mm) | 6.4351 | 7.6986 | 12.1624 | 15.2198 | 6.5256 | 4.7115 | 2.3776 | 2.0155 | 2.0727 | 2.2290 | 2.4768 | 3.4724 | 5.9165 |
| SST medium mesh (mm) | 6.3852 | 7.6428 | 12.1447 | 15.1597 | 6.0952 | 4.6767 | 2.3269 | 1.9677 | 2.0225 | 2.1779 | 2.4090 | 3.3711 | 5.8081 |
| SST coarse mesh (mm) | 6.3403 | 7.5589 | 12.0473 | 15.2093 | 6.5252 | 4.6499 | 2.2817 | 1.9098 | 1.9505 | 2.1029 | 2.3374 | 3.2521 | 5.5843 |
| Rel. Error (fine to exp.) | 19.14% | 20.66% | 25.64% | 27.04% | 33.88% | 23.44% | 4.62% | 0.77% | 7.01% | −10.38% | 4.34% | 1.55% | −17.26% |
| Rel. Error (medium to fine) | −0.78% | −0.73% | −0.15% | −0.40% | −6.82% | −0.74% | −2.16% | −2.40% | −2.45% | −2.32% | −2.78% | −2.96% | −1.85% |
| Rel. Error (coarse to medium) | −0.71% | −1.10% | −0.80% | 0.33% | 6.81% | −0.57% | −1.96% | −2.99% | −3.63% | −3.50% | −3.02% | −3.59% | -3.93% |
| Experimental (mm) | 5.3108 | 6.2568 | 9.3987 | 11.5946 | 4.6352 | 3.7230 | 2.2703 | 2.0000 | 1.9325 | 2.4730 | 2.3716 | 3.4189 | 7.0338 |
| SA fine mesh (mm) | 6.1274 | 7.2940 | 11.3322 | 14.4704 | 6.3664 | 4.6301 | 2.3285 | 1.9750 | 2.0251 | 2.1694 | 2.3982 | 3.2684 | 5.3129 |
| SA medium mesh (mm) | 6.1019 | 7.2670 | 11.3463 | 14.3841 | 5.9822 | 4.6167 | 2.3026 | 1.9526 | 2.0026 | 2.1372 | 2.3769 | 3.2297 | 5.3106 |
| SA coarse mesh (mm) | 6.1584 | 7.3110 | 11.4325 | 14.6143 | 6.4907 | 4.6748 | 2.3088 | 1.9493 | 2.0002 | 2.1509 | 2.3815 | 3.2517 | 5.3431 |
| Rel. Error (fine to exp.) | 14.28% | 15.31% | 18.65% | 22.07% | 31.47% | 21.72% | 2.53% | −1.26% | 4.68% | −13.08% | 1.11% | −4.50% | −27.88% |
| Rel. Error (medium to fine) | −0.42% | −0.37% | 0.12% | −0.60% | −6.22% | −0.29% | −1.12% | −1.14% | −1.12% | −1.49% | −0.89% | −1.19% | −0.04% |
| Rel. Error (coarse to medium) | 0.92% | 0.60% | 0.76% | 1.59% | 8.15% | 1.25% | 0.27% | −0.17% | −0.12% | 0.64% | 0.19% | 0.68% | 0.61% |

Table A2.
Relative error of the momentum thickness.
Table A2.
Relative error of the momentum thickness.
| Stations (mm) | 596 | 710 | 867 | 1015 | 1139 | 1183 | 1345 | 1469 | 1596 | 1665 | 1730 | 1862 | 1990 |
| SST fine mesh (mm) | 4.3102 | 5.0204 | 6.9113 | 8.0405 | 4.5770 | 3.6047 | 1.9612 | 1.6479 | 1.6661 | 1.7738 | 1.9503 | 2.6493 | 4.1432 |
| SST medium mesh (mm) | 4.2982 | 5.0054 | 6.9092 | 8.0269 | 4.4109 | 3.5962 | 1.9384 | 1.6272 | 1.6437 | 1.7511 | 1.9145 | 2.5915 | 4.0891 |
| SST coarse mesh (mm) | 4.2629 | 4.9495 | 6.8559 | 8.0036 | 4.5478 | 3.5571 | 1.8894 | 1.5681 | 1.5744 | 1.6807 | 1.8486 | 2.4937 | 3.9427 |
| Rel. error (fine to exp.) | 6.45% | 6.47% | 4.46% | 0.79% | 15.57% | 10.55% | −0.06% | −8.22% | −12.27% | −12.73% | −3.12% | 1.51% | −0.87% |
| Rel. error (medium to fine) | −0.28% | −0.30% | −0.03% | −0.17% | −3.69% | −0.23% | −1.17% | −1.27% | −1.36% | −1.29% | −1.86% | −2.20% | −1.31% |
| Rel. error (coarse to medium) | −0.82% | −1.12% | −0.77% | −0.29% | 3.06% | −1.09% | −2.56% | −3.70% | −4.31% | −4.10% | −3.50% | −3.85% | −3.64% |
| Experimental (mm) | 4.0407 | 4.7058 | 6.6096 | 7.9771 | 3.9158 | 3.2434 | 1.9625 | 1.7892 | 1.8840 | 2.0151 | 2.0122 | 2.6097 | 4.1793 |
| SA fine mesh (mm) | 4.2706 | 4.9702 | 6.8606 | 8.1599 | 4.5825 | 3.6021 | 1.9310 | 1.6236 | 1.6401 | 1.7414 | 1.9069 | 2.5261 | 3.8347 |
| SA medium mesh (mm) | 4.2728 | 4.9717 | 6.8777 | 8.1362 | 4.4378 | 3.6099 | 1.9285 | 1.6236 | 1.6401 | 1.7335 | 1.9083 | 2.5151 | 3.8494 |
| SA coarse mesh (mm) | 4.2944 | 4.9844 | 6.9055 | 8.1997 | 4.6345 | 3.6316 | 1.9211 | 1.6079 | 1.6246 | 1.7312 | 1.8979 | 2.5165 | 3.8549 |
| Rel. error (fine to exp.) | 5.53% | 5.46% | 3.73% | 2.27% | 15.69% | 10.48% | −1.62% | −9.71% | −13.84% | −14.57% | −5.37% | −3.26% | −8.60% |
| Rel. error (medium to fine) | 0.05% | 0.03% | 0.25% | −0.29% | −3.21% | 0.22% | −0.13% | 0.00% | 0.00% | −0.45% | 0.07% | −0.44% | 0.38% |
| Rel. error (coarse to medium) | 0.50% | 0.26% | 0.40% | 0.78% | 4.34% | 0.60% | −0.39% | −0.97% | −0.95% | −0.14% | −0.54% | 0.06% | 0.14% |

Table A3.
Summary ofrelative errors for the displacement/momentum thickness.
Table A3.
Summary ofrelative errors for the displacement/momentum thickness.
| Average Error (%) | Maximum Error (%) | |
| SST | 2.29 | 6.82 |
| SA | 1.19 | 8.15 |
| Average Error (%) | Maximum Error (%) | |
| SST | 1.84 | 3.69 |
| SA | 0.56 | 4.34 |
References
- Baskaran, V.; Smits, A.; Joubert, P. A turbulent flow over a curved hill Part 1. Growth of an internal boundary layer. J. Fluid Mech. 1987, 182, 47–83. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Science Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. AIAA Paper 92-0439. [Google Scholar]
- Li, Q.; Schlatter, P.; Brandt, L.; Henningson, D.S. DNS of a spatially developing turbulent boundary layer with passive scalar transport. Int. J. Heat Fluid Flow 2009, 30, 916–929. [Google Scholar] [CrossRef]
- Warhaft, Z. Passive scalars in turbulent flows. Ann. Rev. Fluid Mech. 2000, 32, 203–240. [Google Scholar] [CrossRef]
- Paeres, D.; Lagares, C.; Araya, G. Assessment of Incompressible Turbulent Flow Over a Curved Hill with Passive Scalar Transport. In Proceedings of the AIAA SciTech, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Cham, Switzerland, 2016; Volume 113. [Google Scholar]
- Lagares, C.J.; Rivera, W.; Araya, G. Aquila: A Distributed and Portable Post-Processing Library for Large-Scale Computational Fluid Dynamics. In Proceedings of the AIAA SciTech, Virtual, 19–21 January 2021. [Google Scholar]
- Lagares, C.J.; Araya, G. Compressibility Effects on High-Reynolds Coherent Structures via Two-Point Correlations. In AIAA AVIATION 2021 FORUM. 2021. Available online: https://arc.aiaa.org/doi/pdf/10.2514/6.2021-2869 (accessed on 14 April 2022).
- Schlatter, P.; Orlu, R. Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 2010, 659, 116–126. [Google Scholar] [CrossRef]
- Simpson, R. Turbulent boundary layer separation. Ann. Rev. Fluid Mech. 1989, 21, 205–234. [Google Scholar] [CrossRef]
- Mollicone, J.P.; Battista, F.; Gualtieri, P.; Casciola, C.M. Effect of geometry and Reynolds number on the turbulent separated flow behind a bulge in a channel. J. Fluid Mech. 2017, 823, 100–133. [Google Scholar] [CrossRef]
- Chaouat, B. The State of the Art of Hybrid RANS/LES Modeling for the Simulation of Turbulent Flows. Flow Turbul. Combust 2017, 99, 279–327. [Google Scholar] [CrossRef]
- Radhakrishnan, S.; Piomelli, U.; Keating, A.; Lopes, A.S. Reynolds-averaged and large-eddy simulations of turbulent non-equilibrium flows. J. Turbul. 2006, 7, N63. [Google Scholar] [CrossRef]
- Purohit, S.; Kabir, I.F.S.A.; Ng, E.Y.K. On the Accuracy of uRANS and LES-Based CFD Modeling Approaches for Rotor and Wake Aerodynamics of the (New) MEXICO Wind Turbine Rotor Phase-III. Energies 2021, 14, 5198. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Sun, M.; Wang, H.; Liu, C.; Yu, J. Effect of the Backward Facing Step on a Transverse Jet in Supersonic Crossflow. Energies 2020, 13, 4170. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlnds, 1983; pp. 96–116. [Google Scholar]
- Lee, C.H. Rough boundary treatment method for the shear-stress transport k-ω model. Eng. Appl. Comput. Fluid Mech. 2018, 12, 261–269. [Google Scholar]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Rumsey, C. The Menter Shear Stress Transport Turbulence Model; Turbulence Modeling Resource, Langley Research Center/National Aeronautics and Space Administration: Hampton, Virginia, 2021. [Google Scholar]
- Milidonis, K.; Semlitsch, B.; Hynes, T. Effect of Clocking on Compressor Noise Generation. AIAA J. 2018, 56, 4225–4231. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, Q.; Yang, D. Experimental and Numerical Analysis of Rotor-Rotor Interaction Characteristics inside a Multistage Transonic Axial Compressor. Energies 2022, 15, 2627. [Google Scholar] [CrossRef]
- Spalart, P.; Shur, M. On the sensitization of turbulence models to rotation and curvature. Aerosp. Sci. Technol. 1997, 1, 297–302. [Google Scholar] [CrossRef]
- Knight, D.; Saffman, P. Turbulence Model Predictions for Flows with Significant Mean Streamline Curvature. In Proceedings of the 16th Aerospace Sciences Meeting, Huntsville, AL, USA, 16–18 January 1978. AIAA 78-258. [Google Scholar]
- Smirnov, P.E.; Menter, F.R. Sensitization of the SST Turbulence Model to Rotation and Curvature by Applying the Spalart–Shur Correction Term. J. Turbomach. 2009, 131. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: La Can˜ada, CA, USA, 2006. [Google Scholar]
- Spalart, P.R.; Rumsey, C.L. Effective Inflow Conditions for Turbulence Models in Aerodynamic Calculations. AIAA J. 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
- Shapiro, A.; Grossman, G.; Greenblatt, D. Simplified Transition and Turbulence Modeling for Oscillatory Pipe Flows. Energies 2021, 14, 1410. [Google Scholar] [CrossRef]
- Raheem, M.A.; Edi, P.; Pasha, A.A.; Rahman, M.M.; Juhany, K.A. Numerical Study of Variable Camber Continuous Trailing Edge Flap at Off-Design Conditions. Energies 2019, 12, 3185. [Google Scholar] [CrossRef]
- Paciorri, R.; Dieudonné, W.; Degrez, G.; Charbonnier, J.M.; Deconinck, H. Exploring the Validity of the Spalart-Allmaras Turbulence Model for Hypersonic Flows. J. Spacecr. Rocket. 1998, 35, 121–126. [Google Scholar] [CrossRef]
- Lagares, C.; Santiago, J.; Araya, G. Turbulence modeling in hypersonic turbulent boundary layers subject to convex wall curvature. AIAA J. 2021, 59, 1–20. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamentals and Applications; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Kays, W.M.; Crawford, M.E. Convective Heat and Mass Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Quinones, C. Transport Phenomena in Crossflow Jets Subject to Very Strong Favorable Pressure Gradient. Master’s Thesis, University of Puerto Rico-Mayaguez, Mayaguez, Puerto Rico, 2020. [Google Scholar]
- Narasimha, R. Relaminarization-magnetohydrodynamic and otherwise. AIAA Progress Astronaut. Aeronaut. 1983, 84, 30–53. [Google Scholar]
- Araya, G.; Castillo, L. DNS of turbulent thermal boundary layers subjected to adverse pressure gradients. Physics of Fluids 2013, 25, 095107. [Google Scholar] [CrossRef]
- Araya, G.; Castillo, C.; Hussain, F. The log behaviour of the Reynolds shear stress in accelerating turbulent boundary layers. J. Fluid Mech. 2015, 775, 189–200. [Google Scholar] [CrossRef]
- Skote, M.; Henningson, D.; Henkes, R. Direct numerical simulation of self-similar turbulent boundary layers in adverse pressure gradients. Flow Turbul. Combust. 1998, 60, 47–85. [Google Scholar] [CrossRef]
- Narasimha, R.; Sreenivasan, K. Relaminarization of fluid flows. Adv. Appl. Mech. 1979, 19, 221–309. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Lagares, C.J.; Jansen, K.E.; Patterson, J.; Araya, G. The effect of concave surface curvature on supersonic turbulent boundary layers. In Proceedings of the 72nd Annual Meeting of the American Physical Society’s Division of Fluid Dynamics, Seattle, WA, USA, 23–26 November 2019. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids-Eng.-Trans. ASME 2008, 130, 078001. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).