Study on Critical Drawdown Pressure of Sanding for Wellbore of Underground Gas Storage in a Depleted Gas Reservoir
Abstract
:1. Introduction
2. Methodology
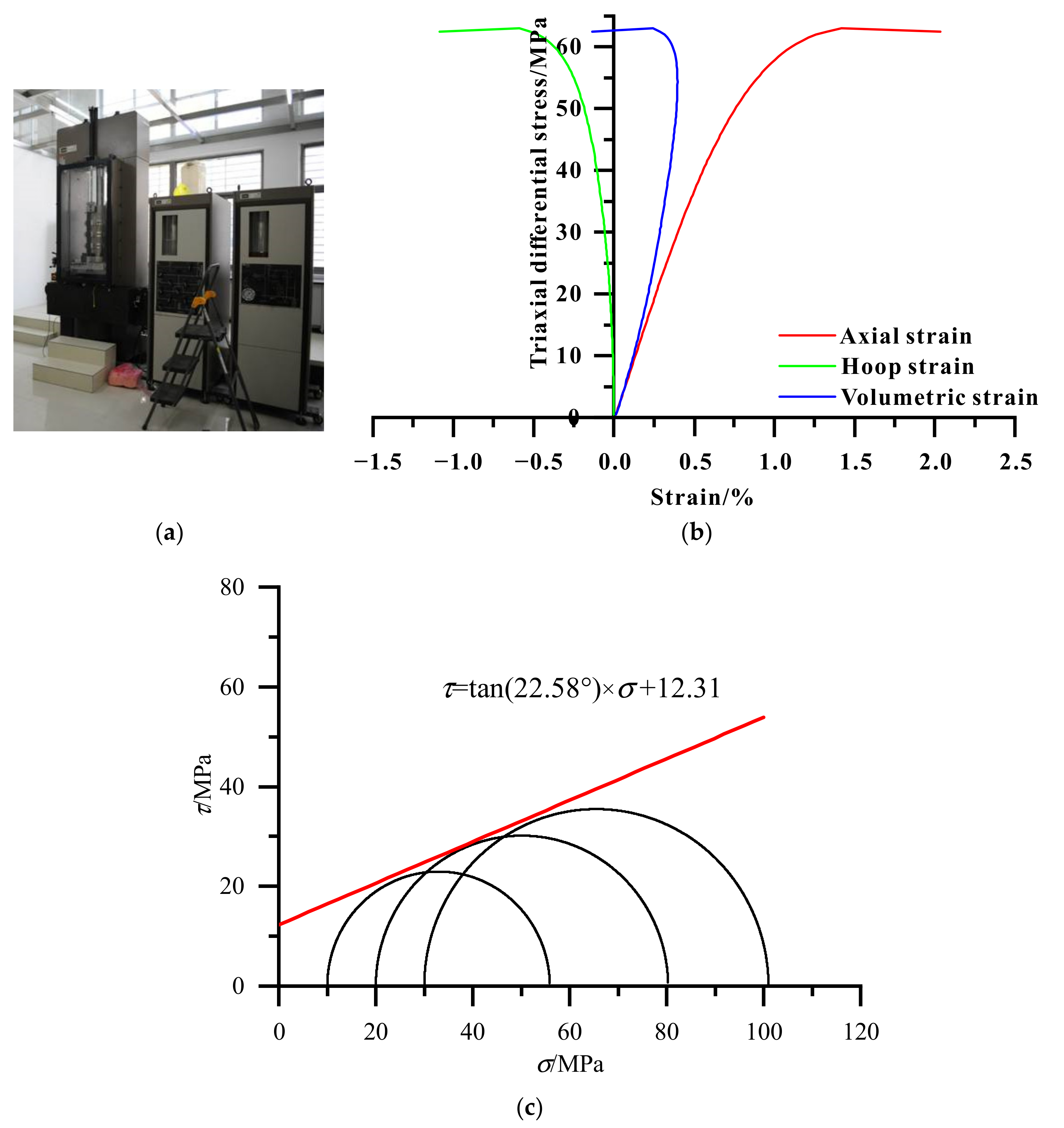
2.1. Experimental Test on Mechanical Properties of Reservoir Rock
2.2. Mathematical Model of the Yield Criterion for Simulation
3. Results and Discussion
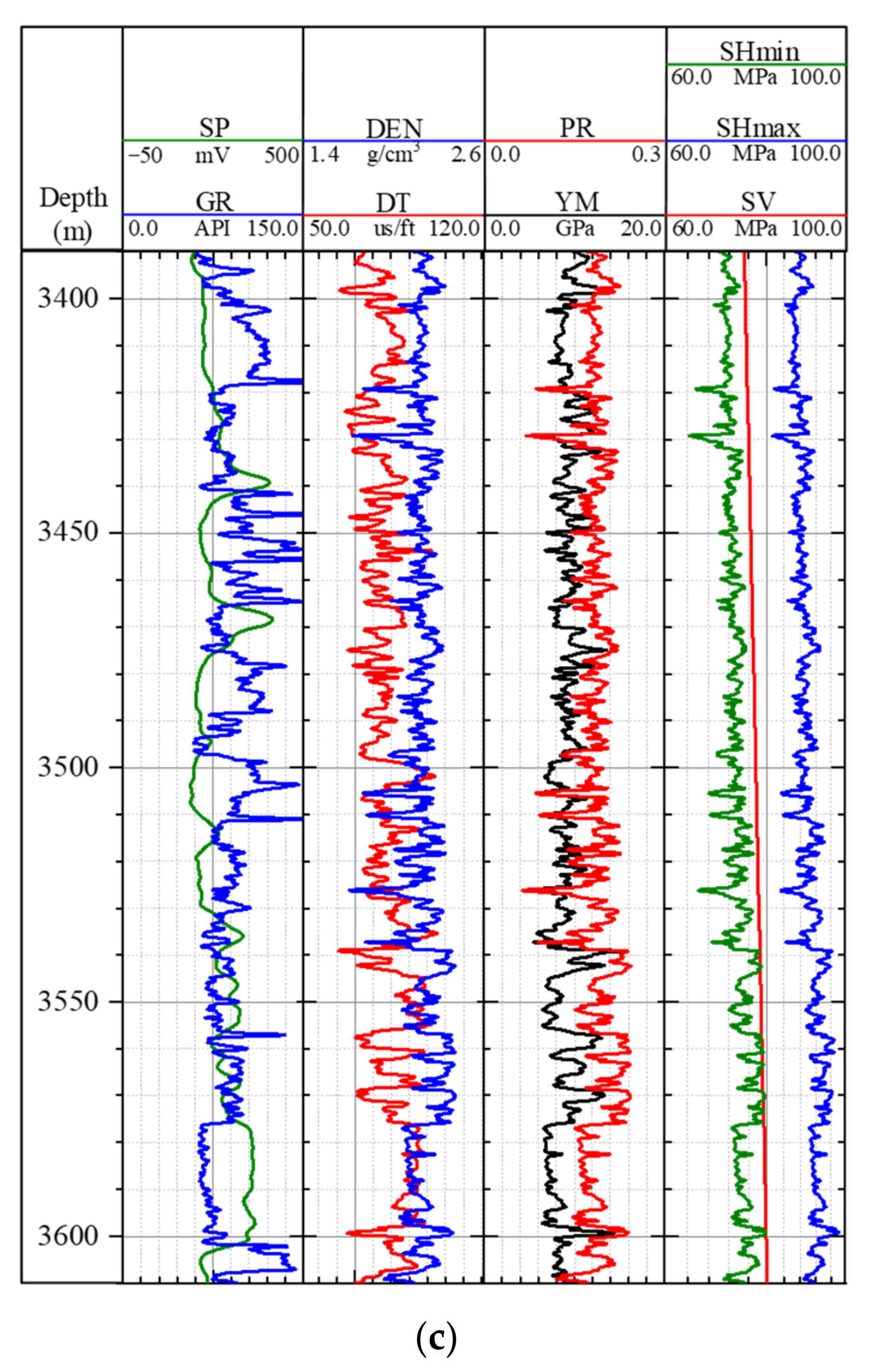
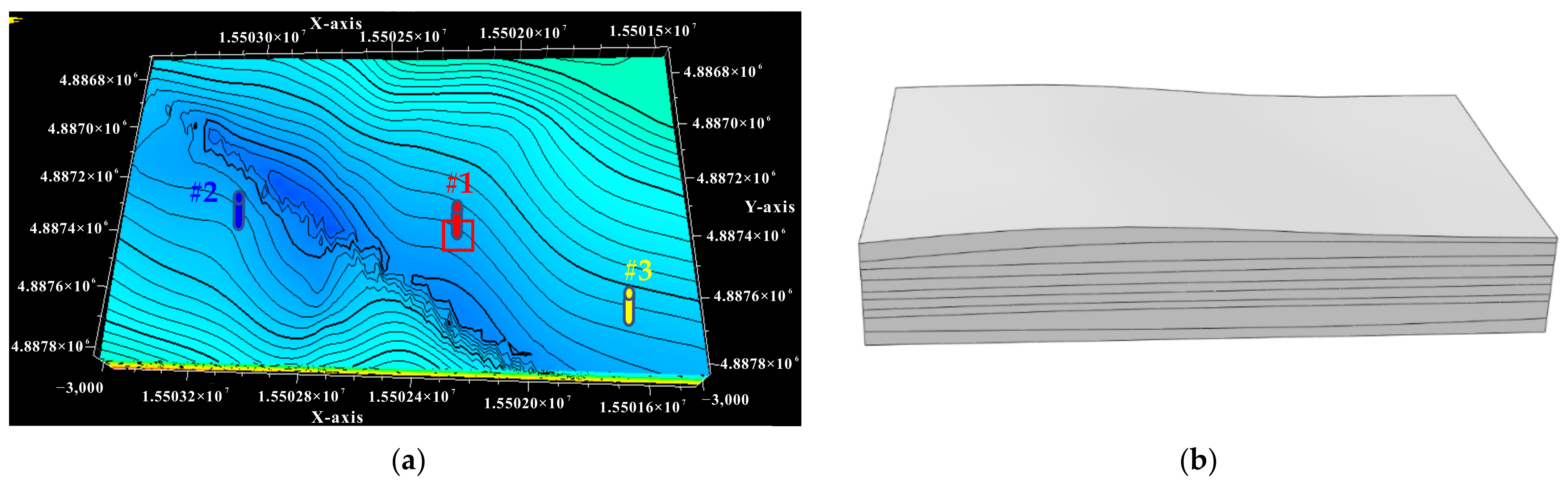
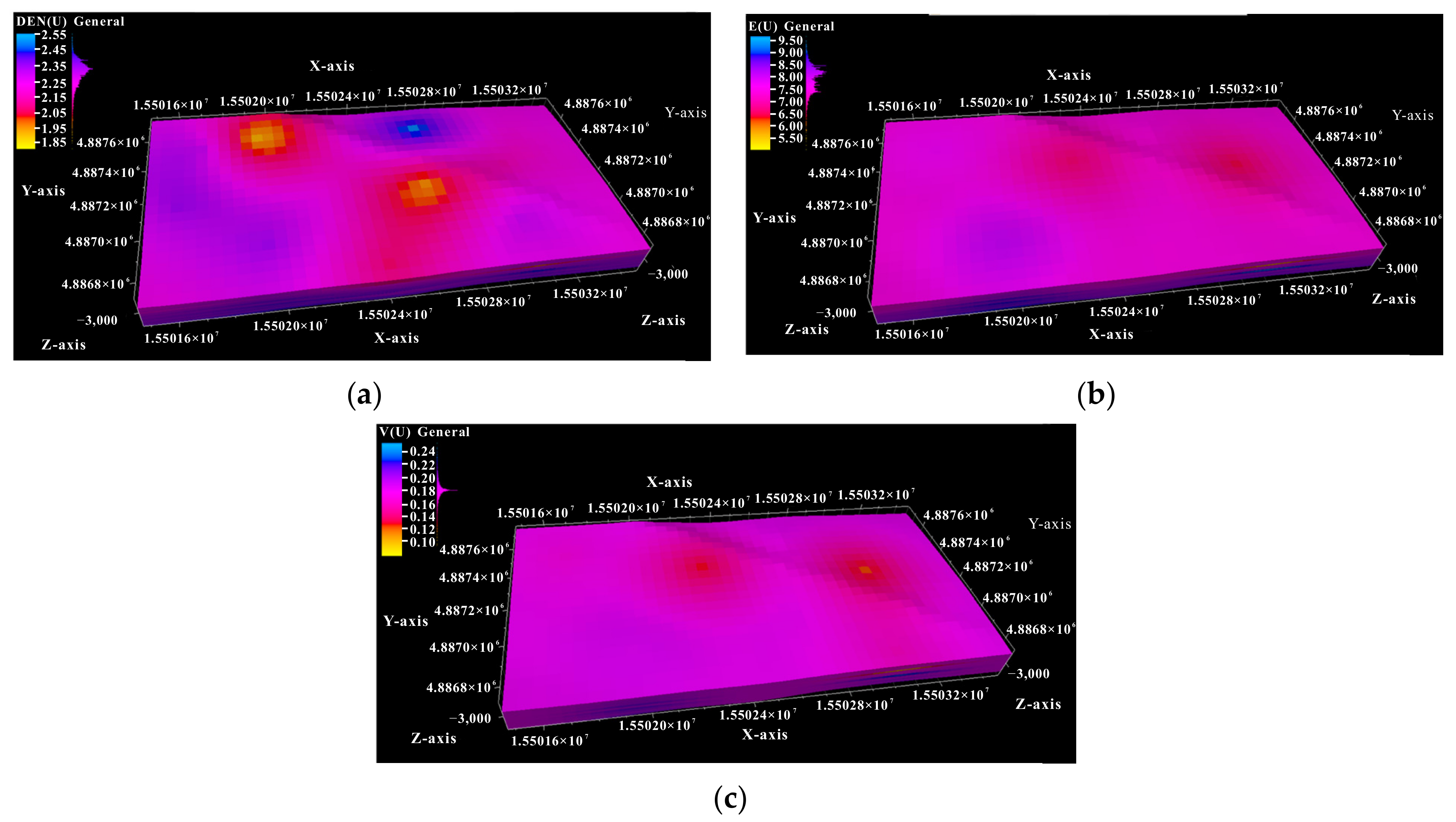
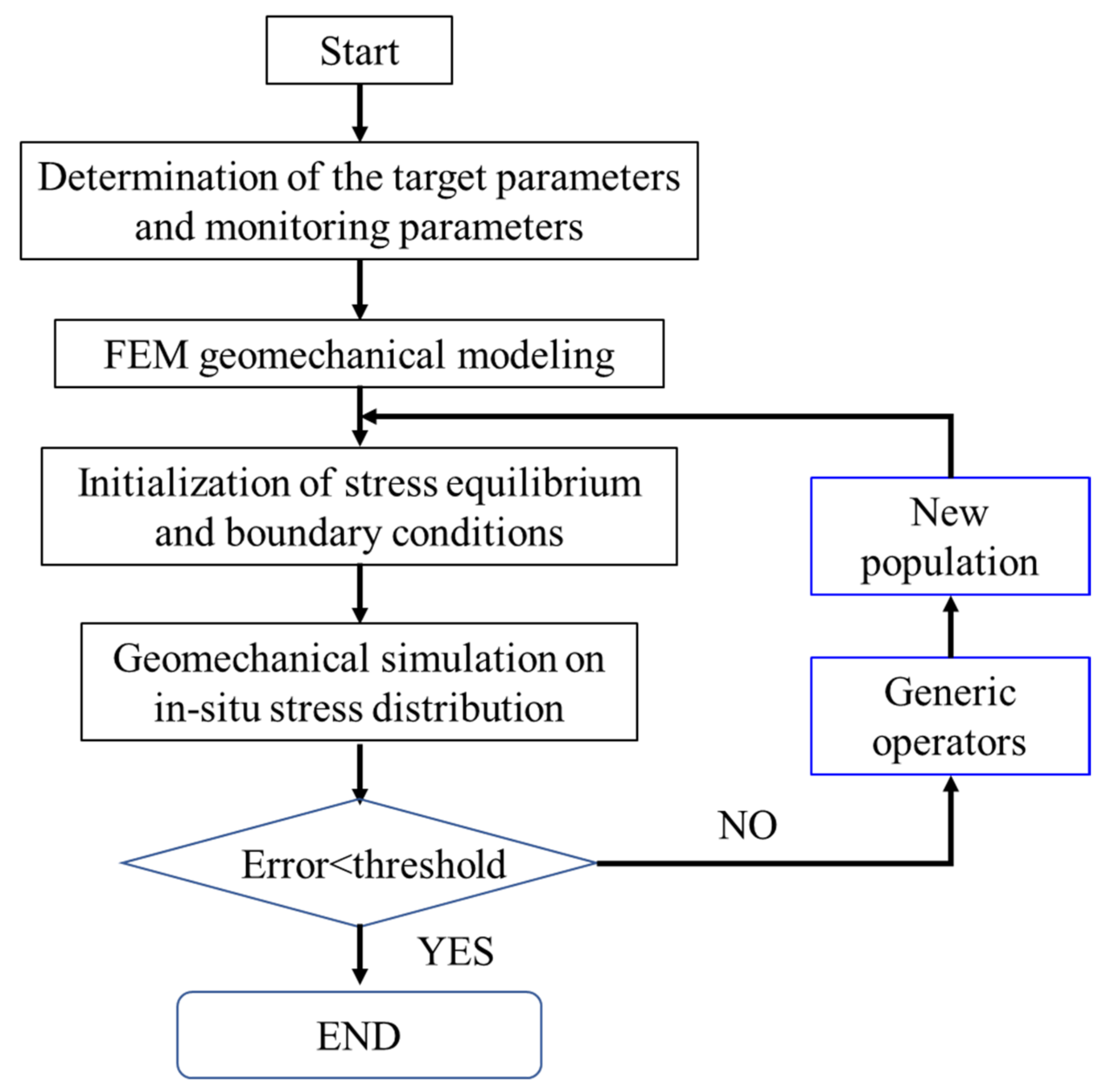
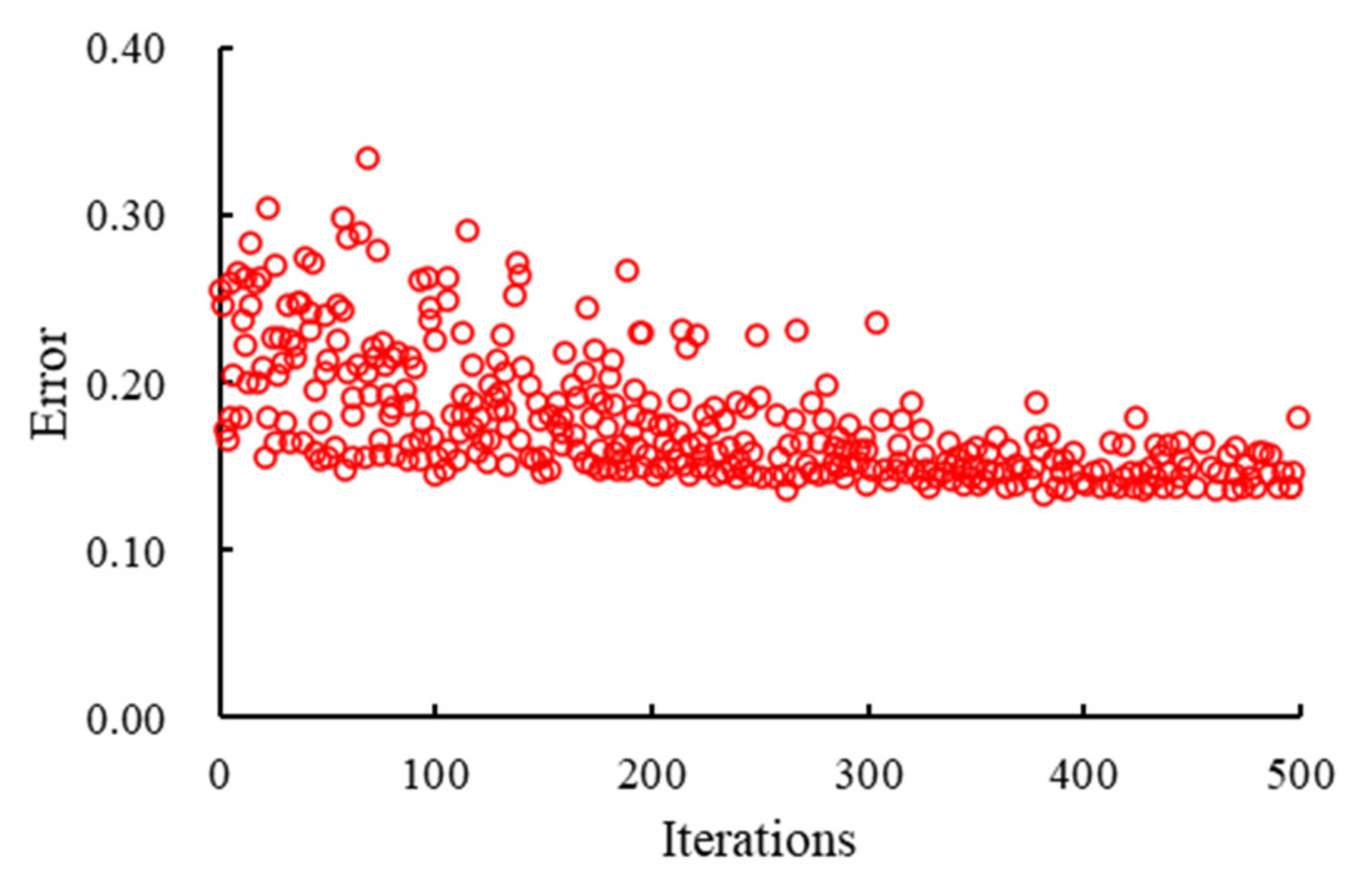
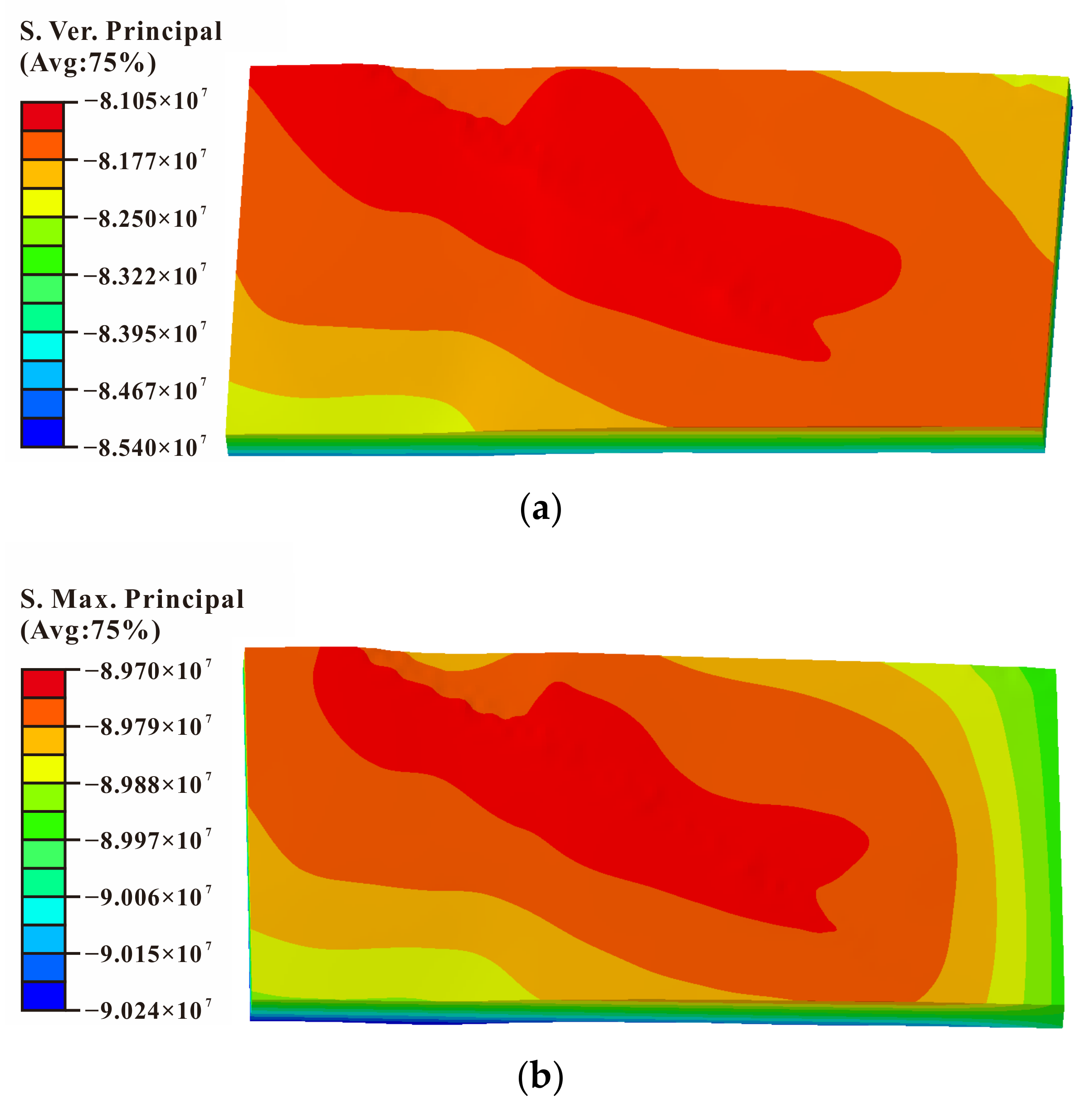
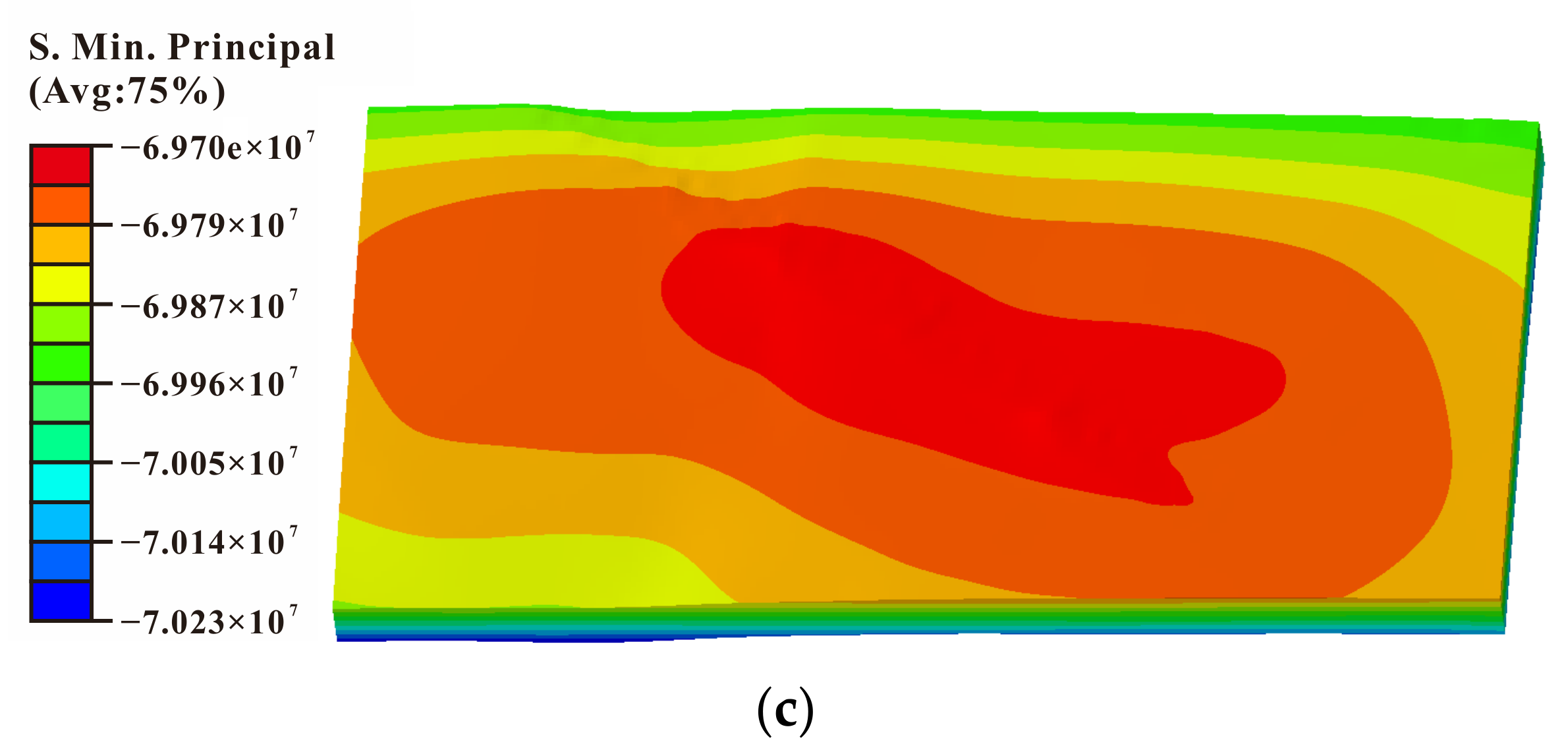
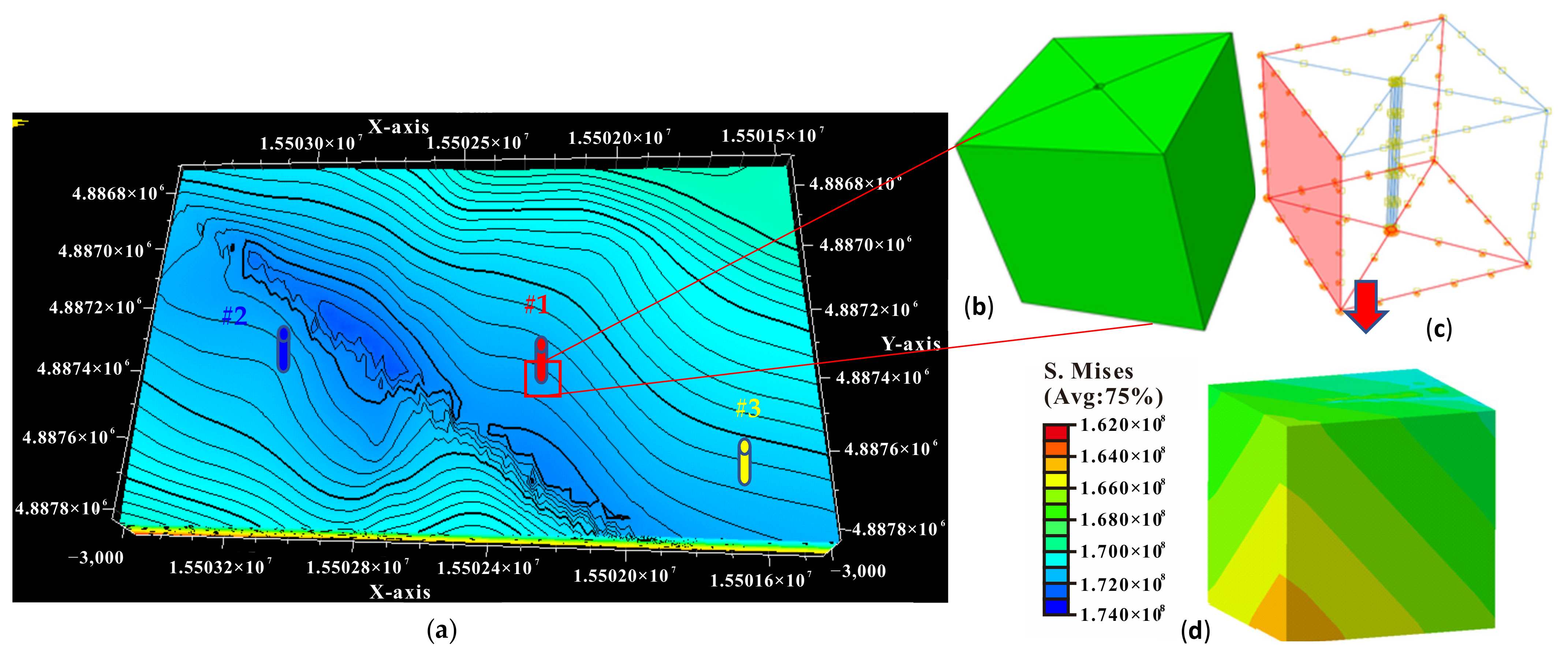
3.1. Inversion of the In-Situ Stress Distribution
3.2. Simulation on Sanding Prediction of Well Failure in UGS
3.3. Influencing Factors of the Critical Pressure Difference for Sanding in UGS
4. Conclusions
- (1)
- Based on the experimental results, the functional relationship between key rock mechanics and rock density, such as compressive strength, elastic modulus, and Poisson’s ratio, was established. Coupling with the well-logging curves, the mechanical properties of the rock in the coring well could be calculated accurately.
- (2)
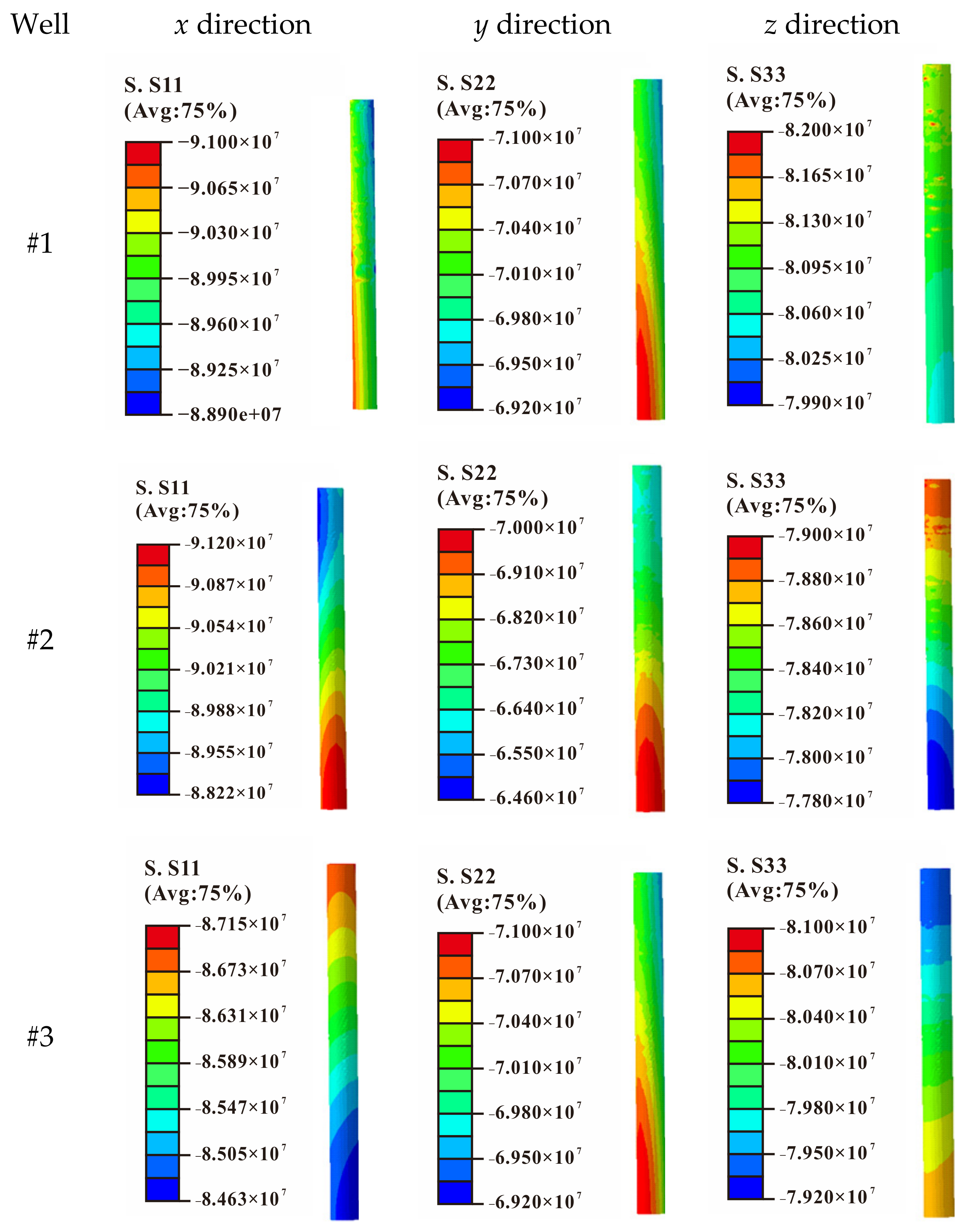
- The 3D geological model of the reservoir for UGS was transformed to a finite element geomechanics model, and was used as inputs for the inversed analysis of in-situ crustal stress. Adopting the measured in-situ stress in the samples of Well #1 as the target parameter, the crustal stress of the reservoir was determined coupling with the genetic algorithm and geomechanical simulation on Abaqus software.
- (3)
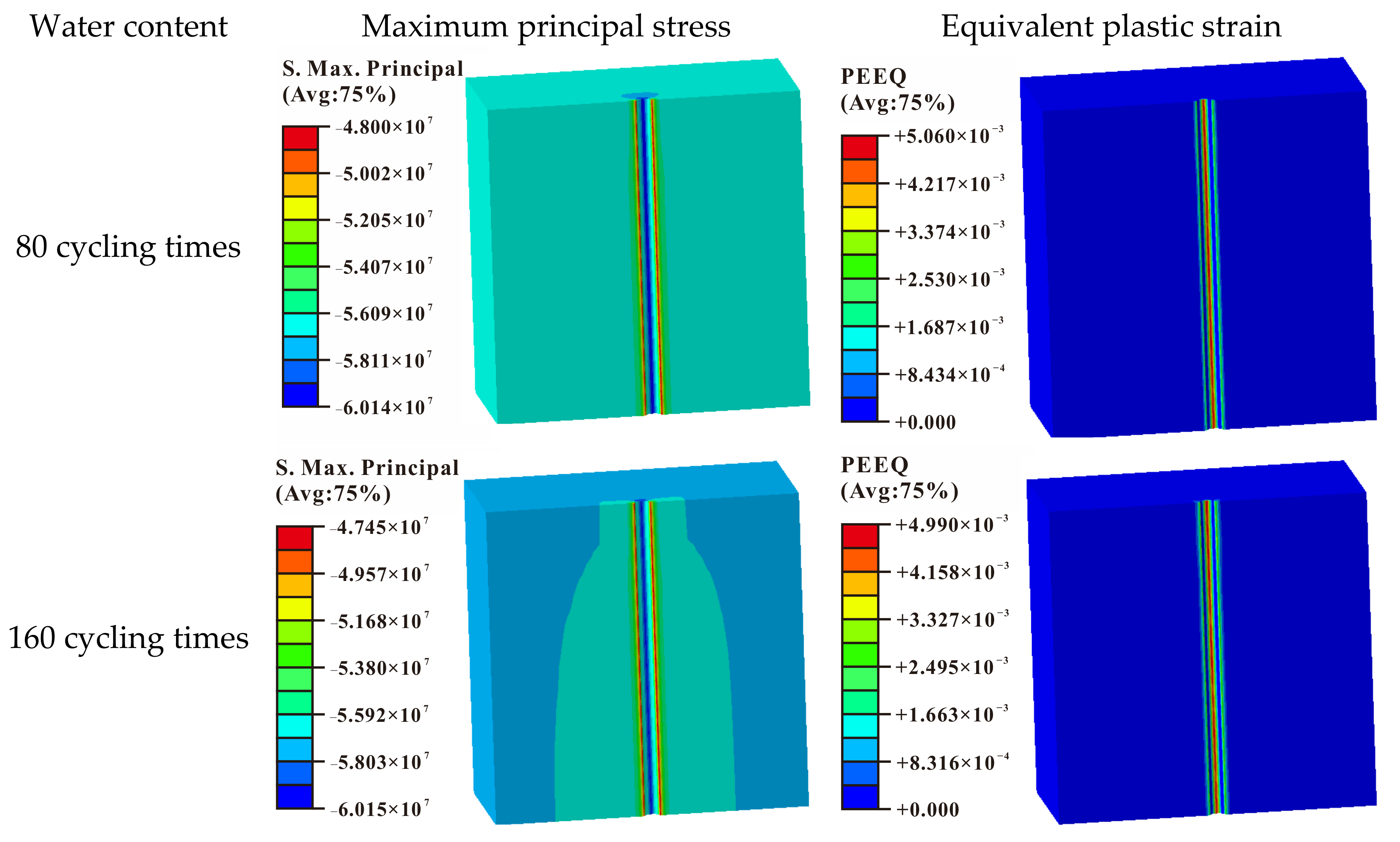
- Based on the stress distribution obtained by inversed analysis, the sub model of the zone near the wellbore was established. Numerical simulations on the well drilling and the cycling of high-speed injection-withdrawal were conducted. Taking the CSL of 5‰ as the sanding criterion of the wellbore, the CDPs of the gas production in the UGS were predicted, which are 5.59 MPa, 3.98 MPa, and 4.01 MPa for well #1, well #2 and well #3 when the pressure of the gas storage is 30 MPa, respectively. The simulation results showed good agreement with the field-measured benchmark data of well #2 and well #3.
- (4)
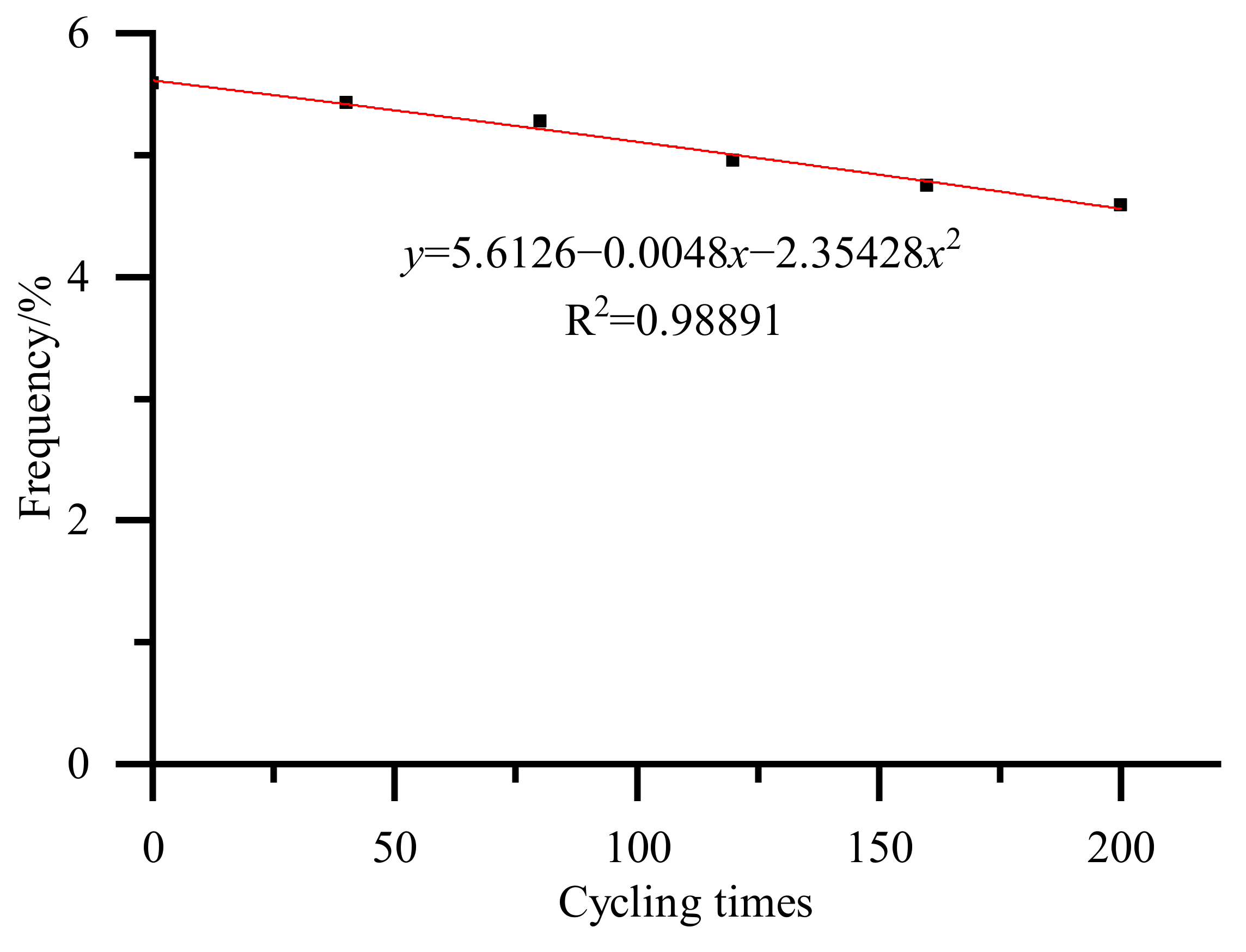
- The effects of moisture contents (ranging from 10% to 40%), and cycling times of gas injection and withdrawal (ranging from 40 to 200 cycling times) on the critical differential pressure were simulated and analyzed. The results indicated that the CDP decreased with increase of the moisture content and the cycling times.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three dimensional |
| ATWC | Advanced thick-walled cylinder () |
| BEM | Boundary Element Method |
| CSL | Critical strain limit |
| CDP | Critical differential pressure |
| DEM | Discrete Element Method |
| FDM | Finite Difference Method |
| FEM | Finite element method |
| GA | Genetic algorithm |
| NG | Natural gas |
| PR | Poisson’s Ratio |
| TWC | Thick-wall cylinder strength |
| UCS | Unconfined compressive strength |
| UGS | Underground gas storage |
| YM | Young’s Modulus |
References
- Song, R.; Cui, M.; Liu, J. Single and multiple objective optimization of a natural gas liquefaction process. Energy 2017, 124, 19–28. [Google Scholar] [CrossRef]
- Song, R.; Sun, S.; Liu, J.; Yang, C. Pore scale modeling on dissociation and transportation of methane hydrate in porous sediments. Energy 2021, 237, 121630. [Google Scholar] [CrossRef]
- Song, R.; Liu, J.; Yang, C.; Sun, S. Study on the multiphase heat and mass transfer mechanism in the dissociation of methane hydrate in reconstructed real-shape porous sediments. Energy 2022, 254, 124421. [Google Scholar] [CrossRef]
- Ali, A. Data-driven based machine learning models for predicting the deliverability of underground natural gas storage in salt caverns. Energy 2021, 229, 120648. [Google Scholar] [CrossRef]
- Gümrah, F.; Katircioglu, D.; Aykan, Y.; Okumus, S.; Kilincer, N. Modeling of gas demand using degree-day concept: Case study for Ankara. Energy Sources 2001, 23, 101–114. [Google Scholar]
- Verga, F. What’s conventional and what’s special in a reservoir study for underground gas storage. Energies 2018, 11, 1245. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Silva, P.P. Overview of large-scale underground energy storage technologies for integration of renewable energies and criteria for reservoir identification. J. Energy Storage 2019, 21, 241–258. [Google Scholar] [CrossRef]
- Confort, M.J.F.; Mothe, C.G. Estimating the required underground natural gas storage capacity in Brazil from the gas industry characteristics of countries with gas storage facilities. J. Nat. Gas Sci. Eng. 2014, 18, 120–130. [Google Scholar] [CrossRef]
- Arfaee, M.I.R.; Sola, B.S. Investigating the effect of fracture–matrix interaction in underground gas storage process at condensate naturally fractured reservoirs. J. Nat. Gas Sci. Eng. 2014, 19, 161–174. [Google Scholar] [CrossRef]
- Vilarrasa, V.; De Simone, S.; Carrera, J.; Villaseñor, A. Unraveling the causes of the seismicity induced by underground gas storage at Castor, Spain. Geophys. Res. Lett. 2021, 48, e2020GL092038. [Google Scholar] [CrossRef]
- Schultz, R.A.; Evans, D.J. Occurrence frequencies and uncertainties for US underground natural gas storage facilities by state. J. Nat. Gas Sci. Eng. 2020, 84, 103630. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, Y.; Sheng, Z.; Yan, X. Uncertainty failure risk quantitative assessments for underground gas storage near-wellbore area. J. Energy Storage 2021, 36, 102393. [Google Scholar] [CrossRef]
- McNulty, J.W. An Experimental Study of Arching in Sand (No. 1); Waterways Experiment Station: Vicksburg, MS, USA, 1965. [Google Scholar]
- Clearly, M.P.; Melvan, J.J.; Kohlhaas, C.A. The Effect of Confining Stress and Fluid Properties on Arch Stability in Unconsolidated Sands. In Proceedings of the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 23–26 September 1979. [Google Scholar]
- Tippie, D.B.; Kohlhaas, C.A. Effect of Flow Rate on Stability of Unconsolidated Producing Sands. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Las Vegas, NV, USA, 30 September–3 October 1973. [Google Scholar]
- Ranjith, P.; Perera, M.; Perera, W.; Wu, B.; Choi, S. Effective parameters for sand production in unconsolidated formations: An experimental study. J. Pet. Sci. Eng. 2013, 105, 34–42. [Google Scholar] [CrossRef]
- Hall, C.J.; Harrisberger, W.H. Stability of Sand Arches: A Key to Sand Control. J. Pet. Technol. 1970, 22, 821–829. [Google Scholar] [CrossRef]
- Rahman, K.; Khaksar, A.; Kayes, T.J. Minimizing Sanding Risk by Optimizing Well and Perforation Trajectory Using an Integrated Geomechanical and Passive Sand-Control Approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Cook, J.M.; Bradford, I.D.R.; Plumb, R.A. A study of the physical mechanisms of sanding and application to sand production prediction. In Proceedings of the European Petroleum Conference, London, UK, 25–27 October 1994. [Google Scholar]
- Bianco, L.C.B.; Halleck, P.M. Mechanisms of arch instability and sand production in two-phase saturated poorly consolidated sandstones. In Proceedings of the SPE European Formation Damage Conference, The Hague, The Netherlands, 21–22 May 2001. [Google Scholar]
- Honari, S.; Seyedi Hosseininia, E. Particulate Modeling of Sand Production Using Coupled DEM-LBM. Energies 2021, 14, 906. [Google Scholar] [CrossRef]
- Al-Shaaibi, S.K.; Al-Ajmi, A.M.; Al-Wahaibi, Y. Three dimensional modeling for predicting sand production. J. Pet. Sci. Eng. 2013, 109, 348–363. [Google Scholar] [CrossRef]
- Arbelaez-Londoño, A.; Osorio, G.; Alzate-Espinosa, G. The Wormholes Formation During the Cold Heavy Oil Production with Sand (CHOPS). In Proceedings of the ISRM 8th International Symposium Geomechanics, Bucaramanga, Colombia, 6–10 May 2019. [Google Scholar]
- Veeken, C.A.M.; Davies, D.R.; Kenter, C.J.; Kooijman, A.P. Sand production prediction review: Developing an integrated approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar]
- Zhang, R.; Shi, X.; Zhu, R.; Zhang, C.; Fang, M.; Bo, K.; Feng, J. Critical drawdown pressure of sanding onset for offshore depleted and water cut gas reservoirs: Modeling and application. J. Nat. Gas Sci. Eng. 2016, 34, 159–169. [Google Scholar] [CrossRef]
- Ou, Q.; Yang, J.; Zhang, Z.; Liu, L.; Qu, X.; Hong, Y. Prediction of high-temperature and high-pressure well sand production in the DF gas field. In Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium, Virtual, 18–25 June 2021. [Google Scholar]
- Zhou, S.; Sun, F. Sand Production Management for Unconsolidated Sandstone Reservoirs; Petroleum Industry Press: Beijing, China, 2016. [Google Scholar] [CrossRef]
- Song, R.; Wang, Y.; Ishutov, S.; Zambrano-Narvaez, G.; Hodder, K.J.; Chalaturnyk, R.J.; Sun, S.; Liu, J.; Gamage, R.P. A Comprehensive Experimental Study on Mechanical Behavior, Microstructure and Transport Properties of 3D-printed Rock Analogs. Rock Mech. Rock Eng. 2020, 53, 5745–5765. [Google Scholar] [CrossRef]
- Zuloaga, P.; Yu, W.; Miao, J.; Sepehrnoori, K. Performance evaluation of CO2 Huff-n-Puff and continuous CO2 injection in tight oil reservoirs. Energy 2017, 134, 181–192. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L.; Li, P.; Zhao, W. The Critical Pressure Difference Prediction of Sand Production in Deepwater Sandstone Gas Reservoirs. Pet. Sci. Technol. 2013, 31, 1925–1932. [Google Scholar] [CrossRef]
- Nordgren, R.P. Strength of well completions. In Proceedings of the 18th US Symposium on Rock Mechanics (USRMS), Golden, CO, USA, 22–24 June 1977. [Google Scholar]
- Almisned, O.A. A Model for Predicting Sand Production from Well Logging Data. Ph.D. Thesis, The University of Oklahoma, Norman, OK, USA, 1995. [Google Scholar]
- Morita, N.; Whitfill, D.L.; Fedde, O.P.; Lovik, T.H. Parametric Study of Sand-Production Prediction: Analytical Approach. SPE Prod. Eng. 1989, 4, 25–33. [Google Scholar] [CrossRef]
- Vaziri, H.; Barree, B.; Xiao, Y.; Palmer, I.; Kutas, M. What is the magic of water in producing sand? In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Rahmati, H.; Jafarpour, M.; Azadbakht, S.; Nouri, A.; Vaziri, H.; Chan, D.; Xiao, Y. Review of Sand Production Prediction Models. J. Pet. Eng. 2013, 2013, 864981. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Perera, M.S.A.; Perera, W.K.G.; Choi, S.K.; Yasar, E. Sand production during the extrusion of hydrocarbons from geological formations: A review. J. Pet. Sci. Eng. 2014, 124, 72–82. [Google Scholar] [CrossRef]
- Subbiah, S.K.; Samsuri, A.; Mohamad-Hussein, A.; Jaafar, M.Z.; Chen, Y.R.; Kumar, R.R. Root cause of sand production and methodologies for prediction. Petroleum 2021, 7, 263–271. [Google Scholar] [CrossRef]
- Nouri, A.; Vaziri, H.; Kuru, E.; Islam, R. A comparison of two sanding criteria in physical and numerical modeling of sand production. J. Pet. Sci. Eng. 2006, 50, 55–70. [Google Scholar] [CrossRef]
- Volonté, G.; Scarfato, F.; Brignoli, M. Sand prediction: A practical finite-element 3D approach for real field applications. SPE Prod. Oper. 2013, 28, 95–108. [Google Scholar] [CrossRef]
- Gui, F.; Khaksar, A.; Van Zee, W.; Cadogan, P. Improving the Sanding Evaluation Accuracy by Integrating Core Tests, Field Observations and Numerical Simulation. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Perth, Australia, 25–27 October 2016. [Google Scholar] [CrossRef]
- Lu, Y.; Xue, C.; Liu, T.; Chi, M.; Yu, J.; Gao, H.; Xu, X.; Li, H.; Zhuo, Y. Predicting the critical drawdown pressure of sanding onset for perforated wells in ultra-deep reservoirs with high temperature and high pressure. Energy Sci. Eng. 2021, 9, 1517–1529. [Google Scholar] [CrossRef]
- Cornelio, J.; Ershaghi, I. A Machine Learning Approach for Predicting Rock Brittleness from Conventional Well Logs. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 15–17 October 2019. [Google Scholar] [CrossRef]
- Jingen, D.; Kangping, W.; Rongzun, H. In-situ stress determination at great depth by using acoustic emission technique. In Proceedings of the 35th US Symposium on Rock Mechanics (USRMS), Reno, NV, USA, 5–7 June 1995. [Google Scholar]
- Park, S.-H.; Bang, K.-H.; Cho, J.-R. Structural Integrity Evaluation of a Reactor Cavity during a Steam Explosion for External Reactor Vessel Cooling. Energies 2021, 14, 3605. [Google Scholar] [CrossRef]
- Santana, C.; Likrama, F. Workflow on Incorporating Thick-Walled Cylinder Test Results in Finite Element Models of near Wellbore for Sanding Prediction Studies. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Deng, F.; Yan, C.; Jia, S.; Chen, S.; Wang, L.; He, L. Influence of Sand Production in an Unconsolidated Sandstone Reservoir in a Deepwater Gas Field. J. Energy Resour. Technol. 2019, 141, 092904. [Google Scholar] [CrossRef]





| Sanding Index | Equation | Threshold |
|---|---|---|
| Porosity [23] | ψ = Volumepore/Volumetotal | Varying with the reservoir types; where Volumepore and Volumetotal are the volume of the pore and the rock, respectively. |
| Acoustic wave travel time [24] | where Vp is the velocity of the P-wave; 95 μs/ft <Δtc < 105 μs/ft, Slight sanding; Δtc ≥ 105 μs/ft, Severe sanding | |
| Combination modulus Ec [25] | where ρr is the rock density; Ec ≥ 2.0 × 104 MPa, No sanding; 2.0 × 104 MPa ≥ Ec ≥ 1.5 × 104 MPa, Slight sanding; Ec < 1.5 × 104 MPa, Severe sanding | |
| Index Bi [26] | where K and G are the volumetric modulus and shear modulus; Bi > 20 GPa, No sanding; 20 GPa > Bi ≥ 1.4 × 104 MPa, Slight sanding (but will sanding seriously after water breakthrough); Bi < 14 GPa, Severe sanding | |
| Schlumberger’s ratio [27] | where μ is the Poisson’s ratio; R ≤ 5.9 × 107 MPa2, Sanding |
| CDP Model | Equation | Nomenclature | Failure Mode |
|---|---|---|---|
| Unconfined compressive strength(UCS)/2 [30] | L is the empirical constant of 0.3~0.5, σUCS is the uniaxial compressive strength | Compressional failure | |
| Nordgren’s model [31] | c is the material constant for non-linearity | ||
| Almisned’s model [32] | B is the Biot’s constant, Pob is the overburden pressure, s and a are Hoek Brown material constants | Shear failure | |
| Morita et al.’s model [33] | |||
| Vaziri et al.’s model [34] | σv is the vertical stress, λ is a factor depending on thick-wall cylinder strength (TWC) test, | ||
| ; | C is the cohesive force, φ is the frictional angle, P0 is the pore pressure | Tensile Failure |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, R.; Zhang, P.; Tian, X.; Huang, F.; Li, Z.; Liu, J. Study on Critical Drawdown Pressure of Sanding for Wellbore of Underground Gas Storage in a Depleted Gas Reservoir. Energies 2022, 15, 5913. https://doi.org/10.3390/en15165913
Song R, Zhang P, Tian X, Huang F, Li Z, Liu J. Study on Critical Drawdown Pressure of Sanding for Wellbore of Underground Gas Storage in a Depleted Gas Reservoir. Energies. 2022; 15(16):5913. https://doi.org/10.3390/en15165913
Chicago/Turabian StyleSong, Rui, Ping Zhang, Xiaomin Tian, Famu Huang, Zhiwen Li, and Jianjun Liu. 2022. "Study on Critical Drawdown Pressure of Sanding for Wellbore of Underground Gas Storage in a Depleted Gas Reservoir" Energies 15, no. 16: 5913. https://doi.org/10.3390/en15165913
APA StyleSong, R., Zhang, P., Tian, X., Huang, F., Li, Z., & Liu, J. (2022). Study on Critical Drawdown Pressure of Sanding for Wellbore of Underground Gas Storage in a Depleted Gas Reservoir. Energies, 15(16), 5913. https://doi.org/10.3390/en15165913








