Abstract
Based on the model of irreversible single resonance energy-selective electron heat engine established in the previous literature, this paper applies finite-time thermodynamic theory and NSGA-II algorithm to perform multi-objective optimization. Single-, bi-, tri- and quadru-objective optimizations are performed when the energy boundary and the resonance width are taken as the optimization variables, and the power output, thermal efficiency, efficient power and ecological function are taken as the optimization objectives. The deviation indexes of different optimization objective combinations are obtained by using LINMAP, TOPSIS and Shannon entropy approaches. The results show that the values of energy boundary and resonance width can be reasonably selected according to the design requirements of the system. When power output and efficiency are optimized, the minimal deviation index is obtained by TOPSIS approach and the value is 0.0748, which is the most ideal design scheme.
1. Introduction
Since the establishment of finite time thermodynamics (FTT) theory, many scholars have introduced it into various cycle studies and have made great progress [1,2,3,4,5,6], including optimal performances [7,8,9,10,11,12,13,14,15] and optimal configurations [16,17,18,19,20,21,22,23,24,25]. The early FTT research objects involved mainly traditional macro thermal devices, such as macro heat engines, refrigerators and heat pumps. The idea of FTT considering various irreversible loss factors to analyze and optimize thermodynamic cycle and process is also of great significance to micro energy conversion devices. With the developments of FTT, the research objects involve quantum cycles [26,27], Brownian motor systems [28,29], electron engine systems [30], and other micro energy conversion devices related to time and rate.
In 2002, Humphrey et al. [31] found that between two electron reservoirs with different electrochemical potentials and temperatures, electrons can be exchanged reversibly by choosing an appropriate energy filter, and this novel electronic device was named as energy selective electron (ESE) heat engine [32]. When not accounting for heat leakage losses, Humphrey [32] applied the FTT theory to explain the operation mechanism of the single resonance ESE heat engine at the earliest and analyzed the efficiency at maximum power (EMP) characteristics of the system. Ding et al. [33] introduced the ecological function [34] into an endoreversible ESE heat engine. Luo et al. [35] further analyzed effect of resonance width. When accounting for heat leakage losses, Ding et al. [36,37,38] studied the power output (POW) and thermal efficiency (TEF) of irreversible single resonance ESE heat engines, and Zhou et al. [39] studied the ecological function performance.
There are also other performance indicators for evaluating thermodynamic devices, besides POW, TEF and ecological function. For example, Yan [40] first took the product of POW and TEF as a new objective function. Later, Yilmaz [41,42] named this new objective function as efficient power (EP). Patodi and Maheshwari [43] studied the maximum EP performance of the macro Atkinson cycle. Singh and Johal [44] and Nilavarasi and Ponmurugan [45] studied the maximum EP performances of low-dissipation heat engines. There is no work concerning the maximum EP performances of an ESE heat engine in the available literature.
The above work focused on single-objective optimization of cycle performance, and there may be contradictions between various objective functions. In order to coordinate the relationship between the objective functions, some scholars have carried out multi-objective optimization (MOO) for macro cycle performances by using NSGA-II algorithm [46,47,48,49,50,51,52,53,54,55,56,57,58], including the thermoelectric generator [46], macro [47] and micro [48] Stirling cycles, Atkinson cycle [49], Diesel cycle [50], Brayton cycle [51], ORC [52], dual cycle [53], porous-medium engines [54,55], MHD plant [56] and chemical reactors [57,58], with objectives of POW, TEF, ecological function and power density.
There is no work concerning the MOO for an ESE heat engine in the available literature. Based on the model of an irreversible single-resonance ESE heat engine established in References [36,39], this paper will perform MOO for the model by applying NSGA-II algorithm. The boundary energy and resonance width will be used as the optimization variables, and the POW, TEF, EP and ecological function will be used as the optimization objectives. The three decision-making methods of LINMAP, TOPSIS and Shannon Entropy will be used to select the optimal scheme with the smallest deviation index (D) under different optimization objective combinations.
2. Model Description
Figure 1 shows the irreversible single-resonance ESE heat engine model [36,39], which consists of two electron sources connected by an energy filter.
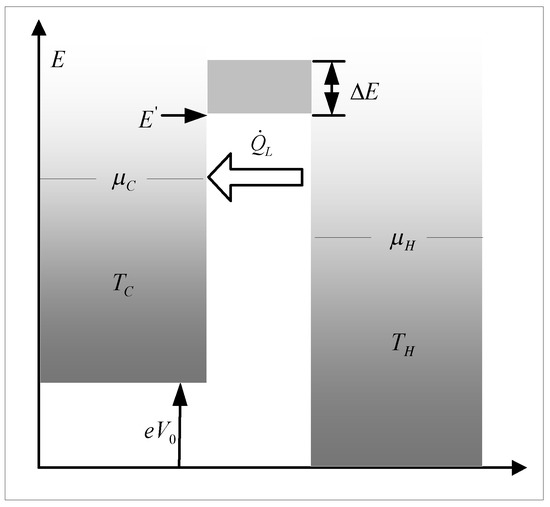
Figure 1.
Model of the ESE heat engine [36,39]. Adapted with permission from Ref. [39]. 2016, Junle Zhou, Lingen Chen, Zemin Ding, Fengrui Sun.
There is no heat exchange between two electron reservoirs, and electrons are exchanged only by filter, which allows for electrons in a specific energy range to be freely transported, and there is also heat leakage loss due to phonon propagation during the transmission process. There are different temperatures, and , and two different electrochemical potentials, and , in two electron reservoirs. is the energy boundary, is the resonance width and is the bias voltage. During the operation of the ESE system, electrons are transferred from the hot electronic reservoir through the energy filter to the cold electronic reservoir due to factors such as electrochemical potential difference and temperature difference. Since the electrons carry energy, the transfer process is accompanied by energy changes, thereby realizing an energy conversion.
The detailed description of the model is shown in Appendix A. From Equations (A8) and (A9) in Appendix A, the POW () and TEF () can be expressed as [39]
where , , and .
Combining Equations (1) and (2), according to the definition of EP () [40,41,42], one has
From Equations (A8) and (A9) in Appendix A, for an ESE heat engine system, the entropy generation rate () is
From Equations (1) and (4), according to the definition formula of ecological function () [34], one has
The dimensionless POW (), EP () and ecological function () are defined as:
3. Multi-Objective Optimizations
For the MOO problem, if the solution cannot be improved for any objective without deteriorating at least one objective, it is a “Pareto optimal solution”, and the corresponding set of objective function values are “Pareto frontiers”. The Pareto frontier contains multiple feasible solutions, and the commonly used three decision-making approaches are LINMAP, TOPSIS and Shannon Entropy. The deviation indices ( s) are used to compare the pros and cons of three decision-making approaches to select the optimal design. The positive and the negative ideal points represent the optimal and worst virtual points for all objective functions, respectively.
The LINMAP decision approach obtains the solution with the smallest distance from the positive ideal point. For the LINMAP approach:
where the value of is normalized, is the proportion of the j-th optimization goal and the value of is weighted. is the normalized and weighted value of the j-th goal of the positive ideal point, is the Euclidean distance between the i-th feasible solution and the positive ideal point and is the best feasible solution.
The TOPSIS decision approach not only requires the solution with the smallest distance from the positive ideal point, but also with the farthest distance from the positive negative point. For the TOPSIS approach:
where is the proportion of the j-th optimization goal, is the normalized and weighted value of the j-th goal of the negative ideal point, is the Euclidean distance between the i-th feasible solution and the negative ideal point and is the best feasible solution.
The Shannon Entropy approach obtains the point when the last objective function of the optimization reaches the maximum. For the Shannon Entropy approach:
where the value of is normalized, is the Shannon Entropy of the j-th optimization objective, is the proportion of the j-th optimization goal and is the best feasible solution.
The is defined as:
The can calculate the average distance between the values obtained by different decision-making methods and the positive and negative ideal points. The smaller is obtained under a certain decision-making approach, which means the design scheme is better. Figure 2 illustrates NSGA-II algorithm flow chart.
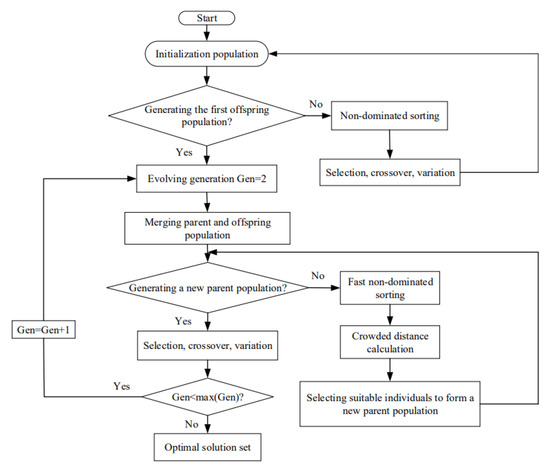
Figure 2.
NSGA-II algorithm flow chart.
This paper takes , , and as optimization objectives; takes the boundary energy () and resonance width () as optimization variables; and applies NSGA-II algorithm to optimize the ESE heat engine with single-, bi-, tri- and quadru-objective optimizations.
According to Reference [39], , , ,, and are set. Ranges of optimization variables and are and , respectively.
Appendix B lists the results of quadru-, tri-, bi- and single-objective optimizations under three decision-making approaches, respectively. When , , and reach their maximum values, it can be seen that s are 0.1007, 0.9331, 0.0882 and 0.1254, respectively. When the is optimized, the s obtained by the TOPSIS and LINMAP decision approaches are both 0.0755, indicating that the result of the optimization of four objectives is more perfect than that of a single objective. The of and obtained by the TOPSIS solution is 0.0748, which is the smallest and the most ideal.
Figure 3 shows the Pareto frontier of quadru-objective () optimization. In Figure 3, the change in color represents the change in the value of . The positive and the negative ideal points are not on the pareto frontier, indicating that the variables and cannot make , , and simultaneously optimal or worse. As increases, continues to decrease, and and first reach their maximum values and then decrease. When reaches the maximum value, reaches the minimum, and and can take into account both and . From Appendix B, for the MOO of , the s obtained by TOPSIS and LINMAP are the same, which is smaller than that obtained by Shannon Entropy, and the result is more ideal.
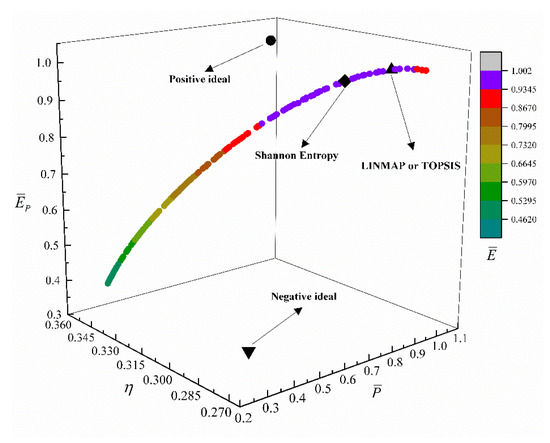
Figure 3.
Pareto frontier with objective.
Figure 4 shows the distributions of and within the value ranges in the Pareto front obtained by taking quadru-objective () optimization. From Figure 4a, is distributed between 13.95 and 14.10, but mostly concentrated between 14.00 and 14.05, with the increase of , the change trends of , , and are not obvious; therefore, the value of can be designed between 14 and 14.05. From Figure 4b, is distributed between 0 and 15, since energy filter allows for electrons in a specific energy range to be freely transported; as the resonance width increases, the number of electrons no longer increases with the increase in resonance width when all electrons in a specific energy range pass through. So as increases, increases, decreases, and increase first and then decrease and the value of can be reasonably selected according to the actual needs.
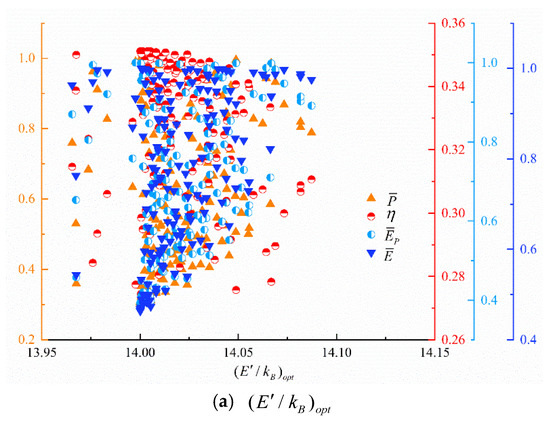
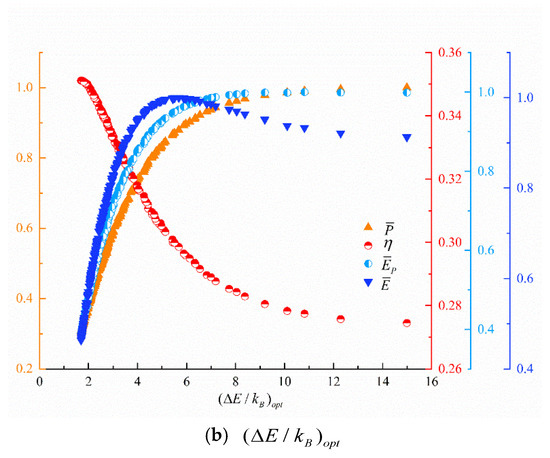
Figure 4.
Distributions of and within the value ranges in the Pareto front.
Figure 5 show the Pareto frontiers obtained by different (six) bi-objective optimization combinations. As increases, , and both decrease. As increases, both and decrease. As increases, decreases. From Appendix B, for the MOO of and , the with the LINMAP approach is better. For the MOO of , and , the with the Shannon Entropy approach is better. For the MOO of , the with TOPSIS approach is better.
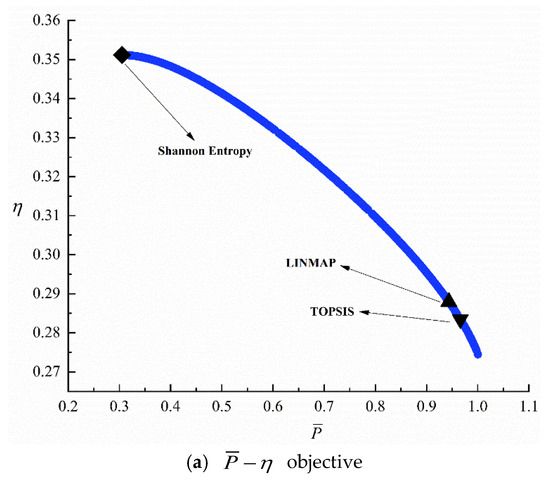
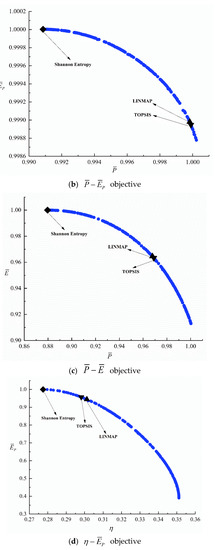
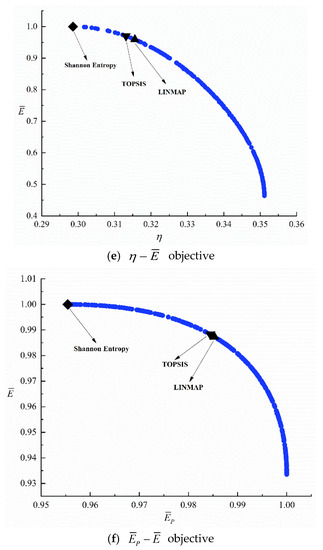
Figure 5.
Pareto frontier for six bi-objective optimizations.
Figure 6 show the Pareto frontiers obtained by different (four) tri-objective optimizations. As increases, decreases, and and reach their maximum values and then decrease. As increases, decreases, and first increases and then decreases.
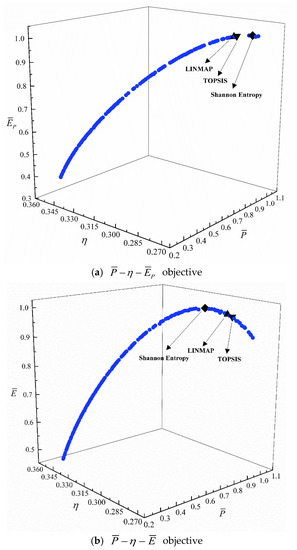
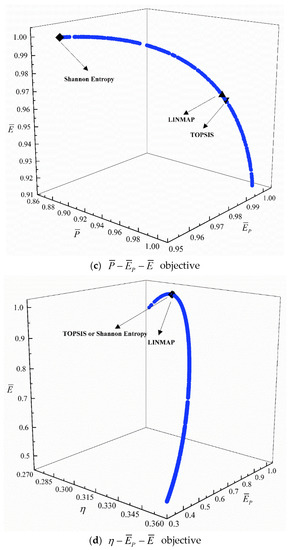
Figure 6.
Pareto frontier for four tri-objective optimizations.
From Appendix B, for the MOO of and , the with the LINMAP approach is better. For the MOO of , the with the TOPSIS approach is better. For the MOO of , the s with the Shannon Entropy and TOPSIS approaches are the same, which is less than that with the LINMAP method.
Figure 7 and Figure 8 show the average distance versus generations and average spread versus generations obtained by taking quadru-objectives () and bi-objectives () as the optimization objectives, respectively. From two figures, if genetic algorithm converges, it will stop. The MOO of and converges at 307 and 1107 generations, respectively.
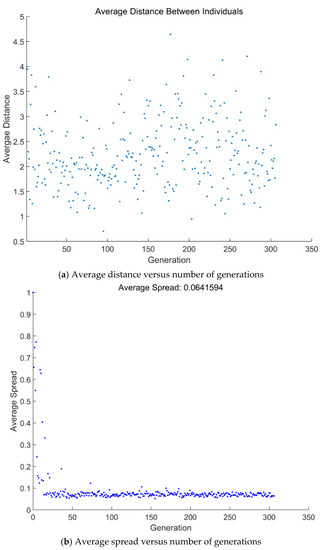
Figure 7.
Average distance and average spread versus number of generations ().
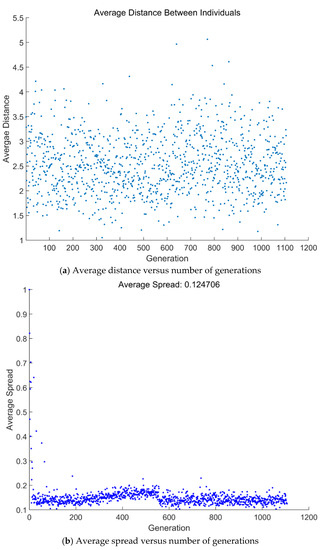
Figure 8.
Average distance and average spread versus number of generations ().
4. Conclusions
Based on the established model of irreversible single ESE heat engine, this paper takes the energy boundary and the resonance width as the optimization variables and the , , and as the optimization objectives to perform MOO by applying the NSGA-II algorithm and FTT theory. The EP performance indicator is introduced to the optimization. The effects of the values of the two variables ( and ) on four optimization objectives are analyzed with the MOO of . The results show that:
- When , , and reach their maximum values, it can be seen that values are 0.1007, 0.9331, 0.0882 and 0.1254, respectively. For the MOO of , the s obtained by the TOPSIS and LINMAP decision approaches are both 0.0755. The obtained by MOO is smaller and better compared with single-objective optimization, which means that the MOO results are better.
- For the MOO of , is distributed between 13.95 and 14.10, and is distributed between 0 and 15. As increases, the change trends of , , and are not obvious; as increases, increases, decreases and and first increase then decrease. In the design of the ESE heat engine, it is very important to choose appropriate values of and .
- For the MOO of , the is the minimum obtained by the TOPSIS approach and the value is 0.0748; at this time, the and are 14.0091 and 8.2266, respectively, which is the most ideal design scheme. For the MOO of other combinations, the appropriate decision-making approach can be selected according to the actual requirements and needs.
- It is meaningful to introduce the MOO to the performance optimization ESE heat engines.
Author Contributions
Conceptualization: L.C. and F.L.; funding acquisition: L.C.; Methodology: J.H.; Software: J.H., Y.G. and S.S.; Supervision: L.C., Y.G. and F.L.; Validation: J.H., Y.G. and S.S.; Writing—Original draft preparation: J.H.; Writing –Reviewing and editing: L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Project Nos. 52171317 and 51779262) and Graduate Innovative Fund of Wuhan Institute of Technology (Project No. CX2021054).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank the reviewers for their careful, unbiased and constructive suggestions, which led to this revised manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Energy boundary () | |
| Bias voltage | |
| Efficient power () | |
| Ecological function | |
| Fermi distributions of electrons | |
| A defined function | |
| Plank constant () | |
| Boltzmann constant () | |
| Heat leakage coefficient () | |
| Power output () | |
| Heat transfer () | |
| Greek symbols | |
| Thermal efficiency | |
| electrochemical potential () | |
| Entropy generation rate () | |
| Resonance width () | |
| Subscripts | |
| Cold reservoir | |
| Heat absorption rate | |
| Hot reservoir | |
| Heat release rate | |
| Heat leakage | |
| Optimal | |
| Environment | |
| Superscripts | |
| Dimensionless |
Abbreviations
| EMP | Efficiency at maximum power |
| EP | Efficient power |
| ESE | Heat exchanger |
| FTT | Finite time thermodynamics |
| MOO | Multi-objective optimization |
| POW | Power output |
| TEF | Thermal efficiency |
Appendix A. Model Description in Detail
In the narrow energy range, the heat release rate of hot reservoir is [31,32]
The heat absorption rate of cold reservoir is
where is the Planck constant.
Fermi distributions of hot and cold reservoirs can be expressed as
where is the Boltzmann constant.
Within the entire energy range of the system, the heat release rate () and the heat absorption rate () are
The heat leakage loss rate () between the two electronic reservoirs is
where is the heat leakage coefficient.
From Equations (A5) and (A6), taking heat leakage into account, the heat release rate () and the heat absorption rate () are
In the process of numerical calculations, there are logarithmic functions with two variables and . The PolyLog function is an ordinary and Nielsen generalized logarithmic function, which is often used for logarithmic integration, and it is necessary to introduce the Nielsen function [35], and the two integral formulas are and .
Appendix B. Optimization Results

Table A1.
Results of quadru-, tri-, bi- and single-objective optimizations.
Table A1.
Results of quadru-, tri-, bi- and single-objective optimizations.
| Optimization Approaches | Decision Schemes | Optimization Variables | Optimization Objectives | Deviation Index | ||||
|---|---|---|---|---|---|---|---|---|
| Quadru-objective optimization ( and ) | LINMAP | 14.0381 | 7.7359 | 0.9566 | 0.2853 | 0.9928 | 0.9737 | 0.0755 |
| TOPSIS | 14.0381 | 7.7359 | 0.9566 | 0.2853 | 0.9928 | 0.9737 | 0.0755 | |
| Shannon Entropy | 14.0006 | 5.6813 | 0.8797 | 0.2986 | 0.9555 | 1.0000 | 0.1254 | |
| Tri-objective optimization ( and ) | LINMAP | 14.0091 | 7.5215 | 0.9613 | 0.2864 | 0.9912 | 0.9785 | 0.0763 |
| TOPSIS | 13.9757 | 7.8488 | 0.9578 | 0.2854 | 0.9934 | 0.9733 | 0.0751 | |
| Shannon Entropy | 13.9975 | 10.8112 | 0.9909 | 0.2774 | 1.0000 | 0.9335 | 0.0882 | |
| Tri-objective optimization ( and ) | LINMAP | 14.0348 | 7.1843 | 0.9430 | 0.2880 | 0.9878 | 0.9831 | 0.0794 |
| TOPSIS | 14.0135 | 7.6952 | 0.9554 | 0.2856 | 0.9554 | 0.9754 | 0.0860 | |
| Shannon Entropy | 14.0000 | 5.6811 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 | |
| Tri-objective optimization ( and ) | LINMAP | 14.0065 | 8.3937 | 0.9712 | 0.4839 | 0.9836 | 0.9953 | 0.0751 |
| TOPSIS | 14.0009 | 8.5764 | 0.9711 | 0.2823 | 0.9973 | 0.9612 | 0.0756 | |
| Shannon Entropy | 14.0000 | 5.6811 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 | |
| Tri-objective optimization ( and ) | LINMAP | 14.0019 | 5.4832 | 0.8677 | 0.3004 | 0.9481 | 0.9995 | 0.1364 |
| TOPSIS | 14.0000 | 5.6810 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 | |
| Shannon Entropy | 14.0000 | 5.6810 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 | |
| Bi-objective optimization ( and ) | LINMAP | 14.0013 | 7.4549 | 0.9498 | 0.2867 | 0.9906 | 0.9795 | 0.0767 |
| TOPSIS | 14.0091 | 8.2266 | 0.9657 | 0.2835 | 0.9959 | 0.9666 | 0.0748 | |
| Shannon Entropy | 14.0001 | 1.6955 | 0.3053 | 0.3511 | 0.3900 | 0.4638 | 0.9331 | |
| Bi-objective optimization ( and ) | LINMAP | 13.9929 | 14.5327 | 0.9998 | 0.2747 | 0.9990 | 0.9143 | 0.1005 |
| TOPSIS | 13.9944 | 14.6054 | 0.9999 | 0.2746 | 0.9989 | 0.9141 | 0.1007 | |
| Shannon Entropy | 13.9975 | 10.8113 | 0.9909 | 0.2774 | 1.0000 | 0.9335 | 0.0882 | |
| Bi-objective optimization ( and ) | LINMAP | 14.0048 | 8.3587 | 0.9678 | 0.2830 | 0.9965 | 0.9646 | 0.0750 |
| TOPSIS | 14.0055 | 8.4334 | 0.9690 | 0.2828 | 0.9968 | 0.9633 | 0.0752 | |
| Shannon Entropy | 14.0000 | 5.6808 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 | |
| Bi-objective optimization ( and ) | LINMAP | 14.0061 | 5.3931 | 0.8621 | 0.3012 | 0.9445 | 0.9990 | 0.1416 |
| TOPSIS | 14.0078 | 5.7264 | 0.8827 | 0.2981 | 0.9572 | 0.9999 | 0.1227 | |
| Shannon Entropy | 13.9985 | 10.8103 | 0.9909 | 0.2774 | 1.0000 | 0.9335 | 0.0882 | |
| Bi-objective optimization ( and ) | LINMAP | 13.9914 | 4.1703 | 0.7526 | 0.3156 | 0.8640 | 0.9591 | 0.2597 |
| TOPSIS | 13.9957 | 4.3475 | 0.7726 | 0.3131 | 0.8801 | 0.9700 | 0.2362 | |
| Shannon Entropy | 13.9998 | 5.6822 | 0.8797 | 0.2986 | 0.9555 | 1.0000 | 0.1254 | |
| Bi-objective optimization ( and ) | LINMAP | 14.0041 | 6.9814 | 0.9363 | 0.2893 | 0.9852 | 0.9874 | 0.0824 |
| TOPSIS | 14.0024 | 6.9264 | 0.9345 | 0.2896 | 0.9845 | 0.9883 | 0.0834 | |
| Shannon Entropy | 14.0000 | 5.6811 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 | |
| Maximum of | —— | 13.9944 | 14.6054 | 1.0000 | 0.2746 | 0.9989 | 0.9141 | 0.1007 |
| Maximum of | —— | 14.0001 | 1.6955 | 0.3053 | 0.3511 | 0.3900 | 0.4638 | 0.9331 |
| Maximum of | —— | 13.9985 | 10.8103 | 0.9909 | 0.2774 | 1.0000 | 0.9335 | 0.0882 |
| Maximum of | —— | 14.0000 | 5.6811 | 0.8796 | 0.2986 | 0.9554 | 1.0000 | 0.1254 |
| Positive ideal point | —— | 1.0002 | 0.3511 | 1.0000 | 1.0000 | —— | ||
| Negative ideal point | —— | 0.3052 | 0.2745 | 0.3899 | 0.4637 | —— | ||
References
- Andresen, B. Finite-Time Thermodynamics; University of Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Hoffmann, K.H.; Burzler, J.M.; Schubert, S. Endoreversible thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22, 311–355. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Andresen, B. Current trends in finite-time thermodynamics. Ange. Chem. Int. Edi. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Sieniutycz, S. Complexity and Complex Chemo-Electric Systems; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Berry, R.S.; Salamon, P.; Andresen, B. How it all began. Entropy 2020, 22, 908. [Google Scholar] [CrossRef] [PubMed]
- Levario-Medina, S.; Valencia-Ortega, G.; Barranco-Jimenez, M.A. Energetic optimization considering a generalization of the ecological criterion in traditional simple-cycle and combined cycle power plants. J. Non-Equilib. Thermodyn. 2020, 45, 269–290. [Google Scholar] [CrossRef]
- Smith, Z.; Pal, P.S.; Deffner, S. Endoreversible Otto engines at maximal power. J. Non-Equilib. Thermodyn. 2020, 45, 305–310. [Google Scholar] [CrossRef]
- Chen, L.G.; Ge, Y.L.; Liu, C.; Feng, H.J.; Lorenzini, G. Performance of universal reciprocating heat-engine cycle with variable specific heats ratio of working fluid. Entropy 2020, 22, 397. [Google Scholar] [CrossRef]
- Diskin, D.; Tartakovsky, L. Efficiency at maximum power of the low-dissipation hybrid electrochemical–otto cycle. Energies 2020, 13, 3961. [Google Scholar] [CrossRef]
- Chen, L.G.; Tang, C.Q.; Feng, H.J.; Ge, Y.L. Power, efficiency, power density and ecological function optimizations for an irreversible modified closed variable-temperature reservoir regenerative Brayton cycle with one isothermal heating process. Energies 2020, 13, 5133. [Google Scholar] [CrossRef]
- Qiu, S.S.; Ding, Z.M.; Chen, L.G.; Ge, Y.L. Performance optimization of thermionic refrigerators based on van der Waals heterostructures. Sci. China Technol. Sci. 2021, 64, 1007–1016. [Google Scholar] [CrossRef]
- Badescu, V. Self-driven reverse thermal engines under monotonous and oscillatory optimal operation. J. Non-Equilib. Thermodyn. 2021, 46, 291–319. [Google Scholar] [CrossRef]
- Valencia-Ortega, G.; Levario-Medina, S.; Barranco-Jiménez, M.A. The role of internal irreversibilities in the performance and stability of power plant models working at maximum ϵ-ecological function. J. Non-Equilib. Thermodyn. 2021, 46, 413–429. [Google Scholar] [CrossRef]
- Wang, R.B.; Chen, L.G.; Ge, Y.L.; Feng, H.J. Optimizing power and thermal efficiency of an irreversible variable-temperature heat reservoir Lenoir cycle. Appl. Sci. 2021, 11, 7171. [Google Scholar] [CrossRef]
- Chen, Y.R. Maximum profit configurations of commercial engines. Entropy 2011, 13, 1137–1151. [Google Scholar] [CrossRef]
- Boikov, S.Y.; Andresen, B.; Akhremenkov, A.A.; Tsirlin, A.M. Evaluation of irreversibility and optimal organization of an integrated multi-stream heat exchange system. J. Non-Equilib. Thermodyn. 2020, 45, 155–171. [Google Scholar] [CrossRef]
- Masser, R.; Hoffmann, K.H. Optimal control for a hydraulic recuperation system using endoreversible thermodynamics. Appl. Sci. 2021, 11, 5001. [Google Scholar] [CrossRef]
- Paul, R.; Hoffmann, K.H. Cyclic control optimization algorithm for Stirling engines. Symmetry 2021, 13, 873. [Google Scholar] [CrossRef]
- Badescu, V. Maximum work rate extractable from energy fluxes. J. Non-Equilib. Thermodyn. 2022, 47, 77–93. [Google Scholar] [CrossRef]
- Paul, R.; Hoffmann, K.H. Optimizing the piston paths of Stirling cycle cryocoolers. J. Non-Equilib. Thermodyn. 2022, 47, 195–203. [Google Scholar] [CrossRef]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Kong, R.; Ge, Y.L. Total entropy generation rate minimization configuration of a membrane reactor of methanol synthesis via carbon dioxide hydrogenation. Sci. China Technol. Sci. 2022, 65, 657–678. [Google Scholar] [CrossRef]
- Paul, R.; Khodja, A.; Fischer, A.; Masser, R.; Hoffmann, K.H. Power-optimal control of a Stirling engine’s frictional piston motion. Entropy 2022, 24, 362. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.; Khodja, A.; Paul, R.; Hoffmann, K.H. Heat-only-driven Vuilleumier refrigeration. Appl. Sci. 2022, 12, 1775. [Google Scholar] [CrossRef]
- Li, J.; Chen, L.G. Optimal configuration of finite source heat engine cycle for maximum output work with complex heat transfer law. J. Non-Equilib. Thermodyn. 2022, 47. [Google Scholar] [CrossRef]
- Kosloff, R. Quantum thermodynamics and open-systems modeling. J. Chem. Phys. 2019, 150, 204105. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.W.; Chen, L.G.; Ge, Y.L.; Feng, H.J.; Wu, F.; Lorenzini, G. Exergy-based ecological optimization of an irreversible quantum Carnot heat pump with spin-1/2 systems. J. Non-Equilib. Thermodyn. 2021, 46, 61–76. [Google Scholar] [CrossRef]
- Qi, C.Z.; Ding, Z.M.; Chen, L.G.; Ge, Y.L.; Feng, H.J. Modelling of irreversible two-stage combined thermal Brownian refrigerators and their optimal performance. J. Non-Equilib. Thermodyn. 2021, 46, 175–189. [Google Scholar] [CrossRef]
- Ding, Z.M.; Ge, Y.L.; Chen, L.G.; Feng, H.J.; Xia, S.J. Optimal performance regions of Feynman’s ratchet engine with different optimization criteria. J. Non-Equilib. Thermodyn. 2020, 45, 191–207. [Google Scholar] [CrossRef]
- Qiu, S.S.; Ding, Z.M.; Chen, L.G.; Ge, Y.L. Performance optimization of three-terminal energy selective electron generators. Sci. China Technol. Sci. 2021, 64, 1641–1652. [Google Scholar] [CrossRef]
- Humphrey, T.E.; Newbury, R.; Taylor, R.P.; Linke, H. Reversible quantum Brownian heat engines for electrons. Phys. Rev. Lett. 2002, 89, 11680. [Google Scholar] [CrossRef]
- Humphrey, T.E. Mesoscopic Quantum Ratchets and the Thermodynamics of Energy Selective Electron Heat Engines. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 2003. [Google Scholar]
- Ding, Z.M.; Chen, L.G.; Sun, F.R. Ecological optimization of energy selective electron (ESE) heat engine. Appl. Mat. Model. 2011, 35, 276–284. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Luo, X.G.; He, J.Z.; Li, C.; Qiu, T. The impact of energy spectrum width in the energy selective electron low-temperature thermionic heat engine at maximum power. Phys. Lett. A 2013, 377, 1566–1570. [Google Scholar] [CrossRef]
- Ding, Z.M.; Chen, L.G.; Sun, F.R. Performance characteristic of energy selective electron (ESE) heat engine with filter heat conduction. Int. J. Energy Environ. 2011, 2, 627–640. [Google Scholar]
- Ding, Z.M.; Chen, L.G.; Wang, W.H.; Ge, Y.L.; Sun, F.R. Exploring the operation of a microscopic energy selective electron engine. Phys. A 2015, 431, 94–108. [Google Scholar] [CrossRef]
- Ding, Z.M.; Chen, L.G.; Sun, F.R. Modeling and performance analysis of energy selective electron (ESE) engine with heat leakage and transmission probability. Sci. China Phys. Mech. Astron. 2011, 54, 1925–1936. [Google Scholar] [CrossRef]
- Zhou, J.L.; Chen, L.G.; Ding, Z.M.; Sun, F.R. Analysis and optimization with ecological objective function of irreversible single resonance energy selective electron heat engines. Energy 2016, 111, 306–312. [Google Scholar] [CrossRef]
- Yan, Z.J. η and P of a Carnot engine at maximum ηP. Chin. J. Nat. 1984, 7, 475. (In Chinese) [Google Scholar]
- Yilmaz, T. A new performance criterion for heat engines: Efficient power. J. Energy Inst. 2006, 79, 38–41. [Google Scholar] [CrossRef]
- Yilmaz, T.; Durmuolu, Y. Efficient power analysis for an irreversible Carnot heat engine. Int. J. Energy Res. 2008, 32, 623–628. [Google Scholar] [CrossRef]
- Patodi, K.; Maheshwari, G. Performance analysis of an Atkinson cycle with variable specific-heats of the working fluid under maximum efficient power conditions. Int. J. Low-Carbon Technol. 2013, 8, 289–294. [Google Scholar] [CrossRef]
- Singh, V.; Johal, R.S. Low-dissipation Carnot-like heat engines at maximum efficient power. Phys. Rev. E 2018, 98, 062132. [Google Scholar] [CrossRef]
- Nilavarasi, K.; Ponmurugan, M. Optimized efficiency at maximum figure of merit and efficient power of power law dissipative Carnot like heat engines. J. Stat. Mech. Theory Exp. 2021, 4, 043208. [Google Scholar] [CrossRef]
- Arora, R.; Kaushikb, S.C.; Arora, R. Multi-objective and multi-parameter optimization of two-stage thermoelectric generator in electrically series and parallel configurations through NSGA-II. Energy 2015, 91, 242–254. [Google Scholar] [CrossRef]
- Rostami, M.; Assareh, E.; Moltames, R.; Jafarinejad, T. Thermo-economic analysis and multi-objective optimization of a solar dish Stirling engine. Energy Sour. Part A 2021, 43, 2861–2877. [Google Scholar] [CrossRef]
- Shah, P.; Saliya, P.; Raja, B.; Patel, V. A multi-objective thermodynamic optimization of a nanoscale Stirling engine operated with Maxwell-Boltzmann gas. Heat Transfer—Asian Res. 2019, 48, 1913–1932. [Google Scholar] [CrossRef]
- Shi, S.S.; Ge, Y.L.; Chen, L.G.; Feng, H.J. Four-objective optimization of irreversible Atkinson cycle based on NSGA-II. Entropy 2020, 22, 1150. [Google Scholar] [CrossRef]
- Shi, S.S.; Chen, L.G.; Ge, Y.L.; Feng, H.J. Performance optimizations with single-, bi-, tri- and quadru-objective for irreversible Diesel cycle. Entropy 2021, 23, 826. [Google Scholar] [CrossRef]
- Baghernejad, A.; Anvari-Moghaddam, A. Exergoeconomic and environmental analysis and multi-objective optimization of a new regenerative gas turbine combined cycle. Appl. Sci. 2021, 11, 11554. [Google Scholar] [CrossRef]
- Teng, S.Y.; Feng, Y.Q.; Hung, T.C.; Xi, H. Multi-objective optimization and fluid selection of different cogeneration of heat and power systems based on organic Rankine cycle. Energies 2021, 14, 4967. [Google Scholar] [CrossRef]
- Ge, Y.L.; Shi, S.S.; Chen, L.G.; Zhang, D.F.; Feng, H.J. Power density analysis and multi-objective optimization for an irreversible Dual cycle. J. Non-Equilib. Thermodyn. 2022, 47, 289–309. [Google Scholar] [CrossRef]
- Zang, P.C.; Ge, Y.L.; Chen, L.G.; Gong, Q.R. Power density characteristic analysis and multi-objective optimization of an irreversible porous medium engine cycle. Case Stud. Therm. Eng. 2022, 35, 102154. [Google Scholar] [CrossRef]
- Zang, P.C.; Chen, L.G.; Ge, Y.L.; Shi, S.S.; Feng, H.J. Four-objective optimization for an irreversible Porous Medium cycle with linear variation of working fluid’s specific heat. Entropy 2022, 24, 1074. [Google Scholar] [CrossRef]
- Wu, Q.K.; Ge, Y.L.; Chen, L.G.; Shi, S.S. Multi-objective optimization of endoreversible magnetohydrodynamic cycle. Energy Rep. 2022, 8, 8918–8927. [Google Scholar] [CrossRef]
- Xie, T.C.; Xia, S.J.; Wang, C. Multi-objective optimization of Braun-type exothermic reactor for ammonia synthesis. Entropy 2022, 24, 52. [Google Scholar] [CrossRef]
- Chen, L.G.; Li, P.L.; Xia, S.J.; Kong, R.; Ge, Y.L. Multi-objective optimization of membrane reactor for steam methane reforming heated by molten salt. Sci. China Technol. Sci. 2022, 65, 1396–1414. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).