An Output Feedback Discrete-Time Controller for the DC-DC Buck Converter
Abstract
1. Introduction
- The presentation of a discrete-time output feedback controller based on the robust exact filtering differentiator for the DC-DC buck converter with saturated input.
- The introduction of a rigorous stability analysis of the discrete-time controller considering the asymmetric saturation of the system.
- An extensive experimental analysis that includes various operating conditions and disturbance scenarios to validate the performance of the controller.
2. Robust Exact Filtering Differentiator
Implicit Discretization of the Robust Exact Filtering Differentiator
- If , then and , where is the unique positive root of the following polynomial:
- If , then and .
- If , then and , where is the unique positive root of the following polynomial:
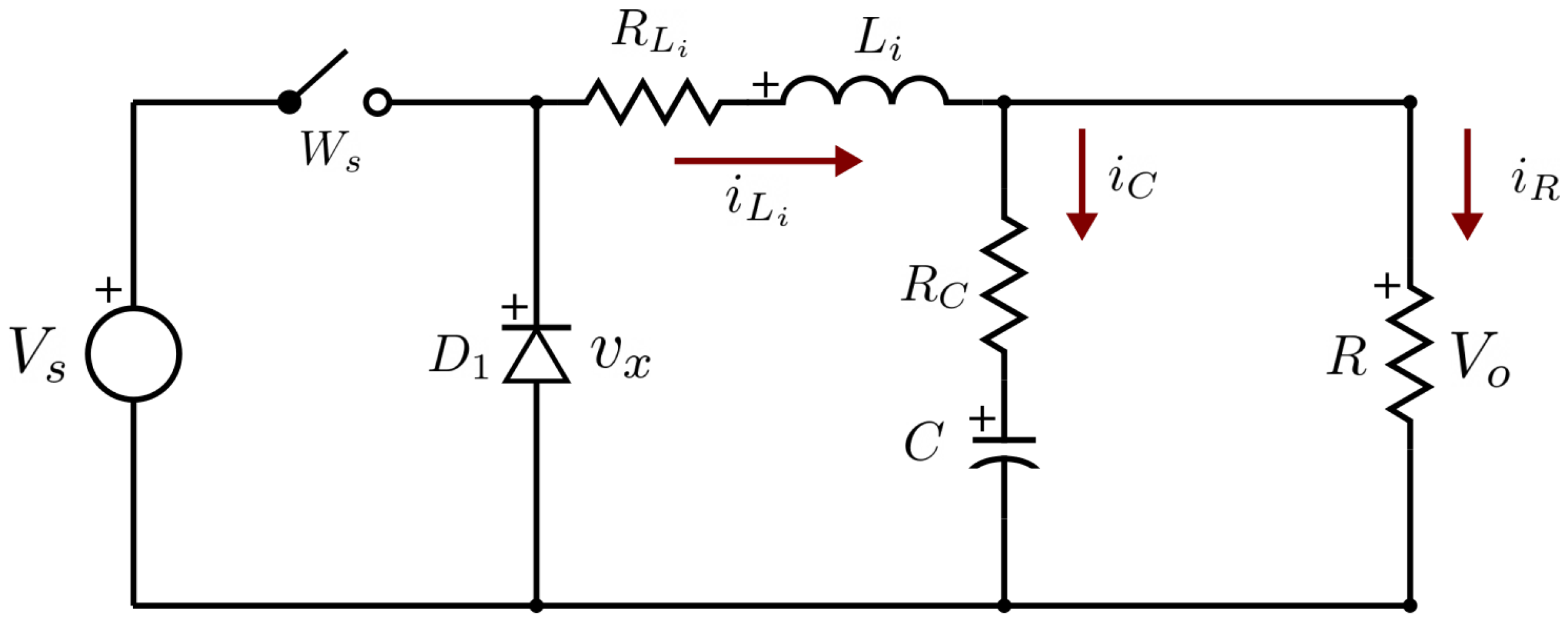
3. DC-DC Buck Converter Analysis
4. Proposed Control Strategy
- is the lowest sampling time such that is saturated for any measurement time greater than and previous to the instant of time , i.e., or for any with .
- is the time instant such that is unsaturated and for the previous measurement time was saturated, i.e., at , and or for any with .
- is the continuous-time function analogous to , defined as
- is the time instant after and such that .
Numeric Example
5. Experimental Results
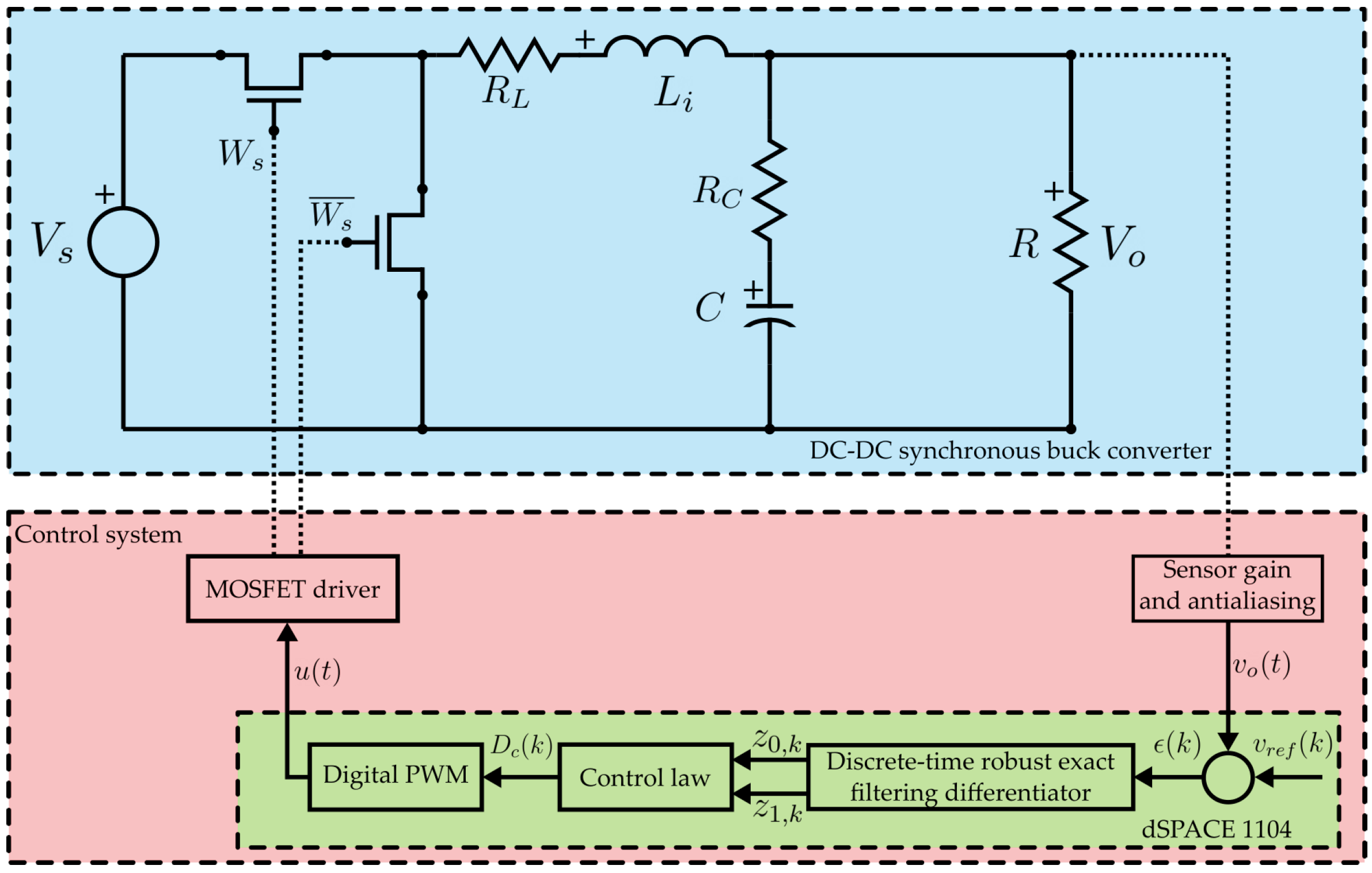
5.1. System Implementation
5.2. Experimental Results
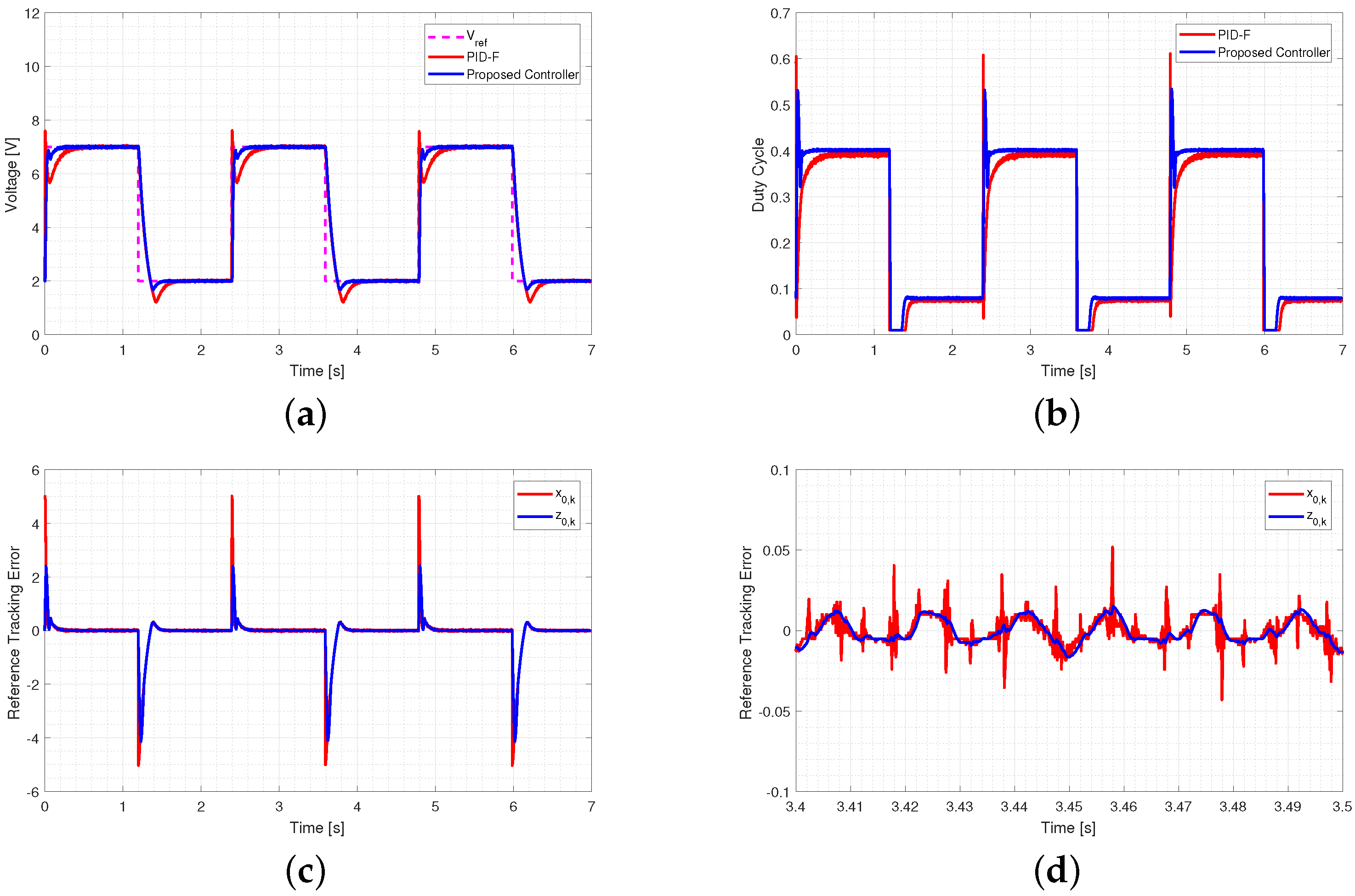
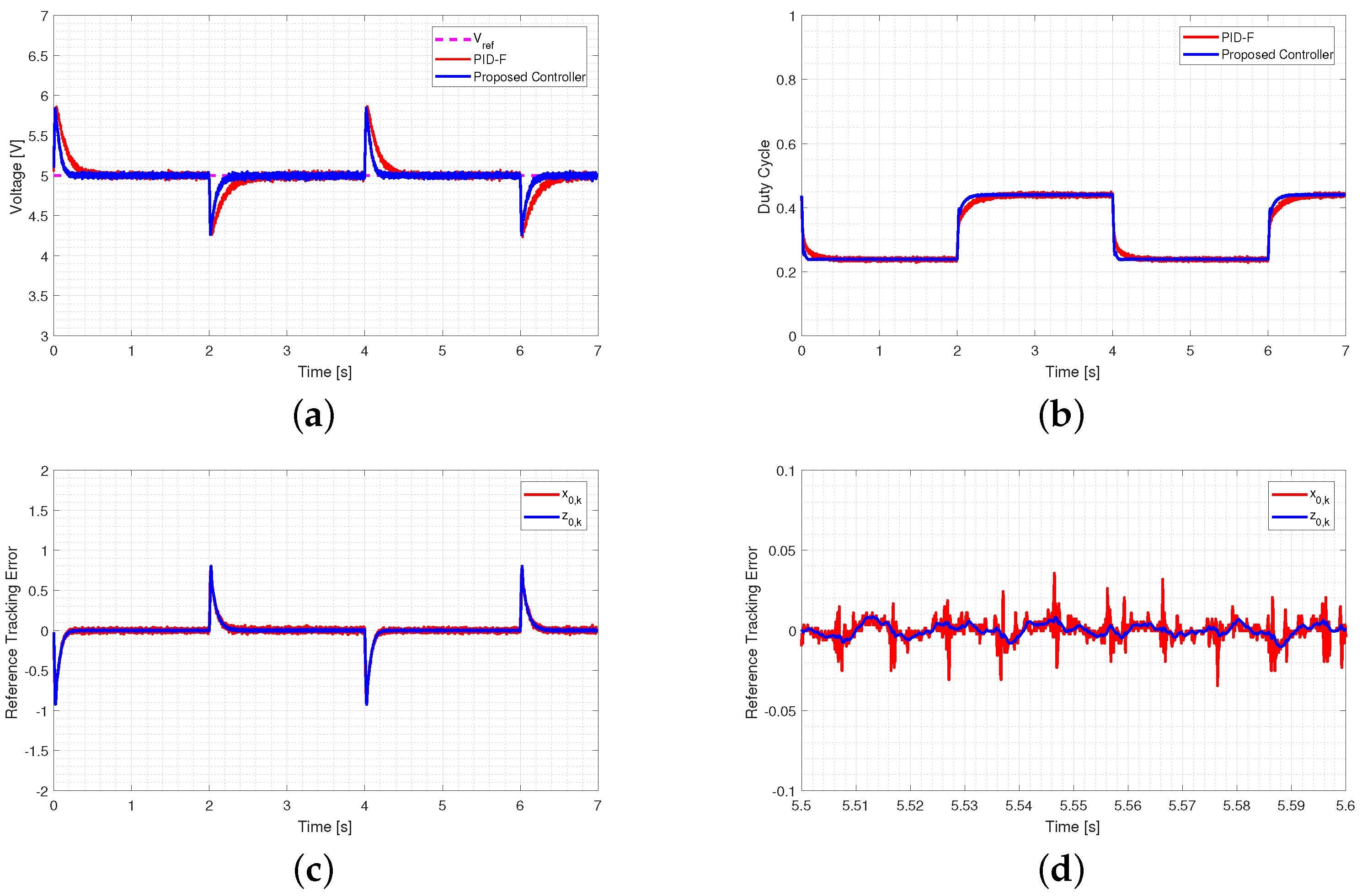
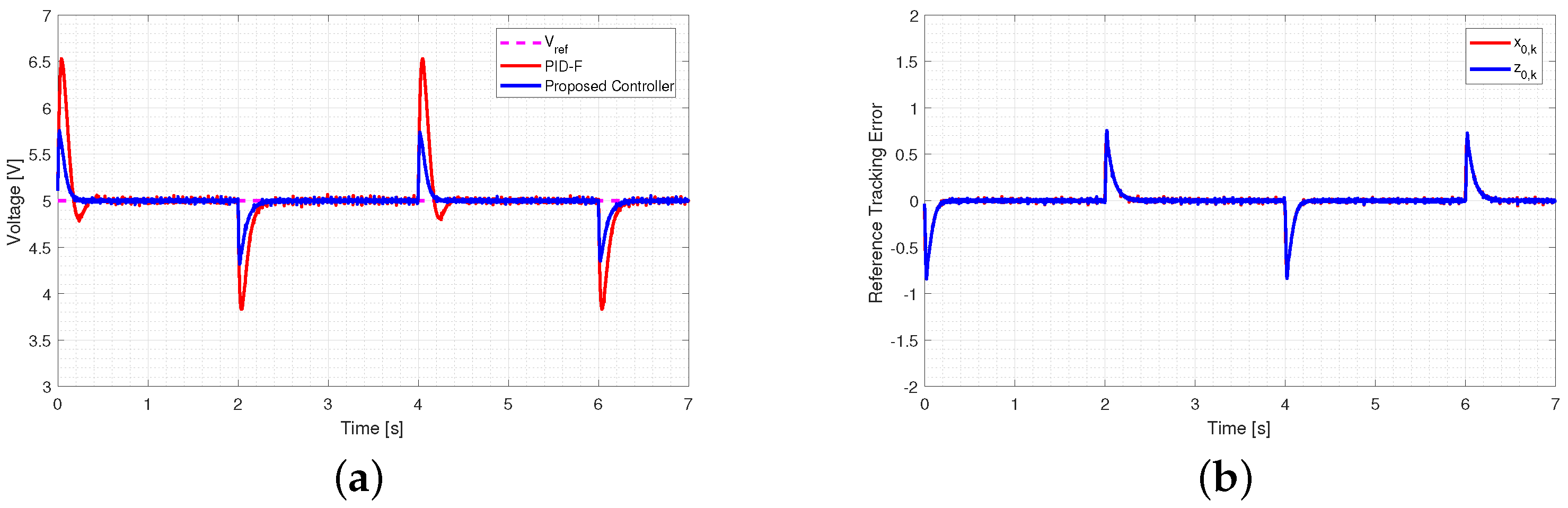
5.2.1. Output Voltage Tracking Performance
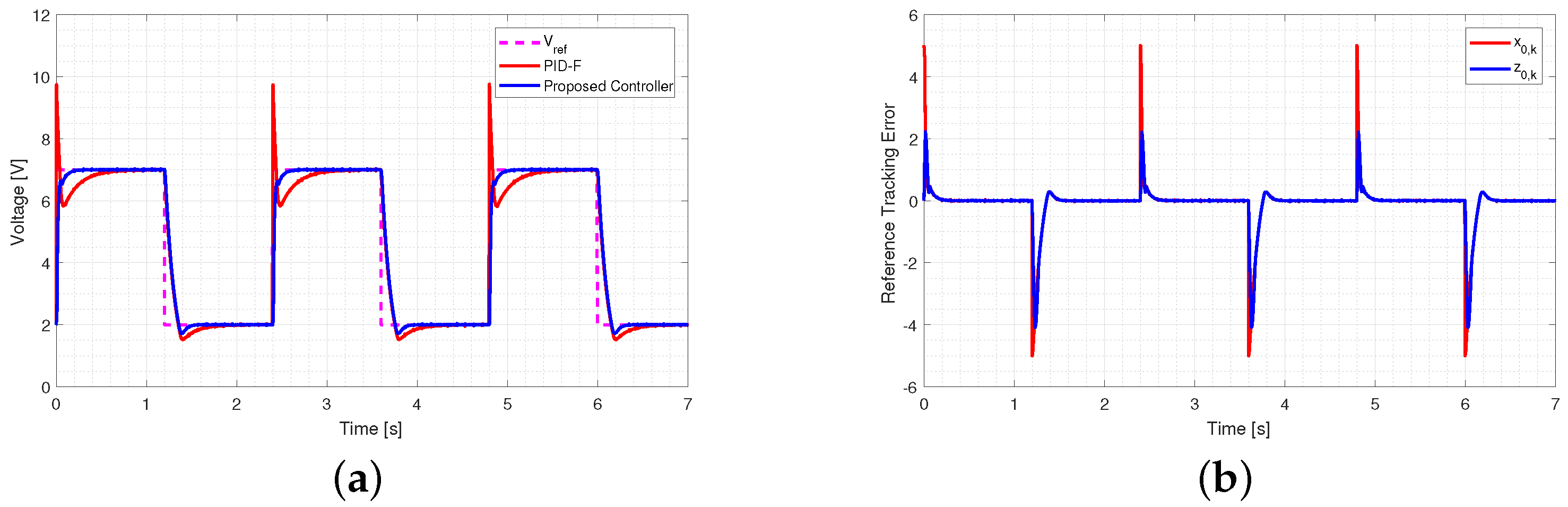
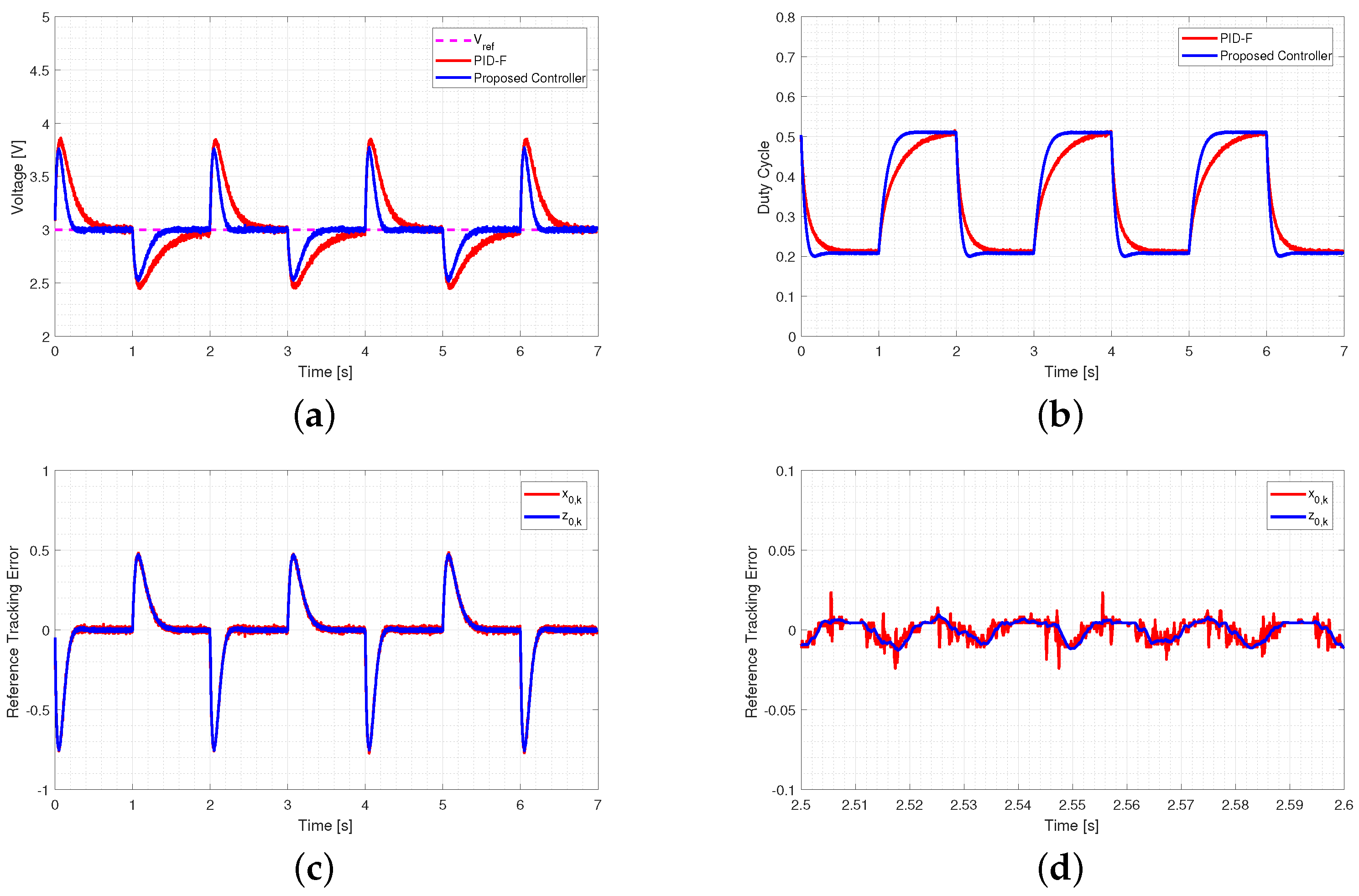
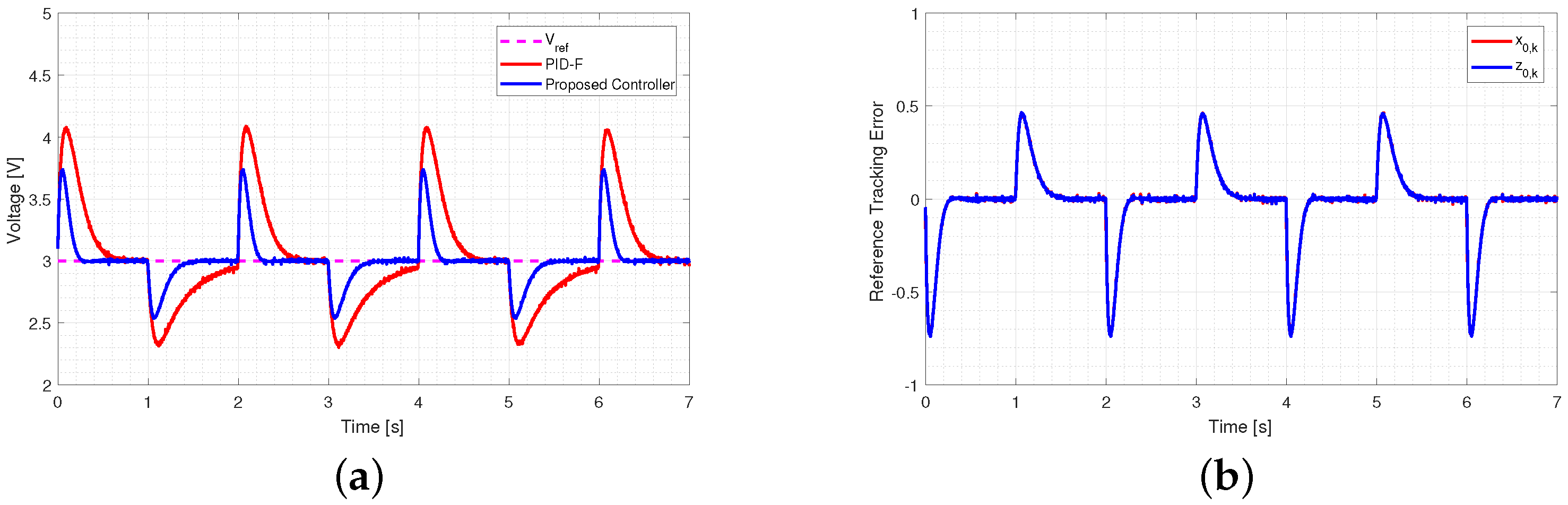
5.2.2. Load Variation Performance
5.2.3. Input Voltage Variation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UPS | Uninterruptible power supply |
| GPI | Generalized proportional integral |
| PID | Proportional integral derivative |
| FPGA | Field-programmable gate array |
| DSP | Digital signal processor |
| SM | Sliding mode |
| PIAW | Proportional integral with anti-windup |
| ESR | Equivalent series resistance |
| CCM | Continuous conduction mode |
| DPWM | Digital pulse-width modulator |
| DCM | Discontinuous conduction mode |
References
- Goyal, V.K.; Shukla, A. Isolated DC–DC Boost Converter for Wide Input Voltage Range and Wide Load Range Applications. IEEE Trans. Ind. Electron. 2021, 68, 9527–9539. [Google Scholar] [CrossRef]
- Wai, R.J.; Lin, C.Y.; Duan, R.Y.; Chang, Y.R. High-Efficiency DC-DC Converter with High Voltage Gain and Reduced Switch Stress. IEEE Trans. Ind. Electron. 2007, 54, 354–364. [Google Scholar] [CrossRef]
- Naayagi, R.T.; Forsyth, A.J.; Shuttleworth, R. High-Power Bidirectional DC–DC Converter for Aerospace Applications. IEEE Trans. Power Electron. 2012, 27, 4366–4379. [Google Scholar] [CrossRef]
- Nagata, H.; Uno, M. Nonisolated PWM Three-Port Converter Realizing Reduced Circuit Volume for Satellite Electrical Power Systems. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3394–3408. [Google Scholar] [CrossRef]
- Dusmez, S.; Hasanzadeh, A.; Khaligh, A. Comparative Analysis of Bidirectional Three-Level DC–DC Converter for Automotive Applications. IEEE Trans. Ind. Electron. 2015, 62, 3305–3315. [Google Scholar] [CrossRef]
- Park, J.; Choi, S. Design and Control of a Bidirectional Resonant DC–DC Converter for Automotive Engine/Battery Hybrid Power Generators. IEEE Trans. Power Electron. 2014, 29, 3748–3757. [Google Scholar] [CrossRef]
- Turksoy, A.; Teke, A.; Alkaya, A. A comprehensive overview of the dc-dc converter-based battery charge balancing methods in electric vehicles. Renew. Sustain. Energy Rev. 2020, 133, 110274. [Google Scholar] [CrossRef]
- Sivamani, D.; Ramkumar, R.; Nazar Ali, A.; Shyam, D. Design and implementation of highly efficient UPS charging system with single stage power factor correction using SEPIC converter. Mater. Today Proc. 2021, 45, 1809–1819. [Google Scholar] [CrossRef]
- Zhan, Y.; Guo, Y.; Zhu, J.; Wang, H. Intelligent uninterruptible power supply system with back-up fuel cell/battery hybrid power source. J. Power Sources 2008, 179, 745–753. [Google Scholar] [CrossRef][Green Version]
- Hong, T.; Geng, Z.; Qi, K.; Zhao, X.; Ambrosio, J.; Gu, D. A Wide Range Unidirectional Isolated DC-DC Converter for Fuel Cell Electric Vehicles. IEEE Trans. Ind. Electron. 2021, 68, 5932–5943. [Google Scholar] [CrossRef]
- Kwon, J.M.; Kim, E.H.; Kwon, B.H.; Nam, K.H. High-Efficiency Fuel Cell Power Conditioning System with Input Current Ripple Reduction. IEEE Trans. Ind. Electron. 2009, 56, 826–834. [Google Scholar] [CrossRef]
- Oh, Y.G.; Choi, W.Y.; Kwon, J.M. Design of a Step-Up DC-DC Converter for Standalone Photovoltaic Systems with Battery Energy Storages. Energies 2022, 15, 44. [Google Scholar] [CrossRef]
- Bereš, M.; Kováč, D.; Vince, T.; Kováčová, I.; Molnár, J.; Tomčíková, I.; Dziak, J.; Jacko, P.; Fecko, B.; Gans, Š. Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources. Energies 2021, 14, 4127. [Google Scholar] [CrossRef]
- Pereira, A.V.C.; Cavalcanti, M.C.; Azevedo, G.M.; Bradaschia, F.; Neto, R.C.; Carvalho, M.R.S.d. A Novel Single-Switch High Step-Up DC–DC Converter with Three-Winding Coupled Inductor. Energies 2021, 14, 6288. [Google Scholar] [CrossRef]
- Qi, Q.; Ghaderi, D.; Guerrero, J.M. Sliding mode controller-based switched-capacitor-based high DC gain and low voltage stress DC-DC boost converter for photovoltaic applications. Int. J. Electr. Power Energy Syst. 2021, 125, 106496. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, S.; Huang, Y.; Tan, C. Non-isolated high step-up DC/DC converter based on a high degrees of freedom voltage gain cell. IET Power Electron. 2017, 10, 2023–2033. [Google Scholar] [CrossRef]
- Park, K.; Chen, Z. Control and dynamic analysis of a parallel-connected single active bridge DC–DC converter for DC-grid wind farm application. IET Power Electron. 2015, 8, 665–671. [Google Scholar] [CrossRef]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power electronic converters modeling and control. Adv. Textb. Control. Signal Process. 2014, 454, 454. [Google Scholar]
- García-Alarcón, O.; Moreno-Valenzuela, J. Analysis and Design of a Controller for an Input-Saturated DC–DC Buck Power Converter. IEEE Access 2019, 7, 54261–54272. [Google Scholar] [CrossRef]
- Mazumder, S. Stability analysis of parallel DC-DC converters. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 50–69. [Google Scholar] [CrossRef]
- Zurita-Bustamante, E.W.; Linares-Flores, J.; Guzman-Ramirez, E.; Sira-Ramirez, H. A Comparison Between the GPI and PID Controllers for the Stabilization of a DC–DC “Buck” Converter: A Field Programmable Gate Array Implementation. IEEE Trans. Ind. Electron. 2011, 58, 5251–5262. [Google Scholar] [CrossRef]
- Seo, S.W.; Choi, H.H. Digital Implementation of Fractional Order PID-Type Controller for Boost DC–DC Converter. IEEE Access 2019, 7, 142652–142662. [Google Scholar] [CrossRef]
- NI, Y.; XU, J. Study of Discrete Global-Sliding Mode Control for Switching DC-DC Converter. J. Circuits Syst. Comput. 2011, 20, 1197–1209. [Google Scholar] [CrossRef]
- Seguel, J.L.; Seleme, S.I. Robust Digital Control Strategy Based on Fuzzy Logic for a Solar Charger of VRLA Batteries. Energies 2021, 14, 1001. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Li, S.; Yang, J.; Li, Q. Finite-Time Output Feedback Control for PWM-Based DC–DC Buck Power Converters of Current Sensorless Mode. IEEE Trans. Control. Syst. Technol. 2017, 25, 1359–1371. [Google Scholar] [CrossRef]
- Aguilar-Ibanez, C.; Moreno-Valenzuela, J.; García-Alarcón, O.; Martinez-Lopez, M.; Acosta, J.A.; Suarez-Castanon, M.S. PI-Type Controllers and Σ − Δ Modulation for Saturated DC-DC Buck Power Converters. IEEE Access 2021, 9, 20346–20357. [Google Scholar] [CrossRef]
- Benzaouia, A.; Soliman, H.M.; Saleem, A. Regional pole placement with saturated control for DC-DC buck converter through Hardware-in-the-Loop. Trans. Inst. Meas. Control. 2016, 38, 1041–1052. [Google Scholar] [CrossRef]
- El Fadil, H.; Giri, F.; Chaoui, F.Z.; El Magueri, O. Accounting for Input Limitation in the Control of Buck Power Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 1260–1271. [Google Scholar] [CrossRef]
- Moreno-Valenzuela, J. A Class of Proportional-Integral with Anti-Windup Controllers for DC–DC Buck Power Converters with Saturating Input. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 157–161. [Google Scholar] [CrossRef]
- Campos-Mercado, E.; Mendoza-Santos, E.F.; Torres-Muñoz, J.A.; Román-Hernández, E.; Moreno-Oliva, V.I.; Hernández-Escobedo, Q.; Perea-Moreno, A.J. Nonlinear Controller for the Set-Point Regulation of a Buck Converter System. Energies 2021, 14, 5760. [Google Scholar] [CrossRef]
- Kaveh, P.; Shtessel, Y.B. Blood Glucose Regulation Using Higher-Order Sliding Mode Control. Int. J. Robust Nonlinear Control. 2008, 18, 557–569. [Google Scholar] [CrossRef]
- Iqbal, M.; Bhatti, A.I.; Ayubi, S.I.; Khan, Q. Robust Parameter Estimation of Nonlinear Systems Using Sliding-Mode Differentiator Observer. IEEE Trans. Ind. Electron. 2011, 58, 680–689. [Google Scholar] [CrossRef]
- Levant, A. Higher-Order Sliding Modes, Differentiation and Output-Feedback Control. Int. J. Control. 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Levant, A.; Livne, M. Robust Exact Filtering Differentiators. Eur. J. Control. 2019, 55, 33–44. [Google Scholar] [CrossRef]
- Carvajal-Rubio, J.E.; Sánchez-Torres, J.D.; Defoort, M.; Loukianov, A.G. On the Discretization of Robust Exact Filtering Differentiators. In Proceedings of the 21st IFAC World Congress 2020—1st Virtual IFAC World Congress (IFAC-V 2020), Berlin, Germany, 12–17 July 2020. [Google Scholar]
- Hanan, A.; Jbara, A.; Levant, A. Non-chattering discrete differentiators based on sliding modes. In Proceedings of the 59th Conference on Decision and Control, Jeju Island, Korea, 14–18 December 2020. [Google Scholar] [CrossRef]
- Brogliato, B.; Polyakov, A.; Efimov, D. The Implicit Discretization of the Super-Twisting Sliding-Mode Control Algorithm. IEEE Trans. Autom. Control. 2020, 65, 3707–3713. [Google Scholar] [CrossRef]
- Carvajal-Rubio, J.E.; Sánchez-Torres, J.D.; Defoort, M.; Djemai, M.; Loukianov, A.G. Implicit and explicit discrete-time realizations of homogeneous differentiators. Int. J. Robust Nonlinear Control. 2021, 31, 3606–3630. [Google Scholar] [CrossRef]
- Mojallizadeh, M.R.; Brogliato, B.; Acary, V. Time-discretizations of differentiators: Design of implicit algorithms and comparative analysis. Int. J. Robust Nonlinear Control. 2021, 31, 7679–7723. [Google Scholar] [CrossRef]
- Levant, A. Filtering Differentiators and Observers. In Proceedings of the 2018 15th International Workshop on Variable Structure Systems (VSS), Estiria, Austria, 9–11 July 2018; pp. 174–179. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Righthand Sides, 1st ed.; Mathematics and its Applications; Springer: Dordrecht, The Netherlands, 1988; Volume 18. [Google Scholar] [CrossRef]
- Carvajal-Rubio, J.E.; Defoort, M.; Sánchez-Torres, J.D.; Djemai, M.; Loukianov, A.G. Implicit and Explicit Discrete-Time Realizations of the Robust Exact Filtering Differentiator. J. Frankl. Inst. 2022, 359, 3951–3978. [Google Scholar] [CrossRef]
- Cheriha, H.; Gati, Y.; Kostov, V.P. On Descartes’ Rule of Signs. arXiv 2019, arXiv:1905.01836. [Google Scholar]
- McNamee, J.M.; Pan, V. Numerical Methods for Roots of Polynomials—Part II; Studies in Computational Mathematics; Elsevier Science: Amsterdam, The Netherlands; London, UK, 2013; Volume 16. [Google Scholar]
- Carvajal-Rubio, J.E.; Sanchez-Torres, J.D.; Defoort, M.; Djemai, M.; Loukianov, A.G. On the Efficient Implementation of an Implicit Discrete-Time Differentiator. Wseas Trans. Circuits Syst. 2021, 20, 70–74. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.J.; Silva-Ortigoza, R. Control Design Techniques in Power Electronics Devices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Faifer, M.; Piegari, L.; Rossi, M.; Toscani, S. An Average Model of DC–DC Step-Up Converter Considering Switching Losses and Parasitic Elements. Energies 2021, 14, 7780. [Google Scholar] [CrossRef]
- Hart, D. Power Electronics; Tata McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- He, Q.; Zhao, Y. The design of controller of buck converter. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010; Volume 15, pp. V15–251–V15–255. [Google Scholar] [CrossRef]
- Garg, M.M.; Pathak, M.K.; Hote, Y.V. Effect of non-idealities on the design and performance of a dc-dc buck converter. J. Power Electron. 2016, 16, 832–839. [Google Scholar] [CrossRef]
- Czarkowski, D. 10-DC-DC Converters. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 275–288. [Google Scholar] [CrossRef]
- Hanan, A.; Levant, A.; Jbara, A. Low-chattering discretization of homogeneous differentiators. IEEE Trans. Autom. Control. 2021, 67, 2946–2956. [Google Scholar] [CrossRef]

| V | ||||
| Description | Symbol | Nominal Value |
|---|---|---|
| Input voltage | 12.3 V–24.7 V | |
| Capacitance | C | 998 F |
| Capacitor ESR | 0.041 | |
| Inductance | 255.81 H | |
| Inductor resistance | 0.32 | |
| Switching frequency | 40 KHz | |
| Minimum load resistance | 5 | |
| Maximum load resistance | 124 | |
| Desired output voltage | 2 V–10.5 V |
| Parameter | Value |
|---|---|
| −3.35 | |
| −0.15 | |
| −0.00002 | |
| 0.01 | |
| 0.99 | |
| L | 2500 |
| 25 s, 250 s | |
| 1.1 | |
| 2.12 | |
| 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alarcón-Carbajal, M.A.; Carvajal-Rubio, J.E.; Sánchez-Torres, J.D.; Castro-Palazuelos, D.E.; Rubio-Astorga, G.J. An Output Feedback Discrete-Time Controller for the DC-DC Buck Converter. Energies 2022, 15, 5288. https://doi.org/10.3390/en15145288
Alarcón-Carbajal MA, Carvajal-Rubio JE, Sánchez-Torres JD, Castro-Palazuelos DE, Rubio-Astorga GJ. An Output Feedback Discrete-Time Controller for the DC-DC Buck Converter. Energies. 2022; 15(14):5288. https://doi.org/10.3390/en15145288
Chicago/Turabian StyleAlarcón-Carbajal, Martin A., José E. Carvajal-Rubio, Juan D. Sánchez-Torres, David E. Castro-Palazuelos, and Guillermo J. Rubio-Astorga. 2022. "An Output Feedback Discrete-Time Controller for the DC-DC Buck Converter" Energies 15, no. 14: 5288. https://doi.org/10.3390/en15145288
APA StyleAlarcón-Carbajal, M. A., Carvajal-Rubio, J. E., Sánchez-Torres, J. D., Castro-Palazuelos, D. E., & Rubio-Astorga, G. J. (2022). An Output Feedback Discrete-Time Controller for the DC-DC Buck Converter. Energies, 15(14), 5288. https://doi.org/10.3390/en15145288







