Decision Support in Selecting a Reliable Strategy for Sustainable Urban Transport Based on Laplacian Energy of T-Spherical Fuzzy Graphs

Abstract

Sustainable transportation has a significant impact on factors related to urban development and economic development. Therefore, much research is being undertaken to select the best strategies to manage sustainable transportation. Transportation requires a carefully designed method to manage the development of mobility modes in terms of the pollution they produce or the use of renewable energy sources. However, due to numerous preferences of decision-makers and data uncertainty problems, it is challenging to select the optimal strategy. In this paper, we focus on creating a framework for determining the best strategy for sustainable transportation management. For this purpose, T-spherical fuzzy graphs will be used, which, together with the combination of Laplacian Energy, can accurately represent decision-makers’ preferences in an uncertain environment. Due to the lack of limitations of T-spherical fuzzy graphs and its numerous membership functions, decision-makers can decide which factor seems most important for selecting the optimal sustainable transportation strategy. Additionally, due to the applicability, the SFS TOPSIS approach has been used in this approach. The obtained results demonstrate the high performance of the proposed approach and the applicability of the approach in management and sustainable transport problems.

1. Introduction

With the increase in global urbanization, the strategies previously pursued related to transportation are starting to become ineffective. Transport is vital to human life primarily because it provides many essential services. Transportation can facilitate mobility, and it also enables economic growth [1]. Transportation modes significantly impact the quality of life of people who use them for daily activities such as commuting and traveling. Therefore, in addition to public transport, they use private means through which they gain some independence.

One of the most crucial transportation issues is sustainable transportation. The issue of sustainable transportation mainly deals with the need to reduce the negative changes in the climate associated with transportation [2]. In order to reduce the pollutants from the burning of fuel for transportation means, there is a great emphasis associated with the development of green sustainable transportation. The topic of green transport includes the disposal of charging of green vehicles (e.g., electric buses, electric cars, electric bicycles) or the choice of energy source for the means of transport (e.g., electricity, hydrogen) [3]. Sustainable transport also relates to choosing the right connections, which are implemented when upgrading, changing, and building missing connections [1]. It involves systems oriented to the disposition of cost and travel time, as well as the integration of high-speed mass transit systems [4,5]. In addition, one of the goals of sustainable transport is to pursue urban modernization related to the idea of an intelligent city [6]. Therefore, research is being conducted on intelligent transportation systems through which technologies related to management, telecommunications, and information technology can be integrated [7].

Decision-making problems related to sustainable urban transportation are an essential aspect addressed by many researchers due to continuous chaotic urbanization, urban sprawl, increased use of transportation networks, and air pollution [8,9]. Based on historical data, there will be a high demand for sustainable transportation systems in future years. Furthermore, demand for transport related to the delivery of goods and services as well as transport related to the movement of passengers is constantly increasing [10], which leads to the need for designing systems responsible for choosing appropriate strategies related to their development.

Sustainable transportation is a frequently discussed topic due to its significant impact on the environment and human life. Bamwesigye and Hlavackova conducted a discussion and analysis of sustainable transport [11]. Their work presented accurate case comparisons of sustainable transportation in the Netherlands, Germany, Kenya, and Uganda. Zhao et al. conducted an extensive review of literature related to the field of sustainable transportation from 2000 to 2019 [12]. This review identified nine popular research topics and four significant knowledge gaps related to sustainable transportation. Badassa et al. reviewed the literature on sustainable transportation infrastructure from a bibliometric and visualization perspective from 2000 to 2019 [13]. In their work, they identified contemporary paradigms, key research areas and connections between research fields related to sustainable transportation infrastructure. Stephenson et al. researched sustainable transport in New Zealand [14]. Their main focus was on the future of sustainable transportation, where they reviewed factors in the policy environment with experts.

Approaches related to sustainable transport are centered around the use of alternative modes of transport [15,16], the analysis of the links between transport and political–economic aspects [17], transport policy [18], formation of demand for transport, a balanced allocation of resources [19] and meeting the demand for freight transport [20]. Kębłowski et al. presented the theoretical and methodological framework of research on transportation [2]. In addition, they considered the influence of various factors such as political–economic embeddedness or power relations and regulatory framework. Sunio and Mateo-Babiano presented a paper on the study of the sustainable transportation system in Metro Manila [21]. This paper considered aspects of the impact of the COVID pandemic crisis through which there would be an opportunity to create resilient transportation systems.

Many studies on sustainable transportation are conducted with the support offered by Decision Support Systems (DSS), designed to solve complex decision-making problems. These systems are mainly based on Multi-Criteria Decision Analysis (MCDA) and Multi-Criteria Decision Making (MCDM) approaches. Due to the high popularity and the difficulty of selecting suitable methodologies for solving multi-criteria problems, MCDA/MCDM techniques are frequently being developed. The most widely used classical approaches for solving MCDA/MCDM problems are Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [22,23], VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) [24,25], Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE) [26], Elimination et Choix Traduisant la Realité (ELECTRE) [27], Analytic Hierarchy Process (AHP) [28], Analytic Network Process (ANP) [29], Multi-Objective Optimization Method by Ratio Analysis (MOORA) [30] and Multi-Attribute Utility Theory (MAUT) [31].

For evaluation, environmentally responsible transport practices (ERTP) were applied with the VIKOR method in the Indian freight transport industry [32]. To assess the public transport, the AHP procedure was used, where the most significant emphasis was placed on engine technologies and combustion characteristics [33]. The VIKOR approach and six other MCDA/MCDM approaches were used in selecting a placement for a road lane in Poland [34]. In evaluating the walkability of selected neighborhoods in the context of public transportation, the ANP method and TOPSIS [35]. To evaluate urban public transport vehicles in terms of economic and environmental criteria the ELECTRE technique was used [36].

New approaches are also gaining popularity in recent years, such as the Characteristic Object’s Method (COMET) [37,38], Stable Preference Ordering Towards Ideal Solution (SPOTIS) [39,40], Sequential Interactive Modelling for Urban Systems (SIMUS) [41], the Full Consistency Method (FUCOM) [42], the Best–Worst Method (BWM) [43], Combined Compromise Solution (COCOSO) [44], Additive Ratio Assessment (ARAS) [45], Multi-Attributive Border Approximation Area Comparison (MABAC) [46] or Potentially All Pairwise Rankings of all Possible Alternatives (PAPRIKA) [47]. These approaches extend classical assumptions about the distance from ideal solutions, compromise evaluation, linear programming or pairwise comparison. Many additionally provide solutions to common problems associated with the difficulty of mapping the decision-maker’s preferences or the phenomenon of reversed rankings.

Novel MCDA/MCDM approaches also find applications in problems related to sustainable transportation issues. Wątróbski et al. used the COMET method to solve a problem related to the sustainable transportation of atomic saltpeter [48]. Pamucar et al. used the FUCOM method with a combination of the MABAC approach [49] for the alternative fuel vehicle problem. Kumar et al. used the BWM approach to determine the significance of the criteria in the battery electric vehicle problem [50]. Zagorskas and Turskis studied retrofitting bicycle networks using the ARAS method [51].

Although we can solve some problems using basic MCDA/MCDM approaches, many problems are related to uncertainty, possibly due to either internal or external factors [52]. The primary sources of uncertainty are contradiction, randomness and partiality of the extracted information [53]. This is also why MCDA/MCDM approaches use tools designed to handle uncertainty. The most popular tool is fuzzy sets, which are used because of their ease in identifying uncertainty. Fuzzy sets (FSs) represent uncertainty using a membership function whose values are from the interval [0, 1].

Due to the possibility of modeling only a particular set membership in fuzzy sets, many generalizations have been made, represented by the

Table 1. Overview of fuzzy set generalizations.

Methods for Uncertainty Determination	Authors	Degrees of Membership	Limitations	Ref.
Fuzzy sets (FSs)	Lotfi A. Zadeh	Degree of membership ($\mu$)	$0\le \mu \le 1$	[60]
Intuitionistic fuzzy sets (IFSs)	Krassimir Atanassov	Degree of membership ($\mu$)	$0\le \mu +\nu \le 1$	[54]
		Degree of non-membership ($\nu$)
Pythagorean fuzzy sets (PyFSs)	Ronald R Yager	Degree of membership ($\mu$)	$0\le {\mu }^2+{\nu }^2\le 1$	[61]
		Degree of non-membership ($\nu$)
Fermatean fuzzy sets (FFSs)	Tapan Senapati	Degree of positive membership ($\mu$)	$0\le {\mu }^3+{\nu }^3\le 1$	[57]
	Ronald R. Yager	Degree of negative membership ($\nu$)
Picture fuzzy sets (PFSs)	Bui Cong Cuong	Degree of positive membership ($\mu$)	$0\le \mu +\eta +\nu \le 1$	[62]
	Vladik Kreinovich	Degree of neutral membership ($\nu$)
		Degree of negative membership ($\eta$)
Neutrosophic fuzzy sets (NFSs)	Florentin Smarandache	Degree of true membership (T)	$0\le T+I+F\le 3$	[63]
		Degree of indeterminate
		membership (I)
		Degree of false membership (F)
Spherical fuzzy sets (SFSs)	Fatma Kutlu Gündoğdu	Degree of membership ($\mu$)	$0\le {\mu }^2+{\eta }^2+{\nu }^2\le 1$	[64,65]
	Cengiz Kahraman	Degree of abstinence ($\eta$)
		Degree of non-membership ($\nu$)

. Atanassov introduced intuitionistic fuzzy sets (IFSs), which additionally considered the degree of the non-membership function for any element in the fuzzy set [54,55]. Because IFSs may not model certain decision situations, Yager introduced Pythagorean fuzzy sets (PyFSs) [56]. Pythagorean fuzzy sets allow for the relaxation of the dependence between the degree of membership and non-membership, which is one of the main contributions of the IFS extension. Another extension of IFS is Fermatean fuzzy sets (FFSs), which Senpati and Yager introduced [57]. They make it possible to present a more extensive set of custom membership degrees. Another extension of IFSs is picture fuzzy sets (PFSs), through which three degrees of membership, i.e., positive, neutral and negative, can be specified. This concept comes from observations on human decision-making, where many response options are formulated as yes, abstain, no and refuse [58]. One generalization of fuzzy sets is neutrosophic fuzzy sets (NFSs), which is challenging to apply to scientific and engineering work due to the mapping of philosophical points of view [59].

This paper will focus on an extension of spherical fuzzy sets (SFSs), namely T-spherical fuzzy sets. SFSs have been introduced by considering the limitations of the PFS domain [66]. Due to the possibility of more accurate identification, they are widely used in work related to pattern recognition [67], the manufacturing domain [68], medical diagnostics [66,69], economics [70], management [64,71] and energy [72]. T-spherical fuzzy sets (TSFSs) have been proposed as a generalization of SFSs, free from the constraints of [67]. Due to their flexibility, TSFSs are continuously developed. A new divergence measure for TSFSs, based on the advantages of Jensen–Shannon divergence, was proposed by Wu et al. [73]. Ullah et al. proposed new correlation coefficients for T-spherical fuzzy sets due to the inapplicability of the correlations derived from IFSs and PFSs [74]. Wu et al. designed nine similarity measures of the T-spherical fuzzy set considering all membership degrees included in TSFSs according to the cosine function [75]. Ali et al. proposed a novel concept of complex T-spherical fuzzy sets (CTSFSs) and their operational laws [76].

1.1. Challenges and Motivation

Based on the overhead review, it can be concluded that the T-spherical fuzzy set tool is a flexible and rapidly developing approach to dealing with uncertainty. This approach was designed recently and therefore needs to be verified with empirical examples. TSFSs are also often used to reflect uncertainty in decision problems. Therefore, combinations of this tool with MCDA/MCDM methods are continuously being developed. Due to the difficulty of choosing the proper MCDA/MCDM techniques, further work on their development should be carried out. Moreover, a frequently addressed issue in TSFSs is the aggregation of expert knowledge. Many numerous aggregation operators need to be continuously investigated.

Given the above constraints associated with T-spherical fuzzy sets, the motivation of this study is as follows:

• There is a lack of comparative analysis between the obtained results from TSFSs in some works;
• Particular works are focused around a single function that aggregates expert knowledge;
• Works considering TSFSs in sustainable transport problems are missing;
• Not many works consider MCDA/MCDM methods in combination with TSFSs.

1.2. Contribution and Novelties

This paper focuses on using the Laplacian Energy of T-spherical fuzzy graphs approach in a sustainable transportation problem. Laplacian Energy is used to determine decision weights based on decision-makers’ preferences. Three decision-makers were involved in the whole process and presented their strategies using T-spherical fuzzy graphs. Then, using the net degree approach, the strategies were evaluated. An additional aspect addressed in the paper is the use of SFS TOPSIS in evaluating the aggregated preferences of the decision-makers. These preferences were also aggregated with four functions, which were compared using Spearman’s weighted correlation coefficient.

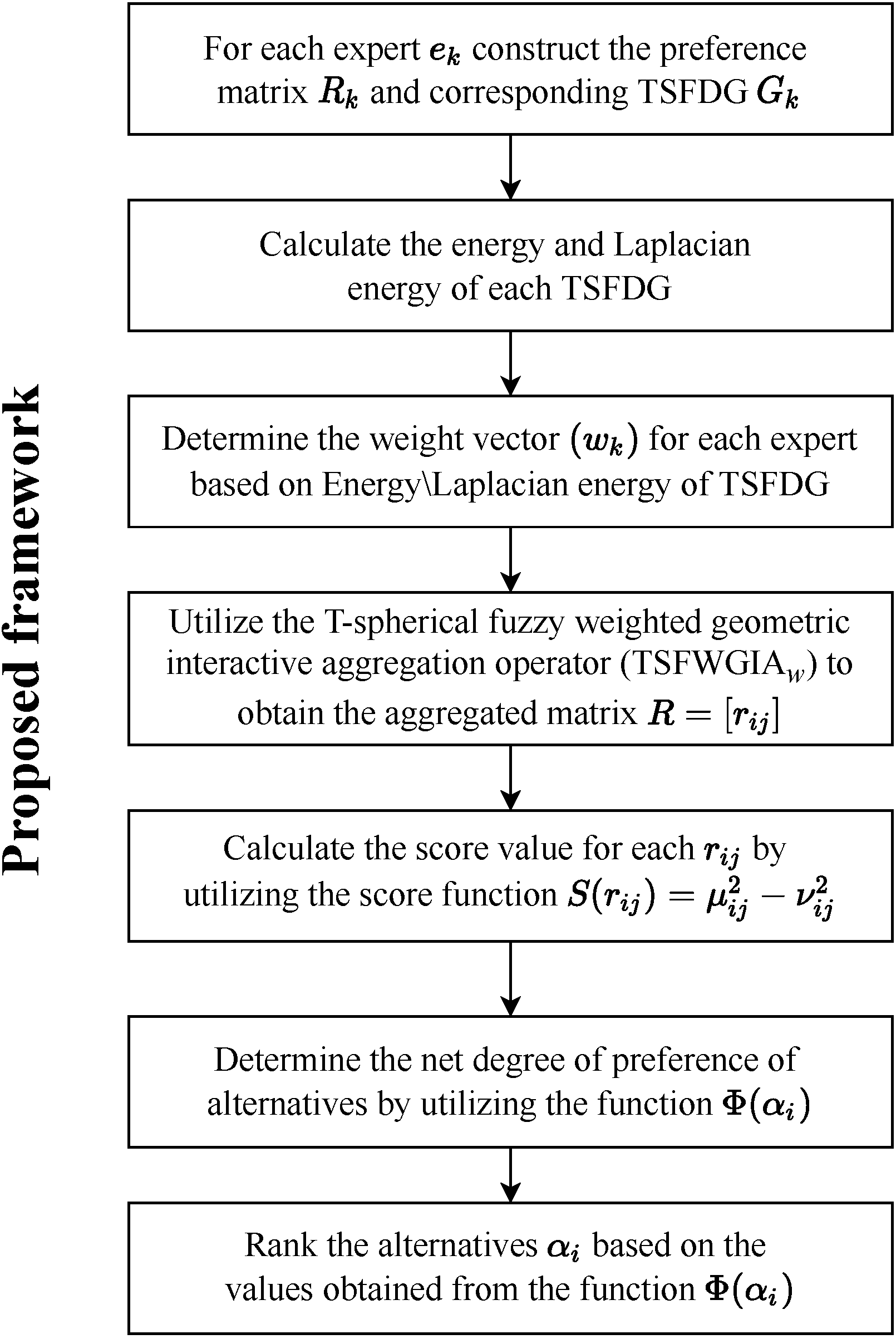
1.3. Framework of This Study

The rest of the paper is organized as follows. Section 2 presents the fundamental concepts related to spherical fuzzy sets. Section 3 presents the assumptions concerning Energy/Laplacian Energy of TSF-directed graph. The TOPSIS method and its main assumptions are presented in Section 4. Section 5 presents a case study on sustainable transportation with a comparative analysis. Finally, Section 6 presents conclusions and future research directions.

2. Preliminaries

Here, some fundamental and basic concepts in connection with Pythagorean fuzzy graph and energy are presented.

Definition 1

([66]). A spherical fuzzy set S in U (universe of discourse) is given by

$$S=\left\{<\alpha ,{\mu }_S(\alpha ),{\eta }_S(\alpha ),{\nu }_S(\alpha )>\mid \alpha \in U\right\};$$

where ${\mu }_S:U\to [0,1]$, ${\eta }_S:U\to [0,1]$ and ${\nu }_S:U\to [0,1]$ denote the degree of membership, degree of neutral membership (abstain) and degree of non-membership, respectively, and for every $\alpha \in U$ satisfying the condition

$${\mu }_S^2(\alpha )+{\eta }_S^2(\alpha )+{\nu }_S^2(\alpha )\le 1\forall \alpha \in U.$$

The degree of refusal for any spherical fuzzy set S and $\alpha \in U$ is given by

$$r_S(\alpha )=\sqrt{1-({\mu }_S^2(\alpha )+{\eta }_S^2(\alpha )+{\nu }_S^2(\alpha ))}.$$

Definition 2

([66]). A T-spherical fuzzy set S in U (universe of discourse) is given by

$$S=\left\{<\alpha ,{\mu }_S(\alpha ),{\eta }_S(\alpha ),{\nu }_S(\alpha )>\mid \alpha \in U\right\};$$

where ${\mu }_S:U\to [0,1]$, ${\eta }_S:U\to [0,1]$ and ${\nu }_S:U\to [0,1]$ denote the degree of membership, degree of neutral membership (abstain) and degree of non-membership, respectively, and for every $\alpha \in U$ satisfying the condition

$${\mu }_S^n(\alpha )+{\eta }_S^n(\alpha )+{\nu }_S^n(\alpha )\le 1\forall \alpha \in U.$$

The degree of refusal for any T-spherical fuzzy set S and $\alpha \in U$ is given by

$$r_S(\alpha )=\sqrt[n]{1-({\mu }_S^n(\alpha )+{\eta }_S^n(\alpha )+{\nu }_S^n(\alpha ))}.$$

• In the case where $n=2$, the T-spherical fuzzy set goes to the spherical fuzzy set.
• If $n=1$, then the T-spherical fuzzy set becomes picture fuzzy set.
• If $n=2$ and $r_S=0$, then the T-spherical fuzzy set becomes Pythagorean fuzzy set.
• If $n=1$ and $r_S=0$, then the T-spherical fuzzy set becomes to intuitionistic fuzzy set.

Definition 3

([77]). An intuitionistic fuzzy graph on U, denoted by $\tilde{G}=(P,Q)$, where P is an intuitionistic fuzzy set on U and Q is an intuitionistic fuzzy relation in $U\times U$ such that

$${\mu }_Q(\alpha ,\beta )\le min\{{\mu }_P(\alpha ),{\mu }_P(\beta )\},$$

$${\nu }_Q(\alpha ,\beta )\ge max\{{\nu }_P(\alpha ),{\nu }_P(\beta )\};$$

satisfying the constraint condition

$$0\le {\mu }_Q(\alpha ,\beta )+{\nu }_Q(\alpha ,\beta )\le 1,\forall \alpha ,\beta \in U.$$

The set P is called the intuitionistic fuzzy vertex set of the graph $\tilde{G}$ and Q is called the intuitionistic fuzzy edge set of the graph $\tilde{G}$.

Definition 4

([78]). Consider a Pythagorean fuzzy graph on U, denoted by $\widehat{G}=(M,N)$, where M is a Pythagorean fuzzy set on U and N is a Pythagorean fuzzy relation in $U\times U$ such that

$${\mu }_N(\alpha ,\beta )\le min\{{\mu }_M(\alpha ),{\mu }_M(\beta )\},$$

$${\nu }_N(\alpha ,\beta )\ge max\{{\nu }_M(\alpha ),{\nu }_M(\beta )\};$$

satisfying the constraint condition $0\le {\mu }_N^2(\alpha ,\beta )+{\nu }_N^2(\alpha ,\beta )\le 1,\forall \alpha ,\beta \in U$. The set M is called the Pythagorean fuzzy vertex set of the graph $\widehat{G}$ and N is called the Pythagorean fuzzy edge set of the graph $\widehat{G}$.

Definition 5

([79]). Let $G^{{}^{\prime }}=(V,E)$ be a graph and $A(G^{{}^{\prime }})$ be its adjacency matrix with eigenvalues ${\lambda }_i$. Then the energy of the graph is the sum of the absolute eigenvalues of $A(G^{{}^{\prime }})$, i.e., $E(G)={\displaystyle \sum _i}|{\lambda }_i|$.

Definition 6

([80]). Let $\tilde{G}=(P,Q)$ be an intuitionistic fuzzy graph and $A(\tilde{G})$ be its adjacency matrix. Consider ${\lambda }_i$ as the eigenvalues of $A_{\mu }(\tilde{G})$ and ${\gamma }_i$ as the eigenvalues of $A_{\nu }(\tilde{G})$. Then the energy of the intuitionistic fuzzy graph is given by $E(\tilde{G}))=\left({\displaystyle \sum _i}|{\lambda }_i|,{\displaystyle \sum _i}|{\gamma }_i|\right).$

Definition 7

([81]). Let U be a universal set. A T-spherical fuzzy graph on U, denoted by $G=(S,R)$, where S is a TSFS on U with ${\mu }_S^n(\alpha )+{\eta }_S^n(\alpha )+{\nu }_S^n(\alpha )\le 1;\forall \alpha \in U$ and R is a T-spherical fuzzy relation in $U\times U$ such that

$${\mu }_R(\alpha ,\beta )\le min\{{\mu }_S(\alpha ),{\mu }_S(\beta )\},{\eta }_R(\alpha ,\beta )\le$$

$$min\{{\eta }_S(\alpha ),{\eta }_S(\beta )\},{\nu }_R(\alpha ,\beta )\le max\{{\nu }_S(\alpha ),{\nu }_S(\beta )\}$$

and satisfying the condition

$${\mu }_R^n(\alpha ,\beta )+{\eta }_R^n(\alpha ,\beta )+{\nu }_R^n(\alpha ,\beta )\le 1;\forall \alpha ,\beta \in U.$$

Here, S and R are the T-spherical fuzzy vertex set and the T-spherical fuzzy edge set of the T-spherical fuzzy graph G, respectively.

Definition 8

([82]). The adjacency matrix $A(\widehat{G})$ of the graph $\widehat{G}$ is a square matrix defined as

$$A(\widehat{G})=\left[a_{ij}\right],where{a}_{ij}=({\mu }_{\widehat{R}}({\beta }_i,{\beta }_j),{\eta }_{\widehat{R}}({\beta }_i,{\beta }_j),{\nu }_{\widehat{R}}({\beta }_i,{\beta }_j)).$$

Here, ${\mu }_{\widehat{R}}({\beta }_i,{\beta }_j),{\eta }_{\widehat{R}}({\beta }_i,{\beta }_j)\&{\nu }_{\widehat{R}}({\beta }_i,{\beta }_j)$ are the membership, neutral membership (abstain) and non-membership components, respectively.

Definition 9.

Thespectrumof $A(\widehat{G})$ of the T-spherical fuzzy graph $\widehat{G}=(\widehat{S},\widehat{R})$ is given by $(\Theta ,\Phi ,\Psi )$, where Θ, Φ and Ψ are the set of the eigenvalues of matrices

$$A({\mu }_{\widehat{R}}({\beta }_i,{\beta }_j))=[{\mu }_{\widehat{R}}({\beta }_i,{\beta }_j)],$$

$$A({\eta }_{\widehat{R}}({\beta }_i,{\beta }_j))=[{\eta }_{\widehat{R}}({\beta }_i,{\beta }_j)]$$

and

$$A({\nu }_{\widehat{R}}({\beta }_i,{\beta }_j)))=[{\nu }_{\widehat{R}}({\beta }_i,{\beta }_j)],$$

respectively.

Definition 10.

Theenergy$E(\widehat{G})$ of the T-spherical fuzzy graph $\widehat{G}$ is defined as

$$E(\widehat{G})=(E({\mu }_{\widehat{R}}({\beta }_i,{\beta }_j)),E({\eta }_{\widehat{R}}({\beta }_i,{\beta }_j)),E({\nu }_{\widehat{R}}({\beta }_i,{\beta }_j)))=$$

$$=\left(\sum _{i=1,{\theta }_i\in \Theta }^m|{\theta }_i|,\sum _{i=1,{\varphi }_i\in \Phi }^m|{\varphi }_i|,\sum _{i=1,{\psi }_i\in \Psi }^m|{\psi }_i|\right).$$

Definition 11

([82]). Let $\widehat{G}=(\widehat{S},\widehat{R})$ be a T-spherical fuzzy graph on m vertices. The degree matrix $D(\widehat{G})=\left[d_{ij}\right]$ of $\widehat{G}$ is an $m\times m$ diagonal matrix defined as:

$$d_{ij}=\left\{\begin{array}{cc}{d}_{\widehat{G}}({\beta }_i)\hfill & ifi=j;\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Definition 12

([82]). Let $\widehat{G}=(\widehat{S},\widehat{R})$ be a TSF graph on m vertices. The Laplacian matrix of a T-spherical fuzzy graph $\widehat{G}$ is defined as $L(\widehat{G})=D(\widehat{G})-A(\widehat{G}),$ where $D(\widehat{G})\&A(\widehat{G})$ are degree and adjacency matrix of the TSF graph $\widehat{G}$, respectively.

Definition 13

([82]). The spectrum of the Laplacian matrix $L(\widehat{G})$ of the T-spherical fuzzy graph $\widehat{G}=(\widehat{S},\widehat{R})$ is given by {$(\Delta ,{\rm Y},\Omega )$}, where Δ, Υ and Ω are the set of the eigenvalues of $L({\mu }_{\widehat{R}}({\beta }_i,{\beta }_j))$, $L({\eta }_{\widehat{R}}({\beta }_i,{\beta }_j))$ and $L({\nu }_{\widehat{R}}({\beta }_i,{\beta }_j))$, respectively.

Definition 14

([82]). The Laplacian Energy of the TSF graph $\widehat{G}=(\widehat{S},\widehat{R})$, denoted by $LE(\widehat{G})$, is defined as

$$LE(\widehat{G})=(LE({\mu }_{\widehat{R}}({\beta }_i,{\beta }_j)),LE({\eta }_{\widehat{R}}({\beta }_i,{\beta }_j)),LE({\eta }_{\widehat{R}}({\beta }_i,{\beta }_j)))=$$

$$\left(\sum _{i=1}^m|{\rho }_i|,\sum _{i=1}^m|{\xi }_i|,\sum _{i=1}^m|{\varsigma }_i|\right);$$

where ${\rho }_i={\delta }_i-\frac{2{\displaystyle \sum _{1\le i<j\le m}}{\mu }_{\widehat{R}}({\beta }_i,{\beta }_j)}{m};$ ${\xi }_i={\upsilon }_i-\frac{2{\displaystyle \sum _{1\le i<j\le m}}{\eta }_{\widehat{R}}({\beta }_i,{\beta }_j)}{m};$ ${\varsigma }_i={\omega }_i-\frac{2{\displaystyle \sum _{1\le i<j\le m}}{\nu }_{\widehat{R}}({\beta }_i,{\beta }_j)}{m}.$

3. Energy/Laplacian Energy of TSF-Directed Graph

In case of the directed graph, $A(\widehat{G})$ of a T-spherical fuzzy directed graph may not be necessarily symmetric. Therefore, the eigenvalues of the adjacency matrix can be complex numbers. This section generalizes the concept of energy/Laplacian Energy for T-spherical fuzzy directed graphs.

Therefore, the eigenvalues of the adjacency matrix can be complex numbers

Definition 15.

Thespectrumof the adjacency matrix $A(\widehat{G})$ of the T-spherical fuzzy directed graph $\widehat{G}=(\widehat{S},\overrightarrow{\widehat{R}})$ is given by $\{(\Theta ,\Phi ,\Psi )\}$, where Θ, Φ and Ψ are the set of the eigenvalues of $A({\mu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))$, $A({\eta }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))$ and $A({\nu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))$, respectively.

Definition 16.

Theenergy of the T-spherical fuzzy directed graph $\widehat{G}$is given as:

$$E(\widehat{G})=(E({\mu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j)),E({\eta }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j)),E({\nu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j)))$$

$$=\left(\sum _{i=1,{\theta }_i\in \Theta }^m|Re({\theta }_i)|,\sum _{i=1,{\varphi }_i\in \Phi }^m|Re({\varphi }_i)|,\sum _{i=1,{\psi }_i\in \Psi }^m|Re({\psi }_i)|\right);$$

where $Re({\theta }_i)$, $Re({\varphi }_i)$ and $Re({\psi }_i)$ represent the real part of the eigenvalues ${\theta }_i$, ${\varphi }_i$ and ${\psi }_i$, respectively.

Definition 17.

Let $\widehat{G}=(\widehat{S},\overrightarrow{\widehat{R}})$ be a TSF graph on m vertices. The out-degree matrix $D^{out}(\widehat{G})=\left[d_{ij}\right]$ of $\widehat{G}$ is an $m\times m$ diagonal matrix defined as:

$$d_{ij}=\left\{\begin{array}{cc}{d}_{\widehat{G}}^{out}({\beta }_i)\hfill & ifi=j;\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Definition 18.

Let $\widehat{G}=(\widehat{S},\overrightarrow{\widehat{R}})$ be a TSF-directed graph on m vertices. The Laplacian matrix of a TSF-directed $\widehat{G}$, denoted by $L(\widehat{G})$ is defined as

$$L(\widehat{G})=D^{out}(\widehat{G})-A(\widehat{G}),$$

where $D^{out}(\widehat{G})\&A(\widehat{G})$ are the out degree matrix and adjacency matrix of the TSF-directed graph $\widehat{G}$, respectively.

Definition 19.

The spectrum of the Laplacian matrix $L(\widehat{G})$ of the TSF-directed graph $\widehat{G}=(\widehat{S},\overrightarrow{\widehat{R}})$ is given by $\{(\Delta ,{\rm Y},\Omega )\}$, where Δ, Υ and Ω are the set of the eigenvalues of $L({\mu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))$, $L({\eta }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))$ and $L({\nu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))$, respectively.

Definition 20.

The Laplacian Energy of the TSF-directed graph $\widehat{G}=(\widehat{S},\overrightarrow{\widehat{R}})$ denoted by $LE(\widehat{G})$ is defined as

$$LE(\widehat{G})=\left(LE({\mu }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j)),LE({\eta }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j)),LE({\eta }_{\overrightarrow{\widehat{R}}}({\beta }_i,{\beta }_j))\right)$$

$$=\left(\sum _{i=1}^m|{\rho }_i|,\sum _{i=1}^m|{\xi }_i|,{\displaystyle \sum _{i=1}^m}|{\varsigma }_i|\right);$$

where ${\rho }_i=Re({\delta }_i)-\frac{{\displaystyle \sum _{i=1,{\delta }_i\in \Delta }^m}Re({\delta }_i)}{m};$ ${\xi }_i=Re({\upsilon }_i)-\frac{{\displaystyle \sum _{i=1,{\upsilon }_i\in {\rm Y}}^m}Re({\upsilon }_i)}{m};$ ${\varsigma }_i=Re({\omega }_i)-\frac{{\displaystyle \sum _{i=1,{\omega }_i\in \Omega }^m}Re({\omega }_i)}{m}.$

To illustrate the proposed definitions, we consider the following example of a T-spherical directed fuzzy graph.

4. Spherical Fuzzy TOPSIS

The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) is a popular approach related to multi-criteria decision-making. Its central premise is based on evaluating alternatives concerning their distance from ideal solutions. The direct distance metric considered in this technique is the Euclidean distance [23,83]. However, research shows the possibility of using other metrics as well. Due to its simplicity, it has numerous extensions to handle uncertainty with fuzzy sets and their generalizations [84,85]. Since this thesis mainly focuses on SFS and, more specifically, TSFS, below are the steps to TOPSIS in the SFS environment. The main concept of SFS TOPSIS is presented in [65], from where its steps are derived.

Step 1.

Create a spherical fuzzy set decision matrix based on Equation (1) with dimensionality $m\times n$, where m is the number of alternatives and n is the number of criteria.

$$D={\left(C_j\left(X_{i}w\right)\right)}_{mxn}=\left(\begin{array}{cccc}\left({\mu }_{11w},v_{11w},{\pi }_{11w}\right)& \left({\mu }_{12w},v_{12w},{\pi }_{12w}\right)& \dots & \left({\mu }_{1nw},v_{1nw},{\pi }_{1nw}\right)\\ \left({\mu }_{21w},v_{21w},{\pi }_{21w}\right)& \left({\mu }_{22w},v_{22w},{\pi }_{22w}\right)& \dots & \left({\mu }_{2nw},v_{2nw},{\pi }_{2nw}\right)\\ :& :& ⋮\\ \left({\mu }_{m1w},v_{m1w},{\pi }_{m1w}\right)& \left({\mu }_{m2w},v_{m2w},{\pi }_{m2w}\right)& \dots & \left({\mu }_{mnw},v_{mnw},{\pi }_{mnw}\right)\end{array}\right)$$

(1)

Step 2.

Create a scoring matrix based on the SFS decision matrix using Equation (2).

$$Score\left(C_j(X_{i}w)\right)={\mu }_{ij}^2-{\nu }_{ij}^2$$

(2)

Step 3.

Determine the ideal solutions of the decision matrix using scoring matrix. A positive ideal solution (PIS) is a solution that achieves the most significant point values from the given criteria (3). On the other hand, as a negative ideal solution (NIS), the solution that achieves the least point values from the given criteria is selected (4).

$$X^{*}=\left\{C_j,\underset{i}{max}<Score\left(C_j\left(X_{iw}\right)\right)>\mid j=1,2\dots n\right\}$$

(3)

$$X^{-}=\left\{C_j,\underset{i}{min}<Score\left(C_j\left(X_{iw}\right)\right)>\mid j=1,2\dots n\right\}$$

(4)

The obtained positive ideal solution and negative ideal solution can be represented successively by Equations (5) and (6).

$$X^{*}=\left\{〈C_1,\left({\mu }_1^{*},v_1^{*},{\pi }_1^{*}\right)〉,〈C_2,\left({\mu }_2^{*},v_2^{*},{\pi }_2^{*}\right)〉\dots 〈C_n,\left({\mu }_n^{*},v_n^{*},{\pi }_n^{*}\right)〉\right\}$$

(5)

$$X^{-}=\left\{〈C_1,\left({\mu }_1^{-},v_1^{-},{\pi }_1^{-}\right)〉,〈C_2,\left({\mu }_2^{-},v_2^{-},{\pi }_2^{-}\right)〉\dots 〈C_n,\left({\mu }_n^{-},v_n^{-},{\pi }_n^{-}\right)〉\right\}$$

(6)

Step 4.

Determine the distance for each alternative from the positive ideal solution and the negative ideal solution according to Equations (7) and (8).

$$D\left(X_i,X^{-}\right)=\sqrt{\frac{1}{2n}\sum _{i=1}^n\left({\left({\mu }_{x_i}-{\mu }_{x^{-}}\right)}^2+{\left(v_{x_i}-v_{x^{-}}\right)}^2+{\left({\pi }_{x_i}-{\pi }_{x^{-}}\right)}^2\right)}$$

(7)

$$D\left(X_i,X^{*}\right)=\sqrt{\frac{1}{2n}\sum _{i=1}^n\left({\left({\mu }_{x_i}-{\mu }_{x^{*}}\right)}^2+{\left(v_{x_i}-v_{x^{*}}\right)}^2+{\left({\pi }_{x_i}-{\pi }_{x^{*}}\right)}^2\right)}$$

(8)

The most significant distance from a negative ideal solution and the smallest distance from a positive ideal solution are determined using Equations (9) and (10).

$$D_{max}\left(X_i,X^{-}\right)=\underset{1\le i\le m}{max}D\left(X_i,X^{-}\right)$$

(9)

$$D_{min}\left(X_i,X^{*}\right)=\underset{1\le i\le m}{min}D\left(X_i,X^{*}\right)$$

(10)

Step 5.

Determine the revised closeness ratio proposed using Equation (11), which Zhang and Xu proposed in [86]. The alternative with the highest score is defined as the best alternative.

$$\xi \left(X_i\right)=\frac{D\left(X_i,X^{-}\right)}{D_{max}\left(X_i,X^{-}\right)}-\frac{D\left(X_i,X^{*}\right)}{D_{min}\left(X_i,X^{*}\right)}$$

(11)

5. Selecting a Reliable Strategy for Sustainable Urban Transport

5.1. Study Case

This section focuses on the study case of the proposed energy/Laplacian Energy of the TSF-directed graph in a real-world problem related to selecting a reliable strategy for sustainable urban transport. As mentioned in the introduction, many European cities have a complex problem with air pollution. Therefore, it is essential to select the most reliable strategy out of the possibilities that quickly reduces pollution and provides appropriate urban transport. Each strategy considered is a mix of basic steps to improve air quality. However, some of them are more or less efficient in terms of time or restrict the possibility of moving around the city. It is, therefore, necessary to identify the most balanced strategy [87].

The preference relation is one of the most utilized techniques to obtain the ranking of the alternatives in which the decision-makers provide their preference concerning the available alternatives/criteria. If the information presented in the preference relation is in the form of TSFNs, then the concept of the TSF preference relation $(TSFPR)$ may be reframed analogously as follows:

Definition 21

([81]). A T-spherical fuzzy preference relation $(TSFPR)$ on the universal set $U=\{{\beta }_1,{\beta }_2,{\beta }_3,\dots ,{\beta }_m\}$ is given by the matrix $\widehat{R}={(\widetilde{r_{ij}})}_{m\times m}$, where for all $i=1,2,\dots ,m,j=1,2,\dots ,m$, we have $\widetilde{r_{ij}}=\left(({\beta }_i,{\beta }_j),\mu ({\beta }_i,{\beta }_j),\eta ({\beta }_i,{\beta }_j),\nu ({\beta }_i,{\beta }_j)\right)$. For convenience, let $\widetilde{r_{ij}}=({\mu }_{ij},{\eta }_{ij},{\nu }_{ij})$, where ${\mu }_{ij}$ represents the degree to which the object ${\beta }_i$ is preferred over the object ${\beta }_j$, ${\eta }_{ij}$ represents the degree to which the decision-maker is confused as to whether to prefer the object ${\beta }_i$ or ${\beta }_j$ and ${\nu }_{ij}$ represents the degree to which the object ${\beta }_i$ is not preferred to the object ${\beta }_j$ and

$$r_{ij}=\sqrt[n]{1-({\mu }_{ij}^n(\beta )+{\eta }_{ij}^n(\beta )+{\nu }_{ij}^n(\beta ))}$$

representing the degree of refusal, with the conditions:

$$0\le {\mu }_{ij}^n(\beta )+{\eta }_{ij}^n(\beta )+{\nu }_{ij}^n(\beta )\le 1,{\mu }_{ij}$$

$$={\nu }_{ji},{\eta }_{ij}={\eta }_{ji},{\nu }_{ij}={\mu }_{ji}and{\mu }_{ii}=1,{\eta }_{ii}={\nu }_{ii}=0;$$

$$\forall i,j=1,2,\dots ,m.$$

Consider the problem of selecting the most reliable strategy for sustainable urban transport, which is formulated supposing that it is based on a comprehensive analysis and survey conducted by the authorities agencies; let there be four possible strategies $({\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4)$ for sustainable urban transport in the city.

To conduct the evaluation process based on the opinion of three experts $(e_k;k=1,2,3)$ who have been independently deputed. Based on the their experience, the expert’s comparative opinions were marked in the form T-spherical fuzzy numbers. Further, T-spherical fuzzy preference relations in the form of matrices were constructed as the initial step for the strategy selection. In view of the proposed energy/Laplacian Energy of TSF-directed graphs with preference relations, we provide an algorithm for solving the above-stated site-selection problem whose flowchart is given below in Figure 1:

Procedural Steps of the Algorithm:

-

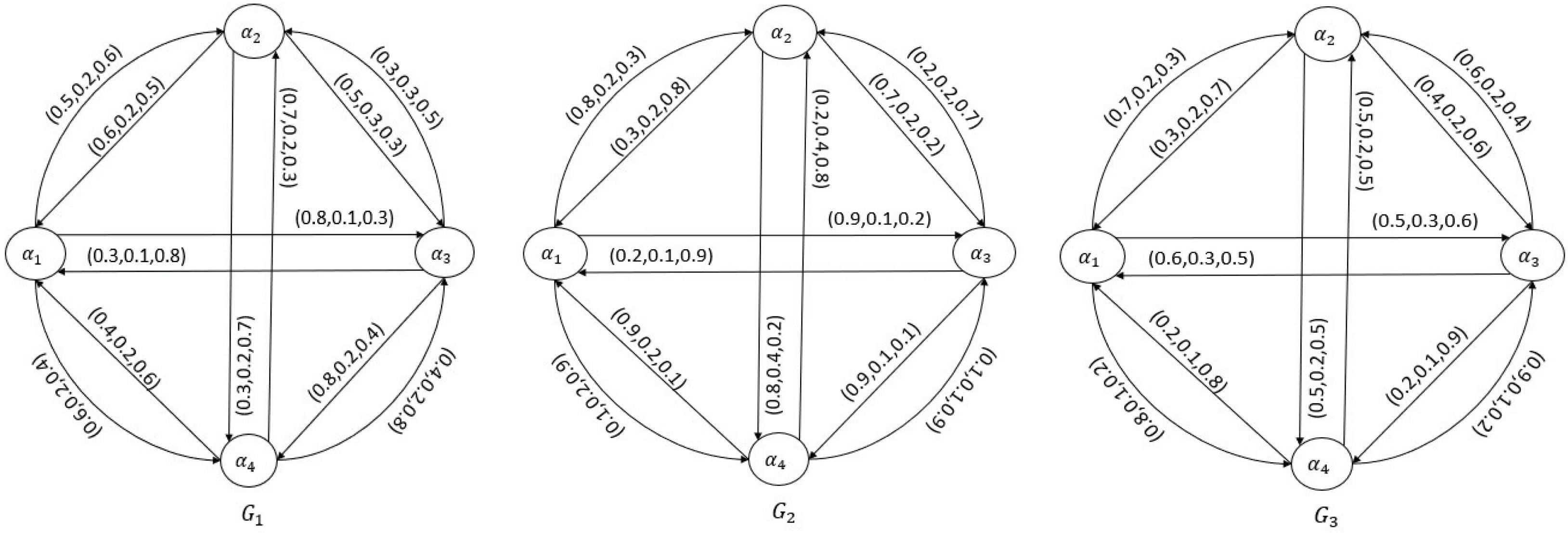
Step 1: The experts compare the involved factors with themselves and present the initial information for computing in the form of TSF preference relations, represented in the form of matrices ${\widehat{R}}_k={({\widetilde{r_{ij}}}^{(k)})}_{4\times 4}(k=1,2,3)$ given by Figure 2 and as follows:

$${\widehat{R}}_1=\left(\begin{array}{cccc}(1.0,0.0,0.0)& (0.5,0.2,0.6)& (0.8,0.1,0.3)& (0.6,0.2,0.4)\\ (0.6,0.2,0.5)& (1.0,0.0,0.0)& (0.5,0.3,0.3)& (0.3,0.2,0.7)\\ (0.3,0.1,0.8)& (0.3,0.3,0.5)& (1.0,0.0,0.0)& (0.8,0.2,0.4)\\ (0.4,0.2,0.6)& (0.7,0.2,0.3)& (0.4,0.2,0.8)& (1.0,0.0,0.0)\end{array}\right);$$

$${\widehat{R}}_2=\left(\begin{array}{cccc}(1.0,0.0,0.0)& (0.8,0.2,0.3)& (0.9,0.1,0.2)& (0.1,0.2,0.9)\\ (0.3,0.2,0.8)& (1.0,0.0,0.0)& (0.7,0.2,0.2)& (0.8,0.4,0.2)\\ (0.2,0.1,0.9)& (0.2,0.2,0.7)& (1.0,0.0,0.0)& (0.9,0.1,0.1)\\ (0.9,0.2,0.1)& (0.2,0.4,0.8)& (0.1,0.1,0.9)& (1.0,0.0,0.0)\end{array}\right);$$

and

$${\widehat{R}}_3=\left(\begin{array}{cccc}(1.0,0.0,0.0)& (0.7,0.2,0.3)& (0.5,0.3,0.6)& (0.8,0.1,0.2)\\ (0.3,0.2,0.7)& (1.0,0.0,0.0)& (0.4,0.2,0.6)& (0.5,0.2,0.5)\\ (0.6,0.3,0.5)& (0.6,0.2,0.4)& (1.0,0.0,0.0)& (0.2,0.1,0.9)\\ (0.2,0.1,0.8)& (0.5,0.2,0.5)& (0.9,0.1,0.2)& (1.0,0.0,0.0)\end{array}\right).$$

-

Step 2: The T-spherical fuzzy directed graph ${\widehat{G}}_k$ corresponding to the $TSFPRs$ given by ${\widehat{R}}_k(k=1,2,3)$ is presented below:

-

Step 3: The energy of each T-spherical fuzzy directed graph is given by

$$E({\widehat{G}}_1)=(3.425,1.213,3.425),$$

$$E({\widehat{G}}_2)=(2.99,1.27,2.99),$$

$$E({\widehat{G}}_3)=(3.02074,1.1237,3.02074).$$

-

Step 4: The weight vector for each expert can be calculated by using

$\begin{array}{c}{w}_k=(w_{\mu }^k,w_{\eta }^k,w_{\nu }^k)=\left(\frac{E{({\widehat{G}}_{\mu })}_k}{{\displaystyle \sum _{l=1}^k}E{({\widehat{G}}_{\mu })}_l},\frac{E{({\widehat{G}}_{\eta })}_k}{{\displaystyle \sum _{l=1}^k}E{({\widehat{G}}_{\eta })}_l},\frac{E{({\widehat{G}}_{\nu })}_k}{{\displaystyle \sum _{l=1}^k}E{({\widehat{G}}_{\nu })}_l}\right);\\ k=1,2,3.\end{array}$ The weight vectors so obtained are listed below:

$$w_1=(0.36297,0.33629,0.36297);$$

$$w_2=(0.31687,0.35209,0.31687);$$

$$w_3=(0.32016,0.31162,0.32016).$$

-

Step 5: In this step, we use the following T-spherical fuzzy weighted geometric interactive aggregation operator recently given by Garg et al. [88],

$$\begin{array}{c}\hfill T-SFWGI{A}_w({\widetilde{r_{ij}}}^{(1)},{\widetilde{r_{ij}}}^{(2)},\dots ,{\widetilde{r_{ij}}}^{(m)})=\\ \hfill (\sqrt[n]{\prod _{j=1}^m{(1-{\nu }_j^n)}^{w_j}-\prod _{j=1}^m{(1-{\mu }_j^n-{\eta }_j^n-{\nu }_j^n)}^{w_j}-\prod _{j=1}^m{({\eta }_j^n)}^{w_j}}\\ \hfill \sqrt[n]{1-\prod _{j=1}^m{(1-{\eta }_j^n)}^{w_j}},\sqrt[n]{1-\prod _{j=1}^m{(1-{\nu }_j^n)}^{w_j}}).\end{array}$$

(12)

We aggregate the three T-spherical fuzzy preference relations ${\widehat{R}}_1,{\widehat{R}}_2$ and ${\widehat{R}}_3$ given in step 1 into a single preference relation $\widehat{R}$, which is obtained as:

$\widehat{R}=\left[r_{ij}\right]=\left(\begin{array}{cccc}(1.0,0.0,0.0)& (0.67,0.20,0.45)& (0.76,0.19,0.42)& (0.50,0.18,0.67)\\ (0.41,0.20,0.69)& (1.0,0.0,0.0)& (0.54,0.24,0.42)& (0.58,0.29,0.54)\\ (0.36,0.19,0.79)& (0.39,0.24,0.56)& (1.0,0.0,0.0)& (0.61,0.14,0.67)\\ (0.56,0.18,0.62)& (0.52,0.29,0.60)& (0.48,0.14,0.77)& (1.0,0.0,0.0)\end{array}\right).$

-

Step 6: We compute the score values by utilizing the score function

$\widehat{S}(r_{ij})={\mu }_{ij}^2-{\nu }_{ij}^2$ and tabulate them in the following matrix:

$$\widehat{S}(\widehat{R})=\left(\begin{array}{cccc}1& 0.25& 0.41& -0.20\\ -0.30& 1& 0.12& 0.04\\ -0.5& -0.16& 1& -0.07\\ -0.08& -0.09& -0.37& 1\end{array}\right).$$

-

Step 7: Determine the net degree of preference of alternatives by utilizing the function $\varphi ({\beta }_i)$ [89] given by

$$\varphi ({\beta }_i)=\sum _{j=1,j\ne i}^m(r_{ij}-r_{ji}),i=1,2,3,\dots m.$$

We obtain $\varphi ({\beta }_1)=1.33,\varphi ({\beta }_2)=-0.14,\varphi ({\beta }_3)=-0.89,\varphi ({\beta }_4)=-0.30.$

-

Step 8: On the basis of the highest value of the net degree, finally we choose the optimal alternative by ranking all the ${\beta }_i^{\prime }s$, i.e,

$${\beta }_1>{\beta }_2>{\beta }_4>{\beta }_3.$$

Hence, we conclude that the strategy ${\beta }_1$ is the most reliable for sustainable urban transport for the proposed methodology and algorithm.

Remark 1.

In step 4, we replace the concept of energy by the concept of Laplacian Energy for the evaluation of weights. In this case, we use the following formula for the calculation of weights:

$$\begin{array}{c}{w}_k=(w_{\mu }^k,w_{\eta }^k,w_{\nu }^k)=\left(\frac{LE{({\widehat{G}}_{\mu })}_k}{{\displaystyle \sum _{l=1}^k}LE{({\widehat{G}}_{\mu })}_l},\frac{LE{({\widehat{G}}_{\eta })}_k}{{\displaystyle \sum _{l=1}^k}LE{({\widehat{G}}_{\eta })}_l},\frac{LE{({\widehat{G}}_{\nu })}_k}{{\displaystyle \sum _{l=1}^k}LE{({\widehat{G}}_{\nu })}_l}\right);\\ k=1,2,3.\end{array}$$

All the computations can similarly by performed for the evaluation process.

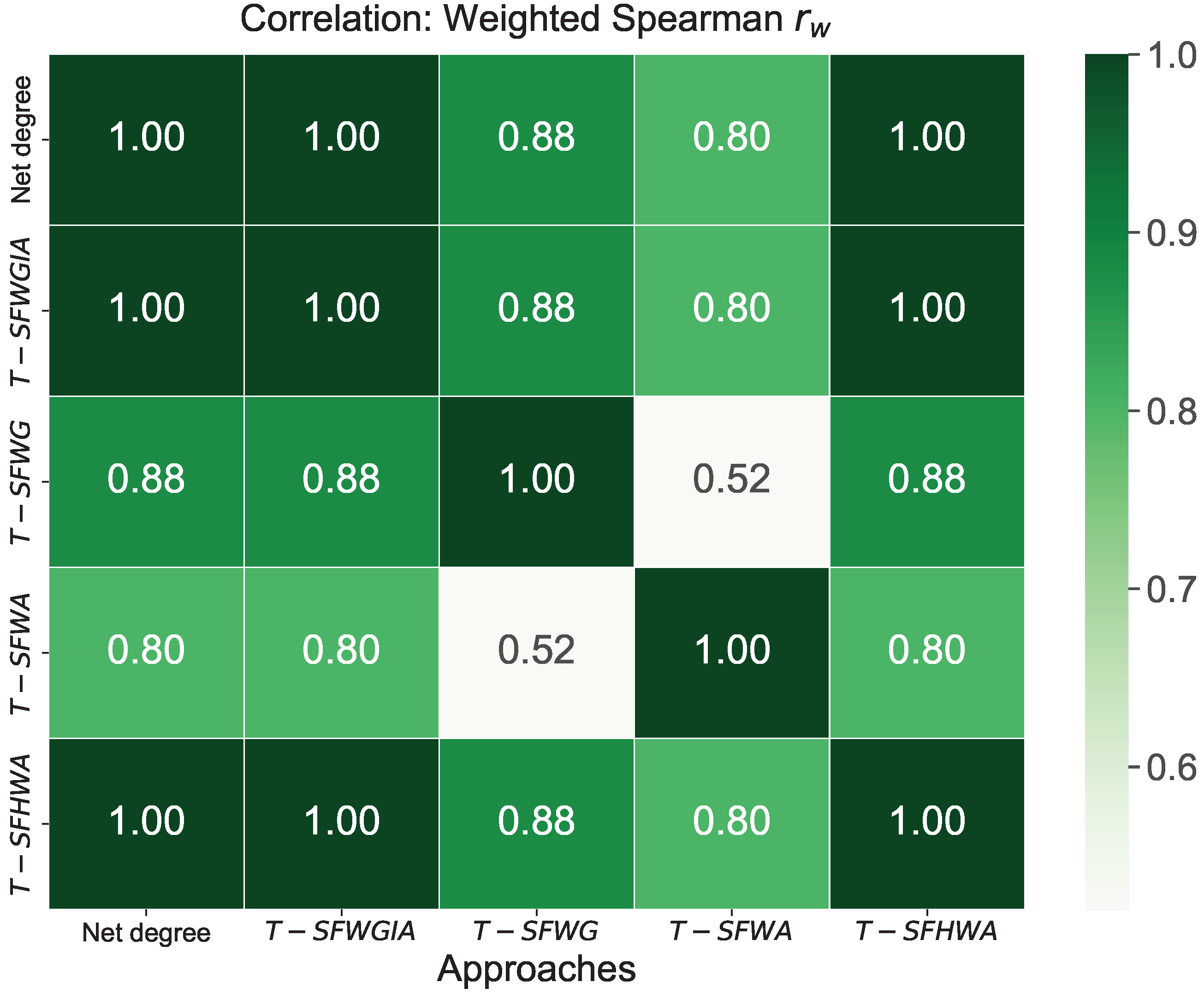
5.2. Comparative Analysis

This section presents a comparative analysis of selected approaches in evaluating sustainable transport strategies. Three additionally selected aggregation functions and the SFS TOPSIS method were used for comparison purposes. The matrices used for aggregation were ${\widehat{R}}_1,{\widehat{R}}_2,{\widehat{R}}_3$ and the weights $w_1,w_2,w_3$, which were determined in the previous section in Step 4. The following approaches aggregated the matrices:

• Mahmood et al. (2019) T-spherical fuzzy weighted geometric (T-SFWG) operator [66]:

  $$T-SFW{G}_w({\widetilde{r_{ij}}}^{(1)},{\widetilde{r_{ij}}}^{(2)},\dots ,{\widetilde{r_{ij}}}^{(m)})=\left(\prod _{j=1}^m{\left({\mu }_j+{\eta }_j\right)}^{w_j}-\prod _{j=1}^m{\eta }_j^{w_j},\prod _{j=1}^m{i}_j^{w_j},\sqrt[n]{1-\prod _{j=1}^m{\left(1-{\nu }_j^n\right)}^{w_j}}\right)$$

  (13)
• Ullah et al. (2019) T-spherical fuzzy weighted averaging (T-SFWA) operator [90]:

  $$T-SFW{A}_w({\widetilde{r_{ij}}}^{(1)},{\widetilde{r_{ij}}}^{(2)},\dots ,{\widetilde{r_{ij}}}^{(m)})=\left(\sqrt[n]{1-\prod _{j=1}^m{\left(1-{\mu }_j^n\right)}^{w_j}},\prod _{j=1}^m{\left({\eta }_j\right)}^{w_j},\prod _{j=1}^m{\left({\nu }_j\right)}^{w_j}\right)$$

  (14)
• Ullah et al. (2020) T-spherical Fuzzy Hamacher-Weighted Averaging (T-SFHWA) operator [91]:

  $$T-SFHW{A}_w({\widetilde{r_{ij}}}^{(1)},{\widetilde{r_{ij}}}^{(2)},\dots ,{\widetilde{r_{ij}}}^{(m)})=\left(\begin{array}{c}\sqrt[n]{\frac{{\prod }_{j=1}^m{\left(1+(\gamma -1){\mu }_j^n\right)}^{w_j}-{\prod }_{j=1}^m{\left(1-{\mu }_j^n\right)}^{w_j}}{{\prod }_{j=1}^m{\left(1+(\gamma -1){\mu }_j^n\right)}^{w_j}+(\gamma -1){\prod }_{j=1}^m{\left(1-{\mu }_j^n\right)}^{w_j}}},\\ \frac{\sqrt[n]{\gamma }{\prod }_{j=1}^m{\eta }_j^{w_j}}{\sqrt[n]{{\prod }_{j=1}^m{\left(1+(\gamma -1)\left(1-{\eta }_j^n\right)\right)}^{w_j}+(\gamma -1){\prod }_{j=1}^m{\left({\eta }_j^n\right)}^{2w_j}}}\\ \frac{\sqrt[n]{\gamma }{\prod }_{j=1}^m{\nu }_j^{w_j}}{\sqrt[n]{{\prod }_{j=1}^m{\left(1+(\gamma -1)\left(1-{\nu }_j^n\right)\right)}^{w_j}+(\gamma -1){\prod }_{j=1}^m{\left({\nu }_j^n\right)}^{2w_j}}}\end{array}\right)$$

  (15)

After performing matrix aggregation, the resulting matrices were evaluated using the net degree approach and SFS TOPSIS. The obtained evaluations are presented in

Table 2. Obtained evaluations of alternatives $A_1$–$A_4$ for the net degree approach and SFS TOPSIS for the considered aggregation functions.

Approach	Aggregation Type	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$
SFS TOPSIS	$T-SFWGIA$	0.00000	−0.35133	−0.53248	−0.49776
	$T-SFWG$	0.00000	−0.36087	−0.51908	−0.57039
	$T-SFWA$	0.00000	−0.52885	−0.74976	−0.47155
	$T-SFHWA$	0.00000	−0.50965	−0.72035	−0.60146
Net degree	$T-SFWGIA$	1.33343	−0.13874	−0.89270	−0.30199
	$T-SFHHG$	1.41580	−0.17622	−0.89400	−0.34558
	$T-SFWA$	1.24570	−0.08991	−0.81010	−0.34569
	$T-SFHWA$	1.19069	−0.11604	−0.67405	−0.40060

. The most significant ratings were obtained for all considered approaches by alternative $A_1$. In the case of the net degree approach, the obtained evaluations at all considered aggregation functions differ slightly and give the same ranking. However, for the SFS TOPSIS approach, the evaluations of alternatives $A_2$–$A_4$ differ.

Table 3. Obtained rankings of $A_1$–$A_4$ alternatives for the net degree method and SFS TOPSIS for the considered aggregation functions.

Approach	Aggregation Type	Rankings
SFS TOPSIS	$T-SFWGIA$	$A_1>A_2>A_4>A_3$
	$T-SFWG$	$A_1>A_2>A_3>A_4$
	$T-SFWA$	$A_1>A_4>A_2>A_3$
	$T-SFHWA$	$A_1>A_2>A_4>A_3$
Net degree	All	$A_1>A_2>A_4>A_3$

shows the rankings for the net degree and SFS TOPSIS approaches under different aggregation functions. In the case of alternative $A_1$, first place is obtained in all rankings. The obtained rankings for the net degree approach at different aggregation functions gave the same ranking of the alternatives, which is the same as the results from SFS TOPSIS for the aggregation functions $T-SFWGIA$ and $T-SFHWA$. Alternative $A_2$ received the second-highest ranking for the SFS TOPSIS approach at aggregation functions $T-SFWGIA$, $T-SFWG$ and $T-SFHWA$. In contrast, for the $T-SFWA$ approach, alternative $A_2$ received the last-place ranking. Referring to alternative $A_3$ for SFS TOPSIS at aggregation functions $T-SFWGIA$, $T-SFWA$ and $T-SFHWA$, it obtained the last place. However, it obtained the second-to-last place for the aggregation functions $T-SFWG$.

Figure 3 presents the Spearman weighted correlation values between the resulting rankings. Most of the obtained rankings have a very high correlation among themselves. The obtained correlation values are in the range [0.52, 1]. The rankings’ minor similarity is between the ranking obtained from the SFS TOPSIS approach with the aggregation function $T-SFWG$ and the SFS TOPSIS approach with the aggregation function $T-SFWA$. The obtained correlation value $r_w$ for this case is 0.52. The highest correlation between the rankings was observed for the net degree, SFS TOPSIS $T-SWGIA$ and SFS TOPSIS $T-SFHWA$ approaches.

6. Conclusions and Future Works

In this paper, a study related to the evaluation of strategies for sustainable transport was conducted. Due to the current uncertainty related to decision-makers’ preferences, it was decided to use Spherical fuzzy sets. The study uses the Laplacian Energy of the TSF-directed graph, and a comparative analysis was conducted using two methods for evaluating alternative strategies and four functions aggregating T-SFS decision matrices.

The results obtained from the studied approach prove its applicability in real problems related to sustainable transport. The ease of expressing the decision-makers’ preferences through the TSF-directed graph provides credible and reliable results. Other directed graphs such as IFS or PyFS do not consider the degree of refusal and do not allow it. From the study results, it can be concluded that the T-SFS decision matrix aggregation functions used did the job. In addition, the aspect of benchmarking that was addressed shows results consistent with the MCDA/MCDM approach. Due to the studied issue of sustainable transportation, the proposed framework fulfills its purpose in this field and can be effectively applied to management problems.

Future research directions should include methods for objective significance determination expressed by metrics such as entropy or standard deviation. Moreover, sensitivity analysis should be applied so that different paths can be taken to improve the approach. Another research direction could be applying the approach to problems related to smart cities. Moreover, the integration of the existing MCDA/MCDM approaches with the Laplacian Energy of the TSF-directed graph should be considered.