1. Introduction
With the scale and complexity of the natural gas pipeline network increasing, the transient simulation of the natural gas pipeline network plays a more significant role in minimizing fuel consumption [
1], pressure amplitude estimation in a gas pipeline [
2], composition tracking [
3], evaluating the effects of hydrogen blending on the characteristics of the natural gas pipeline and pipe network [
4], and many other fields in the natural gas pipeline network. Since the middle of the 19th century, it has been studied extensively and abundant research results have been obtained, such as different numerical methods for solving the governing equations of natural gas transient simulation. Since the time step and the space step are relatively independent [
5], which makes it possible to use a larger time step for a long-term natural gas pipeline transient simulation, it has been widely accepted in commercial network simulation software, and its convenient property also provides support for the adaptive time step. However, the transient simulation of natural gas pipelines requires a set of nonlinear equations to be solved at each time level. The matrix becomes quite large for a complicated pipe network, and the time to solve the matrix becomes excessive [
6]. Therefore, lots of studies have been devoted to improving the transient simulation efficiency of the natural gas pipeline.
The convective term has been changed from being neglected [
6] in the early stage to being linearized at the previous time level by Taylor expansion [
7,
8]. To weaken the connection between the hydraulic system of the governing equations and their thermodynamic system, the decoupled solution strategy was proposed [
9], which increased the efficiency by 20%. The density and velocity were taken as the dependent variables, by which the calculated efficiency could be improved by 1.5 times [
10]. In recent years, an approach based on the intelligent algorithm was proposed, whose resolving time was more than two hundred times faster than that of the traditional algorithm [
11]. Based on the divide and conquer concept, Wang proposed a fast simulation method, whose efficiency was 1.5 times higher than that of SPS [
12]. Recently, the GPU-accelerated transient simulation method for natural gas pipeline networks was proposed, and its speed-up ratio was up to 57.57 compared with that of SPS [
13]. Devices were modelled as modes instead of the graph edge, which made numerical solutions simpler and the computation costs cheaper [
14].
The above-mentioned methods have greatly improved the efficiency of natural gas transient simulation. However, these methods have a common feature in that the fixed time step was used. Since the time step could be adjusted by the adaptive time step method according to the system state changes, that is, when the system state changes dramatically, a smaller time step is applied to accurately describe the system changes, and when the system changes slowly, a larger time step should be used to quickly complete the simulation process due to the slow system state changes. The benefits of the adaptive time step are that it improves the balance between accuracy and efficiency, as well as enhances the reliability of numerical computations [
15]. Based on the advantage of the adaptive time step, it has been widely used to solve various engineering problems, such as solving the incompressible Navier–Stokes equations [
16], fluid–structure interaction solvers [
17], and transient diffusion equation [
18]. However, in the field of natural gas pipe network simulation, corresponding research has been gradually developed in recent years. An adaptive method of lines algorithm was formulated for the solution of Euler equations [
19], which was developed based on the method of lines, and its time step was restricted by the spatial step. The technical overview provided by Energy Solutions International details that Pipeline Studio uses a dynamic time step to maintain accuracy and stability [
20], whereas no relevant technical details have been retrieved. The time step is dependent on the local error technique [
21]. In order to improve the sensitivity of truncation error to mass flow change, Wang [
22] improved the estimation of truncation error. However, transient simulation calculation, which is the most time-consuming step, is used to judge whether the estimated time step is appropriate in all of these methods. In other words, when the time step needs to be reduced, the most time-consuming step will be performed many times, which leads to a low time step adjustment efficiency.
As the state of the pipeline network is changed due to the drastic change in boundary conditions, this paper proposes an adaptive time step strategy for the natural gas pipeline network, which takes boundary conditions into consideration. In addition, the trial calculation processes are optimized, and the efficiency of the time step adaptive process is improved in this method.
Firstly, the implicit finite difference method is briefly introduced. Then, the improved adaptive time step strategy for the simulation process is presented. Finally, the performance of the improved adaptive time step method is evaluated by numerical experiments.
3. Improved Adaptive Time Step Method
The boundary conditions are always given for the transient simulation, and the state change in the natural gas pipeline system is caused by that of boundary conditions. Thus, the boundary conditions are taken into consideration to improve the efficiency of the adaptive time step strategy.
3.1. The Procedures of the Improved Adaptive Time Strategy
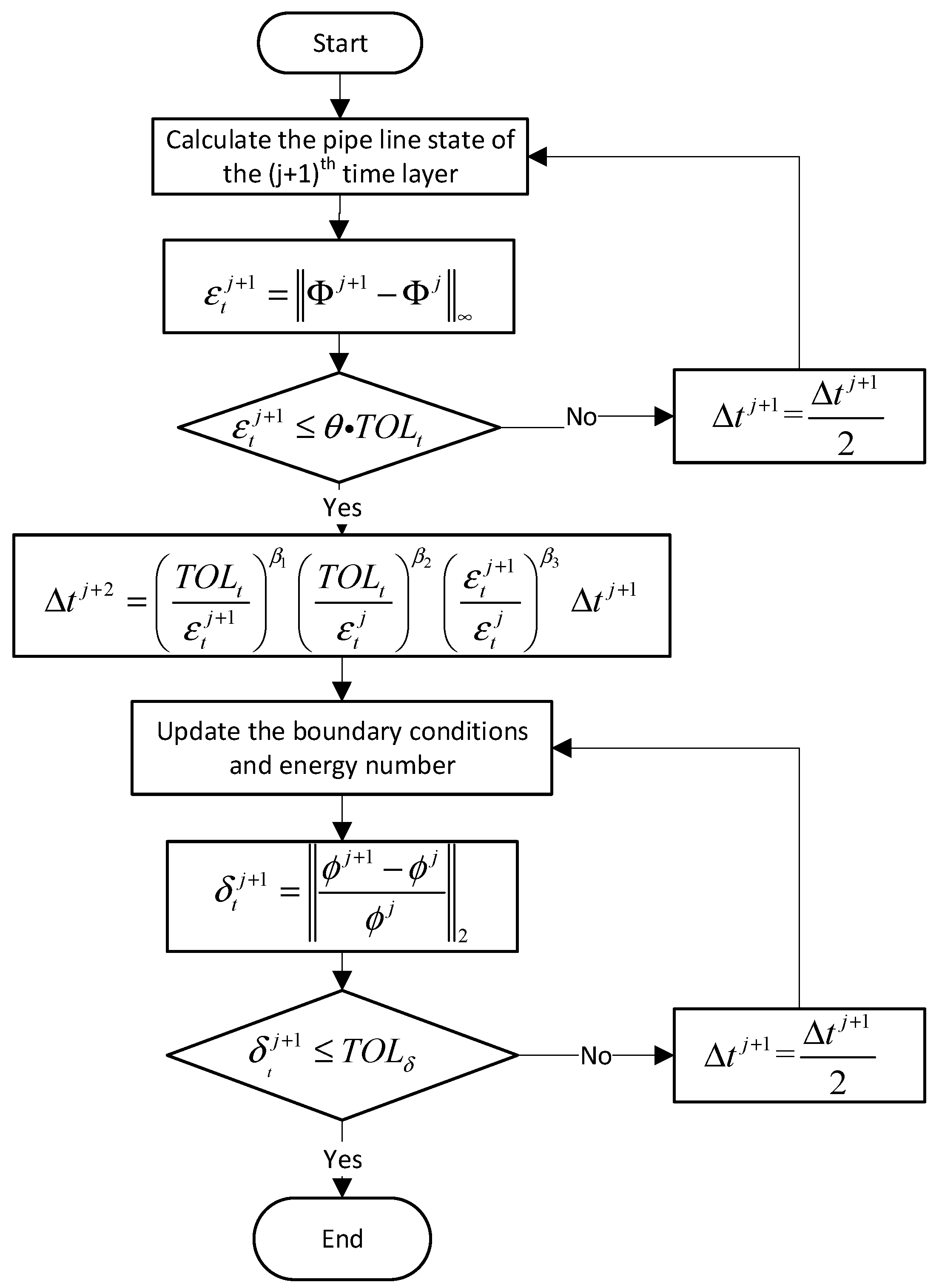
The steps of the improved adaptive time method are shown in
Figure 1.
Step 1. Use the known time step to conduct the pipeline transient simulation at the th time level through Equations (7) and (15), which is the most time-consuming step.
Step 2. Estimate the local error of the
th time level.
where
is the local error;
is the state of the natural gas pipeline at the
th time level.
Step 3. Compare the local error with that of tolerable error :
If , it means that the error is intolerable; then, the time step is reduced by , returning to conduct the pipeline transient simulation at the th time level. This means if the error is intolerable, the most time-consuming step will be executed again with the reduced time step.
If
, the error is tolerable, and the next time step
is calculated by a PID controller, which is shown in Equation (21).
where
,
and
are the parameters of the controller, respectively. H211b controllers [
21] are adopted in this paper;
,
,
, and
.
Then, the error caused by the change of boundary conditions is estimated.
where
is the error caused by the change in boundary conditions, and
is the energy number.
Step 4. Compare the value with the tolerable error .
If , the error in the th time level is intolerable. Then, the time step is reduced to , and the boundary conditions with the new time step are updated and the error (22) is re-estimated.
If , go to Step 1, as should be used in the transient simulation of the next time level.
3.2. The Energy Number
There are various types of boundary conditions for natural gas pipe network simulation such as pressure (Pa) and mass flow (kg/s), which lead to different dimensions in the boundary conditions. The change in boundary conditions ultimately causes the change in system energy. Therefore, the concept of energy number
is proposed for the dimensionless process. The energy number of boundary conditions for different parameters is shown in
Table 3.
3.3. Notes
The value of is always greater than 1, because of the H211b controller. Equation (21) itself has the function of adjusting the time step. When , the values of and in Equation (21) are less than 1, and the time step of the next time layer will decrease, which also plays a role in adjusting the time step. Compared with the estimation method of , the change in time step is relatively mild, which is the first point of improvement.
Energy number,
, is a synthetic parameter that needs to be calculated after the transient simulation of each time layer. It can directly judge whether the time step adjustment is appropriate, rather than changing the pipe network state [
2], so as to reduce the calculation of transient simulation in the process of adjusting the time step and improve the efficiency of the time step adjustment, which is the second point of improvement.
The time step should be in a suitable range to avoid time steps too small or large.
The tolerable error should also be suitable. Referring to the adaptive simulation of the natural gas pipeline [
22], the tolerable errors are set as
,
, and
.
4. Results and Discussion
It has been proved that the adaptive time step could reduce the computing time to complete the simulation, ensuring calculation accuracy compared to that of the fixed time step. Therefore, the accuracy, effect, and efficiency of both the improved adaptive time step method and the adaptive time step method are compared with the help of a virtual pipeline and an actual pipeline in this section.
4.1. The Virtual Pipeline
In the virtual pipeline simulation, the time step adjustment process is discussed when boundary conditions change suddenly, and the accuracy, effect, and efficiency of the improved method are compared.
4.1.1. Simulation Case
The state equation and resistance equation are the BWRS equations [
25] and the Colebrook formula [
26]. The standard state is 101.325 kPa and 20 °C. The simulation conditions are listed in
Table 4. In addition, the components of the studied natural gas are shown in
Table 5.
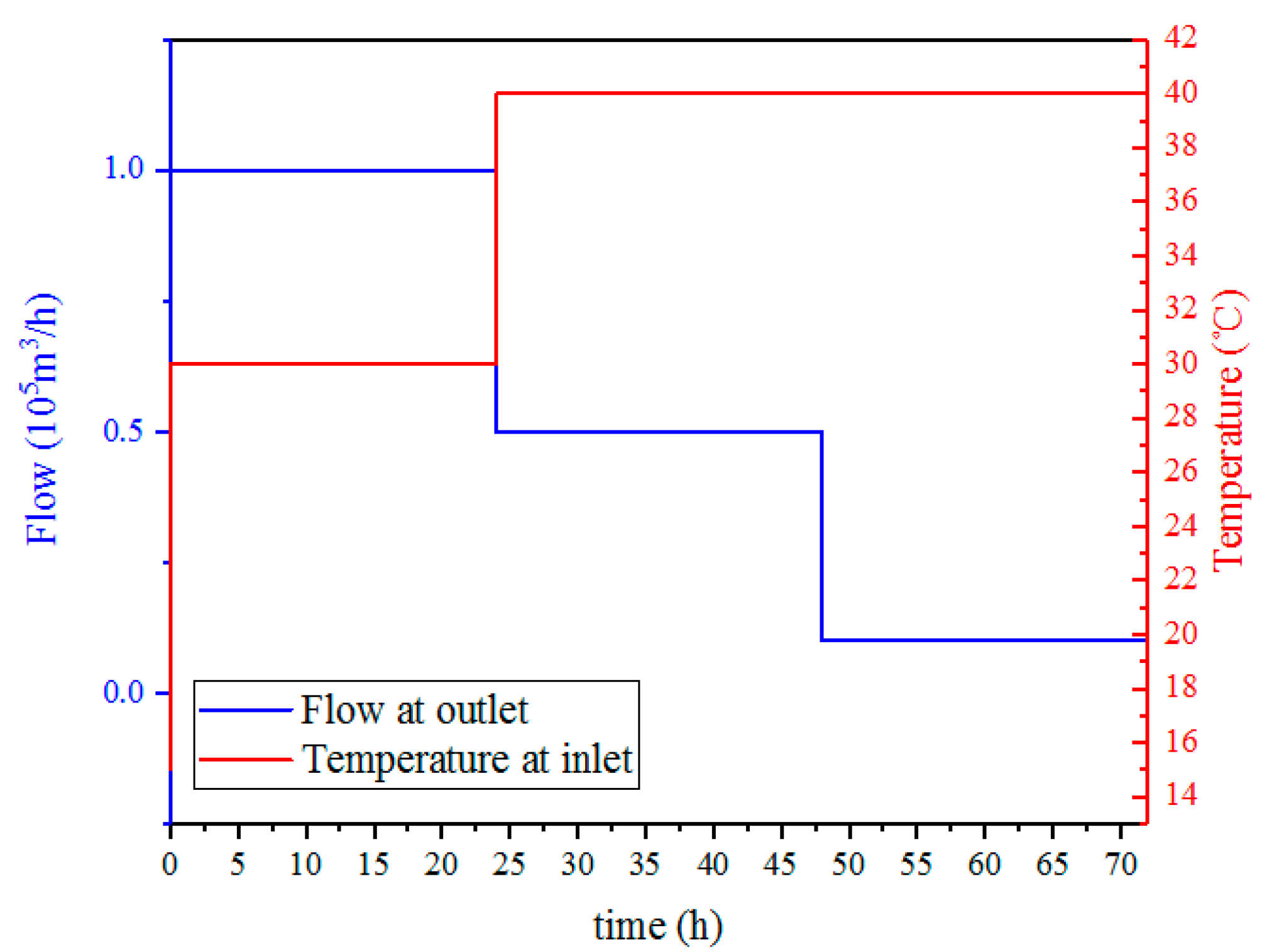
The spatial mesh size is the certain value of 0.4 km. The initial conditions are that the flow rate, temperature, and pressure are 0 Nm
3/h, 15 °C, and 3 MPa, respectively. The outlet flow rate changes suddenly from 0 Nm
3/h to 1.0 × 10
5 Nm
3/h at the beginning, jumps to 0.5 × 10
5 Nm
3/h at the 24th hour, and then jumps to 0.1 × 10
5 Nm
3/h at the 48th hour; one more time, the inlet temperature jumps from 15 °C to 30 °C at the beginning and jumps to 40 °C at the 24th hour, as shown in
Figure 2. The inlet pressure remains 3 MPa during the entire 72 h.
The rapid change in the boundary conditions will cause a drastic change in the pipeline states. Therefore, the moments that the pipeline boundary conditions change dramatically are the 0th, 24th and 48th hours, respectively. So, the transient simulation and time step adjustment at the corresponding time were analyzed.
4.1.2. The Computational Accuracy
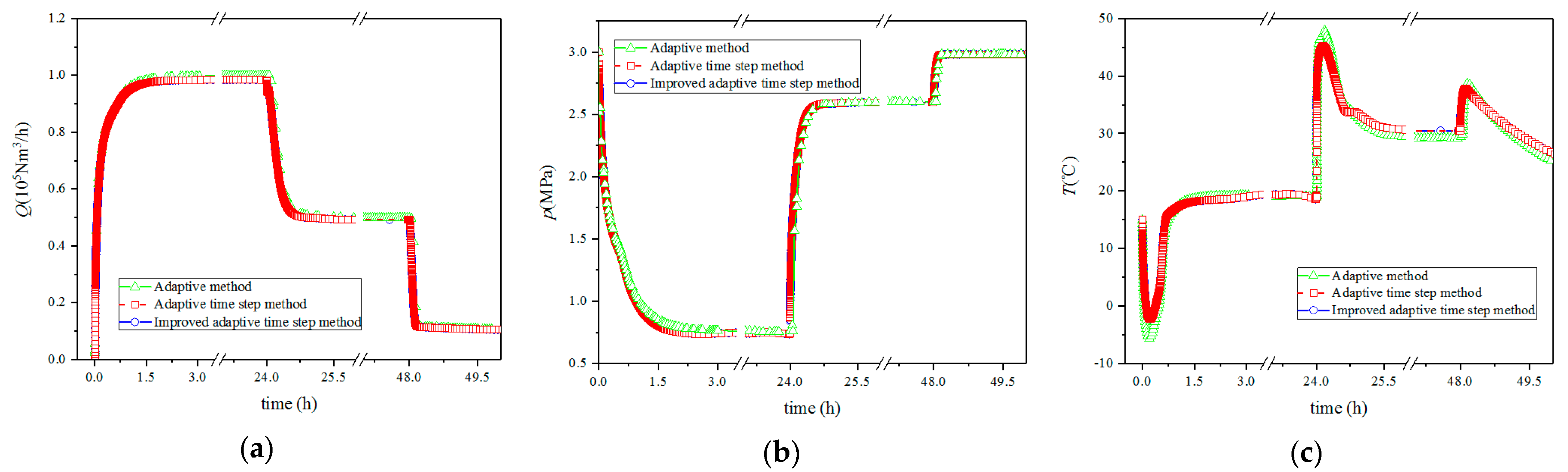
The inlet flow rate, outlet pressure, and outlet temperature were compared and are shown in
Figure 3, where the adaptive method refers to the numerical results obtained by both the adaptive time step and the special step proposed by Wang [
22]. The adaptive time step method refers to the results obtained only by the adaptive time step without the consideration of boundary conditions, and the improved time step method refers to the numerical results obtained by the improved adaptive time step method proposed in this paper.
Figure 3 clearly shows the parameter situation during the entire 72 h simulation. (1) All three methods can describe the changes in the network system. (2) The inlet flow rate, the inlet pressure, and the outlet temperature are all in good agreement with those of the adaptive method prosed by Wang.
4.1.3. The Effect
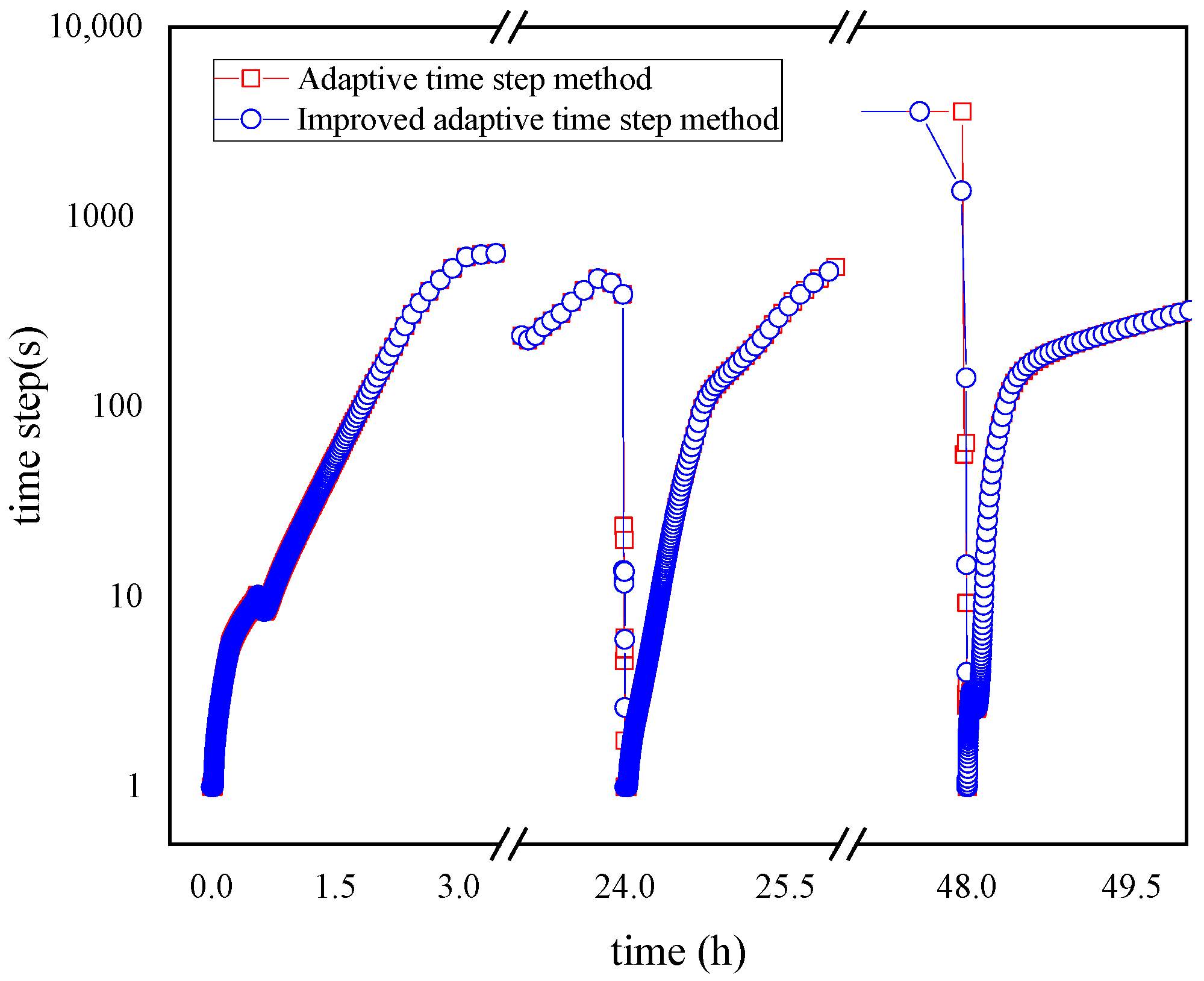
The effect of the improved method was analyzed, and the results are shown in
Figure 4. At the beginning of the simulation, the time step increased slowly from 1 s to 1000 s until approaching the 24th hour. When the boundary conditions changed, the time step rapidly decreased from 1000 s to 1 s, then increased again to 3600 s, and remained constant until approaching the 48th hour. Then, the time step gradually reduced to 1 s, then increased gradually. The time step changed with the change in the pipeline state. The more drastic the change in the pipeline state was, the shorter the time step was. In comparison to the adaptive time step method, the improved adaptive time method has a similar effect in terms of time step adaptation. This is because the same time step adjustment strategy is used in both methods when the boundary conditions are not changed.
4.1.4. The Efficiency
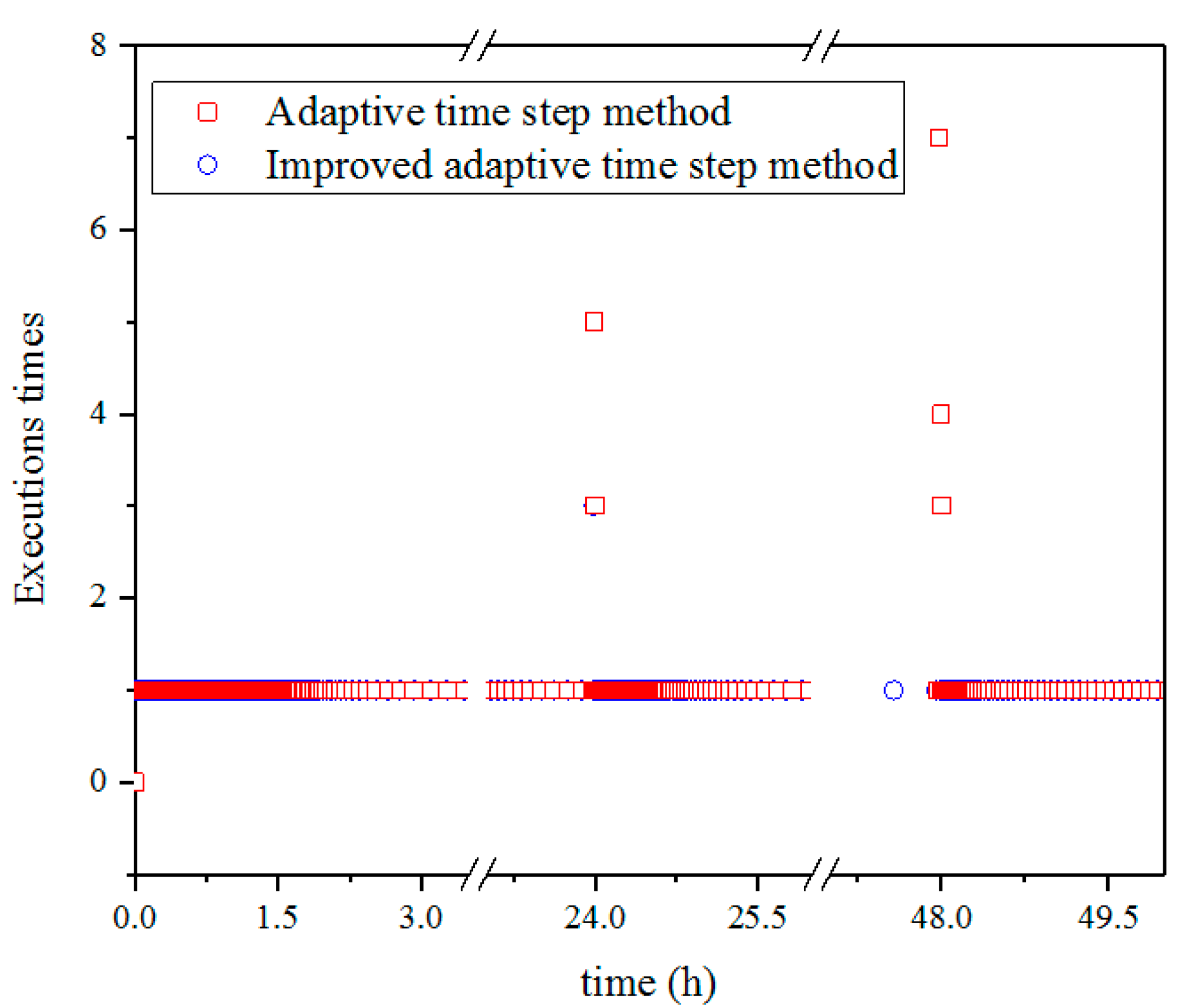
As solving equations is applied to Step 1, Step 1 is the most time-consuming step in the entire time step adjustment process. In order to analyze the efficiency of the improved method, the number of times executed by Step 1 is performed during the time step adjustment, especially when the boundary conditions change. It is clearly shown in
Figure 5 that both the methods adjust the time step without trial calculation from the 0th hour to the 50th hour, except for the 24th hour and the 48th hour. At the 24th hour, the adaptive time step method adjusts the time step from 1000 s to 1 s, and the time step adjustment program is executed five times, but the improved adaptive time step method is only executed three times. In addition, at the 48th hour, the adaptive time step method requires execution up to seven times; however, the improved adaptive time step method requires execution only once, which means that the efficiency of the improved adaptive time step method is much higher compared to the adaptive time step method.
4.2. The Actual Pipeline
As the boundary conditions in the virtual pipeline case remained constant for a long time, the efficiency of the improved method was not fully reflected. Therefore, the operation data of the XB pipeline in China were employed for further tests.
4.2.1. Simulation Case
The length, inner diameter, thickness, and roughness of the pipeline are 11.4 km, 412 mm, 8 mm and 0.02286 mm, respectively. As the XB section is the end of the pipeline, the transportation temperature remains constant, considered as isothermal transportation, and the natural gas temperature is 15 °C. The standard state, equation of state, and friction coefficient formula are all the same as the virtual pipeline simulation case. The detail components of the natural gas are listed in
Table 6.
The inlet of the pipeline is equipped with a pressure transmitter, and the outlet is equipped with both a pressure transmitter and a flow transmitter. The sampling period of the data acquisition system is 30 s, and the measured values of pipeline inlet pressure and outlet flow rate from 00:00 to 24:00 are taken as the boundary conditions. The flow rate of the outlet changes dramatically at the 0th hour, 7th hour, 18th hour and 22nd hour, but changes slowly at other times. For the influence of the pipeline upstream, the pressure at the inlet increased from 2.3 MPa to 2.42 MPa, then decreased to 2 MPa, and finally increased to 2.05 MPa, as shown in
Figure 6.
4.2.2. The Computational Accuracy
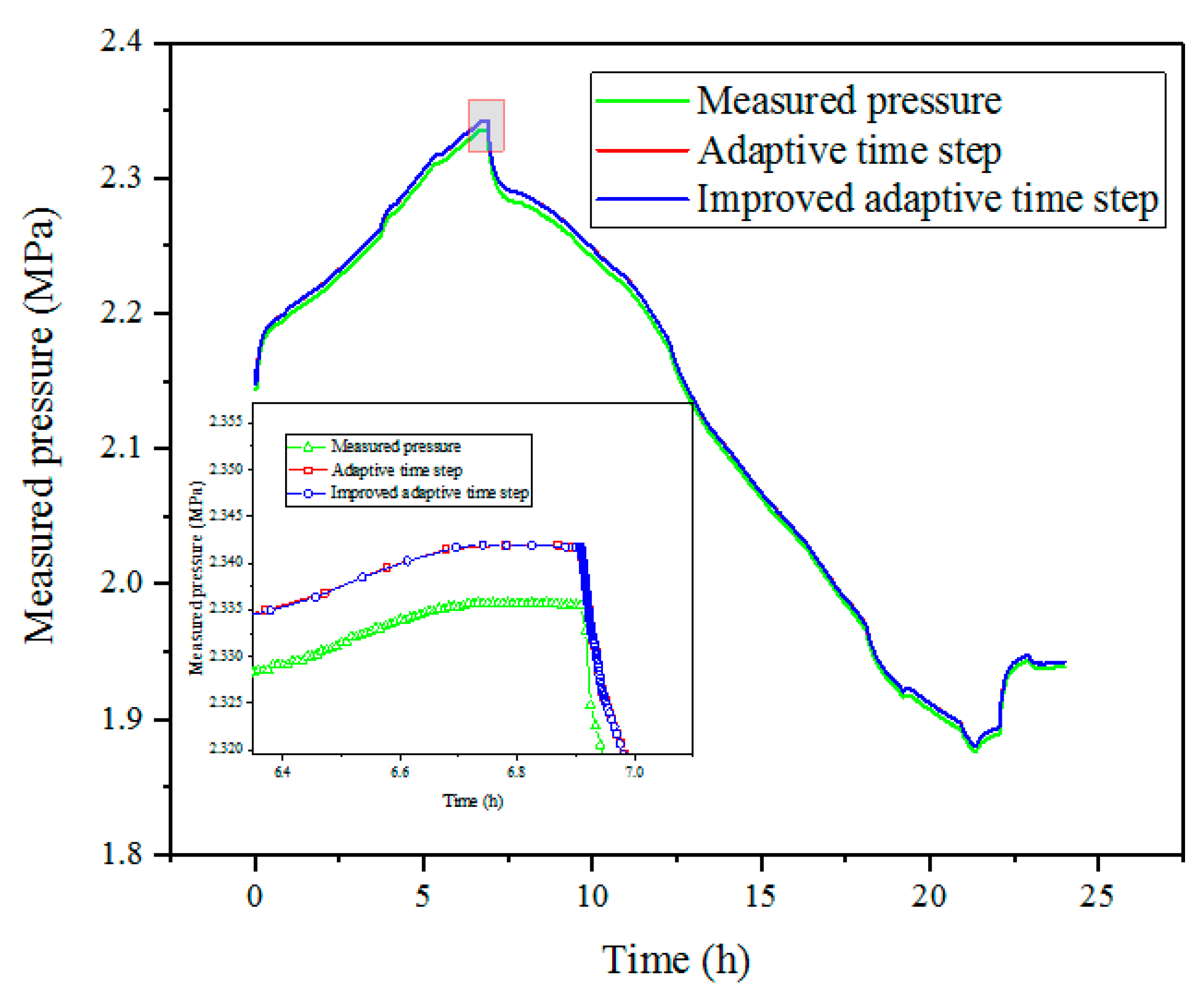
The outlet pressure was selected as the comparison parameter to verify the accuracy of the improved method, and the result is shown in
Figure 7. The pressures calculated by both the adaptive time step method and the improved adaptive time step method are basically the same because their mathematical models are the same, but only the time step is different. In comparison to the measured pressure, the pressure relative errors of both the adaptive time step and the improved adaptive time step at the last moment are all 0.184%, which means the improved adaptive time step method can accurately describe the change process of the pipeline within 24 h, and its calculation accuracy is the same as that of the adaptive time step method.
4.2.3. The Effect
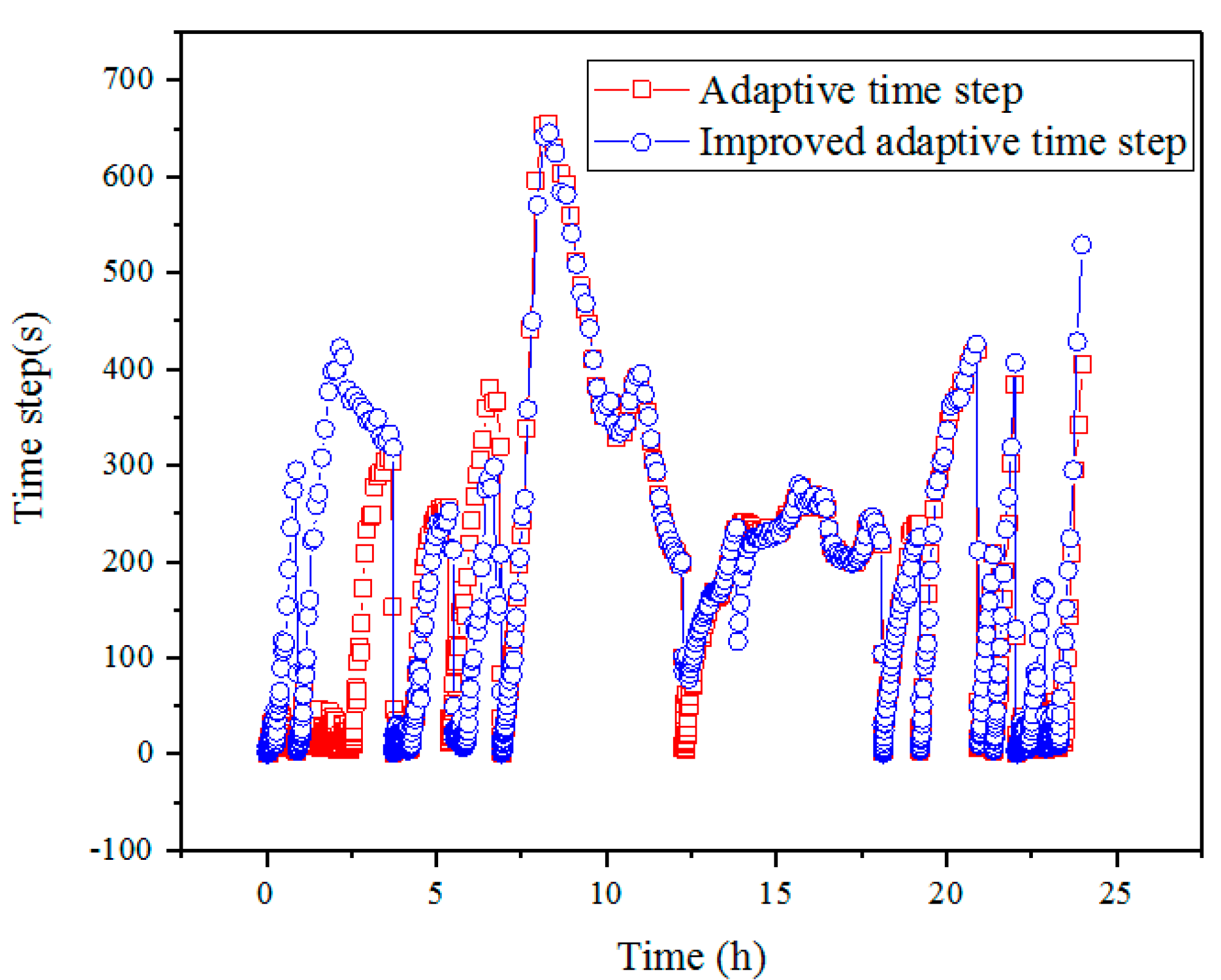
The change in time step was also analyzed as shown in
Figure 8.
As shown in
Figure 8, the time step of both methods can be adjusted with the change of the pipe state, and the time step of the improved adaptive time step method is larger than that of the adaptive time step, from the 1st hour to the 4th hour. This means that in the dynamic simulation, except for the process from the 1st hour to the 4th hour, the time steps of the two methods have the same trend. The computing level of the improved adaptive time step method is lower than that of the adaptive time step method, that is, the efficiency of the improved adaptive time step method is higher than that of the adaptive time step method.
4.2.4. The Efficiency
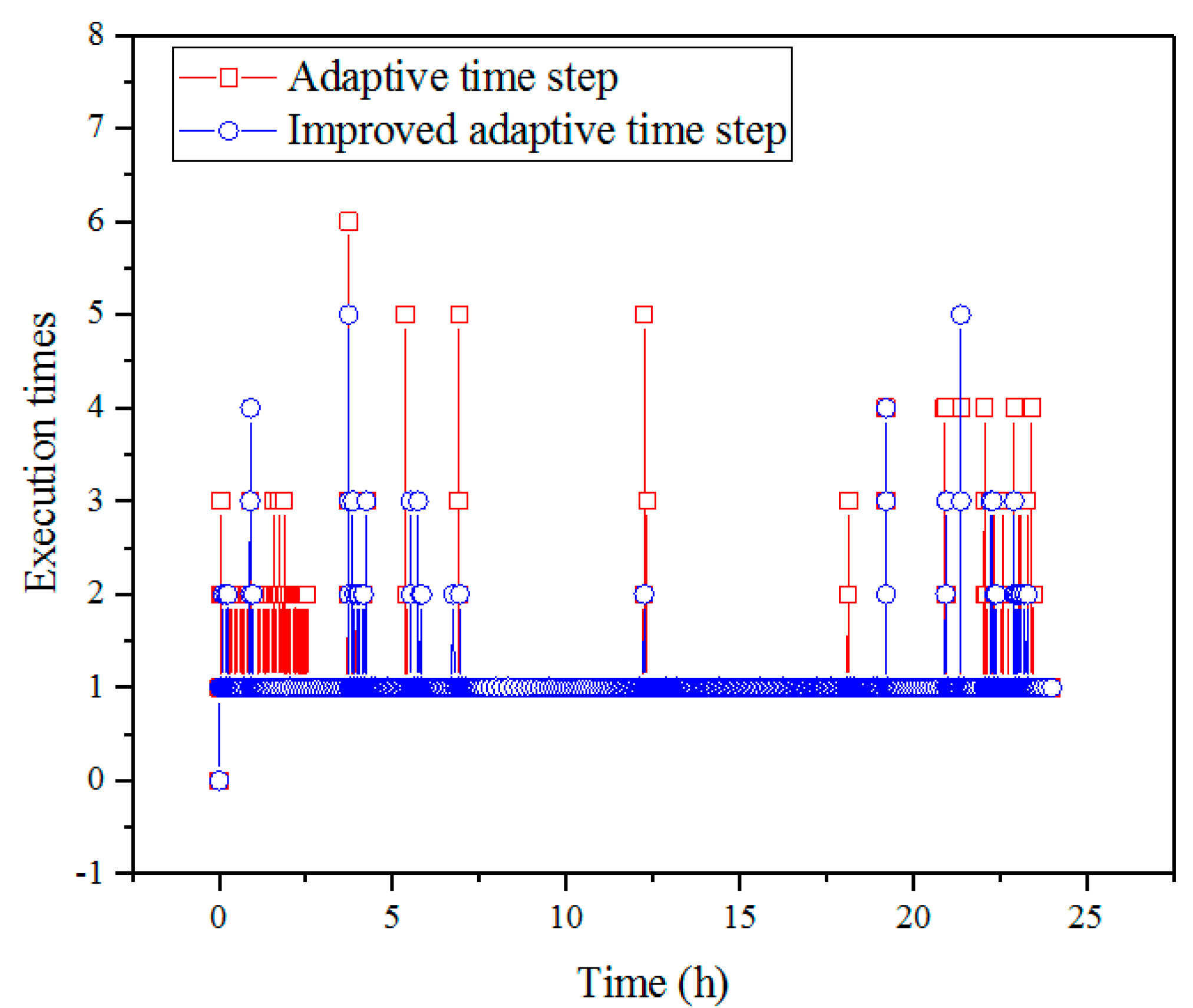
The execution times of the time step adjustment program were analyzed, and the results are shown in
Figure 9. In most cases, the execution times of the time step adjustment program for the improved adaptive time step method are lower than that of the adaptive time step method, which means that the efficiency of the improved adaptive time step method is much higher than that of the adaptive time step method in adjusting the time step.
For the 24 h transient simulation process, the total times and time levels of the time step adjustment program executed by both methods are shown in
Table 7. The total number of executions indicates the total number of times that Step 1 was performed. In addition, the number of time levels means the total number of time levels for completing the 24 h simulation. Since simulation needs to be performed at least once at each time level, the difference between the total number of executions and the time levels indicates extra executions when the time step is adjusted during the 24 h simulation process.
It is clear that the total number of executions for both methods is 2174 and 1587, respectively, which means that Step 1 was performed 2174 times and 1587 times, respectively, during the 24 h transient simulation. In addition, the number of time levels for both methods are 2008 and 1507, respectively. The differences between the total number of executions and the number of time levels for both methods are 166 and 80, respectively, which means that the total number of executions, the number of time levels and the difference of the improved adaptive time step method are 27.00%, 24.95%, and 51.81%, respectively, less than that of the adaptive time step method. So, in other words, the efficiency of the improved adaptive time step method is 27% higher than that of the adaptive time step method.
4.3. Discussion
It can be ascertained from the above two cases that the improved adaptive time step method can adjust the time step according to the transient simulation changes of the boundary conditions, which does not affect the simulation results and can describe the dynamic simulation process of the pipeline well. When the boundary conditions are constant, both the adaptive time step method and the improved method are consistent for time step adjustment, while for the conditions with drastic boundary conditions, the improved method has a higher efficiency, because the improved method takes the boundary conditions into consideration and reduces the number of times in Step 1, which is the most time-consuming step in the natural gas transient simulation. In the production process of the actual pipeline, the consumption of users and the start and stop of the compressor situation change frequently. Therefore, for the actual pipeline, the improved method is more efficient for adjusting the time step.